A Comparative Study on the End-Bearing Capacity of Toe-Wing & Spiral Screw Piles in Cohesionless Soil
Abstract
1. Introduction
2. Materials and Methods
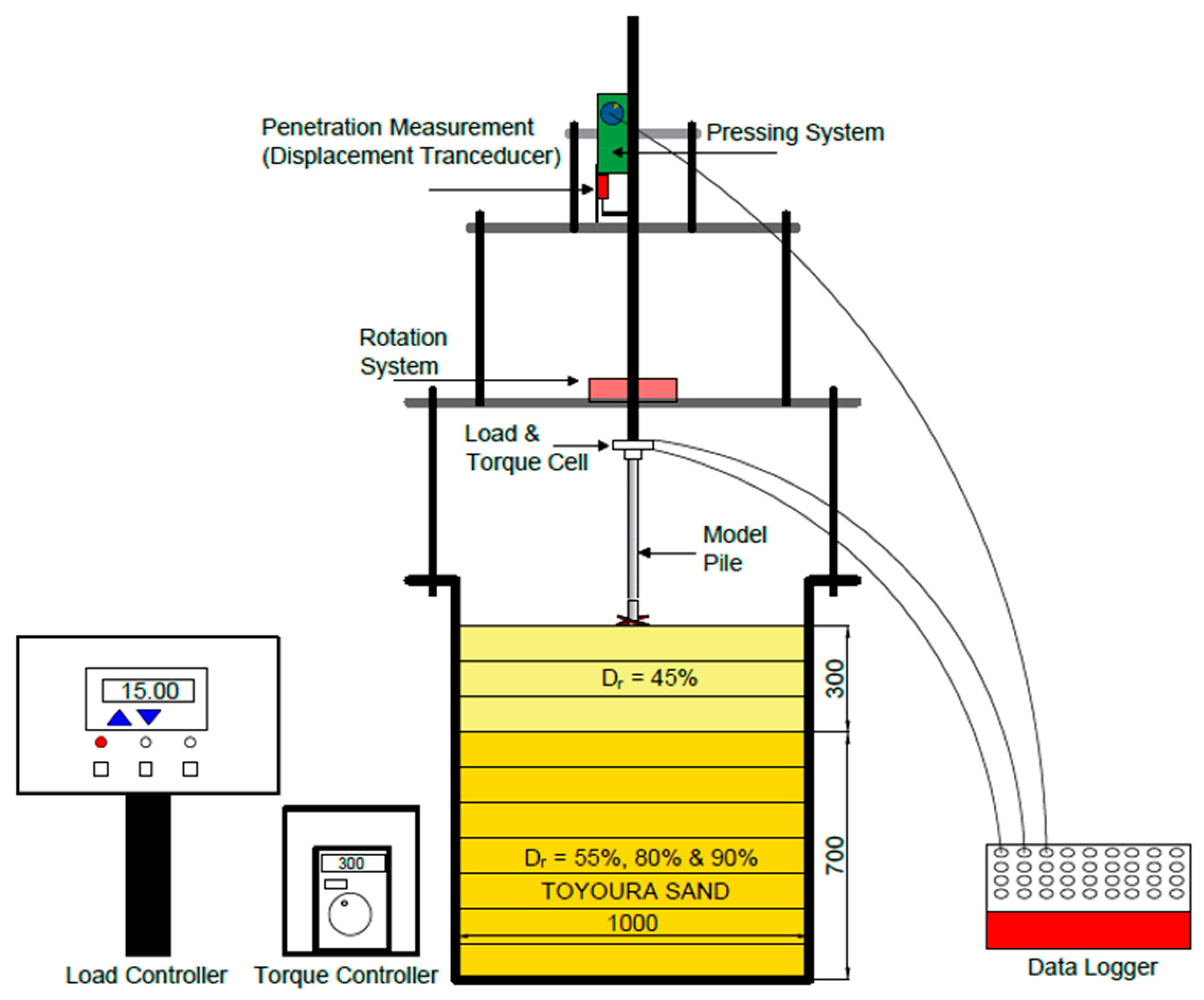
2.1. Testing Procedure
2.2. Model Container
2.3. Model Screw Piles with Toe-Wing (Tsubasa Pile) & Spiral Screw Piles
3. Results and Discussions
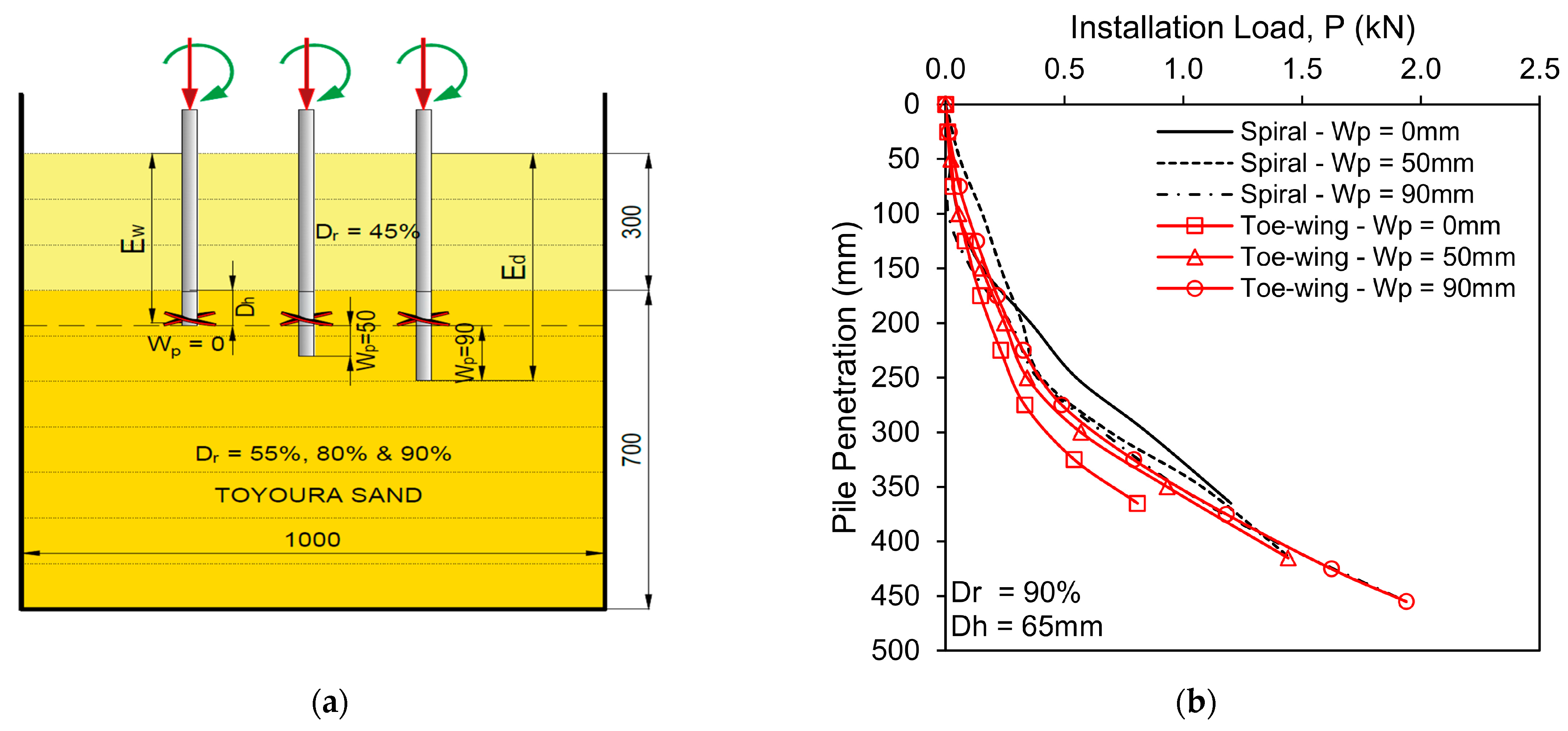
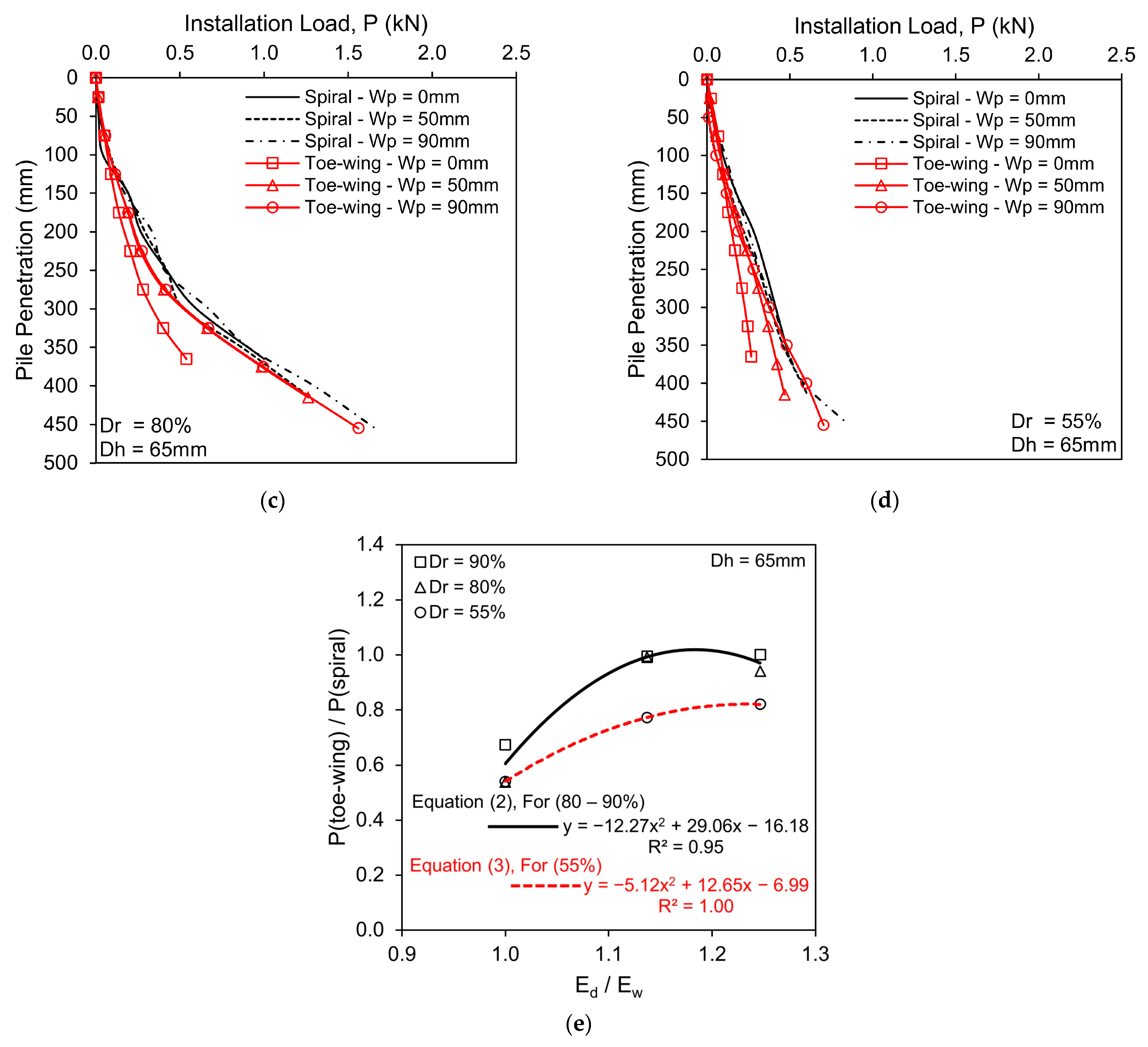
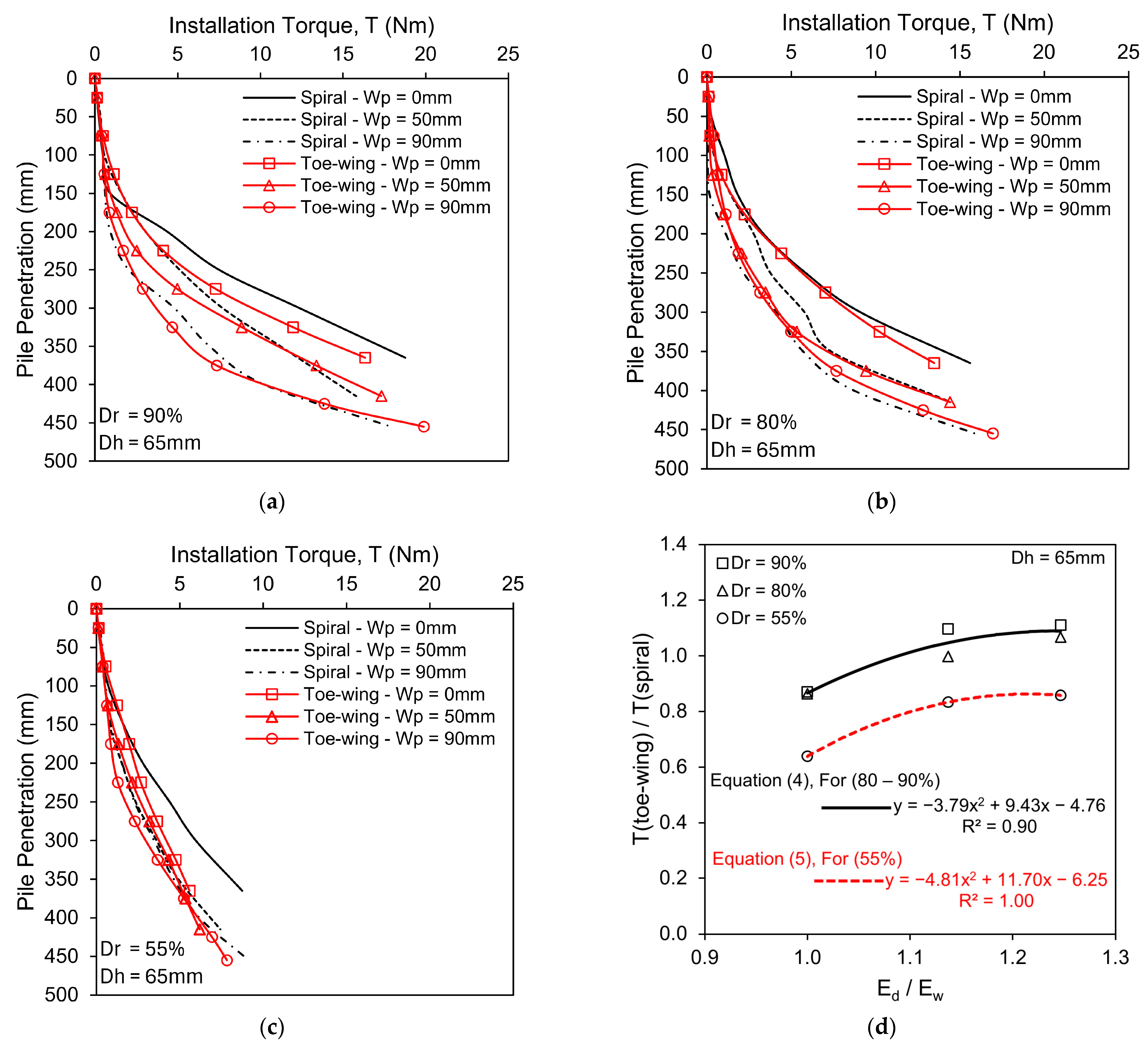
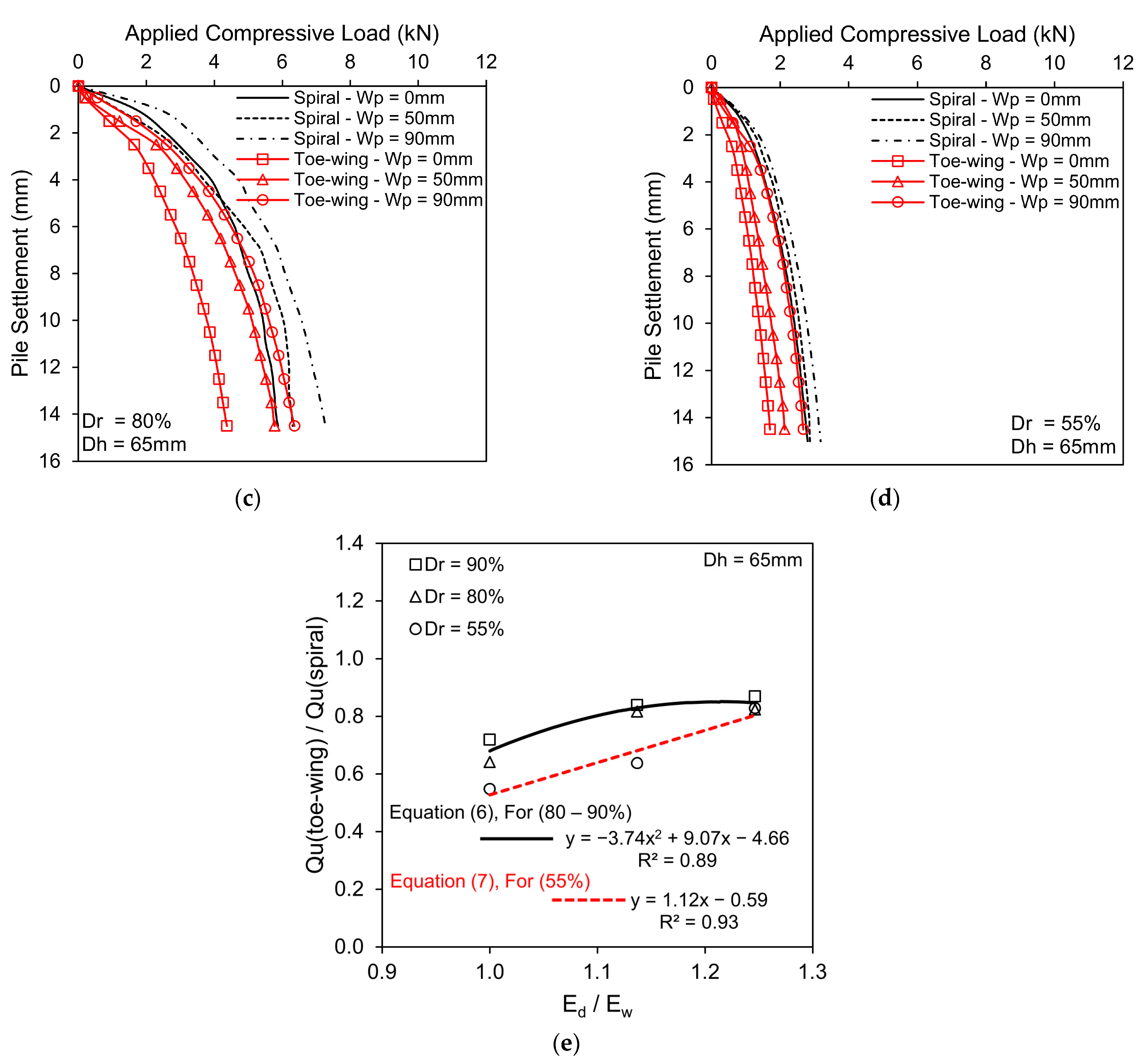
3.1. Scenario 1—Fixed Helix/Toe-Wing Position with Increasing Pile Tip Depth from 0 to 90 mm
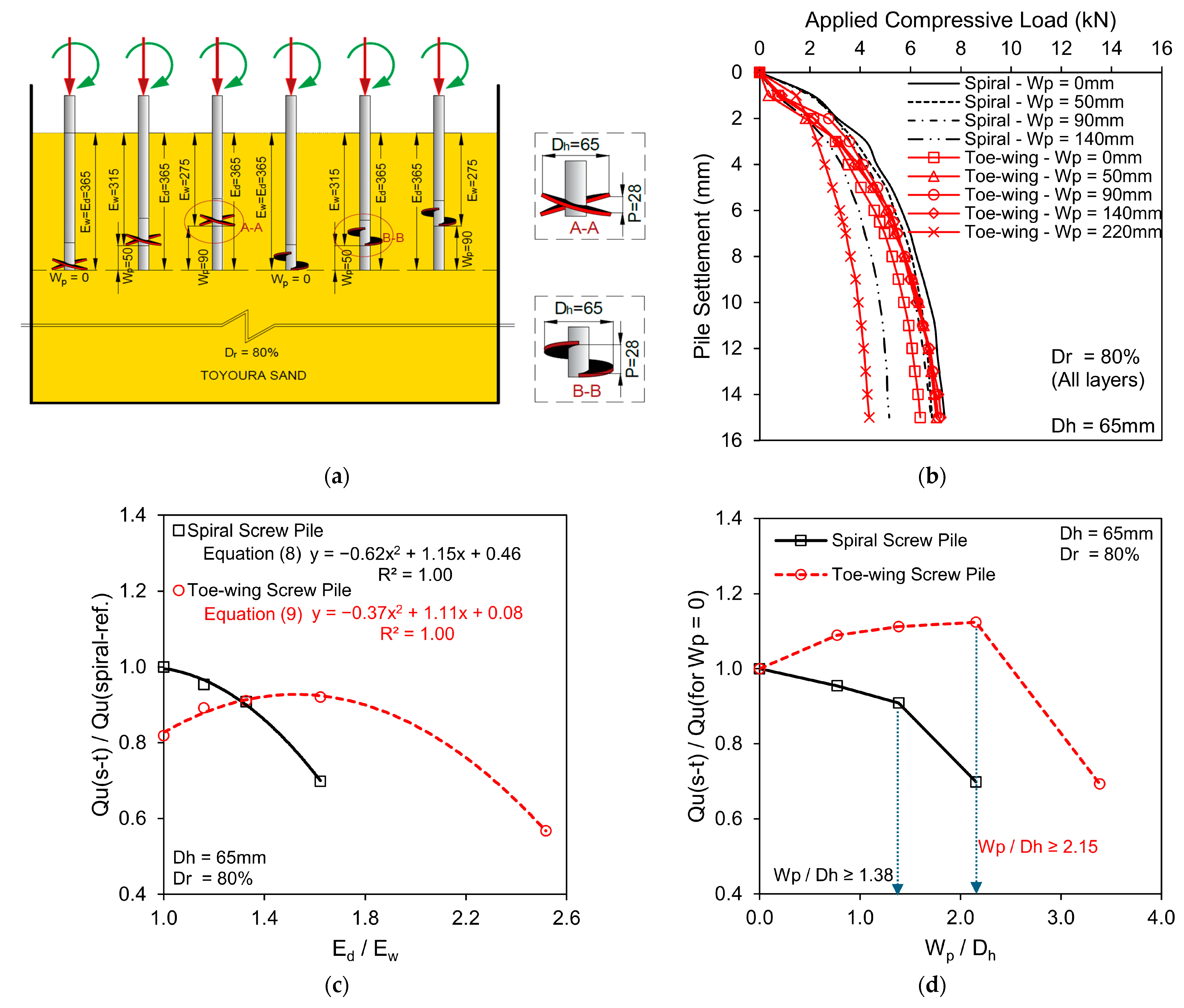
3.2. Scenario 2—Varying Helix/Toe-Wing Position with Constant Pile Tip Depth
4. Conclusions
- In the case of fixed helix/toe-wing position with increasing pile tip embedment (Scenario 1), the toe-wing screw pile showed lesser installation load requirements than the spiral screw pile. As the helix distance from the pile tip increased (Wp, 0–90 mm), the spiral screw pile installation requirements decreased, whereas, for the toe-wing screw pile, the behavior was reversed, i.e., increased. The installation torque decreased as the helix/toe-wing moved away from the pile tip (Wp > 0) for both types of piles. However, at Wp = 0 (helix/toe-wing at pile tip), less installation torque is needed for the toe-wing screw pile than for the spiral screw pile. Empirical Equations (2) and (3) for installation load requirements and Equations (4) and (5) for installation torque requirements can be used to convert the installation load and torque from one type of pile to another within the considered range of the Ed/Ew ratio (1.0–1.25).
- In Scenario 1, the spiral screw piles showed higher load-carrying resistance than the toe-wing screw piles at relative densities of 55%, 80%, and 90%. At the initial stage of the load-settlement curve, the spiral screw pile showed a stiffer response than the toe-wing screw pile, and this indicates that the soil–helix contact is better than the soil–toe-wing. The result indicated that with the increase in Ed/Ew ratio from 1.0 to 1.25 under Dr = 80–90%, the ultimate pile capacity difference between toe-wing and spiral screw piles decreased from 33% to 16.5%, as the ultimate pile capacity of toe-wing screw pile increased. Moreover, for Dr = 55% with Ed/Ew = 1.0, 1.14, and 1.25, the ultimate pile capacity of the toe-wing screw pile is 47%, 31.75, and 19.4%, respectively, less than the spiral screw pile. Empirical Equations (6) and (7) can convert the ultimate pile capacity of one type of pile to another within the provided range of Ed/Ew, i.e., 1.0–1.25.
- In the case of fixed pile tip depth (Ed) with varying helix/toe-wing position (Scenario 2), spiral screw piles have higher load-carrying resistance than toe-wing screw piles when the helix/toe-wing position is less than 90 mm (Wp < 90 mm). Both piles showed a similar ultimate pile capacity at Ed/Ew = 1.33. In the case of spiral screw piles, the result indicated that with the increase in Ed/Ew (1.0–1.62) or increase in Wp from 0 to 140 mm, the ultimate pile capacity, Qu(s) decreased from 5% to 30%. Moreover, when comparing the ultimate pile capacity of the toe-wing screw pile with the spiral screw pile having helix position at Wp = 0, it is found that the toe-wing screw pile capacity increased, and the difference between the capacities of both piles reduced from 18% to 8% as the toe-wing position (Wp) increased from 0 to 140 mm. However, a further increase in the toe-wing position decreased the pile capacity, resulting in an increase in the pile capacity difference between the two piles by 43%. Empirical Equations (8) and (9) can convert the ultimate pile capacity from one pile type to another with varying Ed/Ew ratio (considered in this study) at a relative density of 80%. It is also found that the spiral screw pile’s helix and central shaft tip act independently when Wp/Dh ratio >1.38. Whereas, in the case of the toe-wing screw pile, the toe-wing and central shaft act independently when Wp/Dh > 2.15.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mori, G. Development of the screw steel pipe pile with toe wing, Tsubasa Pile. In Deep Foundations on Bored and Auger Piles; Van Impe, W.F., Ed.; Millpress: Rotterdam, The Netherlands, 2003; pp. 171–176. [Google Scholar]
- Nagata, M.; Hirata, H. Study on the uplift resistance of screwed steel pile. Nippon Steel Tech. Rep. 2005, 92, 73–78. [Google Scholar]
- Chi, Y.; Hao, D.; Chen, R.; Zhang, N. Numerical Investigation of Uplift Failure Mode and Capacity Estimation for Deep Helical Anchors in Sand. J. Mar. Sci. Eng. 2023, 11, 1547. [Google Scholar] [CrossRef]
- Shahzad, F.; Malik, A.A.; Kuwano, J.; Maejima, T. Performance of open and close-end screw piles in bearing layer. In Proceedings of the 47th Annual Conference on Deep Foundations, National Harbor, MD, USA, 4–7 October 2022; Deep Foundation Institute: National Harbor, MD, USA, 2022. [Google Scholar]
- Saleem, M.A.; Malik, A.A.; Kuwano, J. End Shape and Rotation Effect on Steel Pipe Pile Installation Effort and Bearing Resistance. Geomech. Eng. 2020, 23, 523–533. [Google Scholar]
- Wada, M.; Tokimatsu, K.; Maruyama, S.; Sawaishi, M. Effects of cyclic vertical loading on bearing and pullout capacities of piles with continuous helix wings. Soils Found. 2017, 57, 141–153. [Google Scholar] [CrossRef]
- Tsuchiya, T.; Nagai, H.; Shimo, N. Statistical study on settlement characteristics at the toe of screw piles. AIJ J. Technol. Des. 2016, 22, 915–918. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Ho, H.M.; Malik, A.A.; Kuwano, J.; Brasile, S.; Tran, T.V.; Mazhar, M.A. Experimental and Numerical Study on Pressure Distribution under Screw and Straight Pile in Dense Sand. Int. J. Geomech. 2022, 22, 04022139. [Google Scholar] [CrossRef]
- Zuo, H.; Jin, N.; Xu, C.Y. Experiment on the vertical bearing capacity of screw grout pile in a cohesive area. J. Shenyang Jianzhu Univ. (Nat. Sci.) 2016, 32, 225–231. [Google Scholar]
- Conte, E.; Pugliese, L.; Troncone, A.; Vena, M. A simple approach for evaluating the bearing capacity of piles subjected to inclined loads. Int. J. Geomech. 2021, 21, 04021224. [Google Scholar] [CrossRef]
- Han, M.; Jia, J.; Li, Z.; Zhu, Z.; Tu, B.; Liu, L. Improved analytical methods for stabilizing piles in loess slope considering nonlinear pile-soil interactions. Int. J. Geomech. 2024, 24, 04024002. [Google Scholar] [CrossRef]
- Spagnoli, G.; Gavin, K.; Brangan, C.; Bauer, S. In situ and laboratory tests in dense sand investigating the helix-to-shaft ratio of helical piles as a novel offshore foundation system. In Frontiers in Offshore Geotechnics III, 1st ed.; Meyer, V., Ed.; CRC Press/Balkema: Leiden, The Netherlands, 2015; Volume 1, pp. 643–648. [Google Scholar]
- Pavan Kumar, P.V.; Patra, S.; Haldar, S. Behaviour of screw pile under axial compressive and lateral loading in sand for offshore energy foundations. In Advances in Offshore Geotechnics, Proceedings of the ISOG2019, Bhubaneswar, India, 5–6 December 2019, 1st ed.; Haldar, S., Patra, S., Ghanekar, R.K., Eds.; Springer: Singapore, 2020; Volume 92, pp. 393–403. [Google Scholar]
- Liu, Z.; Guo, G.; Luo, L.; Xing, Z. Comparative research on mechanical behaviors between SDS piles and HS piles. In Tunneling and Underground Construction; Ding, W., Li, X., Eds.; Geo-Shanghai International Conference; ASCE: Reston, VA, USA, 2014; pp. 205–215. [Google Scholar]
- Malik, A.A.; Kuwano, J. Single Helix Screw Pile Behavior Under Compressive Loading/Unloading Cycles in Dense Sand. Geotech. Geol. Eng. 2020, 38, 5565–5575. [Google Scholar] [CrossRef]
- Gil-Hernandez, J.A.; Ibarra-Pengagos, G.; Trivino-Oviedo, C.A. Parametric study of helical piles subjected to compression and tension loading through finite element analysis: A case study. Indian Geotech. J. 2024, 55, 443–454. [Google Scholar] [CrossRef]
- Buse, E. Physical and Finite Element Models for Determining the Capacity and Failure Mechanism of Helical Piles Placed in Weak Soil. Appl. Sci. 2024, 14, 2389. [Google Scholar] [CrossRef]
- Majid, H.; Hanifi, C.; Khaleel, O. Performance of Multi-Helix Pile Embedded in Organic Soil Under Pull-out Load. Transp. Infrastruct. Geotech. 2019, 6, 56–66. [Google Scholar]
- Sarici, T.; Özcan, M. Investigation of Screw Pile Behavior in Cohesive Soil Under Uplift and Compressive Forces by Experimental Studies and Numerical Analyses. Arab. J. Sci. Eng. 2024. [Google Scholar] [CrossRef]
- Sarici, T.; Özcan, M. Using geopolymer coated and uncoated geotextile as a hybrid method to improve the uplift capacity of screw piles in cohesionless soil. Adv. Eng. J. 2024, 105, 666–681. [Google Scholar] [CrossRef]
- Yang, Z.X.; Jardine, R.J.; Zhu, B.T.; Rimoy, S. Stresses Developed around Displacement Piles Penetration in Sand. J. Geotech. Geoenviron. Eng. 2014, 140, 1022. [Google Scholar] [CrossRef]
- Ghaly, A.; Hanna, A. Experimental and Theoretical Studies on Installation Torque of Screw Anchors. Can. Geotech. J. 1991, 28, 353–364. [Google Scholar] [CrossRef]
- Spagnoli, G.; Mendez Solarte, C.M.; Cavalcanti Tsuha, C.H.; Oreste, P. Parametric Analysis for the Estimation of the Installation Power for Large Helical Piles in Dry Cohesionless Soils. Int. J. Geotech. Eng. 2018, 144, 1–11. [Google Scholar] [CrossRef]
- Jardine, R.J.; Zhu, B.T.; Foray, P.; Yang, Z.X. Measurement of Stresses Around Closed-Ended Displacement Piles in Sand. Geotechnique 2013, 63, 1–17. [Google Scholar] [CrossRef]
- Dijkstra, J.; Broere, W.; Heeres, O.M. Numerical simulation of pile installation. Compute. Geotech. 2011, 38, 612–622. [Google Scholar] [CrossRef]
- Siegel, T.C.; NeSmith, W.M.; NeSmith, W.M.; Cargill, P.E. Ground improvement resulting from the installation of drilled displacement piles. In Proceedings of the DFI’s 32nd Annual Conference Deep Foundations, Colorado Springs, CO, USA, 11–13 October 2007; pp. 129–138. [Google Scholar]
- Malik, A.A.; Ahmed, S.I.; Ali, U.; Shah, S.K.H.; Kuwano, J. Advancement Ratio Effect on Screw Pile Performance in the Bearing Layer. Soil Found. 2024, 64, 101537. [Google Scholar] [CrossRef]
- Malik, A.A.; Ahmed, S.I.; Kuwano, J.; Maejima, T. Effect of Change in Penetration to Rotation Rate on Screw Pile Performance in Loose Sand. In Climate Change Adaptation from Geotechnical Perspectives, Proceedings of the CREST 2023, Fukuoka, Japan, 20–22 November 2023; Hazarika, H., Haigh, S.K., Chaudhary, B., Murai, M., Manandhar, S., Eds.; Lecture Notes in Civil Engineering; Springer: Singapore, 2023; Volume 447. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, Y.; Tang, Y.; Ren, G.; Qiu, Z.; Luo, W.Y.Z. Numerical Analysis of the Installation Process of Screw Piles Based on the FEM-SPH Coupling Method. Appl. Sci. 2022, 12, 8508. [Google Scholar] [CrossRef]
- Robinsky, E.I.; Morrison, C.F. Sand Displacement and Compaction around Model Friction Piles. Can. Geotech. J. 1964, 1, 81–93. [Google Scholar] [CrossRef]
- Meyerhof, G.G. Compaction of Sands and Bearing Capacity of Piles. J. Soil Mech. Found. Div. 1959, 85, 29. [Google Scholar] [CrossRef]
- Szechy, C. The Effects of Vibration and Driving Upon the Voids in Granular Soil Surrounding a Pile. Soil Mech. Found. Eng. 1961, 2, 61–164. [Google Scholar]
- Kawai, M.; Ichikawa, K.; Kono, K. Development of New Type of Screwed Pile with Large Bearing Capacity and Ecological Driving Method “Tsubasa Pile TM”. In Proceedings of the 4th Congress International de Geotechnique—Ouvrages—Structures, CIGOS217, Ho Chi Minh City, Vietnam, 26–27 October 2017; Tran-Nguyen, H.H., Wong, H., Ragueneau, F., Ha-Minh, C., Eds.; Lecture Notes in Civil Engineering. Springer: Berlin/Heidelberg, Germany, 2018; Volume 8, pp. 411–425. [Google Scholar]
- Ichikawa, K.; Kono, K. Bearing Capacity and Driving Efficiency of Ecological Screw Pile: “Tsubasa Pile TM”. JFE GIHO 2013, 31, 39–45. [Google Scholar]
- Garnier, J.; Gaudin, C.; Springman, S.; Cullingan, S.M.; Goodings, D.; Konig, D.; Kutter, B.; Phillips, R.; Randolph, M.F.; Thorel, L. Catalogue scaling laws and similitude questions in geotechnical centrifuge modeling. Int. J. Phys. Model. Geotech. 2007, 3, 1–24. [Google Scholar]
- Rakotonindriana, M.H.J.; Kouby, A.L.; Buttigieg, S.; Derkx, F.; Thorel, L.; Garnier, J. Design of an instrumented model pile for axial cyclic loading. In Physical Modeling in Geotechnics, Springman; Laue, J., Seward, L., Eds.; Taylor & Francis Group: London, UK, 2010; pp. 991–996. [Google Scholar]
- Tsuchiya, T.; Kohsaka, M. Statistical study on the vertical bearing capacity of screw piles. AIJ J. Technol. Des. 2015, 21, 991–994. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Kishida, H. Stress distribution of model piles in sand. Soils Found. 1963, 4, 1–23. [Google Scholar] [CrossRef]
- Yu, F.; Yang, J. Bearing capacity of open-ended steel pipe piles in sand. J. Geotech. Geoenviron. Eng. 2012, 138, 1116–1128. [Google Scholar] [CrossRef]
- Randolph, M.F.; Worth, C.F. Analysis of deformation of vertically loaded piles. J. Geotech. Eng. Div. 1978, 104, 1465–1488. [Google Scholar] [CrossRef]
- JIS G 3444:2015; Carbon Steel Tubes for General Structure. Japanese Standards Association: Tokyo, Japan, 2005.
- Zhang, D.J.Y.; Chalaturnyk, R.; Robertson, P.K.; Sego, D.C.; Cyre, G. Screw anchor test program (Part I & II): Instrumentation, site characterization, and installation. In Proceedings of the 51st Canadian Geotechnical Conference, Edmonton, AB, Canada, 4–7 October 1998. [Google Scholar]
- Nasr, M.H. Performance-based design for helical piles. In Contemporary Topics in Deep Foundations, 1st ed.; American Society of Civil Engineers: Reston, VA, USA, 2009; pp. 496–503. [Google Scholar]
- Zhao, Q.; Hu, K.; Wang, Y.; Tang, Y.; Ren, G. Analysis on torque and pile-soil interaction of anti-flood screw pile during the installation process. Arab. J. Geosci. 2022, 15, 1018. [Google Scholar] [CrossRef]
- Venkatesan, V.; Muthukumar, M. Design parameters and behavior of helical piles in cohesive soils—A review. Arab. J. Geosci. 2020, 13, 1194. [Google Scholar]


| Test Materials | Specific Gravity | D50 | Emax | Emin |
|---|---|---|---|---|
| Dry Toyoura Sand | 2.645 | 0.19 | 0.973 | 0.609 |
[mm] | [mm] | [mm] | [mm] | [°] | [mm] | [mm] |
|---|---|---|---|---|---|---|
| 500 (Toe-wing) | 21.7 | 65 | 3.6 | 25 | 0, 50, 90 | 365, 415, 455 |
| 500 (Spiral) | 21.7 | 65 | 3.6 | 0, 50, 90 | 365, 415, 455 |
| Screw Pile Type | Dh (mm) | Wp (mm) | Pitch (mm) | Ew (mm) | Wp/Dh |
|---|---|---|---|---|---|
| Toe-wing Screw Pile | 65 | 0, 50, 90, 140, 220 | 28 | 365 | 0, 0.77, 1.38, 2.15, 3.38 |
| Spiral Screw Pile | 65 | 0, 50, 90, 140 | 28 | 365 | 0, 0.77, 1.38, 2.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sahil, A.W.; Uchimura, T.; Malik, A.A.; Kabir, M.R. A Comparative Study on the End-Bearing Capacity of Toe-Wing & Spiral Screw Piles in Cohesionless Soil. Buildings 2025, 15, 525. https://doi.org/10.3390/buildings15040525
Sahil AW, Uchimura T, Malik AA, Kabir MR. A Comparative Study on the End-Bearing Capacity of Toe-Wing & Spiral Screw Piles in Cohesionless Soil. Buildings. 2025; 15(4):525. https://doi.org/10.3390/buildings15040525
Chicago/Turabian StyleSahil, Ahmad Waheed, Taro Uchimura, Adnan Anwar Malik, and Md Raihanul Kabir. 2025. "A Comparative Study on the End-Bearing Capacity of Toe-Wing & Spiral Screw Piles in Cohesionless Soil" Buildings 15, no. 4: 525. https://doi.org/10.3390/buildings15040525
APA StyleSahil, A. W., Uchimura, T., Malik, A. A., & Kabir, M. R. (2025). A Comparative Study on the End-Bearing Capacity of Toe-Wing & Spiral Screw Piles in Cohesionless Soil. Buildings, 15(4), 525. https://doi.org/10.3390/buildings15040525







