Next Article in Journal
Study on the Failure Mode and Bearing Capacity of Unreinforced Steel Fiber-Reinforced Concrete Segment Joints
Previous Article in Journal
An Optimization Procedure for Improving the Prediction Performance of Failure Assessment Model
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Buildings
Volume 15
Issue 24
10.3390/buildings15244486
buildings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Study of Liquefaction Characteristics of Saturated Sand–Rubber Mixture Under Cyclic Torsional Shear Loading

by
Xiaojun Zhu
1,*,
Wenshuai Li
2 and
Yabin Wang
3
1
School of Civil Engineering and Transportation, Yangzhou University, Yangzhou 225127, China
2
School of Civil Engineering, Southeast University, Nanjing 210096, China
3
Anhui Hongyuan Power Tower Co., Ltd., Hefei 237463, China
*
Author to whom correspondence should be addressed.
Buildings 2025, 15(24), 4486; https://doi.org/10.3390/buildings15244486
Submission received: 20 October 2025 / Revised: 15 November 2025 / Accepted: 26 November 2025 / Published: 11 December 2025
(This article belongs to the Section Building Materials, and Repair & Renovation)
Browse Figures
Versions Notes

Abstract

Scrap tire-derived geomaterial has been gaining attention recently as an alternative material for improving the ground. This paper presents a fundamental experimental investigation into sand–rubber mixtures using hollow cylinder torsional shear apparatus, with the aim of enhancing our understanding of the integrated effects of rubber content and cyclic stress ratio (CSR) on the liquefaction characteristics of the mixtures. The results show that the incorporation of granular rubber into sand not only reduces excess pore water pressure during cyclic loading but also alters the generation mode of pore water pressure. The liquefaction resistance of the sand–rubber mixture increases significantly when the rubber gravimetric proportion exceeds 10%. The energy dissipation per loading cycle decreases with increasing rubber content, whereas the cumulative dissipative energy exhibits an opposite trend, showing a positive correlation with rubber content. In addition, this rubber-enhanced effect shows CSR dependence; the cumulative energy dissipation significantly diminishes at a high CSR. Therefore, the effect of granular rubber addition to sand on pore water pressure tends to become more pronounced at higher rubber contents.

1. Introduction

With the vigorous development of automobile engineering in recent decades, the disposal of vast numbers of scrap tires has become a significant global environmental challenge. However, tires have a number of potential options for being repurposed in civil engineering infrastructure, such as integrating recycled tire shreds into soil matrices as innovative geomaterials, thereby achieving the dual goals of managing scrap tires and improving soil properties. Soil–rubber mixtures are employed in various geotechnical applications, such as backfilling behind retaining walls, caisson-type quay walls and bridge abutments to reduce lateral displacement and soil pressure [1,2,3], and subgrade filling for railways or highways to mitigate settlement [4,5,6], owing to their light weight and high strength. In addition, soil–rubber mixtures are also used as a sound-barrier filler [7], an insulation layer to limit frost penetration [8], and a drainage layer in sorption barriers for liquid- and vapor-phase organic chemicals in landfills [9,10,11,12]. One of the more interesting applications of rubber-enhanced soil focuses on its mixture with sand, called a sand–rubber mixture, which can be used in geotechnical seismic isolation systems due to its unique mechanical property of having a high vibration-absorption capacity [13,14,15,16,17,18,19,20,21,22,23,24]. And in this regard, its dynamic properties, such as its shear modulus, damping ratio, and liquefaction performance, have attracted the attention of many scholars and researchers.
Previous studies [25,26,27,28,29,30,31] have compiled experimental results demonstrating the variations in the dynamic properties of sand–rubber mixture. The literature coincides that the shear modulus was directly proportional to confining pressure and inversely proportional to the shear strain, and that both the maximum shear modulus and minimum damping ratio exhibit a clear correlation with the granulated rubber content. However, it should be noted that Okur et al. (2018) [32] obtained contrary results through resonant column tests, indicating that under shear strain amplitudes of less than about 0.05%, the damping ratio decreases with the rubber content irrespective of rubber size, while at shear strain amplitudes greater than about 0.05%, the opposite trend is observed. It can be seen that there is still a lack of consensus on this matter, with some unconsolidated or even contradictory findings, which is possibly due to the nonlinear enhancement phenomenon caused by rubber, and the varying experimental materials and methods used by different scholars.
Other scholars have pointed out that sand–rubber, as a foundation layer for the seismic isolation, not only plays the role of the isolation layer but also prevents soil liquefaction. For instance, Tsang and Pitilaki (2019) [33] studied the mechanism of geotechnical seismic isolation using sand–rubber mixtures through numerical analysis, and further, Vratiskidis and Pitiakis (2023) [24] also conducted a field test of sand–rubber mixtures used in geotechnical seismic isolation. Later, Hazarika et al. (2020) [16] conducted a nonlinear soil–structure interaction analysis of a framed structure resting on a geotechnical seismic isolation technique using a sand–rubber mixture, and Tsang et al. (2021) [18] and Tsiavos et al. (2019) [34] also conducted similar studies. On the other hand, Hyodo et al. (2007) [35] found that the liquefaction occurred when the gravimetric proportion of tire chip in the mixtures was less than 50% through a series of cyclic triaxial tests, and no liquefaction occurred when the rubber content exceeded 50%. Therefore, they concluded that the presence of tire chips in the mixture controls the liquefaction properties and noted that it was ineffective for mixtures with a tire chip gravimetric proportion of less than 30% by considering the influence of compaction on cyclic shear strength. Kaneko et al. (2013) [36] and Mashiri et al. (2016) [37] pointed out that the addition of granulated rubber to sand, within the range of 20% to 40% by weight, leads to a significant reduction in liquefaction potential. However, Promputthangkoon et al. (2007) [38] found that there is no sign of a decrease in liquefaction potential for mixtures containing less than 15% rubber through cyclic triaxial tests. On the contrary, according to the analysis performed by Ding et al. (2021) [39] on the static and dynamic characteristics of sand–rubber mixtures, an optimum granulated rubber content of approximately 10% is recommended. In summary, although conclusions on the liquefaction potential of sand–rubber mixtures are not consistent, existing research demonstrates that tire rubber has promising applications as an energy dissipation material for isolation layers.
Therefore, the application of granular rubber as a sand modifier thus remains an area with considerable exploration potential, especially concerning the dynamic properties of the mixtures. This study employed stress-controlled cyclic torsional shear tests with a hollow torsional shear apparatus to assess the improvement in sand’s liquefaction potential and energy dissipation due to granulated rubber, with rubber content, confining pressure, relative density, and the CSR as the key variables. Here, the CSR is a key parameter used to quantify the seismic demand or level of cyclic shear stress that an earthquake imposes on a soil layer, relative to the soil capacity.

2. Materials and Experimental Methods

2.1. Test Materials

In the present study, the sand–rubber mixture was mixed with the Chinese ISO standard sand and granular rubber. To clarify the role of the particles in the mixture, nearly medium-fine sand was used, which is commercially available. Chinese ISO standard sand passed standard sieve No. 14 and was retained on No. 200. Hence, the size of the sand particles ranged from 0.075 to 1.0 mm. The granulated rubber is the product featuring a particle size ranging from 2 to 4 mm and comprises commercially available recycled scrap tires obtained from local industry. The mean particle size of sand was measured to be 0.23 mm, the specific gravity of sand was 2.66, and the specific gravity of rubber was 1.16 g/cm3. Geotechnical physical and mechanical tests were conducted on the sand and rubber specimens as per specifications to obtain physical parameters, as shown in Table 1. The particle size distribution curves are presented in Figure 1, and a photograph of the soil specimens is presented in Figure 2.

2.2. Test Equipment and Specimen Preparation

In this study, all the tests were conducted using a GDS Instruments (UK) hollow cylinder apparatus (HCA) manufactured by Global Digital Systems Ltd., provided by the Geotechnical Research Center of Yangzhou University, as shown in Figure 3. The tests were conducted using an HCA, which consists of magnetic field coils, a servoactuator, a pneumatic loading unit, and a digital control system. A dry deposition method was employed to simulate in situ applications, as these mixtures are often constructed above groundwater, as shown in Figure 4. The sand was dried out at 105 °C for 24 h, while the granular rubber was stored at room temperature for 24 h. Subsequently, both materials were mixed using a mechanical mixer for 15 min. In addition, the rubber gravimetric proportions (Rf) vary from 5% to 30% in the present study, because once the rubber content exceeds 30%, the volumetric strain of the specimen exceeds 5% and hardly remains constant (Sarajpoor et al. 2020) [40]. The specimens were prepared by depositing the sand/rubber in 10 equal-mass layers into the hollow space between two aluminum molds, with the outer mold being gently tapped using a wooden hammer during placement to attain the target relative density (Dr), as shown in Figure 5. The relative density (Dr) of the specimen is determined by converting its dry density, utilizing the maximum dry density (ρdmax) and minimum dry density (ρdmin) as reference values, as shown in Table 2. After the molds were removed, the specimen with a height of 200 mm, an inner diameter of 60 mm, and an outer diameter of 100 mm was prepared, and then a loading cap was placed on top of the specimen with a small pressure, and a chamber pressure of 20 kPa was applied to prevent the collapse of the specimen.

2.3. Testing Procedure

After specimen formation, carbon dioxide (CO2) was passed through the specimen from bottom to top for at least 60 min. Then, distilled deaired water was exuded into the specimen, and a back pressure of 200 kPa was applied to achieve saturation, until Skempton’s B-value was greater than 0.96. After saturation, the specimen was isotopically consolidated at effective mean principal stress (EMPS) (p’). Following that, a torsional harmonic cyclic torsional shear load (τc) with a constant amplitude of 4.0 N·m was applied to the top of the specimen by an electric motor at a frequency (f) of 0.5 Hz. In this test program, the specimen was sheared cyclically at various cyclic stress ratios (CSR = τc/p’) of 0.15 and 0.2 to develop resistance curves. A summary of the experimental scheme for the cyclic liquefaction tests is provided in Table 3.

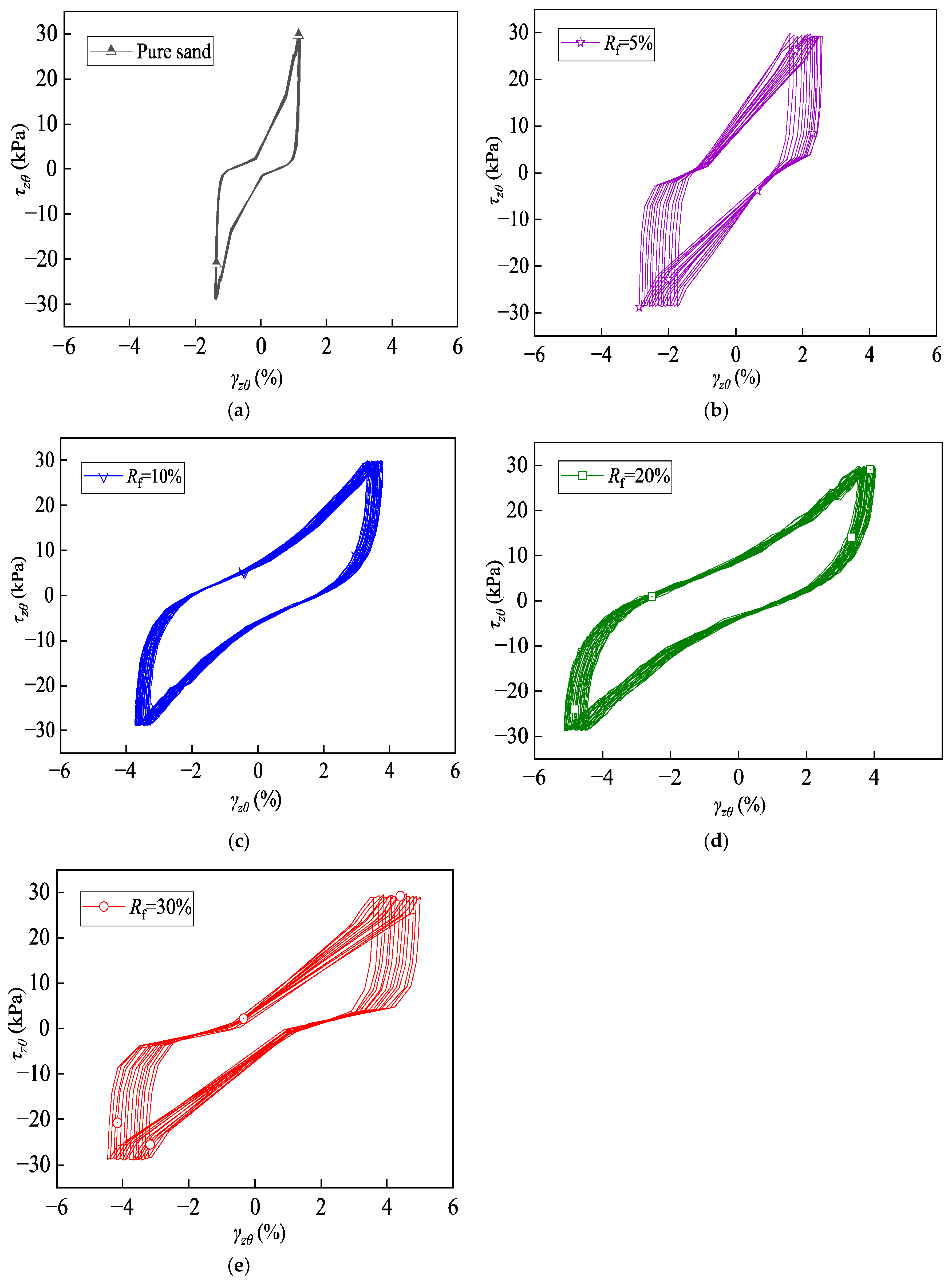
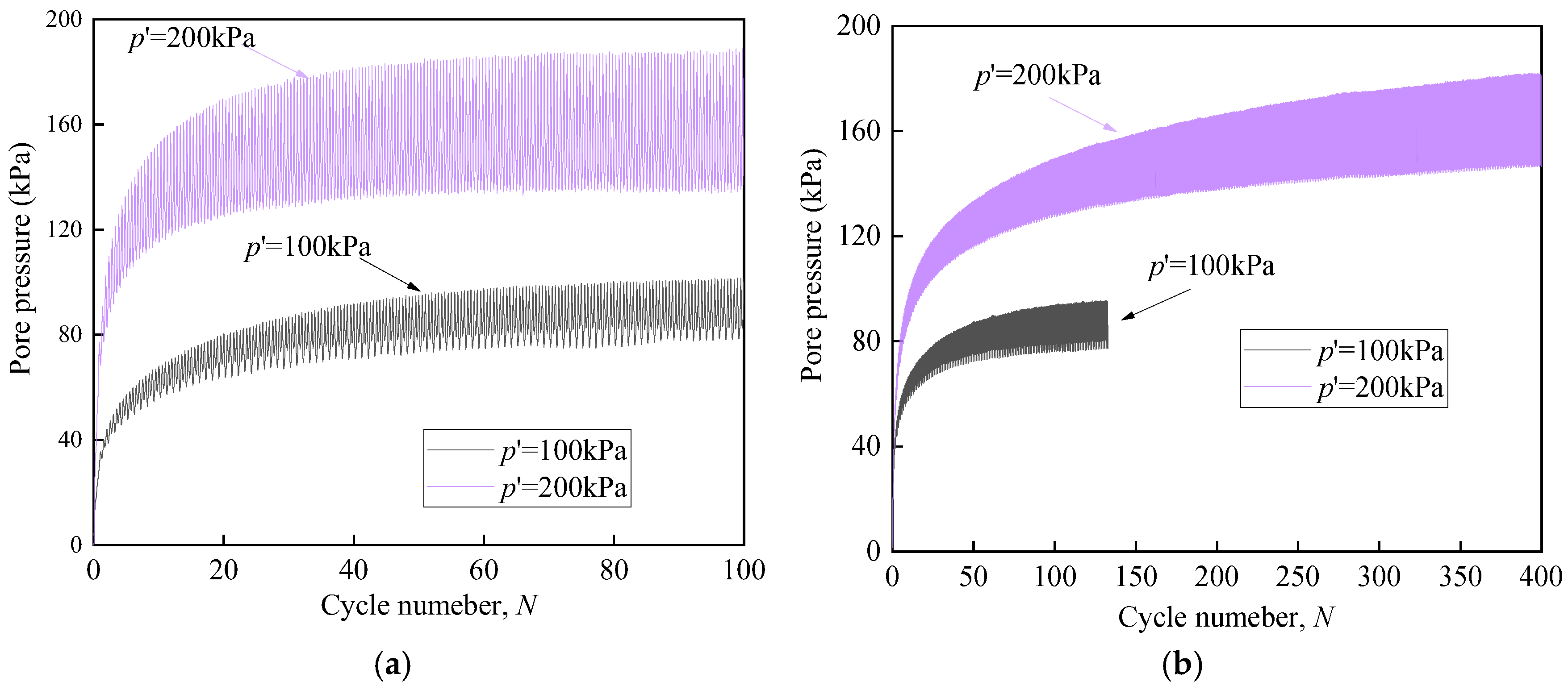
3. Experimental Results and Analysis

3.1. Liquefaction Response

Figure 6 represents curves of the excess pore water pressure ratio (Ru) and shear strain variations versus cycle number at a pressure of 100 kPa and a CSR of 0.15. As can be seen, the specimens experienced a continuous accumulation of excess pore water pressure and shear strain throughout the cyclic loading until Ru reached a value of 0.95 (i.e., initial liquefaction state). The excess pore water pressure buildup pattern of specimens with Rf = 5%, 10% is similar to that of pure sand, showing a B-type pattern—that is, “fast, slow and rapidly grow to stability”—but the rate of excess pore water pressure buildup decreases slightly as the granulated rubber in the specimen increases. The specimen with Rf = 5% liquefied after the 30th cycle, similar to pure sand, but its double-amplitude (DA) shear strain was larger than that of pure sand, reaching 5.0%. In contrast, the DA shear strain of the pure sand was very small before the 25th cycle, and then it rapidly increased to about 3.0%; at this time, the generation of pore water pressure was accelerated to accumulate. In addition, at Rf = 10%, liquefaction occurred after the 50th cycle, demonstrating the substantial benefit of granular rubber inclusion in improving liquefaction resistance; coincidentally, the 7.5% DA shear strain of the specimen meets the satisfaction of the other criterion (Ru = 0.95).
The excess pore water pressure buildup pattern of specimens with Rf = 20%, 30% is different from that of pure sand, showing the A-type pattern of “rapidly grow to stability”. The excess pore water pressure ratio of the specimen with Rf = 20% reached 0.8 at 15 loading cycles and gradually increased to 0.9 during the next 100 loading cycles, but its shear strain increased rapidly and reached the criterion (7.5% DA shear strain) in the 55th cycle. It takes 110 cycles for the excess pore water pressure ratio of the specimen with Rf = 30% to reach 0.9, and the pore water pressure remained nearly constant in the subsequent loading cycles. At this moment, the shear strain continued to increase rapidly, reaching 7.5% DA shear strain in the 65th cycle. The experimental observations indicate that in mixtures with Rf = 20%, 30%, the 7.5% DA shear strain was met many cycles earlier than the other liquefaction criterion (Ru = 0.95). Moreover, the specimen with a higher rubber content had a greater liquefaction resistance, similar to adding gravel to pure sand to increase the permeability, and thereby increasing the liquefaction resistance, which also explained the distinction in the excess pore water pressure buildup. A further effect is the increased compressibility imparted by the low elastic modulus of rubber so that the contact force and friction between particles in the specimen are more stable than the case with rigid sand particles, where the contact is not easily lost as the pore water pressure increases. Additionally, specimens with a higher rubber content had better compressibility and were more easily compressed, thus reducing the excess pore water pressure during cyclic loading. Therefore, the pressure of excess pore water buildup was reduced.
However, the high elastic property of granulated rubber also causes the deformation of the specimen to increase, which can also be seen from the phenomenon that the shear strain of the specimen increases with the rubber content, as reflected in Figure 6. Such a response was correlated with a gradual reduction in both stiffness and strength as the rubber content increased, as shown in Figure 7, which plots the variation in the hysteretic loops of the specimens in the last few cycles. Based on Figure 7, the deformation modes of all specimens in the cyclic liquefaction test were symmetric, and the hysteresis curve of the specimen was transformed from a Z shape to an anti-S shape with the increase in the rubber content in sand, reflecting the weakening of the sliding influence and the enhancement of the energy dissipation capacity. In addition, the area of the hysteretic loop of the sand–rubber mixtures was larger than the pure sand, meaning that more energy was required to rearrange and rotate the particles of the mixture; thus, the contraction of the mixture easily occurred, resulting in a continuous increase in shear strain from the initial loading stage, which was completely different from the phenomenon that the shear strain of pure sand is almost zero before the 25th cycle.
Figure 8 depicts the correlation between the pore water pressure ratio and loading cycles for specimens with Rf = 10~30% under CSRs of 0.15 and 0.2. As illustrated in the figure, the specimens subjected to CSR = 0.2 exhibited a significantly faster rate of pore water pressure accumulation compared to those under CSR = 0.15. Under CSR = 0.15, the specimen with Rf = 10% reached initial liquefaction (Ru = 0.95) at the 35th cycle, while under CSR = 0.2, liquefaction occurred significantly earlier at the 22nd cycle. The Rf = 20% specimen exhibited high liquefaction resistance at CSR = 0.15 but experienced liquefaction at the 40th cycle when subjected to the higher CSR = 0.2. Notably, specimens with Rf = 30% maintained Ru values below the liquefaction criterion under both CSR conditions. However, increasing the CSR from 0.15 to 0.2 resulted in an 18% acceleration in pore water pressure accumulation during the initial 40 loading cycles, as indicated by the increased slope steepness of the Ru-N curves.
Figure 9 demonstrates the influence of relative density on the pore water pressure generation of the specimens with Rf = 30%. While both specimens exhibited qualitatively similar pore pressure generation patterns, the specimen with Dr = 0.5 achieved liquefaction criterion significantly earlier than its Dr = 0.7 counterpart, accompanied by more intense fluctuation amplitudes in cyclic pore pressure. This divergence arises from density-dependent soil fabric characteristics: the looser specimen (Dr = 0.5) possesses a weaker metastable soil skeleton with reduced interparticle locking, predisposing it to rapid liquefaction through contractive collapse. Conversely, the denser specimen (Dr = 0.7) maintains enhanced particle interlocking that delays liquefaction onset but facilitates progressive plastic-strain accumulation through cyclic loading.
Figure 10 illustrates the influence of the confining pressure on the generation of the pore water pressure of the specimens with Rf = 30%. For specimens with Dr = 0.7, consistent pore pressure evolution patterns were observed under both 100 kPa and 200 kPa confining pressures, with pore pressure values scaling proportionally to the confining pressure; notably, neither condition met the pore pressure failure criterion. In contrast, the specimen with Dr = 0.5 demonstrated distinct behavior: under 100 kPa confining pressure, the liquefaction criterion was satisfied after the 80th loading cycle. However, at 200 kPa confining pressure, the specimen exhibited a maximum pore pressure ratio of 0.9, falling short of the liquefaction criterion despite prolonged cyclic loading, and the cumulative pore pressure stabilized and ceased to accumulate, while cyclic pore pressure exhibited more pronounced fluctuations during subsequent loading cycles.
In Figure 11, the number of cycles required to achieve liquefaction (i.e., Ru = 0.95, or gDA = 7.5%), NL, is plotted against the CSR for specimens with varying rubber contents. Experimental data reveal that increasing the proportion of gravimetric rubber increases the number of cycles, causing initial liquefaction across all tested relative densities (Dr = 0.5, 0.7). For Rf = 10% specimens, cyclic resistance decreased with reducing relative density: Dr = 0.5 specimens required 35 cycles (CSR = 0.15) and 22 cycles (CSR = 0.2) to liquefaction, representing 30% and 42% reductions relative to Dr = 0.7 specimens (50 and 38 cycles, respectively). However, this density-dependent discrepancy progressively diminishes with rubber content elevation when Rf exceeds 20%. This phenomenon arises from granulated rubber’s ability to counteract density-dependent liquefaction resistance variations through enhanced interparticle locking and energy dissipation mechanisms.

3.2. Effective Stress Path

Figure 12 depicts the characteristic evolution of the effective stress path in sand–rubber mixtures. To elucidate the governing mechanical mechanisms, representative experimental data are systematically presented with EMPS (p’) plotted on the horizontal axis and shear stress (τc) on the vertical axis. While specimen-specific variations in stress path trajectories were recorded during cyclic loading, three characteristic stages in the development of EMPS universally emerged (Figure 12a–c):
Stage I—Destabilization Phase:
Rapid devolution of p’ manifested during initial cyclic loading (0–3 cycles), accounting for 20–40% of the total stress reduction. Paradoxically, this occurred despite an increase in the relative density, suggesting that stress-induced granulated rubber buckling overwhelmed the densification effects.
Stage II—Transitional Stabilization:
Decaying p’ reduction rates remain constant, accompanied by a stable figure-eight hysteresis loop pattern, reflecting partial shear stiffness recovery. This metastable regime persisted for 10–40 cycles, governed by particle elimination and rearrangement of local instabilities at contact points.
Stage III—Terminal Critical State:
The terminal equilibrium phase revealed progressive convergence of stress paths with developing butterfly loops, marking the progressive stabilization of the stress level of the specimen, as illustrated in Figure 13. As shown in the figure, point A represents the phase transformation point, with the line connecting this point to the origin identified as the phase transformation line (PTL). Upon reaching the phase transformation threshold at point A, a critical state transition occurred, and the specimen’s behavior shifted from contraction to dilation.
Contrastingly, the low-density specimen at a higher CSR (Dr = 0.5, CSR = 0.2, Figure 12d) exhibited a distinctive stress path evolutionary pattern, omitting Stage II entirely. The stress path fails to manifest the characteristic secondary hardening phase observed in denser specimens, instead exhibiting a continuous degradation trajectory of effective mean stress (p’) toward a critical state. This anomalous response originates from the inherently unstable skeleton of the loose mixture, like the matrix material, which facilitates rapid shear-induced particle rearrangement. The metastable granular architecture triggers an accelerated phase transformation (Ishihara et al. 1975) [41], ultimately leading to full liquefaction within fewer than 30 loading cycles, a behavior contrasting sharply with the dilatant responses of the denser specimens documented in Figure 12c.

3.3. Liquefaction Based on Energy Concept

Figure 14 depicts the hysteresis loops of various specimens under identical stress–strain conditions. The centrally symmetric strain distribution induced by shear stress is evident in the plots. Notably, specimens with a higher Rf demonstrate narrower hysteresis loops, indicative of reduced energy dissipation per loading cycle, which is attributed to the elastic properties of the granular rubber incorporated in the specimen. This phenomenon can be attributed to the enhanced elastic behavior imparted by increased granulated rubber in the sand–rubber mixture. The augmented elasticity promotes greater recoverable deformation during cyclic loading, thereby diminishing cumulative dissipated energy. Consequently, the improved deformation recovery capacity mitigates cumulative damage during cyclic loading, ultimately enhancing the deformation resistance of the specimen.
Extensive research efforts have been devoted to implementing energy-based liquefaction evaluation methodologies, with seminal studies demonstrating their efficacy in geotechnical characterization [42,43,44]. This investigation systematically quantified cumulative energy dissipation behavior in sand–rubber mixtures, where the dissipated energy is calculated according to the area of hysteretic loops, and the cumulative dissipated energy is calculated as the summation of hysteretic area up to a certain cycle. Figure 15 illustrates the relationship between cumulative dissipated energy and double-amplitude shear strain for specimens with Rf = 0~30% under CSRs of 0.15 and 0.2. In general, the cumulative dissipated energy is sensitive to both rubber content and the CSR in each cyclic liquefaction case. For these specimens, the cumulative dissipated energy accumulated slowly until γDA = 3.0%, above which large dissipated energy develops rapidly until a γDA of at least 7.5% is reached, especially under a CSR of 0.15 (Figure 15a), and this acceleration becomes more pronounced at a high rubber content. This observed trend contrasts with the single hysteresis loop behavior described previously (Figure 14), which can be attributed to the fact that specimens with a higher rubber content require more loading cycles to reach the 7.5% DA shear strain criterion. Specimens with a higher rubber content (Rf ≥ 20%) manifest particularly pronounced energy dissipation disparities, particularly under a large γDA in excess of 5.0%. At γDA = 5.0%, the specimen with Rf = 30% achieved approximately 60%, 110%, and 140% greater cumulative dissipated energy compared to specimens with Rf = 20%, 10%, and 5%, respectively. This enhanced energy dissipation capacity correlates with improved resistance to liquefaction failure in sand–rubber mixtures, requiring extended cyclic loading periods to reach the criterion of 7.5% DA shear strain. Notably, this rubber-enhanced effect shows CSR dependence; the cumulative energy dissipation significantly diminishes at a high CSR. Under a CSR of 0.2 (Figure 15b), the energy dissipation differentials become substantially less pronounced at γDA = 5.0%; the 30% rubber content specimen demonstrates only 16%, 28%, and 33% higher dissipated energy values relative to its 20%, 10%, and 5% rubber content counterparts.
Figure 15c more distinctly illustrates the correlation between the cumulative dissipated energy and rubber content at 5.0% DA shear strain. The data reveal that more dissipative energy was needed for the specimen at CSR = 0.15, and when Rf ≤ 10%, the difference in cumulative energy dissipation under the two CSRs remains basically constant. However, beyond this threshold (i.e., Rf > 10%), the disparity in cumulative energy dissipation between the two CSRs increases, with a higher rubber content yielding more substantial differences. This phenomenon can be attributed to the enhanced elasticity of specimens with an elevated rubber content, which facilitates greater recoverable deformation under lower CSRs, thus delaying failure and generating higher cumulative dissipated energy. These findings systematically confirm that rubber-enriched specimens possess superior liquefaction resistance characteristics, particularly under lower CSR conditions.

4. Conclusions

In this study, we have conducted a series of undrained cyclic tests using a hollow cylinder torsional apparatus. On this basis, the following conclusions are drawn:
(1) Sand–rubber mixtures exhibit distinctly mechanical behavior from pure sand, even at low rubber contents, and the pore water pressure generation pattern of the specimen changes from B-type to A-type with increasing granulated rubber in the mixture. A lower rate of increase in the pore water pressure of the mixture is observed, and the number of loading cycles required to reach the initial liquefaction state increases with the rubber content; thus, the mixture with a high rubber content has greater liquefaction resistance.
(2) The specimens subjected to CSR = 0.2 exhibited a significantly faster rate of pore water pressure accumulation compared to those under CSR = 0.15. Furthermore, the specimen with Dr = 0.5 reached the liquefaction criterion substantially earlier than its Dr = 0.7 counterpart. In contrast, the pore pressure generation pattern exhibited minimal correlation with variations in confining pressure.
(3) There are three characteristic stages in the EMPS development of the dense mixture, namely the destabilization phase, the transitional stabilization, and the terminal critical state. However, the low-density mixture exhibits a continuous degradation trajectory of effective mean stress toward a critical state.
(4) The cumulative dissipated energy is governed by both rubber content and the CSR. Specifically, specimens subjected to a lower CSR (0.15) exhibit greater energy dissipation, particularly when the rubber fraction (Rf) exceeds 10%. Beyond this threshold, the difference in cumulative dissipated energy between different CSRs becomes more pronounced, with specimens containing a higher rubber content showing substantially larger variations.

Author Contributions

X.Z.: Conceptualization; investigation; supervision; writing—original draft; W.L.: Data curation; visualization; Y.W.: Review; funding acquisition. All authors have read and agreed to the published version of the manuscript.

Funding

This study was supported by the National Natural Science Foundation of China (Project no. 51778557).

Data Availability Statement

The experimental data used in this study are available from the corresponding author upon request.

Conflicts of Interest

Author Yabin Wang was employed by the company Anhui Hongyuan Power Tower Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

  1. Kaneda, K.; Hazarika, H.; Yamazaki, H. The numerical simulation of earth pressure reduction using tire chips in backfll. In Proceedings of the International Workshop on Scrap Tire Derived Geomaterials—Opportunities and Challenges, Yokosuka, Japan, 23–24 March 2007. [Google Scholar]
  2. Tsoi, W.Y.; Lee, K.M. Mechanical properties of cemented scrap rubber tyre chips. Geotechnique 2011, 61, 133–141. [Google Scholar] [CrossRef]
  3. Cabalar, A.F.; Karabash, Z.; Mustafa, W.S. Stabilising a clay using tyre bufngs and lime. Road Mater. Pavement Des. 2014, 15, 872–891. [Google Scholar] [CrossRef]
  4. Edeskar, T. Use of Tyre Shreds in Civil Engineering Applications-Technical and Environmental Properties. Ph.D. Dissertation, Division of Mining and Geotechnical Engineering, Department of Civil and Environmental Engineering, Lulea University of Technology, Luleå, Sweden, 2006. [Google Scholar]
  5. Humphrey, D.N. Tire derived aggregate as lightweight fill for embankments and retaining walls. In Proceedings of the International Workshop on Scrap Tire Derived Geomaterials—Opportunities and Challenges, Yokosuka, Japan, 23–24 March 2007. [Google Scholar]
  6. Wang, Z.; Wang, J.; Wu, H.N.; Zhang, R.; Zhang, G.Y.; Zhang, F.; Mariani, S. Investigation of the microstructure, mechanical properties and thermal degradation kinetics of EPDM under thermo-stress conditions used for joint sealing of floating prefabricated concrete platform of offshore wind power. Constr. Build. Mater. 2025, 485, 141897. [Google Scholar] [CrossRef]
  7. Pincus, H.; Edil, T.; Bosscher, P. Engineering Properties of Tire Chips and Soil Mixtures. ASTM Geotech. Test. J. 1994, 17, 453–464. [Google Scholar] [CrossRef]
  8. Humphrey, D.; Sandford, T. Tire Chips as Lightweight Subgrade Fill and Retaining Wall Backfill. In Proceedings of Recycling Ahead; US Department of Transportation, Federal Highway Administration: Denver, CO, USA, 1993. [Google Scholar]
  9. Das, S.; Bhowmik, D. Small-Strain Dynamic Behavior of Sand and Sand–Crumb Rubber Mixture for Different Sizes of Crumb Rubber Particle. J. Mater. Civ. Eng. 2020, 32, 1–9. [Google Scholar] [CrossRef]
  10. Karmokar, A. Use of scrap tire derived shredded geomaterials in drainage application. In Proceedings of the International Workshop on Scrap Tire Derived Geomaterials—Opportunities and Challenges, Yokosuka, Japan, 23–24 March 2007; pp. 127–138. [Google Scholar]
  11. Zeybek, A.; Eyin, M. Experimental Study on Liquefaction Characteristics of Saturated Sands Mixed with Fly Ash and Tire Crumb Rubber. Sustainability 2023, 15, 2960. [Google Scholar] [CrossRef]
  12. Pokhrel, A.; Chiaro, G. Pore Water Pressure Generation and Energy Dissipation Characteristics of Sand–Gravel Mixtures Subjected to Cyclic Loading. Geotechnics 2024, 4, 1282–1303. [Google Scholar] [CrossRef]
  13. Yasuhara, K. Recent Japanese experiences on scrapped tires for geotechnical applications. In Proceedings of the International Workshop on Scrap Tire Derived Geomaterials—Opportunities and Challenges; Hazarika, H., Yasuhara, K., Eds.; Taylor & Francis: London, UK, 2007; pp. 17–40. [Google Scholar]
  14. Kawata, S.; Hyodo, M.; Orense, P.; Yamada, S.; Hazarika, H. Undrained and drained shear behavior of sand and tire chips composite material. In Proceedings of the International Workshop on Scrap Tire Derived Geomaterials—Opportunities and Challenges, Yokosuka, Japan, 23–24 March 2007; pp. 277–283. [Google Scholar]
  15. Hazarika, H.; Yasuhara, K.; Kikuchi, Y.; Karmokar, A.K.; Mitarai, Y. Multifaceted potentials of tire derived three dimensional geosynthetics in geotechnical application and their evaluation. Geotext. Geomembr. 2010, 28, 303–315. [Google Scholar] [CrossRef]
  16. Hazarika, H.; Pasha, S.M.K.; Ishibashi, I.; Yoshimoto, N. Tire chips reinforced foundation as liquefaction countermeasure for residential buildings. Soils Found. 2020, 60, 315–326. [Google Scholar] [CrossRef]
  17. Tsang, H.H.; Lo, S.H.; Xu, X.; Sheikh, M.N. Seismic isolation for low-to-medium-rise buildings using granulated rubber–soil mixtures: Numerical study. Earthq. Eng. Struct. Dyn. 2012, 41, 2009–2024. [Google Scholar] [CrossRef]
  18. Tsang, H.H.; Tran, D.P.; Hung, W.Y.; Pitilakis, K.; Gad, E.F. Performance of geotechnical seismic isolation system using rubber-soil mixtures in centrifuge testing. Earthq. Eng. Struct. Dyn. 2021, 50, 1271–1289. [Google Scholar] [CrossRef]
  19. Senetakis, K.; Anastasiadis, A.; Pitilakis, K. Dynamic properties of dry sand/rubber (SRM) and gravel/rubber (GRM) mixtures in a wide range of shearing strain amplitudes. Soil Dyn. Earthq. Eng. 2012, 33, 38–53. [Google Scholar] [CrossRef]
  20. Pitilakis, K.; Karapetrou, S.; Tsagdi, K. Numerical investigation of the seismic response of RC buildings on soil replaced with rubber–sand mixtures. Soil Dyn. Earthq. Eng. 2015, 79, 237–252. [Google Scholar] [CrossRef]
  21. Pitilakis, D.; Anastasiadis, A.; Vratsikidis, A.; Kapouniaris, A. Confguration of a gravel-rubber geotechnical seismic isolation system from laboratory and feld tests. Soil Dyn. Earthq. Eng. 2024, 178, 108463. [Google Scholar] [CrossRef]
  22. Abate, G.; Fiamingo, A.; Massimino, M.R. FEM investigation of full-scale tests on DSSI, including gravel-rubber mixtures as geotechnical seismic isolation. Soil Dyn. Earthq. Eng. 2023, 172, 108033. [Google Scholar] [CrossRef]
  23. Chiaro, G.; Palermo, A.; Banasiak, L.; Tasalloti, A.; Granello, G.; Hernandez, E. Seismic response of low-rise buildings with ecorubber geotechnical seismic isolation (ERGSI) foundation system: Numerical investigation. Bull. Earthq. Eng. 2023, 21, 3797–3821. [Google Scholar] [CrossRef]
  24. Vratsikidis, A.; Pitilakis, D. Field testing of gravel-rubber mixtures as geotechnical seismic isolation. Bull. Earthq. Eng. 2023, 21, 3905–3922. [Google Scholar] [CrossRef]
  25. Feng, Z.Y.; Sutter, K.G. Dynamic Properties of Granulated Rubber/Sand Mixtures. ASTM Geotech. Test. J. 2000, 23, 338–344. [Google Scholar] [CrossRef]
  26. Pamukcu, S.; Akbulut, S. Thermoelastic enhancement of damping of sand using synthetic ground rubber. J. Geotech. Geoenvironmental Eng. 2006, 132, 501–510. [Google Scholar] [CrossRef]
  27. Anastasiadis, A.; Senetakis, K.; Pitilakis, K. Small-strain shear modulus and damping ratio of sand-rubber and gravel-rubber mixtures. Geotech. Geol. Eng. 2012, 30, 363–382. [Google Scholar] [CrossRef]
  28. Edincliler, A.; Baykal, G.; Saygili, A. Infuence of diferent processing techniques on the mechanical properties of used tires in embankment construction. Waste Manag. 2010, 30, 1073–1080. [Google Scholar] [CrossRef] [PubMed]
  29. Edincliler, A.; Yildiz, O. Effects of processing type on shear modulus and damping ratio of waste tire-sand mixtures. Geosynth. Int. 2022, 29, 389–408. [Google Scholar] [CrossRef]
  30. Badarayani, P.; Cazacliu, B.; Ibraim, E.; Artoni, R.; Richard, P. Sand Rubber Mixtures under Oedometric Loading: Sand-like vs. Rubber-Like Behavior. Appl. Sci. 2023, 13, 3867. [Google Scholar] [CrossRef]
  31. Wang, Z.; Lyu, H.M.; Zhang, R. Water-swelling behavior and self-reinforcing mechanical properties of joint sealing material in underground prefabricated structure. Constr. Build. Mater. 2025, 490, 142451. [Google Scholar] [CrossRef]
  32. Okur, D.V.; Umu, S.U. Dynamic Properties of Clean sand Modified with Granulated Rubber. Adv. Civ. Eng. 2018, 2018, 5209494. [Google Scholar] [CrossRef]
  33. Tsang, H.H.; Pitilakis, K. Mechanism of geotechnical seismic isolation system: Analytical modeling. Soil Dyn. Earthq. Eng. 2019, 122, 171–184. [Google Scholar] [CrossRef]
  34. Tsiavos, A.; Alexander, N.A.; Diambra, A.; Ibraim, E.; Vardanega, P.J.; Gonzalez-Buelga, A.; Sextos, A. A sand-rubber deformable granular layer as a low-cost seismic isolation strategy in developing countries: Experimental investigation. Soil Dyn. Earthq. Eng. 2019, 125, 105731. [Google Scholar] [CrossRef]
  35. Hyodo, M.; Yamada, S.; Orense, R.P.; Okamoto, M.; Hazarika, H. Undrained Cyclic Shear Properties of Tire Chip-Sand Mixtures. In Proceedings of the International Workshop IW-TDGM2007, Yokosuka, Japan, 23–24 March 2007; Taylor and Francis: London, UK; pp. 187–196. [Google Scholar]
  36. Kaneko, K.; Orense, R.P.; Hyodo, M.; Yoshimoto, N. Seismic Response Characteristics of Saturated Sand Deposits Mixed with Tire Chips. J. Geotech. Geoenviron. Eng. 2013, 139, 633–643. [Google Scholar] [CrossRef]
  37. Mashiri, M.S.; Vinod, J.S.; Sheikh, M.N. Liquefaction potential and dynamic properties of sand-tyre chip (stch) mixtures. Geotech. Test. J. 2016, 39, 20150031. [Google Scholar] [CrossRef]
  38. Promputthangkoon, P.; Hyde, A. Compressibility and liquefaction potential of rubber composite soils. In Proceedings of the International Workshop on Scrap tire Derived Geomaterials—Opportunities and Challenges, Yokosuka, Japan, 23–24 March 2007; Taylor and Francis Group: London, UK; pp. 161–170. [Google Scholar]
  39. Ding, Y.; Zhang, J.; Chen, X.; Wang, X.; Jia, Y. Experimental investigation on static and dynamic characteristics of granulated rubber-sand mixtures a new railway subgrade filler. Constr. Build. Mater. 2021, 273, 121955. [Google Scholar] [CrossRef]
  40. Sarajpoor, S.; Kavand, A.; Zogh, P.; Ghalandarzadeh, A. Dynamic behavior of sand-rubber mixtures based on hollow cylinder tests. Constr. Build. Mater. 2020, 251, 118948. [Google Scholar] [CrossRef]
  41. Ishihara, K.; Tatsuoka, F.; Yasuda, S. Undrained deformation and liquefaction of sand under cyclic stresses. Soils Found. 1975, 15, 29–44. [Google Scholar] [CrossRef]
  42. Kokusho, T.; Kaneko, Y. Energy evaluation for liquefactioninduced strain of loose sands by harmonic and irregular loading tests. Soil Dyn. Earthquake Eng. 2018, 114, 362–377. [Google Scholar] [CrossRef]
  43. Kokusho, T. Energy-based liquefaction evaluation for induced strain and surface settlement–evaluation steps and case studies. Soil Dyn. Earthquake Eng. 2021, 143, 106552. [Google Scholar] [CrossRef]
  44. Kokusho, T.; Tanimoto, S. Energy capacity versus liquefaction strength investigated by cyclic triaxial tests on intact soils. J. Geotech. Geoenviron. Eng. 2021, 147, 04021006. [Google Scholar] [CrossRef]
Buildings 15 04486 g001
Figure 1. Particle size distribution curves of sand and rubber.
Figure 1. Particle size distribution curves of sand and rubber.
Buildings 15 04486 g001
Buildings 15 04486 g002
Figure 2. Size distribution of sand and rubber particles.
Figure 2. Size distribution of sand and rubber particles.
Buildings 15 04486 g002
Buildings 15 04486 g003
Figure 3. The photo of hollow cylinder apparatus.
Figure 3. The photo of hollow cylinder apparatus.
Buildings 15 04486 g003
Buildings 15 04486 g004
Figure 4. Specimen preparation process: (a) mold installation; (b) sample preparation; (c) mold closure.
Figure 4. Specimen preparation process: (a) mold installation; (b) sample preparation; (c) mold closure.
Buildings 15 04486 g004
Buildings 15 04486 g005
Figure 5. Equipment and experimental process: (a) filling the inner cavity with water; (b) demolding molding; (c) closed pressure chamber.
Figure 5. Equipment and experimental process: (a) filling the inner cavity with water; (b) demolding molding; (c) closed pressure chamber.
Buildings 15 04486 g005
Buildings 15 04486 g006aBuildings 15 04486 g006b
Figure 6. Variation in pore water pressure and shear strain with cycle number at p’ = 100 kPa, Dr = 0.7: (a) pure sand; (b) Rf = 5%; (c) Rf = 10%; (d) Rf = 20%; (e) Rf = 30%.
Figure 6. Variation in pore water pressure and shear strain with cycle number at p’ = 100 kPa, Dr = 0.7: (a) pure sand; (b) Rf = 5%; (c) Rf = 10%; (d) Rf = 20%; (e) Rf = 30%.
Buildings 15 04486 g006aBuildings 15 04486 g006b
Buildings 15 04486 g007
Figure 7. Stress–strain relation: (a) pure sand; (b) Rf = 5%; (c) Rf = 10%; (d) Rf = 20%; (e) Rf = 30%.
Figure 7. Stress–strain relation: (a) pure sand; (b) Rf = 5%; (c) Rf = 10%; (d) Rf = 20%; (e) Rf = 30%.
Buildings 15 04486 g007
Buildings 15 04486 g008
Figure 8. Variation in pore water pressure with cycle number at Dr = 0.5: (a) Rf = 10%; (b) Rf = 20%; (c) Rf = 30%.
Figure 8. Variation in pore water pressure with cycle number at Dr = 0.5: (a) Rf = 10%; (b) Rf = 20%; (c) Rf = 30%.
Buildings 15 04486 g008
Buildings 15 04486 g009
Figure 9. Variation in relative density with cycle number at Rf = 30%: (a) CSR = 0.15; (b) CSR = 0.2.
Figure 9. Variation in relative density with cycle number at Rf = 30%: (a) CSR = 0.15; (b) CSR = 0.2.
Buildings 15 04486 g009
Buildings 15 04486 g010
Figure 10. Variation in confining pressure with cycle number at Rf = 30%: (a) Dr = 0.5; (b) Dr = 0.7.
Figure 10. Variation in confining pressure with cycle number at Rf = 30%: (a) Dr = 0.5; (b) Dr = 0.7.
Buildings 15 04486 g010
Buildings 15 04486 g011
Figure 11. Effect of rubber content on dynamic strength of sand–rubber mixtures.
Figure 11. Effect of rubber content on dynamic strength of sand–rubber mixtures.
Buildings 15 04486 g011
Buildings 15 04486 g012
Figure 12. Excess pore water pressure ratio versus cycle number under different rubber content: (a) Rf = 5%, Dr = 0.7, CSR = 0.15; (b) Rf = 10%, Dr = 0.7, CSR = 0.15; (c) Rf = 20%, Dr = 0.7, CSR = 0.15; (d) Rf = 20%, Dr = 0.5, CSR = 0.2.
Figure 12. Excess pore water pressure ratio versus cycle number under different rubber content: (a) Rf = 5%, Dr = 0.7, CSR = 0.15; (b) Rf = 10%, Dr = 0.7, CSR = 0.15; (c) Rf = 20%, Dr = 0.7, CSR = 0.15; (d) Rf = 20%, Dr = 0.5, CSR = 0.2.
Buildings 15 04486 g012
Buildings 15 04486 g013
Figure 13. Shear strain versus cycle number under different rubber content: (a) Rf = 5%, Dr = 0.7, CSR = 0.15; (b) Rf = 10%, Dr = 0.7, CSR = 0.15; (c) Rf = 20%, Dr = 0.7, CSR = 0.15; (d) Rf = 20%, Dr = 0.5, CSR = 0.2.
Figure 13. Shear strain versus cycle number under different rubber content: (a) Rf = 5%, Dr = 0.7, CSR = 0.15; (b) Rf = 10%, Dr = 0.7, CSR = 0.15; (c) Rf = 20%, Dr = 0.7, CSR = 0.15; (d) Rf = 20%, Dr = 0.5, CSR = 0.2.
Buildings 15 04486 g013
Buildings 15 04486 g014
Figure 14. Hysteretic loops under identical stress–strain conditions: CSR = 0.15, Dr = 0.5, f = 0.2 Hz, p0 = 100 kPa, γzθ = 1.0 ± 0.03%.
Figure 14. Hysteretic loops under identical stress–strain conditions: CSR = 0.15, Dr = 0.5, f = 0.2 Hz, p0 = 100 kPa, γzθ = 1.0 ± 0.03%.
Buildings 15 04486 g014
Buildings 15 04486 g015
Figure 15. Cumulative dissipated energy versus DA shear strain: (a) CSR = 0.15; (b) CSR = 0.2; (c) γDA = 5.0%.
Figure 15. Cumulative dissipated energy versus DA shear strain: (a) CSR = 0.15; (b) CSR = 0.2; (c) γDA = 5.0%.
Buildings 15 04486 g015
Table 1. Physical parameters of sand and rubber.
Table 1. Physical parameters of sand and rubber.
SpecimenParticle Size Range (mm)Specific GravityMean Particle Size (mm)Uniformity Coefficient, CuCurvature Coefficient, CcMaximum Dry Density (g/cm3)Minimum Dry Density (g/cm3)
Sand0.075~1.02.660.233.640.921.611.32
Granulated rubber2~41.163.271.401.130.670.41
Table 2. Initial properties of sand–rubber mixture specimens.
Table 2. Initial properties of sand–rubber mixture specimens.
Rf (%)ρdmin (g·cm−3)ρdmax (g·cm−3)ρd (g·cm−3)DrmS (g)mR (g)
0 (pure sand)1.321.611.510.71469.50
51.281.571.470.71412.341.4
101.261.541.450.71355.667.4
201.201.521.410.71241.5138.8
301.151.411.320.71091.7209.3
Note: Rf, the rubber gravimetric proportion; Dr, the relative density; mS, the mass of sand; mR, the mass of granular rubber.
Table 3. Scheme of cyclic liquefaction tests.
Table 3. Scheme of cyclic liquefaction tests.
Rf (%)p’ (kPa)Dr (%)CSR
0 (Pure sand)1000.70.15, 0.2
51000.70.15, 0.2
101000.5, 0.70.15, 0.2
201000.5, 0.70.15, 0.2
30100, 2000.5, 0.70.15, 0.2
Note: p’, the effective mean principal stress; CSR, the cyclic stress ratio.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zhu, X.; Li, W.; Wang, Y. Study of Liquefaction Characteristics of Saturated Sand–Rubber Mixture Under Cyclic Torsional Shear Loading. Buildings 2025, 15, 4486. https://doi.org/10.3390/buildings15244486

AMA Style

Zhu X, Li W, Wang Y. Study of Liquefaction Characteristics of Saturated Sand–Rubber Mixture Under Cyclic Torsional Shear Loading. Buildings. 2025; 15(24):4486. https://doi.org/10.3390/buildings15244486

Chicago/Turabian Style

Zhu, Xiaojun, Wenshuai Li, and Yabin Wang. 2025. "Study of Liquefaction Characteristics of Saturated Sand–Rubber Mixture Under Cyclic Torsional Shear Loading" Buildings 15, no. 24: 4486. https://doi.org/10.3390/buildings15244486

APA Style

Zhu, X., Li, W., & Wang, Y. (2025). Study of Liquefaction Characteristics of Saturated Sand–Rubber Mixture Under Cyclic Torsional Shear Loading. Buildings, 15(24), 4486. https://doi.org/10.3390/buildings15244486

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop