Analytical Calculation Method for Transverse Internal Force of Single-Box Double-Cell Box Girder with Inclined Webs Considering the Influence of Distortion Resistance Stiffness
Abstract
1. Introduction
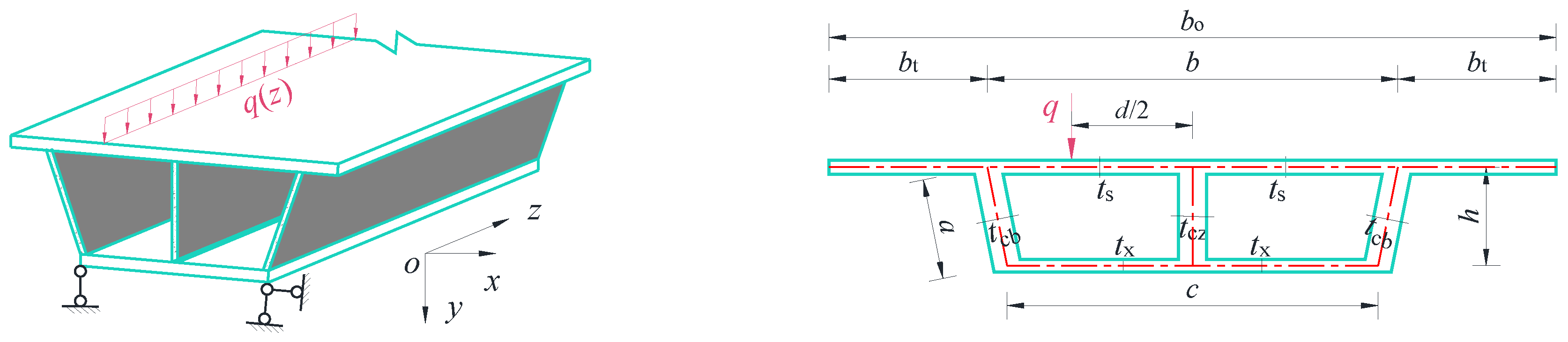
2. Assumptions and Releases of Supports
- The axial deformation of each plate component constituting the frame is negligible, meaning the perimeter of the box-shaped cross-section is considered incompressible, with a transverse strain of 0.
- When a box girder undergoes distortion-induced warping, the individual plates constituting the box section serve as the cross-sections of longitudinal plate girders, each satisfying the plane-section assumption.
- Neglecting the influence of the thickness of each plate component of the box girder on warping, i.e., the shear stress and warping normal stress are uniformly distributed along the wall thickness.
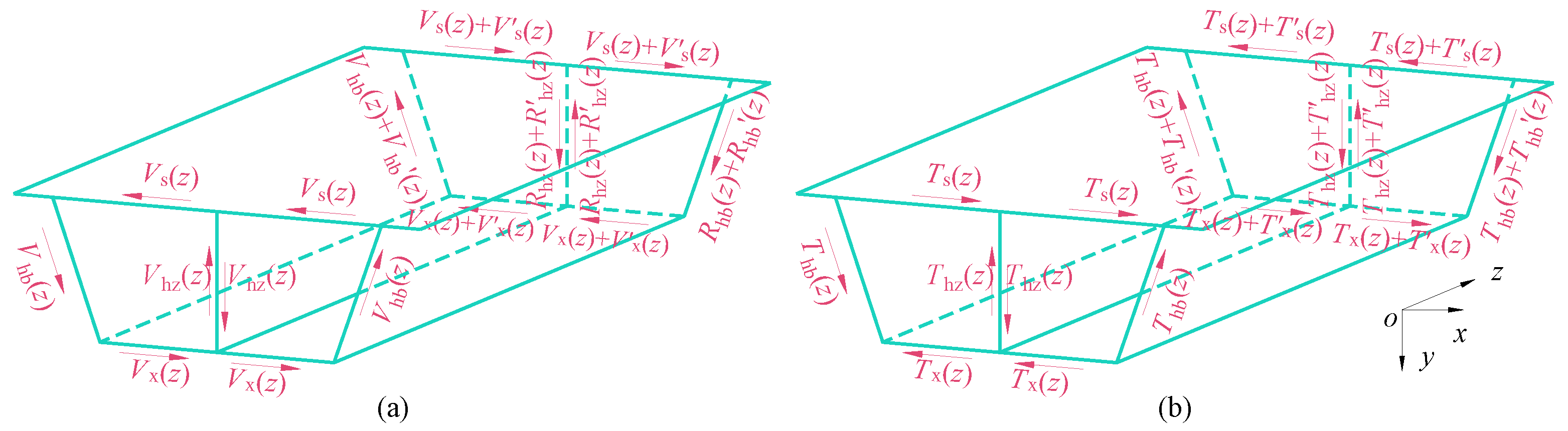
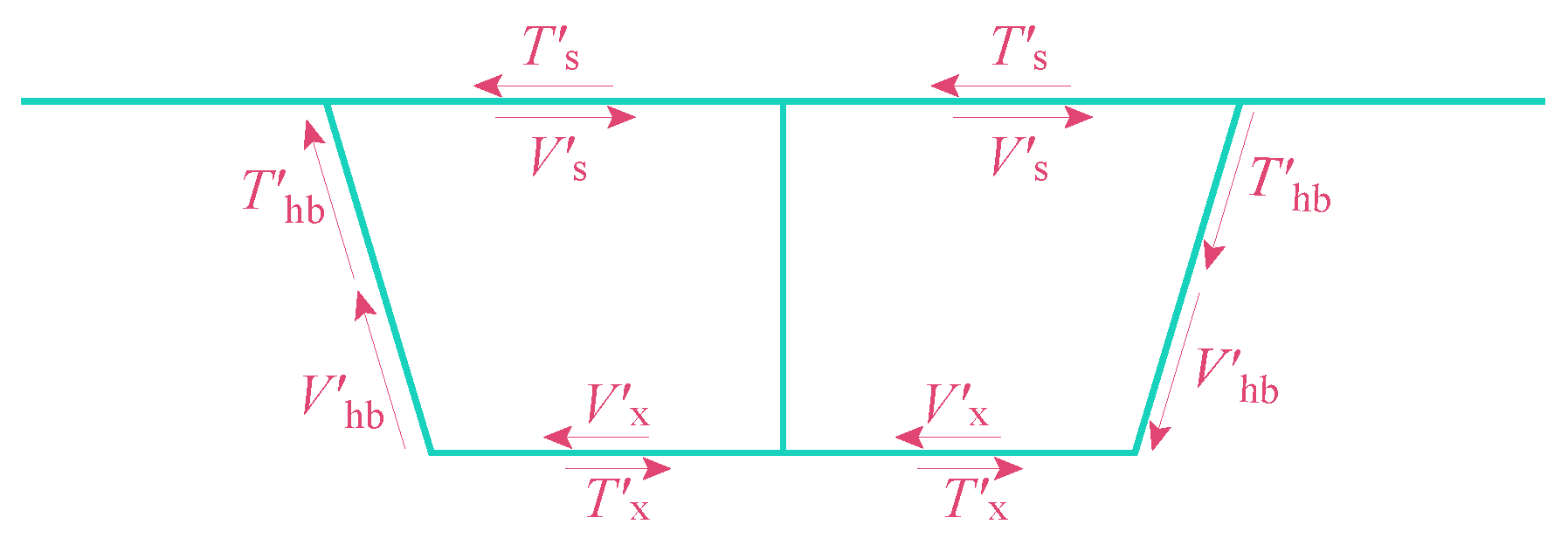
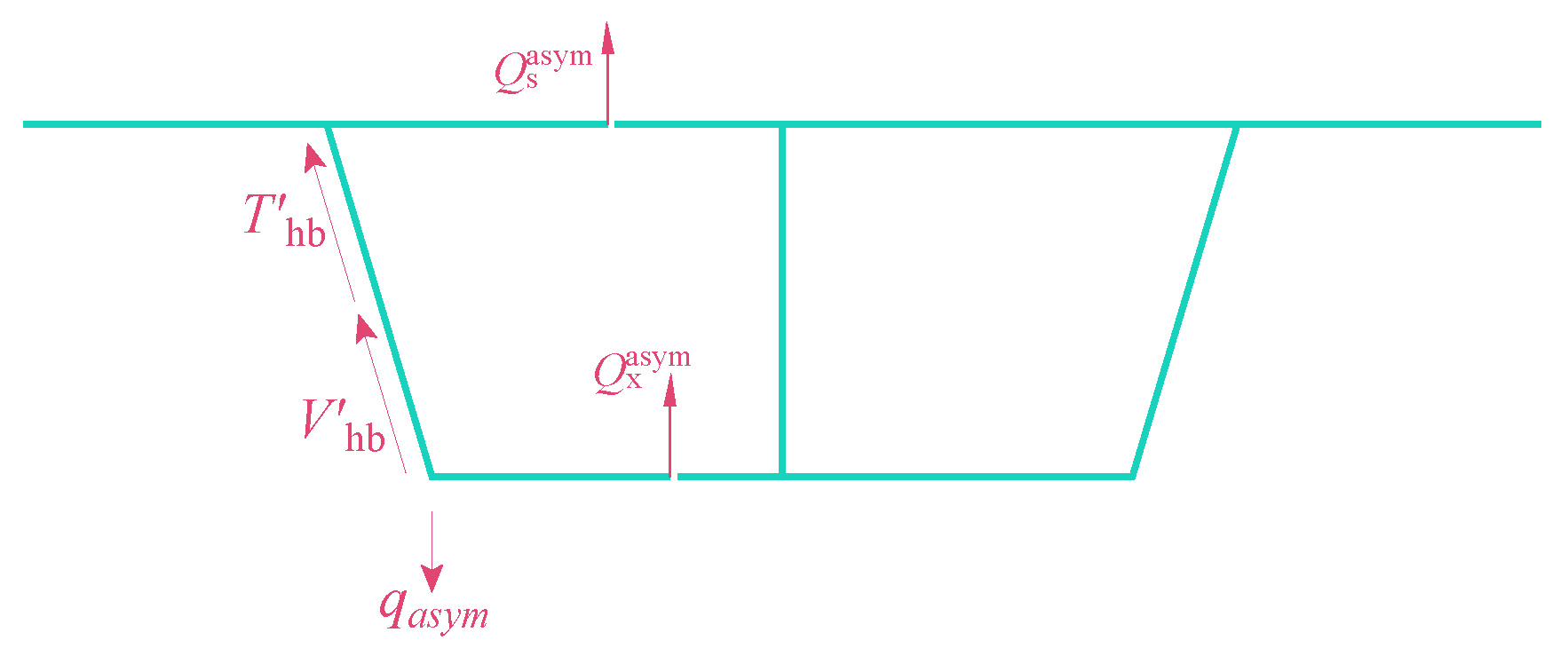
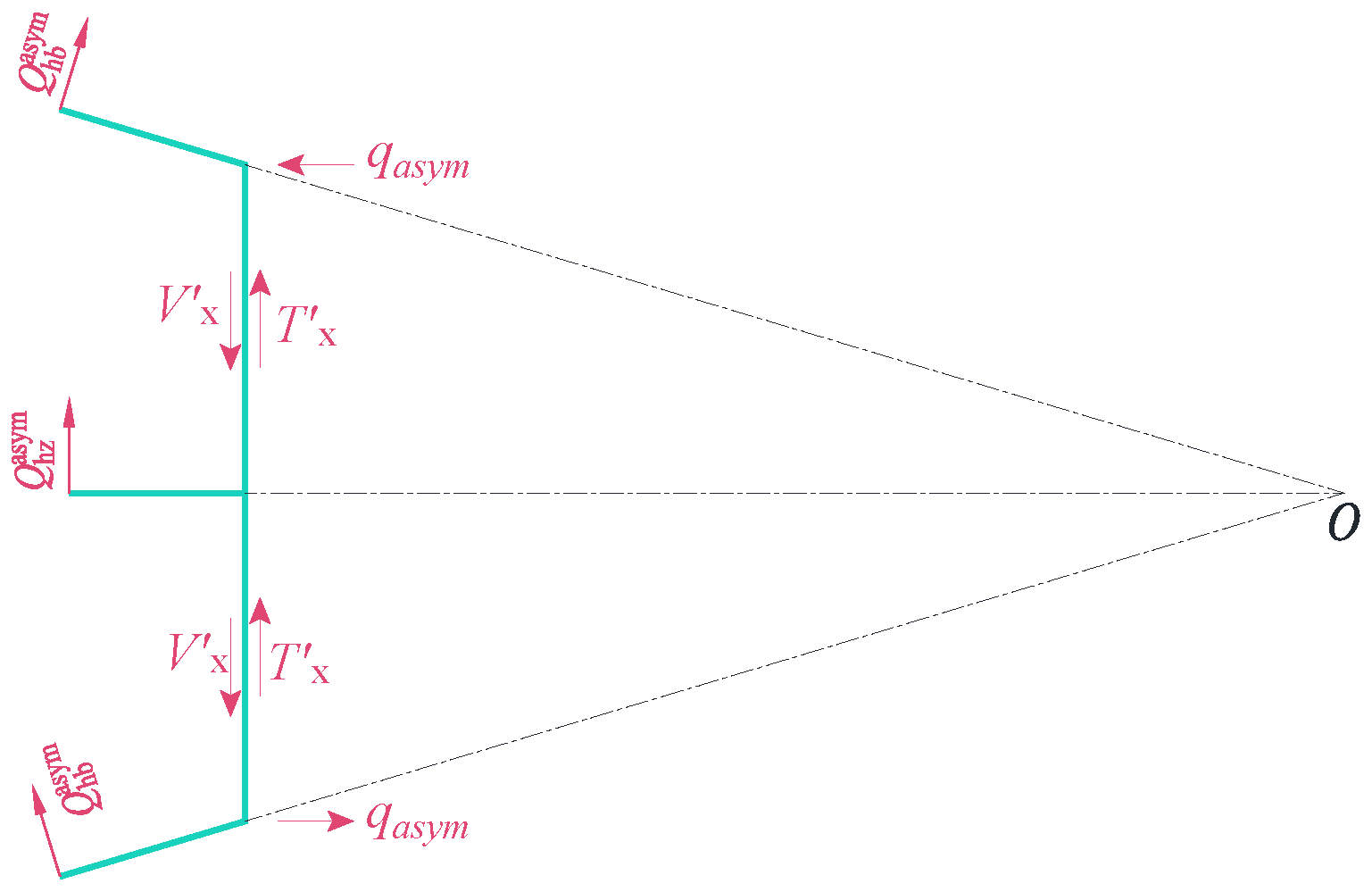
3. Torsion Mode
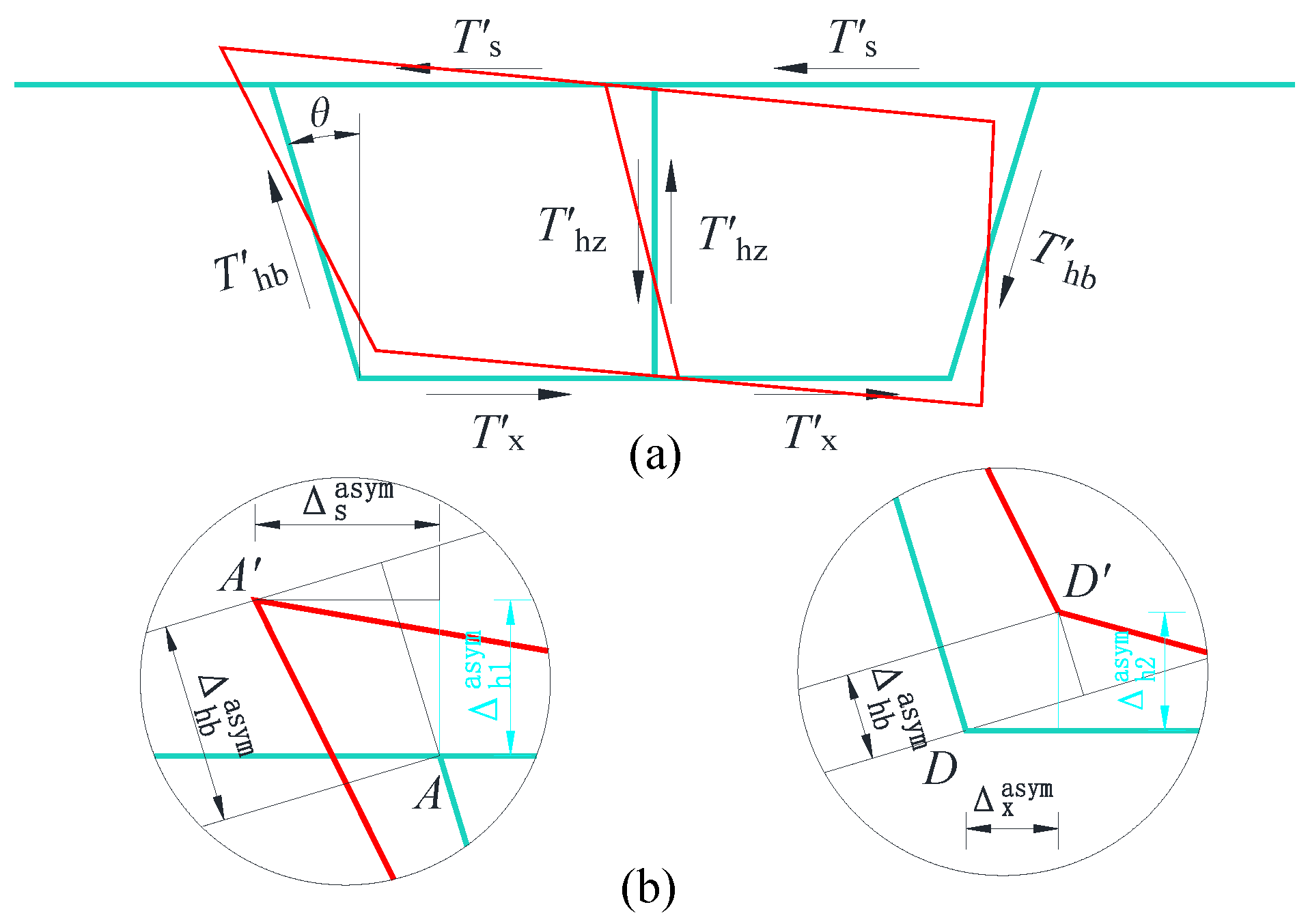
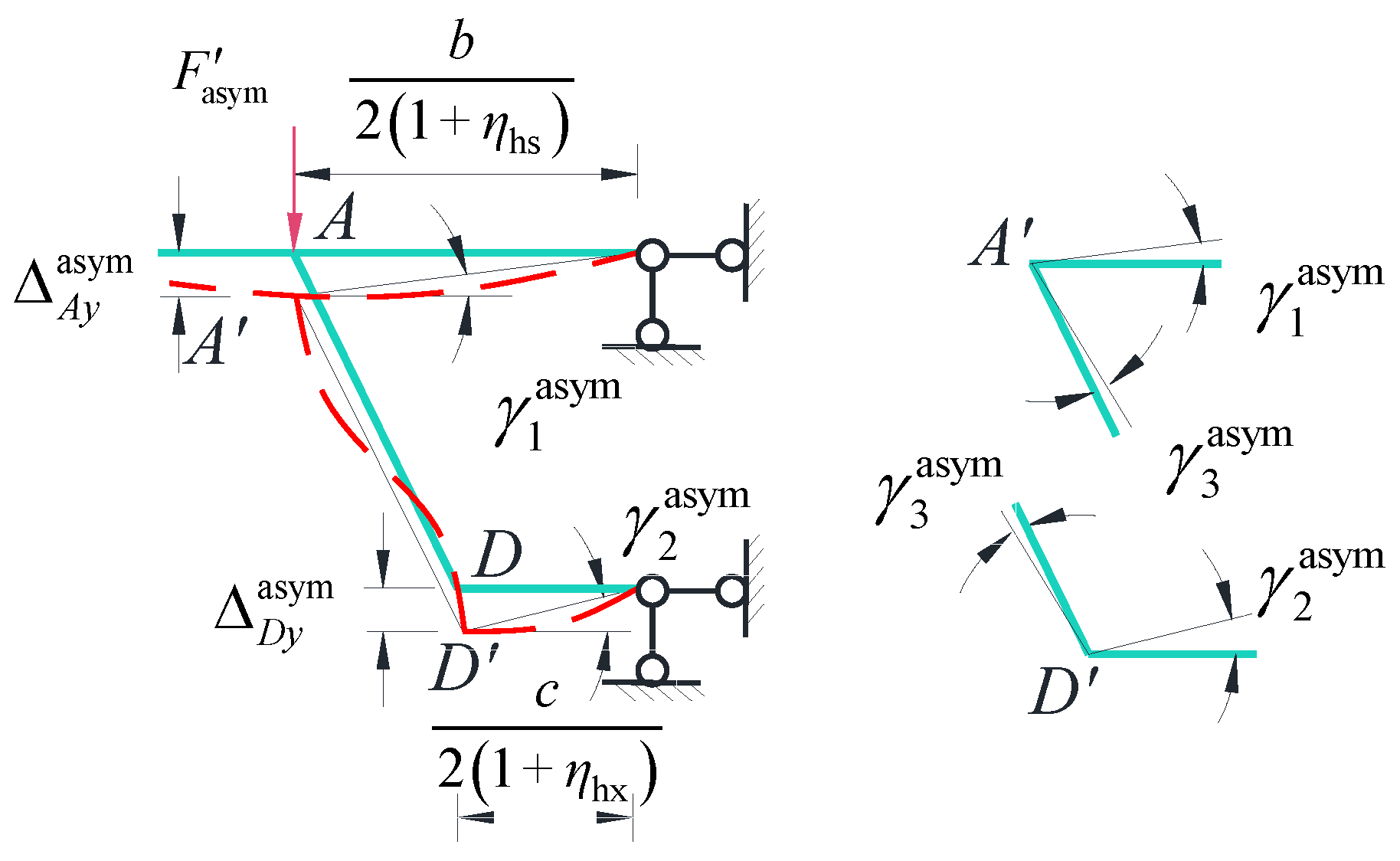
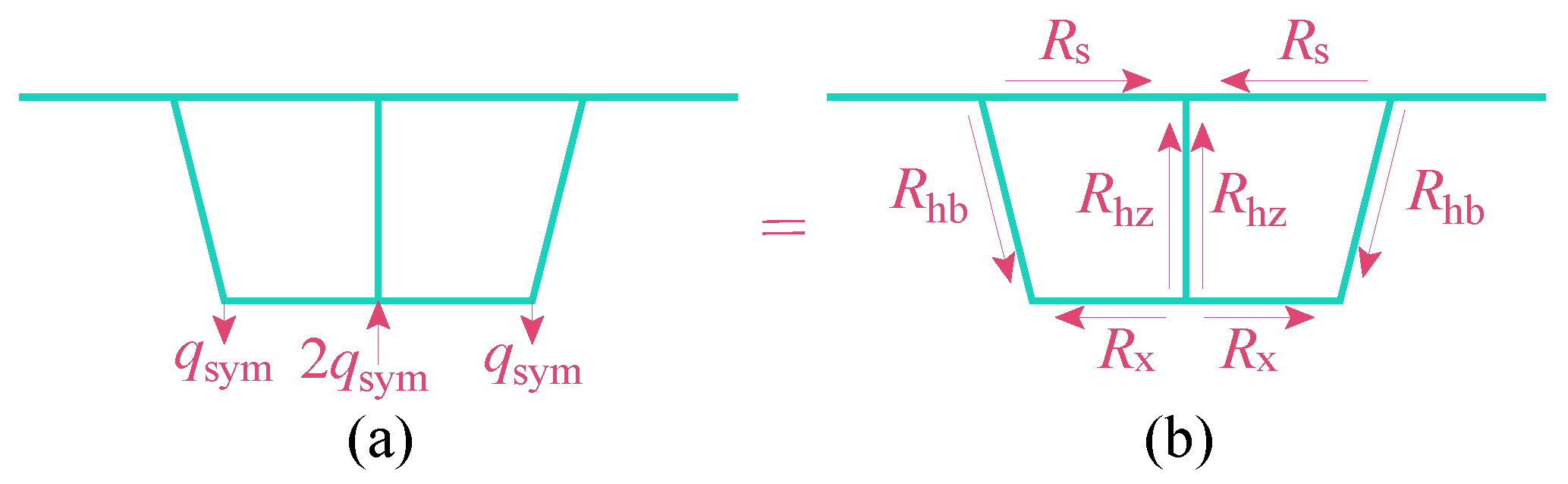
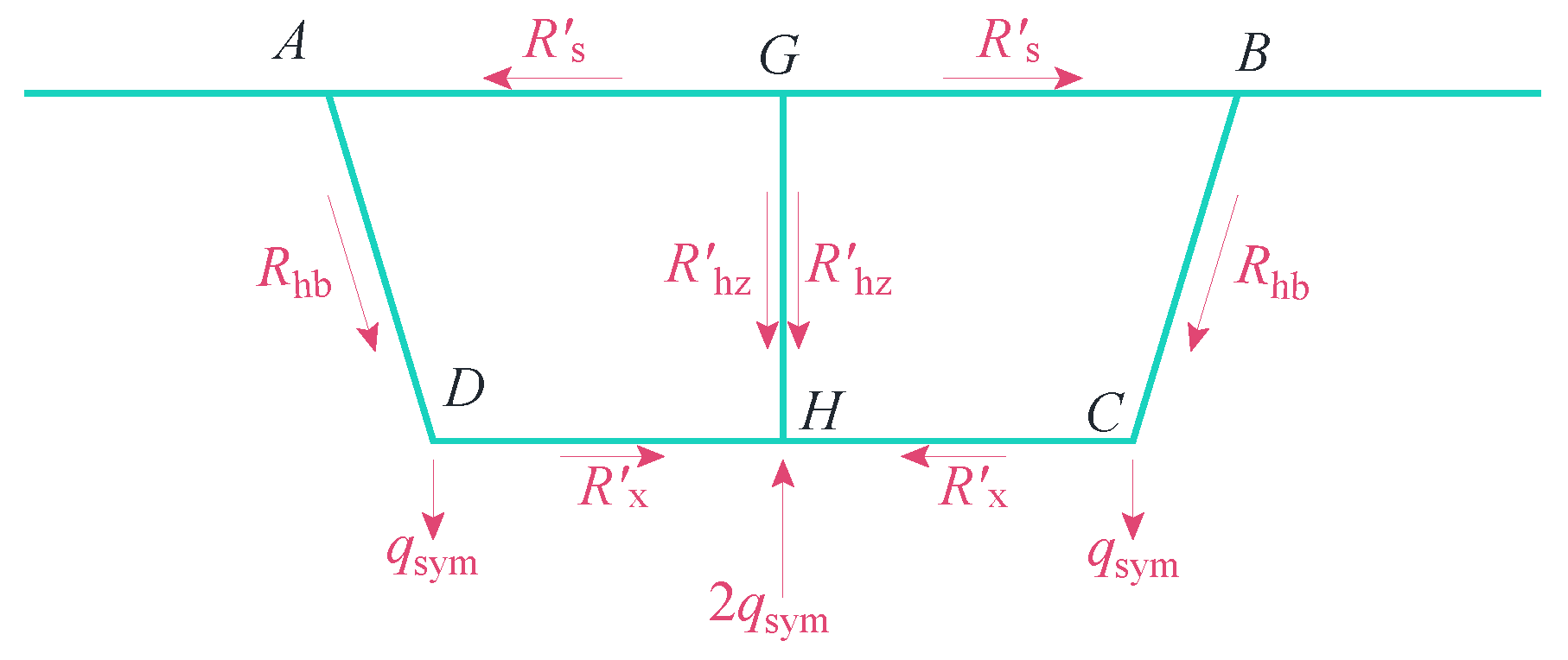
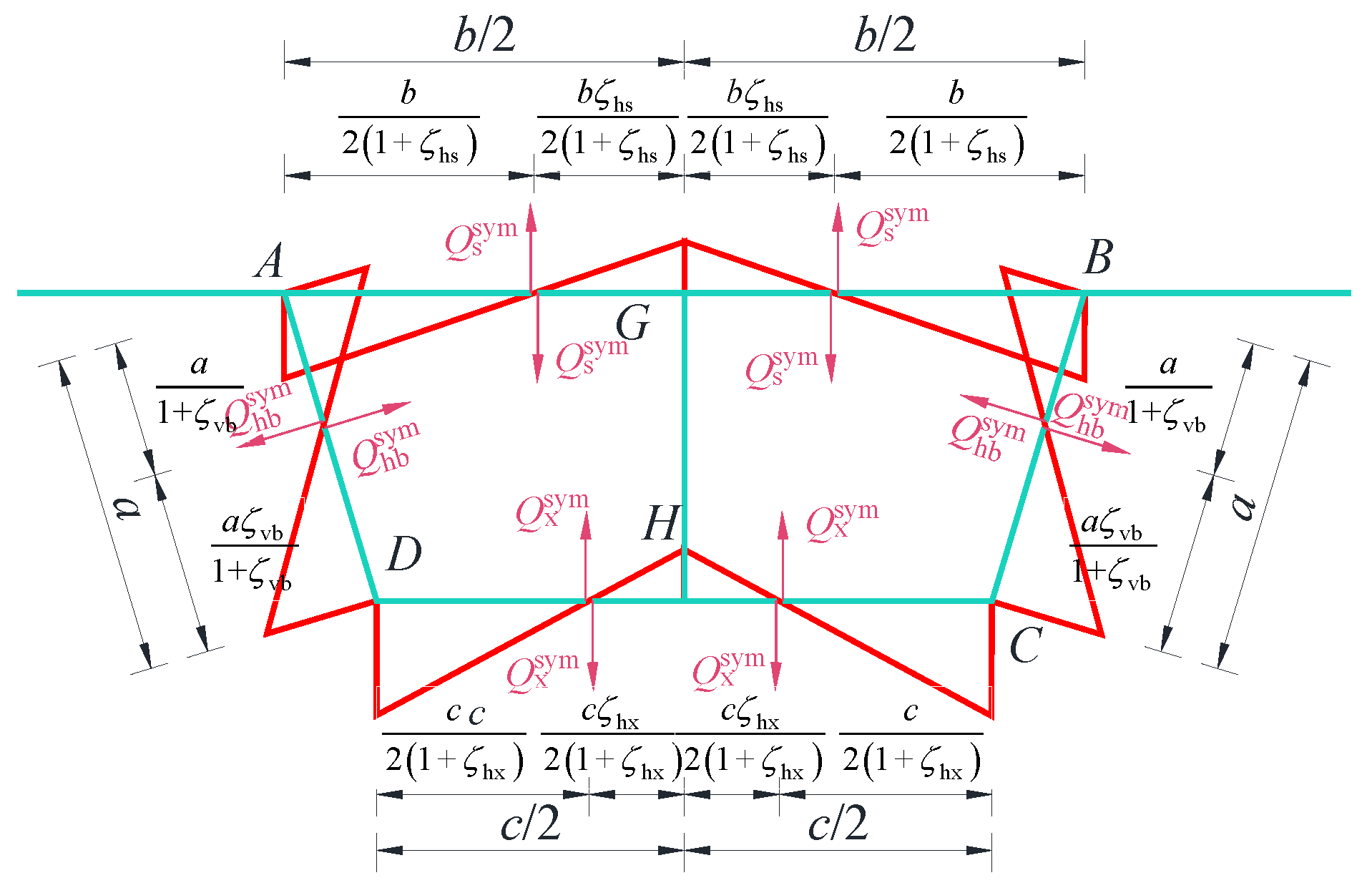
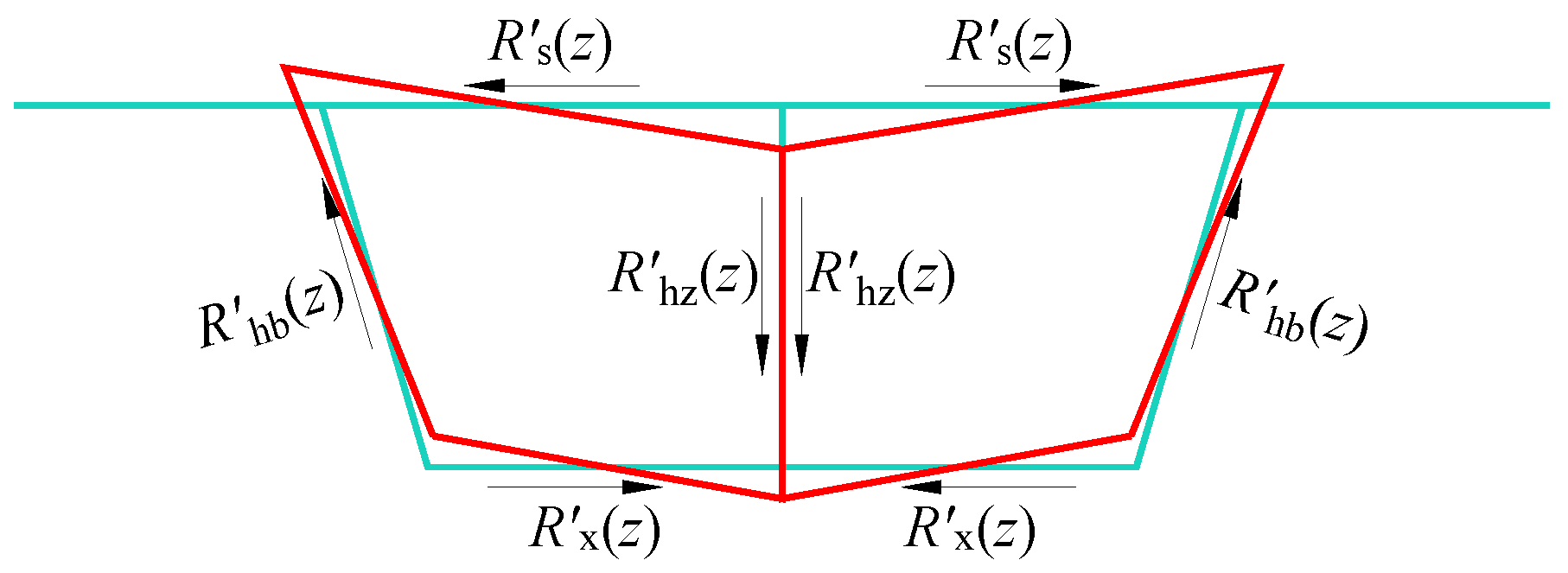
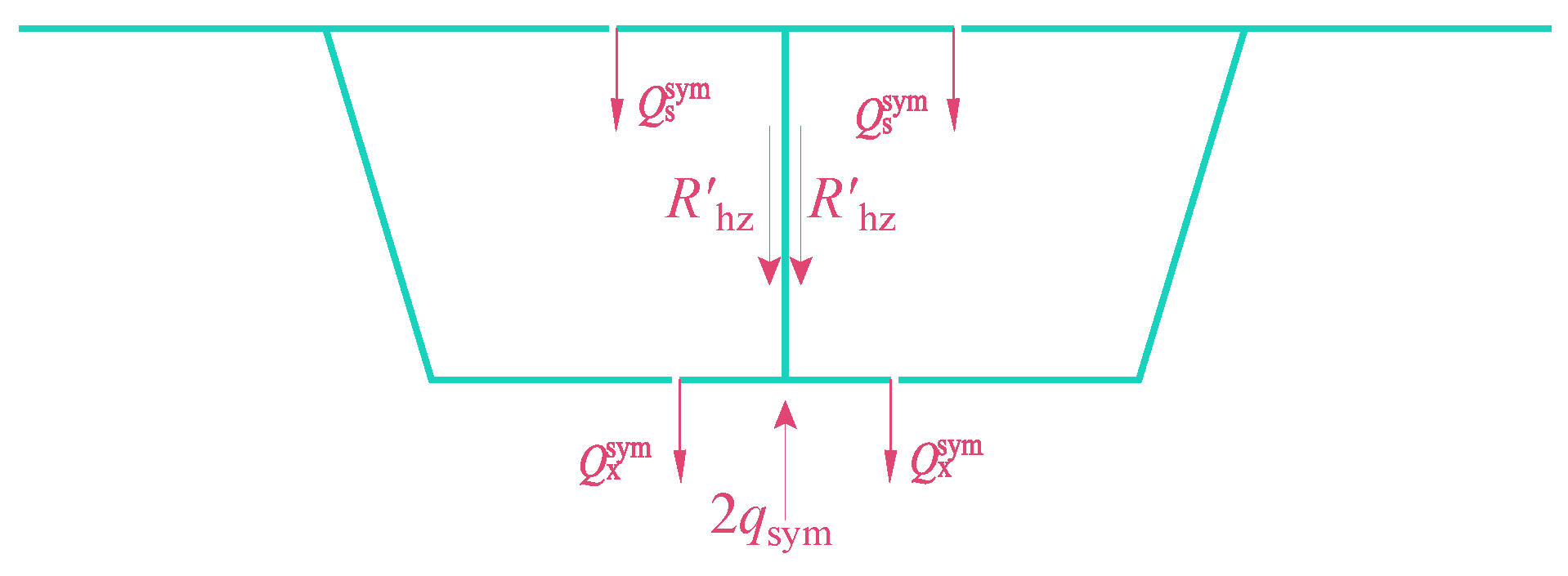
4. Distortion Mode
5. Numerical Example Analysis
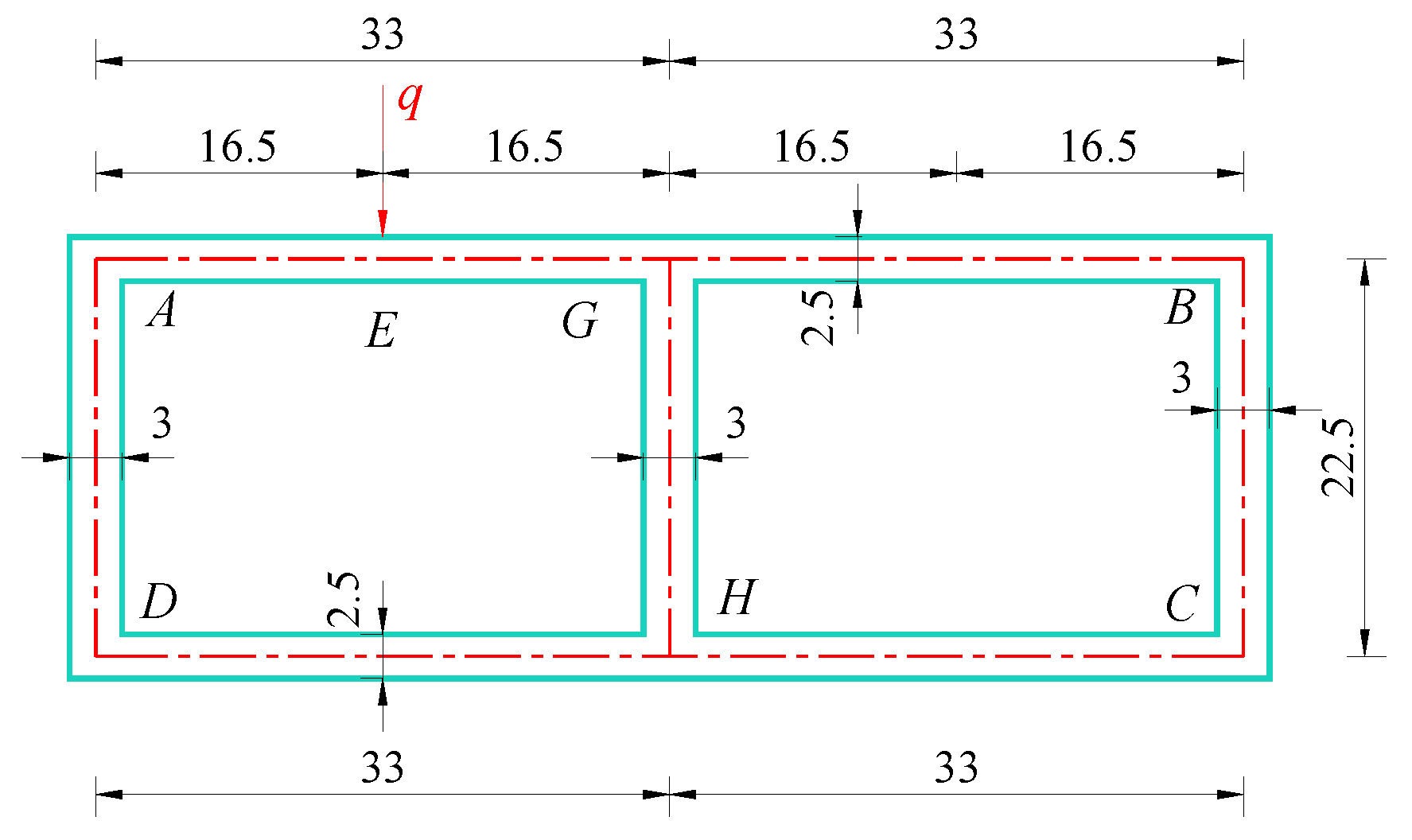
5.1. Numerical Example 1
5.2. Numerical Example 2
6. Parameter Analysis
7. Conclusions
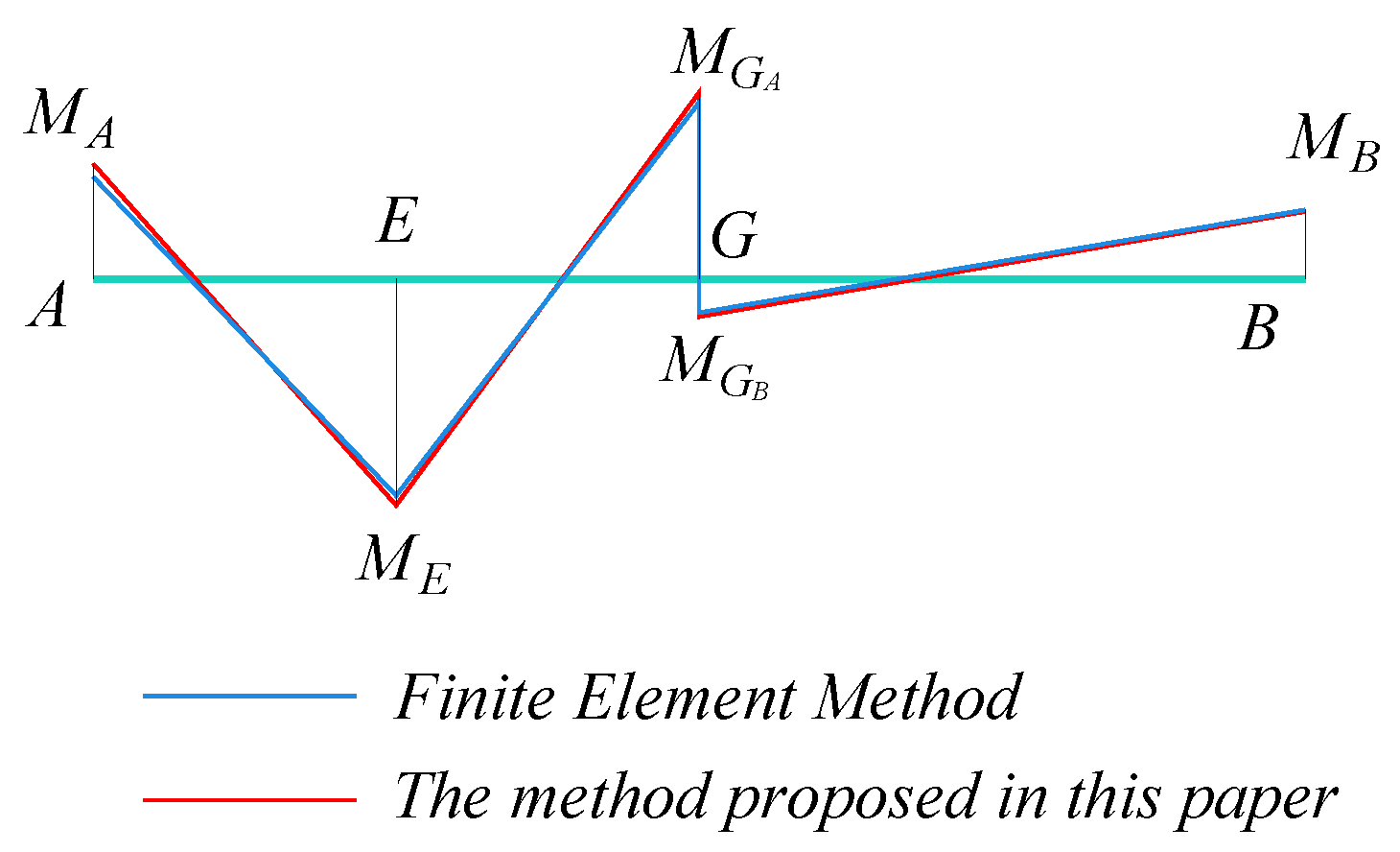
- This study employs frame analysis to systematically explore the structural behavior of twin-cell inclined web box girders. A generalized formula is derived to compute the transverse internal forces resulting from both symmetric and anti-symmetric distortion modes. Validation through case studies demonstrates a strong correlation between the proposed formula and finite element analysis (FEA) results, with relative errors consistently maintained below 7%.
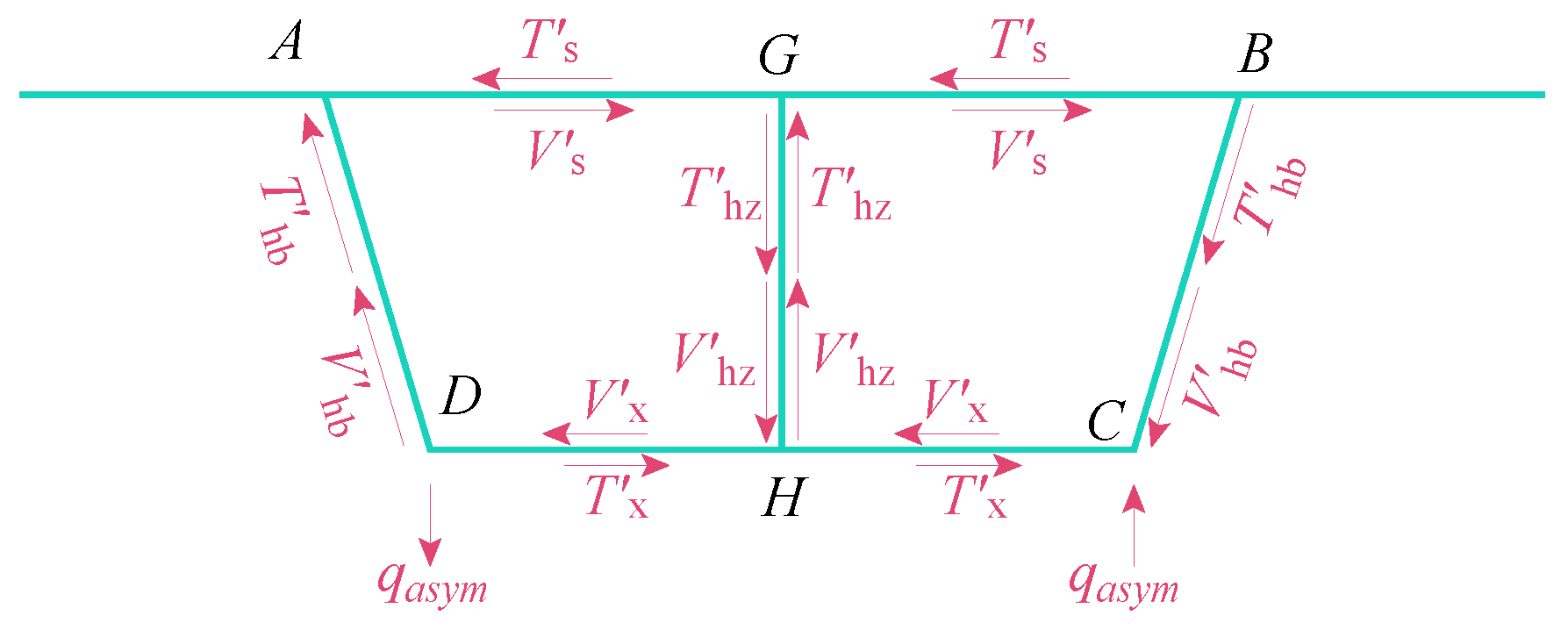
- During the release of virtual support loads, three primary deformation modes are identified: torsion, distortion, and bending. Among these, the transverse internal forces in the box girder are predominantly influenced by torsion and distortion modes, with the distortion mode not directly affecting transverse internal forces in the mid-web. In the case studies presented in this paper, while the distortion mode induces tension-compression effects on the top and bottom slabs distinct from those of the torsion mode, the transverse force magnitudes in both modes remain comparable. As the load application point approaches the mid-web, the impact of the distortion mode becomes increasingly significant.
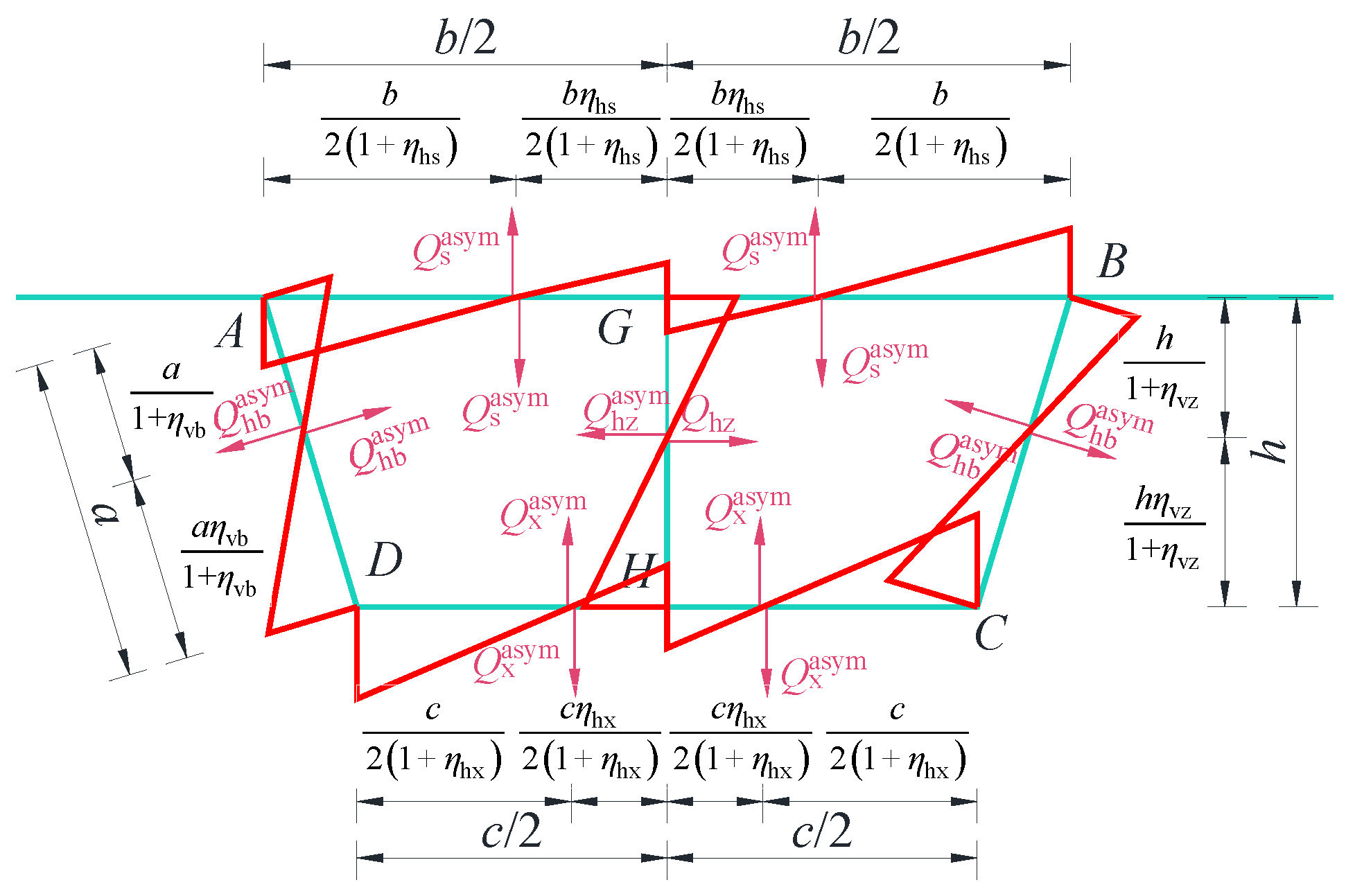
- This study systematically investigates the distribution patterns of transverse internal force inflection points in single-box, twin-cell box girders with inclined webs under torsion mode and distortion mode. The findings indicate that the widely accepted assumption of placing the transverse bending moment inflection point at the center of the single-side top plate is inaccurate. Instead, the position of the inflection point is shown to be significantly influenced by the relative stiffness of individual plate components, necessitating a more holistic consideration of stiffness distribution in engineering design.
- For engineering design purposes, when calculating the transverse internal force of single-box twin-cell box girder with inclined web, it is possible to estimate by using the rectangular section with the same top slab, and the transverse internal force has a considerable safety reserve. However, the influence of the thickness of the middle web plate on transverse internal forces requires special attention. When the middle web thickness is smaller than that of the side web, significant variations in transverse internal forces occur at the calculation points. As the thicknesses become equal, the fluctuations in transverse internal forces stabilize. Further increasing the central web thickness causes no notable changes in the transverse internal forces at each point. For detailed design, the calculation method in this paper can be required.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
| Load Mode | Parameter | Meaning | Unit |
|---|---|---|---|
| Torsion | torsional shear force difference | kN·m/m | |
| anti-symmetric distortion shear difference | kN·m/m | ||
| shear force at the inflection points of bending moment on the simplified structure | kN·m/m | ||
| shear force at the inflection points of bending moment on the unit-length frame | kN·m/m | ||
| The proportion coefficient of the plate lengths on both sides of the inflection point | / | ||
| The coordination proportional coefficient of distortion displacement | / | ||
| Distortion | symmetric distortion shear difference | kN·m/m | |
| shear force at the inflection points of bending moment on the simplified structure | kN·m/m | ||
| shear force at the inflection points of bending moment on the unit-length frame | kN·m/m | ||
| The proportion coefficient of the plate lengths on both sides of the inflection point | / | ||
| The coordination proportional coefficient of distortion displacement | / |
References
- Li, H. Review on Special Issues in Prestressed Concrete Box Girders with Corrugated Steel Webs. J. Basic Sci. Eng. 2018, 26, 440–454. (In Chinese) [Google Scholar]
- Maguire, M.; Moen, C.D.; Roberts-Wollmann, C.; Cousins, T. Field Verification of Simplified Analysis Procedures for Segmental Concrete Bridges. J. Struct. Eng. 2014, 141, D4014007. [Google Scholar] [CrossRef]
- Kurian, B.; Menon, D. Correction of Errors in Simplified Transverse Bending Analysis of Concrete Box-Girder Bridges. J. Bridge Eng. 2005, 10, 650–657. [Google Scholar] [CrossRef]
- Guo, J.; Zheng, Z. Analysis of Transverse Internal Forces in Box Girder Bridges with Cantilevers. China Civ. Eng. J. 1986, 3, 59–72. (In Chinese) [Google Scholar]
- He, J.; Zhang, Y.; Huang, H. Research on Modification Factor of Transverse Internal Force of Thin-walled Box Girder considering Distortion Effect. J. China Railw. Soc. 2022, 44, 140–146. (In Chinese) [Google Scholar]
- Wang, Z. Investigation of the transverse internal force of a box girder using the energy variational principle. Gradevinar 2024, 76, 235–245. [Google Scholar]
- Zhou, M.; Zhang, J.; Yang, D.; Hassanein, M.F.; An, L. Transverse Analysis of a Prestressed Concrete Wide Box Girder with Stiffened Ribs. J. Bridge Eng. 2017, 22, 4017046. [Google Scholar] [CrossRef]
- Shushkewich, W. Transverse Analysis of Strutted Box Girder Bridges. J. Bridge Eng. 2006, 11, 33–47. [Google Scholar]
- Xu, F.; Cheng, Y.; Wang, K.; Zhou, M. Transverse Analysis of Box Girders with Corrugated Steel Webs. Buildings 2024, 14, 574. [Google Scholar] [CrossRef]
- Choi, Y.; Oh, B. Transverse Modeling of Concrete Box-Girder Bridges for Prediction of Deck Slab Ultimate Load Capacity. J. Bridge Eng. 2013, 18, 1373–1382. [Google Scholar] [CrossRef]
- Park, N.; Choi, S.; Kang, Y. Exact distortional behavior and practical distortional analysis of multi cell box girders using an expanded method. Comput. Struct. 2005, 83, 1607–1626. [Google Scholar]
- Razaqpur, A.; Li, H. Thin-Walled Multi cell Box-Girder Finite Element. J. Struct. Eng. 1991, 117, 2953–2971. [Google Scholar] [CrossRef]
- Wei, Y.H.; Zhang, Y.H. Analysis on distortion effect of twin-cell box girders with inclined side webs based on finite beam-segment element. Thin-Walled Struct. 2025, 212, 113137. [Google Scholar] [CrossRef]
- Li, X.; Li, L.; Zhou, M.; Wan, S.; Chen, J.; Kang, A. Refined beam finite element model for thin-walled multi-cell box girders considering distortion and secondary distortional moment deformation effect. Eng. Struct. 2024, 298, 117042. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, C.; Zhang, X.; Li, Y. Exact distortional behavior of single-box multi cell curved composite box girders with corrugated steel webs in the elastic stage. Eng. Struct. 2023, 297, 116961. [Google Scholar] [CrossRef]
- Chithra, J.; Praveen, N.; Sajith, A. Transverse Bending Analysis of Twin-Cell Concrete Box Girder Bridges Using Simplified Frame Analysis. Pract. Period. Struct. Des. Constr. 2023, 28, 1–9. [Google Scholar]
- Chithra, J.; Nagarajan, P.; Sajith, A. Simplified method for the transverse bending analysis of twin celled concrete box girder bridges. IOP Conf. Ser. Mater. Sci. Eng. 2018, 330, 012118. [Google Scholar] [CrossRef]
- Zhao, P.; Ye, J. Transverse force study of single box multi-chamber with corrugated steel webs. J. Harbin Eng. Univ. 2018, 39, 1109–1115. (In Chinese) [Google Scholar]
- Wang, Z.; Zhang, Y. Research on Transverse Internal Force of Single Box Double Cell Composite Box Girder with Corrugated Steel Webs. J. China Railw. Soc. 2019, 41, 106–112. (In Chinese) [Google Scholar]
- Zhang, S.H. The Finite Element Analysis of Thin-Walled Box Spine-Beam Bridges; University of London: London, UK, 1982. [Google Scholar]





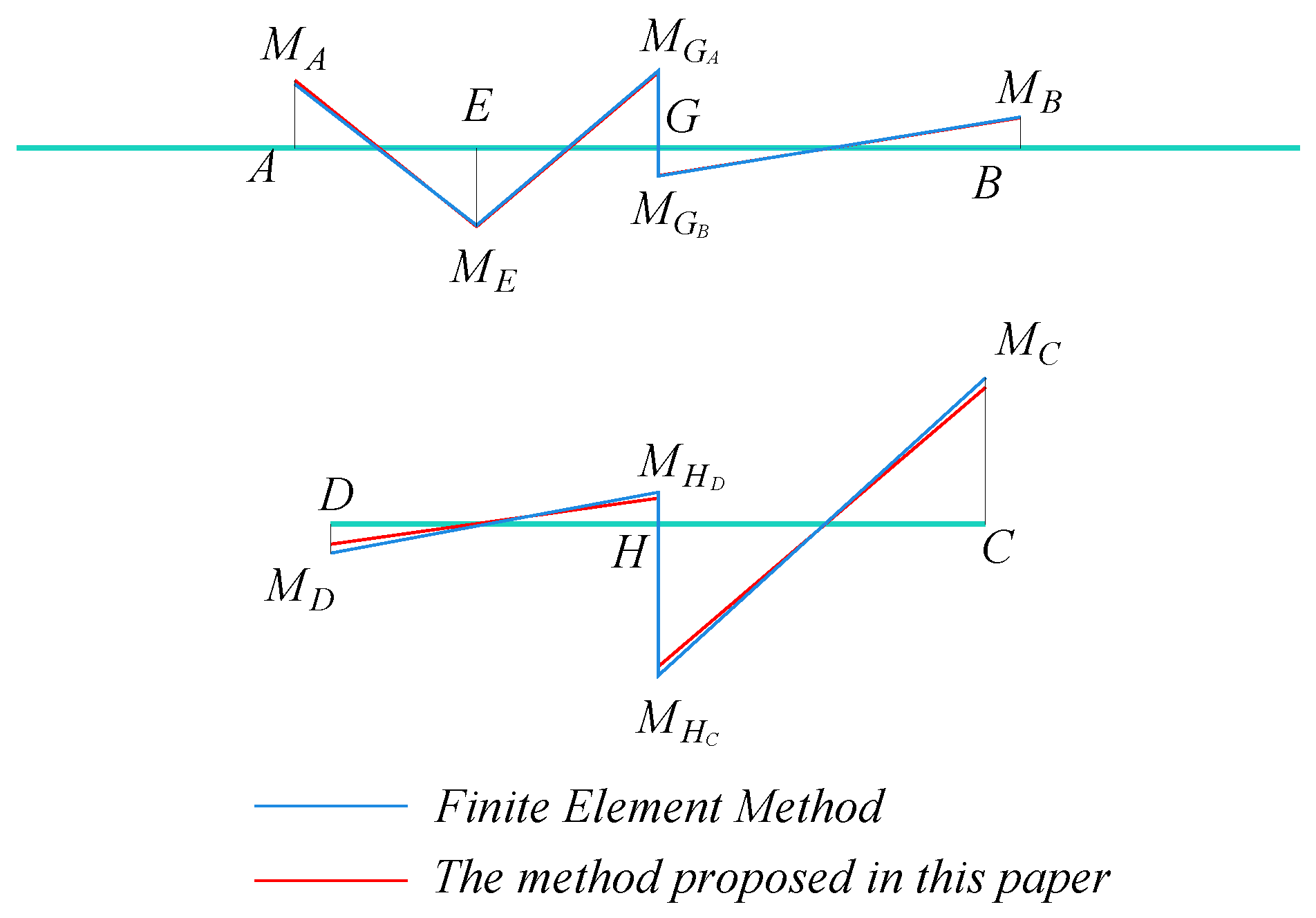
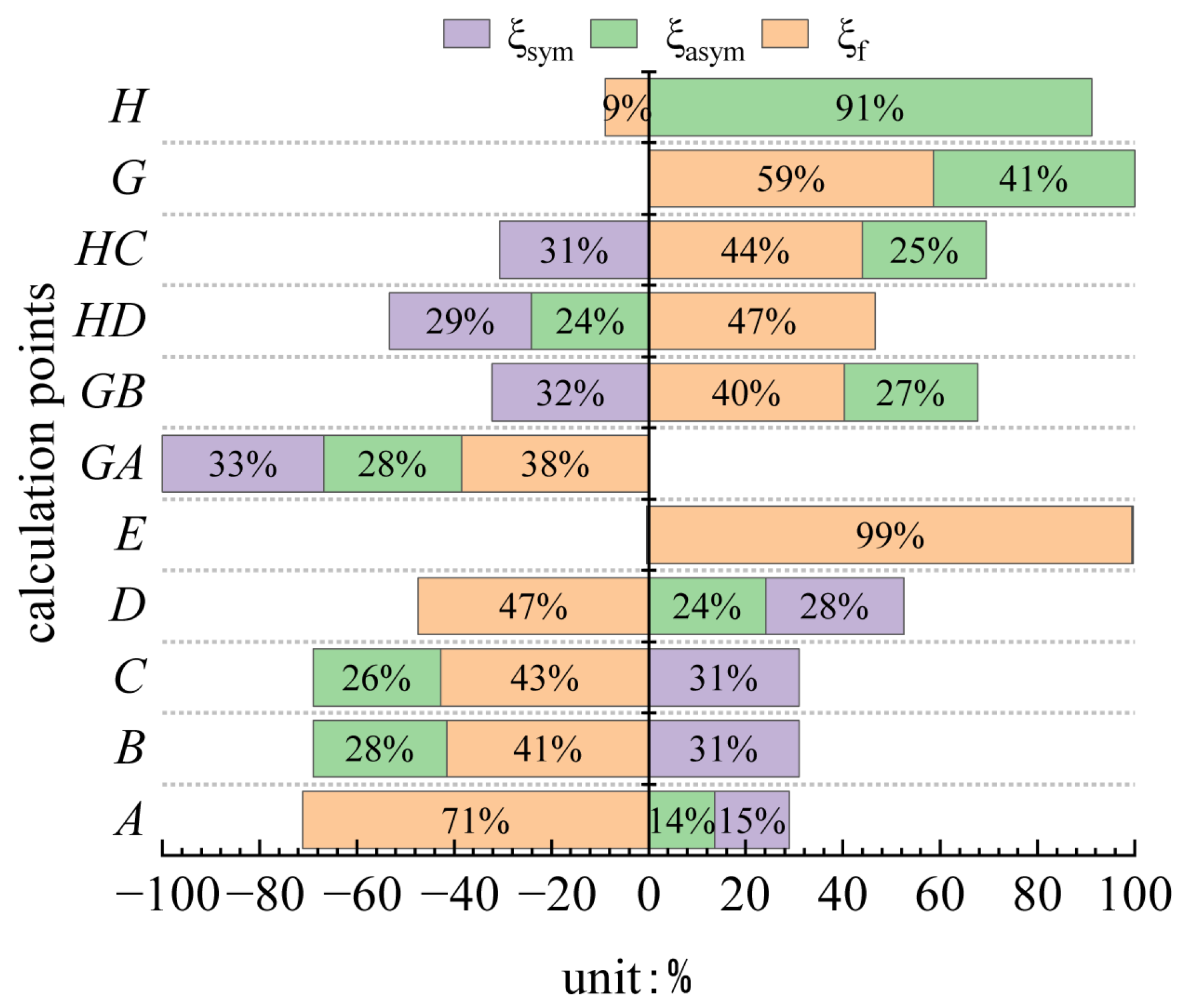
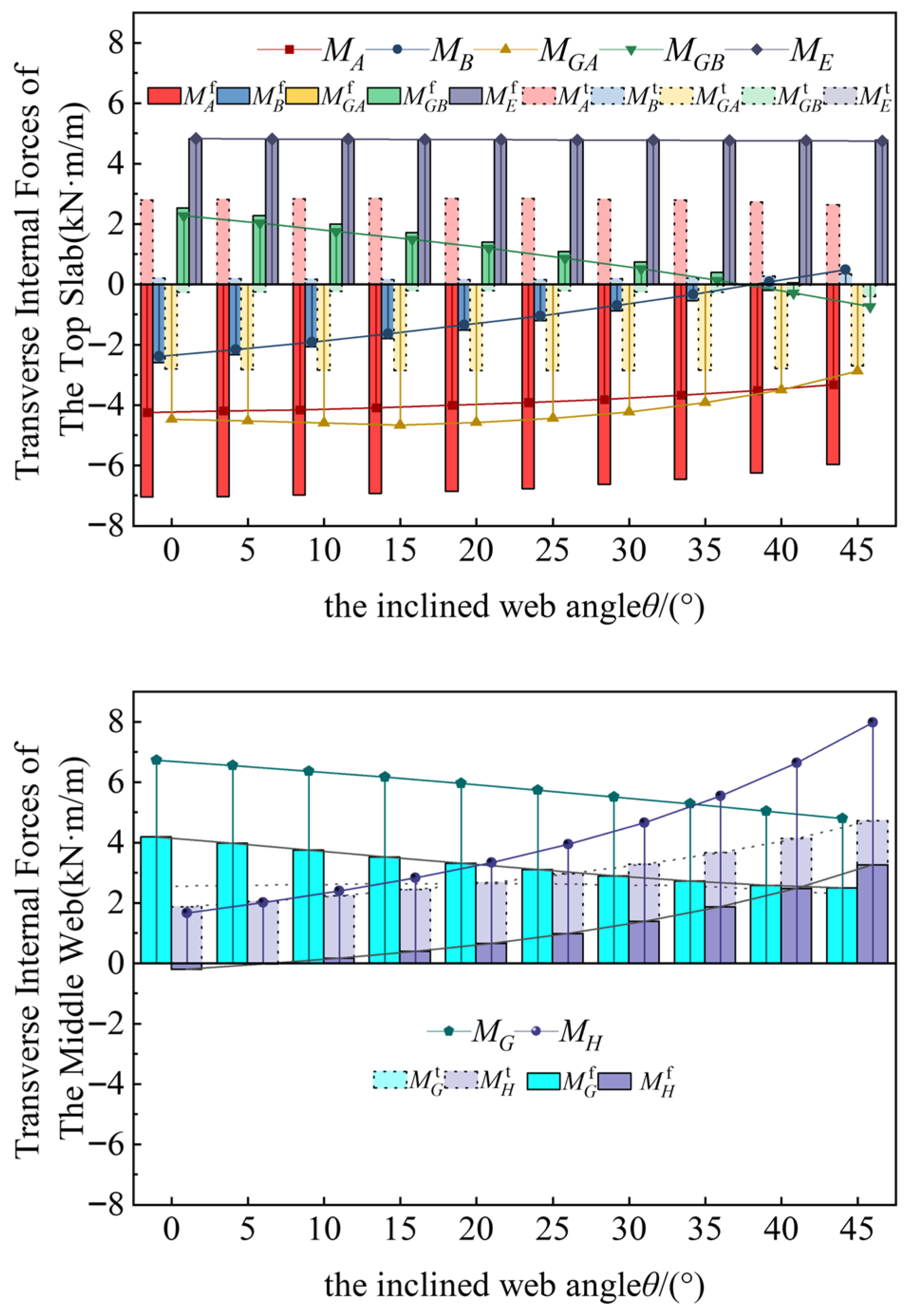

| Proportional Coefficients | Calculated Value | Proportional Coefficients | Calculated Value |
|---|---|---|---|
| ηhs | 0.8959 | ζhs | 1.1315 |
| ηhx | 0.8958 | ζhx | 1.1315 |
| ηvb | 1 | ζvb | 1 |
| ηvh | 1 | ζsym | 0.2064 |
| ηasym | 0.3823 |
| Key Points | M | δ | ||||
|---|---|---|---|---|---|---|
| A | −0.4886 | 0.1084 | 0.1285 | −0.2517 | −0.2230 | 12.9 |
| B | −0.1671 | −0.1084 | 0.1285 | −0.1470 | −0.1509 | −2.6 |
| E | 0.4981 | 0.0057 | −0.0084 | 0.4954 | 0.4743 | 4.4 |
| GA | −0.1652 | −0.0971 | −0.1453 | −0.4076 | −0.3857 | 5.7 |
| GB | 0.1312 | 0.0971 | −0.1453 | 0.083 | 0.0741 | 12.0 |
| Proportional Coefficients | Calculated Value | Proportional Coefficients | Calculated Value |
|---|---|---|---|
| ηhs | 0.9790 | ζhs | 1.0223 |
| ηhx | 0.9875 | ζhx | 1.0138 |
| ηvb | 0.8653 | ζvb | 0.9076 |
| ηvh | 0.8728 | ||
| 0.0963 × 103 | 0.0982 × 103 | ||
| 0.9154 × 103 | 3.2679 × 103 |
| Key Points | M | δ | ||||
|---|---|---|---|---|---|---|
| A | −6.9686 | 1.3357 | 1.5003 | −4.1326 | −3.8940 | 6.13 |
| B | −2.0060 | −1.3357 | 1.5003 | −1.8414 | −1.8877 | −2.45 |
| C | −1.8769 | −1.1557 | 1.3617 | −1.6709 | −1.7883 | −6.56 |
| D | −2.2709 | 1.1557 | 1.3617 | 0.2465 | 0.3554 | −30.64 |
| E | 4.8057 | 0.0141 | −0.0168 | 4.8030 | 4.7380 | 1.37 |
| GA | −1.7699 | −1.3076 | −1.5338 | −4.6113 | −4.7127 | −2.15 |
| GB | 1.9208 | 1.3076 | −1.5338 | 1.6946 | 1.7205 | −1.51 |
| HD | 2.2055 | −1.1413 | −1.3805 | −0.3163 | −0.3883 | −18.55 |
| HC | 1.9840 | 1.1413 | −1.3805 | 1.7448 | 1.8546 | −5.92 |
| G | −3.6907 | −2.6152 | 0 | −6.3059 | −6.4517 | −2.26 |
| H | −0.2215 | 2.2826 | 0 | 2.0611 | 2.1841 | −5.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Zhou, F.; Zhang, Y.; Zhang, Y.; Wei, Y. Analytical Calculation Method for Transverse Internal Force of Single-Box Double-Cell Box Girder with Inclined Webs Considering the Influence of Distortion Resistance Stiffness. Buildings 2025, 15, 4478. https://doi.org/10.3390/buildings15244478
Yu J, Zhou F, Zhang Y, Zhang Y, Wei Y. Analytical Calculation Method for Transverse Internal Force of Single-Box Double-Cell Box Girder with Inclined Webs Considering the Influence of Distortion Resistance Stiffness. Buildings. 2025; 15(24):4478. https://doi.org/10.3390/buildings15244478
Chicago/Turabian StyleYu, Jianbo, Fucheng Zhou, Yuanhai Zhang, Yuyuan Zhang, and Yanhong Wei. 2025. "Analytical Calculation Method for Transverse Internal Force of Single-Box Double-Cell Box Girder with Inclined Webs Considering the Influence of Distortion Resistance Stiffness" Buildings 15, no. 24: 4478. https://doi.org/10.3390/buildings15244478
APA StyleYu, J., Zhou, F., Zhang, Y., Zhang, Y., & Wei, Y. (2025). Analytical Calculation Method for Transverse Internal Force of Single-Box Double-Cell Box Girder with Inclined Webs Considering the Influence of Distortion Resistance Stiffness. Buildings, 15(24), 4478. https://doi.org/10.3390/buildings15244478








