Seismic Reliability Analysis of Reinforced Concrete Arch Bridges Considering Component Correlation

Abstract

To more effectively account for the correlation between components in the seismic reliability analysis of reinforced concrete arch bridges, this study proposes a system seismic reliability analysis method based on the D-vine Copula function. First, based on the theories of seismic vulnerability and hazard, the seismic vulnerability curves of key components (arch ring, piers, main girder, columns) and the site hazard curves are obtained. Second, a trial algorithm is used to determine alternative combinations of Pair-Copula functions. The maximum likelihood estimation method is employed to solve for the parameter θ, and the optimal Pair-Copula function is selected based on AIC and BIC information criteria. The optimal Pair-Copula function for each layer in the D-vine structure is determined through hierarchical iteration, ultimately constructing a seismic reliability evaluation framework for arch bridge systems that incorporates component correlations. The results show that the damage probability of the arch ring is consistently the highest, followed by the piers and main girder, with the columns having the lowest probability. Compared to ignoring component correlation, the seismic reliability indices of the system under minor, moderate, severe damage, and complete failure states all decrease when correlation is considered, indicating that component correlation significantly affects system reliability. Ignoring correlation leads to an overestimation of the system’s seismic performance. The seismic reliability indices obtained by the D-vine Copula method and Monte Carlo simulation are in good agreement, with a maximum relative error not exceeding 2.26%, verifying the applicability and accuracy of the D-vine Copula method in the reliability analysis of complex structural systems. By constructing an accurate joint probability distribution model, this study effectively accounts for the nonlinear correlation characteristics between components. Compared to the traditional Monte Carlo simulation, which relies on large-scale repeated sampling, the D-vine Copula method significantly reduces computational complexity through analytical derivation, improving computational efficiency by over 80%.

1. Introduction

As critical nodes in transportation systems, the seismic performance of bridges directly affects post-earthquake traffic recovery and regional economic sustainability [1]. In China’s vast and complex geographical environment, reinforced concrete arch bridges are widely used in mountainous areas, gorges, and urban landscapes due to their excellent spanning capacity, reasonable mechanical performance, and cost-effectiveness [2]. However, their inherent arch structural characteristics lead to complex mechanical behavior under seismic action, posing significant failure risks in high-intensity seismic zones. Traditional seismic design and analysis methods based on single components or simplified assumptions may introduce systematic deviations in predicting the actual response of complex structural systems under real ground motions [3]. Therefore, conducting a seismic reliability analysis of reinforced concrete arch bridges that considers component correlations can provide a theoretical basis and technical support for optimizing their seismic design.

Research on the seismic performance of arch bridges has long relied on deterministic and probabilistic theoretical analyses [4,5,6,7,8]. Nguyen et al. [9] proposed a vulnerability analysis method based on multiple strip analysis, establishing an effective process for evaluating the seismic performance of modular underground arch Bridges and verifying its feasibility. Deng et al. [10] used ABAQUS software to model a certain RC arch bridge, measured the longitudinal and transverse seismic performance of the RC arch bridge under different intensities, discussed the seismic response of the bridge, and proposed a section safety factor to quantitatively describe the failure degree of the spring section under longitudinal excitation. Lei [11] applied IDA to study the seismic vulnerability of pile foundations in reinforced concrete arch bridges under scour conditions, providing vulnerability curves for different scour depths. These studies have significantly enriched the theoretical understanding of arch bridge seismic performance and provided important references for seismic design. However, deterministic analyses often depend on specific ground motion inputs and structural parameters, making it difficult to systematically quantify the combined effects of various random factors—such as ground motion randomness, material variability, and geometric uncertainties—on overall structural safety. Moreover, current probabilistic methods for seismic performance analysis of arch bridges rarely consider correlations between components.

In actual reinforced concrete arch bridges, key load-bearing components (e.g., different sections of arch ribs, piers, and columns) do not work independently; their seismic performances exhibit significant statistical correlations [12]. The damage evolution of one component (e.g., stiffness degradation) can alter the internal force redistribution path, affecting the stress state and failure probability of other components. This performance coupling, caused by load effect transmission, dynamically reflects the correlation in seismic performance among components [13]. Traditional seismic reliability analyses of arch bridges often treat components as statistically independent units or use simplified correlation models (e.g., assuming full correlation or independence) [14], which tends to overestimate system reliability. Internationally, the use of Copula functions, particularly flexible vine Copula constructions, has gained significant traction for modeling high-dimensional dependencies in structural system reliability analysis of various infrastructures, including offshore platforms, wind turbines, and frame buildings [15,16]. Concurrently, machine-learning-enhanced methods, such as those employing active learning Kriging or neural network surrogates, have emerged as powerful tools for handling computationally expensive reliability problems [17,18]. While these advanced probabilistic frameworks have been extensively applied in various fields, their tailored application to the seismic system reliability of reinforced concrete arch bridges, explicitly addressing their unique component interaction patterns, remains limited.

To address this, this study proposes a system seismic reliability analysis method that considers component correlations. First, based on seismic vulnerability and hazard theories, the seismic vulnerability curves of key components (arch ring, piers, main girder, columns) and the site hazard curve are obtained. Second, a trial algorithm is used to determine alternative Pair-Copula function combinations. The maximum likelihood estimation method is applied to solve for the parameter θ, and the optimal Pair-Copula function is selected based on AIC and BIC information criteria. The optimal Pair-Copula function for each layer in the D-vine structure is determined through hierarchical iteration, ultimately constructing a seismic reliability evaluation framework for arch bridge systems that incorporates component correlations. The proposed method is compared with cases ignoring component correlation and with Monte Carlo simulation results via an engineering example. While vine Copula methods have been employed for system reliability analysis of other bridge types, their application to RC arch bridges necessitates a tailored framework due to the distinct, non-hierarchical interaction among their primary components. This study contributes by: (1) proposing and validating a D-vine Copula model specifically adapted to capture the peer-to-peer correlation structure typical of arch bridge systems; (2) integrating this model within a comprehensive seismic reliability framework encompassing nonlinear dynamic analysis, hazard analysis, and uncertainty quantification; and (3) deriving new quantitative insights into the system-level seismic performance and correlation sensitivity of RC arch bridges, supported by a detailed engineering case study.

2. Seismic Reliability Analysis

Bridge seismic reliability refers to the probability that a bridge structure maintains its intended function during its design service life under potential seismic actions. Its core lies in quantifying bridge safety under earthquakes through probabilistic methods. The performance function for bridge seismic reliability can be characterized by seismic capacity and seismic demand, as shown in Equation (1) [19]:

$$Z=C-D$$

(1)

where Z, C, and D represent the structural seismic reliability performance function, seismic capacity, and seismic demand, respectively.

Given the significant uncertainties in seismic action and structural seismic capacity, probabilistic methods are commonly used to quantify seismic reliability. The mathematical expression is given by Equation (2) [19]:

$$P_f={\displaystyle \sum P\left[C\le D\left|PGA=x\right.\right]}={\displaystyle \int F_R}\left(x\right)\left|dH\left(x\right)\right|$$

(2)

where P_f is the seismic failure probability; F_R(x), H(x) are the seismic hazard function and seismic vulnerability function, respectively; PGA is the peak ground acceleration.

2.1. Seismic Hazard Analysis

Seismic hazard analysis aims to quantitatively assess the probability of different intensity seismic disasters occurring in a specific region over a certain future period. Existing research [20] shows that the probability distribution of the maximum seismic intensity in mainland China over the next 50 years follows a Type III extreme value distribution. The probability distribution of seismic intensity over 50 years, F₅₀(i), can be expressed as:

$$F_{50}\left(i\right)=\exp \left[-{\left({\displaystyle \frac{w-i}{w-\epsilon }}\right)}^k\right]$$

(3)

where i, w are the seismic intensity and upper intensity limit, respectively, w = 12; k is the shape parameter derived from regional seismic activity statistics; ε is the mode of seismic intensity, ε = I₀ − 1.55, where I₀ is the design fortification intensity.

The adoption of the Type III extreme value distribution (Weibull distribution) for F₅₀(i) is a well-established model in probabilistic seismic hazard analysis for mainland China. This choice is empirically supported by statistical fits to historical seismic intensity data and is widely used in regional seismic hazard studies and the development of Chinese seismic zoning maps [21,22]. The distribution is particularly appropriate as it has an upper bound (w = 12), which aligns with the physical limit of seismic intensity. The parameters (k, ε) can be calibrated to regional seismicity characteristics; the relationship ε = I₀ − 1.55 follows from established empirical correlations derived from Chinese intensity records [20].

The seismic hazard function H(x) can be expressed as:

$$H\left(x\right)=\exp \left[-{\displaystyle \frac{T_M}{50}}{\left({\displaystyle \frac{w-i}{w-\epsilon }}\right)}^k\right]=\exp \left\{-{\displaystyle \frac{T_M}{50}}{\left[{\displaystyle \frac{w-\left(\frac{\lg x+2.115}{\lg x}\right)}{w-\epsilon }}\right]}^k\right\}$$

(4)

where T_M is the design service life of the bridge.

2.2. Seismic Vulnerability Analysis

Bridge seismic vulnerability refers to the probability of a bridge structure experiencing specific damage states (e.g., minor damage, severe damage, or collapse) under different intensity seismic actions, reflecting the bridge’s sensitivity and resistance to seismic effects. Its mathematical expression is:

$$P_f=P\left[D\ge C\left|IM\right.\right]$$

(5)

where IM is the ground motion intensity measure. In this study, Peak Ground Acceleration (PGA) is adopted as the intensity measure (IM) for seismic reliability analysis. While it is recognized that Peak Ground Velocity (PGV) or spectral accelerations at fundamental periods (e.g., Sa(T₁)) might exhibit better correlation with the displacement-dependent responses of certain bridge components, PGA was selected primarily for its widespread availability in ground motion databases (e.g., NGA-West2 used herein) and its established use in probabilistic seismic hazard analysis (PSHA). This choice facilitates the efficient generation of a large number of analysis scenarios required for the system-level reliability assessment and the construction of vulnerability curves. The primary focus of this study is on the methodological framework for incorporating component correlations, and the proposed D-vine Copula approach is general and can be adapted to other IMs if deemed more appropriate for specific structural types or failure modes.

The relationship between the mean seismic demand, S_D and IM can be expressed as [19]:

$$S_D=a\cdot I{M}^b$$

(6)

where a and b are determined via linear regression on the logarithms of the median engineering demand parameter (S_D) and the intensity measure (IM) obtained from the ensemble of nonlinear time-history analyses.

The seismic vulnerability function can be further derived as:

$$F_R\left(x\right)=P\left[D\ge C\left|IM\right.\right]=\Phi \left[{\displaystyle \frac{\ln \left(S_D/S_C\right)}{\sqrt{{\beta }_c^2+{\beta }_d^2}}}\right]=\Phi \left[{\displaystyle \frac{\ln \left(a\ln x+b\right)-\ln S_C}{0.5}}\right]$$

(7)

where S_C is the mean seismic capacity.

3. Vine Copula Theory

Vine Copula is a flexible method for modeling multivariate dependency structures. It constructs high-dimensional joint distributions by hierarchically combining multiple bivariate Copulas (Pair-Copulas). The core idea is to decompose complex multivariate dependencies into a series of conditional bivariate dependencies, essentially forming a hierarchical structure of Pair-Copulas.

3.1. Pair-Copula Functions

Assume the joint density function of a multidimensional random variable is f(x₁, x₂, …, x_n). According to the conditional density function theory:

$$f\left(x_1,x_2,\cdots ,x_n\right)=f_n\left(x_n\right)f\left(x_{n-1}\left|x_n\right.\right)f\left(x_{n-2}\left|x_{n-1},x_n\right.\right)\cdots f\left(x_1\left|x_2,\cdots ,x_n\right.\right)$$

(8)

Using the chain rule, it can be derived that:

$$f\left(x_1,x_2,\cdots ,x_n\right)=c_{1\cdots n}\left[F_1\left(x_1\right),F_2\left(x_2\right),\cdots ,F_n\left(x_n\right);\theta \right]\cdot f_1\left(x_1\right)\cdots f_n\left(x_n\right)$$

(9)

where $c_{1\cdots n}\left[F_1\left(x_1\right),F_2\left(x_2\right),\cdots ,F_n\left(x_n\right);\theta \right]$ is the Pair-Copula density function, θ is the Copula parameter, and common Pair-Copula functions and their parameter ranges are listed in

Table 1. The function expressions and parameter values of commonly used pair-Copula functions.

Copula	Copula Function Expression c = (u1,u2;θ)	Generator φ(t)	Parameter Range θ
Gaussian Copula	${\Phi }_{\theta }\left[{\Phi }^{-1}\left(u_1\right),{\Phi }^{-1}\left(u_2\right)\right]$	/	(−1, 1)
Clayton Copula	${\left(u_1^{-\theta }+u_2^{-\theta }-1\right)}^{-1/\theta }$	${\displaystyle \frac{1}{\theta }}\left(t^{-\theta }-1\right)$	(0, +∞)
Gumbel Copula	$\exp \left\{-{\left[{\left(-\ln u_1\right)}^{\theta }+{\left(-\ln u_2\right)}^{\theta }\right]}^{1/\theta }\right\}$	${\left(-\ln t\right)}^{\theta }$	[1, +∞)
Frank Copula	$-{\displaystyle \frac{1}{\theta }}\ln \left[1+{\displaystyle \frac{\left(e^{-\theta u_1}-1\right)\cdot \left(e^{-\theta u_2}-1\right)}{e^{-\theta }-1}}\right]$	$-\ln {\displaystyle \frac{e^{-\theta t}-1}{e^{-\theta }-1}}$	(-∞, +∞)\{0}

[23]; and $F_n\left(x_n\right)$ are $f_n\left(x_n\right)$ the marginal distribution function and marginal density function of the i-th random variable, respectively.

Assume a three-dimensional random variable X = (x₁, x₂, x₃). Its joint probability density function can be decomposed as:

$$f\left(x_1,x_2,x_3\right)=f\left(x_1\left|x_2\right.,x_3\right)\cdot f\left(x_2\left|x_3\right.\right)\cdot f\left(x_3\right)$$

(10)

According to Sklar’s theorem:

$$f\left(x_2\left|x_3\right.\right)={\displaystyle \frac{f\left(x_2,x_3\right)}{f\left(x_3\right)}}=c_{23}\left[F_2\left(x_2\right),F_3\left(x_3\right)\right]f_2\left(x_2\right)$$

(11)

$$f\left(x_1\left|x_2\right.,x_3\right)={\displaystyle \frac{f\left(x_1,x_3\left|x_2\right.\right)}{f\left(x_3\left|x_2\right.\right)}}=c_{13\left|2\right.}\left[F\left(x_1\left|x_2\right.\right),F\left(x_3\left|x_2\right.\right)\right]f\left(x_1\left|x_2\right.\right)$$

(12)

Further:

$$\begin{array}{ll}f\left(x_1,x_2,x_3\right)=& c_{13\left|2\right.}\left[F\left(x_1\left|x_2\right.\right),F\left(x_3\left|x_2\right.\right)\right]\cdot c_{12}\left[F_1\left(x_1\right),F_2\left(x_2\right)\right]\\ & \cdot c_{23}\left[F_2\left(x_2\right),F_3\left(x_3\right)\right]\cdot f\left(x_3\right)\cdot f\left(x_2\right)\cdot f\left(x_1\right)\end{array}$$

(13)

Equations (10)–(13) illustrate the construction of Pair-Copula functions. As shown in Equation (13), a three-dimensional Copula joint distribution function can be decomposed into a product of conditional bivariate Copula functions and marginal Copula functions. The decomposition process is non-unique, leading to multiple possible decomposition forms for Pair-Copula functions.

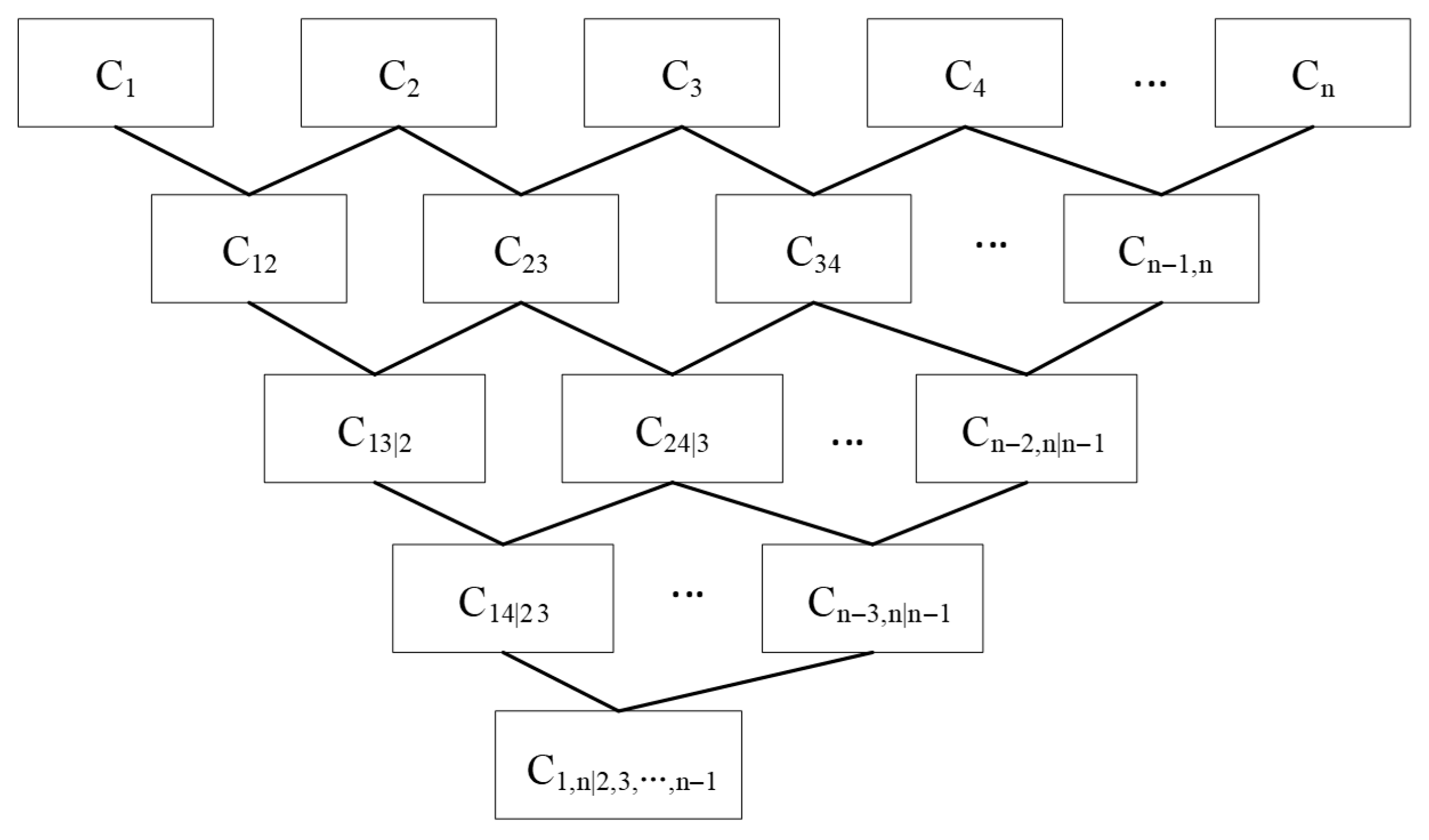
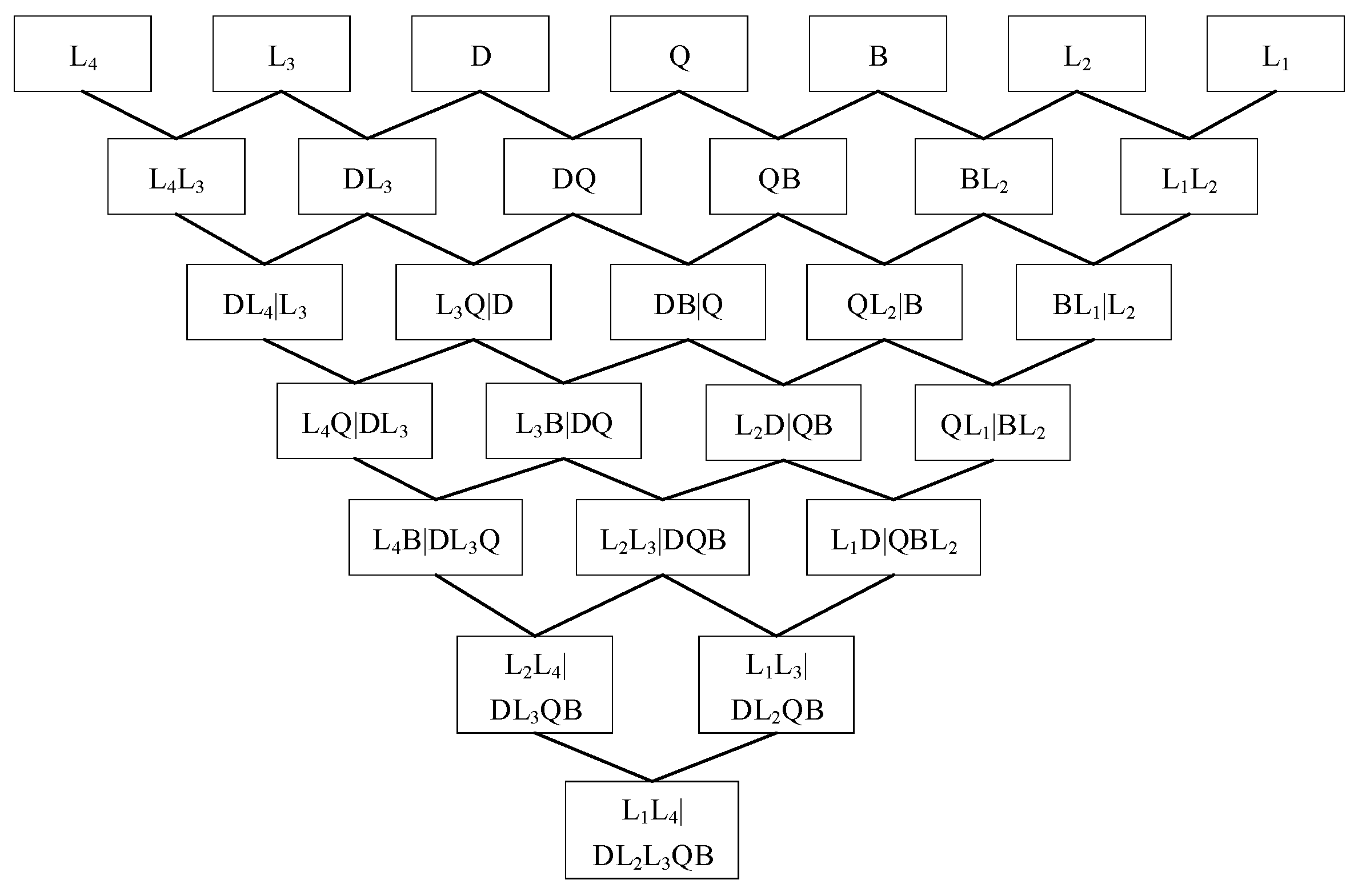
3.2. Vine Copula

Traditional multivariate Copula functions are constrained by structural singularity when constructing joint distributions, requiring all random variables to follow the same dependency structure. This makes it difficult to accurately capture complex bivariate correlation characteristics within multidimensional systems. Vine Copula, based on graph theory and Pair-Copula decomposition principles, achieves a full decomposition representation of high-dimensional joint distributions by hierarchically constructing conditional probability density functions. Among various decomposition architectures, C-vine and D-vine have significant application value due to their clear tree-like topological rules [24]. This study selects the D-vine structure, which suits the non-hierarchical correlation characteristics of the seismic reliability of bridge components (i.e., peer-to-peer relationships among component failure modes), to establish a multi-component vulnerability dependency model. The structural logic is shown in Figure 1. The diagram illustrates the hierarchical decomposition of a 4-variable joint distribution into a cascade of bivariate Pair-Copula functions (C). Variables (e.g., Q, B, D, L₄ representing bridge components) are arranged in a specific order, with dependencies modeled conditionally in successive trees, providing a flexible framework for capturing complex, non-hierarchical correlations.

The joint probability density function of the D-vine Copula can be expressed as:

$$f\left(x_1,x_2,\cdots ,x_n\right)={\displaystyle \prod _{k=1}^n{f}_k\left(x_k\right)}\cdot {\displaystyle \prod _{i=1}^{n-1}{\displaystyle \prod _{j=1}^{n-i}{c}_{i,i+j\left|j+1,\dots ,i+j-1\right.}\left[F\left(x_i\left|x_1,\dots ,x_{i-1}\right.\right),F\left(x_{i+j}\left|x_1,\dots ,x_{i-1}\right.\right)\right]}}$$

(14)

The conditional distribution function $F\left(x\left|u\right.\right)$ can be calculated by:

$$F\left(x\left|u\right.\right)={\displaystyle \frac{\partial C_{x,u_i\left|u_{-i}\right.}\left[F\left(x\left|u_{-i}\right.\right),F\left(u_i\left|u_{-i}\right.\right)\right]}{\partial F\left(u_i\left|u_{-i}\right.\right)}}$$

(15)

where u_i is a component of the d-dimensional vector.

3.3. Determining the Optimal Pair-Copula Function

Candidate Pair-Copula functions must first be screened. This study uses the Copula functions listed in Table 1 as candidates. In the parameter estimation stage, the maximum likelihood estimation method is used to optimize the parameter θ of the Pair-Copula function [25]. The likelihood function form for a random variable sample is:

$$L\left(\theta \right)={\displaystyle \prod _{i=1}^{n}c\left[F_1\left(x_{1,i}\right),F_2\left(x_{2,i}\right);\theta \right]}\cdot f_1\left(x_{1,i}\right)\cdot f_2\left(x_{2,i}\right)$$

(16)

Taking the logarithm of Equation (16):

$$\ln L\left(\theta \right)={\displaystyle \sum _{i=1}^n\ln }c\left[F_1\left(x_{1,i}\right),F_2\left(x_{2,i}\right);\theta \right]+{\displaystyle \sum _{i=1}^n\ln }{f}_1\left(x_{1,i}\right)+{\displaystyle \sum _{i=1}^n\ln }{f}_2\left(x_{2,i}\right)$$

(17)

Further, the Pair-Copula parameter θ can be obtained by:

$$\theta =\arg \max \ln L\left(\theta \right)$$

(18)

The parameter vector θ for each candidate Pair-Copula function is estimated by maximizing the log-likelihood function (Equation (17)) using numerical optimization techniques. This calibration process is performed independently for each bivariate pair at each tree level in the D-vine structure.

Among the candidate Pair-Copula models, the current mainstream optimization screening method is based on an information criterion evaluation framework. Specifically, by systematically calculating the Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) statistics for each candidate Copula function, the “minimum value preference principle” is used for model selection—i.e., when the AIC or BIC value of a Copula function reaches the global minimum in the candidate set, it is selected as the current optimal Pair-Copula function.

The expressions for AIC and BIC are given by Equations (19) and (20):

$$AIC=-2{\displaystyle \sum _{i=1}^N\ln C\left(u_{1i},u_{2i},\theta \right)}+2m$$

(19)

$$BIC=-2{\displaystyle \sum _{i=1}^N\ln C\left(u_{1i},u_{2i},\theta \right)}+m\ln N$$

(20)

where m is the number of Copula function parameters.

The trial algorithm enumerated all possible Pair-Copula functions from the four candidate families listed in Table 1 (Gaussian, Clayton, Gumbel, Frank) for each pair of variables in the D-vine structure. For each candidate, the parameter θ was estimated by maximizing the log-likelihood (Equation (17)) using a BFGS quasi-Newton optimization algorithm. The optimization was considered converged when the relative change in the log-likelihood value and the Euclidean norm of the parameter change between successive iterations both fell below 1 × 10⁻⁶. The AIC and BIC values were then computed for the converged model. The Pair-Copula function yielding the minimum AIC (and consistently, BIC) value among the four candidates was selected as the optimal model for that specific pair.

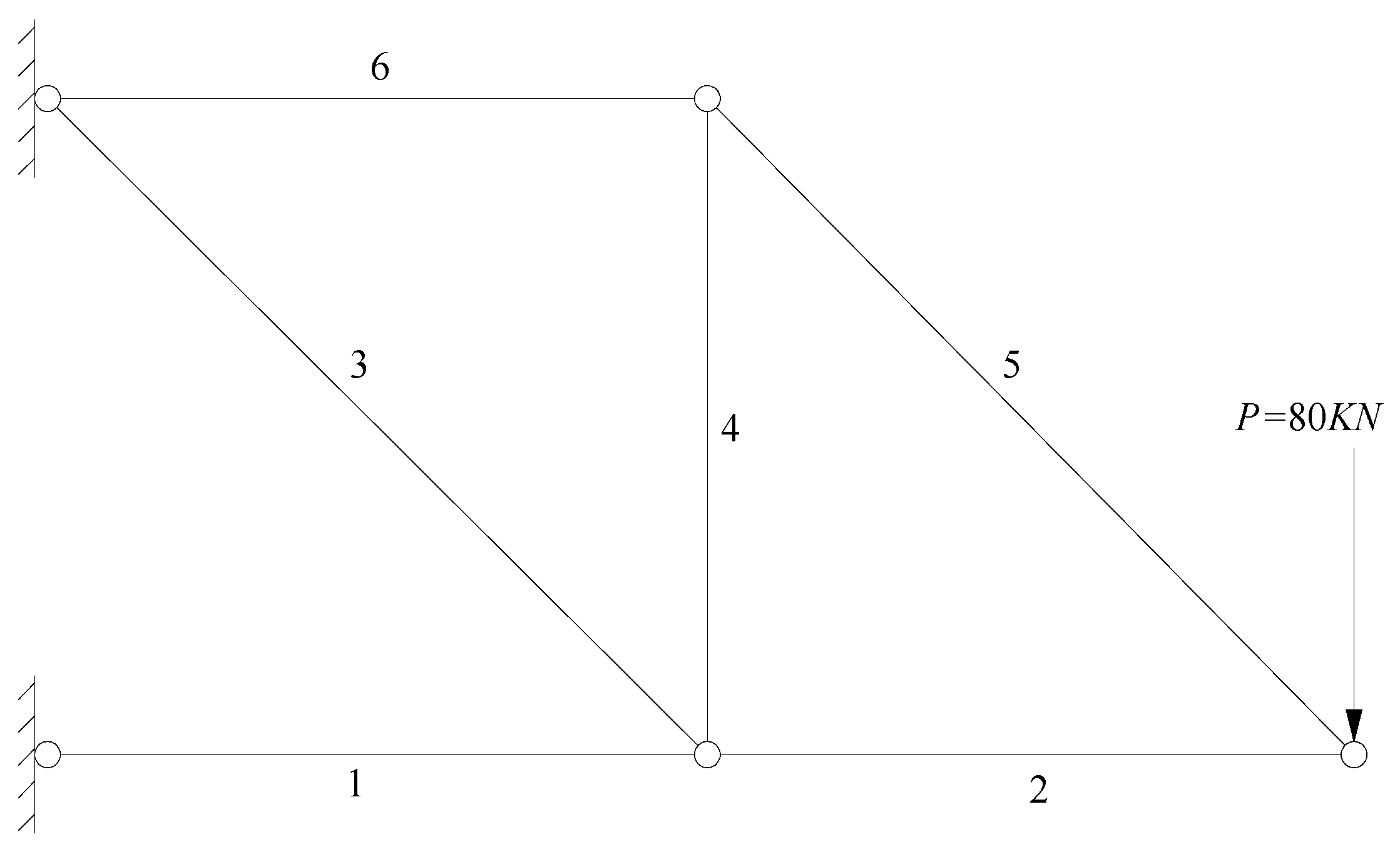
4. Example Verification

To verify the feasibility of the Copula method, a plane truss structure (Figure 2) is used as an example. Relevant parameter values are listed in

Table 2. Examples of structural parameters and statistical characteristics of plane truss.

Parameter Meaning	Probability Distribution	Mean	Coefficient of Variation
Member elastic modulus/MPa	Normal distribution	2 × 105	0.08
Length of members 1, 2, 4, 6/mm	Normal distribution	1 × 103	0.05
Length of members 3, 5/mm	Normal distribution	1.4 × 103	0.05
Cross-sectional area of members 2, 4, 6/mm2	Normal distribution	1 × 104	0.05
Cross-sectional area of members 1, 3, 5/mm2	Normal distribution	2 × 104	0.05
Concentrated load/N	Normal distribution	8 × 104	0.1

.

To evaluate the structural system reliability, a strain threshold of 0.05 is used as the failure criterion for members. A numerical model of the truss structure is established on the ANSYS 19.2 platform. The Monte Carlo simulation benchmark was obtained using 1 × 10⁶ random samples. The simulation was considered stable when the coefficient of variation in the failure probability estimate fell below 0.01. Comparing the results of the proposed method with Monte Carlo simulation shows that when the proposed method is executed 80 times, the obtained system failure probability is 83.37%; the benchmark value obtained from 1 × 10⁶ Monte Carlo samples is 81.95%. The absolute error between the two is only 1.42%, verifying the effectiveness and computational accuracy of the proposed method while significantly reducing computational costs under ensured engineering precision. The comparison results shown in Figure 3 visually demonstrate the good consistency between the two methods in failure probability distribution.

5. Engineering Example

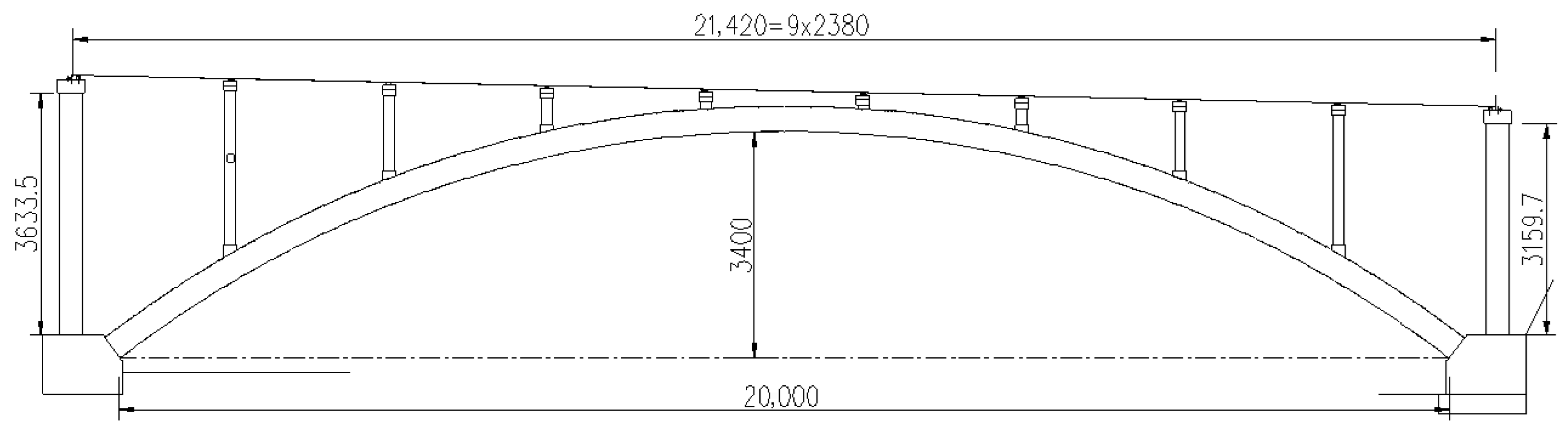
5.1. Engineering Background

This study takes a reinforced concrete arch bridge in China as the engineering background. The arch ring adopts a catenary reinforced concrete box section with a clear span of 210 m, a clear rise of 42 m, a rise-to-span ratio of 1/5.882, and an arch axis coefficient of 1.85. The main arch ring is a single-box double-chamber section with a single box width of 8.0 m and a box height of 3.8 m, using C55 concrete. The main girder uses C50 concrete, while the columns and piers use C40 concrete. The seismic basic intensity of the bridge site is VI degree, and seismic measures are taken for level 7. The general layout of the bridge is shown in Figure 4.

A three-dimensional mechanical model of the bridge structure is built using Midas Civil. The main girder, arch rib columns, and cap beams are discretized using spatial beam elements, while the arch ring structure is accurately described through shared node elements. The finite element model is shown in Figure 5. The reference model parameters of the reinforced concrete arch bridge in the case study are shown in

Table 3. Baseline model parameters for the case-study RC arch bridge.

Category	Parameter	Value/Description
Material Properties	C55 Concrete (Arch Ring)	fc = 55 MPa; E = 3.55 × 104 MPa; ν = 0.2; ρ = 2600 kg/m3
	C50 Concrete (Main Girder)	fc = 50 MPa; E = 3.45 × 104 MPa; ν = 0.2; ρ = 2600 kg/m3
	C40 Concrete (Piers & Columns)	fc = 40 MPa; E = 3.30 × 104 MPa; ν = 0.2; ρ = 2600 kg/m3
	Reinforcement Steel (HRB400)	Yield Strength fy = 400 MPa; E = 2.0 × 105 MPa
Boundary Conditions	Arch Springings	Fully fixed
	Pier Bases	Fully fixed
	Deck-Column Connections	Rigid connection (full moment transfer)
	Column-Arch Connections	Rigid connection
	Deck Expansion Joints	Released longitudinal translational DOF
Primary Loads (Static)	Self-weight	Automatically calculated by software
	Superimposed Dead Load	80 kN/m uniformly distributed on the deck

.

The nonlinear structural responses of the bridge under seismic excitation were computed through nonlinear time-history analysis (NLTHA). This method was employed to accurately capture the inelastic behavior and damage progression of key components under a suite of ground motion records. The finite element model in Midas Civil incorporated material nonlinearity to simulate this behavior. For concrete components, a nonlinear constitutive model accounting for cracking and crushing was adopted, while the reinforcement was modeled with a bilinear stress–strain curve considering kinematic hardening. The analysis solved the equations of motion step-by-step for each ground motion record, directly yielding the time-history responses (e.g., curvatures, moments, strains) from which the engineering demand parameters (EDPs) for vulnerability analysis were extracted.

Under seismic action, key components of the reinforced concrete arch bridge—including the arch ring, columns, main girder, and piers—exhibit high vulnerability. Based on structural system reliability analysis requirements, this study constructs a series system consisting of the arch ring (Q), main girder (B), columns, and piers. Considering the overall symmetry of the bridge and the large number of column components, the study focuses on the left half of the column system, with columns horizontally numbered L₁ to L₄, and the left pier defined as unit D, establishing a complete system failure mode analysis framework.

5.2. Uncertainty Analysis

Given the uncertainties in key parameters such as concrete elastic modulus, steel tensile strength, and structural geometric dimensions, and their non-negligible impact on structural seismic response characteristics, the seismic reliability assessment of reinforced concrete arch bridges must systematically consider the coupling effects of these parameter uncertainties on component performance degradation and overall system failure probability. The uncertainty characteristics and probability distribution forms of relevant parameters are listed in

Table 4. Structural parameters and distribution characteristics of reinforced concrete arch Bridges.

Random Variable	Distribution Type	Mean	Coefficient of Variation
C55 concrete elastic modulus E1/MPa	Normal distribution	3.55 × 104	0.10
C50 concrete elastic modulus E2/MPa	Normal distribution	3.45 × 104	0.10
C40 concrete elastic modulus E3/MPa	Normal distribution	3.3 × 104	0.10
Arch rib cross-sectional area A1/m2	Lognormal distribution	0.6322	0.05
Column cross-sectional area A2/m2	Lognormal distribution	1.7624	0.05
Main girder cross-sectional area A3/m2	Lognormal distribution	4.2861	0.05
Arch rib moment of inertia I1/m4	Lognormal distribution	0.02184	0.05
Main girder moment of inertia I2/m4	Lognormal distribution	3.1347	0.05

[26,27,28].

To systematically evaluate the dual uncertainties of structural parameters and ground motion input in seismic demand analysis, a stratified sampling strategy is adopted to construct coupled samples of the reinforced concrete arch bridge and ground motions. Specifically, Latin Hypercube Sampling (LHS) is first used to efficiently sample key structural parameters, generating 120 sets of statistically representative numerical models of the arch bridge. This sampling method ensures parameter space coverage while significantly improving computational efficiency. Second, based on the bridge site characteristics, 120 ground motion records are selected from the NGA-West2 database [29], with PGA covering the range of 0–1.2 g, meeting the statistical requirements of ground motion intensity measures. This method ensures comprehensive coverage of structural parameter uncertainties while fully characterizing the randomness of ground motion input, providing reliable data support for subsequent seismic reliability analysis.

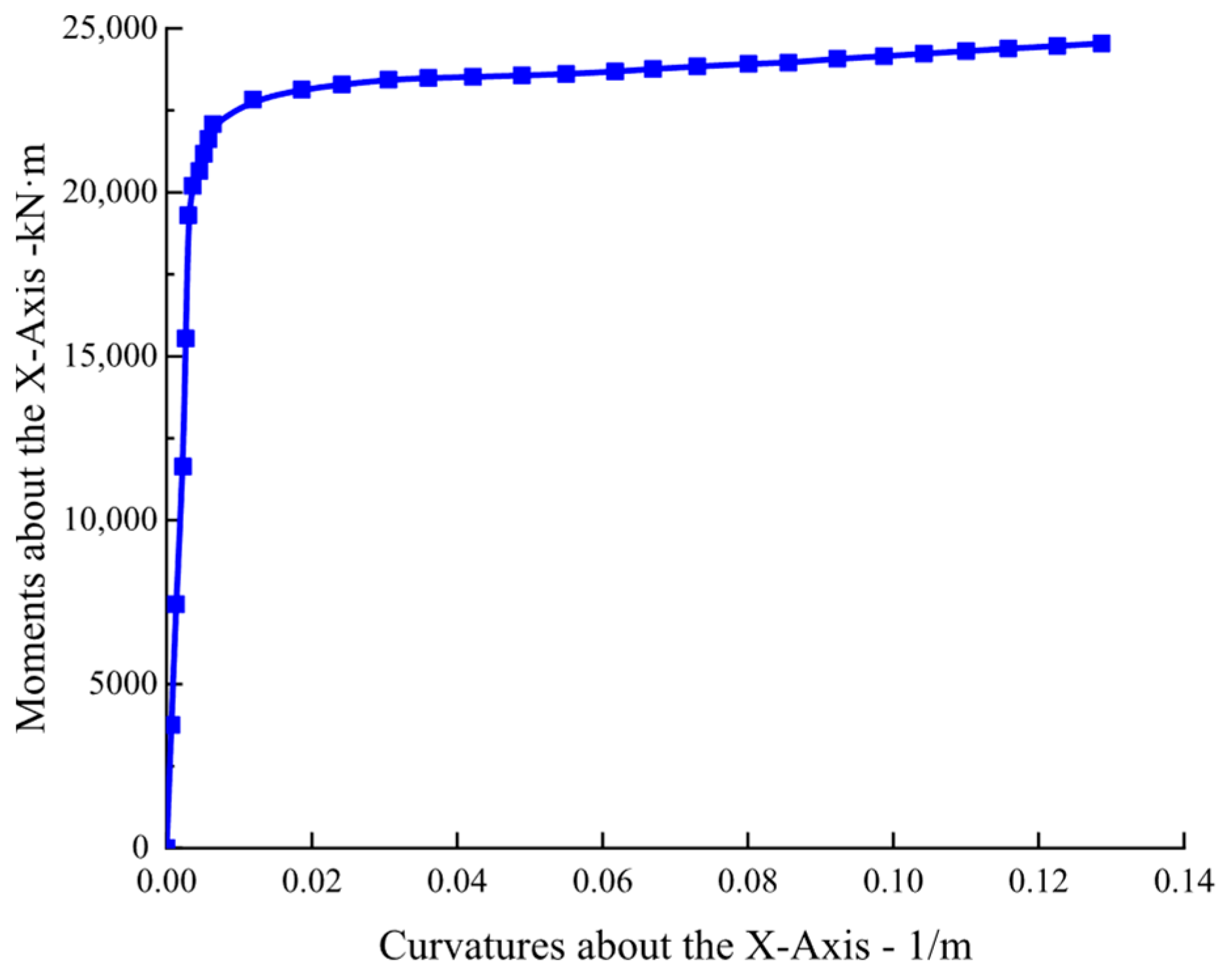
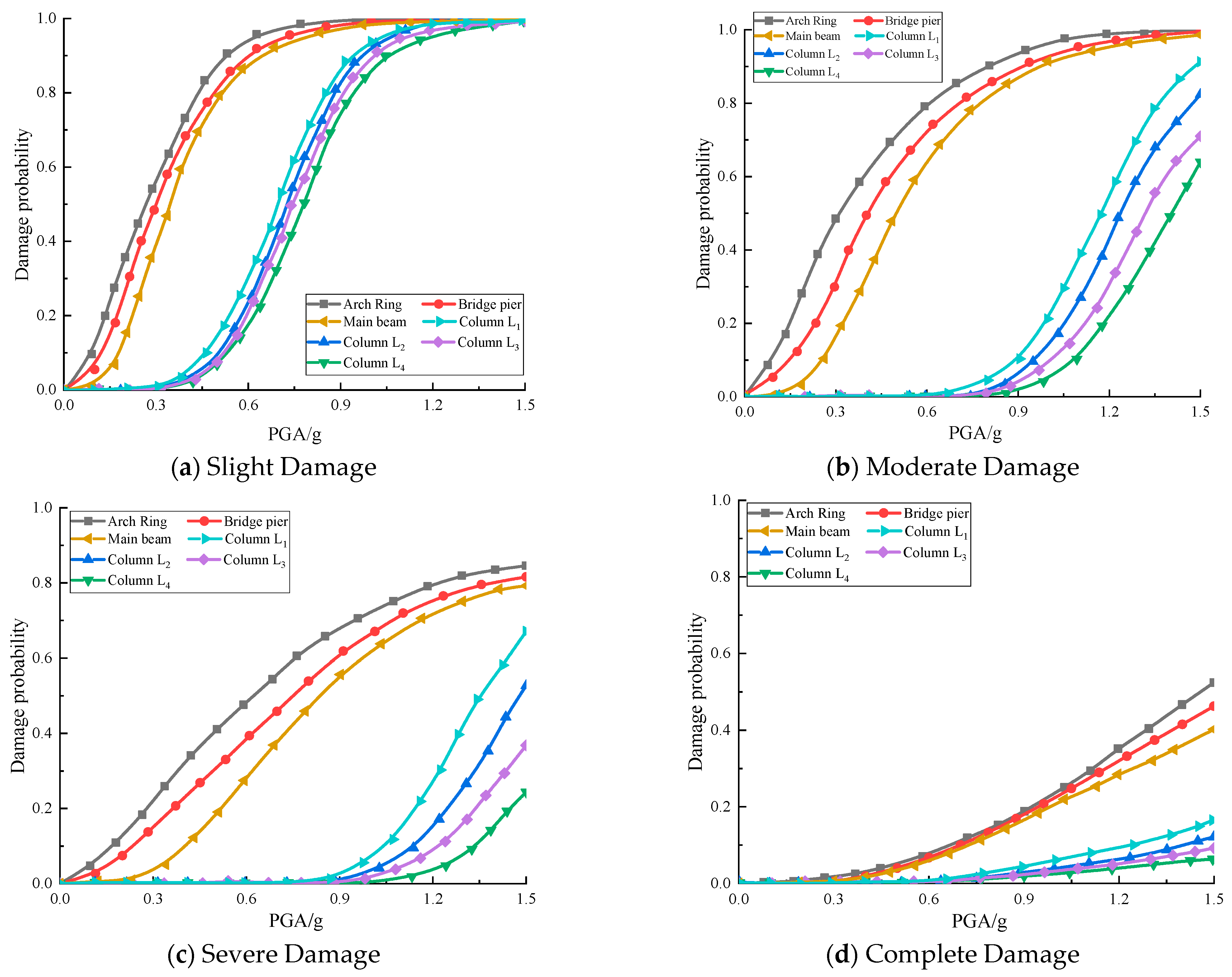
5.3. Component Seismic Vulnerability Analysis

Determining critical indicators for different damage levels is key to component seismic vulnerability analysis. This study uses curvature ductility ratio to define pier damage indicators, strain ratio for arch ring and column damage indicators, and moment–curvature for main girder damage indicators. Specific results are listed in

Table 5. Division of damage indicators for reinforced concrete arch bridge components.

Damage State	Bridge Pier	Main Arch Ring		Columns	Main Beam
	Pier Curvature Ductility Ratio λ	Arch Ring Steel Strain ε1	Arch Ring Steel Strain ε2	Column Strain Ratio ε3	Girder Moment–Curvature γ
Slight Damage	λ ≤ 1.45	ε1 ≤ 0.01	ε2 ≤ 0.0035	ε3 < 2.25	γ < 0.0145
Moderate Damage	1.45 < λ ≤ 3.78	0.01 < ε1 ≤ 0.03	0.0035 < ε2 ≤ 0.0050	2.25 < ε3 < 2.5	0.0145 < γ < 0.0437
Severe Damage	3.78 < λ ≤ 12.59	0.03 < ε1 ≤ 0.05	0.0050 < ε2 ≤ 0.0080	2.5 < ε3 < 3.0	0.0437 < γ < 0.102
Complete Damage	λ > 12.59	ε1 > 0.05	ε2 > 0.0080	ε3 ≥ 3.0	γ ≥ 0.102

[30,31].

To clarify the nonlinear characteristics of the materials and sections underlying the analysis, this subsection details the constitutive models and key sectional responses. The uniaxial stress–strain relationship for concrete was modeled using the modified Kent-Park constitutive law, which accounts for confinement effects in critical regions (e.g., core concrete in piers and columns). The parameters for the concrete grades used (C55, C50, C40) are summarized in Table 3. Reinforcement steel was modeled with a bilinear stress–strain curve incorporating kinematic hardening, with a yield strength of 400 MPa and an elastic modulus of 200 GPa.

The moment–curvature (M-φ) relationships for the critical cross-sections (e.g., arch springing, pier base, mid-span of the main girder) were derived through fiber-section analysis, integrating the material constitutive laws under the appropriate axial load level. Figure 6 presents the typical M-φ backbone curves for the arch springing section. These curves form the basis for translating the global seismic demands (curvatures, moments) obtained from NLTHA into the local damage states used in the vulnerability assessment, thereby verifying the mechanical consistency of the defined damage thresholds.

Based on Equation (7) and the defined damage indicators, the seismic vulnerability curves of the reinforced concrete arch bridge components are obtained, as shown in Figure 7.

The results in Figure 6 show that under the same damage state, the damage probability of the arch ring is always the highest, followed by the piers and main girder, while the overall damage probability of all columns is the lowest, with their complete failure probability almost zero. Comparing the vulnerability of similar components at different positions shows that under the same conditions, column L₁ is relatively more prone to failure.

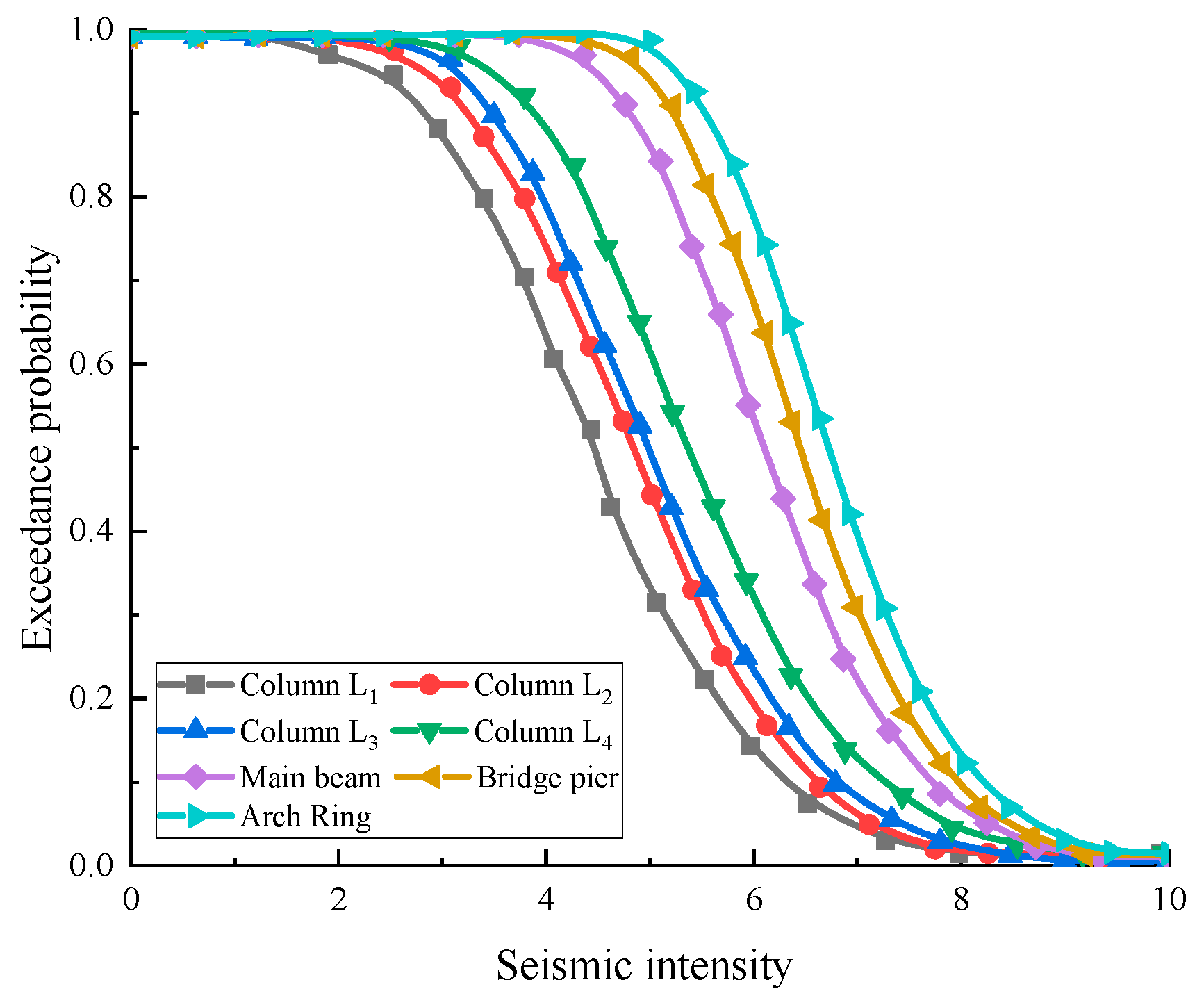
5.4. Component Seismic Hazard Analysis

Using Equations (3) and (4), the seismic hazard curves for different components of the reinforced concrete arch bridge are obtained, as shown in Figure 8.

Figure 8 shows that when the seismic intensity exceeds a certain critical value, the exceedance probability of seismic hazard for reinforced concrete arch bridge components continuously decreases with increasing seismic intensity, with the decreasing rate being fast initially and then slowing down. At the same seismic intensity, the arch ring has the highest exceedance probability, followed by the piers, main girder, and columns. For example, at a seismic intensity of 6, the exceedance probabilities for the arch ring, piers, main girder, column L₄, L₃, L₂, and L₁ are 0.768, 0.682, 0.546, 0.348, 0.249, 0.182, and 0.143, respectively.

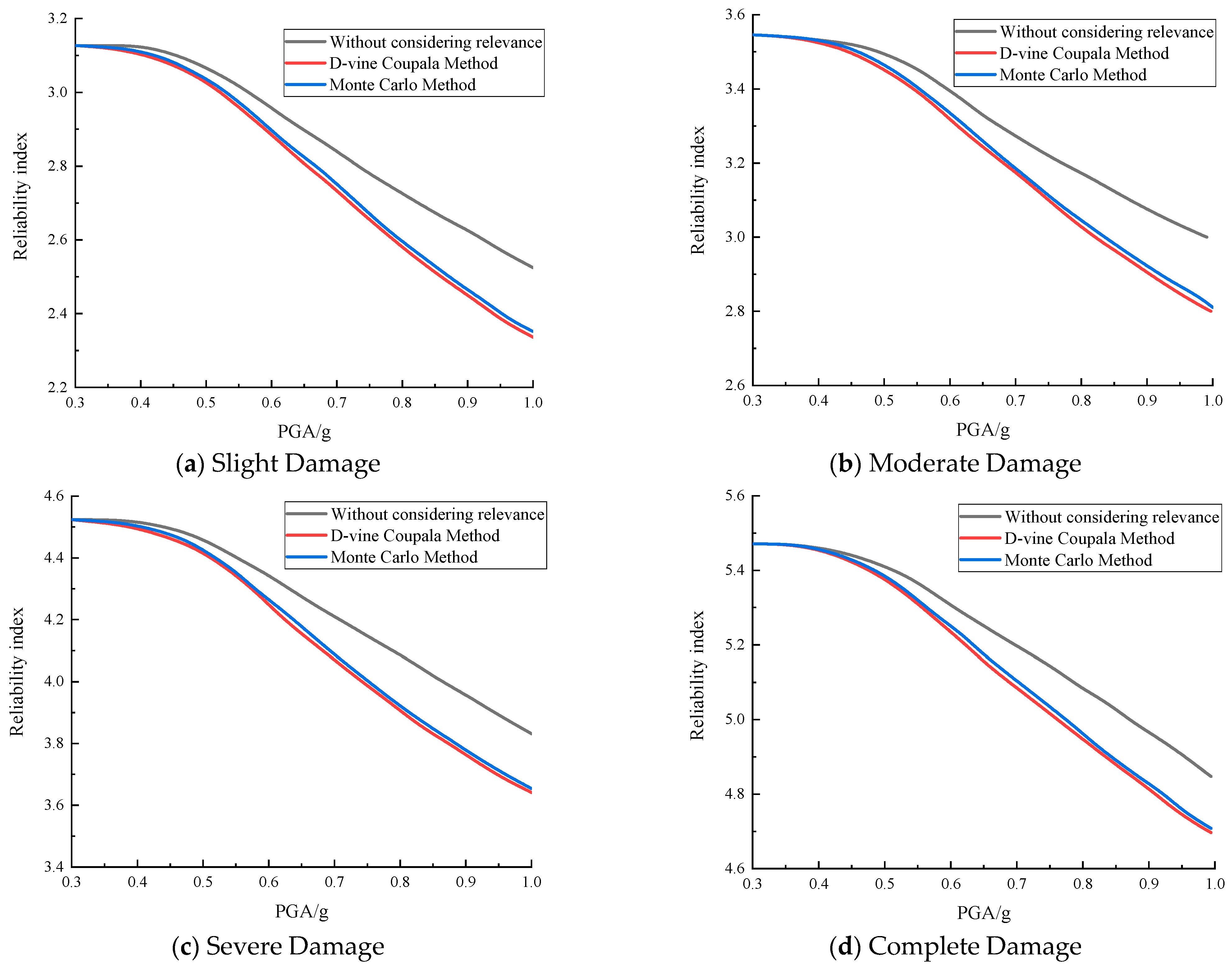
5.5. System Seismic Reliability Analysis

Based on the seismic vulnerability and hazard curves obtained in Section 5.3 and Section 5.4, combined with Equation (2), the seismic reliability of the reinforced concrete arch bridge system can be calculated. To obtain the system seismic reliability considering component correlation, the D-vine structure and Pair-Copula functions must first be determined.

The D-vine Copula construction requires specifying an order for the variables (components) in the first tree. This order influences the hierarchical dependency modeling. To determine an optimal and physically interpretable sequence, a two-step strategy was employed. First, an initial ordering was postulated based on the structural system logic and the primary seismic load-transfer path, starting from the most critical component (the arch ring). Second, to objectively identify the best order, the Dissimilarity Selection Algorithm was used in conjunction with the Akaike Information Criterion (AIC). Several candidate orders were evaluated by constructing the full D-vine model for each and computing its global AIC. The variable sequence that resulted in the model with the minimum AIC value (i.e., the best fit–complexity trade-off) was selected as the final structure, as shown in Figure 9. This approach ensures that the chosen D-vine order effectively captures the dominant dependency patterns in the data.

After determining the D-vine structure and Pair-Copula functions, the seismic reliability of the reinforced concrete arch bridge system, considering component correlation, is calculated using Equation (2). The results are shown in Figure 10. To clarify the impact of component correlation on system seismic vulnerability, the results are compared with those ignoring component correlation. The comparison is also shown in Figure 10.

Meanwhile, to verify the accuracy of the D-vine Copula method, it is compared with the system seismic reliability obtained by the Monte Carlo method. Given that the Monte Carlo method is a primary method for bridge system seismic analysis and its results can be regarded as accurate when the sample size is sufficiently large, it is used as the verification benchmark. The comparison results are also shown in Figure 10.

Comparing the seismic reliability results of the arch bridge system obtained by the D-vine Copula method and the method ignoring component correlation in Figure 10 shows that when component correlation is considered, the seismic reliability indices of the reinforced concrete arch bridge system under minor, moderate, severe damage, and complete failure states are all lower than those ignoring correlation. For example, at PGA = 0.6 g, the seismic reliability indices considering component correlation are reduced by 0.06, 0.07, 0.05, and 0.08 for the four damage states, respectively, compared to ignoring correlation. The results indicate that component correlation significantly affects the seismic reliability of reinforced concrete arch bridge systems. Ignoring this correlation leads to an overestimation of the system’s seismic performance. This conclusion has practical engineering significance for improving the accuracy of bridge system seismic reliability analysis.

A comparison of the system seismic reliability results obtained by the D-vine Copula method and the Monte Carlo method in Figure 10 shows that the deviations between the two methods under all four damage states remain within an acceptable range, with the maximum relative error not exceeding 2.26%. The Monte Carlo benchmark was generated using 1 × 10⁶ samples of the system limit state function. Sampling was performed until the estimated failure probabilities for all damage states exhibited a relative variation of less than 1% over the last 200,000 samples, ensuring convergence. While the MC simulation required approximately 9.5 h of computational time (due to the need for repeated structural analyses), the proposed D-vine Copula method produced results of comparable accuracy in under 1.7 h after the component-level fragility models were constructed. These results not only validate the applicability and accuracy of the D-vine Copula method in reliability analysis of complex structural systems, but also highlight its dual advantages: firstly, by constructing an accurate joint probability distribution model, the method effectively captures the nonlinear correlation characteristics among components; secondly, compared to the traditional Monte Carlo simulation, which requires tens of thousands or even millions of repeated samplings, the D-vine Copula method significantly reduces computational complexity through analytical derivation, with experimentally verified computational efficiency improvements of over 80%. The above conclusions demonstrate that the proposed method offers a practical approach for seismic reliability assessment of bridge structures that balances both accuracy and efficiency.

5.6. Parametric Sensitivity and Generality Analysis

To substantiate the generality of the proposed D-vine Copula framework and investigate the influence of key design parameters, a parametric sensitivity study was conducted. Based on the established model of the 210 m RC arch bridge, four critical parameters were varied one at a time, while keeping others at their baseline values:

(1)

Arch Axis Coefficient (m): 1.75, 1.85 (baseline), 1.95.

(2)

Rise-to-Span Ratio: 1/5.0, 1/5.882 (baseline), 1/6.5.

(3)

Concrete Grade for Arch Ring: C50, C55 (baseline), C60.

(4)

Site Condition (affecting selected ground motions): Site Class II, Site Class III (baseline), Site Class IV.

For each variant, the entire workflow—including nonlinear time-history analysis, component vulnerability derivation, D-vine Copula modeling (with re-optimized Pair-Copula selection), and system reliability calculation—was repeated. The primary outcomes are summarized in

Table 6. Results of parametric sensitivity analysis (Complete damage state, PGA = 0.6 g).

Varied Parameter	Value	System Reliability Index (β)	Optimal Copula for (Q-B) Pair	Parameter θ
Baseline	/	2.45	Clayton	2.15
Arch Axis Coefficient (m)	1.75	2.38	Clayton	2.08
	1.95	2.51	Clayton	2.22
Rise-to-Span Ratio	1/5.0	2.31	Clayton	2.31
	1/6.5	2.58	Frank	3.05
Arch Concrete Grade	C50	2.29	Gumbel	1.78
	C60	2.62	Clayton	2.40
Site Class	II	2.61	Clayton	2.33
	IV	2.28	Clayton	1.95

, which reports the system reliability index (β) for the complete damage state at PGA = 0.6 g and the optimal Copula family for the critical arch-ring-to-main-girder (Q-B) pair.

The analysis leads to two main observations confirming the framework’s utility and generality: (1) The system reliability index logically varies with parameter changes (e.g., higher concrete strength increases β, softer soil decreases it), demonstrating the model’s consistent and physically meaningful response. (2) The D-vine Copula model successfully captured the dependency structure across all variants, with the Clayton Copula remaining the optimal choice for the (Q-B) pair in most cases, indicating a persistent lower-tail dependence. The shift to a Frank Copula for a flatter arch (rise-to-span = 1/6.5) suggests a change in the correlation characteristic, which the method can adaptively capture. This parametric study confirms that the proposed framework is not case-specific but can be reliably applied to assess RC arch bridges with varying designs and site conditions, provided component-level vulnerability analysis is performed.

6. Discussion

6.1. Conclusions

Based on the D-vine Copula function method and the theories of seismic vulnerability and hazard, this study constructs a seismic reliability evaluation framework for reinforced concrete arch bridge systems that considers the correlations among key components such as the arch ring, piers, main girder, and columns. Using a reinforced concrete arch bridge as an engineering example, the seismic vulnerability and hazard curves of its components are obtained, and the system seismic reliability is calculated. Comparisons are made with cases, ignoring component correlation and with Monte Carlo simulation results. The main conclusions are as follows:

(1)

Under the same damage state, the damage probability of the arch ring is always the highest, followed by the piers and main girder, while the overall damage probability of all columns is the lowest, with their complete failure probability almost zero. Comparing the vulnerability of similar components at different positions shows that under the same conditions, column L₁ is relatively more prone to failure.

(2)

When component correlation is considered, the seismic reliability indices of the reinforced concrete arch bridge system under minor, moderate, severe damage, and complete failure states are all lower than those ignoring correlation, indicating that component correlation significantly affects system seismic reliability. Ignoring correlation leads to an overestimation of the system’s seismic performance.

(3)

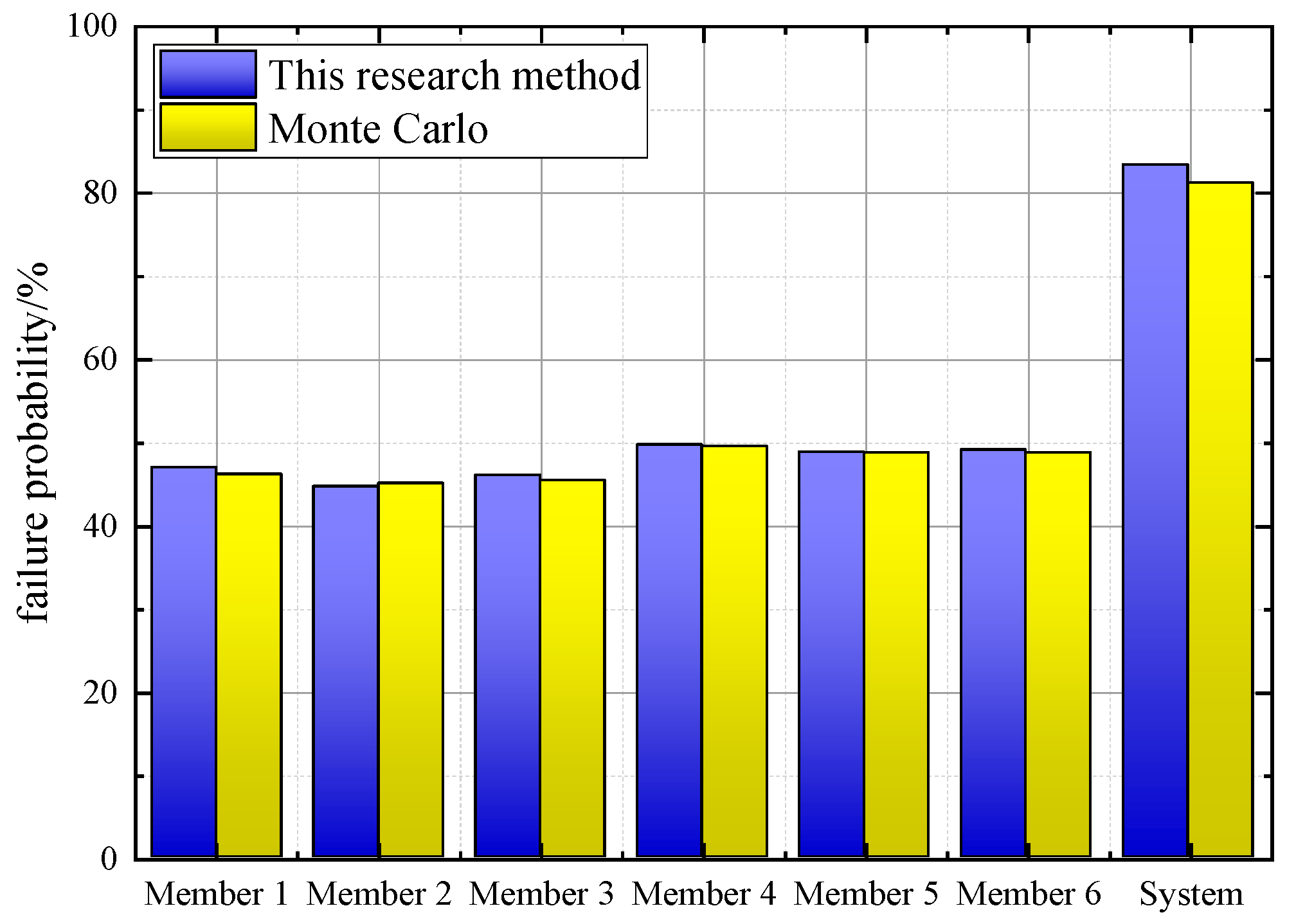
The system seismic reliability obtained by the D-vine Copula method and the Monte Carlo method differs slightly, with a maximum relative error not exceeding 2.26%, verifying the applicability and accuracy of the D-vine Copula method in the reliability analysis of complex structural systems.

(4)

The proposed method effectively captures the nonlinear correlation characteristics between components by constructing an accurate joint probability distribution model. Compared to the traditional Monte Carlo simulation, which requires large-scale repeated sampling, the D-vine Copula method significantly reduces computational complexity through analytical derivation, improving computational efficiency by over 80%.

6.2. Limitations and Future Research

(1)

The uncertainty quantification in this study focuses on key material, geometric, and ground motion intensity parameters, which are sampled independently. Correlations among these input variables (e.g., between concrete strengths in different components) are not considered, which is a common simplification in such system-level analyses; incorporating them remains a topic for future research. Furthermore, structural damping is treated as deterministic, and soil–structure interaction effects are not explicitly modeled, with foundations assumed fixed. These assumptions are consistent with the design basis of the case-study bridge, founded on competent rock. While these choices keep the current analysis focused and tractable for illustrating the novel component-correlation framework, future work could explore the influence of these additional uncertainties and interactions on the system reliability of arch bridges.

(2)

The proposed D-vine Copula framework provides an analytical model for system reliability that considers component correlations. Future research could explore the synergy between this type of model and data from structural health monitoring systems [32]. For example, monitoring data from in-service RC arch bridges [33] could be used to calibrate or validate the correlation parameters within the Copula model, moving towards a more empirically grounded and continuously updated reliability assessment paradigm.

(3)

This work establishes a foundation for several promising extensions. First, the framework could be enhanced by incorporating non-stationary ground motion models to better represent the spectral characteristics of near-fault or long-duration earthquakes. Second, a powerful synergy could be achieved by integrating the proposed Copula-based joint failure probability model with Bayesian updating techniques. Finally, investigating the correlation between material/geometric uncertainties (inputs) and the resulting performance correlations (outputs) remains an important area for refining the overall uncertainty quantification.