Effect of Rehabilitative Wall–Foundation Anchorage Types on the Seismic Behaviour of Weak Reinforced Concrete Frames

Abstract

Installing shear walls in a load-bearing system is one of the most rational, economical, and effective strengthening methods for improving a building system that is vulnerable to seismic effects. One of the most significant points to consider in a reinforced concrete building strengthened with a shear wall is the sufficiency and reliability of anchorage elements in the shear wall–foundation joints, where significant bending moments will occur due to the impact of lateral loads. This study investigated the behaviour of different foundation anchorage methods, including internal anchorage (anchor bars) and external anchorage (steel angle and carbon-fibre-reinforced polymer (CFRP)) applied at the wall–foundation interface in retrofitted weak reinforced concrete frames, which were multi-span, multi-storey, lacking sufficient seismic detailing, and strengthened using wing-type shear walls, under quasi-static lateral loading. It was also aimed to determine the most effective anchorage method for improving the structural performance. A total of six undamaged, but seismically deficient, two-storey, two-span reinforced concrete frames were strengthened with added shear walls that incorporated different anchorage details at the shear wall–foundation joint. According to the test results, the addition of wing-shaped reinforced concrete rehabilitative walls significantly increased the lateral load-carrying capacity, lateral stiffness, and energy dissipation capacity of reinforced concrete frames with poor seismic behaviour. It was observed that additional strengthening was not required in the edge columns of frames with rehabilitative walls of a sufficient length, but that additional measures were required in the foundation anchors at the base of the strengthening wall due to the further increase in the rehabilitative wall capacity. Consequently, the most suitable shear wall foundation anchorage arrangement was achieved with test specimens where one internal anchor bar was used for each vertical shear reinforcement, independently of the shear wall length, and the development length was the highest.

1. Introduction

Reinforced concrete buildings that are still in use, but do not meet the appropriate rigidity, resistance, and ductility criteria essential for earthquake engineering in regions with a high earthquake risk urgently need to be strengthened or demolished if they are weakened. The typical characteristics that are observed in weak reinforced concrete frames during earthquakes, and that were considered in this study, are generally as follows: a low concrete quality, the use of plain reinforcement in existing buildings, the lack of stirrup densification in beam–column joint regions, the absence of column stirrups at beam height in beam–column joint regions, the lap splicing of column longitudinal reinforcement at floor level, and the insufficient lap splicing of beam reinforcement. System improvements are generally achieved via reinforced concrete jacketing, FRP, steel bracings, or reinforced concrete fillings placed in gaps in the frame [1,2,3,4,5]. Reinforced-concrete-infilled frames are more rigid compared to frames retrofitted with steel bracings. Additionally, steel bracings transfer forces to the beam–column joints [6]. This can cause damage to a weak building that lacks stirrups in its beam–column joints and fails to meet earthquake safety regulations. Evaluating the behaviour of reinforced concrete joints under seismic effects is of great importance in load-bearing systems [7,8]. The seismic rehabilitation of reinforced concrete buildings is widely achieved with reinforced concrete walls thanks to their seismic-damage-reducing properties [9]. This retrofitting process is generally carried out by installing a shear wall across the entire span between columns. There have been many experimental studies on this topic, e.g., [10,11,12,13]. However, in some cases, the span between the columns cannot be fully filled with shear walls due to usage, which necessitates the installation of shear walls by adding wing-type walls to one or two sides of the columns. In addition, it may be necessary to leave an opening in the shear wall [14]. There are fewer frame-level experimental studies that have investigated shear wall applications involving the addition of a shear wall to columns [15,16,17,18,19,20]. More recently, many theoretical and experimental studies have been conducted on the effects of different types of shear walls placed in various locations on the seismic behaviours of existing reinforced concrete buildings [21,22,23,24].

Weak points such as the split tensile strength of buildings to be retrofitted can generally limit the benefits of system improvements [25]. The most significant problems in reinforced concrete buildings strengthened by installing fully infilled or wing-type shear walls are expected to occur in the shear wall–foundation joint or the shear wall–beam joints. Therefore, additional strengthening methods should be implemented for shear wall–foundation joints [26,27,28].

There are also studies in the literature that have addressed precast shear walls instead of cast-in-place shear walls [29,30]. For example, Zhang et al. investigated the seismic performance and usability of a different type of precast hollow shear wall rather than a reinforced concrete shear wall [31].

Reinforced concrete buildings suffer considerable damage during earthquakes for a variety of reasons, including a low concrete quality, a lack of sufficient confining reinforcement in beam–column joints and confinement zones, inadequate lap splices and anchor development lengths of longitudinal reinforcement in columns, and an insufficient structural rigidity [32,33]. By installing a shear wall in existing structural systems, load-bearing systems can attain sufficient rigidity and strength levels. Transforming frame columns into shear walls is a frequently used method in practice.

One of the most common strengthening methods involves creating a new lateral load-bearing system by completely filling some of the openings in frames that have an insufficient strength and rigidity with reinforced concrete infill. Reinforced concrete infill frames act like shear walls, carrying a significant portion of the lateral load and increasing the lateral rigidity of the building. In structures rehabilitated with reinforced concrete shear walls between columns, it is often necessary in practice to leave openings in the additional reinforced concrete infill walls for doors and windows, in accordance with the intended use. Shear walls positively affect the behaviour of the structural system, increasing the strength and rigidity of the structure under gravity and lateral loads, and altering the static and dynamic characteristics of the system. Increasing the rigidity ensures that the second-order moments occurring under seismic effects remain within acceptable limits; it also reduces seismic damage to non-structural elements by lowering the relative displacement between floors. In this study, wing walls were added to both sides of the frame’s central column to form a shear wall, enabling the creation of voids that must be left in the structure according to its intended use. The use of wing walls to rehabilitate the reinforced concrete frames examined in this study and the conversion of the column into a shear wall resulted in an increase in the system’s strength and ductility.

This study investigated the best anchoring method that could be used in the connection between the additional shear wall and the existing foundation. This is one of the most critical problems in the rehabilitation of insufficiently and weak reinforced concrete buildings against seismic effects using shear walls, one of the most common structural strengthening methods in practice. This study specifically examined the effectiveness of different anchorage types that can be applied in the additional wing-type shear wall–foundation connection details, particularly in cases where the frame voids cannot be filled with reinforced concrete shear walls due to their intended use.

2. Properties of Test Specimens

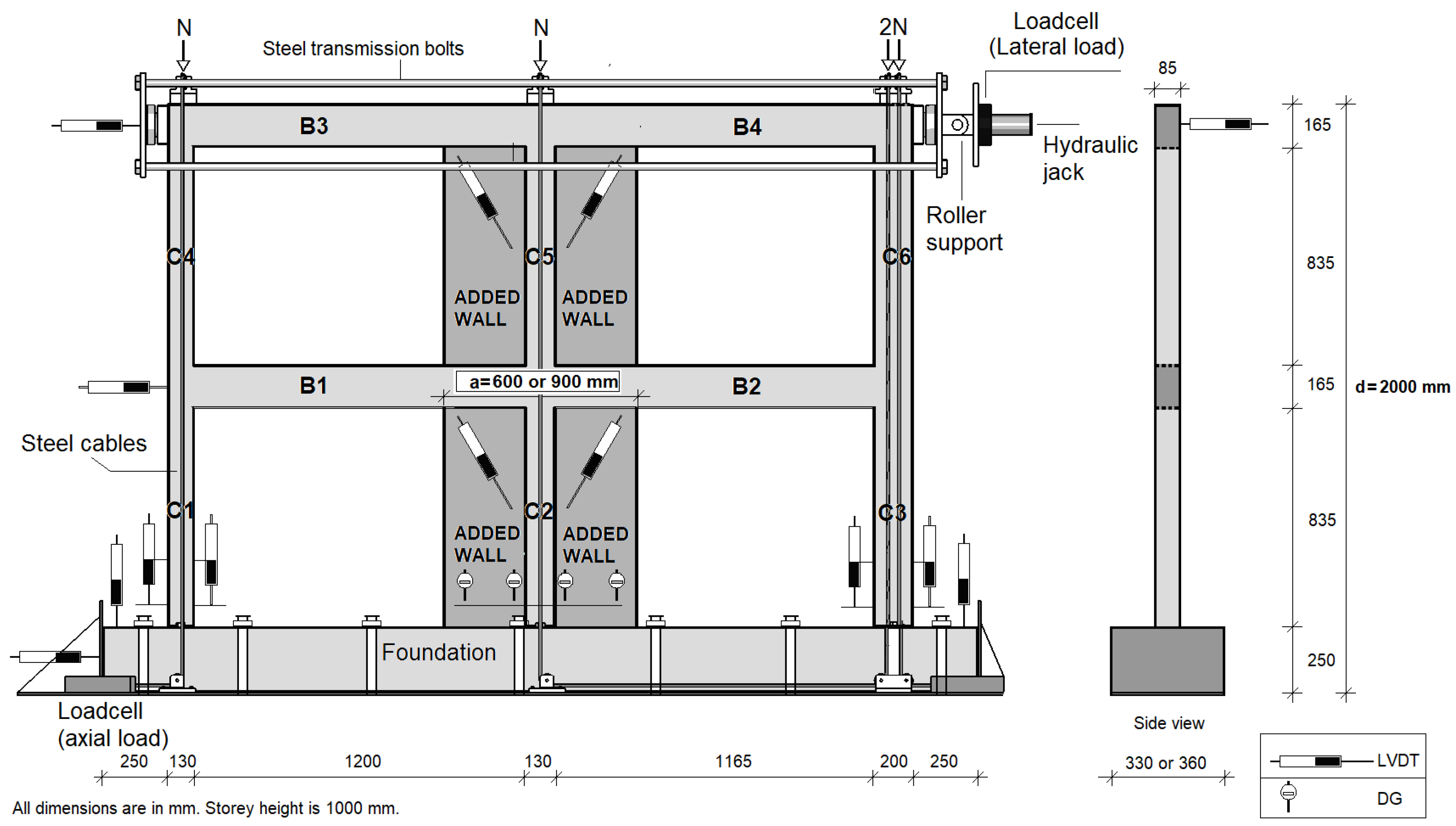
This study focused on the seismic behaviours of different types of reinforced concrete rehabilitative wall–foundation anchorages. Six frame specimens strengthened with reinforced concrete wing walls were tested under quasi-static reversed cyclic lateral loading. The behaviours of these six frames were studied within two groups, with a total of 600 mm and 900 mm of rehabilitative wall. The specimens were alike in terms of failing to fulfil specific earthquake-resistant criteria; they had low-quality concrete, plain reinforcement bars, the absence of stirrup confinement in beam–column joints, a lack of column stirrups extending through the beam depth within the joints, inadequate lap splices of column longitudinal bars at storey levels, insufficient development in beam reinforcement, and 90° hooks used in columns and beam stirrups. However, they had different shear wall anchorage details, as they were strengthened with reinforced concrete shear walls with 1/3-ratio, two-storey, two-span frames and different lengths under a quasi-static lateral load that simulated the effects of an earthquake. An axial force of approximately 0.10–0.15 A_cf_c (as per Turkish Building Code TBC-500-2000 [34]) was applied to the frame columns using steel ropes.

Table 1. Properties of test specimens.

Specimen	Total Wall Length (mm)	Concrete Compressive Strength (N/mm2)		Foundation Anchorage Type
		Frame	Wall
S600-1	600	14	30	Internal (rod)
S900-1	900	14	30	Internal (rod)
S600-2	600	10	22	Internal (rod) + external (angles with bolts)
S900-2	900	10	22	Internal (rod) + external (CFRP laminate)
S600-3	600	14	36	Internal (increased rod)
S900-3	900	14	36	Internal (increased rod)

and Figure 1 show the classification and general properties of the test specimens.

Three specimens had a 600 mm shear wall installed on either side of the middle column (S600-1, S600-2, and S600-3), and the other three specimens had a 900 mm shear wall installed on either side of the middle column (S900-1, S900-2, and S900-3). In this study, “a” is the total shear wall length and “d” is the total shear wall height. The length of the total shear wall was determined on the basis of a mean value of 2.5 for the ratio of the height of the shear wall to the length of the shear wall (a/d), which is accepted as the limit value for short corbel shear wall behaviour for situations that would produce bending and shear walls [35]. When determining shear wall lengths, a flexural wall (a/d = 3.3 > 2.5, S600 specimens) and a shear wall (a/d = 2.2 < 2.5, S900 specimens) were considered for installation. In the shear wall–foundation joint, only internal anchor bars were used in four specimens, while in two specimens, external anchorage methods were used in addition to the internal anchorage. The effects of the anchorage type on the frame behaviour were subsequently investigated. Furthermore, the test results obtained for the strengthened reinforced concrete frames—whose general properties are presented in Table 1 and Figure 1—were evaluated and their overall behavioural characteristics were identified.

This study investigated the behaviour of new load-bearing systems obtained as a result of strengthening reinforced concrete frames, which were manufactured to represent existing buildings lacking sufficient seismic safety properties, as described above. These frames involved partial reinforced concrete shear walls with different shear wall–foundation anchorage details requiring strengthening, and they were subjected to a quasi-static two-way and repetitive lateral load that simulated an earthquake. 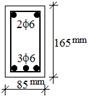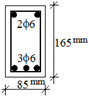A total of six reinforced concrete frames were accordingly manufactured at a 1/3 ratio; their dimensions are shown in Figure 2. For three of these frames, the middle columns were transformed into a 600 mm long shear wall, while for the other three, the middle columns were transformed into shear walls of 900 mm in length. By selecting different sizes for the side columns of the frames, the behaviours of asymmetrical load-bearing systems were studied, such as combinations of a strong column and a weak beam (C3-C6-B2 connection) or a strong beam and a weak column (C1-C4-B1 connection). Stirrups of ϕ4 (4 mm) in diameter, placed at 100 mm intervals, were used for all the columns and beams of the frames. The hook lengths of the stirrups were 10ϕ (ϕ: bar diameter) and they were bent at 90°. Since the lateral load level applied to the columns was small, no additional processes such as jacketing were applied to the side columns.

2.1. Material Properties

The concrete compressive strengths of existing reinforced concrete buildings that have collapsed or been damaged in past earthquakes were observed to be at low values of approximately 10–12 MPa. Therefore, to represent weak and seismically deficient reinforced concrete buildings, the target cylinder compressive strength of the concrete in the test frames was set to 12 MPa, while the cylinder compressive strength of the rehabilitative shear walls was 30 MPa. The mean cylindrical compressive strength of concrete for the specimens was found to be approximately 14 MPa for S600-1, S600-3, S900-1, and S900-3 and 10 MPa for S600-2 and S900-2. After fabricating the test frames, a strengthening process was carried out using partially reinforced concrete shear walls, and the concrete compressive strength of the created shear walls was found to be 30 MPa for S600-1 and S900-1, 22 MPa for S600-2 and S900-2, and 36 MPa for S600-3 and S900-3 (

Table 2. Concrete compressive strength properties of test specimens.

Specimen Group	Average Concrete Compressive Strength (N/mm2)
	Frame	Rehabilitative Wall
1st group (S600-1; S900-1)	14.24	30.24
2nd group (S600-2; S900-2)	10.39	22.53
3rd group (S600-3; S900-3)	13.75	36.05

).

Table 3. Reinforcement properties of test frame members.

Diameter (mm)	Yield Strength fy (MPa)	Ultimate Strength fsu (MPa)	Rupture Strain εsu	Type
4	333	469	0.1496	Plain
6	541	638	0.1285	Plain
8	447	653	0.2303	Plain
6 1	529	664	0.2709	Deformed
8 1	525/508	766/757	0.2153	Deformed

¹ Used in rehabilitative shear walls.

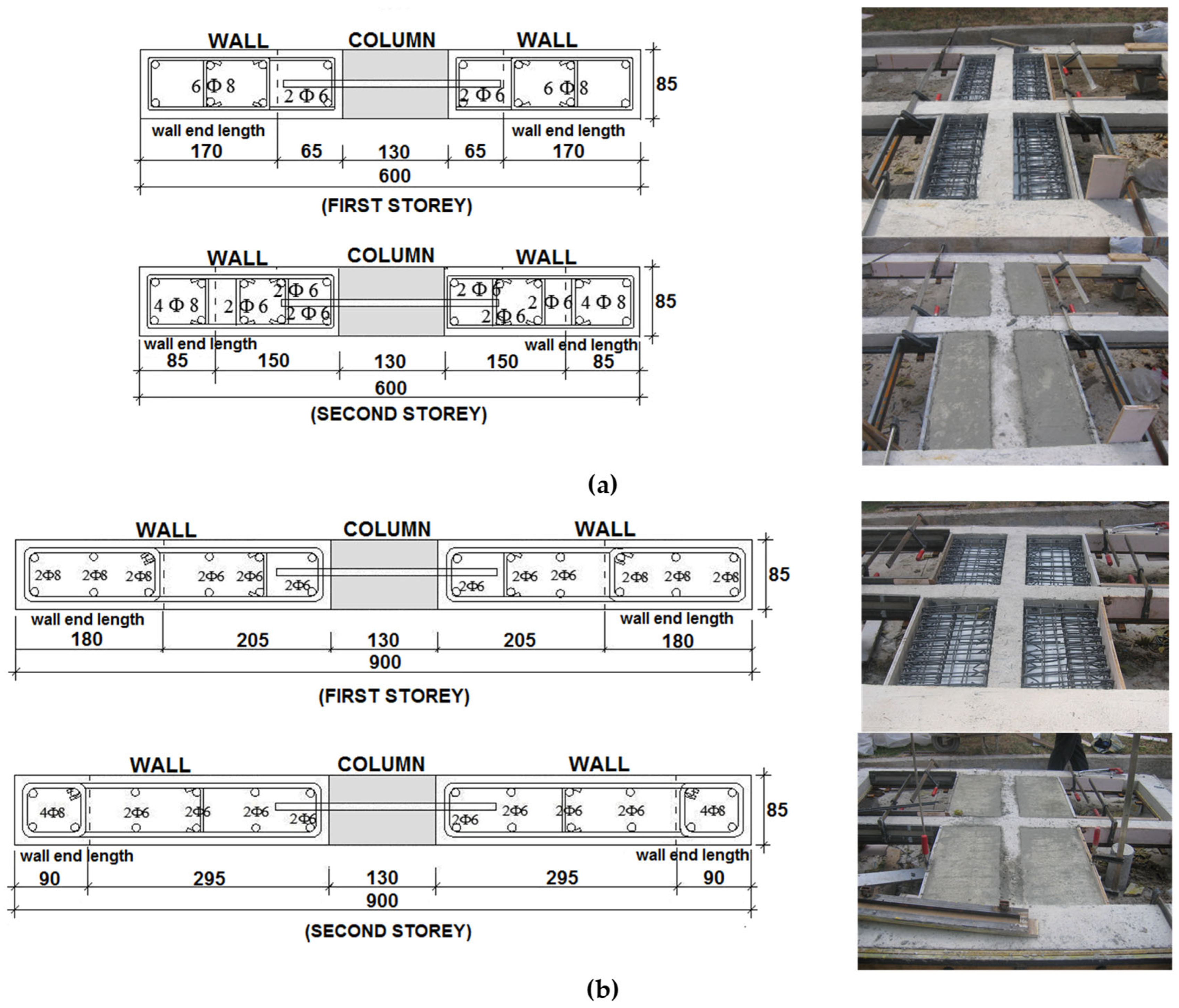
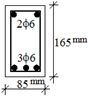
presents the characteristic material properties of the reinforcements used in the test specimens. For the 200 mm wide column, 6 plain bars of 8 mm in diameter were used as reinforcement. For the 130 mm wide column, 4 plain bars of 8 mm in diameter were used, and in the beams, 3 plain bars (lower) of 6 mm in diameter and 2 plain bars (upper) of 6 mm in diameter were used. CFRP sheets were used in the external FRP anchors; they had a uniaxial tensile strength of 4100 MPa, a modulus of elasticity (E_f) of 231,000 MPa, and a thickness of 0.12 mm. The integrity of the FRP and the shear wall–plaster composite was maintained using FRP dowels. A two-component, thixotropic epoxy-based impregnation resin and adhesive was used to bond the CFRP laminate. The approximate technical specifications of the epoxy resin were as follows: the modulus of elasticity in bending was 3800 MPa, the tensile strength was 30 MPa, the modulus of elasticity under tension was 4500 MPa, the rupture elongation was 0.9%, and the tensile bond strength was higher than 4 MPa. The dimensions and reinforcement layouts of the frame members (columns and beams) are shown in

Table 4. Dimensions and reinforcement layouts of columns and beams.

COLUMNS *			BEAMS *
Specimen Type	C1, C2, C4, C5	C3, C6	Support Region B1, B2, B3, B4	Midspan Region B1, B2, B3, B4
S600
S900

* All stirrups for columns and beams had a diameter of 4 mm and were spaced at 100 mm. The hook length of the stirrups was 10ϕ, where ϕ is the bar diameter.

for all the frames [18].

The shear wall dimensions and reinforcement layout are provided in Figure 3. In the rehabilitative shear walls, in accordance with the requirements of the Turkish Earthquake Code [36], six vertical reinforcement bars of 8 mm in diameter were used in the boundary regions of the shear walls within the critical wall height (first storey), and four vertical reinforcement bars of 8 mm in diameter were used in the boundary regions beyond the critical wall height (second storey). In the regions outside the boundary zones of the shear walls, along the critical wall height, the S600 specimens included two vertical reinforcement bars of 6 mm in diameter on each side, while the S900 specimens included six vertical bars of 6 mm in diameter on each side. Beyond the critical wall height, six vertical bars of 6 mm in diameter were used on each side in the S600 specimens, while eight vertical bars of 6 mm in diameter were used on each side in the S900 specimens (Figure 3). In the additional shear walls, a horizontal reinforcement of 4 mm in diameter (considering a 1/3 geometric scale) spaced at 40 mm was used in the boundary zones within the critical wall height, while a horizontal reinforcement of 4 mm in diameter spaced at 85 mm was used in the boundary zones beyond the critical wall height. The lateral reinforcements on both storeys outside the boundary zones were placed at 80 mm intervals.

2.2. Internal Anchor Bars and External Anchorages

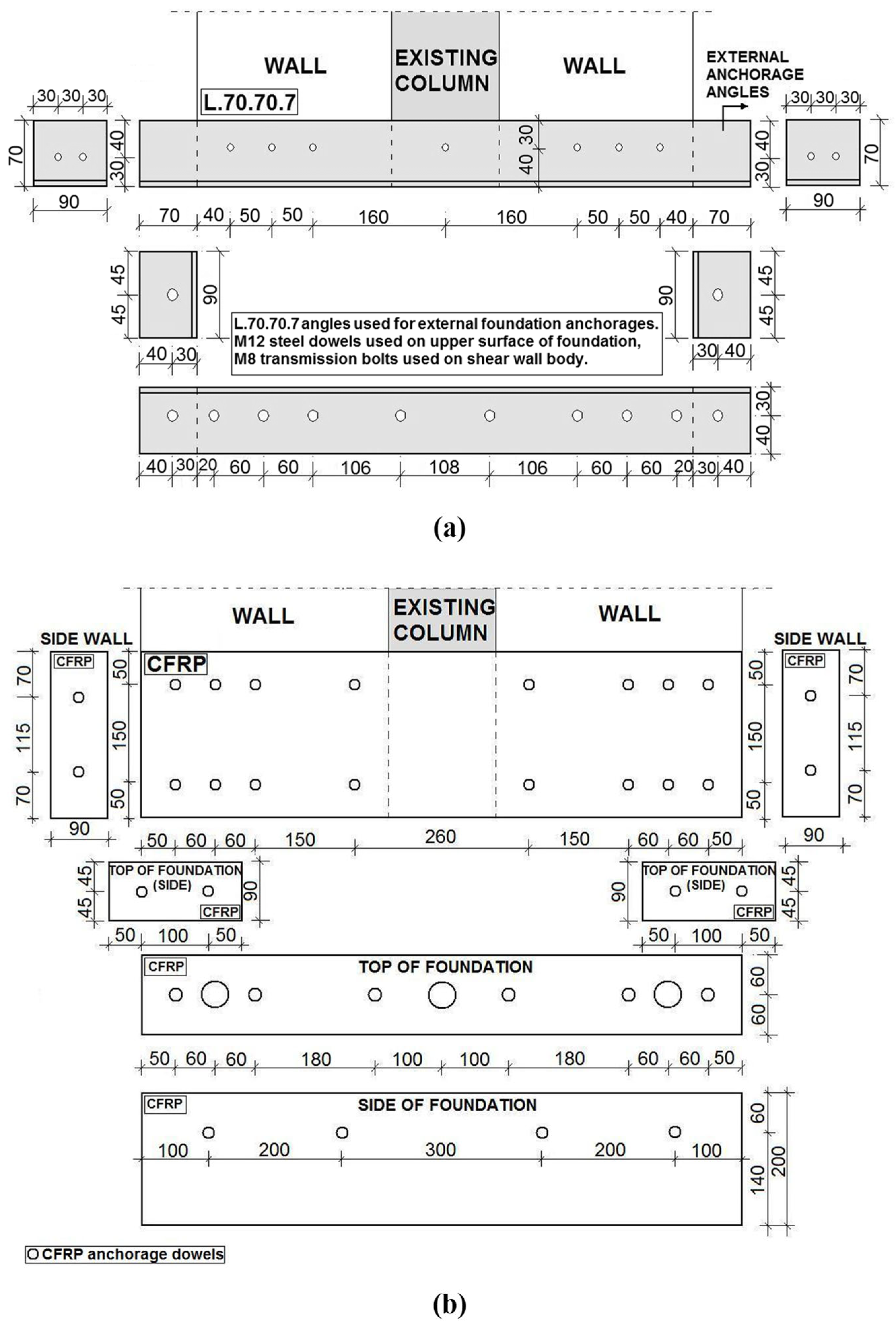
To establish force transfer between the pre-existing reinforced concrete frame and the newly added reinforced concrete shear wall pieces, and to achieve shear wall behaviour, the test specimens’ cross-sectional sizes were also taken into consideration and 8 mm ribbed anchor bars were used. The holes drilled to place these anchor bars inside the concrete were 10 mm in diameter, and they were cleaned of dust using compressed air to avoid the pull-out of the anchor bars. Subsequently, the bars were fixed using epoxy [37]. The interval between the anchor bars was 150 mm for all columns and 145 mm for all beams. On the foundation level, the internal anchors in specimens S600-1, S600-2, S900-1, and S900-2 were placed at 70 mm intervals, while the anchors in S600-3 and S900-3 were placed such that one anchor was provided for each vertical reinforcement bar. In S600-1, S600-3, S900-1, and S900-3, only internal anchor bars were used. In the S600-2 test specimen, in addition to internal anchors, an external anchorage was applied using steel with an L70.70.7 angle profile fixed with bolts, fully enclosing the outer edges of the shear wall. In the S900-2 test specimen, external anchorage was also applied in addition to internal anchorage by fully enclosing the outer edges of the shear wall using custom wires and carbon-fibre-reinforced polymer (CFRP) bar anchors [6], as well as CFRP laminates bonded with epoxy. For all specimens, the lap splice length of the anchor in the upper-storey beam was taken as 15 times the diameter of the anchor bar. For the foundation anchor bars, this length was taken as 20 times the bar diameter for specimens S600-1, S600-2, S900-1, and S900-2 and 30 times the bar diameter for specimens S600-3 and S900-3. For the column and middle floor beams, the anchorage holes were maintained throughout the cross-section; the development length of the anchor bars inside the shear wall was taken as 20 times the anchor reinforcement diameter for the anchors in the columns and beams [37]. The development length in the foundation anchors was 30 times the reinforcement diameter for specimens S600-1, S600-2, S900-1, and S900-2 and 60 times the reinforcement diameter for specimens S600-3 and S900-3. The internal anchor bars used in the shear wall–foundation joints are shown in Figure 4 and the external anchorages are shown in Figure 5.

2.3. Loading and Measurement Setup

The experiments were conducted on a rigid steel loading frame with a capacity of 250 kN. Quasi-static reversed cyclic lateral loads were implemented at the second-storey beam level in such a way as to transfer the load onto both surfaces of the beam with four transmission bolts fixed on the boundary zones of the specimen. To simulate column behaviour, an axial load of approximately 0.10–0.15 f_cA_c was applied to the columns using steel cables, where f_c is the characteristic compressive strength of concrete and A_c is the total cross-sectional area of concrete in the columns. Figure 6 displays the measurement setup and loading frame used for the test specimens [18]. To prevent the lateral displacement of the test specimens, an additional external steel stability frame was added to the loading setup. Since lateral displacements increase significantly after the yielding stage, the loading protocol for all the test frames was force-controlled until yielding occurred in the frame and displacement-controlled after yielding (Figure 7). In addition, the loading protocol was updated during testing based on the behaviour of the specimens.

3. Test Results

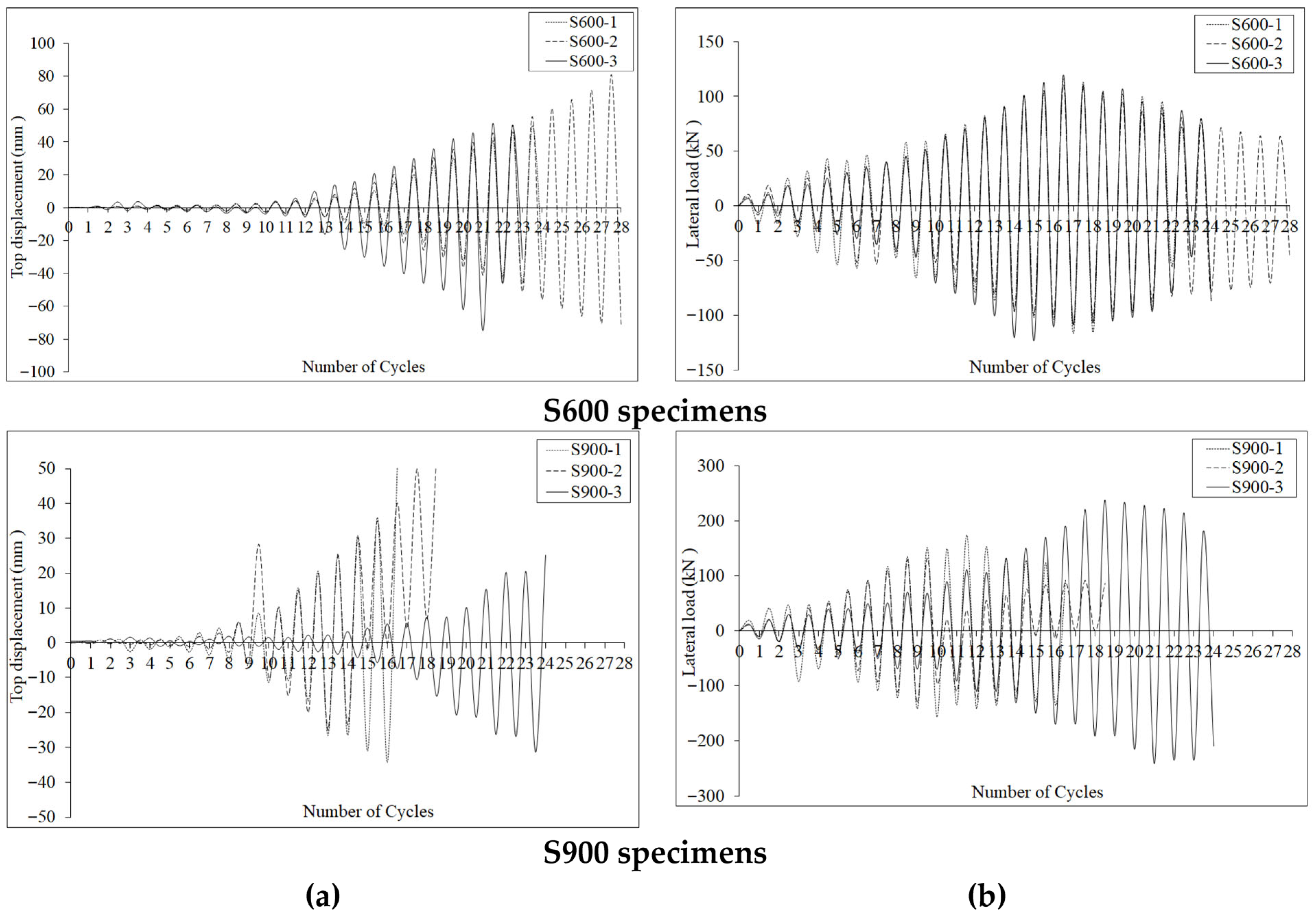
Hysteresis curves of the test specimens are provided in Figure 8 and the experimental envelope curves (lateral load–lateral top displacement) are given in Figure 9.

It was observed that the hysteresis curves of all the test specimens with 600 mm shear walls and different foundation anchors generally exhibited regular behaviour in both the forward and reverse cycles (Figure 8). Figure 9 shows that the initial stiffnesses of the test specimens with 600 mm shear walls were almost identical, and the maximum load values in the forward cycle were also the same. Except for the S600-1 specimen, the maximum peak displacement values of the other two specimens were very close to each other. When examining the hysteresis curves of all the test specimens with 900 mm shear walls and different foundation anchors, it was observed that the hysteresis curves of the specimens with internal anchors were smoother. In the S900-2 specimen with internal anchors and external FRP anchors, when the yield load was reached in the forward cycle, the CFRP laminate separated from the shear wall base at a horizontal load of 130 kN and a peak displacement of 6.05 mm in the ninth forward cycle. At this point, the peak displacement suddenly reached 28.32 mm and the maximum load was measured as 132.46 kN. Loading continued in a displacement-controlled manner in subsequent cycles. Figure 9 shows that the initial stiffnesses of all the test specimens were similar. In contrast, different envelope curves were observed for the three test specimens. The S900-3 specimen, which had increased internal anchors, exhibited the maximum strength value compared to the other specimens. The most brittle behaviour was observed for the S900-3 specimen.

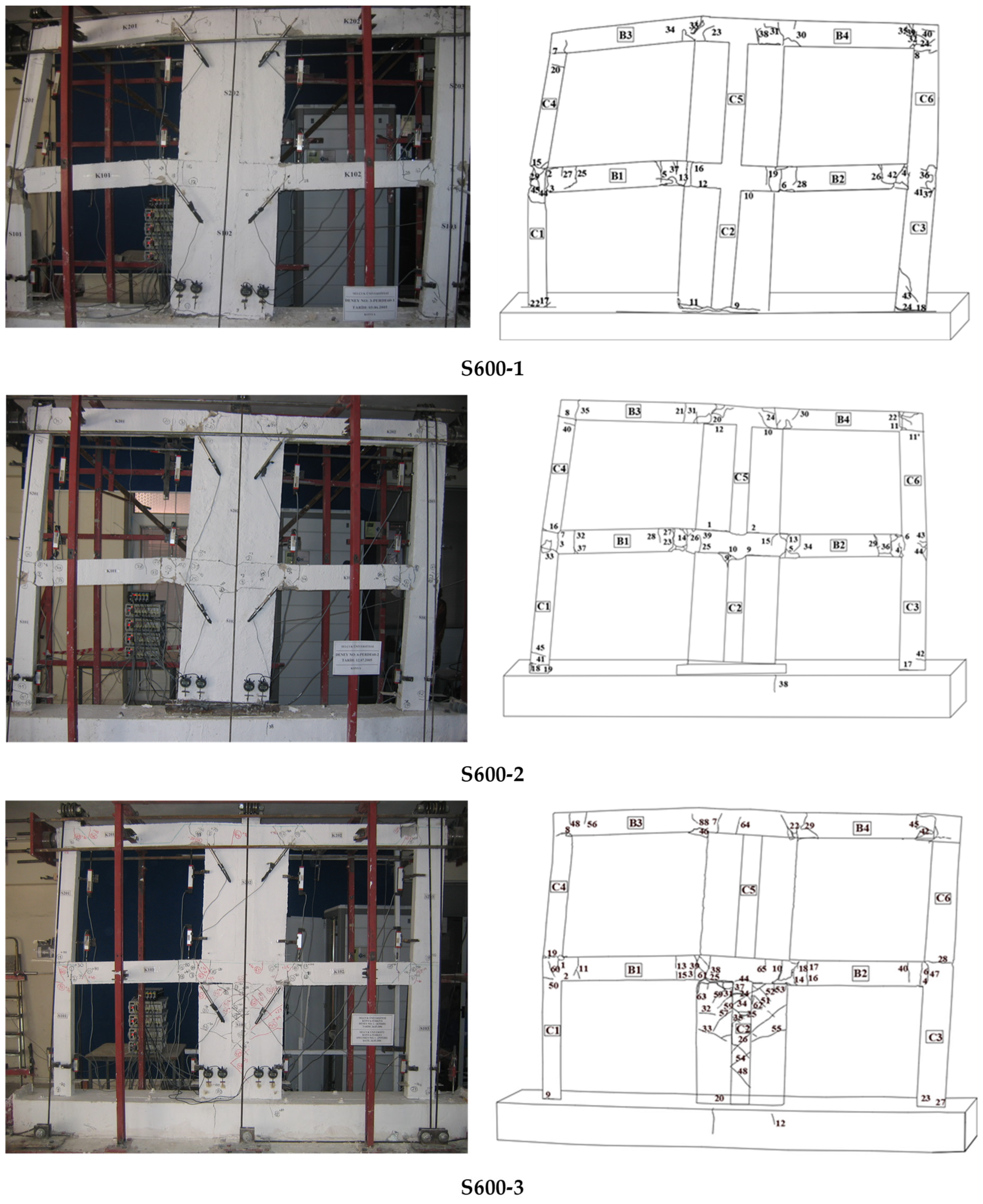
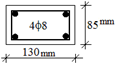
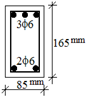
Figure 10 and Figure 11 present representations of the damage and schematic cracking patterns observed at the end of the tests for the frames retrofitted with rehabilitative shear walls of 600 mm and 900 mm in total length, respectively. The damage that occurred to the shear wall–foundation joints of all frames after testing is shown in Figure 12.

The most important parameter considered in this study was the effect of different shear wall–foundation anchorage applications on general load-bearing system behaviours. Accordingly, it was aimed to determine the most suitable anchorage type to be implemented when strengthening shear walls. By examining the lateral load–lateral top displacement of the experimental envelope curves of frames with 600 mm rehabilitative shear walls, it was seen that the curves were very close to each other in both directions (i.e., push and pull), especially up to the yielding load. For the 900 mm shear wall frames, a similar behaviour was observed for specimens S900-1 and S900-2, which had the same internal anchorage. For S900-3, a major increase in the maximum carried load was observed, especially for the frame (maximum increase of ~51% compared to S900-1 and maximum increase of ~82% compared to S900-2). These results show that, when the shear wall length is greater, the importance of the shear wall–foundation anchorage increases. Simultaneously, increasing the internal anchorage is of significance in reaching the full potential of a load-bearing system. For test specimens S600-1 and S900-1, the pull-out of the internal anchor bars occurred in the shear wall–foundation joints. This indicates that the number of anchor bars used and/or the adherence length was insufficient. For specimen S600-2, with additional steel angles and external anchorage, there was no pull-out of the internal anchor bars, but the holes created on the shear wall caused this region to fall apart in subsequent steps. The shear wall accordingly consumed the majority of the energy on the frame with the anchorage application, and the damage to other frame members was reduced. For specimen S600-3, for which the internal anchorage was increased, no anchor pull-out failure was observed in the shear wall–foundation joints. The cracks occurring in S600-3 and S900-3 due to the lateral load were predominantly concentrated in the shear wall. This showed that the shear wall–foundation anchorage was sufficient. Based on these findings, it was concluded that the best foundation anchorage entails installing an anchor bar on every vertical wall reinforcement, and the length of the bars inside the foundation and shear wall was sufficient.

In specimen S900-2, at the ninth forward cycle, the CFRP laminate began to separate from the base of the shear wall under a horizontal load of 130 kN and a peak displacement of 6.05 mm. After reaching the yield load in the 10th forward cycle, the horizontal displacement reached a value of 28.32 mm. At this stage, the load did not increase after 137 kN of horizontal load. When 50 mm of horizontal displacement was reached, an opening of approximately 30 mm occurred at the right end of the shear wall base.

In frames for which a 600 mm rehabilitative shear wall was created, damage to the columns could not be prevented. In contrast, with a 900 mm rehabilitative shear wall, the lateral load-bearing capacity increased significantly at the same displacement stage as that seen for the 600 mm shear wall frame, the damage level of the load-bearing system members decreased, and no significant damage was observed on the columns. These findings confirm that a 900 mm shear wall, which is more rigid, is sufficient for system improvement, and strengthening the other members of the load-bearing system is not necessary. In this case, limited shear cracking was observed, particularly at the left-end joints, where a strong beam–weak column pairing was present, together with vertical cracks in the support zones extending along a length approximately equal to the beam depth.

In test specimen S900-2, for which the shear wall–foundation joints were bound with CFRP, no shear cracks were observed at the corner joints at the same lateral displacement level. This was in contrast to specimen S600-2 from the same group, as well as specimen S900-1, which had the same wall length, but only internal anchorage. Thus, for S900-2, the damage level of the frame decreased and the CFRP laminate contributed at least partially to the structural behaviour of the specimen. When the CFRP laminates that were used in S900-2 for additional external anchorage in the shear wall–foundation joint were removed, no damages were observed on the foundation’s surface (Figure 13). In addition, only a small crack was observed on the foundation surface in specimen S600-2, where the steel angles were used as additional external anchorage. In the second group of test specimens, for which external foundation anchors were used, it was observed that the specimen with a 600 mm shear wall and additional angle anchors sustained damage to the region around the bolts of the steel angle. In the specimen with a 900 mm long shear wall and CFRP anchors, the slippage of the internal anchor bars and the rupture of the external CFRP anchors were observed.

Figure 14 presents the sequence of plastic hinge formation in the experimental test specimens. It was seen that the first plastic hinges generally occurred on the edges of the beams, where there were no shear walls. In the third test specimens, the number of plastic hinge formations was lower compared to the other specimens, despite a much higher lateral load resistance.

Shear hinge formation occurred at the first-floor left-hand edge nodes of the S600-1 and S900-1 specimens in Group 1, which only had internal anchors. For both specimens, the hinge formed in the fifth row at the rehabilitative wall–foundation connection. Due to the inadequacy of the anchors used, significant damage occurred at the shear wall–foundation joint and shear damage at the left-hand beam–column joint, resulting in collapse. This led to the formation of a relatively small number of plastic hinges and, consequently, a lower energy dissipation capacity. The highest number of hinge formations was observed in the second group for the S600-2 and S900-2 specimens, which had both internal and external anchors. This situation demonstrates that external anchors also contribute to the behaviour of the load-bearing system. In the third group, which contained the S600-3 and S900-3 specimens, shear hinges formed in the rehabilitative wall. In this group of samples, as a result of the anchors at the shear wall–foundation connection being adequate, the shear wall carried most of the lateral load, the damage level in the other structural elements decreased, and the energy was consumed by shear cracks in the shear wall. In all the test specimens, the first four hinge formations occurred at the beam ends on the first floor.

The maximum lateral load obtained for the test frames, the lateral load in the yielding and collapsing positions, and the lateral top displacement values are shown in

Table 5. Experimental lateral load and displacement values.

Loading Cycle	Specimen	Yielding Load *		Maximum Lateral Load			Failure Load **		Disp. Ductility Ratio
		Load (kN)	Top Displ. (mm)	Load (kN)	Top Displ. (mm)	Load Ratio	Load (kN)	Top Displ. (mm)
Forward	S-600-1	87.50	6.74	116.67	15.63	1.06	93.34	43.58	6.47
	S-600-2	82.70	5.97	110.26	10.87	1.00	88.20	39.81	6.67
	S-600-3	89.72	10.41	119.63	20.93	1.08	95.70	41.89	4.02
Reverse	S-600-1	87.32	7.17	116.43	12.13	1.08	93.14	41.14	5.74
	S-600-2	80.66	5.82	107.55	7.27	1.00	86.04	41.20	7.08
	S-600-3	92.50	9.51	123.33	25.33	1.15	98.66	51.23	5.39
Forward	S900-1	130.98	5.65	174.64	15.81	1.32	139.71	25.51	4.52
	S900-2	99.35	3.16	132.46	10.60	1.00	105.97	29.34	9.28
	S900-3	181.12	7.46	241.49	15.33	1.82	193.19	25.29	3.39
Reverse	S900-1	117.66	4.82	156.88	6.40	1.20	125.50	31.00	6.43
	S900-2	98.42	2.18	131.23	5.51	1.00	104.98	14.89	6.83
	S900-3	178.34	6.47	237.79	15.33	1.81	190.23	28.44	4.39

*: Yielding load values were determined based on 75% of the maximum lateral load. **: Failure displacement values were determined based on the ultimate displacement corresponding to a 20% decrease in the lateral load capacity.

, while the rigidity at the maximum load is provided in

Table 6. Maximum lateral load stiffnesses.

Specimen	S600-1	S600-2	S600-3	S900-1	S900-2	S900-3
Stiffness (kN/mm)	8.40	12.01	5.19	14.93	16.37	15.63

. The yielding load values were determined based on 75% of the maximum lateral load. The failure displacement values were determined based on the ultimate displacement corresponding to a 20% decrease in the lateral load capacity [38]. In this context, the rigidity at the maximum load was calculated based on the maximum lateral loads and the corresponding displacement values obtained from both forward and reverse loading cycles. S600-2 and S900-2 were considered to be reference specimens, as they were identified to have the lowest lateral load-bearing capacity for both shear wall sizes. Accordingly, increases were observed only in specimens S600-1 and S900-1 with internal anchorage, with a maximum increase of 8% and 32%, respectively, and in specimens S600-3 and S900-3 with increased internal anchorage, with an increase of 15% and 82%, respectively (Table 5). For the second group of test frames, it was concluded that the minimum lateral load-bearing capacity could be obtained due to the frame and the shear wall having the lowest concrete compressive strength. Compared to the reference S600-2 specimen, S600-1 exhibited increases of 6% and 8% in the forward and reverse loading directions, respectively, while S600-3 showed increases of 8% and 15%. For the frames with 900 mm shear walls, using S900-2 as the reference, S900-1 had increases of 32% and 20% and S900-3 had increases of 82% and 81% in the forward and reverse loading directions, respectively.

The maximum values were observed for S600-2 and S900-2 with different shear wall lengths in terms of the final lateral top displacement. Accordingly, when considering the forward loading cycles, the specimens with both internal and additional external anchors exhibited increases in the ultimate lateral top displacement of 62% in specimen S600-2 and 9% in specimen S900-2 compared to the first group of specimens that had the same amount of internal anchorage only.

An examination of the cumulative energy consumption capacity of the test specimens revealed that the capacity increased substantially in the second group of specimens, which utilized external anchorage in addition to internal anchorage for the shear wall–foundation joints, compared to the first group of specimens, which had only internal anchorage (

Table 7. Cumulative energy consumption capacities.

Specimen	S600-1	S600-2	S600-3	S900-1	S900-2	S900-3
Energy consumption (kNmm)	20,096	35,394	35,287	20,362	26,856	37,099

).

4. Load-Bearing Capacity of Internal Anchor Bars

The theoretical load-bearing capacity of the internal anchor bars used in the rehabilitative shear walls was determined while considering the relevant limitations, as influenced by the tensile and shear effects described in ACI318-19 (Chapter 17) [39]. The experimental results were compared with those theoretical findings. Figure 15 presents the possible concrete anchorage collapse modes that might occur under the tensile and shear loadings given in ACI318-19 [39].

Post-installed adhesive anchors are commonly used in strengthening applications for load transfer. The load transfer in adhesive anchors is carried out through contact between the anchor and the adhesive (epoxy) and between the adhesive (epoxy) and the concrete along the bonded area [40]. According to ACI318-19, the tension failure modes of adhesive anchors related to concrete include concrete breakout failures and bond failures. The shear failure modes of adhesive anchors related to concrete include concrete breakout failures and concrete pryouts. Furthermore, a steel failure under both tensile and shear loads is a failure mode for adhesive anchors. An evaluation of the bond strength applies only to adhesive anchors. Single anchors with a small embedment loaded to failure under tension may exhibit concrete breakout failures, while deeper embedments produce bond failures. Adhesive anchors that exhibit bond failures when loaded individually may exhibit concrete failures in a group or in a near-edge condition. The influence of the anchor spacing and the edge distance on both the bond strength and the concrete breakout strength must be evaluated for adhesive anchors [39]. In the case of the concrete breakout strength, the stress pattern has a direct relationship with concrete breakout failures. A concrete breakout failure occurs due to the low tensile capacity of concrete [41]. In his study on epoxy-bonded anchors, Cook (1993) [42] observed that anchor behaviour cannot be reliably predicted with sufficient safety after the elastic limit is exceeded [43].

According to ACI318-19, for the concrete breakout resistance of an anchor in tension, the nominal concrete breakout strength of a single anchor in tension, N_cb, can be calculated with Equation (1). In these equations, A_Nc is the total projected concrete failure area of a single anchor or group of anchors and A_Nco is the projected concrete failure area for a single anchor. In addition, N_cb is the nominal concrete breakout strength in tension of a single anchor, N_cbg is the nominal concrete breakout strength in tension of a group of anchors, ψ_ed,N is the breakout edge effect factor, ψ_c,N is the breakout cracking factor, ψ_c,pN is the breakout splitting factor, and ψ_ec,N is the breakout eccentricity factor.

Table 8. Coefficients used in calculations for anchor bars based on ACI318-19 [39].

${\Psi }_{ec,N}$: Breakout eccentricity factor	${\Psi }_{ec,N}={\displaystyle \frac{1}{\left(1+\frac{{2e}_N^{\prime }}{3h_{ef}}\right)}}\le 1.0$
${\Psi }_{ed,N}$: Breakout edge effect factor	If Ca,min ≥ 1.5hef, then ${\Psi }_{ed,N}$ = 1.0 If Ca,min < 1.5hef, then ${\Psi }_{ed,N}=0.7+0.3{\displaystyle \frac{c_{a,min}}{1.5h_{ef}}}$
${\Psi }_{c,N}$: Breakout cracking factor	$1.4$ for post-installed anchors
${\Psi }_{cp,N}$: Breakout splitting factor	If Ca,min ≥ Cac, then ${\Psi }_{cP,N}=1.0$ If Ca,min < Cac, then ${\Psi }_{cP,N}={\displaystyle \frac{C_{a,min}}{C_{ac}}}\ge {\displaystyle \frac{1.5h_{ef}}{C_{ac}}}$ For all other casese, including cast-in anchors, ${\Psi }_{cP,N}$ shall be taken as 1.00.

h_ef: effective embedment depth of anchor. e’_N: distance between resultant tension load on a group of anchors loaded in tension and the centroid of the group of anchors loaded in tension. C_a,min: minimum distance from the centre of an anchor shaft to the edge of the concrete. C_a,c: critical edge distance required to develop the basic strength as controlled by concrete breakout or the bond of a post-installed anchor in tension in uncracked concrete without supplementary reinforcement to control splitting.

provides the conditions and equations needed to calculate the relevant coefficients in these equations. The basic concrete breakout strength in tension of a single anchor in cracked concrete, N_b, can be calculated with Equation (2). The steel strength of anchors in shear can be calculated with Equation (3). The strength reduction factor is taken to be ϕ = 1.0.

$$\begin{gathered} \mathrm{For} \mathrm{a} \mathrm{single} \mathrm{anchor}: N_{cb}={\displaystyle \frac{A_{Nc}}{A_{Nco}}}{\Psi }_{ed,N}{\Psi }_{c,N}{\Psi }_{cp,N}{N}_b \\ \mathrm{For} \mathrm{an} \mathrm{anchor} \mathrm{group}: N_{cbg}={\displaystyle \frac{A_{Nc}}{A_{Nco}}}{\Psi }_{ec,N}{\Psi }_{ed,N}{\Psi }_{c,N}{\Psi }_{cp,N}{N}_b \end{gathered}$$

(1)

Here, ${\Psi }_{ec,N}=1.0$, ${\Psi }_{ed,N}=0.76$, ${\Psi }_{c,N}=1.4$, and ${\Psi }_{cp,N}=0.75$ are used for the coefficients in Equation (1).

The basic breakout strength of a single anchor, N_b, is as follows:

$$N_b=k_c{\lambda }_a\sqrt{f_c^{\prime }}{h}_{ef}^{1.5}$$

(2)

In this equation, the value of the coefficient for the basic concrete breakout strength in tension k_c was accepted as 7 (for post-installed anchors), while the modification factor λ_a was taken as 1.0 and h_ef was taken as equal to the length of the embedded bar. In this equation, f_c′ is the specified compressive strength of concrete and h_eff is the effective embedment depth of the adhesive anchors.

The steel strength of the anchors in shear, V_sa, can be calculated as follows:

$$V_{sa}=0.6A_{se,V}{f}_{uta}$$

(3)

Here, $A_{se,V}$ is the effective cross-sectional area of an anchor in shear (mm²) and the specified tensile strength of anchor steel, $f_{uta}$, is min (1.9$f_{ya}$ or 860 MPa). $f_{ya}$ signifies the yield strength of the anchor steel.

Table 9. Comparison of theoretical and experimental values based on ACI318-19 under the influence of tensile and shear effects in internal anchors.

Tension						Shear
Loading Cycle	Specimen	Moment (kNm)	Tension Force (kN)			Maximum Load (kN)	Shear Force (kN)
			T1	T1-theoretical	Texp./Ttheo.		V1	V1-theoretical	Vexp./Vtheo.
Forward	S-600-1	223.66	170.99	73.46	2.33	116.67	19.45	15.75	1.23
	S-600-2	211.37	161.60	86.905	1.86	110.26	18.38	15.75	1.17
	S-600-3	229.33	147.01	159.68	0.92	119.63	7.48	15.24	0.49
Reverse	S-600-1	223.20	170.64	73.46	2.32	116.43	19.41	15.75	1.23
	S-600-2	206.17	157.62	86.905	1.81	107.55	17.93	15.75	1.14
	S-600-3	236.42	151.55	159.68	0.95	123.33	7.71	15.24	0.51
Forward	S900-1	334.78	114.45	73.46	1.56	174.64	17.46	15.75	1.11
	S900-2	253.93	86.81	86.905	1.00	132.46	13.25	15.75	0.84
	S900-3	462.94	140.16	159.68	0.88	241.49	10.06	15.24	0.66
Reverse	S900-1	300.74	102.82	73.46	1.40	156.88	15.69	15.75	1.00
	S900-2	251.57	86.01	86.905	0.99	131.23	13.12	15.75	0.83
	S900-3	455.84	138.01	159.68	0.86	237.79	9.91	15.24	0.65

presents the results of the calculations for the internal shear wall–foundation anchors in the test specimens based on ACI318-19 [39]. These calculations were performed for the concrete breakout resistance under tensile loading for adhesive anchors and the steel strength of anchors under shear loading.

Table 9 presents only the calculation results for internal anchors. According to these values, the internal anchor bars in the third group of specimens are sufficient for tensile and shear effects. Due to the high number of internal anchor bars, the experimental load value per reinforcement decreased in the S600-3 and S900-3 specimens, and the T_exp./T_heo. values appeared particularly low. In the 600 mm rehabilitative wall specimens, it was observed that the force applied to each anchor reinforcement in the S600-2 specimen with internal anchors + external steel angle anchors was reduced compared to the S600-1 specimen under tensile and shear effects, and that the external anchors were partially effective. Similarly, in the S900-2 specimen with internal anchors + CFRP external anchors, the load applied to each anchor reinforcement was significantly reduced compared to the S900-1 specimen, and the external CFRP anchor was observed to be effective. For the second group’s S600-2 specimen, it was determined that damage may occur in the internal anchor bars under tensile stress, while the internal anchor bars in the S900-2 specimen were at the limit value under tensile stress. For the first group’s S600-1 and S900-1 specimens, it was determined that damage may occur under tensile stress.

As seen in Table 9, only S600-1, S600-2, and S900-1 were theoretically expected to exhibit concrete breakout due to tensile effects in terms of internal anchorage; no damage was expected for S600-3, and the damages were expected to be at the threshold limits for S900-2 and S900-3. Similar results were obtained for shearing effects with the same specimens.

Table 10. Damage that occurred at the shear wall–foundation joints of the specimens.

Specimen	S600 Specimens (a/d = 3.3)	S900 Specimens (a/d = 2.2)
1st group	Sliding of anchor bars (bond failure)	Sliding of anchor bars (bond failure + concrete splitting), concrete breakout
2nd group	Shear wall damage at web arm of angle’s bolt region	Sliding of internal anchor bars, rupture of external CFRP anchorage (bond failure)
3rd group	No failure (concrete splitting)	No failure (concrete splitting)

presents all of the damage that occurred in the shear wall–foundation joints for all the test specimens. When the damages sustained by the test specimens were examined, bond failures, concrete splitting, the sliding of anchor bars, and concrete breakouts were observed from among the collapse modes specified in ACI318-19.

Although the shear wall length was determined with consideration of both flexural and shear wall behaviour, shear cracking occurred in the shear walls of the third group of test specimens, where the anchor reinforcement was deemed sufficient. In contrast, the damages were concentrated at the shear wall–foundation interface in the first and second groups of specimens.

Since all the experimental members displayed the behaviour of a monolithic shear wall together with the wing-type shear wall pieces, columns, and beams used to improve the systems, it was concluded from the test results that the anchor bars were sufficient along the column and beam cross-sections.

5. Conclusions

In this study, structural strengthening was carried out by adding reinforced concrete rehabilitative shear walls with wings of two different dimensions in terms of their total length. As a result of quasi-static seismic loading tests on six two-storey, two-span reinforced concrete frames with different shear wall–foundation connection details, the following findings were obtained:

*

The anchors in the shear wall–foundation joints of the first and second groups of specimens were insufficient; the load-bearing capacity of the frame was reached either through the failure of the internal anchors or through damage occurring at the joints between the external anchors and the shear wall. For the third group of specimens, where the number of internal anchor bars and the development length were increased, no splitting or damage was observed in the shear wall–foundation joints. It was concluded that the splitting in the shear wall–foundation joints in the first and second groups of test specimens was due to an insufficient number of internal anchor bars in the foundation, the insufficient anchor length and development length of the bars, and the ineffectiveness of the additional external processes.

*

Considering the maximum lateral load-carrying capacity of the test frames, the smallest values were obtained for the specimens with additional external anchors. In addition, these specimens had the lowest concrete compressive strength and achieved the maximum values of final lateral top displacement.

*

Under the maximum lateral load, the highest rigidity values were obtained for the second group of test specimens, for which internal and external anchors were used together.

*

For specimen S600-1, a pull-out failure occurred in the anchor bars at the shear wall–foundation connection. For specimen S600-2, although no pull-out was observed in the internal anchor bars, the holes drilled in the body of the shear wall led to localized degradation in this region during later stages of loading. Therefore, the shear wall consumed the majority of the energy on the frame with the anchorage application, and the damage to other frame members was reduced. For specimens S600-2 and S600-3, higher displacement levels were achieved in the frames compared to S600-1. However, no significant damage or deterioration was observed, particularly at the beam–column joints or the column bases.

*

Although lap splice lengths exceeding the minimum requirements specified in ACI318-19 were used in the test specimens, bar fractures occurred in the anchor bars at the shear wall–foundation joints in only the third group of specimens, where the number of internal anchor bars was higher. In contrast, pull-out failures were observed in the shear wall–foundation anchor reinforcements of the first group of specimens, which had the same concrete compressive strength as the third group. This shows that the number of anchorage reinforcements is a significant parameter in reinforcement pull-out.

*

For specimen S600-2, shear cracks did not occur at the edge joints at the same lateral displacement level, in contrast to specimen S600-1, with only internal anchor bars. This shows that the damage level of the frame decreased and that the additional steel angle contributed at least partially to the structural behaviour. No damage was observed on the foundation surface when the steel angles used for external anchorage in the shear wall–foundation joint were removed.

*

In S900-2, with the shear wall–foundation joint wrapped in CFRP, and S900-3, in which the number of internal anchors was increased, shear cracks did not occur at the edge joints at the same lateral displacement level as that observed for the other frames. This indicates a reduction in the damage level of the frame and also demonstrates the effectiveness of both the CFRP laminate and the enhanced internal anchors.

*

Cracks in the third group of test specimens started at the level where the vertical anchorage reinforcements used in the foundation of the shear wall ended; they occurred in the form of shearing cracks. The anchor reinforcements from the foundation contributed to the moment-bearing strength as vertical reinforcement of the shear wall. Since the point where the anchor ended was the point where an instant decrease was observed in the shear wall vertical reinforcements, it was also deemed the point where the low moment capacity began.

*

Generally, for the three types of specimens, damage occurred in the columns before the shear wall could reach its bearing strength in the frames with 600 mm shear walls. The shear wall length (a/d ratio: 3.3) was insufficient for the columns to prevent damage, indicating that the columns required strengthening.

*

Considering the general status of the frames with 900 mm shear walls, no major damage occurred in elements other than the columns and shear walls. This indicates the adequacy of the length of the shear wall in this system, suggesting that no additional strengthening—such as sheathing, especially around the columns—would be needed in such cases. If sufficiently long walls are used, both lateral drifts are restricted, and time-consuming and expensive processes, such as the strengthening of other frame members that lack sufficient capacity, are not required.

*

Shear cracks occurred in the joint regions of the specimens at the first-storey beam–column joint on the left edge due to the absence of stirrups in the joint area (i.e., weak column). Therefore, it was clearly seen that the stirrups must be continued along the columns in joints. Vertical cracks also occurred on the edges of beams.

This study demonstrated that the most effective shear wall–foundation anchorage for partially reinforced concrete shear walls entails the use of a single anchor bar for each vertical shear wall reinforcement, as is generally applied in practice, with a sufficient development length within both the foundation and the shear wall. It is obvious that the type of anchorage examined in this study, which significantly improved the overall structural behaviour of the frame with a very low concrete compressive strength requiring seismic strengthening, would be even more effective if the concrete compressive strength was relatively high. In larger structural dimensions, the group effect, anchor spacing, edge distance, nearby edges, and adjacent loaded anchors about this optimal anchorage method must be evaluated.

This method can be applied to all reinforced concrete buildings that are insufficiently resistant to seismic effects. Since the rehabilitation wall is between the existing beam–column system, full connection can be provided. If the existing foundation system is continuous, there may be no need to change the foundation system through a simple strengthening operation on the foundation.

Future studies should investigate whether extending the vertical reinforcement used in the end regions of reinforced concrete wing shear walls to the base can prevent the reinforcement from slipping and the anchors from loosening, thereby enabling the shear walls to achieve a higher load-bearing capacity. Where the length of the shear wall is insufficient to prevent damage, particularly at joints, the overall behaviour can be examined when these areas are reinforced with CFRP laminates, CFRP strips, steel strips, or steel profiles. The overall system behaviour and the behaviour of the reinforced shear wall–foundation region can be examined when the axial load level in the columns is increased.