Study on the Influence Mechanism of Metro-Induced Vibrations on Adjacent Tunnels and Vibration Isolation Measures

Abstract

To investigate the effectiveness of vibration mitigation and isolation measures for adjacent tunnels in a metro-induced vibration environment, this study employed a similarity theory-based scaled model test at a ratio of 1:15. The prototype was the Guangzhou 500 kV Suixi-Chuting power transmission tunnel project. The experimental methodology was designed to simulate the vibration impact on adjacent tunnels from metro loading and to evaluate the performance of various countermeasures. The vibration response mechanisms induced by different mitigation materials were analyzed. The results demonstrate the theoretical feasibility of the overall design of the scaled model test, which accurately reproduces the vibration influence on adjacent tunnels from metro loads. Both Expanded Polystyrene (EPS) and rubber particles were found to provide measurable vibration reduction. However, the attenuation achieved by EPS was significantly greater than that of rubber particles, indicating the superior performance of EPS as a vibration isolation material. Furthermore, the isolation mechanisms of both materials were discussed based on observations of their behavioral changes during the vibration isolation process. The findings of this study offer valuable insights and a reference for selecting appropriate vibration mitigation materials in practical engineering applications.

1. Introduction

The ongoing urbanization drives the rapid expansion of underground utility tunnels and metro systems. While power cable tunnels are forming critical energy networks, their paths often intersect with metro lines. A key challenge arising from this coexistence is the impact of train-induced vibrations on the power infrastructure, particularly its vibration-sensitive components such as precision instruments and cables. These vibrations can compromise equipment functionality, accuracy, and long-term reliability. Although the need for vibration control is recognized, the specific effectiveness of different isolation materials in protecting adjacent power tunnels remains insufficiently explored. This study aims to address this gap by systematically evaluating the performance of various mitigation measures, providing essential insights for the design and protection of resilient urban underground infrastructure.

Numerous scholars have conducted extensive research on vibrations induced by metro systems and other rail transit, alongside corresponding mitigation and isolation strategies. Focusing on the source of vibrations, Zhen et al. [1] investigated the dynamic response and properties of tunnel surrounding soil under cyclic loading. Their study, based on a typical soil strain model, identified metro vibration loads as the primary factor influencing long-term settlement.

Regarding vibration propagation and characteristics, Li et al. [2], based on a crossing project in Nanjing, monitored vibrations during blasting excavation. They found significant differences in frequency distribution along the tangential, radial, and vertical directions of the tunnel, with major vibration energy concentrated in the high-frequency band. Similarly, Cai et al. [3] coupled vehicle and track-ground subsystems, demonstrating that dynamic loads significantly contribute to the dynamic response in a porous elastic space, predominantly in high-frequency ranges. Tang [4], using FLAC3D, reported that vibration responses in ground and structures decrease with distance from the metro, but an amplification zone can occur at a certain range. Chen and Zhang et al. [5] investigates face stability in earth pressure shield tunnelling. A 3D computational framework reveals that dynamic cutterhead excavation and soil spatial variability jointly reduce stability. The findings underscore the necessity of considering both factors in chamber pressure design, and a new safety factor-based method is proposed and validated.

On the dynamic response of tunnel structures, Yan et al. [6] numerically analyzed impact damage during train operation, finding that the damage at the tunnel bottom was less severe than at the top, with tensile damage dominating over compressive damage. Yan Q et al. [7], combining numerical simulation with model tests, studied tunnel lining response under different train speeds and clear spacings. They observed that increased speed reduces the energy spectrum values of the vibration load, and that the sidewall experiences less dynamic response than the crown and bottom. They also noted that acceleration in a lower tunnel decreases with increasing spacing, but the attenuation trend diminishes. Zucca and Crespi et al. [8] investigated the influence of shallow subsurface structures on the evaluation of seismic signals. Research on mitigation materials and methods is also extensive. Ding et al. [9,10,11] explored the application of metamaterials for vibration and seismic isolation, discussing design principles related to local resonance, nonlinear behavior of saturated porous media, and the isolation capabilities of auxetic materials. Liang et al. [12] proposed using rubber concrete as a vibration-damping backfill layer for railway tunnels. Sadeghi J [13] demonstrated, via FEM, that a soft grouting layer combined with stiff soil effectively attenuates metro vibrations.

Concerning structural reinforcement, Chango I [14] investigated Carbon Fiber Reinforced Polymer (CFRP) for strengthening tunnel linings under metro vibrations, confirming its effectiveness through field tests and numerical simulation.

For seismic isolation, Kim et al. [15] highlighted that circular tunnels are susceptible to deformation during earthquakes, and suggested that a thin coating on the tunnel lining can effectively mitigate seismic damage. Hasheminejad et al. [16] numerically verified the effective shock absorption of a lining-coating structure for circular tunnels. Furthermore, Wang et al. [17], using ABAQUS to simulate EPS buffer layers with different elastic moduli, found that seismic isolation improves with decreasing modulus and increasing thickness. The elastic modulus had a more pronounced effect than thickness, with the softest EPS providing the best isolation even at smaller thicknesses.

Building upon the current research progress in vibration mitigation for underground structures, this study addresses an identified research gap: the lack of comparative model tests evaluating the isolation effectiveness of different materials under metro-induced vibrations. To bridge this gap, the present study first synthesizes the characteristics of various mitigation materials used in underground structures and consolidates the existing knowledge on metro vibration impacts on adjacent tunnels. Informed by an understanding of potential hazards to power tunnels, the Guangzhou 500 kV Suixi-Chuting power transmission project is selected as the prototype.

A comprehensive experimental program involving a scaled model test (1:15) was designed and implemented. This involved the meticulous design and calculation of all internal components and parameters of the model test setup, including:

• Determination of the similarity ratios.
• Fabrication of the model box, including the metro and power tunnels.
• Selection of the model soil.
• Design of the excitation system to simulate train vibrations.
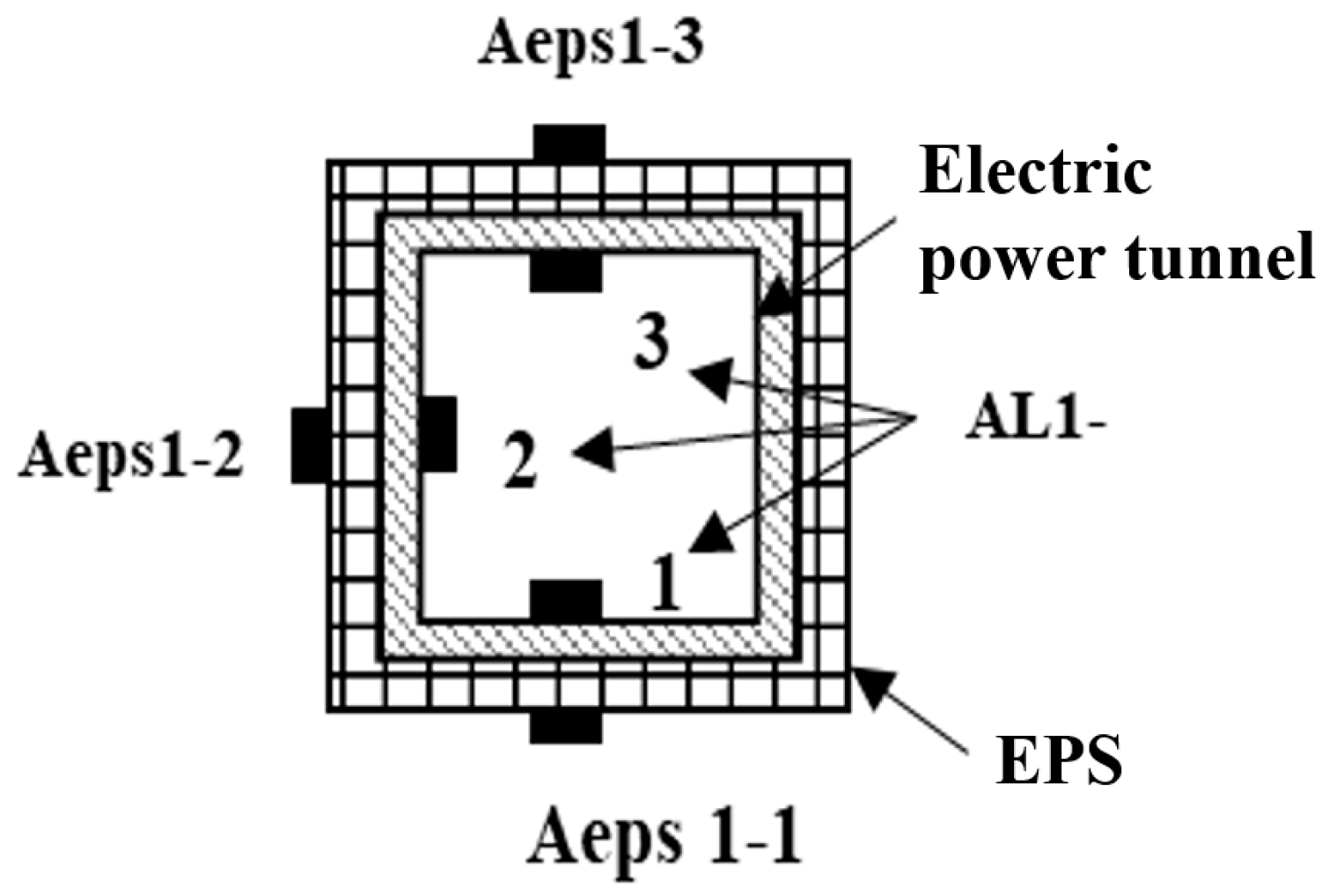
• Layout of key measurement points and instrumentation.
• Selection and configuration of the vibration isolation materials (EPS and rubber particles).

Subsequently, the dynamic responses at key measurement points of the adjacent tunnel were analyzed under three conditions: without any mitigation measure, with an EPS isolation layer, and with a rubber particle isolation layer. The analysis revealed the vibration response pattern of the adjacent tunnel under simulated metro train loads and evaluated and compared the isolation effectiveness of EPS and rubber particles. The findings provide valuable references and a basis for selecting appropriate vibration isolation materials in practical tunnel engineering.

2. Test Method

2.1. Test Device and Principle

The design of the scaled model was primarily guided by the similarity theory to establish the scaling relationships between the model and the prototype parameters. For dynamic testing, dynamic similarity must also be satisfied. Based on the objectives and characteristics of this study, the following key similarity constants were adopted: a geometric scale ratio (S_l) of 15 (prototype:model), an elastic modulus scale ratio (S_E) of 7, and a density scale ratio (Sρ) of 1. The subscript “m” denotes the physical model, while “p” represents the prototype. The specific derivation procedure is as follows:

The Second Similarity Theorem, also known as the π-theorem, was proposed by the American scholar E. Buckingham in 1914 and has since been extensively studied and applied by numerous researchers. It can be described as follows: Suppose a physical system consists of n distinct physical quantities, denoted as X₁, X₂, …, X_n, and can be characterized by the equation f(X₁, X₂, …, X_n) = 0. If there exist k dimensionally independent physical quantities, where k < n, then the functional relationship among these n physical quantities can be expressed using n − k dimensionless parameters. By introducing this association into the dimensionless π terms of the similarity criterion, the relationship can be formulated as follows:

$$F\left({\pi }_1,{\pi }_2,{\pi }_3,\dots ,{\pi }_{n-k}\right)=0$$

(1)

For two physical phenomena, each governed by their respective functional relationships, if they are considered similar phenomena, then a one-to-one correspondence must exist between their dimensionless π terms (${\pi }_{1p}={\pi }_{1m},{\pi }_{2p}={\pi }_{2m}{,\pi }_{3p}={\pi }_{3m},\dots ,{\pi }_{(n-k)p}={\pi }_{(n-k)m}$);

$$F{\left({\pi }_1,{\pi }_2,{\pi }_3,\dots ,{\pi }_{n-k}\right)}_p=0$$

(2)

$$F{\left({\pi }_1,{\pi }_2,{\pi }_3,\dots ,{\pi }_{n-k}\right)}_m=0$$

(3)

This experiment primarily investigates the vibration responses of the metro tunnel–soil–power tunnel system under sinusoidal loading at different frequencies and sweep-frequency loading simulating train-induced excitation. Since the model deformations remain within the elastic range and in accordance with the similitude requirements and characteristics of the scaled model test, similarity relationships for the following 18 physical quantities are considered, as summarized in

Table 1. Eighteen Fundamental Physical Quantities.

Name of Physical Quantity	Physical Quantity	Name of Physical Quantity	Physical Quantity	Name of Physical Quantity	Physical Quantity	Name of Physical Quantity	Physical Quantity
Length	L	Mass	M	Poisson’s Ratio	ν	Velocity	v
Displacement	u	Time	T	Density	ρ	Acceleration	a
Area	A	Frequency	F	Cohesion	C	Gravitational Acceleration	g
Stress	σ	Concentrated Load	F	Friction Coefficient	μ	Surface Load	p
Strain	ε	Elastic Modulus	E

.

According to the Second Similarity Theorem, the phenomena observed in the model test can be represented by a functional relationship composed of these 18 physical quantities, expressed as:

$$f(l,u,A,\sigma ,\epsilon ,E,v,\rho ,C,\mu ,m,t,f,v,a,g,F,P)=0$$

(4)

Based on the dynamic characteristics of the test, the elastic modulus $E$, length $l$, and density $\rho$ were selected as the fundamental physical quantities. Their dimensions are $\left[L\right]$, $\left[M\right][L{]}^{-3}$, and $\left[M\right]\left[L{]}^{-1}\right[T{]}^{-2}$, respectively, where $\left[M\right]$ denotes the mass dimension and $\left[T\right]$ the time dimension. According to the Second Similarity Theorem, with $n=18$ (the total number of physical quantities) and $k=3$ (the three fundamental quantities being mutually independent), a total of 15 dimensionless $\pi$ terms can be derived, as follows:

$${\mathit{\pi }}_{\mathsf{1}}={\displaystyle \frac{\mathit{u}}{\mathit{l}}},{\mathit{\pi }}_{\mathsf{2}}={\displaystyle \frac{\mathit{A}}{{\mathit{l}}^{\mathsf{2}}}},{\mathit{\pi }}_{\mathsf{3}}={\displaystyle \frac{\mathit{\sigma }}{\mathit{E}}},{\mathit{\pi }}_{\mathsf{4}}=\mathit{\epsilon },{\mathit{\pi }}_{\mathsf{5}}=\mathit{v},{\mathit{\pi }}_{\mathsf{6}}={\displaystyle \frac{\mathit{C}}{\mathit{E}}},{\mathit{\pi }}_{\mathsf{7}}=\mathit{\mu },{\mathit{\pi }}_{\mathsf{8}}={\displaystyle \frac{\mathit{m}}{\mathit{\rho }{\mathit{l}}^{\mathsf{3}}}},{\mathit{\pi }}_{\mathsf{9}}={\displaystyle \frac{\mathit{t}}{\mathit{l}{\mathit{\rho }}^{\mathsf{1}/\mathsf{2}}{\mathit{E}}^{-\mathsf{1}/\mathsf{2}}}}$$

(5)

$${\mathit{\pi }}_{\mathsf{10}}={\displaystyle \frac{\mathit{f}}{{\mathit{l}}^{-\mathsf{1}}{\mathit{\rho }}^{-\mathsf{1}/\mathsf{2}}{\mathit{E}}^{\mathsf{1}/\mathsf{2}}}},{\mathit{\pi }}_{\mathsf{11}}={\displaystyle \frac{\mathit{v}}{{\mathit{\rho }}^{-\mathsf{1}/\mathsf{2}}{\mathit{E}}^{\mathsf{1}/\mathsf{2}}}},{\mathit{\pi }}_{\mathsf{12}}={\displaystyle \frac{\mathit{a}}{{\mathit{l}}^{-\mathsf{1}}{\mathit{\rho }}^{-\mathsf{1}}\mathit{E}}},{\mathit{\pi }}_{\mathsf{13}}={\displaystyle \frac{\mathit{g}}{{\mathit{l}}^{-\mathsf{1}}{\mathit{\rho }}^{-\mathsf{1}}\mathit{E}}},{\mathit{\pi }}_{\mathsf{14}}={\displaystyle \frac{\mathit{F}}{{\mathit{l}}^{\mathsf{2}}\mathit{E}}},{\mathit{\pi }}_{\mathsf{15}}={\displaystyle \frac{\mathit{P}}{\mathit{E}}}$$

(6)

In the model, these π terms must correspond one-to-one and be equal in value to their counterparts in the prototype, leading to 15 relational expressions that must be satisfied among the similarity constants. Based on the objectives and characteristics of this scaled model test, the following key similarity constants were adopted: a geometric scale ratio (prototype to model) of S_l = 15, an elastic modulus similarity constant of S_E = 7, and a density similarity constant of Sρ = 1. Using the derived similarity relationships, the dimensions and similarity ratios (prototype to model) for the remaining physical quantities beyond the fundamental set were calculated and are summarized in

Table 2. Dimensional Relationships, Similarity Relations, and Scaling Ratios.

Name of Physical Quantity	Fundamental Dimensions	Similarity Relation	Scaling Ratio	Name of Physical Quantity	Fundamental Dimensions	Similarity Relation	Scaling Ratio
Length	[$L$]	$S_l$	15	Friction Coefficient	—	$S_{\mu }=1$	1
Displacement	[$L$]	$S_u=S_l$	15	Concentrated Load	[$M$][$L$][$T$]−2	$S_F=S_E{S_l}^2$	875
Area	[$L$]2	$S_A={S_l}^2$	125	Surface Load	[$M$][$L$]−1[$T$]−2	$S_P=S_E$	7
Stress	[$M$][$L$]−1[$T$]−2	$S_{\sigma }=S_E$	7	Mass	[$M$]	$S_m=S_{\rho }{S_l}^3$	3375
Strain	—	$S_{\epsilon }=1$	1	Time	[$T$]	$S_t=S_l{S_{\rho }}^{1/2}{S_E}^{-1/2}$	5.66
Elastic Modulus	[$M$][$L$]−1[$T$]−2	$S_E$	7	Frequency	[$T$]−1	$S_f={S_l}^{-1}{S_{\rho }}^{-1/2}{S_E}^{1/2}$	0.17
Poisson’s Ratio	—	$S_{\nu }=1$	1	Velocity	[$L$][$T$]−1	$S_v=S_{\rho }^{-1/2}{S}_E^{1/2}$	2.64
Density	[$M$][$L$]−3	$S_{\rho }$	1	Acceleration	[$L$][$T$]−2	$S_a={S_l}^{-1}{S_{\rho }}^{-1}{S}_E$	0.466
Cohesion	[$M$][$L$]−1[$T$]−2	$S_c=S_E$	7	Gravitational Acceleration	[$L$][$T$]−2	$S_g=1$	1

.

The model container was constructed as a rigid box with internal dimensions of 2.2 m in length, 2.2 m in width, and 2.0 m in height. The main frame of the model container was constructed from hollow rectangular steel tubes with cross-sectional dimensions of 60 mm in width, 40 mm in height, and a wall thickness of 3 mm. The connections between tubes were primarily made by welding, supplemented with bolting for reinforcement. Corrugated plates were installed as inner wall surfaces and securely fastened to the frame using bolts. To minimize wave reflections at the boundaries and prevent boundary effects, the base and all four inner walls of the container were lined with 60 mm-thick Expanded Polystyrene (EPS) boards. Consequently, the effective internal soil space measured 2.0 m in each dimension (length, width, and height) after accounting for the EPS layers. The metro tunnel was modeled with an outer diameter of 0.4 m, an inner diameter of 0.36 m, and a wall thickness of 0.02 m. It was assembled from segmented linings, simulating a typical ring structure composed of standard, adjacent, and key segments, with a total longitudinal length of 2 m. The power tunnel, with a longitudinal length of 2 m, was positioned parallel to and 0.8 m directly above the metro tunnel. Its cross-section was square, with an outer side length of 0.19 m, an inner side length of 0.15 m, and a wall thickness of 0.019 m. The instrumentation scheme included accelerometers, displacement transducers, earth pressure cells, and resistance strain gauges installed on both the inner and outer surfaces of both tunnel models. Additionally, accelerometers were embedded within the soil mass to monitor wave propagation. The configuration of the model container is illustrated in Figure 1, while the sensor layout and the overall experimental setup are detailed in Figure 2.

2.2. Materials

(1)

Model Soil

This test simulated multiple soil layers to a total depth of 30 m. To facilitate model construction, the original strata were homogenized into a single layer by calculating a thickness-weighted average of the soil properties. A large-scale model container was employed to minimize testing distortion, and the soil was sourced from the deep foundation pit excavation of the Guangzhou 500 kV Suixi-Chuting power transmission project. In accordance with the Standard for Geotechnical Testing Methods (GB/T 50123-2019) [18], the prototype soil was tested using a laboratory liquid-plastic limit combination apparatus, yielding a liquid limit of 42.7% and a plastic limit of 22.4%. While maintaining the same density as the prototype soil, the shear modulus of the model soil was reduced by adjusting its dry density and water content. Laboratory resonant column tests were conducted, with the testing process illustrated in Figure 3, to determine the key physical parameters of the soil model, as summarized in

Table 3. Physical Properties of the Soil.

Structure	Type	Unit Weight (kN/m3)	Elastic Modulus (kN/m2)	Shear Modulus (G/MPa)	Poisson’s Ratio (ν)
Soil	Prototype	19.7	72.9	28.1	0.3
	Model	19.7	14.56	6.27	0.3

.

(2)

Tunnel Materials

The metro tunnel lining segments feature an outer diameter of 6 m, wall thickness of 0.3 m, and inner diameter of 5.4 m. The lining system consists of precast reinforced concrete segments with concrete strength class C50. Circumferential connections between segments are established using two M27 high-strength bolts per joint, with six joint surfaces per ring resulting in twelve high-strength bolts total. Longitudinal connections between adjacent rings are made with ten M24 high-strength bolts per ring. Based on the geometric scaling ratio of S_l = 15 for this model test, the dimensions of the metro tunnel lining segments were determined as follows: a ring thickness of 0.02 m, an outer diameter of 0.4 m, and an inner diameter of 0.36 m. To satisfy the similitude requirements for material properties, micro-concrete was used for casting. Through elastic modulus testing and laboratory uniaxial compressive strength tests, the final mix proportion was determined as 1:1.07:3.72:5.12 (water:cement:fine sand:fine aggregate). The achieved concrete strength grade was C25, with an elastic modulus of 23.17 GPa, essentially meeting the similitude requirements.

The prototype track bed was made of plain concrete with a strength grade of C30. The model track bed was also cast using plain concrete, with a mix ratio of 0.27:0.81:1.16:2.12 (water:cement:fine sand:coarse sand). The model track bed dimensions were 2 m in length, 0.175 m in width, and 0.04 m in height. Rails and sleepers were installed within the track bed. The prototype rail was 60 kg/m, scaled down to 1.21 kg/m in the model. Due to the geometric scaling constraints, steel springs and rail fastenings were too small to fabricate and install reliably and were therefore omitted. The rails and sleepers were connected by welding the sleepers to the rails, maintaining the required similitude relationship with the prototype.

The power tunnel utilizes precast segments with concrete strength class C60, featuring a square cross-section with side length of 2.9 m and wall thickness of 0.3 m. The reinforcement follows a double-layer configuration using HRB400 grade steel bars. Identical reinforcement arrangements are employed in both the top and bottom layers, each consisting of five φ16 mm bars uniformly distributed in the transverse direction, with longitudinal bars spaced at 200 mm intervals. Each side wall layer contains six φ16 mm bars in the transverse direction, maintaining the same reinforcement ratio as the top and bottom sections. For the power tunnel, scaling from the prototype using the similarity ratios yielded a model with an outer side length of 0.19 m, a wall thickness of 0.019 m, and an inner side length of 0.15 m. The simulated segments were also constructed from micro-concrete, with a mix proportion of 1:0.75:3.57:4.98:0.19 (water:cement:fine sand:fine aggregate:fly ash). The reinforcement scheme for the model was designed based on the principle of equivalent strength. It featured double-layer reinforcement, with each longitudinal layer consisting of 24 φ1.4 mm bars spaced at 40 mm, and each transverse layer consisting of 75 φ1.4 mm bars spaced at 40 mm. Diagrams of the tunnel lining model and the power tunnel model are shown in Figure 4. Based on the similitude requirements for material properties and the principle of equivalent strength, micro-concrete was used for casting. The key physical parameters of the model structure were determined through elastic modulus testing and laboratory uniaxial compressive strength tests, and the key physical parameters of the model structures are summarized in

Table 4. Key Physical Parameters of the Model Structures.

Structure	Type	Unit Weight (kN/m3)	Compressive Strength (MPa)	Elastic Modulus (kN/m2)
Metro Segment	Prototype	24.2	60	34.5
	Scaled Model	24.4	10.1	7.2
Trackbed	Prototype	23.7	30	30
	Scaled Model	23.9	6.3	6.1
Power Tunnel	Prototype	23.9	40	32.5
	Scaled Model	24.1	8.3	6.2

.

(3)

Vibration Mitigation and Isolation Materials

The vibration isolation materials adopted in this study are EPS and rubber particles. Expanded Polystyrene (EPS) foam is manufactured through a series of processes including bead expansion, curing, and mold shaping. Its unique cellular structure consists of numerous closed-cell compartments containing trapped air, which account for a significant portion of its volume. This structure gives EPS its low density, excellent compressibility, and moderate elasticity. Since its first application in embankment engineering in Norway in 1972, EPS has gained increasing attention in geotechnical engineering due to its favorable mechanical and physical properties. The EPS boards used in this study have a thickness of 60 mm.

Rubber particles, classified by source material and mechanical characteristics, commonly include types derived from shoe soles and waste tires. Particles produced from waste tires exhibit properties such as corrosion resistance, heat tolerance, wear resistance, and certain elasticity, developed through long-term environmental exposure including rain erosion, high temperatures, elastic deformation under pressure, and abrasion. The rubber particles used in this study are manufactured from recycled tires, showing minimal inter-particle variability. Their application also contributes to environmental sustainability by repurposing waste tires and reducing associated pollution. The rubber particles have a grain size of 5–8 mm, cubical shape, and micro-textured surfaces. The thickness of the rubber particle vibration mitigation layer employed in this study is 60 mm.

With reference to existing research [19], the material parameters of EPS and rubber particles adopted in this study are listed in

Table 5. Material Parameters of EPS and Rubber.

Material	Compressive Strength (MPa)	Poisson’s Ratio	Coefficient of Friction with Concrete	Coefficient of Friction with Soil
EPS	1.6	0.075	0.69	0.3
Rubber particles	1.8	0.48	0.31	0.34

.

2.3. Test Loads

Based on the Guangzhou 500 kV Suixi-Chuting power transmission project, this experiment was designed to investigate the effectiveness of different vibration mitigation and isolation materials for power tunnels in a metro-induced vibration environment. The test scenarios included the following conditions directly above the metro tunnel at a 0.8 m vertical distance and 0-degree crossing angle: a power tunnel without any mitigation materials, one with EPS isolation, and one with rubber particle isolation, all under different loading conditions. To account for the high-frequency components of irregular dynamic loads, the tests without isolation measures applied a sinusoidal excitation to the shaker with a 1800 mV input voltage, 15 s duration, and three distinct frequencies: 25 Hz, 75 Hz, and 225 Hz. For tests with isolation measures (EPS or rubber particles), the excitation was set at 1800 mV, 15 s duration, and a fixed frequency of 75 Hz. The dynamic cart maintained a travel speed of 0.35 m/s throughout all tests. Figure 5 shows the time-history curve of the sinusoidal load.

A self-designed adjustable reaction system was developed for this test. By adjusting the position of clamping plates and beams, the circular beam and the integrated dynamic cart could be repositioned as needed, thereby preventing derailment and ensuring close contact between the loading system and the tunnel. Furthermore, to overcome the limitations of conventional single-point or multi-point excitation methods—such as excessive force concentration at a single point and the difficulty in simulating continuous load superposition and speed variations—a movable dynamic system was custom-built. This system utilizes a mobile controller to operate an electric hoist, which drives the cart. The speed of the hoist is regulated to simulate different train velocities, while a vibration exciter applies the dynamic load. This setup significantly enhances the realism of the test results. The model of the dynamic cart is shown in Figure 6.

Based on the test objectives and characteristics, a combined loading scheme of moving and fixed harmonic loads was adopted. For the moving load component, the target speed derived from the similitude relationships ranged from 3.15 to 9.46 m/s. However, due to equipment limitations and safety considerations, the actual travel speed of the dynamic cart during testing was maintained between 0 and 0.55 m/s. Specific speeds within this operable range were selected, with a total travel distance of 2 m. Accordingly, a speed reduction factor was applied during data processing to correct the test results and ensure their validity under the intended similitude conditions.

Table 6. Test Conditions.

Condition	Spatial Parallel Angle and Distance (m)	Axis Intersection Angle	Excitation Load	Frequency (Hz)	Velocity (m/s)
1	Power tunnel 0.8 m directly above metro tunnel	0°	Sinusoidal Load	15, 75, 225	0.35
2	Power tunnel 0.8 m directly above metro tunnelEPS polyethylene foam vibration isolation and damping	0°	Sinusoidal Load	75	0.35
3	Power tunnel 0.8 m directly above metro tunnelRubber particle isolation and vibration reduction	0°	Sinusoidal Load	75	0.35

shows the different test conditions.

3. Test Results and Analysis

3.1. Structural Response of the Power Tunnel Without Vibration Isolation Measures

(1)

Acceleration Response

Figure 7 compares the acceleration time-history curves measured at the bottom of the metro tunnel under sinusoidal excitation at 15 Hz, 75 Hz, and 225 Hz. Under the low-frequency excitation (15 Hz), the acceleration amplitude is small (0.017 m/s²) and the waveform appears irregular, lacking a distinct sinusoidal pattern, which is attributed to its higher susceptibility to environmental noise interference. As the excitation frequency increases to 75 Hz, the waveform becomes markedly more sinusoidal, and the acceleration amplitude rises significantly to 0.072 m/s². A further increase in frequency to 225 Hz results in an even clearer sinusoidal waveform and a substantial growth in acceleration amplitude, reaching 0.163 m/s². These observations indicate that low-frequency vibrations (below 25 Hz) are prone to environmental noise contamination, whereas vibrations within the 25–200 Hz range exhibit well-defined sinusoidal waveforms and considerably larger acceleration amplitudes.

The time-domain curve of vibration acceleration provides a clear observation of how acceleration changes over time, but it fails to reveal the contribution of different frequency components to the overall vibration. Therefore, the acceleration time-domain signal is converted into the frequency domain via Fourier transform, a mathematical method. Using MATLAB (version R2022a; The MathWorks Inc., Natick, MA, United States), the time-domain curve is transformed into a frequency-domain curve, as shown in Figure 8. Analysis of measurement point A10-3 indicates that the dominant frequency bands of vibration at the top of the metro tunnel lining are 175–250 Hz and 300–350 Hz, with relatively large amplitudes. When the vibration propagates to the soil above the lining, a comparison between points A10-3, At3, and At7 shows a significant reduction in the high-frequency range of 150–400 Hz. As the vibration transmits from At3 to At7, the frequency components in the 100–150 Hz range also decrease noticeably. However, near the power tunnel at point At7, the acceleration amplitude in the 50–100 Hz range increases compared to that at At3. This suggests that the soil attenuates high-frequency vibrations while amplifying certain low-frequency components.

Based on multiple tests, it was determined that the magnitude of vertical vibration acceleration is greater than that in the transverse and longitudinal directions, and the attenuation of vertical acceleration is slower. Therefore, vertical vibration is dominant. The peak vertical accelerations at each measurement point without vibration isolation materials are shown in Figure 9 The peak vibration accelerations at point A10-1 (tunnel bottom) and point A10-3 (tunnel crown) of the metro tunnel are 0.124 m/s² and 0.076 m/s², respectively. The peak vibration accelerations at points At3 and At7 in the soil between the metro tunnel and the power tunnel are 0.0412 m/s² and 0.0468 m/s², respectively. The peak accelerations at the bottom and top measurement points on the inner wall of the power tunnel are 0.0358 m/s² and 0.0294 m/s², respectively. The peak acceleration at point At10 in the soil above the power tunnel is 0.0132 m/s². This indicates that the vibration acceleration decreases as it propagates upward through the soil, with attenuation ratios of 39%, 46%, 13%, and 55%, respectively. It can be concluded that the vibration acceleration generally attenuates during propagation from the metro tunnel through the soil to the power tunnel.

In summary, as the propagation distance from the vibration source increases through the soil, the metro-induced vibration acceleration generally decreases overall, with high-frequency vibrations attenuating rapidly. In contrast, mid-to-low frequencies attenuate more slowly compared to high frequencies. During upward propagation through the overlying strata or upon encountering structures, not all frequency components decrease monotonically; some mid-to-low frequency components may rebound and increase at certain distances from the foundation or structures. This phenomenon can be attributed to two main reasons. Firstly, the soil layer has a significant capacity to absorb and filter wave energy, particularly resulting in considerable attenuation of high-frequency vibration responses after penetrating the soil, while low-frequency components experience less attenuation. Secondly, as vibrations propagate upward through the soil, wave refraction and reflection occur when they reach the bottom of the power tunnel. The reflected waves superimpose in the soil near the tunnel bottom, leading to an increase in the wave acceleration amplitude.

(2)

Dynamic Strain Response

This section analyzes test results obtained under a 75 Hz sinusoidal excitation applied by the shaker and a travel speed of 0.35 m/s. The dynamic strain of the metro tunnel lining and the power tunnel segments under vibrational loading is shown in Figure 10. The dynamic strain in the tunnel structure exhibits periodic variation over time, with tensile strain defined as positive and compressive strain as negative.

Regarding the dynamic strain of the tenth ring segment of the metro tunnel, at the same cross-section along the longitudinal direction, the peak dynamic strain near the vibration source at the tunnel invert is 1.5με, with roughly equal magnitudes of tensile and compressive stress. The peak dynamic strains at the sidewall and crown are 0.87με and 0.63με, respectively. This indicates that the longitudinal dynamic strain alternates between tension and compression along the metro segment. In the circumferential direction, the peak dynamic strains from the invert, sidewall, to crown are 1.2με, 0.36με, and 0.021με, respectively, and are primarily tensile. Thus, when ignoring the sign of dynamic strain, the absolute peak values of both longitudinal and circumferential dynamic strain decrease progressively from the invert to the crown. The reduction is more pronounced from the invert to the sidewall and becomes gentler from the sidewall to the crown.

Comparing the circumferential and longitudinal dynamic strains at the invert, sidewall, and crown of the tunnel structure reveals that the longitudinal dynamic strain response is greater than the circumferential. Moreover, from the invert to the crown, the longitudinal strain gradually becomes more dominant compared to the circumferential strain. Therefore, greater attention should be given to the longitudinal dynamic strain in the design and maintenance of the segments, particularly at the invert location.

The variation patterns of dynamic strain at the invert, sidewall, and crown of cross-section 1 and cross-section 2 of the power tunnel are generally consistent. The following discussion uses cross-section 1 as an example. As shown in Figure 11, the peak dynamic strain values at each measurement point show little variation, indicating that changes in train speed have a relatively minor influence on the dynamic strain response of the power tunnel segments.

(3)

Earth Pressure Response

This section analyzes test results obtained under a 75 Hz sinusoidal excitation applied by the shaker and a travel speed of 0.35 m/s. The time-history curve of the contact pressure between the metro tunnel lining and the surrounding soil is shown in Figure 12. Due to the high frequency of vibration and data sampling, the readings from the earth pressure cells are notably dense. As shown in Figure 12, the contact pressure between the tunnel structure and the soil exhibits a regular cyclical pattern under vibrational loading. Measurement points T10-1, T10-2, and T10-3, located at the invert, left sidewall, and crown of the tenth ring segment, respectively, recorded peak contact pressures of 1.85 kPa, 0.8 kPa, and 0.1 kPa. During the vibration process, the contact pressure between the lining and the soil generally ranged from 0 to 1.85 kPa, demonstrating a gradual decrease from the tunnel invert to the crown.

Therefore, under metro-induced loading, the contact pressure between the segment and the soil transitions from compression at the invert to tension at the crown, with the most significant dynamic interaction occurring at the tunnel bottom. Special attention should be given to the pressure from the underlying soil during segment design and construction. Furthermore, the variation in contact pressure between the power tunnel and the surrounding soil follows a consistent pattern under different train speeds.

3.2. Structural Response of the Power Tunnel with Vibration Isolation Measures

(1)

Acceleration Response

Figure 13 and Figure 14 show the sensor layout schematic diagrams under the conditions of EPS and rubber particle vibration isolation materials, respectively. Figure 15 and Figure 16 show the actual on-site arrangement of EPS and rubber particles in the model box, respectively. Figure 17 and Figure 18 show the acceleration results at different locations under the two types of vibration isolation materials, respectively.

For the EPS isolation material under sinusoidal excitation, the recorded peak vibration accelerations were as follows: 0.12 m/s² at point A10-1 (tunnel invert) and 0.04 m/s² at A10-3 (tunnel crown) of the metro tunnel; 0.038 m/s² and 0.025 m/s² at soil measurement points At3 and At6 located between the metro tunnel and the power tunnel; 0.037 m/s² at the bottom of the EPS cushion layer; 0.0148 m/s² and 0.008 m/s² at the bottom and top of the power tunnel inner wall, respectively; and 0.0042 m/s² at soil point At10 above the power tunnel. These results clearly illustrate the continuous attenuation of metro-induced vibration as it propagates from the metro tunnel through the soil to the power tunnel, with the soil exhibiting the greatest attenuation, followed by the metro tunnel, and the power tunnel showing the least. Notably, as vibrations passed through the EPS layer to the power tunnel base, the peak acceleration decreased from 0.032 m/s² to 0.0121 m/s²—a significant attenuation of 62%. This demonstrates EPS’s considerable capacity to dissipate vibration energy and its effective vibration-damping performance. The sharp slope of the attenuation curve in this segment further confirms the substantial damping effect. The underlying mechanism involves the compression of enclosed gas within the foam structure—sometimes leading to cell rupture—and the resulting compressive deformation of the foam, both of which consume vibrational energy. Additionally, sliding friction between foam particles further dissipates energy, collectively contributing to the isolation effect.

In the case of rubber particle isolation material under sweep-frequency loading, measured peak accelerations were: 0.152 m/s² at A10-1 (tunnel invert) and 0.11 m/s² at A10-3 (tunnel crown); 0.042 m/s² and 0.028 m/s² at soil points At3 and At4; 0.029 m/s² at the bottom of the rubber particle layer; 0.0171 m/s² and 0.0089 m/s² at the bottom and top of the power tunnel inner wall; and 0.0042 m/s² at At10. These data similarly confirm the progressive attenuation of vibration during propagation from the metro tunnel through the soil to the power tunnel. When vibrations transmitted through the rubber particle layer to the power tunnel base, the peak acceleration reduced from 0.029 m/s² to 0.0171 m/s², corresponding to a 41% attenuation. This indicates that rubber particles can dissipate vibration energy, providing a moderate damping effect. The vibration reduction mechanism involves minor elastic deformation of the rubber particles upon energy input, which consumes part of the vibration energy. Simultaneously, relative sliding occurs between particles. Owing to the non-smooth surfaces of the rubber particles, inter-particle sliding friction also dissipates energy, and the compaction of gaps between particles further enhances the overall vibration damping.

(2)

Dynamic Strain Response

This section analyzes the test results obtained under a 75 Hz sinusoidal excitation applied by the shaker and a travel speed of 0.35 m/s. As shown in Figure 19, the dynamic strains at the bottom and sidewall of cross-section 1 of the power tunnel—located directly above the metro vibration source—under different vibration isolation measures are presented. Without isolation measures, the peak dynamic strains at the bottom and sidewall are 2.4με and 1.8με, respectively. With EPS isolation, the corresponding peak dynamic strains, as indicated in the figure, are 1.4με and 1.38με, varying within a range of 0–1με. With rubber particle isolation, the peak dynamic strains are 2.1με and 1.78με, varying within a range of 0–0.3με. These results demonstrate that both EPS and rubber particle isolation lead to reductions in dynamic strain at both the bottom and sidewall compared to the unisolated case, although the extent of reduction is relatively small.

(3)

Earth Pressure Response

This section analyzes test results obtained under a 75 Hz sinusoidal excitation and a travel speed of 0.35 m/s. As shown in Figure 20, the contact earth pressures at the invert and sidewall of cross-section 1 of the power tunnel, located directly above the metro vibration source, are presented for different vibration isolation measures.

For the EPS isolation material, the peak contact pressures at the invert and sidewall are 0.8 kPa and 0.39 kPa, respectively. With EPS isolation installed, the corresponding peak pressures at the invert and sidewall of cross-section 1 are 0.38 kPa and 0.13 kPa, varying within a range of 0–0.42 kPa. For the rubber particle isolation material, the peak contact pressures at the invert and sidewall are 0.2 kPa and 0.1 kPa, varying within a range of 0–0.6 kPa.

These results indicate that both EPS and rubber particle isolation reduce the contact earth pressure at both the invert and sidewall compared to the unisolated case, although the reduction is relatively modest.

3.3. Comparison of Power Tunnel Structural Responses Under Different Vibration Isolation Measures

As observed in Figure 21: (1) The peak accelerations for both EPS and rubber particles are lower than those in the unisolated case, demonstrating that both materials provide effective vibration mitigation and isolation. (2) At the location of the isolation layer, the curve exhibits a steeper slope, indicating a more rapid attenuation of acceleration. This confirms that both EPS and rubber particles effectively reduce metro-induced vibrations, with EPS exhibiting a greater degree of attenuation compared to rubber particles, thus demonstrating superior vibration isolation performance.

Regarding the dynamic strain of the tunnel and the earth pressure, the variations under different vibration isolation conditions are relatively minor; therefore, a comparative discussion of these aspects is not provided here.

4. Limitations

While the scaled model test employed in this study effectively captures the general patterns of metro-induced vibration effects on adjacent tunnels, several limitations should be acknowledged. Firstly, although the 1:15 geometric scaling ratio satisfies primary similitude requirements, it may not fully replicate the complex responses observed in real-world engineering scenarios, particularly concerning high-frequency vibrations and material nonlinear behavior. Secondly, despite the installation of EPS boards along the model container boundaries to mitigate wave reflections, it remains challenging to accurately simulate the infinite domain boundary conditions present in actual strata, which may affect the authenticity of vibration wave propagation. Furthermore, the model soil and vibration-damping materials used in the test involved idealized parameters, differing from the non-uniformity and long-term performance variations in materials in practical engineering applications. Nevertheless, these limitations are inherent challenges in model testing and do not undermine the main conclusions of this study regarding the performance comparison of vibration isolation materials and the general patterns of vibration propagation.

5. Conclusions

Based on a combination of field investigations, literature review, and scaled model tests, this study addresses the vibration-induced damage in adjacent tunnels caused by metro operations. Using the Guangzhou 500 kV Suixi-Chuting power transmission project as the prototype, a 1:15 scaled model test was designed to simulate the vibration impact on adjacent tunnels and evaluate the effectiveness of vibration mitigation measures. The vibration response mechanisms of different mitigation materials were analyzed, leading to the following main conclusions:

(1)

Vibration Acceleration Attenuation Pattern: The vibration acceleration generally decreases with increasing distance from the source. The soil exhibits a stronger suppressive effect on high-frequency vibrations, which attenuate more rapidly, while mid-to-low frequency vibrations attenuate relatively more slowly. The acceleration is highest in the soil beneath the tunnel lining, followed by the side sections, and is relatively lower in the upper part.

(2)

Spatial Variation and Special Phenomena in Vibration Propagation: During upward propagation, vibrations attenuate in all directions, with the fastest attenuation in the transverse direction, followed by the longitudinal direction, and the slowest in the vertical direction. When propagating to a certain distance near the ground surface or structures, some mid-to-low frequency vibrations do not continue to decrease but may rebound and increase.

(3)

Vibration Mitigation Effectiveness of EPS and Rubber Particles: The model tests show that the attenuation ratios of vibration acceleration for EPS and rubber particles are 60% and 41%, respectively. Both materials can reduce the peak acceleration. A steeper attenuation slope is observed at the isolation layer location, and EPS demonstrates superior vibration attenuation compared to rubber particles, indicating better overall performance.

(4)

Based on comparative observations of material changes before and after testing, and in light of the material properties and existing research [20], the vibration isolation mechanisms of the two materials are inferred as follows: EPS dissipates vibration energy through compression-induced gas release and foam deformation, accompanied by inter-particle sliding friction, while rubber particles achieve energy dissipation via minor elastic deformation, inter-particle sliding friction, and gap filling effects.

In summary, for the design of vibration-sensitive tunnels adjacent to metro lines, it is recommended to adopt an EPS layer as the primary vibration isolation material, which should be arranged at both the tunnel invert and sidewalls to achieve significant vibration attenuation. Rubber particles may serve as a supplementary measure when necessary. Additionally, dynamic response monitoring and protective measures should be strengthened, particularly in the tunnel bottom region.