Influence of Bolt Arrangement on the Shear Performance of Circumferential Joints of Segments in Super-Large Cross-Section Shield Tunnels

Abstract

To evaluate the shear performance of circumferential joints in super-large cross-section shield tunnels featuring inclined bolts and distributed mortises and tenons, refined numerical models were developed for three distinct configurations: single-bolt aligned mortise and tenon (SAB), single-bolt offset (SOB), and double-bolt offset (DOB). This study focuses on assessing how variations in bolt arrangement influence the shear behavior of these joints. The results are as follows: Under the effect of the ordinal shearing loading scenario (OSLS), bolts can significantly bear the load, resulting in the superior shear performance of DOB over SAB and SOB. Under the reverse shearing loading scenario (RSLS), bolts exhibit noticeable pullout phenomena, leading to minimal differences in the shear-dislocation curves of the three bolt arrangement pattern joints. The shear mechanical performance of SOB is notably better than that of SAB and SOB under OSLS, but this difference is less evident under RSLS. The mechanical behavior of bolts remains consistent across different bolt arrangement pattern joints during shear deformation. The bolt holes in SAB passing through the mortise and tenon weaken them, and contact failure between bolts and bolt holes further damages the mortise and tenon.

1. Introduction

In recent years, an increasing number of large-section shield tunnels have been constructed to meet the growing demands of transportation [1]. During construction, issues such as segment uplift, and during operation, issues such as external disturbances often lead to severe dislocation at circumferential joints. These phenomena significantly affect the safety, watertightness, and durability of the tunnel structure [2,3], while also weakening its overall structural resilience. Structural resilience reflects the ability of a structure to resist damage, maintain functionality, and delay failure under external loads and disturbances [4]. Therefore, investigating the shear mechanical performance of circumferential joints in shield tunnels is not only crucial for controlling joint deformation, but also essential for enhancing the structural resilience and long-term service reliability of shield tunnel structures.

Extensive research has been conducted on the mechanical behavior of longitudinal joints using theoretical analyses, full-scale experiments, and numerical simulations. In contrast, studies focusing on the mechanical performance of circumferential joints remain limited. For example, Zhang et al. [5] examined the shear behavior and failure modes of joints composed of inclined bolts and mortise-and-tenon connections. Similarly, Zuo et al. [6] investigated the overlap, shear stiffness, and failure characteristics of gas tunnel joints under both positive and negative shear loading. Zhang et al. [7] explored the stress conditions of positioning tenon and bolts using numerical calculation model, revealing the reinforcement effect of positioning tenon. Zhang et al. [8] studied the shear performance of small-diameter subway joints constructed using dowel structure through full-scale tests, analyzing the stress states of each component. Guo et al. [9] combined full-scale experiments with a numerical calculation model to investigate the mechanical performance of inclined bolt with mortise and tenon joints under different directional shear forces, employing distributed optical fiber for detailed bolt stress monitoring. Zhou et al. [10] researched the load-bearing process of sleeve-straight bolt combination type connection joints under shear and compared the differences in shear stiffness of joints under positive and negative shear conditions. Han et al. [11] investigated the effect of bolts on joint shear stiffness and evaluated the overall shear stiffness of circumferential joints through numerical simulations.

The primary design for circumferential joints in super-large cross-section shield tunnels combines distributed mortises and tenons with inclined bolts arranged in three main configurations [3]. The first configuration involves a single inclined bolt aligned with the mortise and tenon joint [12], as seen in the Shiziyang Tunnel on the Foshan-Dongguan Intercity Railway. The second arrangement features a single inclined bolt offset from the mortise and tenon joint [9,13], utilized in tunnels such as the Jinan Yellow River Tunnel and the Suzhou-to-Nantong GIL UHV Power Gallery Tunnel. The third arrangement places two bolts on either side of the mortise and tenon joint [14], adopted in tunnels like the Qinwang Tunnel, the Jiangyin-Jingjiang Tunnel, and the Haizhu Bay Tunnel.

Although these three bolt arrangements are widely employed in super-large cross-section shield tunnels, their differences in shear mechanical behavior remain unclear. Therefore, a comprehensive study is necessary to elucidate how these bolt configurations influence the shear performance of circumferential joints in large-section shield tunnels. In light of this, leveraging the Haizhu Bay shield tunnel as the engineering context, this study establishes refined numerical calculation models for three bolt arrangement configurations: single-bolt aligned mortise and tenon arrangement (SAB), single-bolt offset mortise and tenon arrangement (SOB), and double-bolt offset mortise and tenon arrangement (DOB). The models adopt the Concrete Damage Plasticity (CDP) model to capture the damage evolution of concrete. This study examines the shear performance of circumferential joints in super-large cross-section shield tunnels with various bolt arrangement configurations.

2. Numerical Simulation

2.1. Project Background

Spanning the Haizhu and Panyu districts in Guangzhou, China, the Haizhu Bay Tunnel begins north of Nanzhou Road and connects to the Dongxiaonan Viaduct. The tunnel passes beneath the Lizijing Waterway of the Pearl River, Luoxi Island, and the Sanzhixiang Waterway, continuing south toward Nanpu Avenue. The project’s total route length is 4350 m, including a shield tunnel section of 2012 m. The primary structure comprises C60 reinforced concrete segments configured in a “1 + 2 + 7” pattern: one key (F) segment, two adjacent (L1, L2) segments, and seven standard (B1–B7) segments. The lining ring has an external diameter of 14.5 m, an internal diameter of 13.3 m, thickness of 600 mm, and width of 2000 mm. The segments are connected using inclined bolts with a strength class of 8.8, corresponding to an ultimate tensile strength of 800 MPa and a yield strength of 640 MPa, in accordance with the Chinese national standard GB/T 3098.1-2010 Mechanical properties of fasteners—Bolts, screws and studs [15]. The circumferential joints utilize 28 distributed mortise-and-tenon connections and 56 longitudinal bolts, each with a diameter of 30 mm, a length of 739 mm, and an installation inclination angle of 58.78°. Figure 1 illustrates the segment structure schematically.

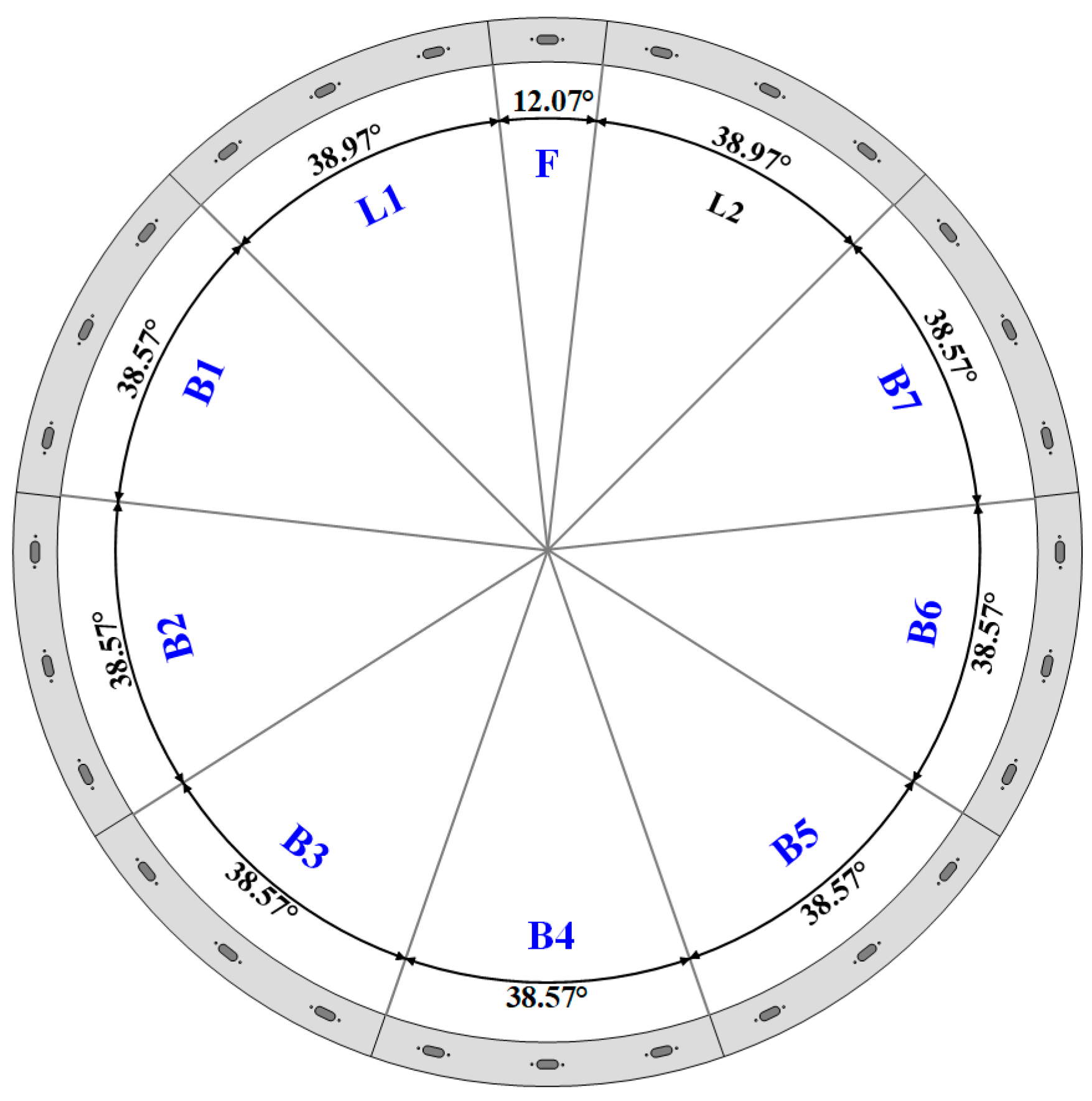
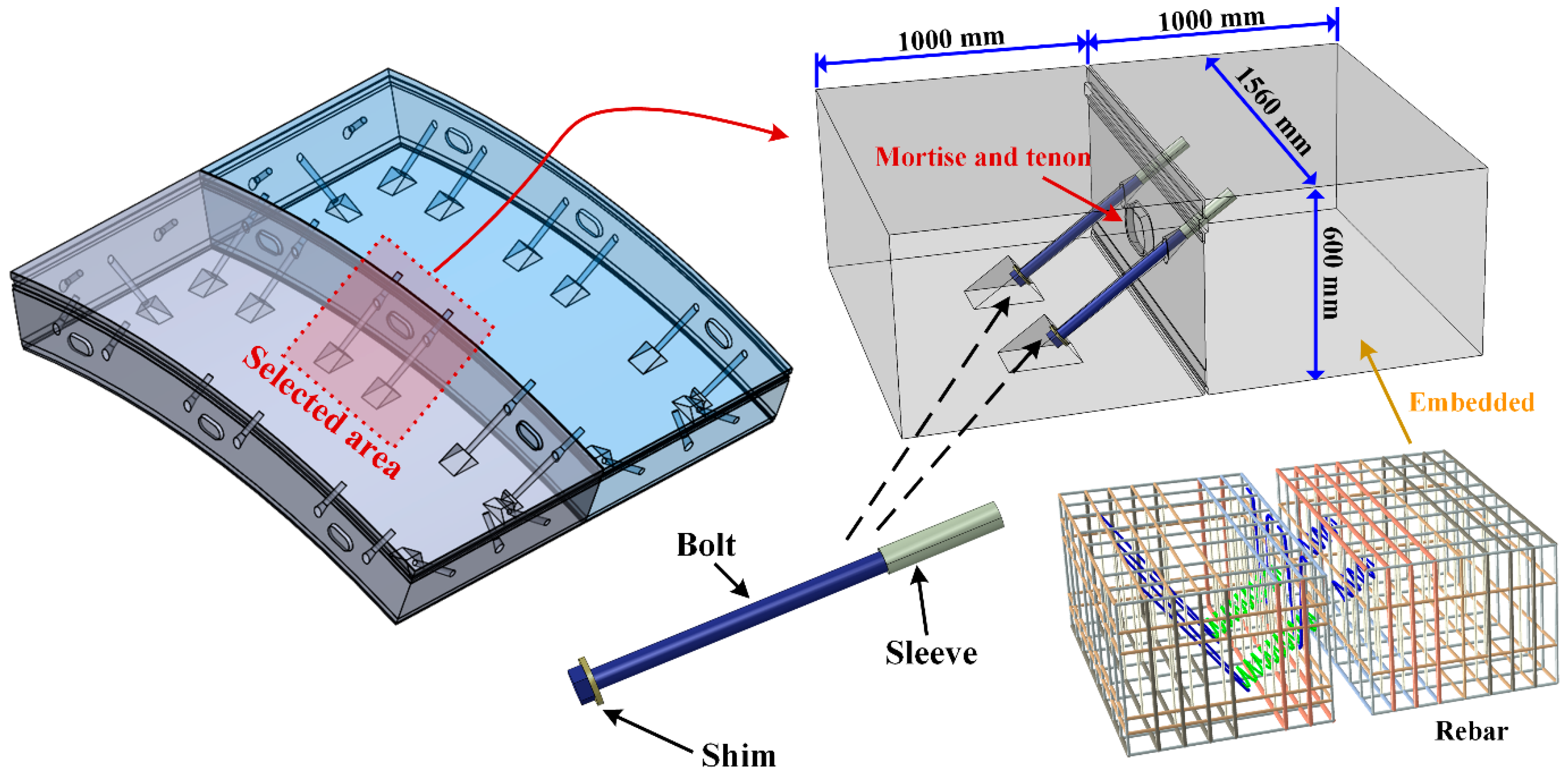
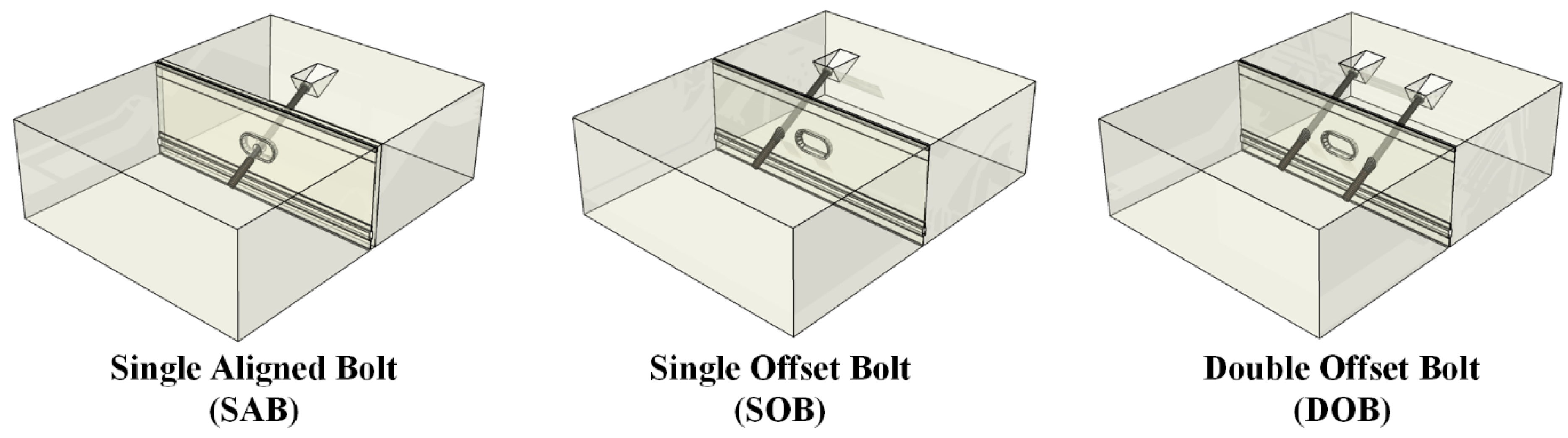
2.2. Overview of the Numerical Model

The segments of the Haizhu Bay Tunnel are connected between rings using a uniform arrangement of 28 units of double bolts and single mortise and tenon. A unit comprising two inclined bolts coupled with a mortise-and-tenon assembly was chosen as the study subject to investigate the shear strength of segment ring joints. This shear joint model is shown in Figure 2. Additionally, considering the tunnel’s maximum outer diameter of 14.5 m and its large curvature radius, the dimensions of the mortise-tenon and inclined bolt joint are comparatively compact. Hence, the impact of curvature on the mechanical behavior of the joints can be disregarded in calculations. As a result, the ring joints are simplified to direct joints for calculation, and this simplification also aids in controlling boundary conditions and applying loads. Nevertheless, the possible secondary influence of curvature will be addressed in future studies.

A three-dimensional refined finite element model of the mortise-and-tenon ring joint incorporating inclined bolts was constructed in ABAQUS (2021) based on the dimensional parameters of the Haizhu Bay Tunnel, as depicted in Figure 2. C3D8R elements were employed to simulate the mortise and tenon, two bolts, sleeves, and shim, while the reinforcement was modeled using T3D2 truss elements. The internal reinforcement cage of the ring joint corresponds to the range of the ring joint, with a width equal to 1/3 of the standard block arc length and a length half the width, ensuring that the distribution and diameter of the reinforcement match those of the original segment [6,16,17]. The bolts were preloaded with a force of 100 kN [3].

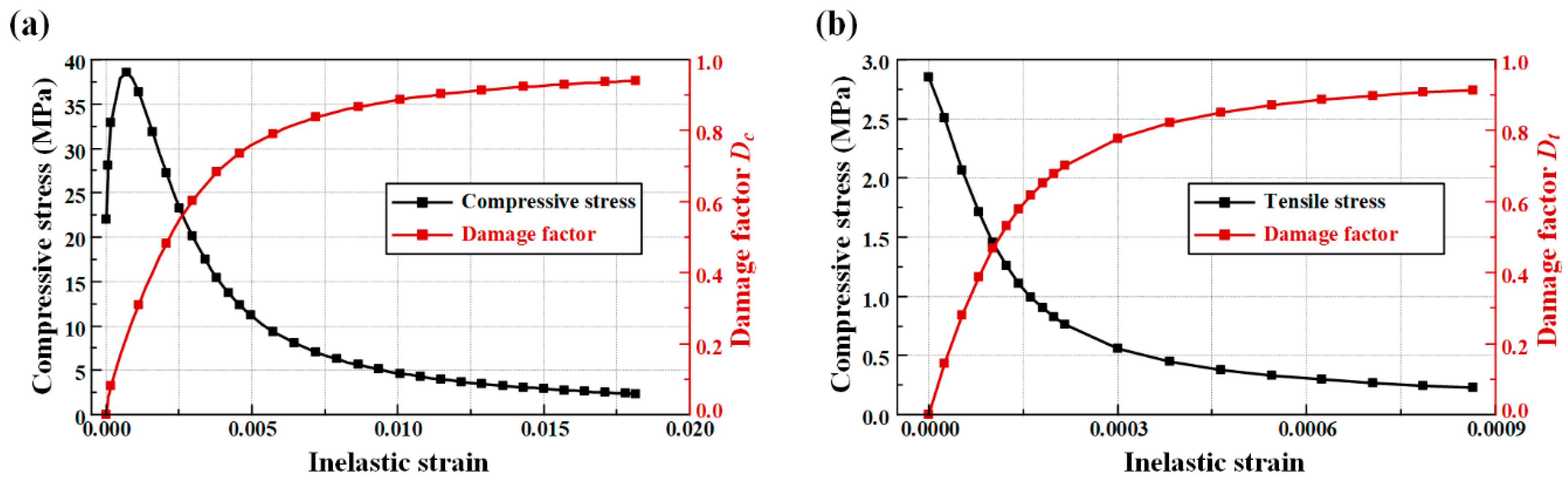
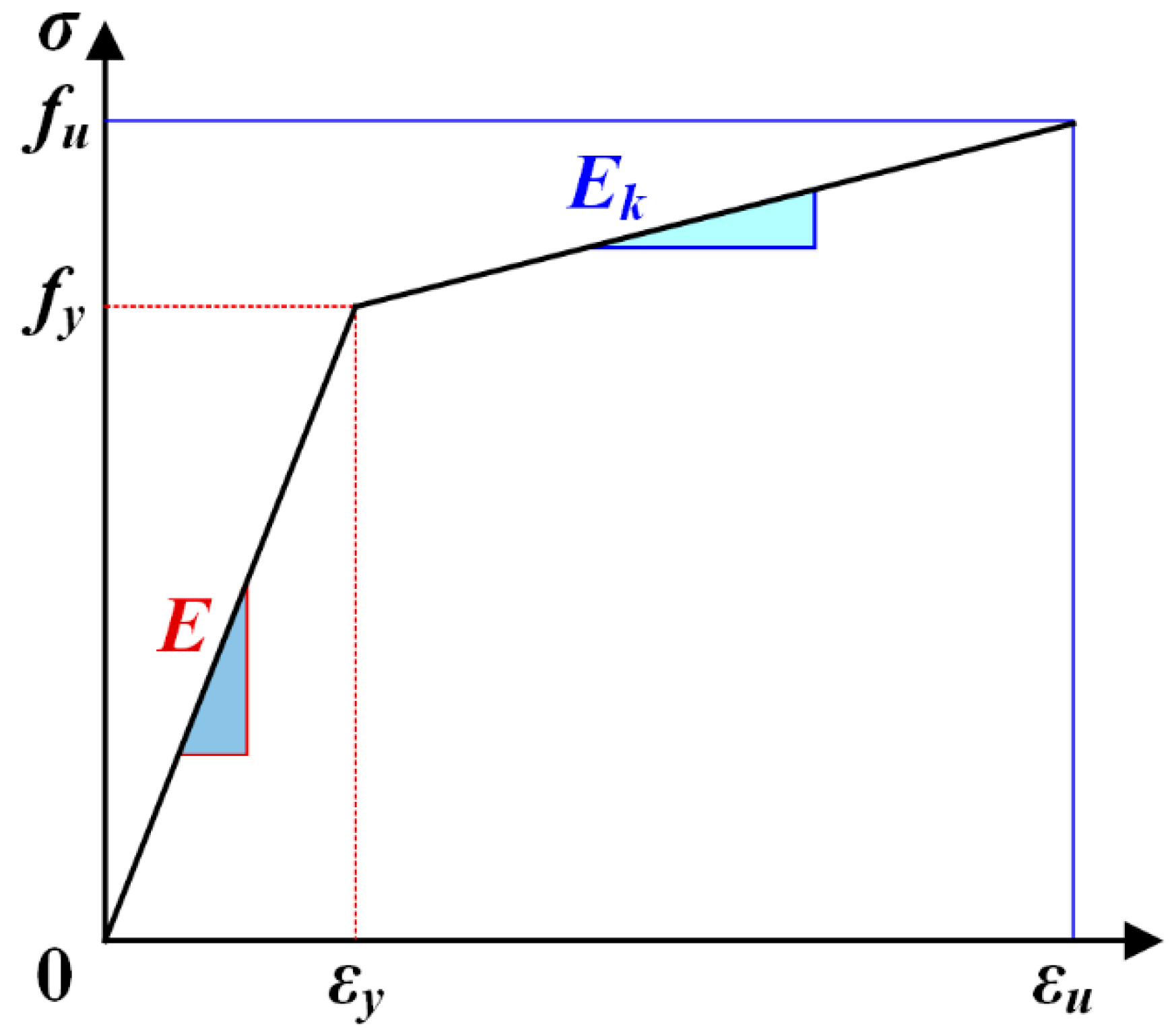
2.3. Material Properties

The Concrete Damage Plasticity (CDP) model was employed in the numerical analysis to accurately capture the mechanical response of concrete. It allows for the distinction between tensile and compressive behaviors and incorporates damage accumulation, thereby providing a realistic representation of concrete failure [18,19]. The segmental structure of the Haizhu Bay Tunnel utilizes C60 concrete, with standard axial compressive and tensile strengths of 38.5 MPa and 2.85 MPa, respectively. In this study, the stress–strain curves for concrete in tension and compression were derived based on the Code for Design of Concrete Structures (GB50010-2010) [20]. Additionally, the equivalent energy method proposed by Sidoroff et al. [21] was employed to determine the damage factors and the stress-inelastic strain relationships for both compressive and tensile loading, as shown in Figure 3.

As shown in Figure 4, the steel reinforcement and bolts were modeled using a bilinear constitutive relationship, with f_y indicating yield stress, f_u representing ultimate stress, E representing elastic modulus, and E_K representing the hardening modulus set at 0.01 times E. Detailed material parameters for the numerical model are listed in

Table 1. Mechanical properties of materials used in the numerical model.

Material	Elastic Modulus (GPa)	Poisson’s Ratio	Yield Strength (MPa)	Ultimate Strength (MPa)
Concrete (Class C60)	0.04	0.20	——	——
Bolt (Grade 8.8)	0.16	0.30	640	800
Reinforcement (HPB300)	210	0.30	300	400
Reinforcement (HRB400)	200	0.30	400	540
Sleeve	2	0.35	——	——
Shim	210	0.33	——	——

.

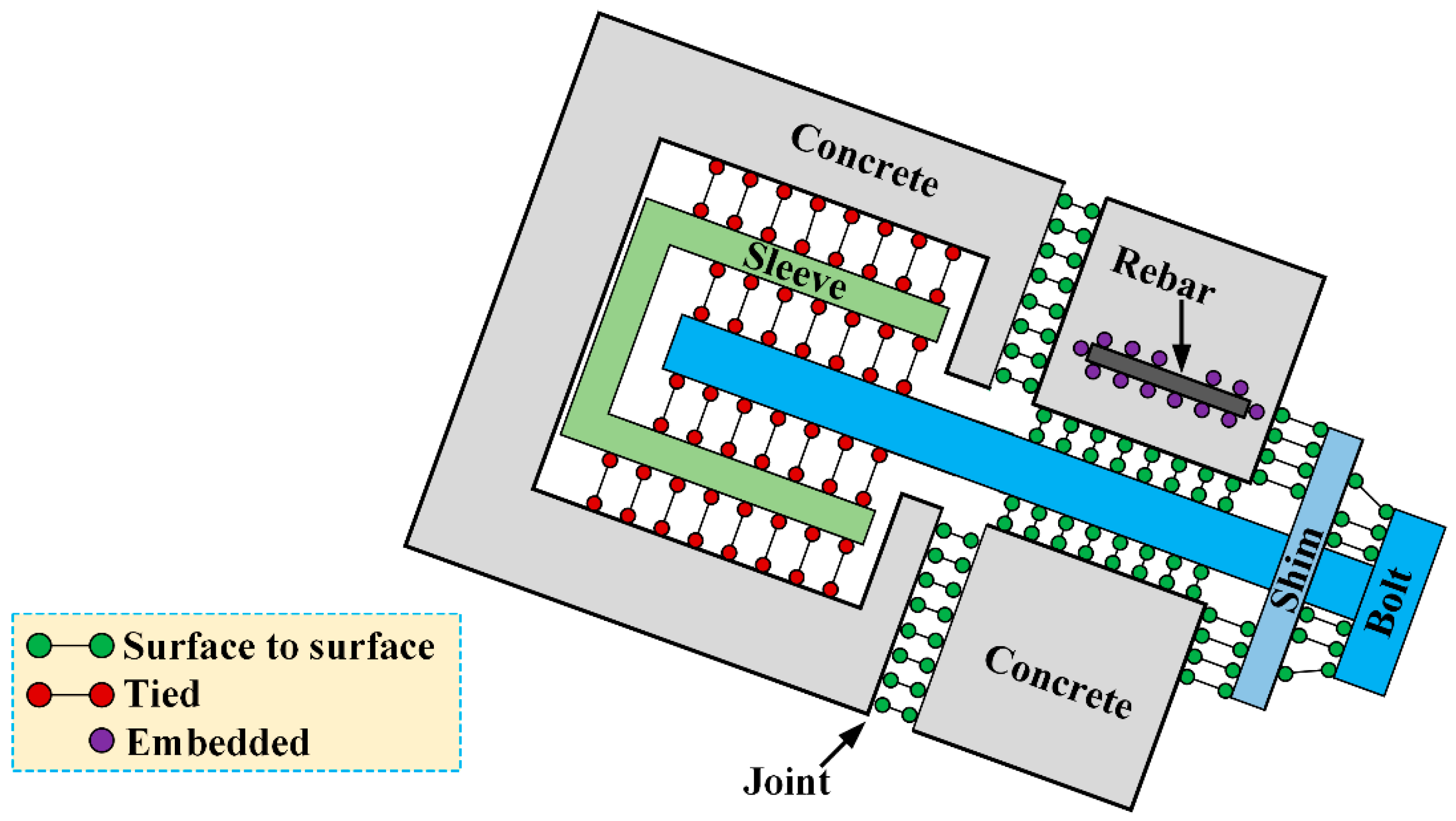
2.4. Interactions

In the numerical model, contact interactions among concrete-concrete, bolt-concrete, and shim-concrete interfaces were simulated using face-to-face contact with a finite sliding formulation and surface discretization. The tangential and normal contact behaviors were modeled using a penalty friction model and hard contact, respectively. According to friction test results and relevant literature, the coefficients of friction were defined as 0.55 for concrete-concrete, 0.15 for bolt-concrete, 0.2 for bolt-shim, and 0.3 for shim-concrete interfaces [22,23]. Embedment constraints were applied between steel reinforcement and concrete to simulate steel stress and concrete deformation [24,25]. According to existing research, there was no significant relative slip between bolt-sleeve and sleeve-concrete interfaces, hence the interaction between sleeve and concrete was set as tied contact, while threaded bolts with sleeves were simplified as tied constraints to more accurately simulate the tightening effect of the threads [26] (Figure 5).

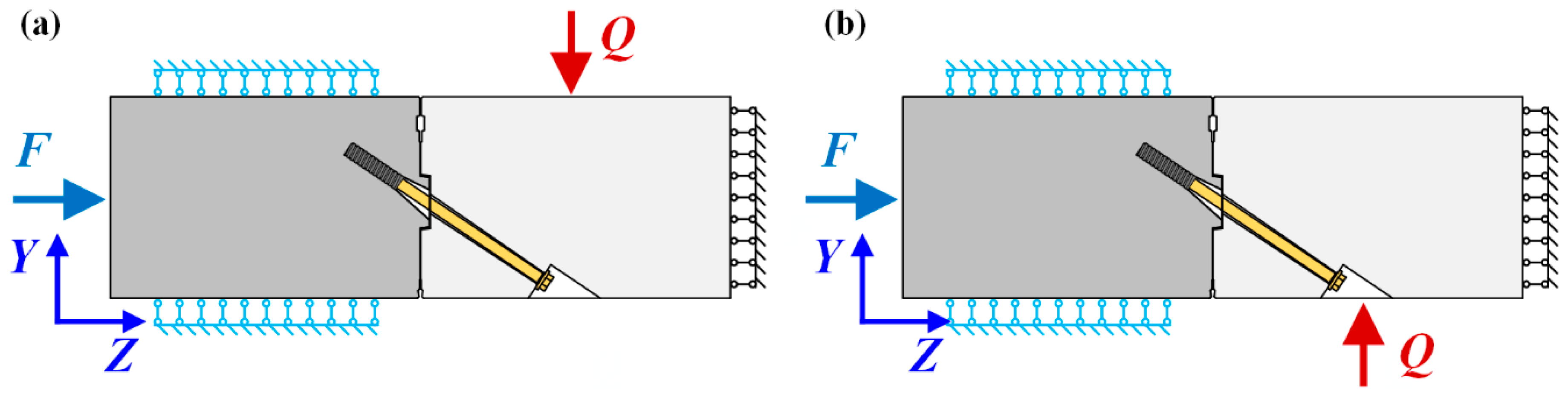
2.5. Boundary and Loading Conditions

In the numerical model, the sleeve was positioned on the left side, with the hand hole located on the right. Displacement constraints in the Y-direction were applied to both the upper and lower surfaces on the left portion of the model, while the Z-direction displacement at the right end face of the right portion was restricted. These boundary conditions prevent structural bending, maintaining the structure in a pure shear state, ensuring the accuracy of the results. The model loading consisted of direct shear loading and reverse shear loading. The model was subjected to a longitudinal force F at the left-end face of the left segment and a shear force Q on the top surface of the right segment. The shear force load caused the model to displace downwards towards the opposite side of the hand hole plane, resulting in ordinal shearing loading scenario (OSLS), while another shear force load caused the model to displace downwards towards the hand hole side plane, leading to the reverse shearing loading scenario (RSLS). Figure 6 illustrates the boundary constraints and loading setup of the model.

This study examined the shear behavior of circumferential joints with various bolt arrangement configurations. Specifically, three of the most common bolt arrangement configurations, namely Single Aligned Bolt (SAB), Single Offset Bolt (SOB), and Double Offset Bolt (DOB) configurations, were selected for study, as illustrated in Figure 7.

Building on the three bolt arrangement configurations, this study conducts an in-depth investigation into the shear behavior of circumferential joints under OSLS and RSLS conditions. In this research, a longitudinal pressure of 1.2 MPa was selected, corresponding to a magnitude of 1123 kN for F, and displacement-controlled loading was applied until the joint dislocation reached 20 mm.

3. Result Analysis

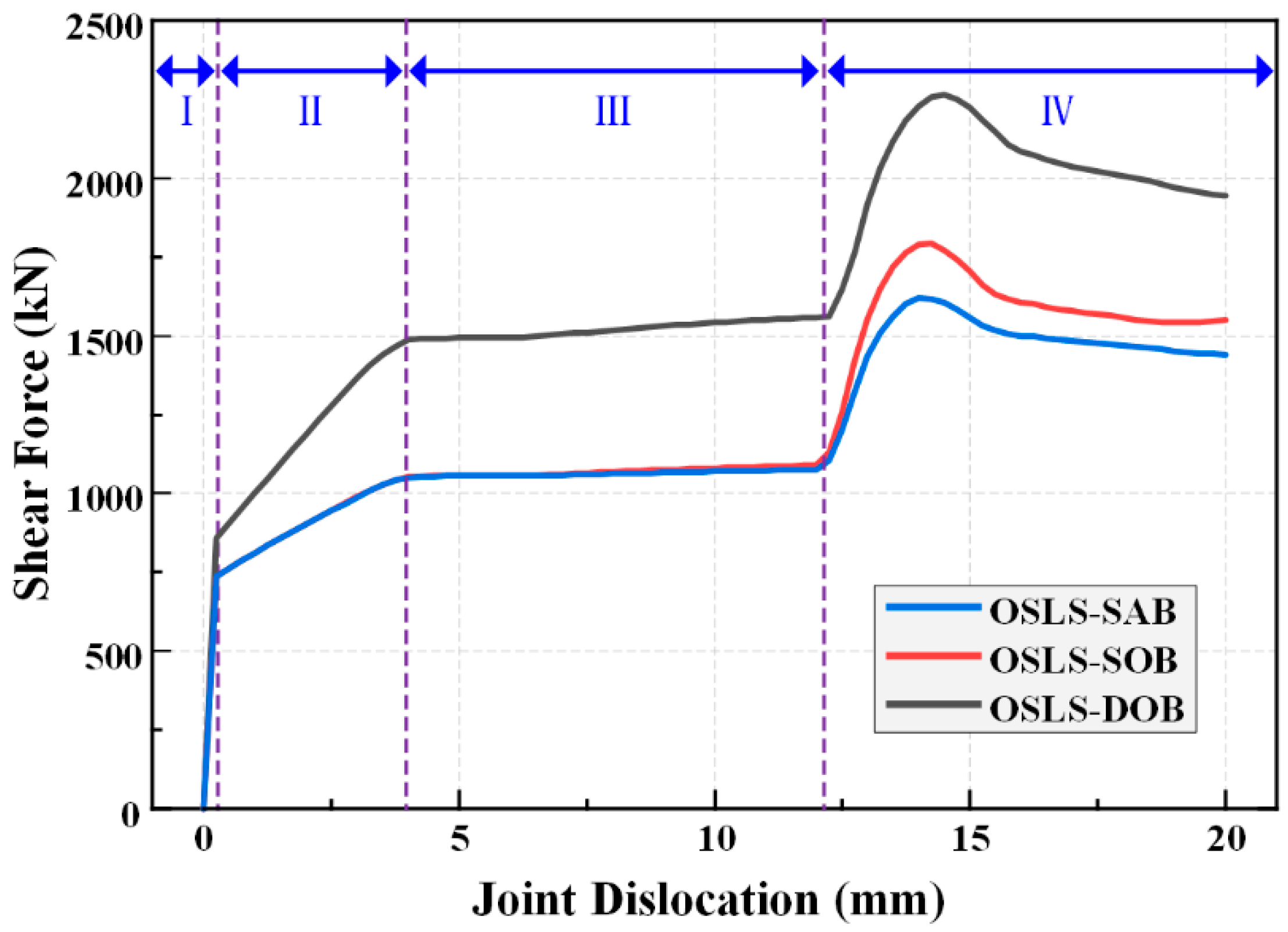
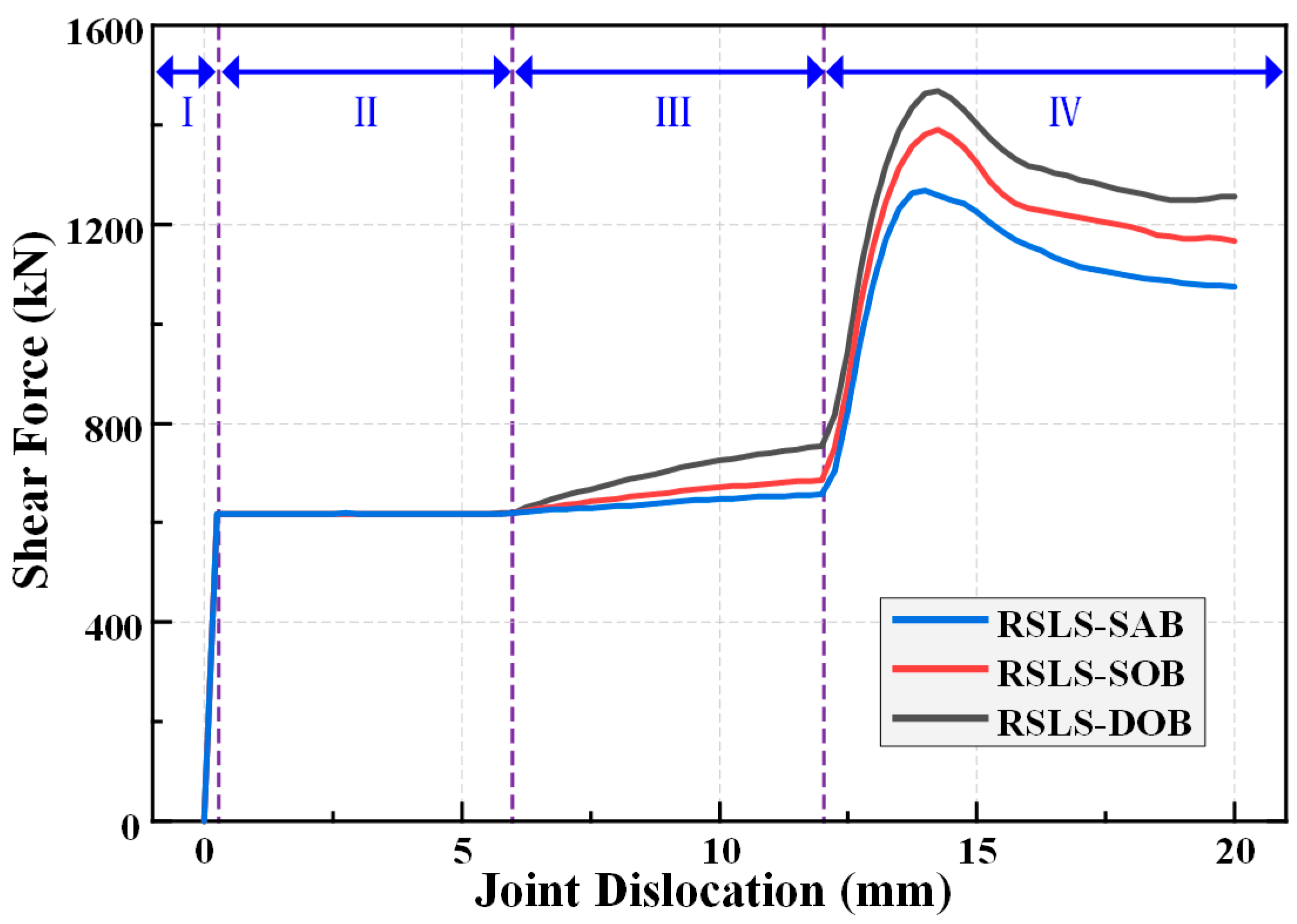
3.1. Correlation Between Shear Force and Joint Dislocation

The correlation between joint dislocation and shear force for circumferential joints with various bolt arrangements under OSLS is shown in Figure 8, highlighting the shear response as dislocation progresses. The horizontal axis, representing joint dislocation, reflects the degree of segment misalignment, which is a critical deformation affecting cracking, leakage, and overall joint performance in shield tunnels.

As shown in Figure 8, the shear force-dislocation curve under OSLS conditions exhibits significant nonlinearity and can be clearly divided into four distinct stages. The first stage corresponds to the static friction phase, where shear resistance is mainly provided by the static friction at the joint interfaces. In this phase, as long as the shear force remains below the maximum static friction threshold, joint dislocation is negligible. The second stage is identified as the gradual sliding phase. Once the shear force exceeds the peak static friction at the interface, relative sliding initiates between joint surfaces, leading to a slow increase in dislocation. Bolts start to play a significant load-bearing role, with bolt stress increasing rapidly as joint dislocation progresses. As joint dislocation continues to increase, the bolts reach a yielding state, transitioning the joint interfaces into the third stage, the rapid sliding stage. In this stage, as the bolts yield, joint dislocation escalates swiftly with increasing shear forces, and bolt deformations increase rapidly. In the fourth stage, contact between the mortise and tenon occurs. The designed clearance for this connection in the present study is 12 mm. When the joint dislocation exceeds this clearance value, the mortise and tenon engage, providing substantial load-bearing capacity. Initially, as the mortise and tenon engage, the shear stiffness of the joint increases rapidly. With continued increase in joint dislocation, shear failure occurs in the mortise and tenon, causing a gradual degradation of shear stiffness and eventual loss of the joint’s shear resistance.

Across different bolt arrangement configurations, the corresponding joint dislocations for each stage of the joint remain largely consistent, a result of the structural characteristics inherent to joints. In the first stage, where only slight slippage occurs at the interfaces, the joint dislocations corresponding to various bolt arrangement configurations are nearly identical. Similarly, for the second and third stages, the joint dislocations when the bolts yield are consistent across different bolt layout patterns. Additionally, the uniformity of the mortise and tenon clearances results in consistent joint dislocation behavior during their contact. The shared mechanical and structural properties lead to nearly consistent joint dislocations corresponding to each loading stage when subjected to shear forces.

Upon contact between the mortise and tenon, the shear stiffness of the joint rises sharply, attaining its peak shear load-bearing capacity at approximately 13.5 mm of dislocation. In this fourth deformation phase, the DOB arrangement maintains a markedly greater load capacity than the SAB and SOB setups, consistent with the previous deformation stages. However, as the circumferential joint progresses into the fourth stage, noticeable discrepancies emerge in the relationship between shear forces and joint dislocations for the SAB and SOB configurations. At equivalent joint dislocations, the shear force supported by the SAB configuration surpasses that of the SOB configuration significantly. The observed discrepancy results from the bolt holes in the SAB arrangement intersecting the mortise and tenon, thereby decreasing the effective mortise-tenon area upon engagement and diminishing the joint’s shear capacity. In contrast, with the bolts arranged separately from the mortise and tenon in the SOB configuration, the mortise and tenon are not weakened by bolt holes, resulting in a notably higher shear load-bearing capacity for the mortise and tenon compared to the SAB configuration.

Figure 9 presents the relationship between joint dislocation and shear force for various bolt arrangements under RSLS conditions. Compared to the OSLS, a distinct divergence is observed in the development trends of shear force and dislocation under RSLS. This variation is primarily attributed to the reduced distance between the handhole and sleeve caused by reverse dislocation, which leads to bolt disengagement from the handhole and consequently limits the bolts’ contribution to load-bearing. As dislocation increases and the bolts separate, the maximum static friction force in the initial stage becomes governed solely by the longitudinal compressive force acting on the joint interface. Given a friction coefficient of 0.55 for the concrete joint interface, the theoretical maximum static friction force is calculated to be 617.65 kN, which aligns well with the results from numerical simulations.

In the initial phase, the shear force–dislocation curves for the SAB, SOB, and DOB configurations are nearly identical. In the second phase, despite the increase in dislocation, the joint shear force exhibits minimal growth, as the bolts are not yet significantly engaged. Once the dislocation exceeds 6.0 mm, the joint transitions into the third phase of shear deformation. At this stage, the bolts begin to contact the bolt holes, and their threads embed into the sleeve, functioning similarly to dowels anchored in concrete and thus capable of transmitting interfacial shear forces. Furthermore, the bolts are still within their elastic range and exhibit limited deformation. In contrast to OSLS conditions, where tensile forces prevail, the bolts under RSLS are primarily subjected to shear loading. Consequently, the load-bearing capacity of the bolts is significantly lower under RSLS compared to OSLS. Therefore, although the double-bolt structure of DOB can provide the joint with higher shear stiffness in the third phase, the difference in shear forces between DOB and the single-bolt structures of SAB and SOB is not pronounced. Following a similar pattern of shear deformation as joints under OSLS, when the joint dislocation reaches 12 mm, the joint deformation enters the fourth phase, the mortise and tenon bearing phase. In this fourth deformation stage, with equivalent dislocations, the shear force experienced by DOB is notably higher than that of SAB and SOB. Similarly, due to the weakening of the mortise and tenon in SAB by bolt holes, the shear resistance of SOB is slightly higher than that of SAB.

Table 2. Ultimate shear capacities of joints under different bolt arrangements.

Loading Condition	Ultimate Shear Load-Bearing Capacity (kN)
	SAB	SOB	DOB
OSLS	1618.76	1791.83	2265.2
RSLS	1266.76	1389.51	1469.17

summarizes the ultimate shear load-bearing capacities of joints with various bolt arrangements under OSLS and RSLS conditions. Under OSLS loading, the DOB configuration exhibits a markedly higher capacity compared to SAB and SOB, with the latter two reaching 71.5% and 79.1% of the DOB capacity, respectively. In the case of RSLS, DOB still exhibits the highest ultimate load-bearing capacity, but the difference from SAB and SOB decreases. Under RSLS conditions, the ultimate shear capacities of SAB and SOB reach 86.2% and 94.6% of that of DOB, respectively. Comparing the two loading scenarios, it is evident that joints exhibit notably reduced load-bearing capacities under RSLS compared to OSLS. This discrepancy arises from the phenomenon of bolt disengagement, which leads to a more adverse loading condition for the bolts under RSLS, resulting in a more limited load-bearing capacity. Under RSLS, the ultimate load-bearing capacities of SAB, SOB, and DOB are 78.2%, 77.5%, and 64.9% of their capacities under OSLS, respectively. These results suggest that a change in shear direction has a more pronounced effect on the ultimate load-bearing capacity of the DOB arrangement.

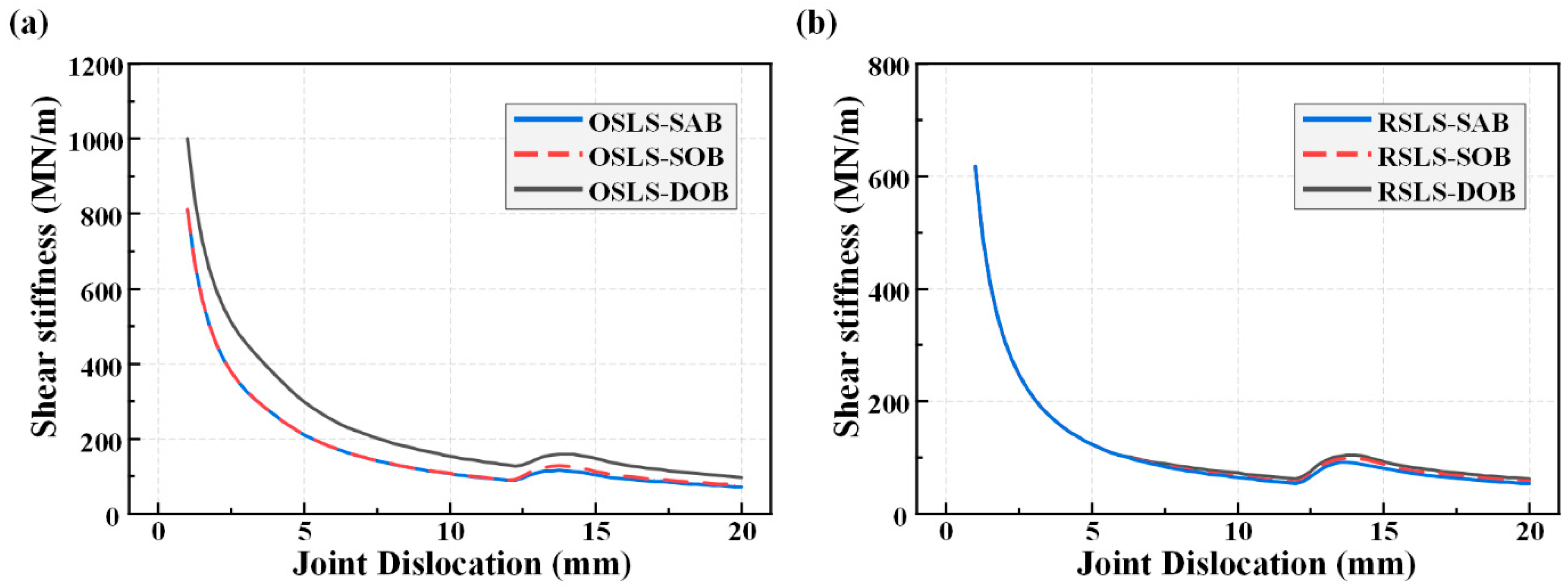
3.2. Shear Stiffness Analysis

In investigations of the shear mechanical behavior of shield tunnel circumferential joints, shear stiffness is a crucial metric representing their shear resistance. The appropriate value of shear stiffness for segmental tunnel lining joints is of significant importance for tunnel design evaluation and model simplification. Figure 10 illustrates the correlation between joint dislocation and shear stiffness for circumferential joints featuring various bolt arrangements, aimed at examining differences in their shear stiffness. The shear stiffness of the joints was determined using the secant stiffness method, defined as the ratio of shear force to joint dislocation.

As shown in Figure 10, the relationship between joint dislocation and shear stiffness for different bolt configurations under OSLS and RSLS exhibits a clear staged behavior. This evolution of shear stiffness with increasing dislocation can be broadly categorized into three phases. In the first stage, shear stiffness gradually declines. During this phase, the joint transitions from relying solely on face-to-face contact for shear resistance to a combined load-bearing mechanism involving both contact surfaces and bolt engagement. Additionally, as the bolts gradually yield, the joint shear stiffness, initially significantly higher at lower dislocation, decreases substantially. Severe attenuation in shear stiffness is observed during this initial stage. The second stage corresponds to the engagement of the mortise and tenon. When joint dislocation exceeds 12 mm, the mortise and tenon begin to interlock, significantly enhancing the load-bearing capacity of the joint and resulting in a noticeable increase in shear stiffness. As dislocation continues to develop, the mortise and tenon gradually deteriorate, which causes a reduction in shear stiffness. This marks the beginning of the third stage, representing the failure phase of the mortise and tenon. Overall, the shear stiffness of the joint shows a declining trend as dislocation increases, with particularly low stiffness observed at larger displacements. Therefore, it is important to consider the substantial reduction in shear stiffness under significant dislocation conditions, emphasizing the necessity of rationally evaluating its impact during structural design and performance assessment.

Figure 10a presents the relationship between joint dislocation and shear stiffness for different bolt configurations under OSLS conditions. The results show that the DOB configuration consistently exhibits significantly higher shear stiffness compared to SAB and SOB, particularly at smaller dislocations. When comparing SAB and SOB, the differences in shear stiffness are minimal across dislocations, as their dislocation-shear force responses during the initial three loading stages are quite similar. Consequently, for dislocations below 12 mm, the stiffness variation between SAB and SOB remains negligible. After the mortise and tenon engage, the SOB configuration exhibits a slight increase in stiffness, but the overall difference between the two remains limited. Under RSLS conditions, as shown in Figure 10b, the relationship between joint dislocation and shear stiffness differs markedly from that observed under OSLS, with more pronounced variations among the bolt arrangements. The occurrence of bolt pullout leads to initially indiscernible differences in shear stiffness development among the three bolt arrangement configurations at the early stages of dislocation. As dislocation progresses to the point where the bolt contacts the hole, there are minor differences in stiffness, with the DOB configuration exhibiting the highest shear stiffness and the SAB configuration displaying the lowest. Throughout the development of joint dislocation until failure, the differences in shear stiffness among the various bolt arrangements are less than 15%.

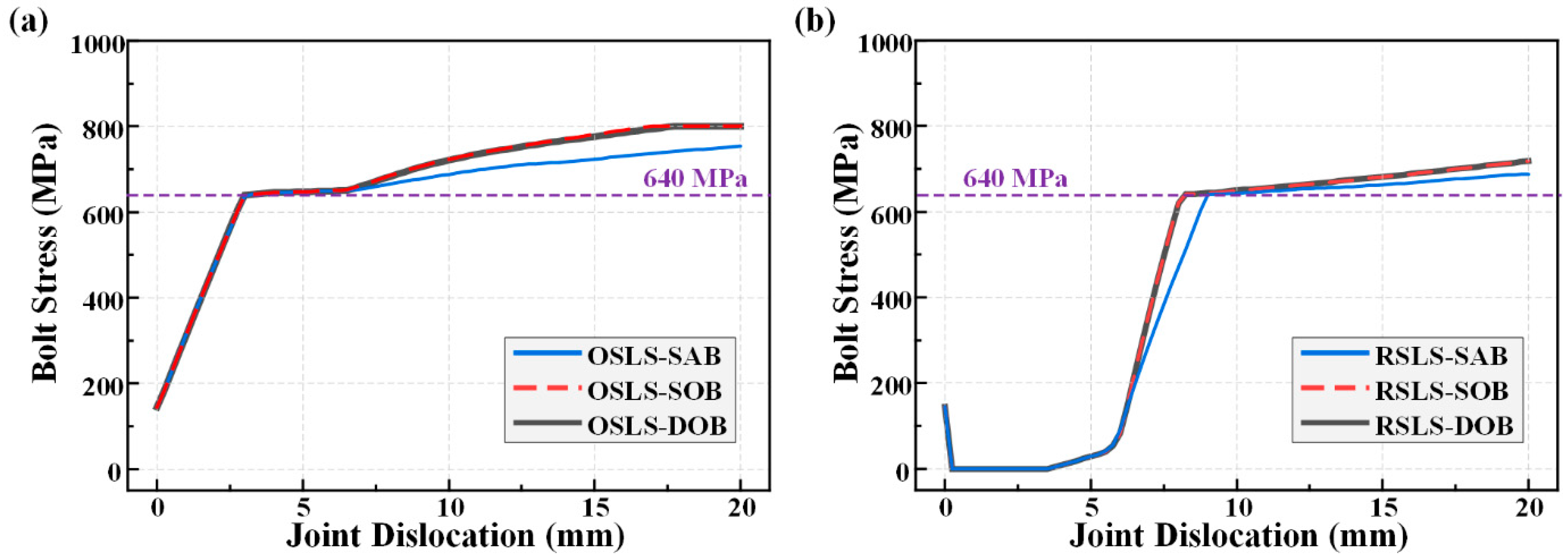
3.3. Bolt Stress

The mechanical behavior of bolts varies significantly under different loading conditions. To better comprehend the stress distribution characteristics of bolts at various dislocation levels, the DOB configuration was selected as a typical example. Corresponding stress contour maps under OSLS and RSLS conditions were extracted and are illustrated in Figure 11. Figure 11a illustrates the stress distribution of bolts under OSLS, while Figure 11b presents the stress distribution of bolts under RSLS.

The stress distribution of bolts in the DOB configuration at various dislocations can be inferred from the contour plot results shown in Figure 11a. When the joint experiences significant misalignment under OSLS, as the dislocation increases, the stress at various bolt positions rises rapidly. Under minor dislocation levels, the bolts undergo coupled tension and shear loading, producing a generally uniform stress profile, with the highest stress localized at the shear-loaded side of the joint interface. This is attributed to the greater bending moments acting on the bolts at this location, where the shear-facing side of the joint interface corresponds to the tension-dominant region of the bolt cross-section, thereby intensifying the stress. Beyond a dislocation of 6.5 mm, the bolt engages the hole, with contact forming between the shear-facing side of the bolt and the joint’s hole boundary. As dislocation grows, shear-induced deformation in the bolts becomes more prominent, causing localized stress accumulation at the contact regions. Figure 11b illustrates the stress distribution of bolts under RSLS. According to the contour plot results, when the joint initially misaligns, the bolt head dislodges from the hole position, leaving the bolt completely unloaded at this stage. As the dislocation further increases, the bolts make contact with the bolt holes, experiencing shear forces only, with significant stresses at the sleeve and joint interface positions, resembling a nail-like loading condition. With larger dislocations, the bolt stresses rapidly escalate, leading to yielding in the sleeve and joint interface regions. It is noteworthy that the phenomenon of bolt dislodgement worsens with increasing dislocation, with the bolt experiencing minimal loading at the bolt head position. Bolts exhibit distinct mechanical characteristics when subjected to OSLS and RSLS load scenarios. Under OSLS, the bolts primarily experience tensile and shear forces, with relatively uniform stress distribution and less pronounced stress concentration. In OSLS, bolt stress rapidly increases with dislocation, reaching yield stress at the critical locations, leading to rapid overall bolt yielding with further dislocation. Under RSLS, the bolts separate from the hole at the onset of loading, and upon contact with the bolt holes, significant shear deformation occurs. Due to the tight connection between the bolt end and the sleeve, the maximum stress in the bolts appears near the threads. In the advanced loading stage, further increases in dislocation lead to intensified shear deformation in the bolts, while tensile deformation remains limited. Compared to OSLS, RSLS induces more severe stress concentrations in the bolts, subjecting them to harsher loading conditions.

Figure 12a further depicts the correlation between joint dislocation and maximum bolt stress for various bolt arrangements under OSLS conditions. The results indicate that when the joint is not misaligned, the bolts are primarily subjected to the preload force, and as the dislocation slowly increases, the bolt stress continues to rise. At a dislocation of 3.0 mm, the bolts reach the yield stress which is 640 MPa. After reaching the yield stress, the bolt stress increases at a slower rate with further dislocation. Once the dislocation attains 6.5 mm, contact occurs between the bolts and bolt holes, causing a rapid rise in bolt stress until the ultimate strength is approached. Comparing the relationship curves between the maximum bolt stress and dislocation for different bolt arrangement configurations, it can be observed that for the SOB and DOB configurations, the bolt stresses are the same at the same dislocation, whereas for the SAB configuration, the correlation between the maximum bolt stress before contacting the bolt hole and dislocation is similar to that of SOB and DOB. However, once the bolts engage with the bolt holes, the peak stress in the SAB configuration is marginally lower compared to SOB and DOB. This difference arises because the bolt hole in the SAB setup traverses a raised and recessed tenon, creating a distinct contact condition from those in SOB and DOB.

Figure 12b further depicts the correlation between joint dislocation and maximum bolt stress for various bolt arrangements under RSLS conditions. When dislocation begins, the stress on the bolts drops to zero due to dislocation. Notably, the bolt contacts the bolt hole at two distinct points. When the dislocation reaches 3.0 mm, the bolt head engages with the hand hole area of the bolt hole. However, since the bolt is anchored at the end, the contact position is far from the fixed position, resulting in a less pronounced increase in stress after contact. After a dislocation exceeds 6.0 mm, the bolts come into contact with the seam position of the bolt hole, leading to a rapid increase in bolt stress until the yield stress is reached. Similarly to the OSLS, once the bolts engage with the bolt holes, the stress experienced by the bolts in the SAB configuration is marginally less than that in SOB and DOB.

Overall, under both OSLS and RSLS, the mechanical behavior of bolts in the three bolt arrangement configurations is essentially the same, and the differences in bolt stress are relatively small at the same dislocation. This suggests that variations in bolt arrangement configurations have a minimal effect on the mechanical performance of the bolts.

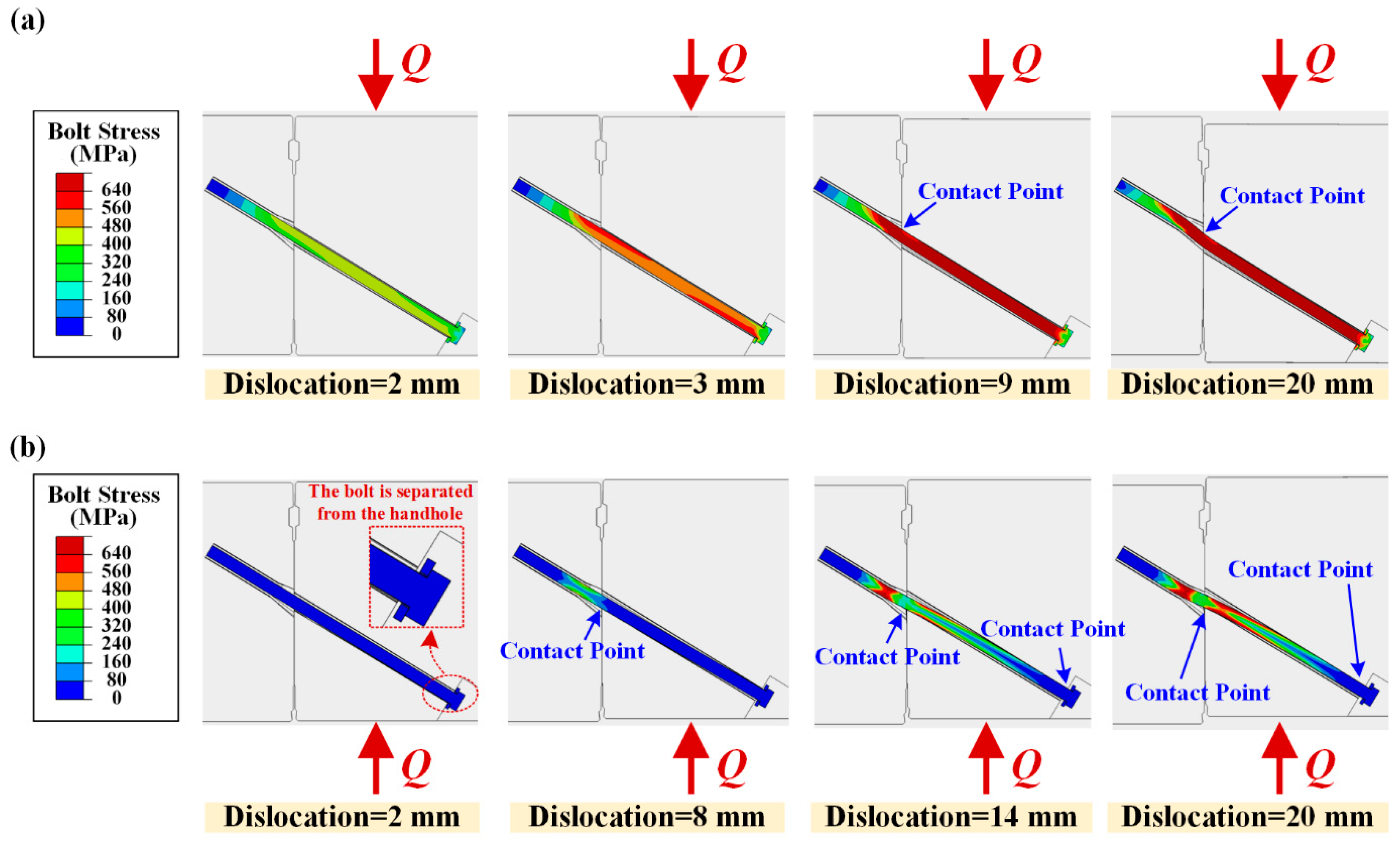
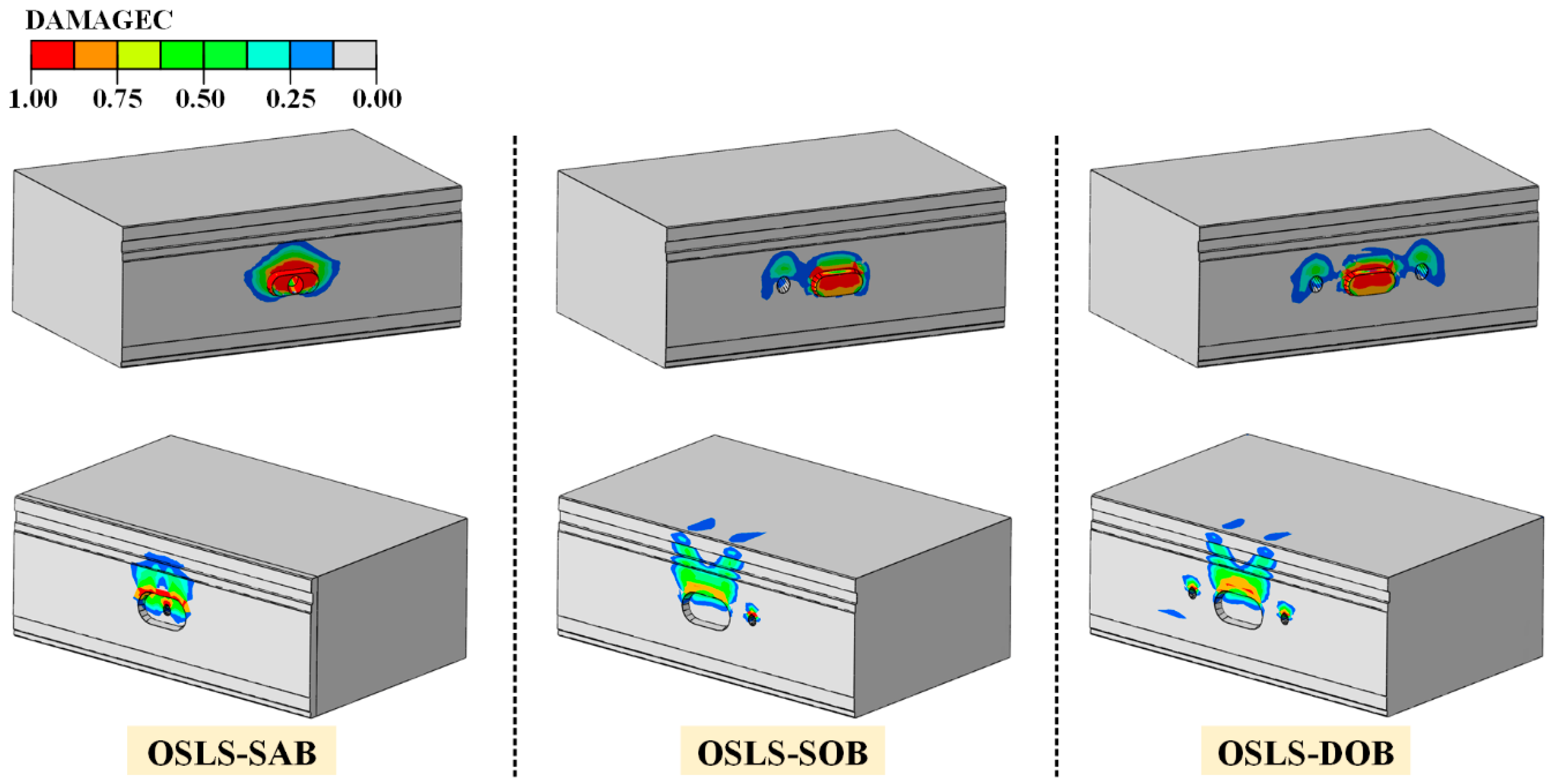
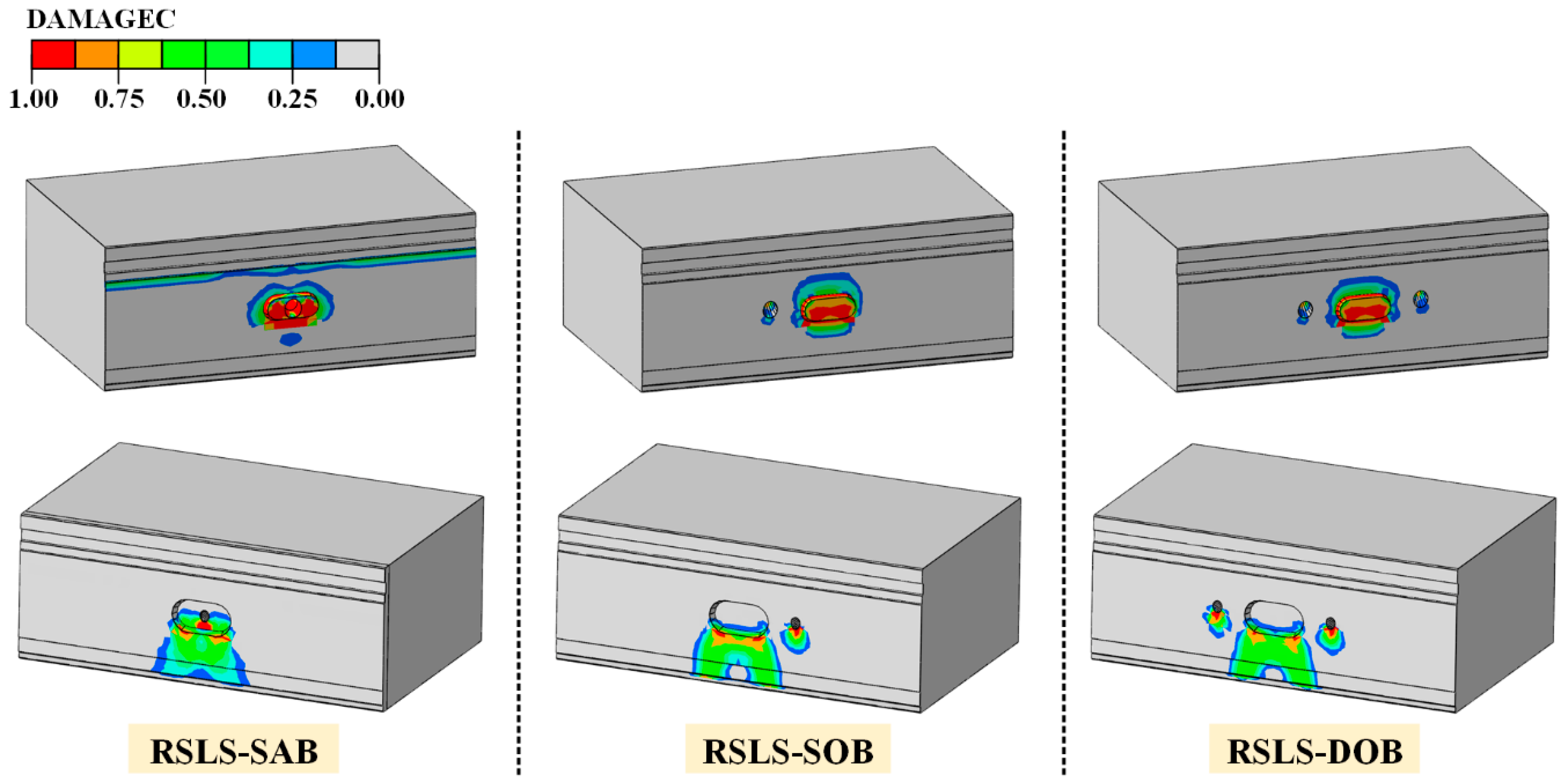
3.4. Failure Characteristics of Joints

As the joint dislocation continues to increase, phenomena such as mortise and tenon engagement and bolt contact with bolt holes can occur, leading to mortise and tenon damage, bolt yielding, and other effects. A comparison of the shear failure characteristics of different bolt arrangement configurations under misalignment of 20 mm under OSLS and RSLS is shown in Figure 13 and Figure 14, respectively.

As depicted in Figure 13, during shear failure of the joint under OSLS, there is a noticeable stress concentration at the contact surface of the tenon and mortise, with contact stress rapidly increasing as dislocation grows. As dislocation increases, the tenon and mortise experience significant damage until complete failure. The damage characteristic of the tenon involves localized concrete fracturing, while the mortise exhibits concrete detachment. The damage area of the mortise extends at a 45° angle from the contact position with the tenon. Apart from tenon and mortise damage, the condition of the bolt holes is also noteworthy. With increasing dislocation, contact between the bolt and the bolt hole leads to concrete compression failure at the bolt hole. Comparing the shear failure modes of different bolt arrangement configurations, the shear failure patterns of SOB and DOB joints are nearly identical, but the shear failure in SAB joints is more severe. One reason for this outcome is that the location of bolt hole damage in SAB coincides with tenon damage, resulting in more severe concrete damage. Additionally, since the bolt hole in SAB passes through the tenon, the tenon shear bearing capacity is weaker, leading to more pronounced damage. From Figure 14, it is evident that the shear failure mode of joints under RSLS conditions is largely similar to that under OSLS, but the locations of tenon and mortise damage differ due to different shear directions. Another noteworthy issue is that the bolt hole damage in joints under RSLS is more severe.

4. Conclusions

This study investigates the shear mechanical performance differences of three joint configurations, namely single-bolt aligned mortise and tenon arrangement (SAB), single-bolt offset mortise and tenon arrangement (SOB), and double-bolt offset mortise and tenon arrangement (DOB), through the establishment of a refined numerical calculation model. The conclusions are as follows:

(1)

When subjected to consistent loading patterns, joints with different bolt arrangements undergo identical force stages with corresponding dislocations. Under OSLS, the joints experience static friction, slow sliding, rapid sliding, and mortise-tenon contact as dislocation increases. Under RSLS, the stages are static friction, rapid sliding, bolt bearing, and mortise-tenon contact.

(2)

Under OSLS, bolts provide significant load-bearing capacity, resulting in DOB having superior shear performance compared to SAB and SOB. Due to the weakening of mortises by bolt holes in SAB, its shear resistance in the later deformation stage is weaker than SOB. Under RSLS, bolts exhibit extraction, and the shear-dislocation curves of the three configurations are similar in the early stages, with only minor differences as deformation progresses.

(3)

DOB demonstrates clearly higher shear performance than SAB and SOB under OSLS, but this difference is less pronounced under RSLS. The ultimate capacities of SAB and SOB are 71.5% and 79.1% of DOB under OSLS and 86.2% and 94.6% of DOB under RSLS.

(4)

The mechanical behavior of bolts is largely consistent across different arrangements. For the same dislocation, the force states, stress distributions, and maximum stresses of bolts in SAB, SOB, and DOB show minimal differences.

(5)

In SAB, bolt holes passing through the mortises weaken the structure, leading to further damage due to contact failure between bolts and bolt holes. As a result, SAB joints suffer more severe shear failure, whereas the failure modes of SOB and DOB joints are nearly identical and less detrimental.

These findings provide a useful reference for the potential development of deformation control criteria and design codes for super-large shield tunnels.