A Two-Stage Support Load Convergence Method for Rock–Support Interaction in Tunnels
Abstract
1. Introduction
2. Problem Statement
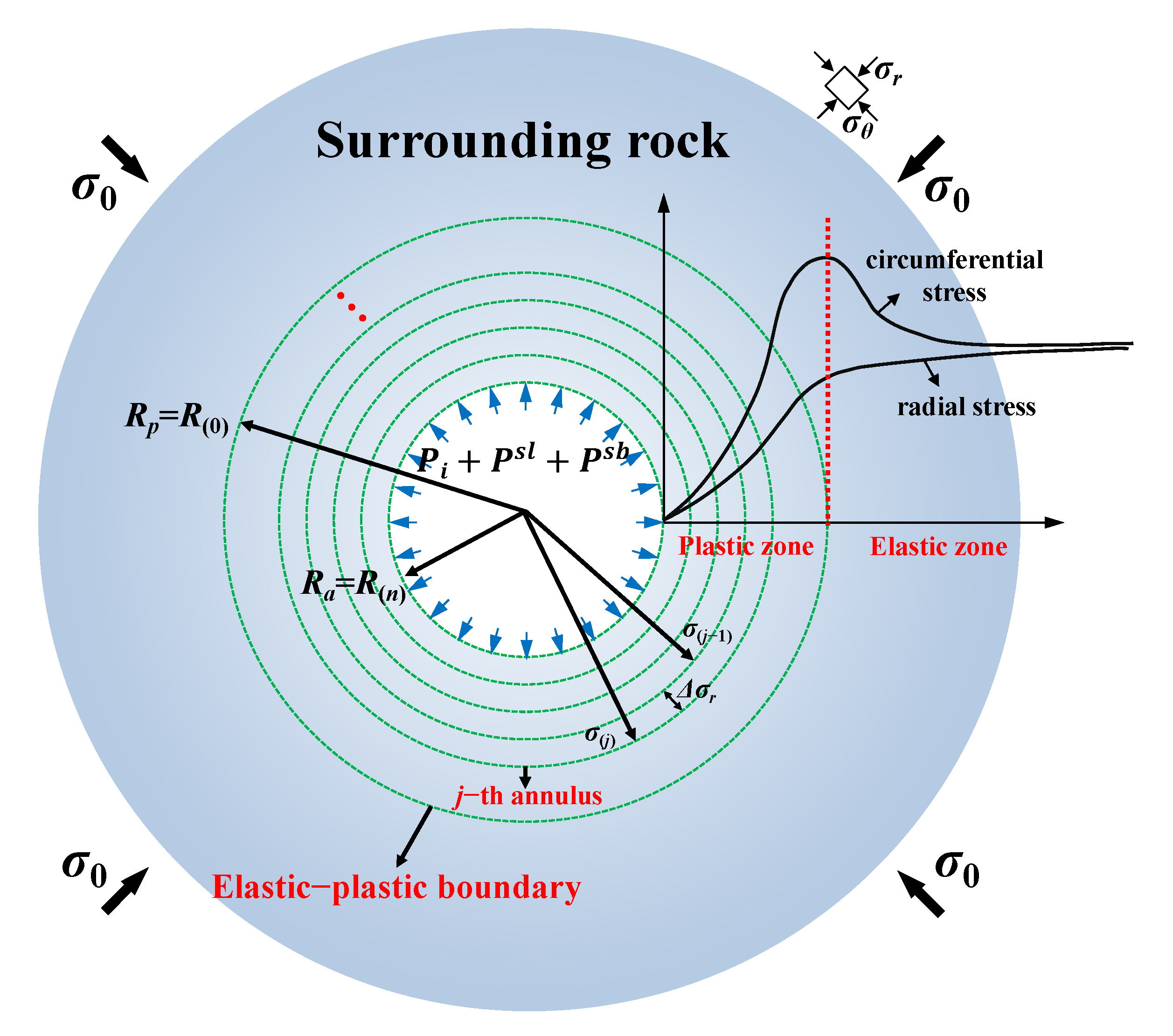
2.1. Basic Assumptions
- (1)
- The surrounding rock is considered an isotropic, homogeneous, and intact medium with strain softening behavior, following the generalized Mohr–Coulomb criterion, while the lining and bolts are linearly elastic.
- (2)
- The in situ stress is assumed to be isotropic, and the stress–strain distribution of both the rock and lining is axially symmetric.
- (3)
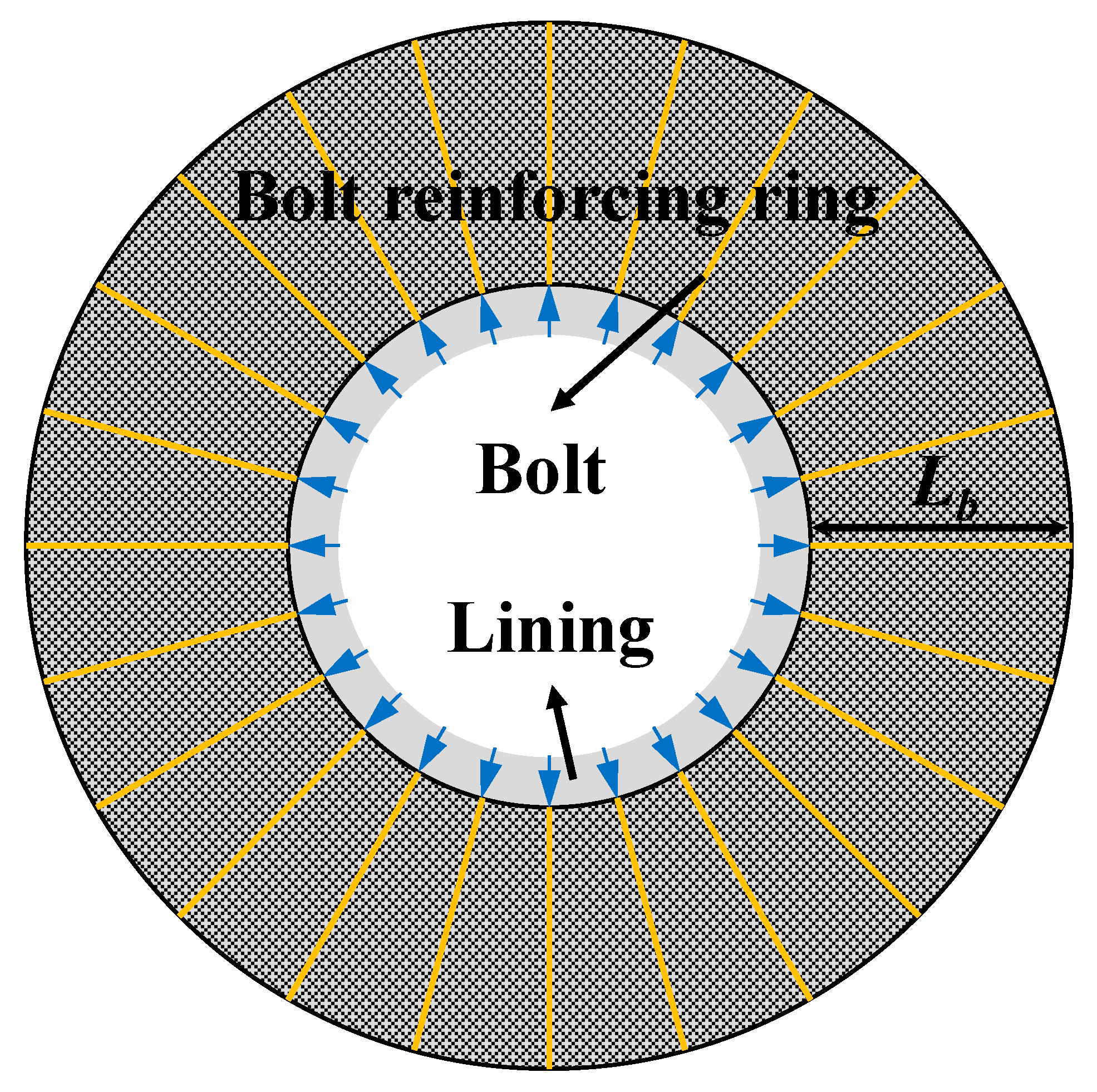
- A perfect bond is assumed between the rock mass and bolts, which share the load and enhance the strength of the reinforced zone.
2.2. Governing Equations
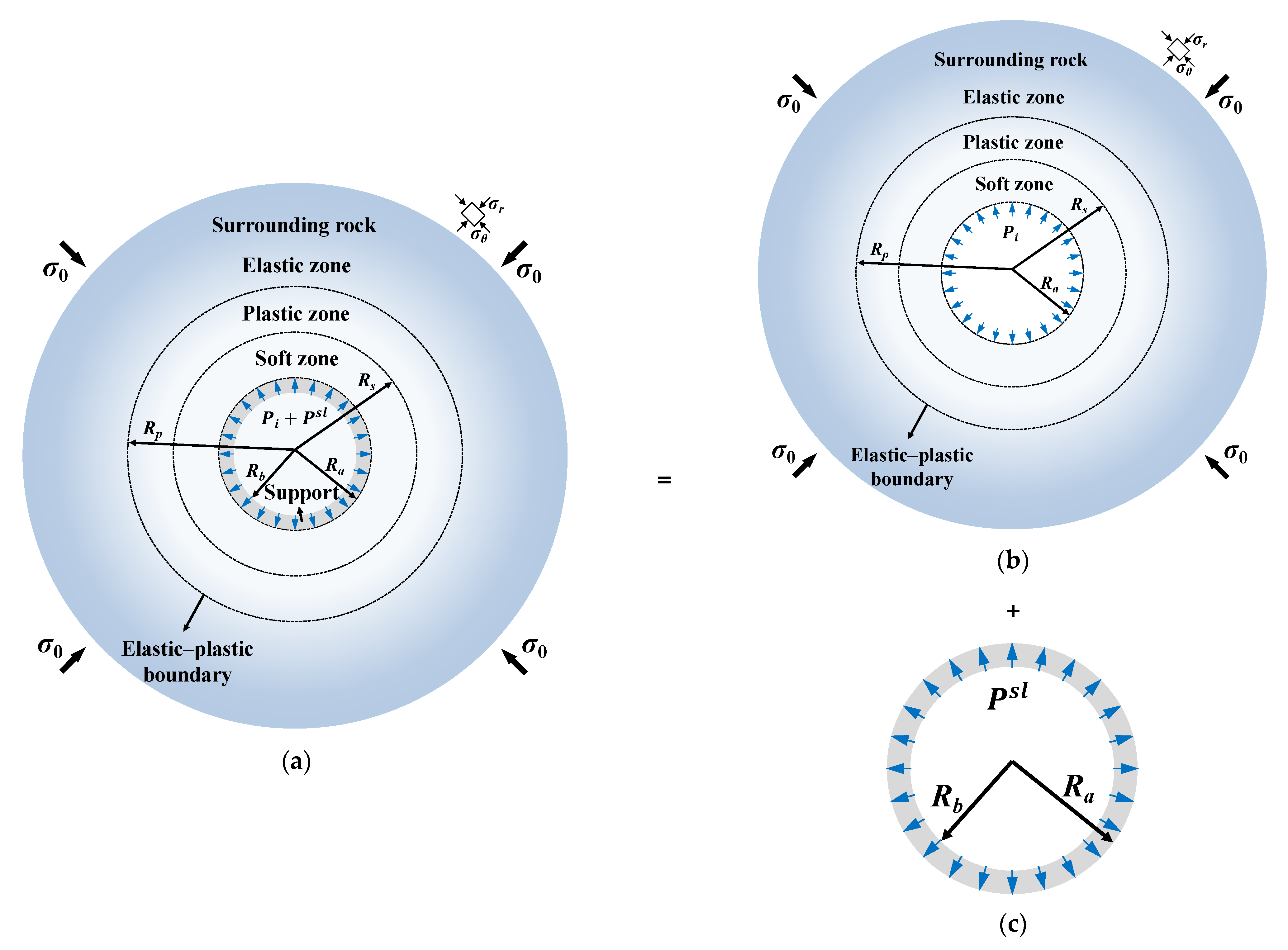
2.3. Boundary Conditions
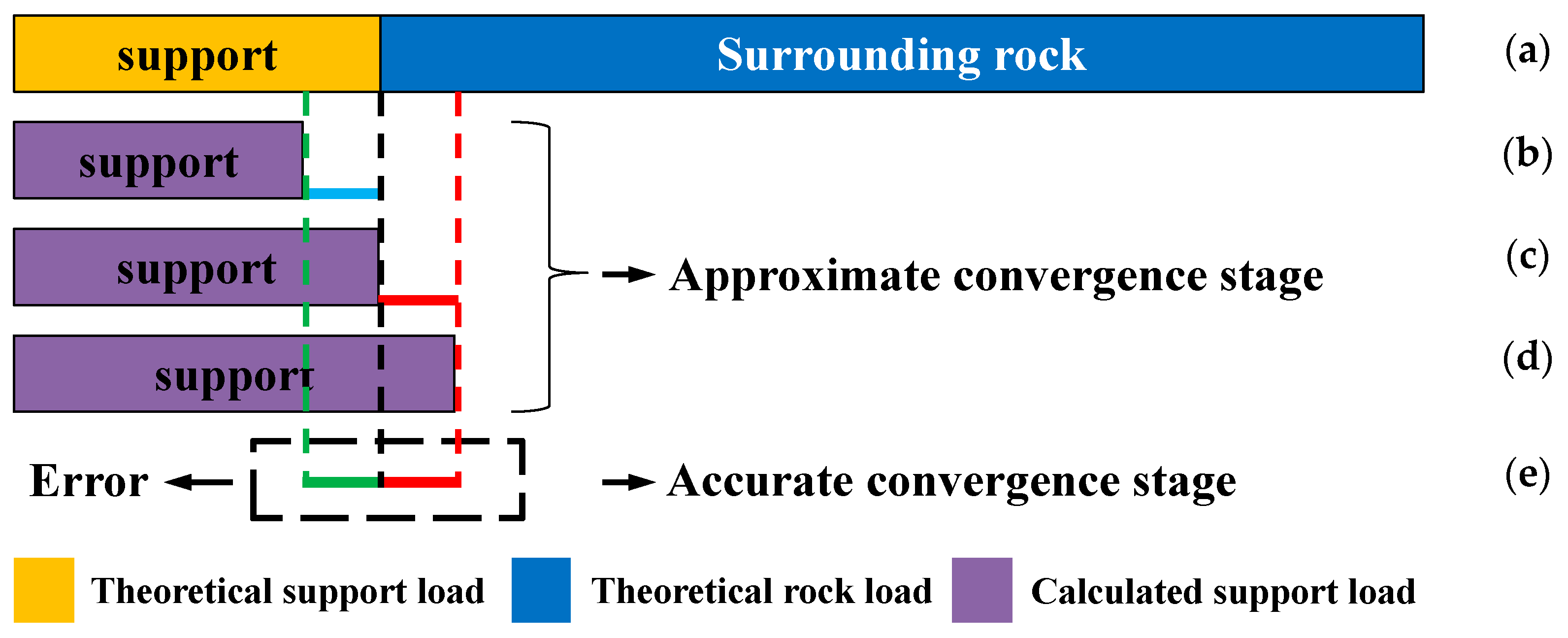
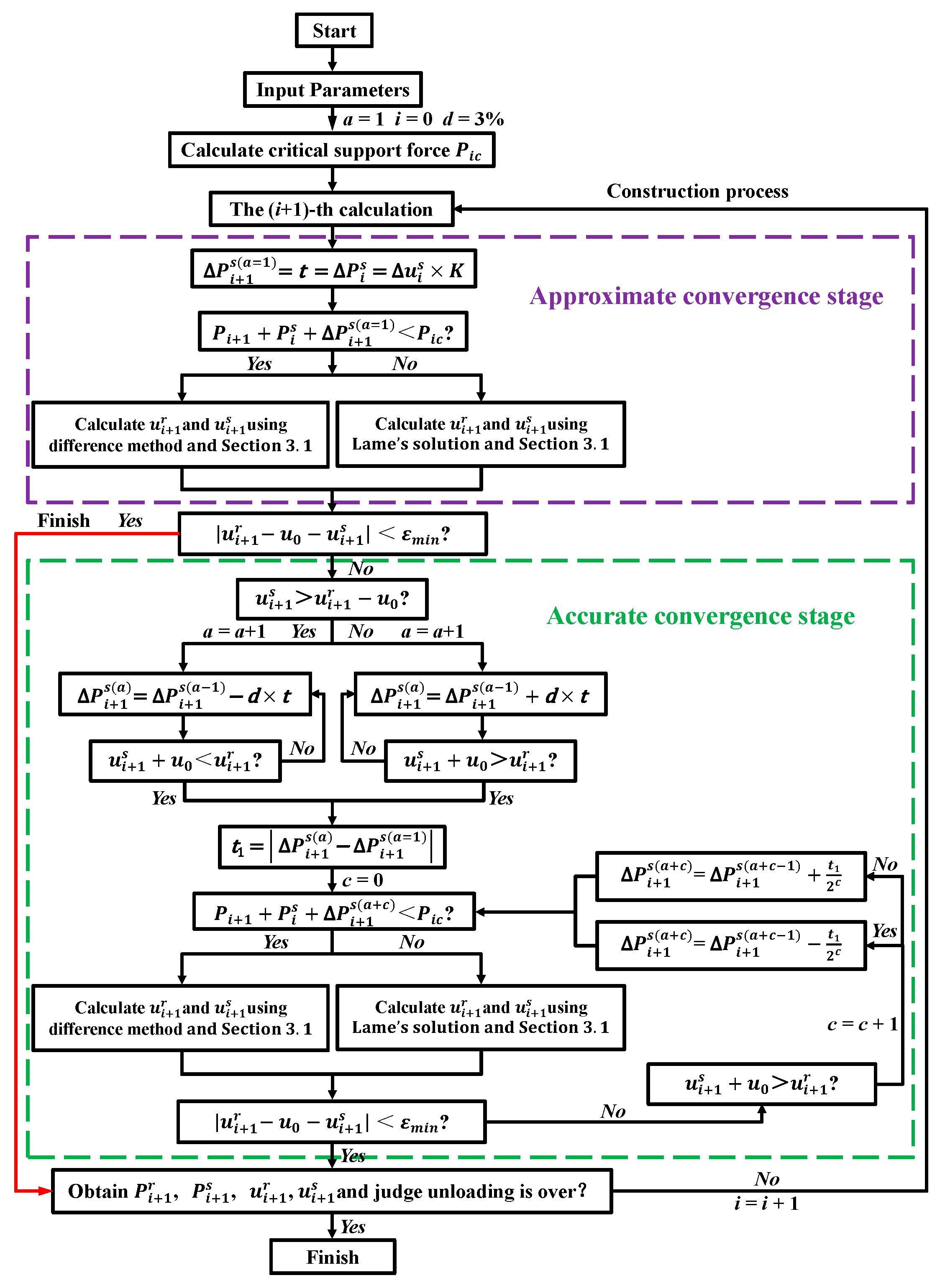
3. Model Solution
3.1. Solution of Rock Subsystem
3.2. Solution of Rock–Support System
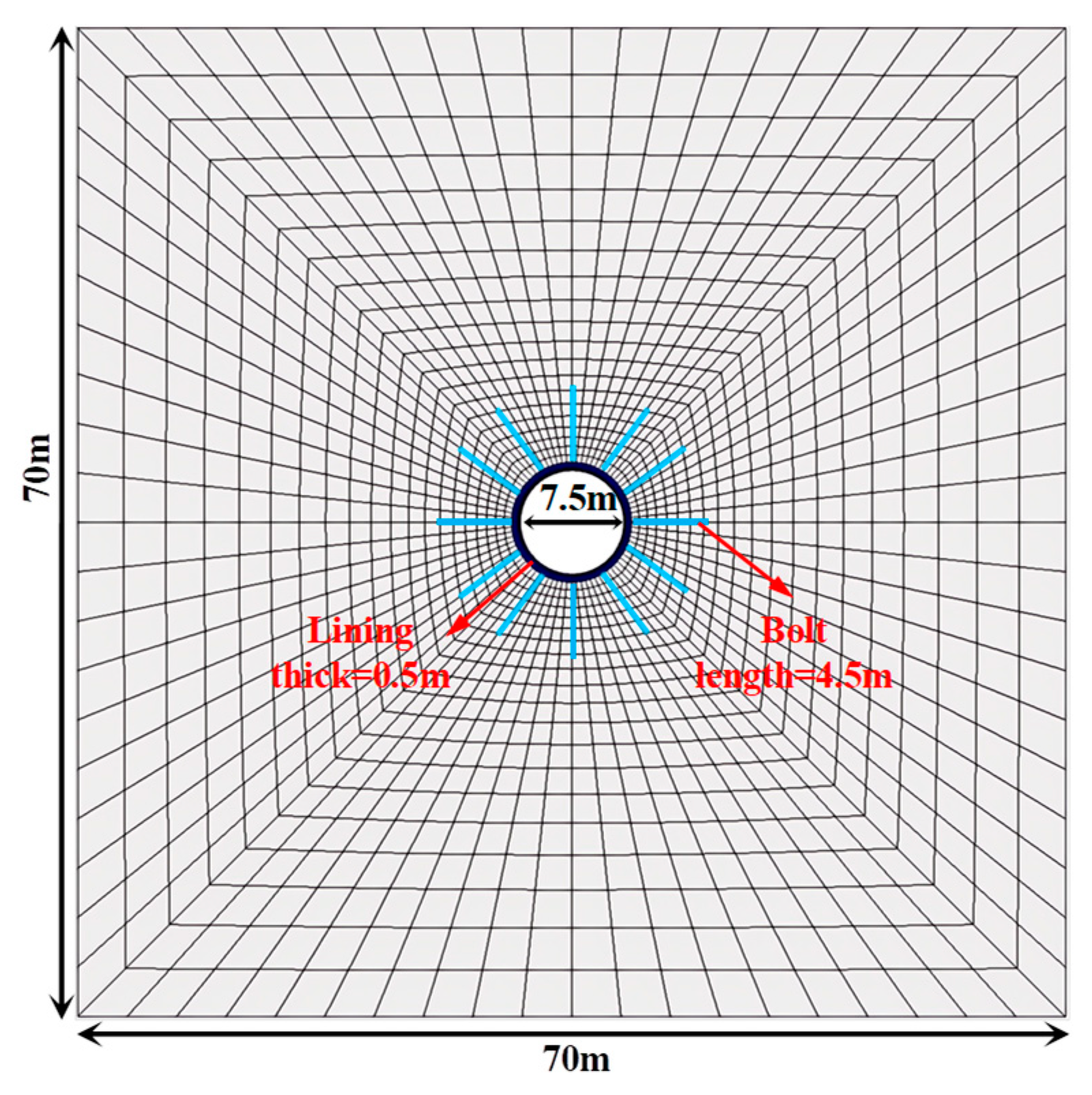
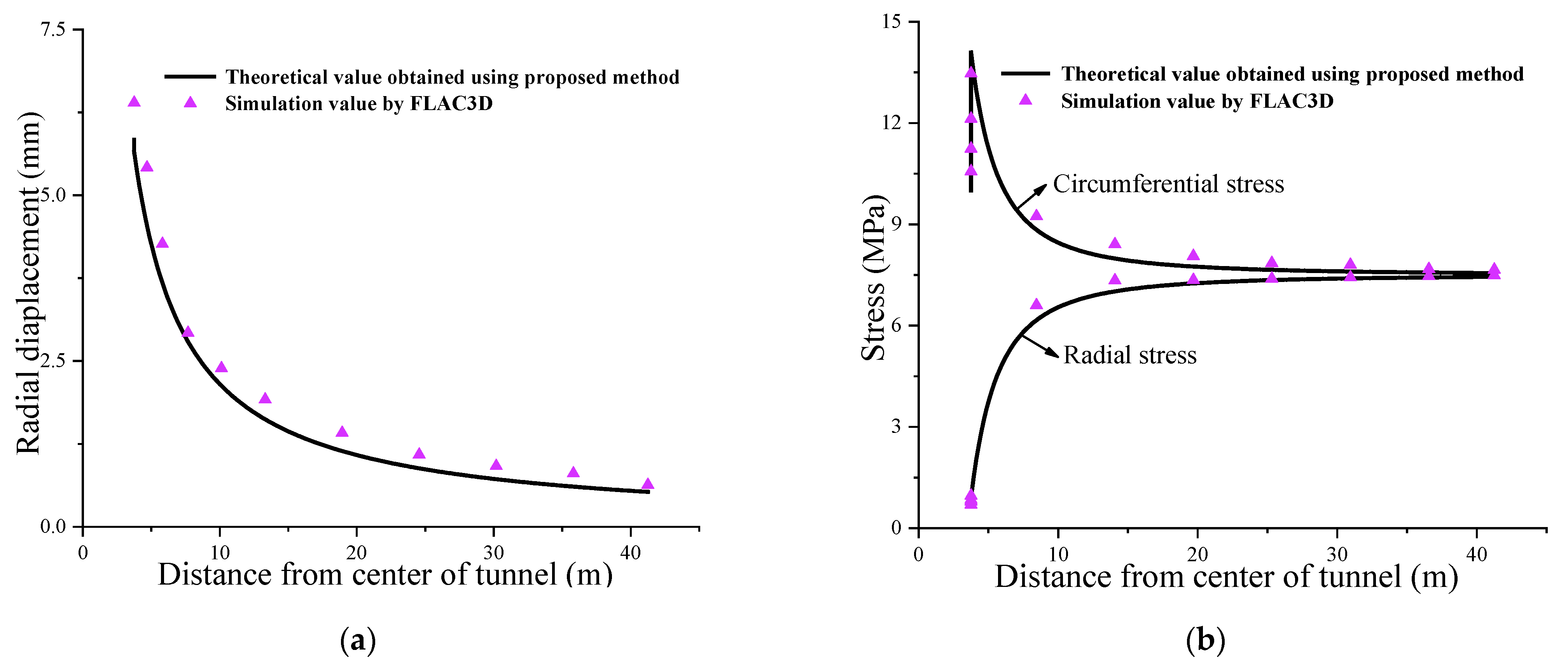
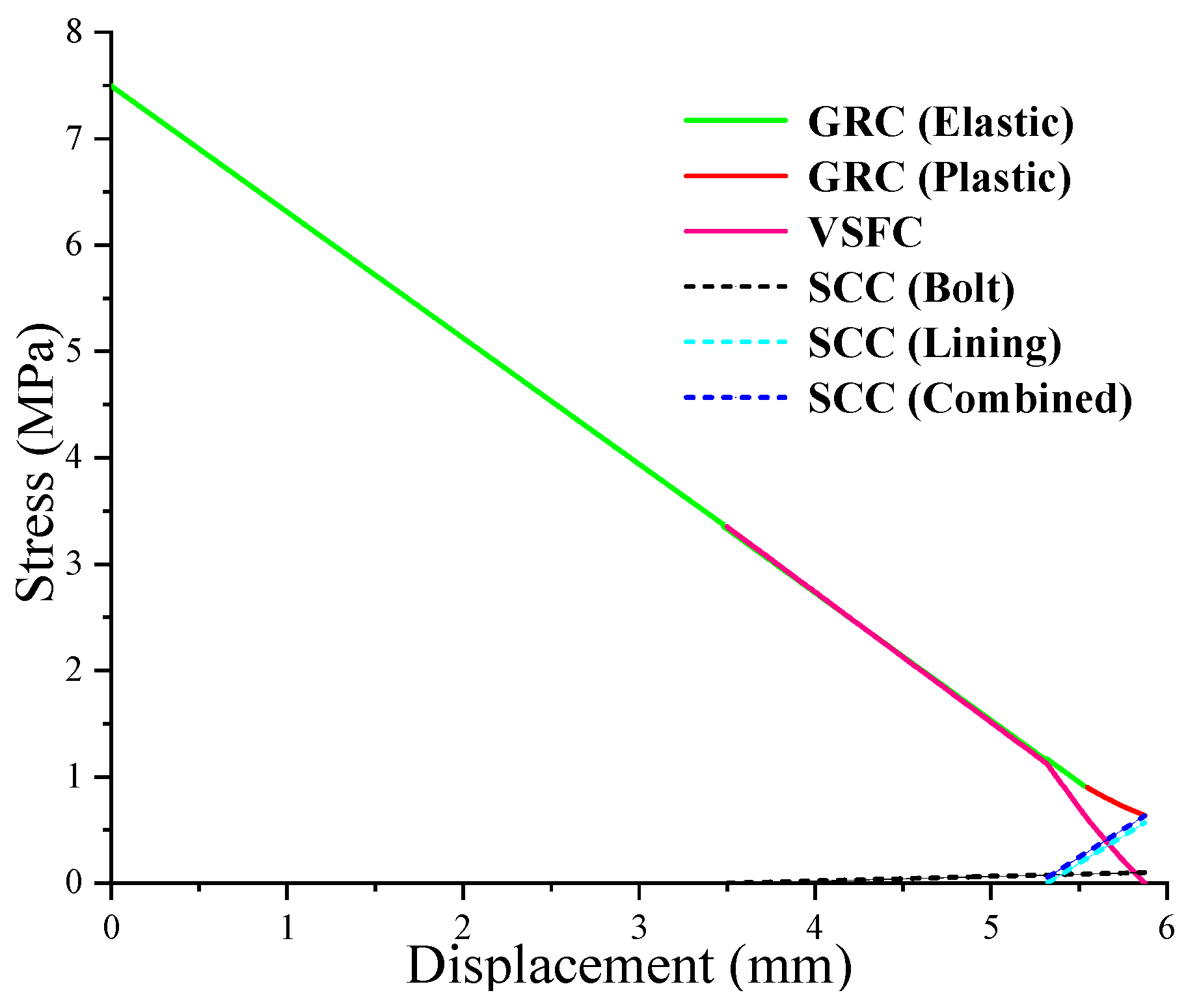
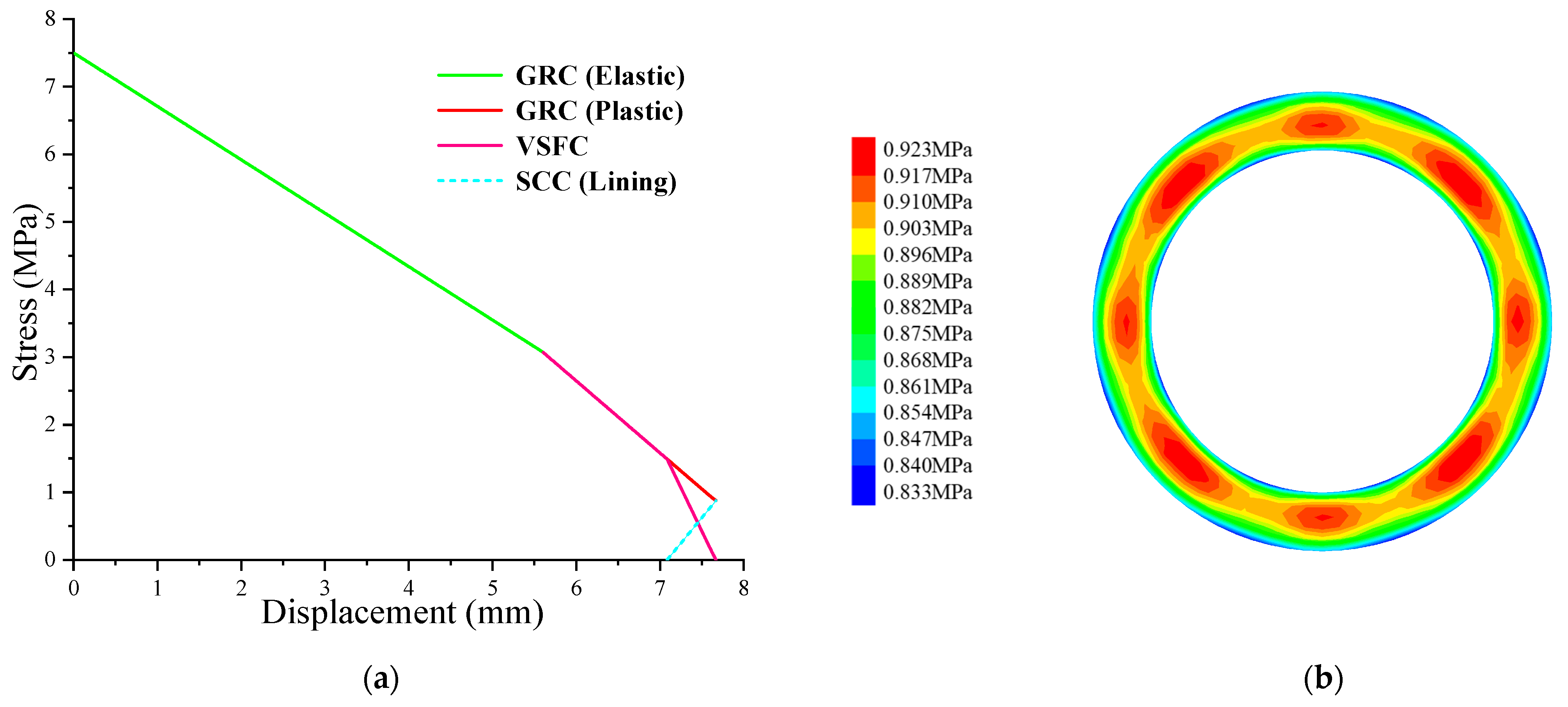
4. Model Verification
4.1. Accuracy Verification of Model 1
4.2. Accuracy Verification of Model 2
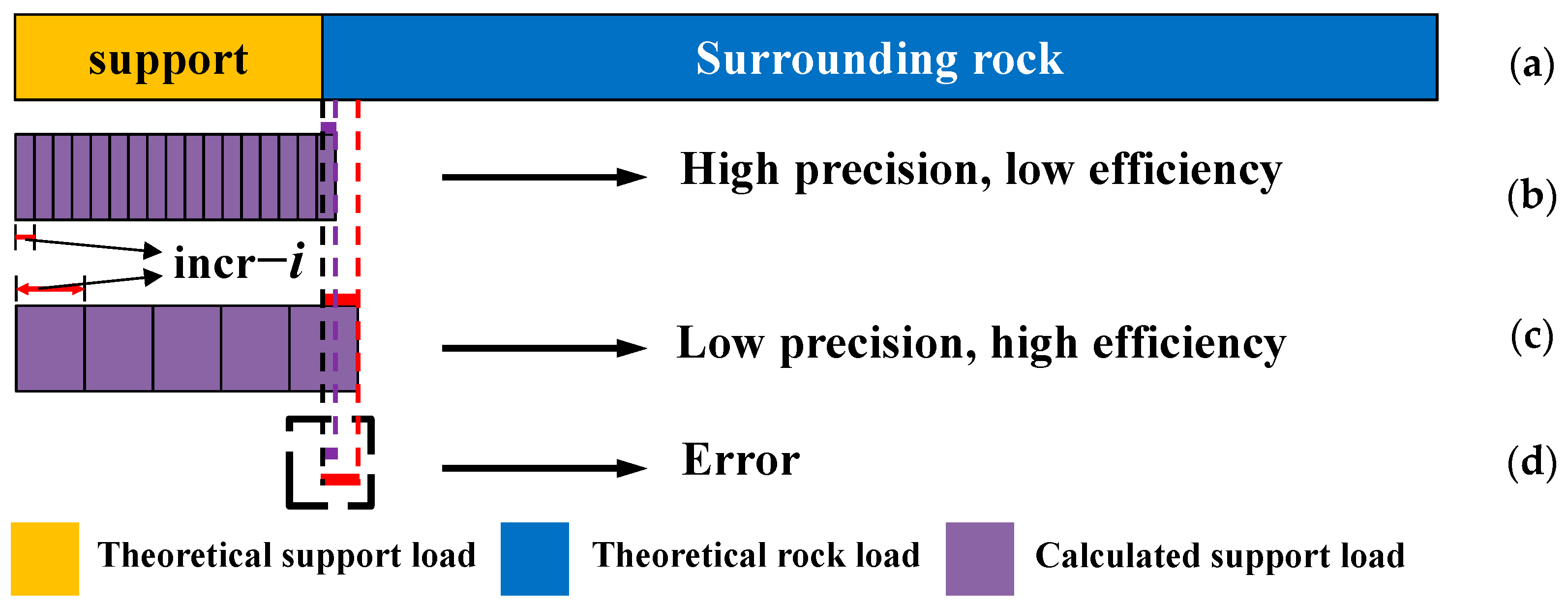
4.3. Verification of Computational Efficiency
5. Discussion
5.1. Effect of Surrounding Rock Mechanical Properties
5.2. Influence of Step Reduction (d) on Computational Efficiency
5.3. Impact of Preset Tolerance on Accuracy and Efficiency
5.4. Engineering Applicability and Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SLCM | Support load convergence method |
| ISLM | Incremental support load method |
| CCM | Convergence–confinement method |
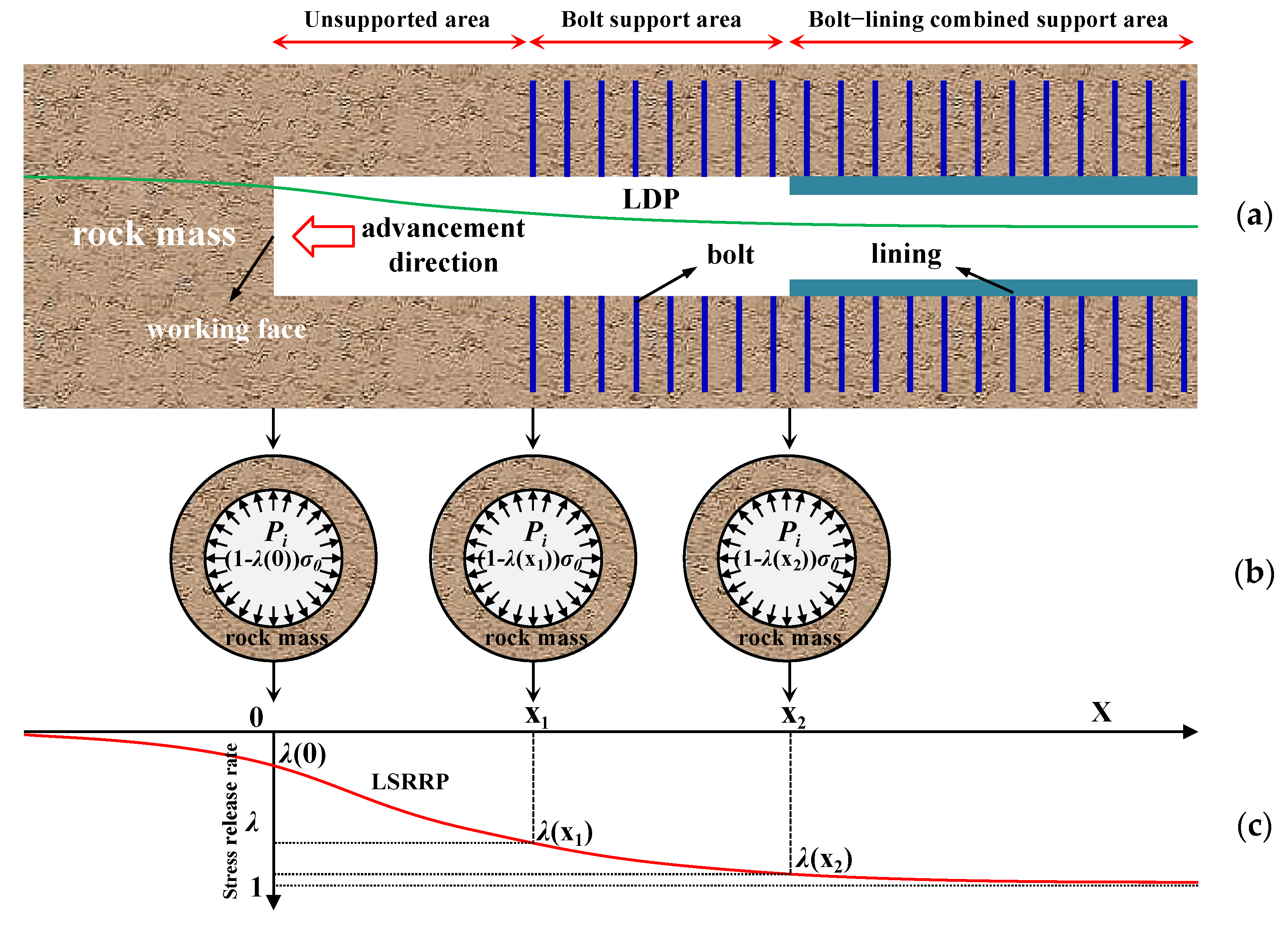
| LDP | Longitudinal displacement profile of the tunnel |
| GRC | Ground reaction curve |
| SCC | Support characteristic curve |
| RMR | Rock mass rating |
| GSI | Geological strength index |
| incr − i | Incremental load |
| The following symbols are used in this manuscript: | |
| Stress release ratio of surrounding rock | |
| Virtual support force | |
| Support force/Support load | |
| Support load carried by lining | |
| Support load carried by bolt | |
| Support force/Support load (i-th step) | |
| Rock load (i-th step) | |
| Critical support force of surrounding rock | |
| Virtual support force reduction (i-th → i + 1-th step) | |
| Support load increment, a = 1, 2, … (i + 1-th step) | |
| Support force increment (i-th step) | |
| In situ stress | |
| Radial stress of surrounding rock | |
| j-th annulus radial stress | |
| Circumferential stress of surrounding rock | |
| j-th annulus circumferential stress | |
| Contact force between surrounding rock and lining | |
| Difference in radial stress between adjacent annuli | |
| Radial strain of surrounding rock | |
| Radial elastic strain of surrounding rock | |
| Radial plastic strain of surrounding rock | |
| Circumferential strain of surrounding rock | |
| Circumferential elastic strain of surrounding rock | |
| Circumferential plastic strain of surrounding rock | |
| j-th annulus circumferential strain | |
| Tunnel radius | |
| Radius of tunnel after lining | |
| Residual radius of surrounding rock | |
| Plastic radius of surrounding rock | |
| Outermost radii | |
| Innermost radii | |
| Radial distance from tunnel center | |
| Radial displacement of tunnel wall | |
| Support displacement (i-th step) | |
| Surrounding rock displacement (i-th step) | |
| j-th annulus radial displacement | |
| Radial displacement of tunnel before support | |
| Radial displacement of lining | |
| Support displacement increment (i-th step) | |
| Softening factor | |
| j-th annulus softening factor | |
| Peak magnitudes of | |
| Residual magnitudes of | |
| Plastic shear strain of surrounding rock | |
| Critical plastic shear strain of surrounding rock | |
| Cohesion of surrounding rock | |
| Internal friction angle of surrounding rock | |
| Dilation coefficient of surrounding rock | |
| Dilation angle of surrounding rock | |
| Shear modulus of surrounding rock | |
| Poisson’s ratio of surrounding rock | |
| Poisson’s ratio of lining | |
| Stiffness of lining | |
| Stiffness of bolt | |
| Stiffness | |
| Elastic modulus of lining | |
| Elastic modulus of bolt | |
| Bolt diameter | |
| Bolt-reinforced zone of surrounding rock/bolt length | |
| Longitudinal spacings of bolt | |
| Circumferential spacings of bolt | |
| Normalized radius | |
| j-th annulus normalized radius | |
| Allowable tolerance | |
| d | Incremental reduction in approximate convergence stage |
References
- Aygar, E.B. Evaluation of new Austrian tunnelling method applied to Bolu tunnel’s weak rocks. J. Rock Mech. Geotech. Eng. 2020, 12, 541–556. [Google Scholar] [CrossRef]
- Zhang, Z.; Pan, Q.; Yang, Z.; Yang, X. Physics-informed deep learning method for predicting tunnelling-induced ground deformations. Acta Geotech. 2023, 18, 4957–4972. [Google Scholar] [CrossRef]
- Zhang, Q.Y.; Ren, M.Y.; Duan, K.; Wang, W.S.; Gao, Q.; Lin, H.X.; Xiang, W.; Jiao, Y.Y. Geo mechanical model test on the collaborative bearing effect of rock-support system for deep tunnel in complicated rock strata. Tunn. Undergr. Space Technol. 2019, 91, 103001. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Wei, G.; Lin, Z.; Wei, X.; Yan, Z.; Yan, J.; Shen, X. Numerical study of excavation face active instability in upward shield tunneling. Buildings 2025, 15, 3371. [Google Scholar] [CrossRef]
- Li, Z.W.; Yang, X.L. Pseudodynamic estimation of 3D active earth pressures with a nonlinear strength criterion. Int. J. Geomech. 2023, 23, 06023013. [Google Scholar] [CrossRef]
- Frenelus, W.; Peng, H.; Zhang, J. Seepage actions and their consequences on the support scheme of deep-buried tunnels constructed in soft rock strata. Infrastructures 2024, 9, 13. [Google Scholar] [CrossRef]
- Liu, K.; Zhao, W.; Li, J.; Ding, W. Design of tunnel initial support in silty clay stratum based on the convergence-confinement method. Sustainability 2023, 15, 2386. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, L.; Chen, J.; Luo, Y.; Guo, H.; Zhai, Y.; Wang, P. Load calculation method for deep-buried layered soft rock tunnel based on back-analysis of structural deformation. Symmetry 2024, 16, 383. [Google Scholar] [CrossRef]
- Lee, Y.K.; Pietruszczak, S. A new numerical procedure for elasto-plastic analysis of a circular opening excavated in a strain-softening rock mass. Tunn. Undergr. Space Technol. 2008, 23, 588–599. [Google Scholar] [CrossRef]
- Nie, X.; Yu, H.; Lu, J.; Zhang, P.; Fan, T. Correlation analysis and dynamic evolution research on safety risks of TBM construction in hydraulic tunnels. Buildings 2025, 15, 3359. [Google Scholar] [CrossRef]
- Carranza Torres, C.; Rysdahl, B.; Kasim, M. On the elastic analysis of a circular lined tunnel considering the delayed installation of the support. Int. J. Rock Mech. Min. Sci. 2013, 61, 57–85. [Google Scholar] [CrossRef]
- El Naggar, H.; Hinchberger, S.D.; Lo, K.Y. A closed-form solution for composite tunnel linings in a homogeneous infinite isotropic elastic medium. Can. Geotech. J. 2008, 45, 266–287. [Google Scholar] [CrossRef]
- Oreste, P.P. A procedure for determining the reaction curve of shotcrete lining considering transient conditions. Rock Mech. Rock Eng. 2003, 36, 209–236. [Google Scholar] [CrossRef]
- Kamiński, P.; Otto, A.; Dawidziuk, P.; Malinowski, L.; Stecuła, K.; Dyczko, A. Determination of the ground reaction curve for an elasto-plasto-fractured rock mass. Appl. Sci. 2024, 14, 5409. [Google Scholar] [CrossRef]
- Zhong, Z.; Tang, T.; Li, Y. Determination of supporting time of tunnels in the Xigeda stratum based on the convergence-confinement method. Appl. Sci. 2023, 13, 13235. [Google Scholar] [CrossRef]
- Dang, T.T.; Tran, M.T.; Nguyen, H.H. Ground characteristic curve and convergence confinement method—A case study. J. Min. Earth Sci. 2022, 63, 68–77. [Google Scholar] [CrossRef]
- Lee, Y.-L.; Kao, W.-C.; Chen, C.-S.; Ma, C.-H.; Hsieh, P.-W.; Lee, C.-M. Inverse analysis for the convergence-confinement method in tunneling. Mathematics 2022, 10, 1223. [Google Scholar] [CrossRef]
- Oreste, P.P. Analysis of structural interaction in tunnels using the covergence–confinement approach. Tunn. Undergr. Space Technol. 2003, 18, 347–363. [Google Scholar] [CrossRef]
- González Nicieza, C.; Álvarez Vigil, A.E.; Menéndez Díaz, A.; González Palacio, C. Influence of the depth and shape of a tunnel in the application of the convergence–confinement method. Tunn. Undergr. Space Technol. 2008, 23, 25–37. [Google Scholar] [CrossRef]
- Ranjbarnia, M.; Rahimpour, N.; Oreste, P. A simple analytical approach to simulate the arch umbrella supporting system in deep tunnels based on convergence confinement method. Tunn. Undergr. Space Technol. 2018, 82, 39–49. [Google Scholar] [CrossRef]
- Chang, L.; Alejano, L.R.; Cui, L.; Sheng, Q.; Xie, M. Limitation of convergence-confinement method on three-dimensional tunnelling effect. Sci. Rep. 2023, 13, 1988. [Google Scholar] [CrossRef] [PubMed]
- González Cao, J.; Alejano, L.R.; Alonso, E.; Bastante, F.G. Convergence-confinement curve analysis of excavation stress and strain resulting from blast-induced damage. Tunn. Undergr. Space Technol. 2018, 73, 162–169. [Google Scholar] [CrossRef]
- Bour, K.; Goshtasbi, K. Study of convergence confinement method curves considering pore-pressure effect. J. Min. Environ. 2019, 10, 479–492. [Google Scholar]
- Ren, M.; Wu, X.; Pan, J.; Liu, H.; Li, N. Theoretical and numerical studies of rock-support interaction by considering imperfect rock-lining interface. Geotech. Geol. Eng. 2023, 41, 1741–1762. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, T.; Li, X.; Dias, D. Bayesian ensemble methods for predicting ground deformation due to tunnelling with sparse monitoring data. Undergr. Space 2024, 16, 79–93. [Google Scholar] [CrossRef]
- Zareifard, M.R.; Fahimifar, A. Analytical solutions for the stresses and deformations of deep tunnels in an elastic-brittle-plastic rock mass considering the damaged zone. Tunn. Undergr. Space Technol. 2016, 58, 186–196. [Google Scholar] [CrossRef]
- Paraskevopoulou, C.; Diederichs, M. Analysis of time-dependent deformation in tunnels using the Convergence-Confinement Method. Tunn. Undergr. Space Technol. 2018, 71, 62–80. [Google Scholar] [CrossRef]
- Guan, Z.; Jiang, Y.; Tanabasi, Y. Ground reaction analyses in conventional tunnelling excavation. Tunn. Undergr. Space Technol. 2007, 22, 230–237. [Google Scholar] [CrossRef]

| Elastic Modulus | Poisson’s Ratio | c | φ | Dilation Angle | ||
|---|---|---|---|---|---|---|
| (GPa) | (MPa) | ° | ° | |||
| Peak value | 5.8 | 0.35 | 2.2 | 40 | 15 | 0.01 |
| Residual value | 5.0 | 0.35 | 0.7 | 22 | 5 |
| Diameter | Length | Longitudinal Spacing | Circumferential Spacing | Elastic Modulus | Poisson’s Ratio |
|---|---|---|---|---|---|
| (m) | (m) | (m) | (m) | (GPa) | |
| 0.03 | 4.5 | 1.15 | 1.96 | 200 | 0.2 |
| Method | Parameter (Pa or %) | Time (s) | Efficiency Improvement (%) | Accuracy |
|---|---|---|---|---|
| ISLM | incr − i = 10 Pa | 5537 | 0.0 | Moderate |
| incr − i = 20 Pa | 3981 | 28.1 | Moderate | |
| incr − i = 50 Pa | 2397 | 56.7 | Moderate | |
| incr − i = 100 Pa | 1473 | 73.4 | Moderate | |
| incr − i = 200 Pa | 936 | 83.1 | Moderate | |
| Bisection Method | 283 | 69.8–94.9 | High | |
| SLCM | d = 3% | 66 | 92.9–98.8 | Very High |
| Step reduction d (%) | 3 | 4 | 5 | 6 | 7 |
| Computation time (s) | 66 | 52 | 41 | 61 | 77 |
| Prescribed Tolerance | Time (s) | Accuracy/Remarks |
|---|---|---|
| 1/100 | 29 | Fast computation, lower accuracy |
| 1/200 | 53 | Recommended minimum for accurate results |
| 1/300 | 66 | Higher accuracy, moderate computation time |
| 1/500 | 97 | Accuracy further improves; computation time increases |
| 1/1000 | 159 | High accuracy, long computation time |
| 1/2000 | 286 | Very high accuracy, very time-consuming |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Z.; Gao, Y.; Song, X.; Chen, X.; Bai, Z.; Li, Z. A Two-Stage Support Load Convergence Method for Rock–Support Interaction in Tunnels. Buildings 2025, 15, 4136. https://doi.org/10.3390/buildings15224136
Xie Z, Gao Y, Song X, Chen X, Bai Z, Li Z. A Two-Stage Support Load Convergence Method for Rock–Support Interaction in Tunnels. Buildings. 2025; 15(22):4136. https://doi.org/10.3390/buildings15224136
Chicago/Turabian StyleXie, Zundang, Yiwei Gao, Xiuchang Song, Xiaonian Chen, Zhengxiong Bai, and Zhen Li. 2025. "A Two-Stage Support Load Convergence Method for Rock–Support Interaction in Tunnels" Buildings 15, no. 22: 4136. https://doi.org/10.3390/buildings15224136
APA StyleXie, Z., Gao, Y., Song, X., Chen, X., Bai, Z., & Li, Z. (2025). A Two-Stage Support Load Convergence Method for Rock–Support Interaction in Tunnels. Buildings, 15(22), 4136. https://doi.org/10.3390/buildings15224136





