Design Spectra for Evaluating the Dynamic Response of Buildings Under Thunderstorm Downbursts
Abstract
1. Introduction
2. Thunderstorm Downburst Wind Flow
3. Thunderstorm Downburst Wind Design Spectra
3.1. Overview of Method
3.2. Wind Design Spectra for Single-Degree-of-Freedom Systems
3.3. Wind Design Spectra for Multi-Degree-of-Freedom Systems
3.4. Scrutinising the Controlling Parameters of Wind Design Spectra for Downburst Outflows
3.5. Applications on Structures
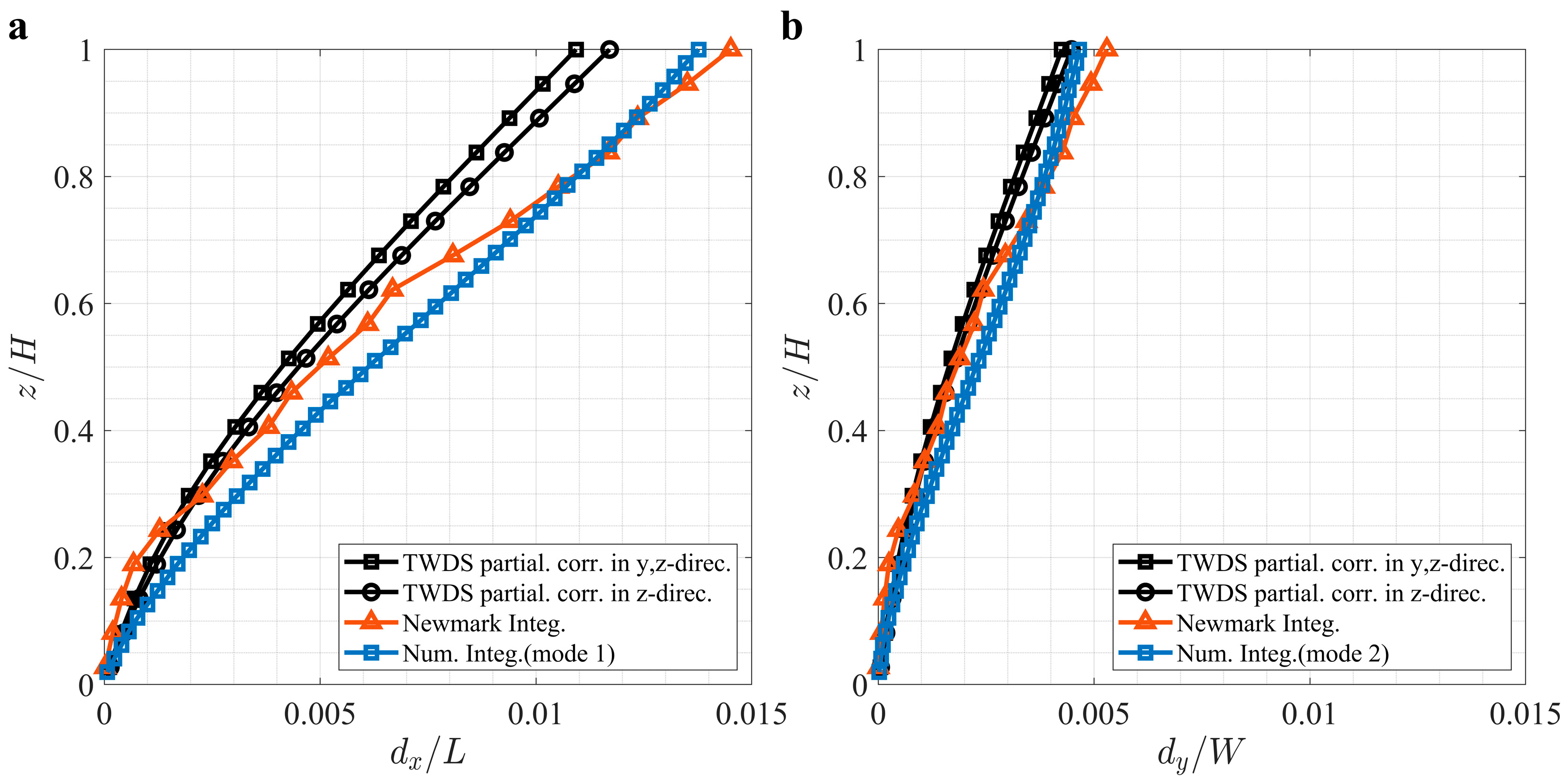
4. Comparison with Other Numerical Methods
4.1. Primary Validation of the Algorithm Referring to WDS for Synoptic Wind
4.2. Simulation of Downburst Outflow Data Series
4.3. Newmark Integration
4.4. Numerical Simulation
5. Sensitivity Discussion and Practice Advancement
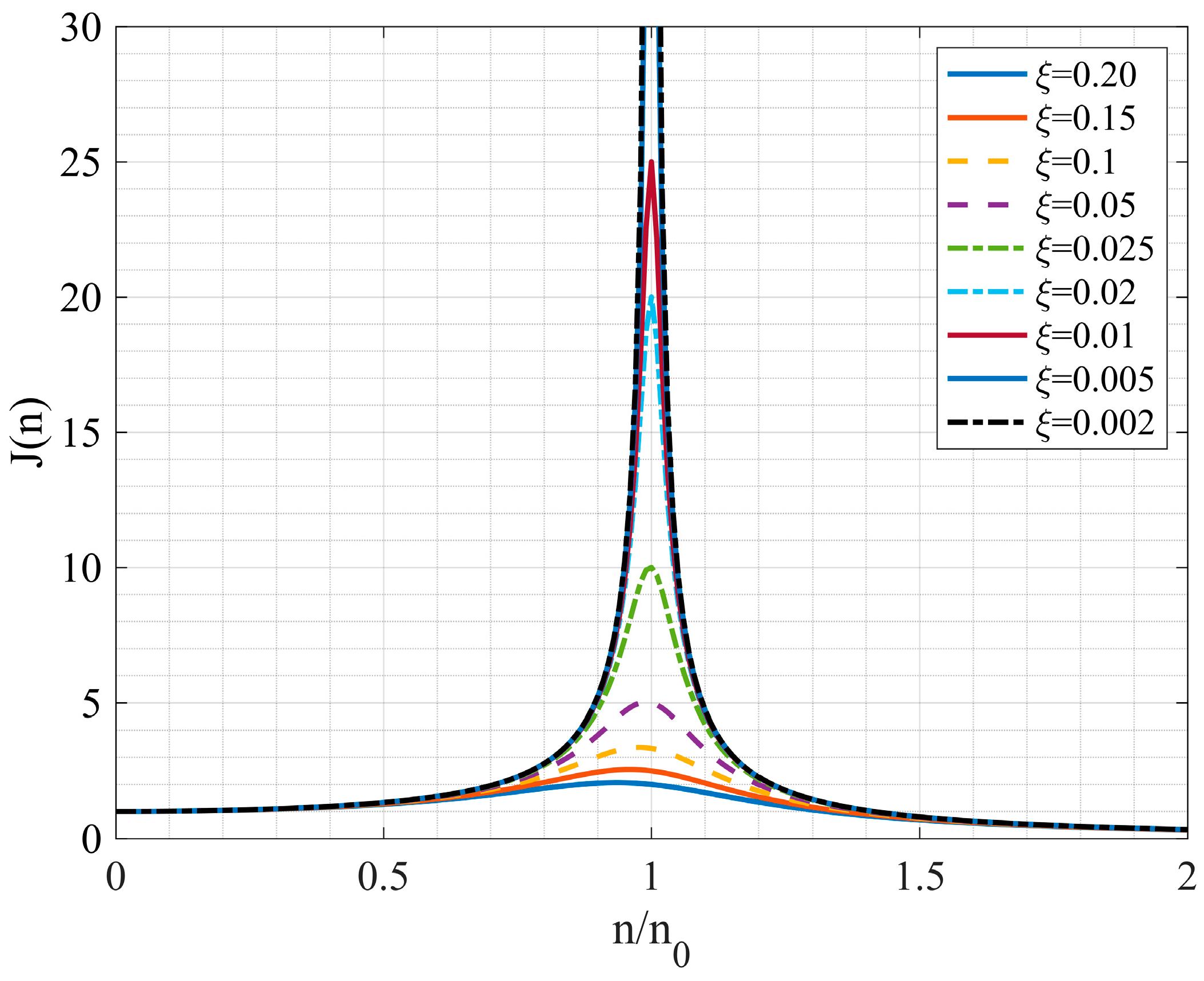
5.1. Sensitivity Discussion
5.2. Practice Advancement
6. Conclusions
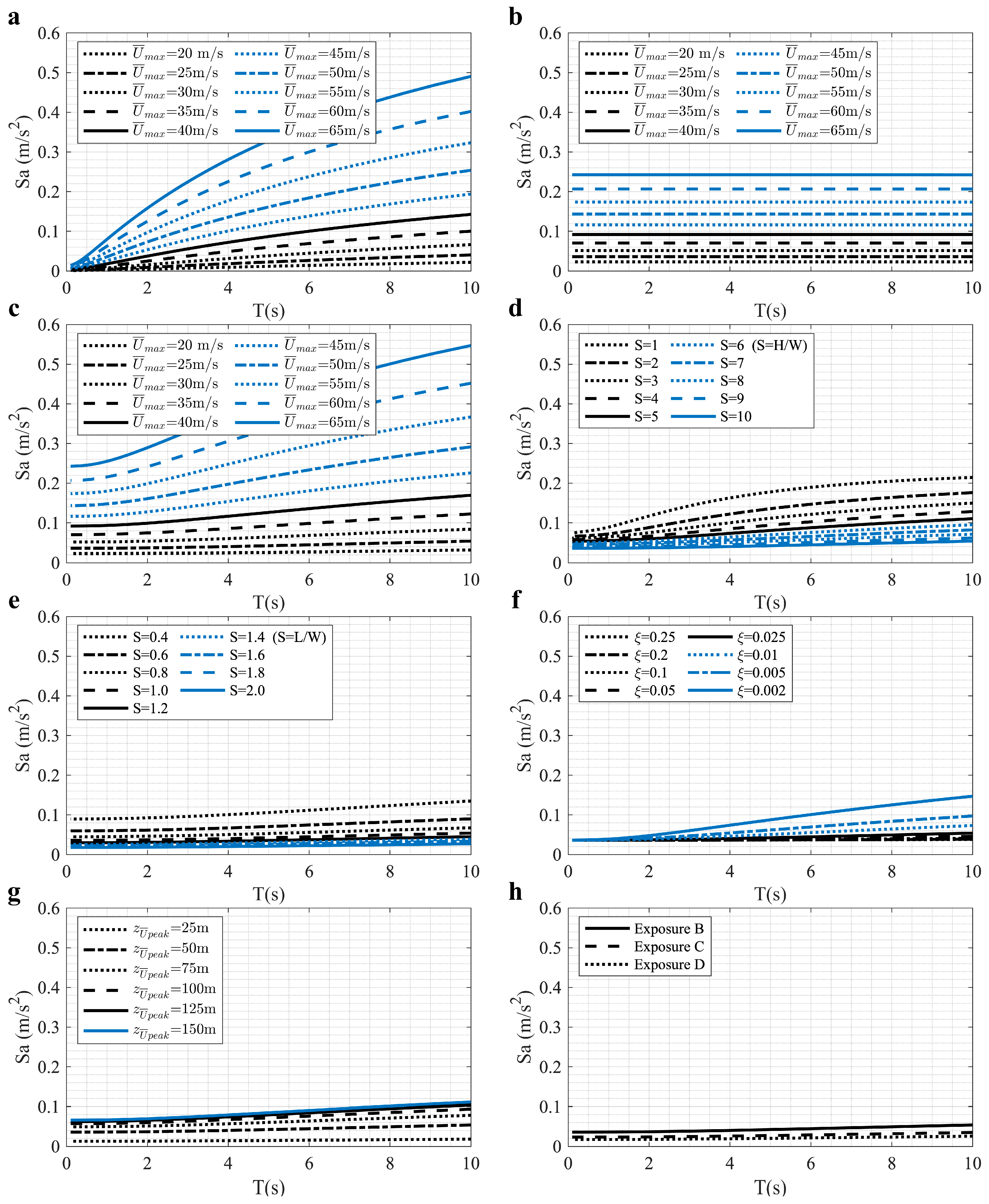
- The investigation for the input parameters of the design spectra illustrates that the design spectra of the output accelerations significantly rise with the increasing velocities of the downburst outflow, particularly in the low-frequency spectral range. To an extent, this is an expected outcome given the energy imparted by low frequency gusts.
- Design spectral ordinates (pseudo-acceleration) decrease with the aspect ratio. This implies that low-rise buildings would undergo higher response acceleration than taller buildings.
- The variations in the damping ratio, although of lower impact, become more evident at the lower frequency range. Furthermore, the changeable heights for the maximum slowly varying mean velocity of the downburst outflow also reflected a slight effect on the design spectra, and the maximum design spectrum is only 0.111 m/s2 when the height of this maximum value is 150 m.
- The comparison between the results of the TWDS in time–frequency domain and the equivalent theoretical integration in the time domain as well as the numerical simulation for the benchmark tall building demonstrate the applicability of the spectral method.
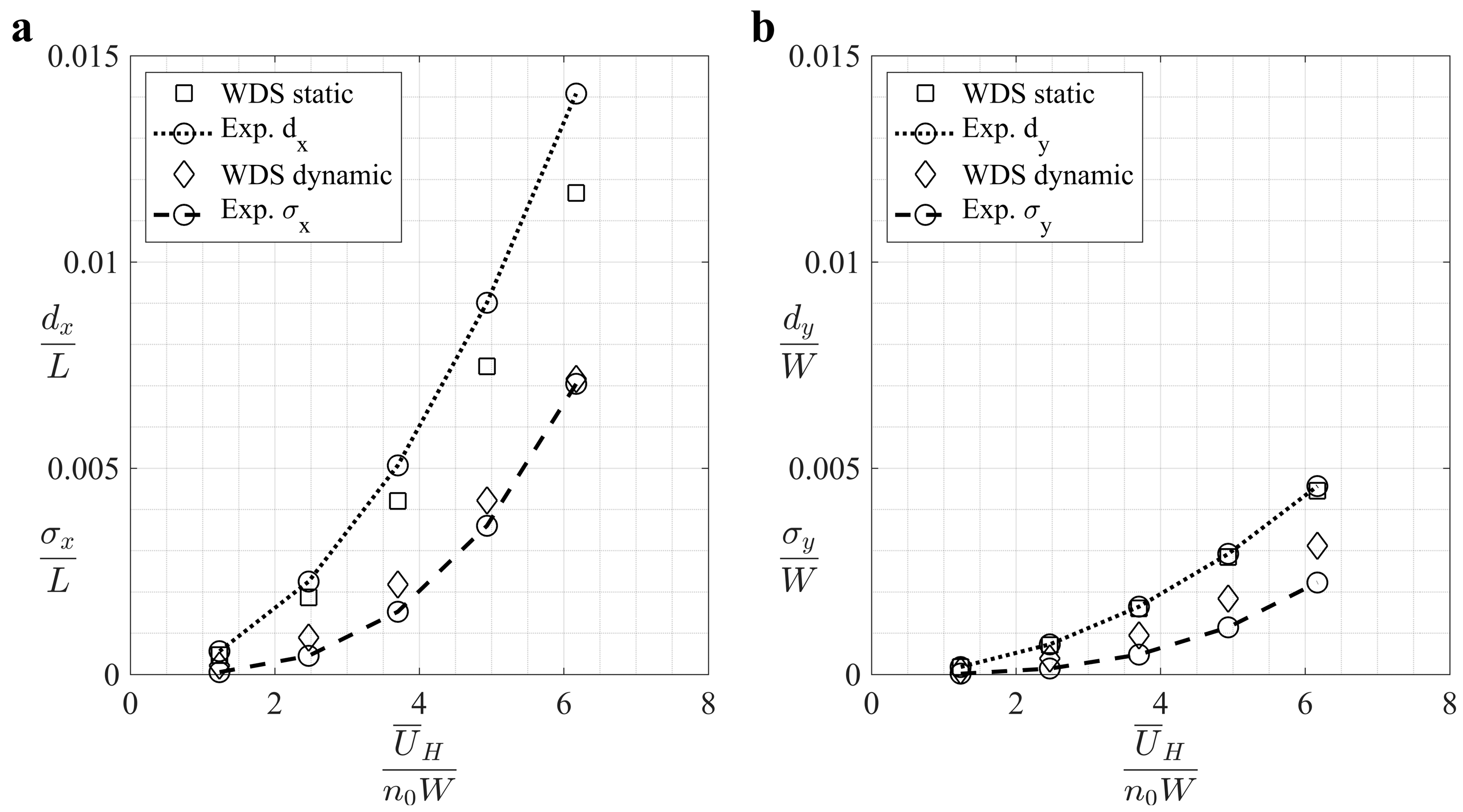
- The peak displacement amplitudes obtained from the simplified and refined modelling under the simulated outflow wind field showed differences with those from the TWDS method ranging between 3.9% and 23.9%, which is the side of the building with the larger exposed area where displacements exhibited larger differences. This seems to be related to the cross-correlation decay, not accurately estimated through simplified modelling based on rigid bars.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviations | |||
| TS | Thunderstorm | WDS | Wind design spectra |
| SDOF | Single-degree-of-freedom | ABL | Atmospheric boundary layer |
| MDOF | Multi-degree-of-freedom | PSD | Power spectral density |
| EPSD | Evolutionary power spectral density | CAARC | Commonwealth Advisory Aeronautical Research Council |
| TWDS | Thunderstorm downburst wind design spectra | ||
| Nomenclature | |||
| Wind velocity | Drag coefficient | ||
| Slowly varying mean wind velocity | Air density | ||
| Residual fluctuating velocity to high-frequency components | Structural surface exposed to wind | ||
| Reduced turbulent fluctuation Rapidly varying fluctuating velocity | Structural stiffness | ||
| Slowly varying standard deviation | (z) | Non-dimensional vertical shape profile of mean value of the turbulence intensity over the measurement time period | |
| Maximum slowly varying mean wind velocity | Non-dimensional horizontal shape profile of turbulence intensity changing with respect to time | ||
| Maximum slowly varying mean wind velocity at reference height | Turbulence intensity factor; Damping coefficient | ||
| Height above the ground | Varying running mean time intervals | ||
| Reference height | Frequency of gust wind | ||
| Turbulence intensity | Turbulence integral length scale | ||
| Mean value of the turbulence intensity over the measurement time period | Autocorrelation function that changes with the time delay | ||
| Time | Time delay | ||
| Non-dimensional vertical shape function of horizontal wind | Friction velocity | ||
| Radius at the maximum horizontal wind velocity | Integral length scale factor | ||
| Radial distance from the storm centre | Exposure constant | ||
| Radial length scale defined as the distance from the ‘low pressure ring’ to the ‘high-pressure ring’ | Power spectra density function for the reduced horizontal fluctuating velocity component | ||
| Non-dimensional time function of horizontal wind | Force spectra | ||
| The height where the velocity is equal to half its maximum value | Input acceleration spectra | ||
| Peak value of maximum slowly varying mean wind velocity along the height above the ground | TWDS of the output acceleration | ||
| erf | error function | Cross-power spectra of the input acceleration | |
| Height for the peak value of maximum slowly varying mean wind velocity | Power spectral density of the generalised input acceleration | ||
| Exponents of power-law | Design spectra of the output acceleration | ||
| Resultant velocity | Mass of the structure excited by the wind force | ||
| Translation velocity | Force factor | ||
| Radial velocity | Aerodynamic admittance | ||
| Observation point | Transfer function | ||
| Initial observation point | Natural frequency of structures | ||
| Offset distance in the transverse direction | Natural period of structures | ||
| Offset distance in the longitudinal direction | Horizontal distance between two points | ||
| Angle between the translation velocity and the radial velocity | Vertical distance between two points | ||
| Damping ratio | Non-dimensional decay constant along with the horizontal direction | ||
| H | Vertical dimension of structures | Non-dimensional decay constant along with the vertical direction | |
| Lateral dimension of structures | Fundamental modal shape at the height above the ground | ||
| Longitudinal dimension of structures | Overall spectral response | ||
| First modal amplitude | Background response components | ||
| Flexibility of the real structure | Resonant response components | ||
| First modal mass | Angular frequency | ||
| First modal stiffness | Static displacement response of structures | ||
| First modal excited masses | Dynamic displacement response | ||
| Total horizontal force on structures | Peak displacement response | ||
| Slowly varying mean component | Stationary Gaussian stochastic process | ||
| Residual fluctuating component | Amplitude modulation function | ||
References
- McDonald, J.R.; Mehta, K.C. A Recommendation for an Enhanced Fujita Scale (EF-Scale); Wind Science and Engineering Center, Texas Tech University: Lubbock, TX, USA, 2006. [Google Scholar]
- Fujita, T.T. The downburst: Microburst and macroburst. University of Chicago. SMRP Res. 1985, 210, 112. [Google Scholar]
- Fujita, T.T. Downbursts: Meteorological features and wind field characteristics. J. Wind Eng. Ind. Aerodyn. 1990, 36, 75–86. [Google Scholar] [CrossRef]
- Kim, J.; Hangan, H. Numerical simulations of impinging jets with application to downbursts. J. Wind Eng. Ind. Aerodyn. 2007, 95, 279–298. [Google Scholar] [CrossRef]
- Chay, M.; Albermani, F. Dynamic response of a SDOF system subjected to simulated downburst wind. In Proceedings of the 10th International Conference on Wind Engineering, Prague, Czech Republic, 11–15 July 2005; Volume 2, pp. 1123–1130. [Google Scholar]
- Chen, L.; Letchford, C. A deterministic–stochastic hybrid model of downbursts and its impact on a cantilevered structure. Eng. Struct. 2004, 26, 619–629. [Google Scholar] [CrossRef]
- Chen, X. Analysis of alongwind tall building response to transient nonstationary winds. J. Struct. Eng. 2008, 134, 782–791. [Google Scholar] [CrossRef]
- Choi, E.C.; Hidayat, F.A. Dynamic response of structures to thunderstorm winds. Prog. Struct. Eng. Mater. 2002, 4, 408–416. [Google Scholar] [CrossRef]
- Holmes, J.; Forristall, G.; McConochie, J. Dynamic response of structures to thunderstorm winds. In Proceedings of the 10th Americas Conference on Wind Engineering (10ACWE), San Juan, Puerto Rico, 22–26 June 2005; pp. 1–6. [Google Scholar]
- Solari, G. Thunderstorm response spectrum technique: Theory and applications. Eng. Struct. 2016, 108, 28–46. [Google Scholar] [CrossRef]
- Chen, L.; Letchford, C. Parametric study on the along-wind response of the CAARC building to downbursts in the time domain. J. Wind Eng. Ind. Aerodyn. 2004, 92, 703–724. [Google Scholar] [CrossRef]
- Solari, G.; De Gaetano, P.; Repetto, M.P. Thunderstorm response spectrum: Fundamentals and case study. J. Wind Eng. Ind. Aerodyn. 2015, 143, 62–77. [Google Scholar] [CrossRef]
- Kareem, A.; Hu, L.; Guo, Y.; Kwon, D.-K. Generalized wind loading chain: Time-frequency modeling framework for nonstationary wind effects on structures. J. Struct. Eng. 2019, 145, 04019092. [Google Scholar] [CrossRef]
- Dyrbye, C.; Hansen, S.O. Wind Loads on Structures, 2nd ed.; Wiley: Hoboken, NJ, USA, 1997. [Google Scholar]
- Peng, L.; Huang, G.; Chen, X.; Yang, Q. Evolutionary spectra-based time-varying coherence function and application in structural response analysis to downburst winds. J. Struct. Eng. 2018, 144, 04018078. [Google Scholar] [CrossRef]
- Le, T.-H.; Caracoglia, L. Computer-based model for the transient dynamics of a tall building during digitally simulated Andrews AFB thunderstorm. Comput. Struct. 2017, 193, 44–72. [Google Scholar] [CrossRef]
- Kwon, D.K.; Kareem, A. Towards codification of thunderstorm/downburst using gust front factor: Model-based and data-driven perspectives. Eng. Struct. 2019, 199, 109608. [Google Scholar] [CrossRef]
- Kwon, D.-K.; Kareem, A. Gust-front factor: New framework for wind load effects on structures. J. Struct. Eng. 2009, 135, 717–732. [Google Scholar] [CrossRef]
- Solari, G.; Rainisio, D.; De Gaetano, P. Hybrid simulation of thunderstorm outflows and wind-excited response of structures. Meccanica 2017, 52, 3197–3220. [Google Scholar] [CrossRef]
- Abd-Elaal, E.-S.; Mills, J.E.; Ma, X. An analytical model for simulating steady state flows of downburst. J. Wind Eng. Ind. Aerodyn. 2013, 115, 53–64. [Google Scholar] [CrossRef]
- Abd-Elaal, E.-S.; Mills, J.E.; Ma, X. Empirical models for predicting unsteady-state downburst wind speeds. J. Wind Eng. Ind. Aerodyn. 2014, 129, 49–63. [Google Scholar] [CrossRef]
- Holmes, J.D.; Oliver, S. An empirical model of a downburst. Eng. Struct. 2000, 22, 1167–1172. [Google Scholar] [CrossRef]
- Li, C.; Li, Q.; Xiao, Y.; Ou, J. A revised empirical model and CFD simulations for 3D axisymmetric steady-state flows of downbursts and impinging jets. J. Wind Eng. Ind. Aerodyn. 2012, 102, 48–60. [Google Scholar] [CrossRef]
- Oseguera, R.M.; Bowles, R.L. A simple, analytic 3-dimensional downburst model based on boundary layer stagnation flow. In NASA Technical Memorandum; Langley Research Center: Hampton, VA, USA, 1988; p. 100632. Available online: https://ntrs.nasa.gov/citations/19880010328 (accessed on 21 October 2025).
- Vicroy, D.D. Assessment of microburst models for downdraft estimation. J. Aircr. 1992, 29, 1043–1048. [Google Scholar] [CrossRef]
- Wood, G.S.; Kwok, K.C.; Motteram, N.A.; Fletcher, D.F. Physical and numerical modelling of thunderstorm downbursts. J. Wind Eng. Ind. Aerodyn. 2001, 89, 535–552. [Google Scholar] [CrossRef]
- Shinozuka, M.; Deodatis, G. Simulation of stochastic processes by spectral representation. Appl. Mech. Rev. 1991, 44, 191–204. [Google Scholar] [CrossRef]
- Skalomenos, K.A.; Hatzigeorgiou, G.D.; Beskos, D.E. Application of the hybrid force/displacement (HFD) seismic design method to composite steel/concrete plane frames. J. Constr. Steel Res. 2015, 115, 179–190. [Google Scholar] [CrossRef]
- Serras, D.N.; Skalomenos, K.A.; Hatzigeorgiou, G.D. A displacement/damage controlled seismic design method for MRFs with concrete-filled steel tubular columns and composite beams. Soil Dyn. Earthq. Eng. 2021, 143, 106608. [Google Scholar] [CrossRef]
- Housner, G.W.; Martel, R.; Alford, J. Spectrum analysis of strong-motion earthquakes. Bull. Seismol. Soc. Am. 1953, 43, 97–119. [Google Scholar] [CrossRef]
- Solari, G. Wind response spectrum. J. Eng. Mech. 1989, 115, 2057–2073. [Google Scholar] [CrossRef]
- Simiu, E.; Scanlan, R.H. Wind Effects on Structures: Fundamentals and Applications to Design, 3rd ed.; Wiley: Hoboken, NJ, USA, 1996. [Google Scholar]
- Martinez-Vazquez, P. Wind-induced vibrations of structures using design spectra. Int. J. Adv. Struct. Eng. 2016, 8, 379–389. [Google Scholar] [CrossRef]
- Martinez-Vazquez, P. Wind design spectra for generalization. Wind Struct. 2020, 30, 155. [Google Scholar] [CrossRef]
- Fujita, T.T. The Downburst, Report of Projects NIMROD and JAWS; University of Chicago: Chicago, IL, USA, 1985. [Google Scholar]
- Chen, L.; Letchford, C. Numerical simulation of extreme winds from thunderstorm downbursts. J. Wind Eng. Ind. Aerodyn. 2007, 95, 977–990. [Google Scholar] [CrossRef]
- Holmes, J.; Hangan, H.; Schroeder, J.; Letchford, C.; Orwig, K. A forensic study of the Lubbock-Reese downdraft of 2002. Wind Struct. 2008, 11, 137–152. [Google Scholar] [CrossRef]
- Lombardo, F.T.; Smith, D.A.; Schroeder, J.L.; Mehta, K.C. Thunderstorm characteristics of importance to wind engineering. J. Wind Eng. Ind. Aerodyn. 2014, 125, 121–132. [Google Scholar] [CrossRef]
- Solari, G.; Burlando, M.; De Gaetano, P.; Repetto, M.P. Characteristics of thunderstorms relevant to the wind loading of structures. Wind Struct. 2015, 20, 763. [Google Scholar] [CrossRef]
- Zhang, S.; Solari, G.; De Gaetano, P.; Burlando, M.; Repetto, M.P. A refined analysis of thunderstorm outflow characteristics relevant to the wind loading of structures. Probabilistic Eng. Mech. 2018, 54, 9–24. [Google Scholar] [CrossRef]
- Hjelmfelt, M.R. Structure and life cycle of microburst outflows observed in Colorado. J. Appl. Meteorol. 1988, 27, 900–927. [Google Scholar] [CrossRef]
- Roncallo, L.; Solari, G. An evolutionary power spectral density model of thunderstorm outflows consistent with real-scale time-history records. J. Wind Eng. Ind. Aerodyn. 2020, 203, 104204. [Google Scholar] [CrossRef]
- Xhelaj, A.; Burlando, M.; Solari, G. A general-purpose analytical model for reconstructing the thunderstorm outflows of travelling downbursts immersed in ABL flows. J. Wind Eng. Ind. Aerodyn. 2020, 207, 104373. [Google Scholar] [CrossRef]
- Aboshosha, H.; Bitsuamlak, G.; El Damatty, A. Turbulence characterization of downbursts using LES. J. Wind Eng. Ind. Aerodyn. 2015, 136, 44–61. [Google Scholar] [CrossRef]
- Burlando, M.; Romanić, D.; Solari, G.; Hangan, H.; Zhang, S. Field data analysis and weather scenario of a downburst event in Livorno, Italy, on 1 October 2012. Mon. Weather Rev. 2017, 145, 3507–3527. [Google Scholar] [CrossRef]
- Choi, E.C. Field measurement and experimental study of wind speed profile during thunderstorms. J. Wind Eng. Ind. Aerodyn. 2004, 92, 275–290. [Google Scholar] [CrossRef]
- Durañona, V.; Sterling, M.; Baker, C.J. An analysis of extreme non-synoptic winds. J. Wind Eng. Ind. Aerodyn. 2007, 95, 1007–1027. [Google Scholar] [CrossRef]
- Orwig, K.D.; Schroeder, J.L. Near-surface wind characteristics of extreme thunderstorm outflows. J. Wind Eng. Ind. Aerodyn. 2007, 95, 565–584. [Google Scholar] [CrossRef]
- Romanic, D.; Chowdhury, J.; Chowdhury, J.; Hangan, H. Investigation of the Transient Nature of Thunderstorm Winds from Europe, the United States, and Australia Using a New Method for Detection of Changepoints in Wind Speed Records. Mon. Weather Rev. 2020, 148, 3747–3771. [Google Scholar] [CrossRef]
- ASCE7. Minimum Design Loads for Buildings and Other Structures (ASCE/SEI 7-10); American Society of Civil Engineers: Reston, VA, USA, 2013. [Google Scholar]
- ASCE. Wind Tunnel Testing for Buildings and Other Structures; American Society of Civil Engineers: Reston, VA, USA, 2012. [Google Scholar]
- von Kármán, T. Progress in the statistical theory of turbulence. Proc. Natl. Acad. Sci. USA 1948, 34, 530. [Google Scholar] [CrossRef]
- Solari, G.; Piccardo, G. Probabilistic 3-D turbulence modeling for gust buffeting of structures. Probabilistic Eng. Mech. 2001, 16, 73–86. [Google Scholar] [CrossRef]
- Kaimal, J.C.; Wyngaard, J.; Izumi, Y.; Coté, O. Spectral characteristics of surface-layer turbulence. Q. J. R. Meteorol. Soc. 1972, 98, 563–589. [Google Scholar] [CrossRef]
- Davenport, A.G. Gust loading factors. J. Struct. Div. 1967, 93, 11–34. [Google Scholar] [CrossRef]
- Vickery, B. Load fluctuations in turbulent flow. J. Eng. Mech. Div. 1968, 94, 31–46. [Google Scholar] [CrossRef]
- Jesson, M.; Lombardo, F.T.; Sterling, M.; Baker, C. The physical simulation of a transient, downburst-like event–How complex does it need to be? J. Wind Eng. Ind. Aerodyn. 2019, 189, 135–150. [Google Scholar] [CrossRef]
- Lombardo, F.T.; Mason, M.S.; de Alba, A.Z. Investigation of a downburst loading event on a full-scale low-rise building. J. Wind Eng. Ind. Aerodyn. 2018, 182, 272–285. [Google Scholar] [CrossRef]
- Letchford, C.; Iverson, R.; McDonald, J. The application of the quasi-steady theory to full scale measurements on the Texas Tech Building. J. Wind Eng. Ind. Aerodyn. 1993, 48, 111–132. [Google Scholar] [CrossRef]
- Mooneghi, M.A.; Irwin, P.; Chowdhury, A.G. Partial turbulence simulation method for predicting peak wind loads on small structures and building appurtenances. J. Wind Eng. Ind. Aerodyn. 2016, 157, 47–62. [Google Scholar] [CrossRef]
- Davenport, A. The prediction of the response of structures to gusty wind. Saf. Struct. Under Dyn. Load. 1977, 1, 257–284. [Google Scholar]
- Kareem, A.; Tamura, Y. Advanced Structural Wind Engineering; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Melbourne, W. Comparison of measurements on the CAARC standard tall building model in simulated model wind flows. J. Wind Eng. Ind. Aerodyn. 1980, 6, 73–88. [Google Scholar] [CrossRef]
- Ondrej. CSi Knowledge Base—SAP2000 21V. 2013. Available online: https://wiki.csiamerica.com/display/sap2000/Home (accessed on 1 January 2013).
- Solari, G.; De Gaetano, P.; Repetto, M.P. Wind loading and response of structures in mixed climates. In Proceedings of the Eight Asia Pacific Conference on Wind Engineering, Chennai, India, 10–14 December 2013. [Google Scholar]
- Deodatis, G. Simulation of ergodic multivariate stochastic processes. J. Eng. Mech. 1996, 122, 778–787. [Google Scholar] [CrossRef]
- Priestley, M.B. Evolutionary spectra and non-stationary processes. J. R. Stat. Soc. Ser. B (Methodol.) 1965, 27, 204–229. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering, 4th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2011; Pearson Education [distributor]: London, UK, 2011. (In English) [Google Scholar]
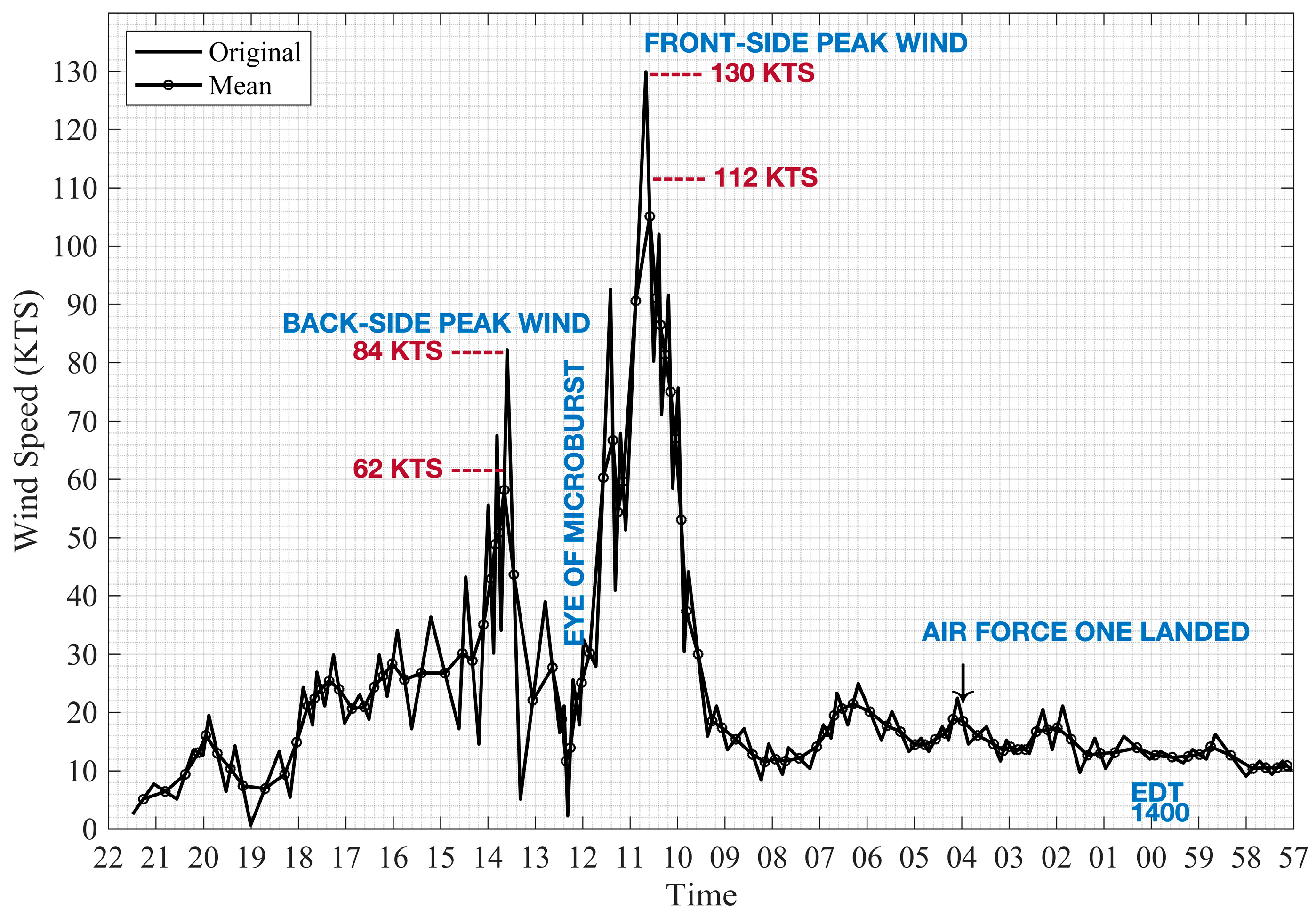
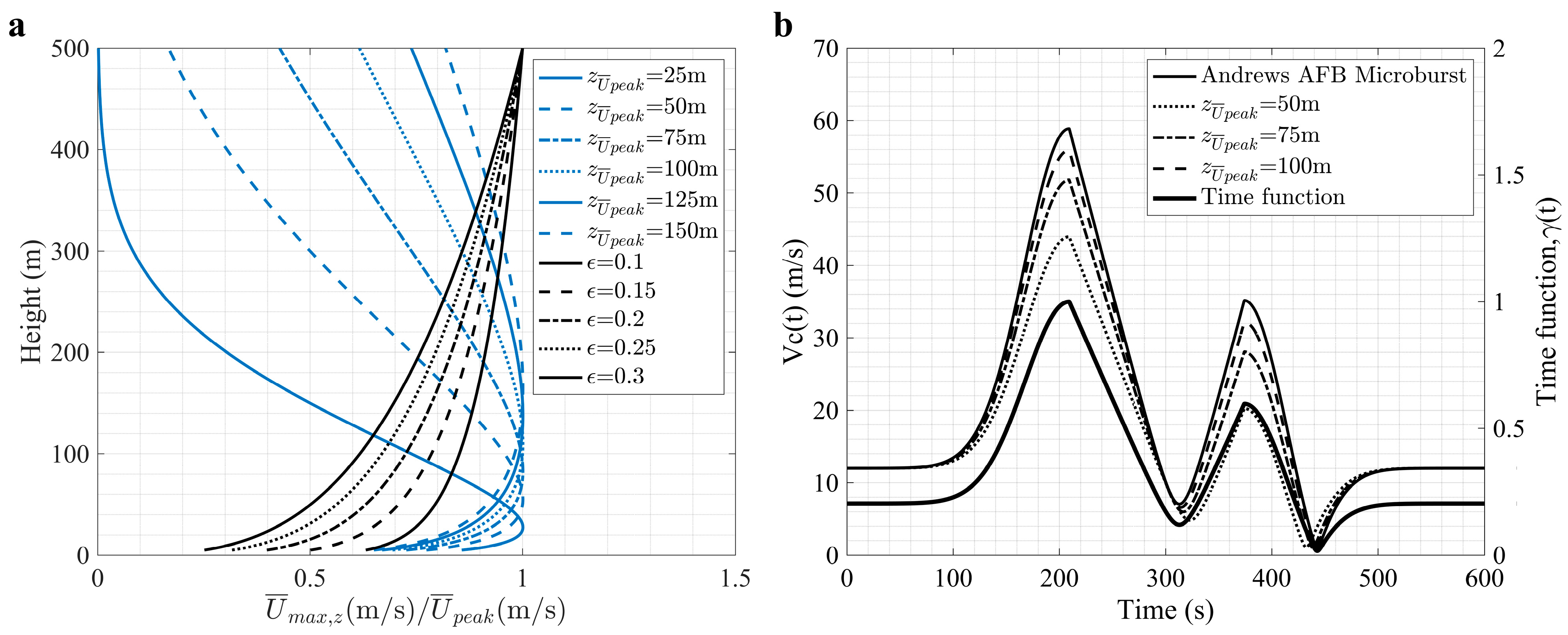
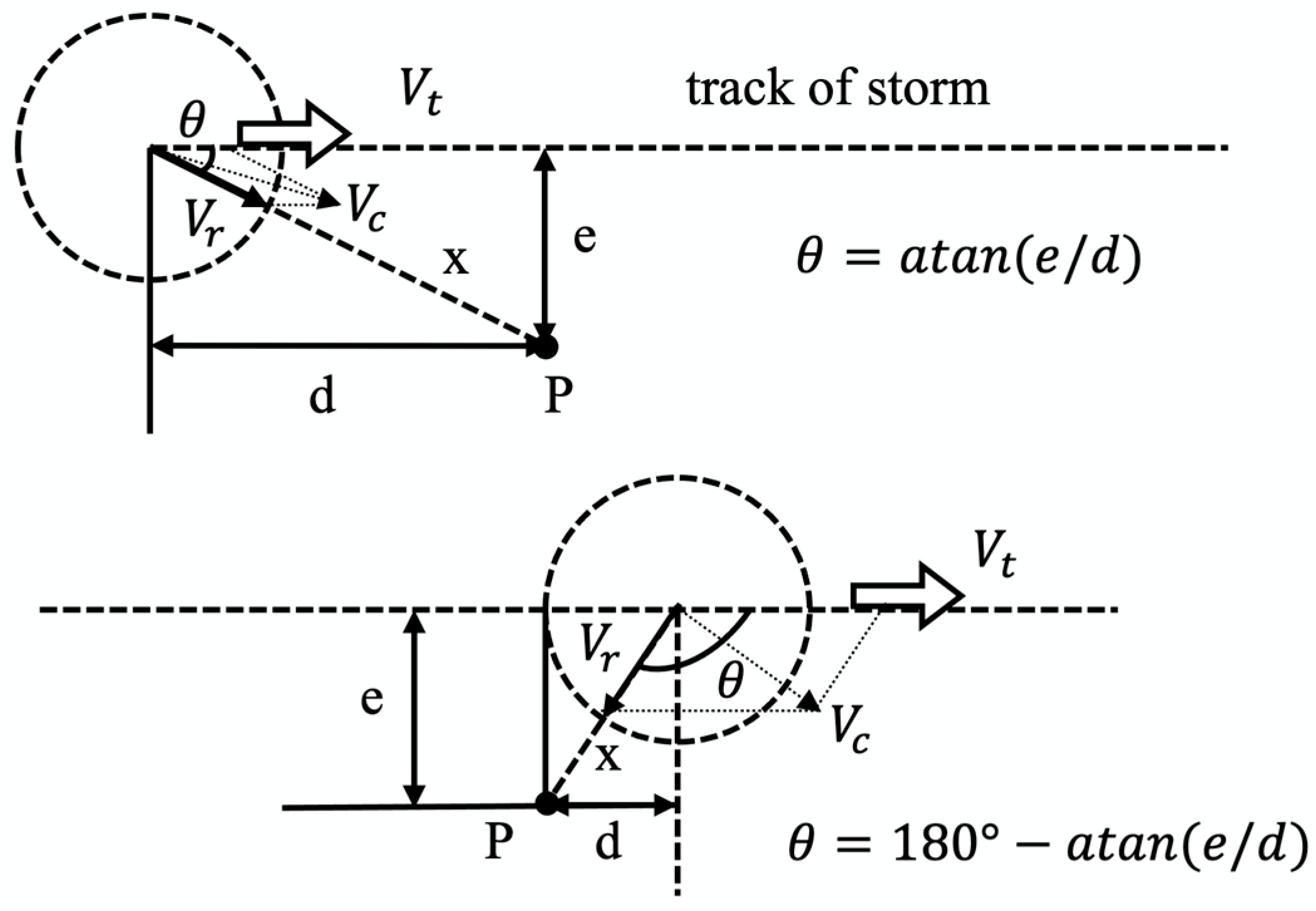
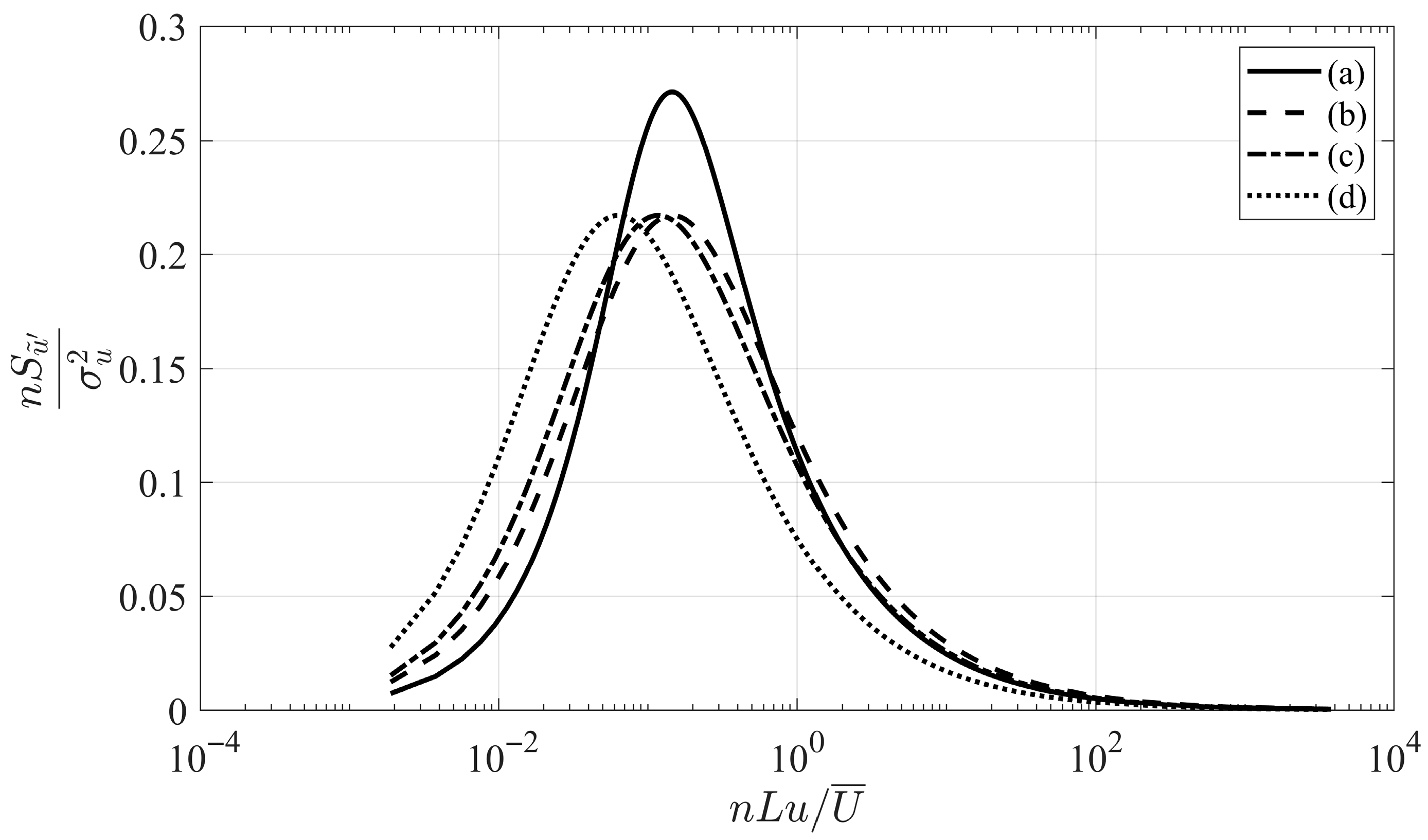

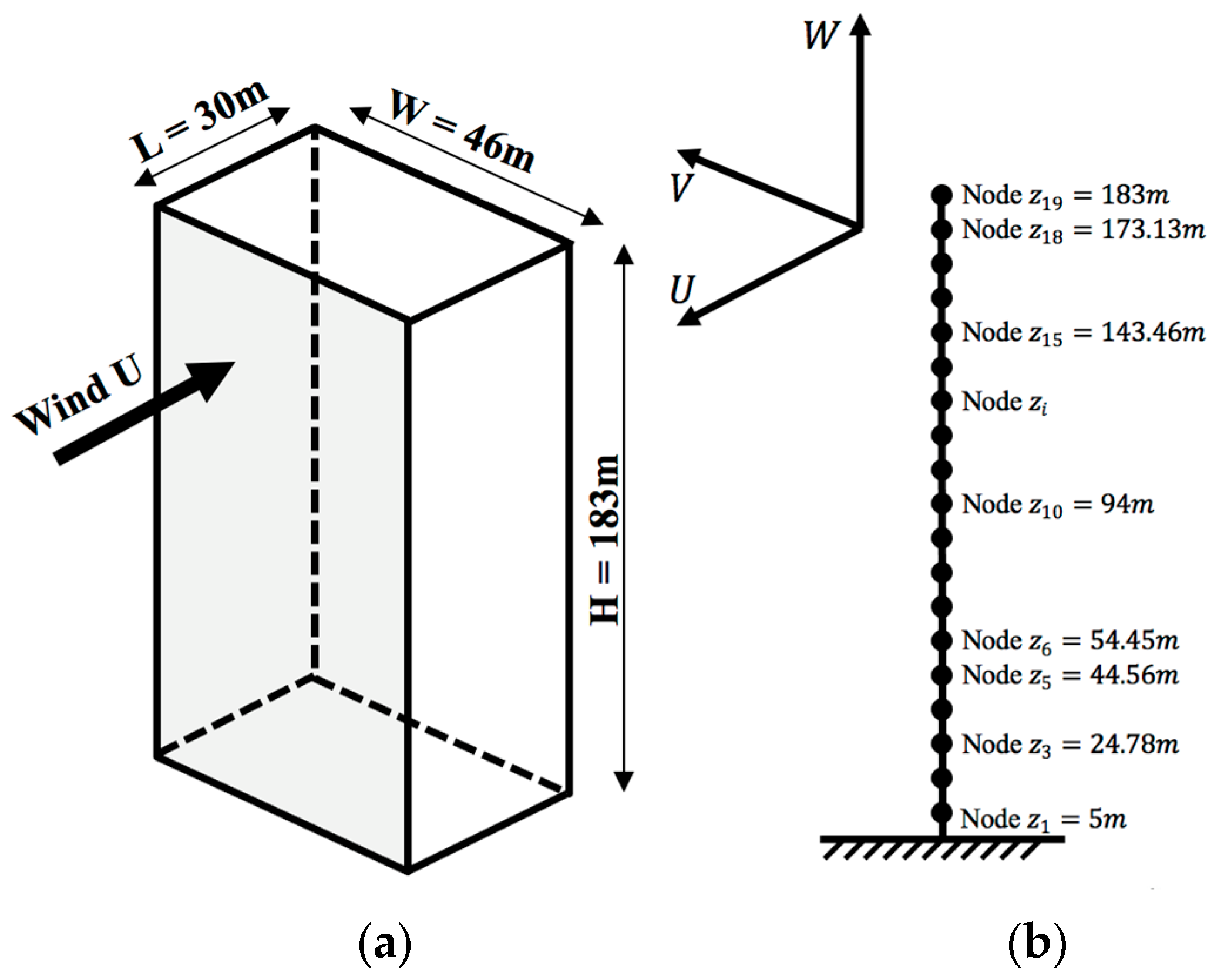

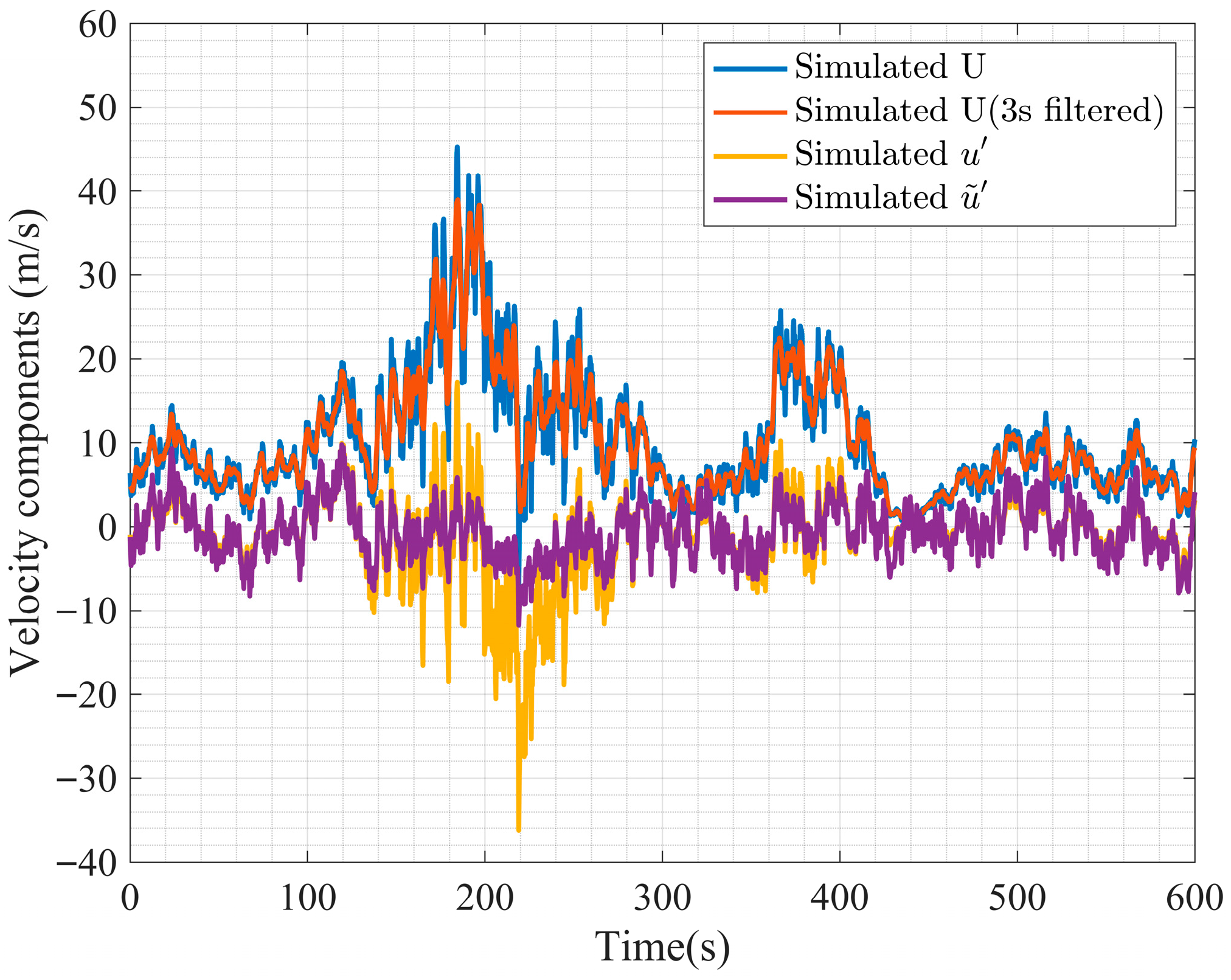
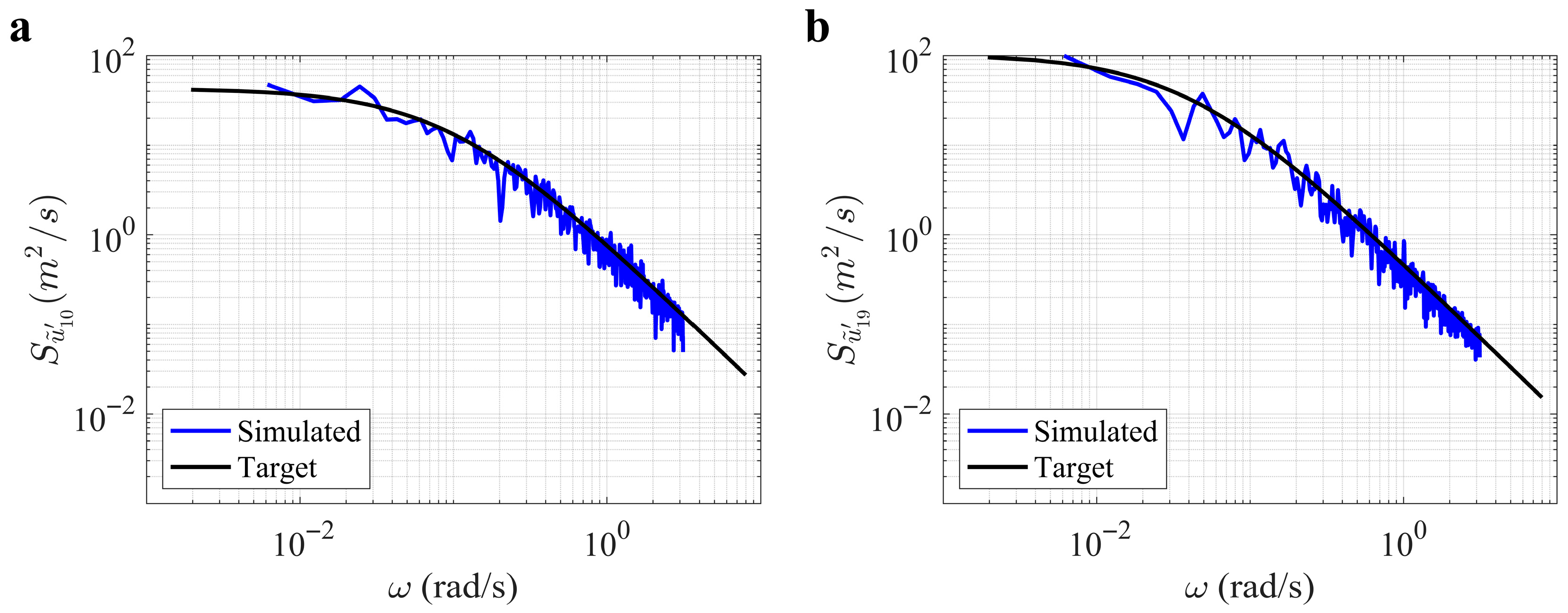
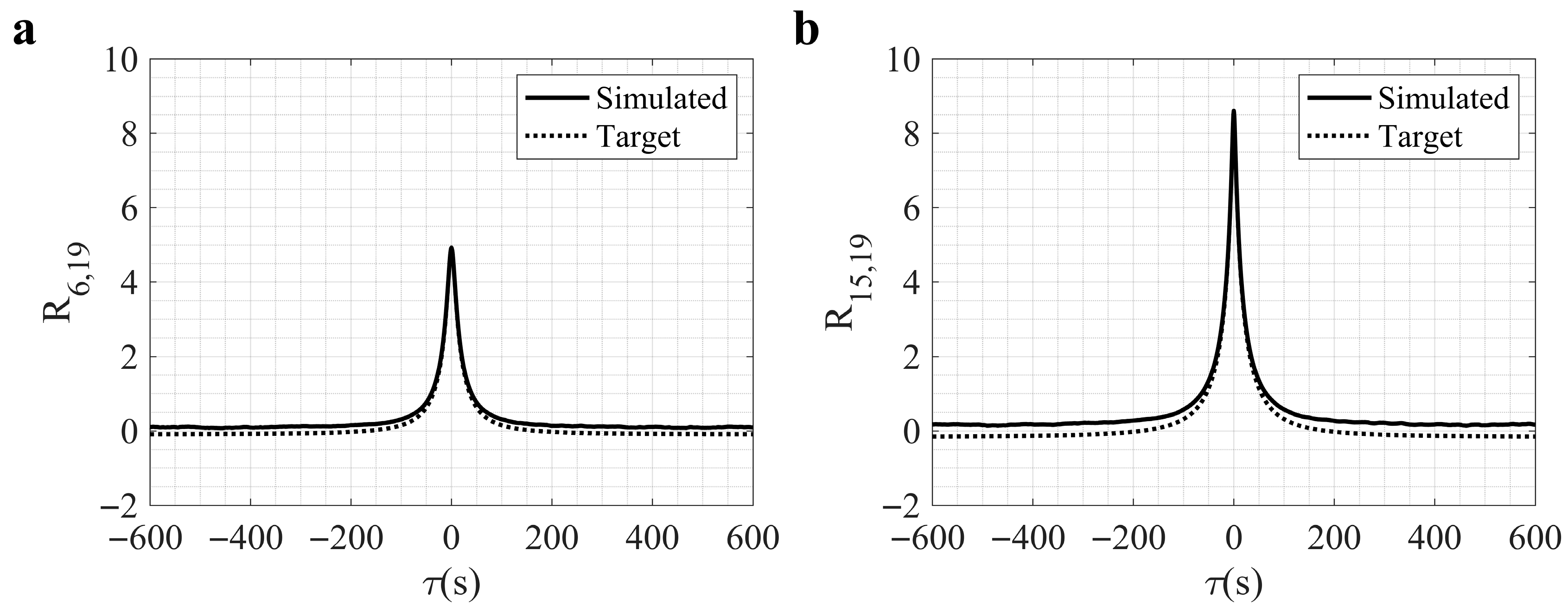
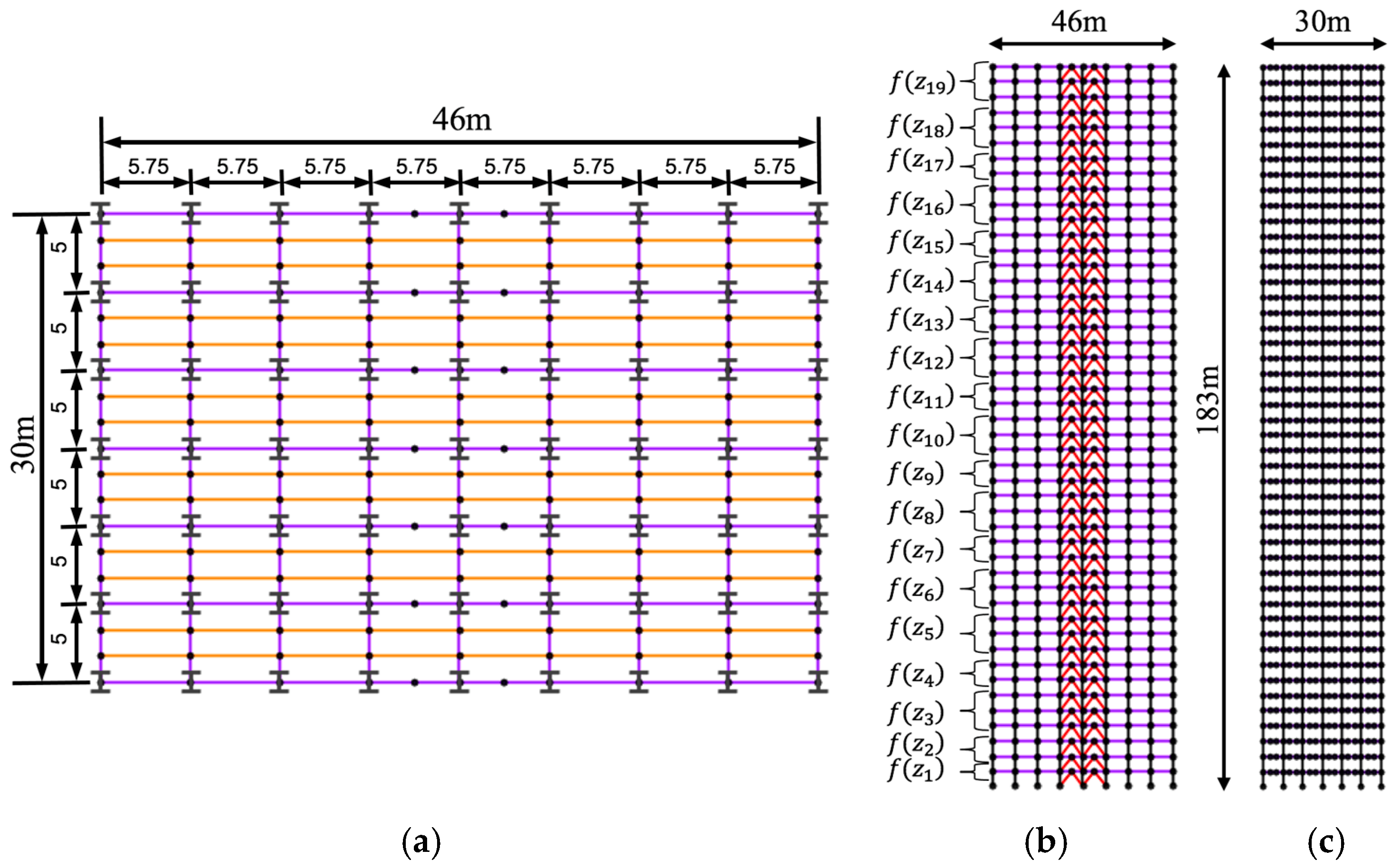
| Parameters | Value |
|---|---|
| (m) | 1000 |
| (m) | 4.9, 50, 75, 100 |
| (m/s) | 47, 32.06, 39.89, 44.01 |
| (m) | 700 |
| (m) | 150 |
| (m/s) | 12 |
| (m) | 3500 |
| (Hz) | 2.56 |
| Point-Like SDOF System | Vertical MDOF System | ||
|---|---|---|---|
| (11) | (18) | ||
| (12) | (19) | ||
| (13) | (20) | ||
| (21) | |||
| (22) | |||
| (23b) | |||
| (14) | (23c) | ||
| (23a) | |||
| (16) | (24) |
| Design Spectra for TS Downburst | Theoretical Integration Newmark | Numerical Analysis | ||||||
|---|---|---|---|---|---|---|---|---|
| (m/s) | Direction | Static | vertical and horizontal cross-correlation | vertical correlation only | vertical correlation only | vertical correlation only | ||
| Dynamic | Total | Dynamic | Total | Total | Total | |||
| 32.06 | x | 0.200 | 0.128 | 0.328 | 0.151 | 0.351 | 0.435 | 0.413 (Mode 1) |
| 0.112 | 0.084 | 0.196 | 0.094 | 0.206 | 0.244 | (Mode 2) | ||
| Wind Direction | (m/s) | (m/s) | Static Response | Dynamic Response | |||
|---|---|---|---|---|---|---|---|
| WDS | Exp. | WDS | Exp. | ||||
| 5 | 11.28 | 1.234 | 0.014 | 0.017 | 0.007 | 0.002 | |
| 10 | 22.56 | 2.468 | 0.057 | 0.069 | 0.027 | 0.014 | |
| 15 | 33.85 | 3.701 | 0.128 | 0.155 | 0.067 | 0.046 | |
| 20 | 45.13 | 4.935 | 0.228 | 0.275 | 0.129 | 0.110 | |
| 25 | 56.41 | 6.169 | 0.356 | 0.429 | 0.218 | 0.215 | |
| 5 | 11.28 | 1.234 | 0.008 | 0.008 | 0.004 | 0.001 | |
| 10 | 22.56 | 2.468 | 0.033 | 0.033 | 0.018 | 0.007 | |
| 15 | 33.85 | 3.701 | 0.073 | 0.075 | 0.043 | 0.022 | |
| 20 | 45.13 | 4.935 | 0.130 | 0.134 | 0.084 | 0.052 | |
| 25 | 56.41 | 6.169 | 0.204 | 0.209 | 0.143 | 0.102 | |
| Storey | Columns | Primary Beams | Secondary Beams | Brace in x-Direction |
|---|---|---|---|---|
| 1–20 | HE1000M | HE800A | HE650A | HE320A |
| 21–40 | HE900B | HE800A | HE650A | HE320A |
| 41–47 | HE800B | HE800A | HE650A | HE320A |
| Material grades | S355 | S275 | S275 | S235 |
| Mode | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Period | 4.98 | 4.95 | 3.76 | 1.46 | 1.43 | 1.22 | 0.74 | 0.73 |
| Frequency | 0.20 | 0.20 | 0.27 | 0.68 | 0.70 | 0.82 | 1.35 | 1.37 |
| Modal participating mass ratio (Sum UX) | 0.70 | 0.70 | 0.70 | 0.70 | 0.88 | 0.88 | 0.88 | 0.92 |
| Modal participating mass ratio (Sum UY) | 0.00 | 0.71 | 0.71 | 0.86 | 0.86 | 0.86 | 0.91 | 0.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Martinez-Vazquez, P.; Skalomenos, K. Design Spectra for Evaluating the Dynamic Response of Buildings Under Thunderstorm Downbursts. Buildings 2025, 15, 4305. https://doi.org/10.3390/buildings15234305
Song J, Martinez-Vazquez P, Skalomenos K. Design Spectra for Evaluating the Dynamic Response of Buildings Under Thunderstorm Downbursts. Buildings. 2025; 15(23):4305. https://doi.org/10.3390/buildings15234305
Chicago/Turabian StyleSong, Jing, Pedro Martinez-Vazquez, and Konstantinos Skalomenos. 2025. "Design Spectra for Evaluating the Dynamic Response of Buildings Under Thunderstorm Downbursts" Buildings 15, no. 23: 4305. https://doi.org/10.3390/buildings15234305
APA StyleSong, J., Martinez-Vazquez, P., & Skalomenos, K. (2025). Design Spectra for Evaluating the Dynamic Response of Buildings Under Thunderstorm Downbursts. Buildings, 15(23), 4305. https://doi.org/10.3390/buildings15234305






