Next Article in Journal
Design Spectra for Evaluating the Dynamic Response of Buildings Under Thunderstorm Downbursts
Previous Article in Journal
Colombian Regulations in the Seismic Design of Reinforced Concrete Buildings with Portal Frames: A Comparative and Bibliometric Analysis
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Buildings
Volume 15
Issue 23
10.3390/buildings15234304
buildings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Shape Coefficient for Soil-Cement: Experimental Determination from Cylindrical and Cubic Specimens

by
Heriberto Pérez-Acebo
1,*,
Alaitz Linares-Unamunzaga
2,
Ángel Aragón-Torre
2 and
Hernán Gonzalo-Orden
2
1
Department of Mechanical Engineering, University of the Basque Country UPV/EHU, Paseo Rafael Moreno Pitxitxi, 2, 48013 Bilbao, Spain
2
Department of Civil Engineering, University of Burgos, c/Villadiego, s/n, 09001 Burgos, Spain
*
Author to whom correspondence should be addressed.
Buildings 2025, 15(23), 4304; https://doi.org/10.3390/buildings15234304
Submission received: 22 October 2025 / Revised: 24 November 2025 / Accepted: 25 November 2025 / Published: 27 November 2025
(This article belongs to the Section Building Materials, and Repair & Renovation)
Browse Figures
Versions Notes

Abstract

The compressive strength is the primary parameter used for the design, control, and performance assessment of cementitious materials. However, this value is strongly influenced by specimen geometry, which has led to the introduction of shape coefficients to convert compressive strength results between different specimen types, particularly between cubes and cylinders. While this topic has been extensively investigated in concrete, very limited research has addressed the shape coefficient in soil-cement or cement-treated base materials, despite their widespread use in pavement construction. Aiming to bridge this gap, this study systematically analyzes the unconfined compressive strength (UCS) of soil-cement specimens with different geometries. Two soil-cement mixtures with distinct physical and chemical characteristics were tested at various curing ages (7, 28, and 90 days) using cylindrical specimens (150 mm diameter × 180 mm height) and cubic specimens (150 mm edge). The results show that the UCS in cylindrical specimens (UCScyl) was consistently higher than that of cubic specimens (UCScub), although the difference decreased with increasing compressive strength. By combining all datasets, a single conversion factor of 1.04 was derived, resulting in an equation, UCScyl = 1.04·UCScub, with an excellent determination coefficient (R2 = 0.99), enabling reliable conversion between cubic and cylindrical UCS results for soil-cement.

1. Introduction

The compressive strength is the foundational parameter used in design, quality control, and performance evaluation of cementitious materials. However, as many researchers have observed, the measured strength depends not only on the material composition but also heavily on the geometry of the specimen used in testing. In particular, the difference between cylindrical specimens and cubic specimens (or prisms or other shapes) has led to the use of a shape coefficient. Specifically, the shape coefficient (often denoted K) is an empirical factor used to translate compressive strength results of cementitious materials between specimens of different geometries, most commonly between standard cubes (e.g., 150 × 150 × 150 mm) and standard cylinders (e.g., 300 mm high × 150 mm diameter), and is defined as shown in Equation (1):
f c y l = K · f c u b e
where fcyl is the strength measured in cylindrical specimens (generally compressive strength), and fcube is the strength measured in cubic specimens. Briefly, this coefficient is able to convert the cube test to equivalent cylinder strengths. Such coefficients are crucial for correlating strength data from different codes, laboratories, and field studies, where different shapes are used.
In practice, a widely cited engineering approximation for concrete specimens assumes that cube strengths exceed cylinder strengths by about 20–25%, corresponding to a conversion factor of roughly 0.80–0.83 [1]. This “rule of thumb” has been embedded in codes and standards where cube-based European data must be compared to cylinder-based American practice. However, a growing body of evidence demonstrates that such a universal constant is an oversimplification, as the cube–cylinder relation varies with concrete strength, aggregate type, curing, loading rate, fiber content, and the presence of recycled materials [2,3].
Experimental programs have systematically investigated these effects. For instance, Dehestani et al. [4] demonstrated that self-consolidating concrete shows measurable variation in cube/cylinder ratios depending on mix design and specimen size, concluding that a fixed factor is not reliable for high-precision applications. Similarly, Li et al. [5] found that shape and size effects are magnified under dynamic loading, which is particularly relevant in impact or blast applications. Their study confirmed that the conversion coefficient K cannot be assumed constant across strain rates, further complicating the interpretation of high-rate testing results.
In fact, the physical mechanisms underpinning these variations are well documented. Cubes, with their lower slenderness ratio, benefit from higher lateral restraint near the loading platens, producing elevated apparent strengths. Cylinders, on the other hand, experience more uniform stress distributions but are more sensitive to capping conditions and eccentric loading [1,6]. Larger specimens statistically incorporate more critical flaws, in line with classical size-effect theories, leading to lower nominal strength as specimen dimensions increase [2]. These explanations are consistent across studies of normal-strength concrete, high-strength concrete (HSC), and ultra-high-performance concrete (UHPC) [7].
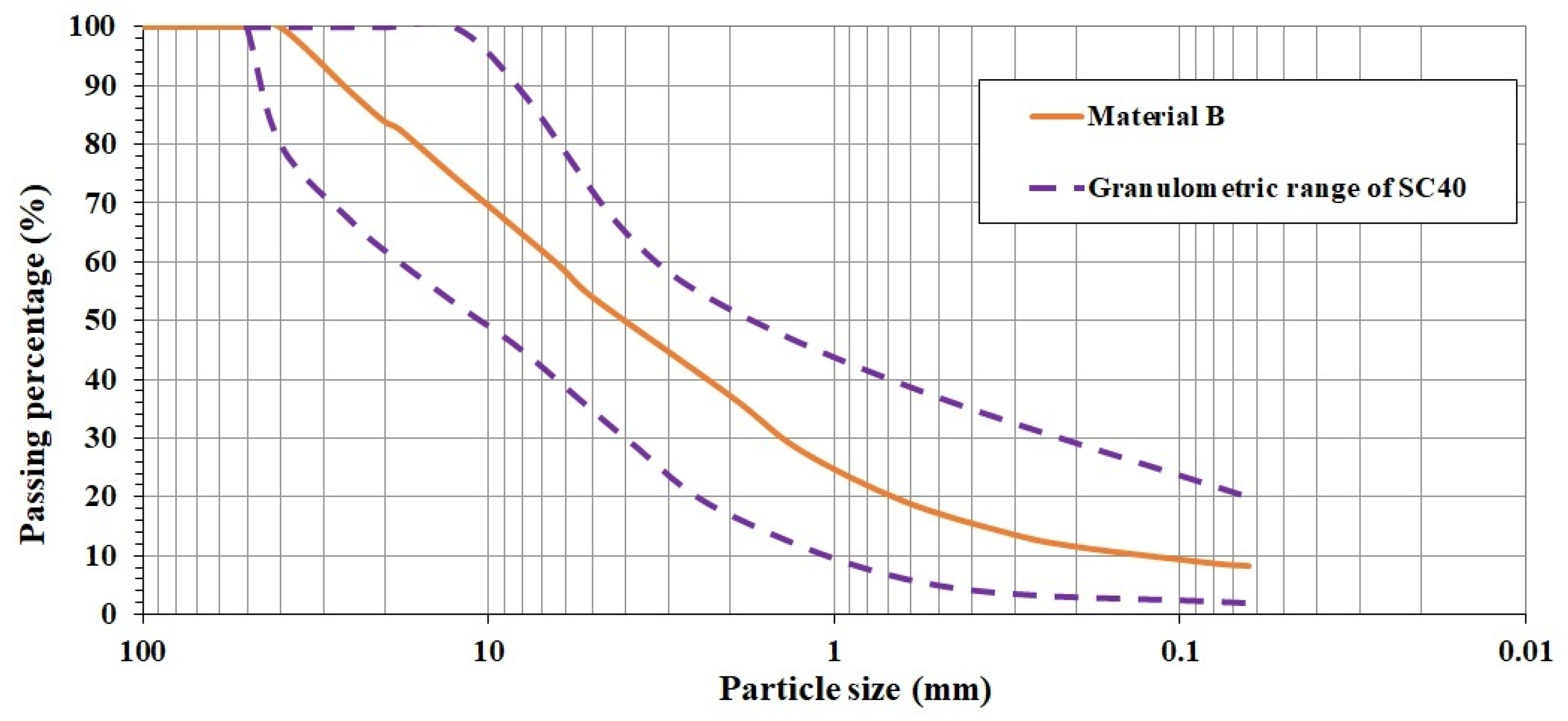
Beyond concrete, however, many engineered pavement base materials make use of cement, such as in cement-treated base materials. These materials are mixtures of natural soil or previously crushed stone (with varying gradation, plasticity, and fines content), duly stabilized by Portland cement (or similar binders). They are widely used in pavement base courses, sub-bases, or stabilization layers, especially in road infrastructure. Some of this type of material is the soil-cement, gravel-cement, or in situ stabilization techniques like the full-depth reclamation (FDR) [8,9,10,11,12,13,14], which form part of the base material of semi-rigid pavements [15,16]. Compared to concrete, they are cheaper and often more sustainable, but their mechanical behavior (strength, stiffness, durability) can differ significantly. Yet, while concrete literature has extensively examined shape and size effects for concrete [17], there is very little work on the shape coefficient in soil-cement or cement-treated base materials.
It can be said that Felt and Abrams [18] provided one of the first analyses of variable strength and other parameters of soil-cement mixtures depending on the shape and size of the samples, apart from other mechanical properties, but without providing a factor as a conclusion. Tariq and Maki [19] investigated the mechanical behavior of cement-treated sand under compression with cylindrical specimens of varying height-to-diameter ratio (H/D) and under tension with notched beam specimens. They concluded that the maximum compressive stress was independent of the specimen size but did not relate the two strengths. Xie et al. [20] conducted research about the fatigue characteristics of cement-treated aggregate base materials under different test conditions (unconfined compressive, indirect tensile, flexural tensile strengths, and fatigue tests). Although they observed the importance of the shape of the specimens and included the shape and scale as parameters in developed models, a correct relationship for converting different types of specimens was not provided. More recently, Lv et al. [21] studied the relationship between the unconfined compressive strength (UCS) and the flexural strength at different curing ages of cement-treated aggregate base materials, but the semi-prismatic parts resulting from the flexural test were not employed for calculating the UCS in cubic specimens.
To the best of our knowledge, no studies have focused on the shape coefficient for soil-cement. Only a few studies address compressive strength with various sample shapes in cement-treated materials, such as soil-cement blocks with waste tire steel fibers [22] or cement-stabilized rammed earth [23]. However, in those studies, the difference between cube vs. cylinder shapes has rarely been compared (or has been compared only in a limited way). Thus, a research question arises: how does the cube vs. cylinder shape coefficient behave in soil-cement and cement-treated base materials? To bridge this gap, this paper analyzes the uniaxial compressive strength values of cylindrical and cubic specimens of soil-cement from different materials at different test ages and, hence, with variable compressive strength.
The research is organized as follows. In the next section, a deeper literature review about the shape coefficient in cementitious materials and, more specifically, in cement-treated pavement base materials is presented. Then, the materials deployed in the research and the applied methodology are described. Subsequently, the obtained results are shown and discussed. Finally, conclusions are deduced from the presented results.

2. Literature Review

2.1. Evolution of Shape for Concrete Specimens

The concept of converting cube test strength to cylinder strength (or vice versa) has long been recognized. Early works [6] noted consistent differences in strength results from cubes vs. cylinders, motivated by differences in boundary conditions, platen restraint, height/diameter ratio (h/d), and confinement effects. Over time, many empirical studies have quantified the cube/cylinder strength ratio across concrete strength classes.
Sim et al. [2] investigated concrete specimens of lightweight concrete and observed that the size effect was stronger with the decrease in the concrete unit weight. This trend was more notable in specimens with an aspect ratio of 2.0 than in those with an aspect ratio of 1.0. Graybeal & Davis [24], in their study of ultra-high-performance concrete (UHPC), reported conversion factors nearer to unity for very high strengths, reflecting decreased influence of specimen geometry. Li et al. [5] confirmed that under different loading rates, especially dynamic loading, shape effects (and thus the coefficient) become more pronounced.
More recently, Pacheco et al. [25] proposed both deterministic and probabilistic models for cube–cylinder conversion based on large datasets of natural and recycled aggregate concretes. They showed that not only does K vary with strength, but also that recycled aggregates tend to shift both their mean and variability, implying that probabilistic approaches provide a more robust basis for design. This probabilistic trend echoes earlier work by Del Viso et al. [26], who emphasized that fracture mechanics and size effects should be accounted for explicitly when comparing different specimen geometries.
The presence of fibers adds another layer of complexity. Zhu et al. [27] demonstrated that steel-fiber-reinforced concrete exhibits altered cube–cylinder ratios because fibers change the crack-bridging mechanisms, thereby influencing peak strength differently in cubes and cylinders. Mardani-Aghabaglou et al. [28] confirmed similar findings for different fiber types, emphasizing that practitioners should avoid generic conversion coefficients for fiber-reinforced concretes and instead rely on material-specific empirical relations.
Beyond material composition, aggregate properties also play a decisive role. Yehia et al. [3] showed that different aggregate types (natural vs. lightweight) shift the cube/cylinder relation, while Gyurkó and Nemes [29] highlighted the combined effects of specimen size, shape, and aggregate type on compressive strength. These findings stress the importance of including detailed specimen and material descriptions in experimental reporting, as shape coefficients derived under one condition may not transfer to another.
National and international standards reflect this diversity of practice. While North America predominantly uses 150 × 300 mm cylinders, Europe and many parts of Asia favor cubes [1,6]. As a result, harmonization is critical for meta-analyses, benchmarking, and design code calibration. Hake [30], for instance, compared compressive strengths obtained from different cylinder sizes (4 × 8 in. vs. 6 × 12 in.), illustrating that even within the same geometry, specimen dimensions affect measured strength and must be normalized.
In light of this accumulated evidence, many researchers argue that codes relying on a single constant conversion factor are outdated.

2.2. Shape Coefficient in Spanish Standards

In the field of concrete in Spain, the cylindrical specimen with a diameter of 15 cm and a height of 30 cm at 28 days of age has always been used as the reference for compressive strength. The Concrete Code of 1968 (EH-68) [31] established the use of the ϕ 15 × 30 cylindrical specimen at 28 days for determining compressive strength, according to standard UNE 7242 [32]. It also included a section regarding conversion factors for specimens of different sizes and shapes (Table 1). These conversion factors were presented as general values with purely informative validity.
The subsequent codes published in later years, EH-73 [33], EH-80 [34], EH-88 [35], EH-91 [36], and EHE-98 [37], adopted the same idea, maintaining the ϕ 15 × 30 cylindrical specimen as the reference for determining compressive strength. The conversion factors remained unchanged and were also provided solely for informational purposes in the absence of real experimental data. It was only in the subsequent update of the code, EHE-08 [38], which established the ϕ 15 × 30 cylindrical specimen at 28 days as the reference, while also allowing the use of cubic specimens with 15 cm or 10 cm edges. The standard regulating the compressive strength test is UNE-EN 12390-3 [39], currently in force. The use of cubic specimens is motivated by the fact that sulfur capping, required for cylindrical specimens, is not necessary, thereby avoiding the generation of highly polluting residues that demand controlled and selective disposal. A conversion factor was established between cubic specimens with 15 cm edges and cylindrical specimens of ϕ 15 × 30, as shown in Equation (1), depending on the compressive strength of the cubic specimen (Table 2).
The regulation currently in force in Spain since 2021 is the Structural Code [40], which essentially reproduces Eurocode 2 [41]. It specifies that compressive strength shall be determined from 28-day compression tests performed on cylindrical specimens with a diameter of 15 cm and a height of 30 cm, in accordance with UNE-EN 12390-3 [39], but it also authorizes the use of cubic specimens with nominal dimensions of 100 mm and 150 mm for determining compressive strength. Specimens of 100 mm nominal dimension may be used, provided that the testing laboratory has the approval of the supervising authority and has established conversion factors derived from reliable correlations with cylindrical specimens of 150 × 300 mm. These correlations must correspond to the same concrete classification, with a minimum recommended number of more than 18 paired results and a recommended correlation coefficient R2 greater than 0.9. For cubic specimens with nominal dimensions of 150 mm, the same procedure described in the EHE-08 Code [38] shall be followed, using the factors presented in Table 2.
It must be indicated that, at present, the use of cubic specimens with 150 mm edges has the advantage of eliminating the need for capping or grinding prior to testing, saving time and reducing health risks. Cubic specimens are placed so that the load is applied perpendicular to the casting direction, i.e., on molded faces. They are also approximately 34% lighter and more manageable than 150 × 300 mm cylindrical specimens. However, for determining the modulus of elasticity and Poisson’s ratio, cylindrical specimens remain the most appropriate choice.

2.3. Shape Coefficient in Cement-Treated Base Materials

On the contrary, while the concrete literature is rich, direct studies of the shape coefficient in soil-cement or cement-treated pavement base materials are sparse. Despite the initial steps conducted by Felt and Abrams [18], who observed that the shape and size of the specimens had to be considered, researchers did not focus on developing a conversion factor, like a shape coefficient, for cement-treated materials in general and for soil-cement in particular. George [42] presented very detailed information about the structural design of cement-treated base materials, comparing design guides and research results from different countries, mainly addressing the fatigue behavior, but there was no comparison between specimens of different shapes.
Furthermore, Nguyen et al. [43] modeled the particle size distribution by means of the discrete element method (DEM) to observe the effect on the flexural strength, but variable shapes of the specimens were not investigated. Similarly, Dong et al. [44] manufactured semicircular specimens that were modeled with DEM, but no relationships with other shapes were presented. Additionally, models to correlate the UCS at 7 days with the UCS at 90 days in cylindrical specimens were proposed, and with flexural strength at 90 days in prismatic samples [10]. However, no relationships between the UCS of the two parts resulted from the prismatic specimen, which could be tested as a cubic sample. Xuan et al. (2015) [45] analyzed the introduction of construction and demolition waste in cement-treated base materials with varying values of masonry, water, and cement content, degree of compaction, and curing time, performing all the tests with cubic samples. Additionally, Rocha et al. [22] analyzed the compressive strength of soil-cement blocks incorporating steel fibers from waste tires, showing strength improvements, but without comparing cube vs. cylinder specimen shape in the same soil-cement mix. Tripura and Das [23] investigated the impact of the shape and size of Cement Stabilized Rammed Earth (CSRE) manufactured in cubes and cylinders, demonstrating that the UCS of cubes is more than that of cylindrical specimens and showing that the size effect in the cubic specimens is more important than in cylinders, where the average strength is approximately constant. On the contrary, after testing cubic and cored specimens of CSRE, Anysz et al. [46] showed that there was no statistically significant difference in the mean UCS, suggesting that it was not necessary to use a shape coefficient.
Beyond that, pavement design or stabilized base manuals (e.g., AASHTO) assume compressive strength values (often unconfined compressive strength, UCS) with certain specimen types (usually cylinders or cubes), but do not always include explicit shape conversion factors for soil-cement materials. For example, in Guidelines for incorporation of cement stabilized reclaimed base (CSRB) in pavement design, some typical strength tests are specified, but do not always compare shapes [47].
In Spanish standards for cement-treated base materials, the UCS must be verified in a cylindrical specimen of 180 mm high and 150 mm diameter at 7 days [48]. As seen, there is a difference with the usual cylindrical samples for concrete, which are 300 mm high and have a diameter of 150 mm. This variation can be explained because the concrete is usually employed for pillars when the height/base ratio is over 2, while soil-cement, or cement-treated base materials in general, are preferably extended in layers in the pavement structure. In concrete pillars, the main stress comes from compression, whereas in soil-cement bases, the main stress corresponds to a flexural tensile stress. Despite not being indicated in the standard, manufacturing cubic specimens of 15 cm can be an adequate alternative to cylindrical ones because the cubic sample provides parallel faces for conducting the UCS test, and, in the case of cylinders, the superior face must be conveniently prepared for the test, as for concrete specimens.
Thus, summarizing the literature review, no work has been identified that systematically investigates the shape coefficient (i.e., cube vs. cylinder for soil-cement or cement-treated base materials). As commented, despite some works indicating that there were differences in the results depending on the size and shape of the specimens, no proposals were given for converting the strength in one shape to another. Consequently, this study aims to bridge this clearly identified gap in the literature.

3. Materials and Experimental Procedure

3.1. Materials

Two types of mixtures were employed to manufacture the soil-cement specimens, identified as Material A and Material B. The difference between mixtures A and B comprises different aggregates, cement type and percentage, and water content. It was preferred to compare two types of soil-cement, produced from different raw materials, to observe if the relationship between cylindrical and cubic samples is maintained regardless of the material.

3.2. Material A

The aggregates composing Material A come from a borrow pit at kilometer point 16 + 400 of the road C-627, in the stretch between Herrera and Villadiego, in the province of Burgos, in Spain.
The granulometry of the material was conducted according to the EN ISO 17892-4:2016 [49] standard and is shown in Table 3. The Spanish standard for soil-cement [48] presents two possible types: SC40 and SC20, according to the maximum aggregate size, 40 mm and 20 mm, respectively. An SC40 soil-cement was preferred because it can be used for all traffic categories, according to the Spanish pavement design guide [50], while the SC20 can be employed only in the traffic categories with the lowest volumes of heavy traffic. As shown in Figure 1, the granulometry of Material A fits adequately in the granulometry range of SC40 established in the standard [48].
Regarding its chemical composition, the soil exhibits an organic matter content of 0.15%, determined according to EN ISO 17892-4:2019 [49], and a total sulfur content of 0.01%, in compliance with EN 1744-1:2009 [51]. The tested aggregate sample exhibited a liquid limit of 21.3, a plastic limit of 13.7, and a plasticity index of 7.6, obtained in accordance with EN ISO 17892-12:2019 [52].
With regard to the cement, a CEM IV B/V 32.5 N cement was employed. It is widely used for soil-cement and soil stabilization in road pavement. It is a pozzolan cement, with a low quantity of clinker and a high quantity of additions. Although it does not achieve high strengths at seven days as CEM II does, it obtains similar strengths in the medium and long term.
Subsequently, the maximum dry density and the optimum moisture content were determined with cylindrical specimens following the modified Proctor test according to the Spanish standard [53], which is very similar to the standard of the ASTM [54]. As a minimum UCS of 2.5 MPa at seven days is required, according to the Spanish standard [48], after some trials, a cement content of 3.5% was selected. With that cement percentage (3.5%), a maximum dry density of 2.19 g/cm3 and an optimum moisture content of 6.7% were obtained with the modified Proctor test [53], as shown in Figure 2.

3.3. Material B

Material B used for manufacturing soil-cement specimens is a gray limestone obtained from the quarries of Hijos de Amantegi, located in Mañaria, in the province of Biscay, in the north of Spain. It is crushed stone and has an internal code AGT0-40C. Its granulometry is shown in Table 4 and Figure 3, and it falls within the grain size range of soil-cement SC-40 [48]. Once again, the gradation of the soil-cement SC40 was preferred due to the possibility of being employed in any type of traffic category. The organic matter content of these aggregates is 0.14% [49], and the total sulfur content is 0.04%, according to EN 1744-1:2010 [51]. Regarding the liquid and plastic limits, both are equal to zero, resulting in a plasticity index of zero.
For producing the soil-cement samples with aggregates described as Material B, a CEM II B-M (V-L) 42.5 R cement was selected because it was the usual one employed by the manufacturer employing those aggregates. It was preferred to maintain the same work formula. This cement is classified as a composite Portland cement, distinguished by its high final mechanical strength, rapid hardening behavior, and a 30% reduction in CO2 emissions compared to conventional cement. Furthermore, it contains a minimum of 20% recycled material. The cement fulfills all the specifications included in the standard EN-197-1:2011 [55].
After some trials, a cement content of 3.5% was chosen for Material B. Once again, with that cement percentage, a modified Proctor test [53] was conducted (Figure 4) to obtain the maximum dry density (2.36 g/cm3) and the optimum moisture content (5.0%).

3.4. Experimental Procedure

The cylindrical specimens were tested in accordance with the Spanish standard for testing the UCS in soil-cement samples [56]. As previously commented, the dimensions of the cylindrical specimens are 180 mm high and 150 mm in diameter. They were manufactured in three layers with a vibrating hammer and a compaction time ranging from 15 to 20 s, depending on the material. According to the Spanish standard [48], a cylindrical sample is correctly produced when its dry density is more than 98% of the maximum dry density obtained in the modified Proctor test [53].
For obtaining the UCS values from cubic samples, cubes of soil-cement were not produced. Instead of that, prismatic specimens with dimensions of 150 mm (height) × 150 mm (width) × 600 mm (length) were manufactured. However, manufacturing prismatic samples of soil-cement with an acceptable quality is a challenging task since it depends on the qualification and experience of the testing team. In this case, prismatic samples were produced using the procedure described by Linares-Unamunzaga et al. [57], with their specific device (Figure 5). The mixture is placed in two or three layers in a mold with inside dimensions of 15 × 15 × 60 cm. Each layer is compacted by collocating some metal sheets (Element 7 of Figure 5) over the metal stand (Elements 5 and 6 of Figure 5) and vibrating the mold with a vibrating table of 40 Hz (Element 1 of Figure 5) for a previously established period of time, generally between 15 and 40 s. This procedure allows achieving compaction densities not less than 98% of the maximum dry density obtained with the Modified Proctor test [53], as established in the Spanish standard [48]. In the case of producing these samples of soil-cement, the material was extended in three layers, 7 metallic sheets were used for compacting, and the vibrating time was between 20 and 30 s, depending on the material (A or B).
After manufacturing the sample, it is placed in the curing room at a temperature of 20 ± 2 °C and at a relative humidity of more than 95%. If the temperature values are below 19.5 or over 20.5, the heating or cooling devices are automatically turned on. The precision of the temperature sensor is 0.1 °C. Similarly, if the sensor of RH detects a value below 95%, the system starts spraying water. The precision of this sensor is ±3%. Additionally, twice a week, we check the values indicated in the display of the curing room with an external device. During this research, no discrepancies were registered. After 24 h, the metal prismatic mold (Element 2 of Figure 5) is removed, maintaining the base of the mold (Element 3 of Figure 5) for seven days to guarantee a minimum resistance and to avoid the rupture of the sample while operating with it.
At a specific age, the prismatic specimen is tested under the four-point flexural beam test, in accordance with the standard EN 12390-5 [58]. The rollers over the samples are placed at a distance of 15 cm (the height of the specimen), and the rollers below the specimen are placed at a distance of 45 cm (three times the height). A plate between the specimen and the rollers over it transmits the applied load at a constant increasing tension in the range of 0.04 MPa/s, which is within the range allowed by the standard [58].
When the four-point flexural beam test is concluded, the specimen results in two semi-prismatic parts of approximately 150 mm (height) × 150 mm (width) × 300 mm (length). Then, the UCS test for cubic samples is conducted in each semi prism, following the standard EN 13286-41 [59], with a load speed in the range of 0.1 ± 0.1 MPa/s. Aiming to simulate the behavior of a cubic specimen, two auxiliary metal sheets are employed; one of them is placed between the top side of the sample and the top plate, and the other one is placed between the lower side of the prismatic sample and the lower plate. Therefore, a uniform tensile distribution in a cube of 150 mm is obtained. Although the cubic specimens were obtained from the two halves resulting from the flexural test, only the extreme ends of each semi prism—away from the mid-span fracture zone—were used for the UCS test, ensuring that the tested material was not affected by flexural cracking. This approach is consistent with previous findings in cement-treated materials and concrete, indicating that flexural fracture is highly localized and does not propagate into the compressive end regions, which remain structurally intact and provide reliable compressive strength measurements [24,26].
In the case of Material A, the following sequence was completed. Ten different mixings were produced, each one on a different day, numbered from A01 to A10. It is supposed that samples from the same mixing have similar properties and can be compared. When producing samples in a laboratory, where low quantities are manufactured in each mixing, and due to the heterogeneity of a material like soil-cement, a wide range of test values can be obtained. However, when comparing values from the same mixing, higher similarities are obtained.
With the quantity of each mixing, it was possible to obtain three cylindrical specimens and a prismatic specimen. Each of the three cylindrical samples of each mixing is tested at a different age: at 7 days, at 28 days, and at 90 days, respectively (Figure 6). Additionally, the prismatic sample is tested under the four-point flexural beam [58] test at 7 days (Figure 7a,b), and one of the semi-prismatic parts is tested under the UCS test for cubic samples on the same day [59] (Figure 7c), e.g., at seven days. The other semi-prismatic part (of approximately 15 × 15 × 30 cm) is placed again in the curing room and is tested at 90 days, at the same time as the corresponding cylindrical sample from the mixing.
Therefore, it is possible to compare the UCS value of a cylindrical sample and the UCS value of a cubic sample produced from the same mixing at 7 days and at 90 days. Consequently, 10 data points from tests at 7 days are available, and 10 data points from tests at 90 days. Apart from comparing values from the same mixing, two different magnitudes of UCS values are employed because it is well known that higher strengths are achieved in cementitious mixes with time. The complete scheme of Material A is displayed in Figure 8.
On the other hand, tests for UCS with Material B were conducted at three different ages: 7, 28, and 90 days. For this purpose, six cylindrical specimens (Figure 9a) and four prismatic specimens were manufactured for each age (Figure 9b), resulting in a total of 6 cylindrical samples and 8 cubic samples (Figure 9c) for comparison at the same age. Mixings for producing these specimens were performed on different days or even on the same day, but separately, and hence, it is not possible to compare UCS values from cylindrical and cubic samples from the same mixing directly. In this case, the average values of UCS values of cylindrical samples at each age (7, 28, and 90 days) are compared with the average UCS values from cubic specimens, resulting in three more data points for the calculation of the shape coefficient.
Additionally, apart from the commented samples, some cylindrical and cubic specimens were manufactured with material from the same mixing, making it possible to compare the values directly. This is the case of a cylinder sample tested at 7 days (BCYL07-7) that was produced from the same mixing as two prismatic samples (BPRIS07-5 and BPRIS07-6), also tested at 7 days. Similarly, a unique mixing produced 2 cylindrical samples (BCYL90-7 and BCYL90-8) and two prismatic samples (BPRIS90-7 and BPRIS90-8), which were all tested at the age of 90 days. As a summary, Figure 10 explains the scheme conducted for Material B.

4. Results and Discussion

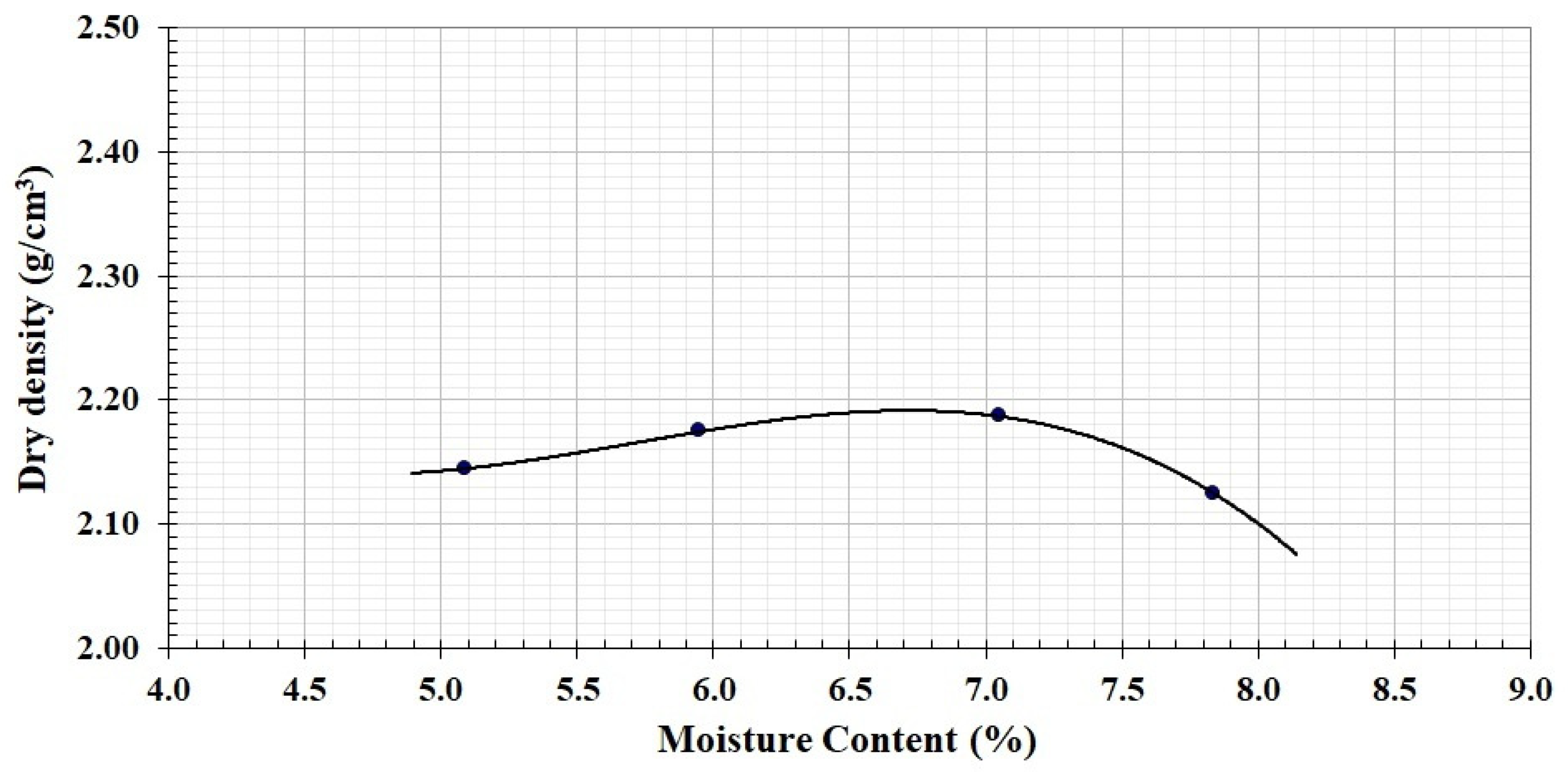
Table 5 presents the UCS values from cylindrical samples of Material A at 7 and 90 days from each of the 10 mixings. Additionally, the dry density of each sample is also exposed.
As could be anticipated, the compressive strength at 90 days is higher than that at 7 days. Additionally, it can be observed that the dry densities of the samples from the same mixing are almost similar. Moreover, the range of values within the same age is wide, underlining the heterogeneity of this type of material, always reported by other researchers [8,9,10,11,13].
Table 6 exposes the UCS values of cubic samples obtained from the semi-prismatic parts at 7 and 90 days, including the density of the prismatic sample.
Once again, the density of the prismatic sample of each mixing is very similar to the corresponding densities of cylindrical samples. This fact highlights the importance of producing mixtures for cylindrical and cubic samples, because their values can be compared adequately. At the same time, as observed in cylindrical samples, the range value at each age is wide, reinforcing the heterogeneity of the material.
As it has been explained in Section 3.4, UCS values from AxxCYL7 can be compared with AxxCUB7. Similarly, values from AxxCYL7 are contrasted against values from AxxCUB90.
If we compare values at 7 days from Material A, Figure 7 is obtained. Two regression lines can be developed, with the intercept (green line) and without the intercept (red line). The red line obtains a lower determination coefficient (R2) because it is forced to pass through the origin (0; 0). However, since the shape coefficient is defined as in Equation (1), the intercept must be omitted, and K is identified with the coefficient of variable x, the UCS value in cubic samples. As shown, the determination coefficient is high, near 0.80, and the shape coefficient indicates that the UCS in cylindrical samples is 1.11 times higher than in cubic samples. In fact, all the data points at 7 days indicate that higher values are obtained in cylindrical samples. The gray line shows the equality line, i.e., y = x. This is contrary to the usual values obtained in a concrete sample. However, as commented, the dimensions of the cylindrical samples are different in height, from 30 cm in concrete (with a diameter of 15 cm) to 18 cm in soil-cement, which obviously influences the result [18,42]. The explanation lies in the particular geometry used in soil-cement testing: cylindrical specimens are only 180 mm in height, compared to the standard 300 mm height used for concrete, resulting in a lower slenderness ratio. This geometry increases the confinement at the loading platens and leads to higher apparent strength. In cubic specimens, the stress distribution is more uniform and less affected by platen restraint, which explains the slightly lower strength values obtained [4,5]. This behavior is consistent with the mechanics of squat cylinders: when the height-to-diameter ratio is close to 1.2, lateral deformation at the ends is strongly restrained by the loading platens, generating localized triaxial compression (“end restraint”) that artificially elevates the apparent UCS. In contrast, the stress field in 150 mm cubes is more uniform and less affected by platen confinement, which explains the lower measured strengths. Similar confinement-induced increases in strength for short cylinders are widely recognized in ASTM D1633 [60] for soil-cement and in studies on concrete [61,62,63].
In Figure 11b, the purple lines show the 95% confidence intervals for the linear regression without an intercept. Except for two points that are near these lines, the rest are in the 95% confidence interval for the predicted values using the proposed shape coefficient.
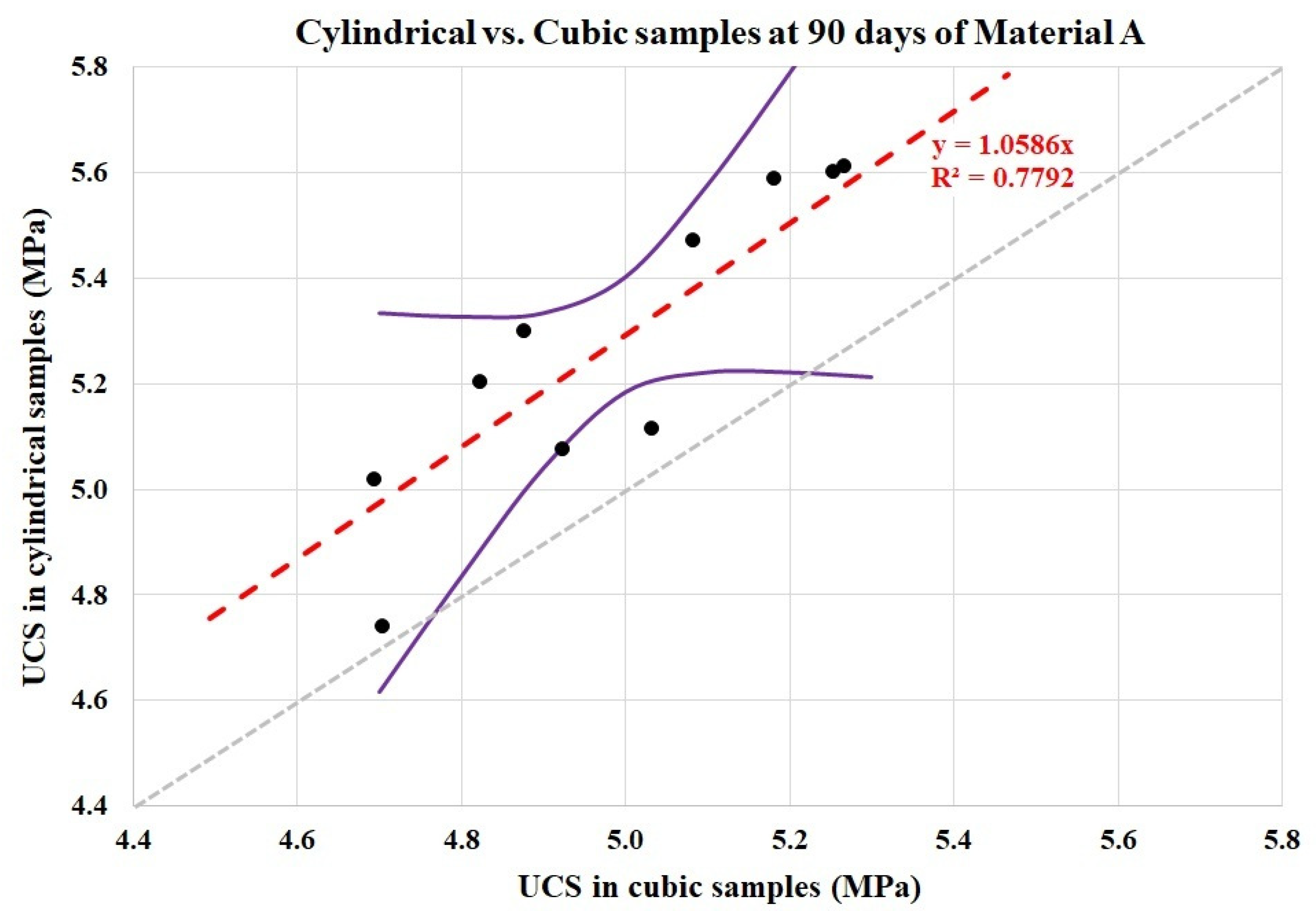
If the same analysis of Figure 11 is repeated for UCS values at 90 days, Figure 12 is developed. As seen, the accuracy of the regression correlating both values is high (R2 = 0.78), similar to that one for 7 days. Once again, all the values from cylindrical values are higher than those from cubic samples. According to the data at 90 days, the shape coefficient should have a value between 1.05 and 1.06, lower than the one developed with data at 7 days. This fact, a lower value, nearer to 1, implies that for higher strength values, the shape coefficient tends to be equal to one, as indicated by some authors with concrete samples [7,24]. In addition, all the data points except for one are inside the 95% CI region.
If the twenty data points are gathered, Figure 13 is created. As observed, the accuracy of the shape coefficient is improved considerably, reaching an R2 value of almost 0.99, implying a very high accuracy. The deduced K achieves a value of 1.068, indicating that strengths in cylindrical samples are almost 7% higher than in cubic specimens. All the data points are between the 95% CI lines.
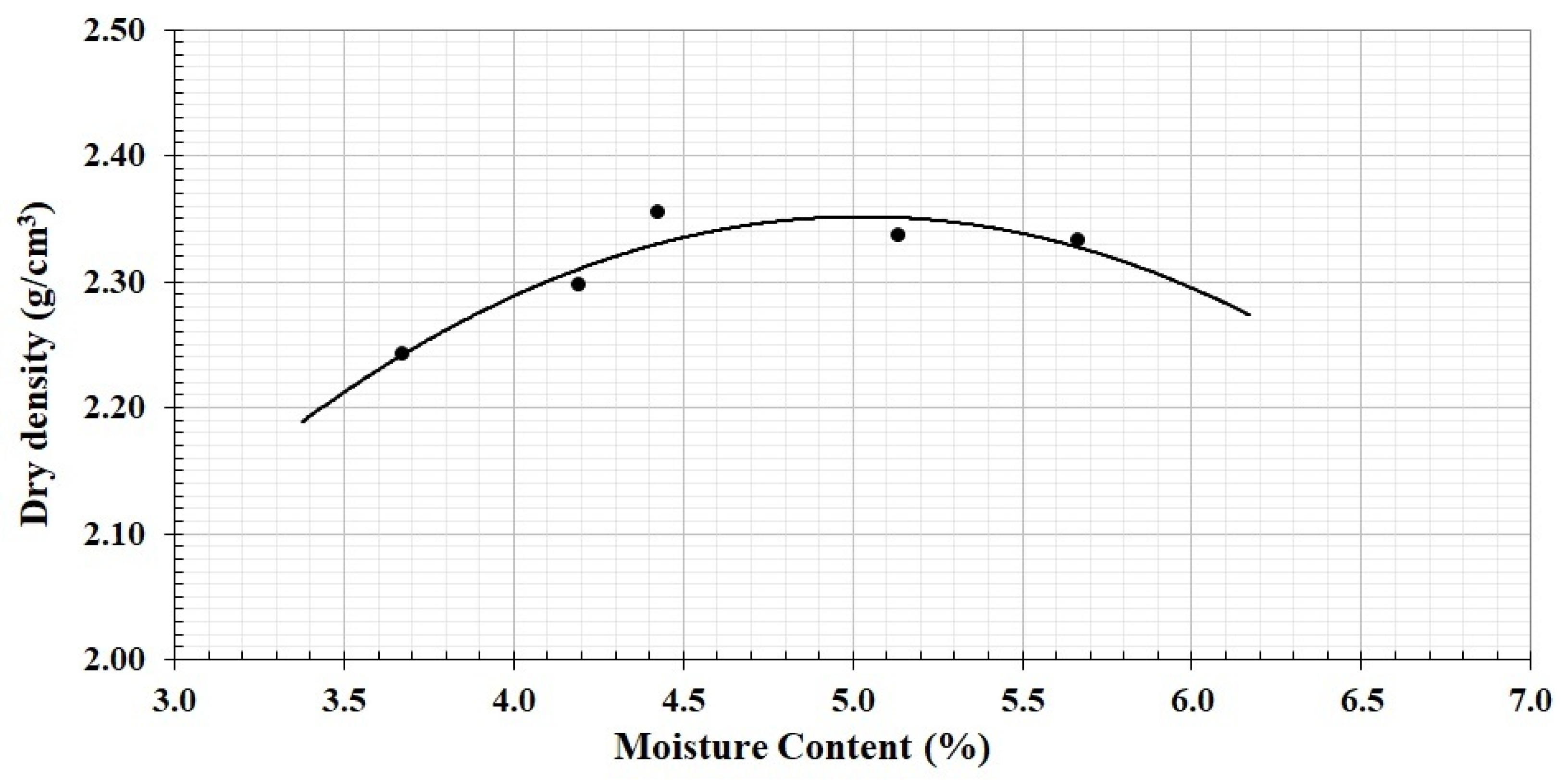
Results from Material B are presented in Table 7, Table 8 and Table 9. Table 7 provides the values of the six cylindrical specimens at each age (7, 28, and 90 days), with the corresponding dry densities and the average values at each age. Similarly, Table 8 exposes the values of the UCS of the eight semi-prismatic parts tested as a cube under the UCS test at each stage, with the average value. Finally, Table 9 presents the results from the specimens manufactured from the same mixing, as commented on in Figure 10.
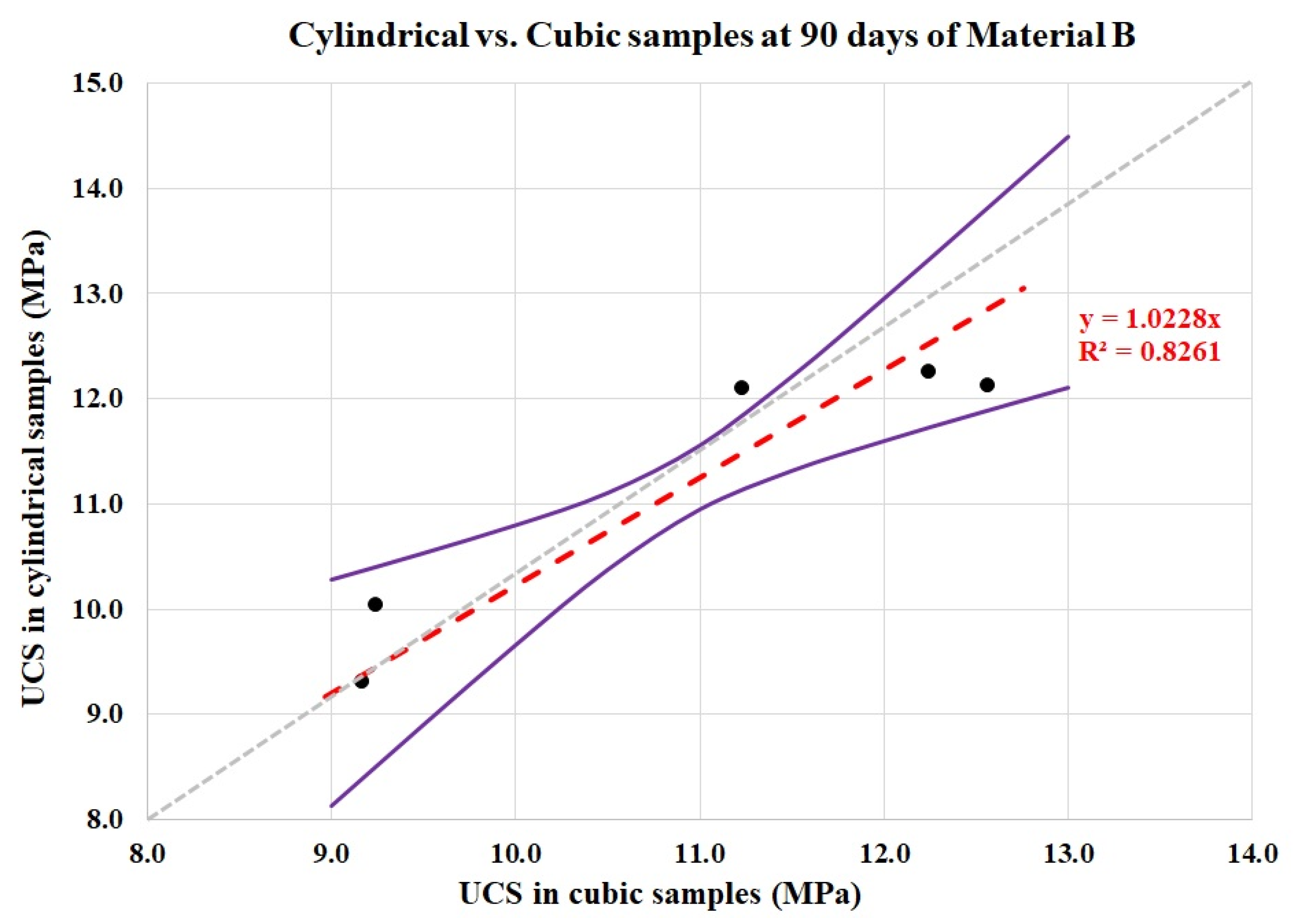
Analyzing the data cloud created with values from Material B (Figure 14), it can be seen that a high correlation coefficient is also obtained (R2 = 0.82). The obtained partial shape coefficient, K = 1.023, is smaller than those obtained from Material A. At this point, it must be noted that the UCS values of the specimens of Material B are in the range between 9 and 13 MPa, which is considerably higher than the range for Material A, even considering the values at 90 days, with UCS around 5 MPa. This fact, a shape coefficient with a trend towards 1, was also observed with concrete specimens with high compressive strength. Researchers [64,65] indicated that the shape coefficient decreases as the concrete strength is increased. In other words, high-strength concrete is not so affected by the shape of the specimen. After analyzing cylinders and cubes of variable sizes and ratios with 11 mixes with UCS values ranging from 20 to 100 MPa, Mansur and Islam [66] verified that the ratio of cube to cylinder compressive strengths decreases when increasing the concrete strengths. This fact is also noted in standards, such as the CEB-FIP Model Code [67] or the EHE-08 code for Spain [38], previously commented on in Section 2.2, which established a value of 1 for K for fcube over 80 MPa. Furthermore, Graybeal and Davis [24] investigated the ratio between cylindrical and cubic specimens for ultra-high-performance fiber-reinforced concrete, with strengths between 80 and 200 MPa, and concluded that cylinders and cubes were interchangeable at this range.
As seen, a similar trend is observable with high-strength soil-cement samples. As the UCS has increased, the shape coefficient has diminished, from a value of 1.11 with UCS around 2.5 MPa, to a value of 1.06 for UCS around 5 MPa, to a value of 1.023 for UCS around 10 MPa. In fact, there is a data point, the one referring to the strength at 28 days, where the value of the cubic samples (12.243 MPa) is practically the same as for cylindrical samples (12.257 MPa) and another one, the one relating the additional cylindrical sample (BCYL07-7) with the cubes from BCUB07-5 and BCUB07-6, where the cubes achieved a greater strength than the corresponding cylindrical specimen. This reflects the idea of trending towards equivalence, which is proposed for other cementitious materials, like concrete [24,66,68,69]. The gradual convergence of cube and cylinder strengths at higher UCS levels also reflects a reduction in lateral dilation and in the influence of end-restraint, meaning that as the material becomes stronger and less deformable, geometric effects diminish and K approaches one [62].
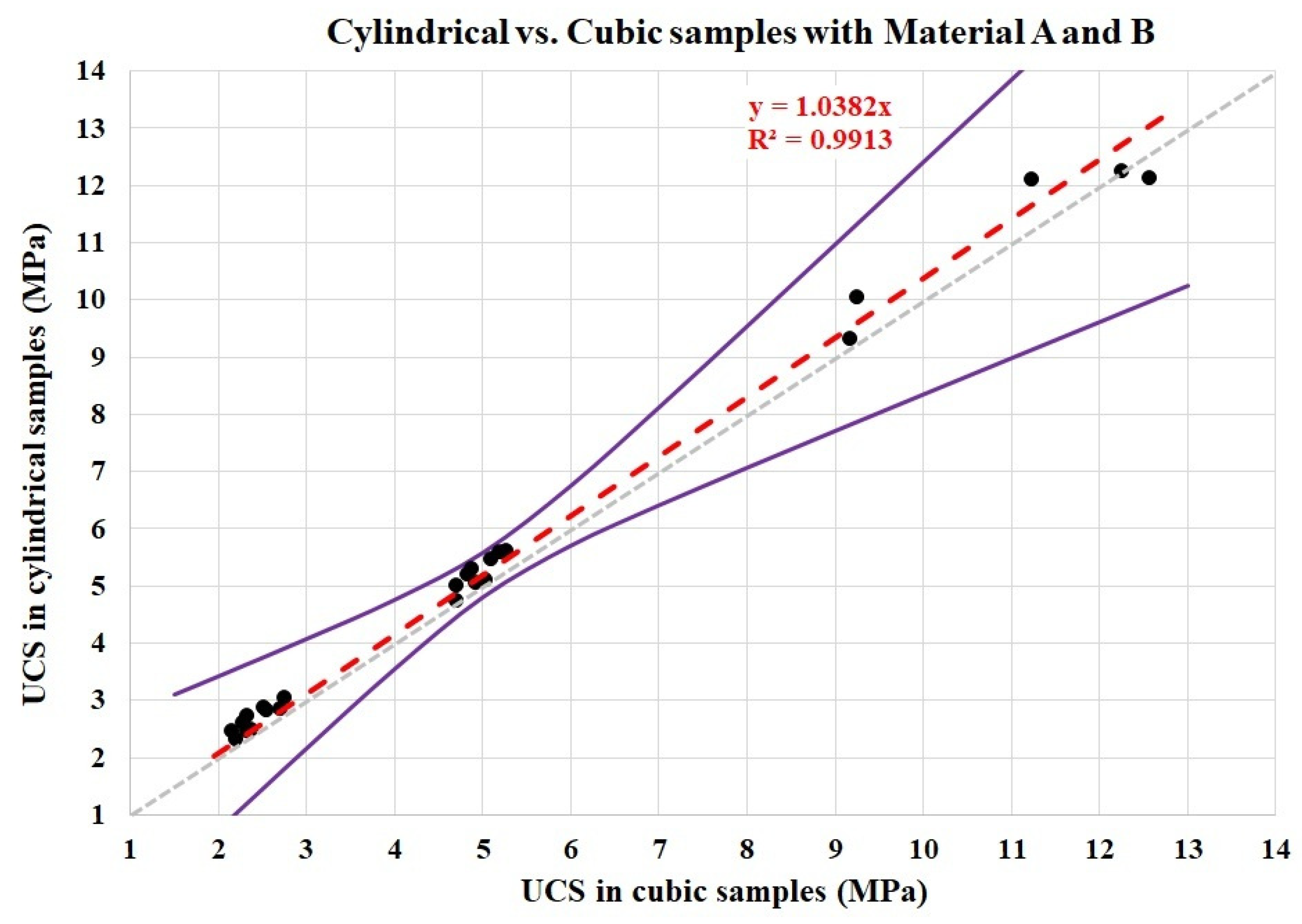
The final stage of the investigation comprises putting all the data points together to calculate a general shape coefficient, which is presented in Figure 15.
The first point to comment on is the resulting value for the shape coefficient. A value of approximately 1.04 is obtained. These average values are fully consistent with the mechanical expectation for squat cylinders, which systematically test stronger than cubes due to confinement effects, as noted in ASTM D1633 [60] for soil-cement and in the literature about mechanics on concrete [61,62,70] and on soil-cement [63,71].
In addition, it could be said that the proposed value of 1.04 comes as an average from 10 points, which were compared using a value of 1.11, 10 points with a value of 1.06, and 5 points that established a value of 1.023. Taking into consideration, it could be deduced that a different shape coefficient was needed according to the range of the UCS, as proposed in other standards [38,67]. Nevertheless, the point to be underlined is that the resulting shape coefficient, 1.04, obtains a higher accuracy than those obtained by the specimens individually in the same range of strength, with all the data points within the 95% CI range. For specimens of Material A tested at 7 days, the determination coefficient of the relationship between them was only 0.77; for samples of Material A tested at 90 days, the R2 value was 0.78; and, finally, the accuracy of the regression for data from Material B was a bit higher, 0.86. However, when gathering all the data together, a very high accuracy is achieved, a determination coefficient of 0.9913. Consequently, instead of proposing various shape coefficients depending on the compressive strength value, as for concrete specimens, it was preferred to propose a unique value, 1.04, for converting UCS values of cubic samples (of 15 cm) to UCS values of cylindrical samples of 18 cm high and 15 cm diameter (Equation (2)). This research has the advantage of comparing different materials and compressive strengths, making it possible to observe the global trend of the soil-cement mixtures instead of being focused on a narrower range for compressive strengths, which would have limited the generalization of the proposed shape coefficient. Our aim was to propose a first shape coefficient for soil-cement for any strength range, which could be applied directly to obtain a magnitude order of the conversion. Finally, although the variability in the UCS range is favorable for the investigation, it must be noted that further analysis is needed to verify the trends observed in this study.
f c y l , s c = 1.04 · f c u b e , s c
where fcyl,sc and fcube,sc are the unconfined compressive strength of soil-cement in cylindrical specimens of 180 mm high and 150 mm diameter, and in cubic specimens of 150 mm, respectively.

5. Conclusions

This study has addressed a long-standing gap in the characterization of cement-treated pavement base materials by examining the influence of specimen geometry on compressive strength testing results, specifically focusing on the development of a shape coefficient for soil-cement. Although shape coefficients are well established in the field of concrete and are embedded in design standards worldwide, equivalent knowledge for soil-cement or cement-treated base materials remains scarce, despite their extensive use in pavement engineering.
To tackle this issue, an experimental program was designed using two different soil-cement mixtures with distinct material characteristics, cement types, and aggregate sources. This was performed deliberately to ensure that the findings would not be restricted to a single material source or mix design. Cylindrical specimens (150 mm diameter × 180 mm height) and cubic specimens (150 mm edge) were tested at various curing ages (7, 28, and 90 days), resulting in a broad range of compressive strength values, from approximately 2.5 MPa to over 12 MPa. The methodology ensured the comparability of results by using specimens manufactured from the same mixing whenever possible and by applying standardized procedures for compaction, curing, and testing. This allowed the observed differences in unconfined compressive strength (UCS) to be attributed mainly to specimen geometry rather than to variability in material production.
The results revealed a systematic trend: cylindrical specimens consistently exhibited higher UCS values than cubic specimens for all mixtures and curing ages. This finding contrasts with typical observations in concrete, where cubic specimens often show higher strengths. The difference can be explained by the geometry used in soil-cement testing. Cylindrical specimens of 180 mm height present a lower slenderness ratio compared to the standard 300 mm height cylinders used in concrete, which leads to greater confinement effects at the platens and higher apparent compressive strength. In cubic specimens, the stress field is more uniform and less influenced by platen restraint, resulting in lower strength values.
A further key observation is that the magnitude of this shape effect decreases with increasing strength. For the lowest UCS range (approximately 2.5 MPa), the shape coefficient (K) was determined to be around 1.11, indicating that cylindrical specimens produced strengths about 11% higher than cubic specimens. At intermediate strength levels (around 5 MPa), the coefficient decreased to 1.06, and at the highest strength levels (around 10 MPa), it was close to unity (1.023). This behavior is consistent with trends observed in concrete, where shape effects become less relevant at higher strengths due to reduced lateral deformation and increased material homogeneity.
When all data points from both mixtures and all ages were combined, a single shape coefficient of K = 1.04 was obtained, resulting in an equation of the form UCScyl = 1.04·UCScub, with a very high coefficient of determination (R2 = 0.9913). This high accuracy suggests that a single value can adequately represent the shape effect for a wide range of soil-cement mixtures and strength levels. From a practical standpoint, this is a significant advantage: using a single coefficient simplifies design, testing, and specification procedures, avoiding the need for strength-dependent correction factors as used in some concrete standards. The proposed coefficient is particularly relevant because cubic specimens present clear operational advantages: they are lighter, easier to handle, and do not require capping prior to testing, thus reducing environmental impacts and simplifying laboratory procedures.
Nevertheless, this research should be considered an initial step towards fully establishing shape conversion rules for soil-cement. The study was conducted with two mixtures representing typical pavement base materials in Spain, and although these mixtures exhibited different properties and strengths, further work is needed to validate the coefficient for a broader range of materials, including those with different cement contents, gradations, moisture conditions, and curing environments. Additionally, other geometries, such as smaller or larger cubes or alternative cylinder dimensions, could be investigated to extend the applicability of the proposed coefficient.

Author Contributions

Conceptualization, H.P.-A., A.L.-U. and Á.A.-T.; methodology, H.P.-A., A.L.-U., Á.A.-T. and H.G.-O.; software, A.L.-U. and H.G.-O.; validation, H.P.-A., A.L.-U. and Á.A.-T.; formal analysis, H.P.-A., A.L.-U. and H.G.-O.; investigation, A.L.-U. and Á.A.-T.; resources, A.L.-U. and H.G.-O.; data curation, H.P.-A., A.L.-U. and H.G.-O.; writing—original draft preparation, H.P.-A. and Á.A.-T.; writing—review and editing, H.P.-A., A.L.-U., Á.A.-T. and H.G.-O.; visualization, Á.A.-T.; supervision, H.P.-A. and Á.A.-T.; project administration, H.P.-A. and H.G.-O.; funding acquisition, H.P.-A. and H.G.-O. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Education Council of the Castille and Leon Government of Spain, under grant numbers BU009A06 and UB 07/03, and by the Provincial Council of Biscay (Bizkaiko Foru Aldundia/Diputación Foral de Bizkaia), under grant number 5/12/IV/2023/00005, ARASC project, of the grant program aimed at promoting innovation in road infrastructure 2023, and under grant 5/12/IV/2024/00005, ARASC 2 project, of the grant program aimed at promoting innovation in road infrastructure 2024. Additionally, financial support was provided through research contracts with Asfaltos Uribe, S.A., under contract numbers 2024.0037, 2024.0819, W58A06, W40B06, W25C06, and W57B06.

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Elwell, D.J.; Fu, G. Compression Testing of Concrete: Cylinders Versus Cubes; No. FHWA/NY/SR-95/119; Transportation Research and Development Bureau, New York State Department of Transportation: Albany, NY, USA, 1995. Available online: https://rosap.ntl.bts.gov/view/dot/38089 (accessed on 4 October 2025).
  2. Sim, J.I.; Yang, K.H.; Kim, H.Y.; Choi, B.J. Size and shape effects on compressive strength of lightweight concrete. Constr. Build. Mater. 2013, 38, 854–864. [Google Scholar] [CrossRef]
  3. Yehia, S.; Abdelfatah, A.; Mansour, D. Effect of aggregate type and specimen configuration on concrete compressive strength. Crystals 2020, 10, 625. [Google Scholar] [CrossRef]
  4. Dehestani, M.; Nikbin, I.M.; Asadollahi, S. Effects of specimen shape and size on the compressive strength of self-consolidating concrete (SCC). Constr. Build. Mater. 2014, 66, 685–691. [Google Scholar] [CrossRef]
  5. Li, M.; Hao, H.; Shi, Y.; Hao, Y. Specimen shape and size effects on the concrete compressive strength under static and dynamic tests. Constr. Build. Mater. 2018, 161, 84–93. [Google Scholar] [CrossRef]
  6. Neville, A. Properties of Concrete, 1st ed.; Longman: London, UK, 1963. [Google Scholar]
  7. Riedel, P.; Leutbecher, T.; Piotrowski, S.; Heese, C. Ratios of compressive strengths of ultra-high-performance concrete specimens of different shapes and sizes. ACI Mater. J. 2019, 116, 139–149. [Google Scholar]
  8. Bagui, S.K. Pavement design for rural low volume roads using cement and lime treatment base. Jordan J. Civ. Eng. 2012, 6, 293–303. [Google Scholar]
  9. López, M.A.C.; Fedrigo, W.; Kleinert, T.R.; Matuella, M.F.; Núñez, W.P.; Ceratti, J.A.P. Flexural fatigue evaluation of cement-treated mixtures of reclaimed asphalt pavement and crushed aggregates. Constr. Build. Mater. 2018, 158, 320–325. [Google Scholar] [CrossRef]
  10. Linares-Unamunzaga, A.; Pérez-Acebo, H.; Rojo, M.; Gonzalo-Orden, H. Flexural strength prediction models for soil–cement from unconfined compressive strength at seven days. Materials 2019, 12, 387. [Google Scholar] [CrossRef]
  11. Pongsivasathit, S.; Horpibulsuk, S.; Piyaphipat, S. Assessment of mechanical properties of cement stabilized soils. Case Stud. Constr. Mater. 2019, 11, e00301. [Google Scholar] [CrossRef]
  12. Gonzalo-Orden, H.; Linares-Unamunzaga, A.; Pérez-Acebo, H.; Díaz-Minguela, J. Advances in the study of the behavior of full-depth reclamation (FDR) with cement. Appl. Sci. 2019, 9, 3055. [Google Scholar] [CrossRef]
  13. Fedrigo, W.; Visser, A.T.; Steyn, W.J.; Núñez, W.P. Flexural behaviour of lightly cement stabilised materials: South Africa and Brazil. Road Mater. Pavement Des. 2021, 22, 397–422. [Google Scholar] [CrossRef]
  14. Diniz, B.C.; Fedrigo, W.; Kleinert, T.R.; Batista, G.D.S.; Núñez, W.P.; Correa, B.M.; Brito, L.A.T. Lime stabilization of tropical soil for resilient pavements: Mechanical, microscopic, and mineralogical characteristics. Materials 2024, 17, 4720. [Google Scholar] [CrossRef]
  15. Pérez-Acebo, H.; Gonzalo-Orden, H.; Findley, D.J.; Rojí, E. Modeling the international roughness index performance on semi-rigid pavements in single carriageway roads. Constr. Build. Mater. 2021, 272, 121665. [Google Scholar] [CrossRef]
  16. Gurrutxaga, I.; Alonso-Solórzano, A.; Isasa, M.; Pérez-Acebo, H. IRI performance models for flexible, semi-rigid and composite pavements in Double-carriageway roads. Civ. Eng. J. 2025, 11, 1712–1738. [Google Scholar] [CrossRef]
  17. Qasim, O.A. A review paper on specimens size and shape effects on the concrete properties. Int. J. Recent Adv. Sci. Technol. 2018, 5, 13–25. [Google Scholar] [CrossRef]
  18. Felt, E.; Abrams, M. Strength and elastic properties of compacted soil-cement mixtures. In Papers on Soils; ASTM International: West Conshohocken, PA, USA, 1957; pp. 152–178. [Google Scholar] [CrossRef]
  19. Tariq, K.A.; Maki, T. Mechanical behaviour of cement-treated sand. Constr. Build. Mater. 2014, 58, 54–63. [Google Scholar] [CrossRef]
  20. Xie, J.; Tang, L.; Lv, S.; Zhang, N.; Huang, T.; Liu, H. Standardization of fatigue characteristics of cement-treated aggregate base materials under different stress states. Appl. Sci. 2018, 8, 1500. [Google Scholar] [CrossRef]
  21. Lv, S.; Xia, C.; Liu, H.; You, L.; Qu, F.; Zhong, W.; Yang, Y.; Washko, S. Strength and fatigue performance for cement-treated aggregate base materials. Int. J. Pavement Eng. 2021, 22, 690–699. [Google Scholar] [CrossRef]
  22. Rocha, J.H.A.; Galarza, F.P.; Chileno, N.G.C.; Rosas, M.H.; Peñaranda, S.P.; Diaz, L.L.; Abasto, R.P. Compressive strength assessment of soil–cement blocks incorporated with waste tire steel fiber. Materials 2022, 15, 1777. [Google Scholar] [CrossRef]
  23. Tripura, D.D.; Das, S. Shape and Size Effects on the Compressive Strength of Cement Stabilised Rammed Earth. In Proceedings of the Architectural Engineering Institute Conference 2017—Resilience of the Integrated Building: A Community Focus, Oklahoma City, OK, USA, 11–13 April 2017; pp. 336–348. [Google Scholar]
  24. Graybeal, B.; Davis, M. Cylinder or cube: Strength testing of 80 to 200 MPa (11.6 to 29 ksi) ultra-high-performance fiber-reinforced concrete. ACI Mater. J. 2008, 105, 603. [Google Scholar]
  25. Pacheco, J.; de Brito, J.; Chastre, C. Probabilistic conversion of the compressive strength between cube and cylinder specimens for natural and recycled aggregate concrete. Materials 2019, 12, 280. [Google Scholar] [CrossRef]
  26. Del Viso, J.R.; Carmona, J.R.; Ruiz, G. Shape and size effects on the compressive strength of high-strength concrete. Cem. Concr. Res. 2008, 38, 386–395. [Google Scholar] [CrossRef]
  27. Zhu, H.; Li, C.; Gao, D.; Yang, L.; Cheng, S. Study on mechanical properties and strength relation between cube and cylinder specimens of steel fiber reinforced concrete. Adv. Mech. Eng. 2019, 11, 1687814019842423. [Google Scholar] [CrossRef]
  28. Mardani-Aghabaglou, A.; Bayqra, S.H.; Nobakhtjoo, A. Specimen size and shape effects on strength of concrete in the absence and presence of steel fibers. Rev. Constr. 2021, 20, 128–144. [Google Scholar] [CrossRef]
  29. Gyurkó, Z.; Nemes, R. Specimen size and shape effect on the compressive strength of normal strength concrete. Period. Polytech. Civ. Eng. 2020, 64, 276–286. [Google Scholar] [CrossRef]
  30. Hake, P.J. Comparison of Compressive Strengths Using 4x8 vs. 6x12 Cylinders for Prestress Concrete; No. RDT 04-005; Missouri Department of Transportation, Research, Development and Technology: Jefferson City, MO, USA, 2004. Available online: https://rosap.ntl.bts.gov/view/dot/62532 (accessed on 2 October 2025).
  31. PG (Presidency of the Government). Decreto 2987/1968, de 20 de Septiembre, Por el Que se Apruebe la Instrucción Para el Proyecto y la Ejecución de Obras de Hormigón en Masa o Armado; BOE de 3 Diciembre de 1968: Madrid, Spain, 1968.
  32. MOP (Ministry of Public Works). UNE 7242. Characteristic Strength and Quality Control; Concrete Permanent Commission: Madrid, Spain, 1972.
  33. PG (Presidency of the Government). Decreto 3062/1973, de 19 de Octubre, Por el Que se Aprueba la Instrucción Para el Proyecto y la Ejecución de Obras de Hormigón en Masa o Armado; BOE de 7 de Diciembre de 1973: Madrid, Spain, 1973.
  34. MOPU (Ministry of Public Works and Urbanism). Real Decreto 2868/1980, de 17 de Octubre, Por el Que se Aprueba la “Instrucción Para el Proyecto y la Ejecución de Obras de Hormigón en Masa o Armado (EH-80); BOE de 10 de enero de 1981: Madrid, Spain, 1981. Available online: https://www.boe.es/eli/es/rd/1980/10/17/2868.
  35. MOPU (Ministry of Public Works and Urbanism). Real Decreto 824/1988, de 15 de Julio, Por el Que se Aprueba la Instrucción Para el Proyecto y la Ejecución de Obras de Hormigón en Masa o Armado (EH-88) y la Instrucción Para el Proyecto y la Ejecución de Forjados Unidireccionales de Hormigón Armado a Pretensado (EF-88); BOE de 28 de Julio de 1988: Madrid, Spain, 1988. Available online: https://www.boe.es/eli/es/rd/1988/07/15/824.
  36. MOPU (Ministry of Public Works and Urbanism). Real Decreto 1039/1991, de 28 de Junio, Por el Que se Aprueba la «Instrucción Para el Proyecto y la Ejecución de Obras de Hormigón en Masa o Armado (EH-91); BOE de 3 de Julio de 1991: Madrid, Spain, 1991. Available online: https://www.boe.es/eli/es/rd/1991/06/28/1039.
  37. MFOM (Ministerio de Fomento). Real Decreto 2661/1998, de 11 de Diciembre, Por el Que se Aprueba la «Instrucción de Hormigón Estructural (EHE); BOE de 13 de Enero de 1999: Madrid, Spain, 1999. Available online: https://www.boe.es/eli/es/rd/1998/12/11/2661.
  38. MP (Ministry of the Presidency). Real Decreto 1247/2008, de 18 de Julio, Por el Que se Aprueba la Instrucción de Hormigón Estructural (EHE-08); BOE de 22 de Agosto de 2008: Madrid, Spain, 2008. Available online: https://www.boe.es/eli/es/rd/2008/07/18/1247.
  39. UNE EN 12390-3:2020; Testing Hardened Concrete—Part 3: Compressive Strength of Test Specimens. AENOR (Asociación Española de Normalización y Certificación): Madrid, Spain, 2020.
  40. MPRCMD (Ministry of the Presidency, Parliamentary Relations and Democratic Memory). Real Decreto 470/2021, de 29 de Junio, Por el Que se Aprueba el Código Estructural; BOE de 10 de Agosto de 2021: Madrid, Spain, 2021. Available online: https://www.boe.es/eli/es/rd/2021/06/29/470.
  41. EN 1992-1-1; Eurocode 2: Design of Concrete Structures. CEN (Comité Européen de Normalisation): Brussels, Belgium, 2004.
  42. George, K.P. Characterization and structural design of cement-treated base. Transp. Res. Rec. 1990, 1288, 78–87. [Google Scholar]
  43. Nguyen, N.H.; Bui, H.H.; Arooran, S.; Nguyen, G.D.; Kodikara, J. Discrete element method investigation of particle size distribution effects on the flexural properties of cement-treated base. Comput. Geotech. 2019, 113, 103096. [Google Scholar] [CrossRef]
  44. Dong, Q.; Zheng, D.; Zhao, X.; Chen, X.; Chen, Y. Mesoscale numerical simulation of fracture of cement treated base material during semi circular bending test with discrete element model. Constr. Build. Mater. 2020, 261, 119981. [Google Scholar] [CrossRef]
  45. Xuan, D.X.; Molenaar, A.A.A.; Houben, L.J.M. Evaluation of cement treatment of reclaimed construction and demolition waste as road bases. J. Clean. Prod. 2015, 100, 77–83. [Google Scholar] [CrossRef]
  46. Anysz, H.; Rosicki, Ł.; Narloch, P. Compressive strengths of cube vs. cored specimens of cement stabilized rammed earth compared with ANOVA. Appl. Sci. 2024, 14, 5746. [Google Scholar] [CrossRef]
  47. Kwon, J.; Seo, Y. Guidelines for Incorporation of Cement Stabilized Reclaimed Base (CSRB) in Pavement Design; No. FHWA-GA-23-2014); Georgia Department of Transportation. Office of Performance-Based Management & Research: Atlanta, GA, USA, 2023. Available online: https://rosap.ntl.bts.gov/view/dot/66670/dot_66670_DS1.pdf.
  48. MFOM (Ministerio de Fomento). Orden FOM/2523/2014, de 12 de Diciembre, Por la Que se Actualizan Determinados Artículos del Pliego de Prescripciones Técnicas Generales Para Obras de Carreteras y Puentes, Relativos a Materiales Básicos, a Firmes y Pavimentos, y a Señalización, Balizamiento y Sistemas de Contención de Vehículos; BOE de 3 de Enero de 2015: Madrid, Spain, 2015. Available online: https://www.boe.es/eli/es/o/2014/12/12/fom2523.
  49. EN ISO 17892-4:2016; Geotechnical Investigation and Testing. Laboratory Testing of Soil. Part 4: Determination of Particle Size Distribution. CEN (Comité Européen de Normalisation): Brussels, Belgium, 2016.
  50. MFOM (Ministerio de Fomento). Orden FOM/3460/2003, de 28 de Noviembre, Por la Que se Aprueba la Norma 6.1-IC “Secciones de Firme”, de la Instrucción de Carreteras; BOE de 12 de Diciembre de 2003: Madrid, Spain, 2003. Available online: https://www.boe.es/eli/es/o/2003/11/28/fom3460.
  51. EN 1744-1:2009; Tests for Chemical Properties of Aggregates—Part 1; Chemical Analysis. CEN (Comité Européen de Normalisation): Brussels, Belgium, 2009.
  52. EN ISO 17892-12:2019; Geotechnical Investigation and Testing—Laboratory Testing of Soil—Part 12: Determination of Liquid and Plastic Limits. CEN (Comité Européen de Normalisation): Brussels, Belgium, 2019.
  53. UNE 103501:1994; Geothecnic. Compaction Test. Modified Proctor. AENOR (Asociación Española de Normalización y Certificación): Madrid, Spain, 1994.
  54. D1557-12e1; Standard Test Methods for Laboratory Compaction Characteristics of Soil Using Modified Effort (56,000 ftlbf/ft3 (2700 kN-m/m3)). American Society for Testing and Materials International (ASTM): West Conshohocken, PA, USA, 2012.
  55. EN 197-1:2011; Cement. Part 1: Composition, Specifications and Conformity Criteria for Common Cements. CEN (Comité Européen de Normalisation): Brussels, Belgium, 2011.
  56. Norma NLT-305/90; Resistencia a Compresión Simple de Materiales Tratados con Conglormerantes Hidráulicos. CEDEX, Direccion General de Carreteras, Ministerio de Obras Públicas y Urbanismo (MOPU): Madrid, Spain, 1990.
  57. Linares-Unamunzaga, A.; Gonzalo-Orden, H.; Minguela, J.D.; Pérez-Acebo, H. New procedure for compacting prismatic specimens of cement-treated base materials. Appl. Sci. 2018, 8, 970. [Google Scholar] [CrossRef]
  58. EN 12390-5:2009; Testing Hardened Concrete—Part 5: Flexural Strength of Test Specimens. CEN (Comité Européen de Normalisation): Brussels, Belgium, 2009.
  59. EN 13286-41:2003; Unbound and Hydraulically Bound Mixtures—Part 41: Test Method for the Determination of the Compressive Strength of Hydraulically Bound Mixtures. CEN (Comité Européen de Normalisation): Brussels, Belgium, 2003.
  60. ASTM D1633-17; Standard Test Method for Compressive Strength of Molded Soil-Cement Cylinders. American Society for Testing and Materials International (ASTM): West Conshohocken, PA, USA, 2017.
  61. Van Vliet, M.R.A.; Van Mier, J.G.M. Experimental investigation of concrete fracture under uniaxial compression. Mech. Cohesive-Frict. Mater. 1996, 1, 115–127. [Google Scholar] [CrossRef]
  62. Talaat, A.; Emad, A.; Tarek, A.; Masbouba, M.; Essam, A.; Kohail, M. Factors affecting the results of concrete compression testing: A review. Ain Shams Eng. J. 2021, 12, 205–221. [Google Scholar] [CrossRef]
  63. Hu, L.; Hao, J.; Wang, L. Laboratory evaluation of cement treated aggregate containing crushed clay brick. J. Traffic Transp. Eng. 2014, 1, 371–382. [Google Scholar] [CrossRef]
  64. Mindess, S.; Young, J.F.; Darwin, D. Concrete; Prentice-Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
  65. Neville, A. Properties of Concrete, 4th ed.; Longman: London, UK, 1993. [Google Scholar]
  66. Mansur, M.A.; Islam, M.M. Interpretation of concrete strength for nonstandard specimens. J. Mater. Civ. Eng. 2002, 14, 151–155. [Google Scholar] [CrossRef]
  67. CEB-FIP. Model Code 1990; Thomas Telford: London, UK, 1990. [Google Scholar]
  68. Day, R.L. Strength measurement of concrete using different cylinder sizes: A statistical analysis. Cem. Concr. Aggreg. 1994, 16, 21–30. [Google Scholar] [CrossRef]
  69. Aitcin, P.C.; Miao, B.; Cook, W.D.; Mitchell, D. Effects of size and curing on cylinder compressive strength of normal and high-strength concrete. Mater. J. 1994, 91, 349–355. [Google Scholar] [CrossRef]
  70. Al-Sahawneh, E.I. Size effect and strength correction factors for normal weight concrete specimens under uniaxial compression stress. Contemp. Eng. Sci. 2013, 6, 57–68. Available online: https://www.m-hikari.com/ces/ces2013/ces1-4-2013/alsahawnehCES1-4-2013.pdf (accessed on 11 November 2025). [CrossRef]
  71. Symons, I.F. The effect of size and shape of specimen upon the unconfined compressive strength of cement-stabilized materials. Mag. Concr. Res. 1970, 22, 45–51. [Google Scholar] [CrossRef]
Buildings 15 04304 g001
Figure 1. Granulometry of Material A.
Figure 1. Granulometry of Material A.
Buildings 15 04304 g001
Buildings 15 04304 g002
Figure 2. Maximum dry density and optimum moisture content of Material A with 3.5% of cement.
Figure 2. Maximum dry density and optimum moisture content of Material A with 3.5% of cement.
Buildings 15 04304 g002
Buildings 15 04304 g003
Figure 3. Granulometry of Material B.
Figure 3. Granulometry of Material B.
Buildings 15 04304 g003
Buildings 15 04304 g004
Figure 4. Maximum dry density and optimum moisture content of Material B with 3.5% of cement.
Figure 4. Maximum dry density and optimum moisture content of Material B with 3.5% of cement.
Buildings 15 04304 g004
Buildings 15 04304 g005
Figure 5. Special device for compacting prismatic specimens of soil-cement or cement-treated bases.
Figure 5. Special device for compacting prismatic specimens of soil-cement or cement-treated bases.
Buildings 15 04304 g005
Buildings 15 04304 g006
Figure 6. Example of a cylindrical specimen of Material A.
Figure 6. Example of a cylindrical specimen of Material A.
Buildings 15 04304 g006
Buildings 15 04304 g007
Figure 7. Example of prismatic specimens of Material A: (a) being tested at the four-point beam test, (b) after the four-point beam test is conducted, and (c) a semi prism being tested at UCS as a cubic sample.
Figure 7. Example of prismatic specimens of Material A: (a) being tested at the four-point beam test, (b) after the four-point beam test is conducted, and (c) a semi prism being tested at UCS as a cubic sample.
Buildings 15 04304 g007
Buildings 15 04304 g008
Figure 8. Experimental procedure for Material A.
Figure 8. Experimental procedure for Material A.
Buildings 15 04304 g008
Buildings 15 04304 g009
Figure 9. Specimens from Material B: (a) cylindrical specimens, (b) prismatic specimens, and (c) semi-prismatic specimens.
Figure 9. Specimens from Material B: (a) cylindrical specimens, (b) prismatic specimens, and (c) semi-prismatic specimens.
Buildings 15 04304 g009
Buildings 15 04304 g010
Figure 10. Experimental procedure for Material B.
Figure 10. Experimental procedure for Material B.
Buildings 15 04304 g010
Buildings 15 04304 g011
Figure 11. UCS in cubic samples vs. UCS in cylindrical samples at 7 days with Material A (a) linear regressions with and without intercept; (b) linear regression without intercept and 95% confidence intervals.
Figure 11. UCS in cubic samples vs. UCS in cylindrical samples at 7 days with Material A (a) linear regressions with and without intercept; (b) linear regression without intercept and 95% confidence intervals.
Buildings 15 04304 g011
Buildings 15 04304 g012
Figure 12. UCS in cubic samples vs. UCS in cylindrical samples at 90 days with Material A.
Figure 12. UCS in cubic samples vs. UCS in cylindrical samples at 90 days with Material A.
Buildings 15 04304 g012
Buildings 15 04304 g013
Figure 13. UCS in cubic samples vs. UCS in cylindrical samples for all the specimens with Material A.
Figure 13. UCS in cubic samples vs. UCS in cylindrical samples for all the specimens with Material A.
Buildings 15 04304 g013
Buildings 15 04304 g014
Figure 14. UCS in cubic samples vs. UCS in cylindrical samples for all the samples with Material B.
Figure 14. UCS in cubic samples vs. UCS in cylindrical samples for all the samples with Material B.
Buildings 15 04304 g014
Buildings 15 04304 g015
Figure 15. UCS in cubic samples vs. UCS in cylindrical samples for all the specimens.
Figure 15. UCS in cubic samples vs. UCS in cylindrical samples for all the specimens.
Buildings 15 04304 g015
Table 1. Shape coefficient to convert strength values to a cylindrical specimen of 15 cm diameter × 30 cm height.
Table 1. Shape coefficient to convert strength values to a cylindrical specimen of 15 cm diameter × 30 cm height.
Specimen TypeDimensionsCoefficient to Convert to the Cylindrical Specimen of 15 cm Diameter × 30 cm Height
Variation LimitsMean Values
Cylinder15 × 30-1.00
Cylinder10 × 200.94 to 1.000.97
Cylinder25 × 501.00 to 1.101.05
Cube100.70 to 0.900.80
Cube150.70 to 0.900.80
Cube200.75 to 0.900.83
Cube300.80 to 1.000.90
Prism15 × 15 × 450.90 to 1.201.05
Prism20 × 20 × 600.90 to 1.201.05
Table 2. Shape coefficient for cubic specimens to cylindrical according to the compressive strength in cubic specimens.
Table 2. Shape coefficient for cubic specimens to cylindrical according to the compressive strength in cubic specimens.
UCS in Cubic Specimen (N/mm2)K
fcube < 600.90
60 ≤ fcube < 800.95
fcube ≥ 801.00
Table 3. Granulometry of Material A.
Table 3. Granulometry of Material A.
Sieve (mm)10080635040252010520.400.080.063
Passing percentage (%)100.0100.0100.097.789.677.873.564.256.649.733.716.815.7
Table 4. Granulometry of Material B.
Table 4. Granulometry of Material B.
Sieve (mm)100805040252012.56.3521.250.630.3150.20.080.063
Passing percentage (%)100.0100.0100.0100.088.983.974.459.654.037.227.919.213.811.58.68.2
Table 5. UCS values from cylindrical samples of Material A.
Table 5. UCS values from cylindrical samples of Material A.
MixingCodeDensity (g/cm3)UCS at 7 Days (MPa)CodeDensity (g/cm3)UCS at 90 Days (MPa)
A01A01CYL72.1512.319A01CYL902.1574.742
A02A02CYL72.1682.730A02CYL902.1575.203
A03A03CYL72.1622.466A03CYL902.1985.300
A04A04CYL72.1572.826A04CYL902.1925.473
A05A05CYL72.1512.628A05CYL902.1685.077
A06A06CYL72.1622.467A06CYL902.1515.02
A07A07CYL72.1622.501A07CYL902.1745.117
A08A08CYL72.1802.897A08CYL902.1805.612
A09A09CYL72.1803.064A09CYL902.1985.603
A10A10CYL72.1682.859A10CYL902.1865.590
Table 6. UCS values from cubic samples of Material A.
Table 6. UCS values from cubic samples of Material A.
MixingDensity of the Prismatic Sample (g/cm3)CodeUCS at 7 Days (MPa)CodeUCS at 90 Days (MPa)
A012.147A01CUB72.199A01CUB904.703
A022.147A02CUB72.321A02CUB904.822
A032.161A03CUB72.314A03CUB904.876
A042.168A04CUB72.533A04CUB905.082
A052.157A05CUB72.269A05CUB904.922
A062.152A06CUB72.144A06CUB904.693
A072.153A07CUB72.363A07CUB905.031
A082.171A08CUB72.513A08CUB905.265
A092.171A09CUB72.740A09CUB905.252
A102.157A10CUB72.696A10CUB905.181
Table 7. UCS values from cylindrical samples of Material B.
Table 7. UCS values from cylindrical samples of Material B.
CodeDensity (g/cm3)UCS at 7 Days (MPa)CodeDensity (g/cm3)UCS at 28 Days (MPa)CodeDensity (g/cm3)UCS at 90 Days (MPa)
BCYL07-12.4498.896BCYL28-12.44615.019BCYL90-12.44812.110
BCYL07-22.4468.975BCYL28-22.4379.518BCYL90-22.44412.110
BCYL07-32.4198.669BCYL28-32.3629.535BCYL90-32.36112.093
BCYL07-42.46210.31BCYL28-42.43212.812BCYL90-42.38512.664
BCYL07-52.40811.77BCYL28-52.43212.913BCYL90-52.38514.572
BCYL07-62.36311.686BCYL28-62.45813.746BCYL90-62.4349.108
Average2.42410.051Average2.42812.257 2.41012.110
Table 8. UCS values from cubic samples of Material B.
Table 8. UCS values from cubic samples of Material B.
Age (Days)CodeDensity of the Prismatic Sample (g/cm3)UCS of the 1st Semi Prism (MPa)UCS of the 2nd Semi Prism (MPa)Average UCS of the Two HalvesAverage at Each Age (MPa)
7BPRIS07-12.39612.17810.1211.1499.236
BPRIS07-22.3187.4447.4367.440
BPRIS07-32.3418.89810.6189.758
BPRIS07-42.3467.8989.2938.596
28BPRIS28-12.36010.13813.00911.57312.243
BPRIS28-22.31412.5969.86211.229
BPRIS28-32.42312.84314.20413.524
BPRIS28-42.29613.28012.00912.644
90BPRIS90-12.36915.10713.44914.27811.227
BPRIS90-22.31610.25811.58210.920
BPRIS90-32.3839.5888.5009.044
BPRIS90-42.35512.0629.26710.665
Table 9. Data from the same mixture with Material B in cylindrical specimens.
Table 9. Data from the same mixture with Material B in cylindrical specimens.
CodeDensity (g/cm3)UCS (MPa)Average Value (MPa)Correlated withDensity of Prismatic Sample (g/cm3)UCS 1st Semi Prism (MPa)UCS 2nd Semi Prism (MPa)Average UCS of the Two HalvesAverage at Each Age (MPa)
BCYL07-72.4809.3199.139BPRIS07-52,44410.8216.1558.4889.164
BPRIS07-62,4209.9909.6889.839
BCYL90-72.41412.84612.138BPRIS90-72.36912.16010.31111.23612.562
BCYL90-82.40211.431BPRIS90-82.31615.20012.57813.889
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Pérez-Acebo, H.; Linares-Unamunzaga, A.; Aragón-Torre, Á.; Gonzalo-Orden, H. Shape Coefficient for Soil-Cement: Experimental Determination from Cylindrical and Cubic Specimens. Buildings 2025, 15, 4304. https://doi.org/10.3390/buildings15234304

AMA Style

Pérez-Acebo H, Linares-Unamunzaga A, Aragón-Torre Á, Gonzalo-Orden H. Shape Coefficient for Soil-Cement: Experimental Determination from Cylindrical and Cubic Specimens. Buildings. 2025; 15(23):4304. https://doi.org/10.3390/buildings15234304

Chicago/Turabian Style

Pérez-Acebo, Heriberto, Alaitz Linares-Unamunzaga, Ángel Aragón-Torre, and Hernán Gonzalo-Orden. 2025. "Shape Coefficient for Soil-Cement: Experimental Determination from Cylindrical and Cubic Specimens" Buildings 15, no. 23: 4304. https://doi.org/10.3390/buildings15234304

APA Style

Pérez-Acebo, H., Linares-Unamunzaga, A., Aragón-Torre, Á., & Gonzalo-Orden, H. (2025). Shape Coefficient for Soil-Cement: Experimental Determination from Cylindrical and Cubic Specimens. Buildings, 15(23), 4304. https://doi.org/10.3390/buildings15234304

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop