Strength Characteristics of Unsaturated Compacted Loess Under Complex Stress Paths
Abstract
1. Introduction
2. Experimental Overview
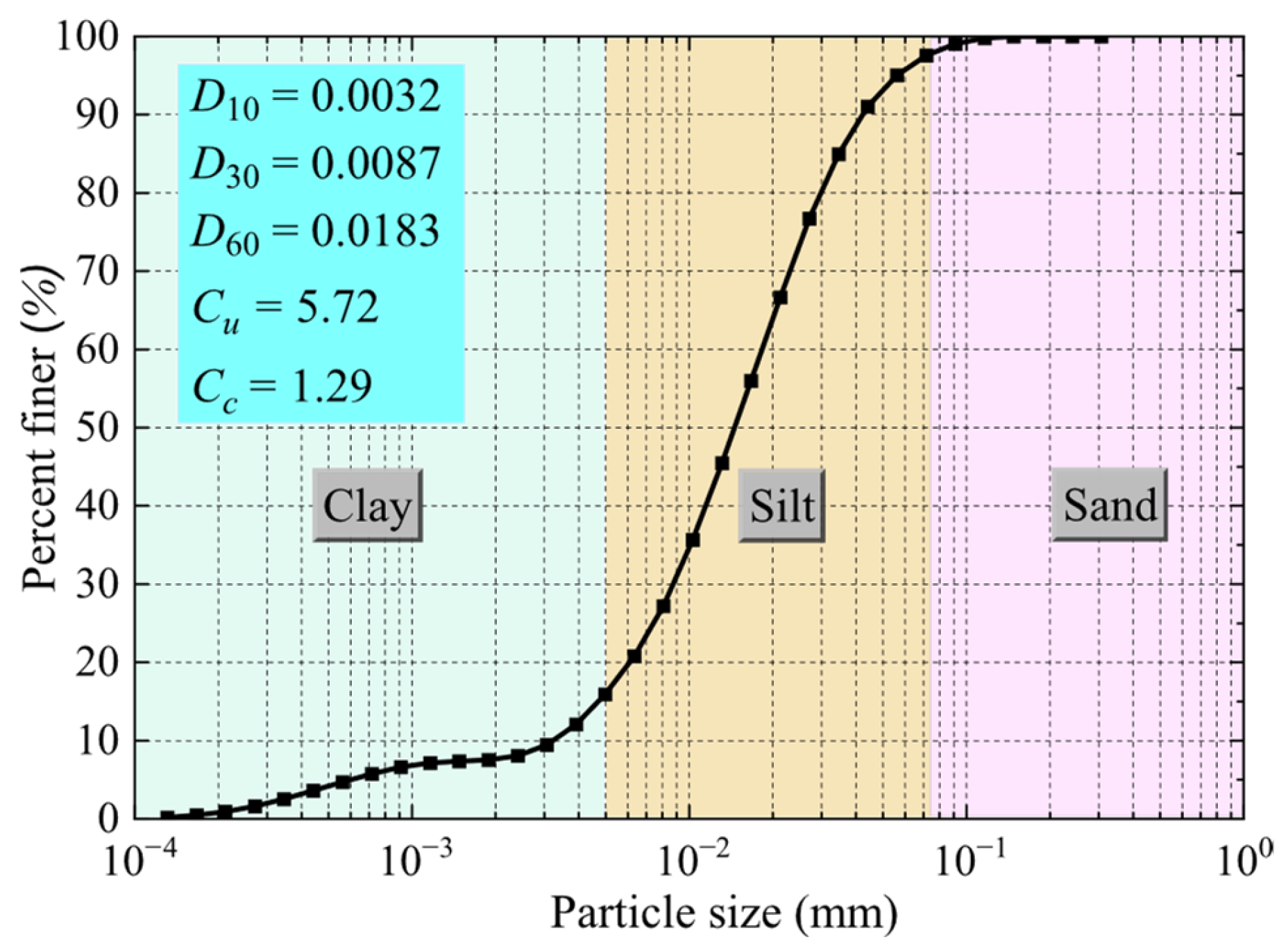
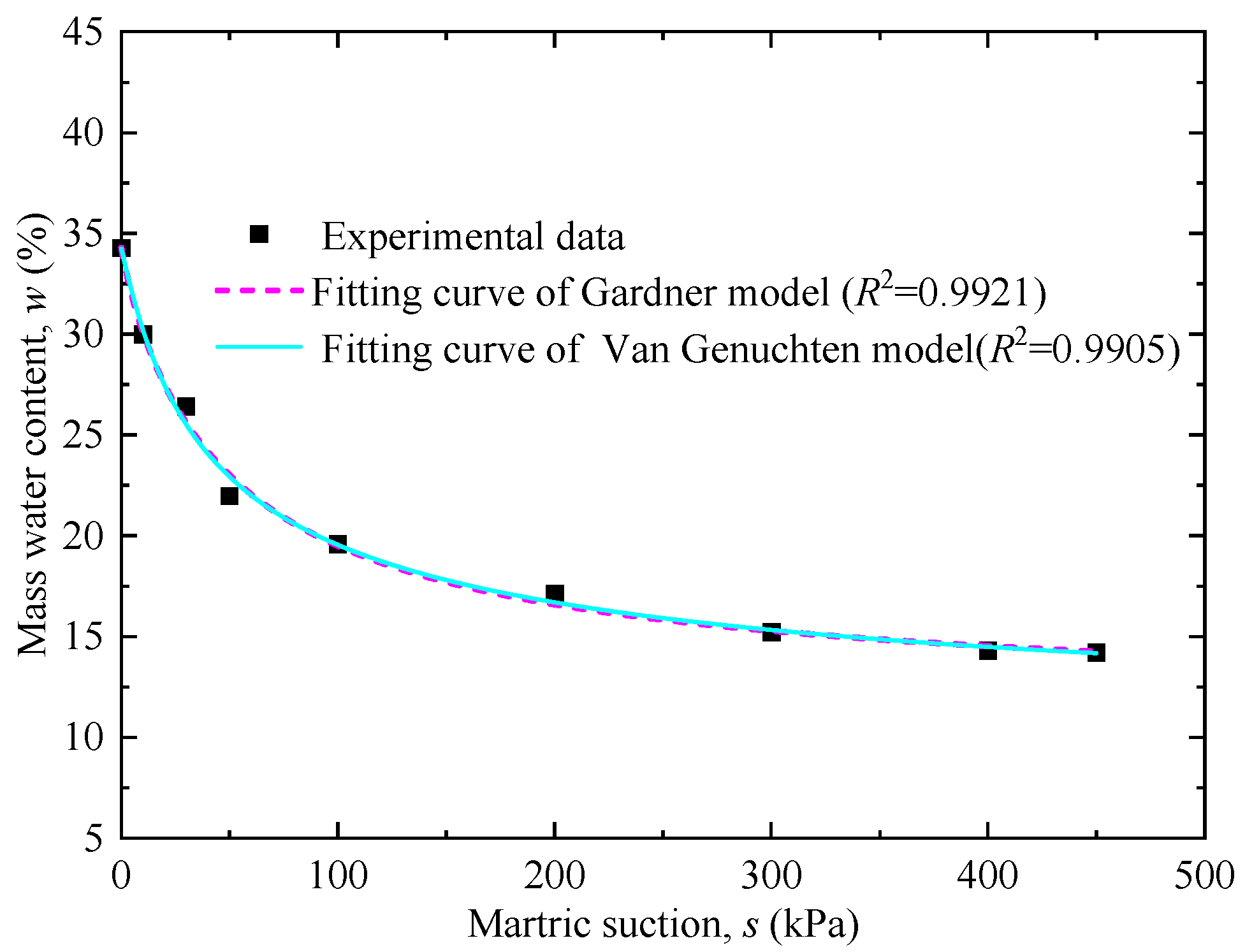
2.1. Sample Preparation
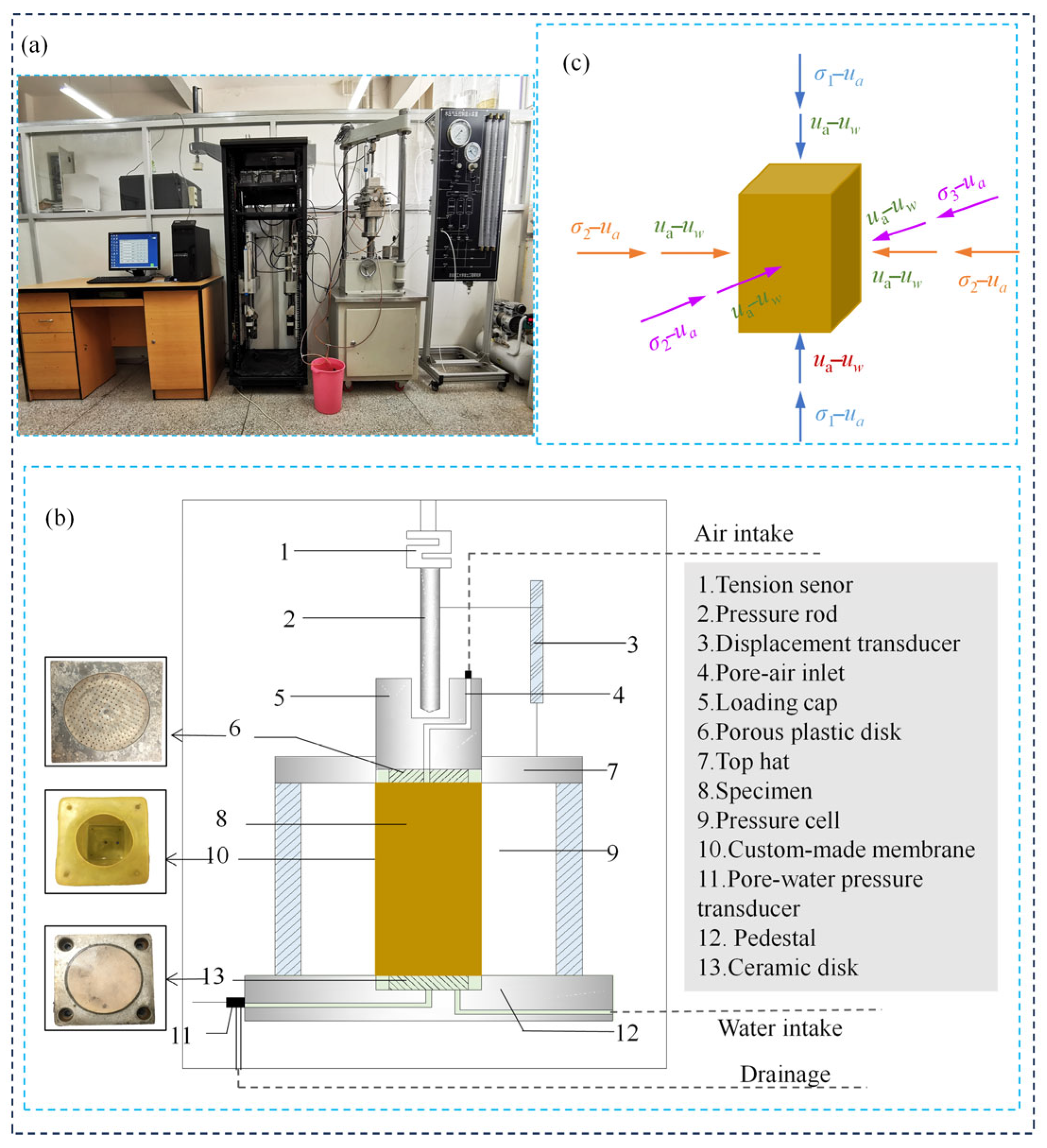
2.2. Test Equipment
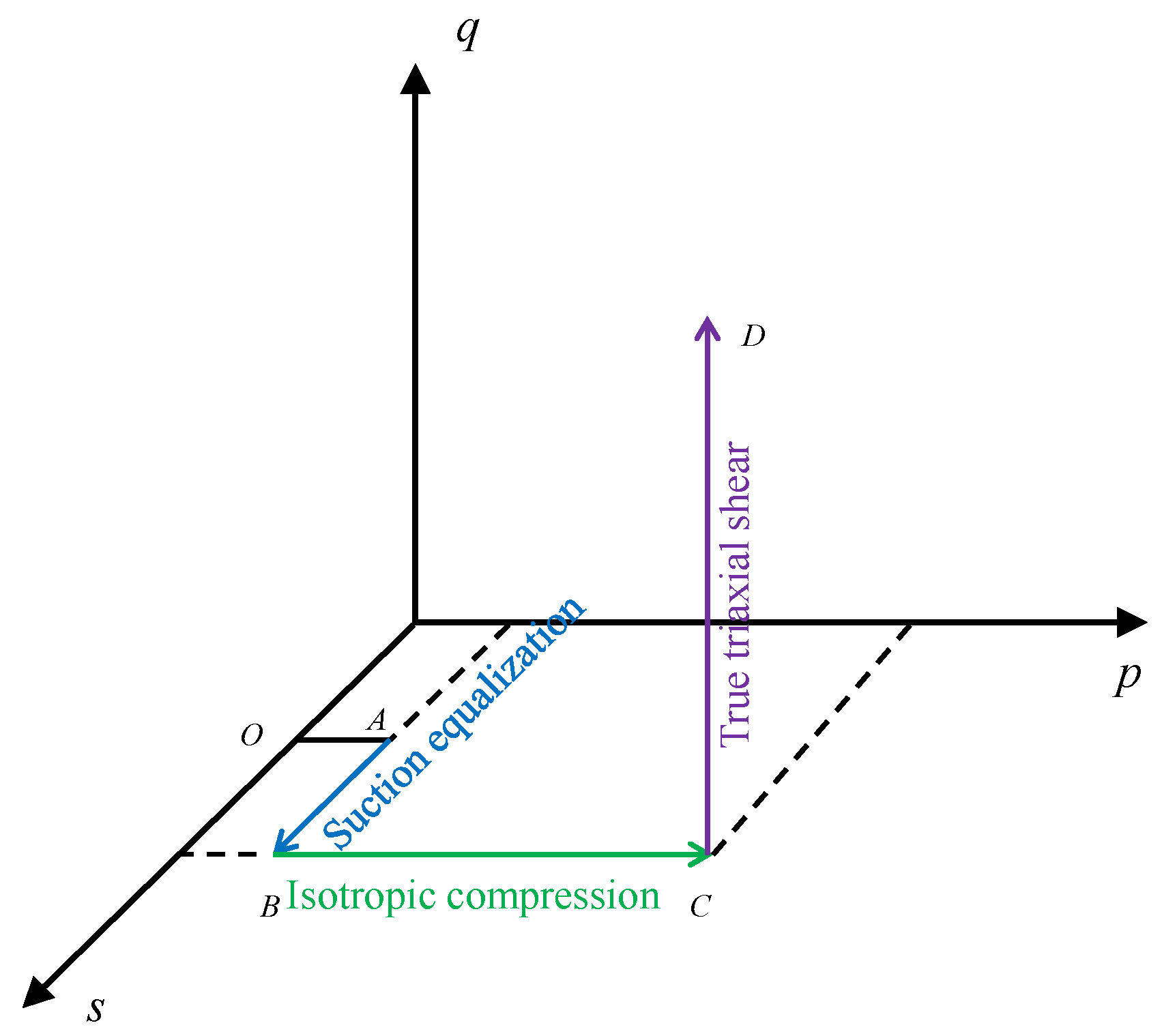
2.3. Test Scheme
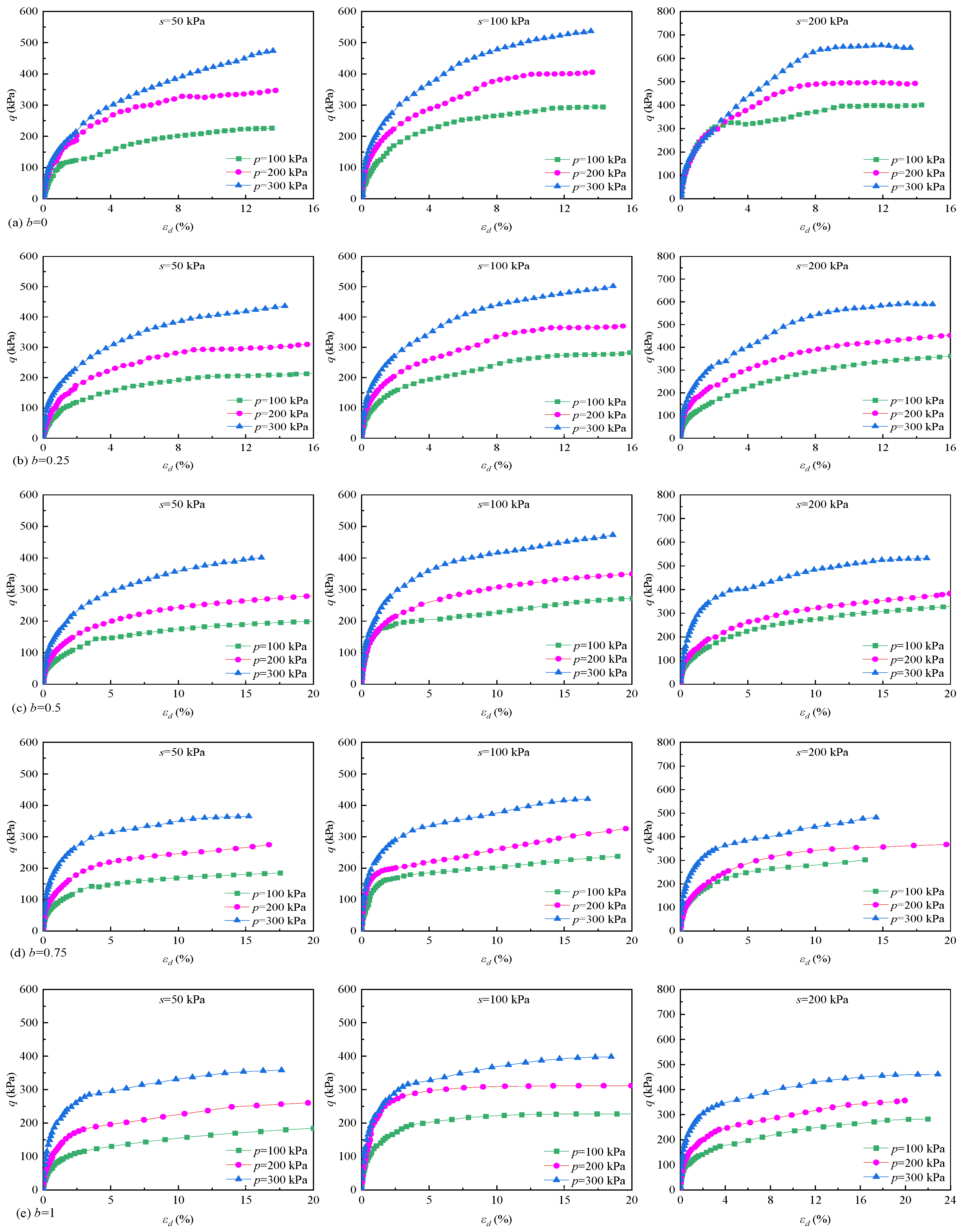
3. Experimental Results
3.1. Stress–Strain Relationship Curve
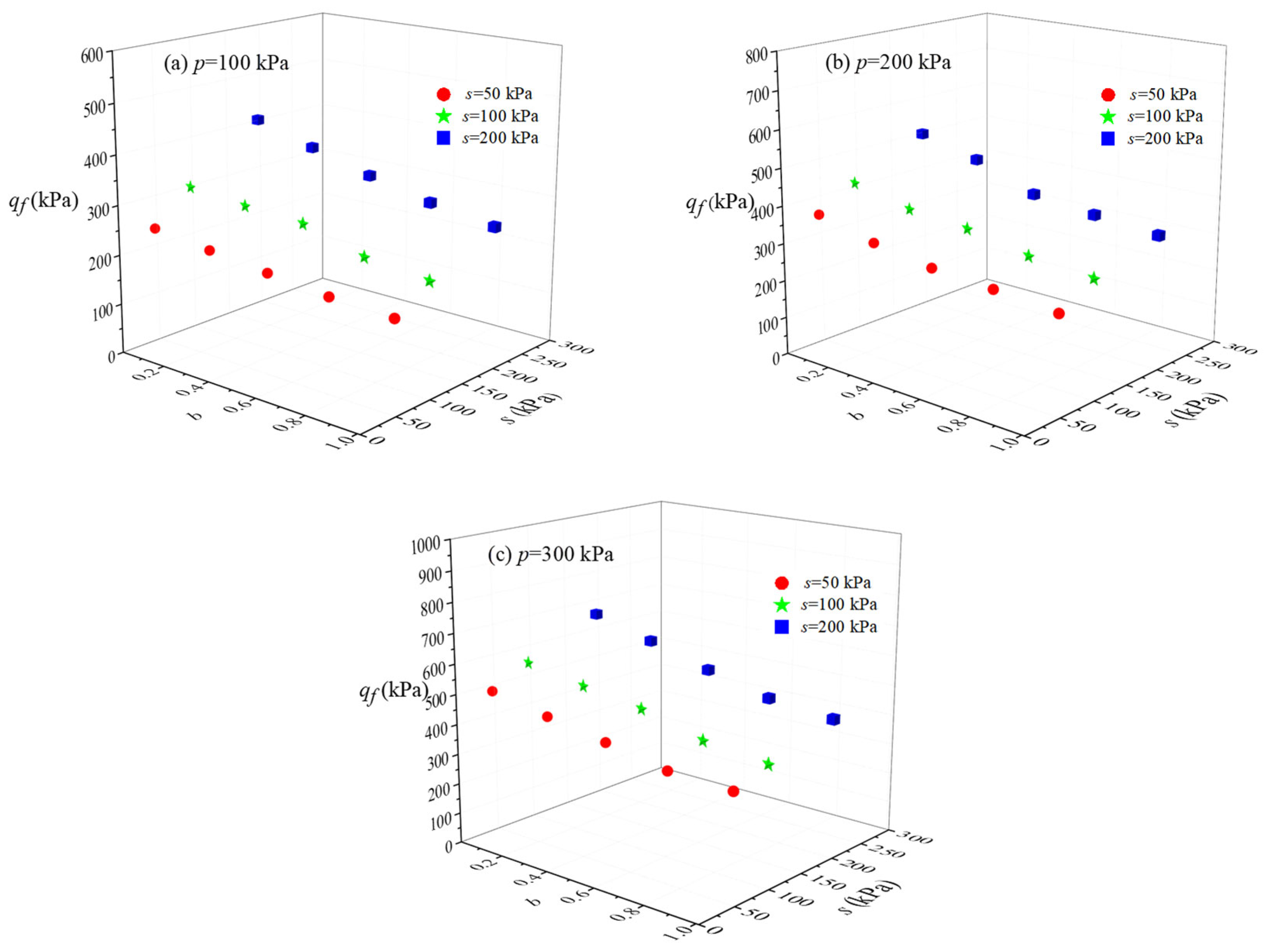
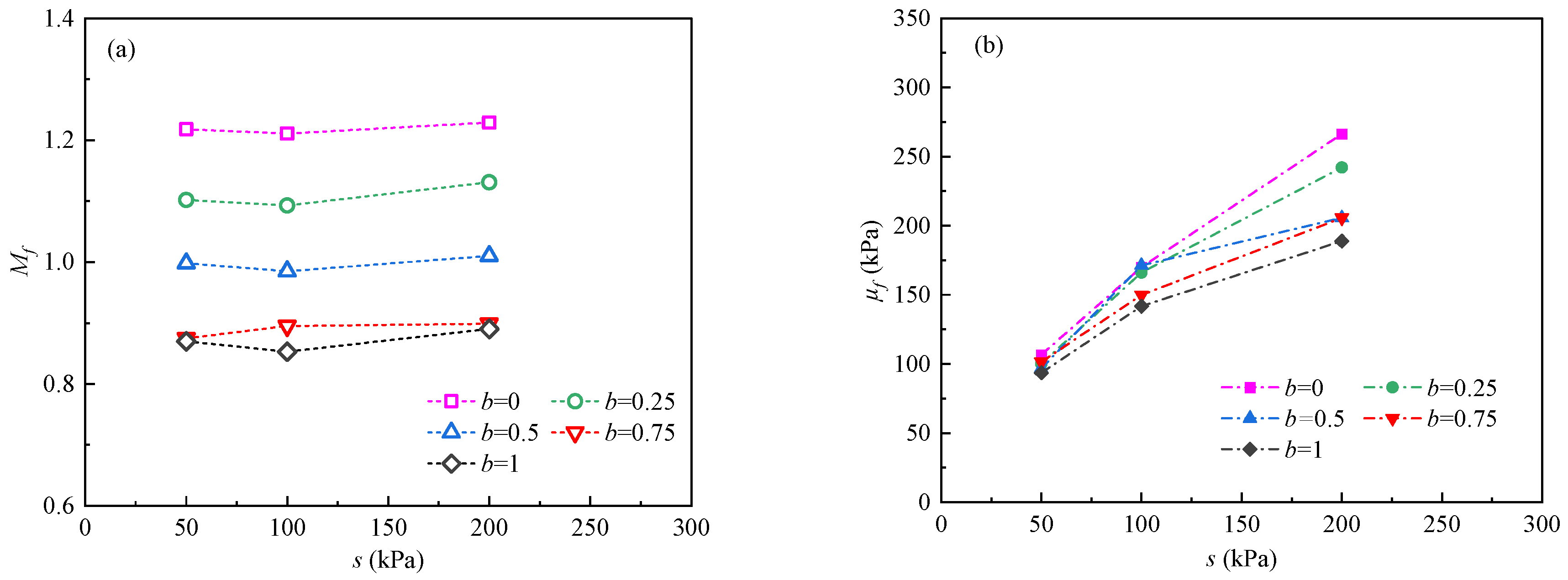
3.2. Failure Stress
4. Analysis and Discussion
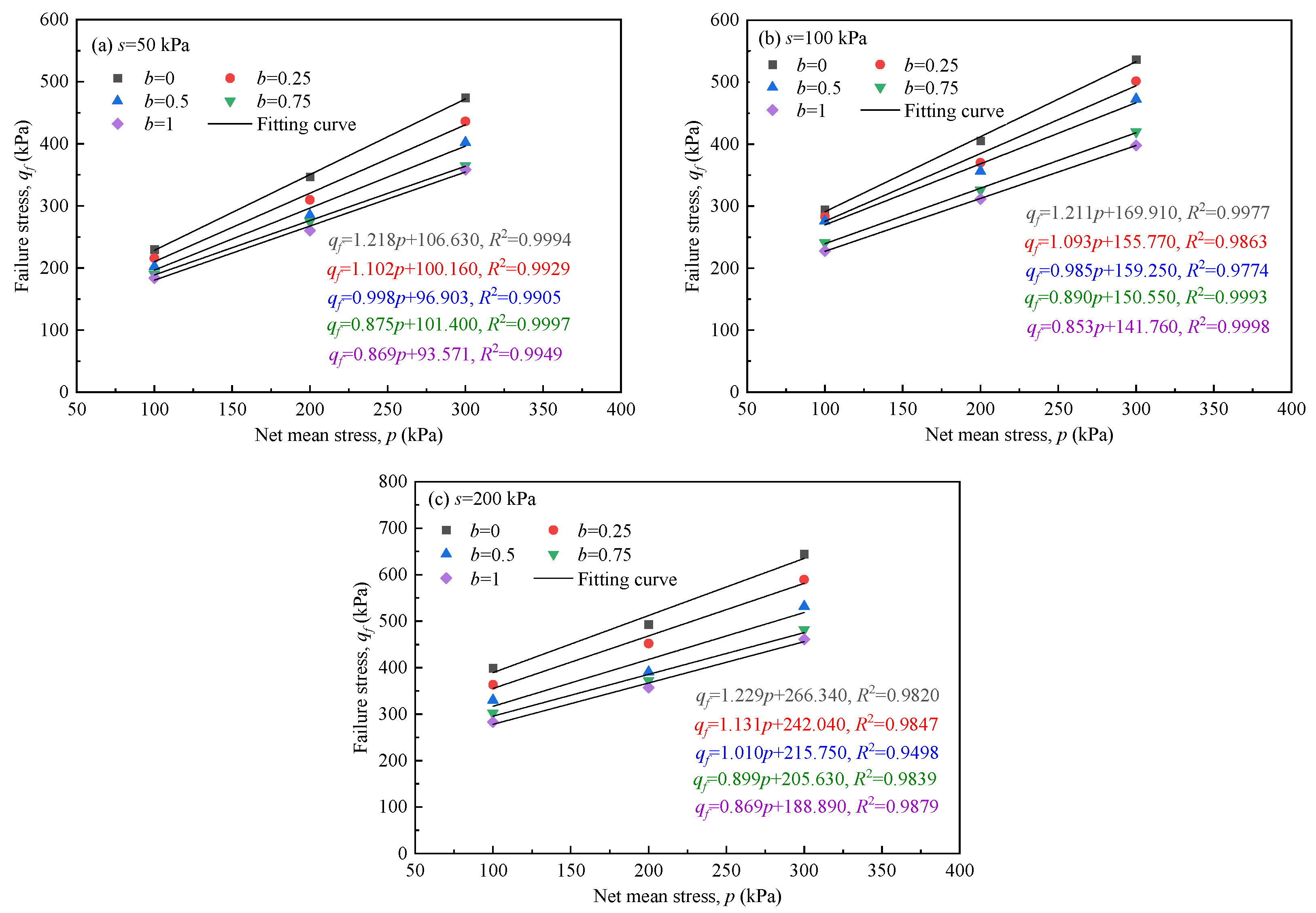
4.1. Strength Failure Line on the Meridian Plane
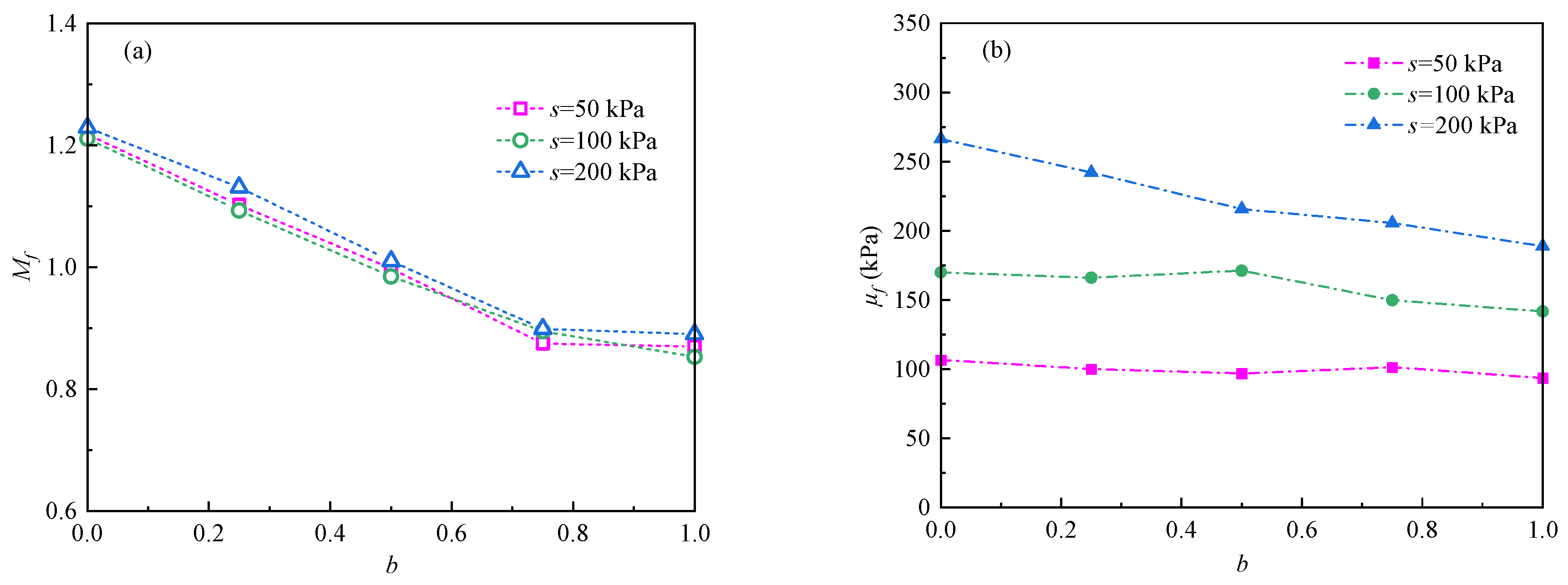
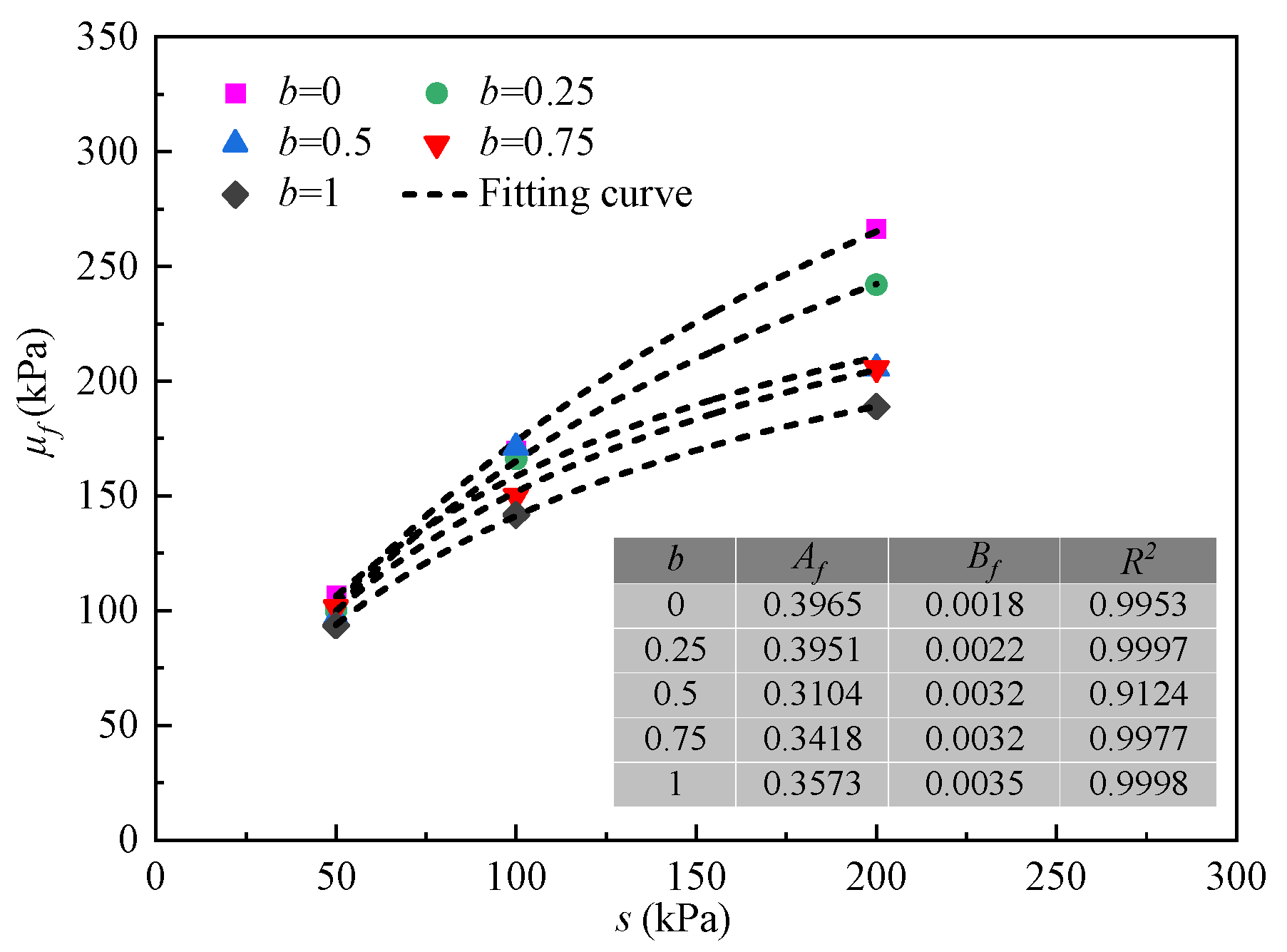
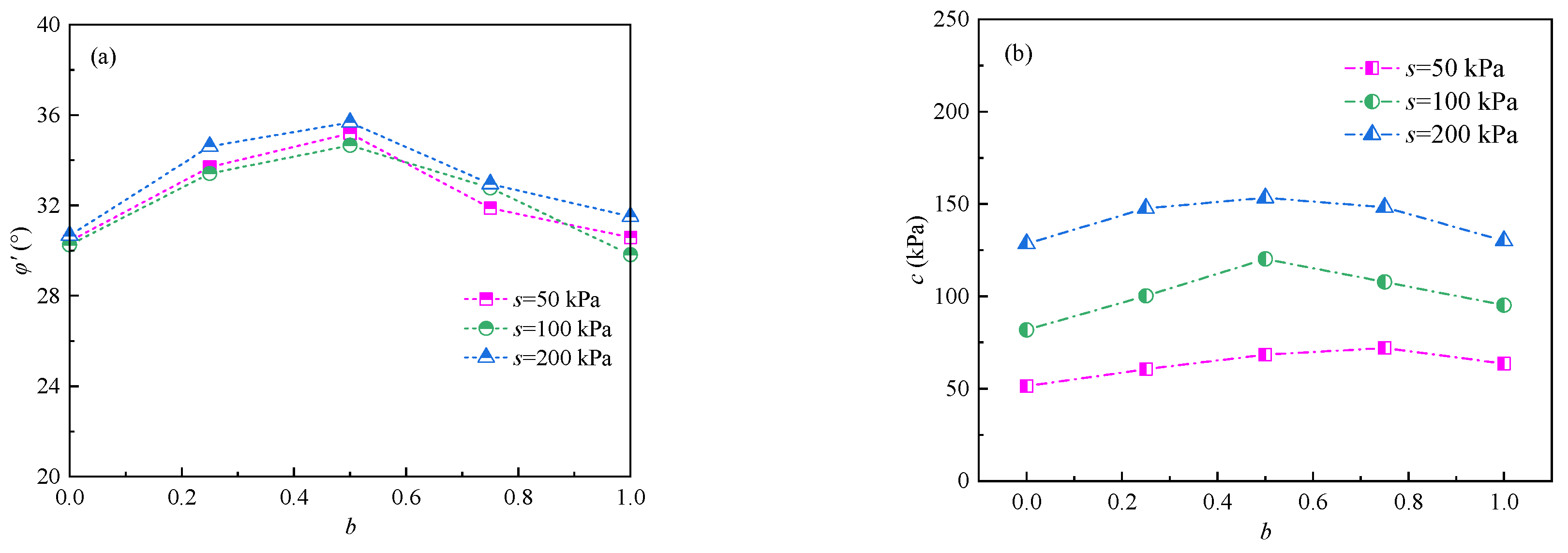
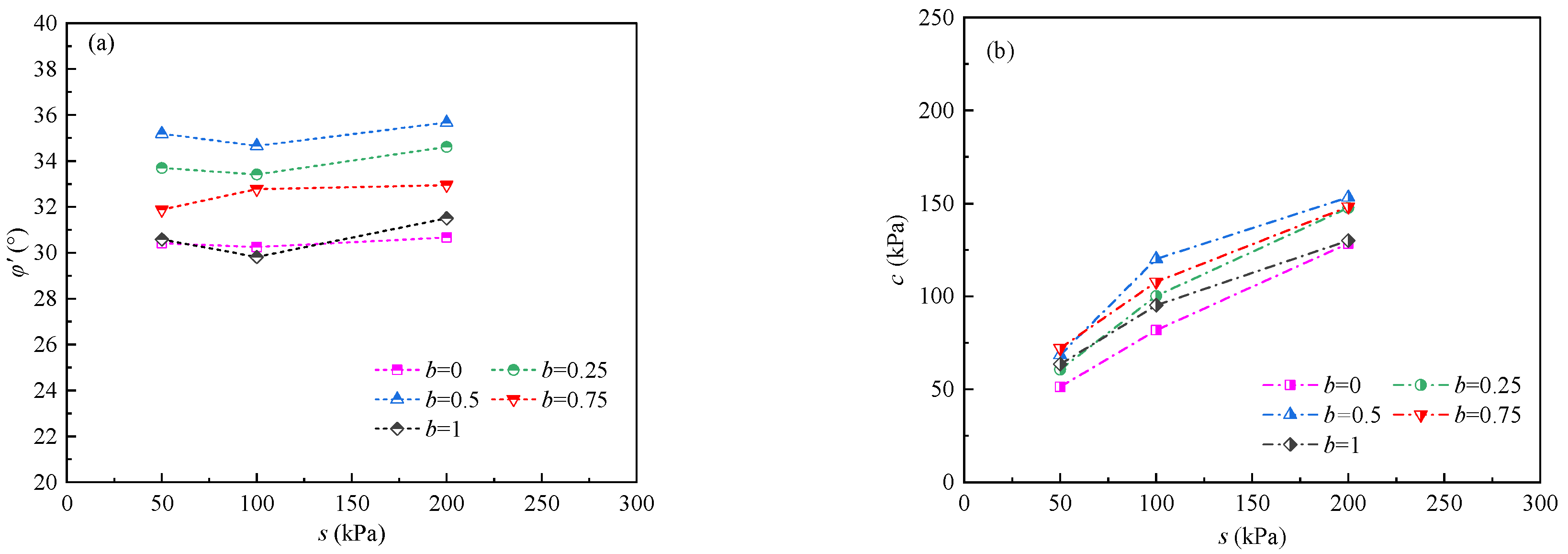
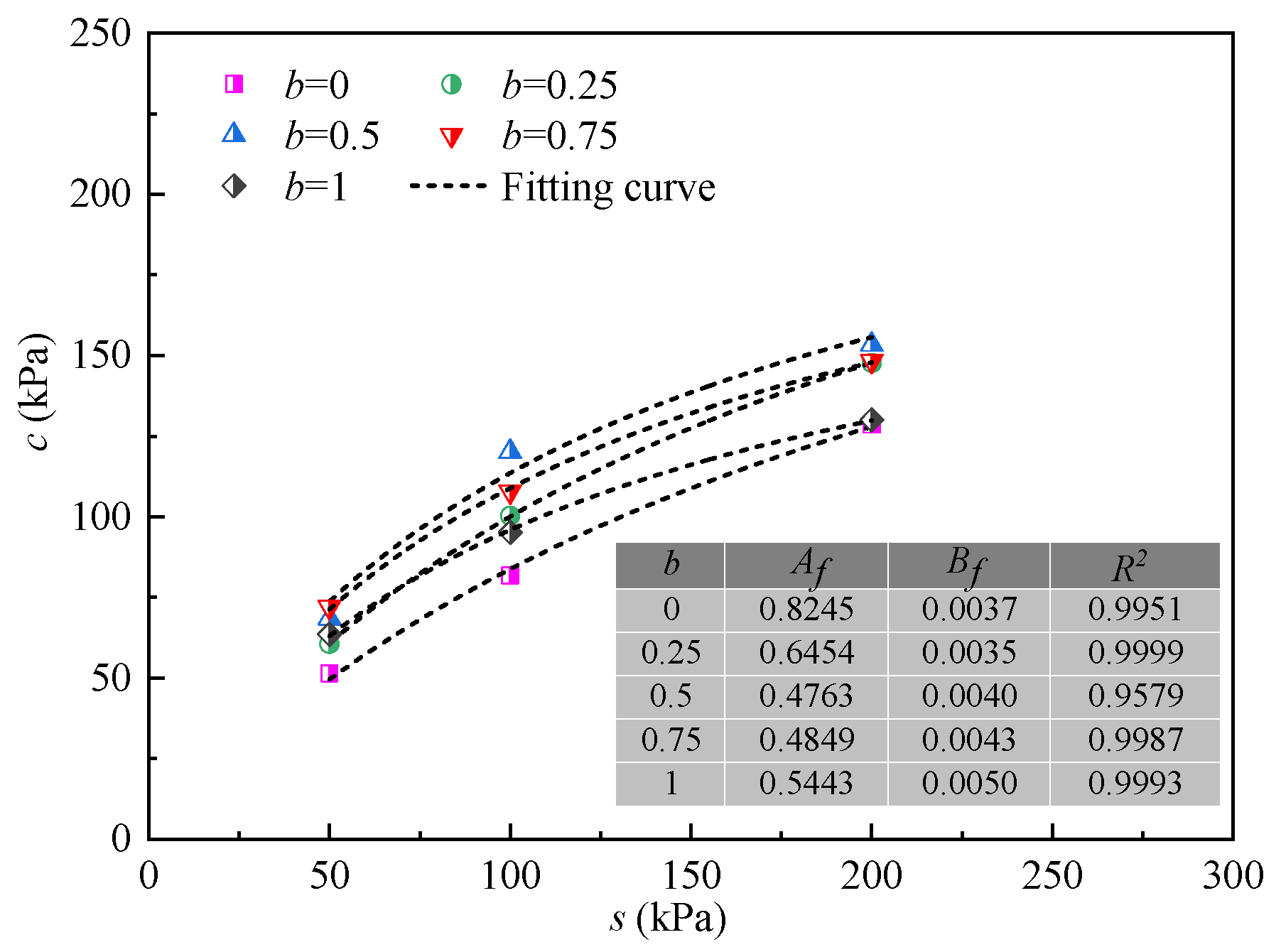
4.2. Strength Parameters
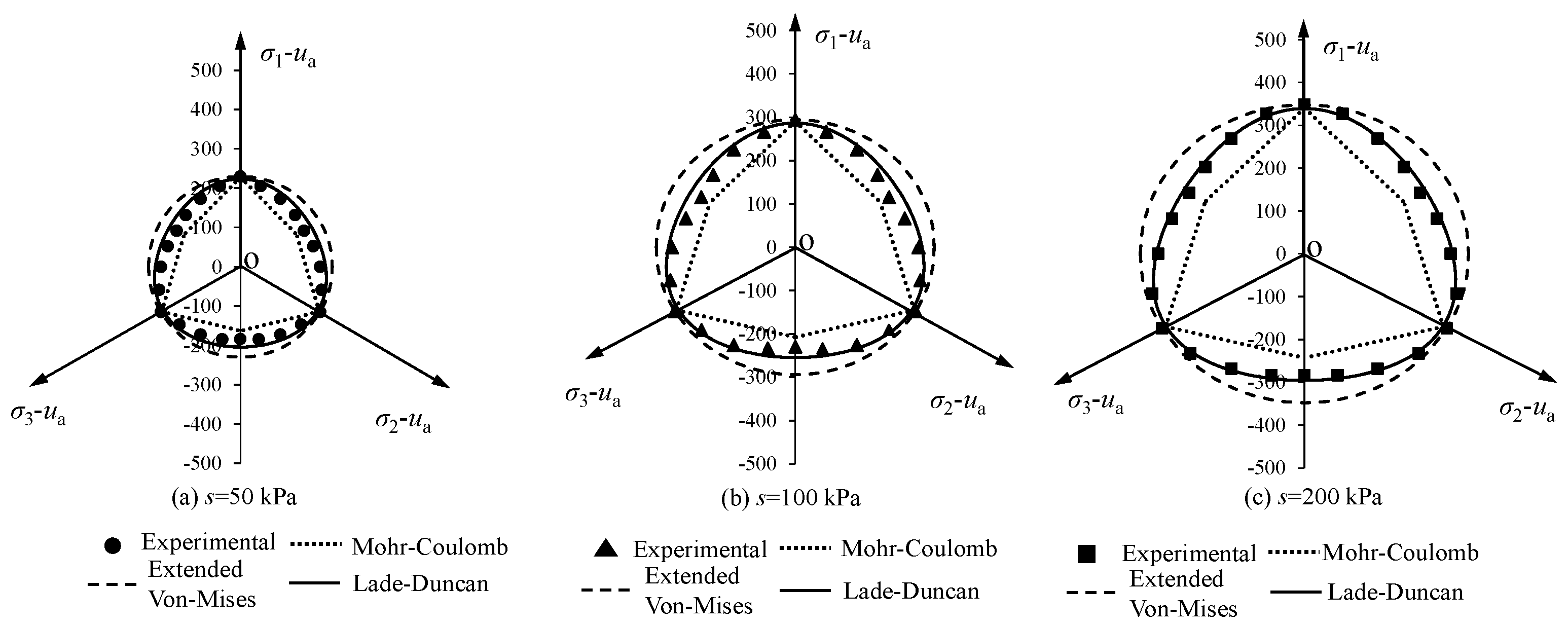
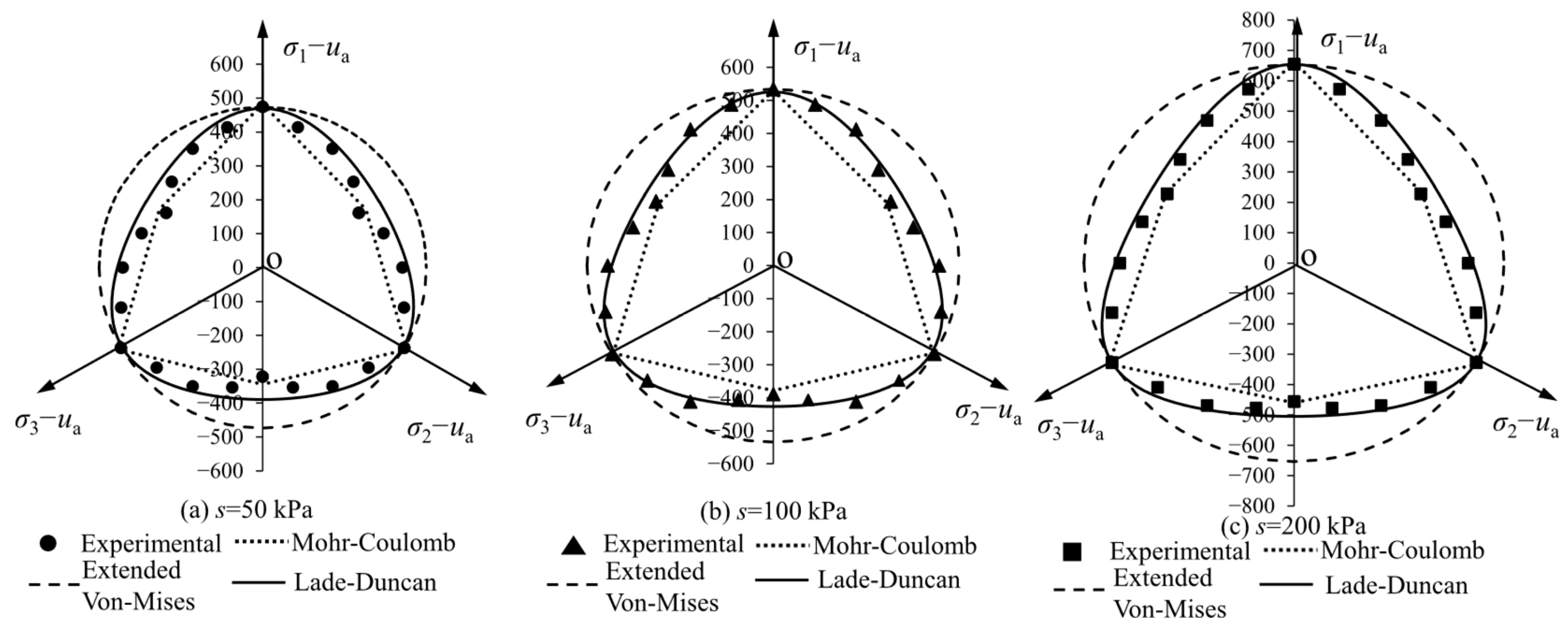
4.3. Applicability of the Strength Criteria
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Z.; Liu, F.; Ma, F.; Wang, M.; Bai, X.; Zheng, Y.; Yin, H.; Zhang, G. Collapsibility, composition, and microstructure of loess in China. Can. Geotech. J. 2015, 53, 673–686. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, L.; Li, Y.; Li, Z.; Zhao, Y. Mechanical, mineralogical, and microstructural characterization of collapsible loess cured by NaOH solution. Constr. Build. Mater. 2024, 421, 135678. [Google Scholar] [CrossRef]
- Li, P.; Vanapalli, S.; Li, T. Review of collapse triggering mechanism of collapsible soils due to wetting. J. Rock. Mech. Geotech. 2016, 8, 256–274. [Google Scholar] [CrossRef]
- Jiang, M.; Li, T.; Thornton, C.; Hu, H.; Affiliations, A. Wetting-induced collapse behavior of unsaturated and structural loess under biaxial tests using distinct element method. Int. J. Geomech. 2017, 17, 6016010. [Google Scholar] [CrossRef]
- Ge, M.; Pineda, J.A.; Sheng, D.; Burton, G.J.; Li, N. Microstructural effects on the wetting-induced collapse in compacted loess. Comput. Geotech. 2021, 138, 104359. [Google Scholar] [CrossRef]
- Gao, D.; Zhao, K.; Jin, S.; Xing, Y. Moistening deformation constitutive model for unsaturated loess. Int. J. Geomech. 2022, 22, 4022123. [Google Scholar] [CrossRef]
- Zhao, X.; Cui, Y.; Zhang, R.; Tian, G.; Satyanaga, A.; Zhai, Q. Experimental investigation of the collapsibility of loess subjected to water invasion. Bull. Eng. Geol. Environ. 2024, 83, 33. [Google Scholar] [CrossRef]
- Xie, B.; Zhang, W.; Sun, X.; Huang, Y.; Liu, L. Experimental study on the effects of freeze–thaw cycles on strength and microstructure of Xining region loess in China. Buildings 2022, 12, 795. [Google Scholar] [CrossRef]
- Jing, J.; Hou, J.; Sun, W.; Chen, G.; Ma, Y.; Ji, G. Study on influencing factors of unsaturated loess slope stability under dry-wet cycle conditions. J. Hydrol. 2022, 612, 128187. [Google Scholar] [CrossRef]
- Zhou, Y.F.; Tham, L.G.; Yan, W.M.; Dai, F.C.; Xu, L. Laboratory study on soil behavior in loess slope subjected to infiltration. Eng. Geol. 2014, 183, 31–38. [Google Scholar] [CrossRef]
- Tang, K.; Liu, D.; Xie, S.; Qiu, J.; Lai, J.; Liu, T.; Fang, Y. Analysis of loess water migration regularity and failure response of tunnel structure under rainfall environment. Bull. Eng. Geol. Environ. 2024, 83, 251. [Google Scholar] [CrossRef]
- Xie, X.; Qi, L.; Li, X. Deformation, strength and water variation characteristics of unsaturated compacted loess. Case Stud. Constr. Mater. 2022, 16, e01129. [Google Scholar] [CrossRef]
- Wang, J.J.; Liang, Y.; Zhang, H.P.; Wu, Y.; Lin, X. A loess landslide induced by excavation and rainfall. Landslides 2014, 11, 141–152. [Google Scholar] [CrossRef]
- Chang, Z.; Huang, F.; Huang, J.; Jiang, S.H.; Zhou, C.; Zhu, L. Experimental study of the failure mode and mechanism of loess fill slopes induced by rainfall. Eng. Geol. 2021, 280, 105941. [Google Scholar] [CrossRef]
- Fredlund, D.H.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; Wiley & Sons, Inc.: Hoboken, NJ, USA, 1993. [Google Scholar]
- Lu, N.; Likos, W.J. Unsaturated Soil Mechanics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Xie, Q.; Huang, Q.; Liu, Y.; Wang, Z.; Yu, D.; Peng, J. Strength behaviors of undisturbed Malan loess under rainfall leaching in Yan’an area, China. Bull. Eng. Geol. Environ. 2023, 82, 53. [Google Scholar] [CrossRef]
- Chertkov, V.Y. Modelling cracking stages of saturated soils as they dry and shrink. Eur. J. Soil Sci. 2002, 53, 105–118. [Google Scholar] [CrossRef]
- Futai, M.M.; Almeida, M.S.S.; Lacerda, W.A. Yield, strength, and critical state behavior of a tropical saturated soil. J. Geotech. Geoenviron. 2004, 130, 1169–1179. [Google Scholar] [CrossRef]
- Chang, D.; Yan, Y.; Liu, J.; Xu, A.; Feng, L.; Zhang, M. Micro-macroscopic mechanical behavior of frozen sand based on a large-scale direct shear test. Comput. Geotech. 2023, 159, 105484. [Google Scholar] [CrossRef]
- Leuther, F.; Schlueter, S. Impact of freeze–thaw cycles on soil structure and soil hydraulic properties. Soil 2021, 7, 179–191. [Google Scholar] [CrossRef]
- Kim, B.; Park, S.; Lohani, T.N.; Kato, S. Characterizing suction stress and shear strength for unsaturated geomaterials under various confining pressure conditions. Transp. Geotech. 2022, 34, 100747. [Google Scholar] [CrossRef]
- Houston, S.L.; Perez-Garcia, N.; Houston, W.N. Shear Strength and shear-induced volume change behavior of unsaturated soils from a triaxial test program. J. Geotech. Geoenviron. 2008, 134, 1619–1632. [Google Scholar] [CrossRef]
- Cai, G.Q.; Zhang, C.; Huang, Z.W.; Li, J.L.; Hou, J.L. Experimental study on influences of moisture content on shear strength of unsaturated loess. Chin. J. Geotech. Eng. 2020, 42 (Suppl. S2), 32–36. (In Chinese) [Google Scholar] [CrossRef]
- Xing, X.; Li, T.; Fu, Y. Determination of the related strength parameters of unsaturated loess with conventional triaxial test. Environ. Earth Sci. 2016, 75, 82. [Google Scholar] [CrossRef]
- Wen, B.P.; Yan, Y.J. Influence of structure on shear characteristics of the unsaturated loess in Lanzhou, China. Eng. Geol. 2014, 168, 46–58. [Google Scholar] [CrossRef]
- Yates, K.; Russell, A.R. The unsaturated characteristics of natural loess in slopes, New Zealand. Géotechnique 2023, 73, 871–884. [Google Scholar] [CrossRef]
- Gao, B.; Su, L. Triaxial mechanical testing of undisturbed unsaturated loess. Soil Mech. Found. Eng. 2020, 57, 57–64. [Google Scholar] [CrossRef]
- Chen, C.L.; Zhang, D.F.; Dong, Y.Z.; Chen, H.; Yu, D.B.; Xue, J.X. Suction and mechanical behaviours of unsaturated intact loess from constant water content triaxial tests. Chin. J. Geotech. Eng. 2014, 36, 1195–1202. (In Chinese) [Google Scholar] [CrossRef]
- Ng, C.W.W.; Sadeghi, H.; Jafarzadeh, F. Compression and shear strength characteristics of compacted loess at high suctions. Can. Geotech. J. 2017, 54, 690–699. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Mu, Q.Y.; Zhou, C. Effects of soil structure on the shear behaviour of an unsaturated loess at different suctions and temperatures. Can. Geotech. J. 2017, 54, 270–279. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, D.; Wang, N.; Gu, T. Mechanisms of wetting-induced loess slope failures. Landslides 2019, 16, 937–953. [Google Scholar] [CrossRef]
- Zhang, J.W.; Mu, Q.Y.; Gang, A.; Liu, F.L.; Cao, J. Shear behavior of unsaturated intact and compacted loess: A comparison study. Environ. Earth. Sci. 2020, 79, 79. [Google Scholar] [CrossRef]
- Wei, Y.Z.; Yao, Z.H.; Chong, X.L.; Zhang, J.H.; Zhang, J. Microstructure of unsaturated loess and its influence on strength characteristics. Sci. Rep. 2022, 12, 1502. [Google Scholar] [CrossRef] [PubMed]
- Gao, D.H.; Chen, Z.H.; Guo, N.; Zhu, Y.P.; Hu, S.X.; Yao, Z.H. The influence of dry density and matric suction on the deformation and the strength characteristics of the remolded unsaturated loess soils. Yanshilixue Yu Gongcheng Xuebao/Chin. J. Rock Mech. Eng. 2017, 36, 736–744. (In Chinese) [Google Scholar] [CrossRef]
- Macari, E.J.; Hoyos, L.R. Mechanical behavior of an unsaturated soil under multi-axial stress states. Geotech. Test. J. 2001, 24, 14–22. [Google Scholar] [CrossRef]
- Hoyos, L.R.; Pérez-Ruiz, D.D.; Puppala, A.J. Refined true triaxial apparatus for testing unsaturated soils under suction-controlled stress paths. Int. J. Geomech. 2012, 12, 281–291. [Google Scholar] [CrossRef]
- Shao, S.; Shao, S.; Wang, J. True triaxial mechanical properties of unsaturated loess in foundation pit engineering. Bull. Eng. Geol. Environ. 2021, 80, 4751–4772. [Google Scholar] [CrossRef]
- Fang, J.; Feng, Y.; Li, Z. Compression and shear strength characteristics of unsaturated intact loess in true triaxial tests. Geotech. Test. J. 2020, 43, 1436–1462. [Google Scholar] [CrossRef]
- Zheng, F.; Shao, S.; Wang, J.; Shao, S. Experimental study on the mechanical behaviour of natural loess based on suction-controlled true triaxial tests. KSCE J. Civ. Eng. 2020, 24, 2304–2321. [Google Scholar] [CrossRef]
- Shao, S.; Wang, Q.; Luo, A.; Shao, S. True triaxial apparatus with rigid-flexible-flexible boundary and remolded loess testing. J. Test. Eval. 2017, 45, 808–817. [Google Scholar] [CrossRef]
- Zheng, F.; Shao, S.; Wang, S. Effect of freeze-thaw cycles on the strength behaviour of recompacted loess in true triaxial tests. Cold Reg. Sci. Technol. 2001, 181, 103172. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, C.; Fan, T.; Liu, J.; Ding, X.; Ma, L.; Wang, L.; Yan, R. Improvement and validation of a newly developed plane strain apparatus based on true triaxial testing. J. Test. Eval. 2023, 51, 4083–4101. [Google Scholar] [CrossRef]
- Vilar, O.M. A simplified procedure to estimate the shear strength envelope of unsaturated soils. Can. Geotech. J. 2006, 43, 1088–1095. [Google Scholar] [CrossRef]
- Niu, G.; Kong, L.; Shao, L.; Wang, H.; Wang, Z. Investigation into the shear strength of a weakly expansive soil over a wide suction range. Acta Geotech. 2024, 19, 3059–3073. [Google Scholar] [CrossRef]
- Banerjee, A.; Puppala, A.J.; Puppala, L.R. Suction-controlled multistage triaxial testing on clayey silty soil. Eng. Geol. 2020, 265, 105409. [Google Scholar] [CrossRef]
- Hoyos, L.R.; Pérez-Ruiz, D.D.; Puppala, A.J. Modeling unsaturated soil response under suction-controlled true triaxial stress paths. Int. J. Geomech. 2012, 12, 292–308. [Google Scholar] [CrossRef]
- Matsuoka, H.; Sun, D.; Kogane, A.; Fukuzawa, N.; Ichihara, W. Stress–strain behaviour of unsaturated soil in true triaxial tests. Can. Geotech. J. 2002, 39, 608–619. [Google Scholar] [CrossRef]


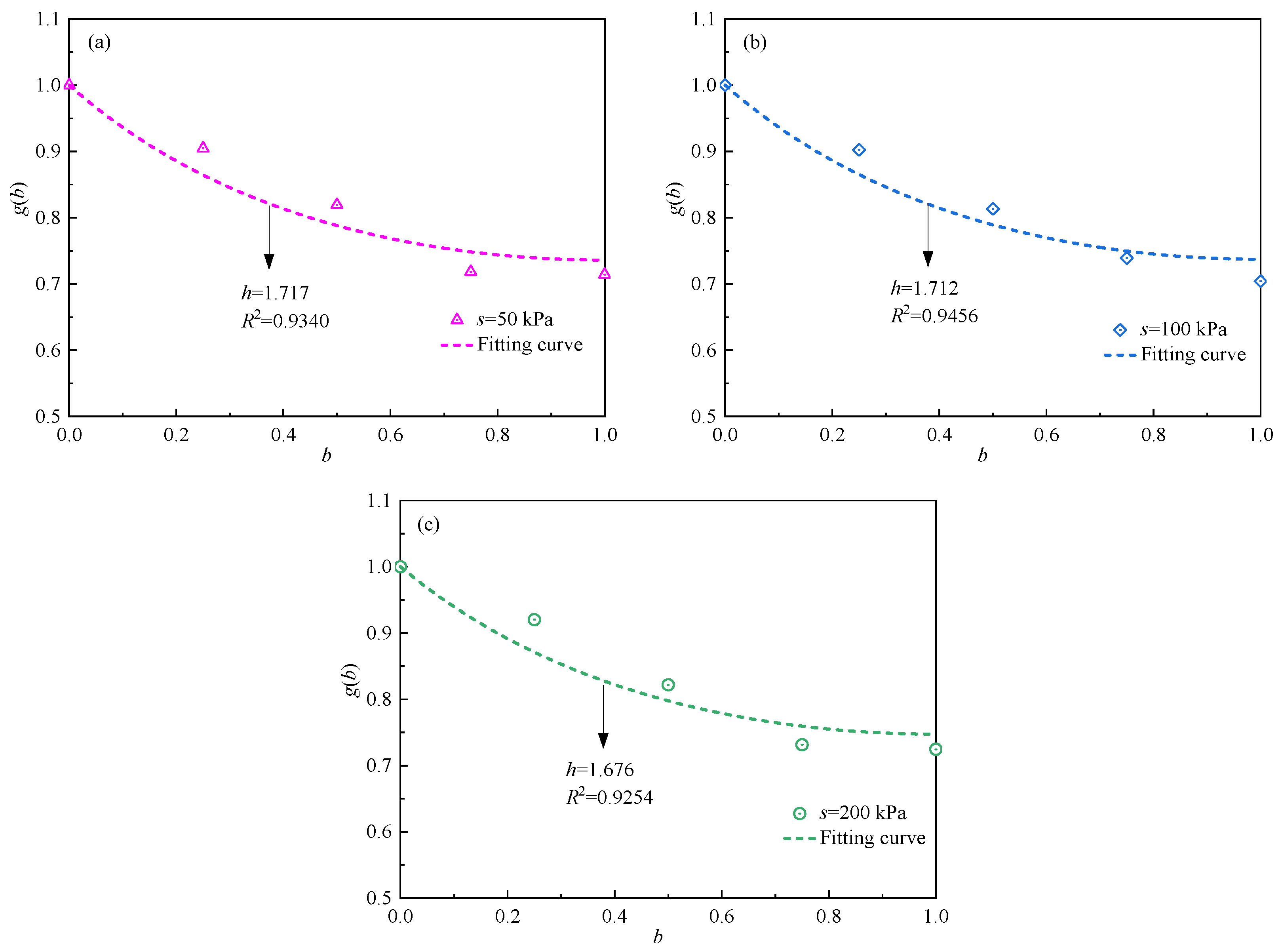


| Parameter | Value | Unit |
|---|---|---|
| Specific gravity | 2.70 | - |
| Liquid limit | 34.2 | % |
| Plastic limit | 18.6 | % |
| Plastic index | 15.6 | - |
| Dry density | 1.40 | g/cm3 |
| Initial pore ratio | 0.93 | - |
| Pore Air Pressure, ua (kPa) | Pore Water Pressure, uw (kPa) | Matric Suction, s (kPa) | Net Mean Stress, p (kPa) | Middle Principal Stress Coefficient, b | Number of Specimens |
|---|---|---|---|---|---|
| 50 | 0 | 50 | 100/200/300 | 0/0.25/0.5/0.75/1 | 15 |
| 100 | 0 | 100 | 100/200/300 | 0/0.25/0.5/0.75/1 | 15 |
| 200 | 0 | 200 | 100/200/300 | 0/0.25/0.5/0.75/1 | 15 |
| Item | Response Results of Different Factors | ||
|---|---|---|---|
| p | s | b | |
| q~εd | minimal impact on the morphology of curve | minimal impact on the morphology of curve | morphology of curve significant changes |
| q | p increases, q increases | s increases, q increases | b increases, q decreases |
| qf | p increases, qf increases | s increases, qf increases | b increases, qf decreases |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, F.; Song, Z.; Zhang, Y.; You, Z. Strength Characteristics of Unsaturated Compacted Loess Under Complex Stress Paths. Buildings 2025, 15, 4287. https://doi.org/10.3390/buildings15234287
Zheng F, Song Z, Zhang Y, You Z. Strength Characteristics of Unsaturated Compacted Loess Under Complex Stress Paths. Buildings. 2025; 15(23):4287. https://doi.org/10.3390/buildings15234287
Chicago/Turabian StyleZheng, Fang, Zhanping Song, Yuwei Zhang, and Zhilang You. 2025. "Strength Characteristics of Unsaturated Compacted Loess Under Complex Stress Paths" Buildings 15, no. 23: 4287. https://doi.org/10.3390/buildings15234287
APA StyleZheng, F., Song, Z., Zhang, Y., & You, Z. (2025). Strength Characteristics of Unsaturated Compacted Loess Under Complex Stress Paths. Buildings, 15(23), 4287. https://doi.org/10.3390/buildings15234287






