Finite Element Analysis and Parametric Study on the Push-Out Performance of Shear Connectors in Long-Span Composite Bridges
Abstract
1. Introduction
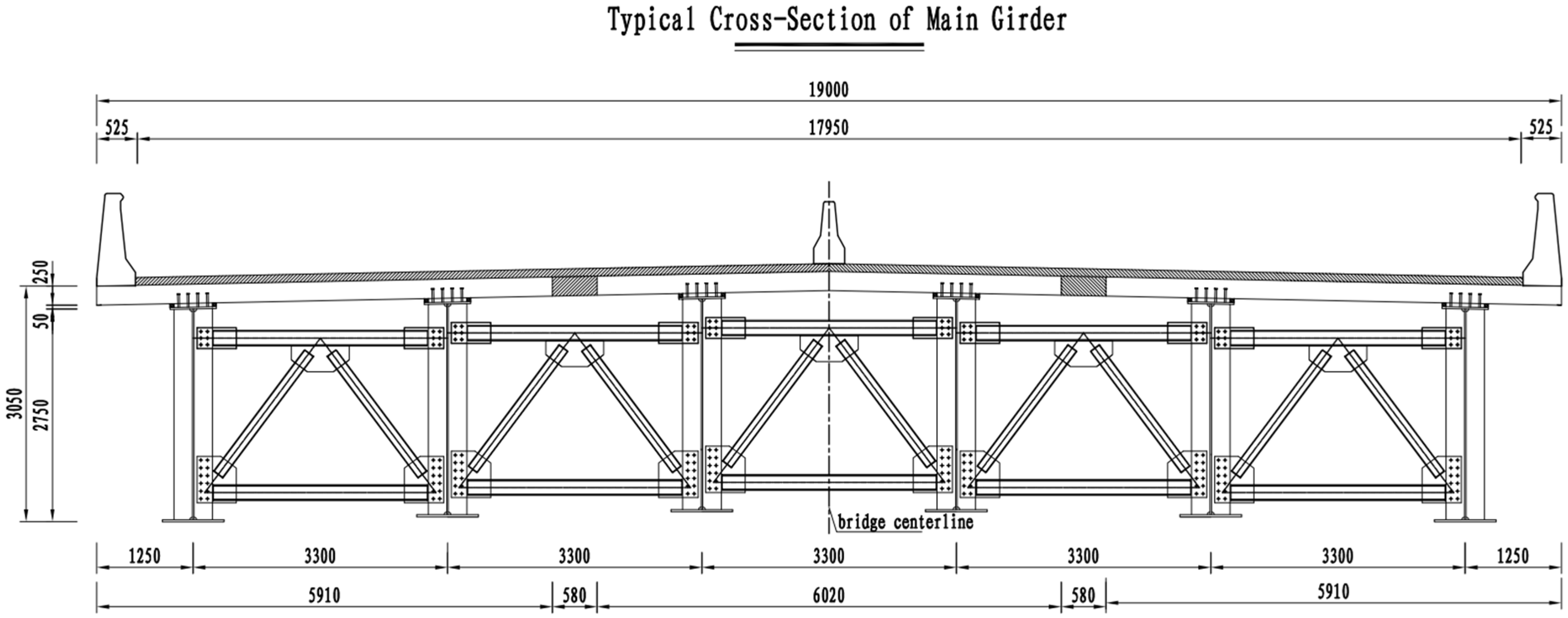
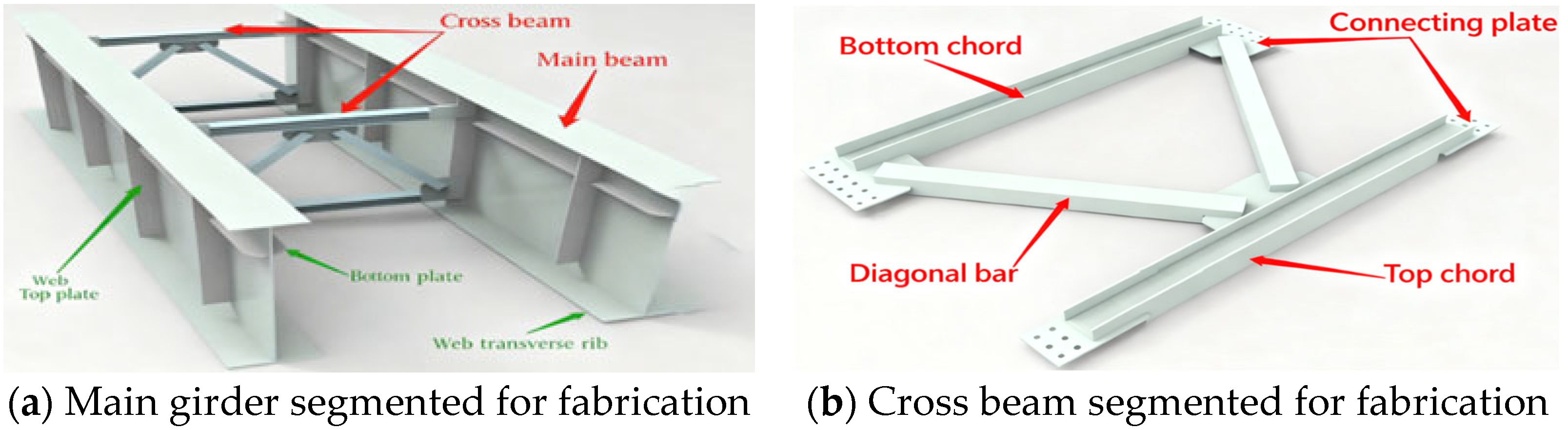
2. Project Overview
3. Numerical Model Development
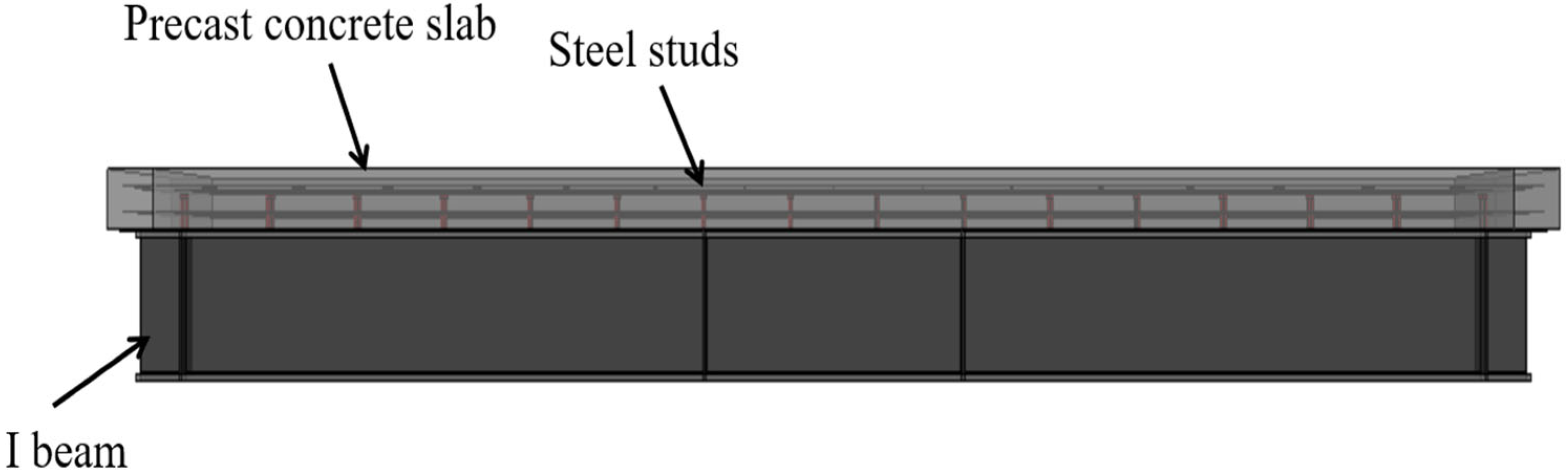
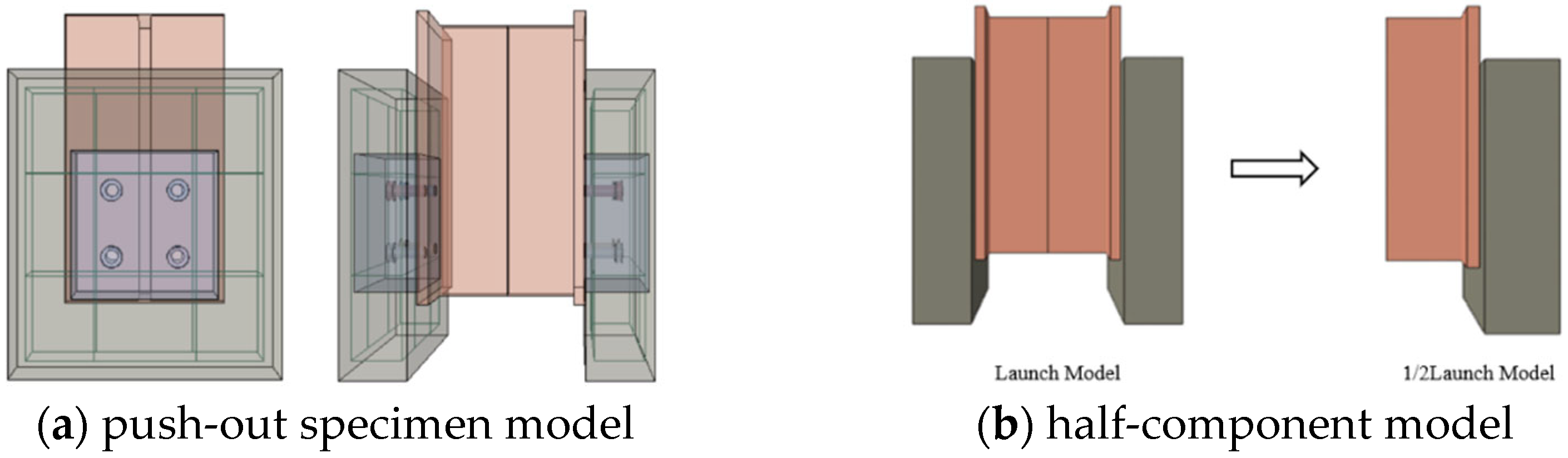
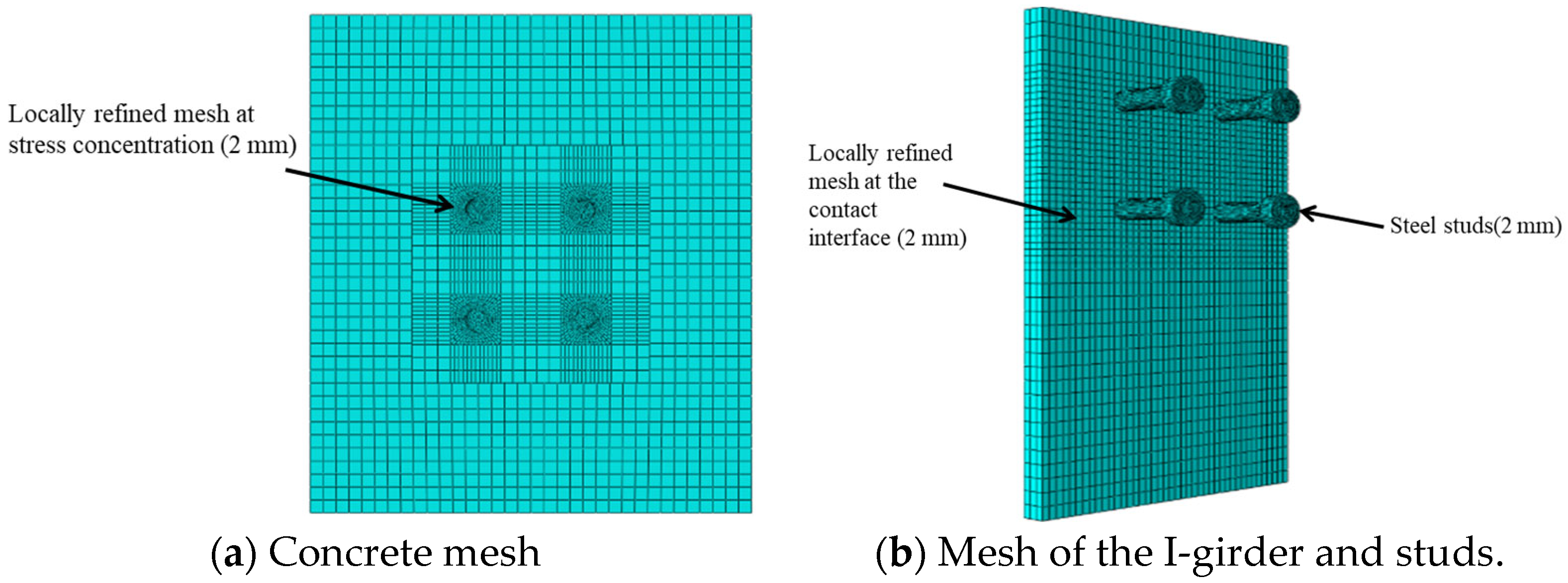
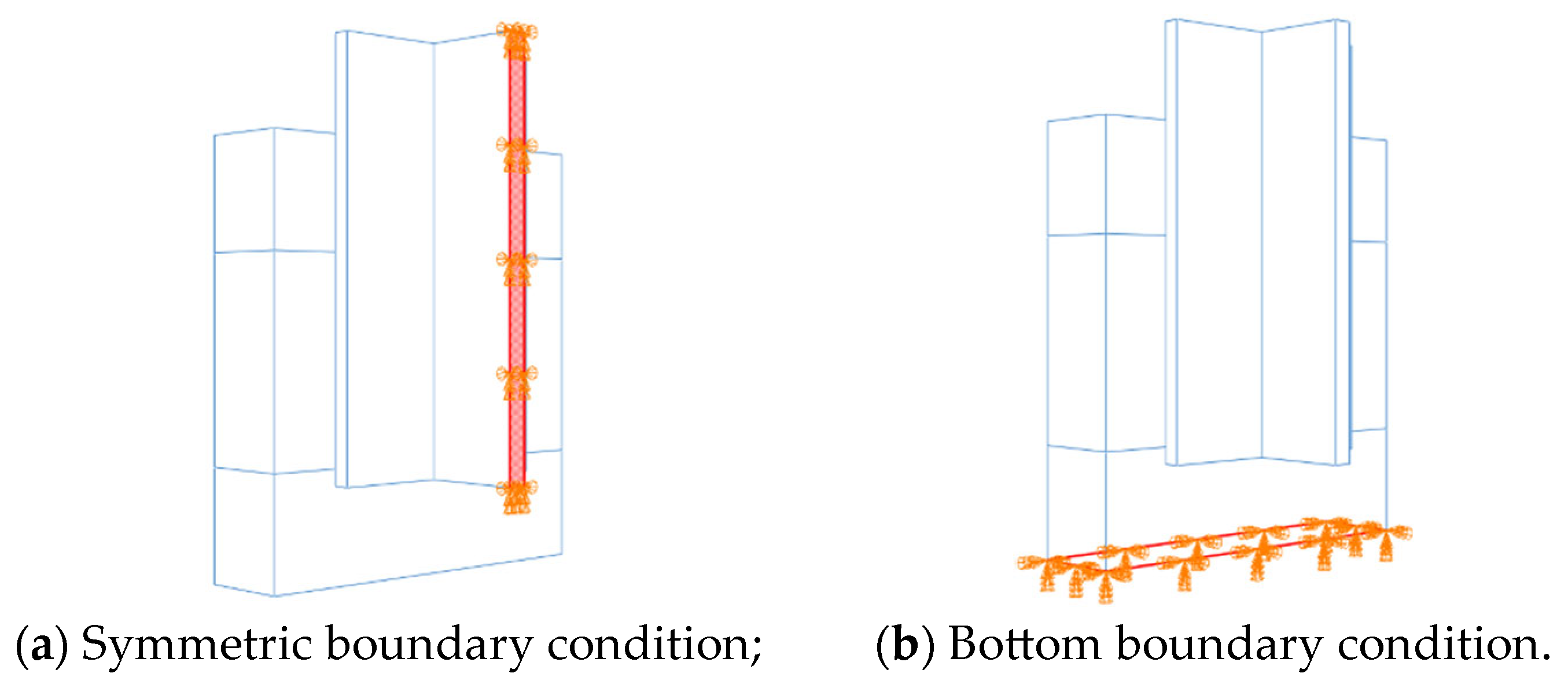
3.1. Finite Element Model
3.2. Material Constitutive Models
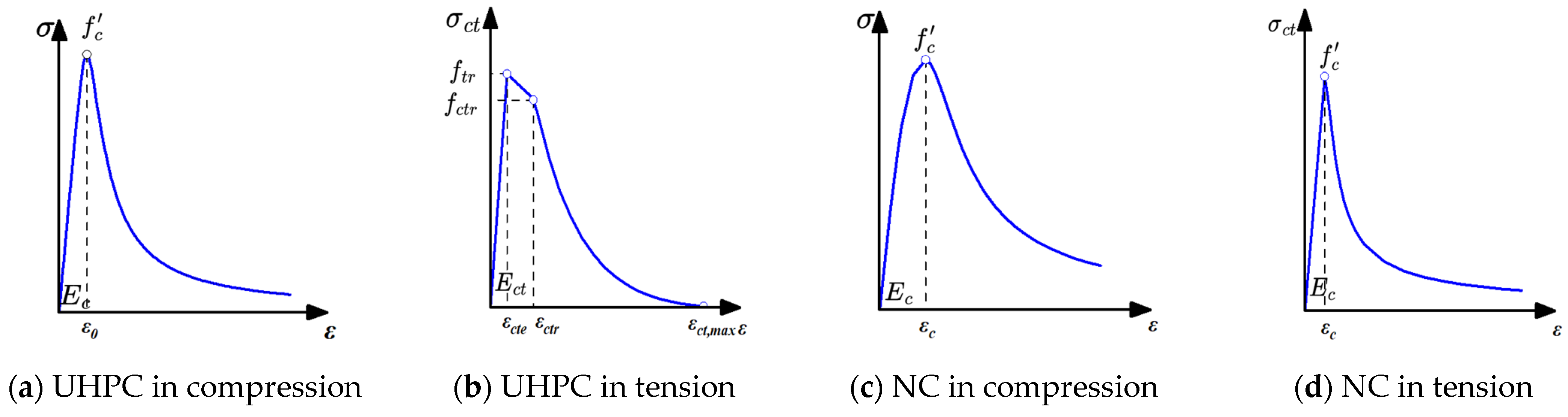
3.2.1. Constitutive Model for Concrete
Compressive Constitutive Relationship of UHPC
Tensile Constitutive Relationship of UHPC
Compressive and Tensile Constitutive Relationships of Normal Concrete
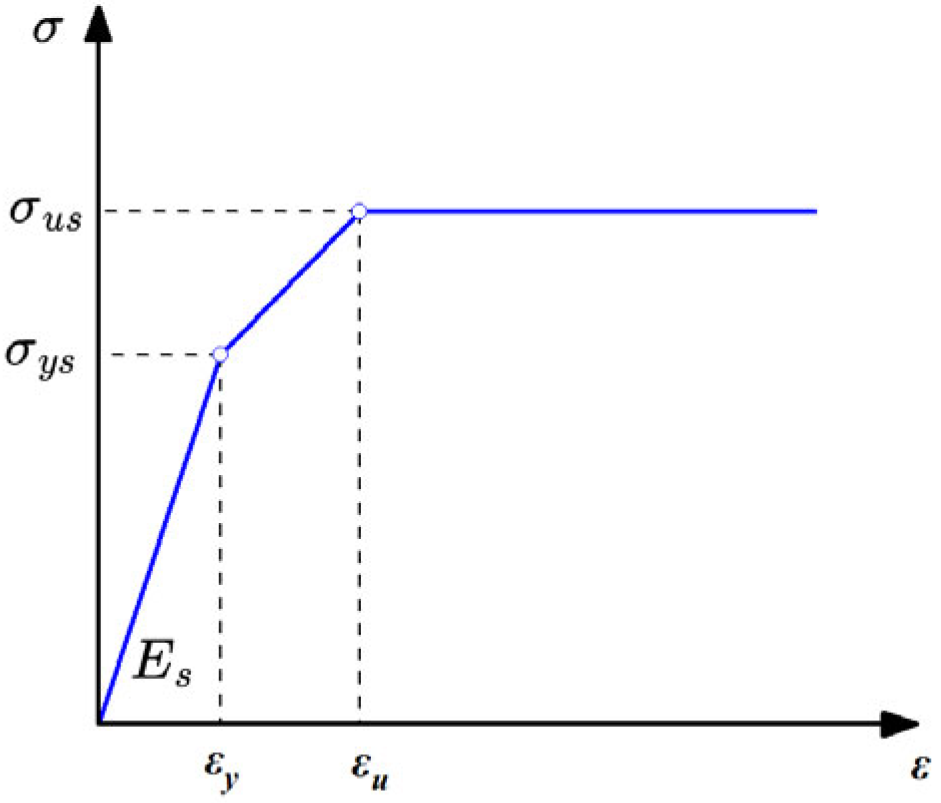
3.2.2. Constitutive Behavior of Steel
3.3. Contact and Constraints
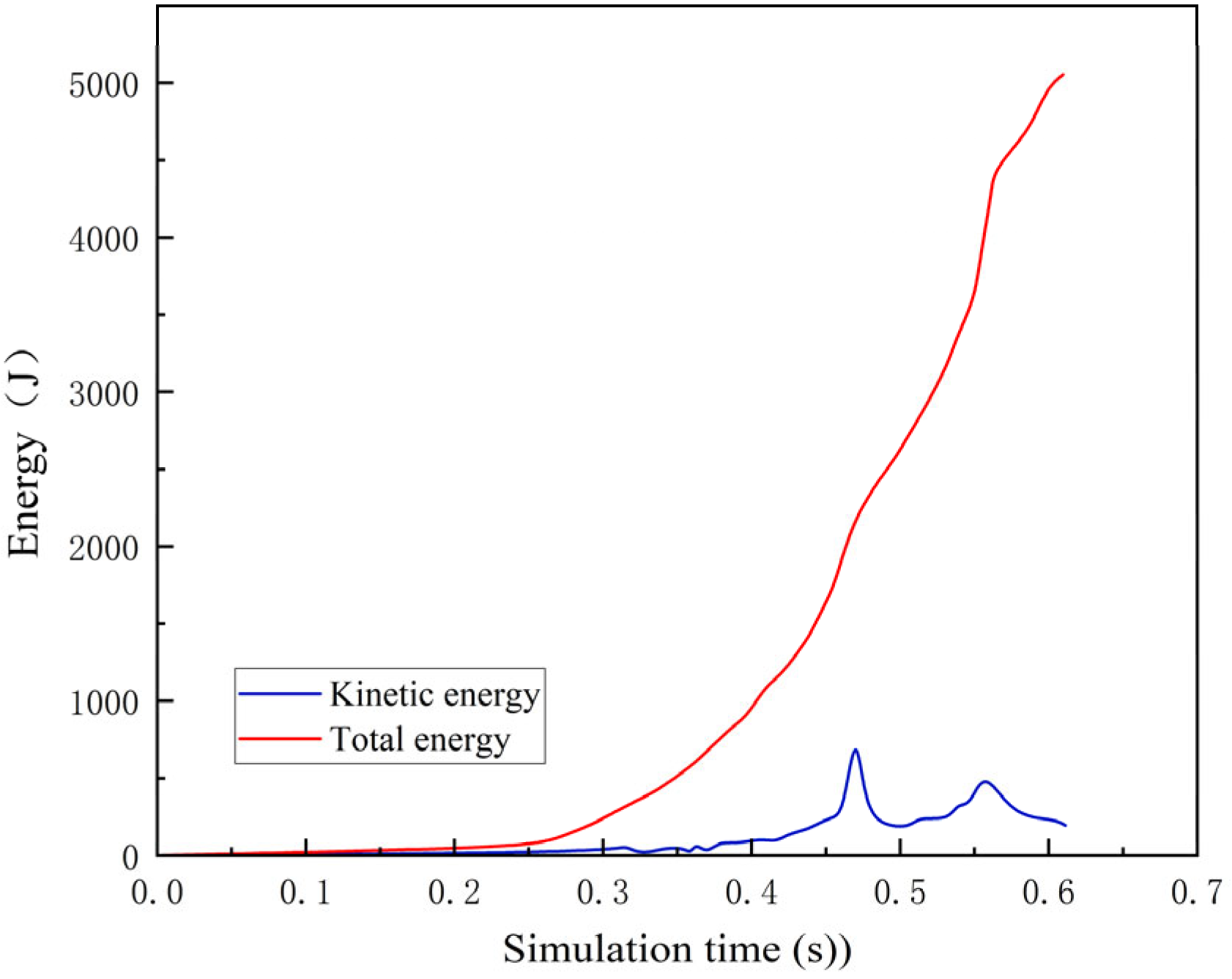
4. Model Validation and Result Analysis
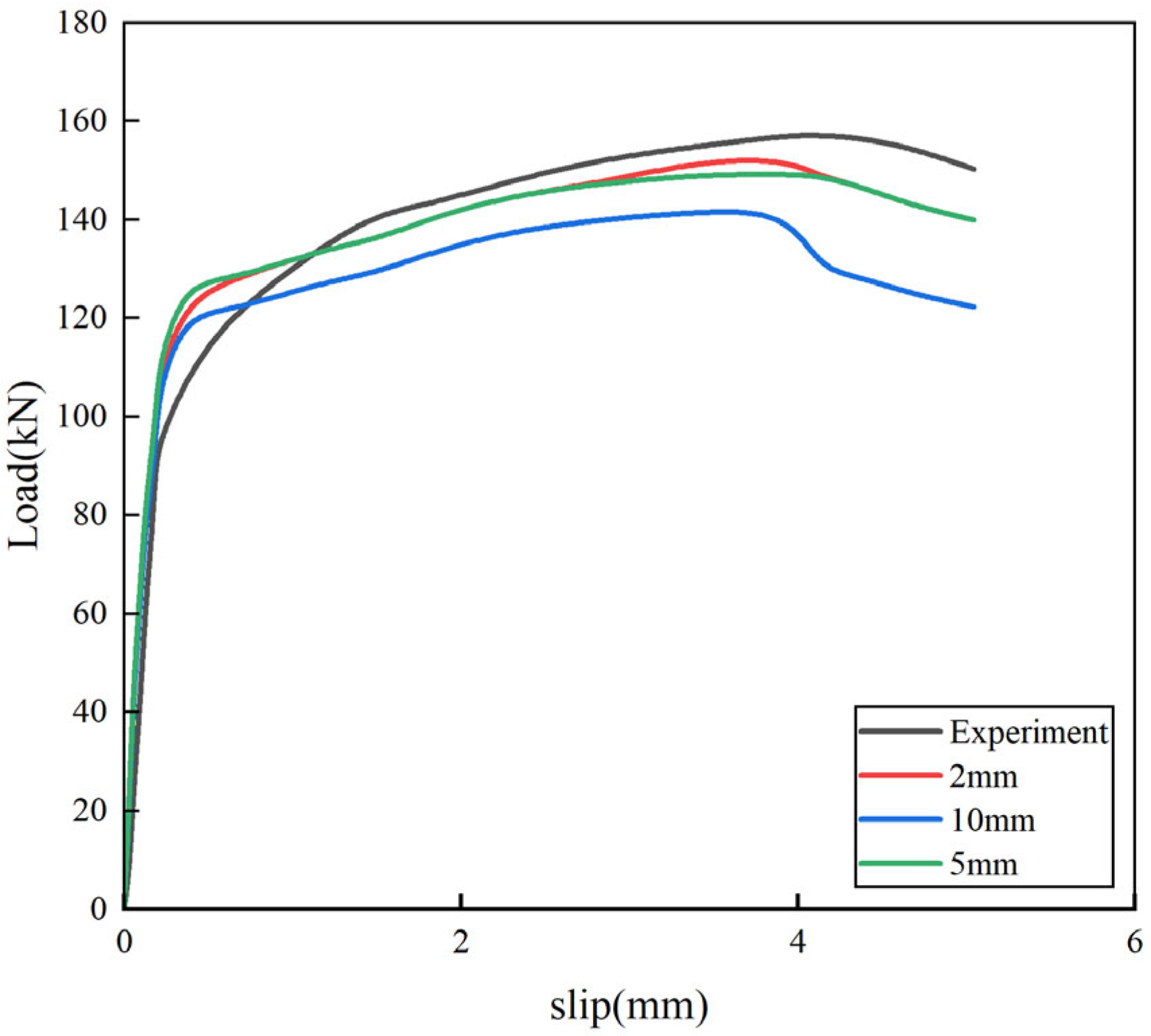
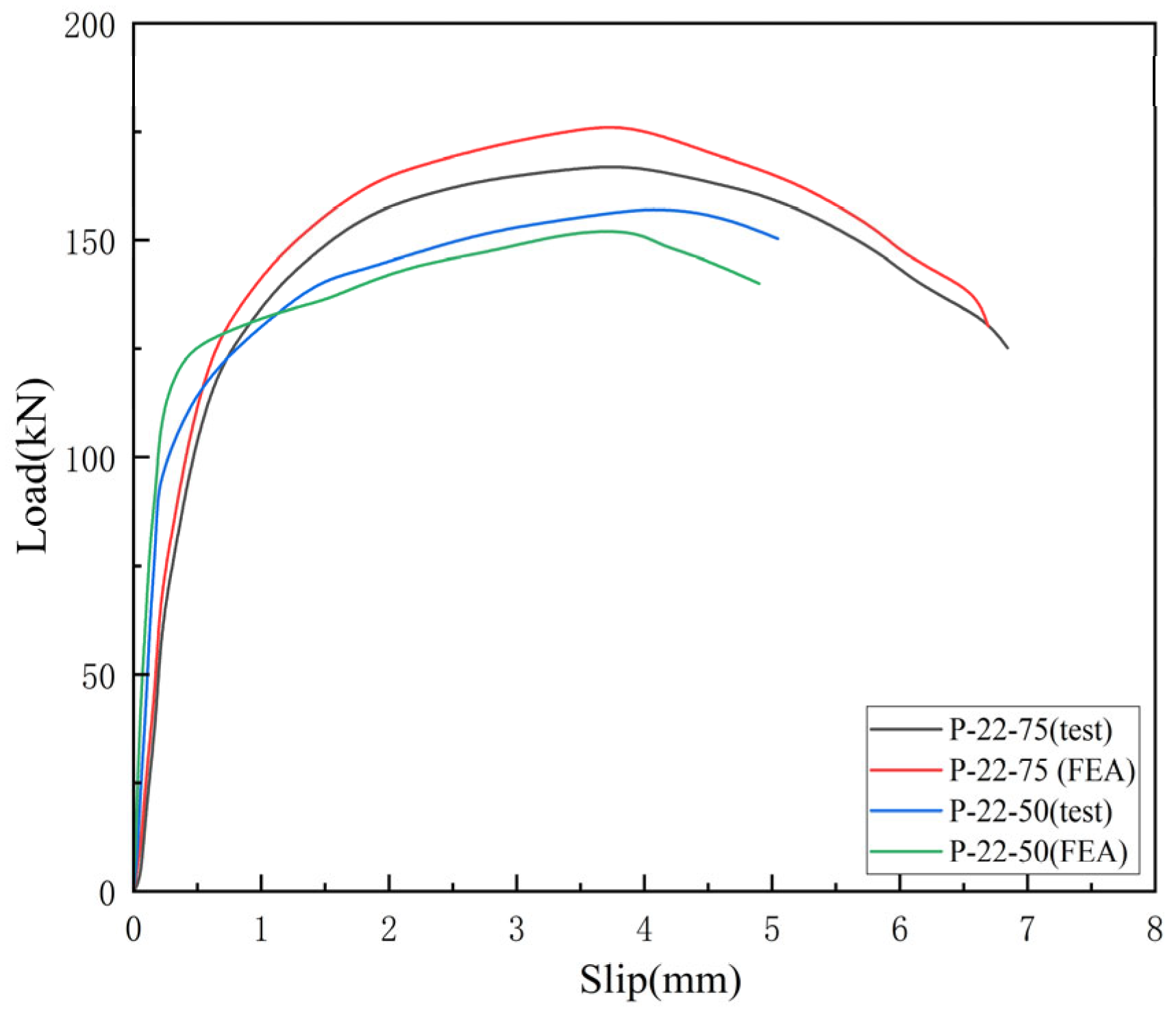
4.1. Model Validation
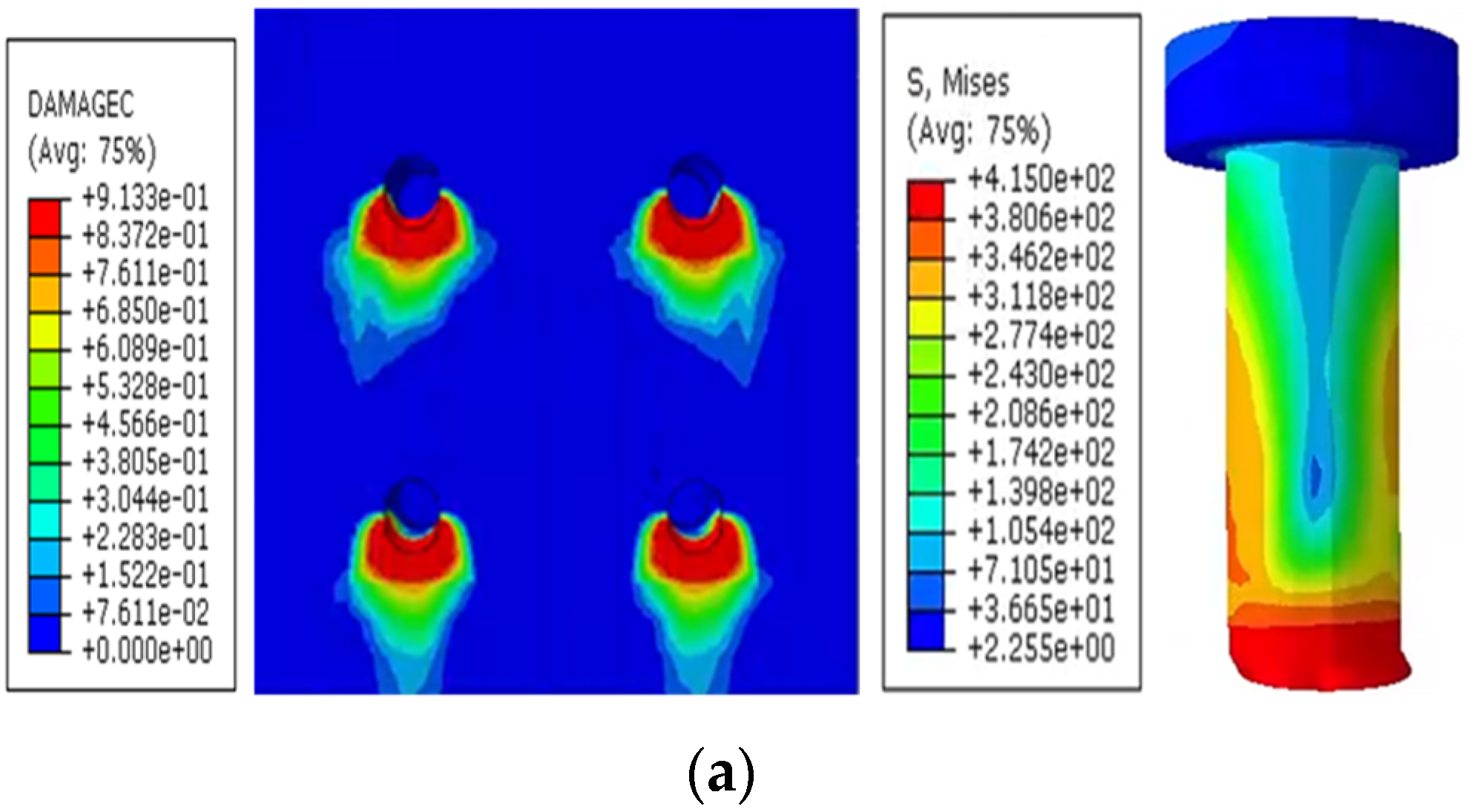
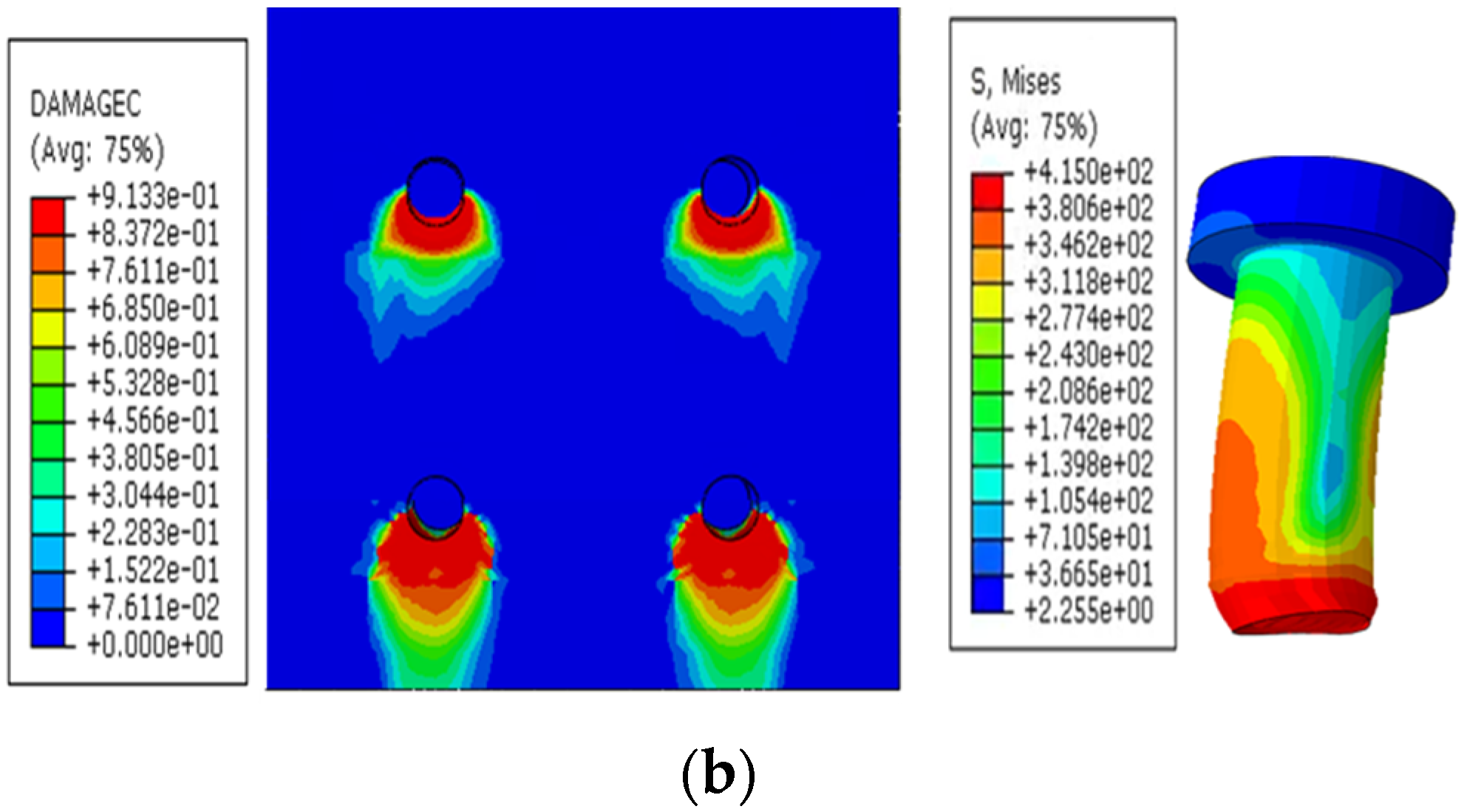
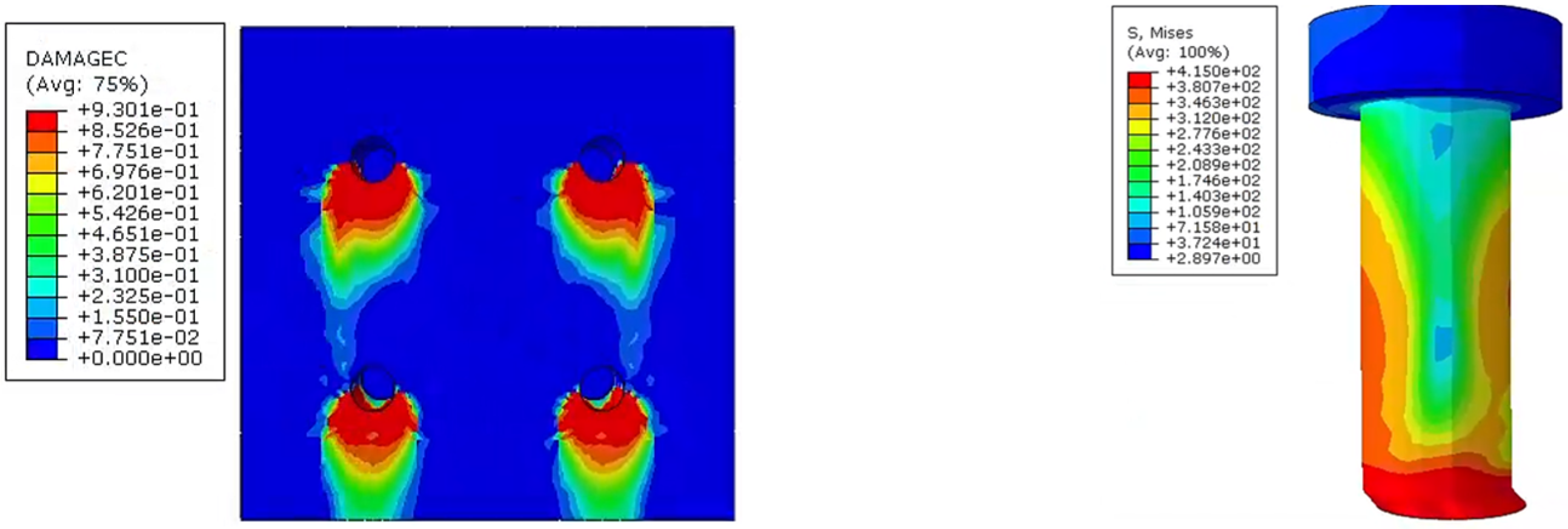
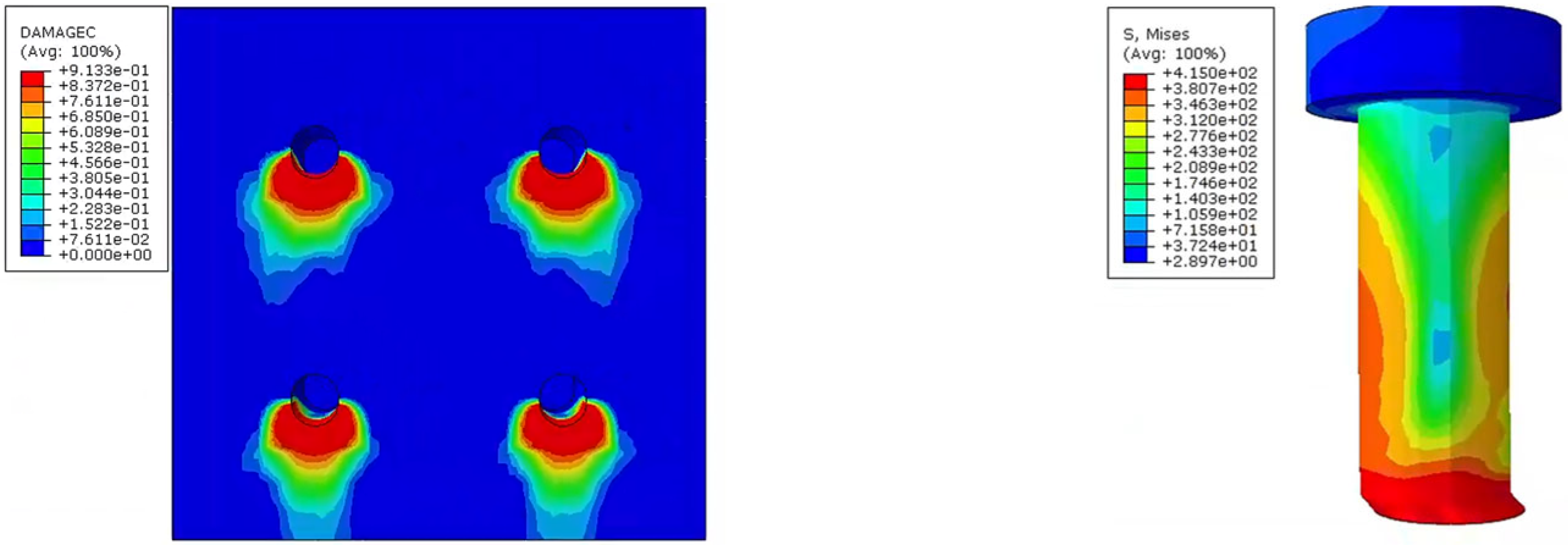
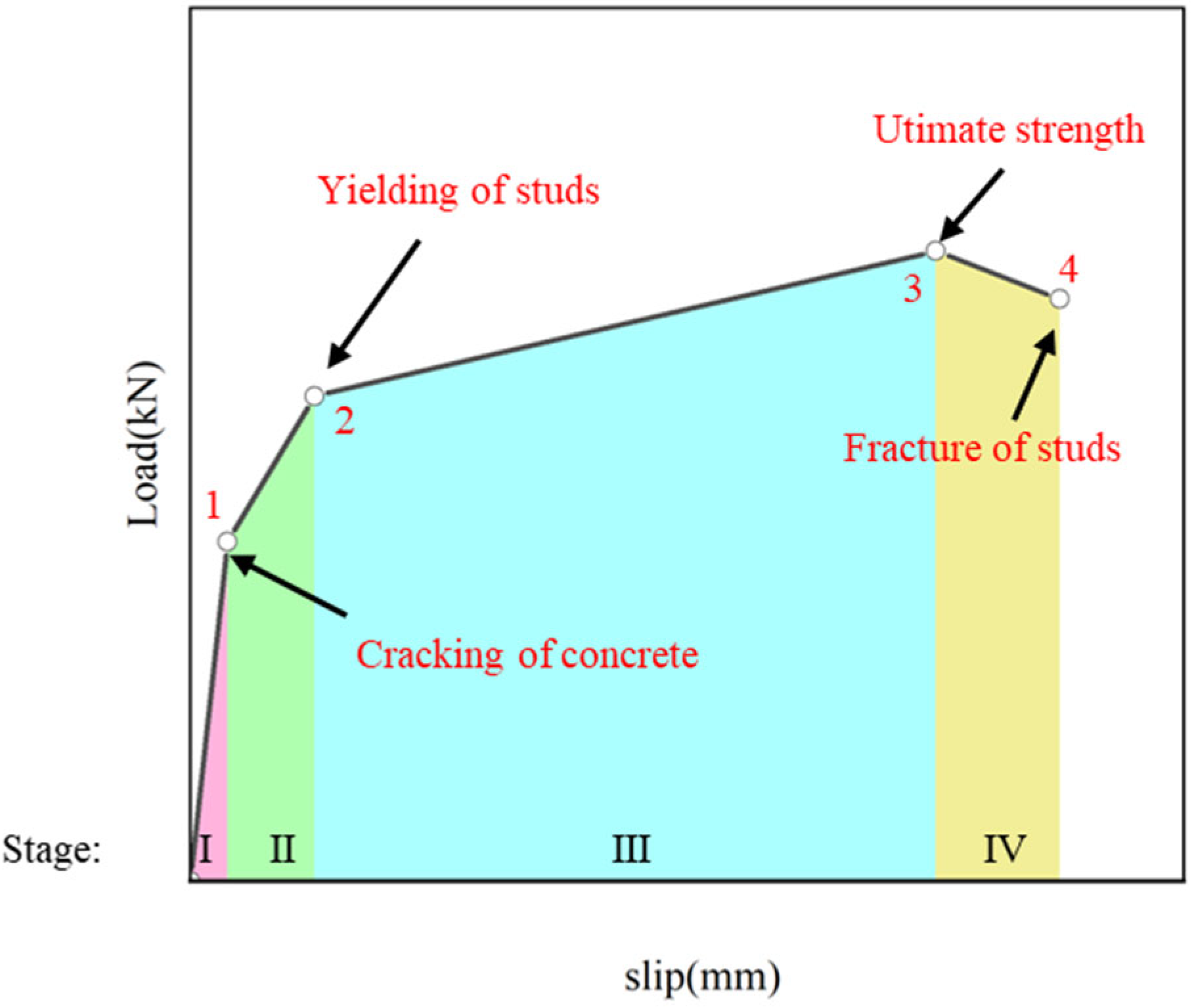
4.2. Failure Modes and Mechanisms
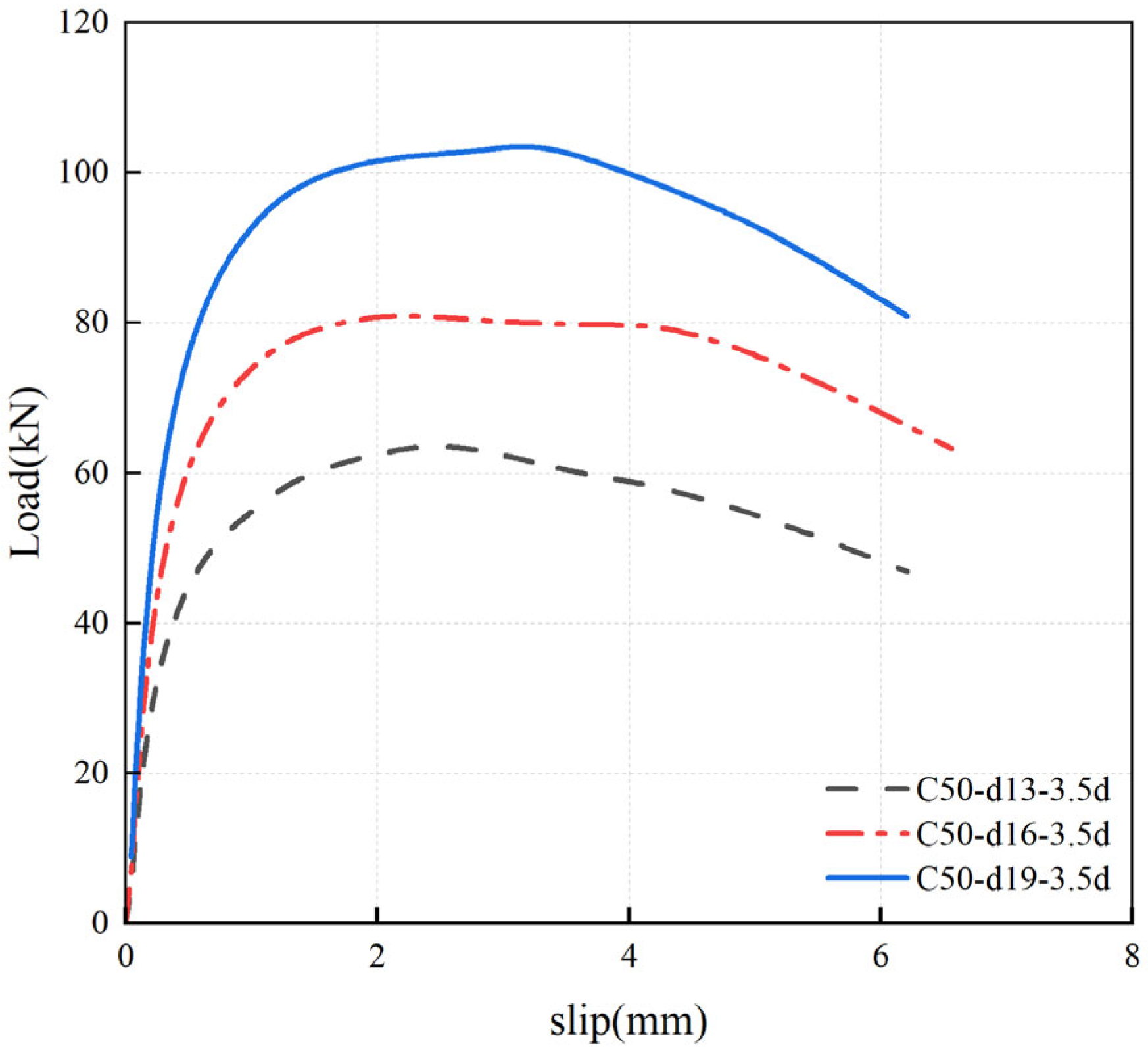
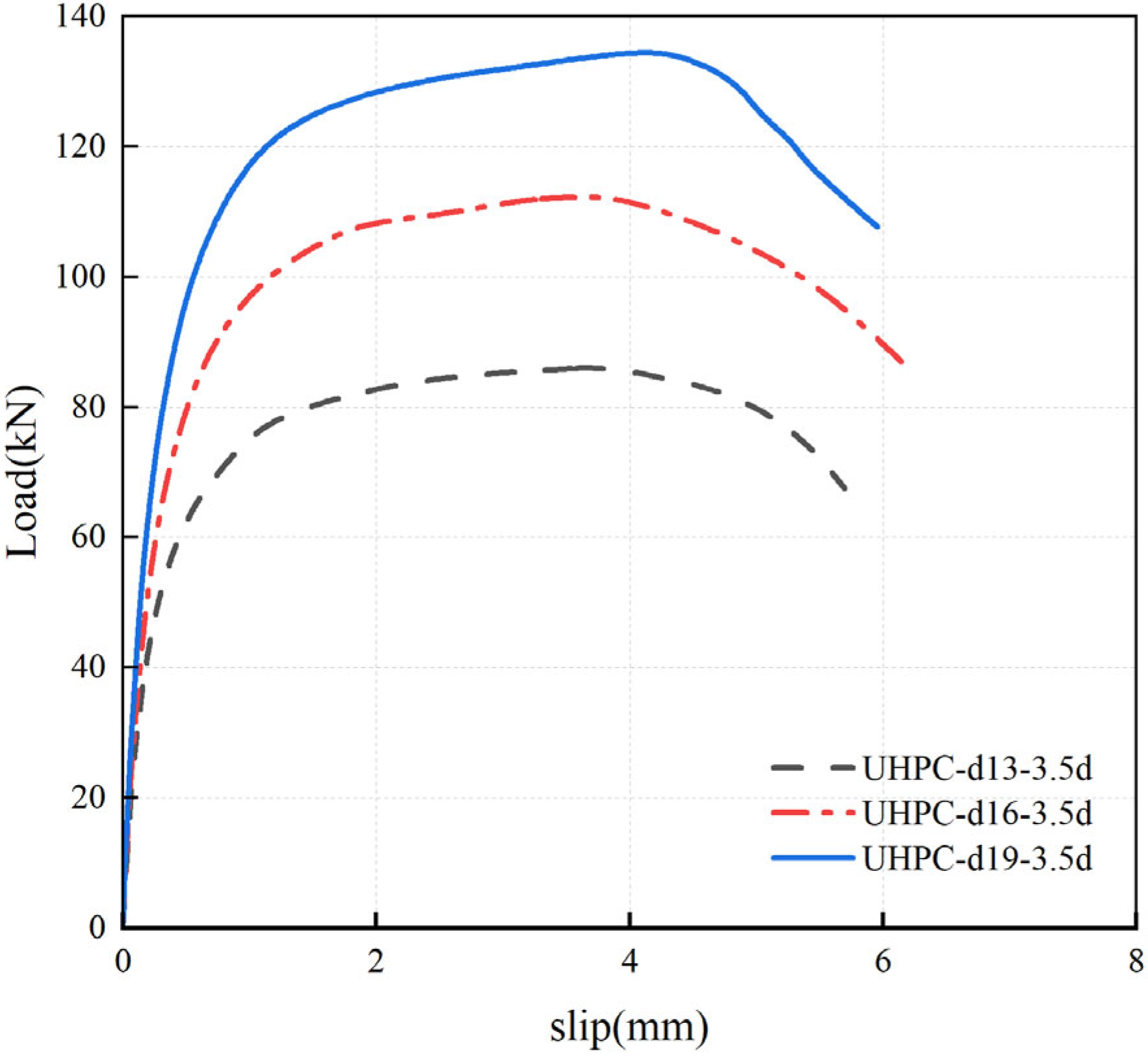
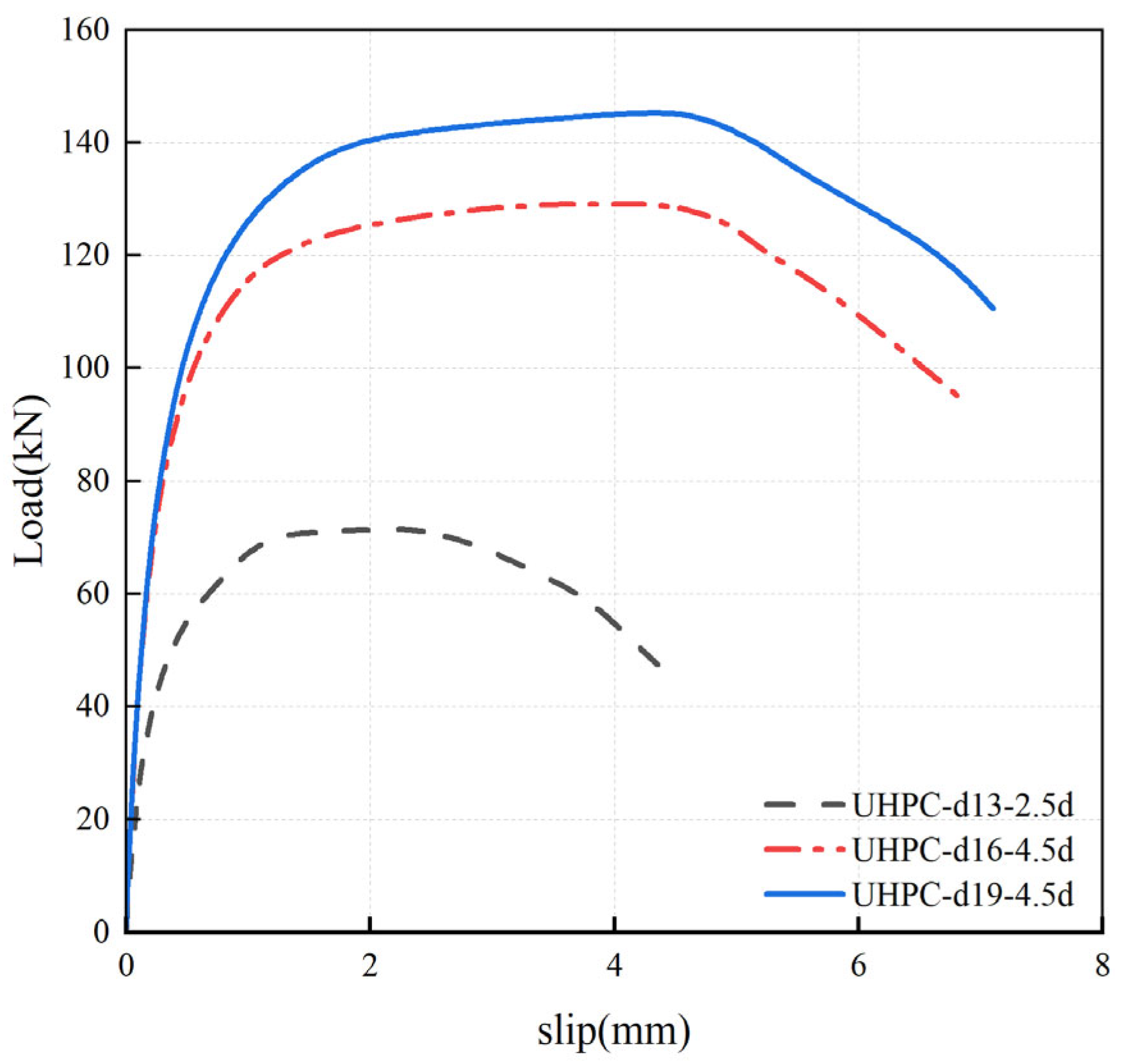
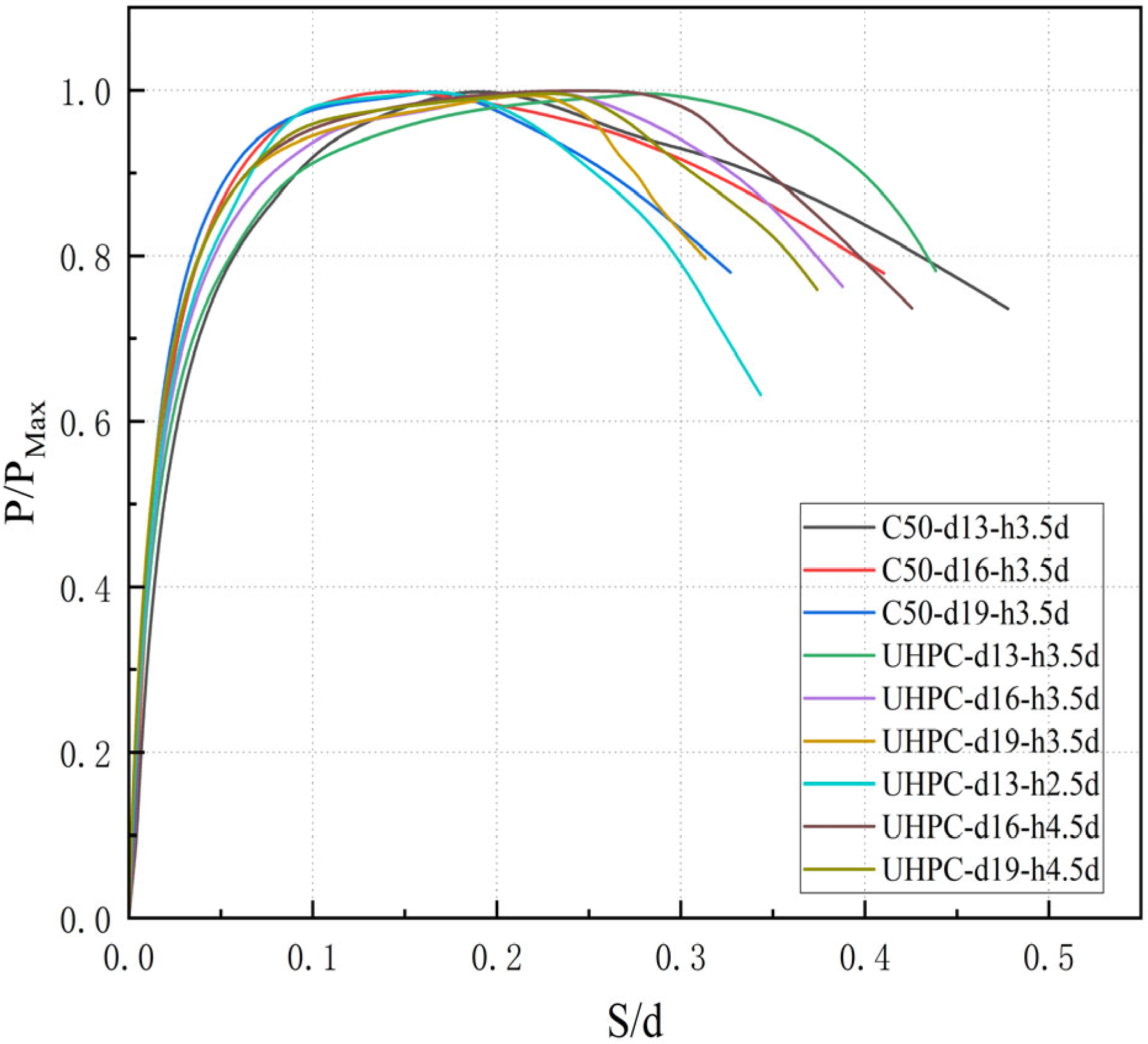
4.3. Load–Slip Curves
4.4. Shear Capacity Calculation
- is the cross-sectional area of the stud shank;
- is the elastic modulus of the concrete;
- is the design axial tensile strength of the concrete; and
- is the tensile strength of the stud material.
4.5. Comparison with Previous Studies and Discussion of Novelty
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fang, Z.; Fang, H.; Huang, J.; Jiang, H.; Chen, G. Static behavior of grouped stud shear connectors in steel–precast UHPC composite structures containing thin full-depth slabs. Eng. Struct. 2022, 252, 113484. [Google Scholar] [CrossRef]
- Ding, J.; Zhu, J.; Kang, J.; Wang, X. Experimental study on grouped stud shear connectors in precast steel- UHPC composite bridge. Eng. Struct. 2021, 242, 112479. [Google Scholar] [CrossRef]
- Ding, J.; Zhu, J.; Shi, T. Performance of grouped stud connectors in precast steel-UHPC composite bridges under combined shear and tension loads. Eng. Struct. 2023, 277, 115470. [Google Scholar] [CrossRef]
- Wang, Y.; Khan, M.; Uy, B.; Katwal, U.; Tao, Z.; Thai, H.-T.; Ngo, T. Long-term performance of steel-concrete composite wall panels under axial compression. Structures 2024, 64, 106606. [Google Scholar] [CrossRef]
- Wang, Y.; Khan, M.; Uy, B.; Lim, L.; Thai, H.-T.; Ngo, T. Behaviour, design and performance of steel-concrete composite walls in fire. J. Constr. Steel Res. 2025, 227, 109408. [Google Scholar] [CrossRef]
- Wang, Y.; Uy, B.; Li, D.; Thai, H.-T.; Mo, J.; Khan, M. Behaviour and design of coupled steel-concrete composite wall-frame structures. J. Constr. Steel Res. 2023, 208, 107984. [Google Scholar] [CrossRef]
- Gao, X.; Yin, C.; Guo, J.; Chen, G.; Huang, H. Experimental and theoretical study on the shear behaviors of an innovative precast UHPC composite beams reinforced with inverted T-shaped steel. J. Build. Eng. 2024, 96, 110504. [Google Scholar] [CrossRef]
- Li, B.; Fang, S.; Wen, J.; Fang, Z.; Ma, Y.; Zhao, G. Flexural and interfacial shear performance of prefabricated steel–UHPC composite beams with high-strength friction-grip bolted shear connectors: Numerical analyses and theoretical investigations. Structures 2025, 80, 109794. [Google Scholar] [CrossRef]
- Hamada, H.; Alattar, A.; Tayeh, B.; Yahaya, F.; Almeshal, I. Influence of different curing methods on the compressive strength of ultra-high-performance concrete: A comprehensive review. Case Stud. Constr. Mater. 2022, 17, e01390. [Google Scholar] [CrossRef]
- Jung, M.; Park, J.; Hong, S.-G.; Moon, J. Electrically cured ultra-high performance concrete (UHPC) embedded with carbon nanotubes for field casting and crack sensing. Mater. Des. 2020, 196, 109127. [Google Scholar] [CrossRef]
- Wang, H.; Wang, N.; Liu, X.-G.; Yue, Q.-R.; Yan, J.-L.; Zhang, Y. Effects of UHPC shear key on strengthening shear performances of wet joint in prefabricated composite beams. Eng. Struct. 2024, 299, 117130. [Google Scholar] [CrossRef]
- Wang, J.; Xu, Q.; Yao, Y.; Qi, J.; Xiu, H. Static behavior of grouped large headed stud-UHPC shear connectors in composite structures. Compos. Struct. 2018, 206, 202–214. [Google Scholar] [CrossRef]
- Luo, J.; Wu, G.; Zhao, G.; Ma, Y.; Fang, Z.; Fang, S. Experimental and numerical analysis on shear performance of single embedded nut bolted shear connectors in prefabricated steel-UHPC composite structures under cyclic loading. Structures 2025, 73, 108446. [Google Scholar] [CrossRef]
- Zhu, J.; Liu, Z.; Yu, X. Study on the shear performance of a novel riveted shear connector for steel-UHPC composite beams. Eng. Struct. 2025, 342, 120924. [Google Scholar] [CrossRef]
- Zong, Z.; An, G.; Gao, Z.; Xie, Q.; Guo, L.; Feng, X. Experimental and numerical investigations on shear behavior of bolt-sleeved connectors embedded in UHPC slabs with glazed hollow beads. J. Build. Eng. 2025, 114, 114396. [Google Scholar] [CrossRef]
- Yang, X.; He, J.; Hu, D.; Xiao, B.; Wang, N. Numerical Simulation Study on the Shear Performance of Stud–PBL Connectors in Corrugated Steel–UHPC Composite Decks. J. Railw. Sci. Eng. 2024, 21, 697–708. [Google Scholar] [CrossRef]
- Chang, X. Mechanical Performance of Steel–UHPC Composite Beam Bridges. Master’s Thesis, Anhui Jianzhu University, Hefei, China, 2022. [Google Scholar]
- Yang, H.; Zheng, Y.; Mo, S.; Lin, P. Push-out tests on studs with UHPC cover embedded in UHPC-NSC composite slab. Constr. Build. Mater. 2022, 331, 127210. [Google Scholar] [CrossRef]
- Zhao, Q.; Huang, G.; Xu, C.; Peng, Y. Push-Out Behavior of Short Headed Stud Connectors in Steel-Ultra High Performance Concrete Composite Deck. KSCE J. Civ. Eng. 2021, 25, 2640–2650. [Google Scholar] [CrossRef]
- Fang, Z.; Jiang, H.; Xiao, J.; Dong, X.; Shao, T. Shear performance of UHPC-filled pocket connection between precast UHPC girders and full-depth precast concrete slabs. Structures 2021, 29, 328–338. [Google Scholar] [CrossRef]
- Fang, Z.; Wu, J.; Xu, X.; Ma, Y.; Fang, S.; Zhao, G.; Jiang, H. Grouped rubber-sleeved studs–UHPC pocket connections in prefabricated steel–UHPC composite beams: Shear performance under monotonic and cyclic loadings. Eng. Struct. 2024, 305, 117781. [Google Scholar] [CrossRef]
- Geng, J.; Cheng, W.; Liu, G. Enhancing interface shear performance and bending resistance of UHPC permanent formwork for composite short beams by different interface treatment. J. Build. Eng. 2024, 85, 108736. [Google Scholar] [CrossRef]
- Gyawali, M.; Sennah, K.; Ahmed, M.; Hamoda, A. Experimental study of static and fatigue push-out test on headed stud shear connectors in UHPC composite steel beams. Structures 2024, 70, 107923. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, X. Static and Fatigue Behavior of Rubber-Sleeved Stud Shear Connectors as Part of Field-Cast Ultra-High Performance Concrete Connections. Materials 2020, 13, 2269. [Google Scholar] [CrossRef] [PubMed]
- Wei, C.; Zhang, Q.; Zhou, Y.; Cheng, Z.; Li, M.; Cui, C. Static and fatigue behaviors of short stud connectors embedded in ultra-high performance concrete. Eng. Struct. 2022, 273, 114888. [Google Scholar] [CrossRef]
- Fang, S.; Zhang, S.; Cao, Z.; Zhao, G.; Fang, Z.; Ma, Y.; Jiang, H. Effects of stud aspect ratio and cover thickness on push-out performance of thin full-depth precast UHPC slabs with grouped short studs: Experimental evaluation and design considerations. J. Build. Eng. 2023, 67, 105910. [Google Scholar] [CrossRef]
- EN 1994-1-1:2004; Eurocode 4: Design of Composite Steel and Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- Zhang, Z.; Zhang, F.; Wu, C. Experimental Study on the Performance of Sustainable Epoxy Resin-Modified Concrete. Sustainability 2025, 17, 6186. [Google Scholar] [CrossRef]
- JTG D60-2015; General Code for Design of Highway Bridges and Ulverts, Ministry of Transport of the People’s Republic of, China. China Communications Press: Beijing, China, 2015.
- Nguyen, H.T.; Kim, S.E. Finite element modeling of push-out tests for large stud shear connectors. J. Constr. Steel Res. 2009, 65, 1909–1920. [Google Scholar] [CrossRef]
- Liu, Y. Measurement and Influence Analysis of Welding Residual Stress of Shear Studs in Steel Plate–Concrete Composite Structures. Master’s Thesis, Shanghai Jiao Tong University, Shanghai, China, 2019. [Google Scholar]
- Jung, D.S.; Park, S.H.; Kim, T.H. Demountable Bolted Shear Connector for Easy Deconstruction and Reconstruction. Appl. Sci. 2022, 12, 1508. [Google Scholar] [CrossRef]
- Fang, Z.; Hu, L.; Jiang, H.; Fang, S.; Zhao, G.; Ma, Y. Shear performance of high-strength friction-grip bolted shear connector in prefabricated steel–UHPC composite beams: Finite element modelling and parametric study. Case Stud. Constr. Mater. 2023, 18, e01860. [Google Scholar] [CrossRef]
- Shi, Z.; Su, Q.; Kavoura, F.; Veljkovic, M. Uniaxial tensile response and tensile constitutive model of ultra-high performance concrete containing coarse aggregate (CA-UHPC). Cem. Concr. Compos. 2023, 136, 104878. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Lee, J.-H.; Yoon, Y.-S. Effect of fiber content on mechanical and fracture properties of ultra high performance fiber reinforced cementitious composites. Compos. Struct. 2013, 106, 742–753. [Google Scholar] [CrossRef]
- GB50010—2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2010.
- Zhang, F. Shear Performance of a Novel Bolted Shear Connector for Prefabricated Steel–UHPC Composite Beams. Ph.D. Thesis, Guangzhou University, Guangzhou, China, 2023. [Google Scholar]
- Pavlović, M.; Marković, Z.; Veljković, M.; Buđevac, D. Bolted shear connectors vs. headed studs behaviour in push-out tests. J. Constr. Steel Res. 2013, 88, 134–149. [Google Scholar] [CrossRef]
- GB 50017-2017; Steel Structure Design Standard. Ministry of Housing and Urban-Rural Development of PRC: Beijing, China, 2017.
- American Association of State Highway and Transportation Officials. AASHTO LRFD Bridge Design Specifications, 8th ed.; with 2019 Interim Revisions; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2017. [Google Scholar]
- Yang, S.; Shi, Z.; Wu, K. Shear performance of small shear studs in steel–concrete composite bridge decks. Railw. Stand. Des. 2025, 69, 96–103. [Google Scholar]
- Qiao, H.; Tang, L.; Zhang, Y. Experimental study on the shear performance of interface studs in steel plate–HPC composite bridge deck. Concrete 2025, 209–214. [Google Scholar]
| Unit | Materials | Modulus of Elasticity (MPa) | Poisson’s Ratio | Yield Strength (MPa) | Ultimate Strength (MPa) |
|---|---|---|---|---|---|
| stud connector | ML15AL | 2.0 × 105 | 0.3 | 404.00 | 532.00 |
| I beam | Q345 | 2.0 × 105 | 0.3 | 348.86 | 530.92 |
| Rebar | HRB400 | 2.0 × 105 | 0.3 | 412.00 | 542.00 |
| Concrete slab | C55 | 3.59 × 104 | 0.2 | — | 61.7 |
| UHPC slab | UHPC | 4.5 × 104 | 0.2 | — | 149.1 |
| SpecID | Concrete | d (mm) | s (mm) | h/d | h (mm) |
|---|---|---|---|---|---|
| C50-d13-h3.5d | C50 | 13 | 100 | 3.0 | 45.5 |
| C50-d16-h3.5d | C50 | 16 | 100 | 3.0 | 56 |
| C50-d19-h3.5d | C50 | 19 | 100 | 3.0 | 66.5 |
| UHPC-d13-h3.5d | UHPC | 13 | 100 | 3.0 | 45.5 |
| UHPC-d16-h3.5d | UHPC | 16 | 100 | 3.0 | 56 |
| UHPC-d19-h3.5d | UHPC | 19 | 100 | 3.0 | 66.5 |
| UHPC-d13-h2.5d | UHPC | 13 | 100 | 2.5 | 32.5 |
| UHPC-d16-h4.5d | UHPC | 16 | 100 | 3.75 | 72 |
| UHPC-d19-h4.5d | UHPC | 19 | 100 | 3.75 | 85.5 |
| Expansion Angle | Eccentricity | Intensity Ratio | K | Coefficient of Viscosity | Expansion Angle |
|---|---|---|---|---|---|
| 36 | 0.1 | 1.16 | 0.59 | 0.0001 | 36 |
| SpecID | Pmax (kN) | K0 (kN/mm) | Pmax Error (%) | Error (%) | Error (%) | K0 Error (%) | ||
|---|---|---|---|---|---|---|---|---|
| P-22-75 (Ref. [1]) | 167.30 | 4.22 | 6.80 | 188.44 | 5.1 | 2.13 | 2.35 | 7.78 |
| P-22-75 (FEA) | 175.82 | 4.31 | 6.64 | 203.10 | ||||
| P-22-50 (Ref. [1]) | 157.22 | 3.62 | 5.04 | 239.96 | 3.03 | 3.31 | 2.58 | 1.25 |
| P-22-50 (FEA) | 152.46 | 3.74 | 4.91 | 243.05 |
| SpecID | Pmax (kN) | K0 (kN/mm) | ||
|---|---|---|---|---|
| C50-d13-h3.5d | 63.60 | 2.44 | 6.31 | 87.02 |
| C50-d16-h3.5d | 81.11 | 2.66 | 6.52 | 128.06 |
| C50-d19-h3.5d | 101.82 | 3.21 | 6.23 | 134.49 |
| UHPC-d13-h3.5d | 82.32 | 3.66 | 5.70 | 156.67 |
| UHPC-d16-h3.5d | 112.60 | 3.76 | 6.05 | 229.15 |
| UHPC-d19-h3.5d | 135.10 | 4.04 | 5.96 | 294.09 |
| UHPC-d13-h2.5d | 71.60 | 2.20 | 4.46 | 167.62 |
| UHPC-d16-h4.5d | 129.90 | 4.21 | 6.81 | 284.22 |
| UHPC-d19-h4.5d | 146.50 | 4.41 | 7.10 | 319.00 |
| SpecID | FE Resultkn | Calculated Value (kN) | Calculated/FE Ratio | ||||
|---|---|---|---|---|---|---|---|
| Equation (10) | Equation (11) | Equation (12) | Equation (10) | Equation (11) | Equation (12) | ||
| C50-d13-h3.5d | 63.60 | 38.56 | 55.08 | 29.38 | 29.38 | 29.38 | 29.38 |
| C50-d16-h3.5d | 81.10 | 58.41 | 83.44 | 44.50 | 44.50 | 44.50 | 44.50 |
| C50-d19-h3.5d | 101.80 | 82.36 | 117.66 | 62.75 | 62.75 | 62.75 | 62.75 |
| UHPC-d13-h3.5d | 86.42 | 38.56 | 55.08 | 29.38 | 29.38 | 29.38 | 29.38 |
| UHPC-d16-h3.5d | 112.50 | 58.41 | 83.44 | 44.50 | 44.50 | 44.50 | 44.50 |
| UHPC-d19-h3.5d | 135.10 | 82.36 | 117.66 | 62.75 | 62.75 | 62.75 | 62.75 |
| UHPC-d13-h2.5d | 71.60 | 38.56 | 55.08 | 29.38 | 29.38 | 29.38 | 29.38 |
| UHPC-d16-h4.5d | 129.90 | 58.41 | 83.44 | 44.50 | 44.50 | 44.50 | 44.50 |
| UHPC-d19-h4.5d | 146.50 | 82.36 | 117.66 | 62.75 | 62.75 | 62.75 | 62.75 |
| Mean | 0.58 | 0.84 | 0.45 | ||||
| Standard deviation | 0.11 | 0.17 | 0.09 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, Z.; Qu, Y.; Zhao, Z.; Wang, S.; Yang, T. Finite Element Analysis and Parametric Study on the Push-Out Performance of Shear Connectors in Long-Span Composite Bridges. Buildings 2025, 15, 4244. https://doi.org/10.3390/buildings15234244
Hou Z, Qu Y, Zhao Z, Wang S, Yang T. Finite Element Analysis and Parametric Study on the Push-Out Performance of Shear Connectors in Long-Span Composite Bridges. Buildings. 2025; 15(23):4244. https://doi.org/10.3390/buildings15234244
Chicago/Turabian StyleHou, Zheng, Youlai Qu, Zhi Zhao, Sirui Wang, and Tao Yang. 2025. "Finite Element Analysis and Parametric Study on the Push-Out Performance of Shear Connectors in Long-Span Composite Bridges" Buildings 15, no. 23: 4244. https://doi.org/10.3390/buildings15234244
APA StyleHou, Z., Qu, Y., Zhao, Z., Wang, S., & Yang, T. (2025). Finite Element Analysis and Parametric Study on the Push-Out Performance of Shear Connectors in Long-Span Composite Bridges. Buildings, 15(23), 4244. https://doi.org/10.3390/buildings15234244






