Research on Seismic Capacity Values of Bridge Pile Group Foundations Based on a Data-Driven Approach

Abstract

Rapid assessment of seismic capacity for bridge pile group foundations under seismic loads is critical. This study employs the second-order central difference method to explore seismic capacity sensitivity and identify critical parameters. Subsequently, 1000 Latin hypercube samples were taken for these parameters, and 1000 analytical models were built. The overall displacement ductility is selected as the capacity indicator, and seismic capacity analysis is conducted on the models to obtain a capacity indicator. A BP model was constructed with the critical parameters as inputs and a capacity indicator as outputs to predict capacity values. Then, a regression function between capacity indicators and critical parameters is fitted to establish a capacity value assessment (CVA) model. Finally, capacity indicators are predicted using both the CVA model and the BP model, and the prediction results are compared. Results indicate that the critical parameters are tensile strength of reinforcing steel, cohesion of soil, cross-sectional area of pile, pile spacing, and longitudinal reinforcement ratio. The BP model can effectively predict the capacity indicators. The computational results of the CAV model show good agreement with the predictions from the BP model, demonstrating the reliability of the assessment model. This study provides a novel approach for disaster prediction of bridge pile group foundations.

1. Introduction

When subjected to seismic loads, pile group foundations for bridges generate internal forces and deformations within the structural system, known as seismic response demands. If these demands are less than the seismic capacity of the pile group foundation, the foundation structure sustains minimal damage. Otherwise, the foundation structure may suffer significant damage. The seismic capacity of pile group foundations is influenced by multiple factors, including the piles configuration, the surrounding soil, and the pile–soil contact. Due to these numerous influencing factors, accurately determining the seismic capacity value during seismic design and verification is highly challenging.

In recent years, building upon traditional research methods, researchers have integrated the artificial intelligence approaches to propose some novel solutions and methodologies for studying the seismic performance of pile foundations under seismic loads. Zhang [1] employed machine learning techniques to predict the maximum seismic response of the soil–pile–superstructure system, utilizing six machine learning algorithms: decision trees, k-nearest neighbors, extreme gradient boosting, random forests, artificial neural networks, and Gaussian process regression. Detailed evaluations demonstrated these models’ effectiveness in predicting maximum displacements of piles and soil. Wang [2] conducted dynamic analyses of nonlinear soil-bridge finite element models using five machine learning algorithms to reliably predict bridge seismic responses under lateral diffusion effects, considering soil, structural, and ground motion characteristics. Results indicated neural networks and gradient tree boosting effectively predict seismic responses of soil-bridge systems. Tang [3] investigated accurate and reliable prediction of maximum pile bending moments in soil–pile–superstructure systems within liquefied soils. A machine learning-based model was developed to predict the maximum pile bending moments. Six machine learning regression algorithms were employed to construct prediction models, with comparative analyses of prediction accuracy conducted. Shokrgozar [4] utilized machine learning techniques—specifically the CatBoost algorithm—to assess the seismic reliability of steel jacket offshore platforms. This was achieved by analyzing the feature importance of 17 variables related to the superstructure, pile foundation, and subgrade. The study employed the Latin hypercube sampling method to simulate 150 models accounting for these uncertainties, followed by nonlinear time-history analysis in OpenSees software (https://opensees.berkeley.edu/, accessed on 13 November 2025) for two seismic hazard levels. Rasheed [5] aimed to accurately assess the maximum settlement of pile-supported structures under seismic loading. Bridging the gap between traditional analytical methods and modern data-driven approaches, the study integrated a Random Forest (RF) model to estimate maximum pile foundation settlement. Results confirmed that the developed data-driven RF seismic settlement prediction method exhibits high accuracy and universality compared to conventional simulation methods. Ozturk [6] employed machine learning algorithms to investigate seismic damage classification for bridges with helical pile foundations in cohesive soils. Numerical data generated from finite element simulations were used to classify damage states based on three key indicators: pier displacement, pile ductility coefficient, and pile settlement rate. Laith [7] constructed a data-driven model to predict seismic response without numerical simulation, ensuring the reliability of tubular pile designs under seismic loads. This study employed genetic programming (GP) to propose innovative lateral displacement and bending moment prediction models for closed-end and open-end pipe piles. Xu [8] achieved outstanding performance in seismic dynamic response analysis of slope pile-anchor composite structures by integrating a hybrid architecture combining convolutional neural networks (CNN), long short-term memory networks (LSTM), and attention mechanisms. Wan [9] conducted earthquake vulnerability analysis for reinforced wharves using artificial neural networks (ANN), simultaneously accounting for uncertainties in soil-cement strength and ANN cognitive uncertainty. This yielded vulnerability surfaces under two damage limit states, enabling more comprehensive performance evaluation of reinforced pile-supported wharves.

The above studies indicate that current research focuses primarily on predicting pile foundation seismic responses using machine learning methods, constructing data-driven models for predictable seismic responses based on machine learning, and investigating the applicability of various machine learning algorithms. These efforts are predominantly directed toward addressing the problem of the seismic responses demand for group pile foundations.

There is relatively little research on seismic capacity values for pile foundations based on machine learning methods. Ahmed [10] presented a hybrid approach combining three-dimensional finite element (FE) modeling and multi-objective genetic algorithm-based evolutionary polynomial regression (EPR-MOGA) to predict the lateral capacity of short straight and step-tapered piles in cohesionless soils. A parametric study using PLAXIS 3D 2020 simulated 580 different pile cases under service-level lateral loads. The FE simulation results were then used to train an artificial intelligence (AI)-based model that produces predictive equations. But this study is based on offshore pile structures, with a focus on soil, and the pile body is modeled with linear elastic materials; in addition, the capacity value indicator uses horizontal force, which may not be applicable to civil buildings. DENG [11] using machine learning algorithms, established prediction models for vertical and horizontal bearing capacities of salteroded pile foundations in salt marsh areas. But the pile body is modeled with linear elastic material, and the research conclusion is mainly used for the static design of piles. Braun [12] developed predictive models that will be able to compute the overall mechanical response of reinforced concrete (RC) piles embedded in unsaturated clay through the use of various machine learning (ML) algorithms. However, this study did not provide a predictive regression equation and only constructed a model based on ML. The research objects of the above studies are all single piles and do not involve pile group foundations. This study aims to propose a data-driven research method for determining the seismic capacity values of bridge group pile foundations, and exploring the material nonlinearity of piles, the selection method of pile characteristic parameters, and the quantification of seismic capacity; these issues are rarely addressed in existing research.

This study employs the second-order central difference method to explore seismic capacity sensitivity and identify critical parameters. Then, 1000 Latin hypercube samples are taken for these parameters, and 1000 analytical models are built. The overall displacement ductility is selected as the capacity indicator, and seismic capacity analysis is conducted on the models to obtain the capacity indicator. A BP model was constructed with the critical parameters as inputs and the capacity indicator as outputs to predict capacity values. Subsequently, a regression function between capacity indicators and critical parameters is fitted to establish a capacity value assessment model (CVA). Finally, the capacity indicators are predicted using both the CVA model and the BP model, and the prediction results are compared. This study provides a novel approach for disaster prediction of bridge group pile foundations.

2. Sensitivity Analysis of Seismic Capacity

The seismic capacity value of a group pile foundation is influenced by factors such as the pile body, surrounding soil, and pile–soil contact. However, the specific factors contributing most significantly to this value remain unclear. Investigating the factors affecting the seismic capacity of a group pile foundation aims to identify the parameters that have the greatest impact on its seismic capacity value. From a systems engineering perspective, this involves conducting a sensitivity analysis to identify the most sensitive component. In practice, it is necessary to integrate the seismic capacity analysis of the pile group foundation with structural response sensitivity analysis to identify the most sensitive component (parameter).

Several scholars have conducted parameter sensitivity studies on pile foundation structures and drawn corresponding conclusions. Hafez [13] conducted a parameter sensitivity analysis on a pile group structure with consolidated pile tops in non-uniform soil layers using the Associated System Method (ASM). They obtained two sets of results: sensitivity factors and sensitivity operators, employing lateral cyclic loading. However, the ASM used is relatively cumbersome and inconvenient for practical application. De Cock [14] investigated the load-displacement characteristic behavior of single piles, primarily analyzing sensitivity factors affecting pile deformation, though their research focused on single-pile structures. Xiao XC [15] performed dynamic response analysis and sensitivity analysis on a pile group structure using a nonlinear Winkelberger foundation beam model. They concluded that the pile–soil stiffness ratio is the most critical sensitivity control parameter. Their research primarily addressed the seismic response demands for pile group structures rather than seismic capacity. This study employs the second-order central difference method to conduct seismic sensitivity analysis on the parameters of the pile group foundation model.

In finite element analysis, continuous structural systems are discretized and represented as a set of algebraic equations (using a static system as an example).

$$K(\tau ,h)q(\tau ,h)=Q(\tau ,h)$$

(1)

In the equation, τ is the (quasi) time variable, h is the system design parameter; K(τ, h) is the N × N order stiffness matrix; Q(τ, h) is the N × 1 order external load matrix, whose explicit dependencies are τ and h; q(τ, h) is the N × 1 order node displacement matrix, whose implicit dependencies are also τ and h. Traditional mechanical analysis assumes design parameters h are constant, whereas structural sensitivity analysis treats the system response characteristics as functions of design parameters h. This is clearly consistent with reality, because actual structural systems differ from ideal ones for various reasons, such as some defects in structural geometry and materials.

Structural response sensitivity (or gradient) refers to the magnitude of change in structural response when structural design parameters undergo a unit change. The response sensitivity (or gradient) indicator is defined as $\psi ={\displaystyle \frac{\Delta q}{\Delta h}}$. There are several methods for calculating $\psi$, primarily including the Finite Difference Method (FDM), Direct Differentiation Method (DDM), Adjoint System Method (ASM), and Semi-Analytical Method [16]. Among these methods, FDM and DDM are simpler to operate and more commonly used, while the other methods are relatively cumbersome and challenging to apply in practice. Although DDM surpasses FDM in efficiency and accuracy, designing algorithms for DDM becomes challenging for nonlinear structural systems. Consequently, FDM holds certain advantages, particularly when employing second-order central differences, which effectively control truncation errors to some extent. Of course, truncation errors also depend on the choice of the difference step size $\Delta h$. Its definition is as follows:

$$\psi ={\displaystyle \frac{\Delta q}{\Delta h}}={\displaystyle \frac{q(h+\Delta h)-q(h-\Delta h)}{2\Delta h}}+0(\Delta h^2)$$

(2)

This study employs a second-order central difference method to conduct sensitivity analysis of seismic capacity values for bridge pile foundations. This is achieved by perturbing several structural system parameters as random variables. The selection of the difference step size $\Delta h$ considers the mean and coefficient of variation in the random variables.

For the seismic capacity values of bridge pile foundations, an elastic-plastic static analysis method is employed, similar to the Pushover analysis. By applying a specific pattern of lateral distributed forces to the structure or components and gradually increasing these forces until the structure reaches a predetermined deformation state or collapse state, the seismic capacity and behavioral characteristics of the structure under ultimate seismic actions are obtained.

During elastic-plastic static analysis, the lateral force loading pattern significantly influences computational results, primarily due to its close association with the inertial loads generated by the structure [17,18]. Under seismic loading, the dynamic interaction between pile group foundations and soil involves both kinematic and dynamic effects. The kinematic effects generated by soil around piles can be conservatively neglected, focusing solely on dynamic effects. In this case, inertial forces comprise three components: seismic inertial forces transmitted from the superstructure above the foundation, seismic inertial forces from the cap, and seismic inertial forces from the pile shaft itself. Analysis of bridge seismic response requirements indicates that the contributions from the first two components are dominant, while the contribution of the third component is relatively minor and can be neglected. The seismic inertial forces transmitted from the superstructure to the base of the cap can be treated as concentrated forces, including axial force, shear force, and bending moment. Therefore, when performing elastic-plastic static analysis on the pile group foundation, the lateral loading mode can adopt a model where a lateral concentrated force is applied at the center of the cap; the axial force and bending moment acting on the cap can be replaced by the axial force and bending moment applied at the center of the cap.

The seismic performance indicators for bridge pile group foundations are displacement, resistance, and ductility. For sensitivity analysis, ductility can be indirectly obtained from the response displacement; therefore, sensitivity studies are conducted only on displacement and resistance herein.

3. Pile Group Foundation Finite Element Model

Under ultimate seismic loading, both the pile and the surrounding soil enter the plastic range. The finite element model for the group pile foundation must account for material nonlinearity and soil–pile interaction effects.

3.1. Overview of the Finite Element Model

A finite element model for the group pile foundation is built in the OpenSees (https://opensees.berkeley.edu/, accessed on 13 November 2025) platform [19] (Figure 1). Piles are modeled using elastoplastic fiber beam–column elements. Each pile is fixed at its base, with rigid arms connecting pile top nodes. The cap weight and superstructure reaction forces are represented by concentrated forces applied at the cap’s centroid (Point A in Figure 1). Surrounding soil is simulated using nonlinear p-y spring elements. In Figure 1, Point B is the bottom center point of the cap, and Point C is the position where the m-method calculation indicates significant bending moments.

3.2. Pile Element

The pile body is modeled using an elastoplastic fiber beam–column element [20]. This element is a nonlinear distributed plasticity element discretized axially into multiple segments. The properties of each segment are represented by its mid-cross-section, which is further subdivided into numerous fibers. Each fiber may correspond to either concrete or reinforcement, as shown in Figure 2. During computation, the bending stiffness of each cross-section is first determined based on the stress–strain relationships of the reinforcement and concrete fibers, respectively. This value is then integrated along the element length to ultimately obtain the element stiffness matrix.

In the OpenSees platform, the dispBeamColumn elastoplastic beam–column element is selected to model the pile body. Simultaneously, the Fiber module is used to define the fiber cross-sections, which are then combined with the dispBeamColumn element to form the elastoplastic fiber beam–column element.

3.3. Pile Material Constitutive Models

The Kent–Scott–Park model [21] is employed as the constitutive model for both confined and unconfined concrete, disregarding concrete tensile behavior. In the OpenSees platform, this model corresponds to the uniaxialMaterial Concrete01 material. A typical monotonic constitutive curve for confined concrete is shown in Figure 3a. Simultaneously, the Giuffré–Menegotto–Pinto model [22] is employed as the constitutive model for the reinforcement. This widely used model closely matches experimental data, with a strain hardening rate set to 0.001. Within the OpenSees platform, this model corresponds to the uniaxialMaterial Steel02 material. Its typical monotonic constitutive curve is shown in Figure 3b.

3.4. Nonlinear Pile–Soil Interaction

Nonlinear p-y elements are commonly employed to simulate lateral pile–soil interactions, t-z elements to model soil friction along the pile side, and q-z elements to represent soil support at the pile tip. This study primarily investigates the lateral seismic resistance of pile group foundations, utilizing only nonlinear p-y elements in the analysis [23]. The nonlinear p-y element in OpenSees is constructed by combining the zeroLength element with the PySimple1 material. The node coordinates at both ends of the element are identical, with one end connected to the pile body and the other end fixed.

The study subject is soft clay, whose soil parameters are determined using Matlock’s recommended formula [24]. In the OpenSees platform, the clay soil parameter variables are P_ult, y₅₀, and C_d; Pult represents the ultimate capacity value of the p-y material (characterizing the cohesion of the soil), y₅₀ denotes the lateral displacement at 50% ultimate capacity P_ult under monotonic loading, and C_d signifies the soil–pile resistance when the soil–pile gap is fully opened; here, P_ult is the core parameter.

Mokwa [25] found that group pile effects cannot be neglected when the pile center spacing is less than 6D (diameter) in the parallel loading direction, or less than 3D in the perpendicular loading direction. A simplified method for accounting for pile group effects involves multiplying the p-y curve of a single pile by a coefficient known as the p-multiplier. The study employs this method, adopting the p-multiplier value from Reference [25].

4. Sensitivity Analysis Example

4.1. Example Description

This example concerns the pile foundation for Pier PM109 of an approach bridge to a Yangtze River bridge in Shanghai. The pile foundation is located within a 7 × 60 m continuous beam bridge. The pile diameter is 1.8 m, with a total length of 61.8 m. The exposed length above the scour line is 10 m, while the buried length below the scour line is 51.8 m. The piles are arranged in a 2 × 3 rectangular grid, with both longitudinal and transverse center-to-center spacings of 4.65 m. The pile cap has longitudinal and transverse plan dimensions of 7.65 × 15.2 m and a thickness of 2.8 m. The pile body uses C40 concrete with longitudinal reinforcement of 35φ32 mm bars (reinforcement ratio 1.24%), with φ12 mm stirrups spaced at 150 mm intervals. The concrete cover is 50 mm thick. The foundation rests in a homogeneous clay layer with an undrained shear strength of 50 kN/m² and an effective unit weight of 10 kN/m³.

4.2. Example Finite Element Model

The finite element model of the example group pile foundation is shown in Figure 1, with some pile elements omitted. All pile elements have a length of 2 m. Fiber divisions are defined as follows: For the core confined concrete, 50 fibers are defined circumferentially and 8 fibers radially, totaling 400 fibers. For the protective layer concrete, fibers are defined circumferentially as for the confined concrete and radially as a single fiber, totaling 50 fibers. For longitudinal reinforcement, each bar is defined as a single element.

Concrete Material Properties: For the core confined concrete, maximum compressive strength 16.73 MPa, corresponding strain at maximum compressive strength 0.0025, ultimate strain 0.016, corresponding ultimate compressive strength 8.365 MPa. For the protective layer concrete, maximum compressive strength is 13.8 MPa, corresponding strain at maximum compressive strength is 0.002, ultimate strain is 0.006, and ultimate compressive strength at ultimate strain is 0.

Reinforcing steel material: yield strength is 280 MPa, elastic modulus is 2.0 × 10⁵ MPa, and post-yield hardening ratio is 0.001.

The p multipliers for Piles 1 to 6 are 0.82, 0.78, 0.82, 0.64, 0.68, and 0.64. Calculation of p-y spring parameters at different depths for each pile is referenced in [22].

4.3. Load Case

A horizontally monotonic quasi-static loading is applied during analysis. The loading point is located at the centroid of the cap (Point A in Figure 1), with loading along the x-direction. Loading is displacement-controlled, with a maximum controlled displacement of 2 m.

The nonlinear finite element equations are solved using the Newton–Raphson method with an energy criterion as the convergence criterion. Due to the presence of inflection points in the material constitutive relationship, displacement control is employed for loading, enabling convergence without the arc length method. Other solution settings are identical to those for conventional static analysis in OpenSees [19].

4.4. Sensitivity Analysis Parameter

For sensitivity analysis, the following parameters were selected as sensitivity control variables: tensile yield strength of pile reinforcement f_s, compressive yield strength of pile concrete f_c, cross-sectional area A of the pile core concrete, and p-y soil parameters P_ult. Since the elastic modulus of concrete is correlated with its compressive strength, it is excluded as a control parameter. Additionally, when the pile length exceeds a certain value, its effect on lateral response becomes negligible; therefore, the pile length is also excluded as a control parameter. For the initial analysis, the differential step size $\Delta h$ was set to ${10}^{-2}\mu$. For comparative analyses, values of ${10}^{-2}\mu$, ${10}^{-3}\mu$, and ${10}^{-4}\mu$ were used, and the $\mu$ representing the mean values of the control parameters.

4.5. Results and Discussion

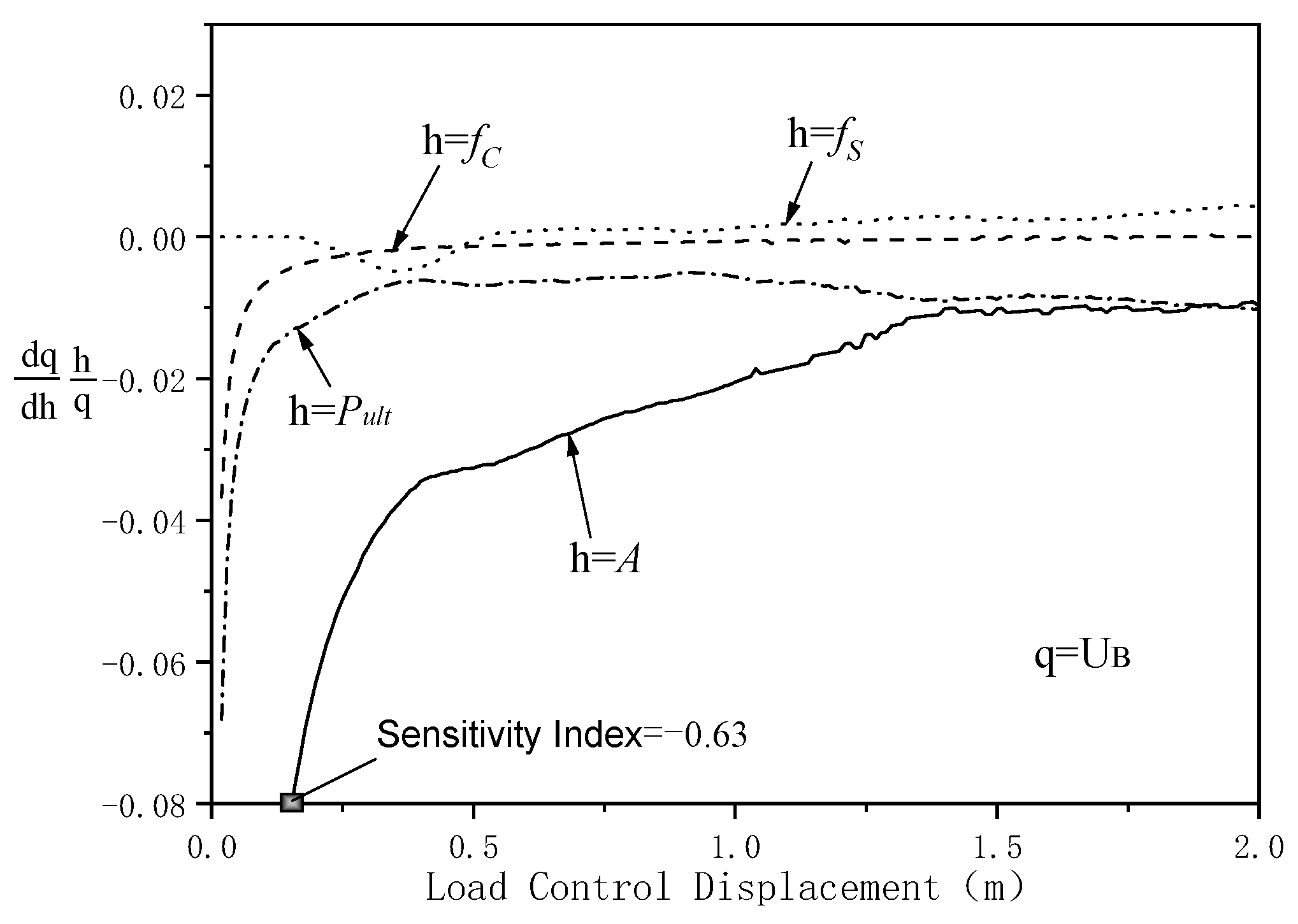
For the seismic performance of the pile group foundation, the sensitivity analysis focuses on the following locations: ① The center of the cap base (Point B in Figure 1); ② The pile body approximately 8 m below the scour line (Point C in Figure 1), where the m-method calculation indicates significant bending moments. The sensitivity analysis focuses on the displacement and horizontal resistance at these locations, along with sensitivity indices relative to control parameters under monotonic quasi-static loading.

The sensitivity analysis subjects q under monotonic quasi-static loading are the horizontal displacement U_B and horizontal resistance F_B at point B, along with the horizontal displacement U_C at point C. The control parameters h are f_s, f_c, A, and P_ult. The study normalizes the sensitivity analysis indices to $\theta$, where the value represents the percentage change in structural response caused by a unit percentage change in the sensitivity control parameter [26]. The derivation formula of $\theta$ is shown in Equation (3). In the formula, q represents the sensitivity analysis subjects and h represents the control parameters.

$$\theta ={\displaystyle \frac{\left(\left( q+dq \right)-q \right) / q}{\left(\left( h+dh \right)-h \right) / h}}={\displaystyle \frac{ dq / q}{dh / h}}={\displaystyle \frac{dq}{dh}}\cdot {\displaystyle \frac{h}{q}}$$

(3)

Figure 4, Figure 5 and Figure 6 show the normalized sensitivity indices of the sensitivity study subjects to control parameters, respectively. These indices are plotted as functions of the applied displacement control. In Figure 4, the sensitivity of U_B to parameter A exhibits significant variation, ranging from −0.63 to 0.14. However, as displacement loading increases, the sensitivity of U_B to parameter P_ult begins to rise, ultimately reaching 0.16 and surpassing that of parameter A. In Figure 5, the sensitivity of F_B to parameter f_s is initially zero during the early displacement loading phase, only beginning to change at a certain displacement value and gradually increasing thereafter. This is because f_s has a negligible effect on the response before reinforcement yielding. Sensitivity to parameter A initially exhibits higher values before gradually stabilizing, reflecting the influence of construction errors on the response. Sensitivity to the remaining two parameters is relatively low. In Figure 6, U_C exhibits sensitivity to parameters f_s and A is similar to F_B; sensitivity to parameter P_ult increases steadily with displacement load, reaching a maximum value close to that for parameter f_s. All sensitivity subjects show relatively low sensitivity to parameter f_c.

Based on the values in these figures, the sensitivity response to parameter f_c is the lowest, being one order of magnitude lower than the other three parameters. U_C exhibits relatively significant sensitivity responses to all three parameters. The occasional sawtooth fluctuations in the figures result from the redistribution of internal forces and deformations within the structure due to complex structural behavior. Sensitivity to parameter f_c decreases gradually with increasing displacement load, consistent with expectations as concrete enters the softening stage after yielding. Sensitivity to parameter f_s increases with displacement load, as reinforcement remains in the strengthening phase after yielding. A similar phenomenon is observed for parameter P_ult. Sensitivity to parameter A remains largely stable with displacement load, reflecting only the impact of structural construction errors on the reaction.

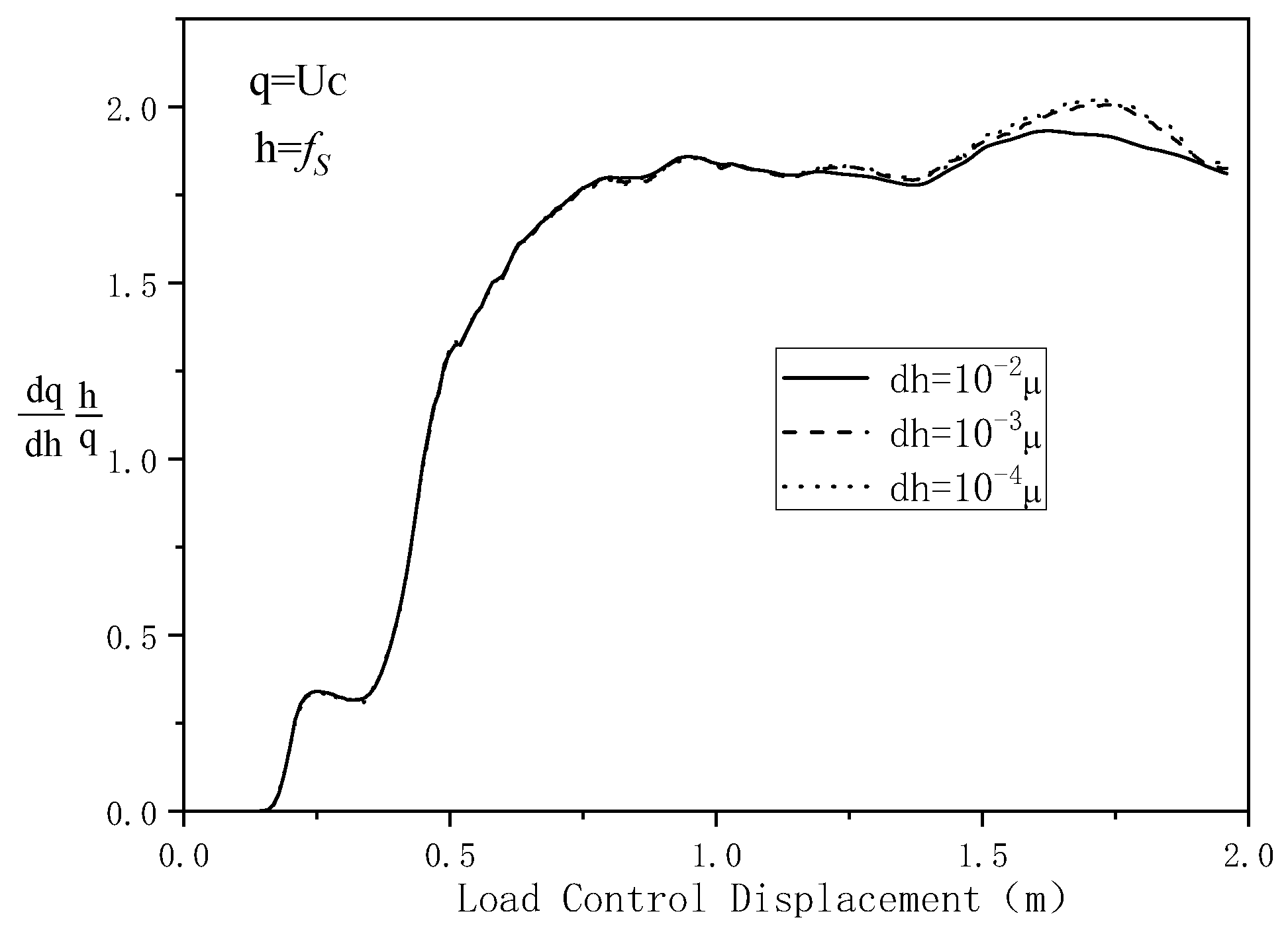
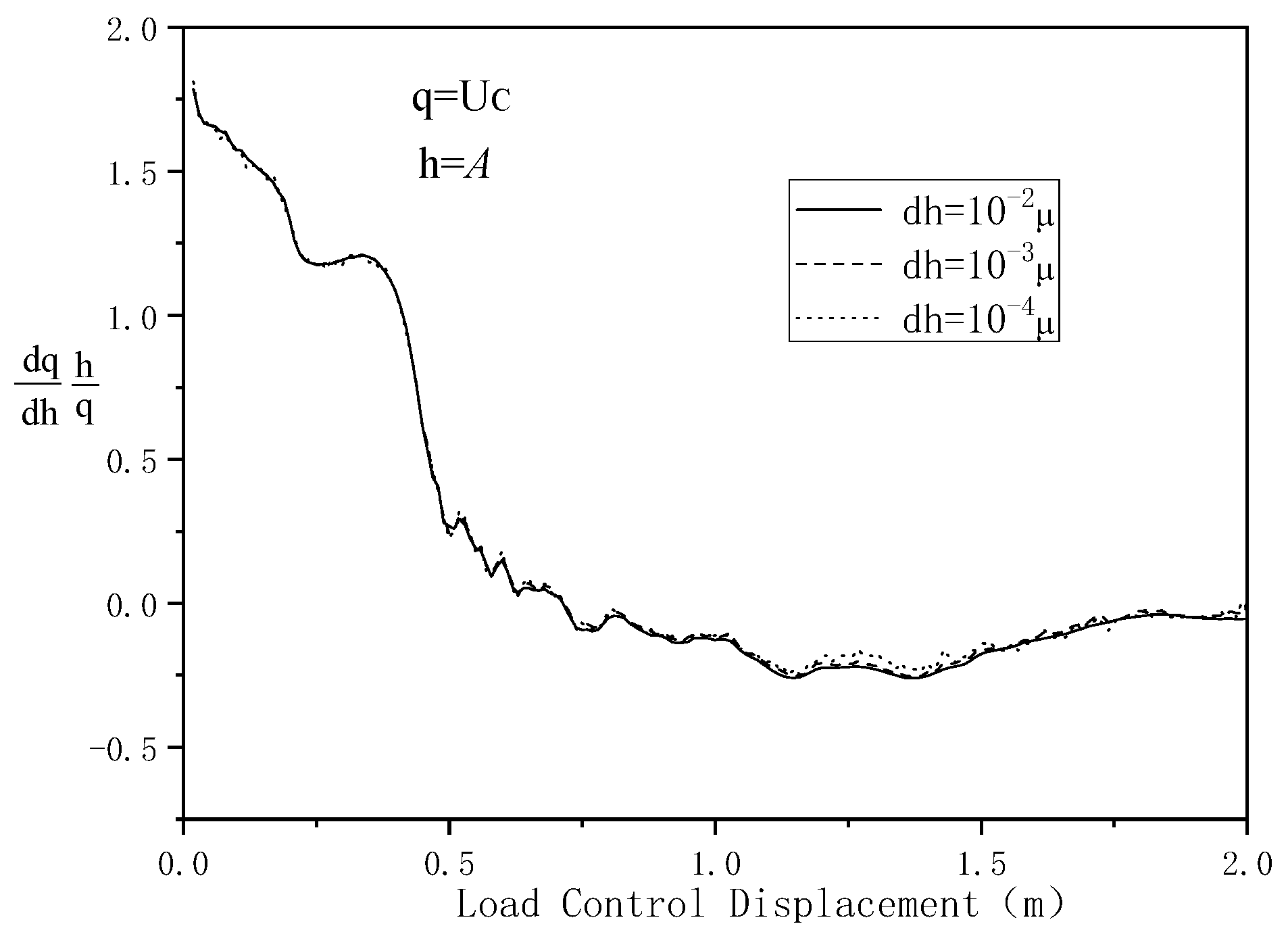
To investigate the impact of differential step size on the response sensitivity calculations, the focus of this study is on the response sensitivities of U_C to f_s, P_ult, and A. In Figure 6, the aforementioned three parameters play a relatively important role in the reaction sensitivity. Figure 7, Figure 8 and Figure 9 show the changes in the response sensitivity values of U_C to f_s, P_ult, and A after considering the differential step size $\Delta h$, with values of ${10}^{-2}\mu$,${10}^{-3}\mu$, and ${10}^{-4}\mu$, respectively. It can be observed that only under larger displacement loading values do the sensitivity values under the three different $\Delta h$ show slight differences. The response sensitivity deviation of U_C to P_ult is the largest, reaching approximately 6%, while the response sensitivity deviation of U_C to A is the smallest, being nearly zero.

In summary, among the various indicators measuring the seismic capacity of group pile foundations, the sensitivity to concrete compressive yield strength is relatively low, while the sensitivity to reinforcing steel tensile yield strength and soil cohesion is relatively high. The sensitivity to the cross-sectional area of the pile core concrete remains relatively stable. Key parameters selected: reinforcing steel tensile yield strength f_s, soil cohesion c, and pile core concrete cross-sectional area A.

5. Development of the Capacity Assessment Model

The seismic capacity of bridge pile group foundations represents one aspect of their seismic performance research. Quantifying the seismic capacity value of pile groups in a rational and efficient manner has long been a challenge. Building upon sensitivity analysis of pile group seismic capacity, the study integrates capacity analysis with a BP neural network model to develop a data-driven assessment model for evaluating the seismic capacity value of pile group foundations. The specific research methodology is illustrated in Figure 10.

5.1. Model Parameter Sampling

This study employs neural networks and data fitting analysis to construct a capacity assessment model, which requires a sufficiently large sample dataset. Latin hypercube sampling (LHS) is a stratified random sampling method widely adopted for its ability to reduce sample size while uniformly increasing sample density.

Based on seismic capacity sensitivity analysis conclusions, the critical model parameters for group pile foundations include the tensile yield strength of reinforcement f_s, soil cohesion c, and the cross-sectional area A of the pile core concrete (taken as the pile diameter d). Considering the characteristics of the research subject, the pile spacing s and the longitudinal reinforcement ratio $\mathsf{\rho }$ of the pile body are also critical parameters in the capacity assessment model. The LHS is performed 1000 times for these five parameters. The pile group layout is designed as 2 × 3. Since the reinforcement ratio correlates with pile diameter, the model adjusts the reinforcement ratio parameter through the reinforcement area A_s. The relationship between reinforcement area and reinforcement ratio is expressed as ${\mathrm{A}}_{\mathrm{s}}={\displaystyle \frac{\mathsf{\pi }}{4}}{\mathrm{d}}^2\mathsf{\rho }$. Therefore, the reinforcement area adjustment factor in the model must also be multiplied by ${\displaystyle \frac{\mathsf{\pi }}{4}}{\mathrm{d}}^2$. The LHS design for model parameters is shown in

Table 1. LHS design for model parameters.

Parameter Name	Original Parameter Value	Parameter Sampling Range	Parameter Adjustment Coefficient	Sampling Step Size
Steel Reinforcement Yield Strength fs	280 MPa	250~330 MPa	0.893~1.179	0.1
Soil cohesion c	50 KPa	30~70 KPa	0.6~1.4	0.01
Pile diameter d	1.8 m	1.2~2.5 m	0.667~1.389	0.001
Pile spacing s	4.65 m	3.5~6.5 m	0.753~1.398	0.001
Reinforcement ratio $\mathsf{\rho }$	1.24%	0.65%~3%	0.524~2.419	0.001

.

5.2. Model Performance Analysis

Based on data from LHS, 1000 sets of analytical models are established. Each model undergoes capacity analysis (Pushover analysis), yielding performance curves. Detailed steps are as follows:

(1)

Identify the most unfavorable pile element within the pile group structure.

(2)

Determine the damage state indicators for the pile body based on internal forces or stresses.

(3)

Identify the corresponding displacement at the cap top for different damage state indicators.

(4)

Calculate the overall ductility of the pile group structure from the displacement.

5.2.1. Determination of the Most Unfavorable Pile Element

For convenience of analysis, the pile plan layout of the FEM model is shown in Figure 11. The six piles have identical longitudinal and transverse spacing of s. Each pile is numbered from 1 to 31, counting from the pile tip to the pile cap.

To identify the most unfavorable pile element, a Pushover analysis is conducted on the original pile group model. The overall Pushover curve for the pile group structure is shown in Figure 12. The distribution of bending moments for each pile element under the maximum push force is extracted and presented in Figure 13. The maximum push force in Figure 12 is 5928.32 kN. As shown in Figure 13, the maximum bending moments in the pile bodies of Piles 1, 2, and 3 are all smaller than those in Piles 4, 5, and 6. This is due to the direction of the horizontal push force loading. Among them, Pile 6 exhibits the largest bending moment in its pile body, occurring in the No. 22 element. The subsequent research in the study will focus primarily on the No. 22 element of Pile 6.

5.2.2. Typical Capacity Curves

The LHS yields 1000 sets of structural key parameters, establishing 1000 analytical models. Capacity analysis (Pushover analysis) is conducted on each model to derive capacity curves. Among these, 10 sets of typical structural key parameters are shown in

Table 2. Parameters of the 10 representative models.

Group ID	Steel Reinforcement Yield Strength (MPa)	Soil Cohesion (KPa)	Pile Diameter (m)	Pile Spacing (m)	Reinforcement Ratio
1	284.48	62.25	1.35	5.57	1.29
2	250.04	34.60	1.94	3.64	2.07
3	278.60	56.20	2.16	6.15	2.35
4	323.68	42.75	2.03	5.71	0.72
5	318.08	52.55	1.51	4.87	2.57
6	301.00	60.00	1.73	6.45	1.90
7	293.72	67.95	2.25	4.28	1.43
8	310.52	30.45	1.65	3.90	2.87
9	272.44	48.15	2.43	5.08	1.62
10	259.84	39.15	1.24	4.42	1.04

, with their capacity curves depicted in Figure 14. As shown in this figure, the push force values for the 10 structural sets exhibit significant dispersion, ranging from a maximum of 9442.17 kN to a minimum of 1983.48 kN. This indicates that the selection of typical structures is reasonably appropriate, effectively covering a broad range of model parameters.

5.2.3. Capacity Failure Indicators

Numerous indicators measure the failure state of group pile foundation, such as cap top displacement (ductility), cap center of gravity rotation angle (ductility), and curvature of the most unfavorable pile cross-section (ductility). Failure states are generally categorized into five types: essentially intact, minor damage, moderate damage, severe damage, and structural collapse.

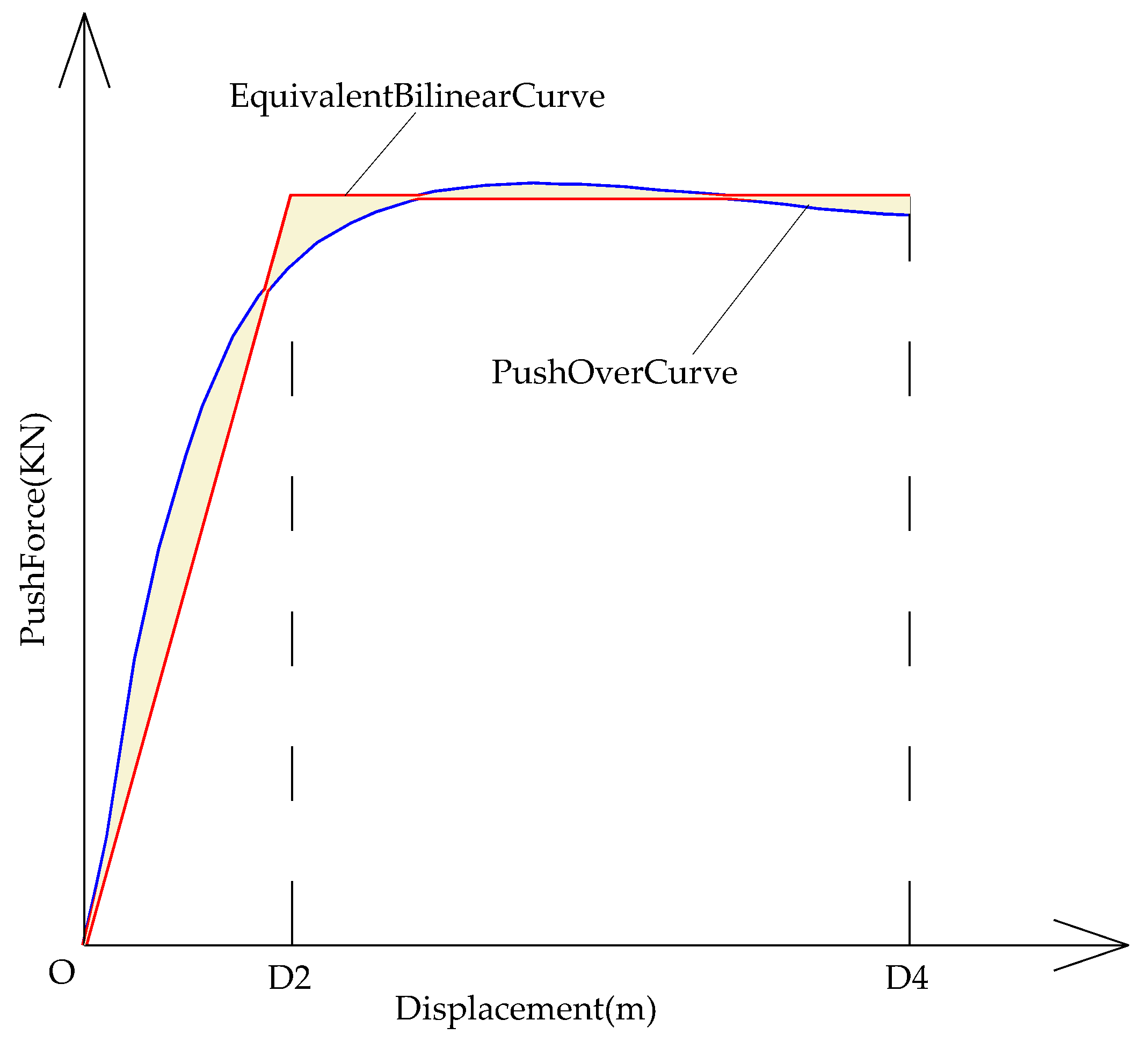
Based on practical considerations, this study defines that the displacement of point A when the tensile stress at the edge reinforcement of the most unfavorable pile cross-section reaches the yield is D1; on the Pushover curve, the equivalent bilinear method is used to obtain the value of D2, as shown in Figure 15; the displacement of point A when the compressive strain at the concrete edges of the non-core zones reaches the limit value is D3; the displacement of point A when the compressive strain at the concrete edges of the core zones reaches the limit value is D4. The overall displacement ductility of the pile group is shown in

Table 3. Capacity failure indicators for group pile.

Destruction Indicators	Pile Cap Top Displacement	Overall Displacement Ductility U
The stress in the edge reinforcement of the tension zone reaches yield	D1	U1 = 1
The equivalent yield point corresponding to the Pushover curve	D2	U2 = D2/D1
The compressive strain at the concrete edge of the non-core zone reaches its limit value	D3	U3 = D3/D1
The compressive strain at the concrete edge of the core zone reaches its limit value	D4	U4 = D4/D1

, and the definition of the failure state is shown in

Table 4. Failure Conditions of Group Pile Foundation.

Damaged State	Judgment Criteria
Essentially intact	U ≤ U1
Minor injury	U1 ≤ U ≤ U2
Moderate injury	U2 ≤ U ≤ U3
Severe injury	U3 ≤ U ≤ U4
Structural failure	U ≥ U4

. In Figure 15, the area enclosed by the Equivalent Bilinear curve and the x-axis is the same as the area enclosed by the Pushover curve and the x-axis.

The overall displacement ductility of the 10 typical model groups is shown in Figure 16. It can be observed that, except for Group 2, the overall displacement ductility values and change patterns of the remaining groups are essentially identical. This discrepancy may be attributed to the relatively low tensile yield strength of the reinforcing steel in Group 2, resulting in a smaller yield displacement and consequently enhanced ductility.

5.3. BP Model Construction

For prediction and fitting tasks in machine learning, BP neural networks, RBF neural networks, single-layer neural networks, and deep neural networks can all be employed. Based on the research subject and structural data characteristics, the BP neural network was selected for modeling.

As noted in Section 5.1, the key parameters for the pile group foundation model are tensile yield strength of reinforcing steel, cohesion of soil, cross-sectional area of pile core concrete (taken as pile diameter), pile spacing within the group foundation, and longitudinal reinforcement ratio of pile bodies. Therefore, the BP model established in this study uses these five parameters as inputs. The outputs are the overall displacement ductility values U2, U3, and U4. Since U1 equals 1, there is no need to treat it as an output parameter.

Based on 1000 sets of model data, a BP neural network model is constructed to predict the overall displacement ductility (U2, U3, and U4). Among them, 900 sets of data are used as training data, and 100 sets of data are used as prediction data. In addition, we select 10 representative sets from the prediction data and present their analysis results [27]. The basic prediction steps are illustrated in Figure 17.

A BP neural network model is constructed in MATLAB R2018b. The data normalization adopts the mapminmax function. The model has 20 hidden layer nodes, 2000 training iterations, a training target error of 1 × 10⁻⁶, and a training learning rate of 0.01. The activation function is the Tanh function, and the training algorithm is the Levenberg–Marquardt algorithm [28]. In addition, setting the parameter net. trainParam.max_fail equals 8, if it exceeds the training, will terminate to prevent overfitting.

After model execution, the residual analysis comparison of prediction results is shown in Figure 18. It can be observed that the residuals between the test data and predicted data for the 10 structural groups are minimal. This is likely attributable to the large database capacity, which enabled the neural network to learn comprehensively and achieve excellent prediction performance.

Table 5. Prediction error of the test dataset.

Evaluation Index	U2	U3	U4
R2 (Coefficient of Determination)	0.992970	0.992970	0.994350
MAE (Mean Absolute Error)	0.010364	0.011515	0.011924
RMSE (Root Mean Square Error)	0.015936	0.017707	0.018645

shows the predictive evaluation of the test dataset, and the results indicate that the predictions are satisfactory.

5.4. Development of Capacity Value Assessment Models

Utilizing existing models and data, nonlinear regression functions between capacity values and model parameters were fitted to construct capacity value assessment models(CVA) for overall displacement ductility (U2, U3, and U4). The capacity value assessment models are expressed as shown in Equation (4).

$${\mathrm{U}}_{\mathrm{i}}=\mathrm{f}(\mathrm{Fs},\mathrm{c},{\mathrm{d}}^2,\mathrm{s},\mathsf{\rho })={ \mathrm{A}}_{\mathrm{i}}·\mathrm{Fs}+{\mathrm{B}}_{\mathrm{i}}·\mathrm{c}+{\mathrm{C}}_{\mathrm{i}}·{\mathrm{d}}^2+{\mathrm{D}}_{\mathrm{i}}·\mathrm{s}+{\mathrm{E}}_{\mathrm{i}}·\mathsf{\rho }$$

(4)

where Fs represents tensile yield strength of reinforcement (MPa), c represents cohesion of soil (kPa), d represents pile diameter (m), s represents pile spacing (m), $\mathsf{\rho }$ represents reinforcement ratio (%). A_i, B_i, C_i, D_i, and Ei represent the regression coefficients for the corresponding parameters, i = 2, 3, 4.

In practice, design engineers need a fast and simple method to obtain the seismic resistance of pile group structures, and combine it with the seismic response requirements of pile groups to carry out seismic design of pile group structures.

The CVA regression model can integrate structural parameters, soil characteristics, deformation control, strength, and performance-based design together, which is exactly the practical computational model that engineers need [29].

5.4.1. Regression Coefficients for Capacity Values

Based on 1000 sets of model data, regression analysis was performed on Equation (3) to derive regression equations for overall displacement ductility (U2, U3, and U4). The regression coefficients are shown in

Table 6. Regression coefficients and root mean square error.

Displacement Ductility	${\mathbf{A}}_{\mathbf{i}}$	${\mathbf{B}}_{\mathbf{i}}$	${\mathbf{C}}_{\mathbf{i}}$	${\mathbf{D}}_{\mathbf{i}}$	${\mathbf{E}}_{\mathbf{i}}$	Root Mean Square Error
U2	0.0017	0.0015	0.24	0.0139	0.0974	1.905
U3	0.0019	0.0017	0.2667	0.0155	0.1083	1.532
U4	0.0018	0.0012	0.3858	0.0162	0.1225	1.789

. The regression results indicate that C_i is greater than the other parameters, primarily due to the relatively small pile diameter values, which increase its regression coefficient.

5.4.2. Validation of Capacity Value Regression Formula

To validate the regression formula, both the capacity value regression formula and the BP model are used to predict the overall displacement ductility (U2, U3, and U4) of the structure, and the results are compared. Validation data utilized the structural data from the 10 typical models listed in Table 2. The comparison of overall displacement ductility validation results is shown in Figure 19, Figure 20 and Figure 21.

5.5. Discussion

When the pile diameter is used as a nonlinear parameter in regression analysis for the capacity value assessment model, the regression coefficient C_i exhibits a higher value than the other parameters. This is primarily due to the relatively small value of the pile diameter, which amplifies its regression coefficient. The regression analysis results are influenced by the characteristics of the original data. If the other four parameters in the model are also selected as nonlinear terms, the establishment of the capacity assessment model would become arbitrary, and its physical significance would be difficult to interpret.

For example, establishing a nonlinear capacity value assessment model as shown in Equation (5).

$${\mathrm{U}}_{\mathrm{i}}=\mathrm{f}({\mathrm{Fs}}^{0.5}, \mathrm{c},{ \mathrm{d}}^2, \mathrm{s} ,\mathsf{\rho })={ \mathrm{A}}_{\mathrm{i}}·{\mathrm{Fs}}^{0.5}+{\mathrm{B}}_{\mathrm{i}}·\mathrm{c}+{\mathrm{C}}_{\mathrm{i}}·{\mathrm{d}}^2+{\mathrm{D}}_{\mathrm{i}}·\mathrm{s}+{\mathrm{E}}_{\mathrm{i}}·\mathsf{\rho }$$

(5)

where Fs represents tensile yield strength of reinforcement (MPa), c represents cohesion of soil (kPa), d represents pile diameter (m), s represents pile spacing (m), $\mathsf{\rho }$ represents reinforcement ratio (%). A_i, B_i, C_i, D_i, and Ei represent the regression coefficients for the corresponding parameters, i = 2, 3, 4.

In Equation (5), the parameter Fs is defined as a nonlinear parameter. Based on 1000 sets of model data, nonlinear regression analysis of Equation (4) can also yield regression equations for overall displacement ductility (U2, U3, and U4). However, the physical significance of Fs^0.5 in the Equation cannot be explained clearly.

Figure 22 shows the comparison of regression results between Equation (3) and Equation (4), indicating that in this study, the effect of nonlinear regression is not as good as that of linear regression. In view of that some parameters in nonlinear regression in Equation (4) have unclear physical meanings, careful consideration is needed when choosing to use complex nonlinear regression formulas.

Although this study is based on a finite element model of a specific pile foundation case and draws research conclusions, the modeling method, data extraction method, neural network model construction, and prediction method provided in this study all have certain generalization ability.

According to the problem-solving approach presented in this article, it is possible to change the soil type and pile configuration, quickly build new models, and obtain corresponding results. Even researchers can be arranged to systematically apply this method to obtain a set of CVA regression models for a certain pile foundation in a certain area, which can be used as a reference for local engineers.

6. Conclusions

In order to assess the seismic capacity of bridge group pile foundations under seismic loads rapidly. The BP model is built using seismic sensitivity analysis and Latin hypercube samples. The overall displacement ductility indicators of the structure are defined, and the capacity value assessment model (CVA) is constructed through regression analysis.

(1)

Among the various indicators measuring the seismic capacity of group pile foundations, the response sensitivity to concrete compressive yield strength is relatively low, while sensitivity to reinforcing steel tensile yield strength and soil cohesion is relatively high. The response sensitivity to the cross-sectional area of the pile core concrete remains relatively stable. Considering all factors comprehensively, the key parameters selected are tensile yield strength of reinforcement, cohesion of soil, cross-sectional area of core concrete (pile diameter), pile spacing, and longitudinal reinforcement ratio of the pile.

(2)

The displacement ductility of the pile group foundations is determined based on the tensile stress at the edge reinforcement of the most unfavorable pile cross-section, the compressive strain at the concrete edges of the core and non-core zones, and the displacement at the cap top. This defines the failure states of the foundation structure, which include essentially intact, minor damage, moderate damage, severe damage, and structural collapse.

(3)

Through 1000 Latin hypercube sampling iterations, 1000 analytical models are established to derive capacity curves and an analytical capacity database, enabling the construction of a BP neural network model. The developed BP model effectively predicts the overall displacement ductility indicators of the structure.

(4)

Using existing data, a regression function was fitted between the model capacity indicators and critical parameters. The constructed capacity value assessment model yielded results that closely matched the BP model predictions, demonstrating the model’s reliability. This provides a novel approach for disaster prediction in bridge pile foundation systems.

This study is based on a specific case, and the scope of the research object is not wide, so the applicability of the research results is relatively narrow. However, according to the problem-solving approach presented in this article, it is possible to change soil types and pile configurations, quickly build new models, and obtain a corresponding set of pile foundation CVA regression models, which can expand the application scope.

In later research, the seismic demand research and capacity research of bridge pile foundations can be combined to form a comprehensive seismic theory system for bridge pile foundations based on data-driven methods.