Theoretical and Experimental Evaluations on Cooperative Bending Behavior of Laminated Channel Beams in Modular Steel Buildings
Abstract
1. Introduction
2. Design of Laminated Beam Structures in Modular Steel Buildings
3. Theoretical Analysis of the Synergistic Flexural Deflection Curve of Laminated Channel Beams in Modular Steel Buildings
3.1. Theoretical Analysis Strategy for the Laminated Beams in Modular Steel Buildings
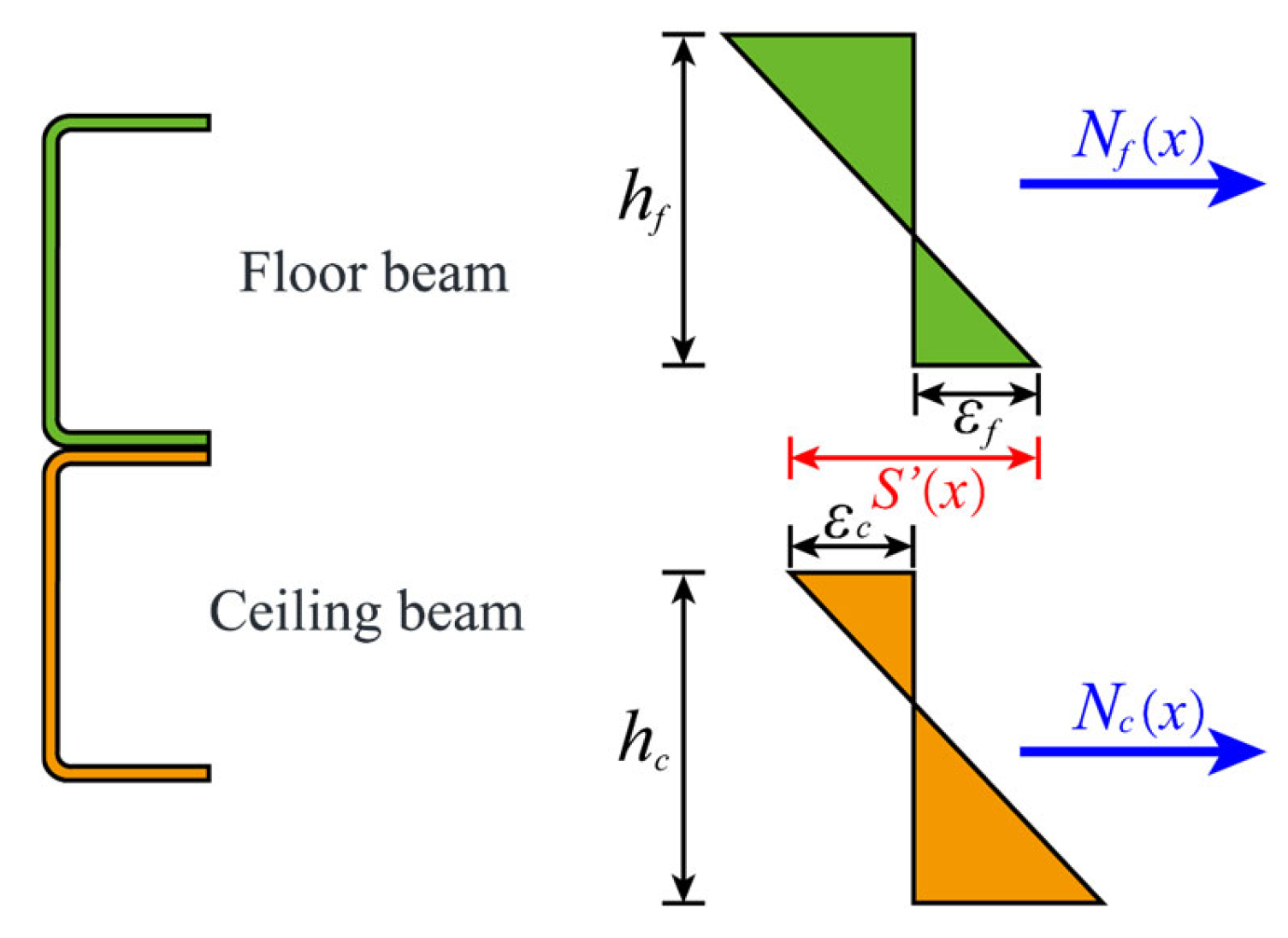
3.2. Theoretical Model of the Deflection Curve for Laminated Beams with Only Friction Restraints in Modular Steel Buildings
3.3. Theoretical Model of the Deflection Curve for Laminated Double Beams That Are Point-Connected in Modular Steel Buildings
3.4. Theoretical Model of the Deflection Curve for Pure Friction Laminated Beams with Fixed Supports in Modular Steel Buildings
3.5. Theoretical Model of the Deflection Curve for Point-Connected Laminated Beams with Fixed Supports in Modular Steel Buildings
4. Equivalent Initial Bending Stiffness Laminated Beams in Modular Steel Buildings
5. Experimental Investigation of the Bending Performance of Laminated Beams in Modular Steel Buildings
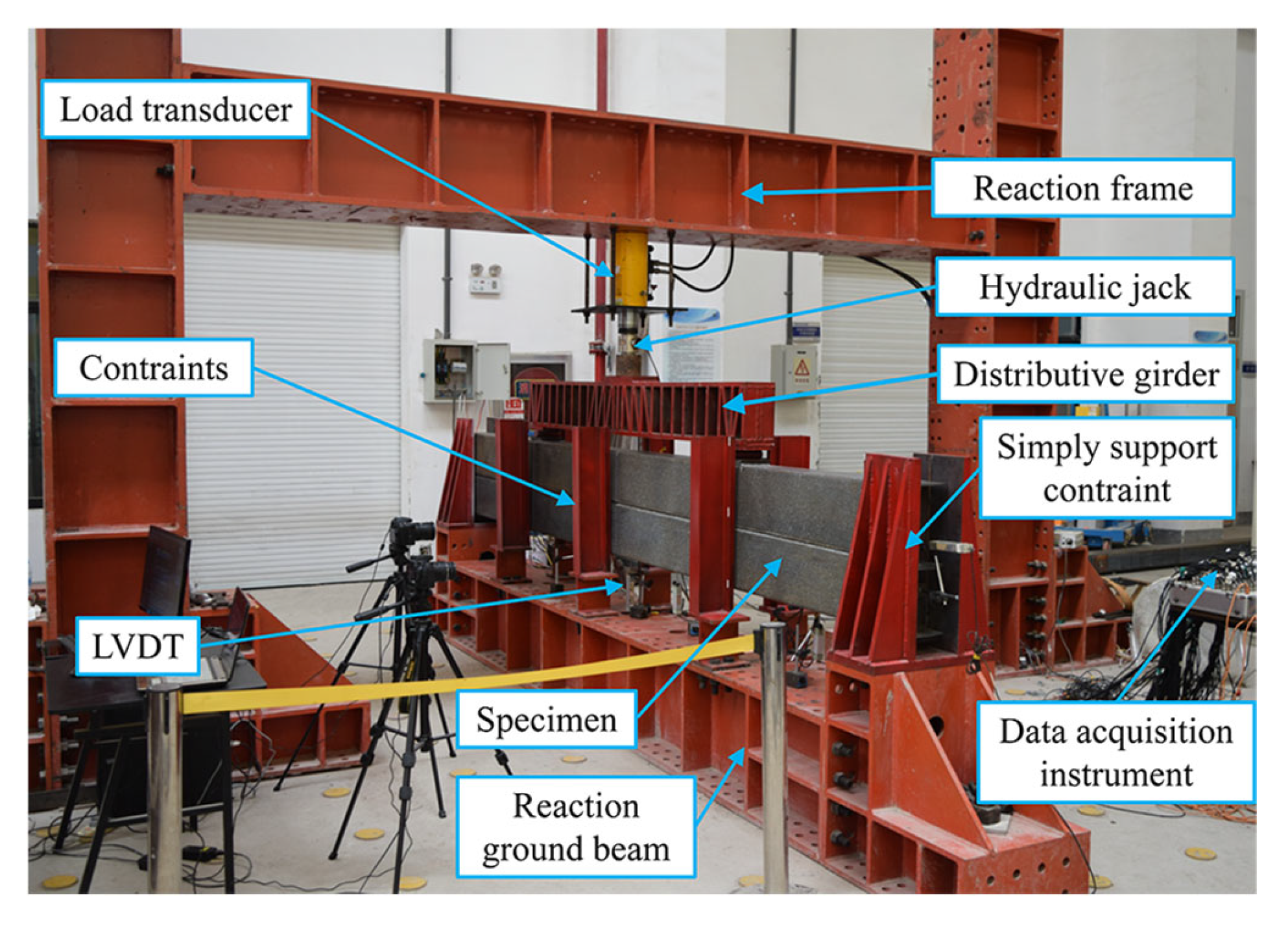
5.1. Set-Up of Bending Tests for the Laminated Beam Specimens
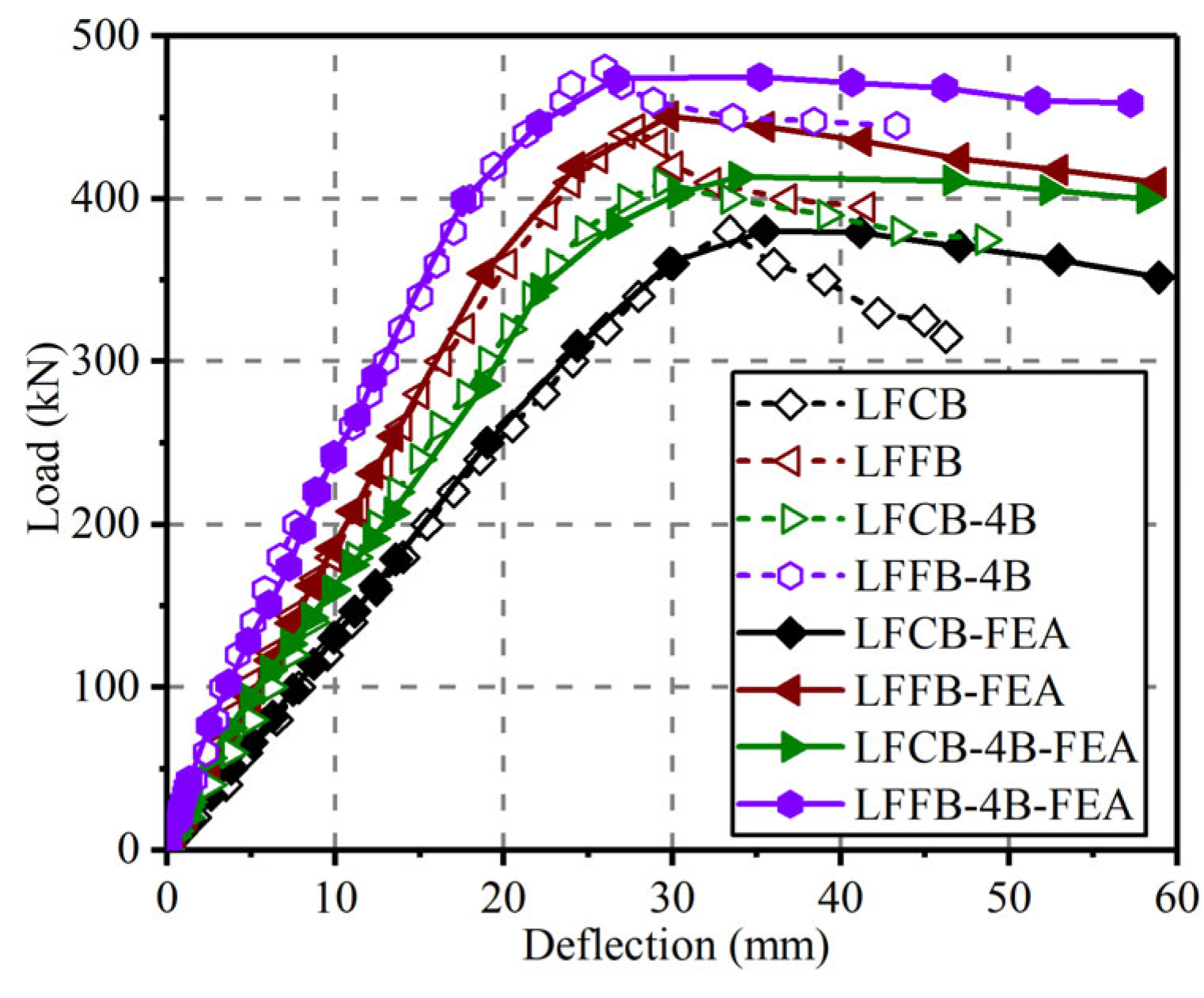
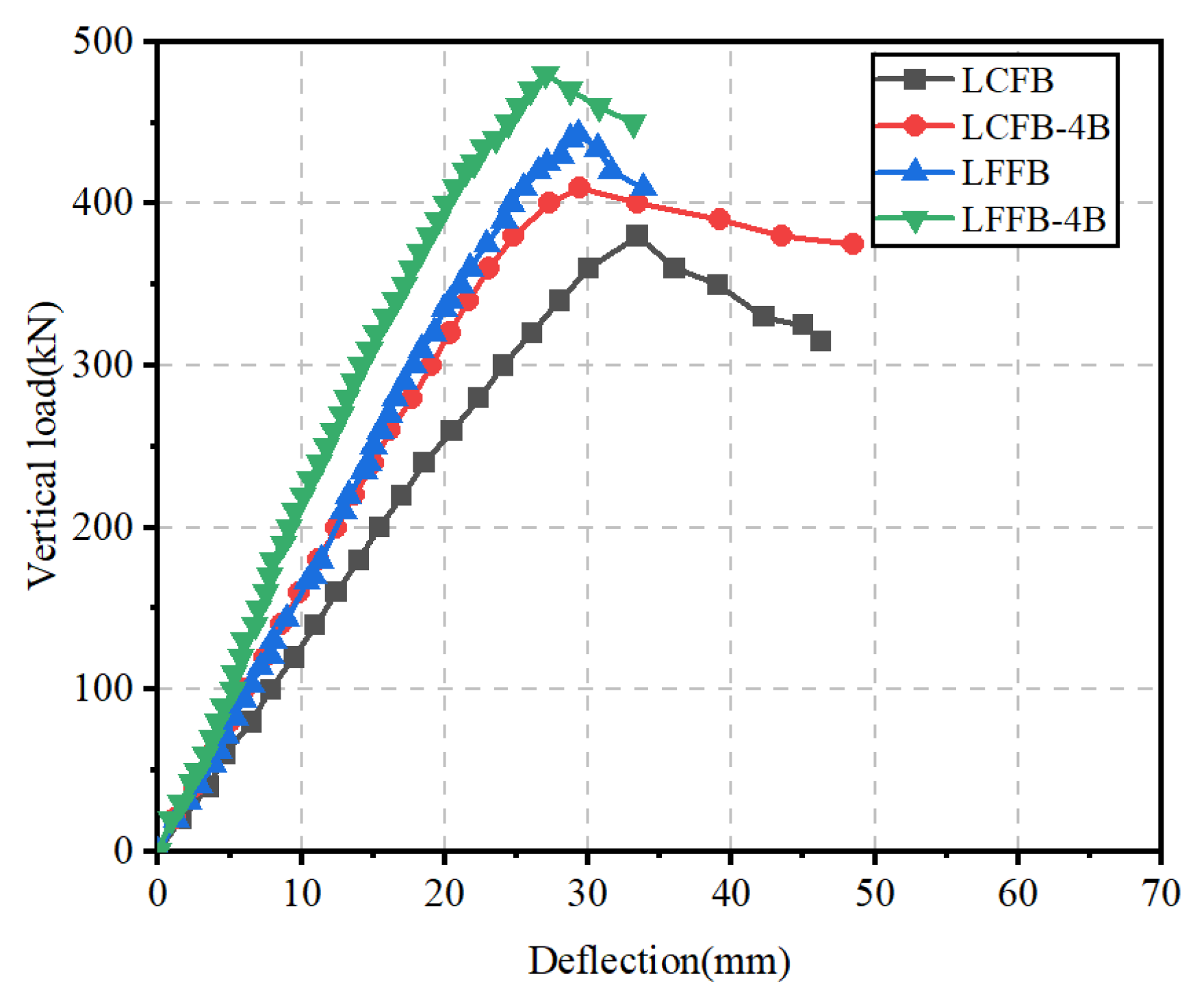
5.2. Flexural Performance of Modular Laminated Beam Specimens
6. Finite Element Modeling and Parametric Analysis of Laminated Beams in Modular Steel Buildings
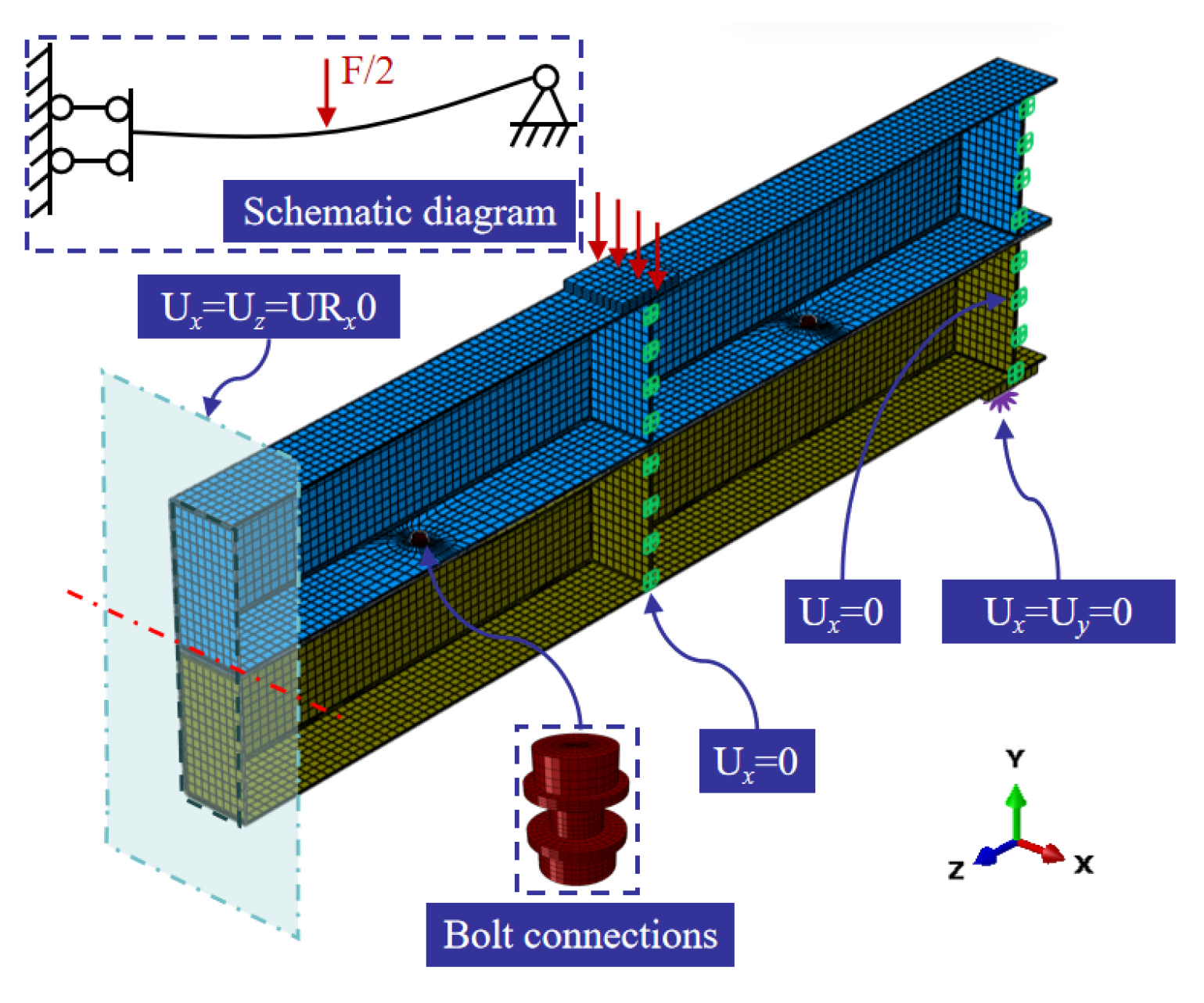
6.1. Finite Element Modeling of Laminated Beam Specimens
6.2. Validation of Finite Element Models
6.3. Parametric Study of Laminated Beam
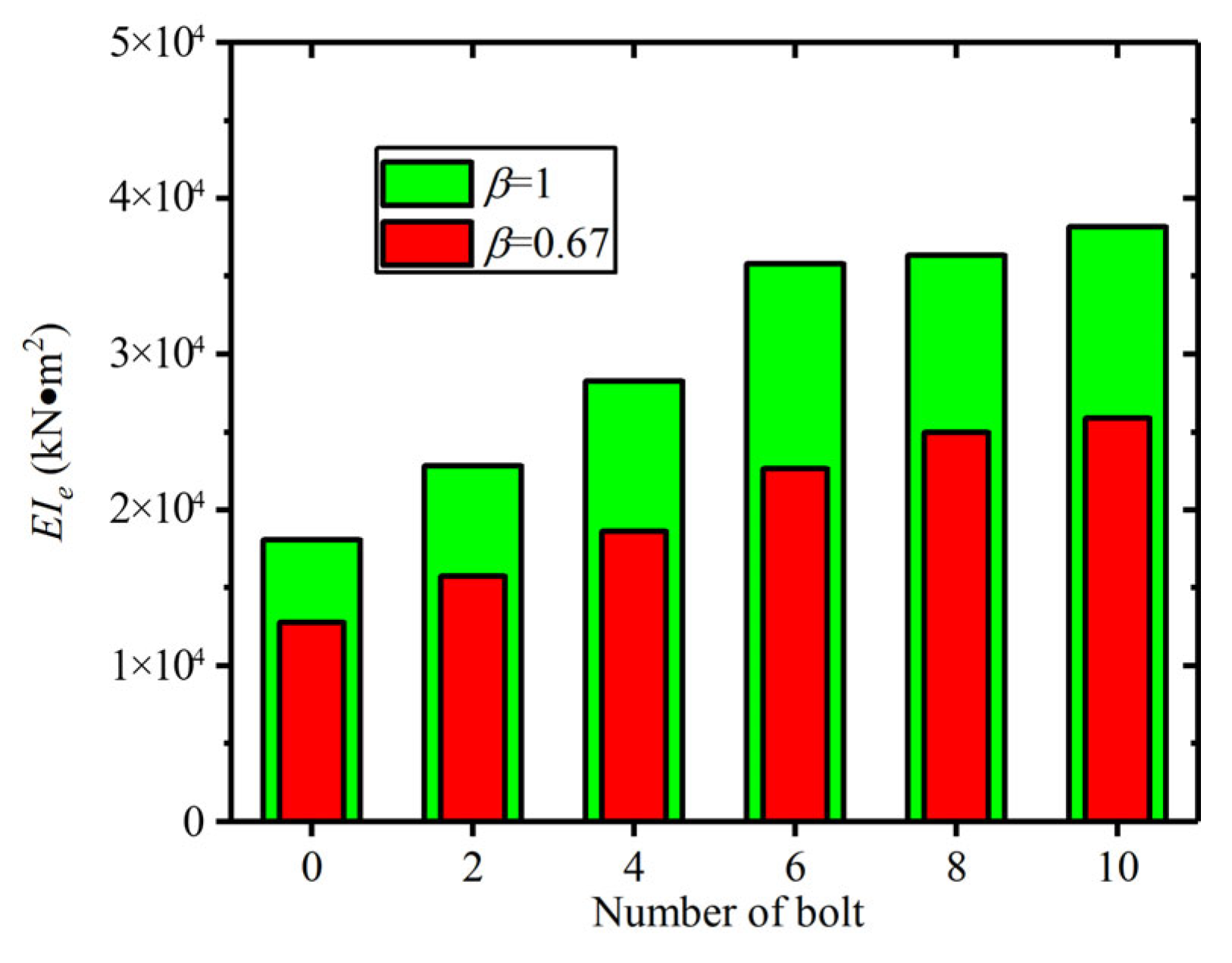
6.3.1. Influence of Bolt Number (n)
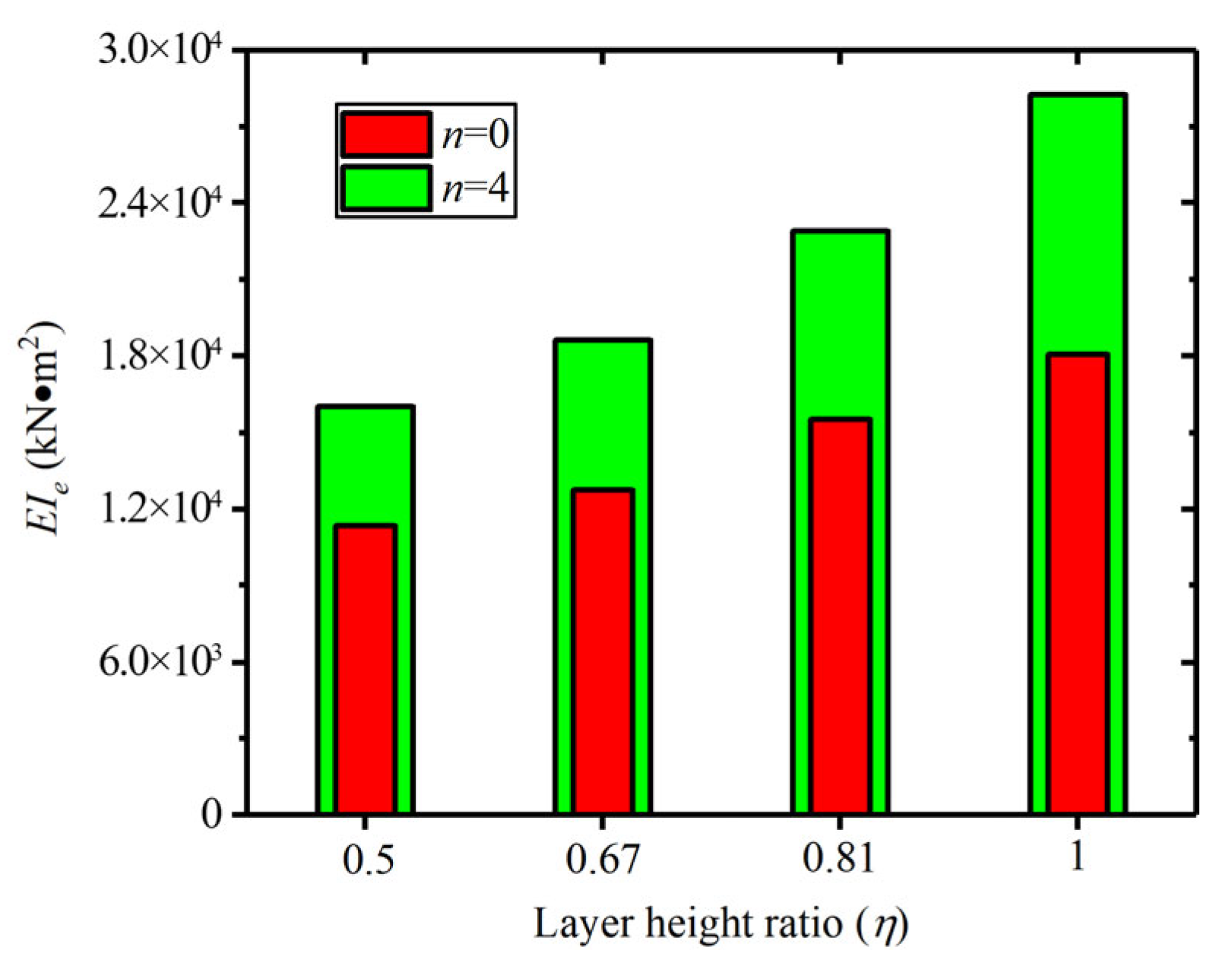
6.3.2. Influence of Layer Height Ratio (η)
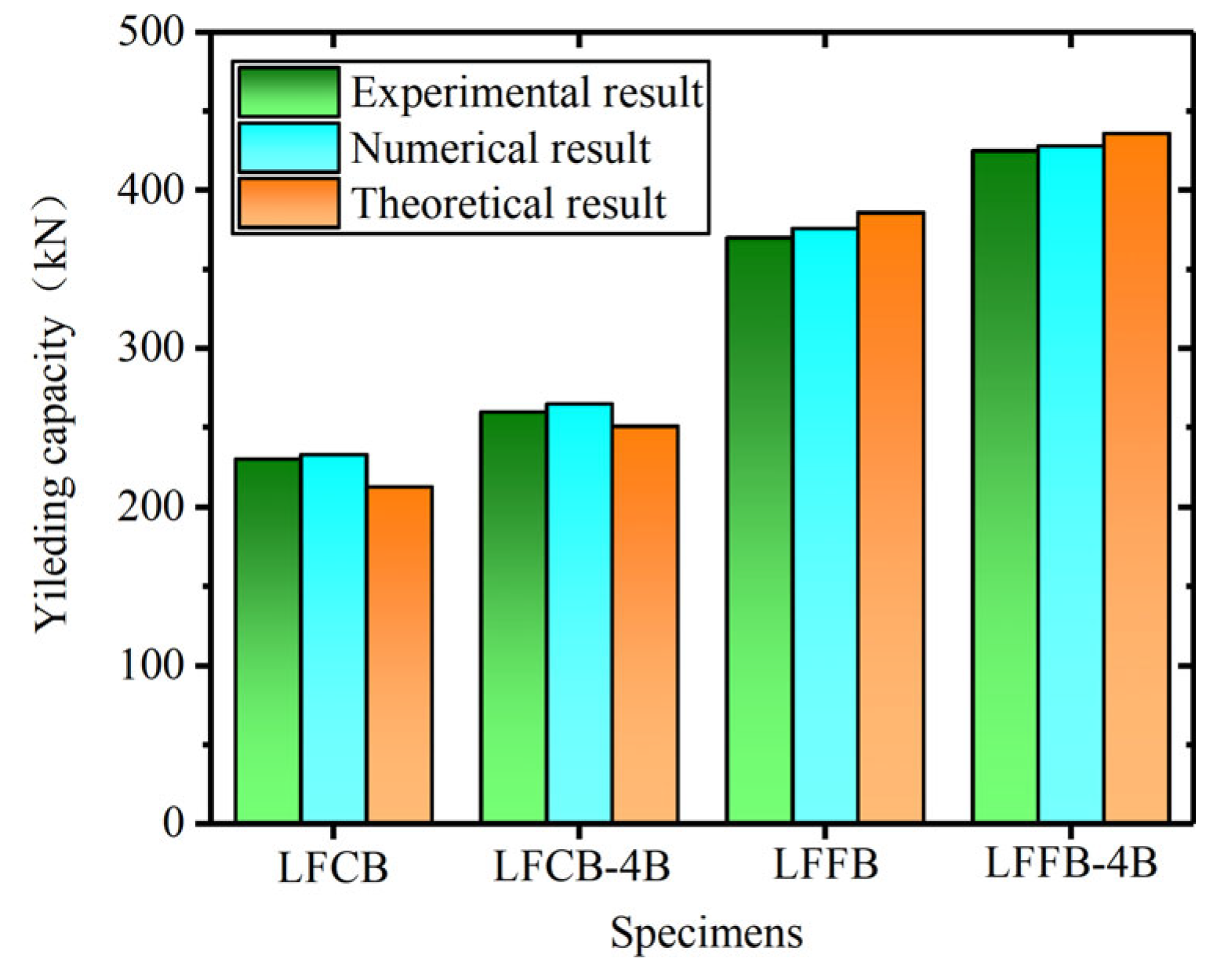
7. Validation of Theoretical Results by Experimental and Numerical Data
8. Conclusions
- Compared with pure friction laminated double beams, bolted laminated double beams in modular steel buildings exhibit significantly improved flexural performance, with load-bearing capacity increased by approximately 8% and initial flexural stiffness increased by 17% to 28%.
- Based on the fundamental differential equation of the typical double-beam segment, the analytical expressions for interfacial slipping strain were established. Then, the theoretical models of interfacial slippage were developed for the modular laminated steel beams with different connections.
- By applying the boundary conditions of simply supported beams, the mathematical expressions were derived for the curvature of modular laminated beams, considering the relative slipping behaviors. In this way, the accurate analytical solutions for deflection and rotation were ultimately obtained.
- More importantly, the initial bending stiffness of laminated beams was theoretically calculated and validated by experimental results, which effectively quantitatively characterized the collaborative bending effect of double beam structures and significantly provided the dependable theoretical basis for the practical design of modular steel buildings.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pasquire, C.L.; Gibb, A.G.F. Considerations for assessing the benefits of standardisation and pre-assembly in construction. J. Financ. Manag. Prop. Constr. 2002, 7, 1–22. [Google Scholar]
- Chen, Z.; Liu, J.; Yu, Y. Experimental study on interior connections in modular steel buildings. Eng. Struct. 2017, 147, 625–638. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, J.; Liu, J.; Khan, K. Seismic behavior and moment transfer capacity of an innovative self-locking inter-module connection for modular steel building. Eng. Struct. 2021, 245, 112978. [Google Scholar] [CrossRef]
- Corfar, D.-A.; Tsavdaridis, K.D. Tsavdaridis, A comprehensive review and classification of inter-module connections for hot-rolled steel modular building systems. J. Build. Eng. 2022, 50, 104006. [Google Scholar] [CrossRef]
- Deng, E.-F.; Du, Y.-P.; Gao, J.-D.; Zhang, Z.; Wang, Y.-B. Seismic performance of an innovative self-centering and repairable connection with SMA bolts in modular steel construction. Thin-Wall Struct. 2024, 205, 112377. [Google Scholar] [CrossRef]
- Khan, K.; Chen, Z.; Liu, J.; Tsavdaridis, K.D. Compressive behaviors of corner-supported modular steel sway frames with rotary inter-modular connections. Thin-Wall Struct. 2023, 193, 111245. [Google Scholar] [CrossRef]
- Lacey, A.W.; Chen, W.; Hao, H.; Bi, K. Structural response of modular buildings—An overview. J. Build. Eng. 2018, 16, 45–56. [Google Scholar] [CrossRef]
- Lacey, A.W.; Chen, W.; Hao, H.; Bi, K. Review of bolted inter-module connections in modular steel buildings. J. Build. Eng. 2019, 23, 207–219. [Google Scholar] [CrossRef]
- Lawson, R.M.; Ogden, R.G.; Bergin, R. Application of modular construction in high-rise buildings. J. Archit. Eng. 2001, 118, 148–154. [Google Scholar] [CrossRef]
- Khan, K.; Chen, Z.; Liu, J.; Tsavdaridis, K.D. Tsavdaridis, Experimental and analytical investigations on compression behaviors of rotary-connected sway column-supported steel modular interior frames. J. Build. Eng. 2023, 78, 107692. [Google Scholar] [CrossRef]
- Lacey, A.W.; Chen, W.; Hao, H.; Bi, K. New interlocking inter-module connection for modular steel buildings: Experimental and numerical studies. Eng. Struct. 2019, 198, 109465. [Google Scholar] [CrossRef]
- Lacey, A.W.; Chen, W.; Hao, H.; Bi, K. Lateral behaviour of modular steel building with simplified models of new inter-module connections. Eng. Struct. 2021, 236, 112103. [Google Scholar] [CrossRef]
- Lacey, A.W.; Chen, W.; Hao, H.; Bi, K. New interlocking inter-module connection for modular steel buildings: Simplified structural behaviours. Eng. Struct. 2021, 227, 111409. [Google Scholar] [CrossRef]
- Mostafaei, H.; Barmchi, M.A.; Bahmani, H. Bahmani, Seismic Resilience and Sustainability: A Comparative Analysis of Steel and Reinforced Structures. Buildings 2025, 15, 1613. [Google Scholar] [CrossRef]
- Li, J.; Deng, L.; Sang, D.; Wang, D. Experimental research on flexural behaviour of laminated steel beams. Ind. Constr. 2015, 45, 115–118+45. [Google Scholar]
- Li, J.; Sang, D.; Wang, D.; Li, L. Experimental Research on Laminated Steel Beamswith Non-continuous Connectors. Struct. Eng. 2013, 29, 125–131. [Google Scholar]
- Chang, H.; Hu, L.; Song, X.; Qin, F.; An, A.; Zhang, S. Experimental test and parametric analysis on flexural performance of laminated square tubular beams in steel box module. J. China Univ. Min. Technol. 2022, 52, 540–549. [Google Scholar]
- Zhang, A.; Liu, J.; Chen, Z.; Chen, T. Bending behavior of detachable tapered-head bolt inter-module connection of steel modular structure. J. Constr. Steel Res. 2024, 220, 108829. [Google Scholar] [CrossRef]
- Zhang, A.L.; Guo, Z.P.; Liu, X.C.; Li, C. Global stability coefficient of prefabricated beams with dual-channel combined section. Eng. Mech. 2018, 35, 67–75. [Google Scholar]
- Zha, X.; Zhai, X.; Wang, Q. Mechanical properties of assembled frame connected bydouble-beam and double-column angle jointswithout on site welding. J. Build. Struct. 2018, 39, 8–15. [Google Scholar]
- Zhai, X.M.; Xiong, C.X.; Gan, Y.L. Experimental study and numerical simulation on assembled frame with double-beam multi-column joints. J. Harbin Inst. Technol. 2020, 52, 81–87. [Google Scholar]
- Zhu, Y.; Zhao, J. Experimental and numerical study on member classification of I-section plate girders. J. Constr. Steel Res. 2017, 137, 192–200. [Google Scholar] [CrossRef]
- Xu, B.; Xia, J.; Chang, H.; Ma, R.; Zhang, L. A comprehensive experimental-numerical investigation on the bending response of laminated double channel beams in modular buildings. Eng. Struct. 2019, 200, 109737. [Google Scholar] [CrossRef]
- Xu, B.; Xia, J.; Chang, H.; Ma, R.; Zhang, L. Flexural behaviour of pairs of laminated unequal channel beams with different interfacial connections in corner-supported modular steel buildings. Thin-Wall Struct. 2020, 154, 106792. [Google Scholar] [CrossRef]
- Xu, B.; Xia, J.; Chang, H.; Ma, R.; Zhang, L. Evaluation of superimposed bending behaviour of laminated channel beams in modular steel buildings subjected to lateral load. Thin-Wall Struct. 2022, 175, 109234. [Google Scholar] [CrossRef]
- Xu, B.; Xia, J.; Chang, H.; Ma, R.; Zhang, L. Experimental and numerical investigation on the lateral force resistance of modular steel sub-frames with laminated double beam. J. Build. Eng. 2022, 46, 103666. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Xia, J.; Ma, R.; Chang, H.; Yang, C.; Zhang, L. Investigation on interfacial slipping response of laminated channel beams with bolt connections in modular steel buildings. J. Build. Eng. 2023, 63, 105441. [Google Scholar] [CrossRef]
- Handbook for the Design of Modular Structures; CRC Press: Boca Raton, FL, USA, 2017.
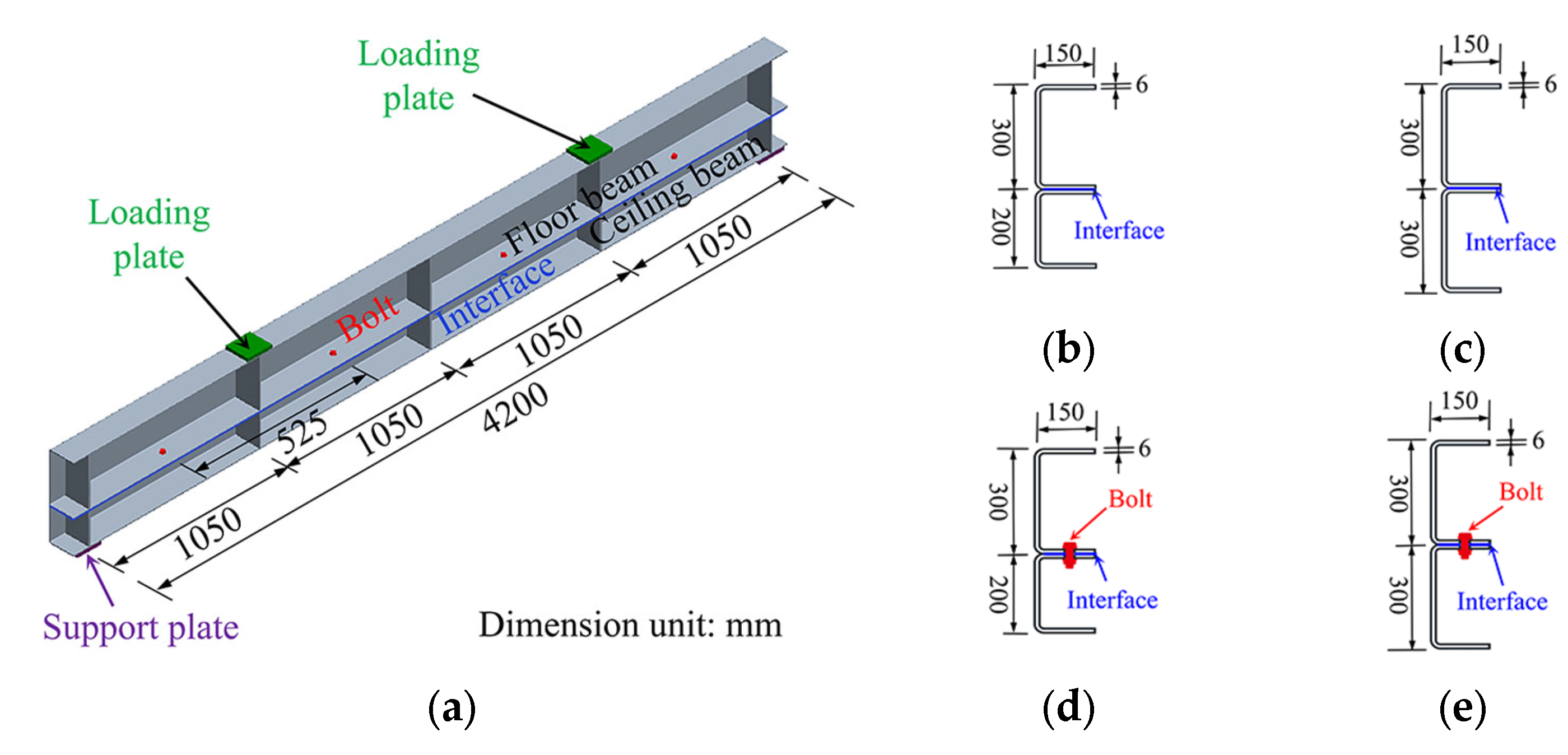
| Specimen | Floor Beam hu × w × tb | Ceiling Beam hu × w × tb | lc | l0 | li |
|---|---|---|---|---|---|
| LFCB | 300 × 150 × 6 | 200 × 150 × 6 | 1550 | 4200 | 500 |
| LFFB | 300 × 150 × 6 | 300 × 150 × 6 | 1550 | 4200 | 600 |
| LFCB-4B | 300 × 150 × 6 | 200 × 150 × 6 | 1550 | 4200 | 500 |
| LFFB-4B | 300 × 150 × 6 | 300 × 150 × 6 | 1550 | 4200 | 600 |
| Fexp (kN) | Dfal (mm) | Sini (kN·m) | Ksec (kN/m) | Hcap | Hins | Hses | |
|---|---|---|---|---|---|---|---|
| LFCB | 380 | 33.42 | 1.35 × 106 | 1.14 × 103 | — | — | — |
| LFFB | 443 | 27.81 | 2.11 × 106 | 1.59 × 103 | — | — | — |
| LFCB-4B | 410 | 29.43 | 1.72 × 106 | 1.39 × 103 | 7.89% | 27.4% | 21.9% |
| LFFB-4B | 480 | 25.99 | 2.69 × 106 | 1.85 × 103 | 8.35% | 27.4% | 16.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Liu, Y.; Li, L.; Zheng, Y.; Chang, H.; Yin, Q.; Du, Z.; Xu, B. Theoretical and Experimental Evaluations on Cooperative Bending Behavior of Laminated Channel Beams in Modular Steel Buildings. Buildings 2025, 15, 4221. https://doi.org/10.3390/buildings15234221
Liu R, Liu Y, Li L, Zheng Y, Chang H, Yin Q, Du Z, Xu B. Theoretical and Experimental Evaluations on Cooperative Bending Behavior of Laminated Channel Beams in Modular Steel Buildings. Buildings. 2025; 15(23):4221. https://doi.org/10.3390/buildings15234221
Chicago/Turabian StyleLiu, Rui, Yong Liu, Lin Li, Yuchao Zheng, Hongfei Chang, Qixiang Yin, Zibo Du, and Bo Xu. 2025. "Theoretical and Experimental Evaluations on Cooperative Bending Behavior of Laminated Channel Beams in Modular Steel Buildings" Buildings 15, no. 23: 4221. https://doi.org/10.3390/buildings15234221
APA StyleLiu, R., Liu, Y., Li, L., Zheng, Y., Chang, H., Yin, Q., Du, Z., & Xu, B. (2025). Theoretical and Experimental Evaluations on Cooperative Bending Behavior of Laminated Channel Beams in Modular Steel Buildings. Buildings, 15(23), 4221. https://doi.org/10.3390/buildings15234221