Structural Performance and Failure Mechanisms in Bend Loading of Steel-Aerated Concrete Fire Wall Composite Panels
Abstract
1. Introduction
2. Experimental Analysis
2.1. Testing Material Properties of the Panel Constituents and the Seam Strength
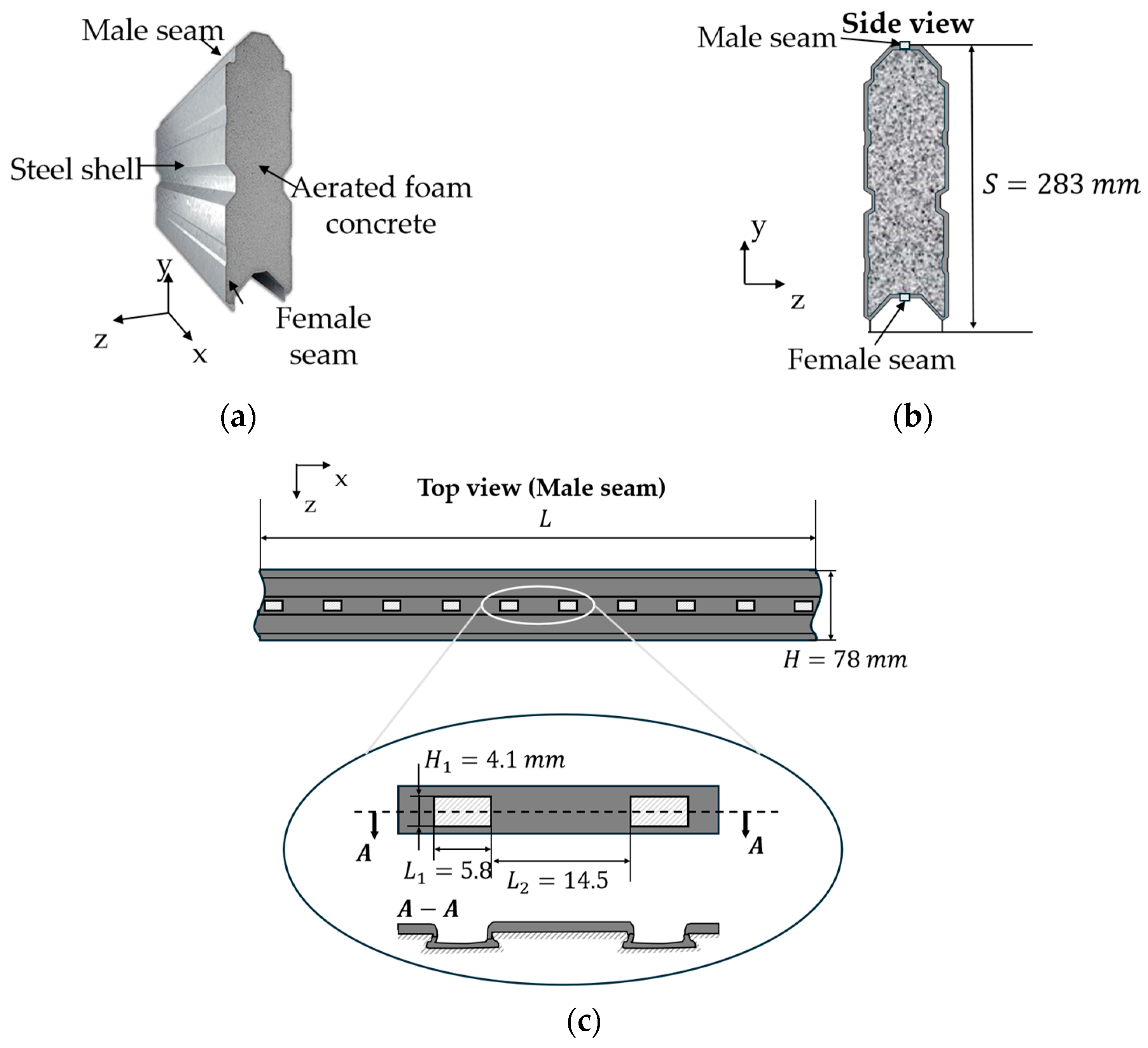
2.1.1. Analysis of the Mechanical Properties of the Outer Steel Shell Material
2.1.2. Analysis of the Aerated Core Structure and Density
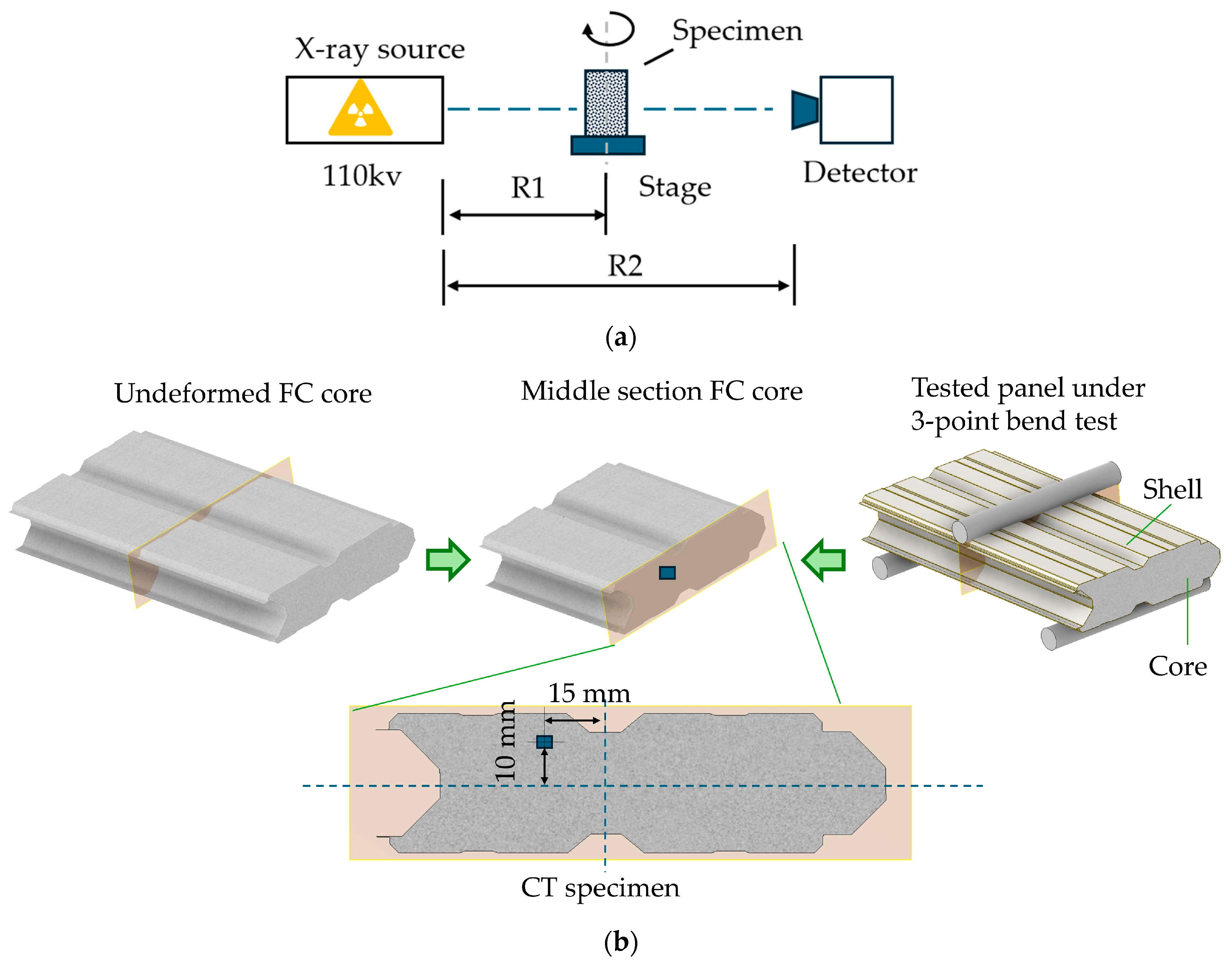
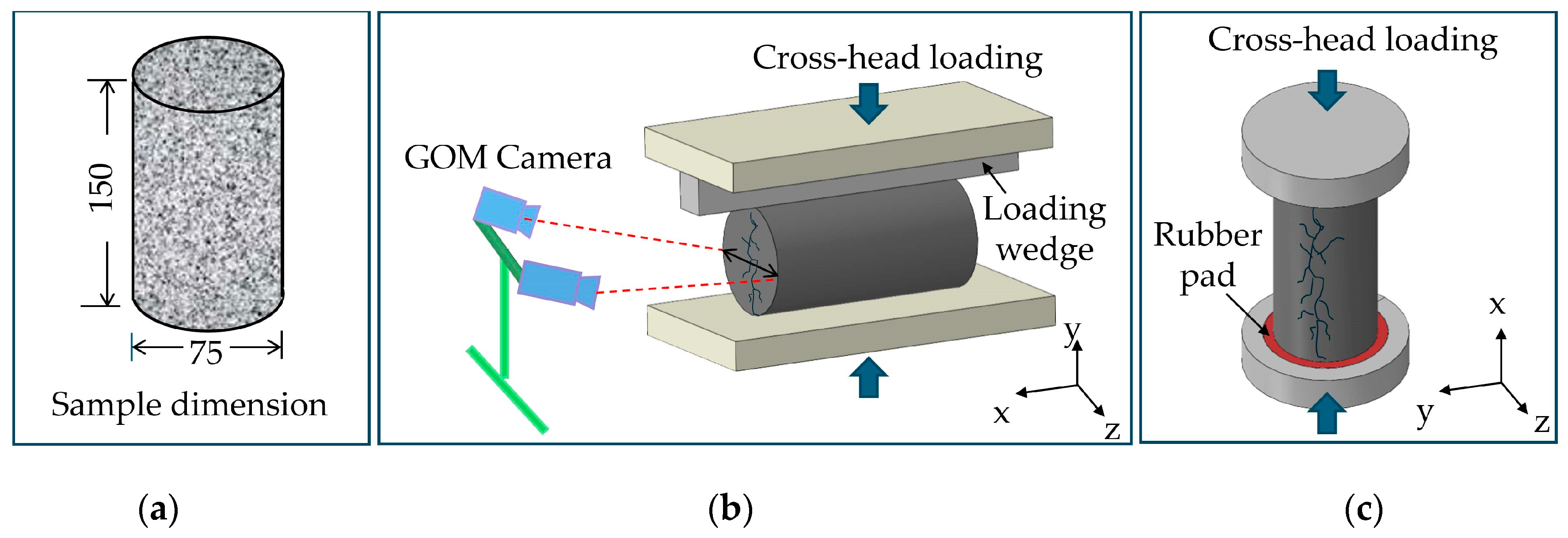
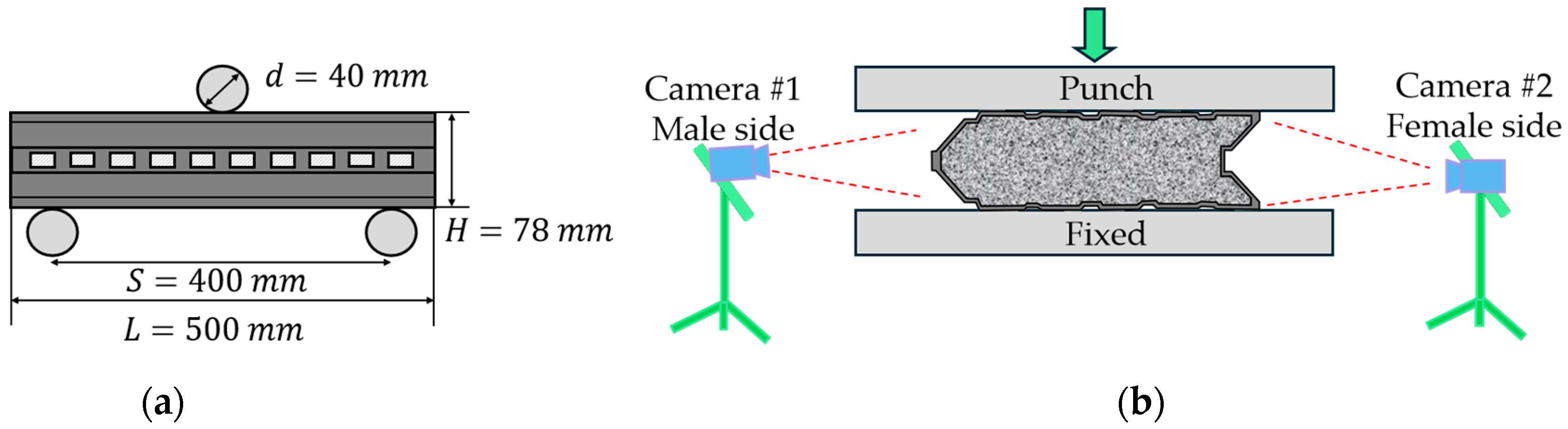
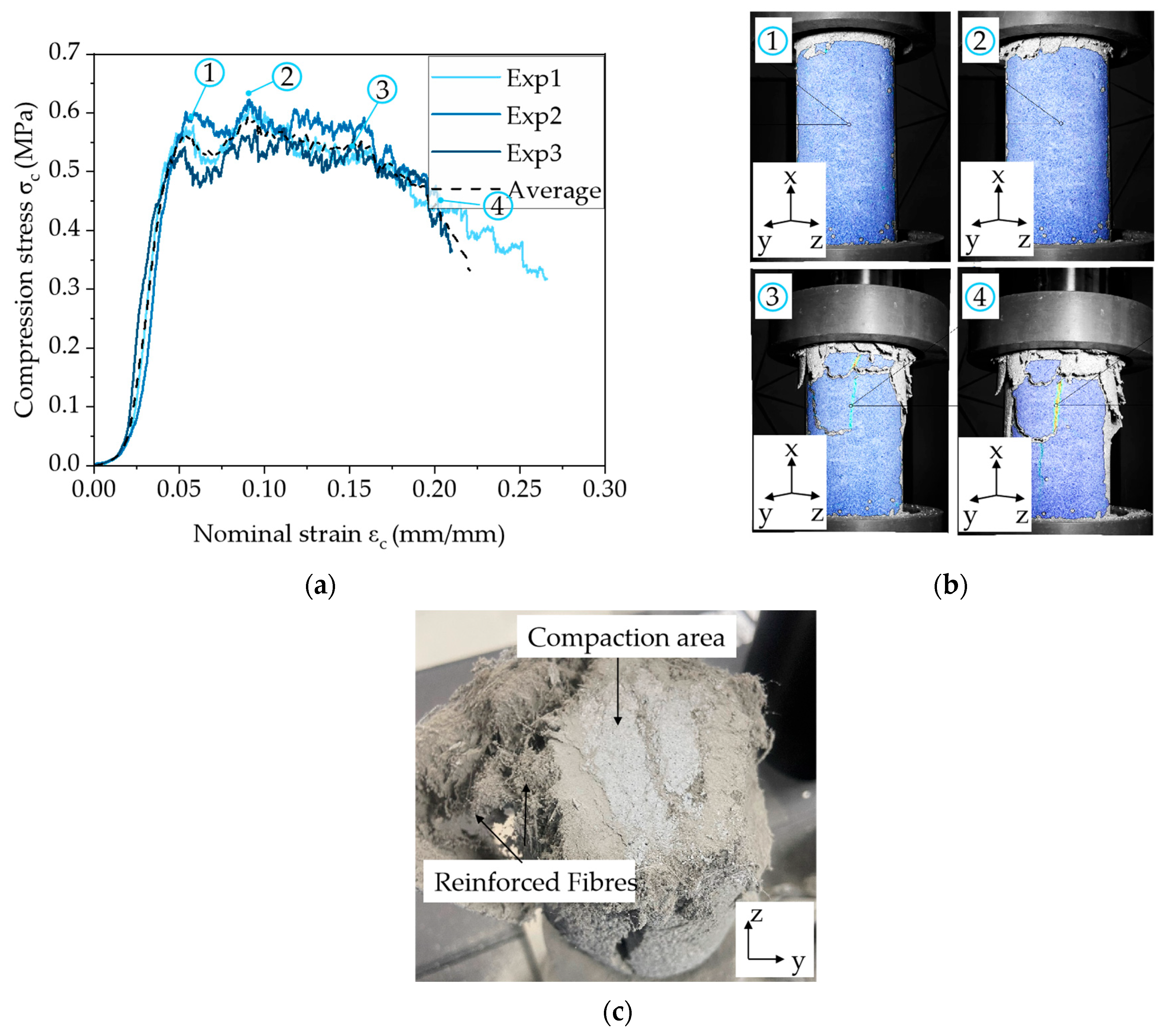
2.1.3. Compression and Splitting Tests on the Aerated Concrete Core
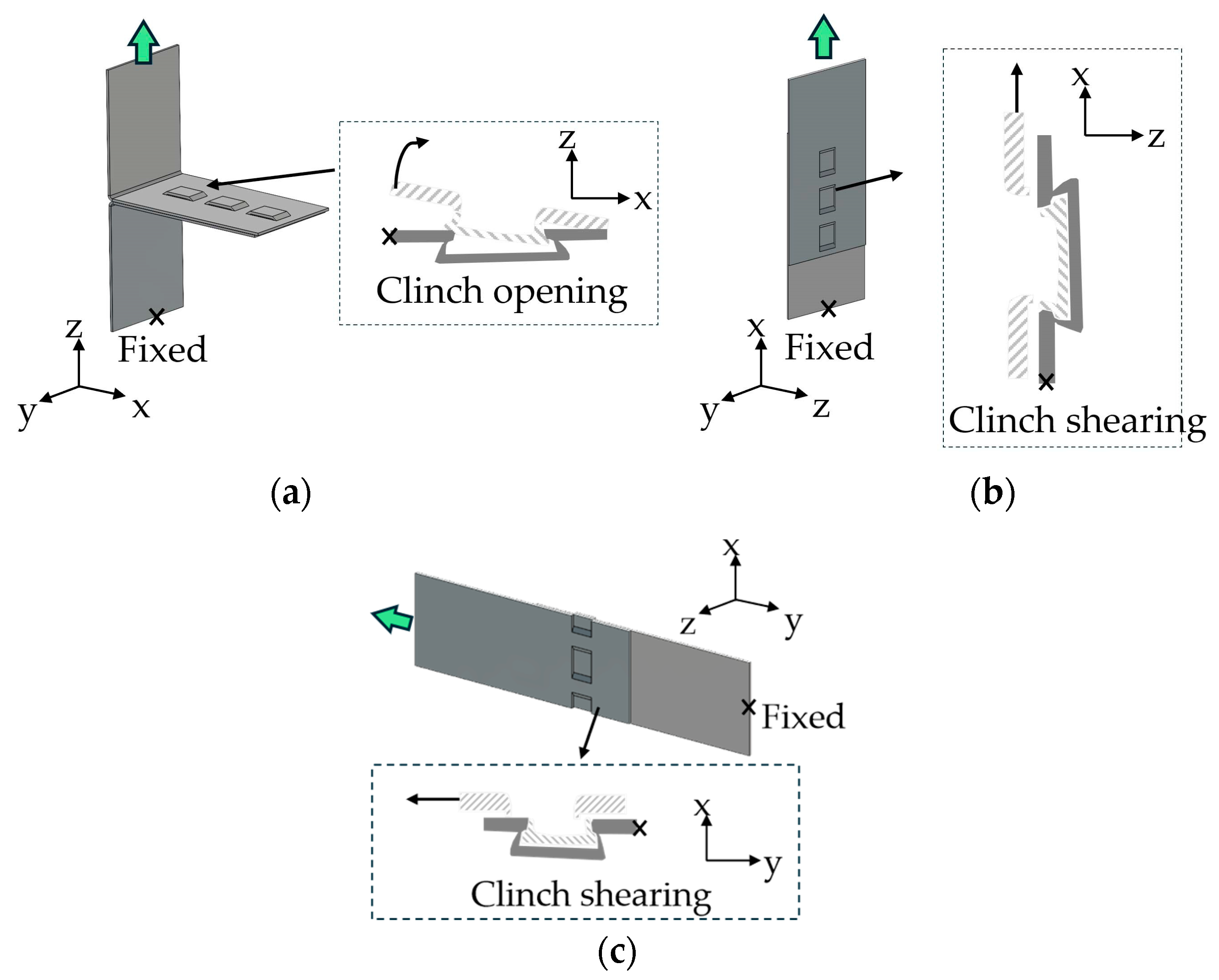
2.1.4. Testing the Strength of the Clinch Joint Connection
2.2. Testing Structural Loading Behaviour
2.2.1. Four-Point Bending Test
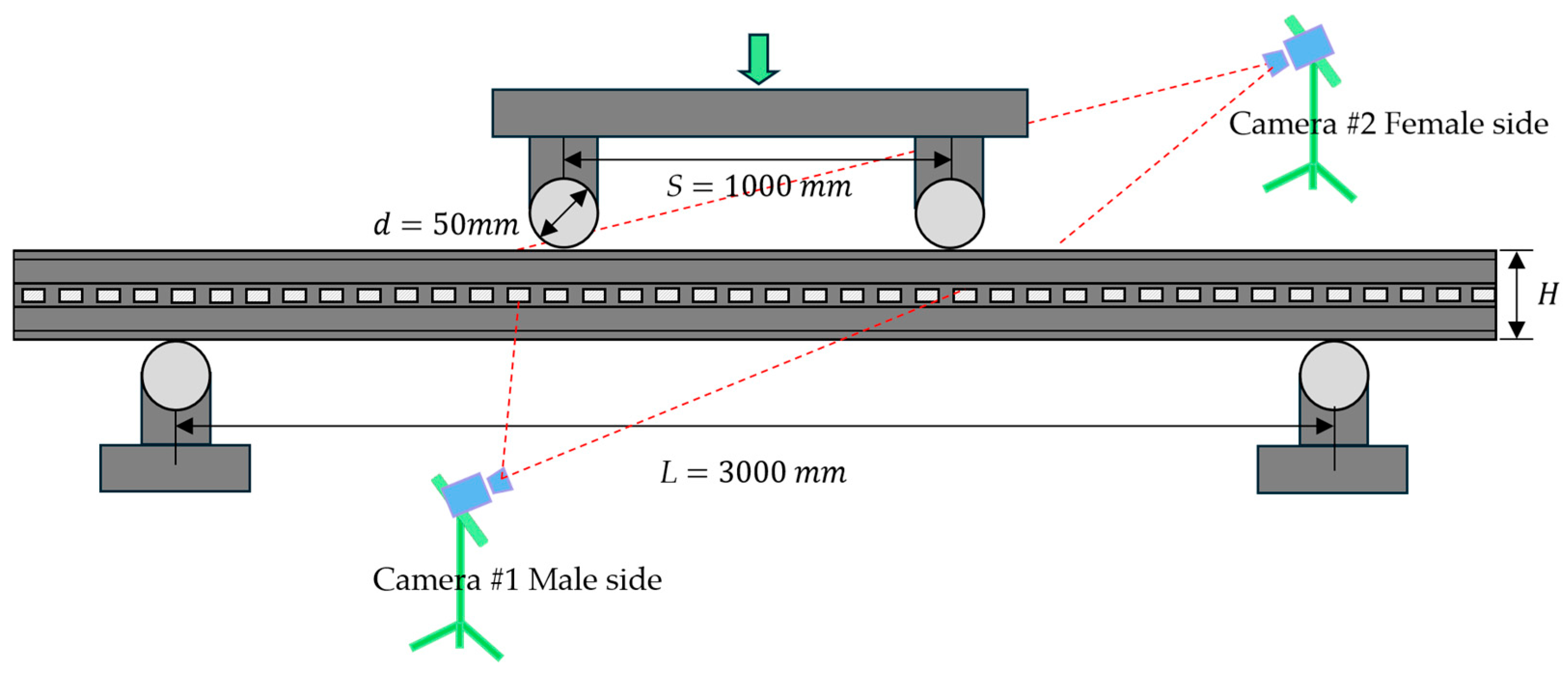
2.2.2. Three-Point Bending Test
3. Experimental Results
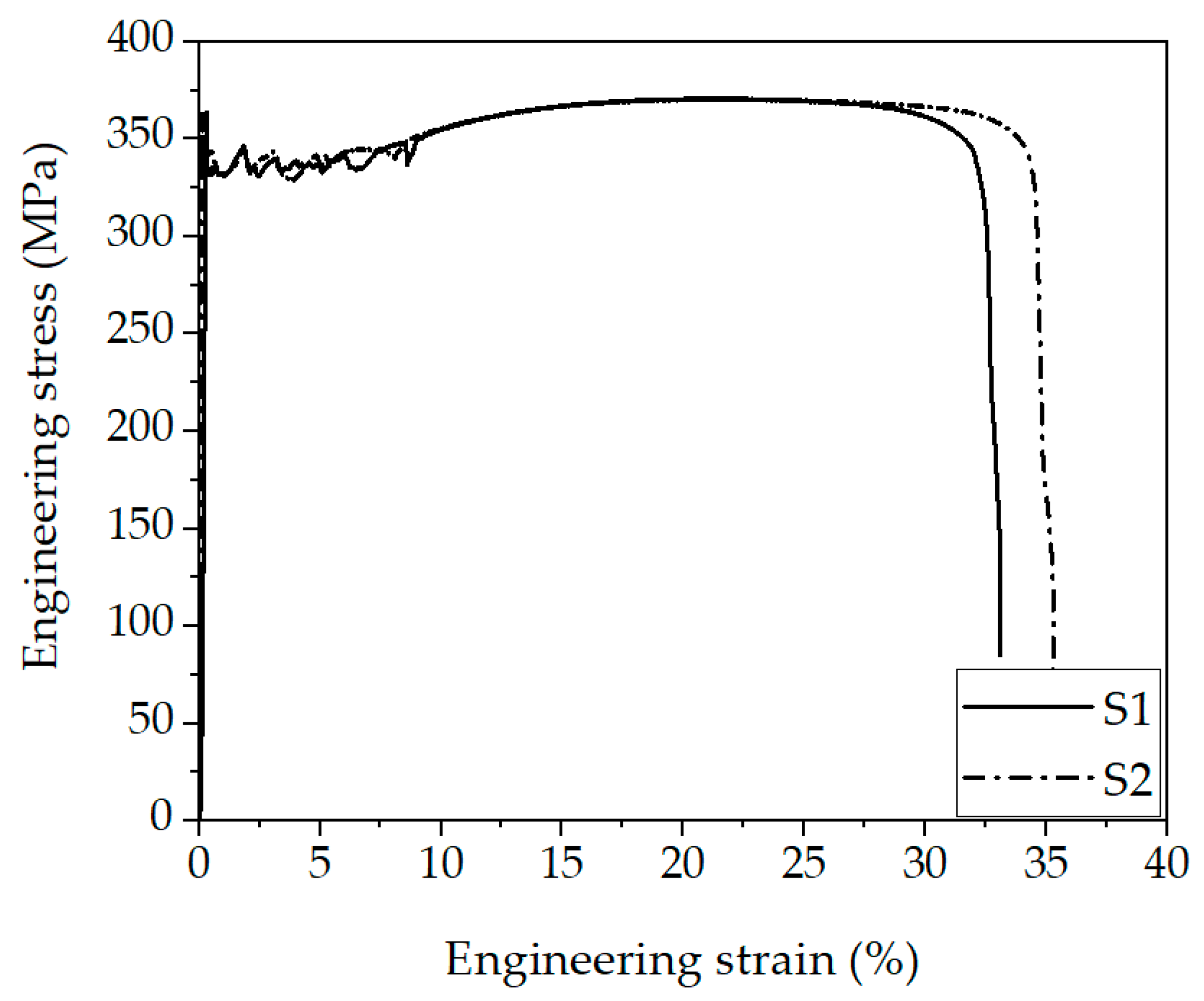
3.1. Mechanical Properties of the Steel
3.2. Structure and Density of the Aerated Concrete Core Before and After Deformation

3.3. Mechanical Properties of the Aerated Core
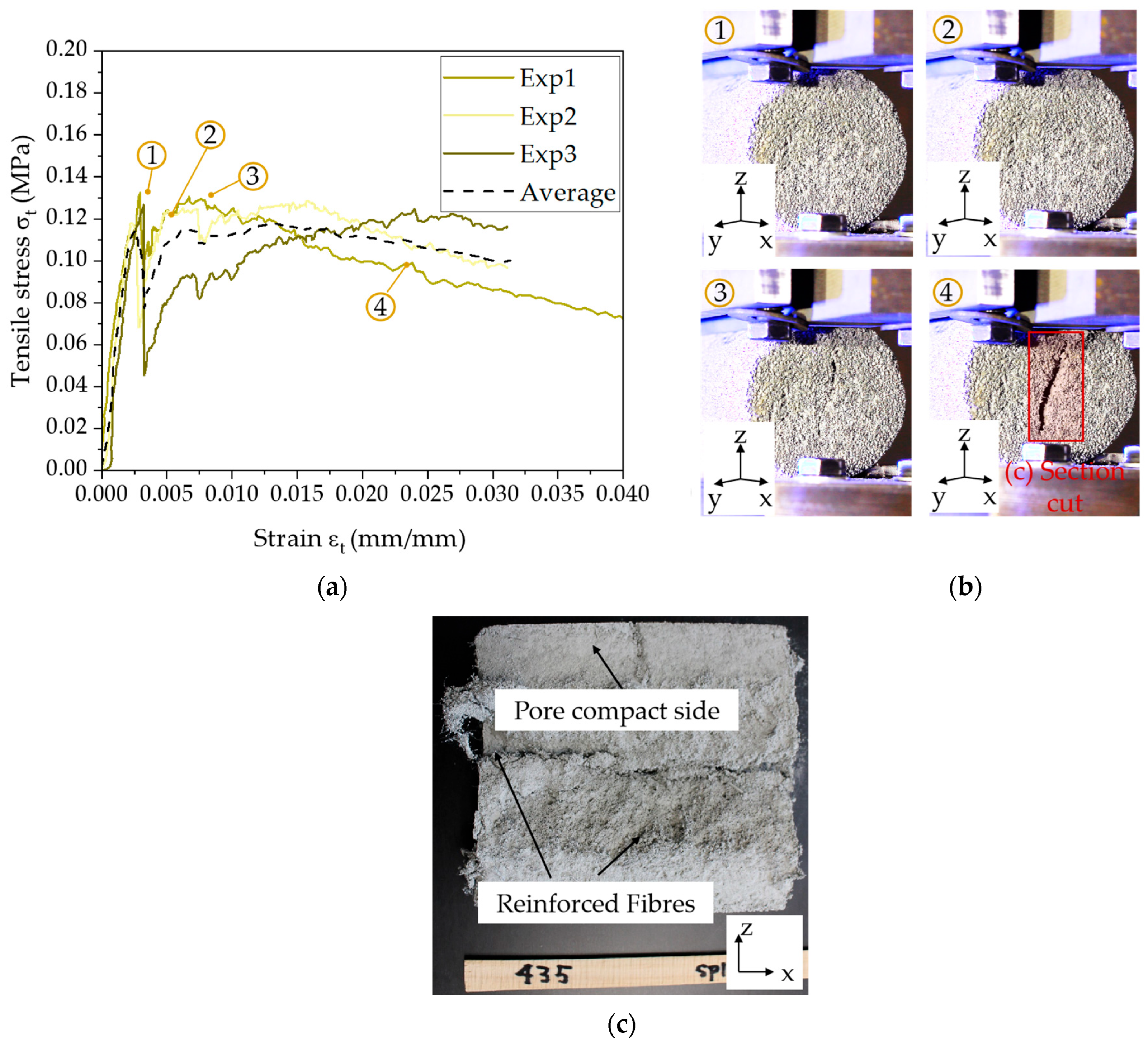
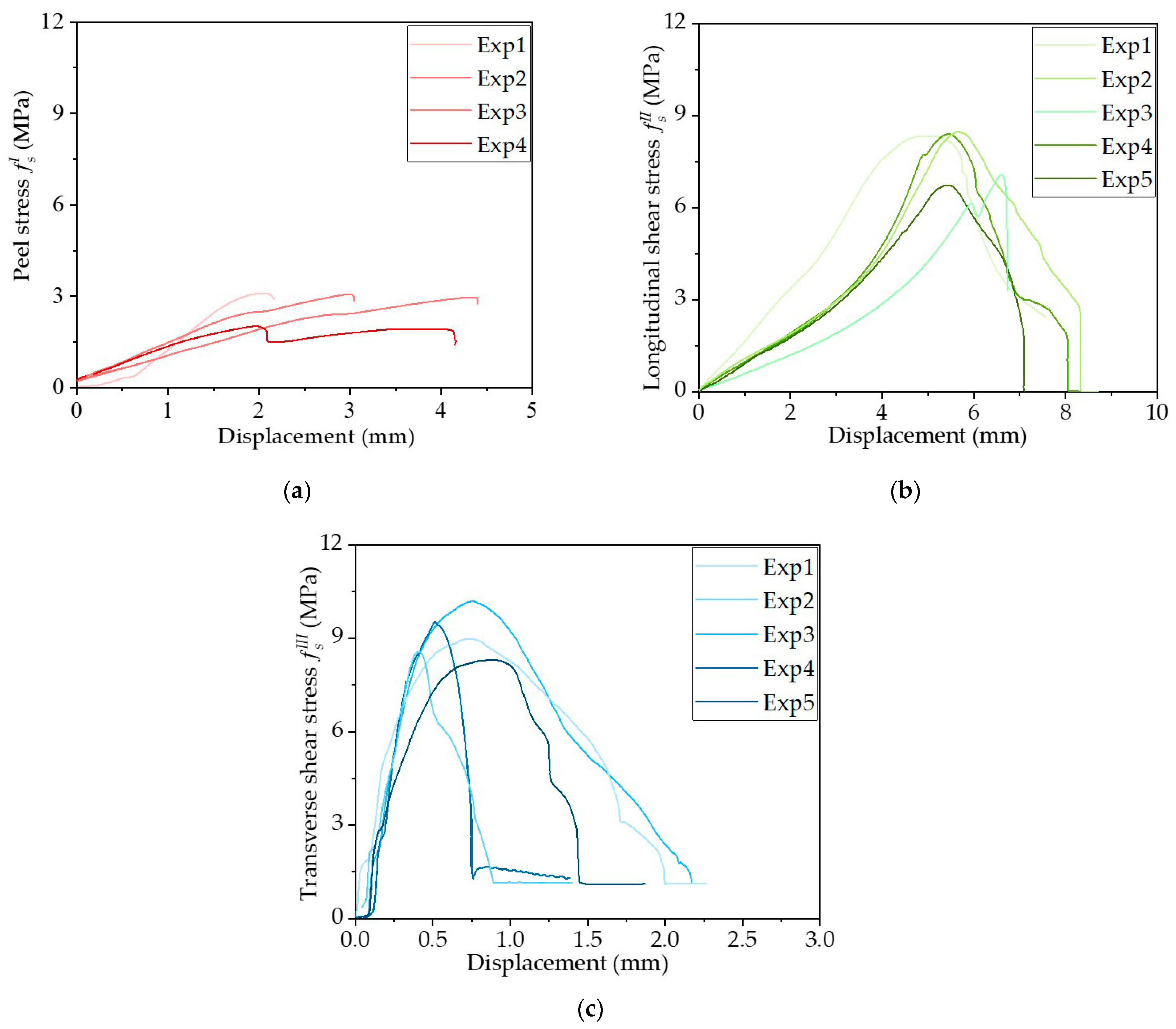
3.4. Clinch Seam Strength
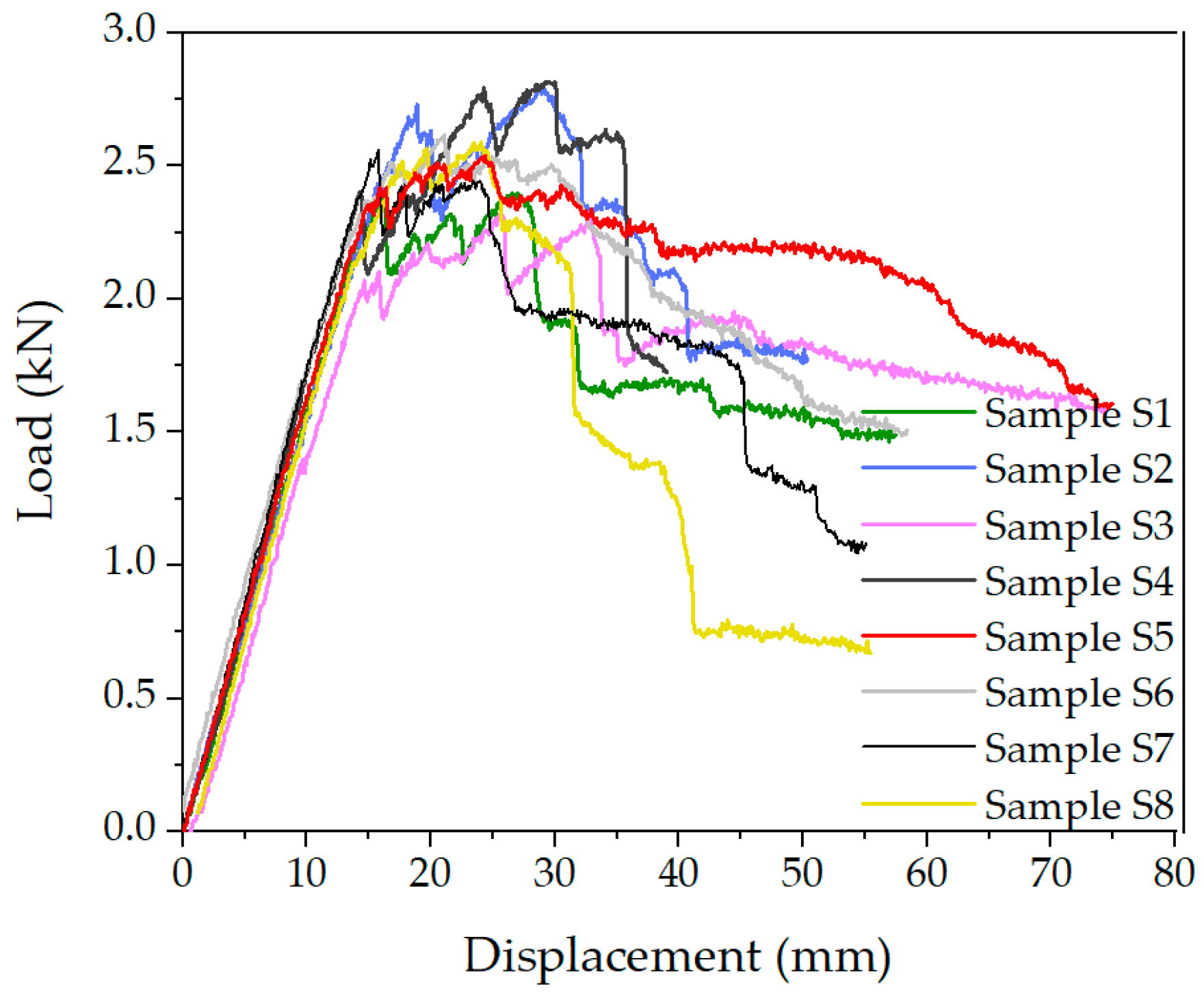
3.5. Structural Loading Behaviour and Failure Modes in Four-Point Bending
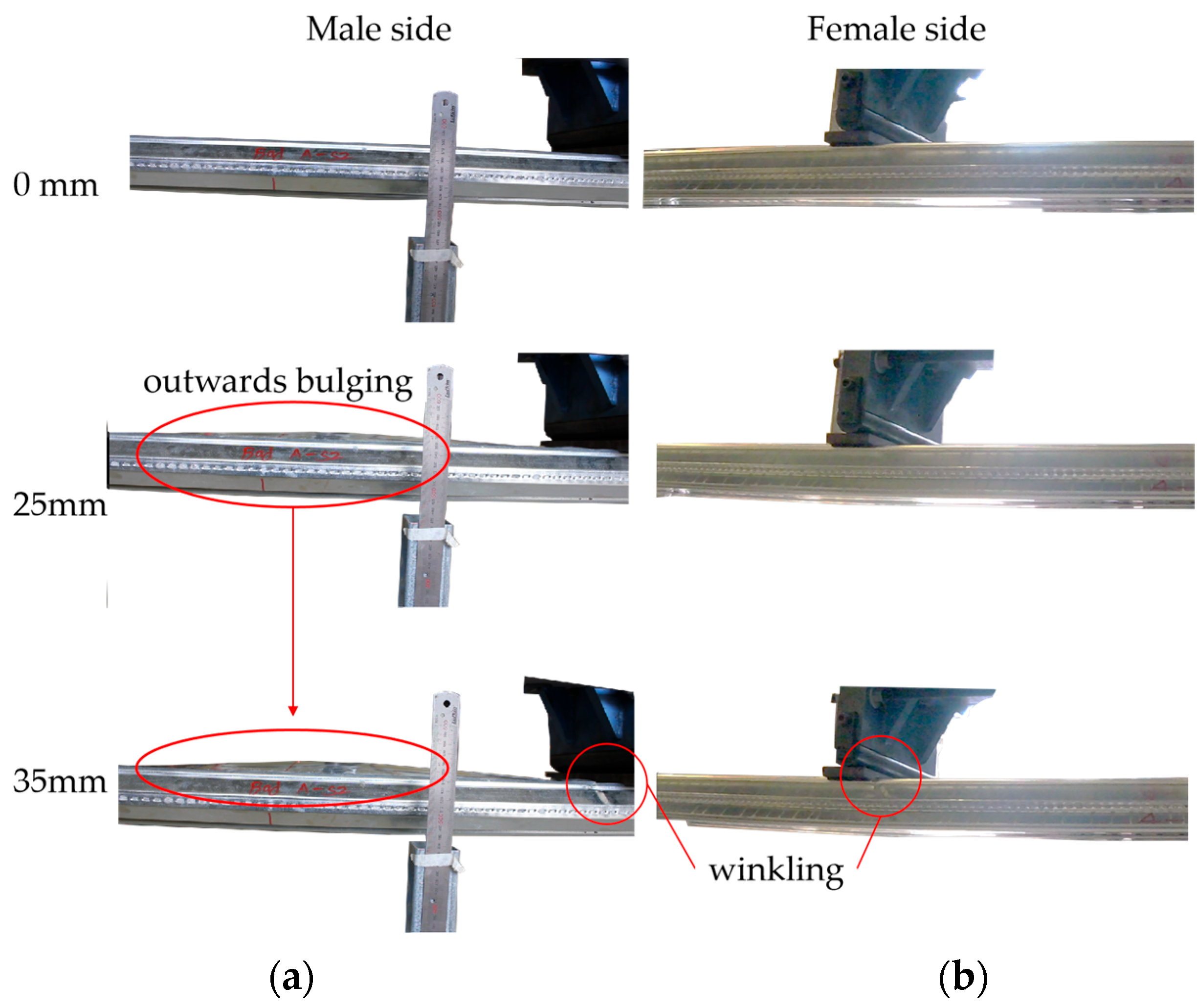
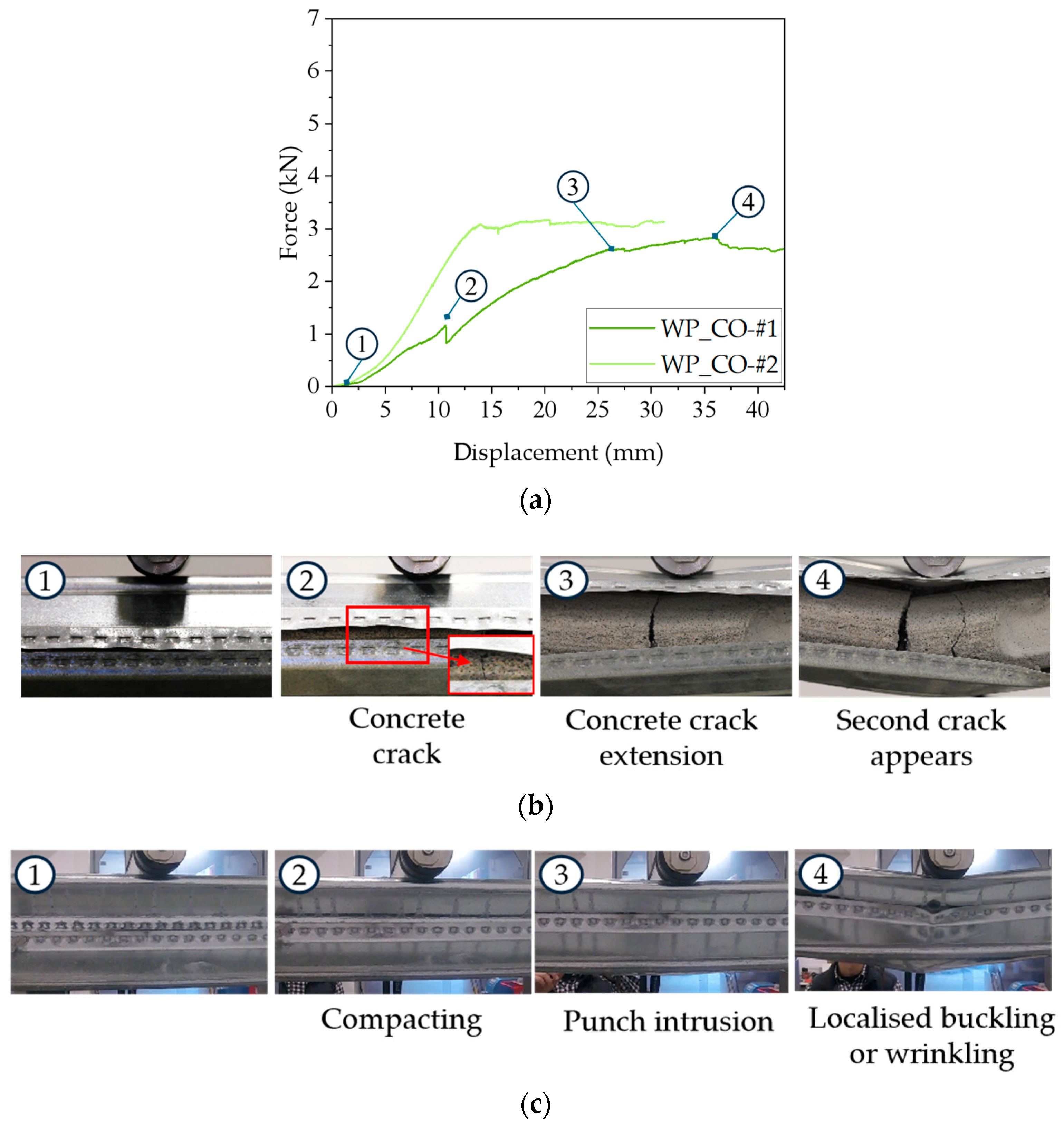
3.5.1. Buckling and Wrinkling of the Steel Outer Shell with the Seam Remaining Intact
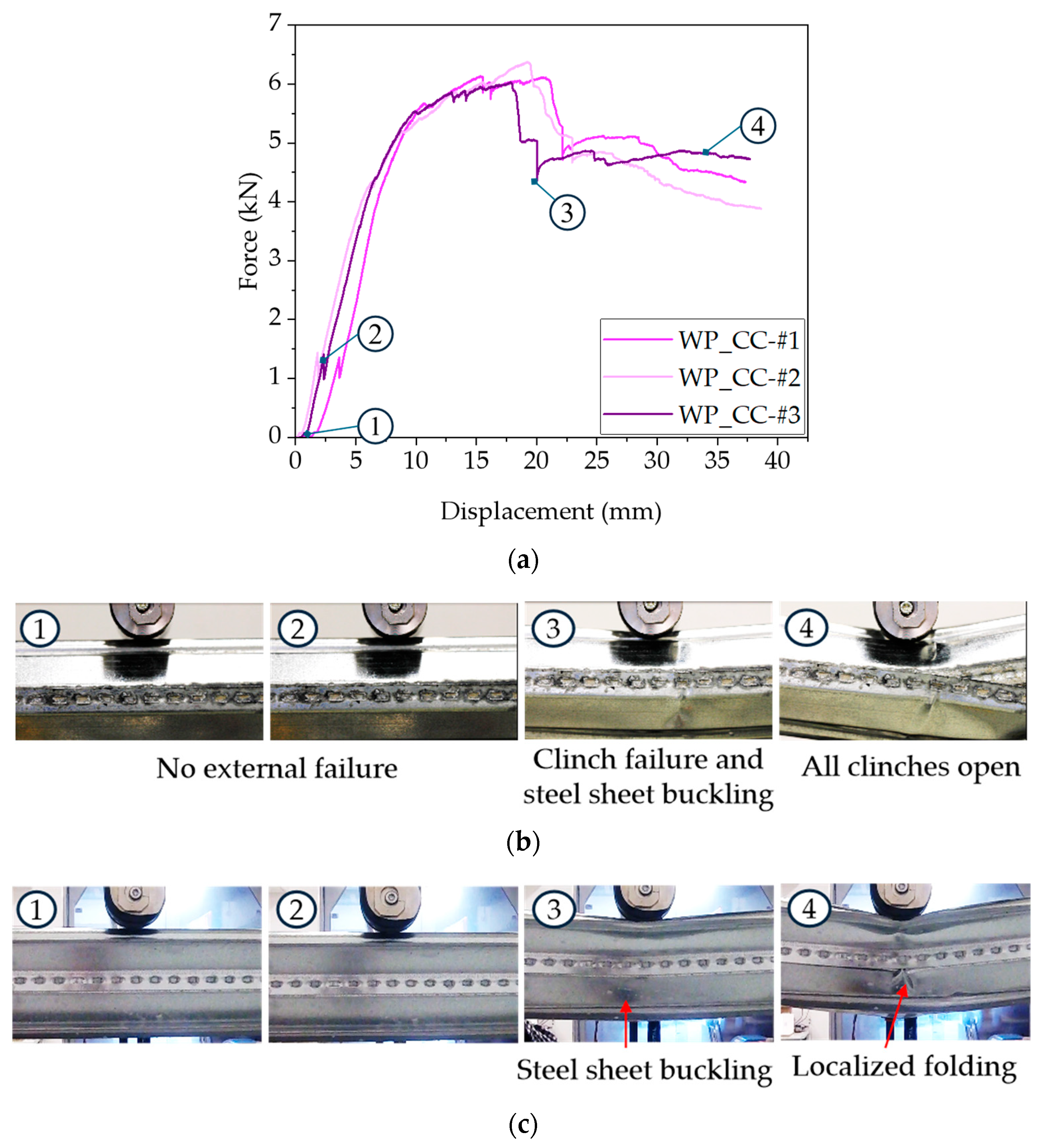
3.5.2. Buckling of the Steel Outer Shell Followed by Seam Failure
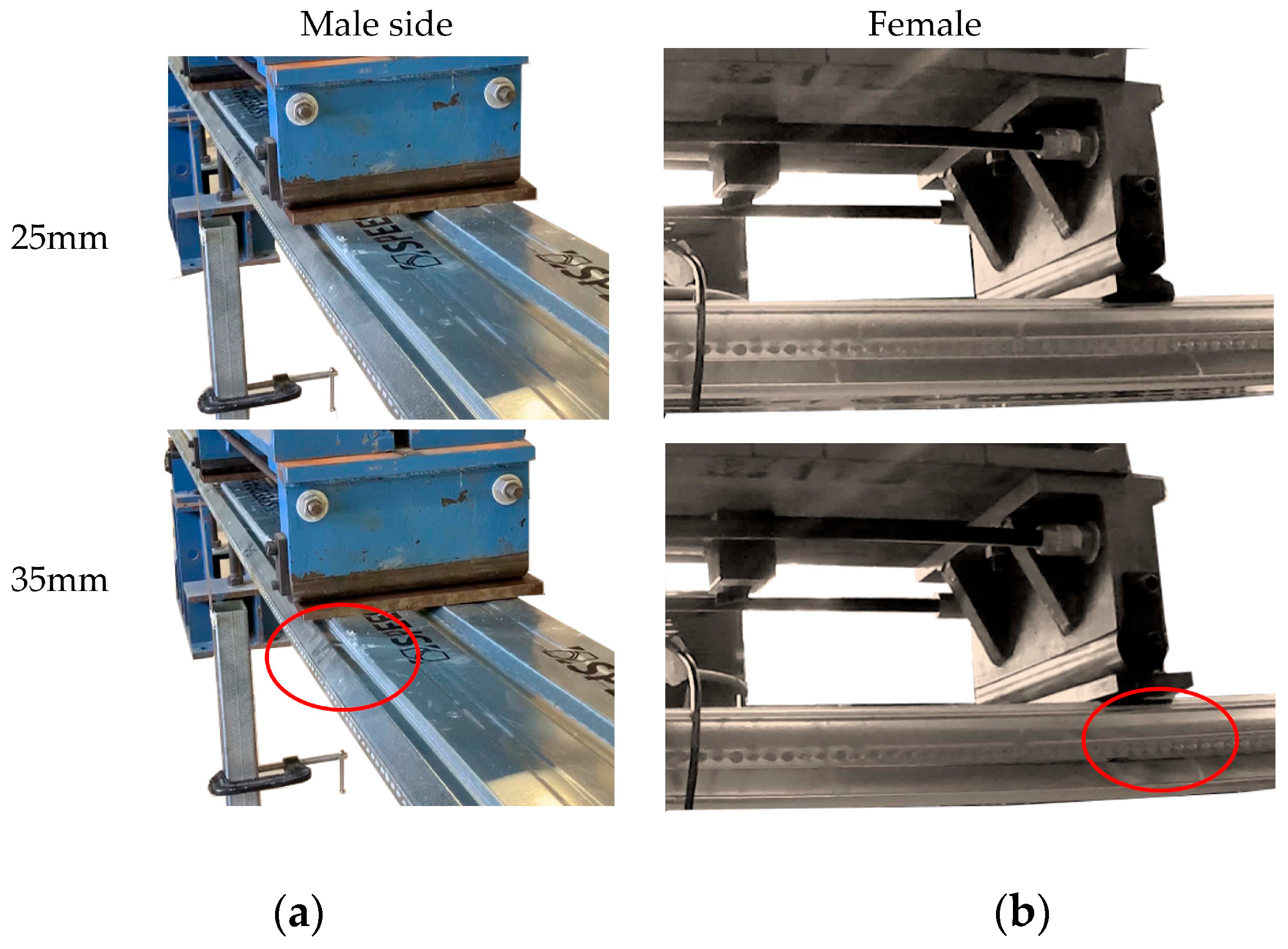
3.5.3. Failure of the Seam on the Male and the Female Side

3.6. The Effect of the Individual Panel Constituents on the Load Bearing Capacity
- Buckling of the steel sheet;
- Buckling of the steel sheet combined with seam failure initiation;
- Catastrophic failure of the clinch seam connection.
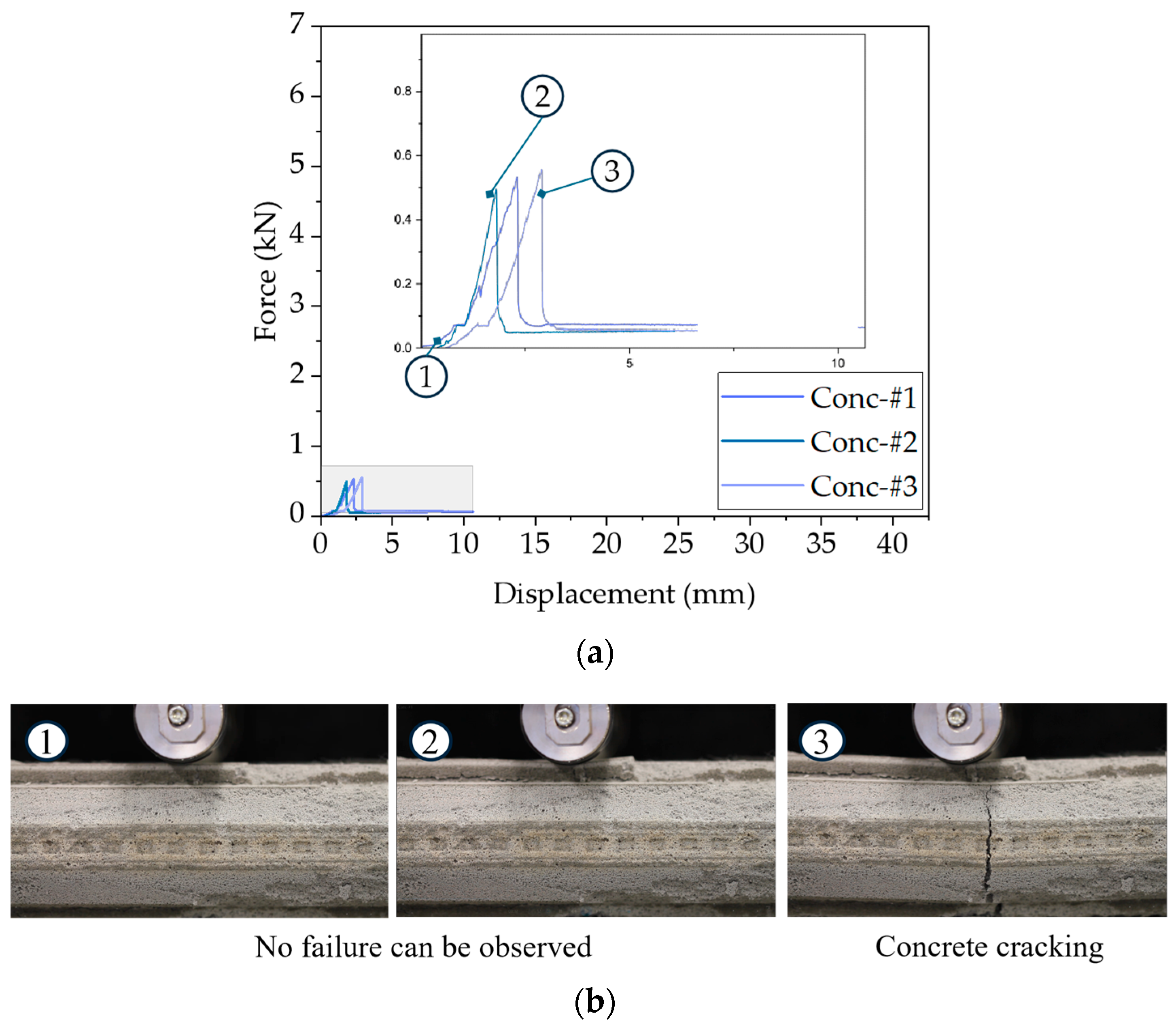
- The concrete core; extracted from the wall panel;
- The wall panel with both clinch seams opened;
- The wall panel with the male and female seams intact and closed.

4. Discussion
4.1. Application of X-Ray Computed Tomography (PCX-CT)
4.2. The Fundamental Mechanics of the Speedpanel DSC Bend Loading Behaviour
4.3. Modes of Failure
4.4. The Effect of Panel Constituents on the Maximum Bend Load
5. Conclusions and Future Work
- X-ray Computed Tomography (PCX-CT) enables the analysis of the size and distribution of air bubbles in aerated concrete. This procedure was validated through concrete density measurements and offers detailed structural information that could be valuable for future material model development and computer-assisted analysis of concrete behaviour.
- The structural performance of the DSC wall panel during bending deformation is primarily governed by the steel outer shells, which are separated by the concrete core and connected by clinch seams on the male and female sides of the panel. In this configuration, the outer steel shells are subjected to tension and compression, while the clinch seams, located at the panel’s thickness centres, experience shear forces. This behaviour aligns with the theory of bending in sandwich panels.
- The aerated concrete core has very low compressive and tensile strengths, and as a result, it contributes minimally to the load-bearing capacity of the wall panel. Its primary role is to separate the outer metal sheets, allowing them to be loaded in tension and compression during bending deformation.
- Panel failure occurs either through buckling of the steel outer shell, clinch seam opening, or a combination of both failure modes. The type of failure does not affect the maximum bending load but only influences the post-failure behaviour after the peak load is reached.
- The results of this study suggest that, in the current wall panel configuration, the concrete core and the clinch seam provide adequate strength to reach the maximum load-bearing capacity of the panel without premature failure. The majority of the stresses are transferred by the steel outer shell material. This indicates that further improvements in bending performance may only be achieved by either increasing the steel thickness or optimizing the cross-sectional shape of the outer shell to enhance its bending rigidity.
- This study is limited to experimental findings. Future work should explore analytical and numerical modelling approaches to theoretically validate the experimental results. Finite element analysis (FEA) could be used to simulate the panel deformation and failure mechanisms under bending loads. Additionally, closed-form model approaches based on the sandwich panel theory could provide further verification. While this study focused on bending behaviour due to its relevance to wind-induced loads, other loading conditions, such as axial compression, shear, and impact should be investigated to provide a more comprehensive assessment of the panel’s structural performance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fiorino, L.; Macillo, V.; Landolfo, R. Experimental characterization of quick mechanical connecting systems for cold-formed steel structures. Adv. Struct. Eng. 2017, 20, 1098–1110. [Google Scholar] [CrossRef]
- Andrade, P.; Veljkovic, M.; Feldmann, M.; Pak, D.; Pyschny, D.; Lundholm, J. Design and execution of a 3D modular building. In Proceedings of the 7th European Conference on Steel and Composite Structures (Eurosteel 2014), Naples, Italy, 10–12 September 2014. [Google Scholar]
- Ferdous, W.; Bai, Y.; Ngo, T.D.; Manalo, A.; Mendis, P. New advancements, challenges and opportunities of multi-storey modular buildings—A state-of-the-art review. Eng. Struct. 2019, 183, 883–893. [Google Scholar] [CrossRef]
- Kamali, M.; Hewage, K. Life cycle performance of modular buildings: A critical review. Renew. Sustain. Energy Rev. 2016, 62, 1171–1183. [Google Scholar] [CrossRef]
- Thai, H.-T.; Ngo, T.; Uy, B. A review on modular construction for high-rise buildings. Structures 2020, 28, 1265–1290. [Google Scholar] [CrossRef]
- Hilo, S.J.; Badaruzzaman, W.H.W.; Osman, S.A.; Al-Zand, A.W.; Samir, M.; Hasan, Q.A. A state-of-the-art review on double-skinned composite wall systems. Thin-Walled Struct. 2015, 97, 74–100. [Google Scholar] [CrossRef]
- Eltayeb, E.; Ma, X.; Zhuge, Y.; Xiao, J.; Youssf, O. Composite walls composed of profiled steel skin and foam rubberized concrete subjected to eccentric compressions. J. Build. Eng. 2022, 46, 103715. [Google Scholar] [CrossRef]
- Ramamurthy, K.; Nambiar, E.K.K.; Ranjani, G.I.S. A classification of studies on properties of foam concrete. Cem. Concr. Compos. 2009, 31, 388–396. [Google Scholar] [CrossRef]
- Clark, J.V.; Lange, D.A. Optimization of cellular concrete microstructure for improved impact resistance. Transp. Res. Rec. 2021, 2675, 237–246. [Google Scholar] [CrossRef]
- Mydin, M.A.O.; Wang, Y.C. Structural performance of lightweight steel-foamed concrete–steel composite walling system under compression. Thin-Walled Struct. 2011, 49, 66–76. [Google Scholar] [CrossRef]
- Karakurt, C.; Kurama, H.; Topçu, İ.B. Utilization of natural zeolite in aerated concrete production. Cem. Concr. Compos. 2010, 32, 1–8. [Google Scholar] [CrossRef]
- Liew, A.C.M. New innovative lightweight foam concrete technology. In Use of Foamed Concrete in Construction: Proceedings of the International Conference, Scotland, UK, 5–7 July 2005; Thomas Telford: London, UK, 2005; pp. 45–50. [Google Scholar]
- Amran, Y.H.M.; Farzadnia, N.; Ali, A.A.A. Properties and applications of foamed concrete; a review. Constr. Build. Mater. 2015, 101, 990–1005. [Google Scholar] [CrossRef]
- Zhang, Z.; Provis, J.L.; Reid, A.; Wang, H. Geopolymer foam concrete: An emerging material for sustainable construction. Constr. Build. Mater. 2014, 56, 113–127. [Google Scholar] [CrossRef]
- Kearsley, E.P.; Wainwright, P.J. The effect of high fly ash content on the compressive strength of foamed concrete. Cem. Concr. Res. 2001, 31, 105–112. [Google Scholar] [CrossRef]
- Falliano, D.; Parmigiani, S.; Suarez-Riera, D.; Ferro, G.A.; Restuccia, L. Stability, flexural behavior and compressive strength of ultra-lightweight fiber-reinforced foamed concrete with dry density lower than 100 kg/m3. J. Build. Eng. 2022, 51, 104329. [Google Scholar] [CrossRef]
- Su, B.; Zhou, Z.; Li, Z.; Wang, Z.; Shu, X. Experimental investigation on the mechanical behavior of foamed concrete under uniaxial and triaxial loading. Constr. Build. Mater. 2019, 209, 41–51. [Google Scholar] [CrossRef]
- Xu, L.; Duan, Y.; Li, Y. Porosity, gradient and impact velocity effects on compressive response of foamed concrete. Constr. Build. Mater. 2022, 315, 125616. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Bui, H.H.; Ngo, T.D.; Nguyen, G.D.; Kreher, M.U.; Darve, F. A micromechanical investigation for the effects of pore size and its distribution on geopolymer foam concrete under uniaxial compression. Eng. Fract. Mech. 2019, 209, 228–244. [Google Scholar] [CrossRef]
- Castillo-Lara, J.F.; Flores-Johnson, E.A.; Valadez-Gonzalez, A.; Herrera-Franco, P.J.; Carrillo, J.G.; Gonzalez-Chi, P.I.; Agaliotis, E.; Li, Q.M. Mechanical behaviour of composite sandwich panels with foamed concrete core reinforced with natural fibre in four-point bending. Thin-Walled Struct. 2021, 169, 108457. [Google Scholar] [CrossRef]
- Jones, M.R.; McCarthy, A. Utilising unprocessed low-lime coal fly ash in foamed concrete. Fuel 2005, 84, 1398–1409. [Google Scholar] [CrossRef]
- Castillo-Lara, J.F.; Flores-Johnson, E.A.; Valadez-Gonzalez, A.; Herrera-Franco, P.J.; Carrillo, J.G.; Gonzalez-Chi, P.I.; Li, Q.M. Mechanical properties of natural fiber reinforced foamed concrete. Materials 2020, 13, 3060. [Google Scholar] [CrossRef]
- Raj, B.; Sathyan, D.; Madhavan, M.K.; Raj, A. Mechanical and durability properties of hybrid fiber reinforced foam concrete. Constr. Build. Mater. 2020, 245, 118373. [Google Scholar] [CrossRef]
- Song, Y.; Lange, D. Influence of fine inclusions on the morphology and mechanical performance of lightweight foam concrete. Cem. Concr. Compos. 2021, 124, 104264. [Google Scholar] [CrossRef]
- Shafighfard, T.; Kazemi, F.; Asgarkhani, N.; Yoo, D.-Y. Machine-learning methods for estimating compressive strength of high-performance alkali-activated concrete. Eng. Appl. Artif. Intell. 2024, 136, 109053. [Google Scholar] [CrossRef]
- Just, A.; Middendorf, B. Microstructure of high-strength foam concrete. Mater. Charact. 2009, 60, 741–748. [Google Scholar] [CrossRef]
- Eltayeb, E.; Ma, X.; Zhuge, Y.; Youssf, O.; Mills, J.E.; Xiao, J.; Singh, A. Structural performance of composite panels made of profiled steel skins and foam rubberised concrete under axial compressive loads. Eng. Struct. 2020, 211, 110448. [Google Scholar] [CrossRef]
- Kozłowski, M.; Kadela, M. Mechanical characterization of lightweight foamed concrete. Adv. Mater. Sci. Eng. 2018, 2018, 6801258. [Google Scholar] [CrossRef]
- Mydin, M.A.O.; Wang, Y.C. Mechanical properties of foamed concrete exposed to high temperatures. Constr. Build. Mater. 2012, 26, 638–654. [Google Scholar] [CrossRef]
- Mahendran, M.; McAndrew, D. Flexural wrinkling strength of lightly profiled sandwich panels with transverse joints in the foam core. Adv. Struct. Eng. 2003, 6, 325–337. [Google Scholar] [CrossRef]
- Ridha, M.M.S.; Li, D.; Clifton, G.C.; Ma, X. Structural behavior of composite panels made of lightly profiled steel skins and lightweight concrete under concentric and eccentric loads. J. Struct. Eng. 2019, 145, 04019093. [Google Scholar] [CrossRef]
- Pokharel, N.; Mahendran, M. An investigation of lightly profiled sandwich panels subject to local buckling and flexural wrinkling effects. J. Constr. Steel Res. 2005, 61, 984–1006. [Google Scholar] [CrossRef]
- Prabha, P.; Marimuthu, V.; Saravanan, M.; Palani, G.S.; Lakshmanan, N.; Senthil, R. Effect of confinement on steel-concrete composite light-weight load-bearing wall panels under compression. J. Constr. Steel Res. 2013, 81, 11–19. [Google Scholar] [CrossRef]
- Liew, J.Y.R.; Yan, J.-B.; Huang, Z.-Y. Steel-concrete-steel sandwich composite structures-recent innovations. J. Constr. Steel Res. 2017, 130, 202–221. [Google Scholar] [CrossRef]
- Negahban, E.; Bagheri, A.; Al-Dujaili, A.; Sanjayan, J. Insulation failure of lightweight composite sandwich panels exposed to flame. Fire Mater. 2020, 44, 943–952. [Google Scholar] [CrossRef]
- Pedreschi, R.; Sinha, B. Predicting the shear strength of mechanical clinching in cold-formed steel structures. J. Mater. Civ. Eng. 2006, 18, 435–442. [Google Scholar] [CrossRef]
- Oudjene, M.; Ben-Ayed, L.; Delamézière, A.; Batoz, J.L. Shape optimization of clinching tools using the response surface methodology with Moving Least-Square approximation. J. Mater. Process. Technol. 2009, 209, 289–296. [Google Scholar] [CrossRef]
- Coppieters, S.; Cooreman, S.; Lava, P.; Sol, H.; Houtte, P.V.; Debruyne, D. Reproducing the experimental pull-out and shear strength of clinched sheet metal connections using FEA. Int. J. Mater. Form. 2011, 4, 429–440. [Google Scholar] [CrossRef]
- Mucha, J.; Boda, Ł.; Witkowski, W. Geometrical parameters and strength of clinching joint formed with the use of an additional rivet. Arch. Civ. Mech. Eng. 2023, 23, 114. [Google Scholar] [CrossRef]
- Breda, A.; Coppieters, S.; Debruyne, D. Equivalent modelling strategy for a clinched joint using a simple calibration method. Thin-Walled Struct. 2017, 113, 1–12. [Google Scholar] [CrossRef]
- Mucha, J.; Witkowski, W. The clinching joints strength analysis in the aspects of changes in the forming technology and load conditions. Thin-Walled Struct. 2014, 82, 55–66. [Google Scholar] [CrossRef]
- Varis, J. Ensuring the integrity in clinching process. J. Mater. Process. Technol. 2006, 174, 277–285. [Google Scholar] [CrossRef]
- ASTM E8/E8M-22; Standard Test Methods for Tension Testing of Metallic Materials. ASTM: West Conshohocken, PA, USA, 2022; p. 31. [CrossRef]
- Mayo, S.C.; Gureyev, T.E.; Nesterets, Y.I.; Thompson, D.A.; Siu, K.K.W.; Wallwork, K. A dedicated micro-CT beamline for the Australian Synchrotron and the Remote-CT project. J. Phys. Conf. Ser. 2013, 463, 012002. [Google Scholar] [CrossRef]
- ASTM C39/C39M-21; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2021. [CrossRef]
- ASTM C496/C496M-17; Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2017. [CrossRef]
- ZEISS. ZEISS Quality Tech Guide: Introduction to Digital Image Correlation and Strain Computation. Available online: https://techguide.zeiss.com/en/zeiss-inspect-2025 (accessed on 30 March 2025).
- Nanayakkara, O.; Xia, J. Mechanical and physical properties of mortar of partially replaced fine aggregates with sawdust. Acad. J. Civil Eng. 2019, 37, 308–313. [Google Scholar] [CrossRef]
- Youssef, A.; Lecompte, T.; Picandet, V.; Challamel, N. Compressive and shearing behavior of lime and hemp concrete. Acad. J. Civil Eng. 2015, 33, 405–411. [Google Scholar]
- Xiao, Q.; Ju, G.; Ye, F.; Wang, Y.; Jin, L.; Fu, W. An innovative approach for assessing the tensile strength of concrete: Experimental and numerical investigations. Constr. Build. Mater. 2024, 417, 135249. [Google Scholar] [CrossRef]
- Plantema, F.J. Sandwich Construction: The Bending and Buckling of Sandwich Beams, Plates, and Shells, 1st ed.; John Wiley and Sons: Hoboken, NJ, USA, 1966. [Google Scholar]
- Zenkert, D. An Introduction to Sandwich Structures, Student ed.; Technical University of Denmark: Copenhagen, Denmark, 1995. [Google Scholar]
- Hou, Y.; Tai, Y.H.; Lira, C.; Scarpa, F.; Yates, J.R.; Gu, B. The bending and failure of sandwich structures with auxetic gradient cellular cores. Compos.-A Appl. Sci. Manuf. 2013, 49, 119–131. [Google Scholar] [CrossRef]
- Ali, S.B.; Kamaris, G.S.; Gkantou, M. Flexural behaviour of concrete-filled double skin aluminium alloy tubes. Eng. Struct. 2022, 272, 114972. [Google Scholar] [CrossRef]
- Hoff, N.J.; Mautner, S.E. Bending and buckling of sandwich beams. J. Aeronaut. Sci. 1948, 15, 707–720. [Google Scholar] [CrossRef]
- Gdoutos, E.E.; Daniel, I.M.; Wang, K.A. Compression facing wrinkling of composite sandwich structures. Mech. Mater. 2003, 35, 511–522. [Google Scholar] [CrossRef]
| Spatial Standard Deviation (-) | Intensity Standard Deviation (-) | Search Window (px) | Local Neighbourhood (px) |
|---|---|---|---|
| 5 | 0.2 | 10 | 3 |
| Ultimate Tensile Strength (UTS) MPa | Yield Strength MPa | Uniform Elongation (UE) % | Total Elongation (TE) % | |
|---|---|---|---|---|
| Specimen 1 | 370.7 | 363.1 | 22.6 | 33.1 |
| Specimen 2 | 370.6 | 363.8 | 22.0 | 35.3 |
| Average | 370.7 | 363.5 | 22.3 | 34.2 |
| Condition | Mortar Volume 3D (mm3) | Pore Volume 3D (mm3) | Pore Percentage (%) | Estimate Density Range (kg/m3) |
|---|---|---|---|---|
| Non-loaded | 160.2 | 217.7 | 57.6 | 572.3–877.5 |
| After the bend test | 145.8 | 232.1 | 61.4 | 518.4–794.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weiss, M.; Hu, X.; Pereira, M.; Zhang, P. Structural Performance and Failure Mechanisms in Bend Loading of Steel-Aerated Concrete Fire Wall Composite Panels. Buildings 2025, 15, 1338. https://doi.org/10.3390/buildings15081338
Weiss M, Hu X, Pereira M, Zhang P. Structural Performance and Failure Mechanisms in Bend Loading of Steel-Aerated Concrete Fire Wall Composite Panels. Buildings. 2025; 15(8):1338. https://doi.org/10.3390/buildings15081338
Chicago/Turabian StyleWeiss, Matthias, Xinyu Hu, Michael Pereira, and Peng Zhang. 2025. "Structural Performance and Failure Mechanisms in Bend Loading of Steel-Aerated Concrete Fire Wall Composite Panels" Buildings 15, no. 8: 1338. https://doi.org/10.3390/buildings15081338
APA StyleWeiss, M., Hu, X., Pereira, M., & Zhang, P. (2025). Structural Performance and Failure Mechanisms in Bend Loading of Steel-Aerated Concrete Fire Wall Composite Panels. Buildings, 15(8), 1338. https://doi.org/10.3390/buildings15081338







