Zero-Carbon Parks’ Electric Load Forecasting Considering Feature Extraction of Multi-Type Electric Load and Dual-Layer Optimization Modal Decomposition
Abstract
1. Introduction
- (1)
- The electric load exhibits pronounced volatility due to the variable and unpredictable nature of renewable energy generation [2].
- (2)
- The industrial electric load exhibits a significant bidirectional temporal correlation feature. An interdependent relationship exists between thermal and electric loads within the park. Furthermore, a strong correlation links current and past values of industrial load.
- (3)
- The electric load is influenced by the diverse energy requirements of various industries, endowing it with a degree of adaptability. The data center, chemical manufacturing company, residence, shopping mall, cement manufacturing plant, and hospital are typical industries. The electric load variations in these typical industries have distinct impacts on the operation management of the park. Some scholars [3,4] proposed that the optimization of electric load not only enhanced the utilization efficiency of renewable energy but also reduced the overall energy costs in zero-carbon parks. Accurate forecasting of electric load can prevent disruptions to production activities that may arise from inadequate or excessive electricity supply. However, conventional load forecasting models fail to capture bidirectional, time-sensitive, and nonlinear effects. This limitation constrains their accuracy in predicting industrial power demand, which remains a critical challenge in the field.
2. Methods
2.1. Framework for the Electric Load Forecasting
2.2. Outlier Correction
2.3. The Dual-Layer Optimization Modal Decomposition Model
2.4. Electric Load Forecasting Based on Multi-Categorical Load Feature Extraction
2.4.1. Extract Features Based on BiLSTM and MIV
2.4.2. Evaluation of the Model
3. Results and Discussion
3.1. Raw Data and Processing
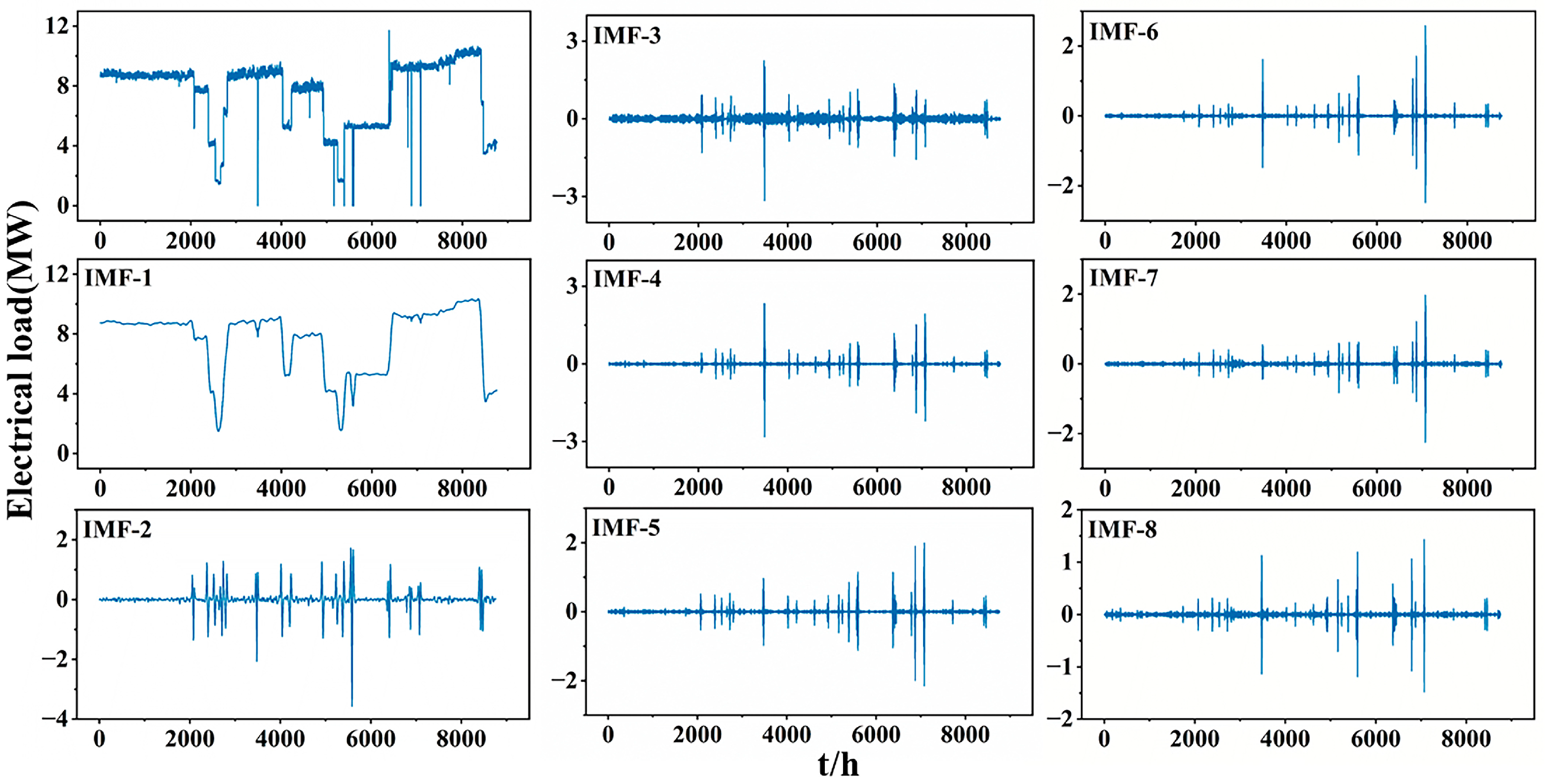
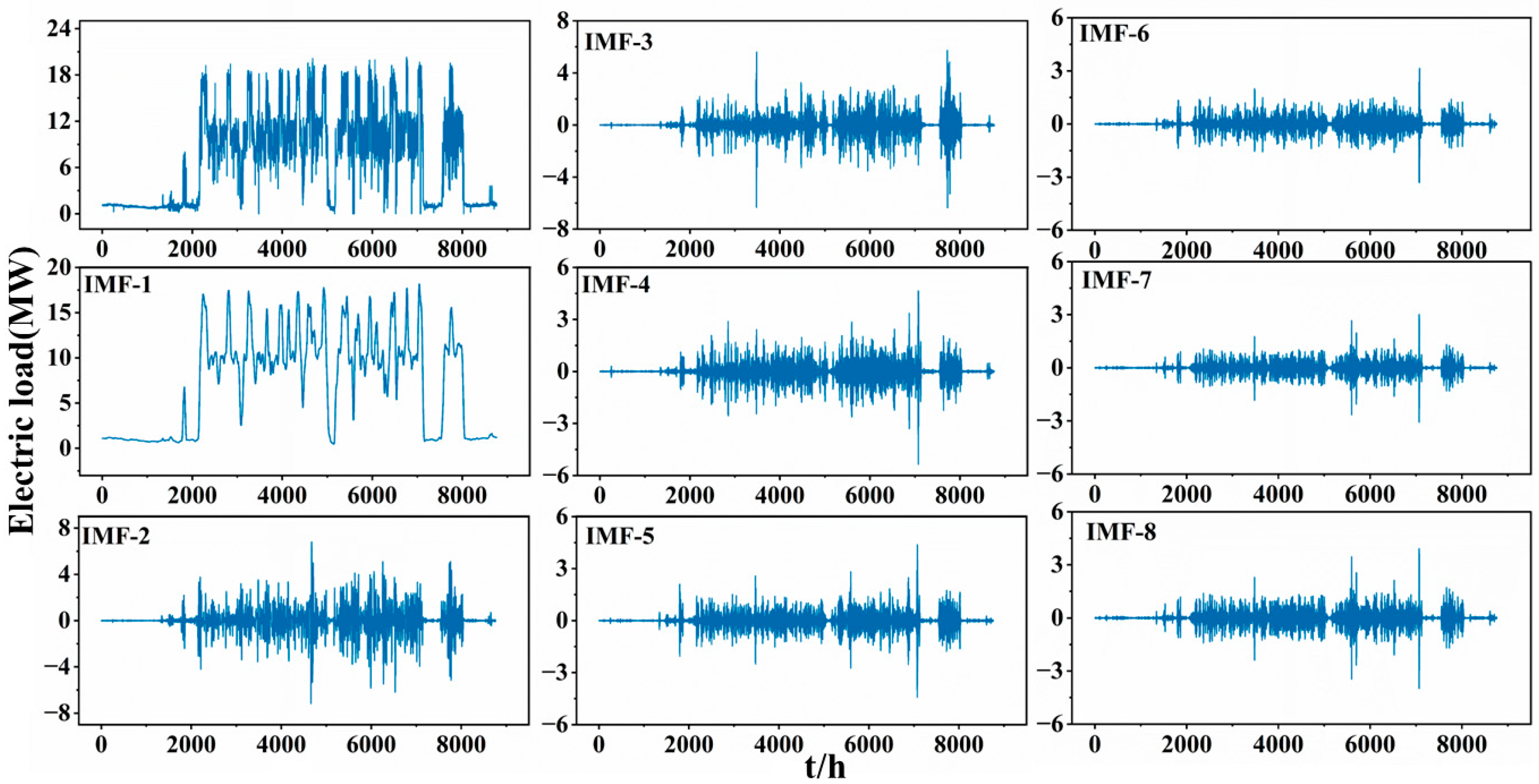
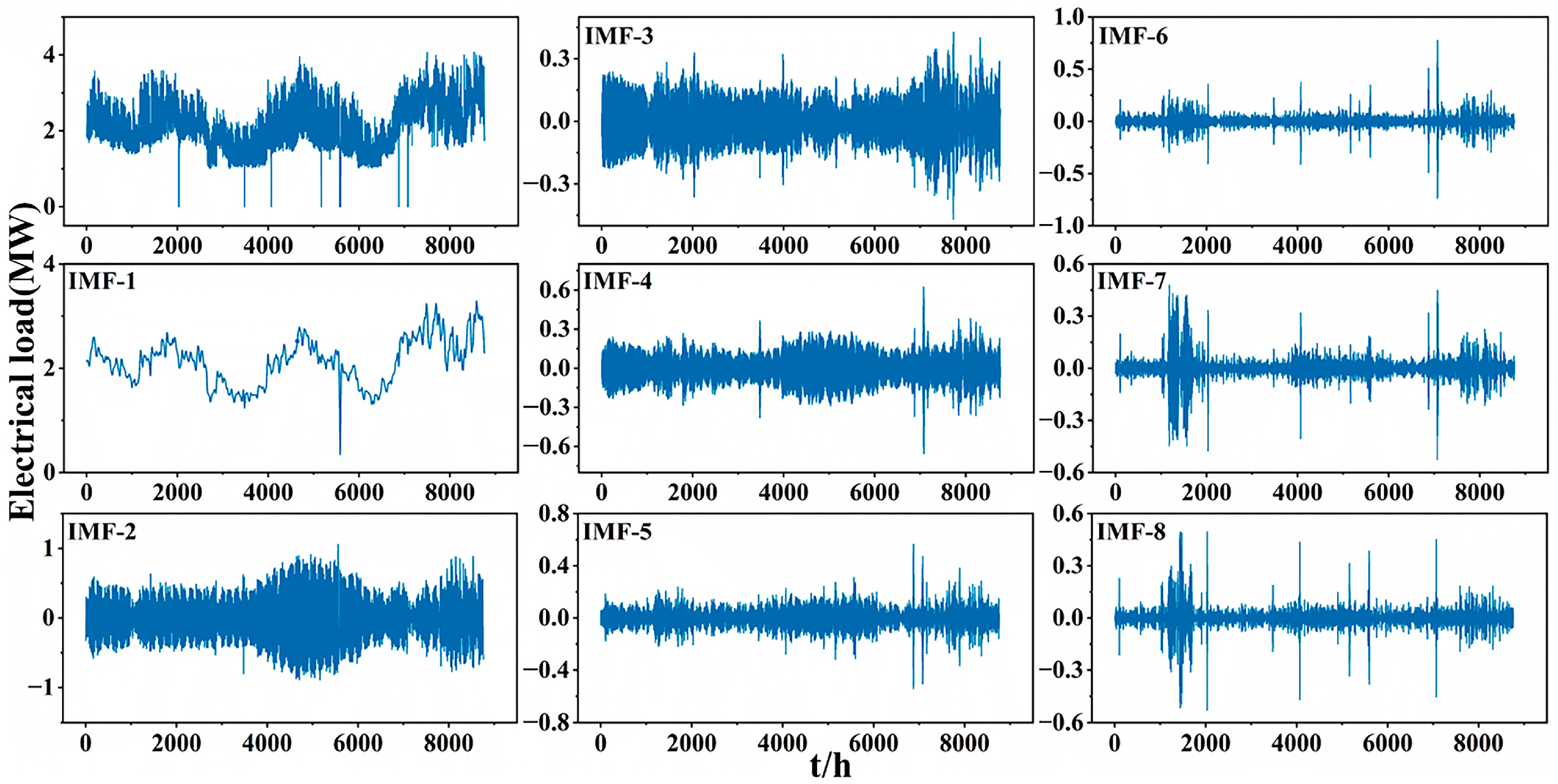
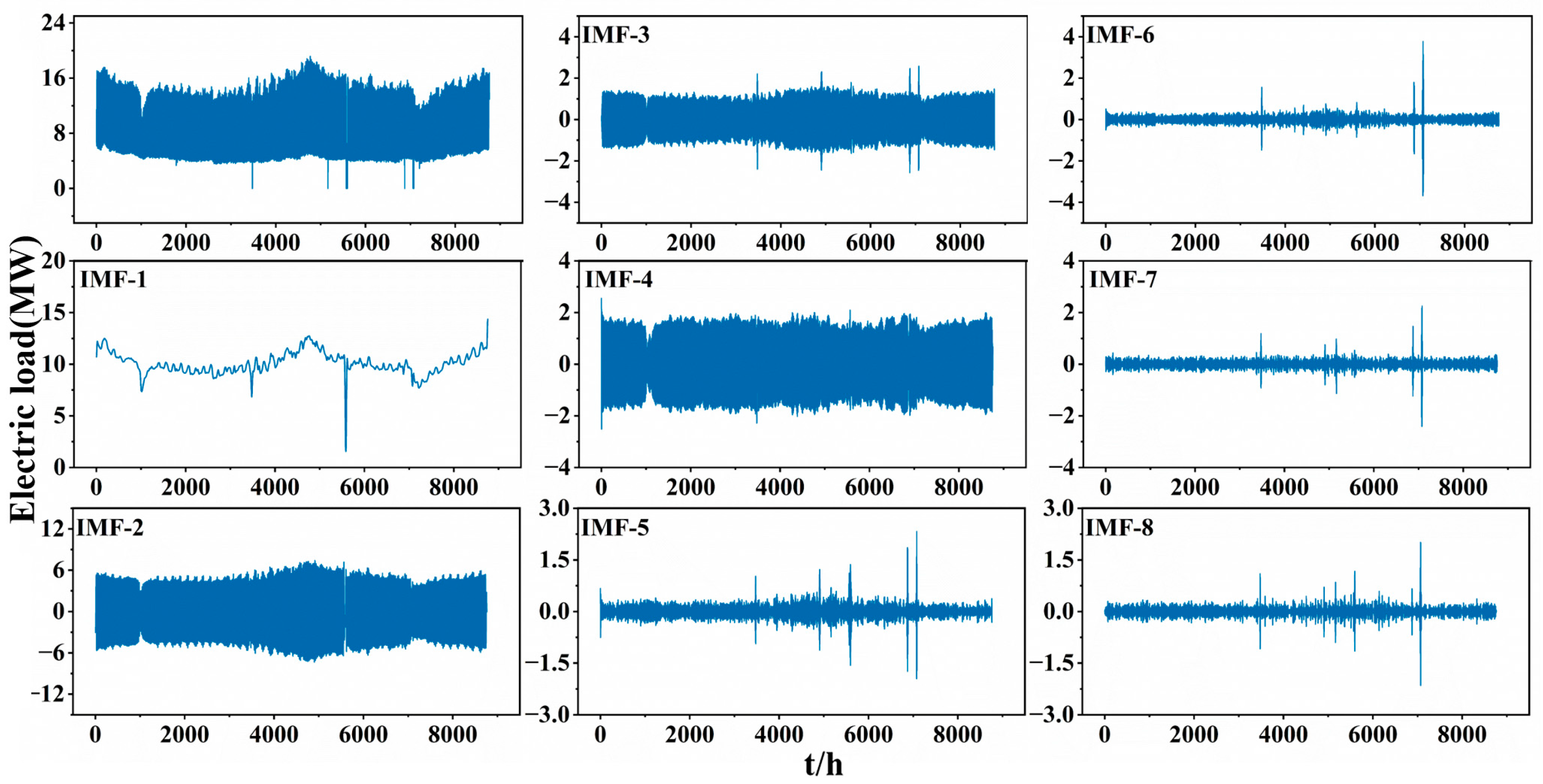
3.2. The Dual-Layer Optimization Modal Decomposition Model (TPE-AVMD)
3.3. Feature Extraction
3.4. Ablation Experiment
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Yin, J.; Jia, H.; Chen, L.; Liu, D.; Mei, S.; Wang, S. Optimal scheduling of zero-carbon park considering variational characteristics of hydrogen energy storage systems. Glob. Energy Interconnect. 2024, 7, 603–615. [Google Scholar] [CrossRef]
- Wang, J.; Gao, J.; Wei, D. Electric load prediction based on a novel combined interval forecasting system. Appl. Energy 2022, 322, 119420. [Google Scholar] [CrossRef]
- Jiao, M.; Qi, X.; Mneg, F.; Wang, T.; Hou, Q.; Zheng, X.; Zhou, H. LSTM-RBF Short-Term Load Forecasting Method Based on Gaussian Similar Days. In Proceedings of the 2023 5th Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 23–26 March 2023; pp. 1189–1194. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, S.; Wu, L.; Kang, L.; Liu, Y. Construction of a Coal Chemical Industry Park with Zero Carbon Emission by Integrating Renewable Energy Based on Life Cycle Analysis. Process Integr. Optim. Sustain. 2024, 8, 1569–1580. [Google Scholar] [CrossRef]
- Pang, X.; Sun, W.; Li, H.; Wang, Y.; Luan, C. Short-term power load forecasting based on gray relational analysis and support vector machine optimized by artificial bee colony algorithm. PeerJ Comput. Sci. 2022, 8, e1108. [Google Scholar] [CrossRef]
- Son, J.; Cha, J.; Kim, H.; Wi, Y.M. Day-Ahead Short-Term Load Forecasting for Holidays Based on Modification of Similar Days’ Load Profiles. IEEE Access 2022, 10, 17864–17880. [Google Scholar] [CrossRef]
- Zhang, D.; Tong, H.; Li, F.; Xiang, L.; Ding, X. An Ultra-Short-Term Electrical Load Forecasting Method Based on Temperature-Factor-Weight and LSTM Model. Energies 2020, 13, 4875. [Google Scholar] [CrossRef]
- Lucas Segarra, E.; Ramos Ruiz, G.; Fernández Bandera, C. Probabilistic Load Forecasting Optimization for Building Energy Models via Day Characterization. Sensors 2021, 21, 3299. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Zhang, C.; Yu, M. A Similar Day Based Short Term Load Forecasting Method Using Wavelet Transform and LSTM. IEEJ Trans. Electr. Electron. Eng. 2022, 17, 506–513. [Google Scholar] [CrossRef]
- Hasan, M.; Mifta, Z.; Papiya, S.J.; Roy, P.; Dey, P.; Salsabil, N.A.; Chowdhury, N.-U.-R.; Farrok, O. A state-of-the-art comparative review of load forecasting methods: Characteristics, perspectives, and applications. Energy Convers. Manag. X 2025, 26, 100922. [Google Scholar] [CrossRef]
- Mamun, A.A.; Sohel, M.; Mohammad, N.; Sunny, M.S.H.; Dipta, D.R.; Hossain, E. A Comprehensive Review of the Load Forecasting Techniques Using Single and Hybrid Predictive Models. IEEE Access 2020, 8, 134911–134939. [Google Scholar] [CrossRef]
- Jin, Y.; Shen, W.; Wu, C.Q. Power Prediction Based on Signal Decomposition and Differentiated Processing with Multi-Level Features. Electronics 2025, 14, 2036. [Google Scholar] [CrossRef]
- Xiao, L.; An, R.; Zhang, X. A Deep Learning Approach Based on Novel Multi-Feature Fusion for Power Load Prediction. Processes 2024, 12, 793. [Google Scholar] [CrossRef]
- Si, C.; Xu, S.; Wan, C.; Chen, D.; Cui, W.; Zhao, J. Electric Load Clustering in Smart Grid: Methodologies, Applications, and Future Trends. J. Mod. Power Syst. Clean Energy 2021, 9, 237–252. [Google Scholar] [CrossRef]
- Syed, D.; Abu-Rub, H.; Ghrayeb, A.; Refaat, S.S.; Houchati, M.; Bouhali, O.; Bañales, S. Deep Learning-Based Short-Term Load Forecasting Approach in Smart Grid With Clustering and Consumption Pattern Recognition. IEEE Access 2021, 9, 54992–55008. [Google Scholar] [CrossRef]
- Agga, F.A.; Abbou, S.A.; Houm, Y.E.; Labbadi, M. Short-Term Load Forecasting Based on CNN and LSTM Deep Neural Networks. IFAC-Pap. 2022, 55, 777–781. [Google Scholar] [CrossRef]
- Lin, J.; Ma, J.; Zhu, J.; Cui, Y. Short-term load forecasting based on LSTM networks considering attention mechanism. Int. J. Electr. Power Energy Syst. 2022, 137, 107818. [Google Scholar] [CrossRef]
- Guo, X.; Liu, R.; Wang, Y.; Ning, Y.; Qu, Q.; Wang, Z.; Cong, W. Short-term power load forecasting for estate-level buildings considering multilevel feature extraction and adaptive fusion. Energy 2025, 337, 138657. [Google Scholar] [CrossRef]
- Maltais, L.-G.; Gosselin, L. Forecasting of short-term lighting and plug load electricity consumption in single residential units: Development and assessment of data-driven models for different horizons. Appl. Energy 2022, 307, 118229. [Google Scholar] [CrossRef]
- Alhussein, M.; Aurangzeb, K.; Haider, S.I. Hybrid CNN-LSTM Model for Short-Term Individual Household Load Forecasting. IEEE Access 2020, 8, 180544–180557. [Google Scholar] [CrossRef]
- Subbiah, S.S.; Chinnappan, J. Deep learning based short term load forecasting with hybrid feature selection. Electr. Power Syst. Res. 2022, 210, 108065. [Google Scholar] [CrossRef]
- Alibrahim, H.; Ludwig, S.A. Hyperparameter Optimization: Comparing Genetic Algorithm against Grid Search and Bayesian Optimization. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, 28 June–1 July 2021; pp. 1551–1559. [Google Scholar] [CrossRef]
- Rong, G.; Li, K.; Su, Y.; Tong, Z.; Liu, X.; Zhang, J.; Zhang, Y.; Li, T. Comparison of Tree-Structured Parzen Estimator Optimization in Three Typical Neural Network Models for Landslide Susceptibility Assessment. Remote Sens. 2021, 13, 4694. [Google Scholar] [CrossRef]
- Andradóttir, S. A Review of Random Search Methods. In Handbook of Simulation Optimization; Springer: Berlin/Heidelberg, Germany, 2015; pp. 277–292. [Google Scholar] [CrossRef]
- Xiao, G.; Xu, F.; Tong, L.; Xu, H.; Zhu, P. A hybrid energy storage system based on self-adaptive variational mode decomposition to smooth photovoltaic power fluctuation. J. Energy Storage 2022, 55, 105509. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Y.; Yu, S.; Guo, Y.; Li, Y.; Han, X.-J.; Zhao, Y.-D.; Chen, S.; Wang, G. An efficient new adaptive variational mode decomposition algorithm for extracting adventitious lung sounds. Biomed. Signal Process. Control 2024, 89, 105700. [Google Scholar] [CrossRef]
- Zeiler, A.; Faltermeier, R.; Keck, I.R.; Tomé, A.M.; Puntonet, C.G.; Lang, E.W. Empirical Mode Decomposition-an introduction. In Proceedings of the The 2010 International Joint Conference on Neural Networks (IJCNN), Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Shen, G.; Tan, Q.; Zhang, H.; Zeng, P.; Xu, J. Deep Learning with Gated Recurrent Unit Networks for Financial Sequence Predictions. Procedia Comput. Sci. 2018, 131, 895–903. [Google Scholar] [CrossRef]
- Wan, R.; Mei, S.; Wang, J.; Liu, M.; Yang, F. Multivariate Temporal Convolutional Network: A Deep Neural Networks Approach for Multivariate Time Series Forecasting. Electronics 2019, 8, 876. [Google Scholar] [CrossRef]
- Jamshidzadeh, Z.; Ehteram, M.; Shabanian, H. Bidirectional Long Short-Term Memory (BILSTM)-Support Vector Machine: A new machine learning model for predicting water quality parameters. Ain Shams Eng. J. 2024, 15, 102510. [Google Scholar] [CrossRef]
- Bennasar, M.; Hicks, Y.; Setchi, R. Feature selection using Joint Mutual Information Maximisation. Expert Syst. Appl. 2015, 42, 8520–8532. [Google Scholar] [CrossRef]
- Liu, S.-Z.; Ma, S.; Chen, H.-Q.; Cui, L.-Z.; Ding, J. Combining KNN with AutoEncoder for Outlier Detection. J. Comput. Sci. Technol. 2024, 39, 1153–1166. [Google Scholar] [CrossRef]
- Liu, P.; Gu, H.; Gu, C.; Wang, Y. A Deformation Prediction Model for Concrete Dams Based on RSA-VMD-AttLSTM. Buildings 2025, 15, 357. [Google Scholar] [CrossRef]
- Shen, K.; Qin, H.; Zhou, J.; Liu, G. Runoff Probability Prediction Model Based on Natural Gradient Boosting with Tree-Structured Parzen Estimator Optimization. Water 2022, 14, 545. [Google Scholar] [CrossRef]
- Abe, K.; Wang, Y.; Watanabe, S. Tree-Structured Parzen Estimator Can Solve Black-Box Combinatorial Optimization More Efficiently. arXiv 2025, arXiv:2507.08053. [Google Scholar]
- Netzell, P.; Kazmi, H.; Kyprianidis, K. Deriving Input Variables through Applied Machine Learning for Short-Term Electric Load Forecasting in Eskilstuna, Sweden. Energies 2024, 17, 2246. [Google Scholar] [CrossRef]
- Zhang, H.; Ping, X.; Wan, H.; Luan, X.; Liu, F. Algae content prediction based on transfer learning and mean impact value. Chemom. Intell. Lab. Syst. 2024, 254, 105244. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H. A new metric of absolute percentage error for intermittent demand forecasts. Int. J. Forecast. 2016, 32, 669–679. [Google Scholar] [CrossRef]
- Chen, M.; Beuchée, A.; Levine, E.; Storme, L.; Gascoin, G.; Hernández, A.I. Model-based characterization of total serum bilirubin dynamics in preterm infants. Pediatr. Res. 2025, 97, 1873–1881. [Google Scholar] [CrossRef] [PubMed]
- Du, S.; Zou, J.; Zheng, X.; Zhong, P. Solar Radiation Prediction Based on the Sparrow Search Algorithm, Convolutional Neural Networks, and Long Short-Term Memory Networks. Processes 2025, 13, 1308. [Google Scholar] [CrossRef]
- Meteorological Data. 2021. Available online: https://energyplus.net/weather (accessed on 10 November 2025).
- Halder, R.K.; Uddin, M.N.; Uddin, M.A.; Aryal, S.; Khraisat, A. Enhancing K-nearest neighbor algorithm: A comprehensive review and performance analysis of modifications. J. Big Data 2024, 11, 113. [Google Scholar] [CrossRef]
- Wang, H.; Liang, Q.; Hancock, J.T.; Khoshgoftaar, T.M. Feature selection strategies: A comparative analysis of SHAP-value and importance-based methods. J. Big Data 2024, 11, 44. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]











| Method | Feature | Reference |
|---|---|---|
| Grid Search | Enumerate all parameter combinations, the cost of calculation increases exponentially with the dimension, and it is completely unintelligent. This approach requires pre-defining a candidate list for each hyperparameter, followed by exhaustive evaluation of all possible combinations. | [22] |
| Tree-structured Parzen Estimator | Improves the predictive accuracy of the model, and automatically finds the globally optimal parameters. The method flow is as follows: based on historical observations, hyperparameters are categorized as “good” or “bad” and modeled using distinct density functions. Subsequent sampling is guided by the improvement probability—the ratio of “good” to “bad” densities—favoring regions most likely to enhance performance. | [23] |
| Random Search | Sampling randomly in the parameter space lacks directional guidance and makes it difficult to find the precise optimal solution. This method entails randomly sampling a set of points within the parameter space, evaluating their performance, and selecting the top-performing candidate. | [24] |
| Variational Mode Decomposition | The method sets bandwidth limits to separate components of different frequencies. Its objective is to minimize the total spectral bandwidth of all principal component functions, thereby effectively suppressing modal confusion. The optimization process requires preset modal parameters. Improper parameter selection may cause over-decomposition or under-decomposition. | [25] |
| Adaptive Variational Mode Decomposition | It is the result of further development of the VMD model. The key advantage is the ability to adaptively determine parameters without the need for manual pre-setting. Core improvement: by using certain criteria (such as envelope entropy, center frequency observation), the optimal modal number K and α are automatically determined, avoiding manual trial and error and making the decomposition results more accurate and objective. | [26] |
| Empirical Mode Decomposition | Sensitive to intermittent signals and noise, and the frequency components of different modalities will be mixed together. The optimization process has no parameters. Each IMF must meet two conditions: the number of extreme points and zero-crossing points must be equal or differ by at most one; at any point, the envelope mean defined by the local maxima and minima is zero. | [27] |
| Gated Recurrent Unit | It has a simpler structure and faster training speed, and can achieve comparable accuracy to LSTM in many scenarios. Core structure consists of two gates: “Update Gate” and “Reset Gate”. | [28] |
| Temporal Convolutional Network | Uses causal convolution to capture the long-term historical dependencies of the sequence and achieves high parallel computing efficiency. The core mechanism involves the use of causal convolution and dilated convolution. | [29] |
| Bidirectional Long Short-Term Memory | It can capture the long-term correlations of time series in addressing specific problems. This method is composed of a forward LSTM and a backward LSTM. The forward LSTM learns information from the past to the future, while the backward LSTM learns information from the future to the past. | [30] |
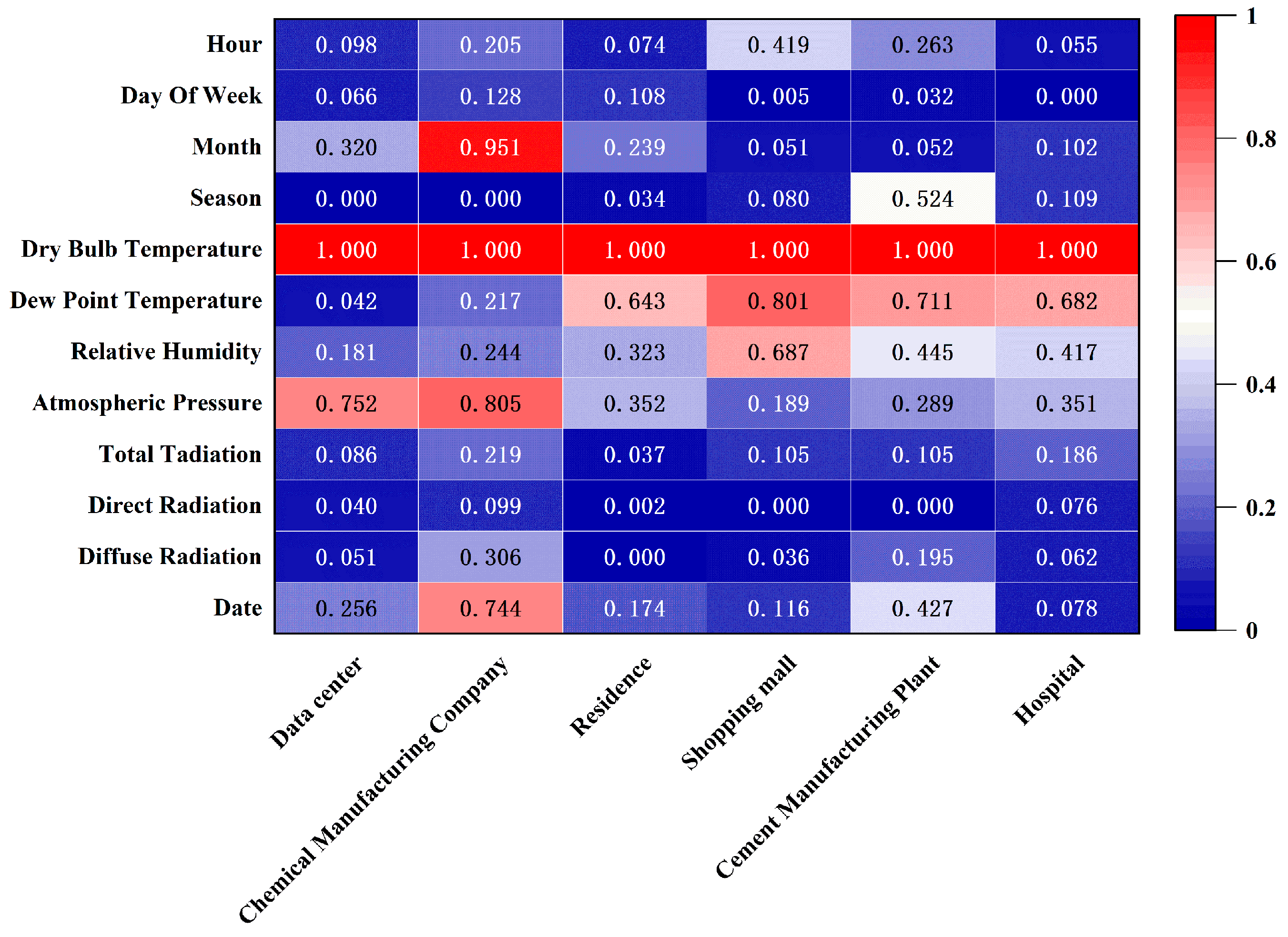
| Building Type | Selected Features |
|---|---|
| Data Center | Dry bulb temperature, atmospheric pressure |
| Chemical Manufacturing Company | Dry bulb temperature, month, atmospheric pressure, date |
| Residence | Dry bulb temperature, dew point temperature |
| Shopping Mall | Dry bulb temperature, dew point temperature, relative humidity |
| Cement Manufacturing Plant | Dry bulb temperature, dew point temperature |
| Hospital | Dry bulb temperature, dew point temperature |
| Prediction Model | Model 1 Training Set/Testing Set—80%/20% | Model 1 Rolling-Origin (Walk-Forward) | |||||
|---|---|---|---|---|---|---|---|
| Test Sample/ Evaluation Index | R2 | EMAE (MW) | ERMSE (MW) | R2 | EMAE (MW) | ERMSE (MW) | EMAE/ERMSE |
| Data Center | 0.9989 | 0.0474 | 0.0726 | 0.9945 | 0.0949 | 0.1630 | 0.5822 |
| Chemical Manufacturing Company | 0.9955 | 0.2269 | 0.3002 | 0.9944 | 0.2365 | 0.3365 | 0.7028 |
| Residence | 0.9989 | 0.0096 | 0.0128 | 0.9987 | 0.0091 | 0.0141 | 0.6453 |
| Shopping Mall | 0.9993 | 0.0784 | 0.1093 | 0.9988 | 0.0880 | 0.1461 | 0.6023 |
| Cement Manufacturing Plant | 0.9945 | 0.2814 | 0.4319 | 0.9947 | 0.2916 | 0.4237 | 0.6882 |
| Hospital | 0.9982 | 0.0181 | 0.0258 | 0.9974 | 0.0197 | 0.0313 | 0.6293 |
| Prediction Model | Model 2 Training Set/Testing Set—80%/20% | Model 2 Rolling-Origin (Walk-Forward) | |||||
| Test Sample/ Evaluation Index | R2 | EMAE (MW) | ERMSE (MW) | R2 | EMAE (MW) | ERMSE (MW) | EMAE/ERMSE |
| Data Center | 0.9969 | 0.0885 | 0.1218 | 0.9922 | 0.1028 | 0.1942 | 0.5293 |
| Chemical Manufacturing Company | 0.9947 | 0.2460 | 0.3267 | 0.9965 | 0.1817 | 0.2667 | 0.6813 |
| Residence | 0.9984 | 0.0120 | 0.0156 | 0.9964 | 0.0182 | 0.0232 | 0.7845 |
| Shopping Mall | 0.9990 | 0.1019 | 0.1332 | 0.9896 | 0.3714 | 0.4239 | 0.8762 |
| Cement Manufacturing Plant | 0.9942 | 0.3054 | 0.4439 | 0.9982 | 0.1676 | 0.2452 | 0.6835 |
| Hospital | 0.9976 | 0.0226 | 0.0300 | 0.9959 | 0.0290 | 0.0390 | 0.7435 |
| Prediction Model | Model 3 Training Set/Testing Set—80%/20% | Model 3 Rolling-Origin (Walk-Forward) | |||||
| Test Sample/ Evaluation Index | R2 | EMAE (MW) | ERMSE (MW) | R2 | EMAE (MW) | ERMSE (MW) | EMAE/ERMS |
| Data Center | 0.9951 | 0.0591 | 0.1540 | 0.9947 | 0.0670 | 0.1595 | 0.4200 |
| Chemical Manufacturing Company | 0.9928 | 0.2679 | 0.3800 | 0.9891 | 0.2749 | 0.4694 | 0.5856 |
| Residence | 0.9982 | 0.0099 | 0.0163 | 0.9979 | 0.0101 | 0.0176 | 0.5738 |
| Shopping Mall | 0.9972 | 0.1094 | 0.2217 | 0.9981 | 0.1081 | 0.1806 | 0.5986 |
| Cement Manufacturing Plant | 0.9946 | 0.2795 | 0.4287 | 0.9938 | 0.2871 | 0.4588 | 0.6257 |
| Hospital | 0.9957 | 0.0276 | 0.0399 | 0.9969 | 0.0212 | 0.0340 | 0.6235 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, R.; Kou, J.; Guo, L.; Wei, S.; Hu, S.; Zhang, Q. Zero-Carbon Parks’ Electric Load Forecasting Considering Feature Extraction of Multi-Type Electric Load and Dual-Layer Optimization Modal Decomposition. Buildings 2025, 15, 4209. https://doi.org/10.3390/buildings15234209
Shi R, Kou J, Guo L, Wei S, Hu S, Zhang Q. Zero-Carbon Parks’ Electric Load Forecasting Considering Feature Extraction of Multi-Type Electric Load and Dual-Layer Optimization Modal Decomposition. Buildings. 2025; 15(23):4209. https://doi.org/10.3390/buildings15234209
Chicago/Turabian StyleShi, Rui, Jianyu Kou, Lei Guo, Shen Wei, Shuai Hu, and Quan Zhang. 2025. "Zero-Carbon Parks’ Electric Load Forecasting Considering Feature Extraction of Multi-Type Electric Load and Dual-Layer Optimization Modal Decomposition" Buildings 15, no. 23: 4209. https://doi.org/10.3390/buildings15234209
APA StyleShi, R., Kou, J., Guo, L., Wei, S., Hu, S., & Zhang, Q. (2025). Zero-Carbon Parks’ Electric Load Forecasting Considering Feature Extraction of Multi-Type Electric Load and Dual-Layer Optimization Modal Decomposition. Buildings, 15(23), 4209. https://doi.org/10.3390/buildings15234209




