Seismic Performance and Collapse Fragility of a 765 kV Transmission Tower–Line System

Abstract

Based on a real-world project in Pakistan, this study investigates the seismic performance and collapse fragility of a 765 kV transmission tower–line system. A refined finite element model, incorporating three towers and four conductor spans, is developed to systematically simulate the system’s dynamic characteristics, seismic response, and nonlinear collapse process. The Incremental Dynamic Analysis (IDA) method is employed for fragility assessments. The results demonstrate that the fundamental frequency of the tower–line system is significantly lower than that of an isolated tower, indicating that the transmission lines substantially reduce the overall structural stiffness. The vulnerable regions in the system are primarily identified at the second and third segments. The mean Peak Ground Acceleration (PGA) triggering collapse is found to be 1.07 g, with the collapse mode characterized by a progressive failure initiated by cumulative damage in the lower members. The derived fragility curves indicate that the probability of system collapse exceeds 55% at a PGA of 1.0 g. These findings can provide a valuable reference for the seismic design and safety evaluation of high-voltage electricity transmission systems.

1. Introduction

As a crucial component of the power supply system, the high-voltage electricity transmission network offers significant advantages, including a large transmission capacity, extensive coverage, high efficiency, and low power loss. Earthquakes, characterized by their strong destructiveness and high frequency, pose a severe threat to power grid security. The collapse of transmission tower–line structures during seismic events can trigger cascading failures, jeopardizing the stability of regional power grids and leading to severe disruptions to social functioning and public safety [1,2,3,4].

Under seismic action, the dynamic response of the transmission tower–line system is complex. In recent years, scholars have conducted extensive research on seismic performance evaluation.

Initially, simplified models were used for the simulation of transmission towers [5,6,7], followed by more sophisticated ones. Suzuki et al. [8] idealized the conductors as springs attached at the cross-arms and simplified the transmission tower as an equivalent beam model. Wu et al. [9] found that the pulse effect of near-fault ground motions significantly amplifies the seismic response of transmission tower–line systems. Du et al. [10] developed collapse fragility curves for hurricane events to avoid the difficulty of quantifying the correlations of failure probabilities across different time intervals within a storm. Miguel et al. [11] compared and analyzed the nonlinear dynamic responses of two typical tower–line systems under different seismic load scenarios, finding that moderate earthquakes can reduce the tower’s resistance to future climatic events. Lai et al. [12] demonstrated that stainless steel tube-confined ultra-high-performance concrete (SS+UHPC) stub columns exhibit excellent ductility and stable residual strength under cyclic loading. This configuration effectively mitigates the brittle failure characteristics of concrete, offering a new material option for the design of seismic-resistant components in structures such as transmission towers.

Given the various characteristics of earthquakes [13,14,15], such as near-fault mainshock–aftershock sequences, Li et al. [16] generated mainshock–aftershock sequences to investigate the damage states of frame structures. Although the repeated synthesis method is straightforward and convenient, it overlooks the randomness and dispersion of ground motions, resulting in significant application limitations. Moustafa et al. [17] employed this method to evaluate the additional damage inflicted by aftershocks on structures. Bruneau et al. [18] introduced the concept of “resilience” into the seismic field of engineering structures, defining community seismic resilience as the ability to mitigate disaster-induced damage, facilitate recovery, and reduce future earthquake impacts. Xu et al. [19] established a database for the recovery time and functional loss of frame structures based on seismic fragility functions. Liu et al. [20] studied the seismic capacity of transmission towers under mainshock–aftershock sequences. Based on a global damage-based fragility assessment method, five damage states for transmission towers were defined. Dynamic analysis considering the steel constitutive model in ABAQUS was conducted to obtain seismic damage under 20 sets of mainshock–aftershock sequences, and fragility curves were derived through a probability density distribution. The results showed that the damage probability of the transmission tower increases significantly with the intensity of aftershocks. Pan et al. [21] adopted the fragility research methodology used for subsea free-span pipelines under spatial ground motions to conduct a seismic fragility analysis of transmission towers. Considering the loss of spatial coherence and directivity effects of ground motions, they evaluated the influence of different input modes on the failure probability. Zheng et al. [22] proposed an explicit dynamic analysis method and used member failure criteria to analyze the progressive collapse of a transmission tower. The results showed that the tower exhibits different collapse failure modes under different seismic waves.

To more accurately assess the seismic safety of high-voltage transmission tower–line systems, this paper, based on a specific 765 kV transmission line project in Pakistan, establishes a refined finite element model of the tower–line system considering conductor coupling effects by utilizing an advanced constitutive model that reflects the hysteretic behavior of steel. Through modal analysis, dynamic response analysis, and IDA, the nonlinear response laws and damage evolution process of the structure are systematically studied. Furthermore, the collapse mechanism of the system is revealed, and its probabilistic fragility curves are established, aiming to provide references for the seismic design of high-voltage transmission projects.

2. Finite Element Model Establishment

2.1. Project Overview

Based on a 765 kV transmission line project in Pakistan, this paper selects a section of the transmission line as the research object, including three transmission towers and four spans of conductors (ground wires). Both the side span length and the middle span length are 550 m. The three transmission towers are identical tangent towers, with design information shown in Figure 1. The main structure of the tangent tower has a total height of 101 m, a nominal height of 53 m, and a base dimension of 20.5 m × 20.5 m. It is equipped with three cross-arms located at elevations of 61 m, 78.5 m, and 96 m, respectively. The members are made of Q420 and Q355 equal-leg angles. The main members are made of Q420, with cross-sectional sizes varying from L220 × 24 to L110 × 8. The bracing members are made of Q355, with cross-sectional sizes varying from L125 × 10 to L45 × 5. Each span of the transmission line is divided into four layers, consisting of six conductors and two ground wires. The ends are suspended at equal height with a sag of 32.46 m. They are connected to the tangent towers via insulators at the cross-arms. The top layer consists of ground wires (type ACS 19 No. 10 AWG aluminum-clad steel strand). The lower three layers consist of six bundle conductors (steel-reinforced-type ACSR 954 KCM Rail aluminum conductor). The specifications and performance indicators of the conductors and ground wires are listed in

Table 1. Design parameters of transmission lines.

Material Properties	Wire	Ground Wire
category	ACSR 954 KCM Rail	ACS 19 No. 10 AWG
outer diameter (mm)	62.8	11.28
cross-sectional area (mm2)	3097	99.93
elastic modulus (GPa)	60.5	162
unit length mass (kg/m)	9.594	0.668
thermal expansion Coefficient (1/°C)	2.08 × 10−5	1.30 × 10−5

.

2.2. Establishment of the Finite Element Model for the Tower–Line System

Based on reference [23], the model adopts a frame form, treating all member connections as rigid connections, allowing members to withstand axial force, shear, bending moment, and torque, to more accurately reflect the complex stress state of rigidly connected members in actual engineering. This study adopted a collaborative modeling strategy using SAP2000 and ABAQUS. The geometric model of the transmission tower–line system was first established in SAP2000 and then imported into ABAQUS for nonlinear dynamic analysis and collapse simulations. Transmission tower members are simulated using beam elements (B31). Conductors and insulators are simulated using truss elements (T3D2). The masses of components such as flanges, bolts, and gusset plates are applied as concentrated mass points to the segments of the finite element model. Compared with previous research [24], a phenomenological hysteretic model [25] was introduced during modeling to simulate the buckling effect of angle steel components under seismic action. Fixed constraints are applied to the base segments of the tower legs, completely restricting their six degrees of freedom (three translations and three rotations), simulating the actual condition of the tower being fixed to the ground. The coordinate system is defined as follows: X-axis parallel to the conductor direction, Y-axis parallel to the cross-arm axial direction, and Z-axis along the tower height direction. The finite element model of the transmission tower–line system is shown in Figure 2.

3. Seismic Performance Analysis of Transmission Towers

3.1. Dynamic Characteristic Analysis

Modal analysis is crucial for structures subjected to dynamic loads and serves as the starting point for dynamic analysis. This section performs modal analysis on the single transmission tower and the tower–line system based on the Lanczos algorithm, comparing the vibration modes and natural frequencies of the structures in different finite element models.

As shown in Figure 3, the first three vibration modes of the isolated tower model are all global modes, sequentially being bending vibration in the X direction, bending vibration in the Y direction, and torsional vibration in the Z direction. In the dynamic characteristic analysis of the tower–line system, due to the much lower stiffness of the conductors compared to the tower, the lower-order modes are predominantly conductor vibration modes. The first three modes of the system are shown in Figure 4. From the natural frequencies listed in

Table 2. Natural frequencies of the isolated tower and the tower–line system (Hz).

Mode Shape	Isolated Transmission Tower	Transmission Tower–Line System	D-Value
1	1.203	0.551	54.2%
2	1.215	0.569	53.2%
3	2.438	1.210	50.4%

for the single tower and the tower–line system, it can also be seen that the inclusion of conductors significantly reduces the natural frequencies of the tower–line system compared to the isolated tower model. This core finding, which highlights that “conductors significantly reduce the system stiffness”, aligns well with conclusions from an existing study [26], providing strong indirect evidence and a rational basis for the reliability of the model’s dynamic characteristics.

3.2. Seismic Response Analysis

This section selects five ground motion records from the Pacific Earthquake Engineering Research Center (PEER) ground motion database (http://peer.berkeley.edu, accessed on 18 March 2025) for the seismic response analysis of the tower–line system. The ground motion information is listed in

Table 3. Ground motion information.

Order	Earthquake Event	Record Stations	Time	Magnitude
1	Imperial Valley	El Centro Array #6	1979	6.53
2	Miyagi Prefecture Building—Top	Tohoku	2011	9.00
3	Taiwan Earthquake	Chiayi Weather Station	2016	6.40
4	Chi-Chi Earthquake	Guanzih	1999	7.60
5	Great Hanshin Earthquake	Kobe Marine S1010	1995	6.90

. The Peak Ground Acceleration (PGA) of the selected records is scaled to 0.2 g. Figure 5 shows the acceleration time-history curves of the scaled Imperial Valley ground motion. For this record, the X-component reaches the peak acceleration of 0.2 g at 2.8 s, and the Y-component reaches 0.2 g at 2.1 s.

We used consistent excitation to input seismic motion and conduct dynamic time-history analysis. Figure 6 shows the Imperial Valley wave as an example and presents the top displacement time-history curve and top acceleration time-history curve of the transmission tower–line system under seismic excitation. From Figure 6a, it can be seen that under seismic excitation in the X direction, the system reaches a displacement peak of 0.21 m at 8 s, while from Figure 6b, it can be seen that its acceleration response reaches a peak of 13.21 m/s² at 9 s. Similarly, Figure 6c shows that the displacement under Y-direction seismic excitation reaches a peak of 0.15 m at 6 s, while the acceleration peak in Figure 6d appears at 11 s with a magnitude of 14.13 m/s². As mentioned earlier, the seismic wave reaches its peak acceleration in 2–3 s, indicating that under seismic excitation, the dynamic response of the transmission tower–line system has a certain time lag, and peak acceleration occurs later than peak displacement. The superstructure’s inertia causes its response to lag after base excitation when seismic ground motion is applied to the foundation. At the peak displacement—a point of zero velocity where the direction is about to reverse—the structure experiences its greatest deformation. On the other hand, as the structure recovers from the maximum displacement position, acceleration—which is directly proportional to the inertial force—peaks. The response parameters have a distinctive phase lag as a result of this sequential sequencing.

Additionally, the stiffness of the transmission tower is typically lower in the Y direction (the cross-arm axial direction) than in the X direction (the conductor direction). This is because the conductors provide additional restraint and stiffness in the X direction, but this restraining effect is weaker in the Y direction. Lower stiffness results in a longer natural period of the structure, leading to greater dynamic responses (including displacement and acceleration) and making the inertia effect more prominent. Consequently, the lag in the acceleration response is more evident in the more flexible Y direction, reflecting the inertia effect of the transmission tower–line system under earthquake action.

To comprehensively evaluate the dynamic response of transmission towers under different seismic excitations, a comparative analysis was conducted on the structural response. The peak displacement, peak acceleration, and peak stress of the transmission tower legs under five seismic wave excitations are listed in

Table 4. Peak dynamic response of the transmission tower–line system.

Ground Motion	Peak Displacement of Tower Top (m)		Peak Acceleration at the Top of the Tower (m/s2)		Peak Stress of Tower Leg (MPa)
	X Direction	Y Direction	X Direction	Y Direction	X Direction	Y Direction
1	0.21	0.15	13.21	14.13	123.7	143.5
2	0.15	0.18	17.51	19.53	113.4	157.6
3	0.44	0.39	17.41	15.47	221.1	184.5
4	0.14	0.19	9.55	8.21	108.4	123.4
5	0.16	0.23	4.89	9.34	78.6	93.1

and further presented in Figure 7a–c.

The dynamic response results of the transmission tower under different ground motions are shown in Figure 7. The peak displacement at the top of the tower ranges from 0.14 m to 0.44 m, while the peak acceleration at the top of the tower ranges from 4.89 m/s² to 19.53 m/s², and the peak stress of the tower leg ranges from 78.6 MPa to 221.1 MPa. All response parameters show significant dispersion, primarily due to differences in spectral characteristics, duration, and energy distribution among the different ground motion records. The maximum tower leg stress (221.1 MPa) is far below the yield strength of the Q420 main member steel (420 MPa) and the Q355 bracing member steel (355 MPa), indicating that the structure remains entirely elastic under 0.2 g PGA seismic action, possesses sufficient safety margin, and meets the requirements for the basic design earthquake in a seismic region of intensity 8.

4. Collapse Failure Analysis of the Tower–Line System

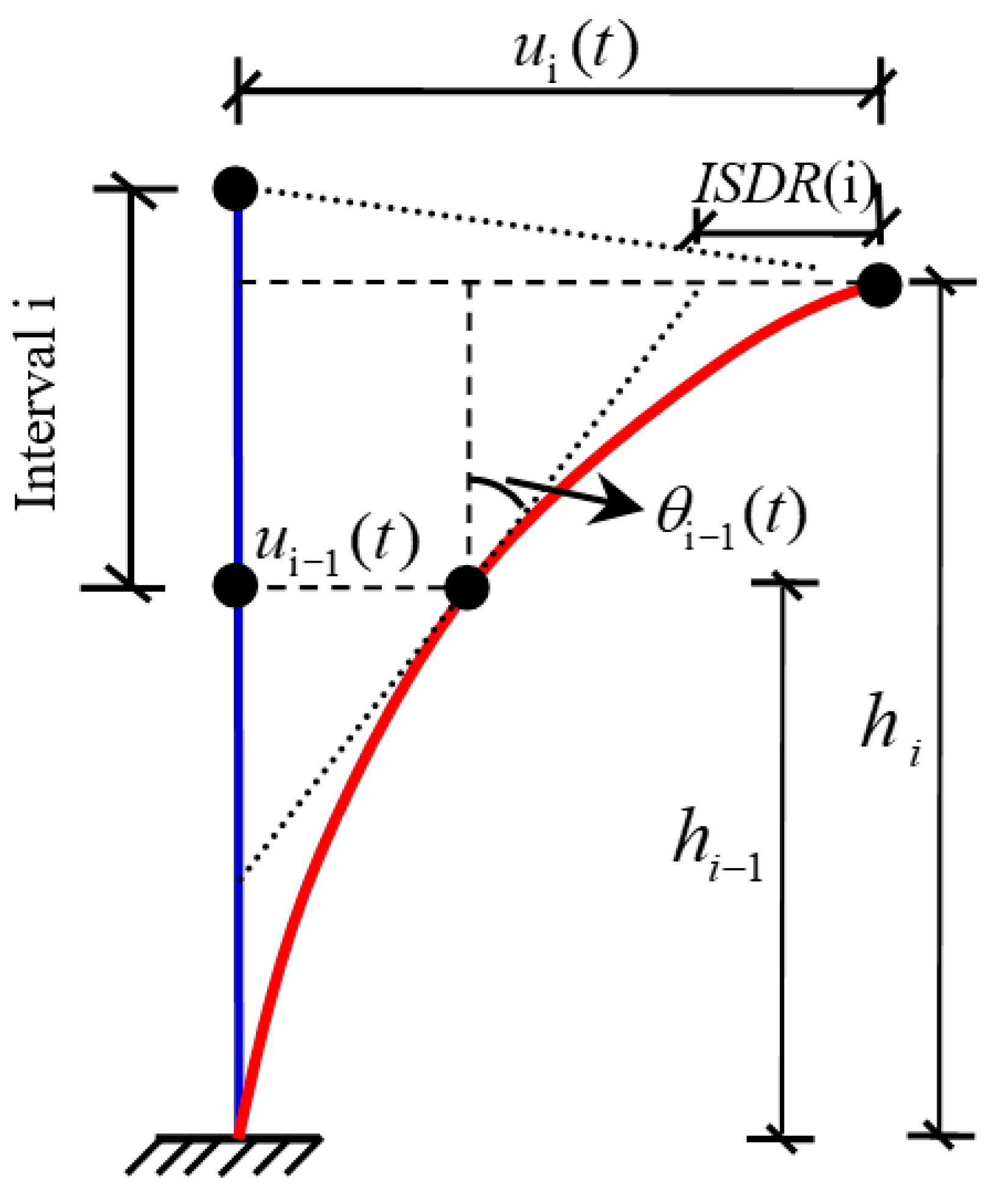
To investigate the collapse failure mechanism of the tower–line system under seismic action, this section employs 10 sets of typical ground motions to perform Incremental Dynamic Analysis (IDA) on the tower–line system. These ground motion records, defined as GM01 to GM10, were selected from the Pacific Earthquake Engineering Research Center (PEER) ground motion database, encompassing actual strong motion records with different magnitudes, spectral characteristics, and durations to ensure the representativeness and statistical significance of the analysis results. The PGA is incrementally increased from 0.2 g to 1.2 g in steps of 0.1 g, obtaining the progressive collapse modes and ultimate seismic capacity under different conditions. The inter-story drift ratio can intuitively present the seismic response along the height and identify potential weak locations under different ground motions, and it is widely used as a failure criterion in building structure seismic research. However, compared to traditional building structures, transmission towers have a large height-to-width ratio and lack floor system support between segments, leading to large rotational deformations in the segments. 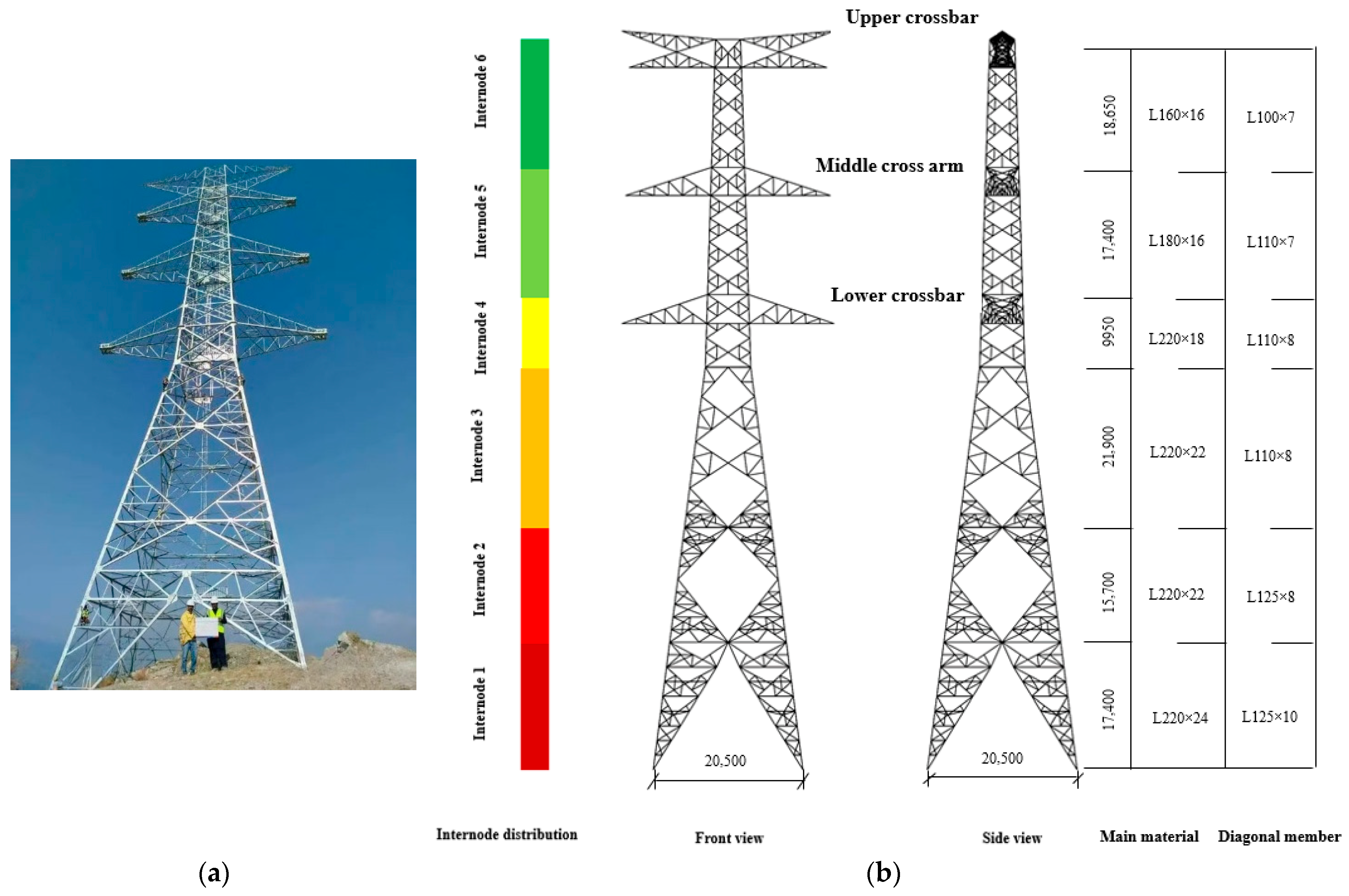Therefore, this paper modifies the traditional inter-story drift ratio by eliminating the effect of rotational deformation [27] and adopting the Inter-Segment Displacement Ratio (ISDR) as the failure criterion for the transmission tower structure. When the ISDR of the transmission tower exceeds 2%, the structure is judged to have collapsed. The segment division is shown in Figure 1. A schematic diagram of the ISDR is shown in Figure 8, and the calculation formula is as follows:

$$ISDR\left(i\right)=max\left[{\displaystyle \frac{u_i\left(t\right)-u_{i-1}\left(t\right)}{h_i-h_{i-1}}}-{\theta }_{i-1}\left(t\right)\right].$$

(1)

In the formula, $i$ is the internode number, which is equal to 1, 2, …, 6; the $ISDR\left(i\right)$ is the internode displacement angle along the ith horizontal node; t is time; $u_i\left(t\right)$ and $u_{i-1}\left(t\right)$ are the displacement time histories of the top and bottom of the ith node along the horizontal direction, respectively; $h_i$ and $h_{i-1}$ are the heights of the top and bottom of the ith internode along the horizontal direction, respectively; and ${\theta }_{i-1}\left(t\right)$ is the time history of torsional displacement along the bottom of the ith node in the horizontal direction.

Figure 8. Inter-segment displacement angle.

Figure 8. Inter-segment displacement angle.

4.1. Weak Location Analysis

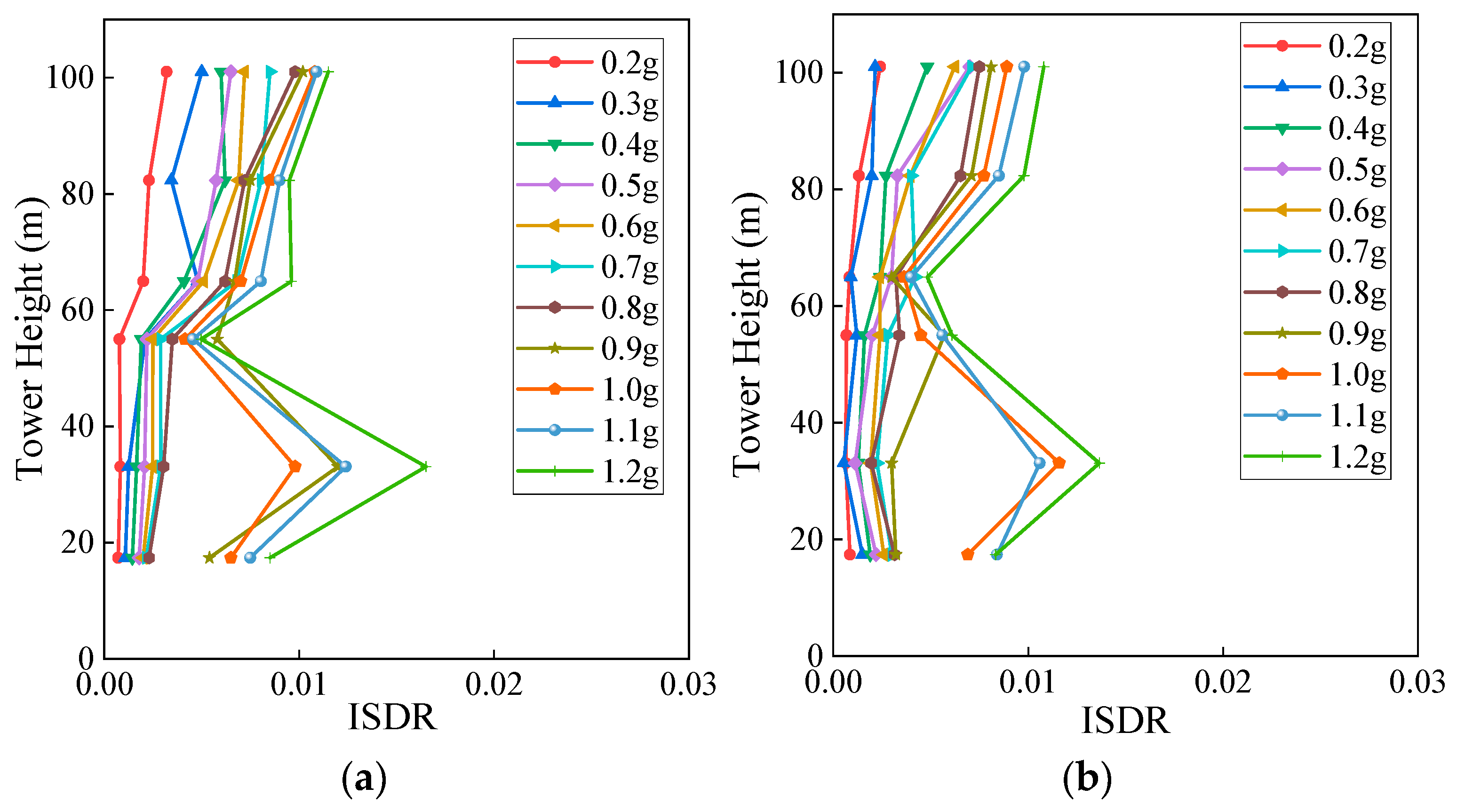
The median displacement angle between transmission towers in the transmission tower–line system under seismic excitation is shown in Figure 9. Figure 9a,b, respectively, provide the median displacement angle between transmission towers in the X and Y directions. It can be seen that when the PGA is small, the trend of the ISDR variation in the transmission tower is basically the same; that is, as the height increases, the ISDR gradually increases. As the PGA increases, the trend of the ISDR of the transmission tower changes, indicating that the transmission tower has entered plasticity. When the PGA is 0.2 g, the ISDRs of the first to sixth segments in the X direction are 0.07%, 0.08%, 0.09%, 0.20%, 0.23%, and 0.32%, respectively. When the PGA is 0.8 g, the ISDRs of the first to sixth segments in the X direction are 0.23%, 0.31%, 0.35%, 0.62%, 0.72%, and 0.98%, respectively. It can be seen that the seismic PGA increases significantly from 0.2 g to 0.8 g in the third and fourth segments. When the PGA is less than 1.0 g, the ISDR of the transmission tower is less than 2%. When the PGA is 1.0 g and 1.1 g, although the ISDR of the transmission tower is less than 2%, there is already a mutation position. When the PGA is 1.0 g, the ISDR mutation position of the transmission tower in the X direction is 17.4 m, and the ISDR is 0.014. When the PGA is 1.1 g, the ISDR mutation position of the transmission tower in the Y direction is 33.1 m, and the ISDR is 0.011. When the PGA of the local seismic intensity is low, the ISDR of the sixth segment is the highest. As the seismic intensity gradually increases, the ISDR of the lower segment of the transmission tower gradually increases. The results above indicate that with the increase in seismic intensity, the damage mode of transmission towers gradually shifts from overall bending deformation to concentrated plastic deformation in the middle and lower segments (such as the second and third segments), clearly revealing the nonlinear evolution process of the structure and the transfer path of weak links.

Table 5. Maximum ISDR locations.

Ground Motion	Maximum ISDR Locations
GM01	Y2
GM02	Y3
GM03	Y1
GM04	Y3
GM05	X3
GM06	Y2
GM07	X2
GM08	Y3
GM09	X3
GM10	Y2

summarizes the locations of the damaged segments in the transmission tower within the tower–line system under ten different seismic excitations. The inter-story locations are defined as follows: X and Y represent the X and Y directions in the finite element model, respectively, and the numbers indicate the segments positions. For example, “Y3” denotes the third segment in the Y direction of the transmission tower. Based on this information, it can be concluded that the weak areas of the transmission tower are located at the second and third inter-story segments, and the mutation points (i.e., the locations most susceptible to damage) differ between the X direction and the Y direction, primarily due to the inherent asymmetry in structural stiffness of the transmission tower–line system.

4.2. Collapse PGA Analysis

Table 6. Collapse PGA (g) of the transmission tower–line system.

Ground Motion	Collapse PGA (g)
GM01	1.2 (Non-collapsed)
GM02	1.0
GM03	1.2
GM04	1.0
GM05	1.0
GM06	0.9
GM07	1.0
GM08	1.1
GM09	1.2 (Non-collapsed)
GM10	1.1
Mean	1.07

lists the collapse PGA and its mean value for the transmission tower–line system under ten different seismic excitations. With the exception of GM01 and GM09, under which the transmission tower–line system did not collapse, the ISDR under all other seismic excitations exceeded the limit of 2%, indicating structural collapse. According to the statistical data in Table 6, the collapse PGA for the transmission tower–line system ranges from 0.9 g to 1.2 g, with a mean value of 1.07 g.

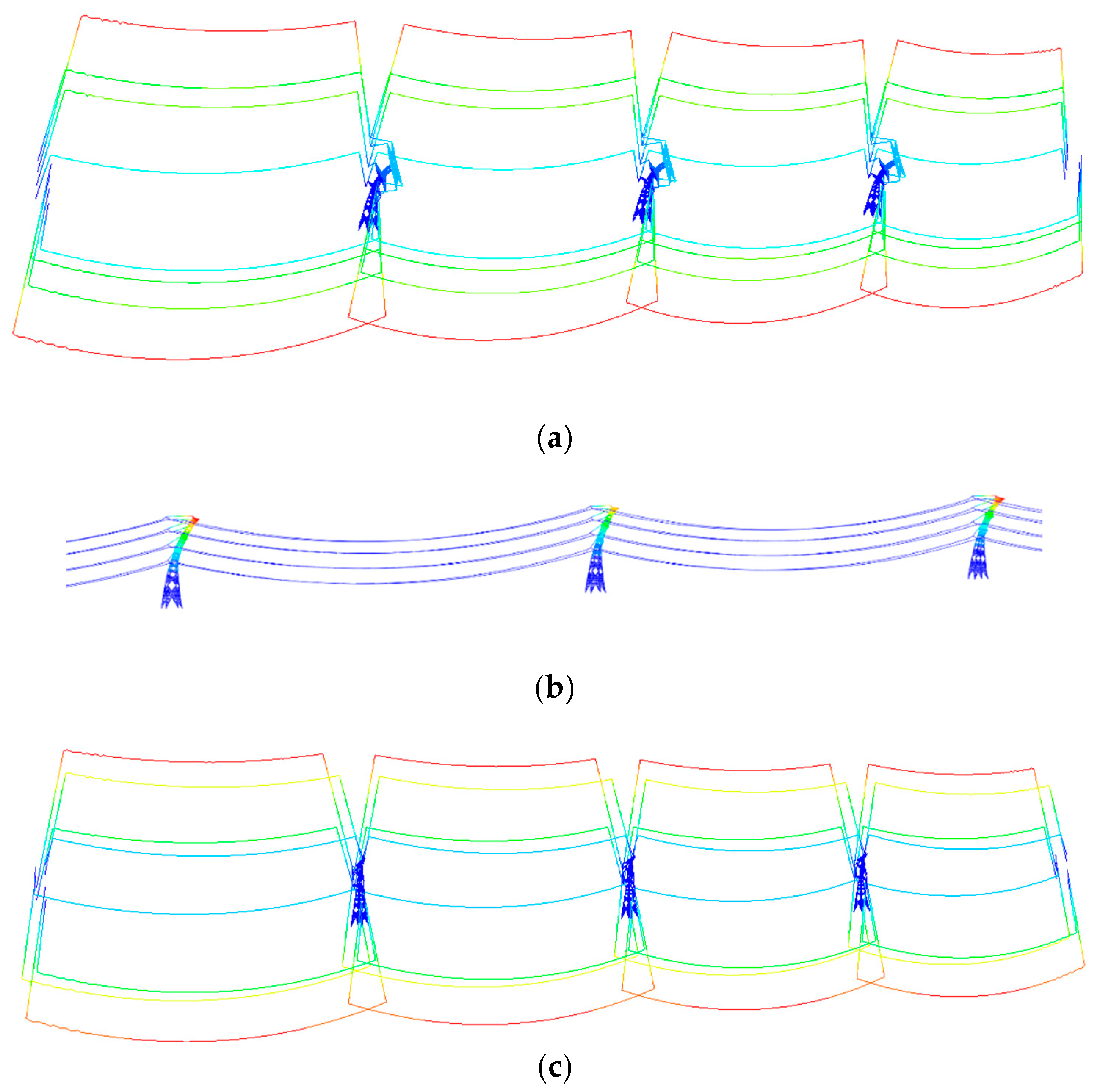
4.3. Collapse–Failure Process Analysis

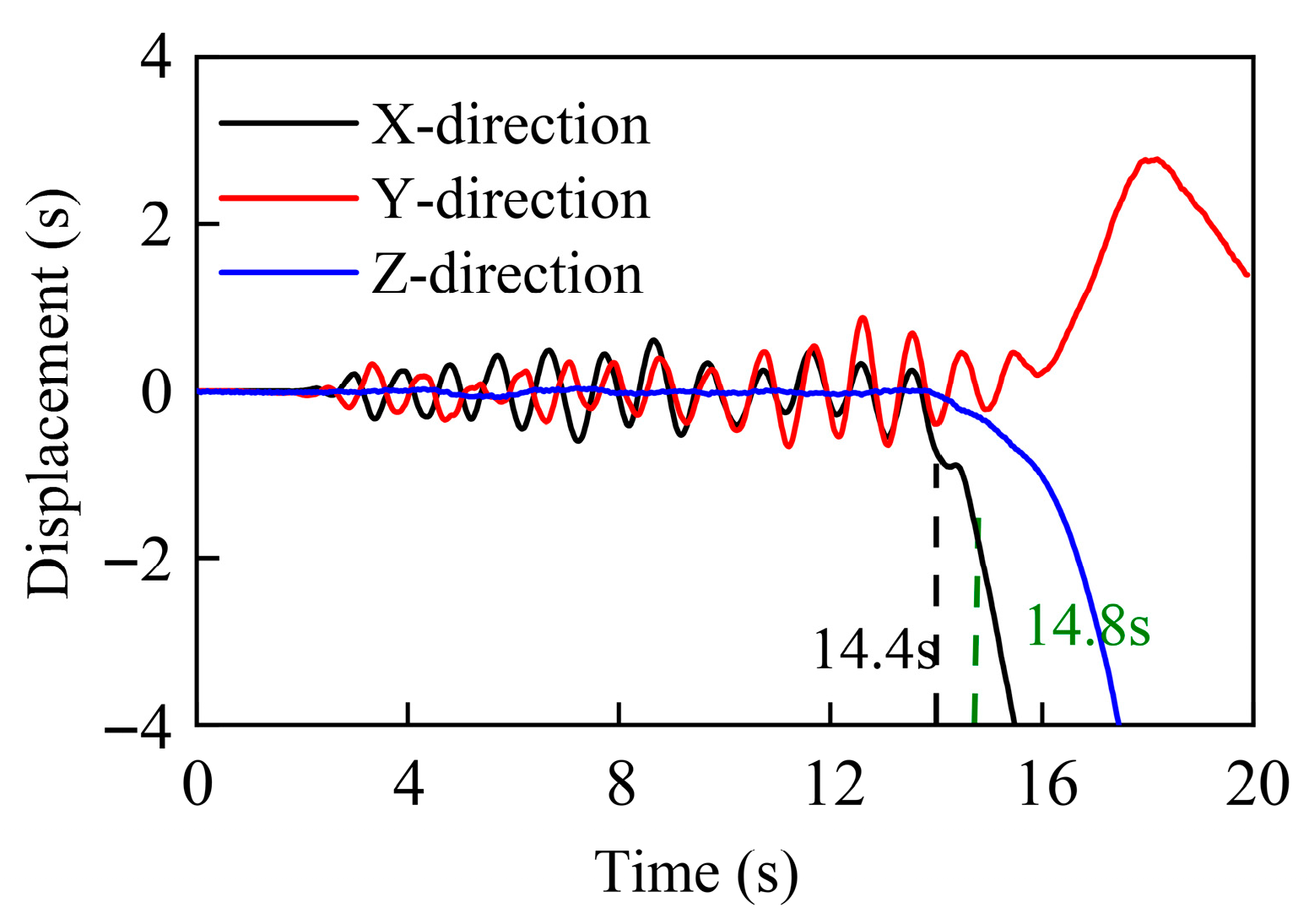
Taking GM07 as an example, Figure 10 presents the time-history curve of the tower-top displacement for the transmission tower–line system under the collapse PGA seismic excitation condition. It can be observed that in the early stage of seismic excitation, the tower-top displacement ranged from −0.738 m to 0.862 m. When the excitation time reached 14.4 s under the collapse PGA, the tower-top displacement began to exhibit a divergent trend, indicating the onset of damage in the transmission tower–line system. At 14.8 s, the ISDR of the transmission tower exceeded 2%, demonstrating that the transmission tower–line system experienced collapse failure.

To further analyze the cumulative damage effect of the transmission tower–line system and clarify the process of its progressive collapse, this section quantitatively presents the cumulative damage in the transmission tower members using the SDV4 parameter from a novel nonlinear hysteretic constitutive model. The value of SDV4 increases progressively with the maximum plastic strain and the cumulative plastic strain in the transmission tower members. This accumulation process is monotonic and irreversible. A value of SDV4 = 0 indicates an intact member, whereas SDV4 = 1 signifies that the member has fractured, so it is removed from the analysis. 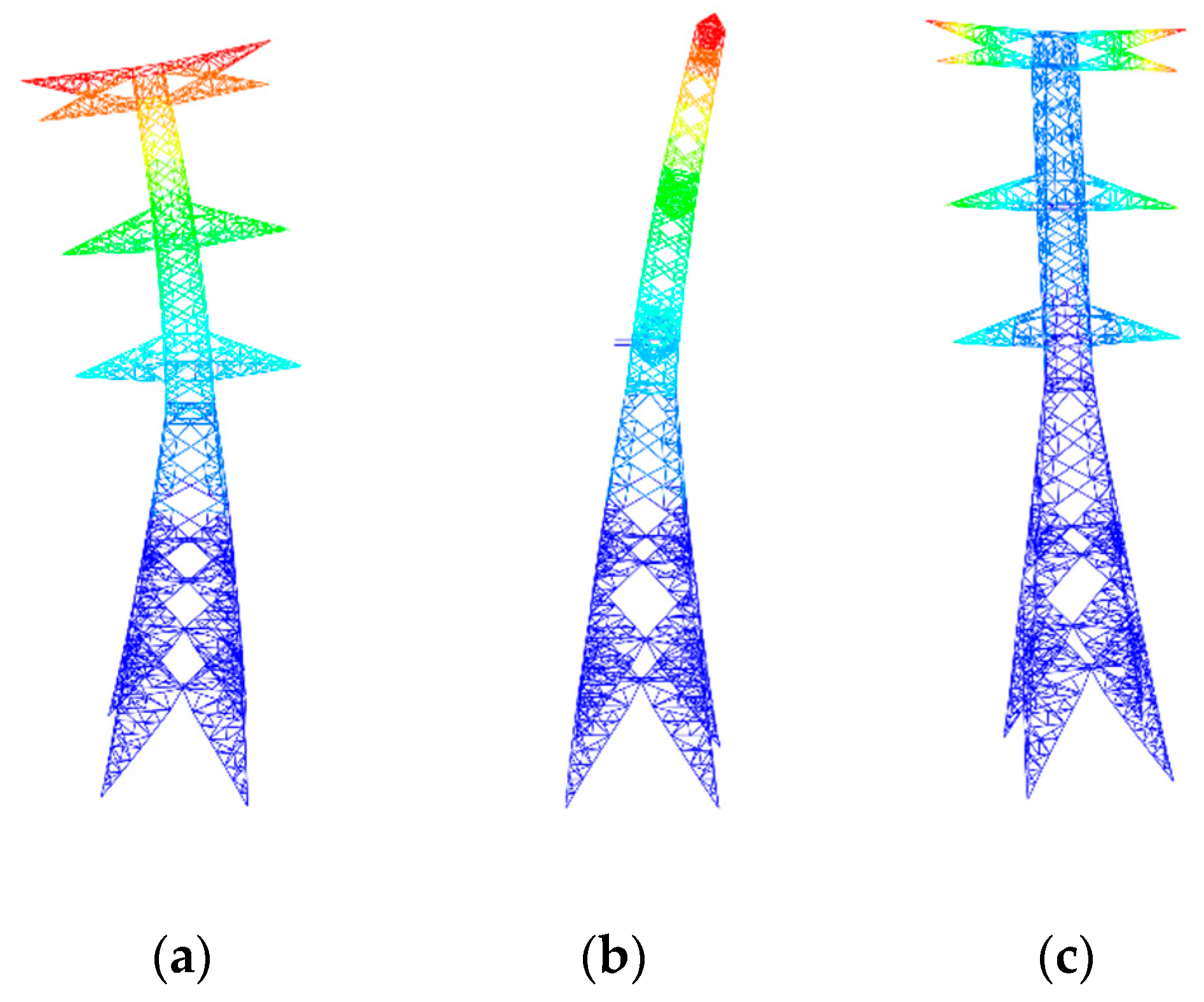Figure 11 shows the damage contour of the transmission tower–line system under this seismic excitation condition.

It can be observed that significant deformation occurred in the lower inter-story segments of the transmission tower, leading to the collapse failure of the tower–line system. The collapse process of the transmission tower is as follows: At t = 3.6 s, multiple diagonal members in the lower inter-story segments began to exhibit cumulative damage. By t = 15.0 s, widespread damage had developed in the diagonal, auxiliary, and cross-diagonal members within these segments. A few components reached SDV4 = 1 (complete failure), and significant global structural deformation was observed. Based on the tower-top displacement time-history curve, the transmission tower was determined to have entered a collapsing state. Subsequently, the progression of member failures accelerated. By t = 18.0 s, most members in the lower inter-story segments were severely damaged, with multiple components reaching SDV4 = 1, resulting in extensive deformation of the overall structure.

5. Fragility Analysis of the Transmission Tower–Line System

Seismic fragility of a structure refers to the probability of the structure reaching a specific performance level under seismic excitations of varying intensities. It serves as a scientific basis for assessing the seismic performance of the structure and estimating the potential extent of damage it may sustain during an earthquake [28,29,30]. Based on the IDA results from Section 4, this section analyzes the seismic performance of a typical transmission tower–line system by developing fragility curves. First, pushover analysis was conducted to quantify the threshold values for different performance levels of the transmission tower. Then, using the maximum ISDR of the tower as the seismic demand parameter and PGA as the seismic intensity measure, the seismic demand relationship of the system was established. Based on this, fragility curves were generated to analyze the seismic damage of the transmission tower system.

5.1. Quantification of Critical States

The fragility analysis workflow for the structural system is shown in Figure 12. The quantitative assessment of different performance levels for the selected transmission tower–line system serves as the starting point of the fragility analysis. According to ‘Seismic Grade Classification for Lifeline Engineering’ (GB/T 24336-2009) [31], the seismic damage grades of the transmission tower system are divided into five phases: Grade I (essentially intact), Grade II (slight damage), Grade III (moderate damage), Grade IV (severe damage), and Grade V (collapse). For a transmission tower subjected to severe damage, under seismic action, damage to its members accumulates rapidly, causing the structure to swiftly enter a collapsing state—that is, to reach a state of complete collapse. It can be considered that once such a transmission tower–line system experiences severe damage during an earthquake, it will inevitably progress to collapse. Therefore, this study categorizes severe damage and collapse of the transmission tower–line system as the same damage grade. Specifically, four damage states (DS) are defined, namely essentially intact (${DS}_1$), slight damage (${DS}_2$), moderate damage (${DS}_3$), and severe damage/collapse (${DS}_4$), as listed in

Table 7. Quantification of performance levels for the transmission tower.

Damage State	Range	Thresholds Determined in This Study
moderate damage (${DS}_1$)	$[0,{LS}_1)$	$[0,0.8\%)$
slight damage (${DS}_2$)	$[{LS}_1,{LS}_2)$	$[0.8\%,1.5\%)$
moderate damage (${DS}_3$)	$[{LS}_2,{LS}_3)$	$[1.5\%,2.0\%)$
severe damage/collapse (${DS}_4$)	$[{LS}_3,~)$	$[2.0\%,~)$

. Correspondingly, there are three limit states ($LS$): ${LS}_1$, ${LS}_2$, and ${LS}_3$.

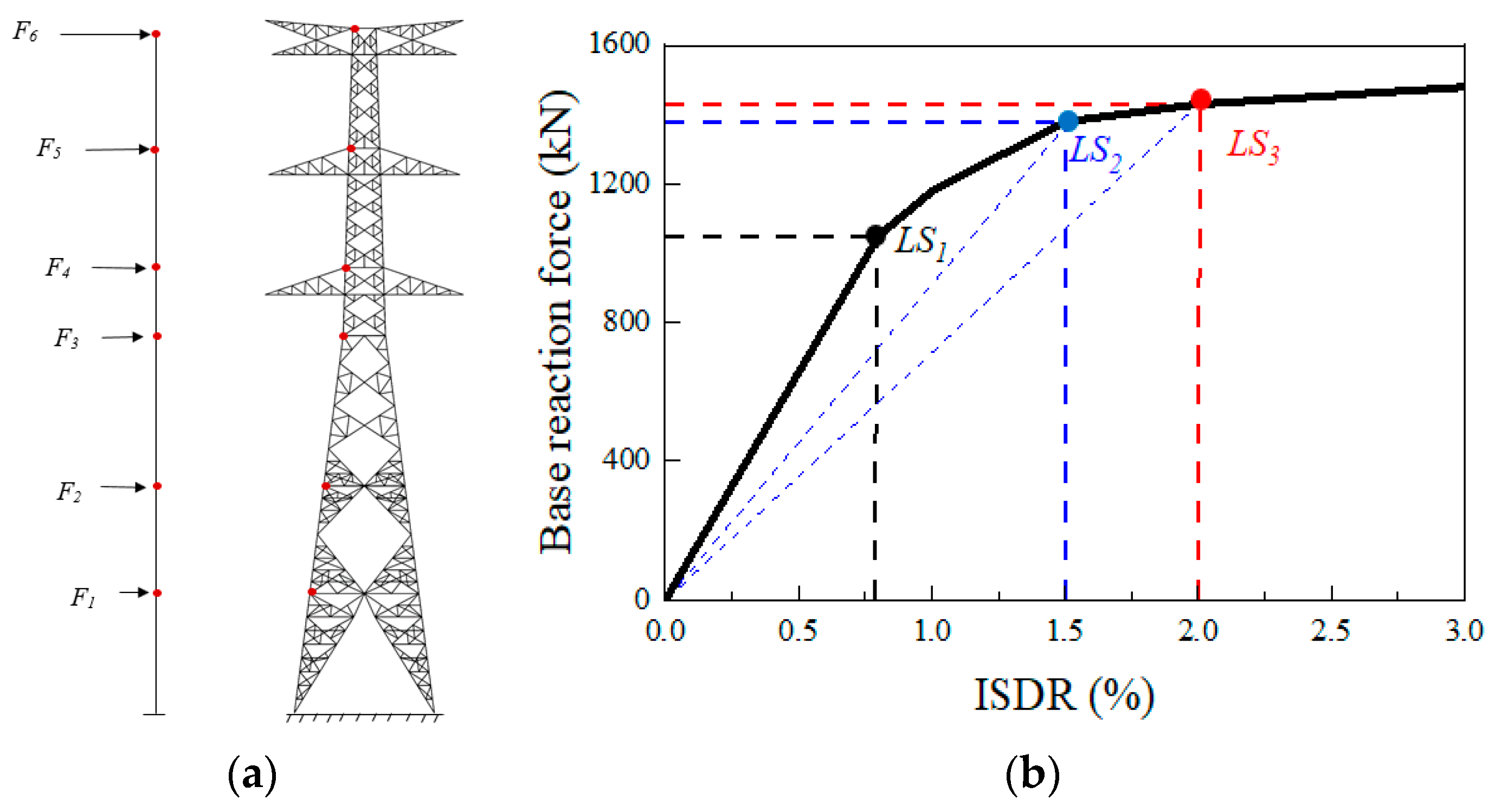
A pushover analysis was conducted on the transmission tower to obtain the relationship curve between the base shear force and the ISDR. This curve was used to determine the various limit states, thereby enabling a quantitative evaluation of the damage grades. The pushover analysis applies laterally distributed forces that incrementally increase according to a specific pattern along the height of the structure, simulating the distribution of story shear forces under seismic action. The reasonableness of the selected lateral force distribution pattern directly affects the accuracy of the pushover analysis results. For slender structures like transmission towers, the story mass can be assumed to be uniformly distributed along the height [32]. Therefore, this chapter employs an inverted triangular distribution load to apply lateral forces to the transmission tower, as shown in Figure 13. We performed a “static” pushover analysis using a fixed inverted triangular load distribution pattern. Its core characteristic is that the lateral force distribution pattern applied to the structure (defined by Equation (2) in the revised manuscript) is predetermined and remains fixed throughout the entire analysis process. The calculation formula for the lateral forces on the transmission tower is as follows:

$$F_i={\displaystyle \frac{m_i{h}_i}{{\sum }_{i=1}^n{m}_i{h}_i}}{V}_b,$$

(2)

In the formula, i is the inter-story segment number, where i = 1, 2, 3, …, 6; n is the total number of inter-story segments; F_i is the lateral force applied to the ith segment; m_i is the mass of the ith segment; h_i is the height of the ith segment; and V_b is the base shear of the transmission tower.

Figure 13. Definition of limit states from the pushover analysis. The images are listed as follows: (a) schematic diagram of lateral force and (b) ISDR–base shear force curve.

Figure 13. Definition of limit states from the pushover analysis. The images are listed as follows: (a) schematic diagram of lateral force and (b) ISDR–base shear force curve.

Based on the pushover analysis, the relationship between the base shear force and the maximum ISDR of the transmission tower was obtained, as shown in Figure 13. The figure also indicates the limit states corresponding to various damage grades of the transmission tower. The linear segment of the curve ends at an ISDR of approximately 0.8%; before this point, the structure can be considered to remain within the elastic range, which is consistent with the findings by Kwon et al. [33]. As loading continues, some members begin to yield, leading to a reduction in the curve’s slope. A more pronounced decrease in slope occurs at an ISDR of 1.5%, suggesting that severe damage has initiated in certain members, beyond which repair of the transmission tower is necessary. When the ISDR reaches 2%, the slope of the curve approaches zero. Since 2% is the predefined collapse limit for the transmission tower, this point is regarded as the structural collapse point. Consequently, the ISDR values corresponding to limit states LS₁, LS₂, and LS₃ are 0.8%, 1.5%, and 2%, respectively. Based on the pushover analysis results, the inter-story drift ratio intervals and limits for the structural damage grades were determined, as listed in Table 7.

5.2. Probabilistic Seismic Demand Model (PSDM)

The core step in conducting a seismic fragility analysis is to establish a probabilistic seismic demand model (PSDM), which describes the probabilistic relationship between an earthquake intensity measure (IM) and an engineering demand parameter (EDP). This relationship is generally assumed to follow a lognormal distribution, and the following expression can be obtained through regression analysis:

$$\mathrm{l}\mathrm{n}\left(EDP\right)=\ln \left(b\right)+a\mathrm{l}\mathrm{n}\left(IM\right),$$

(3)

In the formula, a and b are regression coefficients determined through linear regression.

Based on the database of ISDR responses of the structure under different seismic records and varying PGAs obtained from Section 4, the IDA curves for the constructed transmission tower–line system were derived. Figure 14a,b present the clusters of IDA curves for the transmission tower in the X and Y directions, respectively, along with the 16th, 50th, and 84th percentile IDA curves. It can be observed that the maximum ISDR in the transmission tower–line system gradually increases with rising PGA. When the PGA reaches a certain critical value, the IDA curves exhibit a distinct inflection point, where the ISDR increases rapidly and exceeds the limit, indicating that the transmission tower–line system experiences severe damage or even collapse. In the 50th percentile curve, the PGA at the inflection point is approximately 1.0 g, which is close to the collapse PGA of the transmission tower–line system.

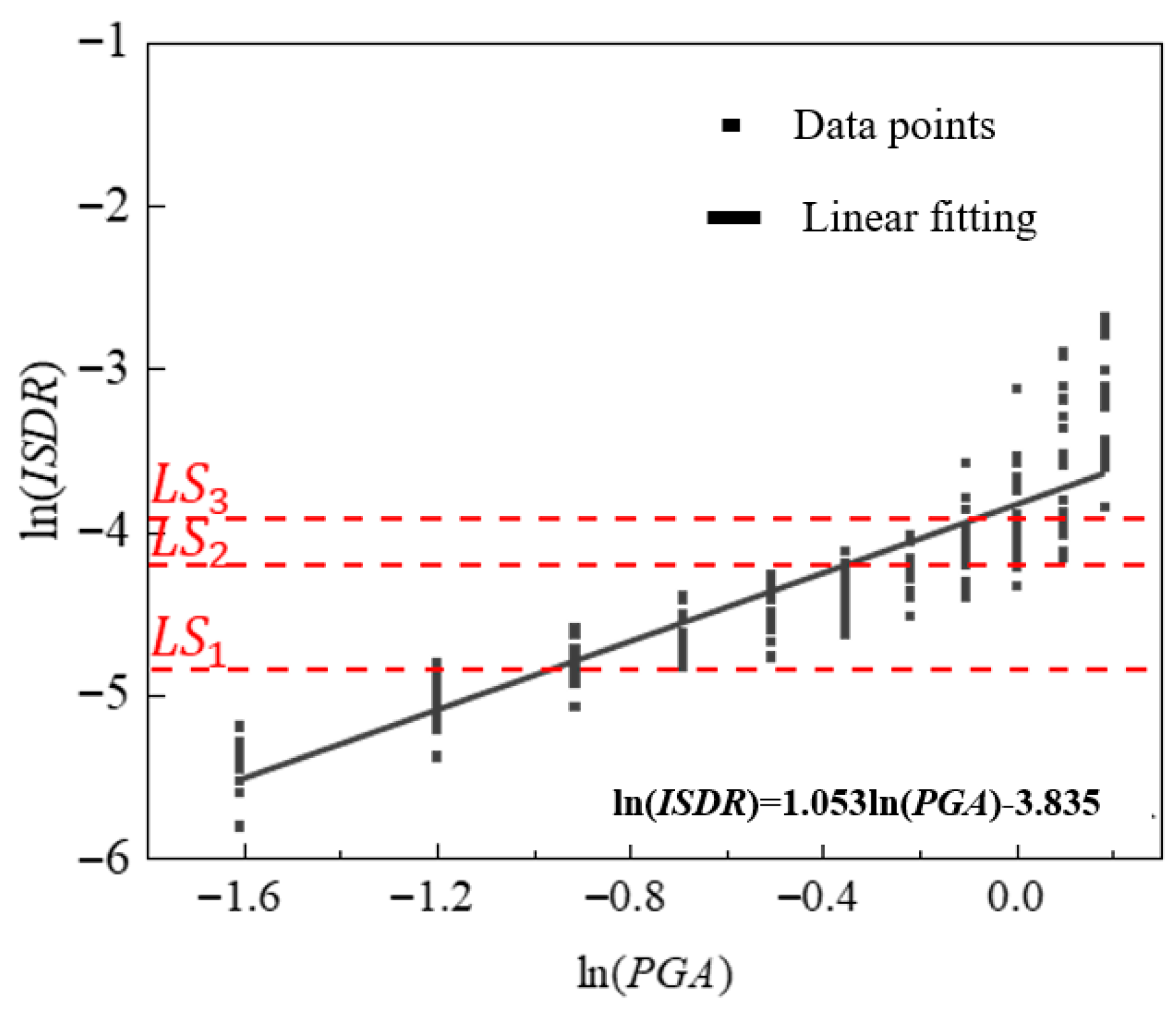
Figure 15 displays the logarithmic scatter distribution of PGA versus the ISDR for the transmission tower–line system and its linear fitting results. In the figure, each column of data points shares the same PGA value, with PGA increasing sequentially from 0.2 g to 1.2 g for different columns. The limit states LS₁, LS₂, and LS₃ defined in Section 5.1 are set at 0.8%, 1.5%, and 2%, respectively, with corresponding logarithmic values of −4.81, −4.18, and −3.95. When the PGA is below 0.7 g, the ISDR values of the transmission tower–line system are mostly below the limit specified by LS₂, indicating that the structure remains primarily in an essentially intact or slightly damaged state. In contrast, under higher seismic intensities, some data points exceed LS₃. For instance, at a PGA of 1.2 g, all data points surpass the LS₃ limit, indicating that the structure has undergone significant deformation and is in a state of severe damage or collapse. Moreover, as the seismic intensity increases, the dispersion of the inter-story drift angles gradually widens. For example, the distribution range of drift angles at a PGA of 1.2 g is noticeably larger than that at 1.0 g, further reflecting the enhanced nonlinear response and more pronounced variability in deformation capacity after the structure enters the plastic stage. Linear regression of ln(PGA) against ln(ISDR) yields fitting coefficients a and b of 1.053 and −3.835, respectively.

5.3. Fragility Analysis

Based on the obtained PSDM, the fragility equation for the transmission tower–line system can be derived using Equation (4).

$$\mathrm{P}\left(D>C|IM\right)=\mathsf{\Phi }\left({\displaystyle \frac{a\mathrm{l}\mathrm{n}\left(IM\right)+\ln \left(b\right)-\mathrm{l}\mathrm{n}\left({LS}_i\right)}{\sqrt{{\beta }_D^2+{\beta }_C^2}}}\right),$$

(4)

In the formula, D represents the seismic demand; C represents the structural capacity; $\mathsf{\Phi }\left(·\right)$ denotes the standard normal distribution function; ${LS}_i$ represents different limit states; and ${\beta }_D$ and ${\beta }_C$ are the logarithmic standard deviations of the seismic demand and structural capacity, respectively. When PGA is used as the intensity measure in the seismic fragility analysis, $\sqrt{{\beta }_D^2+{\beta }_C^2}$ is taken as 0.5.

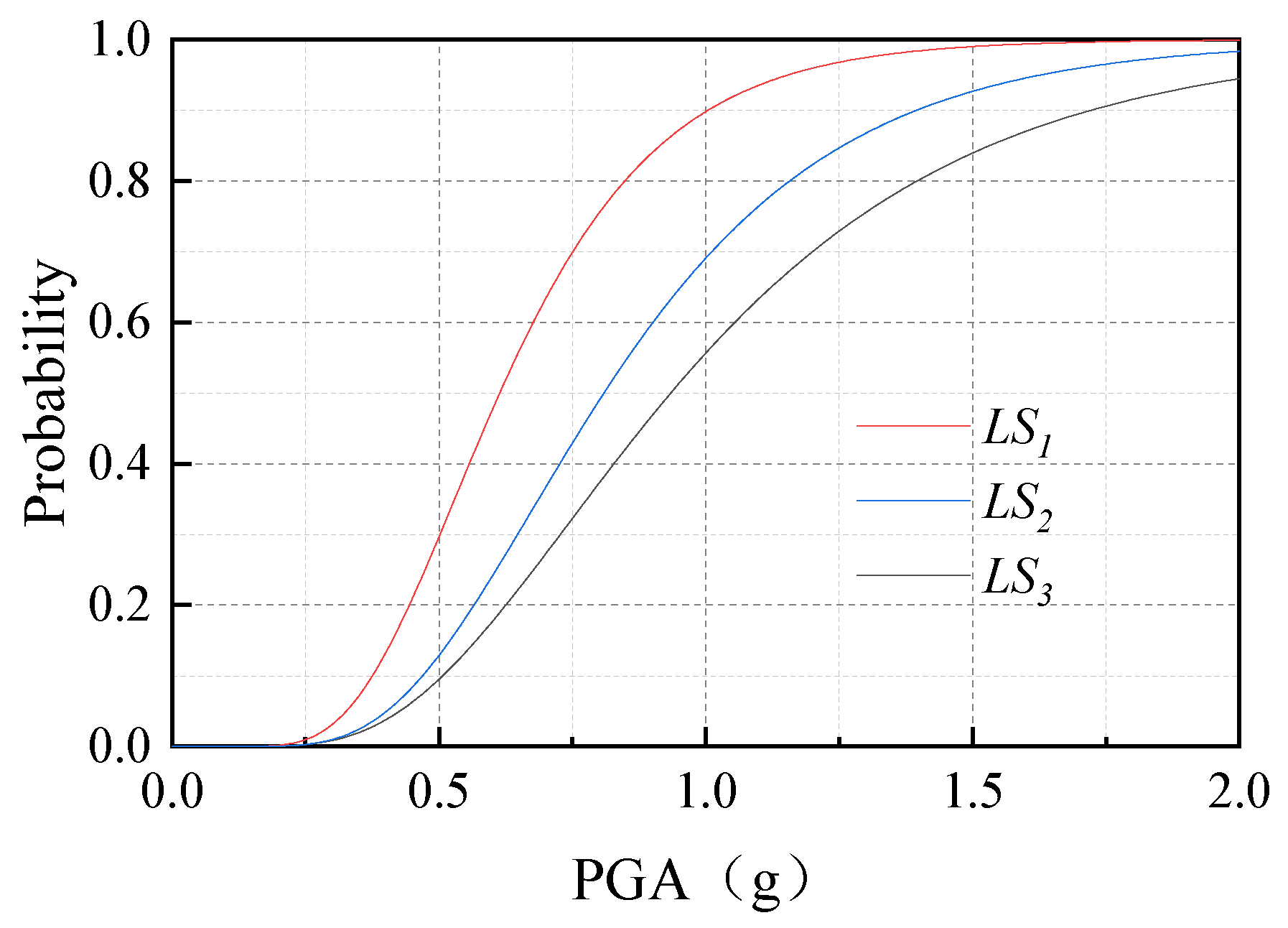
Figure 16 shows the fragility curves of the transmission tower–line system. It can be observed that the probability of structural failure gradually increases with rising seismic intensity. The probabilities of exceeding limit states LS₁, LS₂, and LS₃ increase rapidly at PGAs of 0.26 g, 0.35 g, and 0.41 g, respectively. When the PGA reaches 1.0 g for LS₁, LS₂, and LS₃, the probabilities of failure exceed 90%, 65%, and 55%, respectively. The trend of the fragility curves corroborates the phenomenon observed in Section 3, where the structural response intensified significantly with increasing PGA, thereby quantifying the safety margin from a probabilistic perspective.

6. Discussion

This study systematically investigates the seismic performance and collapse fragility of a 765 kV transmission tower–line system through refined numerical modeling and incremental dynamic analysis. While the findings provide valuable insights into the dynamic behavior, failure mechanisms, and probabilistic seismic capacity of the system, several limitations and future research directions warrant further discussion.

• Limitation of experimental validation and planned shaking table tests: Although the finite element model developed in this study incorporates advanced constitutive laws and has been validated against existing theoretical and numerical benchmarks, it lacks direct experimental verification. The absence of physical testing may limit the generalizability of the hysteretic model and the accuracy of the predicted collapse modes. To address this gap, we plan to conduct large-scale shaking table tests in future work. These tests will enable a more realistic validation of the numerical model, particularly in capturing the nonlinear interaction between the tower and conductors under severe seismic excitations.
• Consideration of ground motion characteristics: The current study employs a set of ground motions scaled to various PGA levels without explicitly distinguishing between near-fault and far-field records or considering mainshock–aftershock sequences. Given that near-fault pulses and repeated seismic events can significantly alter the structural response and cumulative damage, future analyses will incorporate a more comprehensive classification of ground motions. This will include separate evaluations of near-fault versus far-field effects, as well as the impact of mainshock–aftershock sequences on the residual capacity and fragility of the tower–line system.
• Inclusion of high-mode effects: The present model primarily focuses on the global dynamic response and lower-order vibration modes. However, under extreme seismic loading, high-mode effects may also contribute to local instabilities and influence collapse progression. Future research will aim to incorporate high-mode effects into the seismic assessment, particularly for tall and flexible tower structures. This will involve a more detailed modal participation analysis and the potential use of multi-mode pushover or modal-based IDA approaches to better capture the complex seismic behavior.

7. Conclusions

In this paper, we investigate the seismic performance and vulnerability of a transmission tower–line system based on a high-voltage transmission line project. A finite element model was developed and subjected to pushover analysis to determine the capacity limit states, followed by a comprehensive vulnerability assessment. The main research findings are outlined as follows:

• The conductors significantly influence the dynamic characteristics and seismic response of the transmission tower–line system. The fundamental frequency of the transmission tower–line system decreases by over 50% compared to that of the isolated tower, indicating a notable reduction in overall stiffness. The seismic responses exhibit strong dispersion, with peak values of the tower-top displacement, tower-top acceleration, and tower-leg stress being significantly affected by the characteristics of seismic excitation.
• The vulnerable segments of the transmission tower–line system under seismic action are concentrated in the second to third inter-story segments, with a mean critical collapse PGA of 1.07 g. Structural collapse manifests as a progressive chain failure triggered by the cumulative plastic damage of diagonal members in the lower segments.
• The fragility curves established based on the ISDR show that the collapse probability of the system exceeds 55% at a PGA of 1.0 g. The developed probabilistic seismic demand model can provide both a theoretical basis and a practical reference for the seismic design and safety assessment of high-voltage transmission towers.