Experimental Performance of Timber–Concrete Slab-to-Concrete Wall Connections Under Gravitational and Lateral In-Plane Loading
Abstract
1. Introduction
2. Hypothesis and Objectives
3. Materials and Methods
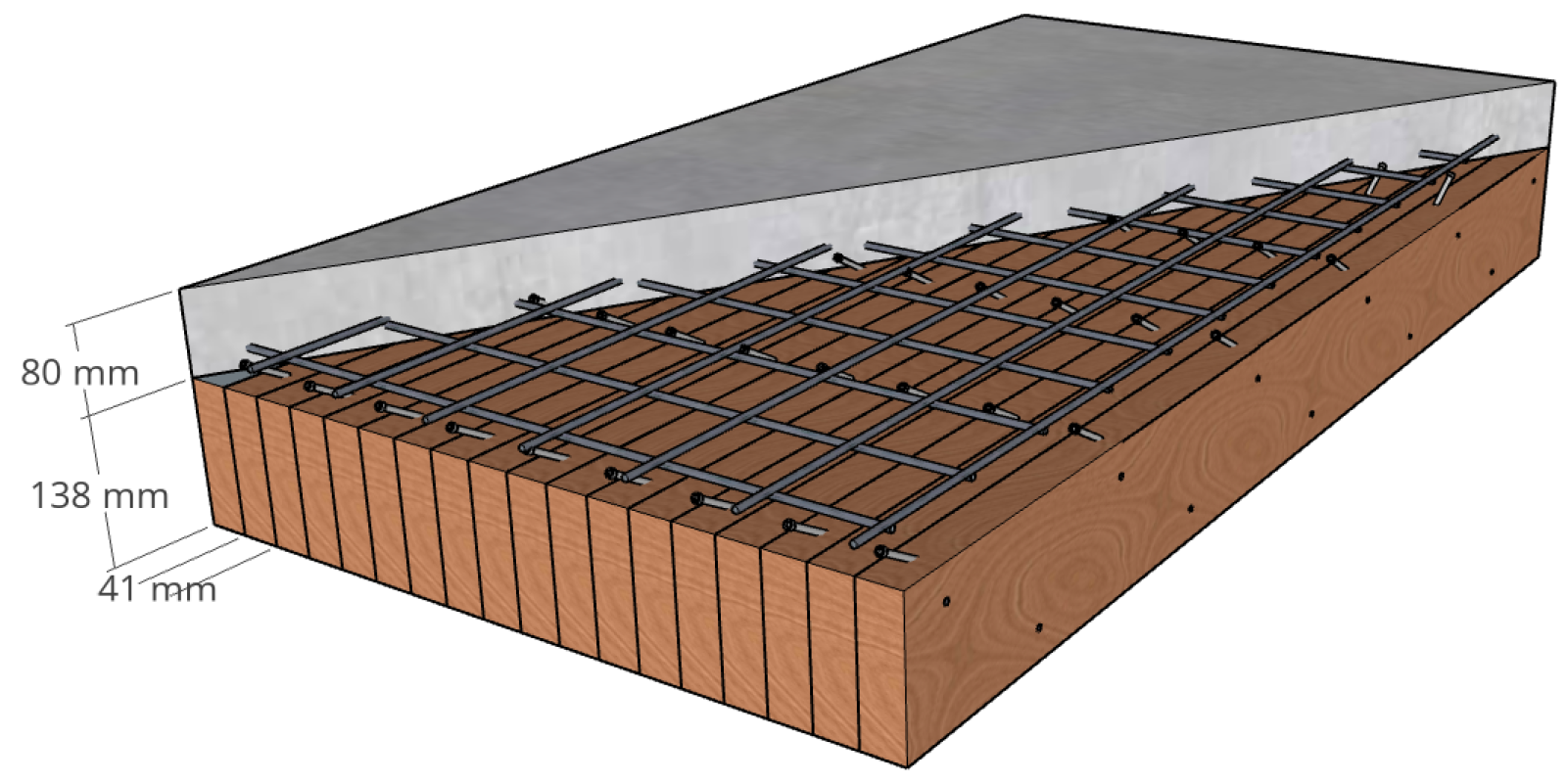
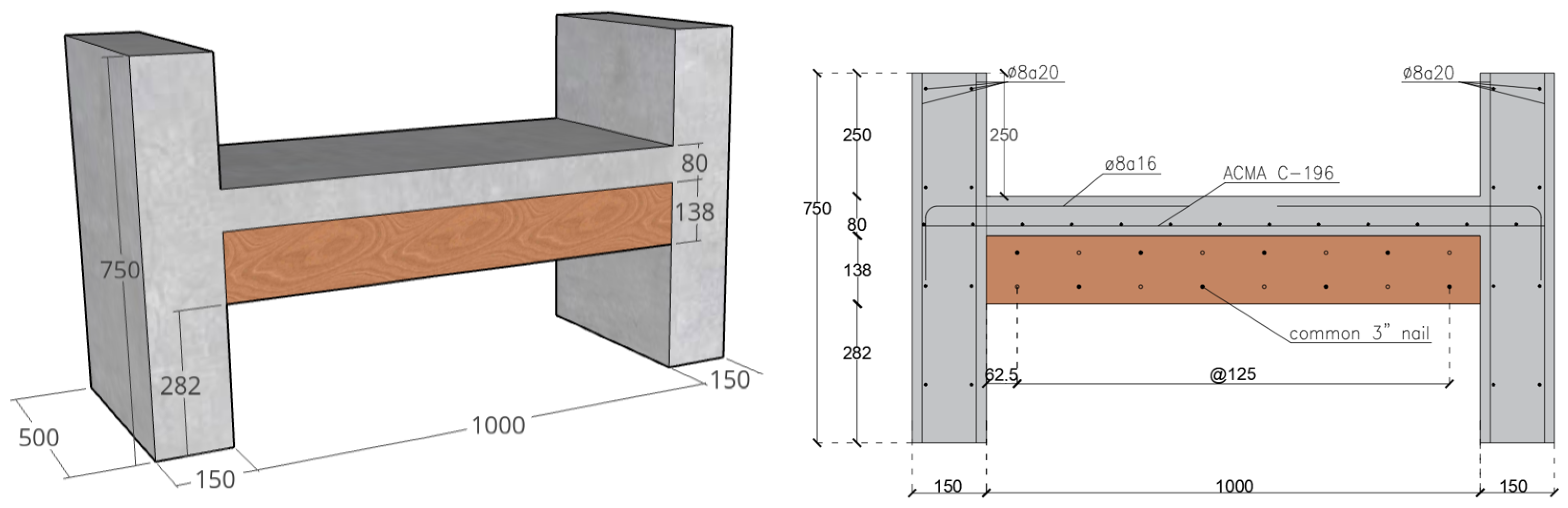
3.1. TCC Slab
3.2. Connections
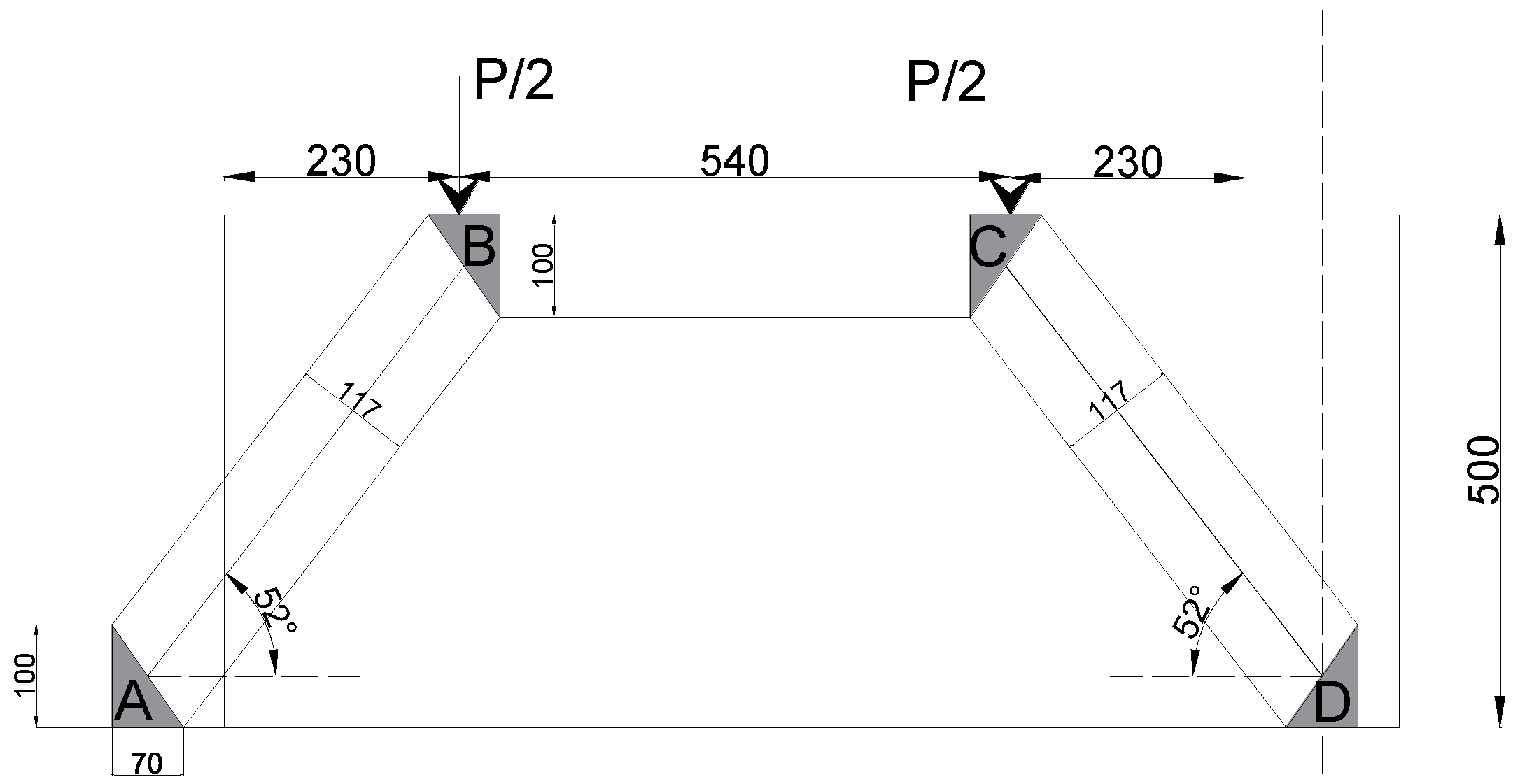
3.3. Test Specimens
3.4. Test Setup and Instrumentation
3.4.1. Gravitational Tests
3.4.2. Lateral Tests
3.5. Loading Protocol
3.5.1. Gravitational Tests
3.5.2. Lateral Tests
4. Results
4.1. Gravitational Tests
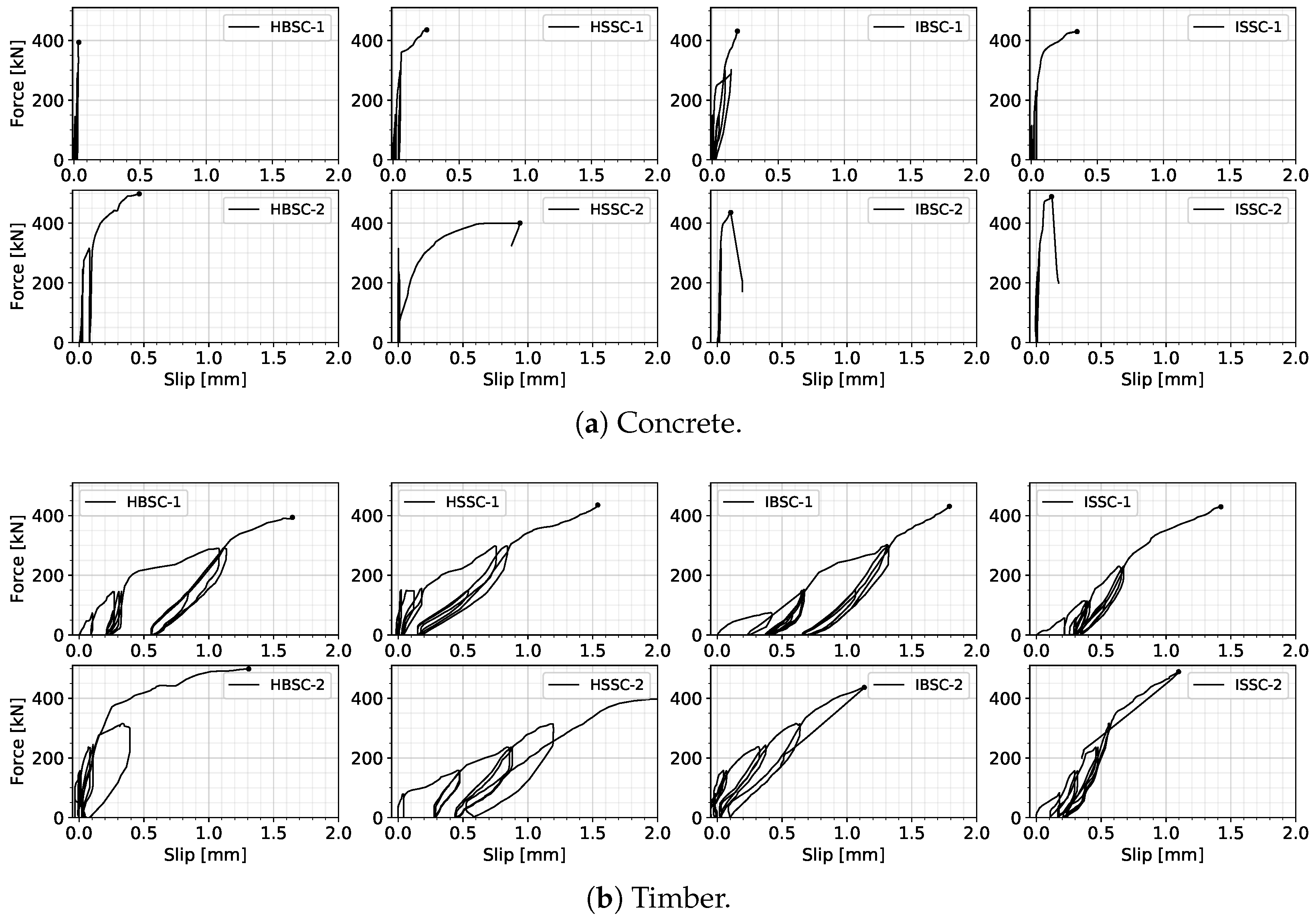
4.1.1. Failure Mode
4.1.2. Load–Slip Curves
4.1.3. Strength
4.1.4. Stiffness
4.2. Lateral Tests
4.2.1. Failure Mode
4.2.2. Load–Slip Relationships
4.2.3. Strength
4.2.4. Stiffness
4.3. Analytical Capacities
4.4. Finite Element Modeling
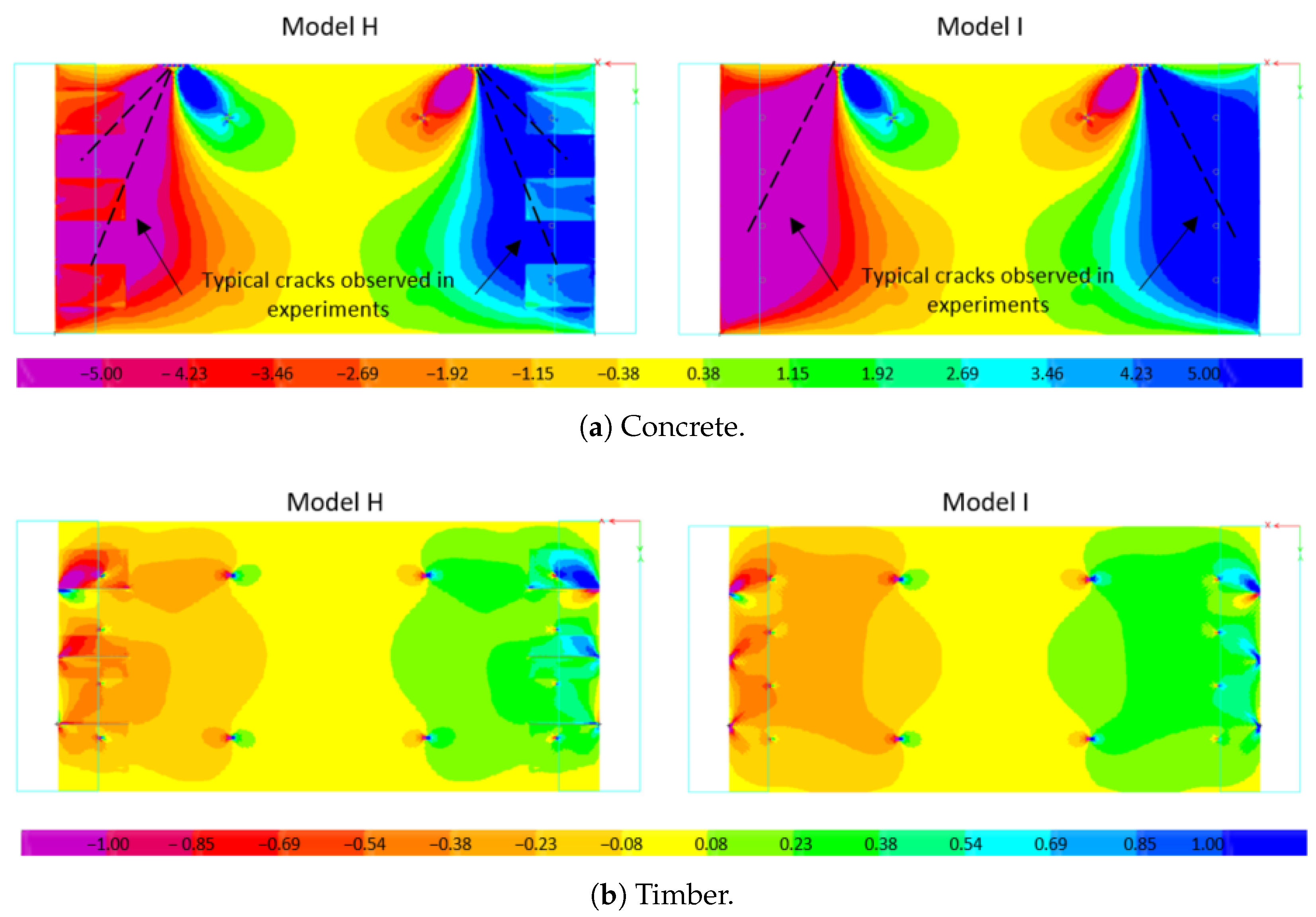
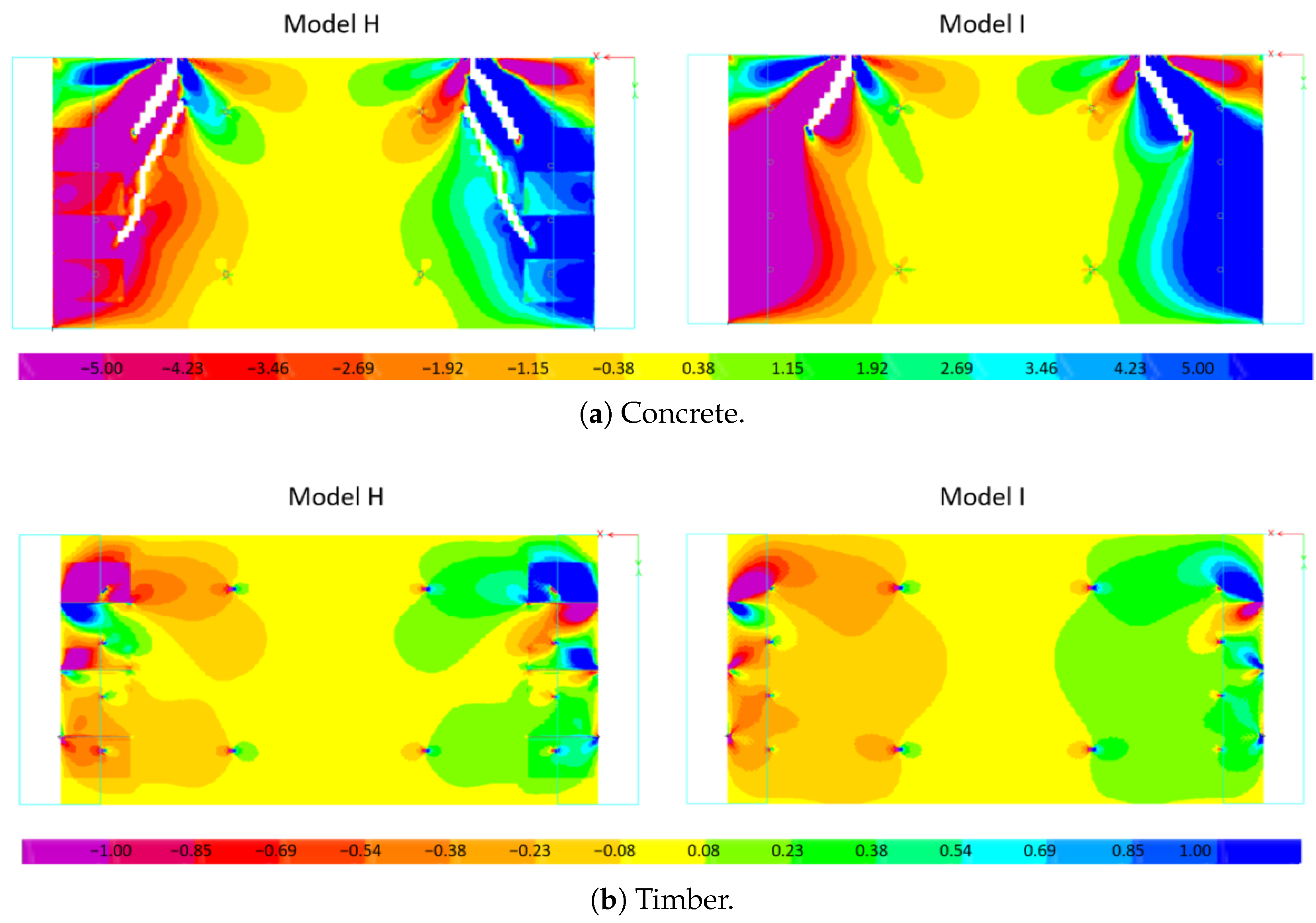
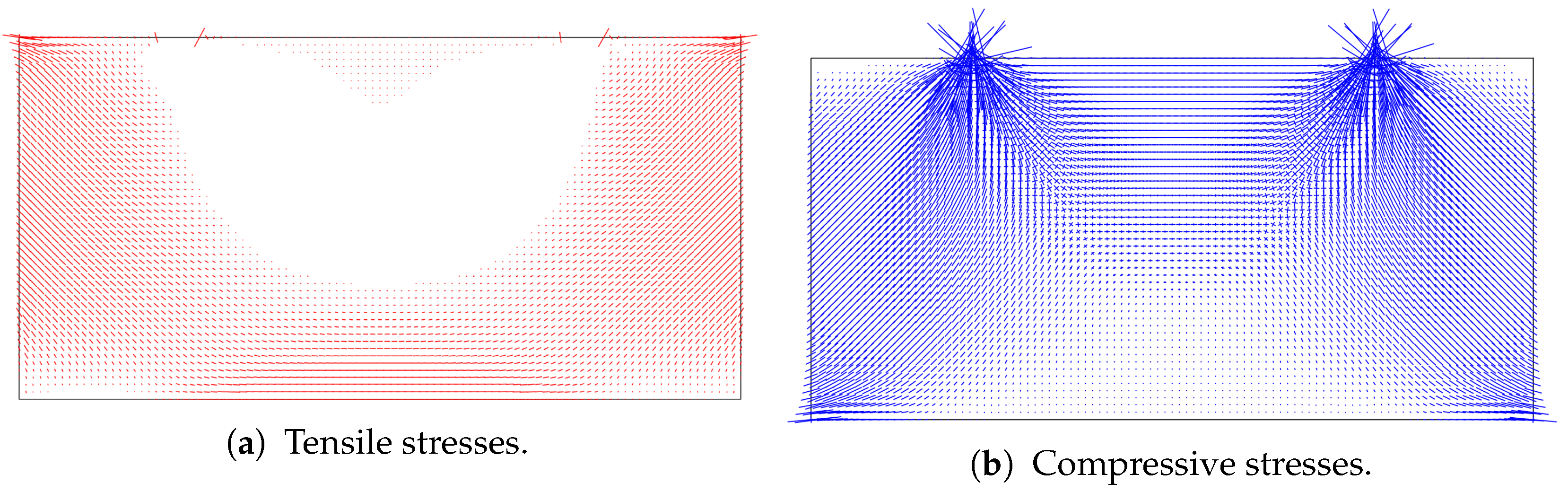
4.4.1. Shear Stress Distribution
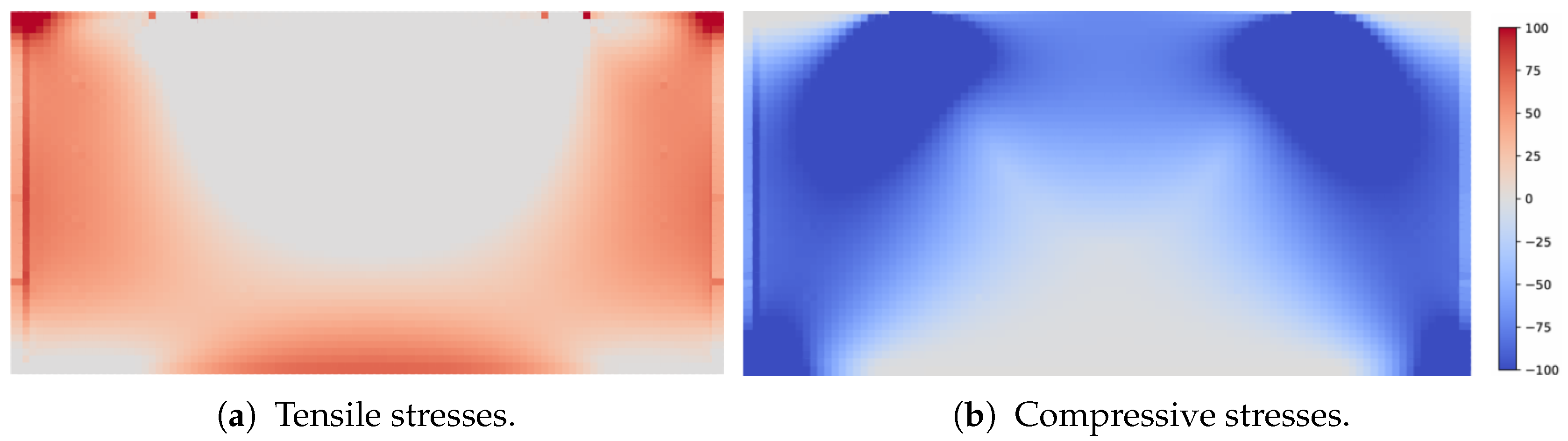
4.4.2. Principal Stresses
4.4.3. Strut-and-Tie Model
5. Conclusions
- Regarding the lateral load response, experimental shear capacities were on average six times larger than design-code predictions, indicating that shear at the slab–wall joint was not the governing mechanism. Finite element analyses revealed that the load was transferred primarily through diagonal compressive stress fields, with localized crushing near load points. A proposed strut-and-tie model captured this behavior more accurately, providing failure load estimates consistent with experimental results.
- No clear trend was observed between the connector type or inclination and ultimate lateral strength. However, crack patterns differed: multiple cracks formed in H-type connections due to stress concentrations in the thicker concrete zones, while I-type connections typically exhibited a single shear crack at the slab–wall interface.
- Timber components remained largely undamaged, with only minor detachment at isolated regions following concrete failure. FE models with explicit cracking modeling confirmed that slab-to-wall connectors attracted greater forces after concrete softening, yet overall connector demand remained well below capacity.
- Regarding the gravitational load response, shear capacities were approximately three times greater than code predictions. Connectors with screws achieved ≈25% higher strength than bar-type connectors, and H-type connections exhibited ≈60% greater secant stiffness than I-type connections. However, stiffness comparisons were influenced by crack locations relative to LVDT measurement points.
- Connectors experienced more damage at failure under gravity loading than under lateral loading with an uneven force distribution, with some connectors yielding while others remained elastic. Concrete–timber detachment occurred in highly sheared zones due to the inability of connectors to enforce composite action after cracking.
- The ultimate loads measured in both lateral and gravitational tests were far above service-level demands for typical residential floors in Chile. For example, a typical residential floor in Chile would be designed with a dead load of D = 1.5 kPa and a live load of L = 2.0 kPa. Therefore, the design should focus on ensuring that connectors resist construction loads, particularly during concrete placement, while ultimate lateral resistance can safely be taken as governed by the concrete slab itself. As a practical consideration, construction is feasible using a single strut support located at the mid-span of the slab, which could also serve for pre-cambering during the casting process. Horizontal connectors were found suitable for pre-installation without interfering with reinforcement, while inclined connectors proved efficient for in situ installation. Both alternatives are considered practical and reliable.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Timber concrete composite | |
| Nail laminated timber | |
| Yield strength | |
| Ultimate strength | |
| Secant stiffness | |
| Ultimate shear capacity | |
| Concrete shear capacity | |
| Specified compressive strength of concrete | |
| Width of cross section | |
| d | Distance from extreme compression fiber to centroid of longitudinal tension reinforcement |
| Material density | |
| E | Modulus of elasticity |
| Poisson’s ratio | |
| Nominal strength of a strut | |
| Confinement modification factor | |
| Factor used to account for the effect of cracking and confining reinforcement | |
| Cross sectional area at one end of a strut |
Appendix A
Appendix A.1. Connection IS, Capacity According to EC5
| Axial capacity | |
| Withdrawal from timber | |
| Pull through of the head | |
| kN | Maximum between pull |
| through of the head or | |
| withdrawal | |
| (thred pull through) | |
| of the remaining part | |
| Tensile capacity of steel | |
| Characteristic axial capacity | |
| of the connection | |
| Characteristic axial capacity | |
| of one screw only towards | |
| the rope effect calculation | |
| Lateral capacity | |
| Mode d without the | |
| rope effect | |
| Mode e without the | |
| rope effect | |
| Mode e with rope effect | |
| Lateral capacity of the | |
| connection | |
| Combined design capacity | |
Appendix A.2. Connection HS, Capacity According to EC5
| Axial capacity | |
| Withdrawal from timber | |
| Tensile capacity of steel | |
| Characteristic axial capacity | |
| Lateral capacity | |
| Mode d without the rope effect | |
| Mode d with the rope effect | |
| Mode e without rope effect | |
| Mode e with the rope effect | |
| Lateral capacity of the | |
| connection | |
| Combined design capacity | |
Appendix A.3. Connection IB, Capacity According to EC5
| Axial capacity | |
| Axial capacity, as well as axial stiffness, is assumed to be very small because the bar is | |
| not glued to the timber. | |
| Lateral capacity | |
| Due to lack of axial stiffness, it is assumed that there is no rope effect. | |
| Mode d | |
| Mode e | |
| Lateral capacity of the | |
| connection | |
Appendix A.4. Connection HB, Capacity According to EC5
References
- Guindos, P. Fundamentos del Diseño y la Construcción con Madera; Ediciones UC: Santiago, Chile, 2019. (In Spanish) [Google Scholar]
- Yeoh, D.; Fragiacomo, M.; Buchanan, A.; Crews, K.; Haskell, J.; Deam, B. Development of semi-prefabricated timber-concrete composite floors in Australasia. In Proceedings of the WCTE2008-10th World Conference on Timber Engineering, Miyazaki, Japan, 2–5 June 2008; Volume 4, pp. 2152–2159. [Google Scholar]
- Otero-Chans, C.; Suarez-Riestra, F.; Martin-Gutiérrez, E.; Estévez-Cimadevila, J. Experimental and numerical analysis of a full-scale timber-concrete-composite beam from simply supported to frame-connected. Eng. Struct. 2025, 327, 119624. [Google Scholar] [CrossRef]
- Rodrigues, J.N.; Providência, P.; Dias, A.M. Sustainability and lifecycle assessment of timber-concrete composite bridges. J. Infrastruct. Syst. 2017, 23, 04016025. [Google Scholar] [CrossRef]
- Nakashima, M. Seismic Resistance Characteristics of Reinforces Concrete Beam-Supported Floor Slabs in Building Structures. Ph.D. Thesis, Lehigh University, Bethlehem, PA, USA, 1981. [Google Scholar]
- Imran, I. Preliminary Study of the Lateral Load Behaviour of a Reinforced Concrete Slab-Wall Assembly. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 1990. [Google Scholar]
- Zenunović, D.; Folić, R. Models for behaviour analysis of monolithic wall and precast or monolithic floor slab connections. Eng. Struct. 2012, 40, 466–478. [Google Scholar] [CrossRef]
- Greeshma, S.; Rajesh, C.; Jaya, K.P.; Division, S.E.; Wing, I.; Complex, E.; Division, S.E. Seismic Behaviour of Shear Wall–Slab Joint Under Lateral Cyclic Loading. Asian J. Civ. Eng. (Build. Hous.) 2011, 13, 455–464. [Google Scholar]
- Greeshma, S.; Jaya, K.P. Effect of Slab Shear Reinforcement on the Performance of the Shear Wall–Floor Slab Connection. J. Perform. Constr. Facil. 2013, 27, 391–401. [Google Scholar] [CrossRef]
- Surumi, R.S.; Jaya, K.P.; Greeshma, S. Modelling and Assessment of Shear Wall–Flat Slab Joint Region in Tall Structures. Arab. J. Sci. Eng. 2015, 40, 2201–2217. [Google Scholar] [CrossRef]
- Arthi, S.; Jaya, K. Seismic performance of precast shear wall-slab connection under cyclic loading: Experimental test vs. numerical analysis. Earthq. Eng. Eng. Vib. 2020, 19, 739–757. [Google Scholar] [CrossRef]
- Xia, K.; Hu, X.; Xue, W. Experimental studies on in-plane connections of composite beam-precast concrete shear wall under reversed cyclic loading. Structures 2021, 34, 1961–1972. [Google Scholar] [CrossRef]
- Han, W.; Zhao, Z.; Qian, J. Global Experimental Response of a Three-Story, Full-Scale Precast Concrete Shear Wall Structure with Reinforcing Bars Spliced by Grouted Couplers. PCI J. 2019, 64, 65–80. [Google Scholar] [CrossRef]
- Lukaszewska, E.; Johnsson, H.; Fragiacomo, M. Performance of connections for prefabricated timber–concrete composite floors. Mater. Struct. 2008, 41, 1533–1550. [Google Scholar] [CrossRef]
- Fragiacomo, M.; Lukaszewska, E. Time-dependent behaviour of timber–concrete composite floors with prefabricated concrete slabs. Eng. Struct. 2013, 52, 687–696. [Google Scholar] [CrossRef]
- Khorsandnia, N.; Valipour, H.; Bradford, M. Deconstructable timber-concrete composite beams with panelised slabs: Finite element analysis. Constr. Build. Mater. 2018, 163, 798–811. [Google Scholar] [CrossRef]
- Krug, S.; Schänzlin, J. Experimental and numerical investigations of timber-concrete composite slabs subjected to negative bending moments. In Wood Material Science & Engineering; Taylor & Francis: Abingdon, UK, 2025. [Google Scholar] [CrossRef]
- van de Lindt, J.W.; Furley, J.; Amini, M.O.; Pei, S.; Tamagnone, G.; Barbosa, A.R.; Rammer, D.; Line, P.; Fragiacomo, M.; Popovski, M. Experimental seismic behavior of a two-story CLT platform building. Eng. Struct. 2019, 183, 408–422. [Google Scholar] [CrossRef]
- Mahr, K.; Sinha, A.; Barbosa, A.R. Elevated Temperature Effects on Performance of a Cross-Laminated Timber Floor-to-Wall Bracket Connections. J. Struct. Eng. 2020, 146, 04020173. [Google Scholar] [CrossRef]
- Newcombe, M.P.; van Beerschoten, W.A.; Carradine, D.; Pampanin, S.; Buchanan, A.H. In-Plane Experimental Testing of Timber-Concrete Composite Floor Diaphragms. J. Struct. Eng. 2010, 136, 1461–1468. [Google Scholar] [CrossRef]
- ACI 318-19; 318-19 Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2019. [CrossRef]
- EN 1995-1-1; Eurocode 5: Design of Timber Structures—Part 1-1: General—Common Rules and Rules for Buildings. Standardization European Commission (EC): Brussels, Belgium, 2004.
- INN—Instituto Nacional de Normalizacion. NCh1198—Diseño en Madera; INN—Instituto Nacional de Normalizacion: Santiago, Chile, 2006; pp. 1–231. [Google Scholar]
- INN—Instituto Nacional de Normalizacion. NCh1037—Hormigón-Ensayo de Compresión de Probetas Cúbicas y Cilíndricas; INN—Instituto Nacional de Normalizacion: Santiago, Chile, 2009. [Google Scholar]
- Jiang, Y.; Chen, H.; Nie, X.; Tao, M. Experimental study on bond and anchorage of steel bars in precast concrete structures with new-to-old concrete interface. Eng. Struct. 2021, 247, 113086. [Google Scholar] [CrossRef]
- Shang, X.; Zheng, M.; Guo, Y.; Zhuang, L.; Liang, H. Experimental Investigation on Static Performance of Novel Precast Concrete Composite Slab–Composite Shear Wall Connections. Buildings 2025, 15, 1935. [Google Scholar] [CrossRef]
- Carmo, R.; Martins, R.; Arruda, M.R.T.; Costa, H.; Valente, D.; Valença, J.; Júlio, E. Reinforcement detailing of connections between perpendicular hollow precast walls. Adv. Struct. Eng. 2023, 26, 1663–1681. [Google Scholar] [CrossRef]
- INN—Instituto Nacional de Normalizacion. NCh 203 Acero Estructural—Requisitos; INN—Instituto Nacional de Normalizacion: Santiago, Chile, 2006. [Google Scholar]
- UNE-EN 26891-1; Timber Structures-Joints Made with Mechanical Fasteners-General Principles for the Determination of Strength, Deformation, Loading. EN—Eurepean Norm: Plzen, Czech Republic, 1991.
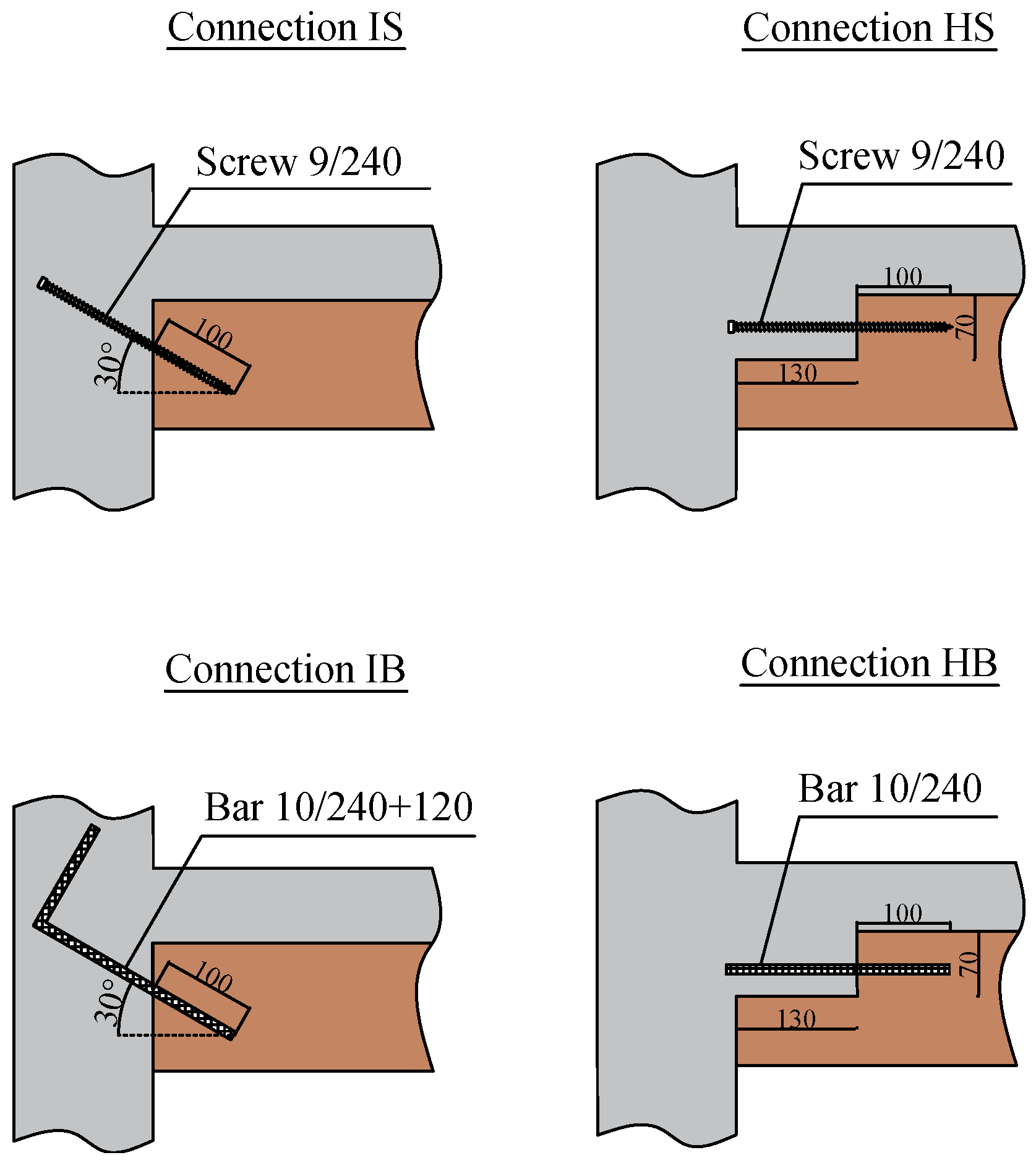






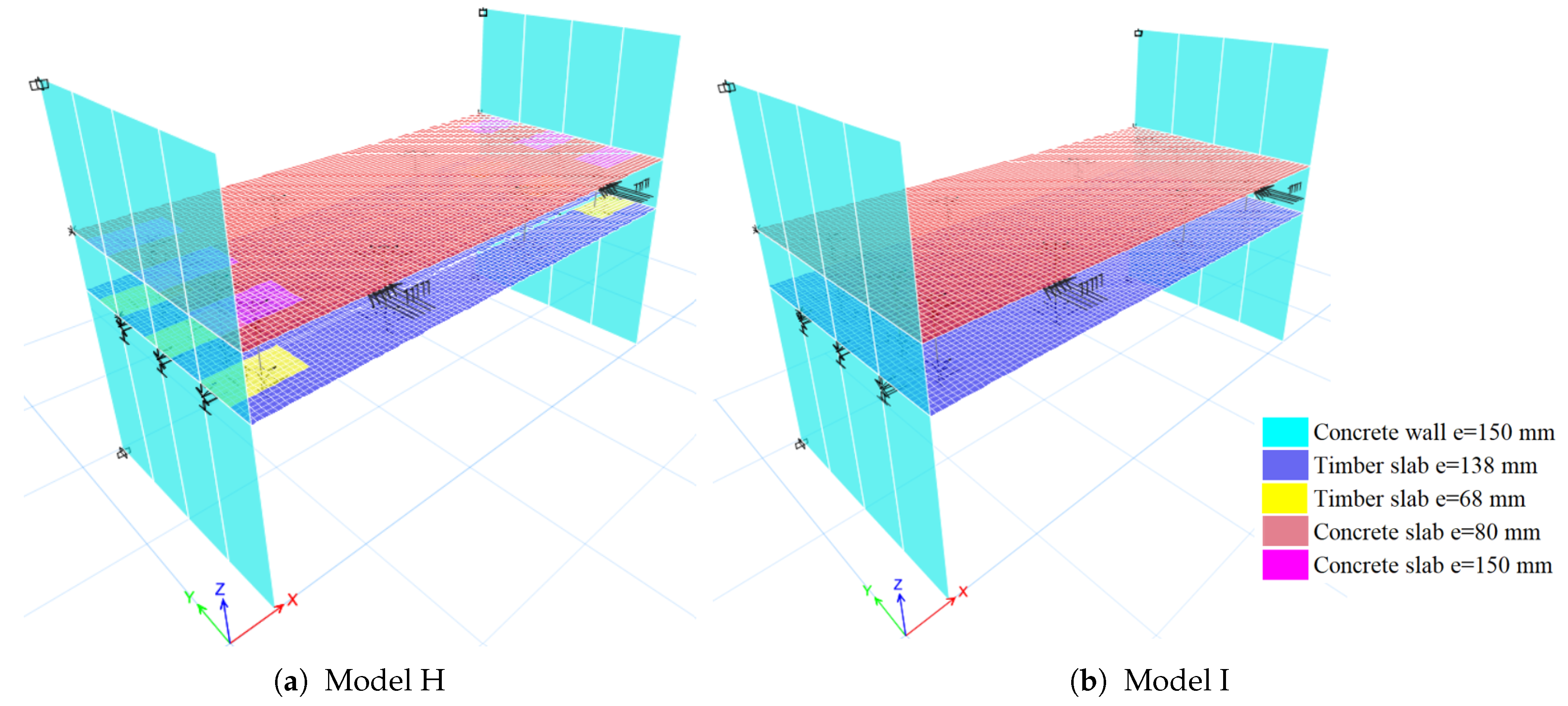
| Connection Type | Connector Type | Loading Direction | Loading Protocol | Connection ID |
|---|---|---|---|---|
| I | S | S | C | ISSC |
| H | S | S | C | HSSC |
| I | B | S | C | IBSC |
| H | B | S | C | HBSC |
| I | S | G | M | ISGM |
| H | S | G | M | HSGM |
| I | B | G | M | IBGM |
| H | B | G | M | HBGM |
| Specimen | (kN/mm) | (kN) | Mean (kN) |
|---|---|---|---|
| HBGM-1 | 15.4 | 133 | 143 |
| HBGM-2 | 9.4 | 152 | |
| HSGM-1 | 6.9 | 153 | 177 |
| HSGM-2 | 10.3 | 200 | |
| IBGM-1 | 11.1 | 129 | 140 |
| IBGM-2 | 6.8 | 151 | |
| ISGM-1 | 0.7 | 170 | 172 |
| ISGM-2 | 0.4 | 175 |
| Serie | (kN/mm) | (kN) | Mean (kN) |
|---|---|---|---|
| HBSC-1 | 8.2 | 394 | 446 |
| HBSC-2 | 7.6 | 498 | |
| HSSC-1 | 6.4 | 436 | 418 |
| HSSC-2 | 13.8 | 400 | |
| IBSC-1 | 12.6 | 432 | 434 |
| IBSC-2 | 7.4 | 437 | |
| ISSC-1 | 6.7 | 430 | 460 |
| ISSC-2 | 12.1 | 490 |
| Connection/Capacity | Lateral (kN) | Axial (kN) |
|---|---|---|
| IS | 41.1 | 18.6 |
| HS | 22.6 | 32.0 |
| IB | 52.7 | 0 |
| HB | 52.7 | 0 |
| Material | (kg/m3) | E (MPa) | (-) |
|---|---|---|---|
| Concrete | 2500 | 25,648 | 0.2 |
| Wood (radiata pine) | 650 | 8897 | 0.2 |
| Spring | (kN/mm) | (kN/mm) | (kN/mm) |
|---|---|---|---|
| Wall-slab I | 0 | 5.2 | 5.2 |
| Wall-slab H | 0 | 5.1 | 2.8 |
| Slab-slab | 8.6 | 1.1 | 1.1 |
| Element | Model I | Model H |
|---|---|---|
| V (kN) | V (kN) | |
| Connector 1 | 4.6 | 3.4 |
| Connector 2 | 4.4 | 3.3 |
| Connector 3 | 3.5 | 3.2 |
| Element | Model I | Model H |
|---|---|---|
| V (kN) | V (kN) | |
| Connector 1 | 6.4 | 4.2 |
| Connector 2 | 4.3 | 3.9 |
| Connector 3 | 3.7 | 3.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maldonado, V.; Santa María, H.; Guindos, P. Experimental Performance of Timber–Concrete Slab-to-Concrete Wall Connections Under Gravitational and Lateral In-Plane Loading. Buildings 2025, 15, 4161. https://doi.org/10.3390/buildings15224161
Maldonado V, Santa María H, Guindos P. Experimental Performance of Timber–Concrete Slab-to-Concrete Wall Connections Under Gravitational and Lateral In-Plane Loading. Buildings. 2025; 15(22):4161. https://doi.org/10.3390/buildings15224161
Chicago/Turabian StyleMaldonado, Valentina, Hernán Santa María, and Pablo Guindos. 2025. "Experimental Performance of Timber–Concrete Slab-to-Concrete Wall Connections Under Gravitational and Lateral In-Plane Loading" Buildings 15, no. 22: 4161. https://doi.org/10.3390/buildings15224161
APA StyleMaldonado, V., Santa María, H., & Guindos, P. (2025). Experimental Performance of Timber–Concrete Slab-to-Concrete Wall Connections Under Gravitational and Lateral In-Plane Loading. Buildings, 15(22), 4161. https://doi.org/10.3390/buildings15224161






