Study on the Vibration Effects of Brick–Concrete Structures Induced by Blasting in Open-Pit Mines
Abstract
1. Introduction
2. Project Background
2.1. Project Introduction
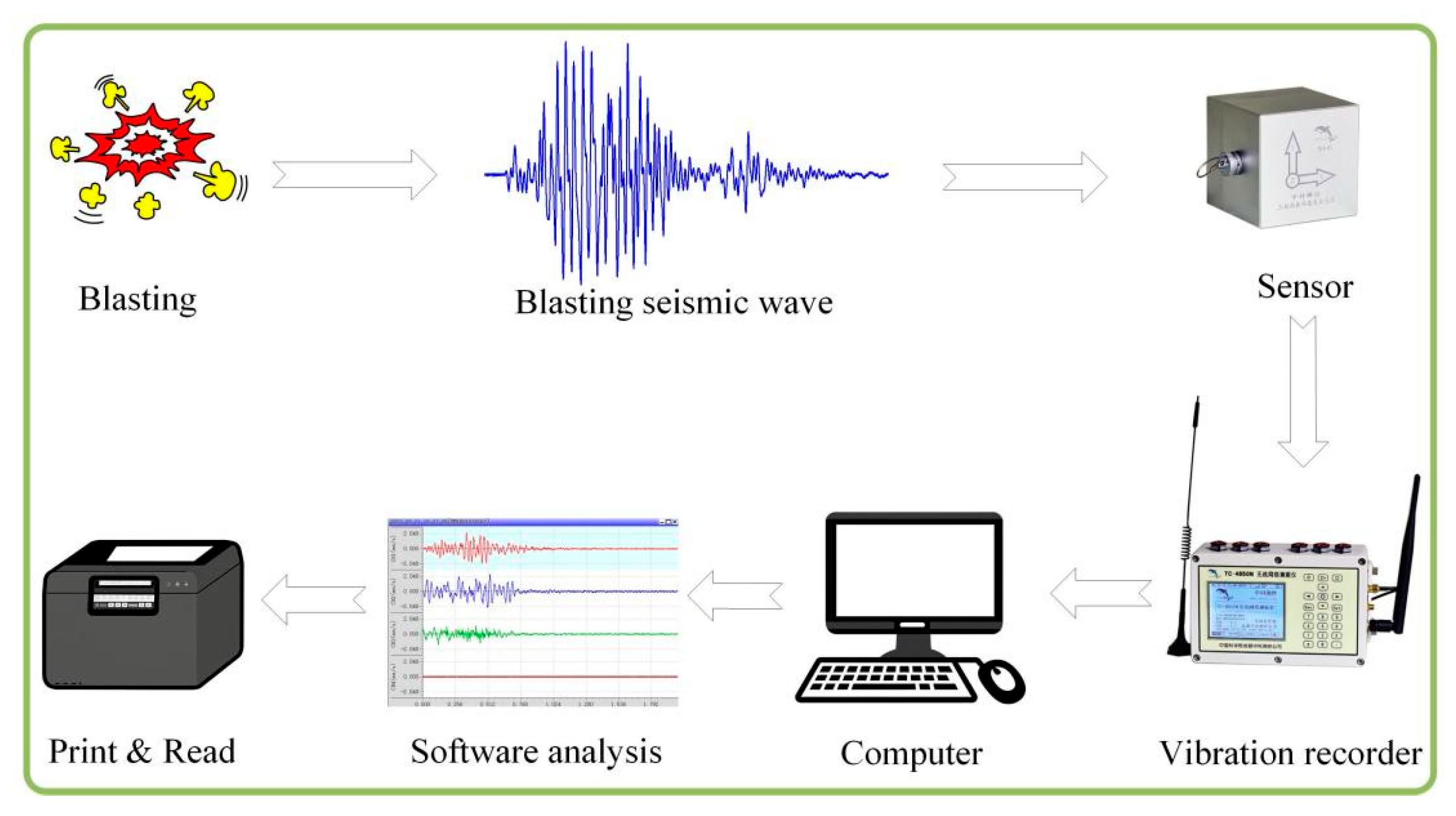
2.2. Blasting Vibration Monitoring Scheme
3. Vibration Monitoring and Analysis of Building Components
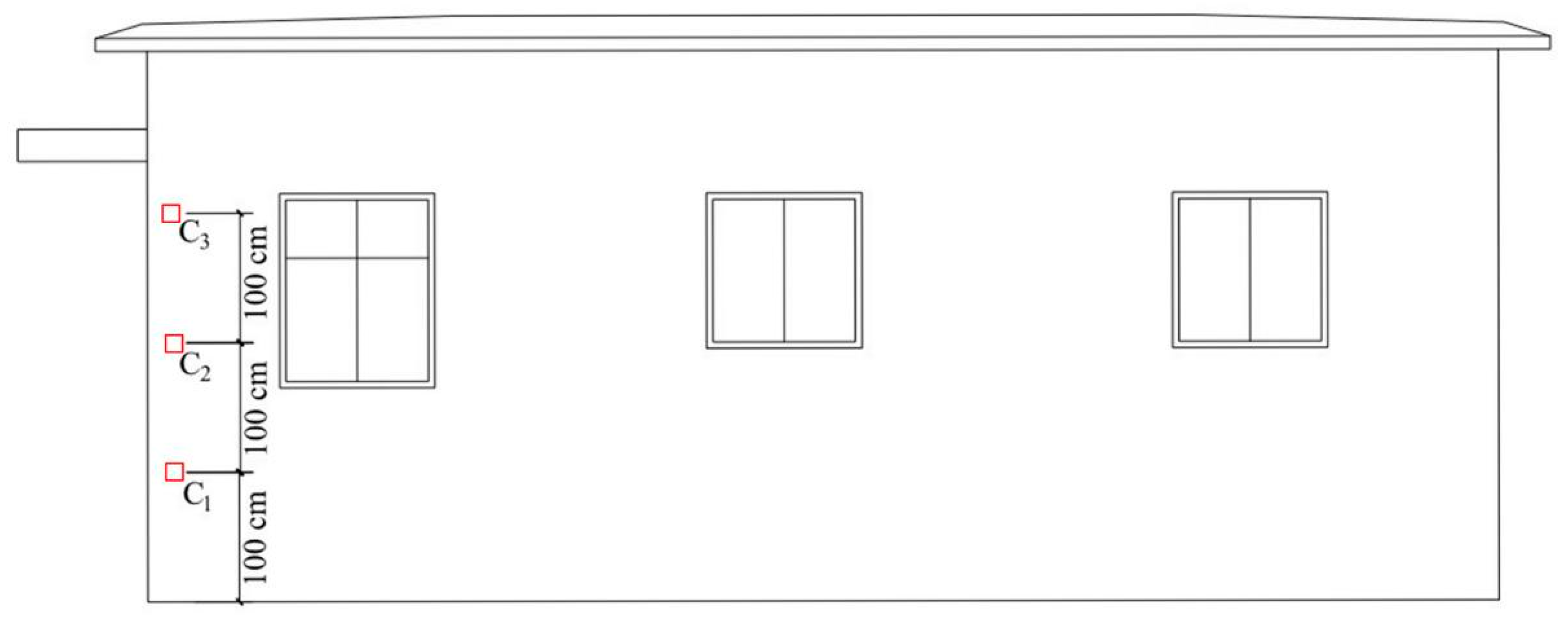
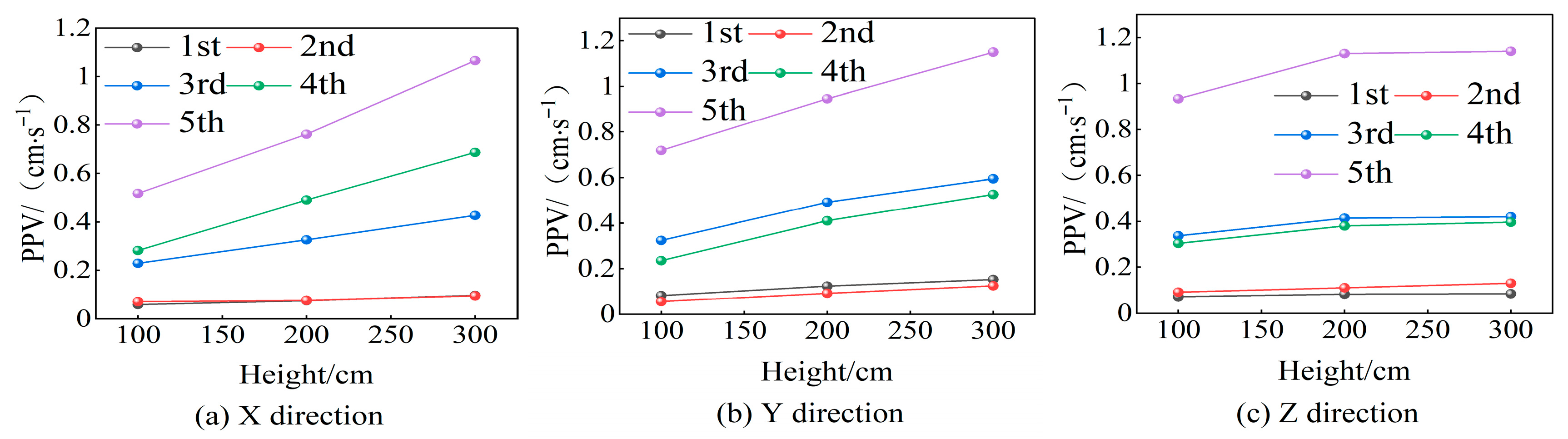
3.1. Monitoring and Analysis of Blasting Vibration of the Structural Column Component
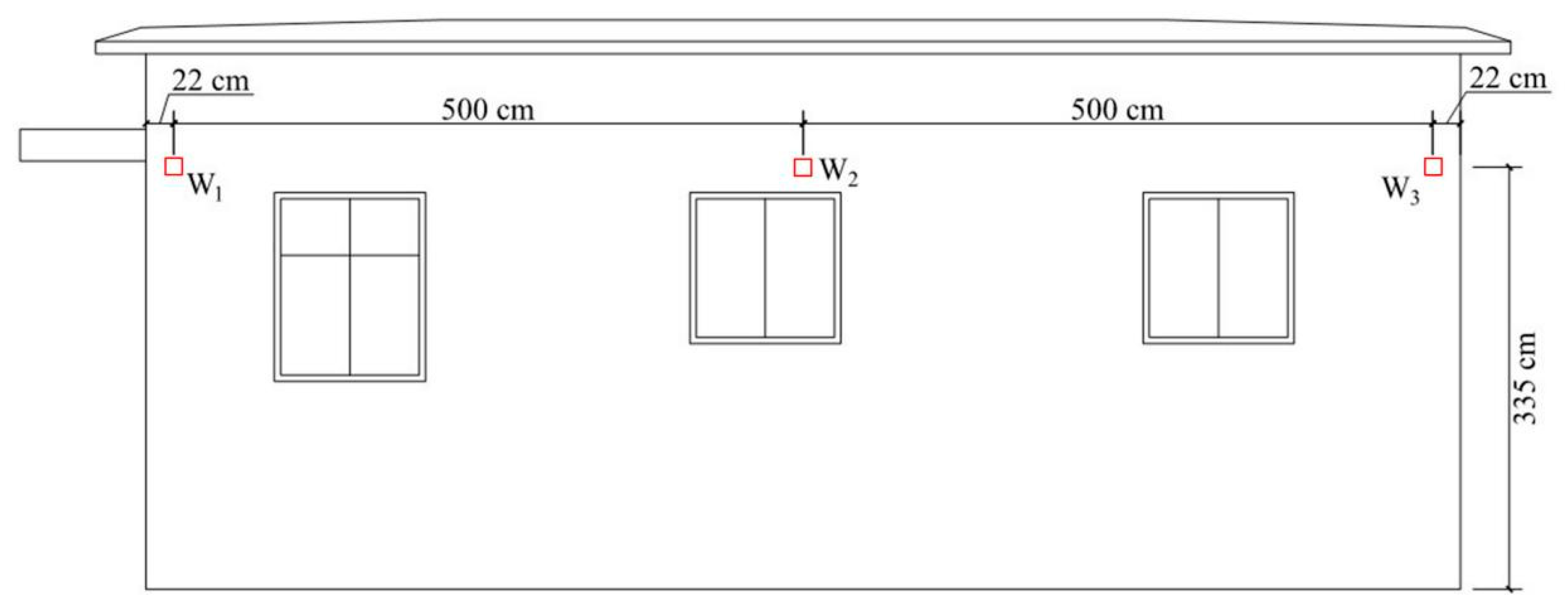
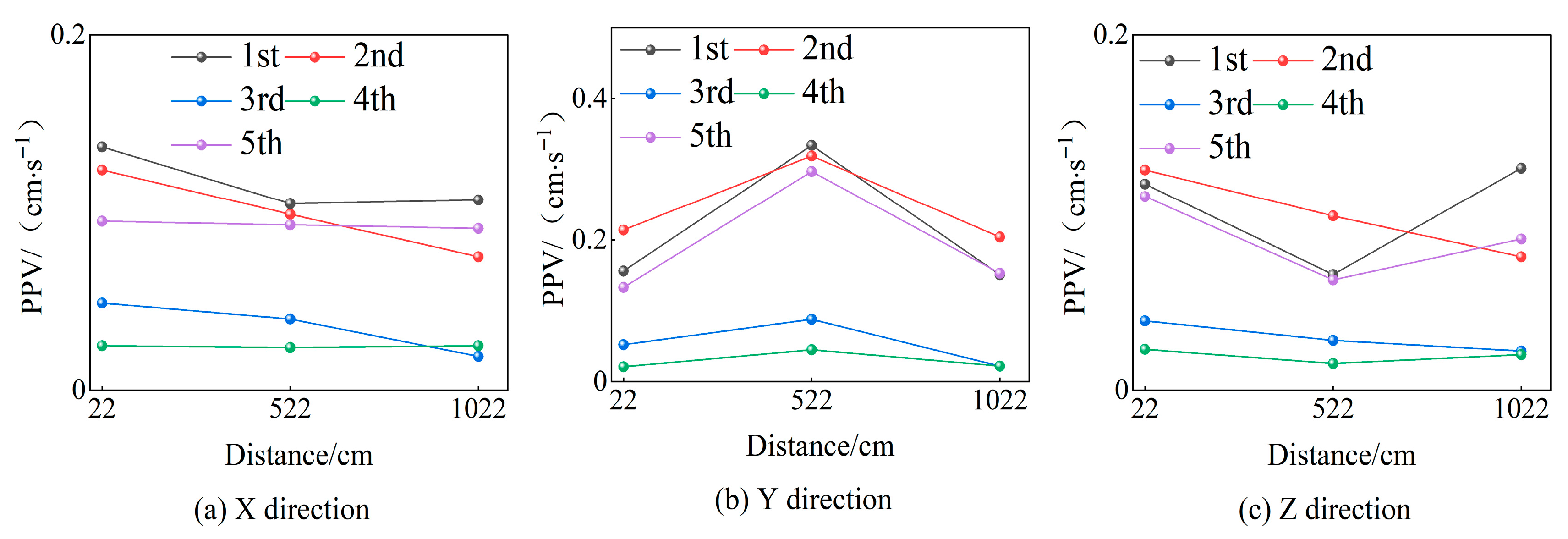
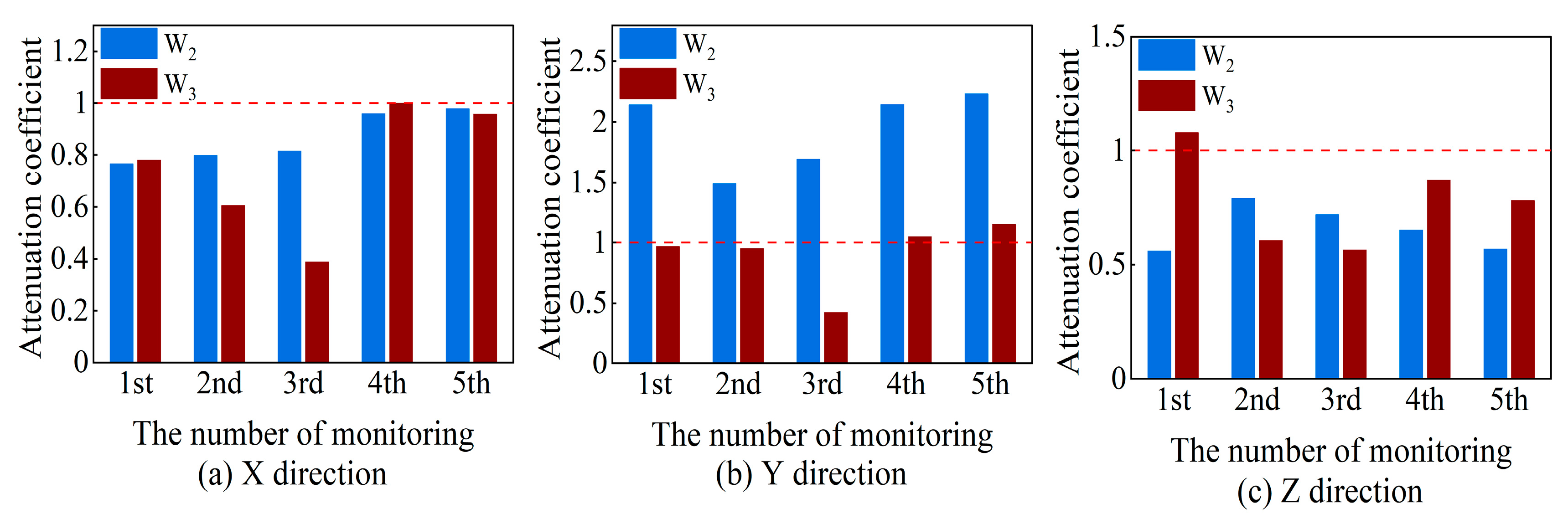
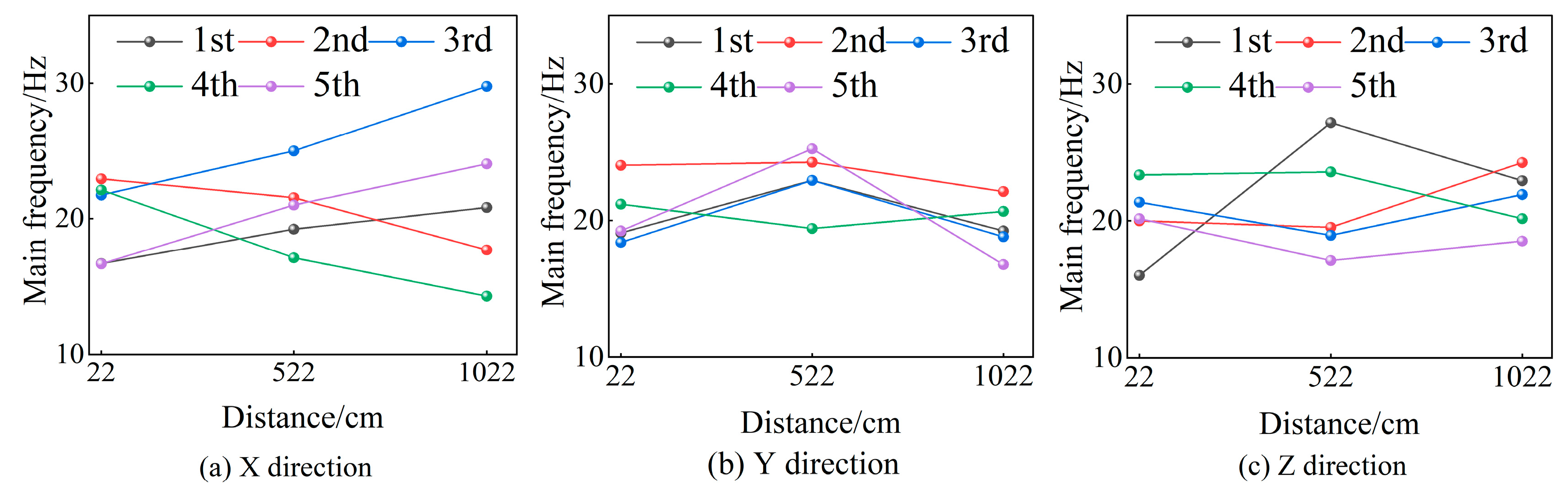
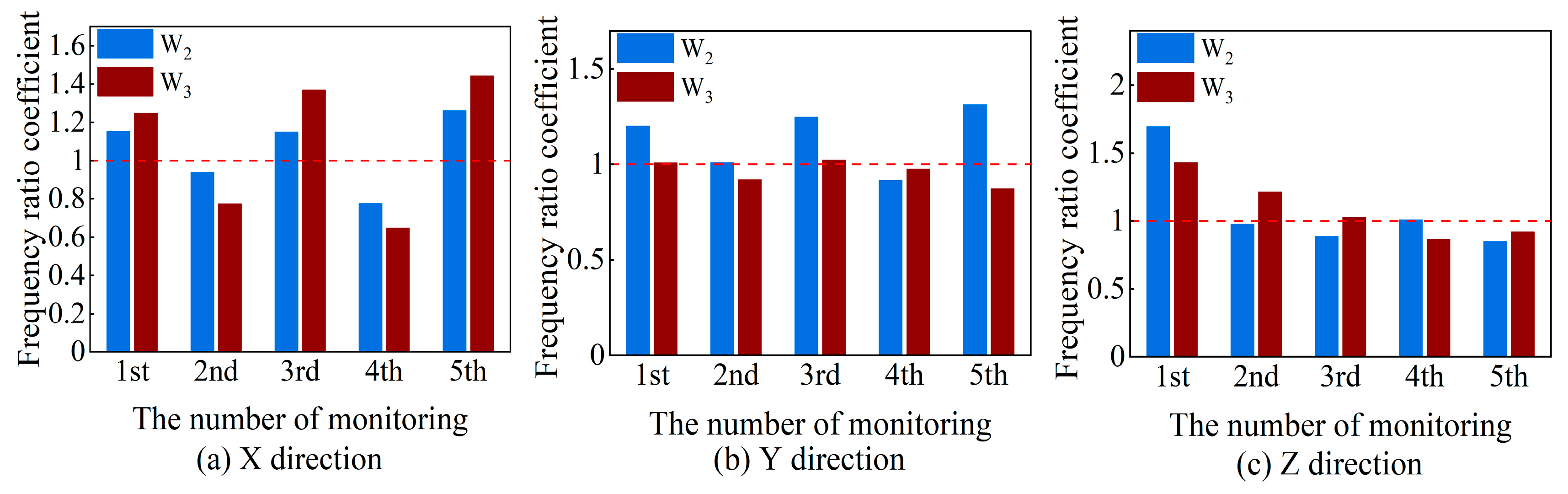
3.2. Monitoring and Analysis of Blasting Vibration of the Masonry Wall Component
4. Dynamic Response of a Building Under Blasting Vibration
4.1. Numerical Model Establishment
4.2. Harmonic Response Analysis of Building Components and Identification of Natural Frequency
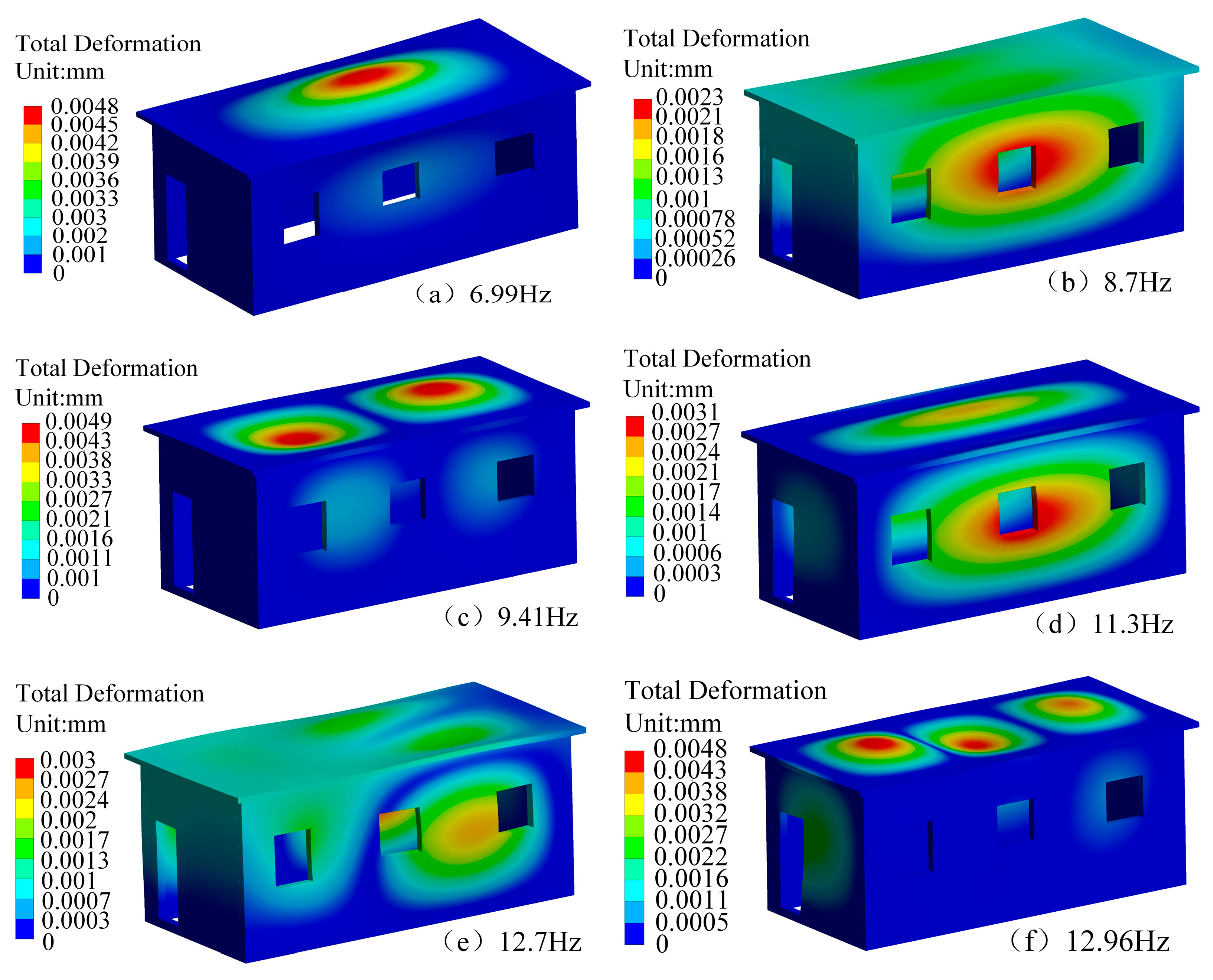
4.2.1. Harmonic Response Analysis of House Components
4.2.2. Identification of Natural Frequency of House Components
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shan, R.; Zhao, Y.; Wang, H.; Liu, Z.; Qin, H. Blasting vibration response and safety control of mountain tunnel. Bull. Eng. Geol. Environ. 2023, 82, 166. [Google Scholar] [CrossRef]
- Xu, S.; Chen, T.; Liu, J.; Zhang, C.; Chen, Z. Blasting Vibration Control Using an Improved Artificial Neural Network in the Ashele Copper Mine. Shock Vib. 2021, 2021, 9949858. [Google Scholar] [CrossRef]
- Zhou, J.; Asteris, P.; Armaghani, D.; Pham, B. Prediction of ground vibration induced by blasting operations through the use of the Bayesian Network and random forest models. Soil Dyn. Earthq. Eng. 2020, 139, 106390. [Google Scholar] [CrossRef]
- Yan, Y.; Hou, X.; Cao, S.; Li, R.; Zhou, W. Forecasting the collapse-induced ground vibration using a GWO-ELM model. Buildings 2022, 12, 121. [Google Scholar] [CrossRef]
- Bao, S.; Fei, H.; Hu, G. Characteristics and energy distribution of blast-induced ground vibration in deep-hole Blasting. Buildings 2023, 13, 899. [Google Scholar] [CrossRef]
- He, R.; Jiang, N.; Li, D.; Qi, J. Dynamic response characteristic of building structure under blasting vibration of underneath tunnel. Shock Vib. 2022, 2022, 9980665. [Google Scholar] [CrossRef]
- Wang, L.; Gaon, W.; Sun, B. Study of dynamic response of High-Rise buildings under blasting earthquake considering model simplifying. Mech. Adv. Mater. Struct. 2020, 27, 2068–2089. [Google Scholar] [CrossRef]
- Huo, R.; Li, S.; Song, Z.; Fujii, Y.; Lei, S.; Mao, J.; Tian, S.; Miao, Z. Analysis of vibration response law of multistory building under tunnel blasting loads. Adv. Civ. Eng. 2019, 2019, 4203137. [Google Scholar] [CrossRef]
- Jiang, N.; Zhang, Y.; Zhou, C.; Wu, T.; Zhu, B. Influence of blasting vibration of MLEMC shaft foundation pit on adjacent high-rise frame structure: A Case Study. Energies 2020, 13, 5140. [Google Scholar] [CrossRef]
- Athanasopoulos, G.; Pelekis, P. Ground vibrations from sheetpile driving in urban environment: Measurements, analysis and effects on buildings and occupants. Soil Dyn. Earthq. Eng. 2000, 19, 371–387. [Google Scholar] [CrossRef]
- Ren, Y.; Xi, S.; Yang, H.; Wan, T.; Wang, H.; Zhao, K. Structural vibration characteristics of the historical building in a nearby blasting test. Front. Earth Sci. 2024, 11, 1304354. [Google Scholar] [CrossRef]
- Ren, K.; Jiang, A.; Guo, X.; Min, Q. Research on Optimization Design of Tunnel Blasting Scheme Adjacent to Buildings. Appl. Sci. 2023, 13, 11509. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, N.; Zhou, C.; Wu, T.; Luo, X.; Xia, Y. Dynamic response of building structures with high-rise framescaused by blasting vibration at adjacent subway foundation pit. J. China Coal Soc. 2019, 44, 118–125. [Google Scholar]
- Guan, X.; Zhang, C.; Zhao, F.; Mou, B.; Ge, Y. Stress response and damage characteristics of local members of a structure due to tunnel blasting vibrations based on the high-order local modal analysis. Shock Vib. 2019, 2019, 7075024. [Google Scholar] [CrossRef]
- Shi, H.; Jiang, N.; Zhou, C.; Zhang, Y.; Yao, Y.; Zhou, W.; Cai, Z. Safety assessment of ancient buddhist pagoda induced by underpass metro tunnel blasting vibration. Eng. Fail Anal. 2023, 145, 107051. [Google Scholar] [CrossRef]
- Jayasooriya, W.; Thambiratnam, D.; Perera, N.; Kosse, V. Blast and residual capacity analysis of reinforced concrete framed buildings. Eng. Struct. 2011, 12, 3483–3495. [Google Scholar] [CrossRef]
- Wu, C.; Hao, H.; Lu, Y. Dynamic response and damage analysis of masonry structures and masonry infilled RC frames to blast ground motion. Eng. Struct. 2005, 27, 323–333. [Google Scholar] [CrossRef]
- Zou, Y.; Yan, P.; Liu, L.; Zhou, T.; Lu, W.; Chen, M. Assessment and control of the blasting vibration effect on local residences during theexcavation of abutment slope in the Baihetan project. J. Vib. Shock 2018, 37, 248–258. [Google Scholar]
- Yuan, Y.; Gao, Z.; He, L.; Lei, Z. Research on the vibration response of high-rise buildings under blasting loadt. Mathematics 2024, 12, 3165. [Google Scholar] [CrossRef]
- Yan, P.; Zhang, Y.; Tian, J.; Wang, H. Blasting vibration signal denoising based on CEEMDAN-K-means algorithm. Blasting 2023, 40, 184–190. [Google Scholar]
- Tang, Z.; Wu, H.; Wu, Z.; Jia, D.; Fu, J. Modal analysis and harmonic response analysis of energy-absorbing and anti-scouring columns. Front. Earth Sci. 2023, 11, 1126120. [Google Scholar] [CrossRef]
- He, Z.; Zhang, X.; Wang, S.; Bai, Y.; Feng, Q. Research on the effect of rail vibration suppression using the stiffness-damping interventional rail vibration reduction device. Constr. Build. Mater. 2024, 411, 134636. [Google Scholar] [CrossRef]
- Zhan, J.; Xia, H. Impact vibration test method for identifying the natural vibration frequency of piers with middle and low heights. China Railw. Sci. 2008, 29, 31–35. [Google Scholar]


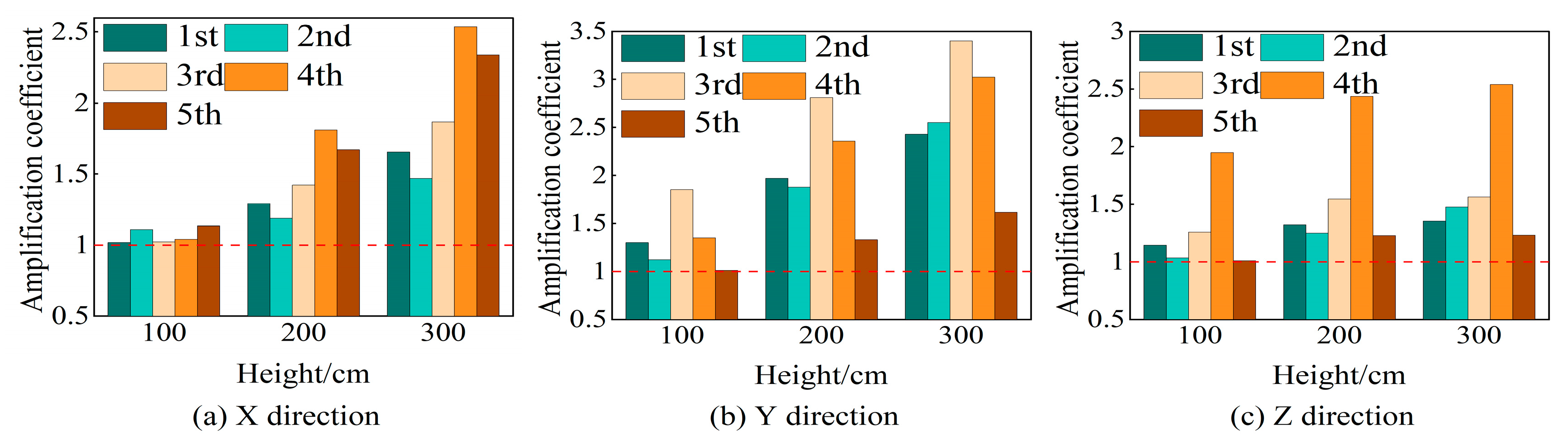
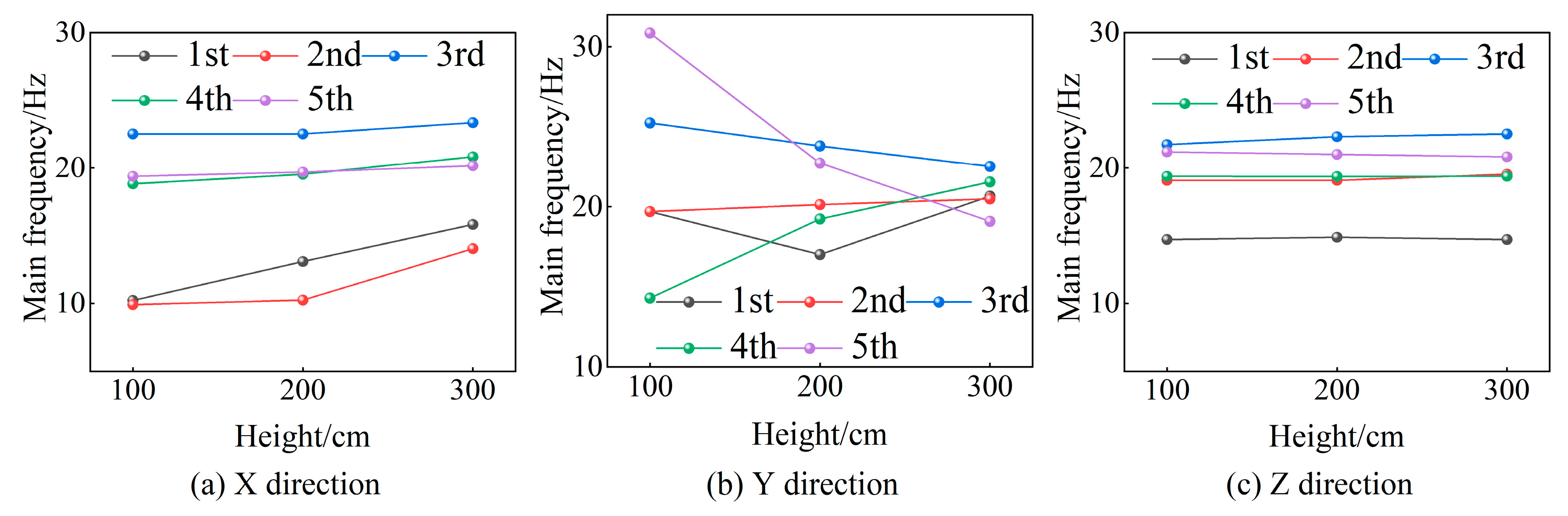

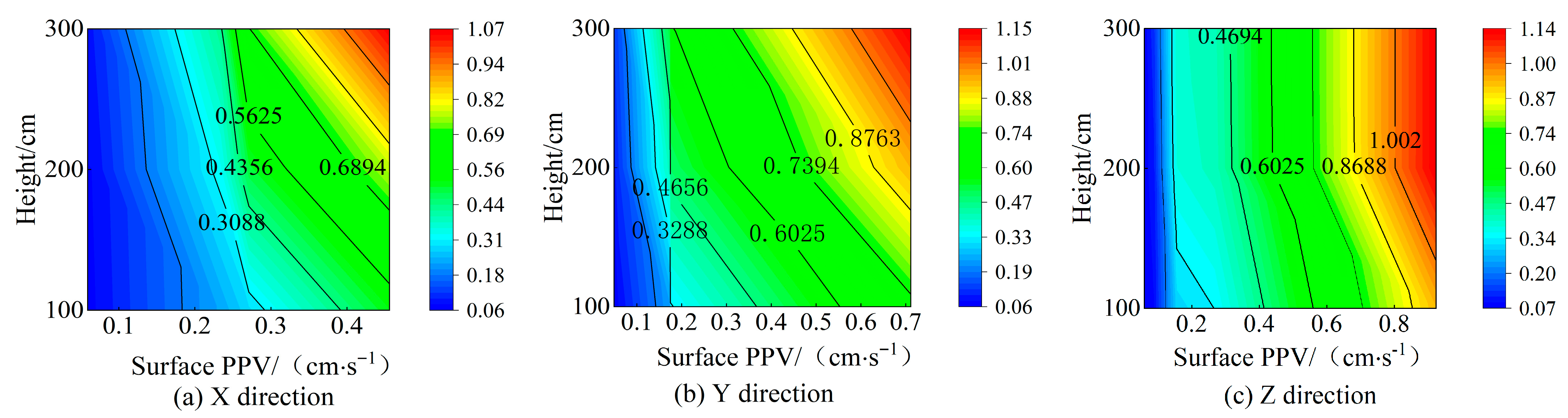

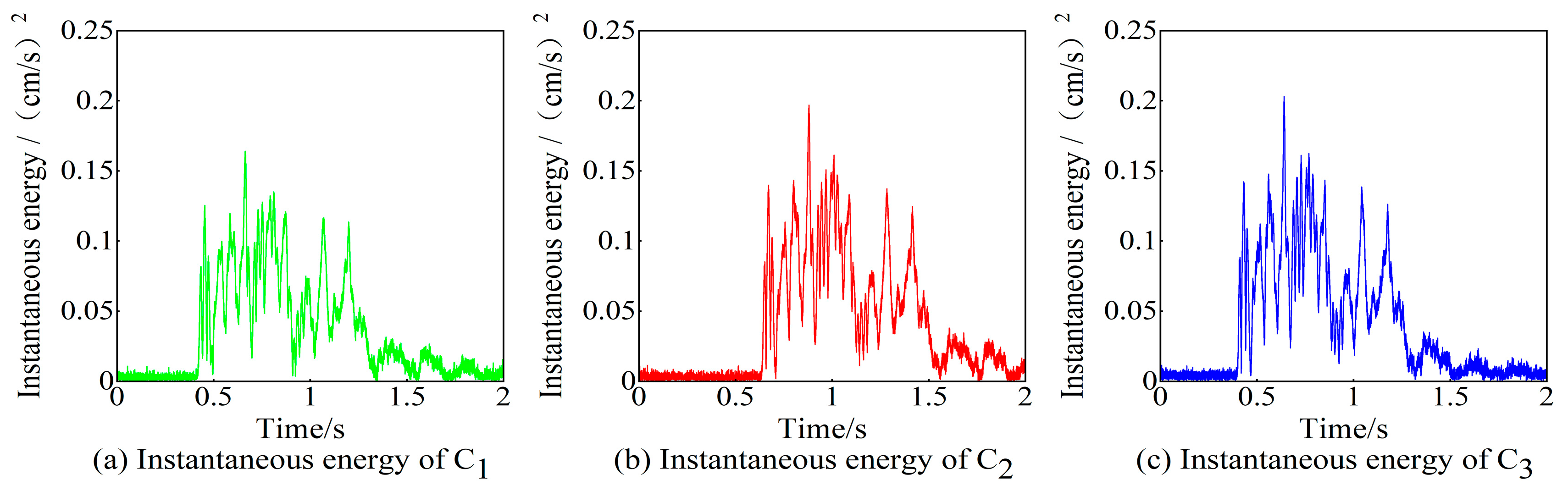

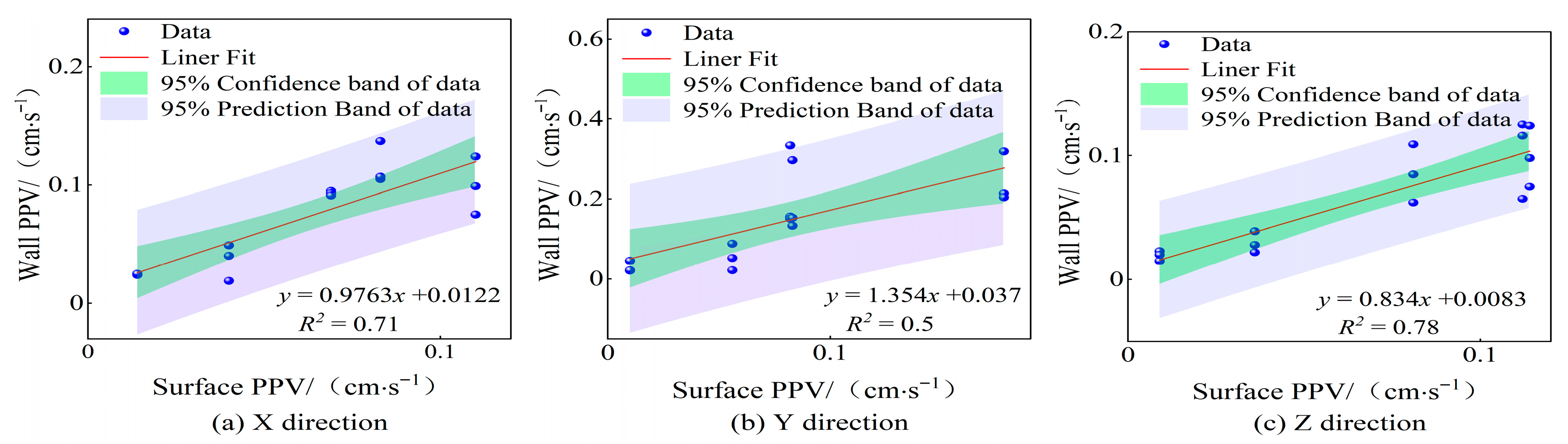
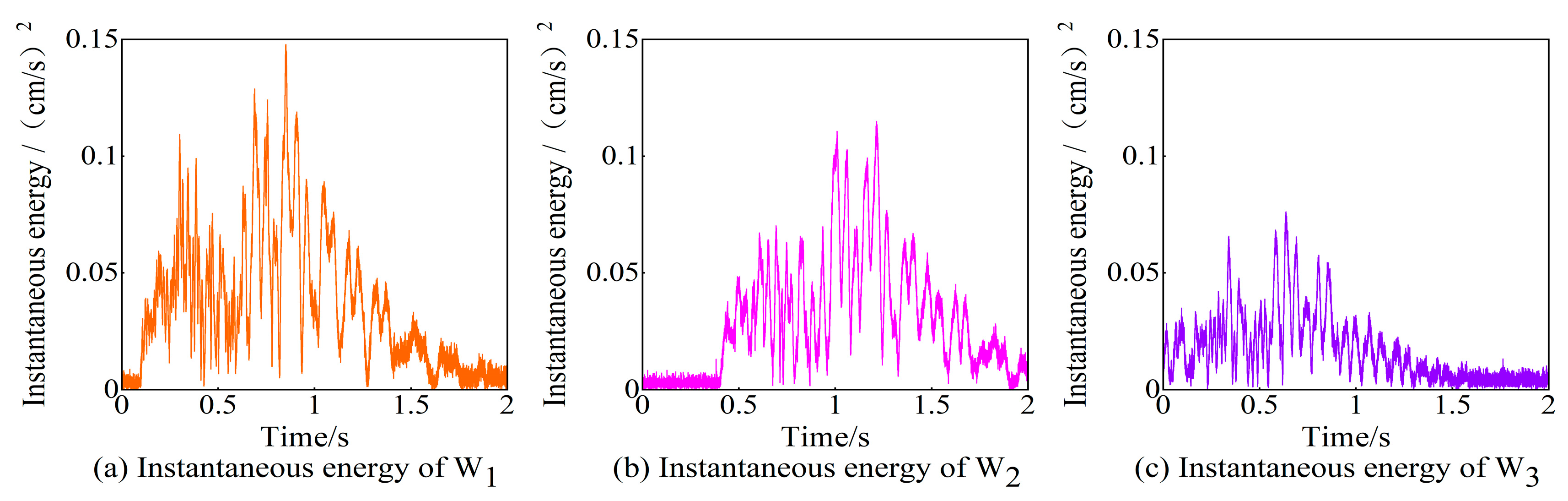



| Time/s | Maximum Explosive Charge per Delay/kg | Blast Center Distance/m | Monitoring Points | Horizontal Radial Direction (X Direction) | Horizontal Tangential Direction (Y Direction) | Vertical Direction (Z Direction) | |||
|---|---|---|---|---|---|---|---|---|---|
| PPV/ (cm/s) | Main Frequency/ Hz | PPV/ (cm/s) | Main Frequency/ Hz | PPV/ (cm/s) | Main Frequency/ Hz | ||||
| 1 | 490 | 581.78 | F | 0.058 | 9.22 | 0.063 | 11.02 | 0.062 | 9.46 |
| 581.80 | C1 | 0.059 | 10.22 | 0.082 | 19.69 | 0.071 | 14.71 | ||
| 581.83 | C2 | 0.075 | 13.09 | 0.124 | 17.01 | 0.082 | 14.88 | ||
| 581.86 | C3 | 0.096 | 15.82 | 0.153 | 20.66 | 0.084 | 14.71 | ||
| 2 | 500 | 591.31 | F | 0.064 | 8.72 | 0.049 | 20.01 | 0.088 | 14.24 |
| 591.32 | C1 | 0.071 | 9.92 | 0.055 | 19.69 | 0.091 | 19.08 | ||
| 591.35 | C2 | 0.076 | 10.25 | 0.092 | 20.13 | 0.112 | 19.08 | ||
| 591.38 | C3 | 0.094 | 14.04 | 0.125 | 20.49 | 0.13 | 19.53 | ||
| 3 | 850 | 328.46 | F | 0.234 | 22.35 | 0.175 | 27.39 | 0.268 | 21.74 |
| 328.55 | C1 | 0.229 | 22.52 | 0.324 | 25.25 | 0.337 | 21.74 | ||
| 328.65 | C2 | 0.326 | 22.52 | 0.492 | 23.81 | 0.414 | 22.32 | ||
| 328.76 | C3 | 0.427 | 23.36 | 0.595 | 22.52 | 0.419 | 22.52 | ||
| 4 | 325 | 198.52 | F | 0.271 | 18.61 | 0.174 | 11.53 | 0.156 | 26.85 |
| 198.79 | C1 | 0.282 | 18.82 | 0.235 | 14.29 | 0.304 | 19.38 | ||
| 199.08 | C2 | 0.49 | 19.53 | 0.410 | 19.23 | 0.380 | 19.37 | ||
| 199.37 | C3 | 0.687 | 20.83 | 0.526 | 21.55 | 0.396 | 19.38 | ||
| 5 | 450 | 219.32 | F | 0.456 | 22.09 | 0.711 | 29.85 | 0.924 | 43.96 |
| 219.66 | C1 | 0.517 | 19.38 | 0.719 | 30.86 | 0.933 | 21.19 | ||
| 220.01 | C2 | 0.762 | 19.69 | 0.946 | 22.73 | 1.135 | 21.01 | ||
| 220.36 | C3 | 1.066 | 20.16 | 1.150 | 19.08 | 1.134 | 20.83 | ||
| Number of Frequency Bands | Frequency Band/Hz | Energy/(cm/s)2 | Proportion/% | ||||
|---|---|---|---|---|---|---|---|
| Signal C1 | Signal C2 | Signal C3 | Signal C1 | Signal C2 | Signal C3 | ||
| 1 | 0~4.8828 | 0.252 | 0.263 | 0.224 | 5.291 | 4.084 | 2.621 |
| 2 | 4.8828~9.7656 | 1.374 | 1.431 | 1.459 | 28.847 | 22.224 | 17.074 |
| 3 | 9.7656~19.5313 | 1.021 | 1.151 | 1.813 | 21.436 | 17.875 | 21.217 |
| 4 | 19.5313~39.0625 | 1.097 | 2.250 | 3.674 | 23.032 | 34.943 | 42.996 |
| 5 | 39.0625~78.125 | 0.665 | 0.666 | 0.689 | 13.962 | 10.343 | 8.063 |
| 6 | 78.125~156.25 | 0.286 | 0.585 | 0.594 | 6.005 | 9.085 | 6.951 |
| 7 | 156.25~312.5 | 0.067 | 0.093 | 0.092 | 1.407 | 1.444 | 1.077 |
| 8 | 312.5~625 | 0.000 | 0.000 | 0.000 | 0 | 0 | 0 |
| 9 | 625~1250 | 0.001 | 0.000 | 0.000 | 0.021 | 0 | 0 |
| 10 | 1250~2500 | 0.000 | 0.000 | 0.000 | 0 | 0 | 0 |
| amount to | 4.763 | 6.439 | 8.545 | 100 | 100 | 100 | |
| Time/s | Maximum Explosive Charge per Delay/kg | Blast Center Distance/m | Monitoring Points | Horizontal Radial Direction (X Direction) | Horizontal Tangential Direction (Y Direction) | Vertical Direction (Z Direction) | |||
|---|---|---|---|---|---|---|---|---|---|
| PPV/ (cm/s) | Main Frequency/ Hz | PPV/ (cm/s) | Main Frequency/ Hz | PPV/ (cm/s) | Main Frequency/ Hz | ||||
| 1 | 700 | 303.41 | F | 0.083 | 16.34 | 0.082 | 16.89 | 0.112 | 22.32 |
| 303.75 | W1 | 0.137 | 16.69 | 0.156 | 19.08 | 0.116 | 16.03 | ||
| 308.72 | W2 | 0.105 | 19.23 | 0.334 | 22.94 | 0.065 | 27.17 | ||
| 313.69 | W3 | 0.107 | 20.83 | 0.151 | 19.23 | 0.125 | 22.94 | ||
| 2 | 800 | 539.83 | F | 0.11 | 22.12 | 0.178 | 24.27 | 0.114 | 25.77 |
| 540.03 | W1 | 0.124 | 22.94 | 0.214 | 24.04 | 0.124 | 20 | ||
| 545.02 | W2 | 0.099 | 21.55 | 0.319 | 24.27 | 0.098 | 19.53 | ||
| 550.01 | W3 | 0.075 | 17.70 | 0.204 | 22.12 | 0.075 | 24.27 | ||
| 3 | 200 | 565.31 | F | 0.04 | 23.36 | 0.056 | 22.32 | 0.036 | 21.01 |
| 565.41 | W1 | 0.049 | 21.74 | 0.052 | 18.380 | 0.039 | 21.37 | ||
| 570.35 | W2 | 0.040 | 25.00 | 0.088 | 22.94 | 0.028 | 18.94 | ||
| 575.3 | W3 | 0.019 | 29.76 | 0.022 | 18.80 | 0.022 | 21.93 | ||
| 4 | 200 | 735.51 | F | 0.014 | 9.9 | 0.01 | 12.74 | 0.009 | 13.7 |
| 735.59 | W1 | 0.025 | 22.12 | 0.021 | 21.19 | 0.023 | 23.36 | ||
| 740.17 | W2 | 0.024 | 17.12 | 0.045 | 19.41 | 0.015 | 23.58 | ||
| 744.76 | W3 | 0.025 | 14.29 | 0.022 | 20.66 | 0.020 | 20.16 | ||
| 5 | 600 | 303.41 | F | 0.069 | 32.47 | 0.083 | 14.71 | 0.081 | 17.01 |
| 303.76 | W1 | 0.095 | 16.67 | 0.133 | 19.23 | 0.109 | 20.16 | ||
| 308.72 | W2 | 0.093 | 21.01 | 0.297 | 25.25 | 0.062 | 17.12 | ||
| 313.69 | W3 | 0.091 | 24.04 | 0.153 | 16.78 | 0.085 | 18.52 | ||
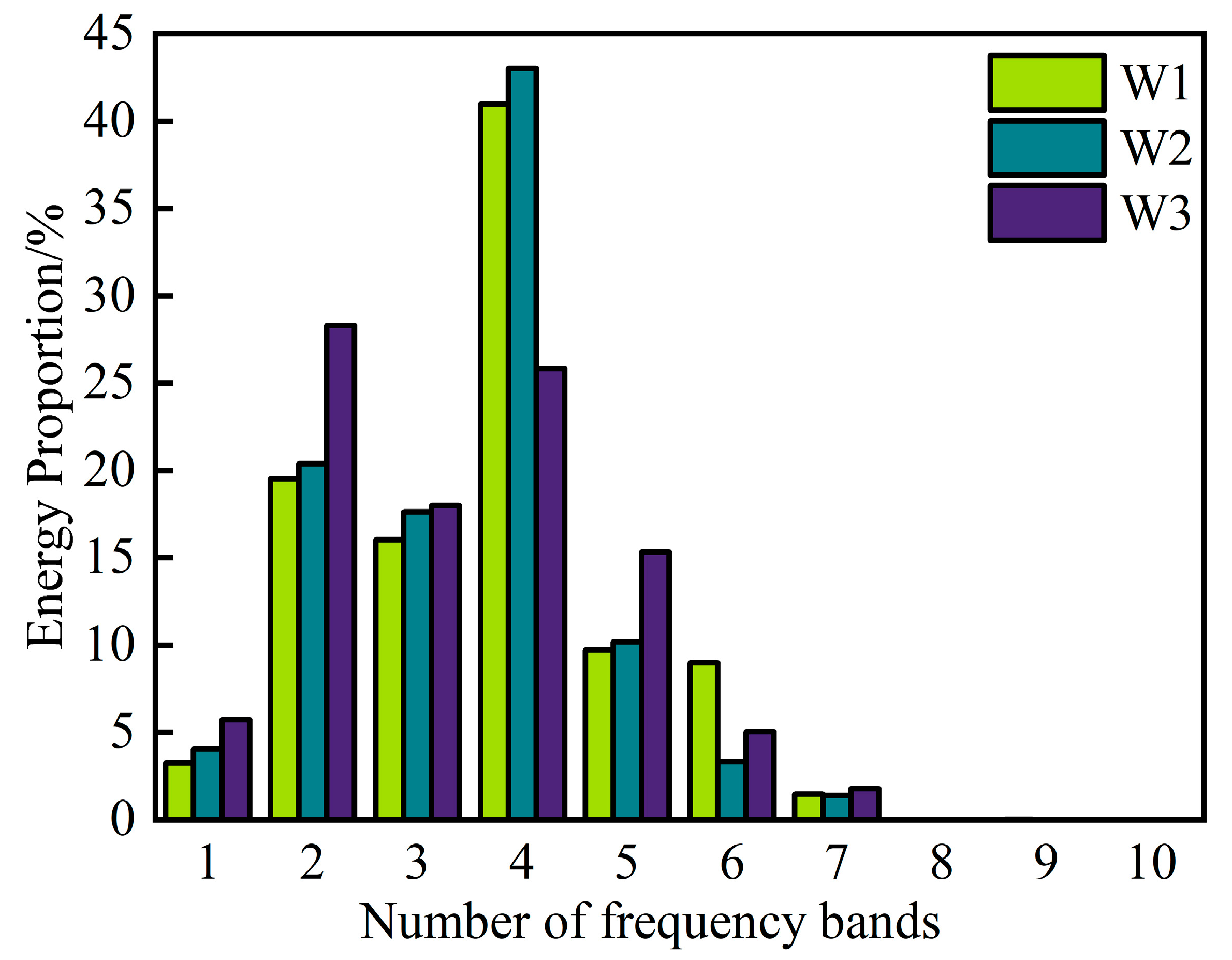
| Number of Frequency Bands | Frequency Band/Hz | Energy/(cm/s)2 | Proportion/% | ||||
|---|---|---|---|---|---|---|---|
| Signal W1 | Signal W2 | Signal W3 | Signal W1 | Signal W2 | Signal W3 | ||
| 1 | 0~4.8828 | 0.209 | 0.211 | 0.191 | 3.256 | 4.06 | 5.715 |
| 2 | 4.8828~9.7656 | 1.252 | 1.061 | 0.946 | 19.508 | 20.416 | 28.306 |
| 3 | 9.7656~19.5313 | 1.029 | 0.915 | 0.601 | 16.033 | 17.606 | 17.983 |
| 4 | 19.5313~39.0625 | 2.631 | 2.235 | 0.864 | 40.994 | 43.006 | 25.853 |
| 5 | 39.0625~78.125 | 0.623 | 0.529 | 0.512 | 9.707 | 10.179 | 15.32 |
| 6 | 78.125~156.25 | 0.578 | 0.174 | 0.168 | 9.006 | 3.348 | 5.027 |
| 7 | 156.25~312.5 | 0.094 | 0.072 | 0.060 | 1.465 | 1.385 | 1.795 |
| 8 | 312.5~625 | 0.000 | 0.000 | 0.000 | 0 | 0 | 0 |
| 9 | 625~1250 | 0.002 | 0.000 | 0.000 | 0.031 | 0 | 0 |
| 10 | 1250~2500 | 0.000 | 0.000 | 0.000 | 0 | 0 | 0 |
| amount to | 6.418 | 5.197 | 3.342 | 100 | 100 | 100 | |
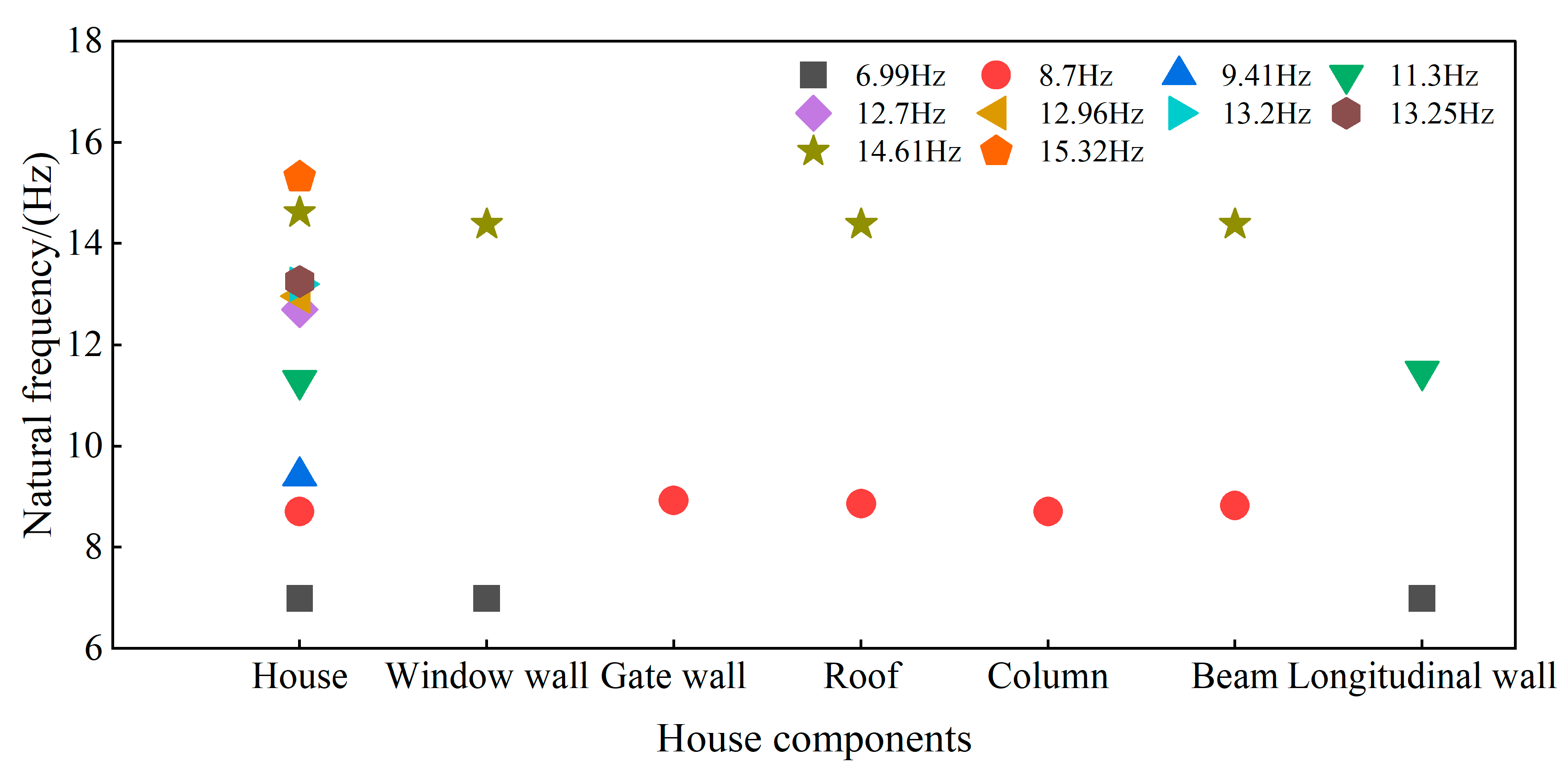
| Order | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Frequency/Hz | 6.99 | 8.7 | 9.41 | 11.3 | 12.7 | 12.96 | 13.2 | 13.25 | 14.61 | 15.32 |
| Component | X Direction | Y Direction | Z Direction | |||
|---|---|---|---|---|---|---|
| Frequency/Hz | PPV/(cm/s) | Frequency/Hz | PPV/(cm/s) | Frequency/Hz | PPV/(cm/s) | |
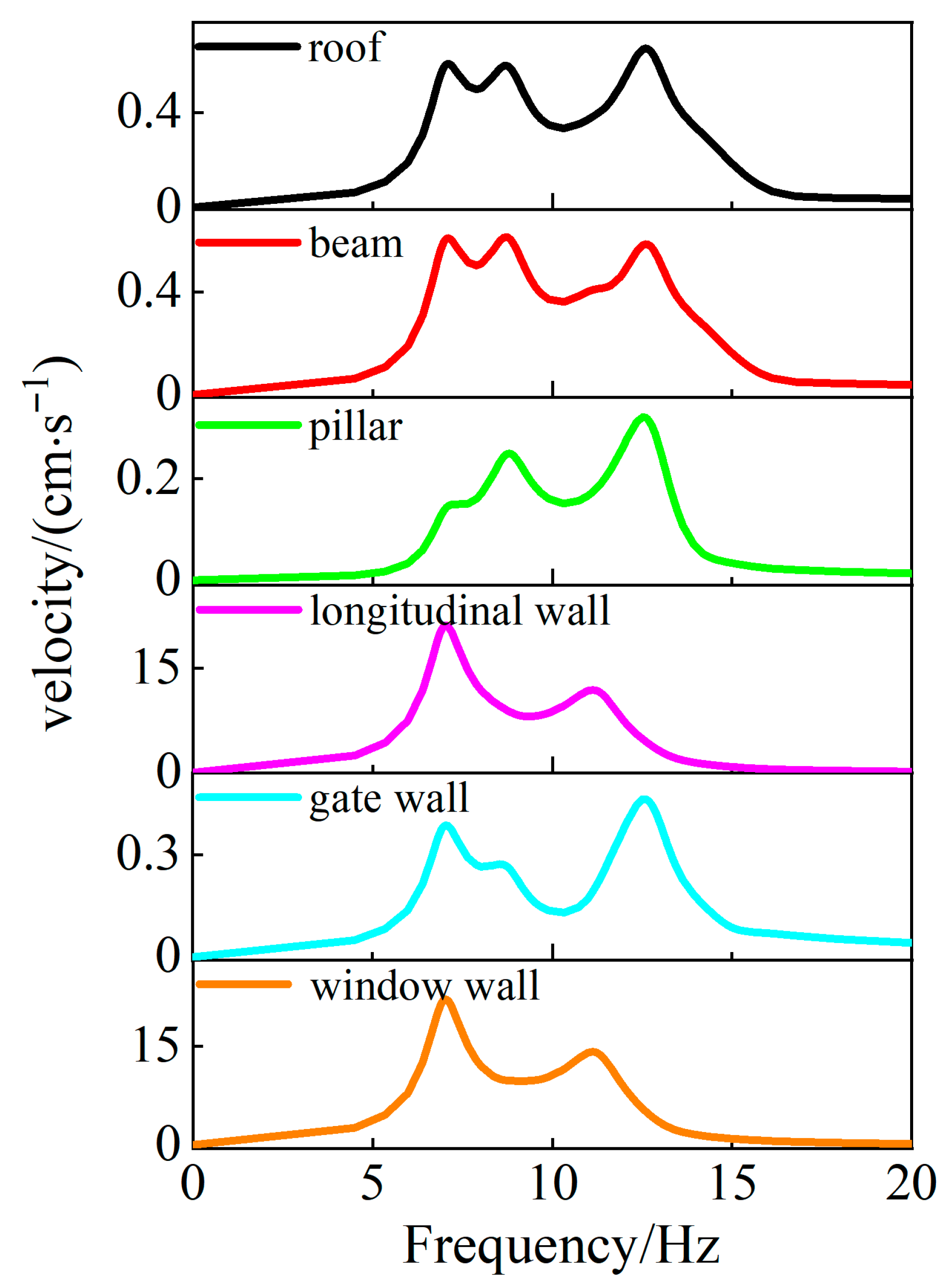
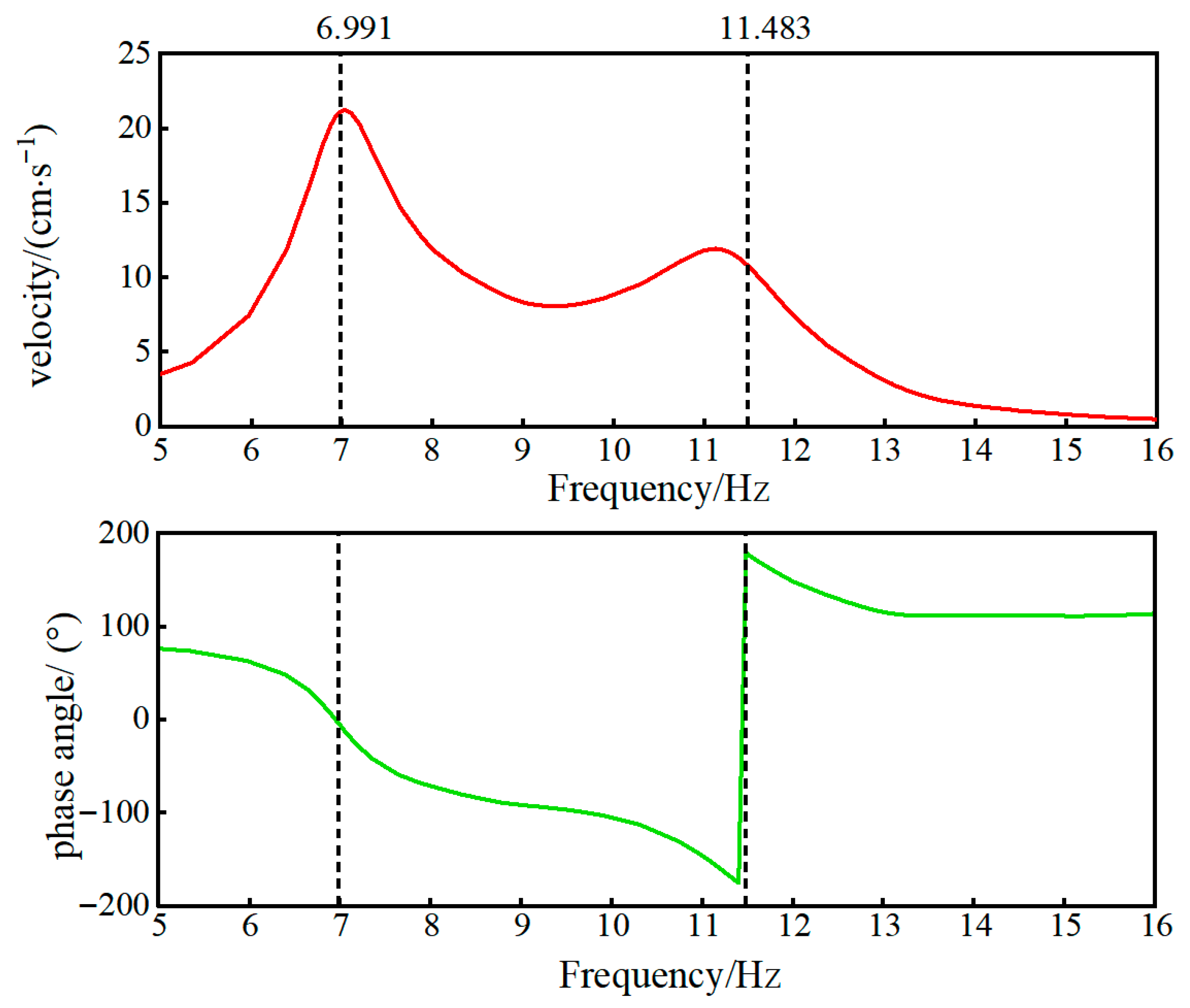
| Window wall | 6.991 | 0.055 | 6.991 | 22.073 | 6.991 | 0.417 |
| 13.138 | 0.137 | 11.124 | 14.164 | 11.483 | 0.179 | |
| 14.384 | 0.111 | — | — | 13.227 | 0.142 | |
| Gate wall | 6.991 | 0.752 | 6.991 | 0.384 | 6.991 | 0.243 |
| 11.358 | 5.032 | 8.918 | 0.245 | 12.896 | 0.251 | |
| 13.138 | 7.448 | 12.592 | 0.463 | — | — | |
| Longitudinal wall | 6.991 | 0.019 | 6.991 | 21.139 | 6.991 | 0.359 |
| 14.384 | 0.101 | 11.483 | 10.780 | 11.402 | 0.152 | |
| — | — | — | — | 13.138 | 0.132 | |
| Pillar | 6.991 | 0.341 | 8.777 | 0.250 | 8.639 | 0.112 |
| 13.138 | 0.468 | 12.592 | 0.321 | 11.402 | 0.059 | |
| — | — | — | — | 13.227 | 0.084 | |
| Beam | 13.317 | 0.303 | 6.991 | 0.598 | 6.991 | 0.642 |
| 14.383 | 0.274 | 8.820 | 0.606 | 11.402 | 0.267 | |
| — | — | 12.642 | 0.585 | — | — | |
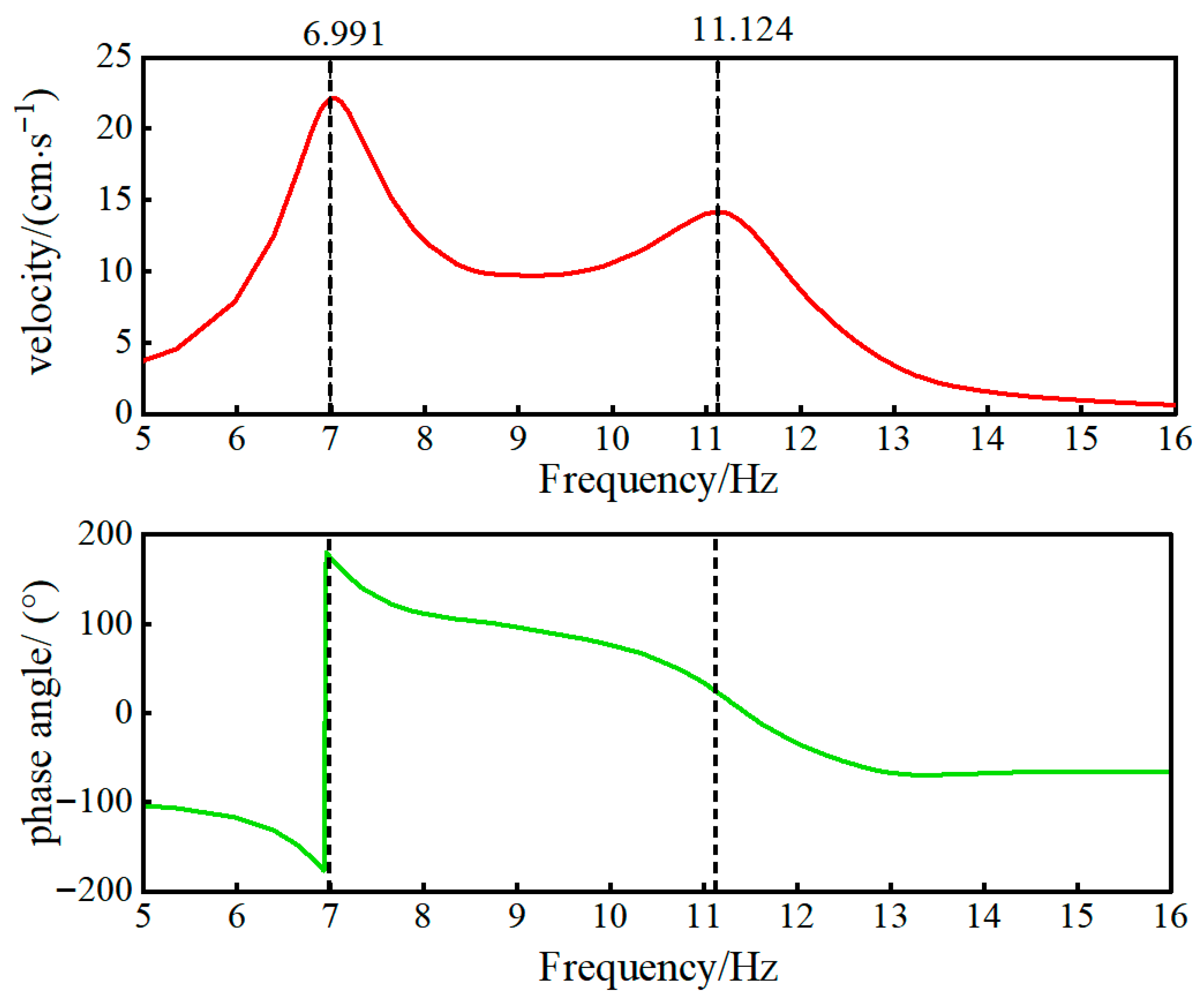
| Roof | 13.317 | 0.238 | 6.991 | 0.594 | 6.991 | 53.680 |
| 14.384 | 0.225 | 8.855 | 0.581 | 11.402 | 10.606 | |
| — | — | 12.642 | 0.668 | — | — | |
| Component | X Direction | Y Direction | Z Direction | |||
|---|---|---|---|---|---|---|
| Frequency/Hz | Phase Angle/° | Frequency/Hz | Phase Angle/° | Frequency/Hz | Phase Angle/° | |
| Window wall | 14.384 | 169.890 | 6.991 | 175.820 | — | — |
| Gate wall | — | — | 8.918 | 176.680 | — | — |
| Longitudinal wall | 6.991 | 179.690 | 11.483 | 178.630 | — | — |
| Pillar | 6.991 | 178.950 | 8.855 | 177.860 | 8.777 | 179.250 |
| Beam | 14.384 | 178.720 | 8.820 | 176.420 | — | — |
| Roof | 14.384 | 175.730 | 8.855 | 177.440 | — | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, P.; Tian, J.; Zhang, Y.; Hao, L. Study on the Vibration Effects of Brick–Concrete Structures Induced by Blasting in Open-Pit Mines. Buildings 2025, 15, 2954. https://doi.org/10.3390/buildings15162954
Yan P, Tian J, Zhang Y, Hao L. Study on the Vibration Effects of Brick–Concrete Structures Induced by Blasting in Open-Pit Mines. Buildings. 2025; 15(16):2954. https://doi.org/10.3390/buildings15162954
Chicago/Turabian StyleYan, Peng, Jie Tian, Yunpeng Zhang, and Liangpeng Hao. 2025. "Study on the Vibration Effects of Brick–Concrete Structures Induced by Blasting in Open-Pit Mines" Buildings 15, no. 16: 2954. https://doi.org/10.3390/buildings15162954
APA StyleYan, P., Tian, J., Zhang, Y., & Hao, L. (2025). Study on the Vibration Effects of Brick–Concrete Structures Induced by Blasting in Open-Pit Mines. Buildings, 15(16), 2954. https://doi.org/10.3390/buildings15162954





