Seismic Performance Testing and Damage Analysis of Reinforced T-Stub Connections
Abstract
1. Introduction
2. Research Overview
2.1. Specimen Design
2.2. Material Property Tests
2.3. Loading Setup
2.4. Loading Protocol and Instrumentation
3. Results Analysis
3.1. Experimental Macroscopic Phenomena
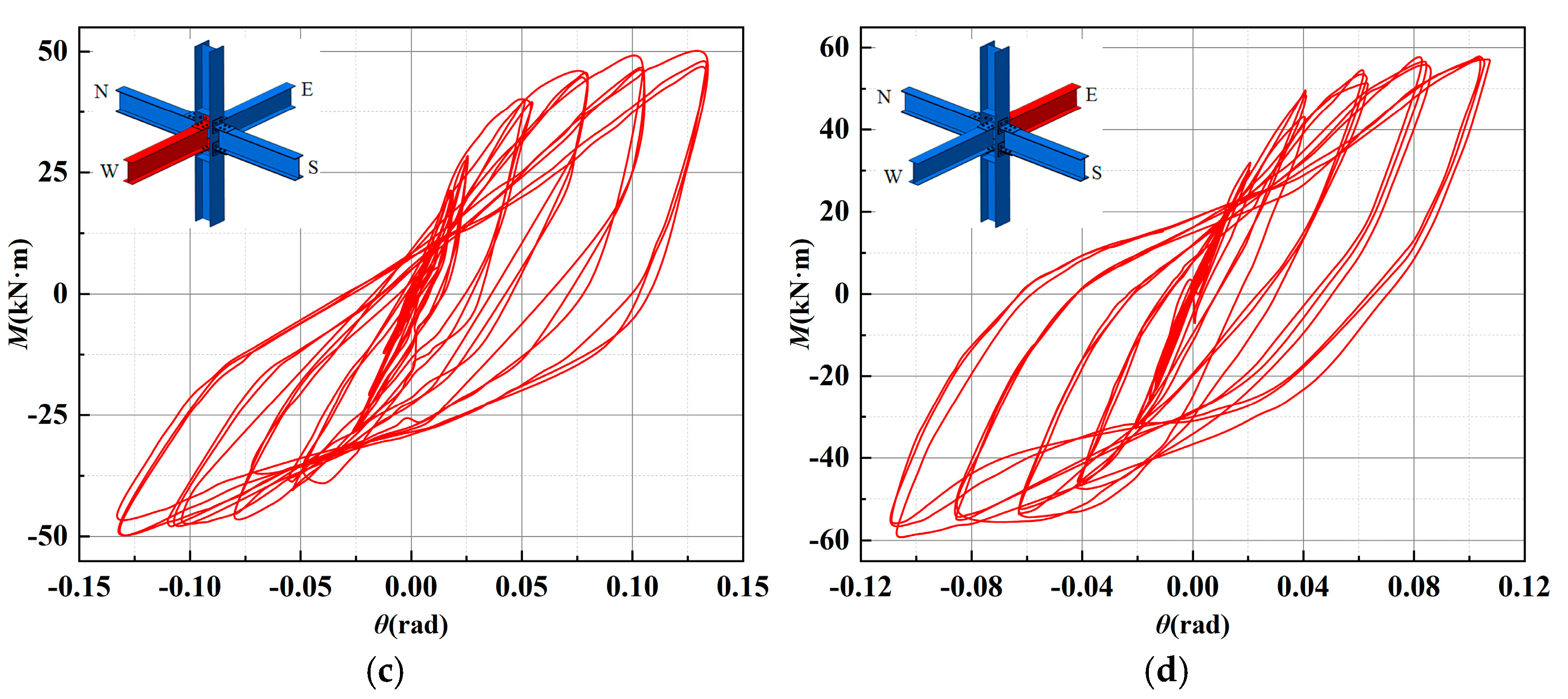
3.2. Hysteretic Curves
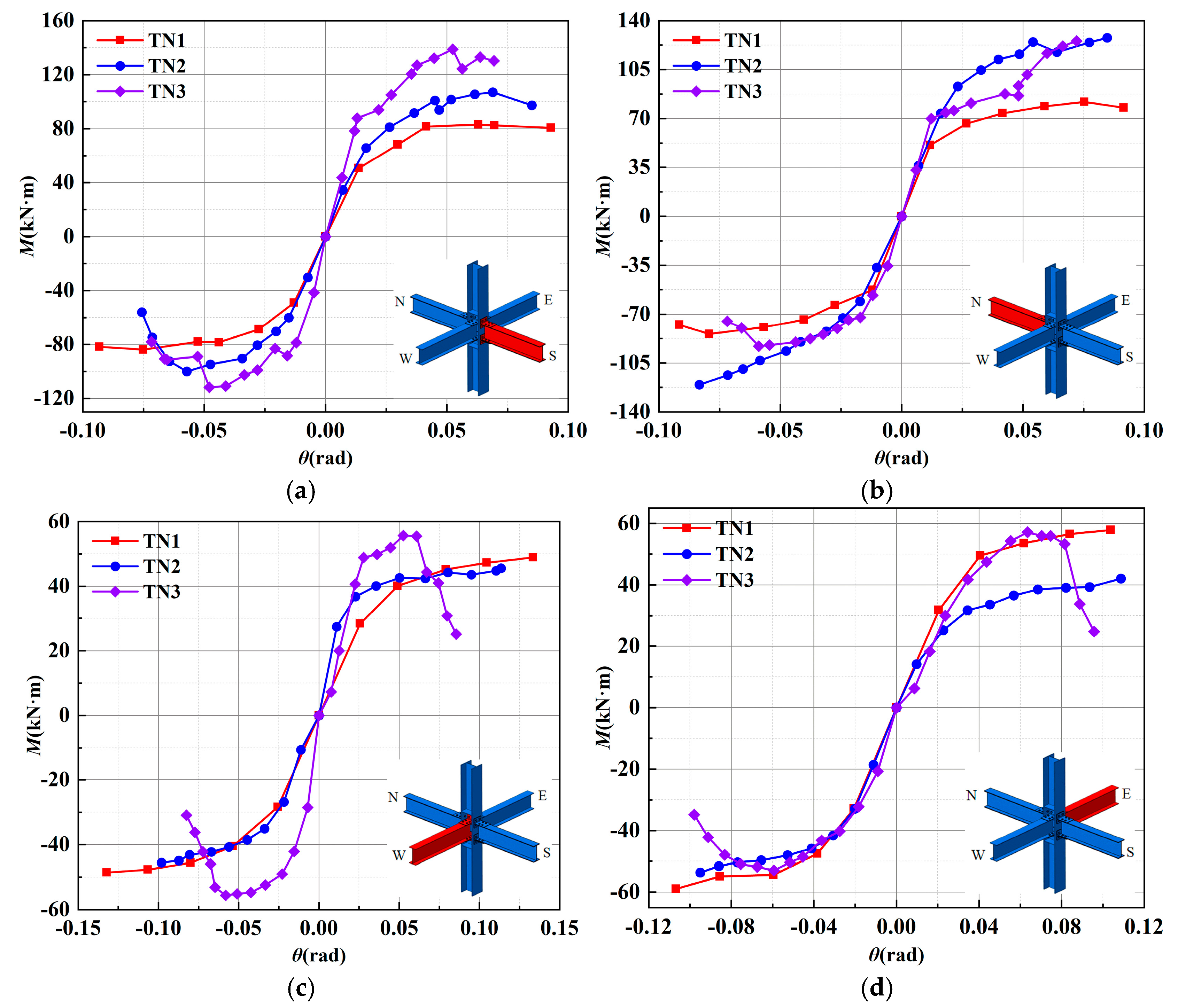
3.3. Skeleton Curves
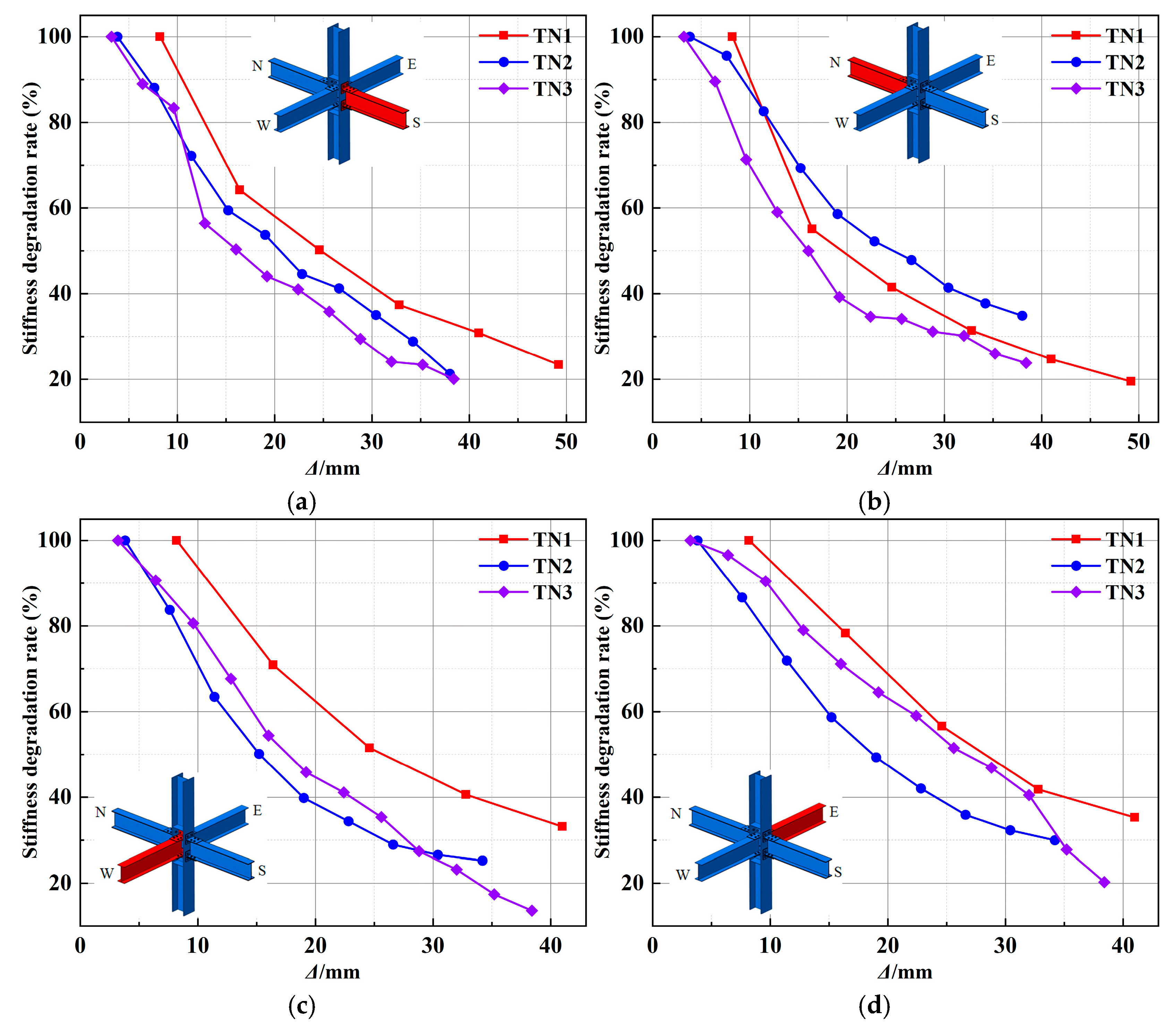
3.4. Stiffness Degradation
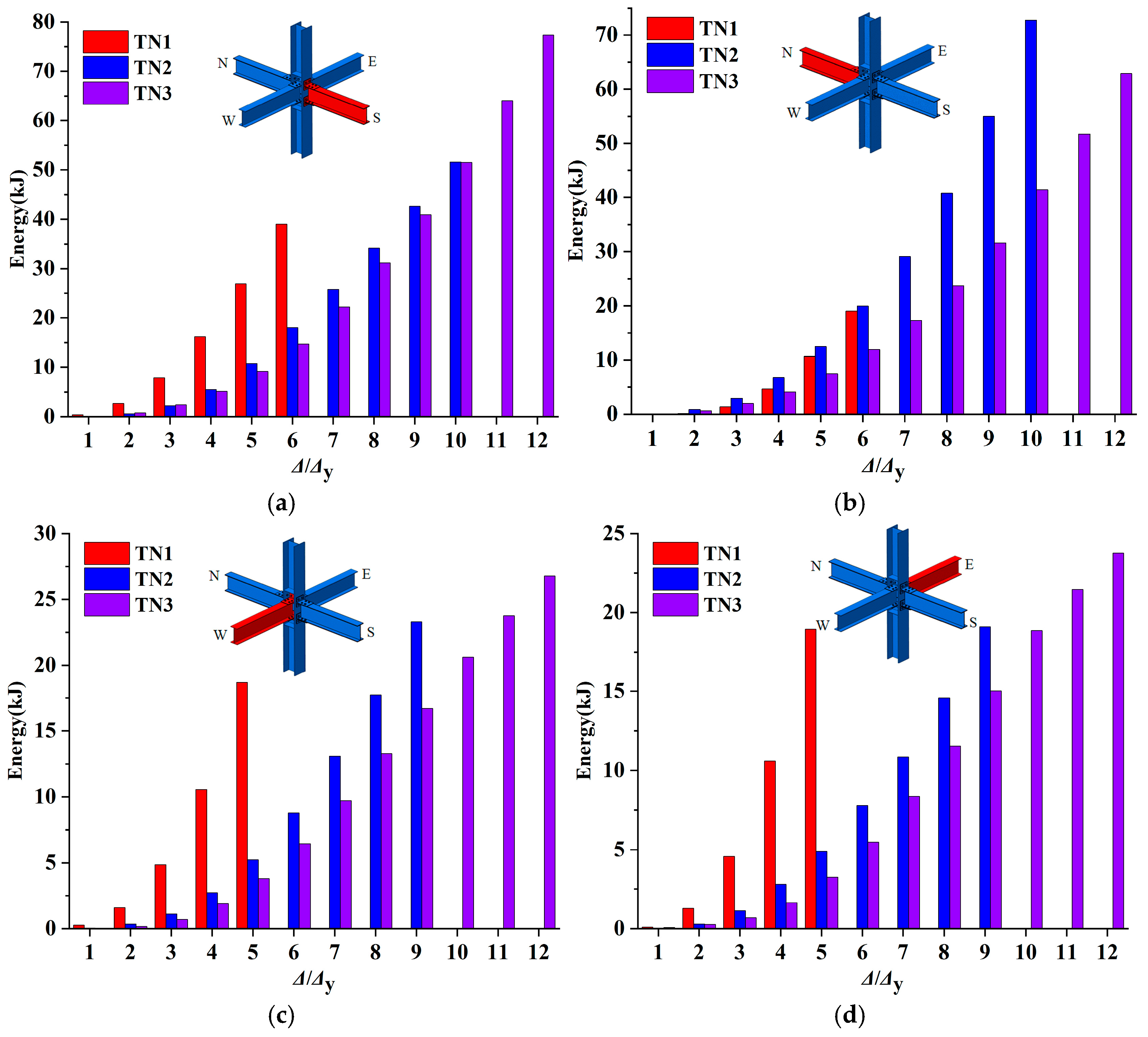
3.5. Energy Dissipation Capacity
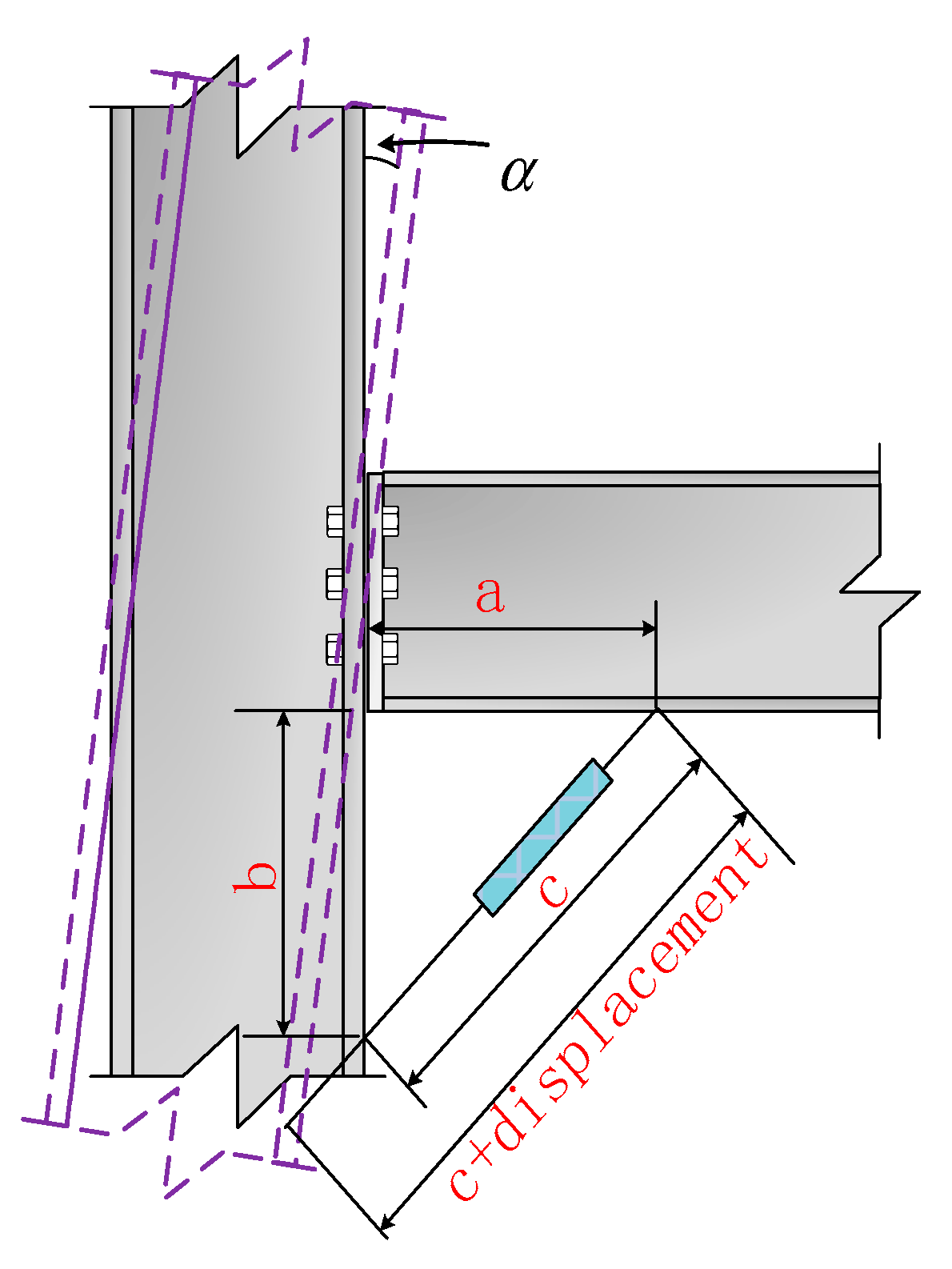
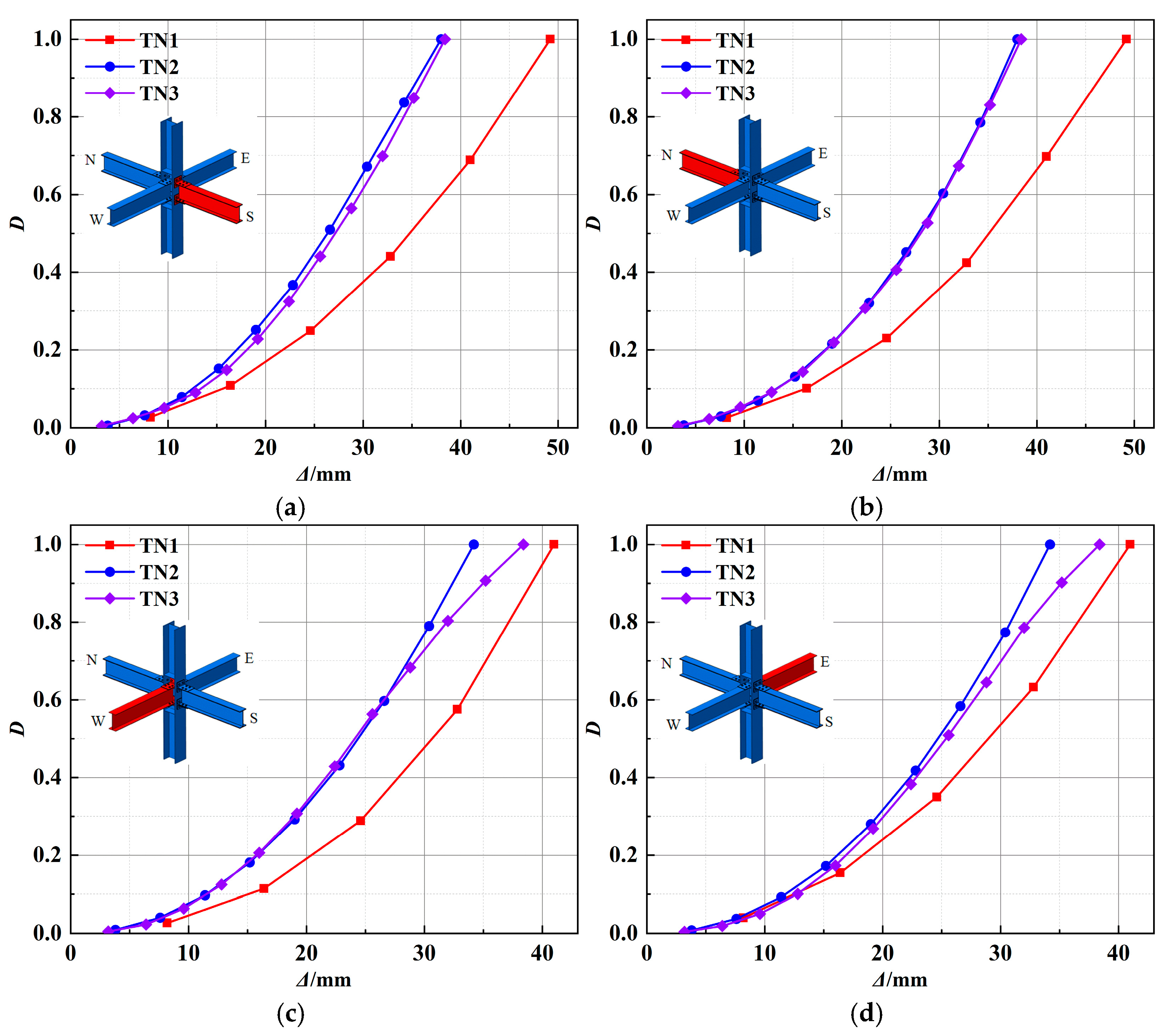
4. Damage Assessment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Simoncelli, M.; Tagliafierro, B.; Montuori, R. Recent development on the seismic devices for steel storage structures. Thin Walled Struct. 2020, 155, 106827. [Google Scholar] [CrossRef]
- Zhang, Y.; Ding, K.W. Study on seismic behavior of fabricated beam-column bolted joint. J. Constr. Steel Res. 2022, 82, 801–812. [Google Scholar]
- Prinz, G.S.; Nussbaumer, A.; Borges, L.; Khadka, S. Experimental testing and simulation of bolted beam-column connections having thick extended endplates and multiple bolts per row. Eng. Struct. 2014, 59, 434–447. [Google Scholar] [CrossRef]
- Bu, X.; Xiao, S.X.; Wu, Z.J.; Li, X.L.; Wang, X.W. Damage Evaluation of T-Stub Connected to Hollow Section Column Using Blind Bolts under Tension. Buildings 2023, 13, 2603. [Google Scholar] [CrossRef]
- Miller, D.K. Lessons learned from the Northridge earthquake. Eng. Struct. 1998, 20, 249–260. [Google Scholar] [CrossRef]
- Bruneau, M. Performance of steel bridges during the 1995 Hyogoken-Nanbu (Kobe, Japan) earthquake—A North American perspective. Eng. Struct. 1998, 20, 1063–1078. [Google Scholar] [CrossRef]
- Chen, W.F.; Goto, Y.; Liew, R.J.Y. Stability Design of Semi-Rigid Frames; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Liu, X.; Hao, Z.M. Constitutive model for rotation behaviour of semi-rigid steel beam-to-column joints. J. Constr. Steel Res. 2022, 198, 107563. [Google Scholar] [CrossRef]
- Majlesi, A.; Asadi-Ghoozhdi, H.; Bamshad, O.; Attarnejad, R.; Masoodi, A.R.; Ghassemieh, M. On the Seismic Evaluation of Steel Frames Laterally Braced with Perforated Steel Plate Shear Walls Considering Semi-Rigid Connections. Buildings 2022, 12, 1427. [Google Scholar] [CrossRef]
- Fan, J.; Wu, Z.F.; Liu, J.H.; Wang, Y.X.; Zheng, H.D.; Tee, K.F. Damage and failure of semi-rigid steel joints during progressive collapse. Structures 2023, 58, 105632. [Google Scholar] [CrossRef]
- Abdalla, K.M.; Drosopoulos, G.A.; Stavroulakis, G.E. Failure Behavior of a Top and Seat Angle Bolted Steel Connection with Double Web Angles. J. Struct. Eng. 2015, 141, 04014172. [Google Scholar] [CrossRef]
- Monaco, A. Numerical prediction of the shear response of semi-prefabricated steel-concrete trussed beams. Constr. Build. Mater. 2016, 124, 462–474. [Google Scholar] [CrossRef]
- Guo, H.C.; Liang, G.; Li, Y.L.; Liu, Y.H. Q690 high strength steel T-stub tensile behavior: Experimental research and theoretical analysis. J. Constr. Steel Res. 2017, 139, 473–483. [Google Scholar] [CrossRef]
- Morrison, M.L.; Schweizer, D.Q.; Quayyum, S.; Hassan, T. An Unstiffened Eight-Bolt Extended End-Plate Moment Connection for Special and Intermediate Moment Frames. J. Struct. Eng. 2019, 145, 04019055. [Google Scholar] [CrossRef]
- Monaco, A.; Colajanni, P.; La Mendola, L. The structural behaviour of hybrid steel-trussed concrete beams: A literature review of experimental tests and theoretical models. Structures 2025, 71, 108018. [Google Scholar] [CrossRef]
- Popov, E.P.; Takhirov, S.M. Bolted large seismic steel beam-to-column connections Part 1: Experimental study. Eng. Struct. 2002, 24, 1523–1534. [Google Scholar] [CrossRef]
- Takhirov, S.M.; Popov, E.P. Bolted large seismic steel beam-to-column connections Part 2: Numerical nonlinear analysis. Eng. Struct. 2002, 24, 1535–1545. [Google Scholar] [CrossRef]
- Latour, M.; Rizzano, G. Experimental Behavior and Mechanical Modeling of Dissipative T-Stub Connections. J. Struct. Eng. 2012, 138, 170–182. [Google Scholar] [CrossRef]
- Latour, M.; Piluso, V.; Rizzano, G. Experimental behaviour of friction T-stub beam-to-column joints under cyclic loads. Steel Constr. 2013, 6, 11–18. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Zhang, J.F.; Jiang, J.Q. A multi-spring component modelling approach for T-stub connections. Adv. Struct. Eng. 2016, 19, 883–896. [Google Scholar] [CrossRef]
- D’Aniello, M.; Cassiano, D.; Landolfo, R. Monotonic and cyclic inelastic tensile response of European preloadable gr10.9 bolt assemblies. J. Constr. Steel Res. 2016, 124, 77–90. [Google Scholar] [CrossRef]
- Tartaglia, R.; D’Aniello, M.; Zimbru, M. Experimental and numerical study on the T-Stub behaviour with preloaded bolts under large deformations. Structures 2020, 27, 2137–2155. [Google Scholar] [CrossRef]
- Liu, X.C.; Zhu, Y.N.; Chen, X.S.; Li, Y.M. Seismic performance of bolted double-web T-stub connections with T-shaped steel column. J. Constr. Steel Res. 2022, 191, 107168. [Google Scholar] [CrossRef]
- Bayat, K.; Shekastehband, B. Seismic performance of beam to column connections with T-shaped slit dampers. Thin-Walled Struct. 2019, 141, 28–46. [Google Scholar] [CrossRef]
- Meng, B.; You, K.; Yang, B.; Kong, D.Y.; Wen, J.L. Anti-progressive collapse performance and design method of novel T-stub connections. Eng. Struct. 2024, 319, 118880. [Google Scholar] [CrossRef]
- Hou, G.L.; Shang, Y.T.; Zhang, L.; Sun, L.L.; Wu, J.Y.; Lu, Y.Y.; Zhu, A.B.; Mou, Y.H. Bending performance of bolted beam-column joints with T-stubs. J. Constr. Steel Res. 2025, 226, 109280. [Google Scholar] [CrossRef]
- Oh, K.; Lee, K.; Chen, L.; Hong, S.B.; Yang, Y. Seismic performance evaluation of weak axis column-tree moment connections with reduced beam section. J. Constr. Steel Res. 2015, 105, 28–38. [Google Scholar] [CrossRef]
- Xu, Y.L.; Hao, J.P. Seismic performance of spatial beam-column connections in steel frame. J. Constr. Steel Res. 2021, 180, 106586. [Google Scholar] [CrossRef]
- Shi, G.; Jiang, S.; Zhang, N.Z.; Hou, L.T.; Zhao, H.T. Seismic performance of double-sided plate-reinforced connections between steel beams and built-up box columns. Thin-Walled Struct. 2025, 208, 112872. [Google Scholar] [CrossRef]
- Saberi, V.; Gerami, M.; Kheyroddin, A. Comparison of bolted end plate and T-stub connection sensitivity to component thickness. J. Constr. Steel Res. 2014, 98, 134–145. [Google Scholar] [CrossRef]
- Wang, P.; Pan, J.R.; Wang, Z.; Chen, S.Z. Experimental and analytical behavior of stiffened angle joints. Steel Compos. Struct. 2018, 26, 67–78. [Google Scholar]
- GB 50017-2017; Standard for Design of Steel Structures. China Architecture & Building Press: Beijing, China, 2017. (In Chinese)
- GB 50011-2010; Code for Seismic Design of Buildings. China Architecture & Building Press: Beijing, China, 2010. (In Chinese)
- Shi, Q.; Yan, S.L.; Kong, L.L.; Bu, X.; Wang, X.W.; Sun, H.S. Seismic behavior of semi-rigid steel joints—Major axis T-stub and minor axis end-plate. J. Constr. Steel Res. 2019, 159, 476–492. [Google Scholar] [CrossRef]
- Lu, S.C.; Wang, Z.; Pan, J.R.; Wang, P. The Seismic Performance Analysis of Semi-rigid Spatial Steel Frames Based on Moment-Rotation Curves of End-plate Connection. Structures 2022, 36, 1032–1049. [Google Scholar] [CrossRef]
- GB/T228.1-2021; Metallic Materials-Tensile Testing-Part 1: Method of Test at Room Temperature. China Standards Press: Beijing, China, 2021. (In Chinese)
- FEMA-461; Interim Testing Protocols for Determining the Seismic Performance Characteristics of Structural and Nonstructural Components. Applied Technology Council: Redwood City, CA, USA, 2007.
- Xiao, S.X.; Bu, X.; Shen, B.; Fan, L.D.; Chen, Y.F.; Wang, X.W. Seismic performance and damage characteristics evolution of spatial beam to corner column connection with T-stubs. J. Build. Eng. 2025, 111, 113186. [Google Scholar] [CrossRef]
- Darwin, D.; Nmai, C.K. Energy dissipation in RC beams under cyclic load. J. Struct. Eng. 1986, 112, 1829–1846. [Google Scholar] [CrossRef]
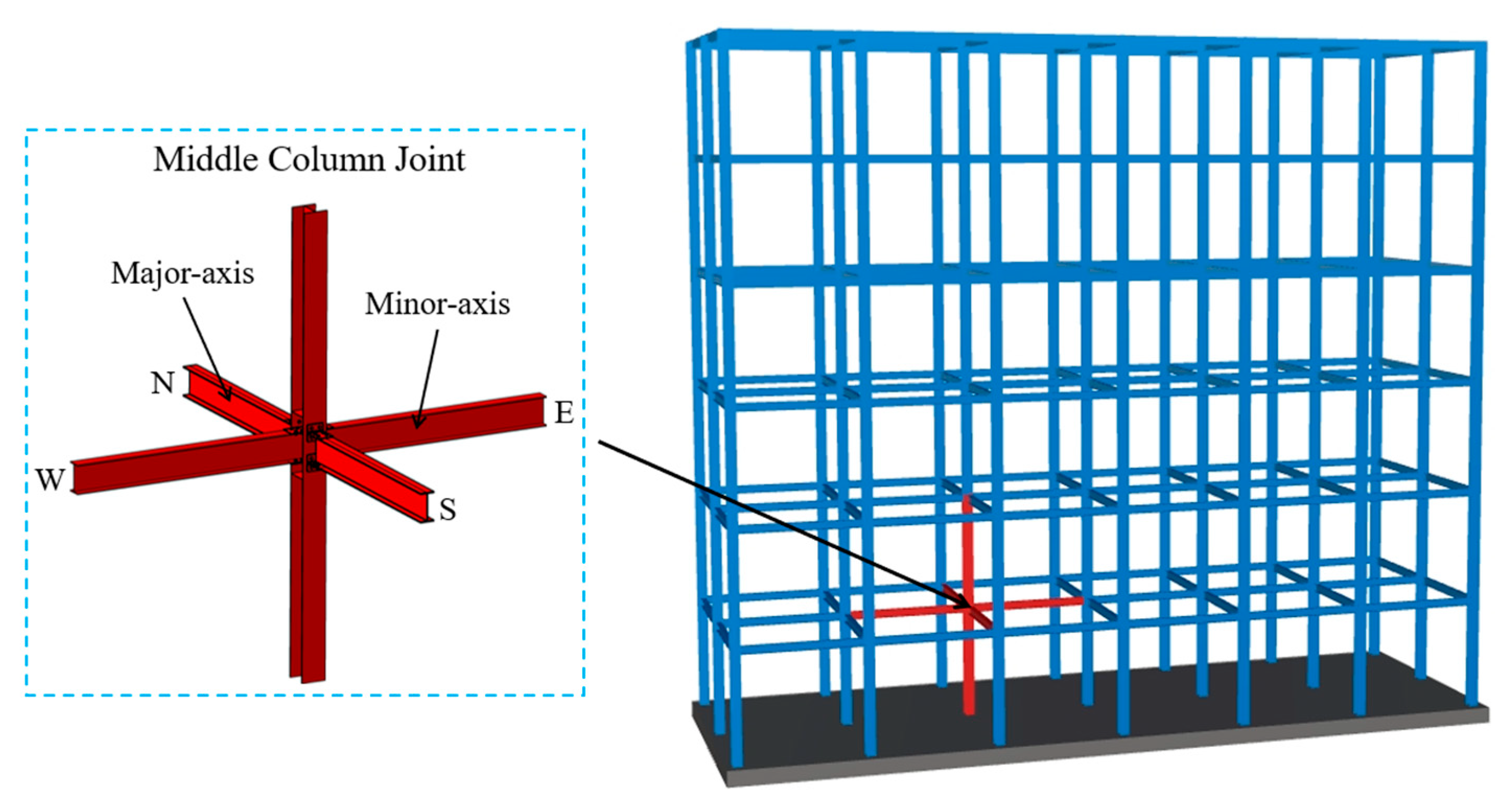
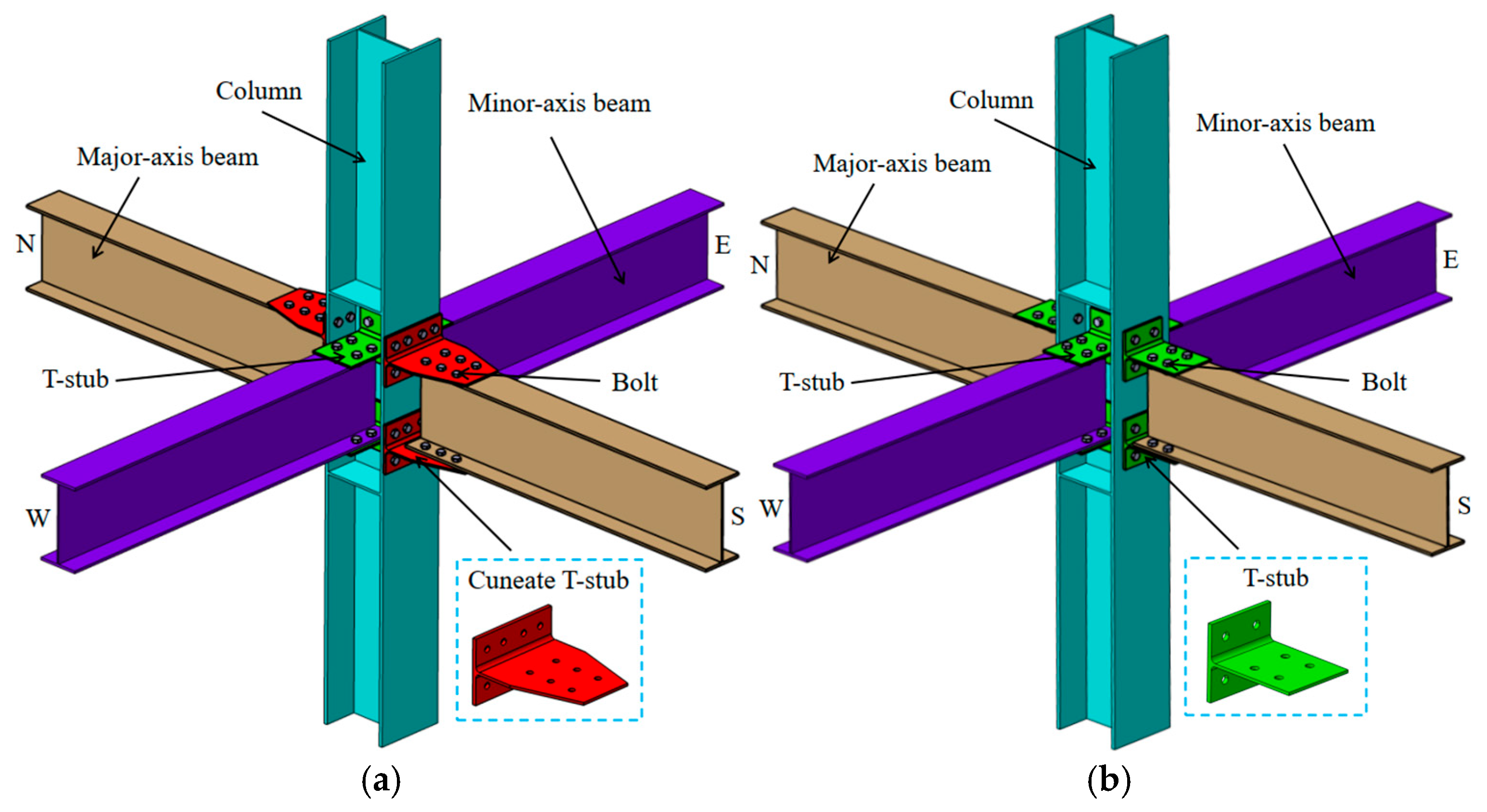
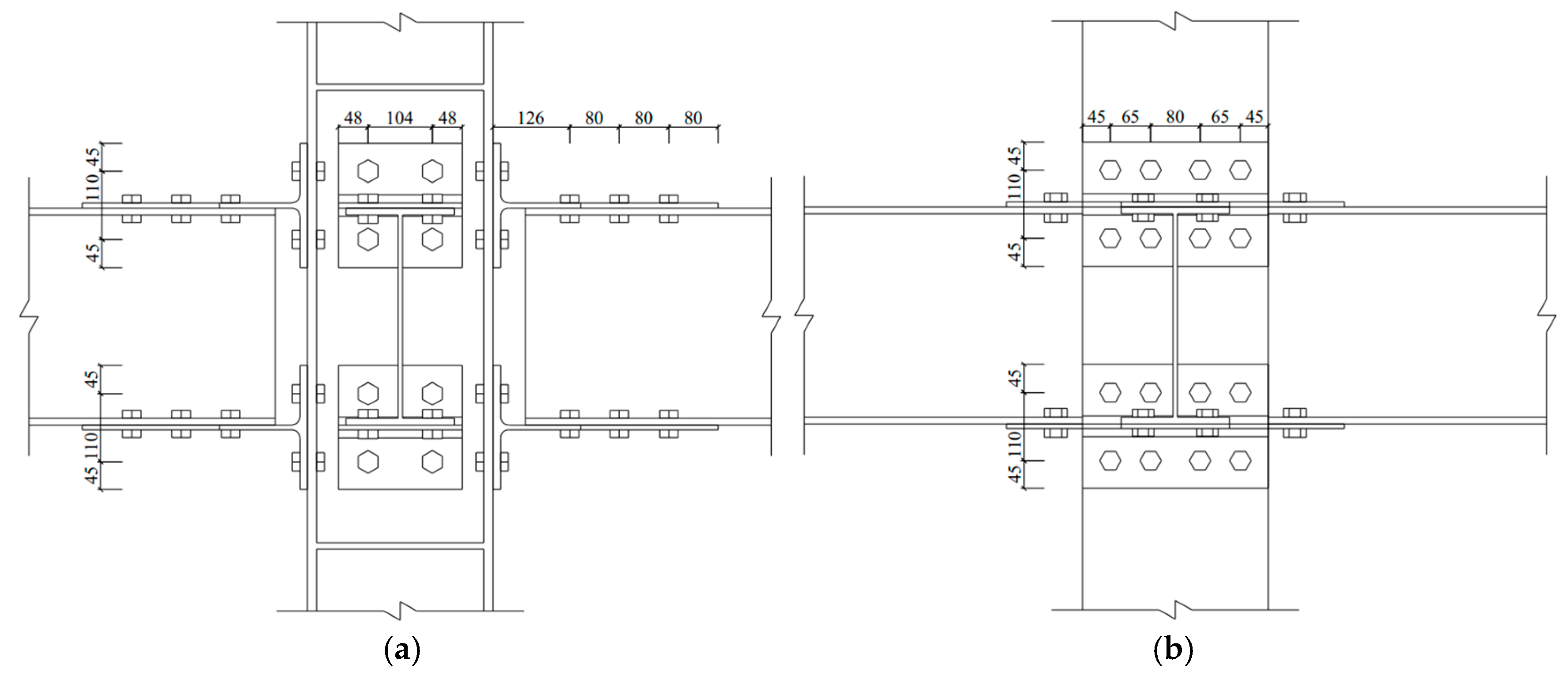

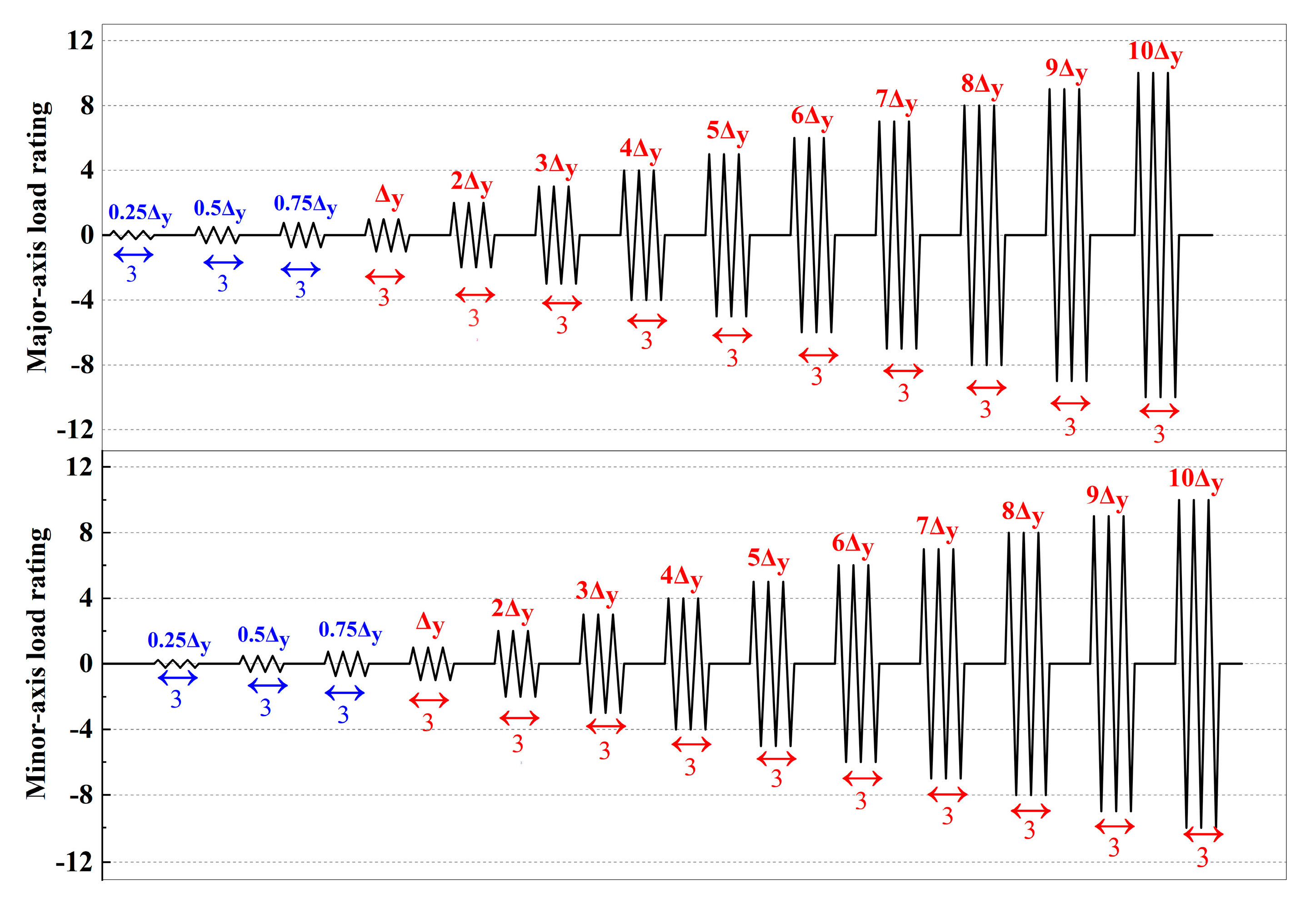






| Specimens Number | The Specimens Used for Dividing T-stubs/mm | Bolts Type | Bolts Quantity | |||
|---|---|---|---|---|---|---|
| Major | Minor | Major | Minor | Major | Minor | |
| TN1 | H270 × 200 × 8 × 12 | H270 × 200 × 8 ×12 | M22 | M22 | 32 | 24 |
| TN2 | H450 × 200 × 8 × 12 | H270 × 200 × 8 × 12 | M20 | M22 | 56 | 24 |
| TN3 | H450 × 200 × 9 × 14 | H270 × 200 × 9 × 14 | M20 | M22 | 56 | 24 |
| Specimen | fy/MPa | fu/MPa | E/GPa | A/% | δ/% | fy/fu |
|---|---|---|---|---|---|---|
| Column flange | 271 | 430 | 209 | 36 | 31 | 0.63 |
| Column web | 274 | 436 | 202 | 40 | 35 | 0.63 |
| Beam flange | 256 | 445 | 203 | 40 | 32 | 0.58 |
| Beam web | 249 | 438 | 201 | 43 | 36 | 0.57 |
| T-stub flange | 286 | 481 | 189 | 35.5 | 33 | 0.59 |
| T-stub web | 290 | 490 | 201 | 36.5 | 35 | 0.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Bu, X.; Shen, B.; Yin, X.; Wang, X.; Huang, Q.; Zhang, Z. Seismic Performance Testing and Damage Analysis of Reinforced T-Stub Connections. Buildings 2025, 15, 4112. https://doi.org/10.3390/buildings15224112
Chen Y, Bu X, Shen B, Yin X, Wang X, Huang Q, Zhang Z. Seismic Performance Testing and Damage Analysis of Reinforced T-Stub Connections. Buildings. 2025; 15(22):4112. https://doi.org/10.3390/buildings15224112
Chicago/Turabian StyleChen, Yifei, Xin Bu, Bing Shen, Xufeng Yin, Xinwu Wang, Qiang Huang, and Zhiwei Zhang. 2025. "Seismic Performance Testing and Damage Analysis of Reinforced T-Stub Connections" Buildings 15, no. 22: 4112. https://doi.org/10.3390/buildings15224112
APA StyleChen, Y., Bu, X., Shen, B., Yin, X., Wang, X., Huang, Q., & Zhang, Z. (2025). Seismic Performance Testing and Damage Analysis of Reinforced T-Stub Connections. Buildings, 15(22), 4112. https://doi.org/10.3390/buildings15224112






