Experimental Test and Finite Element Analysis on a Concrete Box Girder of a Cable-Stayed Bridge with W-Shaped Prestressed Concrete Diagonal Braces
Abstract
1. Introduction
2. Experimental Research
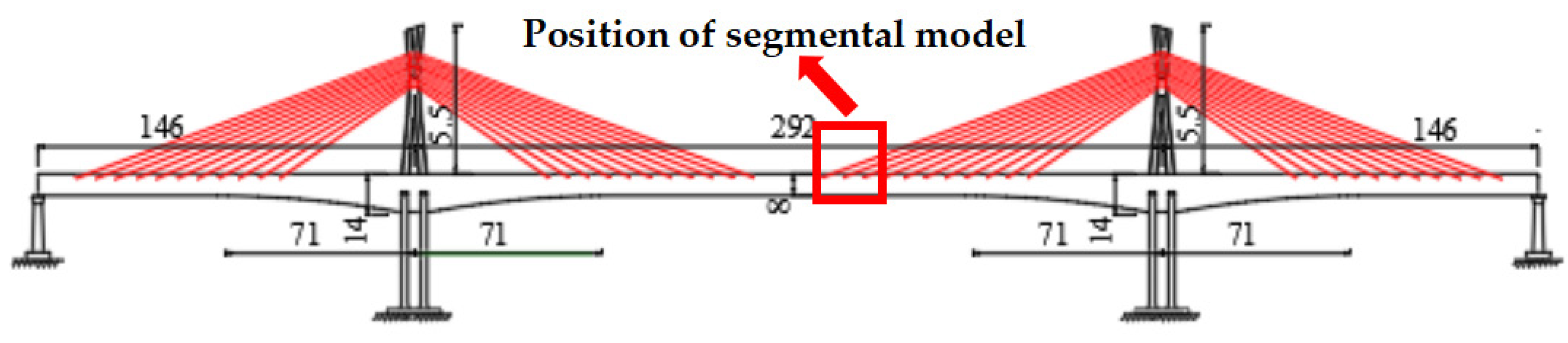
2.1. Project Overview
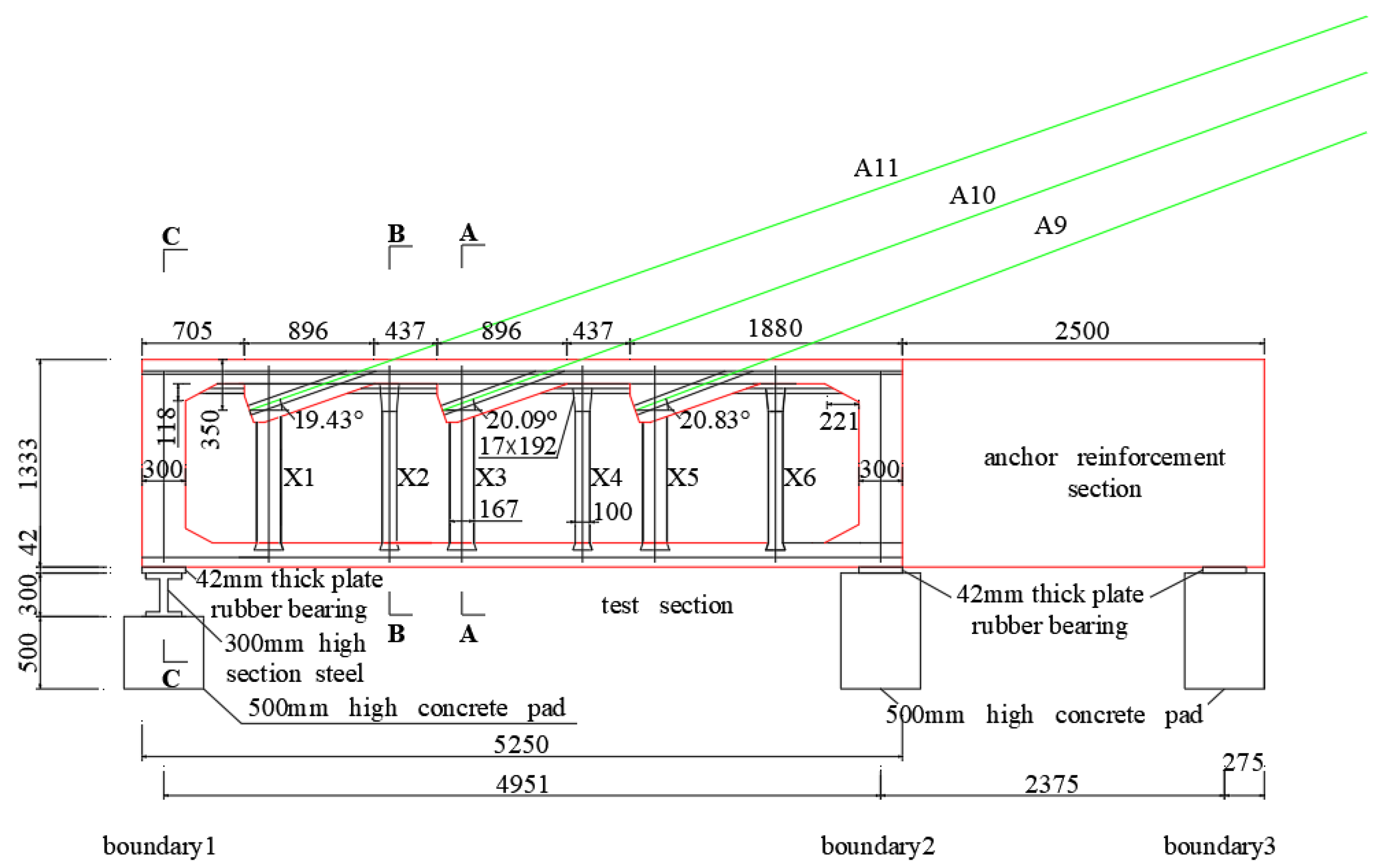
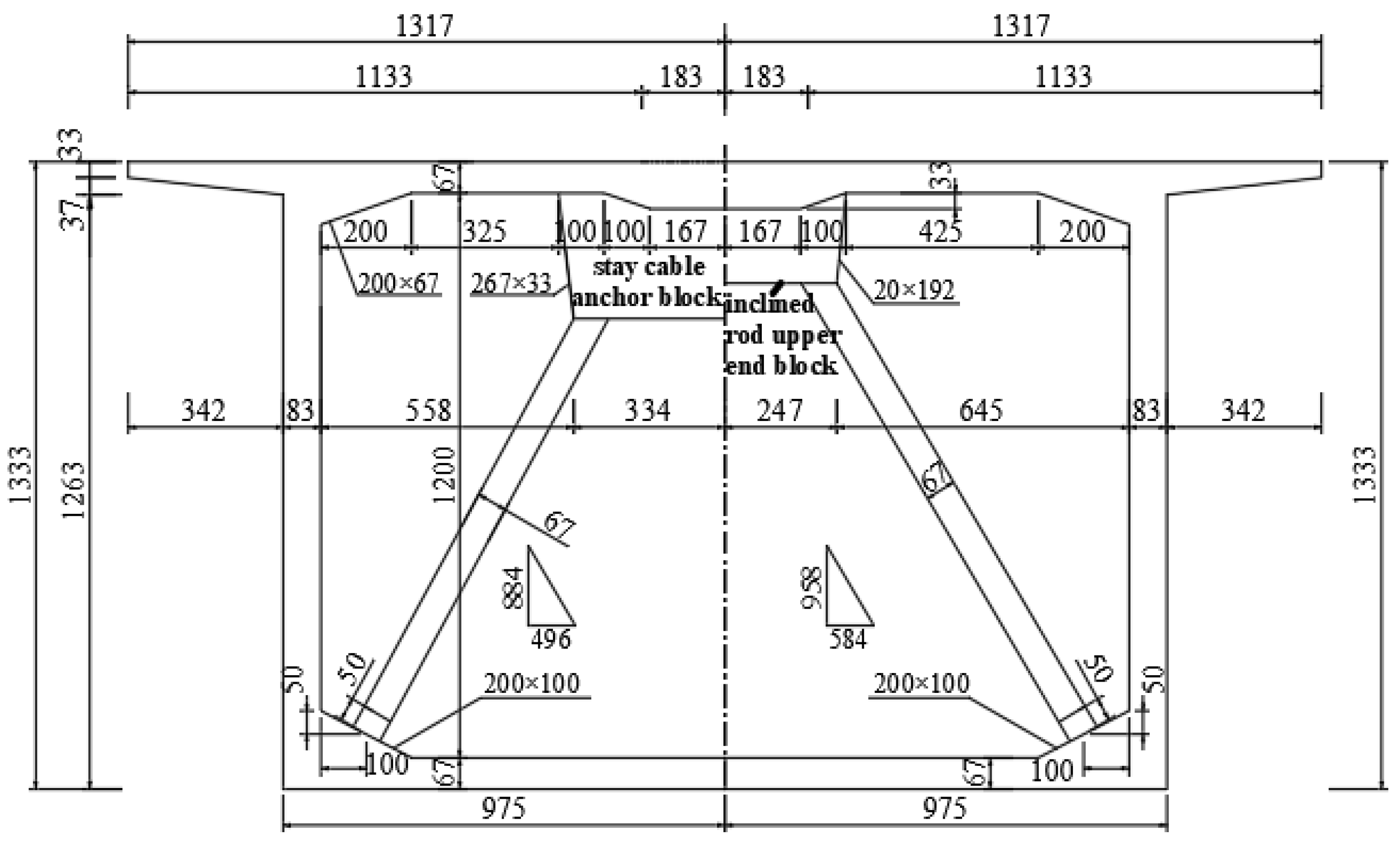
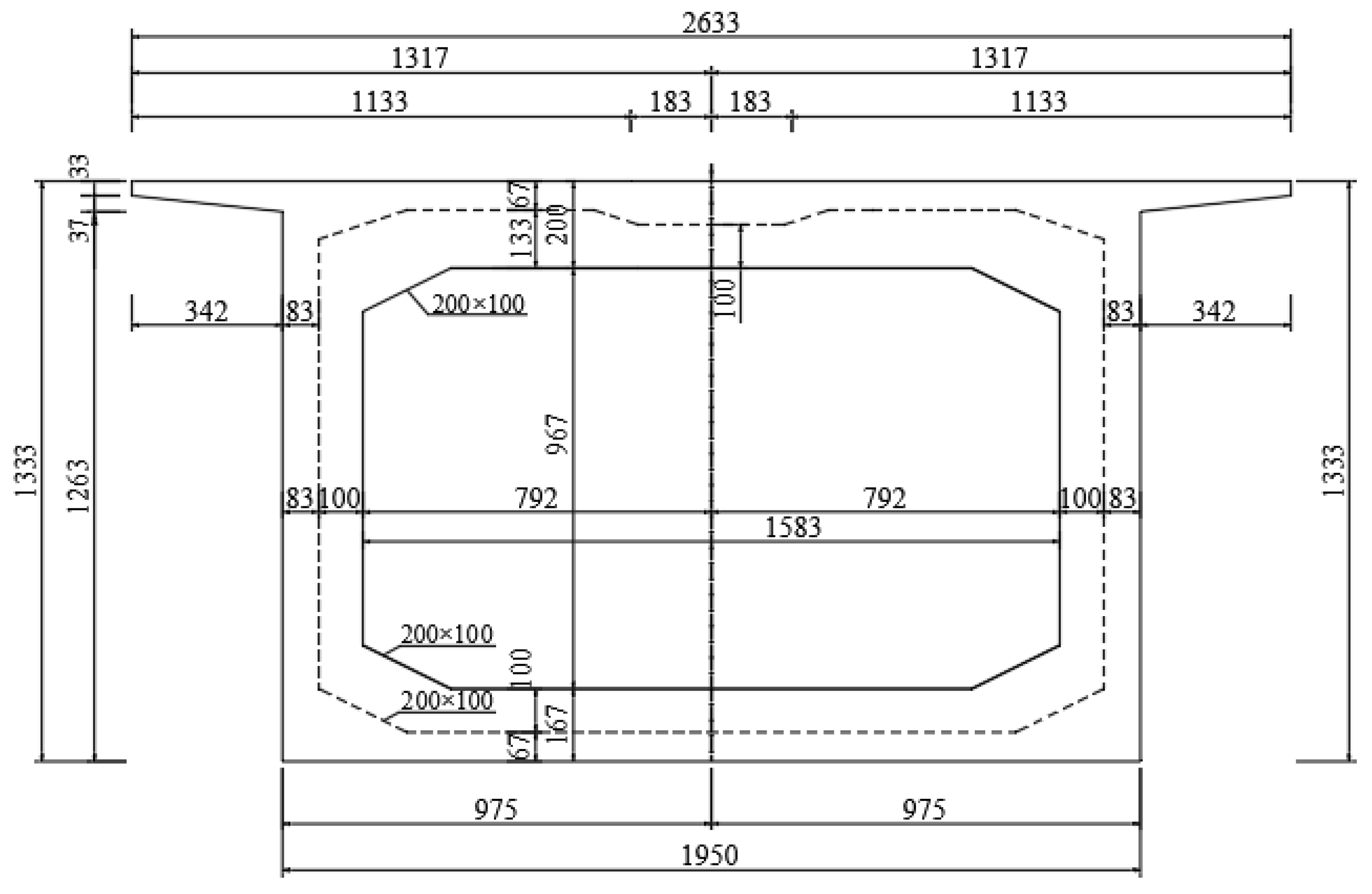
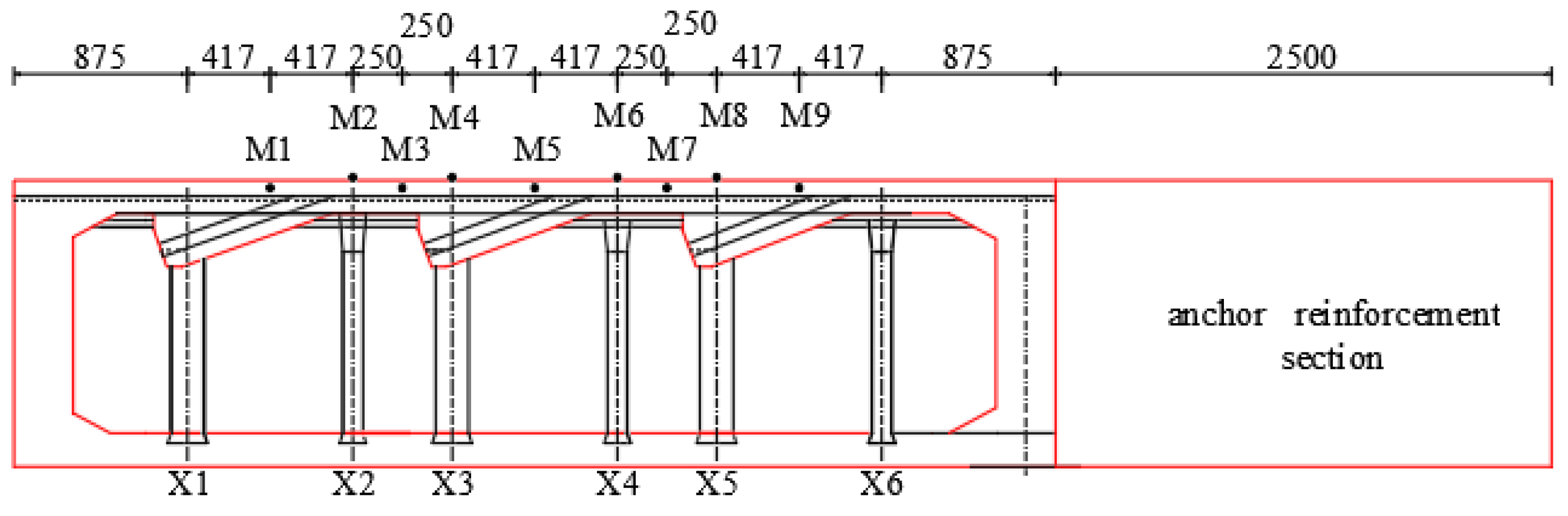
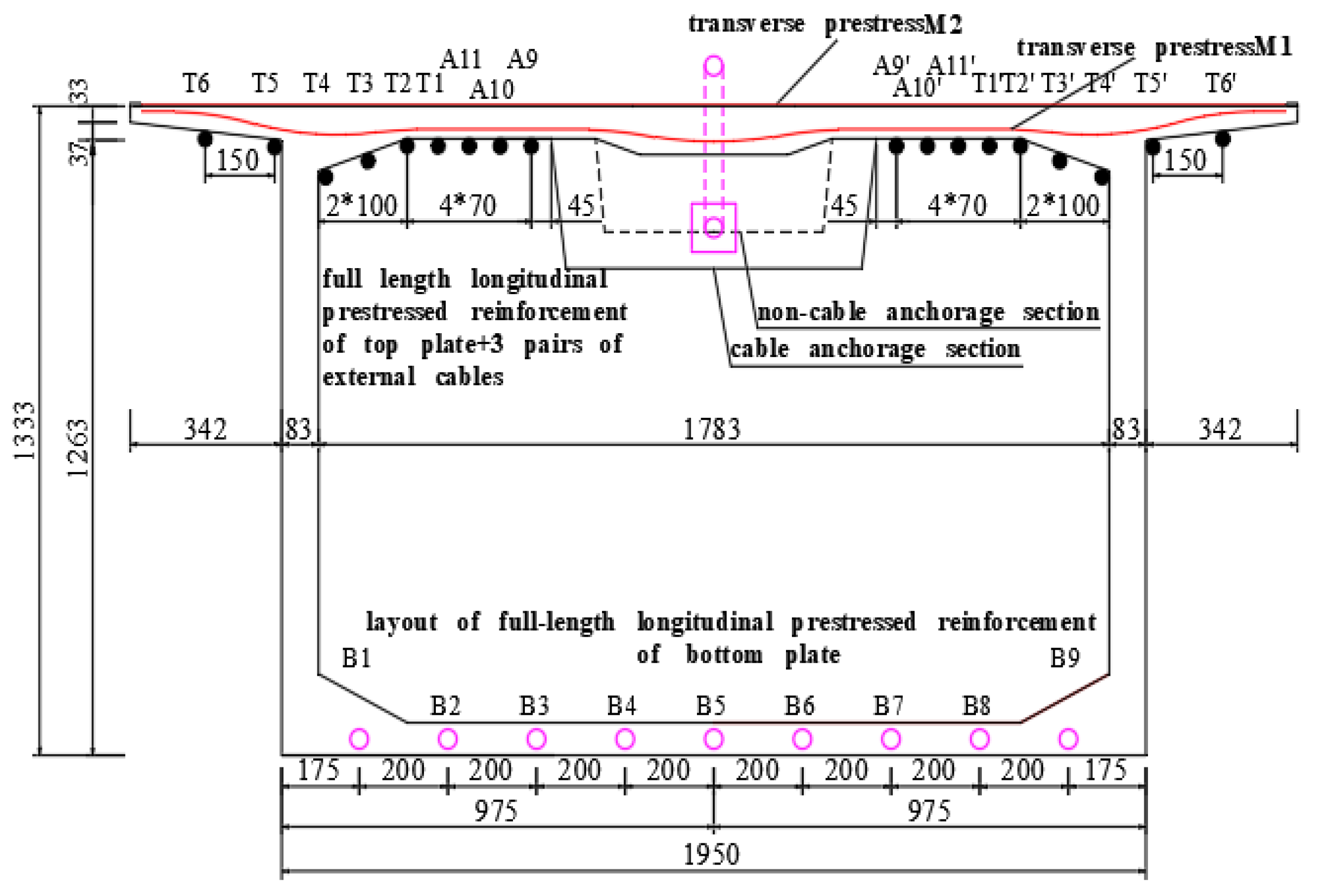
2.2. Test Model
2.3. Test Program
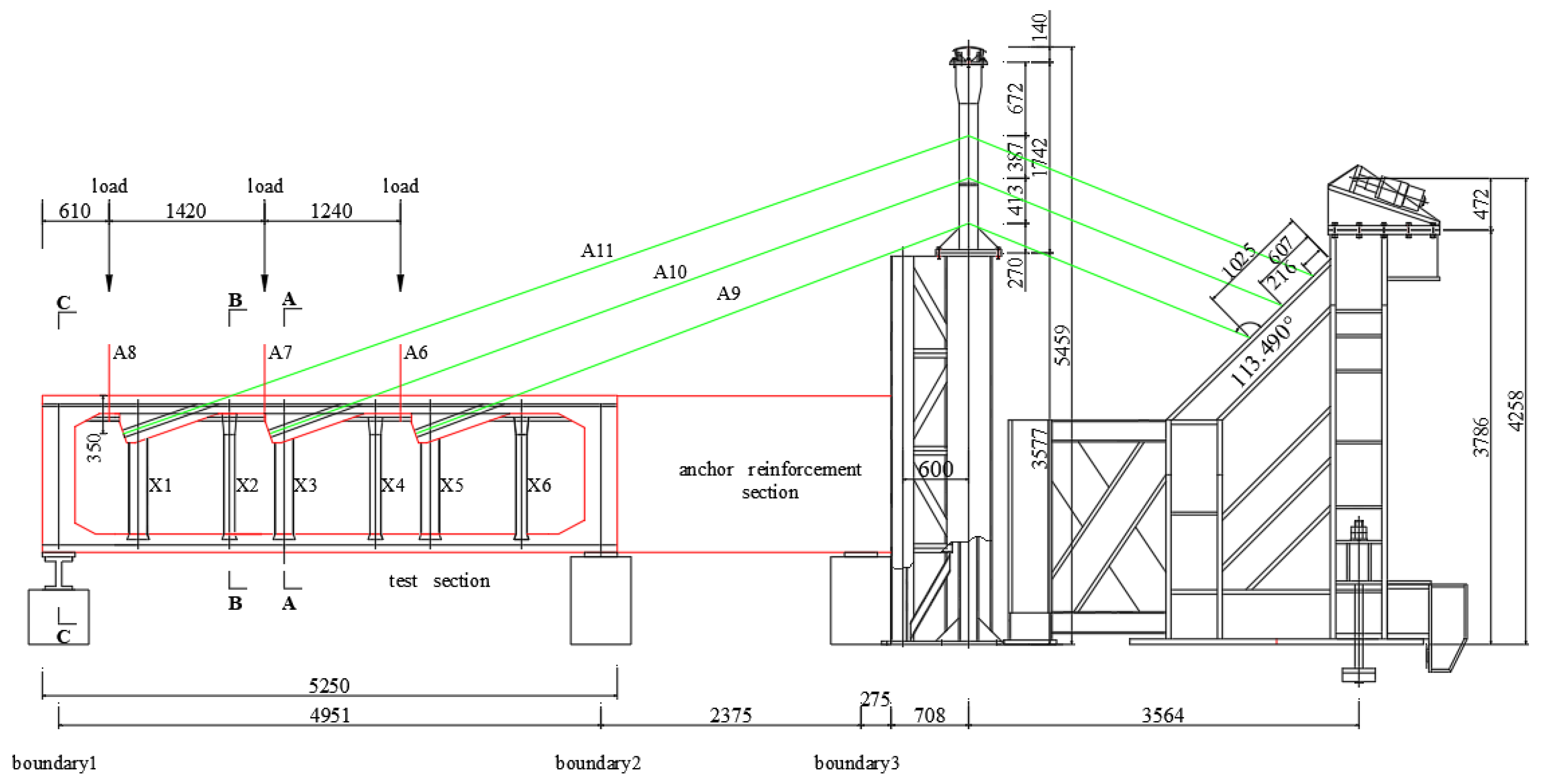
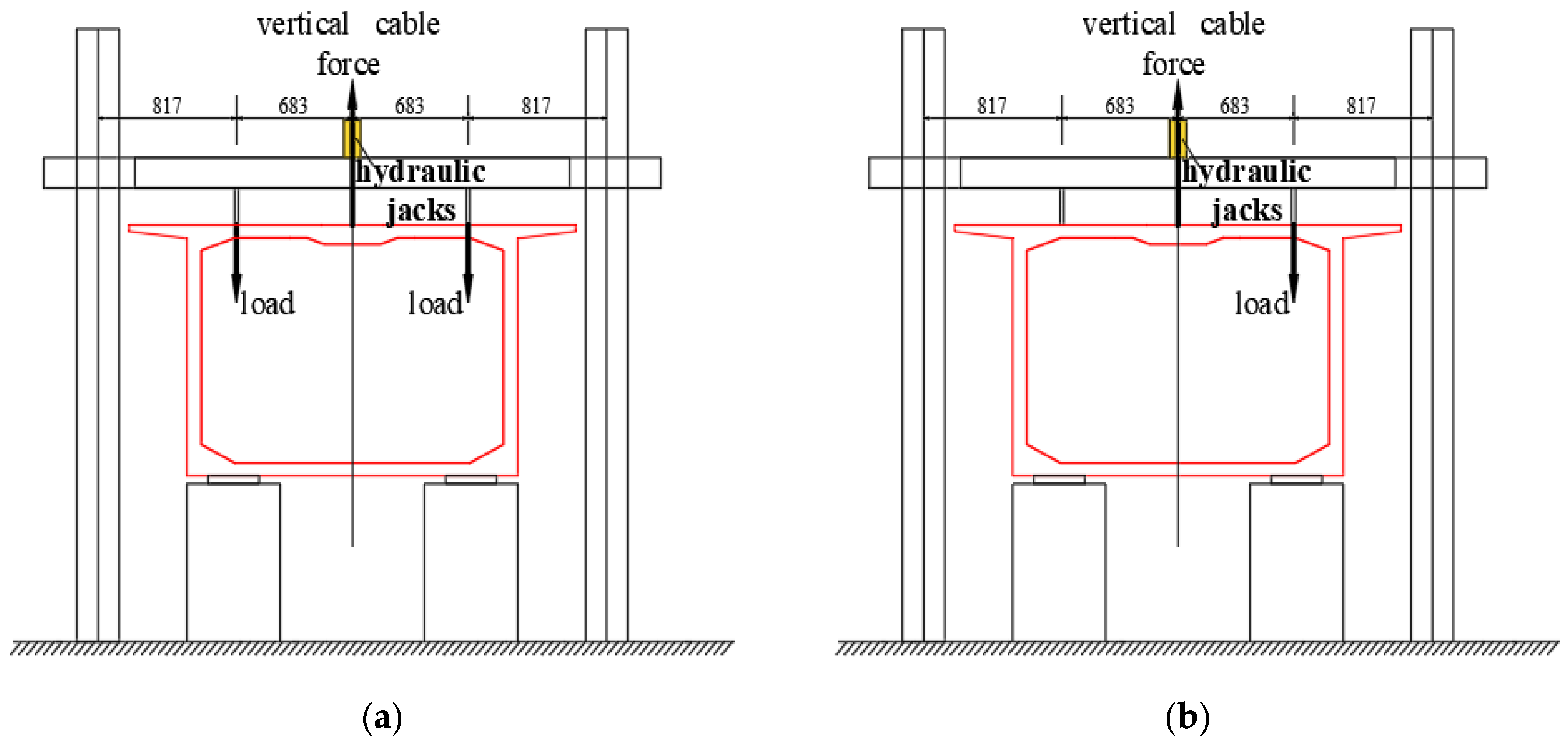
2.3.1. Test Setup
2.3.2. Loading Protocol
2.3.3. Instrument Layout
3. Test Results and Discussions
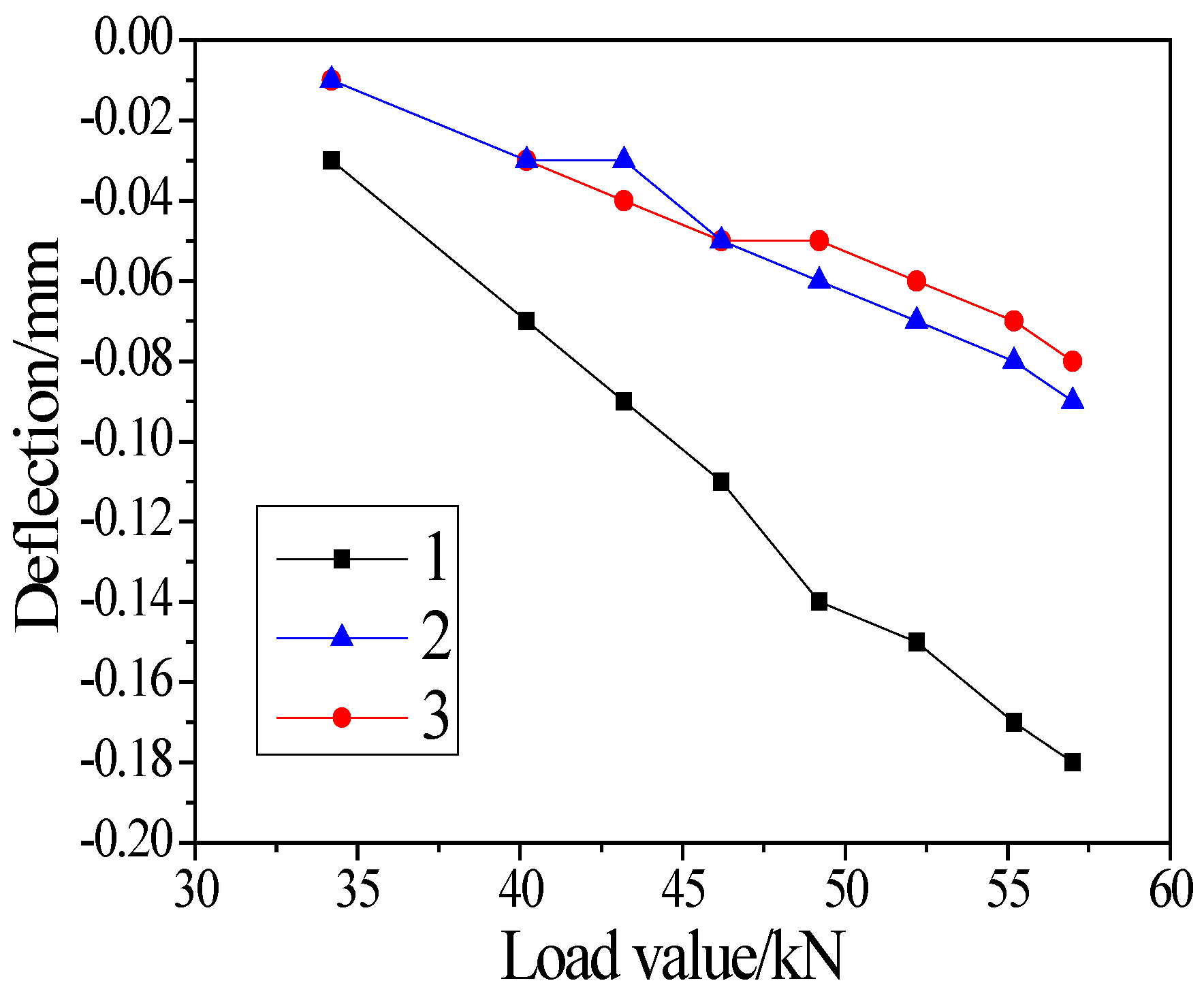
3.1. Deflection of the Girder
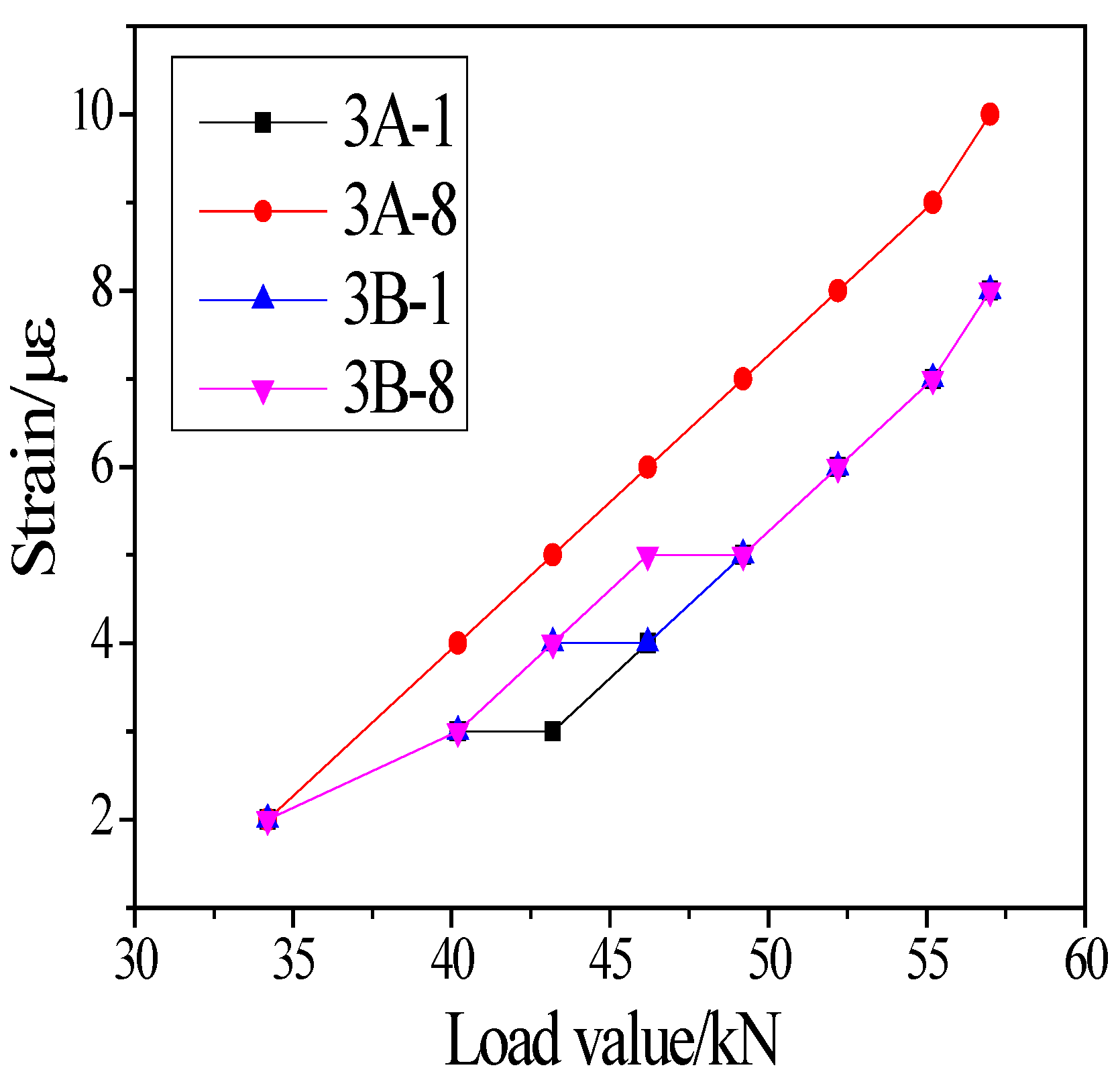
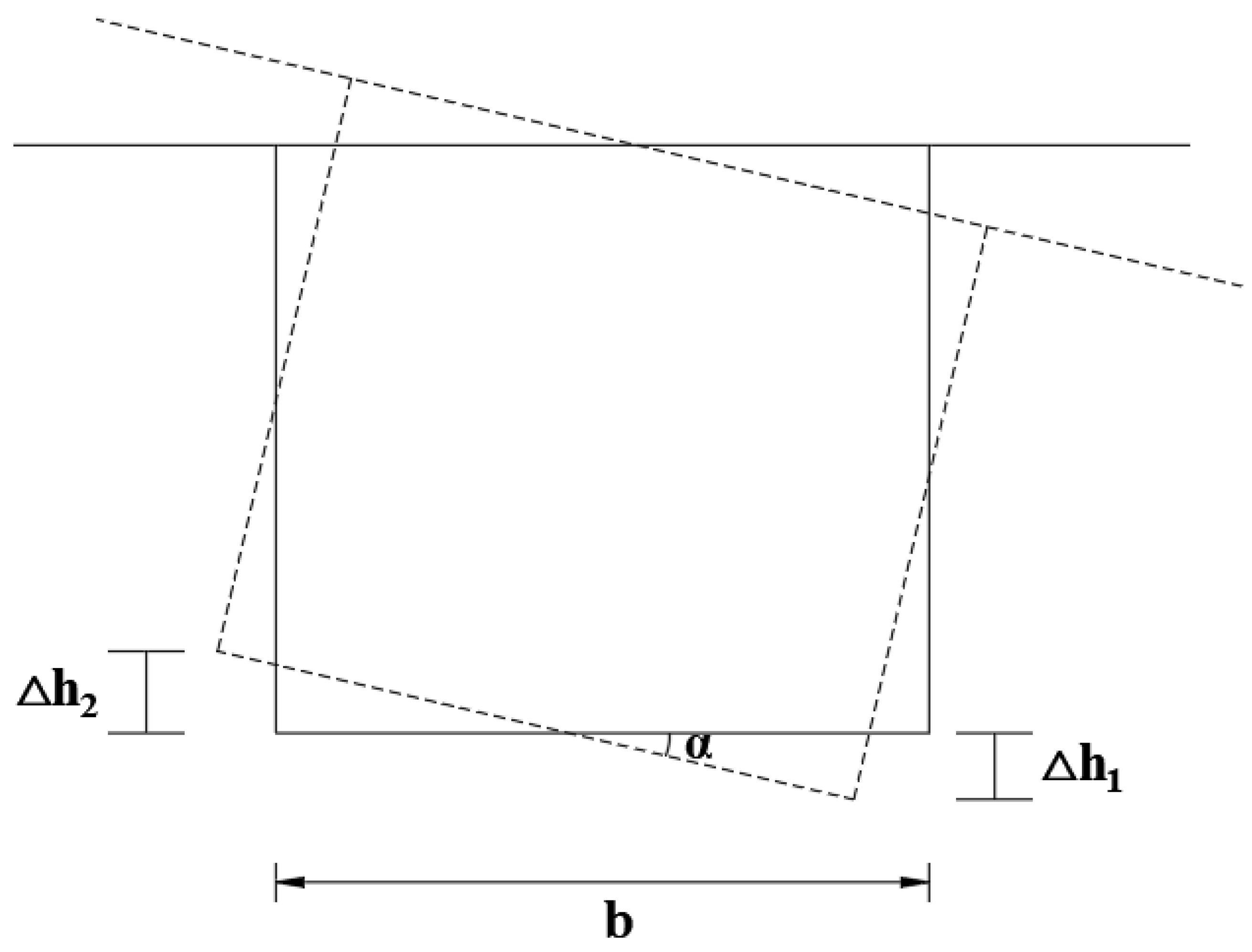
3.2. Strain Results
4. Finite Element Analysis
4.1. Numerical Model
4.2. Analysis Results
4.2.1. Comparison between Modelling and Test Results of the Deflection
4.2.2. Comparison of the Strains
4.3. Torsional Performance of the W-Shaped Web Box Girder
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lenglet, C. Brotonne Bridge Longest Prestressed Concrete Cable Stayed Bridge. In Cable-Stayed Bridges, Structural Engineering Series; Bridge Division, Office of Engineering, Federal Highway Administration: Washington, DC, USA, 1978. [Google Scholar]
- Svensson, H.S.; Christopher, B.G.; Saul, R. Design of a cable-stayed steel composite bridge. J. Struct. Eng. 1986, 112, 489–504. [Google Scholar] [CrossRef]
- Hao, Q.; Jufeng, S.; Pingming, H. Study on dynamic characteristics and seismic response of the extradosed cable-stayed bridge with single pylon and single cable plane. J. Civ. Struct. Health Monit. 2017, 7, 589–599. [Google Scholar] [CrossRef]
- Huang, W.; Pei, M.; Liu, X.; Wei, Y. Engineering, C. Design and construction of super-long span bridges in China: Review and future perspectives. Front. Struct. Civ. Eng. 2020, 14, 803–838. [Google Scholar] [CrossRef]
- Soto, A.G.; Caldentey, A.P.; Peiretti, H.C.; Benítez, J.C. Experimental behaviour of steel-concrete composite box girders subject bending, shear and torsion. Eng. Struct. 2020, 206, 110169. [Google Scholar] [CrossRef]
- Arici, M.; Granata, M.F.; Longo, G. Symplectic analysis of thin-walled curved box girders with torsion, distortion and shear lag warping effects. Thin Wall. Struct. 2022, 175, 109244. [Google Scholar] [CrossRef]
- He, X.; Sheng, X.; Scanlon, A.; Linzell, D.; Yu, X. Skewed concrete box girder bridge static and dynamic testing and analysis. Eng. Struct. 2012, 39, 38–49. [Google Scholar] [CrossRef]
- Zhu, M.; Yan, Z.; Chen, L.; Lu, Z.; Chen, Y.F. Experimental study on composite mechanical properties of a double-deck prestressed concrete box girder. Adv. Struct. Eng. 2019, 22, 2545–2556. [Google Scholar] [CrossRef]
- Campo-Rumoroso, I.; Ramos-Gutiérrez, Ó.R.; Cambronero-Barrientos, F. Distortion analysis of horizontally curved trapezoidal box girder bridges. Eng. Struct. 2023, 282, 115798. [Google Scholar] [CrossRef]
- Kim, K.; Yoo, C.H. Ultimate strength interaction of bending and torsion of steel/concrete composite trapezoidal box girders in positive bending. Adv. Struct. Eng. 2006, 9, 707–718. [Google Scholar] [CrossRef]
- Chidolue, C.; Amadou, A.; Ezeagu, C. Torsional-distortional performance of multi-cell trapezoidal box girder with all inclined web members. Int. J. Eng. Res. 2015, 5, 45–51. [Google Scholar]
- Li, L.; Zhou, C.; Wang, L. Distortion analysis of non-prismatic composite box girders with corrugated steel webs. J. Constr. Steel Res. 2018, 147, 74–86. [Google Scholar] [CrossRef]
- Mo, Y.; Fan, Y.-L. Torsional design of hybrid concrete box girders. J. Bridge Eng. 2006, 11, 329–339. [Google Scholar] [CrossRef]
- National Railway Administration of the People’s Republic of China. Code for Design on Railway Bridge and Culvert; China Railway Publishing House: Beijing, China, 2017. [Google Scholar]
- Simulia, D.S. Abaqus 6.12 Documentation; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2012. [Google Scholar]
- Li, Q.; Hu, S.; Shi, L.; Su, Y. Analysis of Torsion Deformation Performance of Railway Simply Supported Box Girder. Railw. Eng. 2021, 61, 1–5. (In Chinese) [Google Scholar]



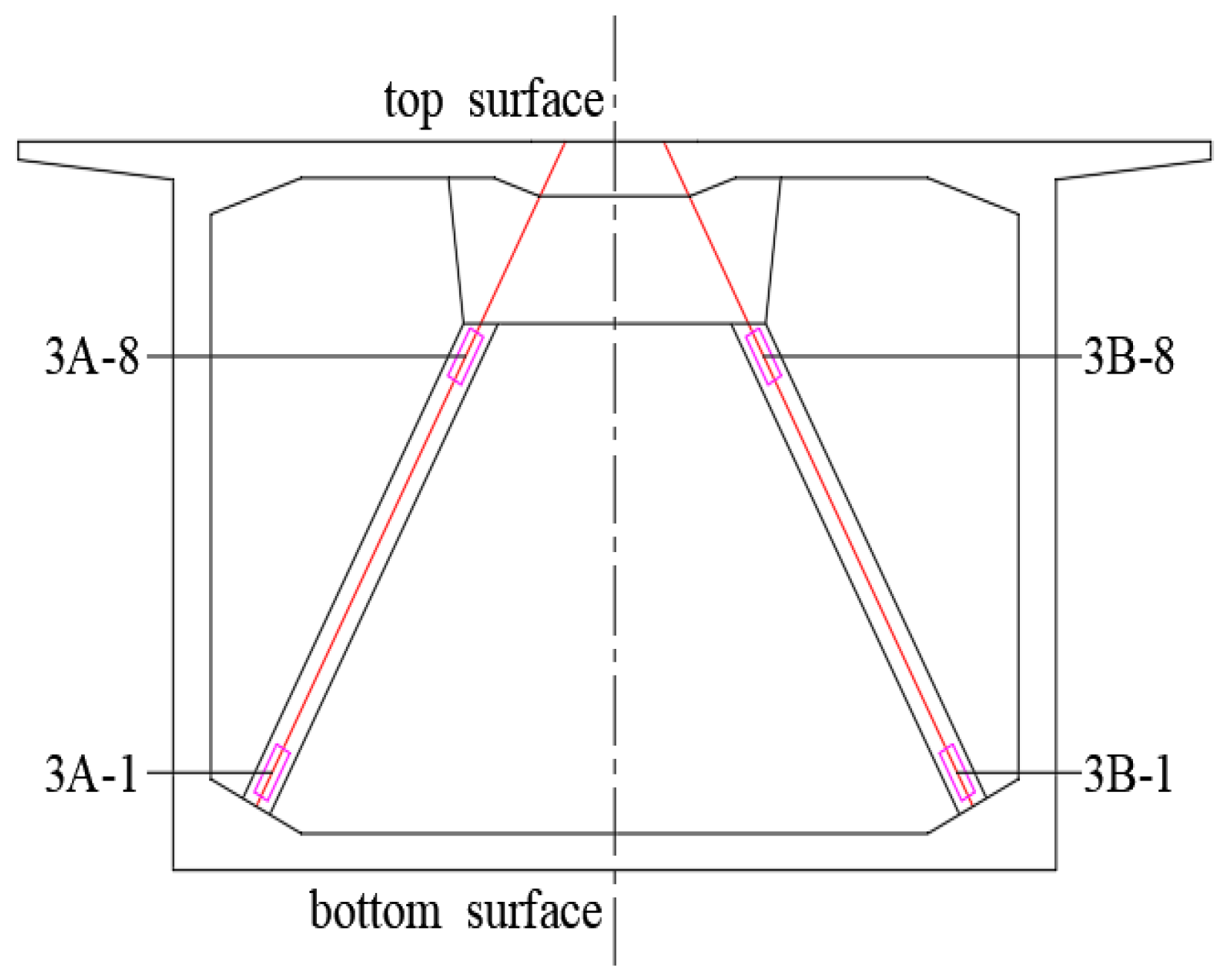

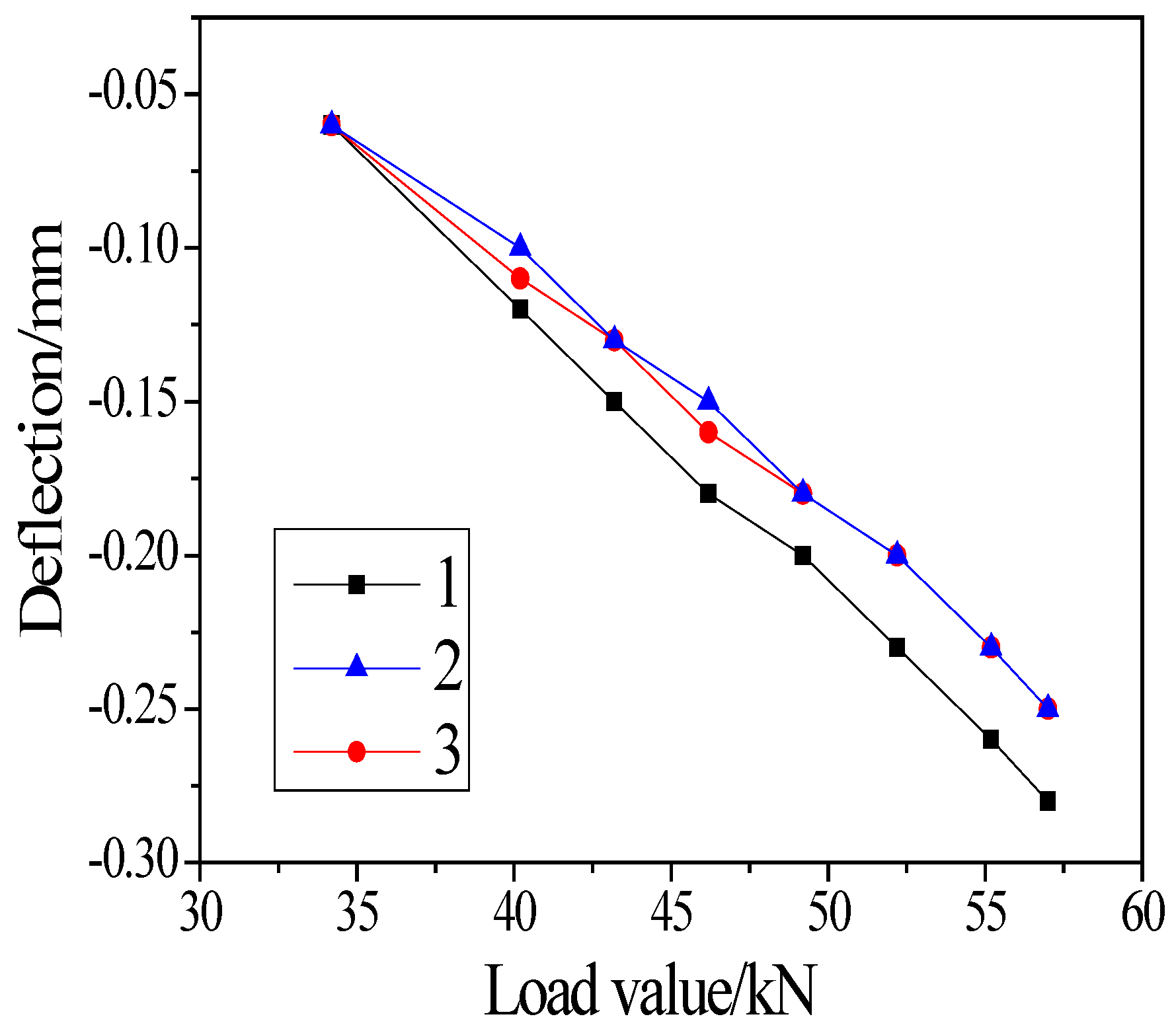


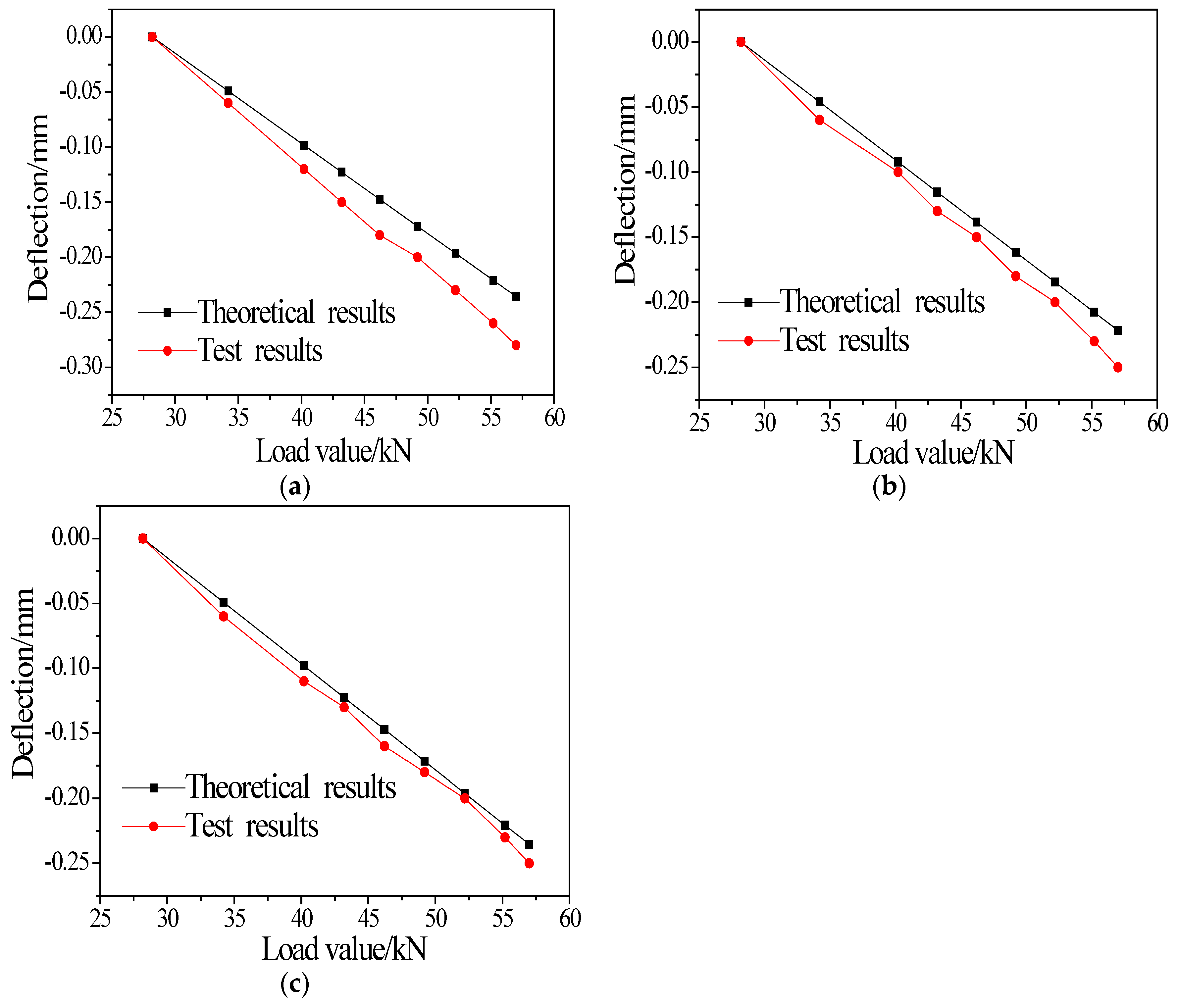
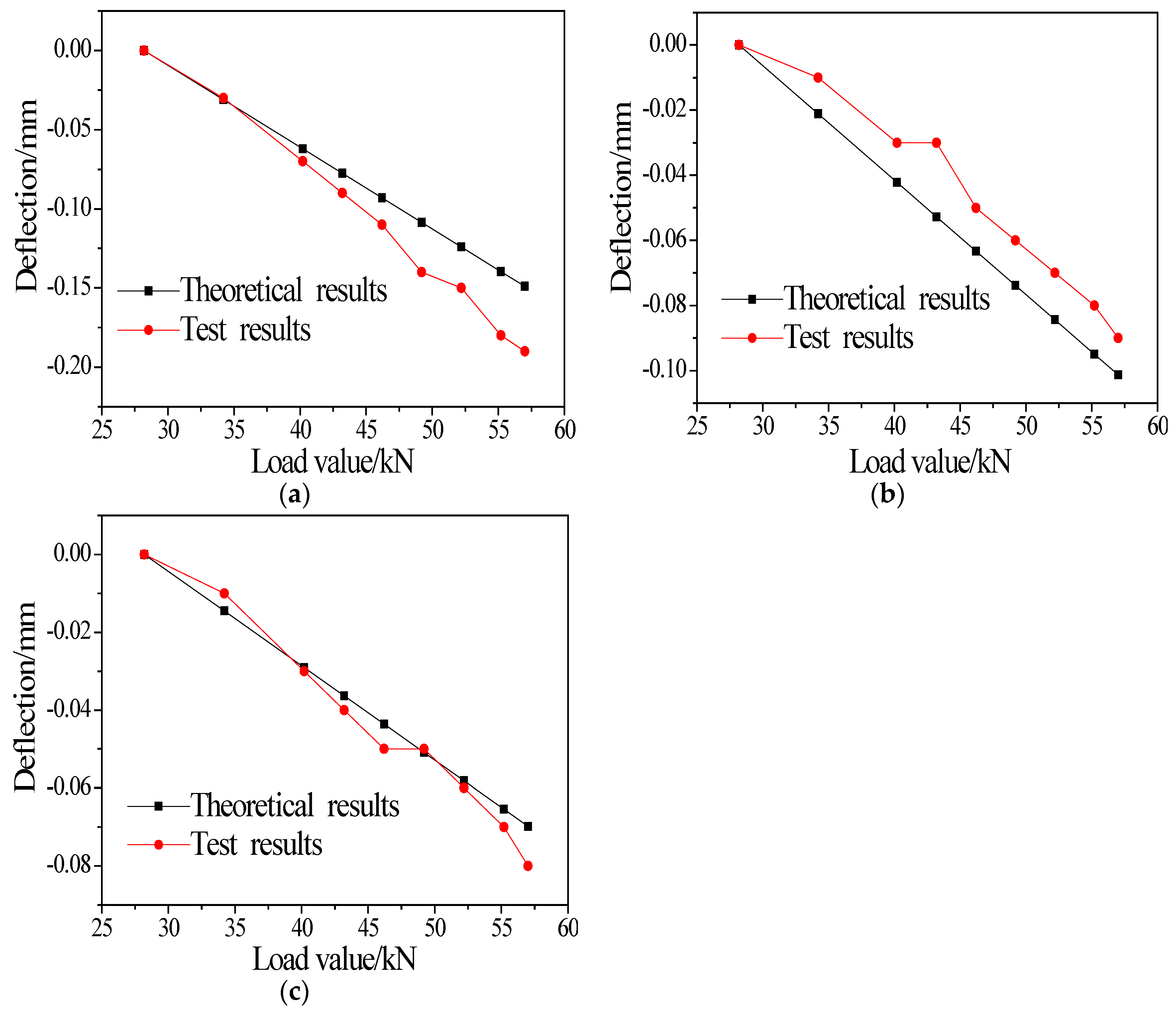
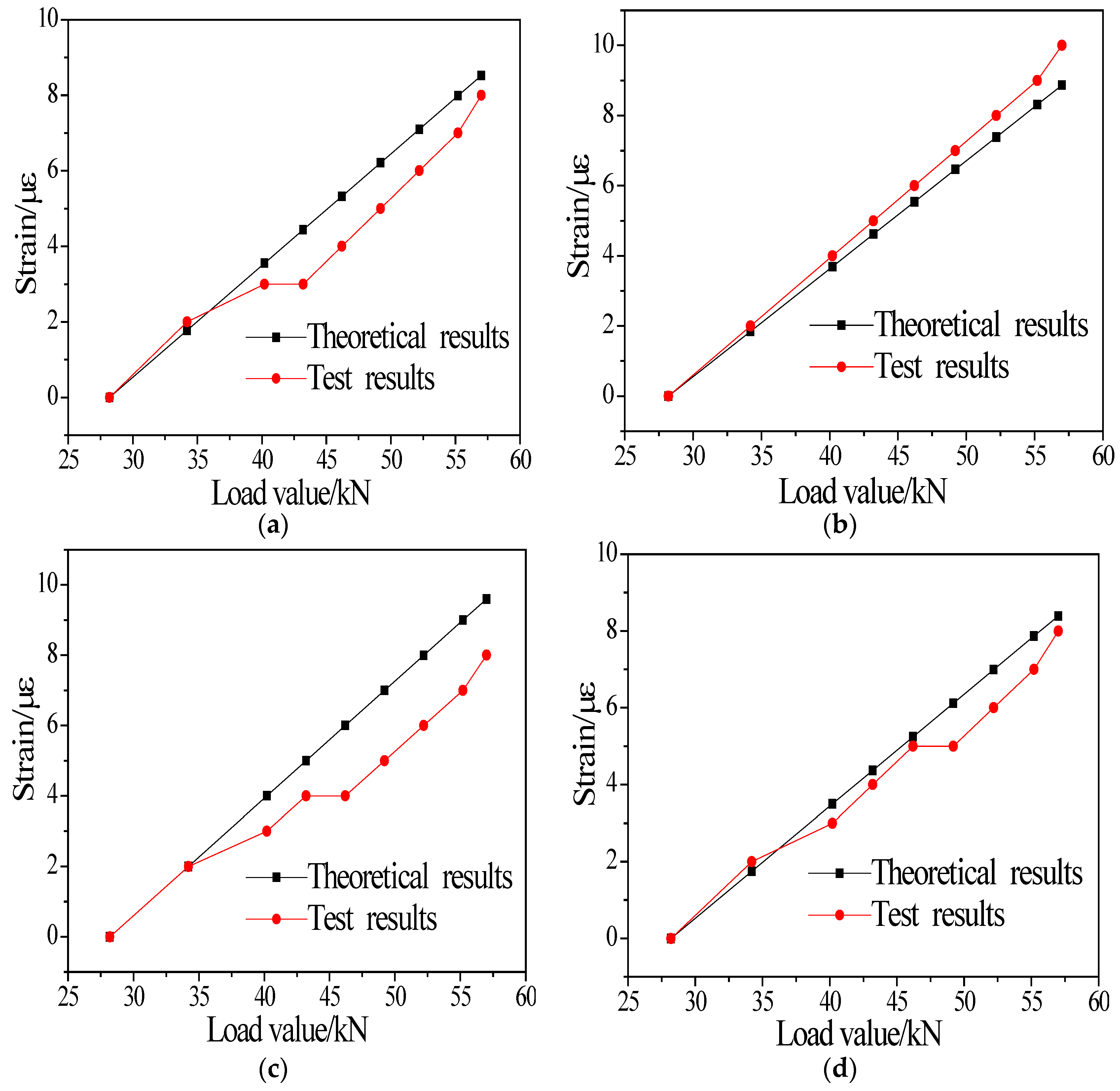
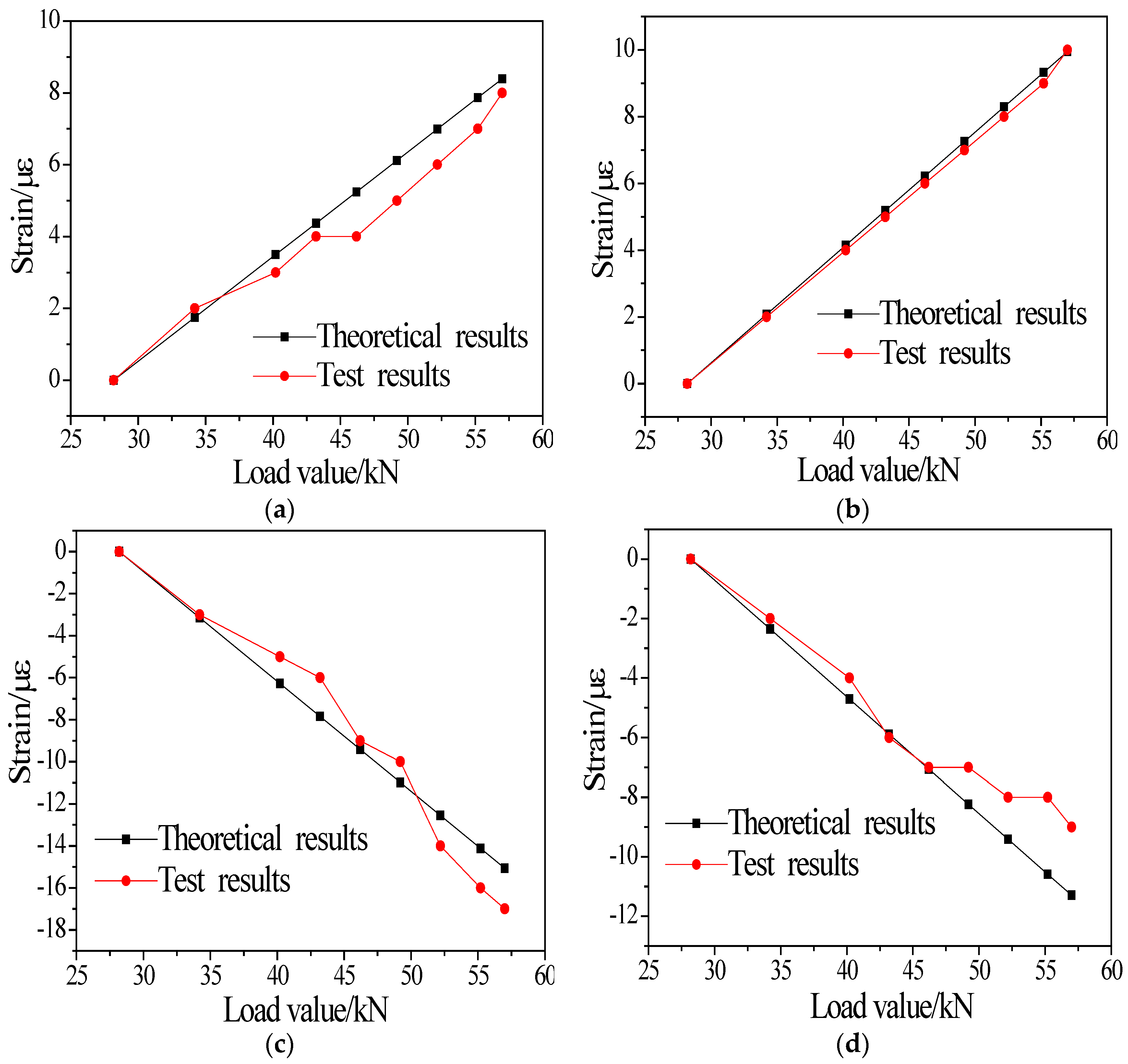

| Load Value | 34.2 kN | 40.2 kN | 43.2 kN | 46.2 kN | 49.2 kN | 52.2 kN | 55.2 kN | 57 kN |
|---|---|---|---|---|---|---|---|---|
| Point 1 | −0.06 | −0.12 | −0.15 | −0.18 | −0.2 | −0.23 | −0.26 | −0.28 |
| Point 2 | −0.06 | −0.1 | −0.13 | −0.15 | −0.18 | −0.2 | −0.23 | −0.25 |
| Point 3 | −0.06 | −0.11 | −0.13 | −0.16 | −0.18 | −0.2 | −0.23 | −0.25 |
| Load Value | 34.2 kN | 40.2 kN | 43.2 kN | 46.2 kN | 49.2 kN | 52.2 kN | 55.2 kN | 57 kN |
|---|---|---|---|---|---|---|---|---|
| Point 1 | −0.03 | −0.07 | −0.09 | −0.11 | −0.14 | −0.15 | −0.17 | −0.18 |
| Point 2 | −0.01 | −0.03 | −0.03 | −0.05 | −0.06 | −0.07 | −0.08 | −0.09 |
| Point 3 | −0.01 | −0.03 | −0.04 | −0.05 | −0.05 | −0.06 | −0.07 | −0.08 |
| Measuring | 34.2 kN | 40.2 kN | 43.2 kN | 46.2 kN | 49.2 kN | 52.2 kN | 55.2 kN | 57 kN |
|---|---|---|---|---|---|---|---|---|
| Points | ||||||||
| 3A-1 | 2 | 3 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3A-8 | 2 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 3B-1 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 |
| 3B-8 | 2 | 3 | 4 | 5 | 5 | 6 | 7 | 8 |
| Measuring | 34.2 kN | 40.2 kN | 43.2 kN | 46.2 kN | 49.2 kN | 52.2 kN | 55.2 kN | 57 kN |
|---|---|---|---|---|---|---|---|---|
| Points | ||||||||
| 3A-1 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 |
| 3A-8 | 2 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 3B-1 | −3 | −5 | −6 | −9 | −10 | −14 | −16 | −17 |
| 3B-8 | −2 | −4 | −6 | −7 | −7 | −8 | −8 | −9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Wang, Z.; Li, C.; Gao, C.; Liu, Y.; Li, C.; Liu, B. Experimental Test and Finite Element Analysis on a Concrete Box Girder of a Cable-Stayed Bridge with W-Shaped Prestressed Concrete Diagonal Braces. Buildings 2024, 14, 506. https://doi.org/10.3390/buildings14020506
He X, Wang Z, Li C, Gao C, Liu Y, Li C, Liu B. Experimental Test and Finite Element Analysis on a Concrete Box Girder of a Cable-Stayed Bridge with W-Shaped Prestressed Concrete Diagonal Braces. Buildings. 2024; 14(2):506. https://doi.org/10.3390/buildings14020506
Chicago/Turabian StyleHe, Xuhui, Zhiyu Wang, Chao Li, Ce Gao, Yongfeng Liu, Changpeng Li, and Bin Liu. 2024. "Experimental Test and Finite Element Analysis on a Concrete Box Girder of a Cable-Stayed Bridge with W-Shaped Prestressed Concrete Diagonal Braces" Buildings 14, no. 2: 506. https://doi.org/10.3390/buildings14020506
APA StyleHe, X., Wang, Z., Li, C., Gao, C., Liu, Y., Li, C., & Liu, B. (2024). Experimental Test and Finite Element Analysis on a Concrete Box Girder of a Cable-Stayed Bridge with W-Shaped Prestressed Concrete Diagonal Braces. Buildings, 14(2), 506. https://doi.org/10.3390/buildings14020506






