Hysteretic Energy-Based Estimation of Ductility Demand in Single Degree of Freedom Systems

Abstract

Ductility, as a fundamental mechanical property, allows structures to undergo inelastic deformations and dissipate seismic energy while maintaining their load-carrying capacity without substantial strength degradation. Thus, the estimation of structural ductility demand has consistently constituted an essential topic of research interest in earthquake engineering. In this study, an iterative procedure for estimating the ductility demand of elastoplastic single-degree-of-freedom (SDOF) systems through dissipated energy is introduced. The proposed procedure helps the determination of ductility demand by use of only elastic response spectra. It initially estimates the hysteretic energy as a proportion of the total input energy. Then, ductility demand is estimated with the help of a developed equation by performing regression analyses based on the nonlinear time history analyses results of elastoplastic single-degree-of-freedom (SDOF) systems with a certain strength. Time history analyses were carried out by using an extensive earthquake ground motion database, which includes a total of 268 far-field records, two horizontal components from 134 recording stations located on firm soil sites.

1. Introduction

Inelastic response and subsequent structural damage are inevitable when structures are subjected to seismic loads that exceed their strength defined by seismic codes. The key target of modern seismic design philosophy is to limit this potential damage and ensure structural safety. Ductility is one of the most essential mechanical properties that enables structures to undergo inelastic deformations and dissipate seismic energy efficiently without experiencing significant loss of strength. Thus, accurately estimating the ductility demand that structures may experience during an earthquake has long been a central topic in earthquake engineering research. Reliable quantification of ductility demand enhances the understanding of structural performance under severe ground motions. In recent decades, performance-based seismic design frameworks have been incorporated into seismic codes worldwide, reflecting the need to evaluate the damage probability of both new and existing structures. These methodologies aim at predicting the peak inelastic displacement demand imposed by seismic ground motions, so that potential structural damage and the corresponding performance level can be rationally estimated. Seismic design codes, such as FEMA 356 [1], FEMA 440 [2], ASCE 41-17 [3], Eurocode 8 [4], and TBEC 2018 [5], generally impose simplified methods to estimate inelastic displacement demand caused by earthquake ground motions. They are generally based on the principle of converting the pushover curves—obtained by nonlinear static analysis—of multi-story structures into the capacity curve of the equivalent single degree of freedom system. They take the ground motion into consideration by only the elastic spectral value of acceleration. These methods aim to estimate the maximum inelastic displacement of an SDOF nonlinear system by adjusting the elastic displacement by the inelastic displacement ratio, which is defined as the ratio between the maximum inelastic and elastic displacement demands of systems with the same period of vibration. These methods are generally based on the findings of studies carried out to investigate the inelastic displacement ratio [6,7,8,9,10,11,12,13,14]. Miranda [6,7,8] presented equations that give the inelastic displacement ratio for the estimation of inelastic displacement demand of elastoplastic SDOF, based on the results obtained from the nonlinear time history analyses of SDOF systems under the effect of 124 ground motions recorded on different soil conditions. Miranda [9] also presented plots which show the inelastic displacement ratio for different soil types, earthquake magnitude, and epicenter distance using 264 earthquake records, and presented an equation for the inelastic displacement estimation of elastoplastic SDOF Systems with constant ductility. Miranda and Ruiz-Garcia [10] examined the inelastic displacement ratio of SDOF systems with constant ductility and lateral strength under the effect of 216 ground motions based on the elastoplastic behavior. They concluded that the value of the inelastic displacement ratio with certain lateral strength is higher than the inelastic displacement ratio for the constant ductility. Ruiz-Garcia and Miranda [11] investigated the effects of soil types, post-yield stiffness, earthquake magnitude, and fault distance and presented a relationship to determine the inelastic displacement ratio with certain lateral force capacity for different soil types. Nassar and Krawinkler [12] presented a Ry-μ-T relation for the constant-ductility SDOF systems with different post-yield stiffness. Aydinoglu and Kacmaz [13] proposed an equation for the estimation of inelastic displacement of elastoplastic systems under the effect of 146 records. However, they did not investigate the effects of soil types. Chopra and Chintanapakdee [14] investigated the sensitivity of the inelastic displacement ratio of bilinear SDOF systems to the characteristics of earthquake ground motions and presented equations to estimate the ratio between the maximum elastic and inelastic displacement of SDOF Systems with a certain lateral load capacity and constant ductility under the effect of 140 ground motions by considering different earthquake magnitude levels and fault distance. Although the methods above are simple, they do not provide information regarding parameters such as the input energy, the period at which the input energy reaches its maximum value, or the hysteretic energy that causes damage.

They observed that the inelastic displacement ratio with certain lateral strength is higher than the inelastic displacement ratio for constant ductility. Ruiz-Garcia and Miranda [11] investigated the effects of soil types, post-yield stiffness, earthquake magnitude, and fault distance and presented a relationship to determine the inelastic displacement ratio with certain lateral force capacity for different soil types. Nassar and Krawinkler [12] presented a Ry-μ-T relationship for bilinear SDOF systems with constant-ductility but several post-yield stiffness ratios. Aydinoglu and Kacmaz [13] proposed an equation for the estimation of the inelastic displacement ratio of elastoplastic systems under the effect of 146 records. However, they did not investigate the effects of soil types. Chopra and Chintanapakdee [14] investigated the sensitivity of the inelastic displacement ratio of bilinear SDOF systems to the characteristics of earthquake ground motions and presented equations to estimate the ratio between the maximum elastic and inelastic displacement of SDOF Systems with a certain lateral load capacity and constant ductility under the effect of 140 ground motions by considering different earthquake magnitude levels and fault distance. Although the methods above are simple, they do not provide information regarding parameters such as the input energy, the period at which the input energy reaches its maximum value, or the hysteretic energy that causes damage.

However, results of numerous studies have shown that structural damage cannot be attributed only to the maximum deformation; rather, it is also significantly affected by the cumulative hysteretic energy dissipated by the structural system along the duration of the earthquake [15,16,17,18,19,20,21,22,23,24,25]. In this sense, as well as displacement, the seismic energy can be an effective tool to estimate the potential seismic damage. Thus, the present study aims to develop a method to estimate the ductility demand of SDOF systems by taking the hysteretic energy into consideration. In the literature, numerous studies have investigated various aspects of seismic energy, including the ratio of hysteretic energy within the total input energy for both SDOF and multi-degree-of-freedom (MDOF) systems, the distribution of energy along the height of multi-story structures, and the relationship between hysteretic energy and ductility. Several researchers have further explored these relationships in detail. Mezgebo and Lui [26] proposed input and hysteretic energy spectra that account for soil conditions, hysteretic behavior, and ductility, and later extended their approach to MDOF moment-resisting steel frames (MRSF) [27]. Homaei [28], through nonlinear time-history analyses, demonstrated that soil–structure interaction notably reduces hysteretic energy demand in short-period systems. Hasanoğlu et al. [29] investigated input and hysteretic energy demands of systems with constant-ductility under near-fault excitations, established empirical correlations between energy-based and conventional intensity measures, and proposed predictive models relating energy parameters to spectral acceleration for varying ductility levels. Gholami et al. [30] carried out a study to determine the vertical distribution of seismic hysteretic energy in buildings with hysteretic dampers. The effects of several parameters, such as target ductility capacity, the ratio of stiffness between frame and damper, and the ratio of stiffness between brace and damper, on the energy distribution along the height of the structure were investigated. They studied 224 steel frame structures, 2 to 14 stories equipped with triangular-plate added damping and stiffness dampers. They concluded that when the ductility demands show a uniform distribution along the height of frame structures with hysteretic dampers, the energy distribution along the height can be assumed similar to the story shear distribution. Nakashima et al. [31] investigated the seismic behavior of MDOF structures with hysteretic steel dampers and remarked that the energy distribution approaches a uniform form with rising post-yield stiffness ratio, α. A simple relationship was also to estimate presented for the estimation of the maximum deformation based on the hysteretic energy. Investigations on MDOF systems showed that, even for high values of α, the total input energy and hysteretic energy of both MDOF and SDOF systems are almost the same. Furthermore, the hysteretic energy distribution can be assumed uniform along the height in case α is high. Shen and Akbas [32] made some observations on the energy input of SMRF with different story and span. They observed that the energy input of soft soil is generally much higher than that of firm soil. They also stated that energy input significantly changes with frame height. They also observed that the energy distribution along the height has a decreasing form and approaches a uniform shape with increasing height of the structure. The observations made in this study also show that the intensity of the ground motion does not affect the distribution of hysteretic energy among the structural elements. The column’s share in hysteretic energy is significant only at the first and top story compared to the hysteretic energy share of columns at other stories. Contrary to Nakashima et al.’s observations [31], the authors conclude that the energy-based approach developed for SDOF systems has limitations when applied to MDOF structures in design practice. As seen from reference [31,32], there are conflicting findings in the literature regarding the use of the results obtained with SDOF systems for MDOF systems. Ridell and Garcia [22] carried out a study to improve the understanding of hysteretic energy dissipation in SDOF systems. They made an investigation into the correlation between ground motion intensity indices and input and dissipated energy. They concluded that peak ground motion parameters and the significant duration of motion (t_d) are most appropriate to normalize hysteretic energy spectra. This paper presents the results of a study that proposes an iterative procedure for estimating the displacement ductility demand of elastic-perfectly plastic SDOF systems through hysteretic energy. The proposed methodology was developed through regression analyses based on the considered ground motions −268 far-field horizontal components from 134 earthquakes recorded on firm sites-, which were also utilized in time-history analyses of SDOF systems. The proposed methodology enables the estimation of ductility demand using only elastic response spectra. Several studies [33,34,35,36] reported that the hysteresis type does not exhibit a remarkable correlation with ductility demand. Moreover, Ibarra et al. [36] demonstrated that the effect of degradation does not play a decisive role along the entire inelastic response history but becomes significant only as the structural system approaches a collapse or near-collapse state. This finding highlights that degradation mainly governs the collapse rather than the earlier phases of seismic response. Dindar et al. [37] compared the hysteretic energy demand of the elastoplastic model and that of models with degradation. They concluded that hysteretic energy spectra, obtained with the elastoplastic hysteretic model, are conservative.

2. Materials and Methods

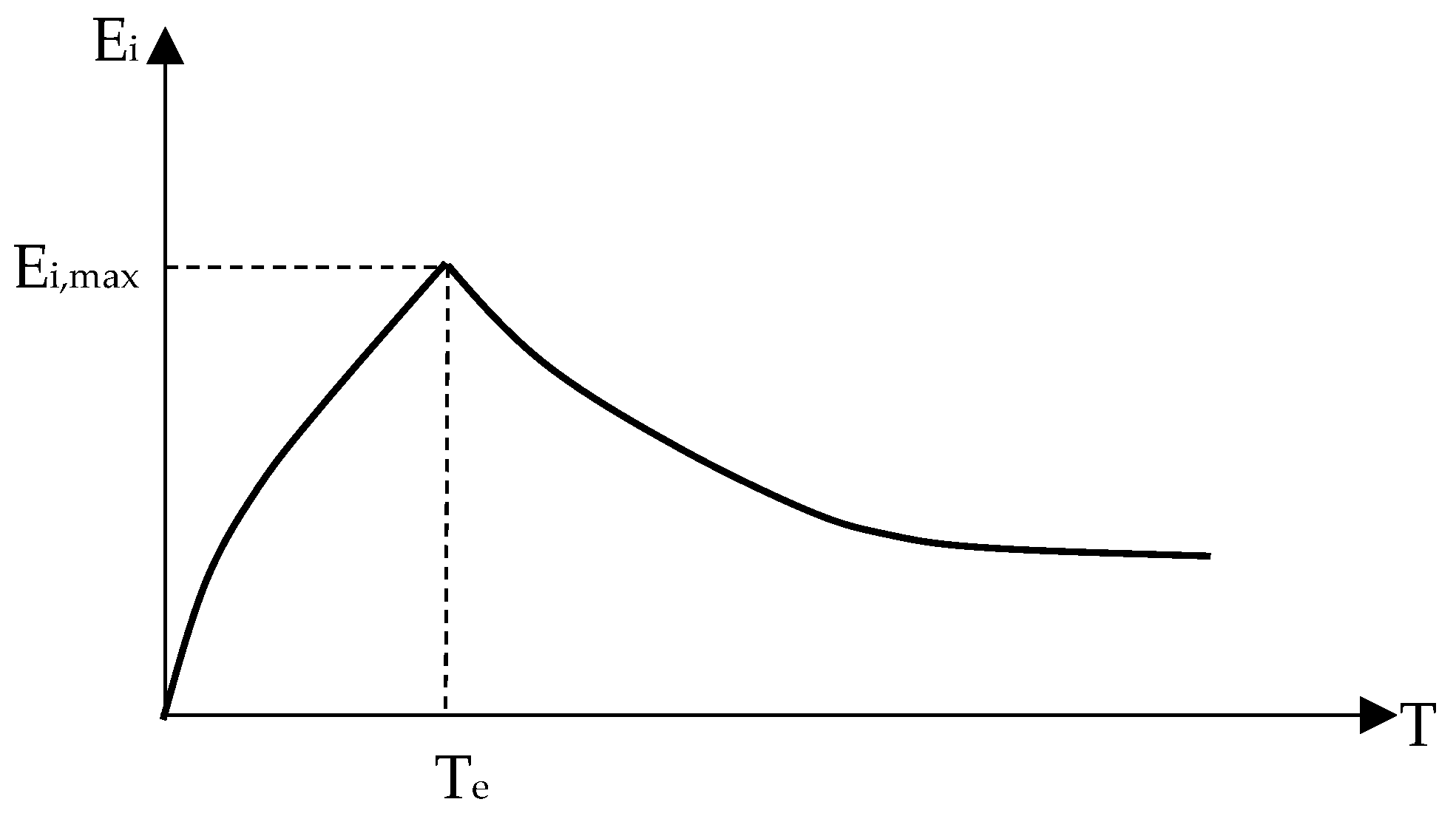
2.1. Seismic Energy

Housner [38] identified four principal components of energy dissipation in structural systems: kinetic energy, viscous damping energy, elastic strain energy, and irrecoverable hysteretic energy. The equation of motion for an elastoplastic, damped SDOF system subjected to ground acceleration is expressed as follows:

$$m\ddot{u}\left(t\right)+c\dot{u}\left(t\right)+f_s\left(u,\dot{u}\right)=-m{\ddot{u}}_g\left(t\right)$$

(1)

where m, c, and f_s represent the mass, viscous damping coefficient, and restoring force, respectively, while u denotes the relative displacement. By substituting $du=\dot{u}\left(t\right)dt$, Equation (1) can be rewritten in the energy balance form as follows:

$$\underset{0}{\overset{u}{\int }}m\ddot{u}\left(t\right)du+\underset{0}{\overset{u}{\int }}c\dot{u}\left(t\right)du+\underset{0}{\overset{u}{\int }}{f}_s\left(u,\dot{u}\right)du=-\underset{0}{\overset{u}{\int }}m{\ddot{u}}_g\left(t\right)du$$

(2)

The right-hand side of Equation (2) defines the relative input energy (E_i) as termed by Uang and Bertero [39], while the first term shows the kinetic energy (E_k). Following Manfredi [21], the total accumulated input energy at the end of the excitation is adopted as the representative measure of seismic input, since it captures the contribution of all inelastic cycles and provides a more consistent basis for cumulative damage assessment. The second term represents the viscous damping energy, while the third term corresponds to the absorbed energy (E_a), defined as the sum of hysteretic (E_h) and the elastic strain (E_s) energies:

$$E_a\left(t\right)=\underset{0}{\overset{u}{\int }}{f}_s\left(u,\dot{u}\right)du=E_h\left(t\right)+E_s\left(t\right)$$

(3)

with

$$E_s\left(t\right)={\displaystyle \frac{{\left[f_s\left(t\right)\right]}^2}{2k}}$$

(4)

E_s is recoverable and vanishes upon completion of the ground motion, the absorbed energy (E_a) becomes equal to the hysteretic energy (E_h).

2.2. Input Energy

Akiyama [16] (1985) proposed the following equation for the determination of Input Energy per mass of a ground motion.

$${\displaystyle \frac{E_i}{m}}={\displaystyle \frac{1}{2}}{\left(V_e\right)}^2$$

(5)

V_e shows the equivalent velocity which is utilized in the calculation of input energy of SDOF systems. Hancıoğlu et al. [40] made an extensive statistical analysis analyze the effect of several seismic parameters on the equivalent velocity including site class, effective period of ground motion, normalized period of SDOF system with respect to effective period, strength reduction factor, peak ground acceleration, peak ground velocity, pseudo-spectral velocity, spectrum intensity, effective duration of strong ground motion and uniform duration of strong ground motion. They observed that the most effective structural parameters are the strength reduction factor and the period of the SDOF System. Pseudo-spectral velocity is the most effective parameter that represents the ground motion. Effective duration of strong ground motion and uniform duration of strong ground motion are also effective and have a similar effect on input energy. Furthermore, using normalized energy and period is proposed to reduce the scatter of estimation, especially at periods close to the characteristic period of ground motion. The most appropriate model was determined as lognormal. Finally, they proposed Equation (6) for the determination of V_e to be used for the calculation of the Input Energy given in Equation (5).

$$V_e=\left\{\begin{array}{cc}0.66 {\displaystyle \frac{PS{V}^{0.86}{t}_d^{0.27}}{R_y^{0.1(T-0.55)}{\left(\frac{T}{T_e}\right)}^{0.2}}}\hfill & T<T_e\\ 0.66{\displaystyle \frac{PS{V}^{0.86}{t}_d^{0.27}}{R_y^{0.1(T-0.55)}}}\hfill & T\ge T_e\end{array}\right\}$$

(6)

PSV, T, T_e, R_y, and t_d are pseudo-spectral velocity, period of SDOF system, effective period of ground motion, strength reduction factor, and effective duration of strong ground motion, respectively. Hancıoğlu et al. [41] proposed Equation (7) for the estimation of characteristic period T_e.

$$T_e=1.23T_s{e}^{\left(-0.18{\displaystyle \frac{T_s}{T_1}}\right)}\hspace{1em}\hspace{1em}{T}_1=2\pi {\displaystyle \frac{{PSV}_{max}}{{PSA}_{max}}}$$

(7)

T_s shows the period of the SDOF System where the 5% damped pseudo-spectral velocity reaches its peak value, while T₁ is the transition period between the acceleration-sensitive and velocity-sensitive parts of the spectrum. PSV_max and PSA_max correspond to the maximum responses of the pseudo-velocity and pseudo-acceleration response spectra, respectively, derived from the considered ground motion records.

As shown from the schematic spectrum given in Figure 1, the input energy spectrum has two characteristic parts. The horizontal axis is the vibration period of SDOF Systems, while the vertical axis shows Input Energy. As illustrated in Figure 1, the spectrum exhibits an ascending shape for SDOF systems with periods shorter than T_e. Beyond T_e, its shape has a descending form.

2.3. Ground Motions

A particularly large number of earthquake ground motions were selected in order to assess the dispersion. A total of 268 far-field records (two horizontal components from 134 recording stations located on firm soil sites) were taken from 22 seismic events with magnitudes ranging from 5.2 to 7.9. It is known that the velocity pulse, as one of the characteristics of near-fault ground motions, imposes high displacement demands, especially in medium and long-period systems. Several studies were conducted to study the near-fault effect on the ductility demand of structures. According to studies by Alavi and Krawinkler [42], near-fault impact can increase ductility demand by a factor of 2–3, especially in the range T > 0.5 s. Iervolino et al. [43] and Tothong and Luco [44] reported that ductility demand under near-fault impacts has both a higher variance and a higher mean value than under far-fault impacts. Furthermore, several criteria had been proposed to define the near field–far field discrimination with considering of both the epicentral distance of the recording stations and the magnitude of the earthquakes; however, the proposed approaches are inconsistent with each other [45] in terms of magnitude and epicentral distance and due to the lack of a widely accepted near-fault definition, the recording stations with the minimum epicentral distance of 40 km were used to eliminate the near field effect. Records that consist of forward directivity or fling pulses were also eliminated from the ground motion database. For the evaluation of the relationship between near-fault motion attributes and structural ductility demand, the study by Hasanoğlu et al. [29] can be referred to. The criteria used for the selection of earthquake records are as follows: (i) recorded on firm sites with average shear wave velocities exceeding 180 m/s in the upper 30 m of the site profile; (ii) records whose at least one horizontal component has a peak ground acceleration higher than 35 cm/s²; (iii) recorded on stations with the minimum epicentral distance of 40 km; (iv) records which did not exhibit forward directivity as well as fling effects. The selected records can be classified into three groups according to the NEHRP local site classification (site classes B, C, and D) [46]. The first group consisted of 56 records taken from stations on rock whose average shear wave velocities changed between 760 m/s and 1500 m/s. The second one consisted of 104 records obtained from stations on very dense soil or soft rock whose average shear wave velocities changed between 360 m/s and 760 m/s, while the third group consisted of 108 records taken from stations on stiff soil with average shear wave velocities between 180 m/s and 360 m/s. All the selected ground motions are shown in

Table 1. Ground motion records used in the regression analysis.

Event	Year	M *1	Repc *2	Site Class *3	Vs30 *4
Big Bear-01	1992	6.5	69	B	822
Chi-Chi, Taiwan	1999	7.6	173	B	1023
Chi-Chi, Taiwan-05	1999	6.2	92	B	845
Denali, Alaska	2002	7.9	68	B	964
Irpinia, Italy-01	1980	6.9	77	B	1000
Loma Prieta	1989	6.9	92	B	895
Morgan Hill	1984	6.2	39	B	1428
Norcia, Italy	1979	5.9	36	B	1000
Northridge-01	1994	6.7	77	B	822
San Fernando	1971	6.6	39	B	969
Sierra Madre	1991	5.6	40	B	996
Whittier Narrows-01	1987	6.0	28	B	1223
Big Bear-01	1992	6.5	118	C	405
Drama, Greece	1985	5.2	47	C	660
Kern County	1952	7.4	126	C	415
Landers	1992	7.3	148	C	368
Loma Prieta	1989	6.9	98	C	597
N. Palm Springs	1986	6.1	60	C	685
Northridge-01	1994	6.7	62	C	446
San Fernando	1971	6.6	75	C	446
Whittier Narrows-01	1987	6.0	77	C	450
Chi-Chi, Taiwan	1999	7.6	116	D	273
Dinar, Turkey	1995	6.4	50	D	339
Friuli, Italy-01	1976	6.5	90	D	275
Imp. Valley-06	1979	6.5	84	D	345
Irpinia, Italy-01	1980	6.9	52	D	275
Kern County	1952	7.4	118	D	316
Kobe, Japan	1995	6.9	136	D	256
Kocaeli, Turkey	1999	7.5	100	D	275
Landers	1992	7.3	75	D	271
Lazio-Abruzzo, Italy	1984	5.8	51	D	200
Loma Prieta	1989	6.9	94	D	249
Manjil, Iran	1990	7.4	87	D	275
Morgan Hill	1984	6.2	80	D	271

*1 M: moment magnitude. *2 Repc: distance from recording site to epicenter. *3 Site Class: NEHRP site classification. *4 Vs30: average shear wave velocity down to 30 m depth (m/s).

with their magnitude, site class, epicentral distance, and shear wave velocity in the upper 30 m of the site profile.

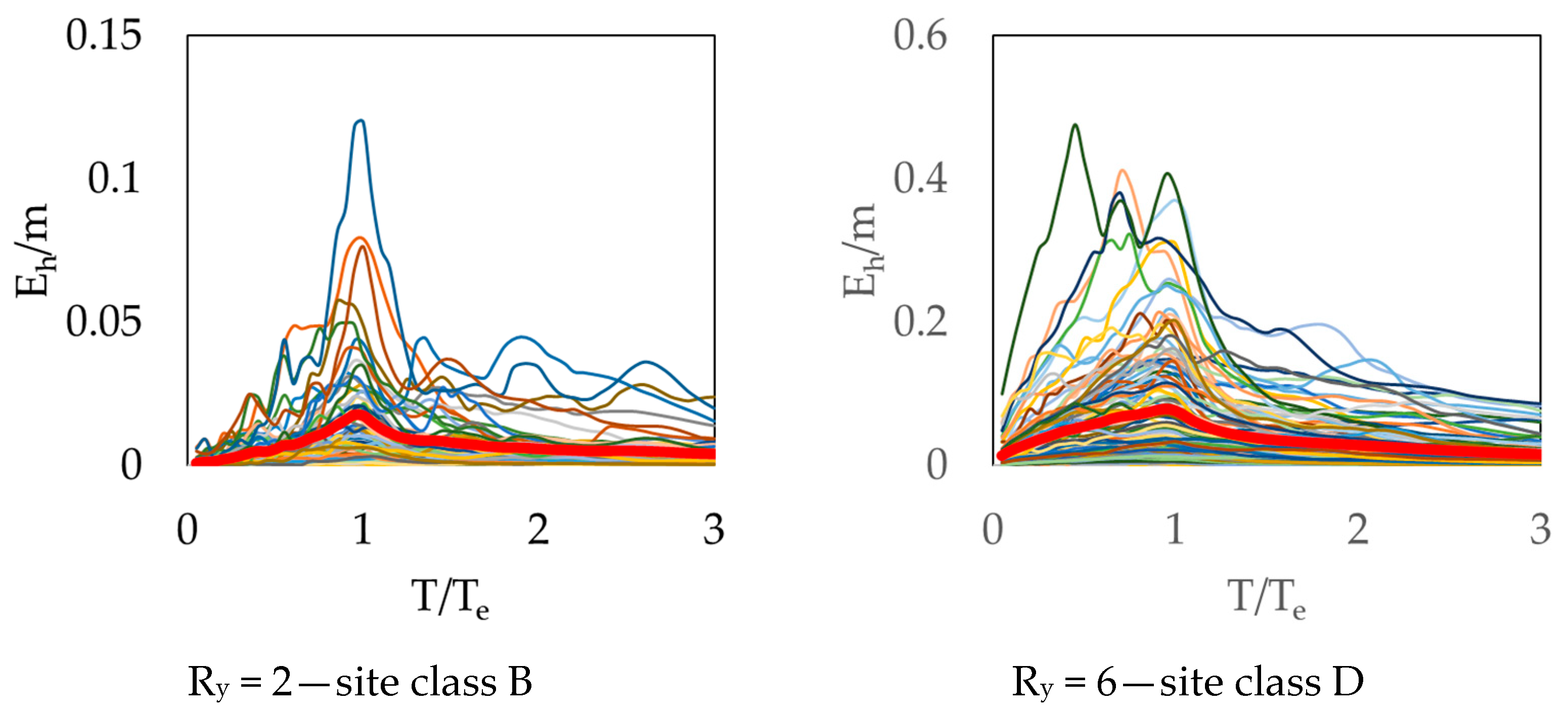
2.4. Hysteretic Energy

The hysteretic energy spectra, obtained with the considered SDOF systems, and the mean spectrum with strength reduction factors of 2 and 6 are shown in Figure 2. The first spectrum corresponds to systems with a reduction factor of 2 subjected to ground motions recorded on site class B, whereas the second corresponds to systems with a reduction factor of 6 subjected to ground motions obtained from site class D. All spectra were shown for SDOF systems with periods ranging from 0.05 s to 3 s, with a constant increase of 0.05 s.

As can be seen from Figure 2, hysteretic energy spectra have a similar shape to input energy spectra, whose schematic representation is given in Figure 1, and reach their maximum value when T = T_e. For the assessment of the hysteretic energy, a common approach is to estimate it through the input energy as given in Equation (8). The ratio between hysteretic energy and input energy, termed α, may be estimated by means of the displacement ductility demand.

$$E_h={\alpha E}_i$$

(8)

Figure 3 and Figure 4 also show hysteretic energy spectra, but in terms of hysteretic energy normalized with respect to the input energy, which is defined by α.

Figure 3 and Figure 4 show that the hysteretic energy ratio is almost constant except for SDOF systems whose period is less than 0.5 T_e. Figure 5 shows the mean hysteretic energy ratio spectra of SDOF systems with different strength reduction factors for each considered site class. Mean spectra are also shown on each figure.

Figure 3, Figure 4 and Figure 5 show that the normalized energy–normalized period relationship has a lower dispersion. Figure 6 shows the mean hysteretic energy ratio of each site class.

Fajfar et al. [19] developed the following equation for the estimation of α in the case of the bilinear hysteretic model:

$$\alpha =1.05{\displaystyle \frac{{\left(\mu -1\right)}^{0.95}}{\mu }}$$

(9)

In the present study, the above equation, whose general form is given in Equation (10), is modified by considering the ground motion database used in this study. Thus, a nonlinear regression analysis [47,48] was performed to minimize the least-squares loss function, which shows the difference between calculated and estimated values of α.

$$\alpha =a{\displaystyle \frac{{\left(\mu -1\right)}^b}{{\mu }^c}}$$

(10)

As a result of the regression analysis, Equation (11) is obtained. The proportion of variance accounted for by the model (R²) is calculated as 77%. The mean error, the weighted mean error, and the coefficient of variation of error are found as 0.005, 0.043, and 0.163, respectively.

$$\alpha =0.72{\left({\displaystyle \frac{\mu -1}{\mu }}\right)}^{0.84}$$

(11)

The α-displacement ductility demand (µ) relationship is given in Figure 7 with the curve that represents the proposed equation for α. Figure 7 indicates that α significantly increases with increasing displacement ductility demand for 1 < μ < 4, while it takes a constant value of approximately 0.72 on average for the systems that have displacement ductility demand greater than 20. Fajfar and Vidic [19] stated that 0.7 could be taken as the average upper limit. The result obtained with this study is slightly higher than this value; however, they are quite close. Finally, Equation (8), which gives the hysteretic energy, can be expressed as follows,

$$E_h=0.72{\left({\displaystyle \frac{\mu -1}{\mu }}\right)}^{0.84}{E}_i$$

(12)

The scatter plot of hysteretic energy demand computed by nonlinear time history analyses and estimated by Equation (12) is given in Figure 8. The proportion of variance was calculated as R² = 97%.

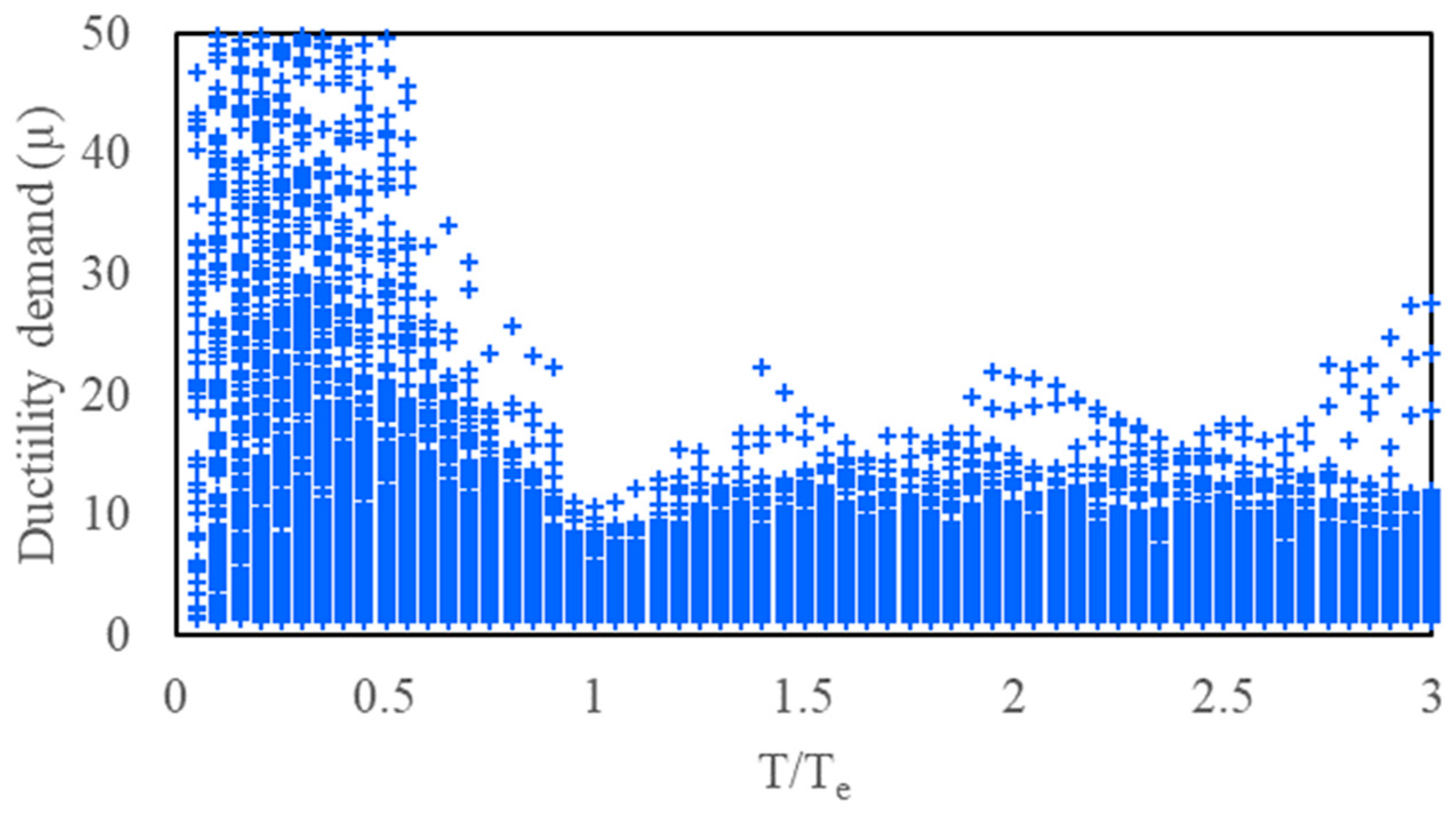
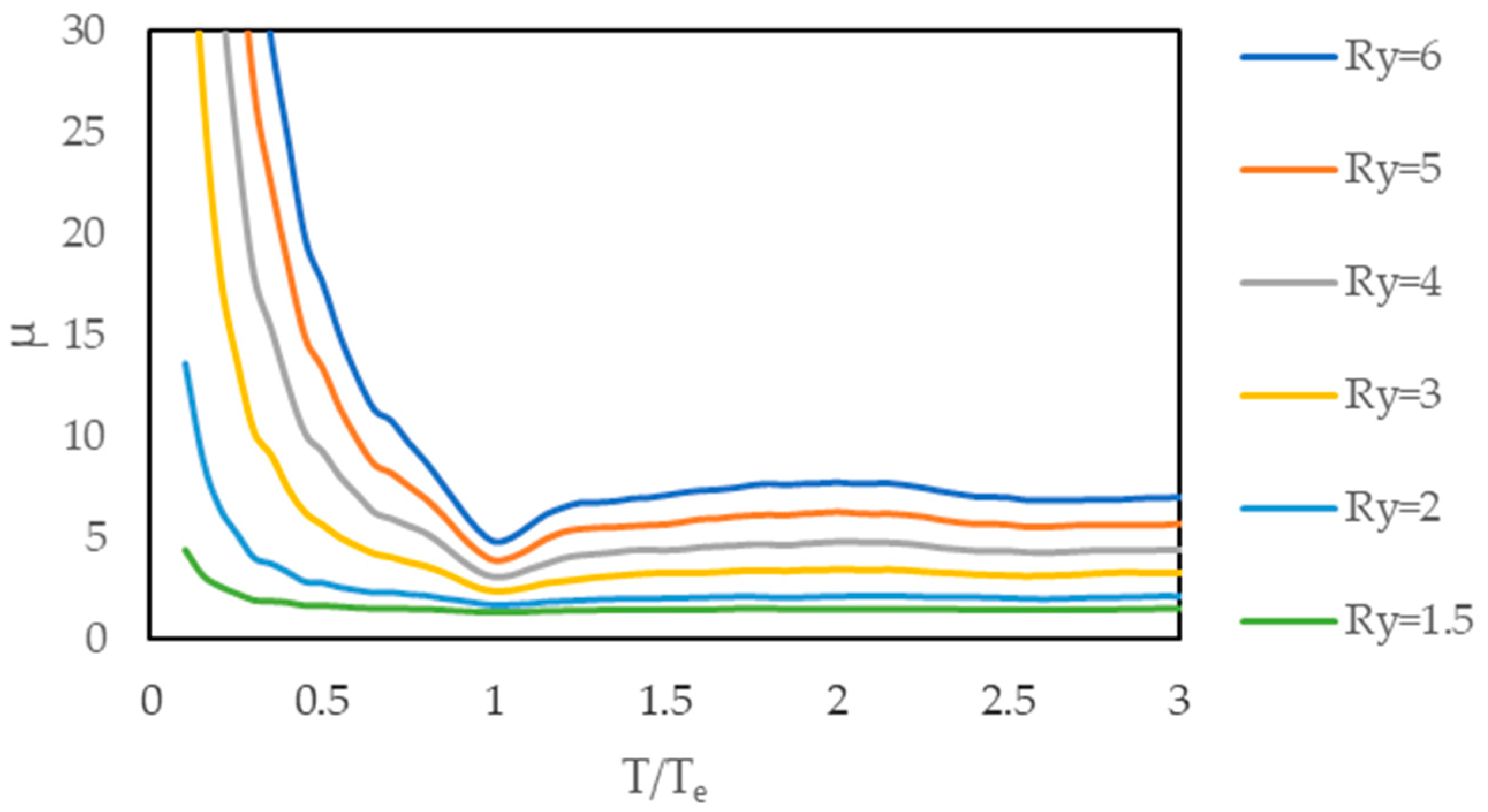
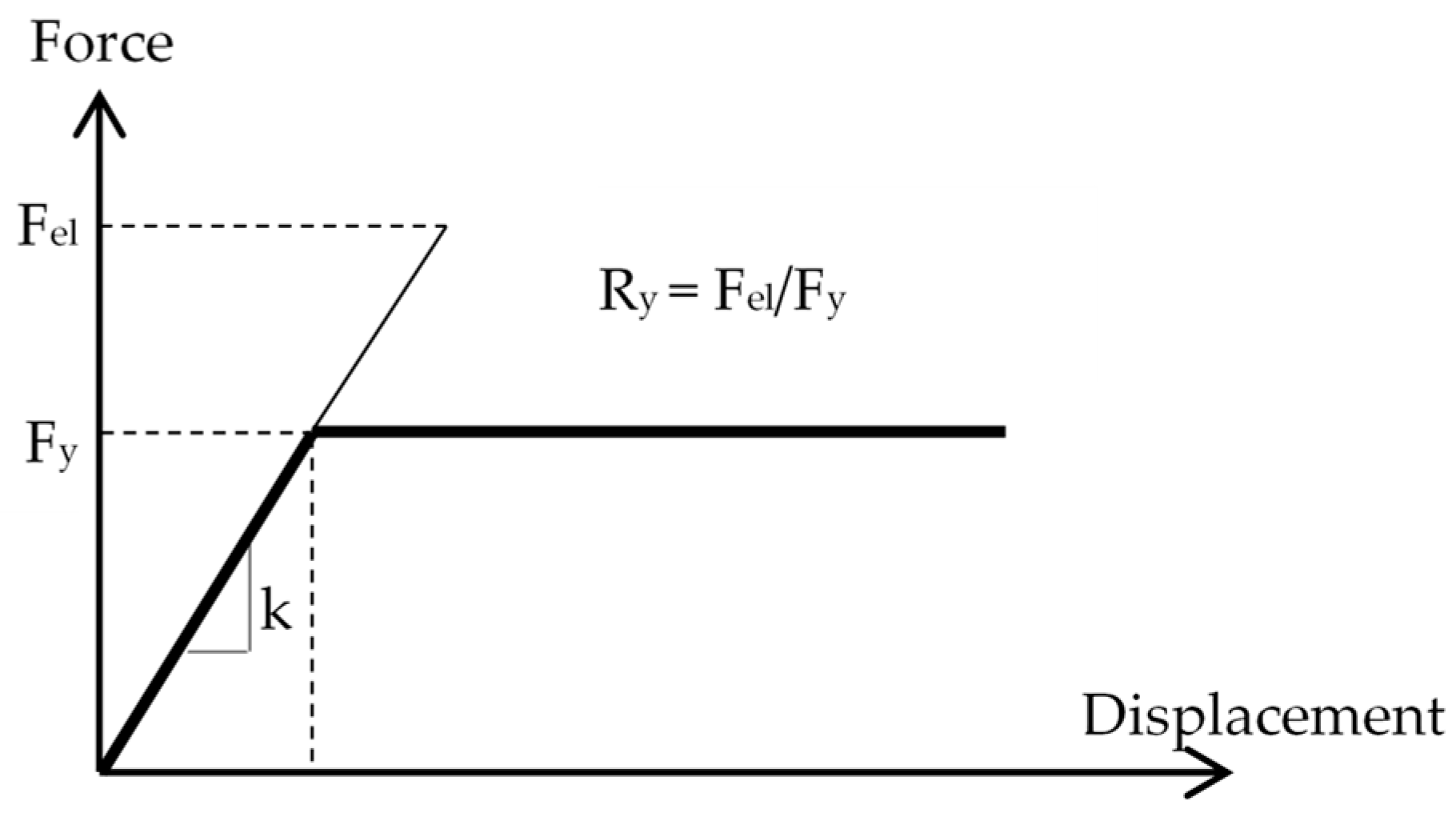
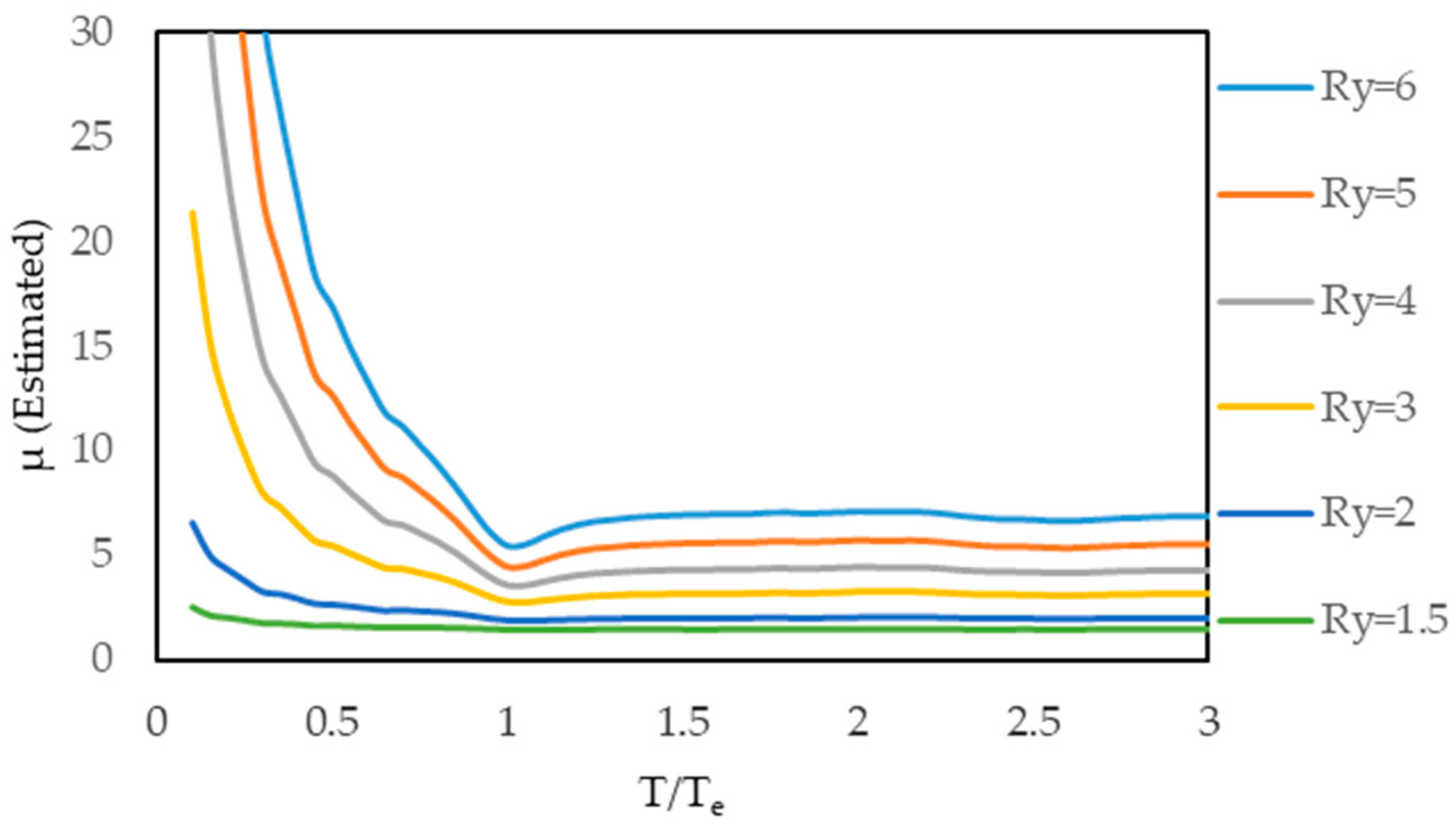
2.5. Estimation of Displacement Ductility Demand

Figure 9, Figure 10 and Figure 11 show the calculated ductility demand value of ground motion records recorded on Soil Types B, C, and D, respectively.

Figure 12 shows all ductility demands regardless of Soil Type.

Figure 13 shows the mean calculated ductility demand values for different strength levels. Mean ductility demand values for each T/T_e ratio were calculated regardless of soil type, since the distribution of ductility demand is similar for all considered soil types.

In order to obtain an equation that estimates the displacement ductility demand, a regression analysis was performed based on the results obtained from nonlinear time history analyses. The proposed equation takes the structural parameters, ground motion characteristics, and energy dissipation capacity of the system into consideration, which are effective on the displacement demand of ground motions. The power function given in Equation (13) has been chosen for the regression model of the equation that gives the mean ductility demand.

$$\mu =1+a{\beta }_1^b{ \beta }_2^c{ \beta }_3^d$$

(13)

where a, b, c, and d are the regression coefficients. β₁ shows the Normalized Hysteretic Energy, given in Equation (14), which is defined as the ratio between the cumulative hysteretic energy, dissipated by an SDOF system through yielding at the end of ground motion, and the maximum recoverable elastic strain energy absorbed by the system during the earthquake.

$$N_h={\displaystyle \frac{E_h/m}{E_{s,max}/m}}={\displaystyle \frac{E_h/m}{\frac{F_y{u}_y}{2m}}}={\displaystyle \frac{E_h/m}{\frac{PSA\times SD}{2R_y^2}}}$$

(14)

where F_y and u_y represent the structural force and displacement corresponding to the yielding of the elastoplastic SDOF system whose force-displacement relationship is given in Figure 14.

PSA refers to the elastic pseudo-spectral acceleration; SD denotes the spectral displacement. The normalized cyclic energy defined in Equation (15) corresponds to the normalized absorbed energy introduced by Chou and Uang [49]. Since the recoverable deformation energy E_s becomes zero at the end of the ground motion, the absorbed energy becomes equivalent to the cyclic energy. The mean hysteretic energy (E_h/m), mean normalized hysteretic (N_h) energy, and ductility demand (µ) spectra are shown in Figure 15. It is observed that the spectral shapes of the mean hysteretic energy (E_h/m) and ductility (µ) demands exhibit different trends, whereas the mean normalized hysteretic energy (N_h) spectrum shows a similar trend to that of the ductility demand spectrum. Figure 16 shows the mean normalized hysteretic energy for different strength levels of SDOF Systems.

β₂ shows the seismic index defined by Cosenza and Manfredi [18], which is used as the primary parameter representing the variation in the characteristics of earthquake ground motions in the regression model. The seismic index ID can be calculated by the following equation:

$$I_D={\displaystyle \frac{I_E}{PGA\times PGV}}$$

(15)

where IE, given in Equation (16), is the acceleration record intensity, PGA and PGV are the peak ground acceleration and velocity, respectively.

$$I_E={\int }_0^t{\ddot{u}}_g^{2}dt$$

(16)

β₃ is T/T_e, which shows the ratio of the period of the SDOF system and the characteristic period of ground motion, which is given with Equation (8). A regression analysis was performed comparing the ductility demands calculated by nonlinear time history analyses with those obtained by the proposed regression model. Relatively high ductility demands are observed under some earthquake ground excitation, especially for SDOF systems with periods of vibration shorter than 0.3 s. This manner causes extremely high deviations in the related period range. In order to compensate for the effect of these deviations, the weighted least squares loss function L was taken as follows:

$$L=\omega {\left[{\mu }_{exact}-{\mu }_{estimated}\right]}^2={\displaystyle \frac{1}{{\mu }_{exact}}}{\left[{\mu }_{exact}-{\mu }_{estimated}\right]}^2$$

(17)

The regression coefficients, minimizing the standard error, were chosen. As a result of regression analysis, the following equation has been developed:

$$\mu =\left\{\begin{array}{cc}1+0.70N_h^{0.70}{I}_D^{-0.35}{\left({\displaystyle \frac{T}{T_e}}\right)}^{\left({\displaystyle \frac{1-R_y}{23}}\right)}\hfill & {\displaystyle \raisebox{1ex}{$T$}\!\left/ \!\raisebox{-1ex}{$T_e$}\right.}<1\\ 1+0.70N_h^{0.70}{I}_D^{-0.35}\hfill & {\displaystyle \raisebox{1ex}{$T$}\!\left/ \!\raisebox{-1ex}{$T_e$}\right.}\ge 1\end{array}\right\}$$

(18)

The proportion of variance accounted for the regression model is calculated as R² = 88%. Estimated mean ductility values are shown in Figure 17. Furthermore, the scatter plot of the ductility demand calculated from nonlinear time history analyses (calculated) and obtained from the proposed equation is given in Figure 18 in logarithmic format.

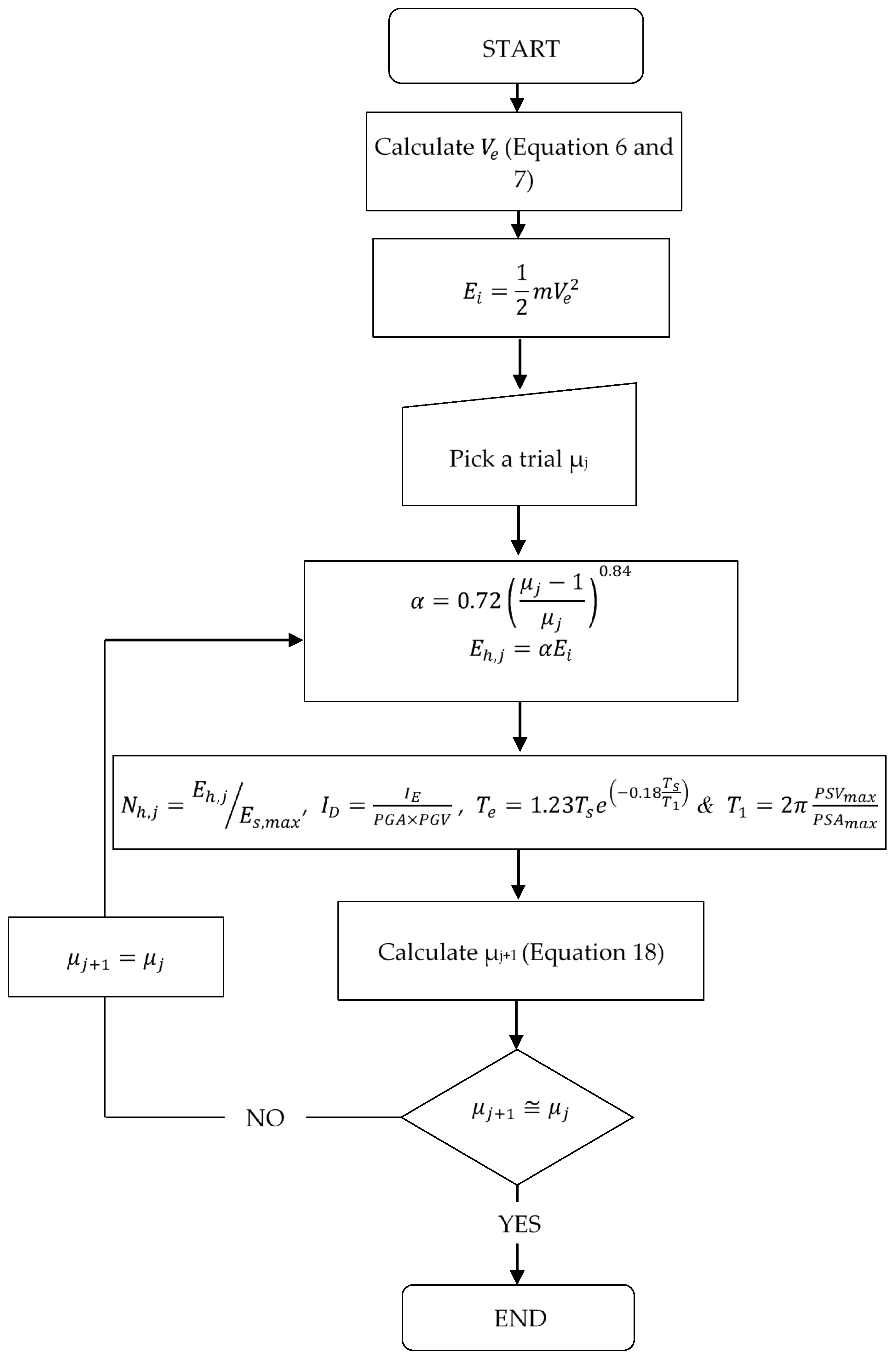
2.6. The Proposed Procedure for Estimating the Displacement Ductility Demand

Equation (19) given above allows estimating the ductility demand in terms of the energy dissipated by the yielding of the SDOF system. Thus, a reliable estimation of the displacement ductility demand through the seismic energy should be obtained by performing an iterative procedure. The flow chart of the proposed iterative procedure is given in Figure 19 and summarized as follows:

• Compute the input energy demand using Equations (5)–(7);
• Pick a trial displacement ductility demand;
• Compute the hysteretic energy dissipation using Equation (12) through the trial displacement ductility demand;
• Normalize the hysteretic energy demand, obtained in the previous step, as defined in Equation (14);
• Compute the Cosenza and Manfredi seismic index using Equations (15) and (16);
• β₃ is T/T_e, which shows the ratio of the period of the SDOF system and the characteristic period of ground motion, which is given with Equation (7).
• Compute a new displacement ductility demand through the normalized hysteretic energy obtained in the previous step using Equation (18);
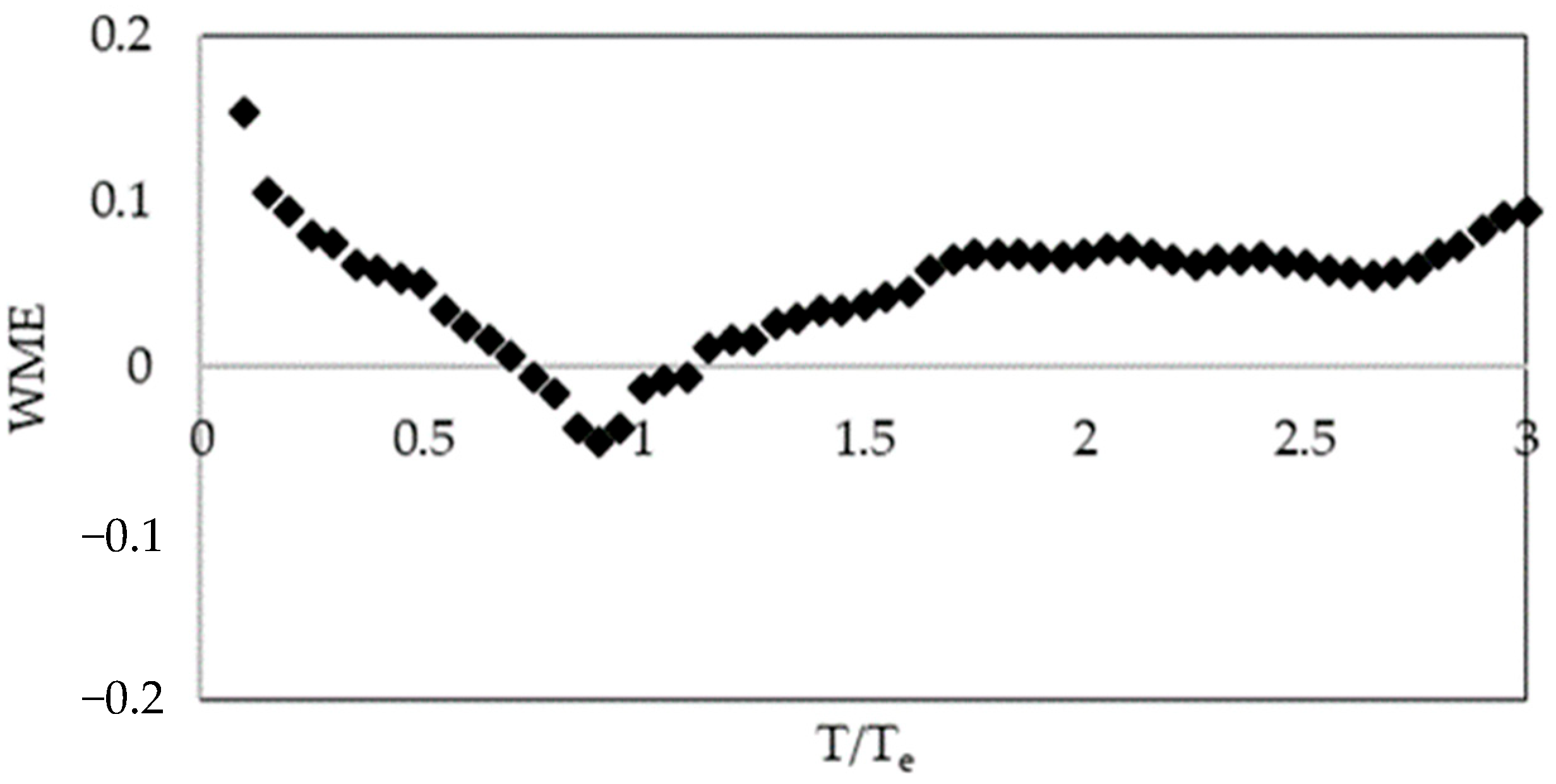
• Compute the relative error by the following expression:

$${\epsilon }_i=\left|{\displaystyle \frac{{\mu }_{i+1}}{{\mu }_i}}-1\right|<{\epsilon }_{limit}$$

(19)

If the absolute value of the relative error (Step 8) is greater than the limit, turn back to Step 3 with assuming the displacement ductility demand computed at the last step as the new trial value. The iteration should be carried on until the absolute value of the relative error (Step 8) becomes smaller than the limit value. Hence, the value of µ computed at the last is assumed as the estimated displacement ductility demand.

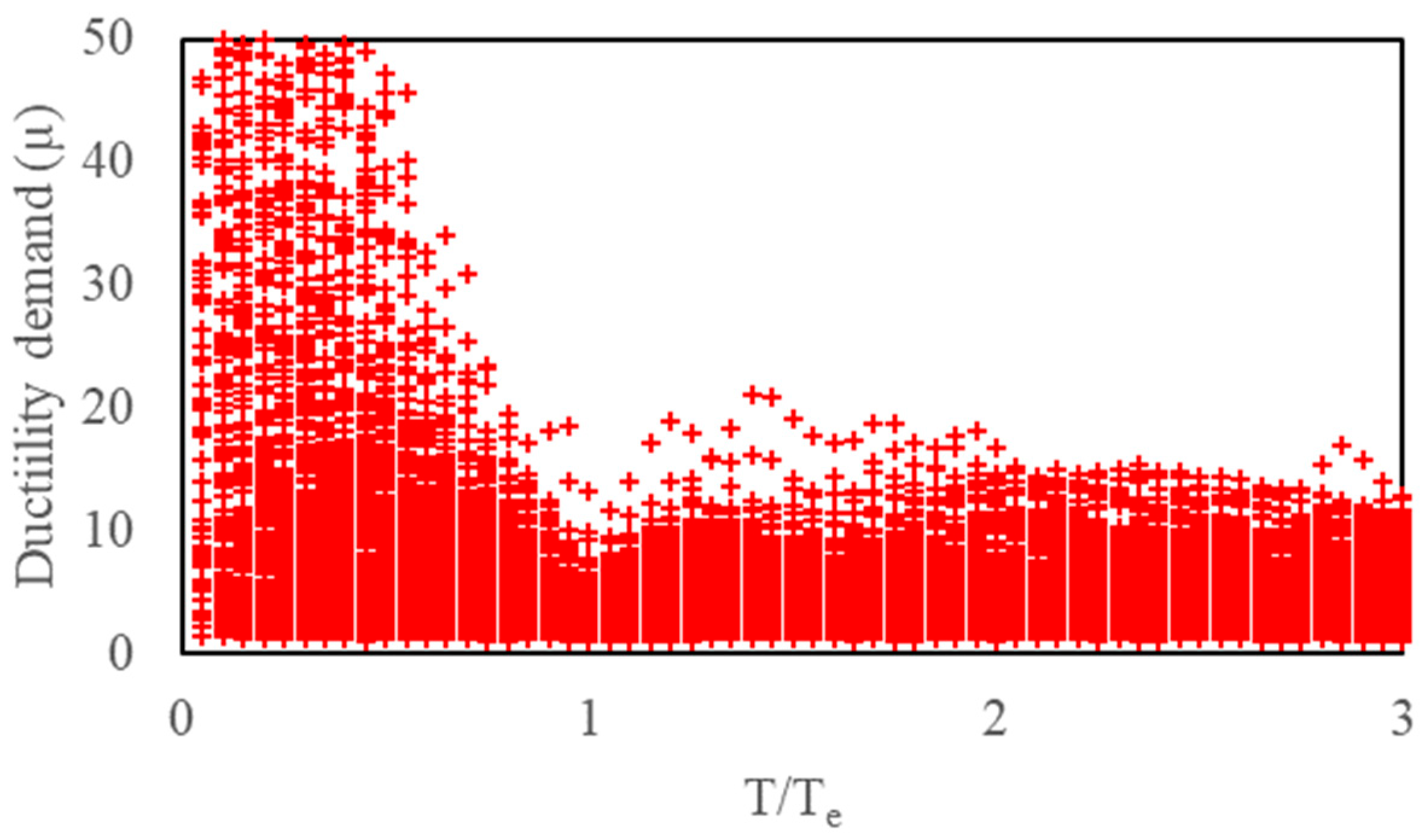
3. Results

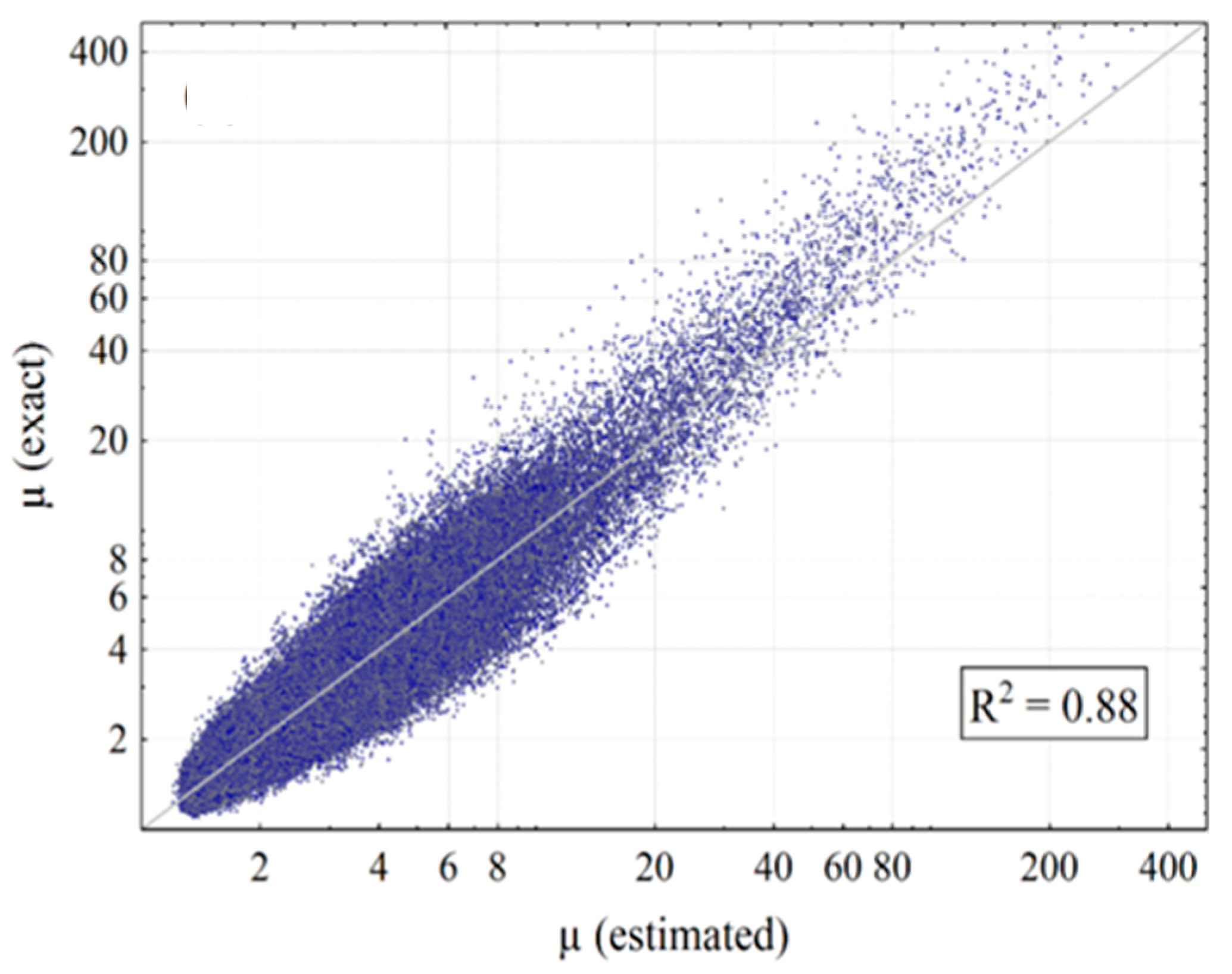
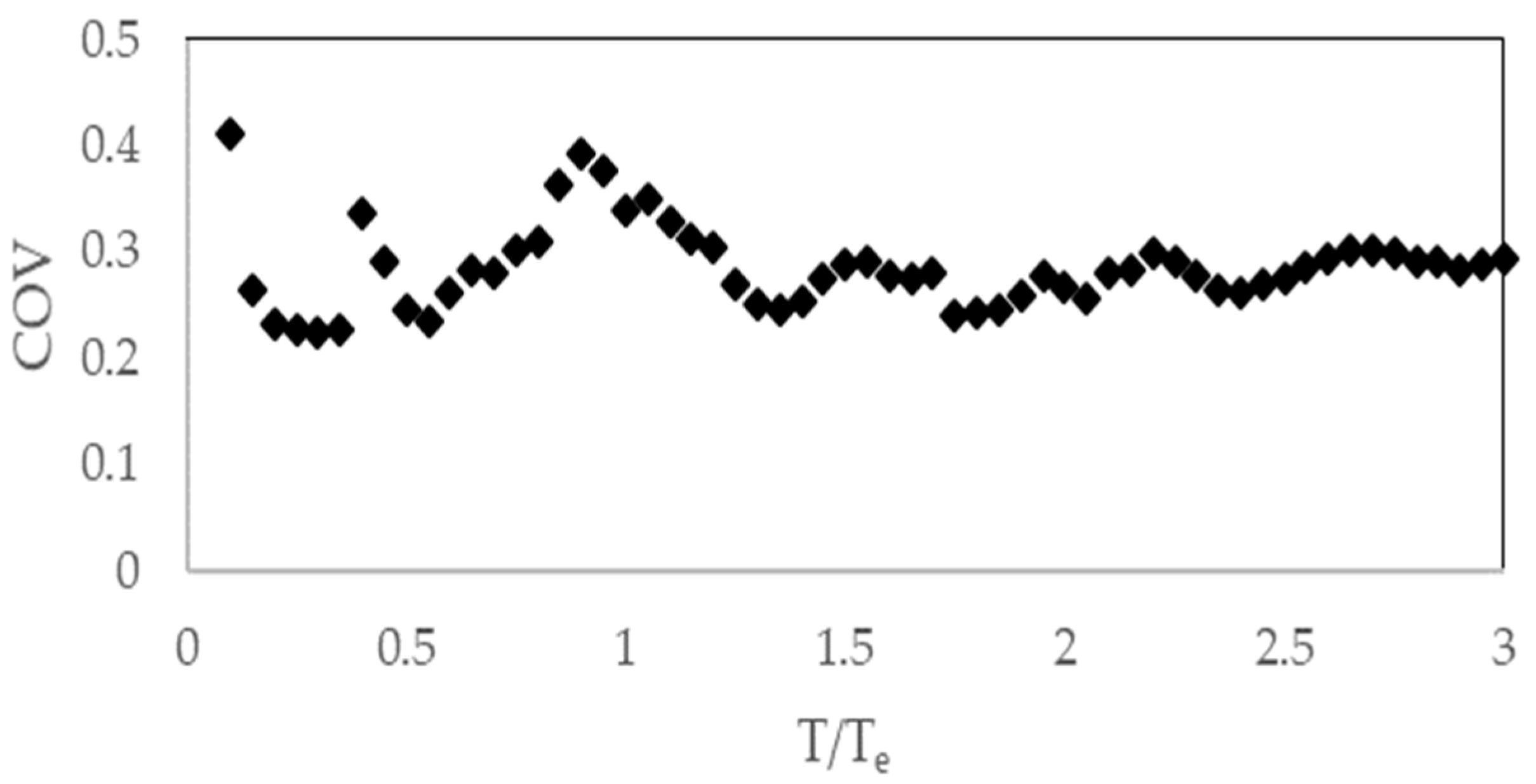
Regression Analysis

The mean spectra of calculated and estimated hysteretic energy spectra are given in Figure 20, regardless of the strength reduction factor (Ry). As shown in Figure 20, there is almost no difference between estimated and calculated values of hysteretic energy along periods that are lower than 0.4 T_e and periods that are higher than T_e. Between 0.4 T_e and T_e, there is a difference between the estimated and calculated hysteretic energy, but this difference is reasonable.

Figure 21 shows the mean calculated and mean estimated hysteretic energy spectra for SDOF systems with different strength levels under the effect of the considered ground motions.

4. Discussion

Figure 6 shows that the site class has no significant effect on the hysteretic energy dissipated by an SDOF system, unlike the input energy. However, the shape of the hysteretic energy spectrum is similar to the input energy spectrum’s shape, as is seen in Figure 2 and Figure 21. As it is shown in Figure 21, the strength reduction factor is significantly effective on hysteretic energy. This result stems from the fact that hysteretic energy is an indicator of structural damage and that structural damage is directly related to strength. Another parameter related to structural damage is the displacement demand caused by ground motion. Therefore, the obtained results indicate that a relationship can be established between hysteretic energy and displacement ductility demand of SDOF systems with a certain strength. The hysteretic energy reaches its maximum value when the period of the SDOF System is equal to T_e. The weighted mean error (WME) and the coefficient of variation of error (COV) of Equation (12) are given in Figure 22 and Figure 23. As mentioned above, Ibarra et al. [36] concluded that degradation is effective only when the structural system approaches or reaches its collapse state. Given that the proposed method does not explicitly account for such degradation, it should be recognized that its accuracy may slightly decrease under near-collapse conditions. Furthermore, Vega and Montejo [50] observed that ground motion duration has a significant influence on damage at moderate damage levels; however, this effect diminishes at severe damage levels. Thus, ductility demands, which may cause moderate damage, would differ from those obtained with the proposed methodology.

5. Conclusions

The purpose of this study is to estimate the displacement ductility demand of SDOF systems through the hysteretic energy demand of existing structures built on firm sites whose lateral strength is known. Based on these results, a number of general conclusions are made as follows:

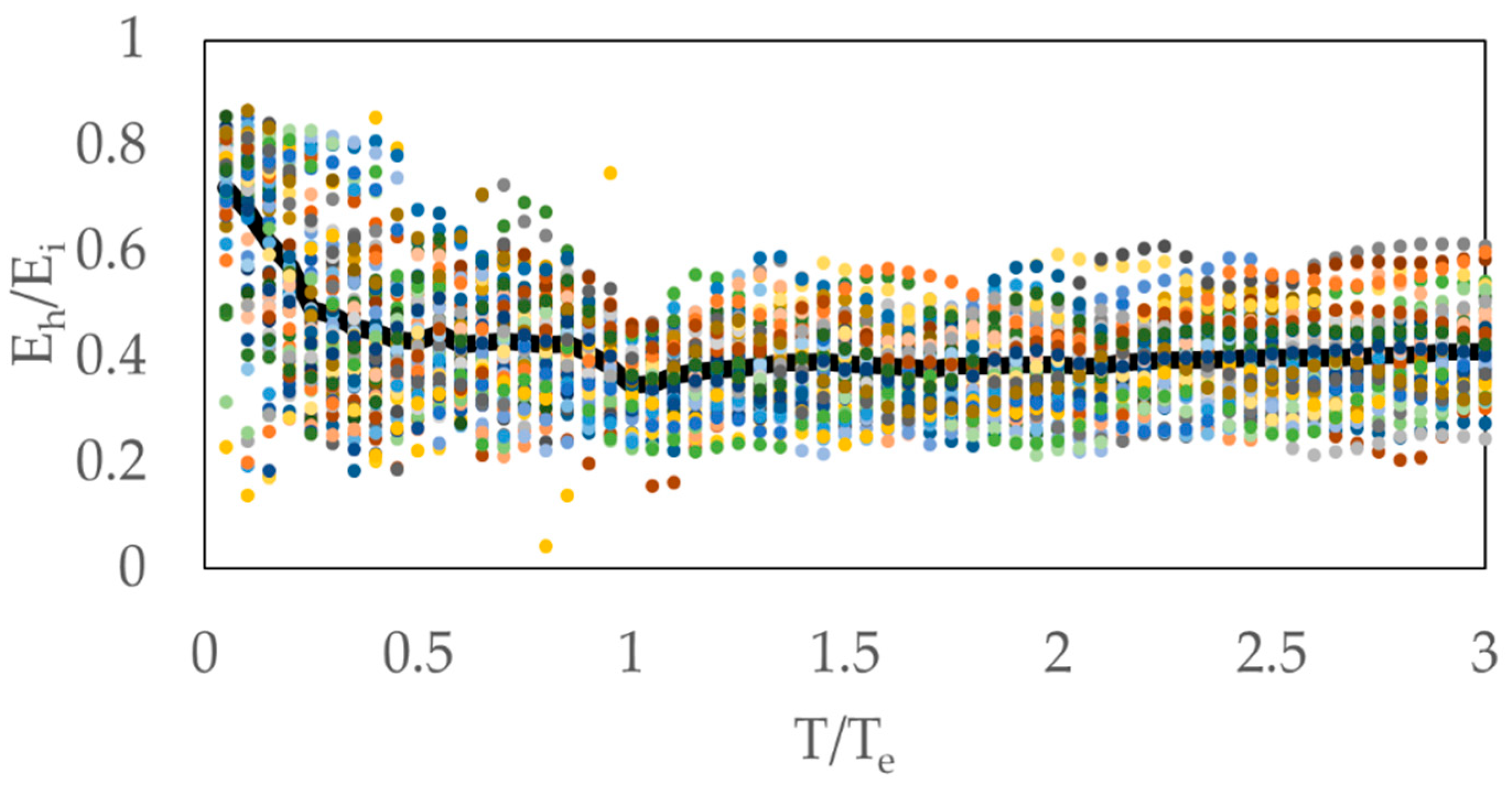
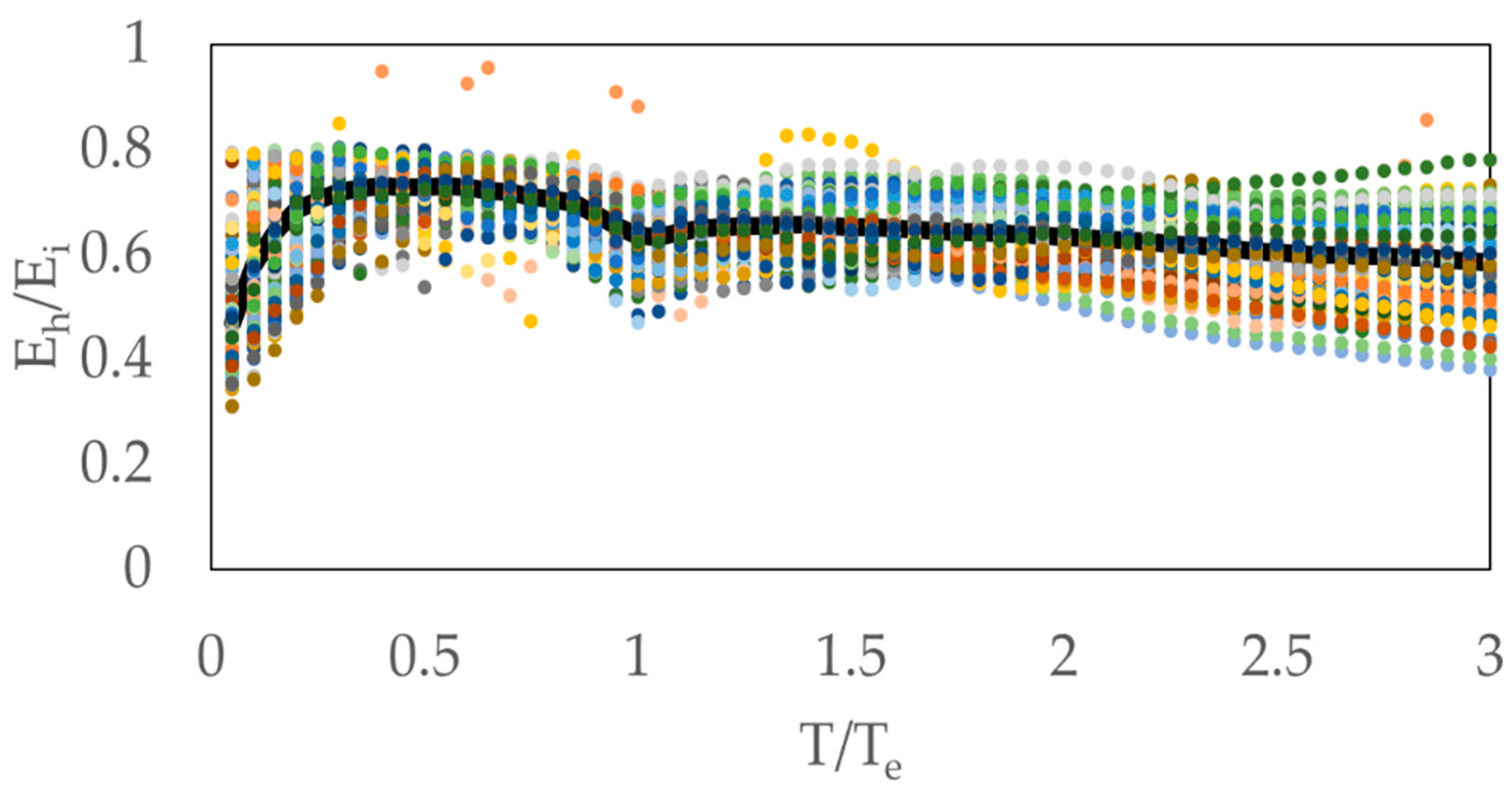
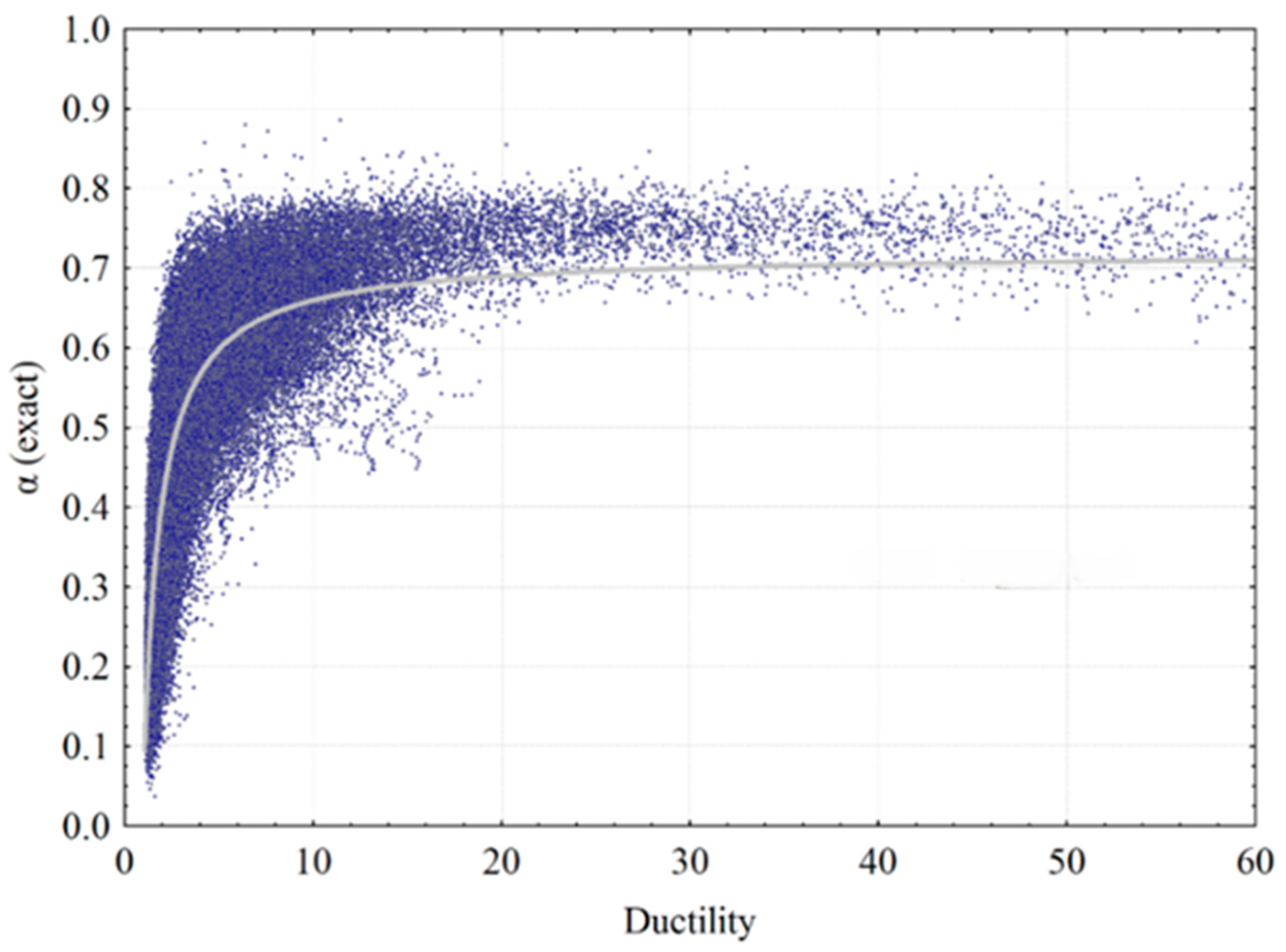
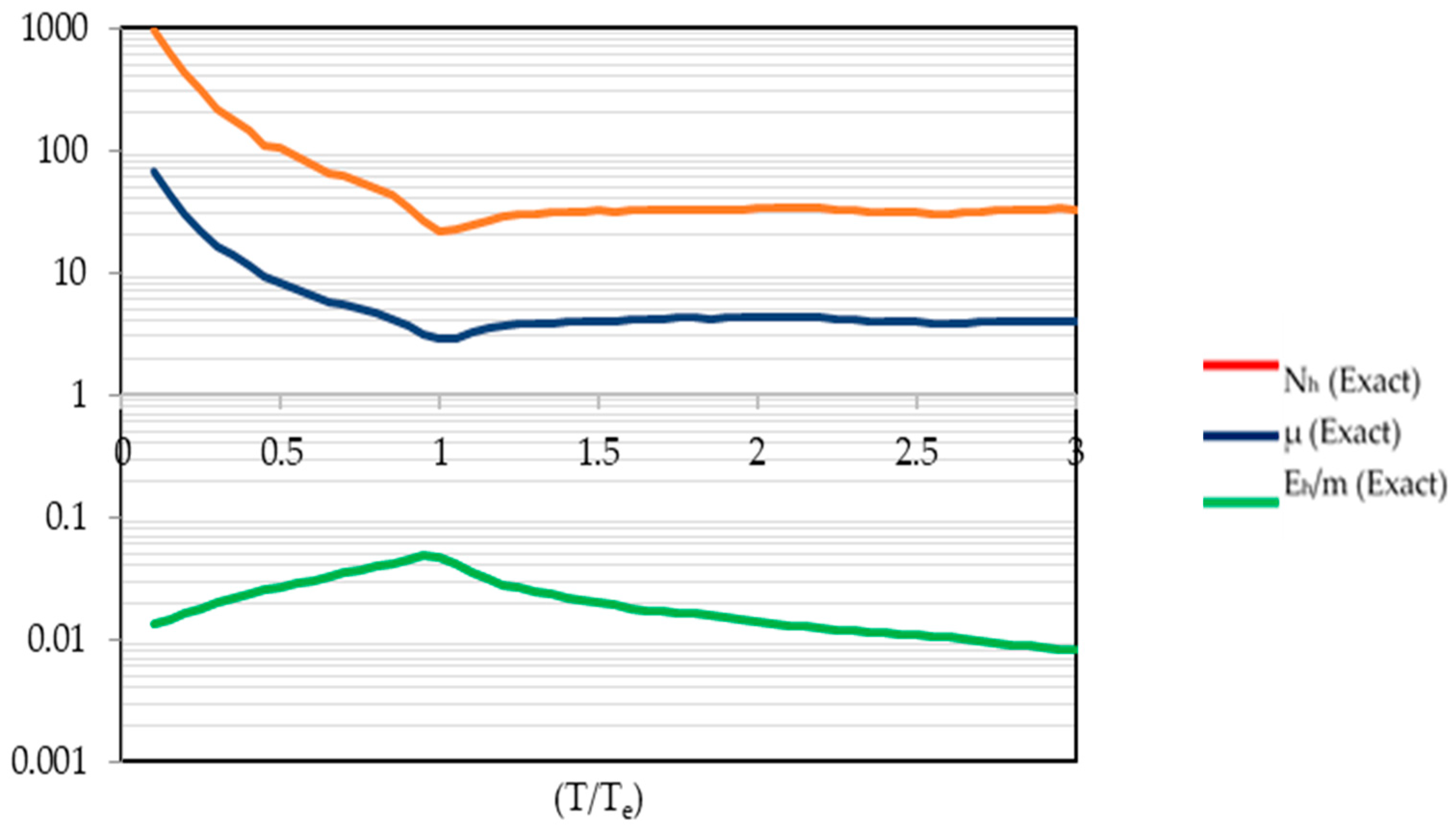
• The ratio between hysteretic energy and input energy, α, rapidly increases up to 0.6 with increasing displacement ductility demand for 1 < μ < 4. However, this increase becomes slower beyond the ductility demand of 4 and becomes constant with increasing ductility. 0.80 may be considered as a conservative value of α, based on results obtained with the considered ground motion database of this study (Figure 7).
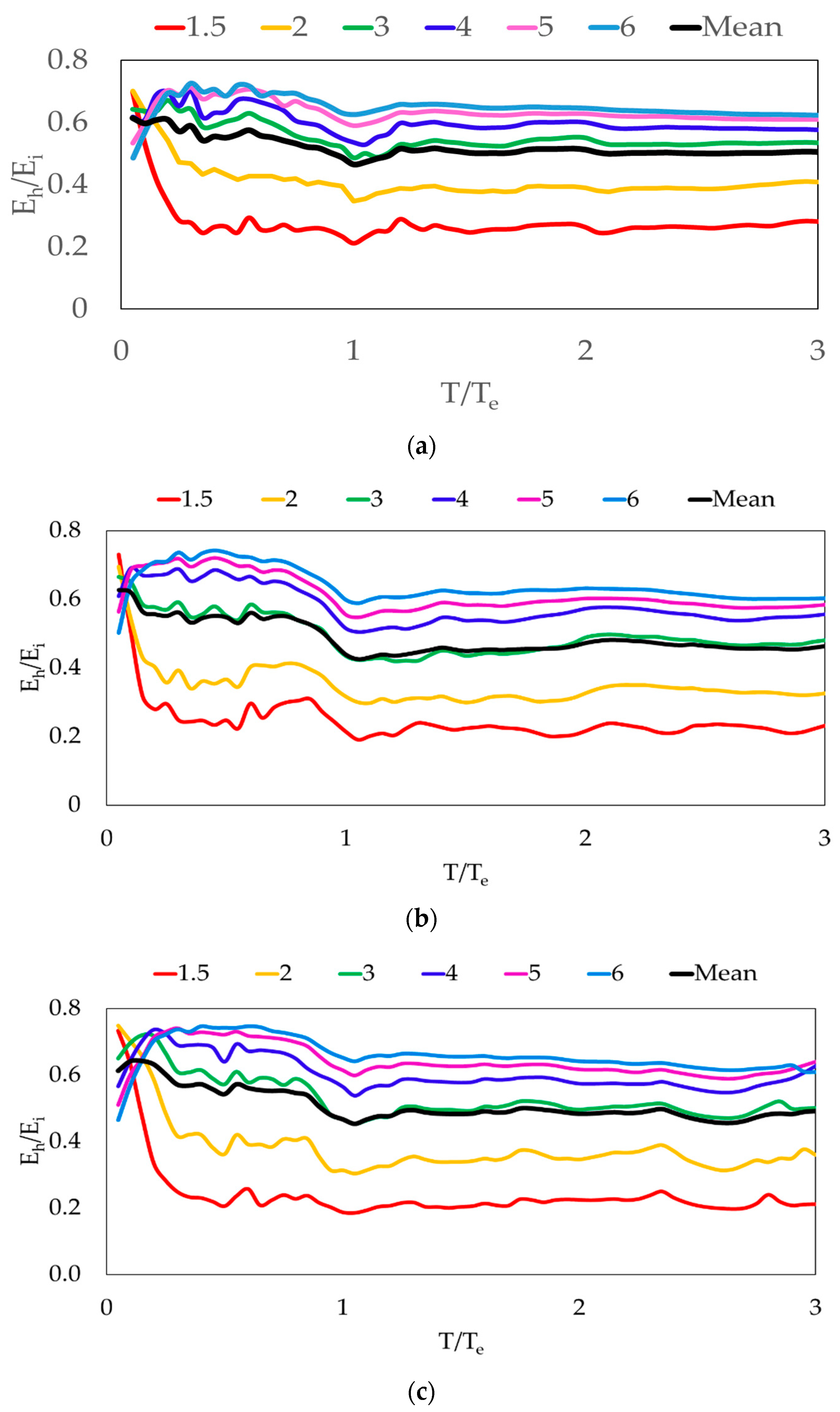
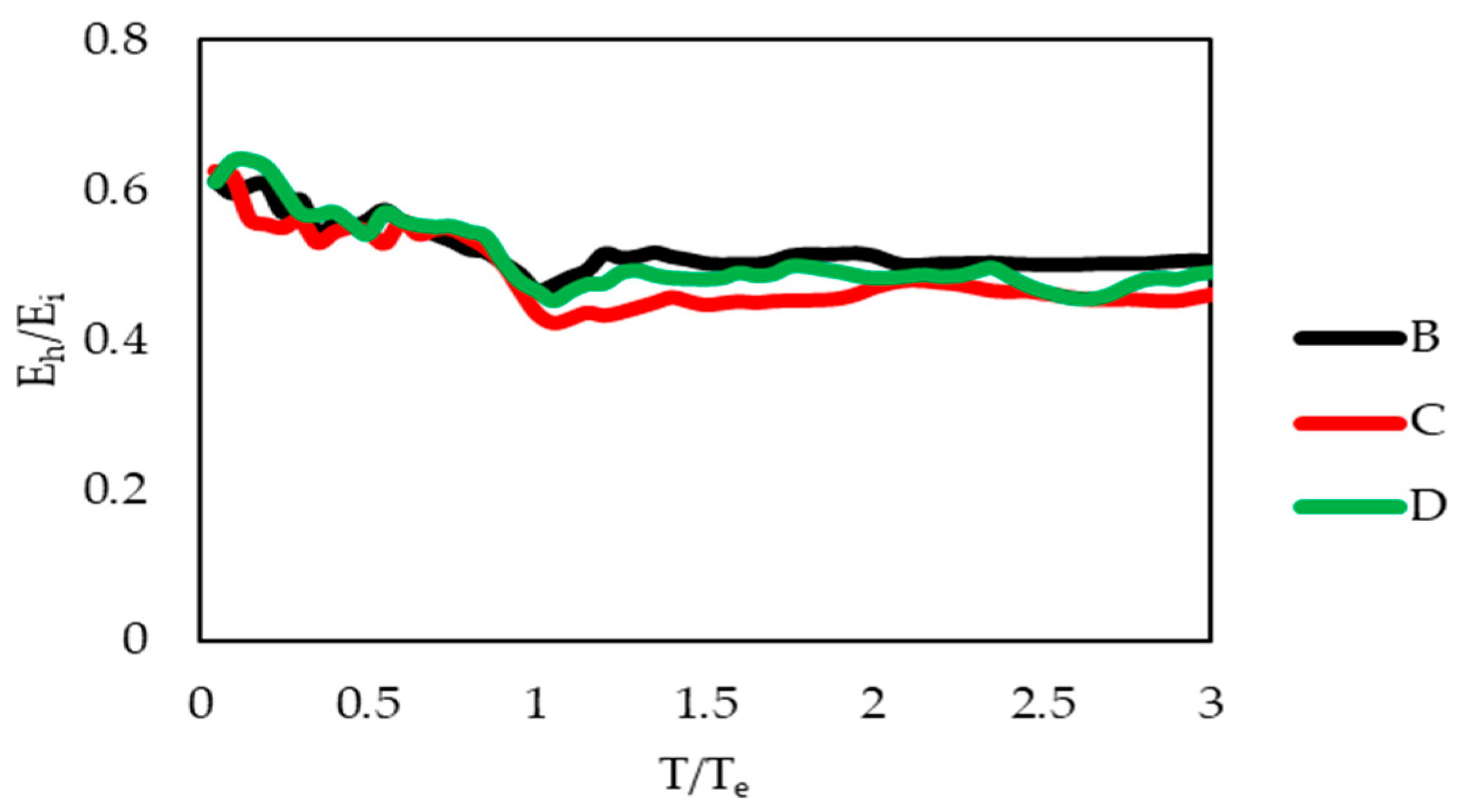
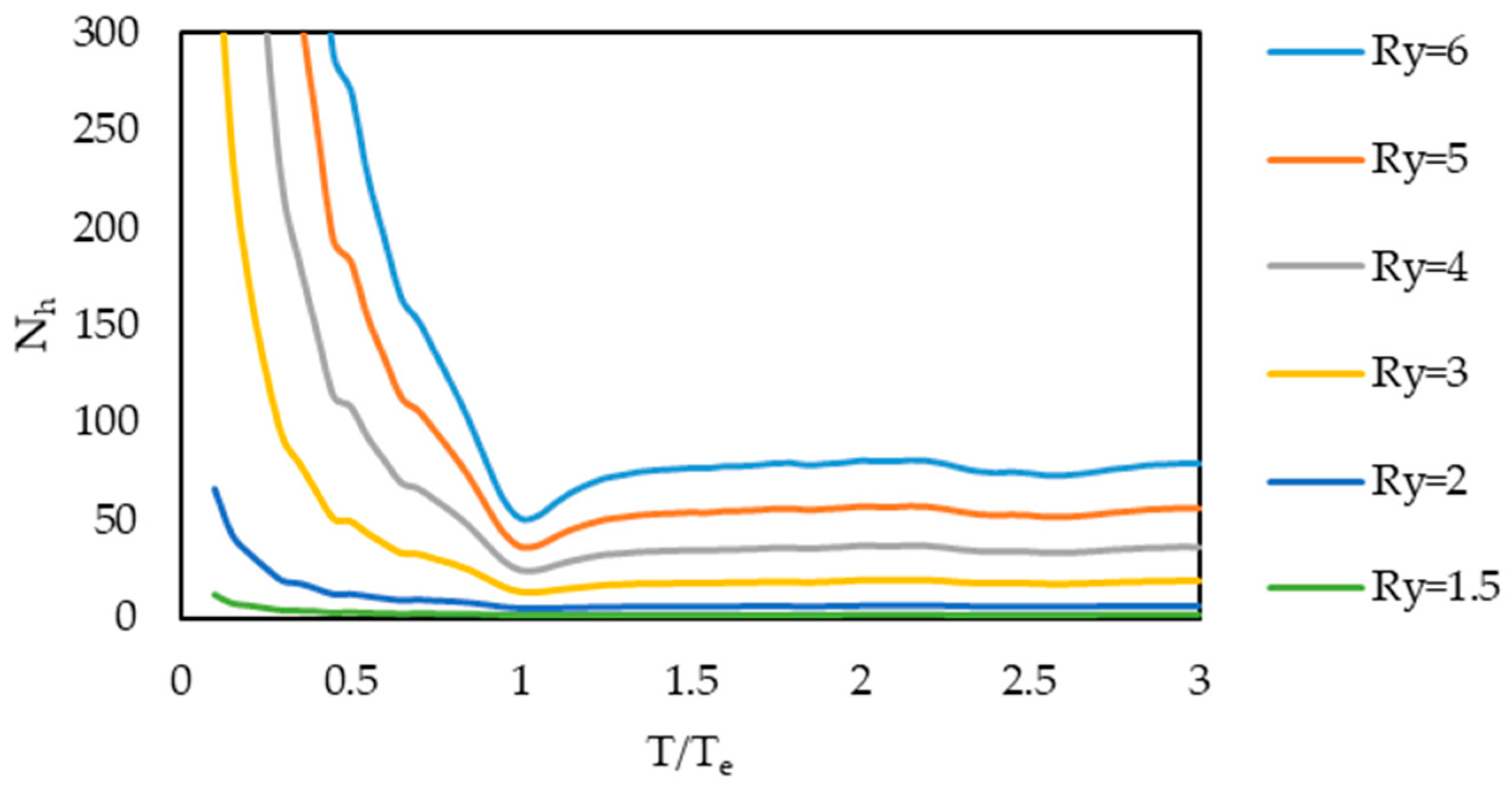
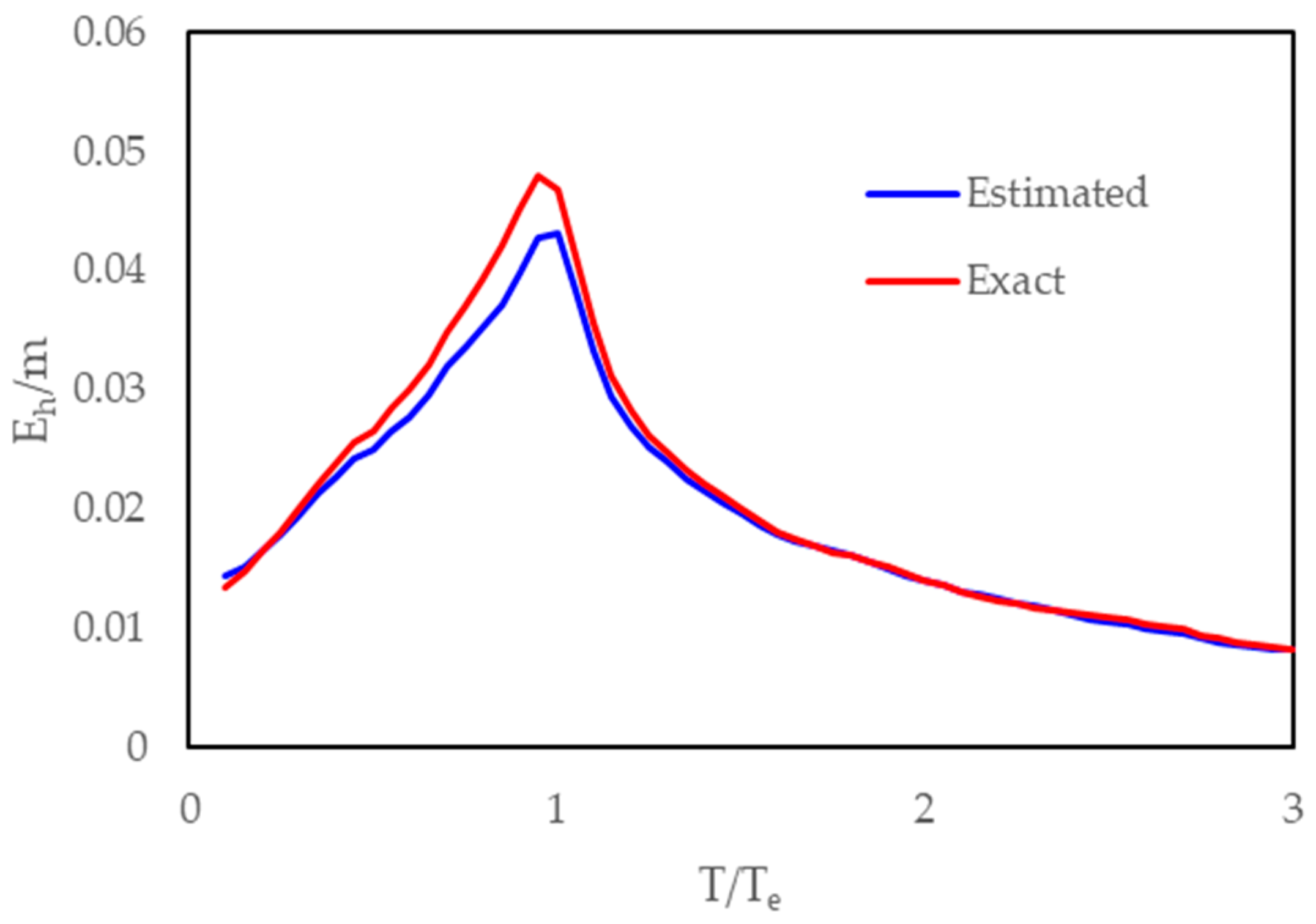
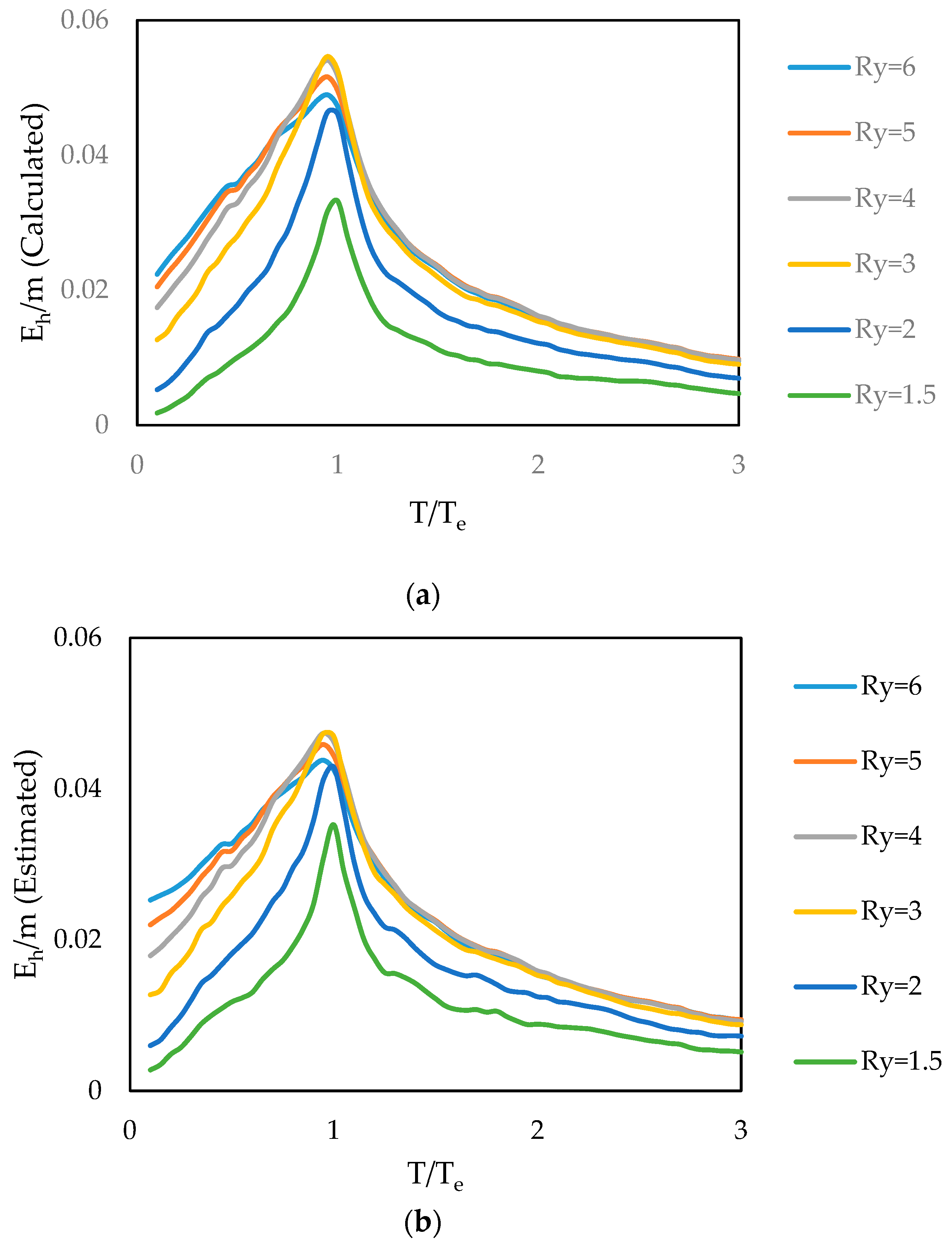
• The mean hysteretic energy demand decreases on average with increasing strength of the system whose period is less than approximately 0.75 T_e and higher than 1.1 T_e. Furthermore, the mean hysteretic energy demand is almost the same for systems with R_y ≥ 3 whose period is higher than 1.1 T_e (Figure 21).
• The spectral shape of the mean hysteretic energy and ductility demands exhibits different trends, while the mean normalized hysteretic energy spectrum shows the same tendency as the mean ductility demand spectrum (Figure 15).
• Normalized hysteretic energy and displacement ductility demands increase on average with decreasing strength (Figure 13 and Figure 16).

In future studies, the applicability of the proposed method under near-fault earthquakes should be investigated. Furthermore, effects of degradation, duration of ground motions, ground motions recorded on soft soils, and soil–structure interaction can also be incorporated. Finally, it is worth noting that all the results obtained within the scope of this study are valid for structural systems that can be represented by equivalent SDOF models with periods falling within the investigated period range. Moreover, as mentioned above, there are conflicting results in the literature concerning the applicability of results derived from SDOF system analyses to MDOF structural systems. However, the authors believe that the equations derived in this paper are valid for systems that exhibit predominantly first-mode response behavior. Further studies are required to determine the numerical limits of the engineering parameters for the use of energy-based methods—developed with the results of single-degree-of-freedom systems—in multi-degree-of-freedom systems.