Abstract
Bridging the gap between Artificial Intelligence (AI)-driven generative design and robotic fabrication remains a critical challenge in architectural automation. While Generative Artificial Intelligence (GenAI) tools have advanced conceptual design workflows, their practical deployment in physical construction is hindered by the absence of structured, fabrication-aware datasets to train suitable AI models. This study introduces GDRF (Geometric Data for Robotic Fabrication), an automated pipeline for the generation, evaluation, and encoding of structurally feasible brick wall designs, enabling the creation of machine-learning-compatible data tailored for architectural robotic assembly. We developed a six-stage process that combines parametric modeling, algorithmic design generation, physics-based simulation, data encoding and storage, toolpath generation and assembly simulation, and physical robotic assembly with a robot. Over 33,000 wall configurations were synthetically generated and evaluated for structural stability, of which approximately 52% met the feasibility criteria. Stable and failed designs were identified through displacement-based criteria and encoded using dot-product-based rotational representation, reducing dimensionality while preserving critical geometric features. Comparative analysis revealed that brute-force generation produced more consistent outcomes, while random sampling achieved slightly higher local diversity. This study delivered a data pipeline and the BrickNet dataset, providing a foundation for future research in generative design, structural prediction, and autonomous robotic assembly.
1. Introduction
The integration of AI and machine learning (ML) into architectural design and construction has led to the emergence of computational workflows that combine algorithmic creativity with data-driven optimization. While Generative AI (GenAI), including models such as Generative Adversarial Networks (GANs) [1], Variational Autoencoders (VAEs) [2], and Diffusion Models [3], has shown promise in early-stage architectural design ideation of spatial compositions [4,5,6], morphological variations [7,8,9], facade typologies [10,11,12], and material variations [13], to date, their successful implementation in robotic fabrication has been limited.
A defining characteristic of such AI-driven workflows is their dependence on extensive, high-quality datasets [14,15,16]. In deep learning (DL), data quality and volume often have a greater impact on the performance of the trained DL models than the underlying architecture or training techniques [17]. The success of GenAI in domains such as 2D layout generation and conceptual design is largely attributable to the availability of large datasets [15]. In contrast, the field of robotic fabrication, particularly within architecture, suffers from a pronounced data scarcity problem. Unlike domains such as computer vision or natural language processing, where large standardized datasets like ImageNet [18] and Common Crawl [19] support scalable model development, architectural robotics lacks publicly available, scalable, and fabrication-aware datasets.
This scarcity stems from several interrelated challenges. High-fidelity fabrication data is difficult and costly to obtain, as physical experimentation in robotic construction is time-consuming, labor-intensive, and highly dependent on material and contextual variables [20]. As a result, most available datasets are narrow in scope, limited in size, or lack structural and physical validation [21]. DL models trained on abstract geometry alone lack awareness of critical constraints such as constructability, stability, robot reachability, and assembly sequence logic [22], all of which are essential for real-world deployment. This deficiency limits the generalizability and practical application of AI models [23,24,25], especially in domains requiring material-aware, constraint-compliant, and physically realizable outputs.
This disconnect leads to a design-to-fabrication gap, which is particularly pronounced in robotic assembly workflows, where digitally created forms must be translated into executable operations for industrial robots. In robotic bricklaying, one of the most studied domains of automated construction [26], designs must satisfy both architectural intention and physical feasibility. This includes collision-free toolpaths, structural stability, geometric tolerances, material behavior, and executable assembly sequences [27,28]. Without structured datasets that embed these criteria in a machine-readable format, most generative design models operate in abstraction, thus limiting their application to virtual simulations and undermining their utility in real-world fabrication contexts.
Despite growing interest in AI-driven generative design, a clear research gap remains: the absence of structured, fabrication-aware datasets that integrate material, structural, and robotic constraints into a machine-readable format suitable for training deep learning models. Existing architectural datasets capture geometry or form but rarely encode the physical and procedural information required for robotic assembly. Consequently, generative models in architecture continue to operate largely in abstraction, with limited capacity for real-world fabrication.
One promising approach to bridging this gap lies in the use of synthetic datasets that explicitly embed fabrication constraints into their structure. Synthetic datasets, which integrate algorithmic design, simulation, and constraint-aware encoding, have already demonstrated substantial success in several deep learning domains. Notable examples include robotic manipulation and control [29], machine vision [30], material defect detection [31], medical imaging [32] and industrial applications [33], where synthetic data has enabled robust model training in the absence of large-scale existing data. Although successful in different domains, their adoption in architectural fabrication has been less explored.
This study aims to address this gap by proposing a structured pipeline for synthetic dataset generation, focused on dry-stacked brick wall designs for robotic assembly as a case study. This article expands upon an earlier version of this work presented at CAADRIA 2025 [34], with substantial extensions and revisions in methodology, dataset evaluation, and physical robotic testing.
This article makes the following primary contributions to the field of AI-driven generative design for architectural robotic assembly:
- A six-stage synthetic data creation pipeline that integrates parametric modeling, algorithmic pattern generation, real-time physics simulation, and robotic toolpath generation for fabrication-aware brick wall designs.
- A domain-specific geometric encoding strategy based on dot-product transformations, enabling dimensionality reduction while retaining essential orientation information for ML-based predictive or generative applications.
- A comparative evaluation of sampling strategies (brute-force vs. stochastic sampling) assessed using entropy metrics, PCA, t-SNE embeddings, and nearest-neighbor distance analyses to quantify dataset diversity and redundancy.
- Physical assessment of selected designs via robotic assembly, highlighting discrepancies between simulation and reality, and identifying opportunities for feedback loops and tolerance-aware robotic control systems.
By providing a reusable, fabrication-aware synthetic data generation methodology, this work contributes essential tools and a dataset toward enabling deep learning techniques within robotic fabrication workflows in architecture. This article serves as both a methodological framework and a proof-of-concept, demonstrating how synthetic data, when embedded with physical constraints and tested with a robot, can bridge the gap between computational creativity and built reality.
The remainder of this article is structured as follows: Section 2 reviews the challenges associated with data scarcity in architectural robotics and highlights related work in generative design, simulation-driven evaluation, and dataset creation for AI-driven fabrication. Section 3 presents our proposed methodology for generating a fabrication-aware synthetic dataset, detailing a six-stage pipeline that integrates parametric modeling, generating wall patterns, physics-based simulation, and data storage, followed by toolpath generation for robot and robotic assembly. This section also introduces and compares three geometric encoding strategies tailored for machine learning applications. Section 4 provides an in-depth analysis of the generated dataset, comparing brute-force and stochastic sampling approaches using statistical measures, dimensionality-reduction techniques, and class-level performance metrics. Then, it outlines the physical assessment process and discusses discrepancies observed between simulated and physical assembly results. Finally, Section 5 offers a critical discussion of the method’s implications, limitations, and generalization potential, while Section 6 concludes with key contributions and directions for future research in AI-assisted robotic construction.
2. Literature Review
2.1. Dataset Limitations in Architectural Robotic Fabrication Research
Recent research in AI-driven architectural design generation has increasingly focused on creating building layouts, particularly for spatial planning. This focus on spatial planning is largely due to availability of existing datasets such as RPlan [35], CubiCasa5K [36], Structured3D [37], and Reco [38]. Additionally, a common approach uses large-scale web scraping to extract design data from public sources, as shown by Park, Gu [39], enabling the compilation of extensive architectural repositories. These datasets fueled growth in spatial planning research using DL techniques.
However, the current trajectory in architectural research and practice has created a widening gap between design concepts and fabrication-ready solutions suitable for robotic construction. At the core of this divide lies a scarcity of high-quality, publicly accessible datasets tailored for robotic fabrication. The difficulty of data acquisition in architecture is not simply a matter of insufficient quantity; it is an inherently complex and multifaceted challenge. Architectural data is fundamentally heterogeneous and multi-modal, spanning geometric forms, structural forces, material properties, environmental conditions, and intricate fabrication constraints, all intertwined with abstract design intent. Collecting and curating such diverse information is not only time-intensive and costly but also riddled with technical obstacles.
Projects such as KnitCone [40] and the Bridge Too Far [41] exemplify the pioneering efforts being made to generate architectural fabrication datasets. The former demonstrates how seven carefully constructed physical samples were expanded into a dataset of 8000 samples through data augmentation, while the latter achieved the capture of 45,000 samples derived from ten panels by 3D scanning. These contributions represent advances in addressing the scarcity of data for robotic fabrication, offering valuable strategies for extending limited physical samples into larger datasets. At the same time, they also underline the considerable effort, resource intensity, and scalability constraints that remain inherent in physical data collection. Together, these projects highlight both the ingenuity of current research and the pressing need for more efficient, scalable, and automated data generation methods in architectural applications.
Common data acquisition methods like 3D scanning, while useful, encounter limitations for certain materials. Shiny, transparent, or highly textured surfaces frequently yield noisy, inaccurate scans as a result of specular reflections, insufficient depth cues, or multi-pathing in structured light systems [41]. These challenges directly compromise the fidelity and consistency of datasets derived from physical objects, fundamentally limiting their utility for training models that require precise geometric or material property understanding for fabrication. Furthermore, these physically derived datasets often lack an inherent encoding of critical fabrication-aware information, such as structural feasibility [42], or assembly sequence logic [43], necessitating laborious manual annotation or computationally expensive post-processing to be machine-actionable.
Attempts to circumvent these challenges through synthetic data generation, as seen in [44] with their parametric dataset of 60,000 volumetric geometries, offer promise in bypassing scanning errors and enabling controlled variability. However, such efforts often prioritize abstract volumetric representation. A dataset composed of 24 × 24 × 24 voxel grids, while computationally tractable, typically lacks granular geometric precision and embedded assembly sequence information that is paramount for direct translation to executable robotic toolpaths. This highlights a crucial, persistent gap: existing synthetic data for architecture largely remains on a conceptual or abstract level, rarely designed from its inception to be “fabrication-aware” or directly integrable into industrial robotic workflows.
2.2. Alternative Approaches in Integrating DL in Generative Design for Robotic Fabrication
Over the past decade, efforts to integrate DL into design and robotic fabrication have seen significant advancements, yet many remain critically limited by the scale, abstraction, and inherent biases of their underlying datasets. While approaches such as Wu and Kilian’s [20] Stochastic Assembly demonstrated an innovative use of computer vision for emergent assembly patterns, their bottom-up, purely vision-driven methodology prioritized structural emergence over explicit architectural design intent. This reliance on emergent behavior can lead to uncontrolled variability and non-deterministic outcomes, posing challenges for the reliability and repeatability demanded by real-world robotic construction where safety and precision are paramount. Moreover, such systems often lack the predictive capacity or inverse design capabilities that would allow a designer to specify desired formal or functional outcomes and reliably generate feasible fabrication sequences.
Reinforcement Learning (RL) presents an appealing alternative to supervised learning by theoretically reducing reliance on extensive pre-labeled datasets. Studies exploring RL for physical assembly, including voxel-based design generation [45,46], blueprint-free bridge construction [47], robotic block stacking [48], or vault construction [49], have shown conceptual promise. However, these RL-based approaches typically operate on highly simplified geometries within idealized, often discretized, simulation environments. While seemingly flexible and physically feasible, this approach can lead to solutions that lack architectural expressiveness or alignment with broader design principles. Furthermore, the long training durations and the inherent sample inefficiency of RL for complex, high-dimensional action spaces common in robotic construction also render it impractical for rapid design iteration in real-world scenarios.
2.3. Bridging the Gap with Constraint-Aware Synthetic Data
Addressing similar challenges across various domains, other fields have successfully leveraged data-efficient ML techniques such as transfer learning [50], active learning [51], one-shot learning [52], multi-task learning [53], and robust data augmentation [54,55]. These strategies have proven invaluable in contexts where labeled data is inherently expensive or scarce, ranging from drug discovery to environmental sensing. However, their direct application to fabrication-aware architectural design remains underexplored, primarily because existing architectural datasets focus on abstract geometric representation or visual aesthetics and lack information on structural integrity, material limitations, collision avoidance, or assembly sequencing logic. For instance, while data augmentation can increase sample size, it cannot introduce new physical principles or validate against fabrication constraints not present in the original, often limited, real-world data. As highlighted by Mitrano and Berenson [56], the core issue is not simply the volume of data, but its semantic richness [57] and physical validity in relation to the specific demands of robotic construction. Most general-purpose ML datasets lack the multi-modal encoding necessary to capture the complex interplay between design intent, material behavior, and robotic executability.
Consequently, despite the advancements in both generative AI and data-efficient learning, a critical void persists. While progress has been made, there remains no widely adopted strategy that can both generate and validate physically fabricable structures at an architectural scale using general-purpose collaborative robotic arms and simultaneously encode fabrication constraints in a machine-readable format for scalable ML training. This research is one of the first steps to overcome this gap.
3. Materials and Methods
This section presents a comprehensive and replicable methodology for generating robust datasets for fabricable structures, focusing on stacked brick walls assembled via robotic arms. The workflow integrates parametric design, physics-based simulation, automated data generation, encoding, and robotic stacking, ensuring machine learning compatibility and structural validity.
3.1. Data Requirements for Robotic Assembly
A fundamental requirement for robotic assembly is the availability of accurate digital representations of all elements involved in the process. These elements include CAD models of the robotic system and the assembly units (in this case, the bricks). Equally essential are the kinematic descriptions of the robot and the specification of target object poses, particularly the relative transformations between components in their assembled state, as emphasized by Thomas and Wahl [58].
In this study, we employed Grasshopper3D (version 1.0.0008) as the parametric modeling environment, utilizing the Robots plugin for robotic task and motion planning. Within this environment, the position of each brick is defined by a local coordinate plane placed at its centroid. These planes include the essential positional and orientational data required for assembly operations, and they serve as the primary data for robot programming. Through inverse kinematics, the Robots plugin computes the necessary robot toolpaths based on these planes. We used a UR10 collaborative robotic arm equipped with a Robotiq 2F-85 servo-electric adaptable gripper, manufactured by Robotiq Inc. in Quebec, Canada, for physical assembly tasks.
3.2. Dataset Framework for Machine Learning
The development of a dataset intended for machine learning applications requires careful consideration of both data quality and structure. To ensure the dataset’s effectiveness, we adopted the recognized “5Vs” framework, which defines the essential characteristics of big data—volume, velocity, variety, veracity, and value—as outlined by Zhou, Pan [59]. Volume refers to the quantity of data within the dataset; velocity concerns the speed at which data is generated; variety addresses the diversity of data; veracity pertains to the accuracy and reliability of the data; and finally, value assesses the usefulness or relevance of the dataset.
To meet these criteria, we developed a data generation workflow, which will be described in detail in the following section. The performance of the proposed workflow, evaluated within the context of the 5Vs framework, will be presented in Section 5 (Discussion).
3.3. Computer Setup
All computations were performed on a workstation equipped with a 12th Gen Intel® Core™ i7-12850HX (2.10 GHz) processor, 32 GB of RAM, and an NVIDIA RTX A4500 GPU, operating on Windows 11 Enterprise.
3.4. Workflow for Data Generation and Physical Assessment
The overall methodology follows a structured workflow consisting of six key stages (Figure 1):
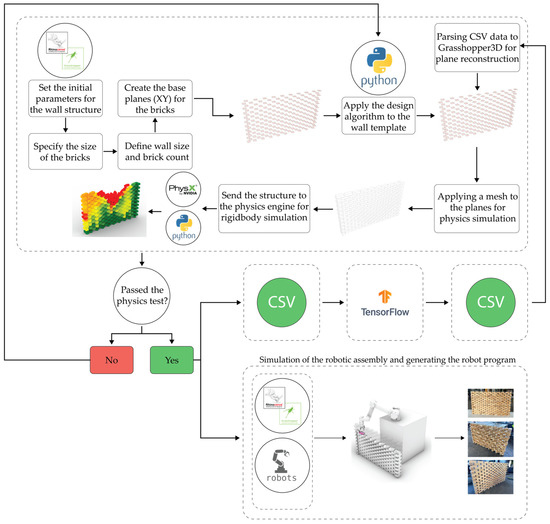
Figure 1.
Diagram showing step-by-step workflow of GDRF workflow.
- parametric modeling
- design generation
- physics simulation
- data storage
- robotic toolpath generation
- robotic assembly
Parametric modeling involves the development of a computational model of dry-stacked brick walls using Grasshopper3D. The model enables precise control over the geometric and structural parameters that define the wall configuration, including brick dimensions, bonding patterns, and wall height and length. In this study, these parameters were fixed to ensure consistent structural and robotic testing conditions; however, they can be modified for other fabrication scenarios. Beyond these basic parameters, the model incorporates a generative parameter, the rotation of individual bricks within the XY plane, which drives the formal variation in wall patterns. The details of the model parameters and their description can be found in Table 1.

Table 1.
This table summarizes the parameters in the parametric model of the walls.
The parametric setup defines one primary variable, brick rotation within a range of 0° to 90°. Because each brick can independently rotate within this interval, the theoretical design space is continuous and combinatorially vast. To generate patterned wall classes, three rotation-driving strategies were implemented: (1) attractor curves, (2) attractor points, and (3) mathematical functions (e.g., sinusoidal wave function).
In attractor-based methods, rotation intensity is determined using Inverse Distance Weighting (IDW), producing smooth gradients of rotation that preserve continuous brick-to-brick contact and avoid destabilizing discontinuities. The IDW method is particularly suitable for this application because it provides a continuous and spatially coherent influence field, in which bricks closer to an attractor experience stronger rotation while distant bricks remain minimally affected. This ensures that geometric transitions remain smooth, avoiding abrupt misalignments that could disrupt physical brick contact and reduce structural stability. IDW is also computationally lightweight, deterministic, and easily parameterized, making it well suited for large-scale generative sampling and for maintaining consistency across thousands of automatically generated wall patterns.
To create a tractable subset of this design space, two sampling strategies were employed: brute-force and random sampling. In the brute-force strategy, systematic sampling was performed over the discretized parametric control variables that generate rotation values for each brick, based on the three algorithmic design methods explained earlier. A standard runner-bond wall template is used as the geometric baseline, and rotation fields are then applied algorithmically to produce patterned wall classes. For Classes 01–10, which are governed by a single attractor curve, two scalar parameters control rotation behavior: (1) a parameter influencing bricks within the attractor’s field of effect (via Inverse Distance Weighting), and (2) a parameter defining the rotation of bricks outside that influence. Both parameters are discretized over a range of 0–90° in 2° increments, yielding 46 × 46 = 2116 unique parameter combinations per class. For each parameter setting, the brick-level rotations are determined deterministically by the parametric model, ensuring systematic and uniform design coverage.
Classes 11–14 utilize attractor points rather than curves and therefore incorporate a third degree of freedom: the position of the attractor point. In these classes, rotation intensity is again discretized over 0–90° at 2° resolution (46 levels), while the attractor position parameter is sampled over 0–1.0 at 0.1 increments (11 levels), and the radius of influence parameter varies from 0.2 to 1.0 in 0.1 increments (9 levels). This produces 46 × 11 × 9 = 4554 combinations for single-point attractor configurations. For dual-attractor cases, symmetry reduces the feasible parameter combinations, resulting in 46 × 5 × 9 = 2070 variations per class.
In parallel, the random sampling strategy draws the same parameter variables from the same bounds as continuous values rather than on a discrete grid. This allows random sampling to explore intermediate states between brute-force grid points while maintaining full comparability between methods.
The generated configurations include examples such as alternating rotations between odd and even brick courses; single vertical attractor curves placed along one edge of the wall; diagonal attractors extending from corner to corner; and other attractor fields such as cross-shaped, circular, V-shaped, and S-shaped curves influencing rotation gradients. Other cases employed dynamic point attractors with variable position, radius, and strength, either singular or paired in horizontal or diagonal alignments, while the final configuration was driven by a sinusoidal mathematical series, producing periodic undulations across the wall surface. Figure 2 shows examples of these wall patterns.

Figure 2.
Samples of various wall patterns that were generated using different parametric techniques, including attractor points, attractor curves, and mathematical functions.
Following the generation of each wall configuration, we conducted structural simulations to evaluate structural feasibility. These simulations were carried out using the NVIDIA PhysX engine (PhysX.GH version 0.1), which enabled real-time rigid-body analyses of the brick assemblies. NVIDIA PhysX was chosen among various simulation engines due to its ease of integration within the Grasshopper3D environment and its superior performance over alternatives such as Bullet in simulating simple geometries [60]. The effectiveness of the PhysX engine for discrete assembly tasks involving brick-like or other rigid components has also been demonstrated in previous studies [61,62,63,64]. For the simulation, the walls were modelled as static dry-stack structures, with bricks assigned the material properties of timber (The material we used to create our bricks and build the walls in this study), including a static friction coefficient of 0.55 and a coefficient of restitution between 0.6 and 0.64, in line with the values reported by Gallego, Fuentes [65].
The structural stability of each wall configuration was evaluated based on a maximum displacement criterion. Any design in which the maximum displacement of a brick exceeded a threshold of 2 mm (mm) under simulated loads was classified as structurally unstable and excluded from the final dataset. This threshold was not arbitrarily chosen but was determined through an empirical calibration process involving iterative simulations across a diverse range of wall designs. These test cases spanned a variety of geometric patterns and structural configurations, providing a robust basis for the evaluation. More conservative thresholds (e.g., 1 mm) were found to be overly restrictive for some cases, often disqualifying designs that maintained sufficient structural integrity and geometric alignment. Consequently, the 2 mm threshold was adopted as a practical and conservative balance between these two competing performance criteria: essential structural performance and the preservation of the intended geometric form and visual appearance.
Each wall configuration was evaluated using a 30-s simulated settling period, discretized into 20 solver steps. This lightweight configuration enables rapid throughput, theoretically allowing the assessment of up to two wall configurations per minute. In cases where displacement values approached the 2 mm stability threshold (borderline cases), the simulation duration was extended to ensure that the final structural state was correctly classified. This approach provides an effective balance between computational efficiency and reliable performance screening across the full dataset. While this simplified settling regime prioritizes scalability over fine-grain physical accuracy, the extended evaluation of marginal cases ensured consistent classification performance where instability was ambiguous. Figure 3 illustrates a sample wall structure in a borderline condition, which was simulated for 150 s for visualization purposes. The color gradient transitions from dark green to light green, then to yellow, orange, and finally red, reflecting increasing levels of displacement and risk of failure. The images from left to right and top to bottom show the condition of the wall in time steps of 10, 30, 60, 90, 120 and 150 s.
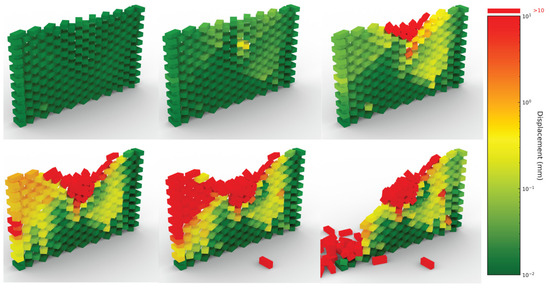
Figure 3.
Snapshots illustrating displacement-based color coding of bricks, indicating the least displaced bricks (dark green) and failed bricks (red).
To automate the generation and evaluation process, Python (version 3.9.1) scripts were embedded within the Grasshopper3D environment to systematically vary input parameters. These scripts implemented both sampling strategies described above, automatically generating the wall geometry, running the stability simulation, and storing the results. For each design iteration, the full workflow was executed without manual intervention, enabling efficient and repeatable dataset creation at scale.
Configurations passing the stability assessment were stored in a tabular format. Each valid configuration was recorded as a CSV (comma-separated values) file containing detailed information for every brick, including dimensions, spatial coordinates, and rotational vectors. This tabular format was selected for its compatibility with common machine learning libraries such as Pandas (https://pandas.pydata.org/, accessed on 15 September 2025), enabling efficient data handling and downstream analysis. Although the computational model developed in this research supports exporting data to multiple file formats, including image formats (such as PNG and JPG), 3D geometry formats (such as OBJ), and structured text-based formats (such as JSON), the CSV format was specifically chosen for its effectiveness in storing structured numerical data.
3.5. Characteristics and Details of Wall Data
The primary data type selected to meet the geometric and construction requirements of the wall design was the plane. In computational design, “planes” are geometric entities that encode both the position and orientation of objects in three-dimensional (3D) space. This information is essential for two key purposes: (1) constructing geometries in Grasshopper3D, and (2) serving as the foundational input for defining target points in robotic fabrication, where toolpaths are derived directly from these planes.
Each plane comprises six essential components: three positional coordinates (x, y, and z) that specify its location in 3D space, and three directional vectors that define its orientation. Each vector contains three parameters (x, y, and z), and together these three vectors define the plane’s orientation in space. As a result, every plane includes a total of twelve numerical features per brick (three for position and nine for orientation).
In this study, each wall was limited to 180 bricks. This quantity balances sufficient geometric and structural complexity with the operational reach of a fixed UR10 robotic arm. Consequently, each wall initially contains 180 × 12 = 2160 features. Such a high-dimensional dataset poses challenges for machine learning (ML) applications, particularly due to the curse of dimensionality, which can lead to poor model performance and computational inefficiency [66].
To address this, we carefully examined the dataset with the aim of reducing dimensionality and simplifying the problem. Notably, in all wall configurations under study, the positional coordinates of bricks remain constant; only the rotational orientation of the bricks varies. Therefore, we excluded the positional data from the dataset, treating it as a static template. Our parametric model was designed accordingly: it first generates the wall geometry using a grid of XY-planes (representing the brick positions), after which the planes are rotated according to various algorithms.
We tested three approaches for representing the rotational data of individual bricks for ML applications:
- (1)
- Full Geometric Representation:
In this approach, we preserved all rotational features. For each wall, the directional vectors of all bricks were recorded, resulting in nine features per brick (three vectors, each with X, Y, and Z components) and thus 9 × 180 = 1620 features per wall. This format retains comprehensive geometric information but remains high-dimensional.
- (2)
- Grayscale Encoding Based on Rotation:
The grayscale encoding process was implemented in Rhinoceros 8 using Grasshopper3D (version 1.0.0008). Each brick’s rotation angle (0–90°) was normalized to an 8-bit grayscale range (0–255), where 0 corresponds to no rotation (lightest tone) and 255 represents maximum rotation (darkest tone); (Figure 4). This drastically reduces the dimensionality to a single feature per brick (i.e., 180 features per wall). However, this approach requires data conversion from rotation angles to color-codes and vice versa, which might result in some precision loss during the conversion process.
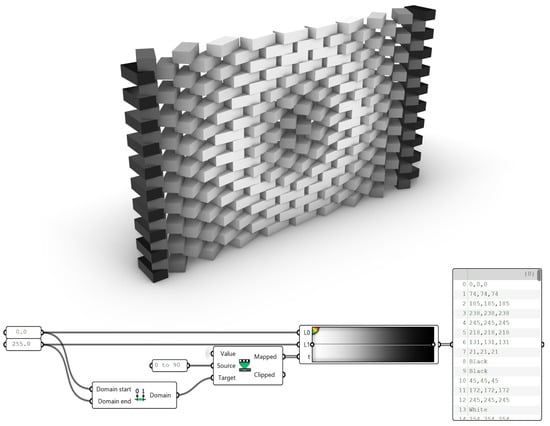
Figure 4.
The bricks in the wall are color-coded using grayscale values ranging from 0 to 255, mapped from rotation angles between 0 and 90 degrees.
As shown in Figure 4, bricks with zero rotation appear white, while those rotated by 90 degrees are shown in black. Intermediate rotation angles are represented by varying shades of gray (higher rotations are darker). The Grasshopper3D definition snippet shown below the wall image illustrates the data-mapping process used to encode these values.
- (3)
- Dot Product-Based Rotation Encoding:
The third and final approach represents brick rotations by calculating the dot product between each brick’s X-direction vector and that of the corresponding brick in the reference (unrotated) wall configuration. The dot product yields a scalar value that corresponds to the cosine of the angle between the two vectors (Figure 5). For rotations ranging from 0 to 90 degrees, this produces values between 0 and 1 [67]. The dot product between two unit vectors inherently produce normalized values in this range. Additionally, the original rotation angles can be easily reconstructed by applying the inverse cosine function to the stored dot product values. This method reduces the dimensionality of the dataset to just one feature per brick resulting in 180 features per wall while preserving essential rotational information. Mathematically, the dot product is expressed as:
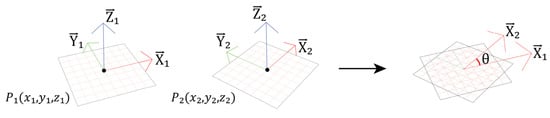
Figure 5.
Planes P1 and P2 are positioned at the same location but differ in their rotations within the XY plane. Because the Y vector is always perpendicular to the X vector, and the Z vector serves as the normal to the plane, both Y and Z can be excluded from the calculation as they can be fully determined from the X vector alone.
When both vectors are normalized to unit length, this simplifies to:
This compact and efficient representation thus offers both simplicity and fidelity for learning tasks.
Finally, the extracted features were stored in a comma-separated values (CSV) file, a simple and widely compatible format that enables easy data exchange between Grasshopper3D and machine learning environments such as Python. The use of CSV ensured minimal storage overhead and straightforward data management. Given the lightweight nature of the extracted features, no significant data storage limitations were encountered during dataset generation or processing. For reference, the file size per sample was approximately 13–15 kilobytes for the full geometric encoding, 4 kilobytes for the dot-product encoding, and 3 kilobytes for the color-coded method, confirming that all datasets remained compact and computationally efficient. The color-coded representation was more compact because it stored integer-based RGB values, whereas the dot-product encoding stored values with decimal points, which require greater precision and, consequently, slightly more storage per entry.
4. Results and Analysis
This section presents a comprehensive comparative analysis between two synthetically generated wall pattern datasets to identify advantages and disadvantages of each method: one dataset constructed through a brute-force strategy and the other via a random sampling approach. Each dataset comprises over 33,000 unique walls across 15 predefined pattern-based classes. To perform this comparative analysis, we employed several quantitative criteria, each chosen for capturing different aspects of dataset quality. Specifically, we used entropy to assess the variability and unpredictability in the dataset, offering insight into overall design diversity. Pairwise distance distributions were used to quantify how similar or different wall designs were from one another, revealing global redundancy or spread. Feature-space diversity was analyzed using PCA and t-SNE to visualize the structural layout and latent variation within the datasets. Nearest-neighbor overlap was used to measure the degree of novelty in the random dataset relative to the brute-force dataset, highlighting the extent of exploration versus redundancy. In addition, an artificial neural network (ANN) predictive model was trained to test and evaluate the dataset. Finally, a few randomly selected samples were tested for their physical validity through robotic assembly.
4.1. Quantitative Analysis of the Datasets
4.1.1. Description of the Synthetic Datasets
Two synthetic datasets correspond to 15 distinct wall classes developed through parametric modeling strategies described earlier. Each wall instance underwent a stability test (physics simulation), where outcomes were classified as either pass or fail based on whether the structure satisfied predefined physical criteria.
Wall typologies were generated using three distinct parametric modeling strategies, all based solely on brick rotation: attractor curves (Classes 01–10), attractor points (Classes 11–14), and a sinusoidal mathematical function (Class 15). For the first group (Classes 01–10), two control parameters set the minimum and maximum rotation angles for the bricks, defining how much each brick could turn within and beyond the attractor’s range. The second group (Classes 11–14) employed a more responsive model with three parameters: one controlling the rotation intensity (the strength of the attractor’s effect), one for defining the location of the attractor point(s), and one adjusting its radius of influence.
The empirical results reflected these modeling distinctions. Classes generated using the attractor-based parametric system (Classes 11–14) consistently achieved noticeably higher pass rates across both sampling methods, ranging from 74% to 82% in the brute-force dataset. In contrast, the earlier classes (Classes 01–10) performed less favorably, with pass rates typically ranging from 34% to 48%, suggesting lower inherent stability under the same test conditions. The random method produced similar aggregate results, with a global pass rate of approximately 52% in both datasets. However, class-specific outcomes varied slightly, as random sampling occasionally favored more structurally viable configurations, as observed in Class 15 (sinusoidal mathematical series). The dataset summary is presented in Table 2.

Table 2.
The table summarizes dataset sizes by wall class along with pass/fail rates.
These datasets offer a robust and controlled environment for investigating the relationships between generative design logic, geometric complexity, and structural performance. Moreover, they provide a valuable foundation for training and benchmarking machine learning models in tasks such as performance prediction, generative design optimization, and automated design space exploration. The inclusion of both sampling strategies and distinct parametric regimes enhances the potential for comparative analysis and supports broader inquiries into the role of geometry and control parameters in data-driven architectural design.
4.1.2. Nearest-Neighbor Distance Analysis Between Sampling Methods
To quantify the geometric similarity between the two sampling strategies, we computed the nearest-neighbor Euclidean distance from each sample in the random method dataset to its closest counterpart in the brute-force generated dataset. The distribution of these distances is visualized in Figure 6, which presents a histogram of the pairwise distances across all dimensions of the design space. The vast majority of distances cluster near zero, indicating that most randomly sampled wall configurations have a structurally similar counterpart in the brute-force-generated dataset. A red dashed line marks the mean nearest-neighbor distance, highlighting the central tendency of the distribution.
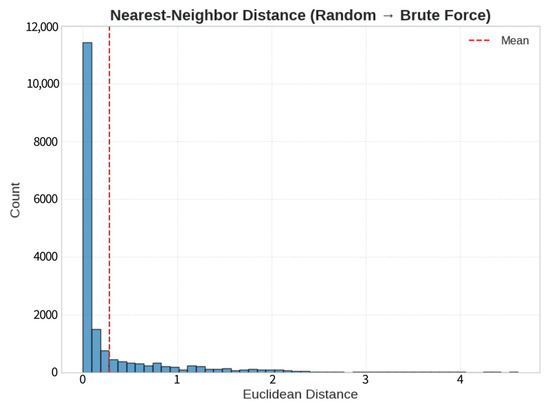
Figure 6.
Histogram displaying distribution of Euclidean distances between each point in the random dataset and its nearest neighbor in the brute-force dataset.
This dense concentration near the origin suggests that the random method did not diverge substantially from the overall design space explored via brute-force enumeration. Instead, it appears to have sampled configurations that are largely redundant or proximate to those already captured by brute-force generation. Nevertheless, the presence of a long-tailed distribution reveals that a smaller subset of random samples lies at a moderate or high distance from any brute-force equivalent. These may represent novel or underrepresented regions of the design space and could contribute added diversity or insight into geometric stability boundaries. Overall, this analysis reinforces the overlap between the two methods, while also suggesting the random method may offer marginal exploration beyond the deterministic brute-force scope.
4.1.3. Entropy Analysis
Figure 7 presents the entropy distribution across individual brick indices for both the brute-force and random generation strategies. Entropy, expressed in bits, is used here as a proxy for measuring the unpredictability and diversity of brick states across the dataset.
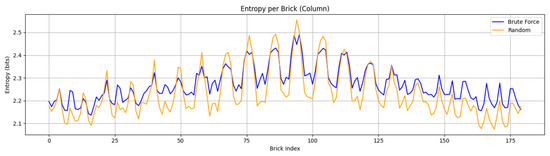
Figure 7.
A plot showing entropy per brick (column) across the dataset, comparing two methods: brute-force (blue) and random (orange). X-axis (brick index): Each number represents a column (brick position) in the wall dataset. Y-axis (entropy in bits): Entropy measures unpredictability or diversity of that brick’s states. Higher entropy means more variation across samples, and lower entropy means more predictable or repetitive patterns.
Overall, both methods exhibit entropy values between 2.1 and 2.5 bits, indicating moderate variability in columnar brick configurations. However, distinct differences in the behavior of the two methods can be observed. The random strategy produces a noisier profile, with frequent local fluctuations and pronounced peaks, suggesting higher variability and less structural consistency. In contrast, the brute-force approach yields a smoother curve, maintaining relatively stable entropy across indices, which points to more regulated distribution patterns.
A notable observation occurs between brick indices 70 and 110, where both methods reach maximum entropy levels (≈2.55 bits). This interval corresponds to the most unpredictable region of the wall dataset. Importantly, the random method consistently overshoots the brute-force method in these regions, highlighting its tendency to generate greater diversity at the expense of consistency. Conversely, at the boundaries of the structure (indices 0–30 and 150–180), entropy levels converge toward 2.1 bits, indicating that bricks at the periphery are more predictable, likely constrained by borderline conditions inherent to the dataset.
These findings suggest that the brute-force method is better suited for applications requiring controlled variation and structural coherence, while the random method is advantageous for maximizing unpredictability and novelty. In practice, the choice between the two depends on whether the design objective prioritizes stability or exploration of diverse configurations.
4.1.4. Dimensionality Reduction and Distributional Comparison of Sampling Strategies
To further investigate the structural distribution and diversity of the brute-force-generated and random datasets, we applied both Principal Component Analysis (PCA) and t-distributed Stochastic Neighbor Embedding (t-SNE) to project the high-dimensional design space into lower-dimensional representations. These visualizations allow for an intuitive assessment of dataset overlap, coverage, and sampling density within the latent geometry of the wall configuration space.
To reduce dimensionality and reveal underlying patterns in the data, PCA, a widely used multivariate statistical technique, was employed. PCA transforms inter-correlated quantitative variables into a smaller set of orthogonal principal components, enabling clearer visualization of similarities among observations while retaining most of the original data variance [68]. The 3D PCA projection (Figure 8) illustrates the first three principal components of the design feature space, capturing the directions of greatest variance. Both datasets exhibit a shared core structure with a dense overlapping region, suggesting that the random method effectively samples from the same dominant subspace as the brute-force method. However, the brute-force-generated dataset (blue) presents a more uniform lattice-like distribution, indicating systematic and even coverage. In contrast, the random dataset (orange) appears denser near the origin but shows sparser and more uneven dispersion along the peripheries of the principal component axes.
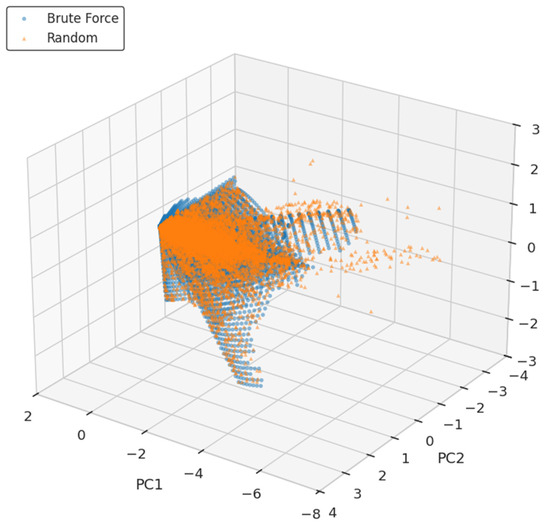
Figure 8.
3D PCA plot of the brute-force-generated dataset (blue) and the random-generated dataset (orange).
This relationship is confirmed in the 2D PCA overlay (Figure 9), which projects the first two principal components. Here, the brute-force-generated samples display clear linear banding, consistent with systematic parametric variation, whereas the random samples are more diffusely distributed within and between these bands. The two datasets substantially overlap, affirming that random sampling does not stray far from the manifold explored by brute-force enumeration; however, the less structured nature of the random dataset may result in redundant concentration near the dataset centroid and insufficient exploration of edge conditions. The overlapping regions suggest shared structural patterns, while dispersion differences indicate variance in sampling or data generation strategies.
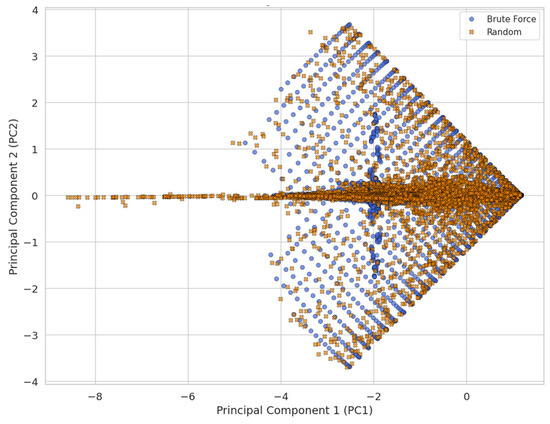
Figure 9.
2D PCA overlay of brute-force and random datasets.
The t-SNE projection (Figure 10) offers a nonlinear perspective, emphasizing local neighborhood relationships and clustering tendencies [69]. The visualization reveals that brute-force-generated samples (red) form well-separated, coherent clusters likely reflecting distinct parametric techniques or wall class boundaries. Random samples (blue), while still covering many of the same clusters, appear more diffuse and scattered, with several areas showing sparse or noisy sampling. Certain clusters present in the brute-force dataset have few or no corresponding random samples, indicating under-sampling of specific localized features or structural configurations.
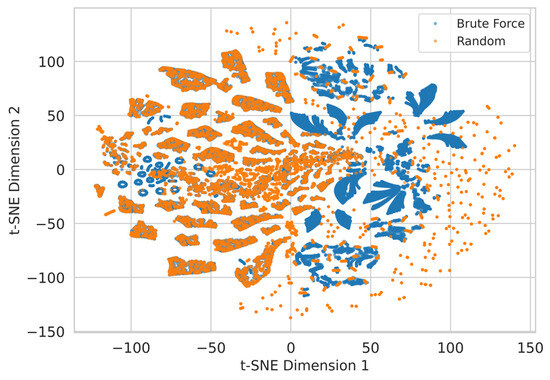
Figure 10.
A Scatter plot visualizing the t-SNE dimensionality reduction in brute-force (blue) and random (orange) datasets. Distinct clustering and shape patterns suggest structural differences in how each dataset samples the underlying feature space, despite partial overlapping in some regions.
Together, these dimensionality-reduction techniques reveal that while the random method does broadly cover the same geometric design space as the brute-force approach, it does so less uniformly and with lower structural granularity. The random dataset’s sampling strategy tends to concentrate near the data centroid and may fail to capture the full diversity of boundary cases or critical transitions. These findings emphasize the importance of sampling strategy in shaping not only dataset structure but also its utility for downstream applications in learning, optimization, or generative design.
4.2. Evaluation of the Dataset
To evaluate the dataset and explore predictive modeling of brick wall stability, we implemented a deep learning approach using numerical encodings of wall configurations. Each wall is represented as a 180-dimensional feature vector, where each value corresponds to a specific brick’s material or geometric parameter. The dataset consists of 17,748 stable walls and 16,289 failed walls, labeled with a binary outcome (1 for stable, 0 for failed). Prior to training, all features were standardized, and an 80/20 stratified train-test split was applied to maintain class distribution.
A fully connected Artificial Neural Network (ANN) was implemented to classify wall stability from the encoded rotation features on both datasets. The architecture included an input layer of 180 neurons (corresponding to brick-level geometric encodings), followed by three hidden layers with 256, 128 and 64 units, activated with the ReLU function and regularized with a dropout rate of 0.25 after the first hidden layer and 0.15 after the second. The output layer was a single sigmoid neuron that produced the predicted stability probability. The model was trained for up to 80 epochs using the Adam optimizer (learning rate: 0.001) with early stopping. Model performance was evaluated using accuracy, AUC, precision, and recall. To mitigate class imbalance and improve sensitivity to failure cases, class weighting was applied to up-weight the failed-wall category.
The performance of the trained ANN model on the encoded wall dataset is illustrated through several diagnostic plots and evaluation metrics. These figures collectively demonstrate the model’s learning behavior, classification capability, and generalization performance.
Figure 11 shows the performance of the ANN trained on the brute-force dataset. The loss curve (Figure 11a) shows both training and validation losses decrease steadily over epochs, indicating effective minimization of the objective function. The validation loss drops from roughly 0.21 to about 0.06 and remains consistently low with only minor fluctuations between epochs 5 and 15. There is no visible divergence between curves; instead, the gap narrows and stabilizes.
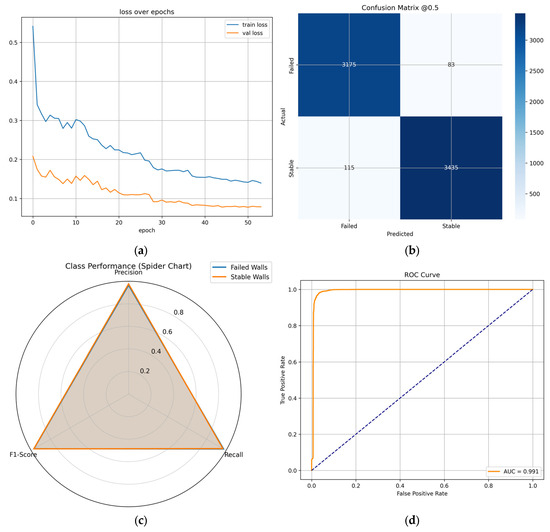
Figure 11.
(a) Shows the loss curve over 50 epochs. (b) A heatmap of the confusion matrix showing prediction outcomes. (c) Compares class-wise performance metrics—including Precision, Recall, and F1-Score—for failed walls (blue) and stable walls (orange). (d) Illustrates the True Positive Rate vs. False Positive Rate across thresholds.
The confusion matrix heatmap (Figure 11b) offers insights into the model’s predictive accuracy across the two target classes: “Failed” and “Stable” walls. The model accurately classifies a substantial number of instances, with 3175 (97.45%) true negatives and 3435 (96.76%) true positives. Misclassification rates are modest, with 83 (2.55%) false positives and 115 (3.24%) false negatives. Overall accuracy is 97.09% indicating a balanced and high-performing classifier, with relatively few misclassifications compared to the total sample size (n = 6808).
The radar chart (Figure 11c) compares precision, recall, and F1-score for each class. All three metrics are consistently high, with values nearing 0.97–0.99 for both classes. The two profiles almost overlap entirely, showing that the model performs symmetrically well across both categories. This indicates that the classifier effectively reduces both false positives and false negatives, and the balanced F1-scores confirm strong stability in prediction quality across classes.
The Receiver Operating Characteristic (ROC) curve (Figure 11d) reinforces the model’s discriminative power. The ROC curve closely follows the upper-left boundary, indicating excellent separation between classes. The area under the curve (AUC) is reported at 0.991, reflecting near-perfect binary classification performance. This high AUC value confirms the model’s strong sensitivity and specificity across varying classification thresholds.
The reported test accuracy of 97.09% aligns with the findings from the other evaluation metrics shown in the radar and ROC analyses, establishing the ANN model as highly effective in distinguishing between structurally “Failed” and “Stable” wall samples based on the encoded input features. Overall, the combination of high AUC, strong F1-scores, and high accuracy supports the conclusion that the trained ANN exhibits both precise and reliable performance on this classification task.
In summary, this work demonstrates the viability of deep learning in structural stability prediction using encoded wall patterns. The model not only performs with high accuracy but also provides interpretable insights into the role of individual bricks. This framework sets the stage for further integration into parametric design and robotic assembly workflows.
4.3. Robotic Assembly
To test the physical validity of the data produced, we randomly selected and built some wall samples from the dataset (Figure 12). We used custom-made timber blocks at ½ scale of an Australian standard brick. Despite acceptable outcomes in real-world tests, discrepancies were noted between digital simulations and physical assemblies, but these differences were marginal. Simulations assumed ideal material conditions (uniform brick dimensions, perfect surface alignment), which did not fully match the real-world conditions on materials such as variability in block size, edge defects, or surface irregularities. Such deviations, even as small as 1–2 mm, occasionally led to structural misalignments or assembly failures, particularly in tightly constrained designs.

Figure 12.
(a) Shows the digital representation of a wall sample. (b) The same wall sample after robotic stacking with timber blocks.
To improve fidelity between simulation and reality, it is critical to maintain a precisely calibrated robot, use dimensionally consistent materials, and ensure a flat, clean assembly surface. Additionally, minor deviations during placement, caused by release force or gripper recoil, can lead to cumulative errors affecting wall stability. Nonetheless, the implemented toolpath and physical setup proved effective, with wall assemblies demonstrating acceptable structural integrity and offering further potential for optimization in speed and reliability.
5. Discussion
The following discussion interprets the results of the proposed dataset generation and evaluation framework in relation to fabrication-aware design, data sampling, and structural performance. The findings reveal how embedding constructability constraints into generative logic transforms parametric design into a fabrication-informed process, while revealing trade-offs between geometric diversity, structural reliability, and computational efficiency in dataset creation.
5.1. Fabrication-Aware Parametric Modeling
A key strength of the proposed framework lies in its structured dataset generation pipeline. By grounding parametric wall generation in real-world fabrication constraints, such as buildable wall geometries, assembly sequence, and robotic limitations, the study moves beyond abstract computational design toward a materially grounded, construction-ready paradigm. Comparable integration of design intent, structural logic, and fabrication constraints has been demonstrated in cooperative human–robot frameworks such as the rule-based “assembly grammar” by Atanasova et al. [70], where geometric parameters and task data are encoded jointly to enable fabrication-aware assembly workflows.
The developed parametric logic establishes a consistent link between design intention and robotic constraints, aligning with the principle of “robotic constraints–informed design” explored by Devadass et al. [71]. Wall typologies are defined through three families of generative functions, each representing a distinct mode of spatial organization and level of geometric complexity, allowing systematic exploration of how local and global rotation fields can be parameterized for fabrication.
This fabrication-informed taxonomy provides the foundation for assessing how algorithmic variation influences structural behavior. By embedding constructability parameters directly within the generative logic, the framework ensures that every pattern produced, regardless of its geometric complexity, remains within the domain of robotic buildability. This approach demonstrates how parametric design can serve not only as a creative engine but also as a constraint-aware system capable of producing fabrication-ready, data-rich geometries for downstream AI workflows.
5.2. Evaluation of Data Sampling Strategies
The two sampling strategies (brute-force and stochastic) demonstrate complementary strengths. The brute-force approach ensures uniform, systematic coverage of the discrete design space, yielding predictable and reproducible structural outcomes. This systematic coverage provides a reliable benchmark for assessing model behavior and serves as a stable training baseline for downstream learning tasks.
In contrast, the stochastic method employs continuous sampling, enabling smoother local variation and, in some cases, generating novel configurations beyond the brute-force grid. The PCA revealed that while some random samples remained clustered within already explored regions of the design space, others extended beyond the areas covered by the brute-force sampling. Although this finding suggests a theoretical potential for finer exploration, the observed benefits were limited in practice, raising questions about the efficiency of unconstrained randomness in high-dimensional design domains. Moreover, geometric novelty does not necessarily correspond to improved structural behavior; diverse configurations may instead introduce instability. Further discussion of these effects is provided in Section 5.3.
The comparison underscores a fundamental trade-off between computational efficiency and fabrication certainty. Continuous random sampling offers speed and exploratory breadth but lacks structural assurance. The brute-force approach, though computationally more expensive, provides the reliability required for fabrication-aware learning, where buildability outweighs novelty. Future work may revisit stochastic sampling as validation mechanisms mature, allowing safer integration of geometric diversity without compromising robotic feasibility.
5.3. Structural Performance Insights from the Datasets
Structural analysis revealed how sampling strategies interact with different generative logics to shape stability outcomes. Classes 01–07 and 09–10, derived from attractor-curve mappings, showed comparable pass/fail ratios under both brute-force and stochastic sampling (≈36–47% pass rate; Table 2), indicating that random variation does not meaningfully alter stability under minor geometric variations. An exception emerged in Class 08, where the V-shaped attractor curve amplified rotation gradients and produced slightly higher failure rates in the brute-force dataset, while continuous stochastic variation occasionally softened these transitions and improved local stability.
By contrast, Classes 11–14, governed by point-attractor logic, showed noticeably higher failure rates in the random dataset (≈4–7% increase). This effect appears linked to continuous sampling of the attractor position, where random draws sometimes locate the attractor in regions that are more structurally sensitive, and the stochastic process can cluster around such regions. Thus, the observed increase in failures reflects sampling and parametrization effects (position and coverage) rather than a fundamental weakness of the point-attractor mechanism. Class 15, defined by a global sinusoidal pattern, behaved inversely; its continuous logic benefited from randomization, which enhanced geometric adaptability.
While the brute-force method provides systematic yet discrete coverage, its coarse resolution may undersample transitional regions where small geometric shifts produce disproportionate structural effects. In principle, the continuous stochastic method could complement this limitation by exploring interstitial zones and improving edge-case coverage. However, such gains were not conclusively observed, suggesting that the theoretical benefits of continuous exploration require further validation through broader geometric testing and structural benchmarking.
When generative logics are compared at a broader level, a more nuanced trend emerges. Under brute-force sampling, curve-based attractors (Classes 01–10) exhibit higher failure rates than point-attractor systems (Classes 11–14), indicating that continuous field geometries are more sensitive to systematic variations. However, under random sampling, the field-based attractors showed similar failure rates, but point-attractor systems showed higher failure rates. This suggests that field-based algorithms tend to amplify structured variations in general regardless of the sampling strategy, and localized point-based systems are more vulnerable to stochastic noise. Overall, the results highlight that robustness is context-dependent, governed as much by the nature of variation as by the generative logic itself.
Together, these results highlight a trade-off between sampling completeness and geometric generalization. Brute-force sampling offers stable, reproducible configurations suitable for training ML models requiring controlled variation, while stochastic sampling contributes diversity for generative exploration. Likewise, localized attractor logic tends to enhance structural resilience compared to global or highly continuous fields. In combination, these findings clarify how different generative and sampling strategies can be balanced to construct fabrication-aware datasets that are both structurally consistent and geometrically diverse.
5.4. Simulation vs. Reality: Insights and Limitations
The study acknowledges and critically engages with one of the most underexplored but consequential limitations in generative AI and robotic fabrication: the gap between simulation and reality. While simulations provide a valuable tool for early evaluation, real-world assemblies introduce unforeseen variables such as material tolerances, surface irregularities, and robot precision drift. These factors, often marginalized in digital workflows, emerged as constraints during the physical testing phase. The observation that even minor variations (1–2 mm) in brick size or robot toolpath could lead to cumulative structural errors underscores the fragility of transitioning from virtual to physical systems.
This highlights the need for more robust physical assessment protocols and possibly feedback-driven correction mechanisms in future AI-robotic fabrication workflows. Integrating sensors, such as cameras [72] and force/torque sensing devices [73], for error detection or developing closed-loop systems that allow for real-time adaptation, could offer pathways to bridge this simulation-reality divide. Furthermore, these discrepancies point to a potential avenue for incorporating uncertainty modeling into the dataset or even leveraging stochastic simulations to better anticipate fabrication-induced deviations.
5.5. Generalization Potential and AI Learning Utility
From a machine learning perspective, the generated datasets present significant potential for training models in both supervised and generative tasks. With over 33,000 unique wall configurations, the volume and variety (as defined in the 5Vs framework) are substantial. The dataset’s structure, organized at the per-brick level, encoded through normalized rotational features, and validated through physics simulation, makes it uniquely positioned for use in generative design optimization, structural prediction models, and robotic assembly planning.
Synthetic data and simulators have emerged as a promising solution to challenges related to data scarcity and annotation. Synthetic datasets are comparatively easier to generate, inexhaustible, pre-annotated, and less expensive. They also avoid ethical (e.g., privacy) and practical (e.g., security) concerns and enable the creation of training data that would be impractical or impossible to collect in the real world [29]. In this context, our fully automated pipeline facilitated the generation of a large and diverse dataset at a consistent rate, satisfying not just volume and variety, but also velocity.
To ensure veracity, we implemented rigorous physics-based stability simulations, allowing us to filter out structurally unsound configurations. Finally, by designing the dataset explicitly for downstream ML tasks like structural prediction and fabrication planning, we ensure its practical value. This holistic alignment with the 5Vs framework underscores the dataset’s utility as a benchmark resource in AI-driven design and construction.
Nonetheless, while the dataset is large in absolute terms, it may still be considered relatively small compared to datasets in other domains (e.g., computer vision). This limitation can be overcome using our developed pipeline, which, when paired with crowdsourcing [74], can be scaled to millions of data points. Furthermore, while this study focuses on dry-stacked brick systems, its principles could be extended to other materials and construction methods, though doing so would require new simulation models and fabrication constraints, thus warranting further investigation.
5.6. Limitations and Future Research
This study presents a method for creating and evaluating a dataset suitable for robotic assembly workflows. Data for robotic fabrication is inherently complex, encompassing multiple dimensions and constraints. While the proposed approach provides a useful foundation, the study also has several limitations. These limitations will be outlined below, along with suggested directions for future research to guide subsequent investigations.
At present, the dataset is limited in both size and variation, focusing on a constrained number of wall patterns and bonding types. A larger and more diverse dataset would enable the framework to capture a richer design space, including variations in scale, wall thickness, walls with openings, curved walls, etc. Expanding the dataset to incorporate more patterns, wall sizes, and bonding will enhance the model’s ability to generalize beyond the tested cases. Furthermore, including examples drawn from historical masonry, vernacular traditions, or contemporary experimental assemblies could help in evaluating the adaptability of the system across different architectural contexts. To achieve this a crowdsourcing approach using the developed pipeline can expand the dataset size to hundreds of thousands of wall patterns and increase the richness of the dataset.
The proposed fabrication-aware synthetic data generation methodology is adaptable within discrete, component-based construction systems such as modular assemblies and façade panels, where geometric relationships, connection logic, and fabrication constraints can be reliably parameterized. It is particularly effective in contexts involving modular or repetitive unit systems, such as brick, block, or modular façade elements, where geometric variation and assembly rules can be encoded synthetically. However, its applicability is more limited in scenarios involving deformable or continuous materials (e.g., clay extrusion, concrete printing, or fabric-based structures), where material flow and deformation introduce complexities not captured by rigid-body simulation.
The use of an NVIDIA PhysX engine provided a fast but simplified stability assessment; contact dynamics, frictional variability, and material heterogeneity are only coarsely approximated. No sensitivity analyses or tolerance studies were conducted, which limits the framework’s ability to quantify uncertainty and error propagation. Moreover, the methodology currently operates at a proof-of-concept scale, emphasizing conceptual feasibility rather than full generalization across fabrication systems. Future research will therefore incorporate higher-fidelity methods (e.g., Discrete Element Method (DEM), Finite Element Method (FEM)) and validate simulation thresholds against standardized performance criteria. Future work will also expand physical testing to larger sample sizes and diverse structural typologies while quantitatively benchmarking placement accuracy, build time, and failure modes, ultimately scaling and adapting the approach to accommodate diverse material behaviors, higher-fidelity physics, and broader construction modalities.
Furthermore, the current study primarily evaluated the dataset using an ANN for predictive purposes. While this demonstrated the feasibility of a data-driven predictive approach, it does not capture the full potential of contemporary generative models. In future research, the dataset should be extended to train and test generative deep learning models such as VAEs, GANs, or more recent architectures like diffusion models and transformers. Such models are capable of synthesizing novel design variations rather than merely predicting performance, and their application could be applied to support creative, automated wall generation. Comparative experiments between these algorithms would also provide a clearer picture of the relative strengths, weaknesses, and design affordances of each generative approach.
Lastly, the developed framework was tested exclusively on wall structures suitable for robotic stacking, with the assumption of discrete, brick-like elements. This choice narrows the application to a particular form of assembly and excludes alternative methods of digital fabrication. Future research should test the adaptability of the framework for other fabrication modalities, such as robotic pick-and-place of irregular units, cooperative multi-robot assembly, or additive processes like robotic 3D printing. Such extensions could help validate whether the proposed data-to-fabrication pipeline is sufficiently robust and generalizable across multiple construction methods.
6. Conclusions
This study tackled a fundamental challenge in AI-driven architectural design research: the absence of structured, fabrication-aware datasets that bridge the gap between generative design and physical realization. To address this, a structured pipeline integrating parametric modeling, physics-based evaluation, and robotic toolpath generation was developed to produce a diverse and fabrication-feasible synthetic wall dataset. Through dual sampling strategies, geometric encoding, and physics simulation, the framework demonstrated how parametrically controlled geometries, when grounded in material and structural logic, can yield stable assemblies suitable for machine learning workflows. The comparative analysis of stochastic and exhaustive sampling revealed crucial trade-offs between coverage, efficiency, and structural stability in exploring generative design spaces.
The study’s findings highlight both the potential and constraints of employing synthetic, fabrication-aware data within machine learning workflows for design and fabrication. Rather than presenting a definitive solution, the results demonstrate that structured synthetic datasets can serve as an effective foundation for training and testing deep learning models, supporting the gradual integration of AI into robotic construction processes. However, the persistent simulation-to-reality gap, where small material or robotic tolerances can accumulate into structural deviations, remains a critical challenge. This emphasizes the necessity of integrating feedback-driven, sensor-informed systems to strengthen the reliability of digital-to-physical transitions. Moreover, while the dataset showed strong potential for supervised and generative machine learning tasks, its scale and scope remain modest relative to other AI domains, pointing to the importance of scaling through automated pipelines and potentially crowdsourced contributions.
Ultimately, this research demonstrates both the promise and the limitations of AI-driven design for robotic construction. It contributes not only a fabrication-informed synthetic dataset but also a methodological framework that bridges generative design and automated fabrication. By extending the dataset to incorporate more diverse wall types; leveraging advanced generative models such as GANs, VAEs, diffusion models, and transformers; and evaluating alternative fabrication methods like 3D printing and multi-robot assembly, future studies can push this agenda further. In doing so, the study moves beyond purely conceptual applications of AI in architecture and provides a foundation for fabrication-informed design.
Author Contributions
Conceptualization, H.R.; Methodology, H.R., M.F.L.A.T., J.D. and T.S.; Software, H.R.; Validation, H.R.; Formal analysis, H.R.; Data curation, H.R.; Writing—original draft, H.R.; Writing—review & editing, M.F.L.A.T., J.D. and T.S.; Visualization, H.R.; Supervision, M.F.L.A.T., J.D. and T.S. All authors have read and agreed to the published version of the manuscript.
Funding
Queensland University of Technology; Building 4.0 CRC.
Data Availability Statement
The dataset can be accessed at: https://researchdatafinder.qut.edu.au/display/n47461.
Acknowledgments
We thank Advanced Robotic Manufacturing HUB (ARMHUB) for providing their facilities to construct the wall assemblies.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| AUC | Area Under the Curve |
| CSV | Comma Separated Values |
| DL | Deep Learning |
| GAN | Generative Adversarial Networks |
| GenAI | Generative Artificial Intelligence |
| IDW | Inverse Distance Weighting |
| ML | Machine Learning |
| PCA | Principal Component Analysis |
| ReLU | Rectified Linear Unit |
| RL | Reinforcement Learning |
| ROC | Receiver Operating Characteristic |
| t-SNE | t-distributed Stochastic Neighbor Embedding |
| UR | Universal Robot |
| VAE | Variational Autoencoder |
References
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems 27, Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. In Proceedings of the Advances in Neural Information Processing Systems 33, Virtual, 6–12 December 2020. [Google Scholar]
- Nauata, N.; Hosseini, S.; Chang, K.H.; Chu, H.; Cheng, C.Y.; Furukawa, Y. House-GAN++: Generative Adversarial Layout Refinement Network towards Intelligent Computational Agent for Professional Architects. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Aalaei, M.; Saadi, M.; Rahbar, M.; Ekhlassi, A. Architectural layout generation using a graph-constrained conditional Generative Adversarial Network (GAN). Autom. Constr. 2023, 155, 105053. [Google Scholar] [CrossRef]
- Lu, Z.; Li, Y.; Wang, F. Complex layout generation for large-scale floor plans via deep edge-aware GNNs. Appl. Intell. 2025, 55, 400. [Google Scholar] [CrossRef]
- Peng, Z.; Zhang, Y.; Lu, W.; Li, X. Data-driven generative contextual design model for building morphology in dense metropolitan areas. Autom. Constr. 2024, 168, 105820. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.; Deng, Q.; Hu, K. Diffusion Probabilistic Model Assisted 3D Form Finding and Design Latent Space Exploration: A Case Study for Taihu Stone Spacial Transformation; Springer Nature: Singapore, 2024. [Google Scholar]
- Li, C.; Zhang, T.; Du, X.; Zhang, Y.; Xie, H. Generative AI models for different steps in architectural design: A literature review. Front. Archit. Res. 2025, 14, 759–783. [Google Scholar] [CrossRef]
- Yu, Q.; Malaeb, J.; Ma, W. Architectural Facade Recognition and Generation through Generative Adversarial Networks. In Proceedings of the 2020 International Conference on Big Data & Artificial Intelligence & Software Engineering (ICBASE), Chengdu, China, 23–25 October 2020. [Google Scholar]
- Sun, C.; Zhou, Y.; Han, Y. Automatic generation of architecture facade for historical urban renovation using generative adversarial network. Build. Environ. 2022, 212, 108781. [Google Scholar] [CrossRef]
- Law, S.; Valentine, C.; Kahlon, Y.; Seresinhe, C.I.; Tang, J.; Morad, M.G.; Fujii, H. Generative AI for Architectural Façade Design: Measuring Perceptual Alignment Across Geographical, Objective, and Affective Descriptors. Buildings 2025, 15, 3212. [Google Scholar] [CrossRef]
- Fui-Hoon Nah, F.; Zheng, R.; Cai, J.; Siau, K.; Chen, L. Generative AI and ChatGPT: Applications, challenges, and AI-human collaboration. J. Inf. Technol. Case Appl. Res. 2023, 25, 277–304. [Google Scholar] [CrossRef]
- Zhang, W.; Li, H.; Li, Y.; Liu, H.; Chen, Y.; Ding, X. Application of deep learning algorithms in geotechnical engineering: A short critical review. Artif. Intell. Rev. 2021, 54, 5633–5673. [Google Scholar] [CrossRef]
- Luo, D.; Xu, W. Adaptable Method for Dynamic Planning of 3D Spatial Wireframes Extrusion with Neural Networks and Robotic Automation. 3D Print. Addit. Manuf. 2022, 9, 255–268. [Google Scholar] [CrossRef] [PubMed]
- Tsuruta, K.; Griffioen, S.J.; Ibáñez, J.M.; Johns, R.L. Deep Sandscapes: Design Tool for Robotic Sand-Shaping with GAN-Based Heightmap Predictions. In Proceedings of the 2022 Annual Modeling and Simulation Conference (ANNSIM), San Diego, CA, USA, 18–20 July 2022. [Google Scholar]
- Greff, K.; Belletti, F.; Beyer, L.; Doersch, C.; Du, Y.; Duckworth, D.; Fleet, D.J.; Gnanapragasam, D.; Golemo, F.; Herrmann, C.; et al. Kubric: A scalable dataset generator. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. ImageNet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami Beach, FL, USA, 20–25 June 2009. [Google Scholar]
- Baack, S. A Critical Analysis of the Largest Source for Generative AI Training Data: Common Crawl. In Proceedings of the 2024 ACM Conference on Fairness, Accountability, and Transparency, Rio de Janeiro, Brazil, 3–6 June 2024; Association for Computing Machinery: New York, NY, USA; pp. 2199–2208. [Google Scholar]
- Wu, K.; Kilian, A. Designing Natural Wood Log Structures with Stochastic Assembly and Deep Learning. In Robotic Fabrication in Architecture, Art and Design 2018; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Fragkia, V.; Foged, I.W.; Pasold, A. Predictive Information Modeling: Machine Learning Strategies for Material Uncertainty. Technol. Archit. Des. 2021, 5, 163–176. [Google Scholar] [CrossRef]
- Ali, A.K.; Lee, O.J.; Song, H. Robot-based facade spatial assembly optimization. J. Build. Eng. 2021, 33, 101556. [Google Scholar] [CrossRef]
- Leng, J.; Zuo, K.; Xu, C.; Zhou, X.; Zheng, S.; Kang, J.; Liu, Q.; Chen, X.; Shen, W.; Wang, L.; et al. Physics-informed machine learning in intelligent manufacturing: A review. J. Intell. Manuf. 2025. [Google Scholar] [CrossRef]
- Wu, Y.; Sicard, B.; Gadsden, S.A. Physics-informed machine learning: A comprehensive review on applications in anomaly detection and condition monitoring. Expert Syst. Appl. 2024, 255, 124678. [Google Scholar] [CrossRef]
- Xu, Y.; Kohtz, S.; Boakye, J.; Gardoni, P.; Wang, P. Physics-informed machine learning for reliability and systems safety applications: State of the art and challenges. Reliab. Eng. Syst. Saf. 2023, 230, 108900. [Google Scholar] [CrossRef]
- Gharbia, M.; Chang-Richards, A.; Lu, Y.; Zhong, R.Y.; Li, H. Robotic technologies for on-site building construction: A systematic review. J. Build. Eng. 2020, 32, 101584. [Google Scholar] [CrossRef]
- Dörfler, K.; Sandy, T.; Giftthaler, M.; Gramazio, F.; Kohler, M.; Buchli, J. Mobile Robotic Brickwork: Automation of a Discrete Robotic Fabrication Process Using an Autonomous Mobile Robot. In Robotic Fabrication in Architecture, Art and Design 2016; Reinhardt, D., Saunders, R., Burry, J., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 204–217. [Google Scholar]
- Piškorec, L.; Jenny, D.; Parascho, S.; Mayer, H.; Gramazio, F.; Kohler, M. The Brick Labyrinth. In Robotic Fabrication in Architecture, Art and Design 2018; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- de Melo, C.M.; Torralba, A.; Guibas, L.; DiCarlo, J.; Chellappa, R.; Hodgins, J. Next-generation deep learning based on simulators and synthetic data. Trends Cogn. Sci. 2022, 26, 174–187. [Google Scholar] [CrossRef]
- Gräßler, I.; Hieb, M. Creating Synthetic Datasets for Deep Learning used in Machine Vision. Procedia CIRP 2024, 126, 981–986. [Google Scholar] [CrossRef]
- Boikov, A.; Payor, V.; Savelev, R.; Kolesnikov, A. Synthetic Data Generation for Steel Defect Detection and Classification Using Deep Learning. Symmetry 2021, 13, 1176. [Google Scholar] [CrossRef]
- Paproki, A.; Salvado, O.; Fookes, C. Synthetic Data for Deep Learning in Computer Vision & Medical Imaging: A Means to Reduce Data Bias. ACM Comput. Surv. 2024, 56, 271. [Google Scholar] [CrossRef]
- Wong, M.Z.; Kunii, K.; Baylis, M.; Ong, W.H.; Kroupa, P.; Koller, S. Synthetic dataset generation for object-to-model deep learning in industrial applications. PeerJ Comput. Sci. 2019, 5, e222. [Google Scholar] [CrossRef]
- Rafizadeh, H.; Teixeira, M.F.L.A.; Donovan, J.; Schork, T. BrickNet: A computational design framework for robust dataset creation for robotic fabrication and design automation. In Architectural Informatics, Proceedings of the 30th International Conference of the Association for Computer-Aided Architectural Design Research in Asia (CAADRIA) 2025, Tokyo, Japan, 26–28 March 2025; The Association for Computer-Aided Architectural Design Research in Asia: Hong Kong, China, 2025; Volume 2. [Google Scholar]
- Wu, W.; Fu, X.M.; Tang, R.; Wang, Y.; Qi, Y.H.; Liu, L. Data-driven interior plan generation for residential buildings. ACM Trans. Graph. 2019, 38, 234. [Google Scholar] [CrossRef]
- Kalervo, A.; Ylioinas, J.; Häikiö, M.; Karhu, A.; Kannala, J. CubiCasa5K: A Dataset and an Improved Multi-task Model for Floorplan Image Analysis. In Image Analysis; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Zheng, J.; Zhang, J.; Li, J.; Tang, R.; Gao, S.; Zhou, Z. Structured3D: A Large Photo-Realistic Dataset for Structured 3D Modeling; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar]
- Chen, X.; Xiong, Y.; Wang, S.; Wang, H.; Sheng, T.; Zhang, Y.; Ye, Y. ReCo: A Dataset for Residential Community Layout Planning. In Proceedings of the 31st ACM International Conference on Multimedia, Ottawa, ON, Canada, 29 October–2 November 2023; Association for Computing Machinery: New York, NY, USA; pp. 397–405. [Google Scholar]
- Park, H.; Gu, H.; Hong, S.; Choo, S. Developing a Robust Training Dataset for AI-Driven Architectural Spatial Layout Generation. Appl. Sci. 2024, 14, 7095. [Google Scholar] [CrossRef]
- Ramsgaard Thomsen, M.; Nicholas, P.; Tamke, M.; Gatz, S.; Sinke, Y.; Rossi, G. Towards machine learning for architectural fabrication in the age of industry 4.0. Int. J. Archit. Comput. 2020, 18, 335–352. [Google Scholar] [CrossRef]
- Tamke, M.; Nicholas, P.; Zwierzycki, M. Machine learning for architectural design: Practices and infrastructure. Int. J. Archit. Comput. 2018, 16, 123–143. [Google Scholar] [CrossRef]
- Das, A.R.; Koskinopoulou, M. Toward Sustainable Manufacturing: A Review on Innovations in Robotic Assembly and Disassembly. IEEE Access 2025, 13, 100149–100166. [Google Scholar] [CrossRef]
- Belousov, B.; Wibranek, B.; Schneider, J.; Schneider, T.; Chalvatzaki, G.; Peters, J.; Tessmann, O. Robotic architectural assembly with tactile skills: Simulation and optimization. Autom. Constr. 2022, 133, 104006. [Google Scholar] [CrossRef]
- Sebestyen, A.; Hirschberg, U.; Rasoulzadeh, S. Using deep learning to generate design spaces for architecture. Int. J. Archit. Comput. 2023, 21, 337–357. [Google Scholar] [CrossRef]
- Akizuki, Y.; Bernhard, M.; Kladeftira, M.; Kakooee, R.; Dillenburger, B. Generative modelling with design constraints–reinforcement learning for object generation. In Proceedings of the RE: Anthropocene, Design in the Age of Humans–Proceedings of the 25th CAADRIA Conference, Bangkok, Thailand, 5–6 August 2020; Association for Computer Aided Architectural Design Research in Asia: Hong Kong, China, 2020. [Google Scholar]
- Wang, D.; Snooks, R. Artificial Intuitions of Generative Design: An Approach Based on Reinforcement Learning. In Proceedings of the 2020 DigitalFUTURES; Springer: Singapore, 2021. [Google Scholar]
- Li, Y.; Kong, T.; Li, L.; Li, Y.; Wu, Y. Learning to Design and Construct Bridge without Blueprint. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Online, 27 September–1 October 2021. [Google Scholar]
- Felbrich, B.; Schork, T.; Menges, A. Autonomous robotic additive manufacturing through distributed model-free deep reinforcement learning in computational design environments. Constr. Robot. 2022, 6, 15–37. [Google Scholar] [CrossRef]
- Vallat, G.; Wang, J.; Maddux, A.; Kamgarpour, M.; Parascho, S. Reinforcement learning for scaffold-free construction of spanning structures. In Proceedings of the 8th ACM Symposium on Computational Fabrication, New York, NY, USA, 8–10 October 2023; Association for Computing Machinery: New York, NY, USA, 2023; p. 12. [Google Scholar]
- Hosna, A.; Merry, E.; Gyalmo, J.; Alom, Z.; Aung, Z.; Azim, M.A. Transfer learning: A friendly introduction. J. Big Data 2022, 9, 102. [Google Scholar] [CrossRef]
- Cacciarelli, D.; Kulahci, M. Active learning for data streams: A survey. Mach. Learn. 2024, 113, 185–239. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, Q.; Kwok, J.T.; Ni, L.M. Generalizing from a Few Examples: A Survey on Few-shot Learning. ACM Comput. Surv. 2020, 53, 63. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Q. A Survey on Multi-Task Learning. IEEE Trans. Knowl. Data Eng. 2022, 34, 5586–5609. [Google Scholar] [CrossRef]
- Gangwal, A.; Ansari, A.; Ahmad, I.; Azad, A.K.; Sulaiman, W.M.A.W. Current strategies to address data scarcity in artificial intelligence-based drug discovery: A comprehensive review. Comput. Biol. Med. 2024, 179, 108734. [Google Scholar] [CrossRef] [PubMed]
- Weber, M.; Banihashemi, F.; Mandl, P.; Jacobsen, H.A.; Mayer, R. Overcoming Data Scarcity through Transfer Learning in CO2-Based Building Occupancy Detection. In Proceedings of the 10th ACM International Conference on Systems for Energy-Efficient Buildings, Cities, and Transportation, Istanbul, Turkey, 15–16 November 2023; Association for Computing Machinery: New York NY, USA, 2023; pp. 1–10. [Google Scholar]
- Mitrano, P.; Berenson, D. Data augmentation for manipulation. arXiv 2022, arXiv:2205.02886. [Google Scholar]
- Trabucco, B.; Doherty, K.; Gurinas, M.; Salakhutdinov, R. Effective Data Augmentation With Diffusion Models. arXiv 2024, arXiv:2302.07944. [Google Scholar]
- Thomas, U.; Wahl, F.M. Assembly Planning and Task Planning—Two Prerequisites for Automated Robot Programming. In Robotic Systems for Handling and Assembly; Schütz, D., Wahl, F.M., Eds.; Springer: Berlin, Germany, 2011; pp. 333–354. [Google Scholar]
- Zhou, L.; Pan, S.; Wang, J.; Vasilakos, A.V. Machine learning on big data: Opportunities and challenges. Neurocomputing 2017, 237, 350–361. [Google Scholar] [CrossRef]
- Connolly, M.; Ramasubramanian, A.K.; Kelly, M.; McEvoy, J.; Papakostas, N. Realistic simulation of robotic grasping tasks: Review and application. Procedia CIRP 2021, 104, 1704–1709. [Google Scholar] [CrossRef]
- Mehdizadeh, S.; Tessmann, O. Roll-locks: A fabrication to self-assembly design-framework for reusable discrete concrete elements. In Advances in Architectural Geometry(AAG); DE Gruyter: Berlin, Germany, 2023. [Google Scholar]
- Song, Y.; Agkathid, A.; Koeck, R. Augmented Performative Design: A Workflow Utilizing Augmented Reality for Structurally Stable Masonry Design. In Computer-Aided Architectural Design. Interconnections: Co-Computing Beyond Boundaries; Springer Nature: Cham, Switzerland, 2023. [Google Scholar]
- Agkathidis, A.; Song, Y.; Zhao, J. Rethinking the Brick: Developing a File to Fabrication Framework for Mortar-Free, Robotic Masonry Wall Assembly. In Computational Design and Digital Manufacturing; Kyratsis, P., Manavis, A., Davim, J.P., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 107–118. [Google Scholar]
- Albaghajati, Z.M.; Bettaieb, D.M.; Malek, R.B. Exploring text-to-image application in architectural design: Insights and implications. Archit. Struct. Constr. 2023, 3, 475–497. [Google Scholar] [CrossRef]
- Gallego, E.; Fuentes, J.M.; Ruiz, Á.; Hernández-Rodrigo, G.; Aguado, P.; Ayuga, F. Determination of mechanical properties for wood pellets used in DEM simulations. Int. AgroPhys. 2020, 34, 485–494. [Google Scholar] [CrossRef]
- Maturo, F.; Rambaud, S.C.; Ventre, V. Advances in statistical learning from high-dimensional data. Qual. Quant. 2025, 59, 1933–1937. [Google Scholar] [CrossRef]
- Issa, R. Essential Mathematics for Computational Design, 4th ed.; Robert McNeel & Associates: Seattle, WA, USA, 2019; pp. 14–16. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal component analysis. WIREs Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Atanasova, L.; Kenny, J.C.; Alexi, E.V.; Chovghi, F.; Mitterberger, D.; Dörfler, K. Building (with) human–robot teams: Fabrication-aware design, planning, and coordination of cooperative assembly processes. Constr. Robot. 2025, 9, 16. [Google Scholar] [CrossRef]
- Devadass, P.; Heimig, T.; Stumm, S.; Kerber, E.; Brell-Cokcan, S. Robotic constraints informed design process. In Proceedings of the 39th Annual Conference of the Association for Computer Aided Design in Architecture (ACADIA), Austin, TX, USA, 21–26 October 2019. [Google Scholar]
- Feng, C.; Xiao, Y.; Willette, A.; McGee, W.; Kamat, V.R. Vision guided autonomous robotic assembly and as-built scanning on unstructured construction sites. Autom. Constr. 2015, 59, 128–138. [Google Scholar] [CrossRef]
- Apolinarska, A.A.; Pacher, M.; Li, H.; Cote, N.; Pastrana, R.; Gramazio, F.; Kohler, M. Robotic assembly of timber joints using reinforcement learning. Autom. Constr. 2021, 125, 103569. [Google Scholar] [CrossRef]
- Roh, Y.; Heo, G.; Whang, S.E. A Survey on Data Collection for Machine Learning: A Big Data-AI Integration Perspective. IEEE Trans. Knowl. Data Eng. 2021, 33, 1328–1347. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).