Integrated Construction Process Monitoring and Stability Assessment of a Geometrically Complex Large-Span Spatial Tubular Truss System

Abstract

This study presents a comprehensive construction monitoring program for a geometrically complex, large-span spatial tubular truss system within a typical center steel exhibition hall. To ensure construction quality and structural integrity throughout the entire process, the monitoring strategy was rigorously aligned with the actual construction sequence. Real-time vertical displacement measurements were acquired at critical structural members and joints. A detailed finite element model of the entire structure was developed to systematically analyze the structural behavior of herringbone columns, primary and secondary trusses, and temporary supports during both installation and removal phases. Displacement patterns at key locations were investigated, and a global stability assessment was performed. Results demonstrate close agreement between finite element predictions and field measurements, confirming the rationality and reliability of the construction scheme. The structural system exhibited excellent stability across all construction stages, satisfying both architectural aesthetics and structural safety requirements. This study provides practical insights for construction control of similar large-span steel structures.

1. Introduction

Recent advancements in modern construction technologies have spurred the widespread adoption of large-span steel structures with nonstandard geometries in public buildings such as convention centers and stadiums [1,2,3]. Their appeal lies in exceptional design flexibility, space adaptability, and superior mechanical properties. However, the construction of such geometrically complex structures presents significant technical challenges, including (1) difficulties in fabrication and installation precision control stemming from intricate cross-sectional geometries; (2) pronounced time-dependent structural behavior under construction loads; (3) substantial displacements of local members during erection phases. These issues can lead to error accumulation, compromising structural performance or safety. Consequently, implementing comprehensive full-process monitoring coupled with rigorous simulation is paramount to ensure the safe construction of these geometrically complex, large-span steel structures.

Significant advances in construction control techniques for large-span steel structures have been achieved through recent research. Zhang et al. [4] investigated the nonlinear behavior and design of steel structures. Their work identified critical areas for future research and development. Teng [5] and Lin et al. [6] demonstrated the application of structural health monitoring systems in large-span steel structures, with the former analyzing temperature and displacement data during the construction of the Shenzhen Bay Sports Center roof, and the latter employing a wireless stress monitoring system for the Guilin Liangjiang International Airport terminal, both providing valuable references for similar engineering projects. Zhu et al. [7] addressed the high risks and limited experience in hoisting converter station steel structures by integrating monitoring and simulation for a long-span case, providing a reference for similar projects. Naresh et al. [8] comprehensively assessed structural health monitoring methods for steel joints, encompassing both bolted and welded connections. Yao et al. [9] employed a case study to compare the one-step and phased forming methods by analyzing the mechanical performance during construction. Shahabsafa [10] and Cai et al. [11] developed novel topology optimization methods for truss design and sizing. Jiang et al. [12] validated the seismic performance of a hotel structure in Shanghai through elasto-plastic time–history analysis, confirming its safety under rare earthquakes. Separately, Li et al. [13] combined finite-element simulation with monitoring to ensure the safety of steel trusses during the construction of a super high-rise building. For enhanced simulation accuracy, Du et al. [14] employed a Bayesian MCMC method to optimize key parameters, significantly reducing the error between simulated and measured displacements in a tower project. Furthermore, Liu et al. [15] investigated a segmented steel antenna housing, analyzing how structural deformation affects its electrical performance and proposing a new deformation control method, which provides a valuable reference for similar designs. Bekdas et al. [16] analyze two tensegrity structures via energy minimization.

Refinements in finite element analysis (FEA) have markedly enhanced the accuracy and reliability of construction process simulations. Notable applications include Fan et al. [17] innovative use of element activation technology for multi-stage construction simulation of the National Stadium; Jin et al. [18] use of finite element inverse analysis to verify construction feasibility for the Bengbu Stadium; Liu et al. [19] development of a mechanics-based zoning method dedicated to structural health monitoring of spoke-type cable-truss structures; and Li et al. [20] identification of lateral instability risks in truss girders through full-process simulation at Xi’an Silk Road International Expo Center and implementation of corresponding control measures. Li et al. [20] demonstrated close agreement between field measurements and FEA results for key joint stresses and vertical loads in a Xi’an super-tall steel truss. Sun et al. [21] proposes a recursive analytical method utilizing structural symmetry to determine member forces in continuous trusses, enabling optimal material selection for large-span bridge design. Liu et al. [22] proposes and validates a digital twin framework for steel structure construction, establishing a three-stage modeling methodology and demonstrating its practical implementation in two major construction projects. Despite these advancements, persistent challenges remain in developing monitoring strategies and simulation frameworks specifically optimized for geometrically complex large-span steel structures.

This paper addresses these challenges through an in-depth investigation of a large-span steel structure with geometrically complex tubular trusses at a major convention center. An integrated methodology combining high-fidelity finite element modeling and real-time structural health monitoring (SHM) was employed to (1) accurately simulate hoisting procedures of primary and secondary trusses; (2) track spatiotemporal evolution of structural deflection and stress through construction; (3) assess global structural stability through geometrically nonlinear analysis; and (4) validate simulation reliability through SHM measurements at critical joints. This study presents dual innovations in structural monitoring and design. The proposed system enables real-time, high-resolution deformation measurement through a non-contact, full-field optical approach. It effectively overcomes the limitations inherent in traditional point-based methods. Structurally, an inverted trapezoidal truss design significantly enhances rigidity and material efficiency. Together, these advances form an integrated framework that improves accuracy, adaptability, and safety in large-scale construction. The method advances stability analysis by shifting from static analysis of completed structures to real-time, process-based tracking with dynamic model correction, effectively addressing the sensitivity of complex spatial structures to initial defects through high-precision model updating. The findings establish actionable theoretical frameworks and field-applicable protocols for constructing geometrically complex large-span steel structures.

2. Project Overview

The convention center comprises two multi-functional halls and six standard exhibition halls, with a total gross floor area of 145,000 m². All halls employ a unified portal frame structural system. The typical structural unit consists of herringbone columns connected to spatial truss beams via pin joints. Standard halls feature a plan dimension of 144 m (length) × 84 m (width) and a maximum structural height of 21.2 m. Their roof structure utilizes an orthogonal grid of primary and secondary trusses: primary trusses are spaced at 24 m intervals (totaling six trusses), and secondary trusses at 12 m intervals (totaling eight trusses).

The multi-functional halls, while maintaining the standard plan dimensions (144 m × 84 m) and achieving column-free large spans through a structural height of 21.2 m, incorporate local reinforcement strategies based on the standard system. Specifically, the two central primary trusses utilize nonstandard geometries designed with significantly increased flexural rigidity to resist the higher load demands resulting from their extended spans.

This study focuses on the mechanical response during the construction of these nonstandard primary trusses within the multi-functional halls. Figure 1 presents a 3D schematic illustrating the spatial configuration of the large-span steel structure in a multi-functional hall.

3. Detailed Design of Trusses and End-Support Herringbone Column

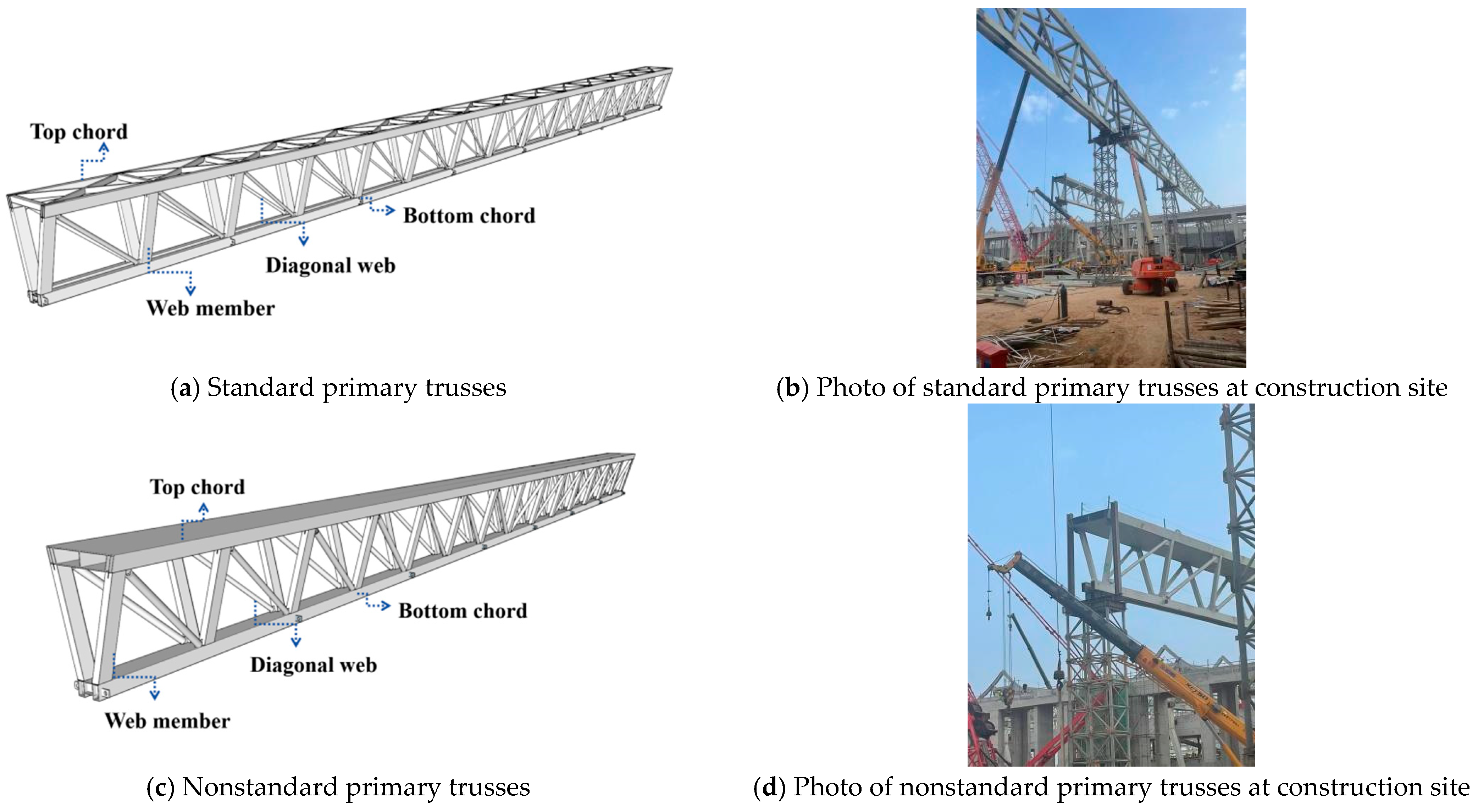
3.1. Design of Standard and Nonstandard Primary Trusses

3.1.1. Standard Primary Truss

The standard primary truss spans 84 m with a constant depth of 4.5 m, as shown in Figure 2a,b. Its structural system features a top chord composed of two parallel longitudinal members utilizing parallelogram-shaped tubes, interconnected by vertical members and diagonal bracing. The cross-sectional dimensions of the parallelogram tubes are 580 × 300 × 20 mm. The bottom chord comprises two longitudinal box-section members joined via I girders, with web members connecting the chords. The box section dimensions are 580 × 300 × 20 mm. This composite configuration, integrating distinct parallelogram-top and box-bottom chords with standardized web members, ensures structural rigidity for spans exceeding 100 m.

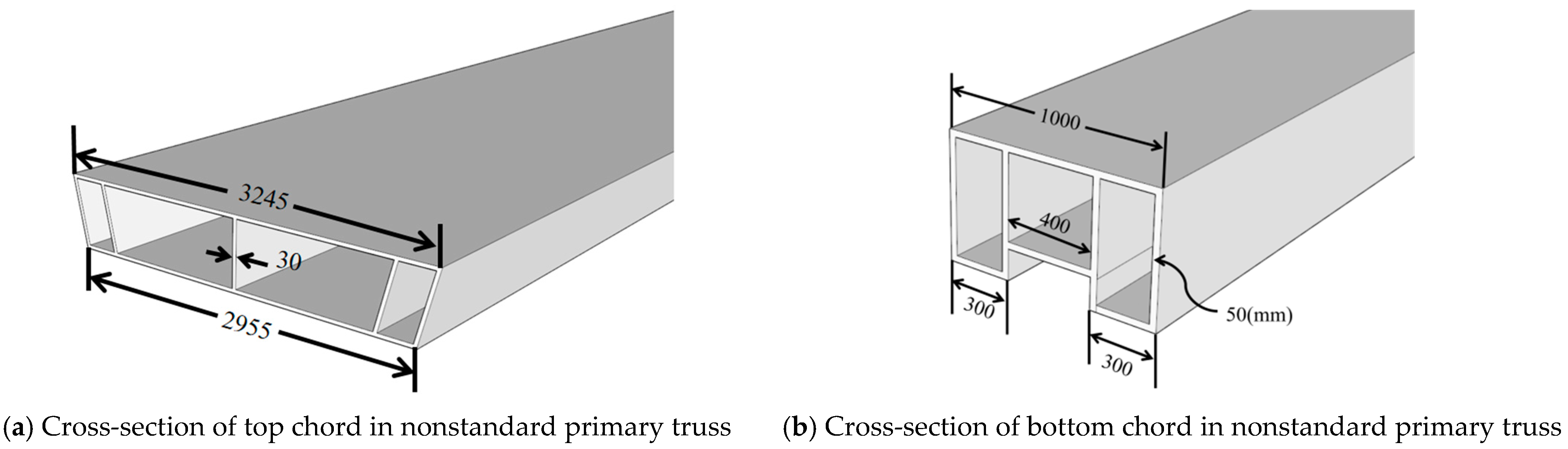
3.1.2. Nonstandard Primary Truss

The central axis of the exhibition hall, perpendicular to the primary truss direction, supports a 144 m super-span arched truss, which serves as the primary load-bearing backbone. Within this central critical zone, two intermediate nonstandard primary trusses directly bear concentrated loads from the arched truss and transfer them to adjacent hall sections (Figure 2c,d). Each of these trusses spans 84 m with a constant depth of 4.5 m and comprises top and bottom chords interconnected by web members.

The top chord features an inverted trapezoidal composite section, combining symmetrical parallelogram box-sections on both flanges with a central inverted trapezoidal box-section (Figure 3a). Conversely, the bottom chord utilizes a composite rectangular section formed by three interconnected box-sections (Figure 3b). Web members consist of diagonal circular hollow sections (CHS) and vertical rectangular hollow sections (RHS), interconnected end-to-end and attached to the chords via gusset plates.

Compared to conventional truss girders, the inverted trapezoidal composite section optimizes the cross-sectional centroid position, concentrating materials at the extreme fibers. This configuration significantly enhances the moment of inertia, flexural rigidity, and torsional stiffness. The resultant enclosed box-sections create a continuous torsional system, improving global stability and anti-overturning capacity. These enhancements improve material utilization efficiency, reduce structural self-weight, and effectively control vertical deflection. Through systematic experimental studies, parametric numerical analysis, and iterative design optimization, the optimal composite section geometry was finally determined.

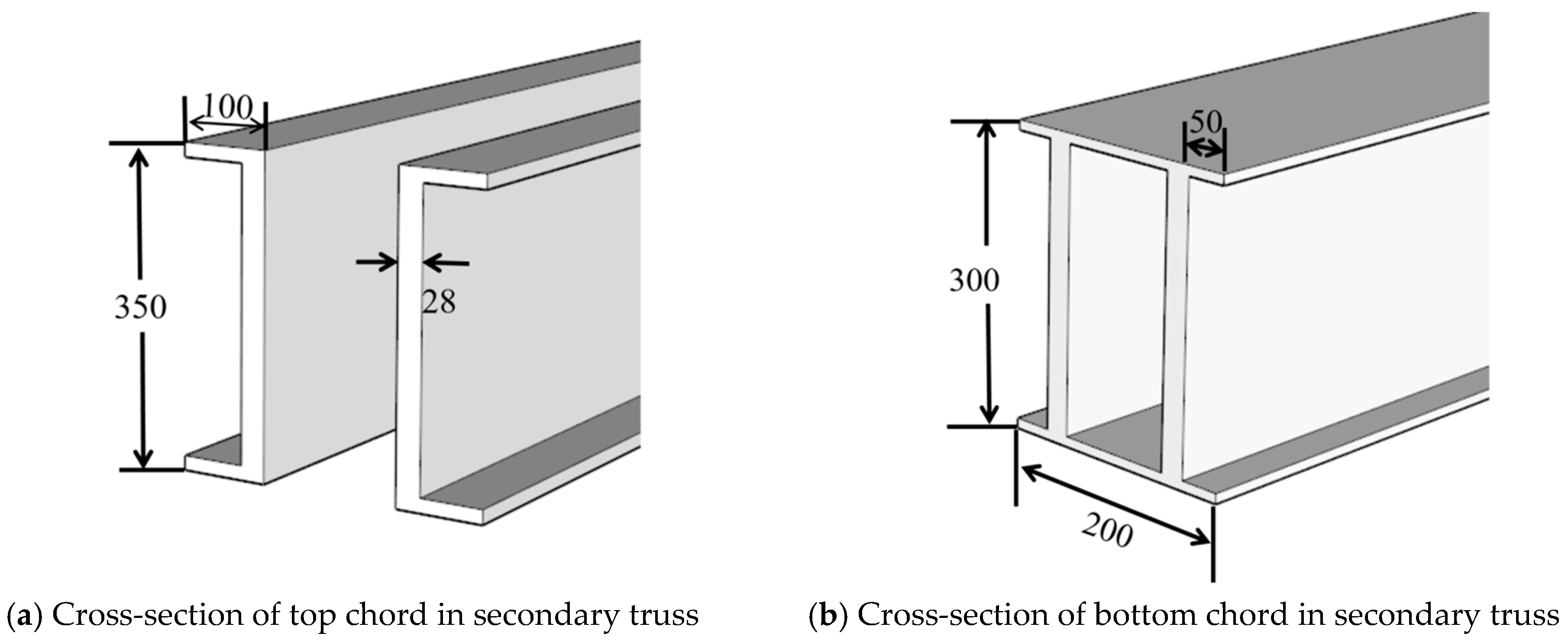
3.2. Design of Secondary Trusses

The secondary trusses feature a continuous 144 m span (Figure 4), with a curved top chord composed of back-to-back channels (Figure 5a), a box-section bottom chord (Figure 5b), and diagonal CHS (circular hollow section) web members providing mechanical connectivity. This configuration optimizes load-bearing behavior by transferring forces predominantly as axial loads while creating distinctive architectural morphology through spatial curvature. The design exemplifies a synthesis of structural efficiency, spatial transparency, and architectural aesthetics. Figure 4 shows the overall design of the secondary trusses. Cross-sectional details of chords are shown in Figure 5. The connection between the secondary trusses and the primary trusses is illustrated in Figure 6.

3.3. Design of End-Support Herringbone Column

With a total height of 14.2 m, the end-support Herringbone Column shown in Figure 7 consists of three structural segments: an upper straight section, a middle load-transfer segment, and a lower knee segment. The box-section upper straight section is pinned to the truss girder ends, thereby directly transferring dead loads, live loads, and lateral loads from the roof system. The middle load-transfer segment incorporates gradually stiffened rib-plates, facilitating the efficient conversion of axial loads into biaxial stresses and distributing concentrated loads uniformly. Specifically, the dimensions of the box section of the upper straight section are 580 × 300 × 25 mm, and the dimensions of the box section of the lower knee segment section are 600 × 480 × 25 mm. This segmented configuration systematically channels truss-originated loads through stress transformation to foundation interfaces, with cross-sectional adaptation optimizing load distribution efficiency.

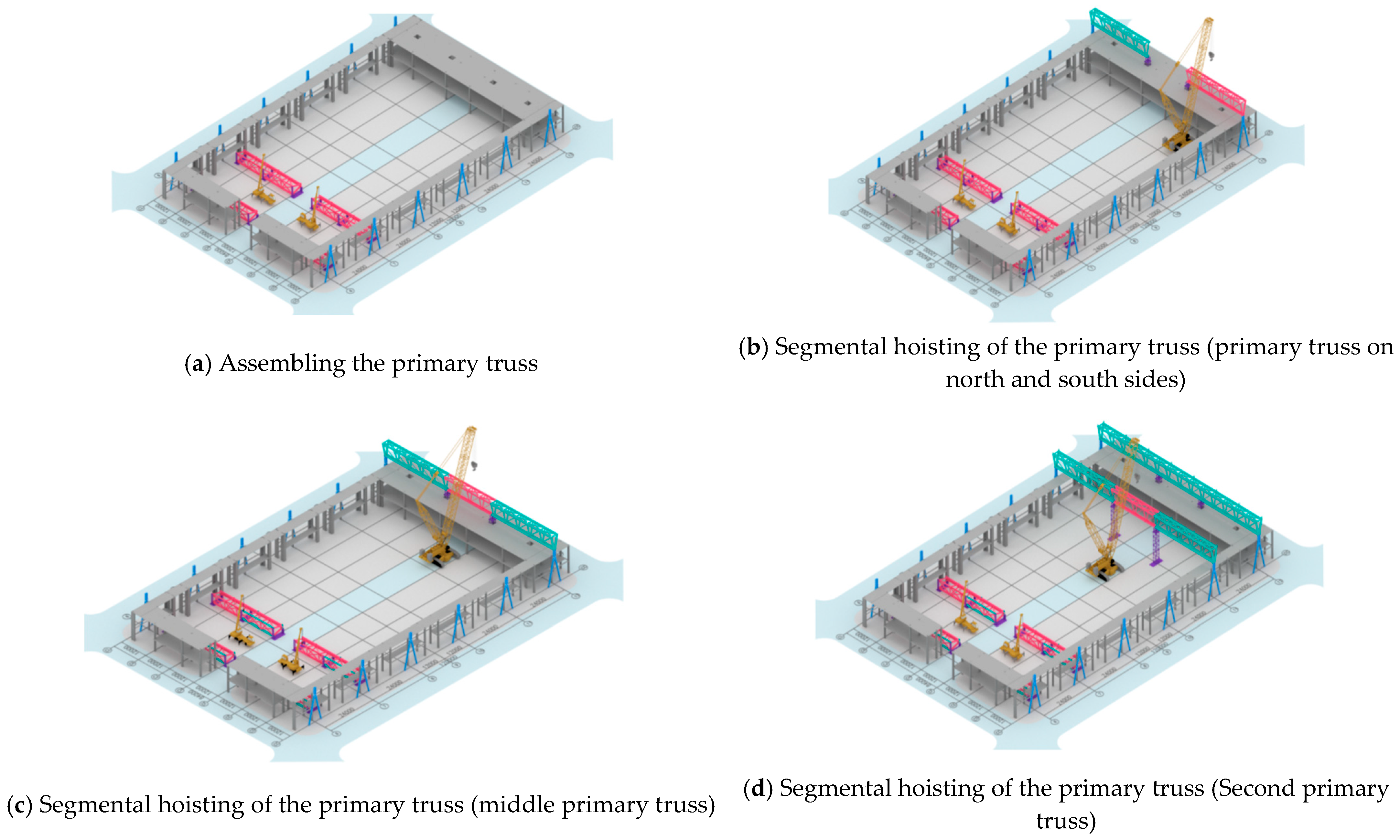
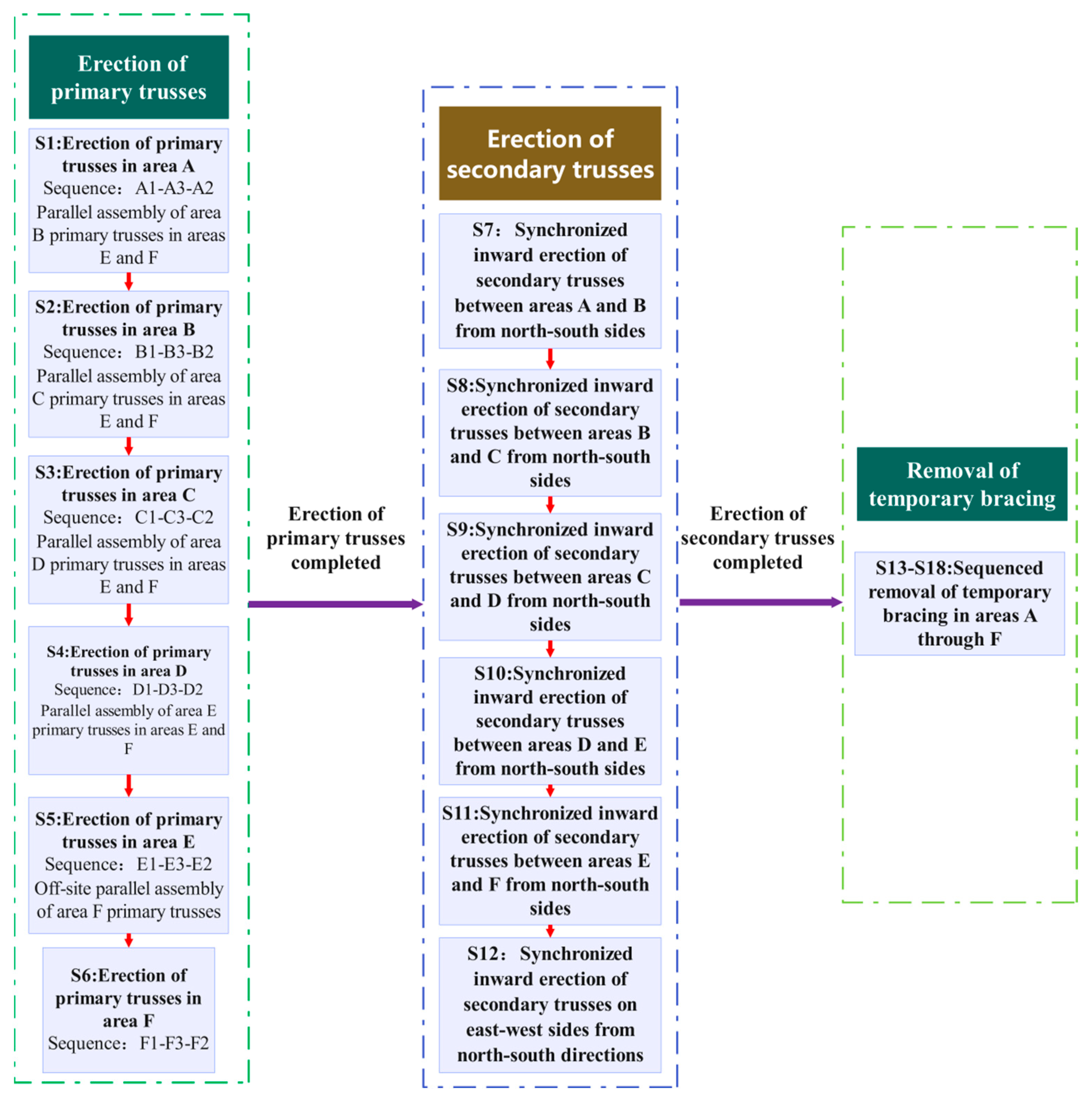
4. Steel Structure Installation Procedures

The steel roof employs an integrated “segmented lifting with temporary bents” methodology for the primary trusses. To accommodate the 84 m maximum span and substantial loads, each primary truss is rationally segmented into three transportable lifting units (Figure 8), maintaining structural integrity while satisfying logistical constraints. On-site heavy-duty lifting operations utilize two 300 t and two 400 t crawler cranes for coordinated multi-crane hoisting. The erection process proceeds sequentially: the six primary trusses are installed progressively from east to west in sequence. Following the erection of the six primary trusses, secondary trusses spanning between adjacent primary trusses are installed progressively from east to west. The installation sequence within each structural bay initiates concurrently at the outermost north and south secondary trusses, progressing symmetrically inward. This methodology ensures installation accuracy and construction safety. Construction sequencing implements spatiotemporal optimization through 18 alpha-numeric zones (Figure 8):

Phase I: Two 50-ton mobile cranes install herringbone columns, establishing dual workfaces progressing from the corridor toward the road. Adjustable temporary supports are erected concurrently.

Phase II: Primary trusses No.1–6 (corresponding to Grids A–F) are segmented and lifted in three segments per truss. Installation strictly follows an end-to-center sequence for each truss (end segments first, followed by mid-span segment).

Phase III: After the primary trusses are installed, the secondary trusses between adjacent main trusses are installed. The installation method of “bidirectional symmetry and layer-by-layer advancement” is adopted. The rigid connections between the primary trusses are completed first, and the cantilever sections are dealt with last.

This construction methodology employs “zoned progression and temporal optimization” principles, substantially improving the construction quality of large-span spatial structures. The assembly and lifting sequence of the primary truss is shown in Figure 9: Figure 9a provides a schematic diagram of the primary truss assembly; Figure 9b shows the lifting of the north and south sections of the first primary truss; Figure 9c illustrates the lifting of the middle section of the first primary truss; and Figure 9d depicts the completed lifting of the second primary truss. Figure 10 further illustrates the step-by-step construction sequences.

5. Full-Process Numerical Simulation of Construction

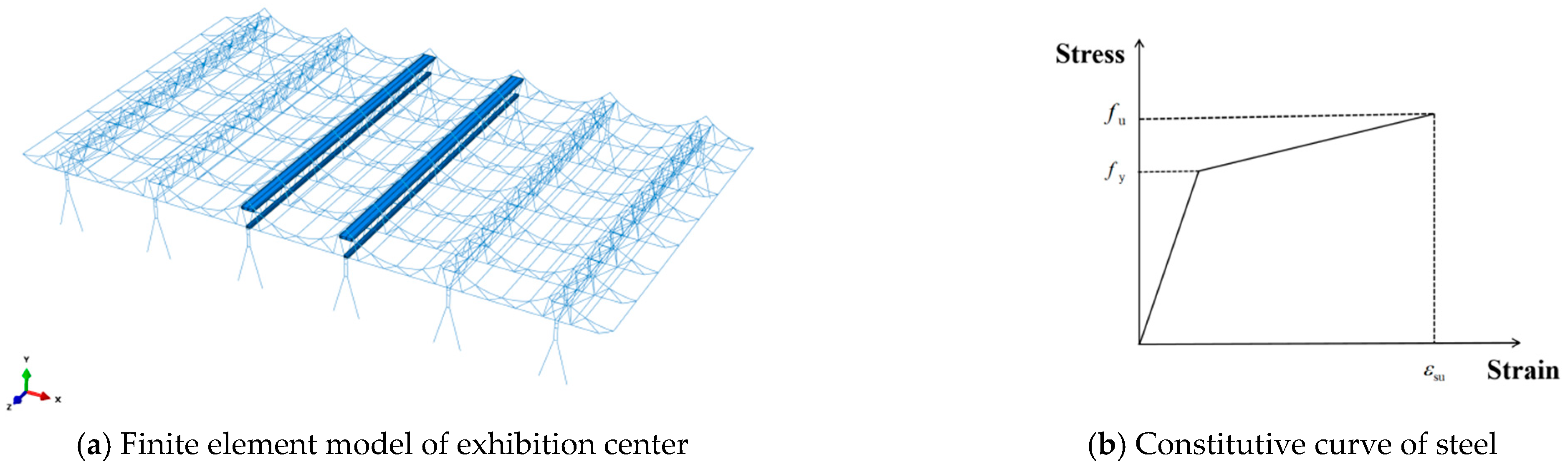
5.1. Establishment of Numerical Models

This study develops a refined finite element model for long-span steel trusses using ABAQUS 2020 (Figure 11). The model adopts a hybrid-element approach: B31 beam elements are used for standard primary trusses, secondary trusses, and herringbone columns, while S4R shell elements characterize nonstandard primary truss chords to capture geometric fidelity. In the finite element modeling of the steel structure, distinct connection types are represented with specific simplifications. Welded connections, such as those within the primary and secondary trusses, are simulated as rigid connections. This idealization may result in a slightly stiffer global model and smaller computed deformations, as it does not account for factors like residual stress. Conversely, bolted connections, including those linking the standard primary trusses to the herringbone columns, are modeled as pinned. Since actual bolted joints exhibit semi-rigid behavior, this assumption may yield slightly conservative predictions, particularly in the form of larger deformation values. Q355B steel is modeled using a bilinear constitutive relationship (Figure 11b). Tie constraints connect primary and secondary trusses; MPC algorithms interface primary trusses with herringbone columns (Model Predictive Control; MPC, simulates bolted connections); fixed constraints are applied at column bases. Structural self-weight is explicitly incorporated. The finite element model incorporated necessary simplifications, including material idealization of steel as homogeneous isotropic elastic–plastic and simplified boundary conditions where temporary flexible supports were modeled as ideal articulations. These idealizations, particularly the boundary condition simplification, represent the primary source of deviation between simulated and measured deformation values. Acknowledging these limitations provides transparency and establishes a basis for future model refinement. Eighteen construction stages (S1–S18) simulate self-weight effects during lifting and temporary support unloading. This approach accurately reproduces time-dependent structural mechanics throughout construction, providing reliable data to elucidate the evolutionary behavior of internal forces and deformations.

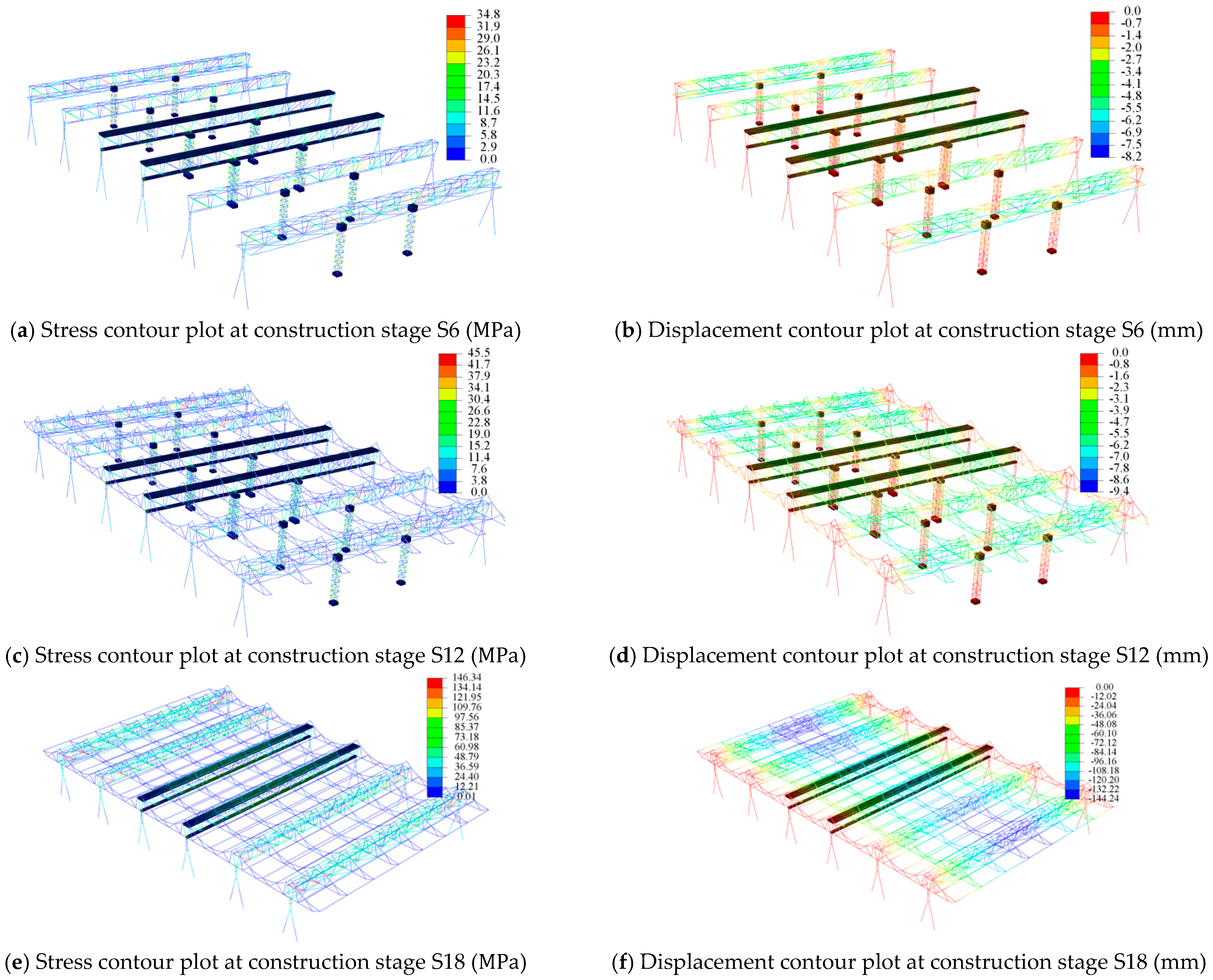
5.2. Dynamic Simulation of Construction Processes

To accurately simulate construction sequences, this study implements ABAQUS 2020 element activation/deactivation techniques. Primary truss elements are sequentially activated with simultaneous application of temporary support constraints. Subsequently, secondary truss elements are incrementally activated in Stages S7–S11, employing tie constraints to model welded connections to primary trusses. Phased removal of temporary supports is then implemented in Stages S13–S18 through progressive constraint deactivation. Structural stress control limits are set at 295 $\mathrm{M}\mathrm{P}\mathrm{a}$ based on the requirements of GB 50017-2017 [23] Tables 4.4.1 and B.2.4-1, with deflection limits of L/250 (L is span length). The following table lists the specific contents.

Given space constraints, Figure 12 presents numerical results for critical stages only: S6 (primary truss completion), S12 (full truss installation), and S18 (temporary support removal). Analysis reveals the following:

Stage S6: Outer web members of Trusses No.1 and No.6 exhibit peak stresses of 34.8 $\mathrm{M}\mathrm{P}\mathrm{a}$ with maximum mid-span deflection of merely 8.2 mm (Figure 11a,b);

Stage S12: Global maximum stress reaches 45.5 $\mathrm{M}\mathrm{P}\mathrm{a}$, accompanied by a maximum mid-span deflection of 9.4 mm (Figure 12c,d);

Stage S18: Critical web members experience sharply elevated peak stresses (146.3 $\mathrm{M}\mathrm{P}\mathrm{a}$), while maximum mid-span deflection rises significantly to 144.2 mm (Figure 12e,f).

All stress and deflection values remain well below specified limits, confirming the reliability of the construction scheme and providing crucial guidance for field implementation.

6. Instrumentation Layout and Monitoring Strategy

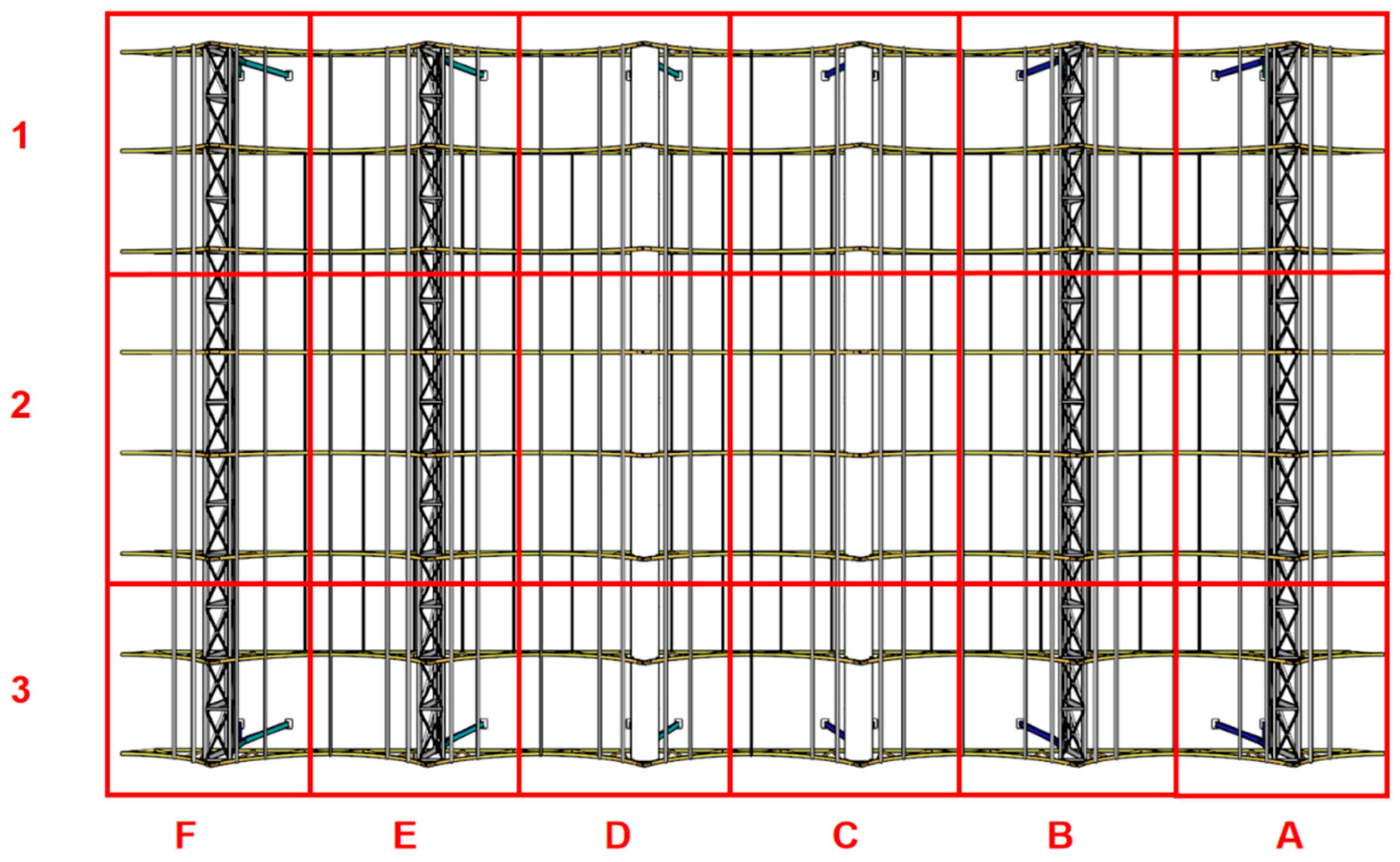
6.1. Layout of Measurement Points

To ensure structural safety during steel truss construction, where component stresses and displacements evolve continuously, this project employed a non-contact optical measurement system based on digital image processing. This system monitored the vertical displacements of the nonstandard primary trusses, specifically targeting ten measurement points (five per truss) on the undersurfaces of the bottom chord. The measurement points for No.3 and No.4 were designated as STL and STR, respectively (Figure 13). The stars are the positions of the measurement points. Monitoring equipment was positioned atop the end-of-span, herringbone column of these trusses. The system employs automated real-time optical target tracking to precisely capture structural responses during temporary support removal. This approach overcomes technical bottlenecks in conventional strain measurement for high-altitude long-span structures, providing reliable displacement data for refined construction safety validation.

6.2. Description of Monitoring Instrumentation

The monitoring equipment used this time is the RMC-01 from Shenzhen Weite Intelligent Technology Co., Ltd. in Shenzhen, China. The monitoring system utilizes RMC-01 online cameras (Figure 14a) and corresponding optical targets (Figure 14b). This non-contact full-field optical measurement system employs advanced digital image processing to enable displacement data acquisition with automated transmission, real-time analysis, and graphical visualization. Designed for long-range, high-precision structural monitoring, the system achieves a displacement resolution of 1/100,000 relative to the field of view with measurement accuracy better than the 0.01 mm-performance specifications typically applied to kilometer-scale bridges. The non-contact optical monitoring system’s accuracy is influenced by several factors: lighting extremes (causing up to ±0.3 mm deviation or 15–20% increased error), calibration stability, and minimal processing delays. These were mitigated through scheduled monitoring during optimal light conditions and regular calibration checks and were deemed negligible for tracking slow structural deformations. Field installation details are documented in Figure 15.

6.3. Construction Monitoring Protocol

Following assembly of all primary and secondary trusses, a high-precision displacement monitoring system is deployed before initiating temporary support removal. The implementation comprises the following:

(1)

Installation of RMC-01 photogrammetric systems on observation platforms atop the herringbone column of critical nonstandard trusses No.3 and No.4, ensuring an unobstructed field of view;

(2)

Mounting of high-contrast retroreflective targets at predetermined measurement points on the bottom chord surfaces.

After system calibration and functional verification, baseline reference data was acquired under full support loading conditions. During stage removal, synchronized data acquisition is triggered immediately following sequential removal of temporary supports beneath each primary truss, capturing transient displacement responses during and after load transfer.

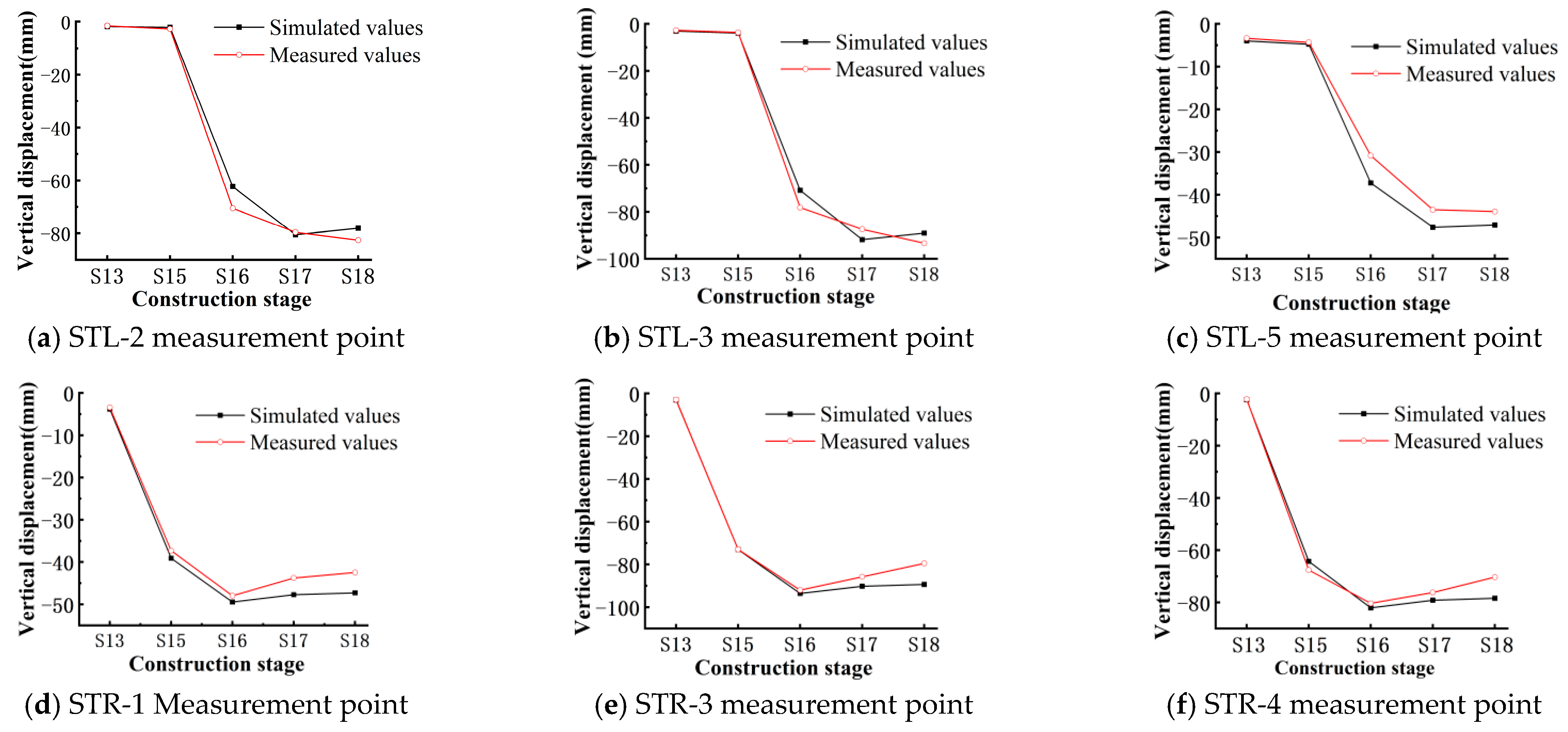
7. Validation of Construction Simulation Against Field Monitoring Data

To validate the reliability of the steel truss construction scheme and finite element model, this study establishes a dual-verification framework integrating numerical simulation accuracy assessment with construction safety evaluation. Vertical deflection of primary truss bottom chords serves as the key control parameter during temporary support removal. Comparative analysis of FEA predictions and field measurements at critical monitoring points (Figure 16,

Table 1. Comparison of vertical displacements at selected measurement points for different construction stages.

Measurement Points Data		Construction Stage
		S13	S15	S16	S17	S18
STL-2	Simulated Values/mm	−1.8426	−2.3363	−63.367	−80.574	−78.1374
	Measured values/mm	−1.6669	−2.7162	−70.569	−79.6275	−82.6381
	Deviation/%	18.07%	−14.81%	−10.3%	1.19%	−5.48%
STR-2	Simulated Values/mm	−1.8354	−64.2866	−82.1174	−79.1754	−78.4462
	Measured values/mm	−1.7536	−66.0528	−82.7360	−77.6251	−76.2787
	Deviation/%	4.57%	−2.8%	−0.75%	2.09%	2.97%
STR-3	Simulated Values/mm	−3.1080	−73.0572	−93.6086	−90.2246	−89.3865
	Measured values/mm	−2.9181	−72.9853	−92.0445	−85.8273	−79.5429
	Deviation/%	6.52%	0.95%	1.69%	5.12%	12.42%
STL-5	Simulated Values/mm	−3.9930	−4.7810	−37.2473	−47.6281	−47.0906
	Measured values/mm	−3.3802	−4.3467	−32.8419	−43.5200	−43.9540
	Deviation/%	18.04%	10.13%	13.39%	9.42%	7.14%

Note: Negative values in Table 1 indicate downward deflections. Deviation = (Simulated − Measured)/Measured × 100%.

) reveals that STL-3 and STR-3 exhibit peak vertical displacements of 92.04 mm during support removal, confirming maximum deflection occurs at midspan regions of nonstandard primary trusses; the average simulation-measurement discrepancy across all points is approximately 10%, with localized extremes at STL-2 (18.07% under Stage S12 loading) and STR-2 (0.75% during Stage S15). The significant errors observed in Table 1 primarily originate from measurement points located near the herringbone columns. At these locations, minor displacement inconsistencies occurred during the temporary support removal process. Based on rigorous analysis, these significant errors are confirmed to fall within the acceptable range. The measured deflections comply with all three standards (GB 50017-2017, Eurocode, AISC 360-10 [24]). Despite differing limit values arising from distinct safety philosophies, our monitoring methodology aligns with international practice by validating serviceability limits through real-time data.

Table 2. Allowable deflection limitations in different codes.

	GB 50017-2017	AISC 360-10	Eurocode
Deflection limits	L/250	L/240	No specific regulations. Satisfy serviceability requirements

summarizes the limit values specified by the design code. In addition, the presence of both positive and negative errors in the table is attributed to several possible factors, including slight shifts in monitoring instruments attached to the trusses during temporary support removal, and simplifications of boundary conditions in the numerical model compared to the actual structural conditions, among other potential influences.

This error distribution demonstrates close alignment between FEA and field measurements, validating both the computational model’s predictive capability and the construction scheme’s structural safety.

8. Truss Stability Analysis

The upper end of the herringbone column supports a large-span spatial grid frame structure comprising interconnected primary and secondary trusses. While distinct from single-layer lattice shells, this structural system falls within the scope of Technical Specification for Space Frame Structures (JGJ 7-2010) [25], which mandates stability verification for long-span spatial structures. Per Article 4.3.1, stability calculations are expressly required for single-layer lattice shells and double-layer shells with a thickness-to-span ratio below 1/50. Given the critical importance of stability in spatial grid frames under asymmetric construction loads, this study conducts comprehensive stability analysis in accordance with the code’s fundamental principles.

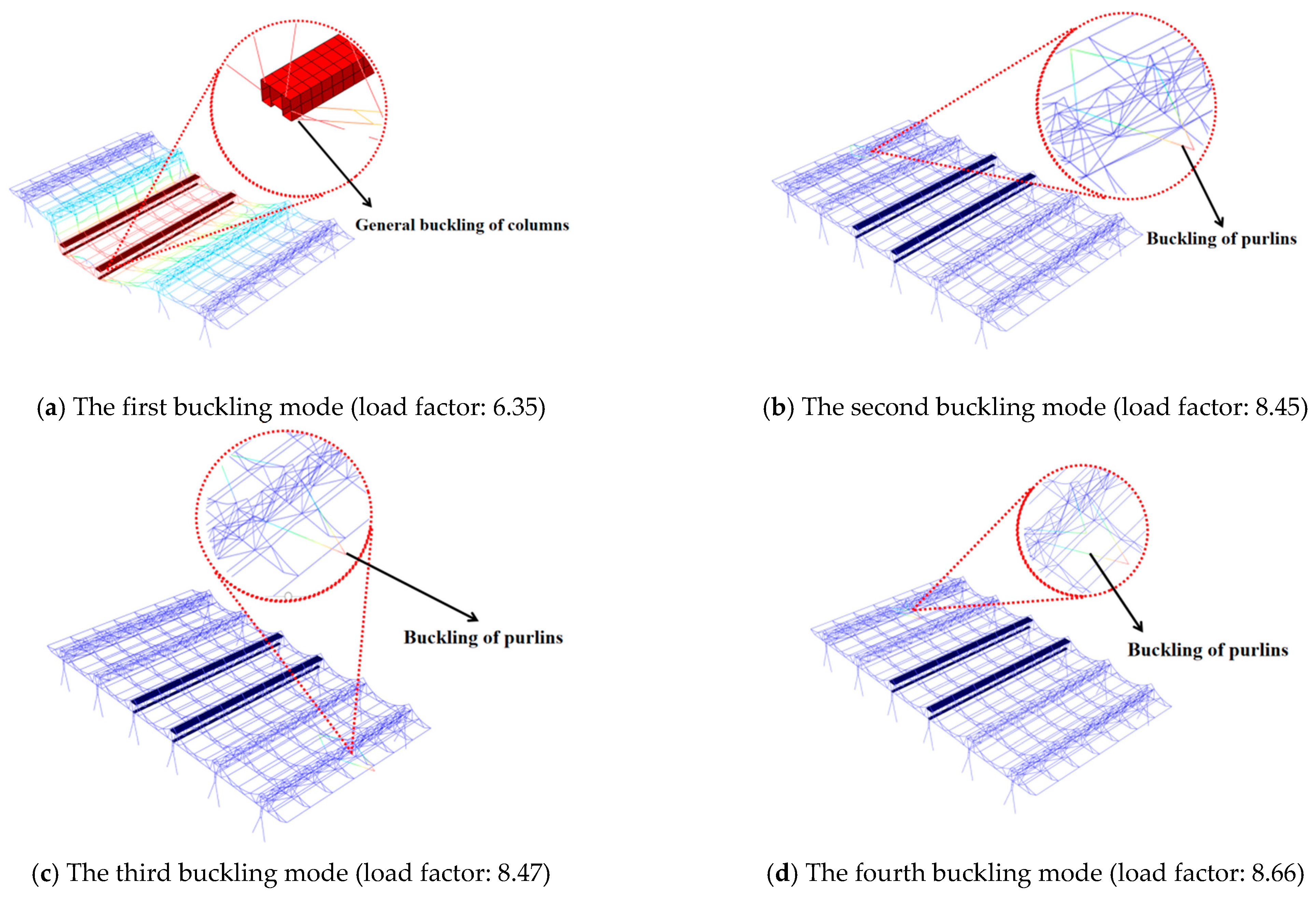
8.1. Eigenvalue Buckling Analysis

Eigenvalue buckling analysis predicts the theoretical elastic buckling capacity of ideal structures by solving linear eigenvalue problems, disregarding initial geometric imperfections and material nonlinearity. This method establishes the upper-bound buckling load and identifies the critical failure mode.

Eigenvalue analysis was performed on steel trusses by using ABAQUS 2020 software, following complete temporary support removal, with load combination 1.0DL (dead load) + 1.0LL (live load) as the reference loading. Figure 17 presents the first four buckling modes and corresponding load factors. All load factors exceed 2.0, satisfying the minimum requirement of Article 4.3.4 of JGJ 7-2010. The fundamental mode (Mode 1) exhibits global instability, while Modes 2-4 exhibit local buckling at roof purlin connections. Key findings and recommendations are as follows:

(1)

Global stability enhancement: Mode 1 (Figure 17a) indicates that nonstandard primary truss end columns initiate destabilization. It is recommended to strengthen lateral restraint systems at the herringbone columns’ upper ends under ultimate load.

(2)

Local buckling mitigation: Thin-walled purlins (6 mm thick 350 mm × 200 mm box-sections) require increased sectional stiffness to reduce stress concentrations from welding constraints, accommodate differential truss deflections, and suppress premature local buckling (Modes 2~4).

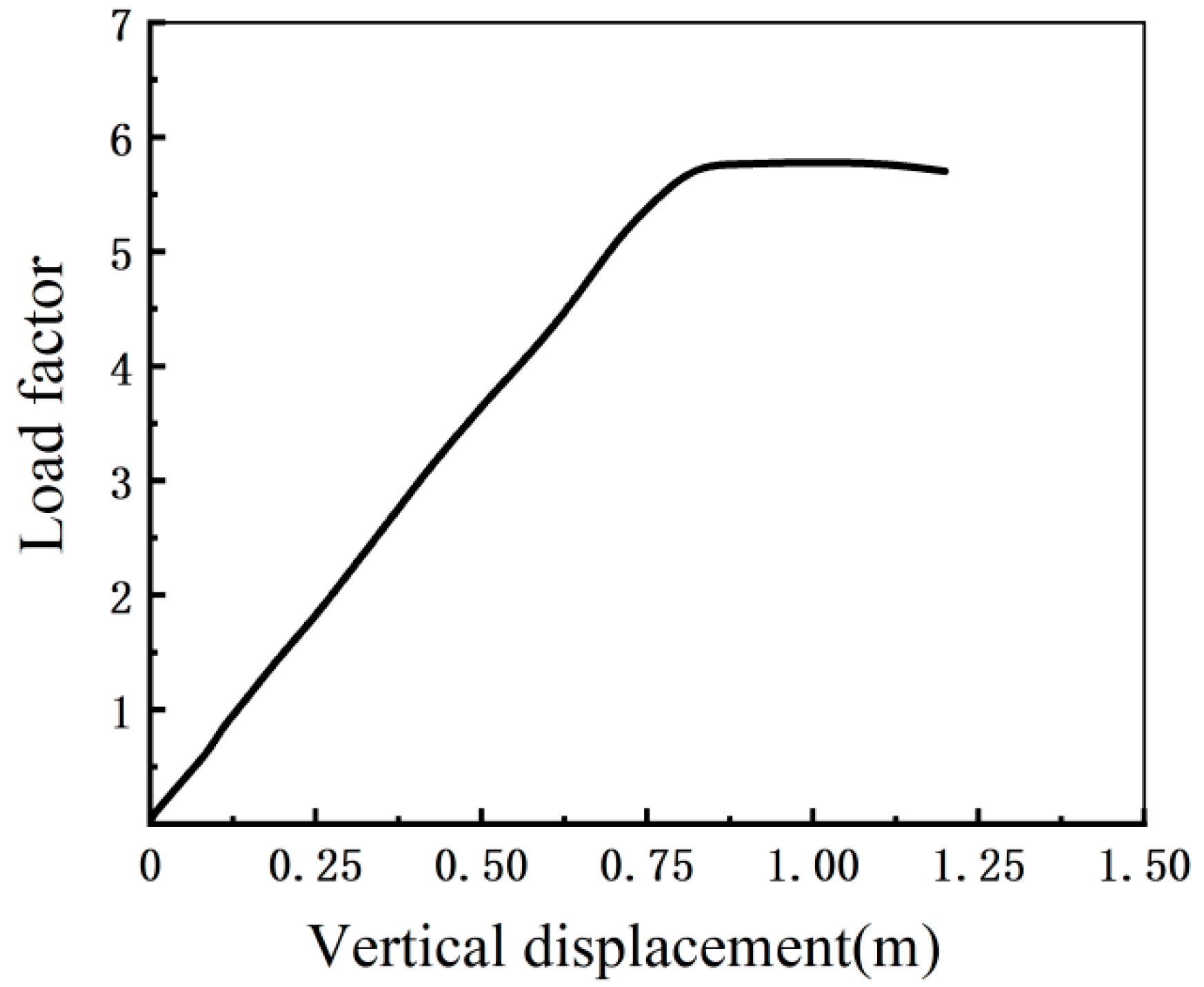
8.2. Geometrically Nonlinear Stability Analysis

Structural nonlinearity encompasses both material and geometric effects. While steel exhibits linear stress–strain behavior initially, geometric nonlinearity dominates when structural displacements significantly alter force distributions. Considering geometric nonlinearity exclusively (material nonlinearity being negligible within the elastic range), the load–displacement curve at the control node exhibits progressive stiffness degradation (Figure 18). The geometrically nonlinear elastic buckling load factor is 5.71, surpassing the minimum requirement of 4.2 specified in JGJ 7-2010 Section 4.3.4 [25] and confirming global stability. This represents a 10.1% reduction from the linear eigenvalue prediction value of 6.35, demonstrating the quantifiable influence of geometric nonlinearity on stability performance. Wind loading was incorporated in the nonlinear buckling analysis. However, variations in live loads during construction could have a potential influence on the structural stability bearing capacity. A detailed sensitivity analysis of the structural response to these load conditions is recommended for future work.

The cited 10% reduction in the global stability coefficient—from 6.35 (linear eigenvalue analysis) to 5.71 (geometrically nonlinear analysis)—stems from the inclusion of large deformation effects. While the linear result meets the code requirement (>2.0), the nonlinear result reflects the actual structural behavior more accurately, particularly the P-Δ effect in critical components such as the herringbone columns and their connections in the central span, where significant lateral deformations induce additional bending moments not captured by linear analysis.

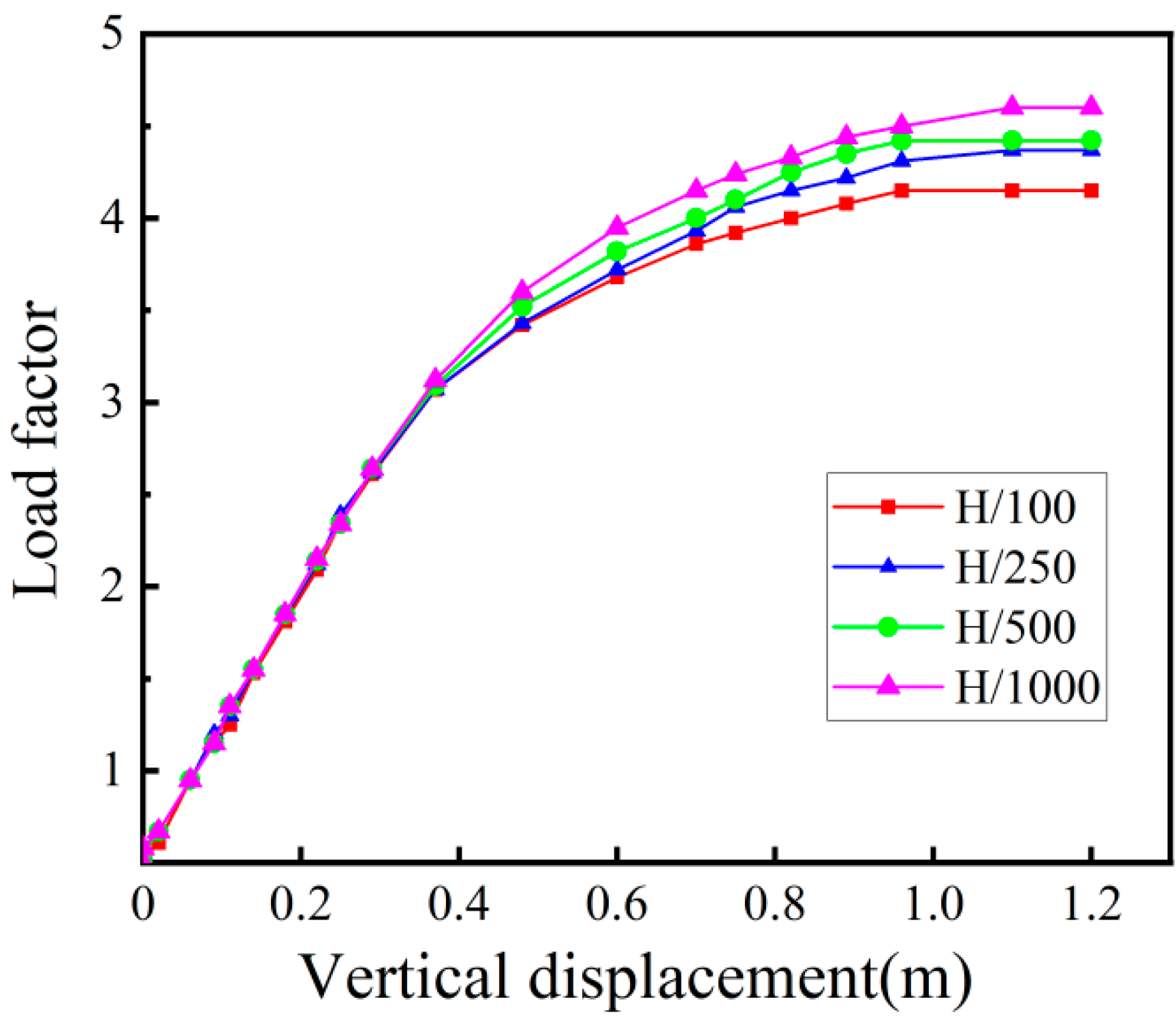
8.3. Analysis of the Effect of Initial Geometric Imperfections

Installation-induced initial geometric imperfections significantly influence structural stability. To investigate their effect on the exhibition hall structure, the sensitivity of the stability bearing capacity to initial imperfections was evaluated by imposing defect distributions based on the fundamental buckling mode shape from eigenvalue analysis. Analyses considered imperfection amplitudes of H/1000, H/500, H/250, and H/100, where H = 21.2 m denotes the structural height. The nonlinear load–displacement curves with different imperfection amplitudes are presented in Figure 19, and the corresponding buckling load coefficients are indicated in

Table 3. Buckling load factors under varying initial imperfection amplitudes.

Initial Imperfection Amplitude	H/1000	H/500	H/250	H/100
Buckling load factors	4.1	3.92	3.87	3.65

.

As shown in Table 3, the buckling load coefficient of the structure progressively decreases with increasing initial imperfection amplitude, declining from 4.1 (H/1000) to 3.65 (H/100), which represents a reduction of approximately 10.9%. Notably, even at the maximum initial imperfection amplitude, the buckling load coefficient (3.65) remains substantially higher than the specified value of 2.0 stipulated in the Technical Specification for Space Frame Structures (JGJ 7-2010) [25], exceeding by 82.5%. While larger imperfections marginally reduce the stability reserve, the maximum reduction magnitude remains below 11%. These results confirm imperfection-insensitive behavior and robust stability reserves in the large-span steel truss system across practical tolerance ranges (H/1000 to H/100), demonstrating full compliance with structural safety standards.

9. Conclusions

Focusing on an irregular spatial steel truss roof in an exhibition center, this study integrates full-process health monitoring with construction simulation and stability analysis during assembly and unloading. The main conclusions are as follows:

(1)

The developed structural health monitoring system enables real-time tracking of vertical displacements at critical nodes of nonstandard primary trusses. Close agreement between monitoring data and FEM simulations confirms the accuracy of the numerical model and validates the reliability of the construction scheme. The results provide a robust technical foundation for optimizing the construction and simulation of similar truss structures.

(2)

Construction monitoring reveals that primary trusses under long-span and heavy-load conditions exhibit symmetrically parabolic vertical displacement profiles, with mid-span maxima reaching 93 mm and end supports stabilizing at 2–3 mm. This underscores the criticality of mid-span vertical displacement control in such structures. To mitigate deformation, pre-camber adjustments are recommended for comparable projects to achieve targeted compensation.

(3)

Linear buckling analysis yields a first-order critical load factor of 6.35, surpassing the minimum threshold of 4.2 and confirming baseline stability. Nonlinear analysis incorporating geometric imperfections of H/100 reduces the buckling load factor to 3.65, showing a 10.9% reduction from the linear result, which still complies with codified stability requirements, demonstrating sufficient safety margins post-construction.

(4)

The core methodology of this study—real-time comparison of full-field monitoring data with finite element predictions—constitutes a universally applicable paradigm for large-scale structural control. While specific monitoring metrics may vary across structures (e.g., displacement in roofs, stress in bridge cables, or settlement in stadium foundations), the integrated monitoring system adapts to diverse geometries, and the analytical framework of model validation and updating through real-time data remains consistently applicable. This “monitor-model-compare” logic ensures the direct transferability of our approach to other long-span structures such as stadium roofs and bridges.