Failure Mechanism and Load Carrying Capacity of Hybrid High-Strength Steel Composite Cellular Beams Under Low Cyclic Loading
Abstract
1. Introduction
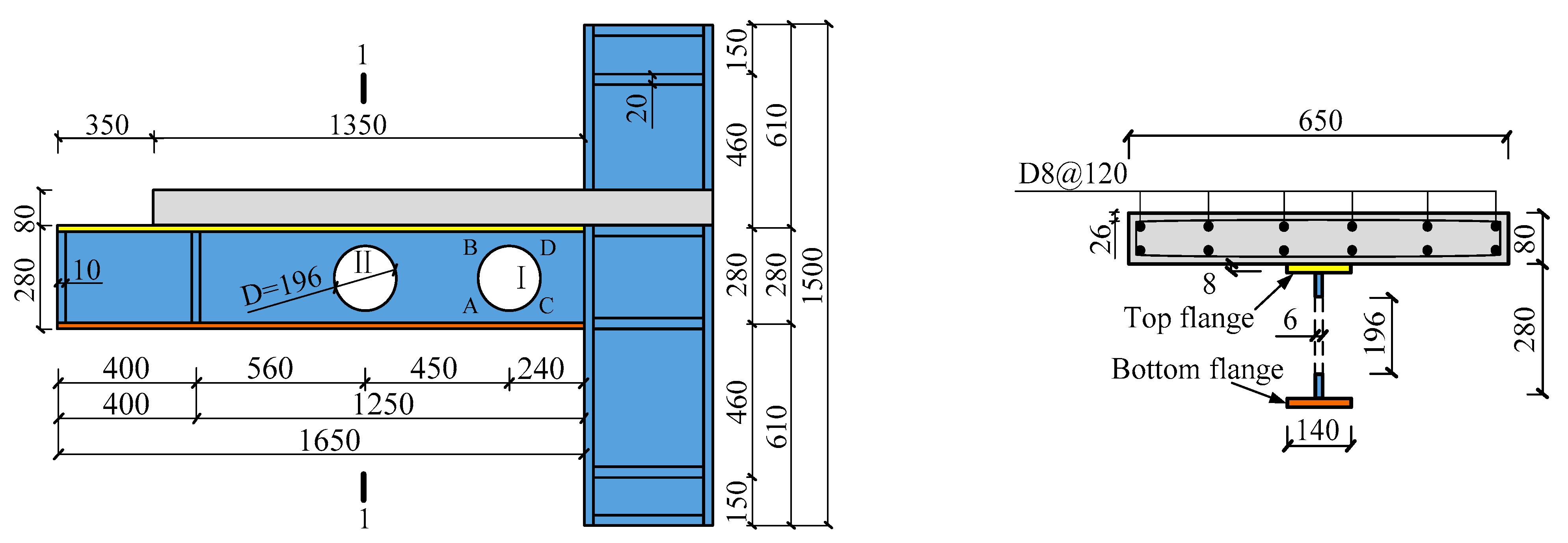
2. Experimental Design
3. Vierendeel Mechanism of HHS-CCBs
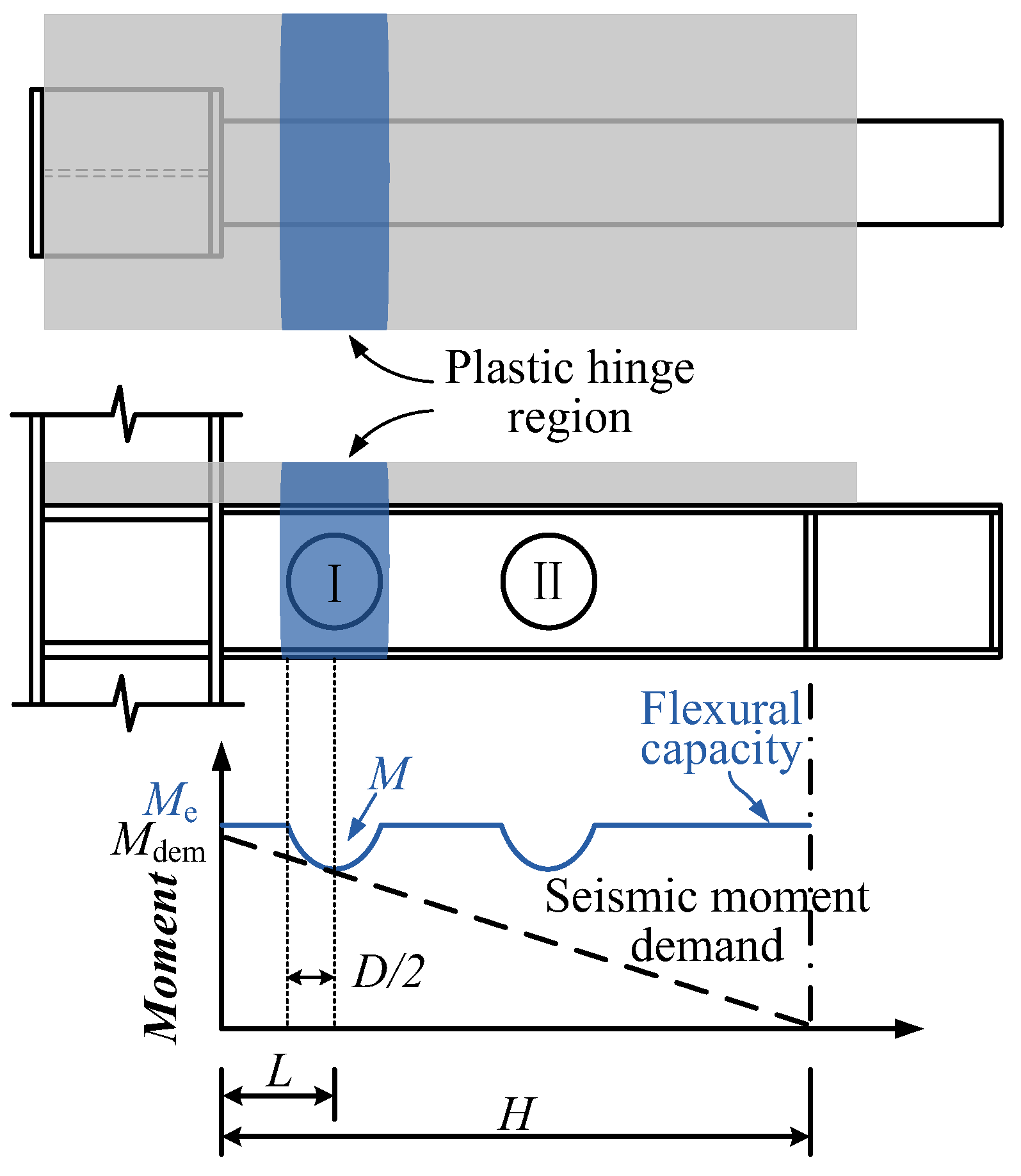
3.1. Failure Modes
3.2. Strain Analysis Around Hole I of the Specimens
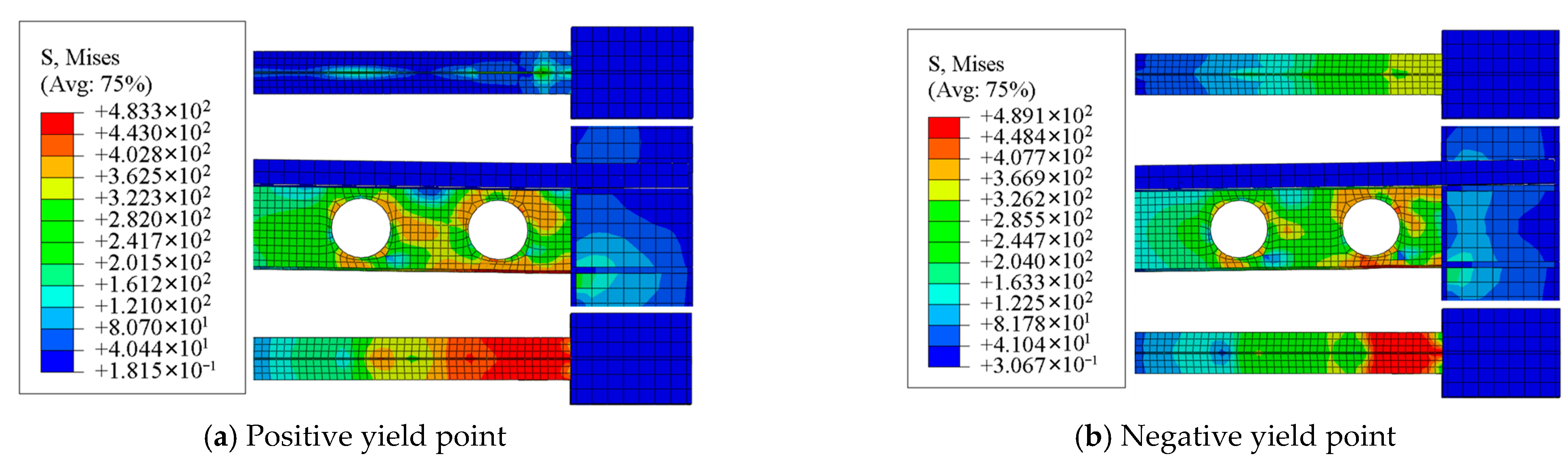
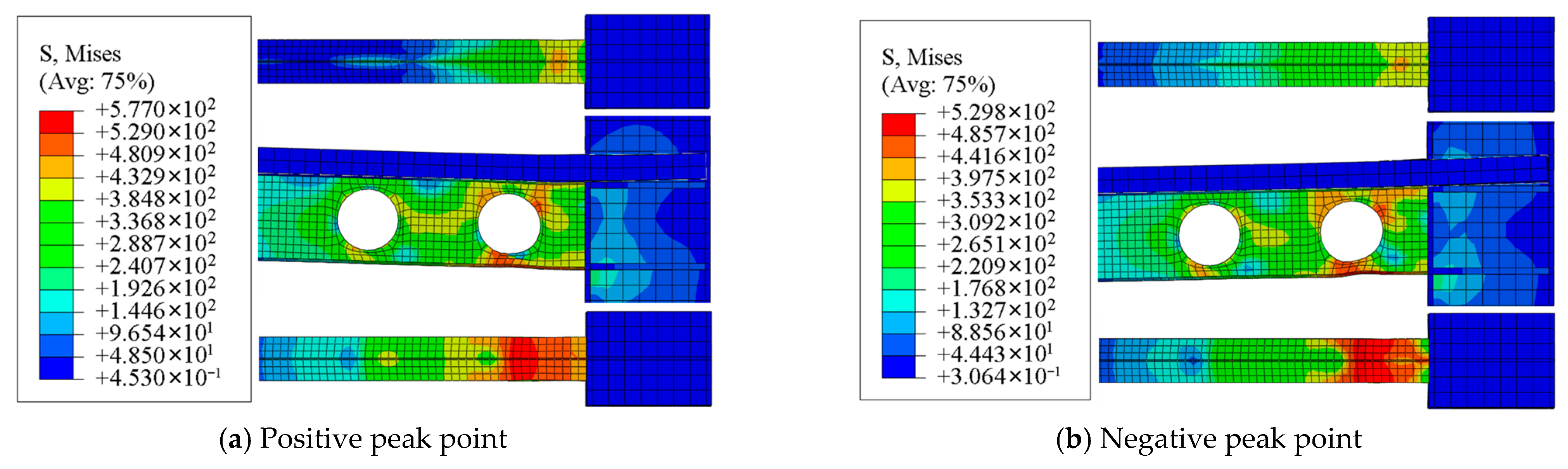
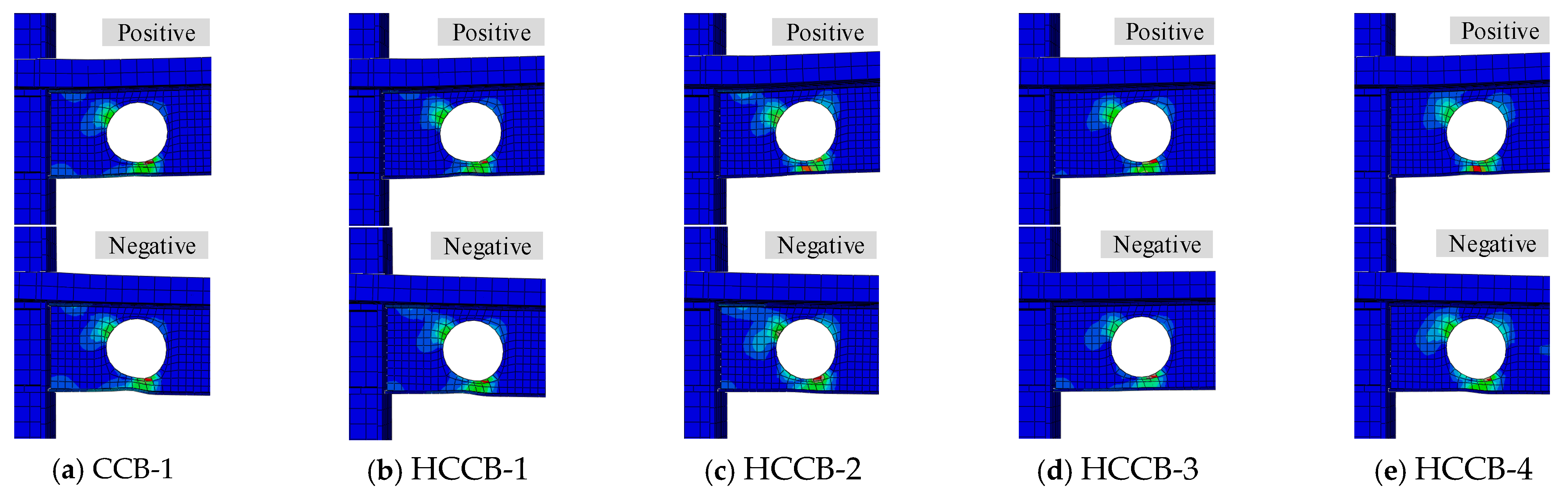
3.3. Finite Element Analysis (FEA) Around Hole I of the Specimens
3.3.1. Stress Distribution Development of Cellular Beam Under Yield Stage
3.3.2. Stress Distribution Development of Cellular Beam Under Peak Stage
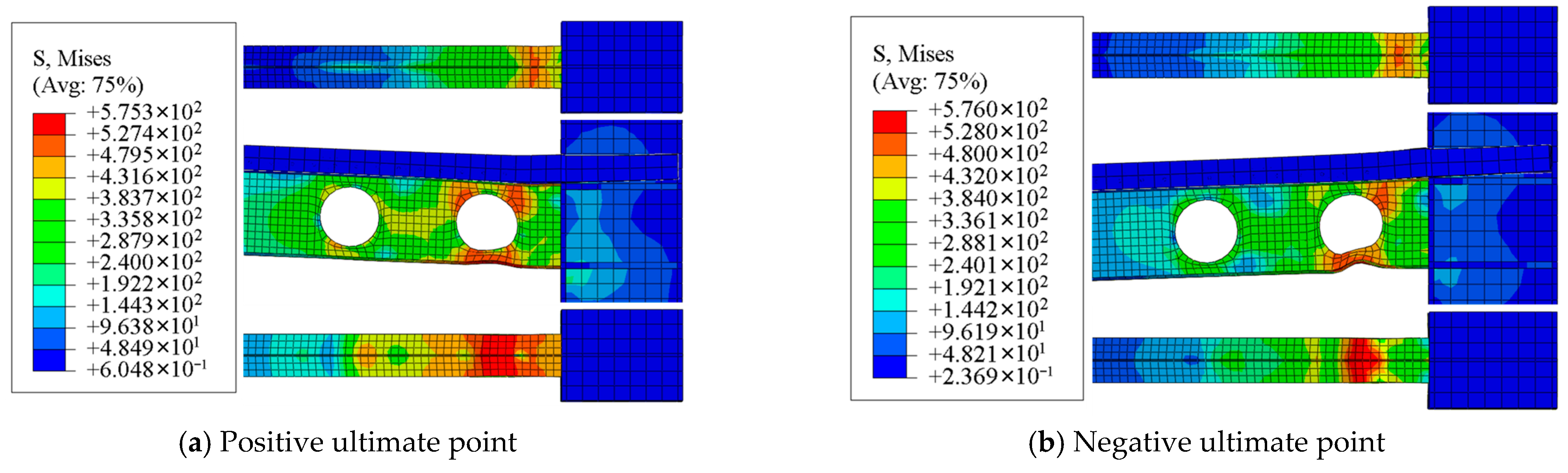
3.3.3. Stress Distribution Development of Cellular Beam Under Ultimate Stage
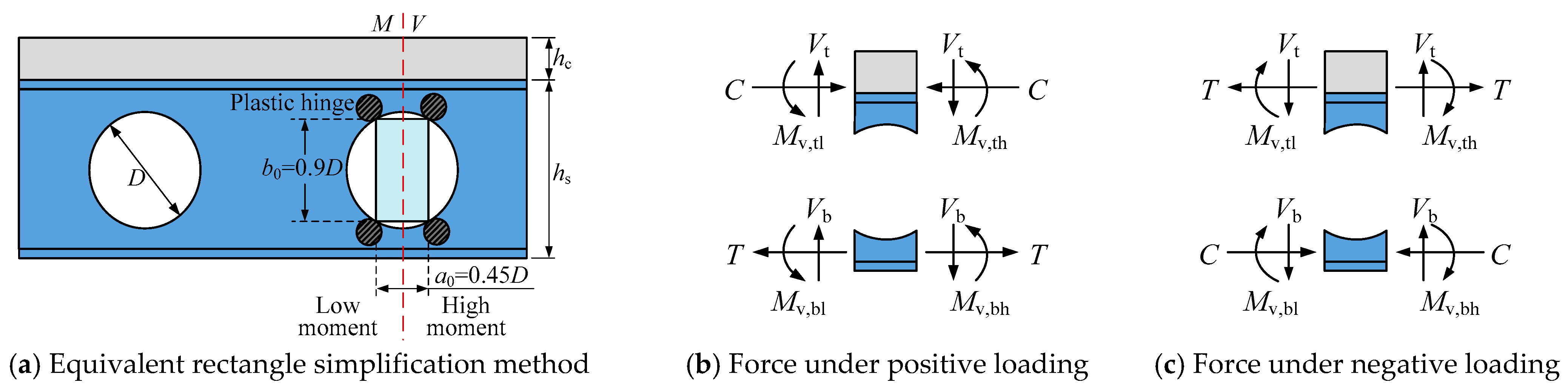
3.4. Mechanical Model of a Composite Beam with Web Opening
4. Applicability of the Calculation Method in SEI/ASCE [23]
5. Design Model of HHS-CCBs with Circular Holes
5.1. Maximum Bending Capacity at the Web Opening
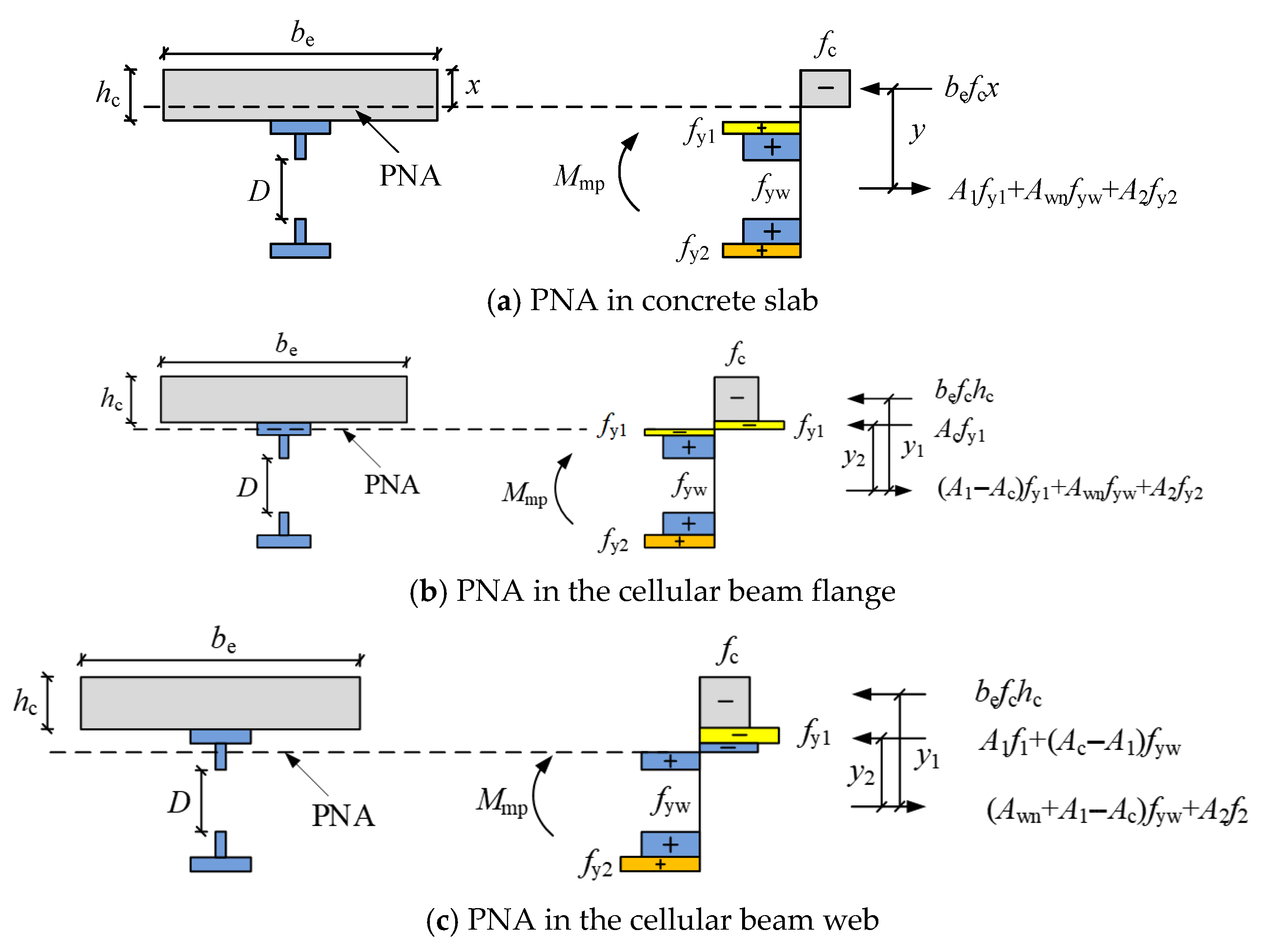
5.1.1. Maximum Bending Capacity at Web Opening Under Positive Loading
- (a)
- PNA in the concrete slab
- (b)
- PNA in the cellular beam flange
- (c)
- PNA in the cellular beam web
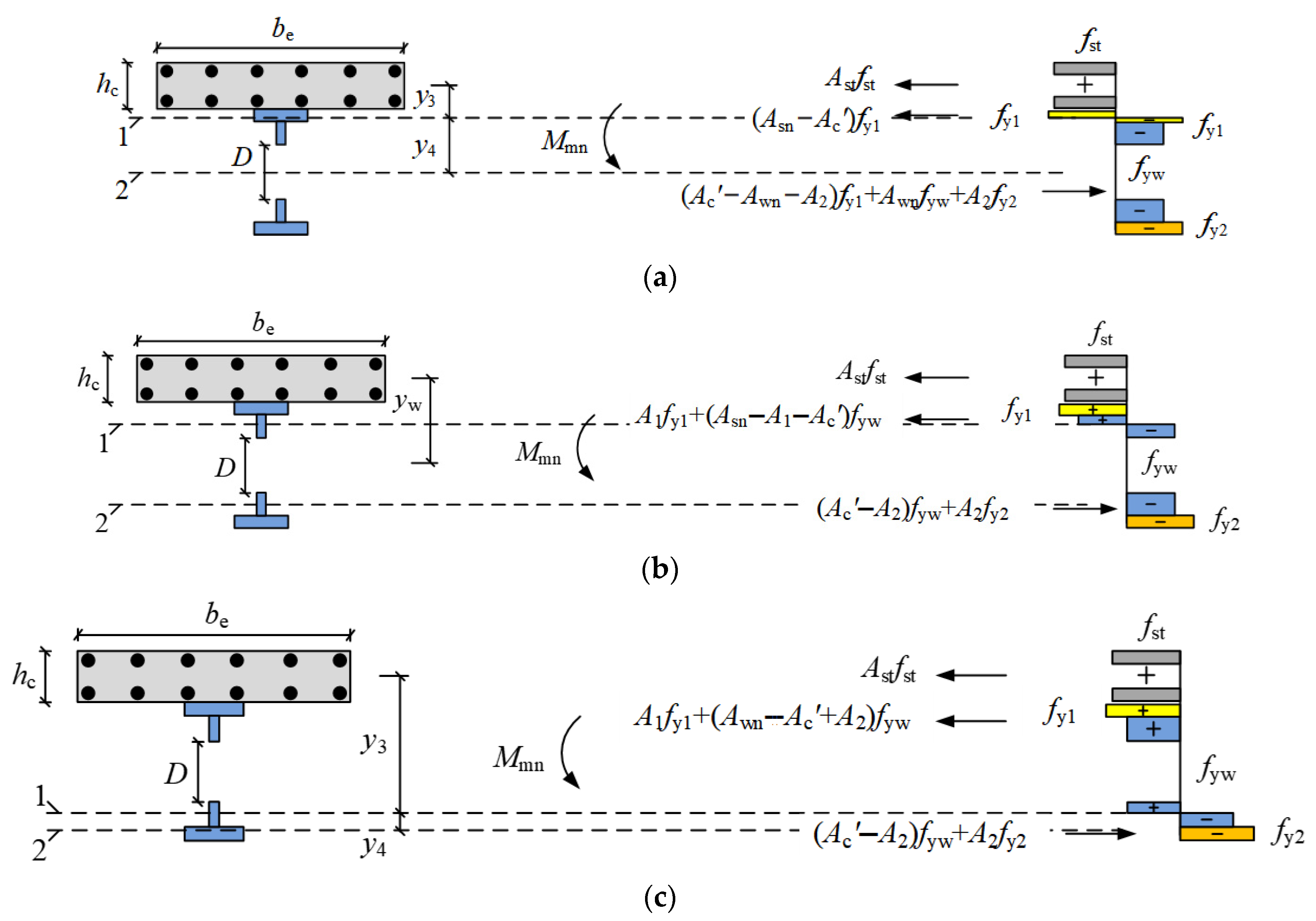
5.1.2. Maximum Bending Capacity at Web Opening Under Negative Loading
- (a)
- 1-axis is located on the upper flange of the cellular beam, and the 2-axis is located at the opening center of the cellular beam
- (b)
- 1-axis is located on the upper T-shape of the cellular beam, and the 2-axis is located at the lower T-shape of the cellular beam
- (c)
- 1-axis is located on the lower T-shape of the cellular beams, and the 2-axis is located at the lower flange of the cellular beam
5.2. Maximum Shear Capacity at the Web Opening
5.2.1. Maximum Shear Capacity at Web Opening Under Positive Loading
5.2.2. Maximum Shear Capacity at the Web Opening Under Negative Loading
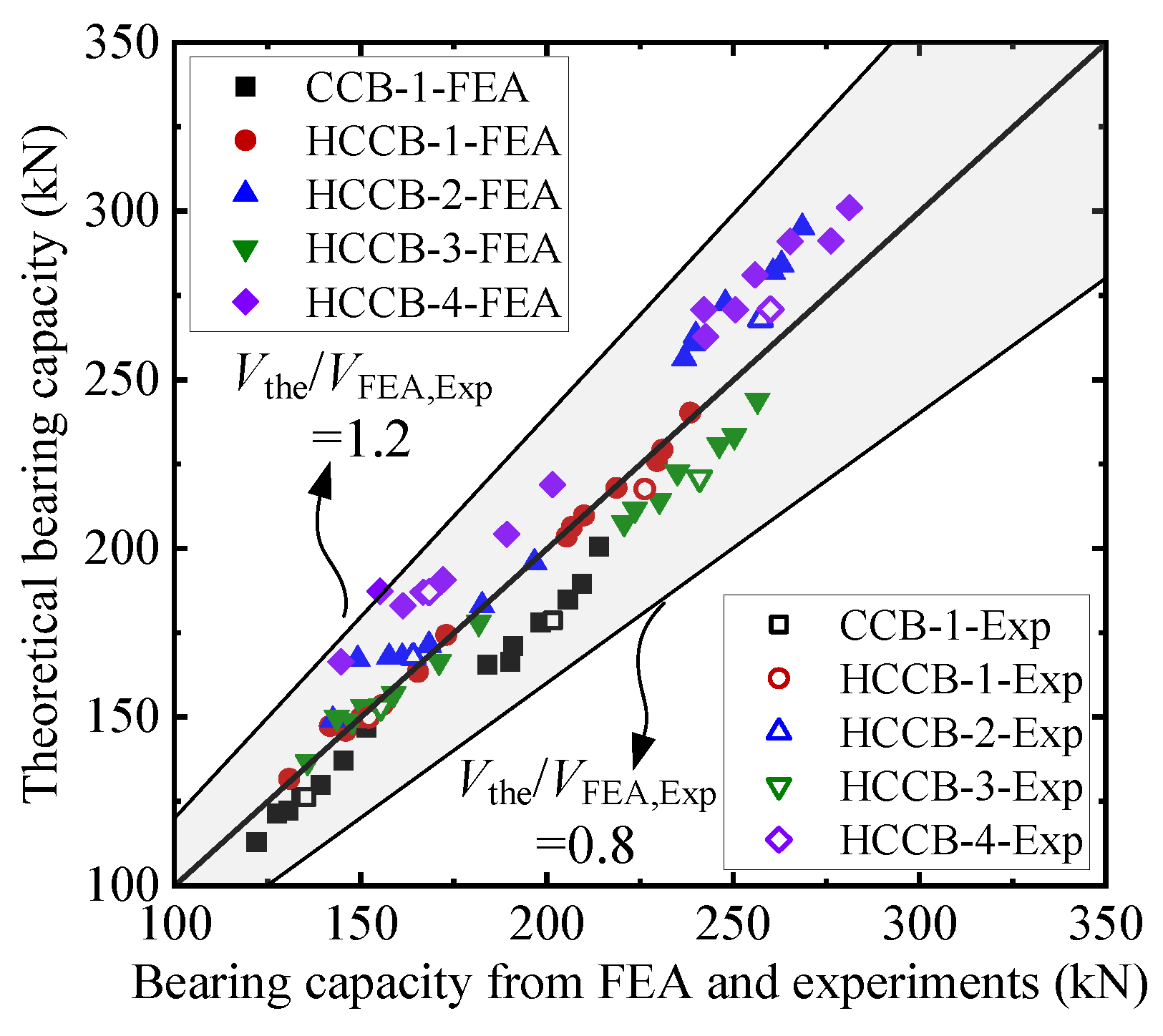
5.3. Comparison of the Experimental and Theoretical Load Carrying Capacities at the Web Opening
6. Comparison of FEA and Theoretical Results
6.1. Weakening Parameter
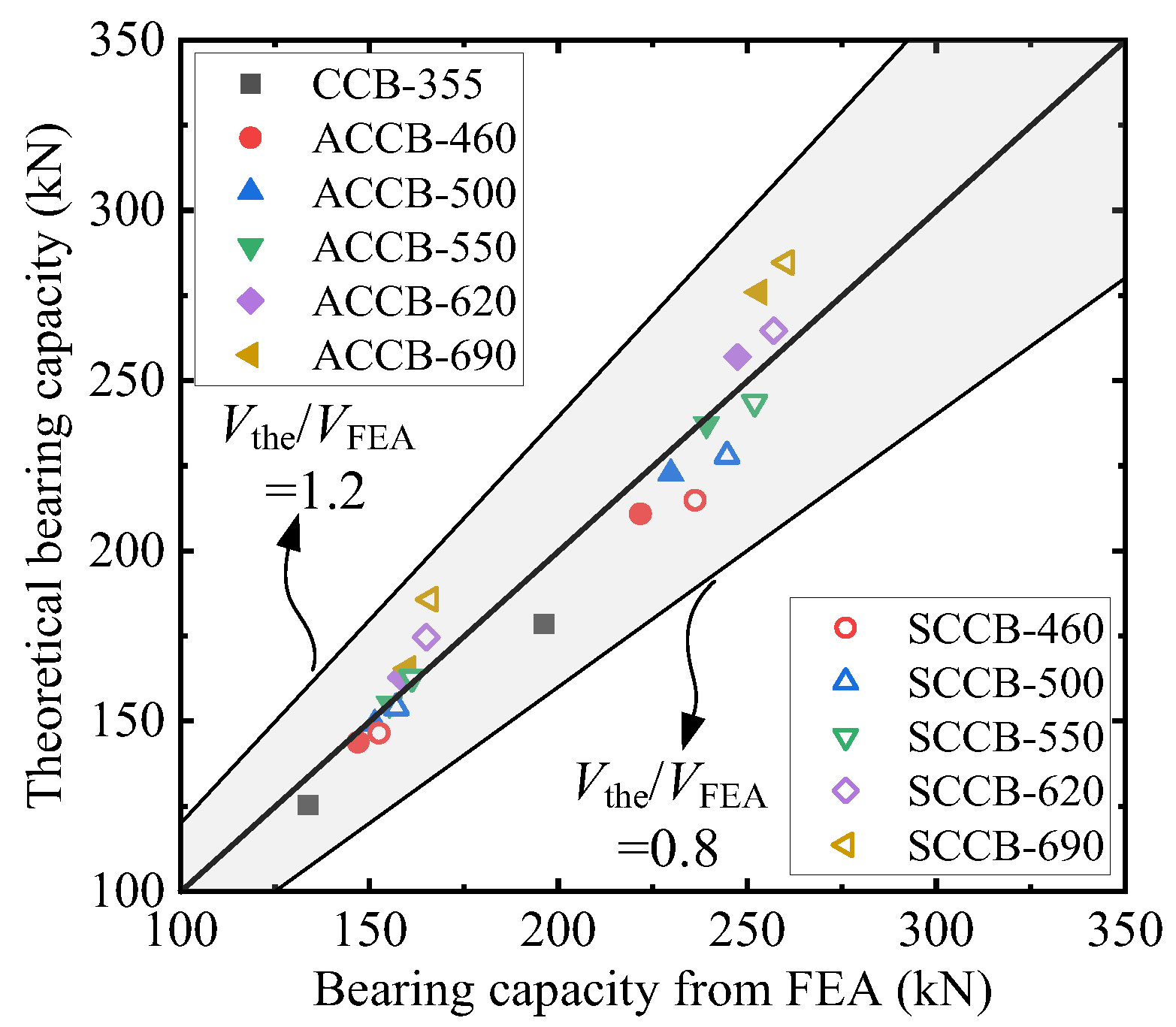
6.2. Strength Matching of the Flange and Web
7. Design Suggestions
8. Conclusions
- (1)
- Based on the Vierendeel mechanism damage at the beam-end opening web, a calculation method for the load-carrying capacity of HHS-CCBs with circular holes was proposed using the cubic interaction curve of the bending moment shear force. Simultaneously, the shear contributions of the flange and concrete slab at the web opening were considered. The calculation results were consistent with the results of the experiments and FEA, and can provide a reference for practical engineering design.
- (2)
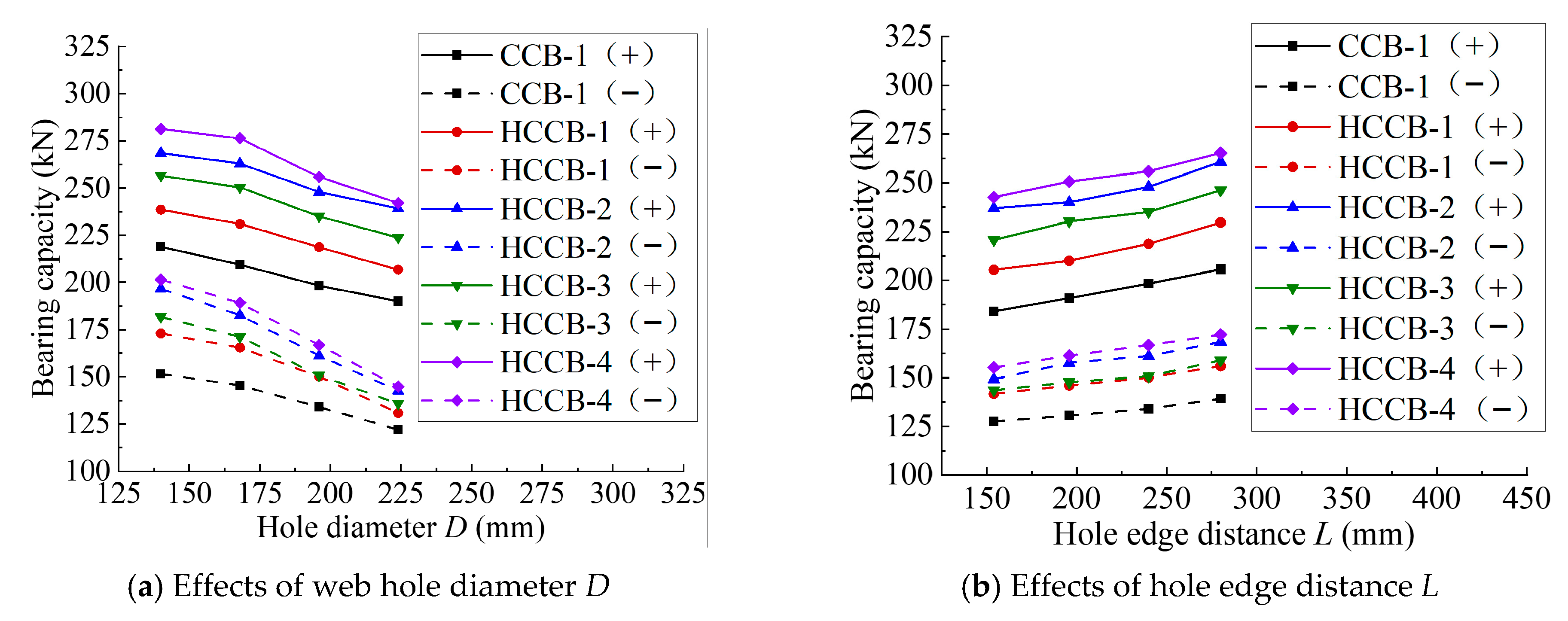
- The weakening parameters at the beam ends determine the failure mode of HHS-CCBs. In practical engineering, to avoid stress concentration at the beam-end welds, ensure the development of the Vierendeel mechanism at the web openings of the beam ends, and prevent excessive reduction in load-carrying capacity, it is recommended that the weakening parameter ranges for HHS-CCBs be set as follows: hole diameter D = 0.6hs − 0.7hs and hole edge distance L = 0.7hs − 1.0hs, respectively. For symmetric HHS-CCBs with a flange strength of up to 690 MPa, the upper limit of the hole edge distance L can be extended to 1.3hs.
- (3)
- The experimental and finite element results indicate that strength matching between the flange and web has almost no effect on the failure mode of the HHS-CCBs. It is recommended that when the web strength of cellular steel beam is 355 MPa, the flange yield strength should not exceed 550 MPa. Additionally, asymmetric HHS-CCBs exhibit both favorable mechanical properties and economic benefits and have greater overall advantages over symmetric HHS-CCBs.
- (4)
- The load-carrying capacity calculation formula can be applied to HHS-CCBs with different section types, where there are circular holes at the beam web and Vierendeel mechanism damage occurs, but the flange width–thickness ratio cannot significantly exceed the limit.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lawson, R.M.; Chung, K.F.; Price, A.M. Tests on composite beams with large web openings to justify existing design methods. Struct. Eng. Lond. 1992, 70, 1–7. [Google Scholar]
- Lawson, R.M. Design for Openings in the Webs of Composite Beams; CIRIA Special Publication and SCI Publication 068; CIRIA, Steel Construction Institute: Bracknell, UK, 1987. [Google Scholar]
- Chung, K.F.; Lawson, R.M. Simplified design of composite beams with large web openings to Eurocode 4. J. Constr. Steel Res. 2001, 57, 135–164. [Google Scholar] [CrossRef]
- Eurocode4: Design of Composite Steel and Concrete Structures; European Committee for Standardization: Brussels, Belgium, 2004.
- Zhou, D. Beitrag zum Tragverhalten und zur Entwicklung der Rechenmodelle von Verbundträgern mit Stegöffnungen; Shaker-Verlag: Düren, Germany, 2003. [Google Scholar]
- Zhou, D. Ein Rechenverfahren für Verbundträgern mit Stegöffnungen-Teil 1. Stahlbau 2003, 72, 626–634. [Google Scholar] [CrossRef]
- Zhou, D. Ein Rechenverfahren von Verbundträgern mit Stegöffnungen-Teil 2. Stahlbau 2003, 72, 744–747. [Google Scholar] [CrossRef]
- Wang, P.; Zhou, D.H.; Wang, Y.H.; Han, C.X. Theoretical study on ultimate bearing capacity of composite beams with reinforced web opening. Eng. Mech. 2013, 30, 138–146. [Google Scholar]
- Li, L.Q. Experimental Study and Theoretical Analysis of Steel-Concrete Continuous Composite Beams with Web Opening. Master’s Thesis, Kunming University of Science and Technology, Kunming, China, 2014. [Google Scholar]
- Todd, D.M.; Cooper, P.B. Strength of composite beams with web openings. J. Struct. Div. 1980, 106, 431–444. [Google Scholar] [CrossRef]
- Donoghue, C.M. Composite beams with web openings: Design. J. Struct. Div. 1982, 108, 2652–2667. [Google Scholar] [CrossRef]
- Redwood, R.G.; Pournbouras, G. Analysis of composite beams with web openings. J. Struct. Eng. 1984, 110, 1949–1958. [Google Scholar] [CrossRef]
- Clawson, W.C.; Darwin, D. Tests of composite beams with web openings. J. Struct. Div. 1980, 108, 145–162. [Google Scholar] [CrossRef]
- Clawson, W.C.; Darwin, D. Strength of composite beams at web openings. J. Struct. Div. 1982, 108, 623–641. [Google Scholar] [CrossRef]
- Cho, S.H.; Redwood, R.G. Slab behavior in composite beams at openings. I Anal. J. Struct. Eng. 1992, 118, 2287–2303. [Google Scholar] [CrossRef]
- Redwood, R.; Cho, S.H. Design of steel and composite beams with web openings. J. Constr. Steel Res. 1993, 25, 23–41. [Google Scholar] [CrossRef]
- Fahmy, E.H. Analysis of composite beams with rectangular web openings. J. Constr. Steel Res. 1996, 37, 47–62. [Google Scholar] [CrossRef]
- Donahey, R.C.; Darwin, D. Performance and Design of Composite Beams with Web Openings; University of Kansas: Lawrence, KS, USA, 1986. [Google Scholar]
- Darwin, D.; Donahey, R.C. LRFD for composite beams with unreinforced web openings. J. Struct. Eng. 1988, 114, 535–552. [Google Scholar] [CrossRef]
- Darwin, D.; Lucas, W.K. LRFD for steel and composite beams with web openings. J. Struct. Eng. 1990, 116, 1579–1593. [Google Scholar] [CrossRef]
- Lucas, W.K.; Darwin, D. Steel and Composite Beams with Web Openings; University of Kansas Center for Research, Inc.: Lawrence, KS, USA, 1990. [Google Scholar]
- Darwin, D. Design of Steel and Composite Beams with Web Openings; Steel Design Guide Series No.2; American Institute of Steel Construction: Chicago, IL, USA, 1990. [Google Scholar]
- American Society of Civil Engineers. Specifications for Structural Steel Beams with Web Openings; American Society of Civil Engineers: Reston, VA, USA, 1999. [Google Scholar]
- Park, J.W.; Kim, C.H.; Yang, S.C. Ultimate strength of ribbed slab composite beams with web openings. J. Struct. Eng. 2003, 129, 810–817. [Google Scholar] [CrossRef]
- Du, H.; Hu, X.; Shi, D.; Fang, B. Effect of reinforcement on the strength of the web opening in steel-concrete composite beam. Eng. Struct. 2021, 235, 112038. [Google Scholar] [CrossRef]
- Chen, T.; Gu, X.; Li, H. Behavior of steel-concrete composite cantilever beams with web openings under negative moment. Int. J. Steel Struct. 2011, 11, 39–49. [Google Scholar] [CrossRef]
- Ma, H.W.; Liu, W.Y.; Lin, L.; Yuan, J.L. Experimental Study on the Bending Capacity of Castellated Composite Beam Under Negative Moment. J. South China Univ. Technol. 2019, 47, 75–85. [Google Scholar]
- GB 50017-2017; Standard for Design of Steel Structures. China Architecture and Building Press: Beijing, China, 2017.
- American Institute of Steel Construction. Load and Resistance Factor Design Specification for Structural Steel Buildings; American Institute of Steel Construction, Inc: Chicago, IL, USA, 1999. [Google Scholar]
- Guo, J.R.; Shi, Q.X.; Li, T.F.; Ma, G. Seismic performance of hybrid high-strength steel composite cellular beam under low cyclic loading. J. Constr. Steel Res. 2023, 203, 107801. [Google Scholar] [CrossRef]
- Zhao, H.; Lu, R.; Guo, J.R.; Hai, L.T. Influence of cold-forming on cyclic behaviors and constitutive model constants of Q460 high-strength steel. J. Constr. Steel Res. 2025, 235, 109793. [Google Scholar] [CrossRef]
- Jia, L.G.; Li, Q.W.; Zhang, Y.G. Analysis of shear behaviour of steel-concrete cellular composite beam. Ind. Constr. 2012, 42, 150–156. [Google Scholar]
- Liu, Y.F. Experimental Study on Shear Performance of Cellular Composite Beam. Master’s Thesis, Shenyang Jianzhu University, Shengyang, China, 2013. [Google Scholar]
- Jia, L.G.; Li, Q.W.; Liu, Y.F. Performance analysis and calculation of shear force resistance for cellular beam. Eng. Mech. 2012, 29, 23–30+56. [Google Scholar]
- Guo, J.R.; Sun, L.H.; Zhao, H.; Hu, X.H.; Hai, L.T. Seismic performance of a novel non-diaphragm joint between concrete-filled cold-formed high-strength square steel tubular columns and composite beams. Eng. Struct. 2025, 339, 120700. [Google Scholar] [CrossRef]
- Zhao, H.; Tao, M.X.; Ding, R. Experimental study on seismic behaviour of composite frames with wide floor slabs considering the effect of floor loads. Eng. Struct. 2020, 220, 111024. [Google Scholar] [CrossRef]
- Chung, K.F.; Liu, C.H.; Ko, A. Steel beams with large web openings of various shapes and sizes: An empirical design method using a generalised moment-shear interaction curve. J. Constr. Steel Res. 2003, 59, 1177–1200. [Google Scholar] [CrossRef]
- Ding, F.X.; Wang, E.; Lv, F.; Wang, L.P.; Yu, Y.J.; Huang, Q.L.; Yu, Z.W. Composite action of steel-concrete composite beams under lateral shear force. Eng. Mech. 2021, 38, 86–98. [Google Scholar]
- Nie, J.G.; Tang, L. Vertical shear strength of composite beams with compact steel sections. Part I: Composite beams subjected to sagging moment. China Civ. Eng. J. 2008, 41, 7–14. [Google Scholar]
- Tang, L.; Nie, J.G. Vertical shear strength of composite beams with compact steel sections. Part II: Composite beams subjected to hogging moment. China Civ. Eng. J. 2008, 41, 15–20. [Google Scholar]
- JGJ/T 483-2020; Standard for Design of High Strength Steel Structure. China Architecture and Building Press: Beijing, China, 2020.
- JGJ 138-2016; Code for Design of Composite Structures. China Architecture and Building Press: Beijing, China, 2020.




| Specimen | Yield Strength fy (MPa) | Section Classification | Schematic Diagram of Section (AISC) | ||||
|---|---|---|---|---|---|---|---|
| Top Flange | Web | Bottom Flange | Top Flange | Web | Bottom Flange | ||
| CCB-1 | 345.65 | 395.13 | 345.65 | Compact | Compact | Compact | 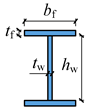 |
| HCCB-1 | 345.65 | 395.13 | 475.45 | Compact | Compact | Non-compact | |
| HCCB-2 | 345.65 | 395.13 | 668.33 | Compact | Compact | Non-compact | |
| HCCB-3 | 475.45 | 395.13 | 475.45 | Non-compact | Compact | Non-compact | |
| HCCB-4 | 668.33 | 395.13 | 668.33 | Non-compact | Compact | Non-compact | |
| Specimens | Experimental Results [30] | SEI/ASCE Method [23] | Proposed Method | Vp,c1/Vp,t | Vp,c2/Vp,t | |||
|---|---|---|---|---|---|---|---|---|
| Mp,t (kN·m) | Vp,t (kN) | Mp,c1 (kN·m) | Vp,c1 (kN) | Mp,c2 (kN·m) | Vp,c2 (kN) | |||
| CCB-1 | 203.67 | 201.65 | 152.52 | 151.01 | 178.67 | 176.90 | 0.749 | 0.877 |
| HCCB-1 | 227.06 | 224.81 | 159.09 | 157.51 | 218.57 | 216.40 | 0.696 | 0.963 |
| HCCB-2 | 259.93 | 257.36 | 169.90 | 168.22 | 273.25 | 270.54 | 0.648 | 1.051 |
| HCCB-3 | 243.40 | 240.99 | 180.63 | 178.84 | 222.93 | 220.72 | 0.737 | 0.916 |
| HCCB-4 | 262.61 | 260.01 | 230.11 | 227.84 | 280.81 | 278.03 | 0.865 | 1.069 |
| Average | 0.739 | 0.975 | ||||||
| Standard deviation | 0.072 | 0.075 | ||||||
| Specimens | Experimental Results [30] | SEI/ASCE Method [23] | Proposed Method | Vp,c1/Vp,t | Vn,c2/Vn,t | |||
|---|---|---|---|---|---|---|---|---|
| Mn,t (kN·m) | Vn,t (kN) | Mn,c1 (kN·m) | Vn,c1 (kN) | Mn,c2 (kN·m) | Vn,c2 (kN) | |||
| CCB-1 | 136.76 | 135.41 | 88.05 | 87.18 | 127.23 | 125.97 | 0.644 | 0.930 |
| HCCB-1 | 153.75 | 152.23 | 88.86 | 87.98 | 150.89 | 149.40 | 0.578 | 0.981 |
| HCCB-2 | 165.72 | 164.08 | 89.05 | 88.17 | 168.81 | 167.14 | 0.537 | 1.019 |
| HCCB-3 | 156.93 | 155.38 | 94.96 | 94.02 | 154.13 | 152.61 | 0.605 | 0.982 |
| HCCB-4 | 170.10 | 168.42 | 99.03 | 98.05 | 188.21 | 186.35 | 0.582 | 1.106 |
| Average | 0.589 | 1.004 | ||||||
| Standard deviation | 0.035 | 0.059 | ||||||
| Group | Weakening Parameters | FEA Results | Proposed Method | Vp,c2/Vp,a | Vn,c2/Vn,a | |||
|---|---|---|---|---|---|---|---|---|
| D (mm) | L (mm) | Vp,a (kN) | Vn,a (kN) | Vp,c2 (kN) | Vn,c2 (kN) | |||
| CCB-1 | 140 | 240 | 213.91 | 151.56 | 199.17 | 146.73 | 0.931 | 0.968 |
| 168 | 240 | 209.43 | 145.39 | 188.15 | 136.95 | 0.898 | 0.942 | |
| 196 | 240 | 198.29 | 134.00 | 176.90 | 125.97 | 0.892 | 0.940 | |
| 224 | 240 | 190.09 | 122.01 | 165.40 | 112.59 | 0.870 | 0.923 | |
| 196 | 154 | 183.99 | 127.46 | 165.39 | 121.23 | 0.899 | 0.951 | |
| 196 | 196 | 190.86 | 130.56 | 170.01 | 122.00 | 0.891 | 0.934 | |
| 196 | 280 | 205.59 | 139.26 | 183.62 | 129.73 | 0.893 | 0.932 | |
| HCCB-1 | 140 | 240 | 238.52 | 173.01 | 238.39 | 174.10 | 0.999 | 1.006 |
| 168 | 240 | 231.01 | 165.41 | 227.54 | 163.02 | 0.985 | 0.986 | |
| 196 | 240 | 218.68 | 150.12 | 216.40 | 149.40 | 0.990 | 0.995 | |
| 224 | 240 | 206.74 | 130.86 | 204.95 | 131.03 | 0.991 | 1.001 | |
| 196 | 154 | 205.34 | 141.76 | 203.29 | 147.08 | 0.990 | 1.038 | |
| 196 | 196 | 209.99 | 146.03 | 208.31 | 145.47 | 0.992 | 0.996 | |
| 196 | 280 | 229.57 | 155.90 | 224.25 | 153.03 | 0.977 | 0.982 | |
| HCCB-2 | 140 | 240 | 268.56 | 196.67 | 292.69 | 195.51 | 1.090 | 0.994 |
| 168 | 240 | 262.99 | 182.61 | 281.83 | 182.55 | 1.072 | 1.000 | |
| 196 | 240 | 247.91 | 161.19 | 270.54 | 167.14 | 1.091 | 1.037 | |
| 224 | 240 | 239.26 | 142.52 | 258.78 | 148.28 | 1.082 | 1.040 | |
| 196 | 154 | 236.90 | 149.19 | 255.97 | 166.73 | 1.080 | 1.118 | |
| 196 | 196 | 240.00 | 157.66 | 261.07 | 163.30 | 1.088 | 1.036 | |
| 196 | 280 | 260.70 | 168.35 | 279.64 | 170.65 | 1.073 | 1.014 | |
| HCCB-3 | 140 | 240 | 256.53 | 181.74 | 244.65 | 177.72 | 0.954 | 0.978 |
| 168 | 240 | 250.33 | 171.08 | 231.32 | 166.08 | 0.924 | 0.971 | |
| 196 | 240 | 235.02 | 150.71 | 220.72 | 152.61 | 0.939 | 1.013 | |
| 224 | 240 | 223.67 | 135.75 | 209.82 | 136.03 | 0.938 | 1.002 | |
| 196 | 154 | 220.72 | 143.58 | 207.38 | 149.66 | 0.940 | 1.042 | |
| 196 | 196 | 230.21 | 147.71 | 212.37 | 148.50 | 0.923 | 1.005 | |
| 196 | 280 | 246.23 | 158.89 | 228.83 | 156.41 | 0.929 | 0.984 | |
| HCCB-4 | 140 | 240 | 281.23 | 201.47 | 297.96 | 218.49 | 1.059 | 1.084 |
| 168 | 240 | 276.26 | 189.22 | 288.08 | 203.65 | 1.043 | 1.076 | |
| 196 | 240 | 255.87 | 166.79 | 278.03 | 186.35 | 1.087 | 1.117 | |
| 224 | 240 | 242.11 | 144.75 | 267.75 | 165.58 | 1.106 | 1.144 | |
| 196 | 154 | 242.61 | 155.17 | 262.55 | 186.83 | 1.082 | 1.204 | |
| 196 | 196 | 250.67 | 161.35 | 267.83 | 182.39 | 1.068 | 1.130 | |
| 196 | 280 | 265.26 | 172.16 | 287.89 | 189.94 | 1.085 | 1.103 | |
| Average | 0.996 | 1.020 | ||||||
| Standard deviation | 0.075 | 0.066 | ||||||
| Components | fy (MPa) | Es (105 MPa) | λ | λl | Section Classification |
|---|---|---|---|---|---|
| Beam Web | 355.00 | 2.06 | 44.00 | 90.57 | Compact |
| Beam flange | 355.00 | 2.06 | 8.75 | 9.15 | Compact |
| Beam flange | 460.00 | 2.06 | 8.75 | 8.04 | Non-compact |
| Beam flange | 500.00 | 2.06 | 8.75 | 7.71 | Non-compact |
| Beam flange | 550.00 | 2.06 | 8.75 | 7.35 | Non-compact |
| Beam flange | 620.00 | 2.06 | 8.75 | 6.92 | Non-compact |
| Beam flange | 690.00 | 2.06 | 8.75 | 6.57 | Non-compact |
| Group | fy (MPa) | FEA Results | Theoretical Results | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Top Flange | Web | Bottom Flange | Vp,a (kN) | Vn,a (kN) | Vp,c (kN) | Vn,c (kN) | |||
| CCB-355 | 355 | 355 | 355 | 196.16 | 133.72 | 177.41 | 125.06 | 0.904 | 0.935 |
| ACCB-460 | 355 | 355 | 460 | 221.72 | 147.00 | 209.40 | 143.35 | 0.944 | 0.975 |
| ACCB-500 | 355 | 355 | 500 | 229.72 | 151.39 | 221.14 | 148.68 | 0.963 | 0.982 |
| ACCB-550 | 355 | 355 | 550 | 239.19 | 155.28 | 235.48 | 154.50 | 0.984 | 0.995 |
| ACCB-620 | 355 | 355 | 620 | 247.42 | 158.39 | 254.96 | 162.17 | 1.030 | 1.024 |
| ACCB-690 | 355 | 355 | 690 | 253.05 | 160.10 | 273.77 | 164.77 | 1.082 | 1.029 |
| SCCB-460 | 460 | 355 | 460 | 236.18 | 152.54 | 213.07 | 146.06 | 0.902 | 0.958 |
| SCCB-500 | 500 | 355 | 500 | 244.60 | 157.15 | 225.86 | 153.44 | 0.923 | 0.976 |
| SCCB-550 | 550 | 355 | 550 | 251.97 | 161.28 | 241.28 | 162.26 | 0.958 | 1.006 |
| SCCB-620 | 620 | 355 | 620 | 256.98 | 165.02 | 261.84 | 173.95 | 1.019 | 1.054 |
| SCCB-690 | 690 | 355 | 690 | 260.23 | 166.04 | 281.63 | 185.01 | 1.082 | 1.114 |
| Average | 0.981 | 1.004 | |||||||
| Standard deviation | 0.062 | 0.047 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Huo, S.; Zhao, H.; Li, T. Failure Mechanism and Load Carrying Capacity of Hybrid High-Strength Steel Composite Cellular Beams Under Low Cyclic Loading. Buildings 2025, 15, 3954. https://doi.org/10.3390/buildings15213954
Guo J, Huo S, Zhao H, Li T. Failure Mechanism and Load Carrying Capacity of Hybrid High-Strength Steel Composite Cellular Beams Under Low Cyclic Loading. Buildings. 2025; 15(21):3954. https://doi.org/10.3390/buildings15213954
Chicago/Turabian StyleGuo, Jiangran, Siyu Huo, He Zhao, and Tengfei Li. 2025. "Failure Mechanism and Load Carrying Capacity of Hybrid High-Strength Steel Composite Cellular Beams Under Low Cyclic Loading" Buildings 15, no. 21: 3954. https://doi.org/10.3390/buildings15213954
APA StyleGuo, J., Huo, S., Zhao, H., & Li, T. (2025). Failure Mechanism and Load Carrying Capacity of Hybrid High-Strength Steel Composite Cellular Beams Under Low Cyclic Loading. Buildings, 15(21), 3954. https://doi.org/10.3390/buildings15213954







