Computational and Experimental Insights into Blast Response and Failure Mechanisms of Square, Rectangular and Circular Reinforced Concrete Columns: A State-of-the-Art Review
Abstract
1. Introduction
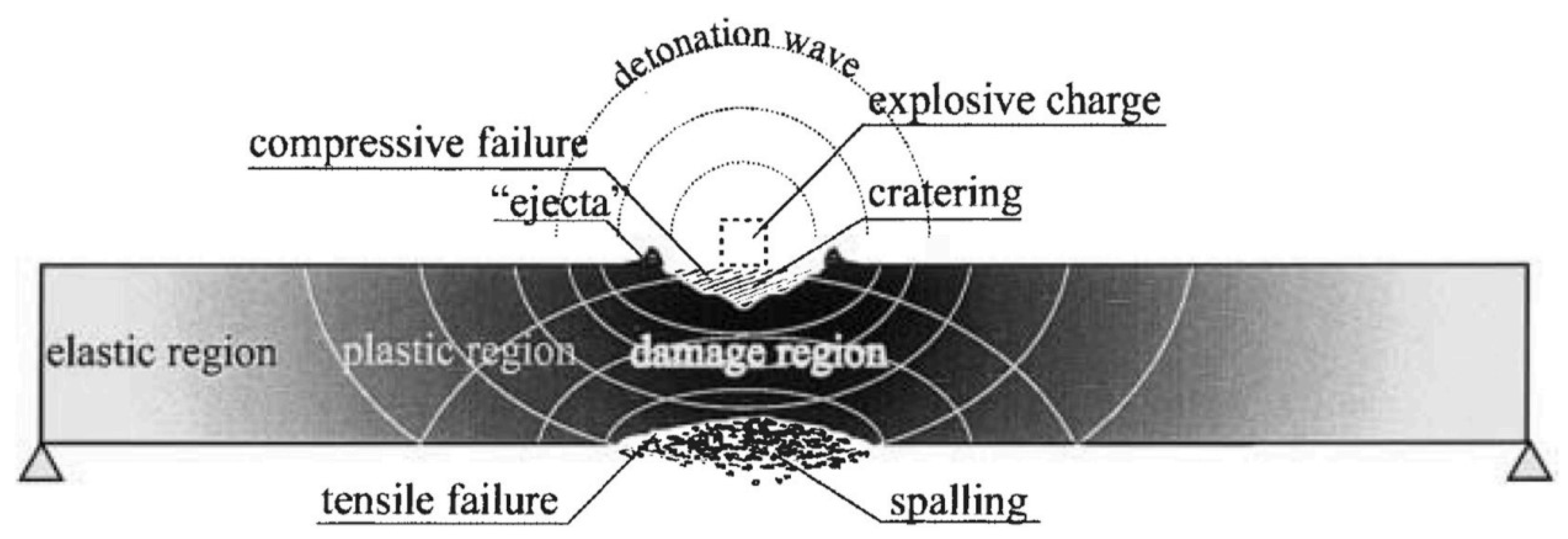
- Spalling: Material is ejected from the rear face of concrete due to high tensile stresses caused by stress wave reflections.
- Scabbing: Fragments of concrete break away from the back face when compressive stress waves surpass the residual tensile strength.
- Shear plug formation: A localized shear failure occurring in RC slabs or walls, caused by concentrated blast pressures over small areas.
- Punching shear failure: Localized penetration or perforation, often in thin plates or slabs, resulting from high-intensity, short-duration pressure pulses [23].
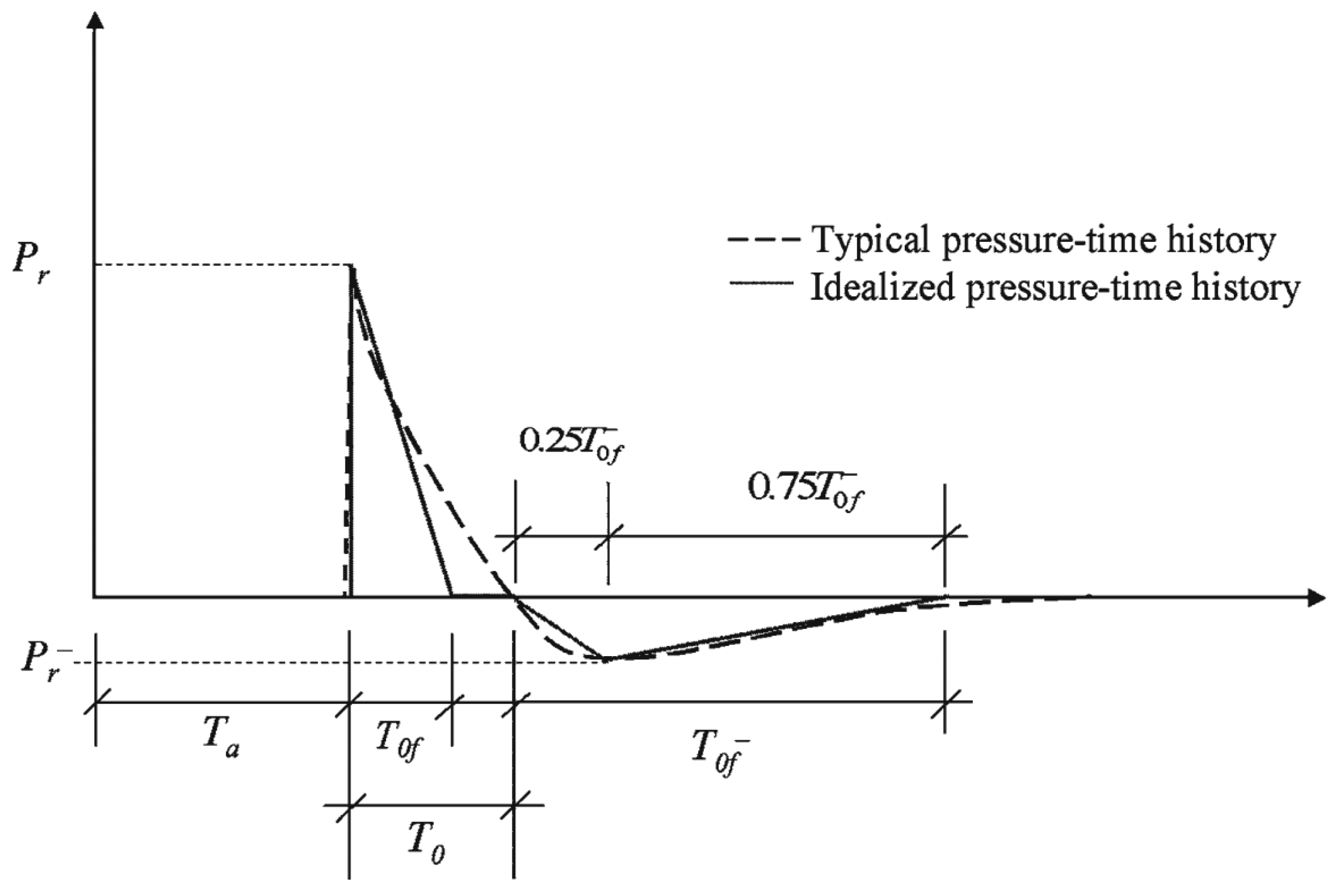
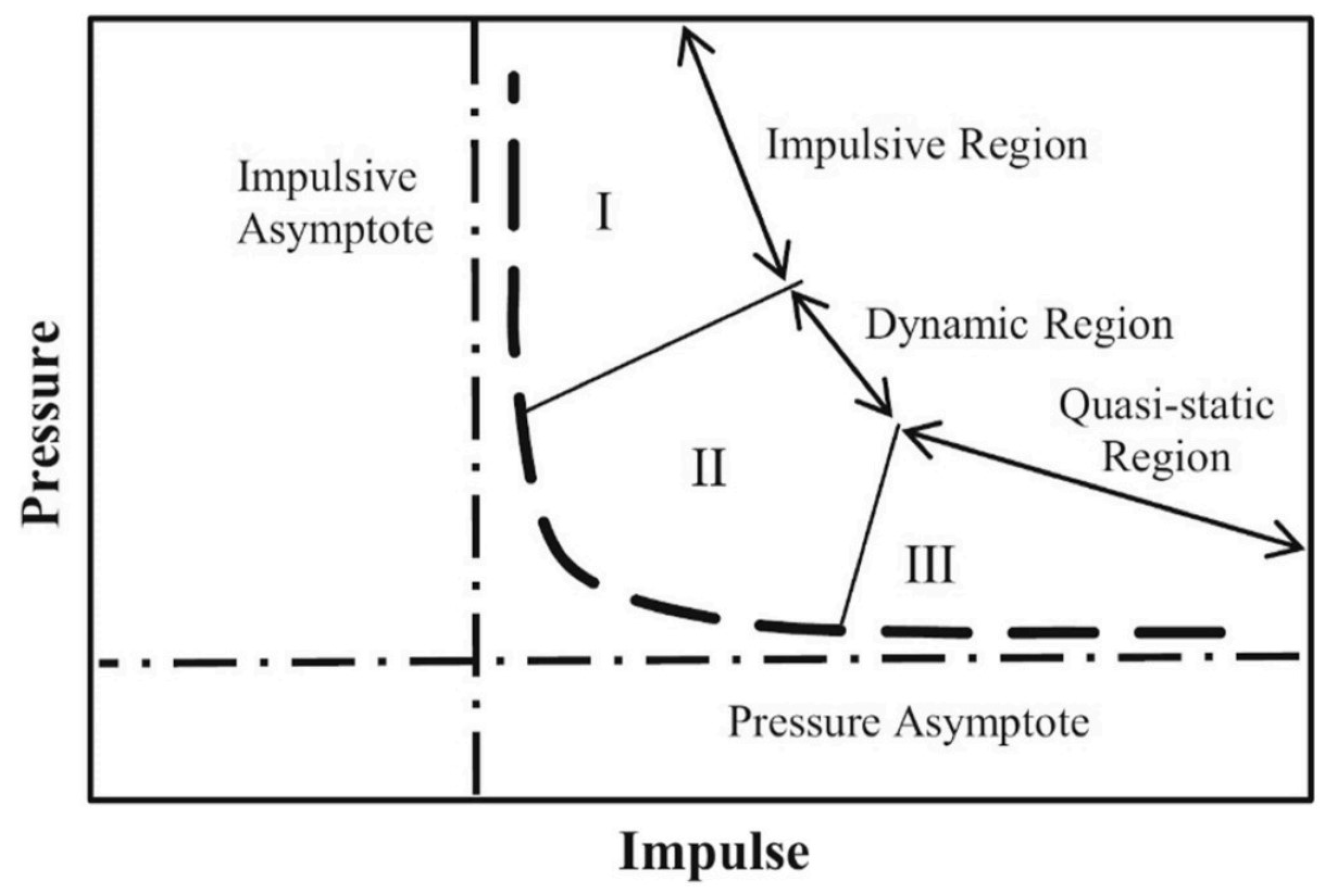
- Impulsive Region (td ≪ Tn): The blast is very short compared to the structural vibration period. The response is mostly controlled by inertia. Deformation depends more on the impulse than on the peak pressure [28]. Single-degree-of-freedom (SDOF) models are often used here, treating the blast as a rapid momentum transfer.
- Dynamic Region (td ≈ Tn): When the blast duration is similar to the natural period, both pressure and impulse affect the response. This is the most complex region, with possible resonance or dynamic amplification [1,28]. Time-history analysis using SDOF or finite element (FE) models is usually needed to capture structural behavior.
- Quasi-static Region (td ≫ Tn): For long-duration blasts, the load changes slowly compared to the structure’s response. In this case, deformation is mainly driven by peak pressure [1]. The structure develops significant plastic deformations before unloading; so, the response can be treated as quasi-static.
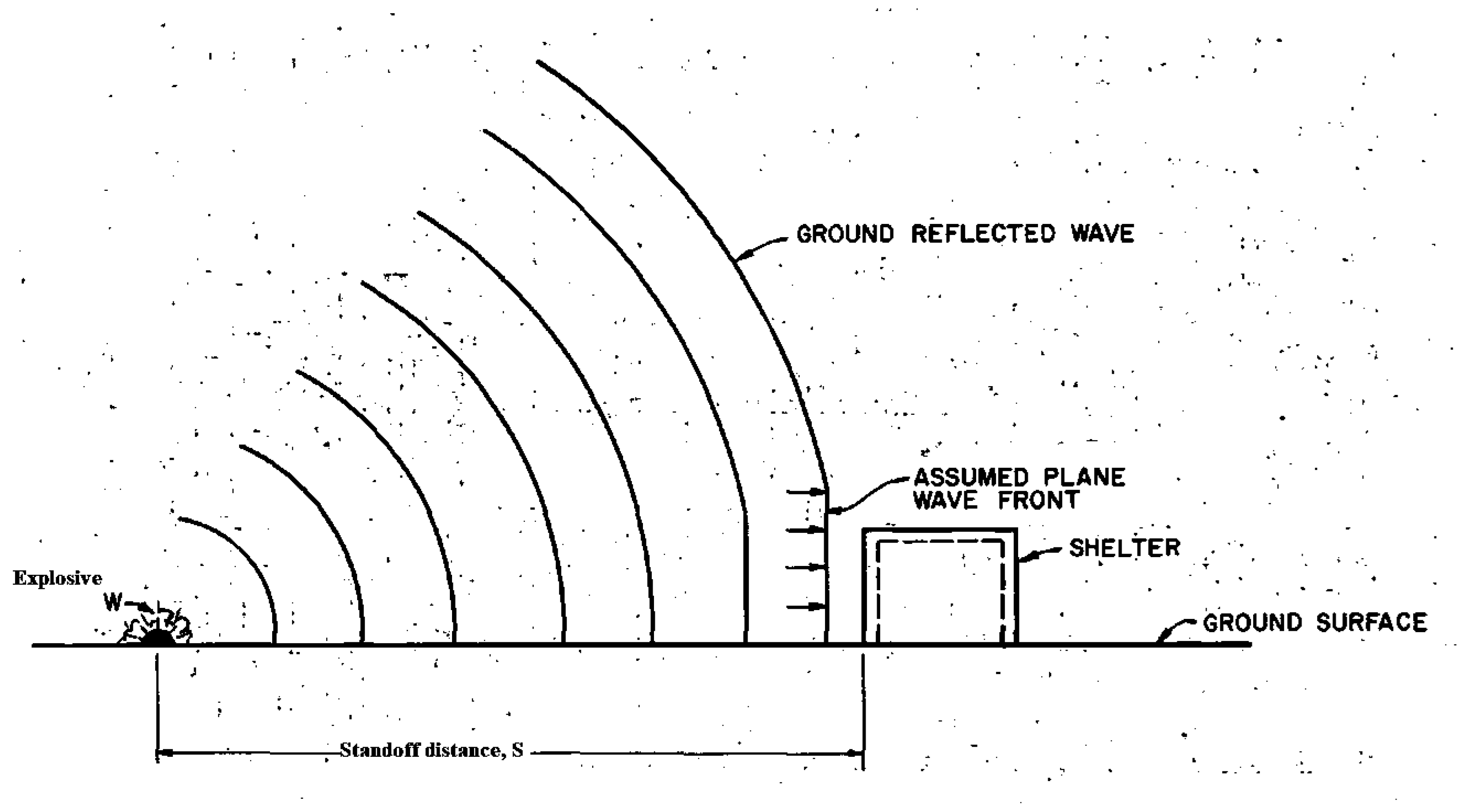
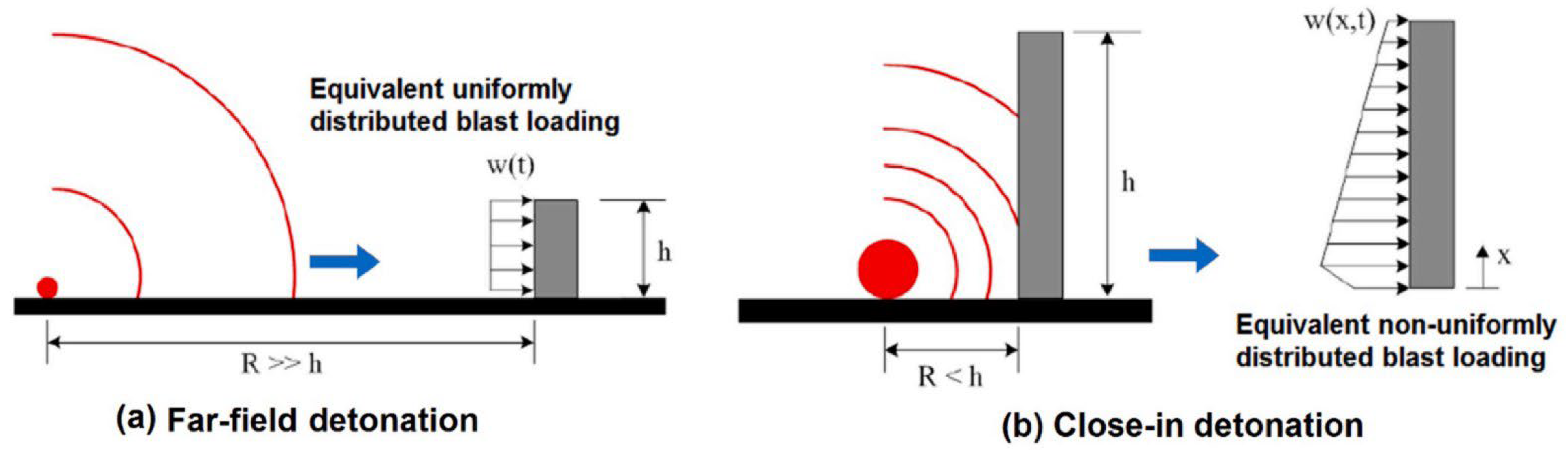
- The blast originates from large explosive charges positioned at a standoff distance sufficient to ensure uniform pressure distribution along the column height, as assumed in SDOF models, though real pressure gradients may occur.
- The column’s lateral response is primarily flexure-dominated, with bending governing failure mechanisms.
- Local core fracturing of concrete is minimal and does not significantly influence the overall response.
1.1. Methods for Simulating Blast Loads
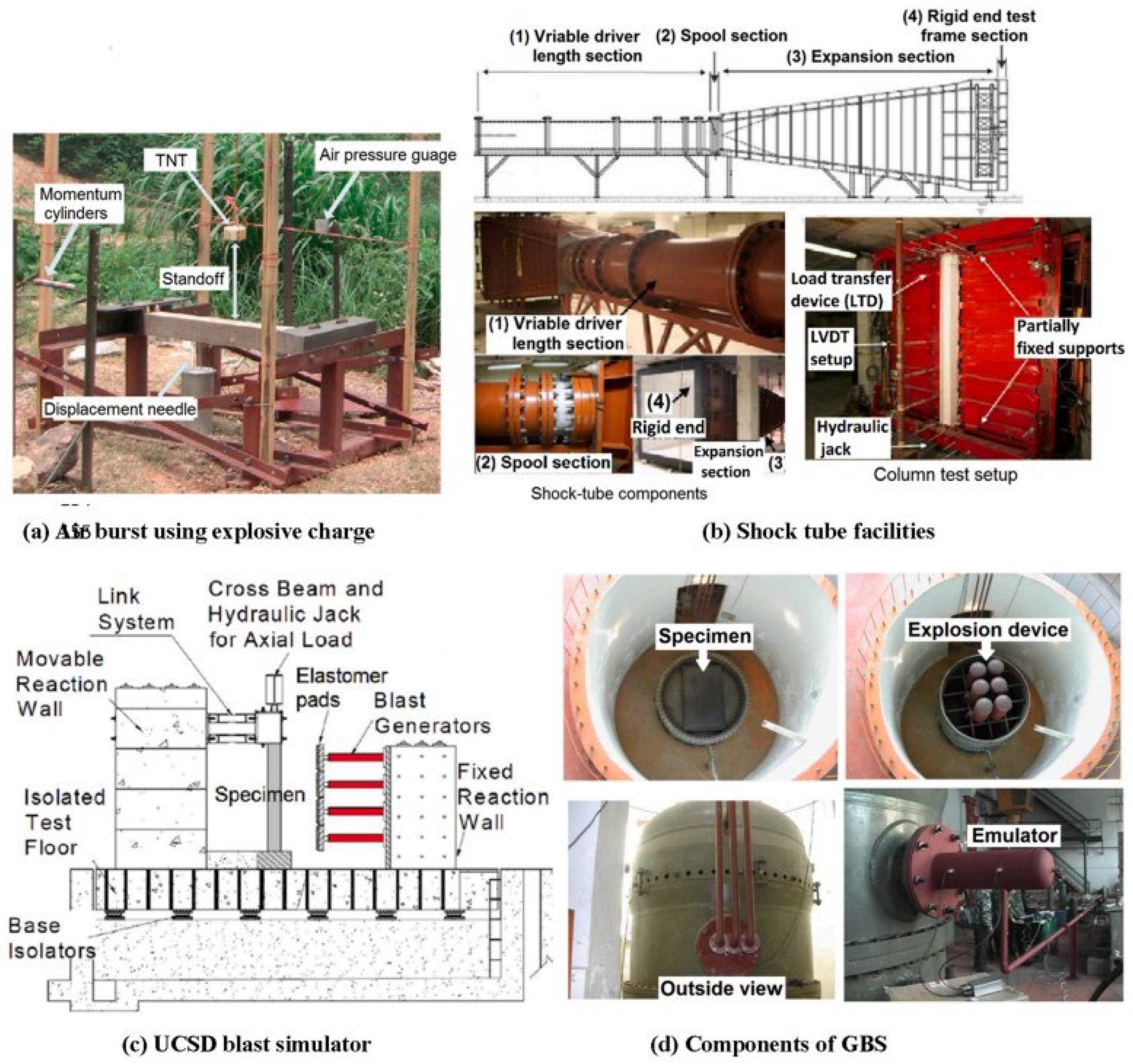
- Air burst using explosive charges (Figure 7a [1]): In this approach, structures are subjected to controlled explosions, often using TNT or other chemical compounds. The explosives vary in geometry, size, and weight, allowing researchers to study different blast intensities and structural responses [35]. Pressure transducers and displacement gauges are commonly used to record pressure–time histories and specimen movements (Figure 7a).
- One major advantage of this method is that it can closely replicate real blast effects, capturing even complex pressure patterns and fragments. However, it also comes with several drawbacks. The setup is costly and risky to operate, testing sites are limited, and results often vary because of unpredictable explosive behavior.
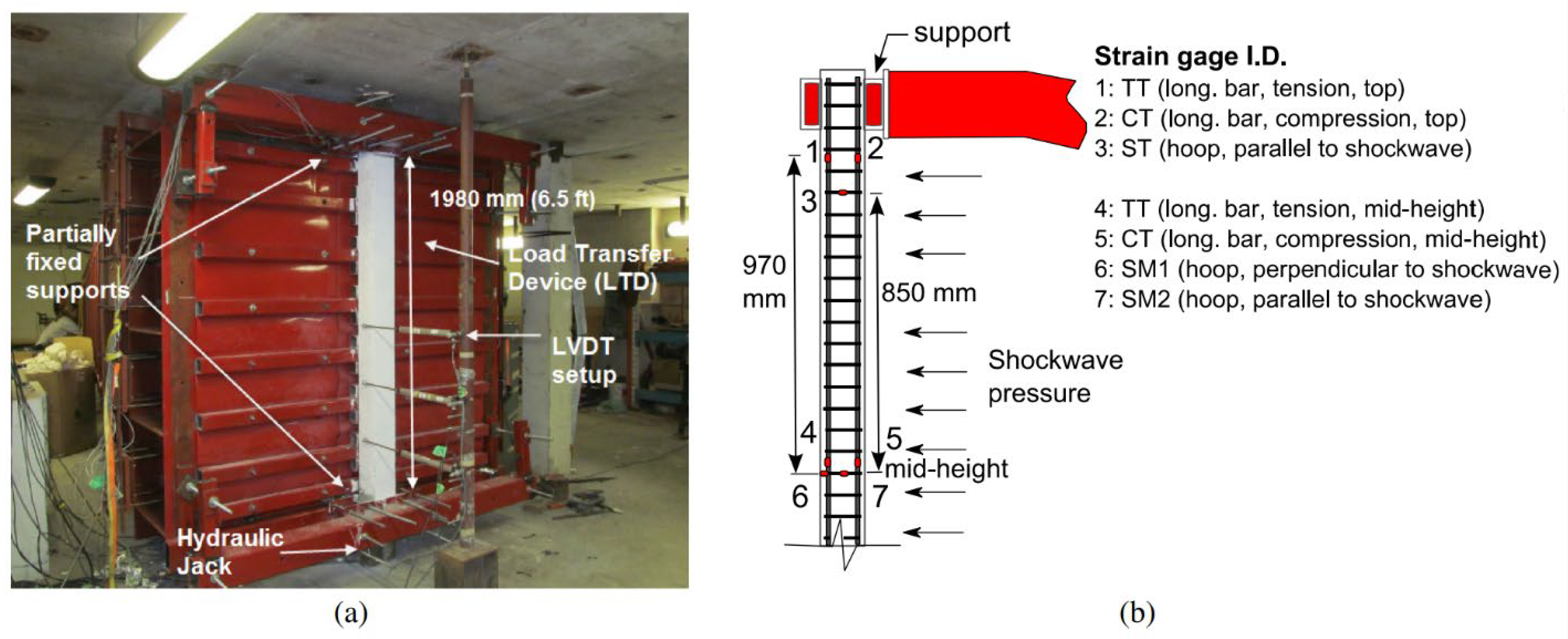
- Shock tube testing (Figure 7b [1]): Shock tubes generate high-pressure waves inside a compression chamber. These waves are then released through a variable-length driver toward the target. A differential pressure diaphragm in the spool section controls the firing. The generated shockwaves travel along an expansion section before striking the target, enabling precise study of blast effects on structures [36]. This approach helps in creating consistent and repeatable loading conditions. Instrumentation such as load cells, LVDTs, and strain gauges are used to measure responses (Figure 7b).
- The main advantages are the ability to repeat blast conditions with precision and to record accurate measurements using LVDTs, load transfer devices, and hydraulic jacks. However, shock tubes often fail to reproduce certain secondary effects such as fragmentation or multiple reflected pressure waves that occur in real explosions.
- UCSD blast simulator (Figure 7c [1]): Developed at the University of California, San Diego, this facility uses hydraulically driven actuators to mimic distributed blast loads. Elastomer pads transfer these simulated impact loads to structural specimens, providing a controlled and repeatable experimental environment [37]. The system includes both movable and fixed reaction walls, along with cross beams and connecting link systems (see Figure 7c). This setup helps in effectively confining and distributing the simulated blast loads to the structural elements. Stability is ensured by using base isolators.
- Major advantages are high repeatability and precise control over how the load is shared. It is also much safer than using real explosives. The drawback is that simulated loads do not always reproduce the very high strain rates, the complex pressure–time patterns, or the shock interactions that occur in real explosions.
- Gas Blast Simulator (GBS) (Figure 7d [1]): Created at the Anti-Explosion and Protective Engineering Ministry Key Laboratory, Harbin Institute of Technology, China, this setup exposes specimens to a series of gas-generated blast waves inside a multifunctional system, allowing for detailed study of structural response under controlled conditions [38,39,40,41,42]. The GBS is made up of an explosion device, an emulator, and sections to place specimens (Figure 7d). It allows different intensities of gas-driven shocks to be recreated with ease. Its modular design makes it possible to observe the blast wave both from inside and from the outside.
- The main advantages of this method are better safety, consistent results, and the ease of controlling the blast intensity as needed. However, it is difficult to recreate very close or extreme explosions, and it does not effectively capture debris impact or fragmentation of structures.
1.2. Typical Modes of Failure of RC Structural Components Under Explosion Loadings
2. Novelty of This State-of-the-Art Review
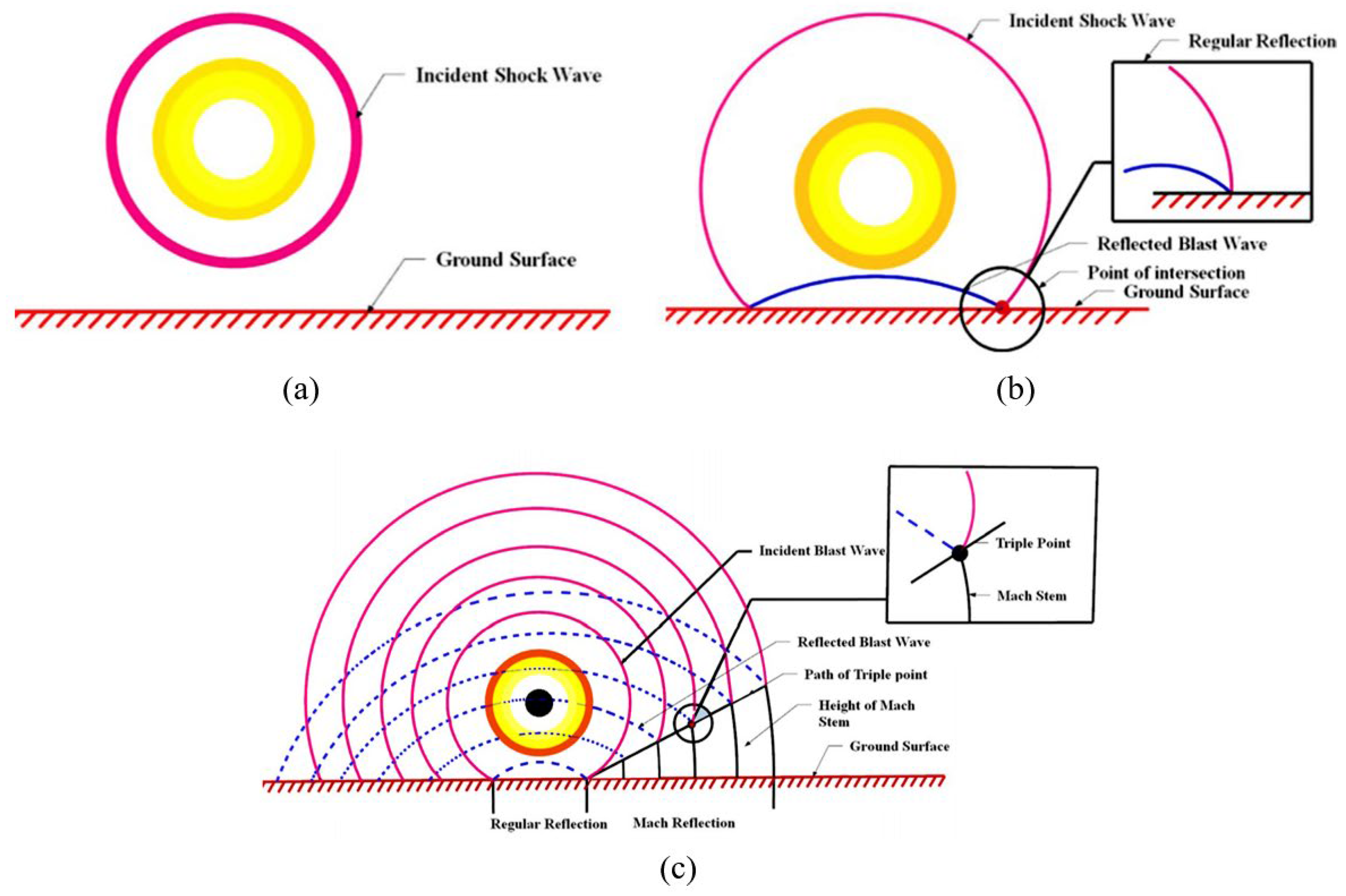
3. RC Columns Under Blast Loading
3.1. Studies on Square Columns
- Effect of Axial Load and Boundary Conditions
- Influence of Concrete Type and Material Properties
- Reinforcement Detailing & Seismic Provisions
- Strengthening/Retrofitting Techniques
- Numerical & Analytical Modelling Approaches
- Experimental vs. Simulated Blast Testing
3.2. Studies on Rectangular Columns
- Damage Assessment & Parametric Studies
- 0 ≤ D < 0.20—Low damage
- 0.20 ≤ D < 0.50—Medium damage
- 0.50 ≤ D < 0.80—High damage
- D ≥ 0.80—Collapse
- i.
- For low damage (D = 0.20) [16]:
- ii.
- For medium damage (D = 0.50) [16]:
- iii.
- For high damage (D = 0.80) [16]:
- Strengthening with FRP Wraps
- Influence of Cross-Section Geometry
3.3. Studies on Circular Columns
- Material Enhancement & Coatings
- Composite/Double-Skin Tubular Columns (DSTC, CFDSST, RPC-FST)
- Experimental Validation of RC Circular Columns
- Multi-Hazard & Retrofit of Bridge Columns
4. Progression of Studies
5. Conclusions
5.1. Observations for Square Columns
- Double-end-initiated cylindrical charges produce peak overpressures and impulses approximately 2–4 times higher than centre-point-initiated charges.
- Reflected blast pressure from cylindrical charges was found to be twice that of spherical charges
- Axial compressive load significantly affects blast resistance. Even less than half of the balanced axial load can considerably reduce the residual capacity under blast as compared to pure flexural capacity.
- UHPFRC columns demonstrate reduced maximum and residual displacements compared to normal- and high-strength RC columns under similar blast pressures.
- Increasing steel fibre content in UHPFRC from 2% to 4% improves column displacement resistance, but content beyond 4% can cause longitudinal bar rupture under close-in blasts.
- Micro steel fibre-reinforced UHPC preserves over 70% axial load capacity after a 35 kg TNT blast, whereas high-strength RC columns retain only 40% capacity after an 8 kg TNT blast at 1.5 m standoff.
- Larger cross-sections, higher transverse reinforcement ratios, reduced stirrup spacing, and thinner concrete covers enhance blast performance.
- The damage criterion proposed by Cui et al. [3] is suitable for rapid damage assessment of RC columns under near-field blasts.
- Increased shear/transverse reinforcement improves residual resistance post-blast.
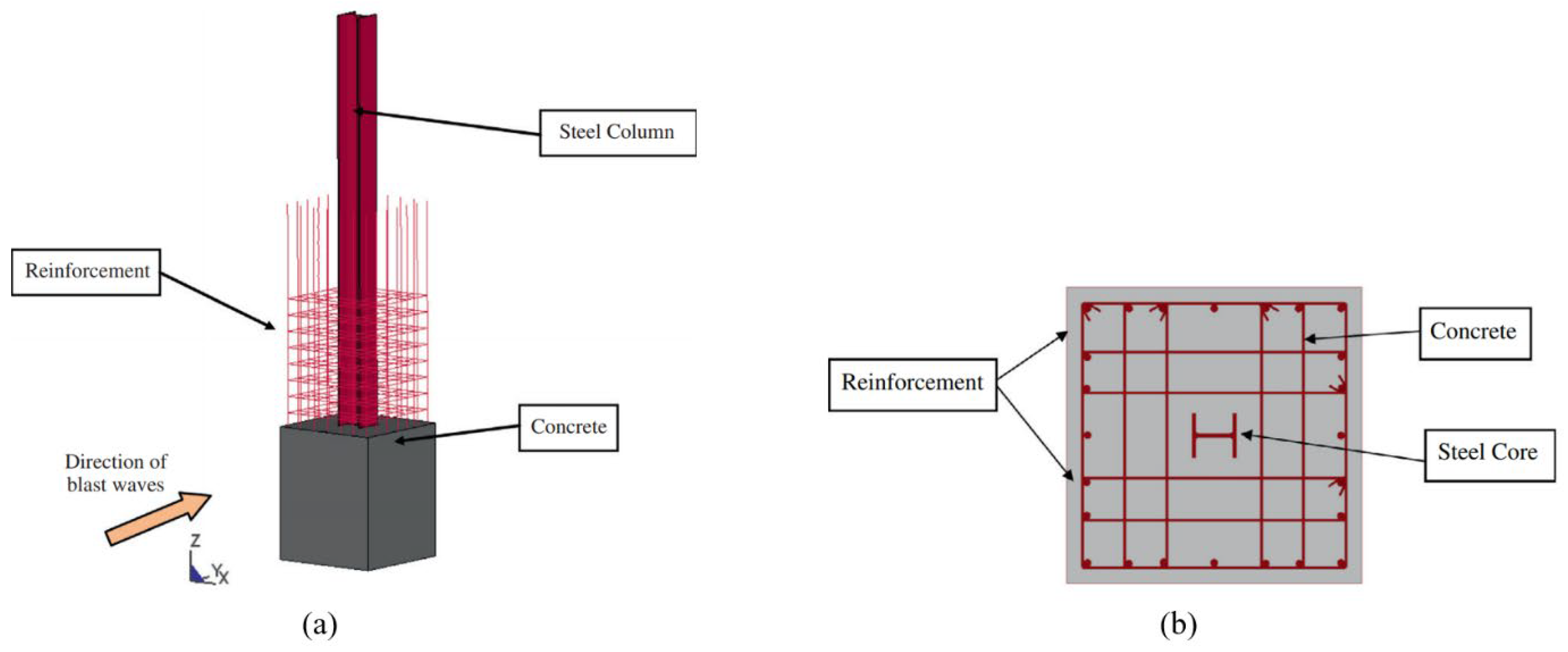
- Concrete-steel composite columns (RC with steel core) exhibit improved blast response and maintain higher post-blast load capacity than conventional RC columns.
- SFRC significantly enhances column performance, reducing both maximum and residual displacements.
- Thicker inner and outer steel tubes in CFDSST columns improve stiffness and reduce displacement, with the outer tube contributing more under close-in blasts.
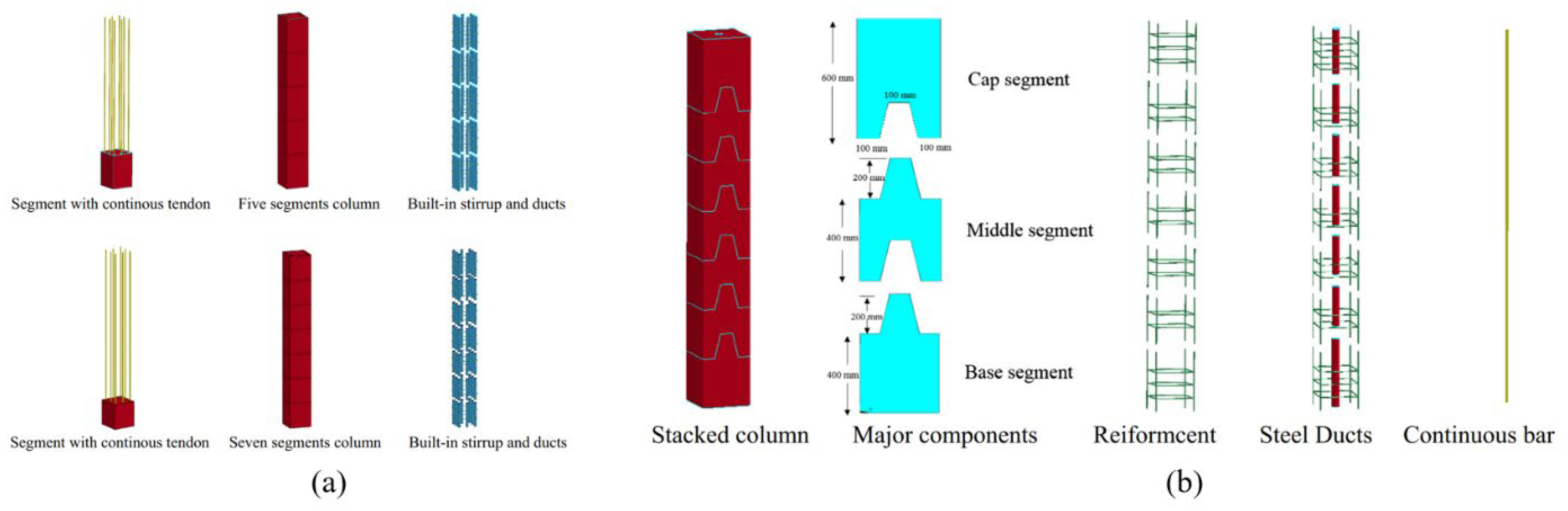
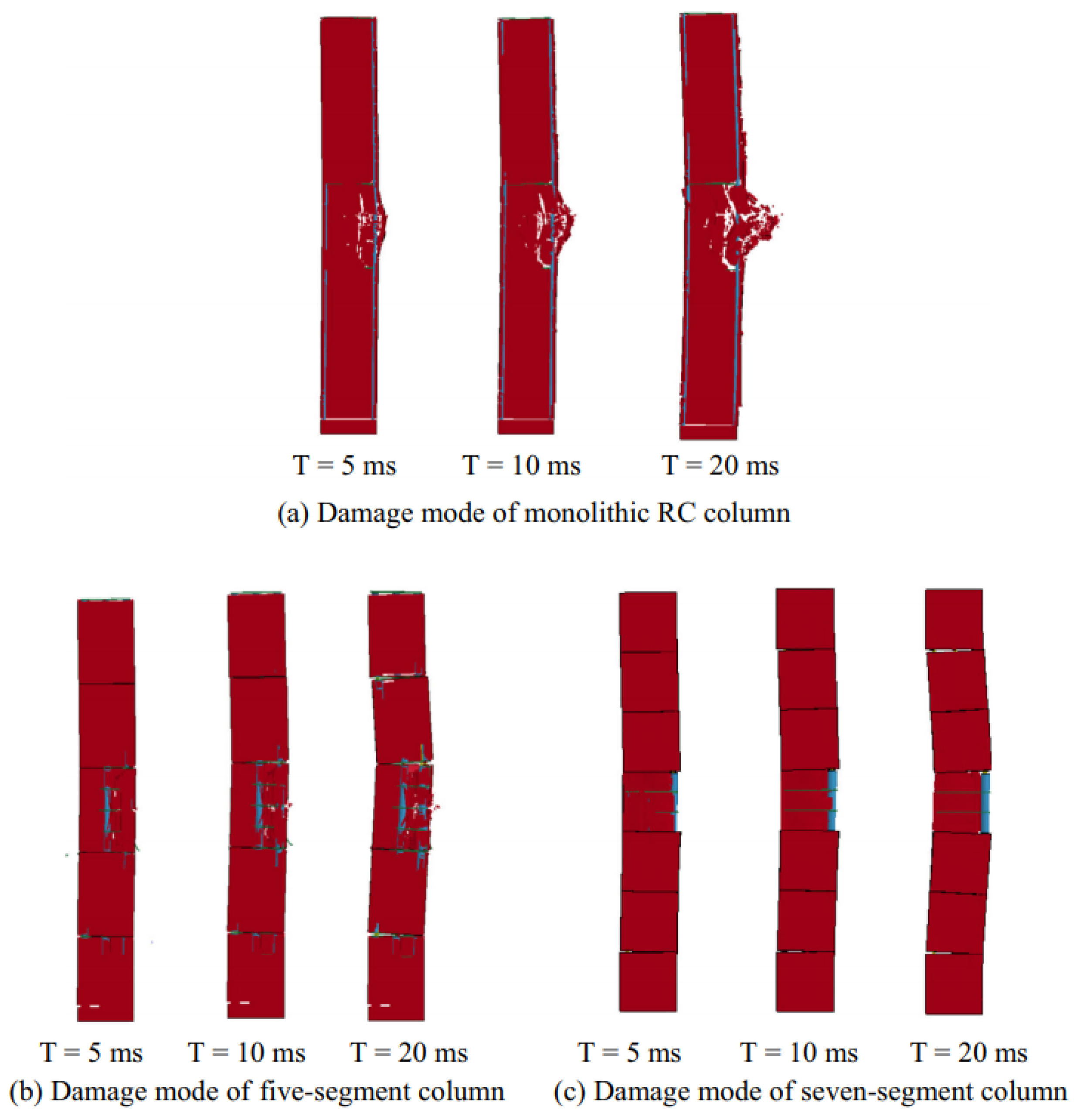
- Segmental columns show reduced spalling and displacement. Energy absorption between segments mitigates damage, and additional shear keys further improve resistance.
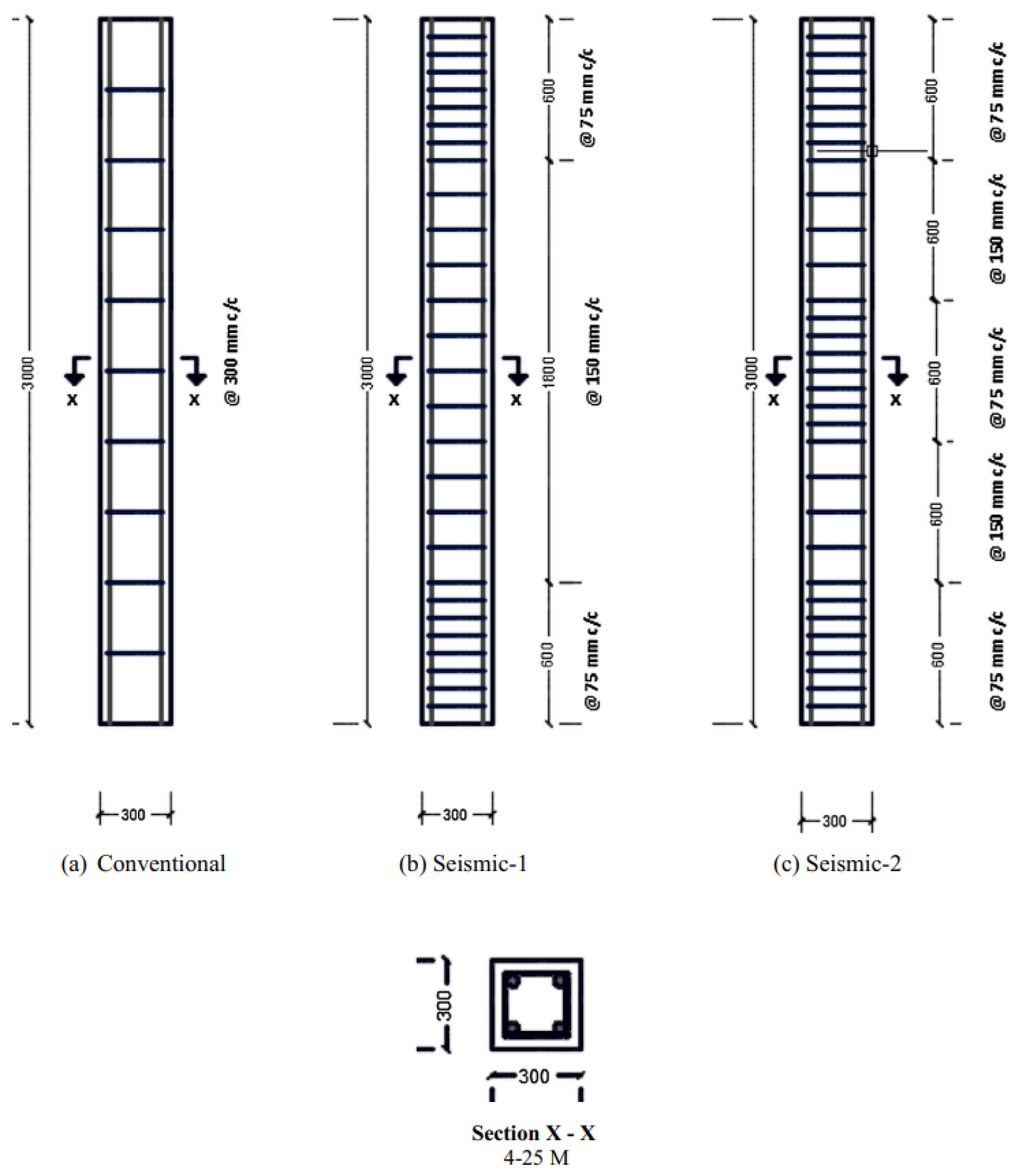
- Confining/seismic reinforcement at the top, bottom, and mid-height regions reduces transverse displacement and cracking under near-field blasts.
- ALR around 0.30 benefits blast resistance at scaled distances Z > 0.40 m/kg1/3, but higher ALR increases mid-height shear damage at Z < 0.40 m/kg1/3 [78].
- Doubling concrete strength increases blast resistance by 1.5 times; while increasing reinforcement ratio 3.5 times raises capacity by 1.2 times under 11.2 MPa peak overpressure [90].
- Steel-FRP wrapping of lower column halves enhances residual load by 10–15%, while two layers of transverse CFRP strips improve cracking resistance and residual capacity under close-in explosions.
- Advanced FE models and ML techniques offer a much better prediction of mid-span displacement, damage indices, and residual capacity. These approaches clearly show where traditional SDOF or purely empirical methods fall short.
- Graph Neural Networks can predict blast damage with very high accuracy in a fraction of the time, reducing computation by more than 10,000 times without losing precision.
- Dimensional analysis along with FE simulations enables a straightforward prediction of mid-span disturbances during blast events. It effectively reflects the influence of explosive weight, standoff distance, and vulnerability limits. Significant damage, such as stirrup rupture and concrete spalling, is observed only when the scaled distance falls below a critical value (Z < 0.07 m/kg1/3).
- Damage indicators that account for both displacement and energy absorption show stronger correlation with residual strength than using displacement alone.
- Uneven chloride-driven corrosion greatly increases blast fragility in the long run, with risks becoming more severe after decades of exposure.
- Assessments based only on ductility or residual strength often give different results; hence, a combined approach is essential for dependable design.
- Off-center blast loading changes the failure behavior in a major way, especially under axial compression, stressing the importance of considering eccentric detonations.
- Microscopic study showed that basalt and polypropylene fibers in RFRCAC columns acted as crack bridges and developed a good bond with the cement matrix. This improved the packing of coral aggregates and gave the columns much higher blast resistance than RCAC and conventional RC columns.
5.2. Observations for Rectangular Columns
- Glass-FRP composite wrapping on all faces enhances blast performance.
- Rectangular RC columns experience less damage under contact explosions compared to square columns, making them preferable for high-rise structures requiring higher blast resistance.
- Aramid FRP (AFRP) jacketing showed a clear reduction in displacement and damage levels. Surrogate ML like ANFIS and DRNN, trained on FE data, provided dependable predictions and helped in balancing cost with performance during retrofit design.
5.3. Observations for Circular Columns
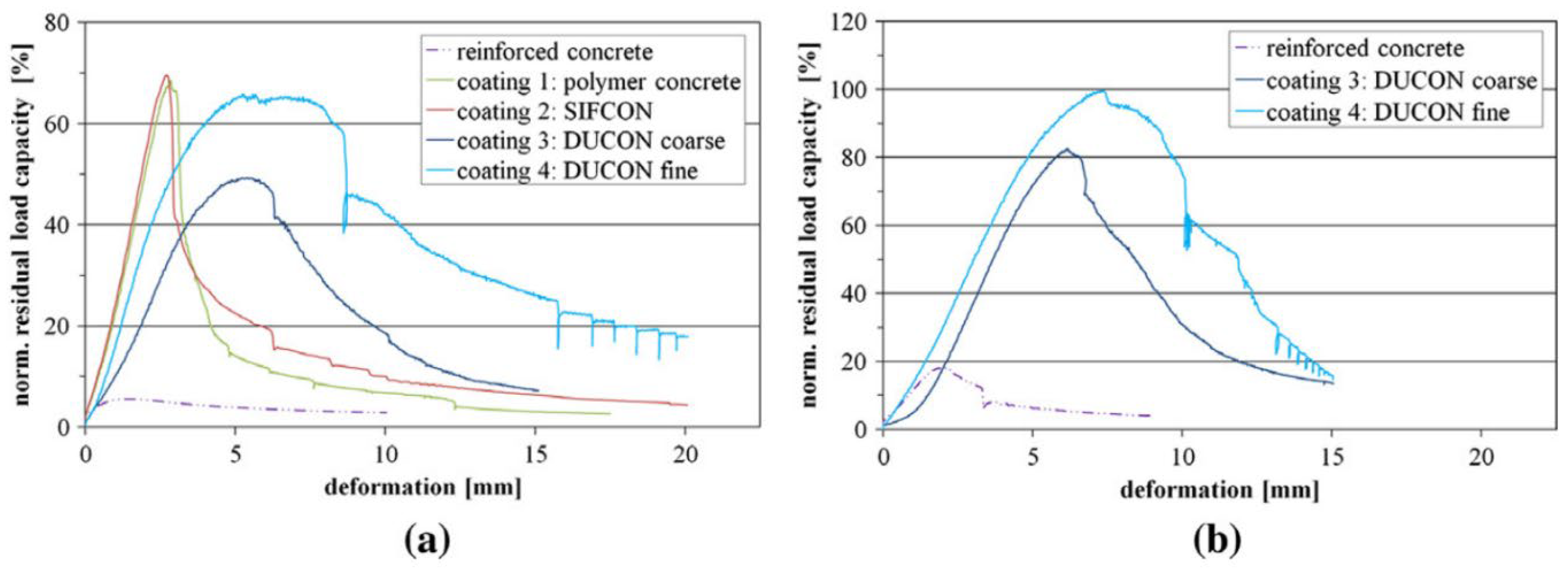
- Thin layers of energy-absorbing materials such as SIFCON, DUCON, and UHPC significantly improve residual load capacity, with SIFCON-coated columns showing the best performance under contact blasts.
- CFDSST columns outperform CFST and hybrid FRP-concrete steel DSTC columns in limiting mid-height transverse displacement under close-in blasts [112]. Steel tubes prevent spall, while plastic deformation of the concrete core contributes to energy absorption. UHPC further enhances performance. Circular CFDSST columns outperform square counterparts.
- Increased thickness of inner and outer steel tubes improves stiffness; the outer tube contributes more to blast resistance.
- Circular RC columns show lower peak deflections than square, hexagonal, and octagonal columns under similar blast conditions [23].
- Numerical models using ANSYS AUTODYN, LS-DYNA, and ABAQUS/CAE with damage models such as Mazars, KCC, and CDP effectively validate the experimental results and simulate blast responses.
- Probabilistic and ML models provide a quick and dependable way to assess displacement and the chances of failure. These models work well alongside experimental studies on axial loads and blast impacts.
- Small-scale shock tube tests using stereoscopic DIC recorded crack initiation and crater formation within milliseconds. The results clearly showed that the reinforcement ratio played a crucial role in determining blast resistance.
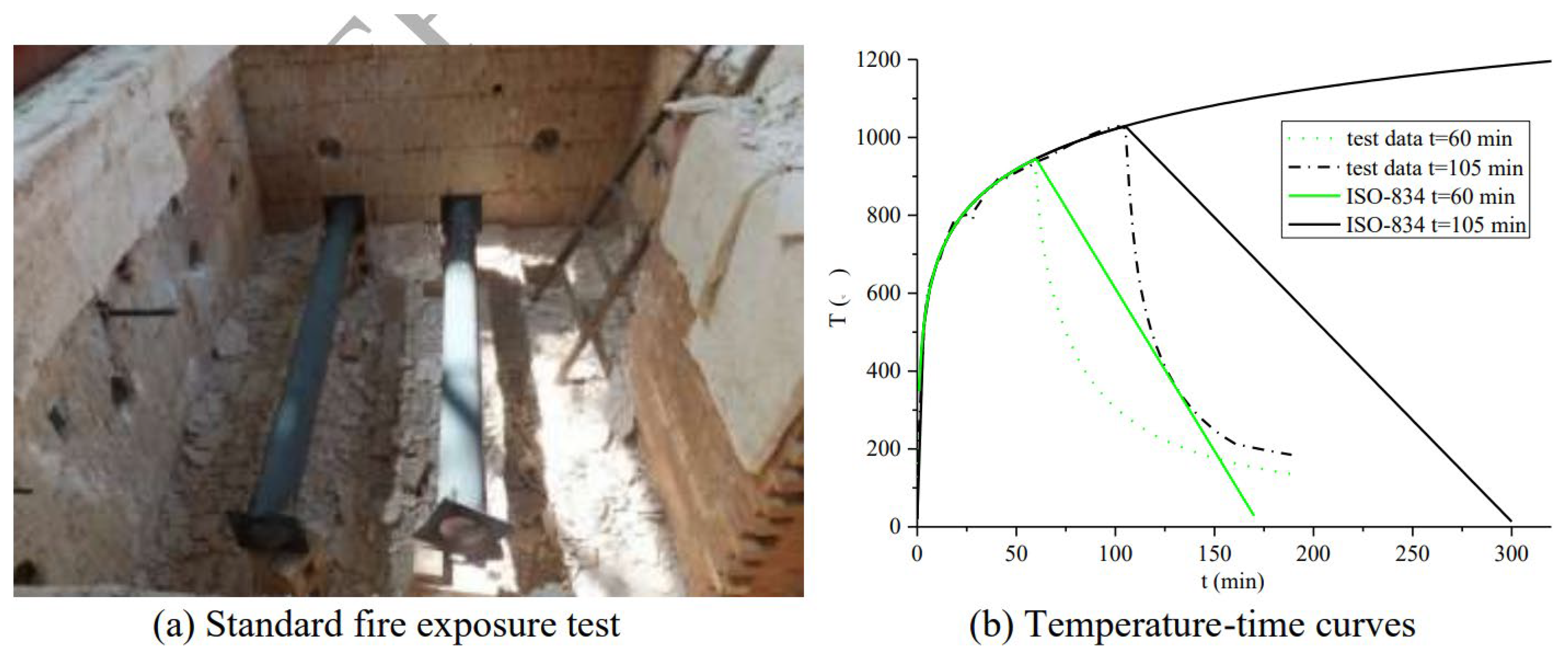
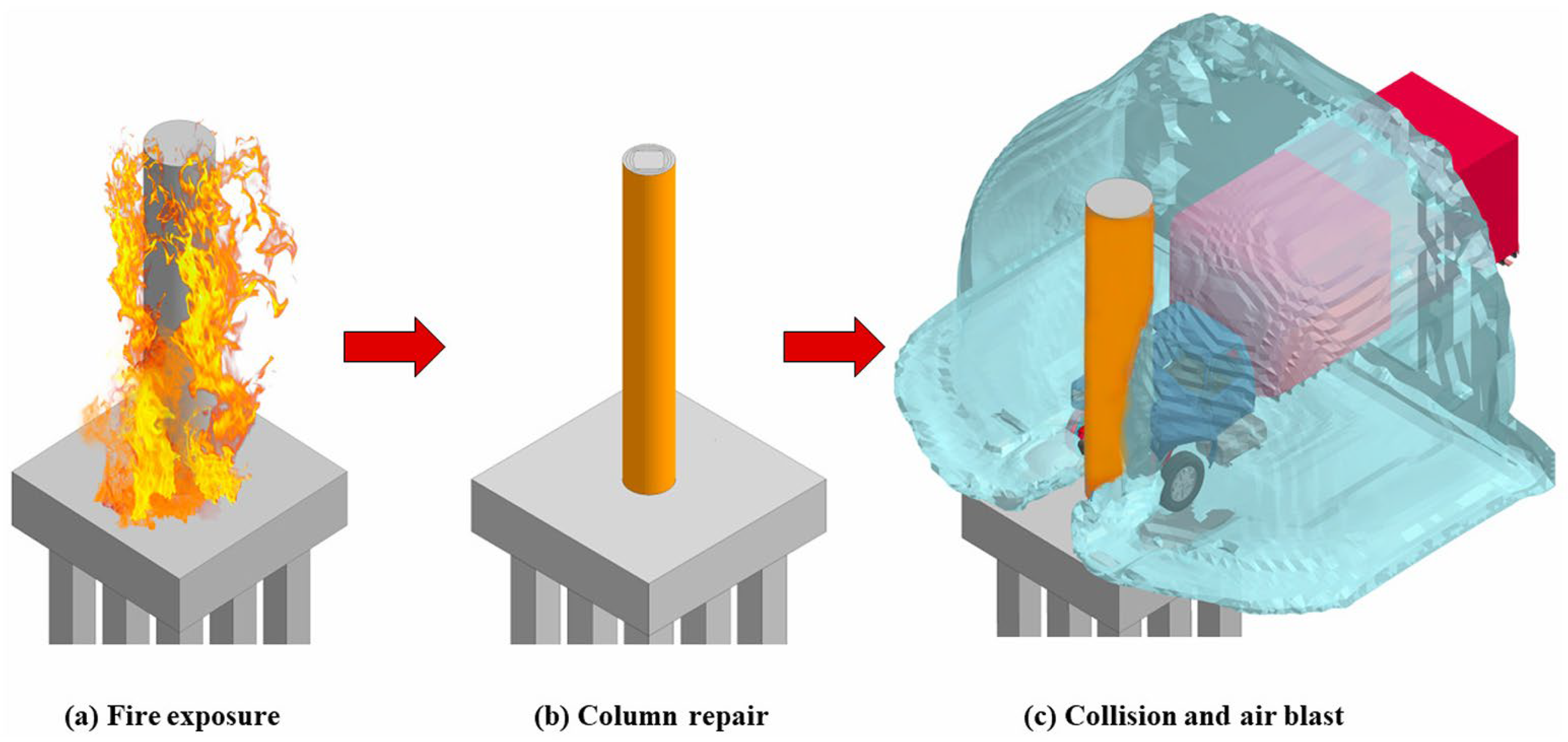
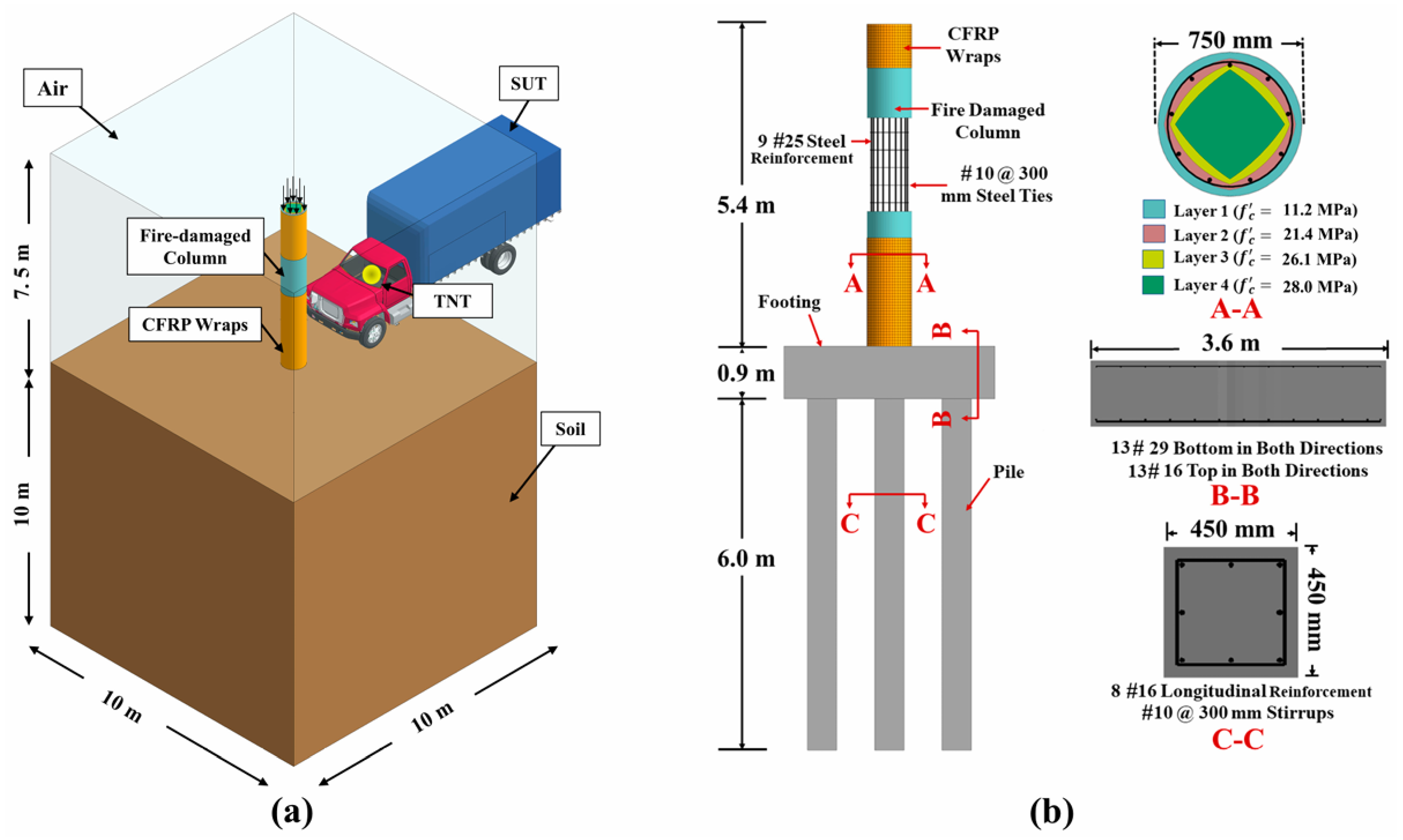
- RC bridge columns subjected to sequential hazards like fire, vehicle impact, and air blast showed cumulative damage. Fire caused a sharp drop in axial capacity, for instance, a 750 mm diameter circular column retained only about 26% of its original strength after 90 min of fire exposure. CFRP retrofitting, especially with full or partial 1.5 mm wraps, proved effective in restoring axial capacity (up to ~54%) and reduced peak displacement and kinetic energy under combined impact and blast conditions.
- Columns with larger diameters showed lower retrofit effectiveness, mainly due to higher axial load demands and reduced slenderness.
6. Directions for Future Research
- Blast loading is affected not just by environmental factors like temperature, humidity, and wind, but also by the characteristics and aging of explosives, as well as their storage and handling. These aspects can change the pressure-time history and impulse distribution, which in turn impacts the behavior of RC columns. It is important that future experiments and numerical models take all these factors into account for more accurate results.
- Effect of additional transverse reinforcement should be studied. This includes increasing bar diameter in the confining zones, mid-height region alone, or both regions, to see its impact on blast resistance.
- There is a need to explore AI and ML methods along with probabilistic approaches for predicting blast damage. Combining these with Monte Carlo simulations can help account for variations in loads and structural properties.
- New methods using GNNs and surrogate models like ANFIS and DRNN have shown quick and precise results for blast prediction. However, they still need to be tested on full-scale columns, multiple hazard cases, and aging conditions.
- Future studies can focus on explainable AI frameworks that connect blast damage prediction with performance-based retrofit methods for RC columns. Tools such as partial dependence plots (PDP) and accumulated local effects (ALE) may be used to define clear retrofit limits for stiffness and confinement.
- Simplified dimensional models should be extended to account for different axial loads, larger column sizes, and various retrofit methods to better predict column behavior under extreme conditions.
- Support conditions in experiments and numerical models often do not match the real-life boundary conditions of actual structures. Laboratory supports, whether pinned, fixed, or simply supported, are idealized and cannot fully represent the interaction with slabs, beams, or the flexibility of foundations. This mismatch can result in differences in observed displacements, failure patterns, and remaining structural capacity.
- Effect of off-center blasts should be studied.
- Spatial variation and correlation of blast pressures from vehicle-borne improvised explosive devices need closer study. Adjacent RC columns are often subjected to related, yet not identical, air blast loads because of vehicle shielding and orientation. Considering this variability in experiments and reliability-based models can make the assessment of progressive collapse risk more accurate.
- There is a need for experimental and numerical studies to validate CFRP retrofitting approaches for fire-damaged columns facing blast or impact, including determination of optimal thickness and coverage for columns of different dimensions.
- Most studies focus on damage or crack patterns under blast loading. Detailed reporting of crack length, width, depth, and energy dissipated during damage will provide a more complete picture.
- Damage evaluation needs common criteria that combine displacement, leftover strength, and energy absorption. Depending only on ductility can give a wrong picture of collapse.
- In future studies, reporting damage indices along with probabilistic confidence intervals would help complement physical crack measurements and provide a more complete understanding of structural behavior.
- The correlation between induced stresses and resulting damage should receive more attention to better understand failure mechanisms.
- Determining the maximum explosive charge that a column can withstand at the minimum standoff distance without failure is critical.
- Most studies have relied on idealized charges, such as spherical or cylindrical TNT equivalents, with uniform standoff distances. Future investigations need to consider irregular, multiple, or sequential blasts.
- Combined influence of axial load, span length, and reinforcement detailing needs careful investigation. High-fidelity FE models should be used, and results must be verified through experiments, as these parameters play a crucial role in determining failure patterns and remaining load-carrying capacity.
- Strategies to enhance blast performance without increasing the column’s cross-section need further exploration.
- Strengthening damaged columns after blast exposure is an important area for study, including repair techniques that restore structural integrity.
- Scaling up lab-scale stereoscopic DIC and shock-tube studies to full-scale members would help validate observed crack initiation and crater formation patterns.
- Variation in bond strength between existing concrete and strengthening materials like UHPC or UHPFRC must be considered, as it affects load transfer and overall performance.
- Special attention should be given to cases where ground shock and air-blast impinge the structure at the same time. This situation represents the most severe loading scenario, causing the highest structural demands because of the combined peak pressures and dynamic impacts.
- Effectiveness of polypropylene fiber (PPF) overlays and other spall-resistant concretes should be systematically tested under near-field blasts.
- A systematic benchmarking of concrete damage models (e.g., CDP, KCC, JHC, Mazars, Mat_Concrete_Damage_Rel3) across different FEM platforms under contact and near-field blasts is required.
- Innovative strengthening concepts, such as using steel angle sections at column corners with batten connections, should undergo experimental and numerical validation for blast performance.
- The comparative effectiveness of helical reinforcement versus traditional circular stirrups in circular RC columns under blast loads should be quantified in terms of confinement efficiency and energy dissipation.
- Blast resistance of RC columns can be improved by using confinement methods that are different from the conventional transverse reinforcement. Innovative options like hexagonal or honeycomb-shaped steel tube confinement around the concrete core may help develop a triaxial stress state, which in turn can strengthen resistance against both penetration and blast.
- Blast behavior of distressed or pre-damaged columns requires attention, as real structures often have existing flaws.
- Fragility studies should account for time-based deterioration like uneven chloride-driven corrosion.
- More detailed investigations are required to understand how RFRCAC columns perform over time in marine conditions. Exposure to corrosion, chloride penetration, and repeated wet-dry cycles can slowly weaken the bond between fibers and matrix, which may eventually reduce their blast resistance and durability.
- Materials like UHPFRC, SIFCON, DUCON, and CFDSST provide very good blast resistance. However, many of these materials are costly, not easily available everywhere, and may not be practical for use in regular buildings. Future research should focus on a complete cost–benefit assessment, covering initial material cost, construction effort, maintenance, and the ability to repair after blast incidents.
- Exploring low-cost alternatives, locally available materials, or hybrid solutions can also be beneficial. Such options may offer adequate blast resistance for non-critical structures without putting too much strain on the budget.
- Most blast research has concentrated on well-engineered RC columns and high-performance buildings. On the other hand, non-engineered structures, low-rise buildings, and informal constructions receive very little attention.
- CFDSST columns under contact explosions deserve dedicated experimental campaigns to establish design guidelines.
7. Research Gaps and Open Issues
- In experimental blast testing, several on-ground challenges often arise. These include slight misalignment of explosive charges, delay or inconsistency in detonation timing, and uneven confinement around the specimen. Reflected pressure waves from nearby boundaries can also affect the results. Free-standing columns may become unstable during testing, and applying or maintaining a steady axial load at the moment of blast is often difficult. Sensors, too, tend to show temporary drift under high strain-rate conditions. Such practical issues are rarely measured or discussed in detail in most available studies.
- Many numerical studies use empirical blast curves or simplified models. These lose accuracy at very short distances. For example, Kingery-Bulmash curves are not very reliable below ~0.40 m·kg−1/3. Better calibration with experiments and clear protocols for near-field or contact blasts are needed.
- Even with recent developments, the use of ML and probabilistic models for assessing RC column blast resistance remains quite limited. More validation is required across different geometries, reinforcement configurations, and loading conditions to ensure broader applicability.
- Latest GNNs and ML surrogates give highly accurate results, but they are still not tested for deterioration cases, eccentric blasts, or large field structures.
- Most ML models used for blast resistance work like “black boxes” and do not give any clear guidance on retrofit parameters, such as stiffness and confinement ratios for RC columns. Studies on explainable AI that can provide understandable thresholds for retrofit design are still very few.
- Different FE damage models (Mazars, KCC, CDP, JHC, Mat_Concrete_Damage_Rel3) give very different predictions for spalling, crushing, and fragment ejection. There is no systematic comparison between software tools yet.
- The influence of spatial variability and partial correlation of blast loads on nearby or adjacent columns is still not clear. Many studies usually consider the pressure to be uniform or fully correlated. However, the results from VBIED tests indicate that the shielding effect of the vehicle causes uneven loading on columns. This gap makes the prediction of progressive collapse less reliable.
- High-quality field tests are rare. Most studies are small-scale or carried out in shock tubes. Factors like weather, crack patterns, and post-blast strength are not consistently reported, making comparisons difficult.
- Combined effects of ground shock and air blast, especially when they happen together, are still not well understood.
- Modern stereoscopic DIC at high speed can capture cracks and crater growth with detail, but till now it has been used only in small-scale tests.
- The impact of eccentric blasts and combined axial compression has hardly been explored, even though both have a major effect on damage behavior and the remaining strength.
- There is little agreement on repair methods that restore strength. The long-term durability and bond of retrofit materials like CFRP or UHPC overlays after blast are not well studied.
- Real structures often have cracks, corrosion, or old damage, but their effect on blast response is not well known.
- There is limited validation of retrofit methods such as CFRP wraps when columns face combined hazards, particularly for larger-diameter or slender columns.
- Dimensional models used for rapid damage assessment under various blast scenarios require more calibration and development to be widely applicable.
- Corrosion caused by chlorides, especially when it is non-uniform, makes structures more fragile with time. Yet, its role in reducing blast resistance has not been validated through experiments.
- Effect of longitudinal and shear reinforcement on blast resistance, especially during close-range explosions, still requires detailed experimental and numerical study.
- Economic comparisons of retrofit options (FRP, SFRP, UHPC overlays, steel jackets, CFDSST) are limited.
- Different studies use different damage measures (residual capacity ratios, displacement-based indices, D-index variants), which makes combining results difficult.
- Predictions based on energy, displacement, and residual strength often do not match, and there is still no common framework to unify them.
- Uncertainty in numerical models needs attention. Predictions are sensitive to mesh, material behavior, boundary conditions, and load representation.
- New materials (UHPFRC, SIFCON, DUCON, PPF overlays, advanced FRPs, CFDSST) show promise in small tests. But broader and field-scale studies are needed to confirm their performance.
- Reinforced textile concrete is gaining attention as a high-performance alternative to traditional RC and FRP-strengthened concrete, without relying on fibers. Its response to high-strain-rate loads, like blasts, is still not fully explored.
- RFRCAC has shown promising benefits in resisting blast effects. However, the absence of standardized design guidelines for coral aggregate-based concretes under such loading makes its direct use in practical engineering work challenging.
- Blast effects are often studied in isolation, but real buildings face multiple hazards, earthquakes, fire, impacts either together or one after another. How damage from one event influences blast behavior, and vice versa, is still an open question.
- Most existing models do not reflect how damage unfolds step by step under multiple threats. For instance, a column may first face local penetration or small-scale damage, and only then be hit by a blast. This order of loading changes the way cracks spread, and failure develops. Yet, such sequential effects are hardly considered in current experiments or FE studies.
- Most research considers simple, single columns. In actual structures, columns connect with beams, slabs, and non-structural elements. The effect of these connections on blast resistance, failure modes, and progressive collapse is not well understood.
- Approaches that combine FE simulations, experimental results, and AI/ML predictions are still rarely used, particularly for near-field scenarios and cases with high axial loads.
- Very little is known about how RC columns behave months or years after a blast. Long-term effects like creep, fatigue from repeated loading, corrosion at damaged areas, and gradual deterioration are rarely studied.
- Probabilistic models can help estimate how a structure will perform over the long term after a blast, considering variations in materials and their gradual deterioration over time.
- Role of cladding, infill walls, partitions, and other non-structural parts in blast response is poorly investigated. These components can change pressure distribution, create additional local damage, or affect spalling patterns, yet they are often ignored in experiments and simulations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABAQUS/CAE | Finite Element Analysis Software |
| AI | Artificial Intelligence |
| ALE | Arbitrary Lagrangian-Eulerian |
| ALR | Axial Load Ratio |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| ANFO | Mixture of Ammonium Nitrate and Fuel Oil |
| ANSYS AUTODYN | Hydrocode for impact/blast simulations |
| ASCE/SEI | American Society of Civil Engineers/Structural Engineering Institute |
| BF, SF, BSF | Bending Failure, Shear Failure, Bending-Shear Failure |
| CDP | Concrete Damage Plasticity |
| CEL | Coupled Eulerian-Lagrangian |
| CFD | Computational Fluid Dynamics |
| CFDSST | Concrete-Filled Double-Skin Steel Tubular |
| CFDST | Concrete-Filled Double-Skin Steel Tube |
| CFRP | Carbon Fiber-Reinforced Polymer |
| CONWEP | Conventional Weapons Effects Program (blast load model) |
| CRC | Compact Reinforced Composite |
| CSC | Continuous Surface Cap Model/Concrete–Steel Composite |
| DIC | Digital Image Correlation |
| DIF | Dynamic Increase Factor |
| DRNN | Deep Recurrent Neural Network |
| DSAS | Dynamic Structural Analysis System |
| DUCON | Ductile Concrete |
| ED | Energy Dissipation |
| FE | Finite Element |
| FEM/FEA | Finite Element Method/Analysis |
| FHWA | Federal Highway Administration |
| FRP | Fiber-Reinforced Polymer |
| FRCM | Fabric-Reinforced Cementitious Matrix |
| GFRP | Glass Fiber-Reinforced Polymer |
| GNN | Graph Neural Network |
| HSRC | High-Strength Reinforced Concrete |
| ISO-834 | Standard Fire Curve |
| JHC | Johnson-Holmquist-Cook |
| JWL | Jones-Wilkins-Lee |
| K-B | Kingery-Bulmash |
| KCC | Karagozian & Case Concrete |
| LS-DYNA | Nonlinear Dynamic Analysis Software (commercial FE solver) |
| LVDT | Linear Variable Differential Transformer |
| Mazars | Mazars Concrete Damage Model |
| ML | Machine Learning |
| NSM | Near-Surface Mounted |
| P-I | Pressure-Impulse |
| PDP | Partial Dependence Plot |
| PETN | Pentaerythritol Tetranitrate |
| PPF | Polypropylene Fiber |
| RC | Reinforced Concrete |
| RCAC | Reinforced Coral Aggregate Concrete |
| RFRCAC | Fiber-Reinforced Coral Aggregate Concrete with Steel Bars |
| RHT | Riedel-Hiermaier-Thoma |
| RPC | Reactive Powder Concrete |
| SDOF | Single Degree of Freedom |
| SFRC | Steel Fiber Reinforced Concrete |
| SFRP | Steel Fiber-Reinforced Polymer |
| SIFCON | Slurry Infiltrated Fiber Concrete |
| TNT | Trinitrotoluene |
| UHPFRC | Ultra-High-Performance Fiber-Reinforced Concrete |
| UHPC | Ultra-High-Performance Concrete |
| VBIED | Vehicle-Borne Improvised Explosive Devices |
References
- Hao, H.; Hao, Y.; Li, J.; Chen, W. Review of the current practices in blast-resistant analysis and design of concrete structures. Adv. Struct. Eng. 2016, 19, 1193–1223. [Google Scholar] [CrossRef]
- Kyei, C.; Braimah, A. Effects of transverse reinforcement spacing on the response of reinforced concrete columns subjected to blast loading. Eng. Struct. 2017, 142, 148–164. [Google Scholar] [CrossRef]
- Cui, J.; Shi, Y.; Li, Z.-X.; Chen, L. Failure Analysis and Damage Assessment of RC Columns under Close-In Explosions. J. Perform. Constr. Facil. 2015, 29, B4015003. [Google Scholar] [CrossRef]
- Do, V.T.; Pham, M.T.; Hao, H. Shock wave propagation and structural response of precast concrete segmental columns under simulated blast loads. Int. J. Impact Eng. 2020, 143, 103595. [Google Scholar] [CrossRef]
- Smith, P.J. Terrorism in Asia: A persistent challenge sustained by ideological, physical, and criminal enablers. In Handbook of Asian Criminology; Springer: New York, NY, USA, 2013; pp. 147–164. [Google Scholar]
- Williamson, E.B.; Winget, D.G. Risk management and design of critical bridges for terrorist attacks. J. Bridge Eng. 2005, 10, 96–106. [Google Scholar] [CrossRef]
- Federal Highway Administration (FHWA). Recommendations for Bridge and Tunnel Security, Blue Ribbon Panel Report; Report No. FHWA-IF-03-036; AASHTO: Washington, DC, USA, 2003.
- TM 5-855-1; Design & Analysis of Hardened Structures to Conventional Weapons Effects; U.S. Department of the Army: Fort Belvoir, VA, USA, 1986.
- TM 5-1300; Structures to Resist the Effects of Accidental Explosions. Joint Department of the Army: Alexandria, VA, USA, 1990.
- UFC 3-340-02; Structures to Resist the Effects of Accidental Explosions; Unified Facilities; Criteria U.S. Army Corporations of Engineers: Washington, DC, USA, 2008.
- Wu, C.; Hao, H. Modelling of simultaneous ground shock and airblast pressure on nearby structures from surface explosions. Int. J. Impact Eng. 2005, 31, 699–717. [Google Scholar] [CrossRef]
- Shirbhate, A.P.; Goel, D.M. A critical review of blast wave parameters and approaches for blast load mitigation. Arch. Comput. Methods Eng. 2021, 83. [Google Scholar] [CrossRef]
- IS 4991; Criteria for Blast Resistant Design of Structures for Explosions Above Ground. Bureau of Indian Standard: New Delhi, India, 1968.
- IS 6922; Criteria for Safety and Design of Structures Subject to Underground Blasts. Bureau of Indian Standard: New Delhi, India, 1773.
- Shi, Y.; Hao, H.; Li, Z.-X. Numerical simulation of blast wave interaction with structure columns. Shock Waves 2007, 17, 113–133. [Google Scholar] [CrossRef]
- Shi, Y.; Hao, H.; Li, Z.-X. Numerical derivation of pressure–impulse diagrams for prediction of RC column damage to blast loads. Int. J. Impact Eng. 2008, 35, 1213–1227. [Google Scholar] [CrossRef]
- Kennedy, W.D. Explosions and Explosives in Air; NDRC: Washington DC, USA, 1946. [Google Scholar]
- Enstock, L.; Smith, P. Measurement of impulse from the close-in explosion of doped charges using a pendulum. Int. J. Impact Eng. 2007, 34, 487–494. [Google Scholar] [CrossRef]
- ASCE/SEI 59-11; Blast Protection of Buildings. American Society of Civil Engineers: Reston, VA, USA, 2011.
- Gel’FAnd, B.E.; Voskoboinikov, I.M.; Khomik, S.V. Recording the Position of a Blast-Wave Front in Air. Combust. Explos. Shock. Waves 2004, 40, 734–736. [Google Scholar] [CrossRef]
- ESL-TR 87-57; Protective Construction Design Manual. U.S. Air Force Engineering and Services Center, Air Force Base: Florida, CA, USA, 1989.
- Kingery, C.N.; Bulmash, G. Air Blast Parameters from TNT Spherical Air Burst and Hemispherical Surface Burst; Ballistic Research Laboratories: Adelphi, MA, USA, 1984.
- Rajkumar, D.; Senthil, R.; Kumar, B.B.M.; AkshayaGomathi, K.; Velan, S.M. Numerical Study on Parametric Analysis of Reinforced Concrete Column under Blast Loading. J. Perform. Constr. Facil. 2020, 34, 04019102. [Google Scholar] [CrossRef]
- CSA 850-12; Design and Assessment of Buildings Subjected to Blast Loads. Canadian Standards Association: Mississauga, ON, Canada, 2012.
- UFC 4-010-01; DoD Minimum Antiterrorism Standards for Buildings; Unified Facilities Criteria. US Department of Defense: Washington, DC, USA, 2012.
- FEMA 427; Primer for Design of Commercial Buildings to Mitigate Terrorist Attacks. Federal Emergency Management Agency: Washington, DC, USA, 2003.
- ASCE. Minimum Design Loads for Buildings and Other Structures (7–10); American Society of Civil Engineers: Reston, VA, USA, 2010. [Google Scholar]
- Krauthammer, T.; Astarlioglu, S.; Blasko, J.; Soh, T.; Ng, P. Pressure–impulse diagrams for the behavior assessment of structural components. Int. J. Impact Eng. 2008, 35, 771–783. [Google Scholar] [CrossRef]
- FEMA 428; Risk Management Series. US Department of Homeland Security: Washington, DC, USA, 2004.
- ASCE. Design of Blast Resistant Buildings in Petrochemical Facilities; American Society of Civil Engineers: Reston, VA, USA, 1997. [Google Scholar]
- NCHRP 12-72; Blast-Resistant Highway Bridges: Design and Detailing Guidelines. National Cooperative Highway Research Program: Washington, DC, USA, 2005.
- EN 1991-1-7; Eurocode 1—Actions on Structures—Part 1–7: General Actions—Accidental Actions. European Committee for Standardization (CEN): Brussels, Belgium, 2006.
- ACI 349-13; Code Requirements for Nuclear Safety-Related Concrete Structures and Commentary. American Concrete Institute (ACI): Farmington Hills, MI, USA, 2013.
- ACI 370R-14; Report for the Design of Concrete Structures for Blast Effects. American Concrete Institute (ACI): Farmington Hills, MI, USA, 2014.
- Zhang, D.; Yao, S.; Lu, F.; Chen, X.; Lin, G.; Wang, W.; Lin, Y. Experimental study on scaling of RC beams under close-in blast loading. Eng. Fail. Anal. 2013, 33, 497–504. [Google Scholar] [CrossRef]
- Aoude, H.; Dagenais, F.P.; Burrell, R.P.; Saatcioglu, M. Behavior of ultra-high performance fiber reinforced concrete columns under blast loading. Int. J. Impact Eng. 2015, 80, 185–202. [Google Scholar] [CrossRef]
- Hegemier, G.A.; Seible, F.; Rodriguez-Nikl, T.; Arnett, K. Blast mitigation of critical infrastructure components and systems. In FIB Proceedings of the 2nd International Congress, Laussane, Switzerland, 21–22 July 2006; FIB: Laussane, Switzerland, 2006. [Google Scholar]
- Zhang, X.H.; Zhang, C.W.; Duan, Z.D. Numerical simulation on shock waves generated by explosive mixture gas from large nuclear blast load generator based on equivalent-energy principles. J. Explos. Shock Waves 2014, 34, 80–86. [Google Scholar]
- Zhang, X.H.; Zhang, Z.D.; Duan, Z.D.; Zhang, C.W. Analysis for dynamic response and failure process of reinforced concrete beam under blast load. J. Northeast For. Univ. 2009, 37, 50–53. [Google Scholar]
- Zhang, X.H.; Zhang, C.W.; Duan, Z.D. Numerical simulation on impact responses and failure modes of steel frame structural columns subject to blast loads. J. Shenyang Jianzhu Univ. 2009, 25, 656–662. [Google Scholar]
- Zhang, X.H.; Duan, Z.D.; Zhang, C.W. Shock responses of steel frame structure near the ground explosion. Earthq. Eng. Eng. Vib. 2009, 29, 70–76. [Google Scholar]
- Zhang, C.; Wang, W.; Zhang, X.; Lu, S. Large scale blast emulator based explosive gas loading methods for structures and recent advances in experimental studies. In Proceedings of the 8th International Conference on Shock and Impact Loads on Structures, Adelaide, Australia, 2–4 December 2009; University of Adelaide: Adelaide, Australia, 2009; pp. 769–780. [Google Scholar]
- Rabczuk, T.; Eibl, J. Modelling dynamic failure of concrete with meshfree methods. Int. J. Impact Eng. 2006, 32, 1878–1897. [Google Scholar] [CrossRef]
- Zhou, Q.X.; Kuznetsov, A.V.; Hao, H.; Waschl, J. Numerical prediction of concrete slab response to blast loading. Int. J. Impact Eng. 2008, 35, 1186–2000. [Google Scholar] [CrossRef]
- Li, J.; Hao, H. Numerical study of concrete spall damage to blast loads. Int. J. Impact Eng. 2014, 68, 41–55. [Google Scholar] [CrossRef]
- Goel, D.M.; Matsagar, V.A. Blast-resistant Design of Structures Practice Periodical on Structural Design and Construction. Pract. Period. Struct. Des. Constr. 2014, 19, 04014007. [Google Scholar] [CrossRef]
- McVay, M.K. Spall Damage of Concrete Structures; No. WES/TR/SL-88-22; Army Engineer Waterways Experiment Station Vicksburg MS Structures LAB: Washington, DC, USA, 1988.
- Yao, S.J.; Zhang, D.; Lu, F.Y.; Wang, W.; Chen, X.G. Damage features and dynamic response of RC beams under blast. Eng. Fail Aanl. 2016, 62, 103–111. [Google Scholar] [CrossRef]
- Magnusson, J.; Hallgren, M.; Ansell, A. Air-blast-loaded, high-strength concrete beams. Part I: Experimental investigation. Mag. Concr. Res. 2010, 62, 127–136. [Google Scholar] [CrossRef]
- Yan, B.; Liu, F.; Song, D.; Jiang, Z. Numerical study on damage mechanism of RC beams under close-in blast loading. Eng. Fail. Anal. 2015, 51, 9–19. [Google Scholar] [CrossRef]
- Li, J.; Hao, H. A two-step numerical method for efficient analysis of structural response to blast load. Int. J. Prot. Struct. 2011, 2, 103–126. [Google Scholar] [CrossRef]
- Liu, Y.; Yan, J.-B.; Huang, F.-L. Behavior of reinforced concrete beams and columns subjected to blast loading. Def. Technol. 2018, 14, 550–559. [Google Scholar] [CrossRef]
- Nagata, M.; Beppu, M.; Ichino, H.; Matsuzawa, R. A fundamental investigation of reinforced concrete beams subjected to close-in explosion. Int. J. Prot. Struct. 2018, 9, 174–198. [Google Scholar] [CrossRef]
- Li, Y.; Algassem, O.; Aoude, H. Response of high-strength reinforced concrete beams under shock-tube induced blast loading. Constr. Build. Mater. 2018, 189, 420–437. [Google Scholar] [CrossRef]
- Anas, S.M.; Alam, M.; Umair, M. Experimental and Numerical Investigations on Performance of Reinforced Concrete Slabs under Explosive-induced Air-blast Loading: A state-of-the-art review. Structures 2021, 31, 428–461. [Google Scholar] [CrossRef]
- Jayasooriya, R.; Thambiratnam, D.P.; Perera, N.J. Blast response and safety evaluation of a composite column for use as key element in structural systems. Eng. Struct. 2014, 61, 31–43. [Google Scholar] [CrossRef]
- Nguyen, K.T.Q.; Navaratnam, S.; Mendis, P.; Zhang, K.; Barnett, J.; Wang, H. Fire safety of composites in prefabricated buildings: From fibre reinforced polymer to textile reinforced concrete. Compos. Part B Eng. 2020, 187, 107815. [Google Scholar] [CrossRef]
- Yuan, S.; Hao, H.; Zong, Z.; Li, J. A study of RC bridge columns under contact explosion. Int. J. Impact Eng. 2017, 109, 378–390. [Google Scholar] [CrossRef]
- Williams, G.D.; Williamson, E.B. Response of Reinforced Concrete Bridge Columns Subjected to Blast Loads. J. Struct. Eng. 2011, 137, 903–913. [Google Scholar] [CrossRef]
- Tang, E.K.; Hao, H. Numerical simulation of a cable-stayed bridge response to blast loads, part I: Model development and response calculations. Eng. Struct. 2010, 32, 3180–3192. [Google Scholar] [CrossRef]
- Hao, H.; Tang, E.K. Numerical simulation of a cable-stayed bridge response to blast loads, part II: Damage prediction and FRP strengthening. Eng. Struct. 2010, 32, 3193–3205. [Google Scholar] [CrossRef]
- Williamson, E.B.; Bayrak, O.; Williams, G.D.; Davis, C.E.; Marchand, K.A.; McKay, A.E.; Kulicki, J.; Wassef, W. Blast-Resistant Highway Bridges: Design and Detailing Guidelines; NCHRP Rep. No. 645; National Cooperative Highway Research Program: Washington, DC, USA, 2010. [Google Scholar]
- Oswald, C.J. Prediction of injuries to building occupants from column failure and progressive collapse with the BICADS computer program. In Proceedings of the ASCE Structures Congress and Exposition, Reston, VA, USA, 20 April 2005; pp. 1–22. [Google Scholar] [CrossRef]
- Williamson, E.B.; Bayrak, O.; Davis, C.; Daniel Williams, G. Performance of bridge columns subjected to blast loads. II: Results and recommendations. J. Bridge Eng. 2011, 16, 703–710. [Google Scholar] [CrossRef]
- Foglar, M.; Kovar, M. Conclusions from experimental testing of blast resistance of FRC and RC bridge decks. Int. J. Impact. Eng. 2013, 59, 18–28. [Google Scholar] [CrossRef]
- Wu, C.; Nurwidayati, R.; Oehlers, D.J. Fragmentation from spallation of RC slabs due to airblast loads. Int. J. Impact. Eng. 2009, 36, 1371–1376. [Google Scholar] [CrossRef]
- Wu, C.; Oehlers, D.; Rebentrost, M.; Leach, J.; Whittaker, A. Blast testing of ultra-high performance fibre and FRP-retrofitted concrete slabs. Eng. Struct. 2009, 31, 2060–2069. [Google Scholar] [CrossRef]
- Ellingwood, B.R. Mitigating Risk from Abnormal Loads and Progressive Collapse. J. Perform. Constr. Facil. 2006, 20, 315–323. [Google Scholar] [CrossRef]
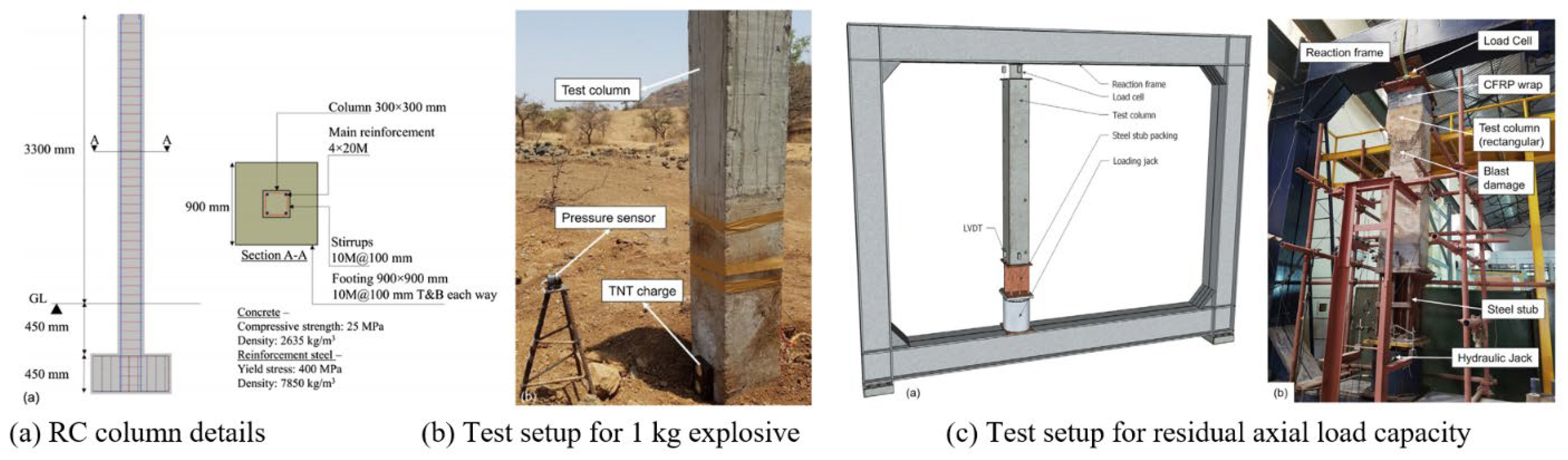
- Dua, A.; Braimah, A.; Kumar, M. Experimental and numerical investigation of rectangular reinforced concrete columns under contact explosion effects. Eng. Struct. 2020, 205, 109891. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Zhou, Y. Why did the world trade center collapse?—Simple analysis. J. Eng. Mech. 2002, 128, 12–18. [Google Scholar]
- Mlakar, F.P.; Corley, G.W.; Sozen, A.M.; Thornton, H.C. The Oklahoma City bombing: Analysis of blast damage to the murrah building. J. Perform. Constr. Facil. 1998, 12, 113–119. [Google Scholar] [CrossRef]
- Sadovskiy, M.A. Mechanical effects of air shock waves from explosions according to experiments. In Selected Works: Geophysics and Physics of Explosion; Nauka Press: Moscow, Russia, 2004. [Google Scholar]
- Fujikake, K.; Aemlaor, P. Damage of reinforced concrete columns under demolition blasting. Eng. Struct. 2013, 55, 116–125. [Google Scholar] [CrossRef]
- Astarlioglu, S.; Krauthammer, T.; Morency, D.; Tran, T.P. Behavior of reinforced concrete columns under combined effects of axial and blast-induced transverse loads. Eng. Struct. 2013, 55, 26–34. [Google Scholar] [CrossRef]
- Astarlioglu, S.; Krauthammer, T. Response of normal-strength and ultra-high-performance fiber-reinforced concrete columns to idealized blast loads. Eng. Struct. 2014, 61, 1–12. [Google Scholar] [CrossRef]
- Xu, J.; Wu, C.; Xiang, H.; Su, Y.; Li, Z.-X.; Fang, Q.; Hao, H.; Liu, Z.; Zhang, Y.; Li, J. Behaviour of ultra high performance fibre reinforced concrete columns subjected to blast loading. Eng. Struct. 2016, 118, 97–107. [Google Scholar] [CrossRef]
- Zhang, F.; Wu, C.; Zhao, X.-L.; Xiang, H.; Li, Z.-X.; Fang, Q.; Liu, Z.; Zhang, Y.; Heidarpour, A.; Packer, J.A. Experimental study of CFDST columns infilled with UHPC under close-range blast loading. Int. J. Impact Eng. 2016, 93, 184–195. [Google Scholar] [CrossRef]
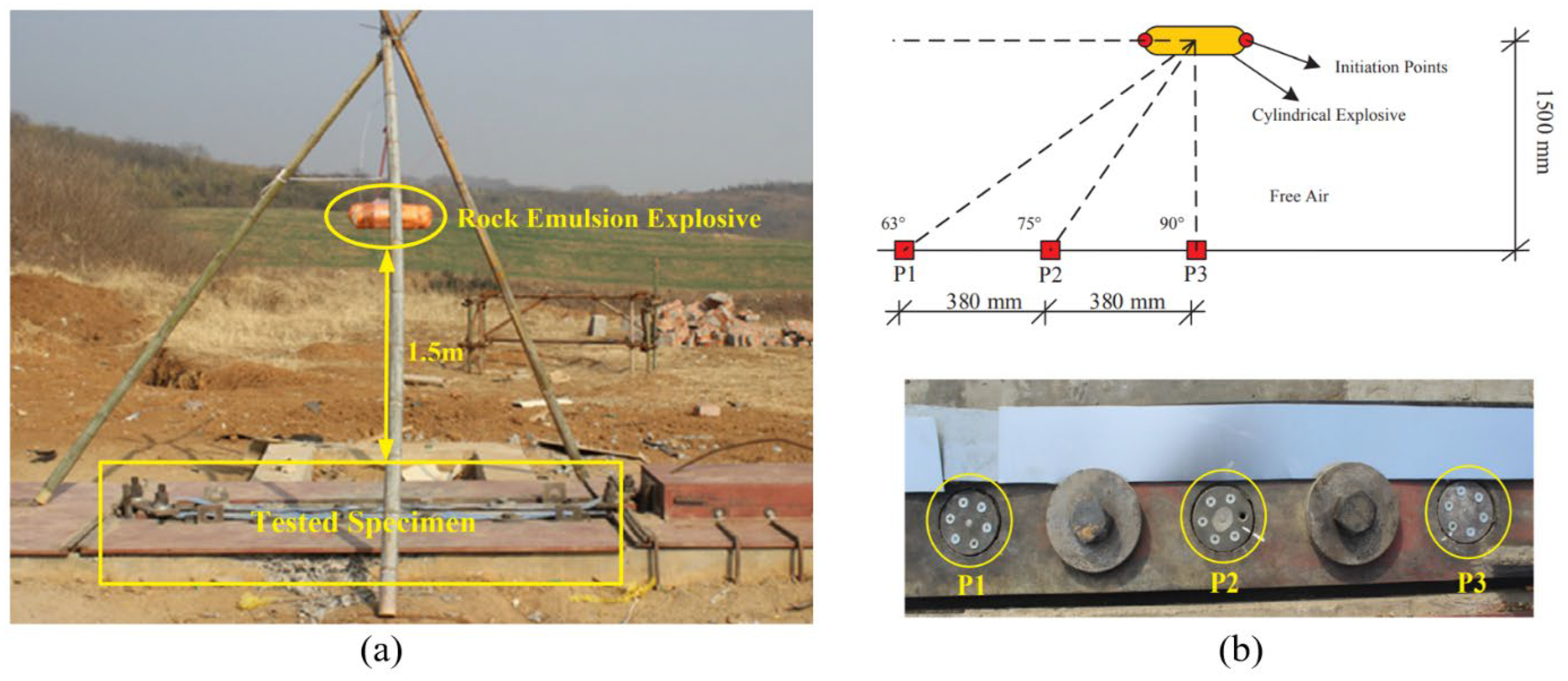
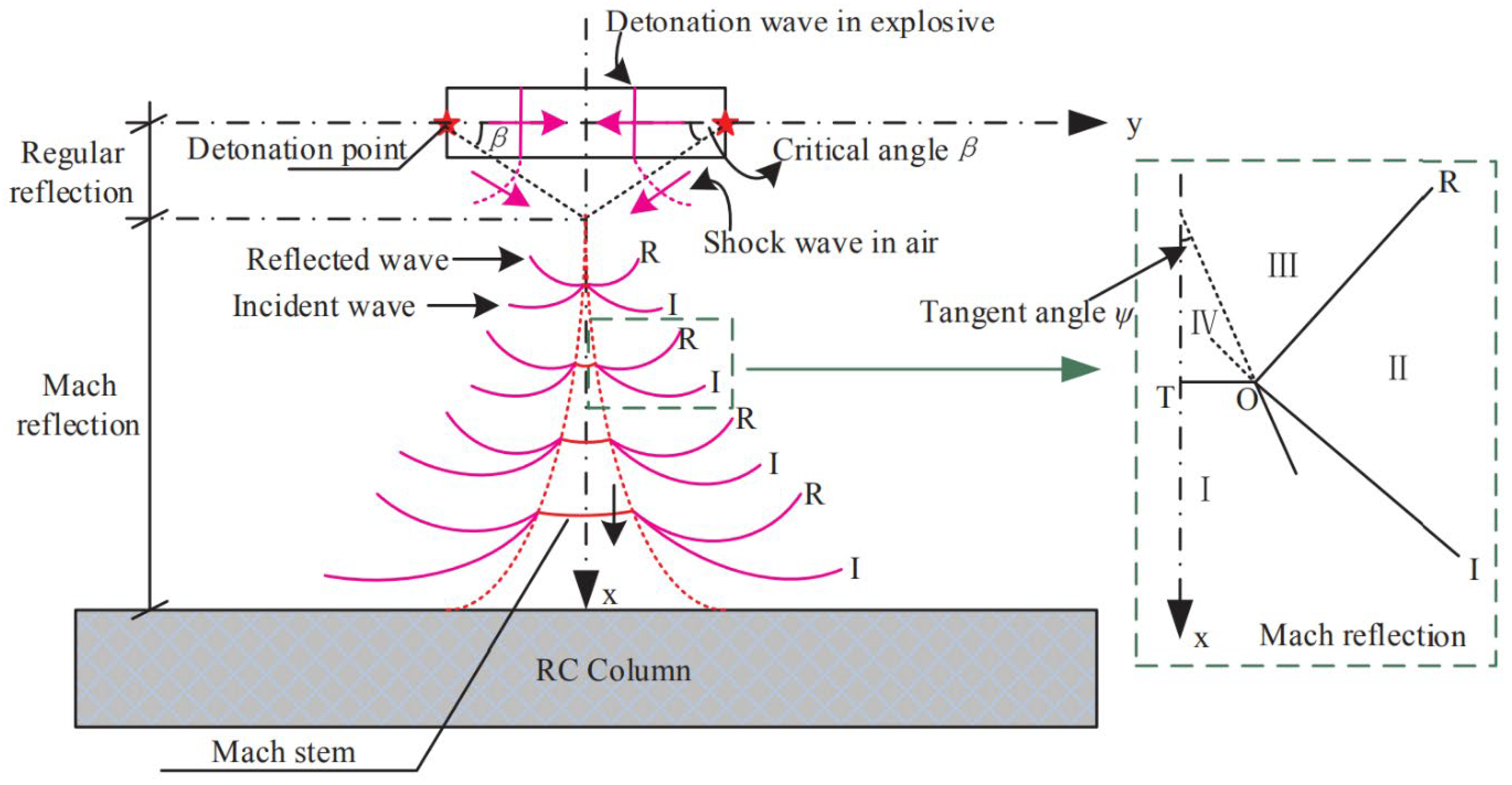
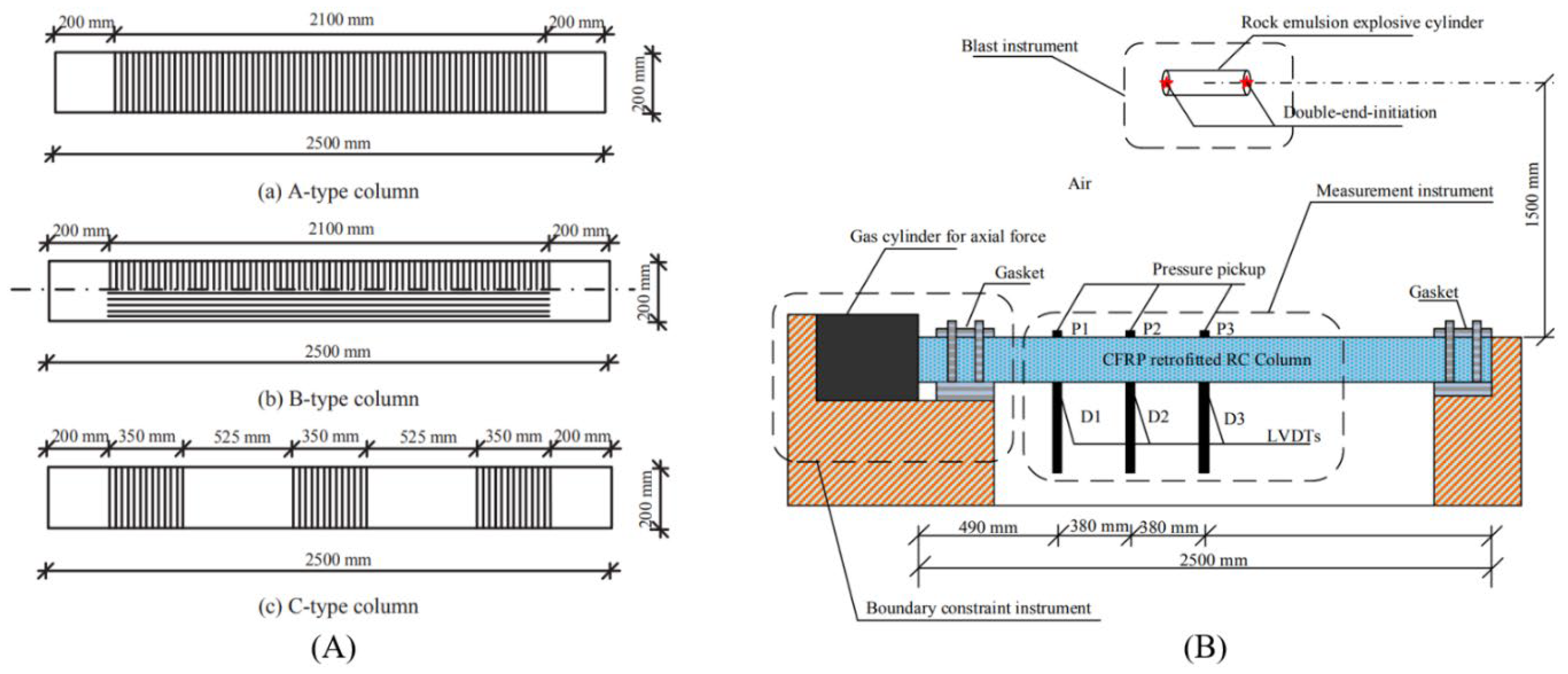
- Chen, L.; Hu, Y.; Ren, H.; Xiang, H.; Zhai, C.; Fang, Q. Performances of the RC column under close-in explosion induced by the double-end-initiation explosive cylinder. Int. J. Impact Eng. 2019, 132, 103326. [Google Scholar] [CrossRef]
- Kim, Y.; Lee, K.; Shin, J. Ductility and residual strength-based blast resistance evaluation of RC columns with various structural details. Structures 2025, 77, 109179. [Google Scholar] [CrossRef]
- Shen, S.; Zheng, R.; Wang, W.; Ye, C. Effect of Charge Eccentric Position on the Response of Reinforced Concrete Columns Under Blast Loading. Buildings 2025, 15, 1898. [Google Scholar] [CrossRef]
- AS 3600; Concrete Structures. Standards Association of Australia: Sydney, Australia, 2018.
- Burrell, R.P.; Aoude, H.; Saatcioglu, M. Response of SFRC Columns under Blast Loads. J. Struct. Eng. 2015, 141, 04014209. [Google Scholar] [CrossRef]
- Li, J.; Hao, H.; Wu, C. Numerical study of precast segmental column under blast loads. Eng. Struct. 2017, 134, 125–137. [Google Scholar] [CrossRef]
- Li, J.; Wu, C.; Hao, H.; Liu, Z. Post-blast capacity of ultra-high performance concrete columns. Eng. Struct. 2017, 134, 289–302. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, L.; Fang, Q.; Xiang, H. Blast loading model of the RC column under close-in explosion induced by the double-end-initiation explosive cylinder. Eng. Struct. 2018, 175, 304–321. [Google Scholar] [CrossRef]
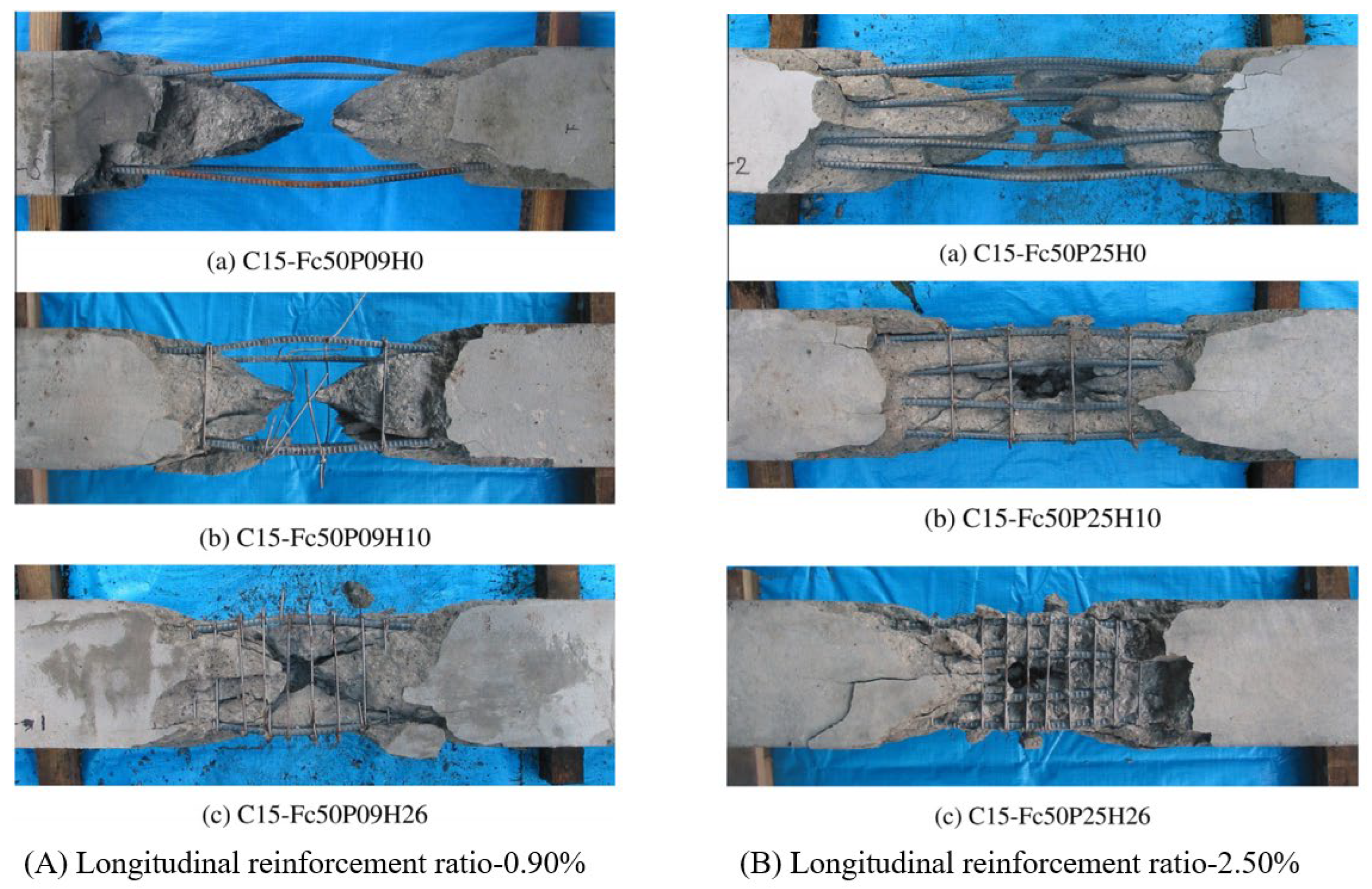
- Yan, Y.; Hou, X.; Zheng, W.; Fei, H. The damage response of RC columns with considering different longitudinal and shear reinforcement under demolition blasting. J. Build. Eng. 2022, 62, 105396. [Google Scholar] [CrossRef]
- Zhang, X.; Niu, D. Experimental study of fiber-reinforced coral aggregate concrete columns with steel reinforcements under blast loading. Structures 2025, 80, 110074. [Google Scholar] [CrossRef]
- Wu, Y.; Xie, Q.; Mu, C. Sensitivity Analysis of Factors Influencing the Blast Resistance of Reinforced Concrete Columns Based on Grey Relation Degree. Sustainability 2023, 15, 12285. [Google Scholar] [CrossRef]
- CSA A23.3; Design of Concrete Structures. Canadian Standards Association (CSA): Mississauga, ON, Canada, 2004.
- Alsendi, A.; Eamon, C.D. Quantitative Resistance Assessment of SFRP-Strengthened RC Bridge Columns Subjected to Blast Loads. J. Perform. Constr. Facil. 2020, 34, 04020055. [Google Scholar] [CrossRef]
- Pathak, A.; Raman, R.; Shestakova, Y.; Aref, A. Numerical simulation of reinforced concrete columns in mid-rise buildings subjected to close by blast loading. In Proceedings of the Structures Congress 2020, St. Louis, MI, USA, 5–8 April 2020. [Google Scholar]
- ASCE/SEI 7-16; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. American Society of Civil Engineers: Alexander Bell Drive Reston, VA, USA, 2016.
- ACI 318-14; Building Code Requirements for Structural Concrete and Commentary. ACI Committee 318: Farmington Hills, MI, USA, 2014.
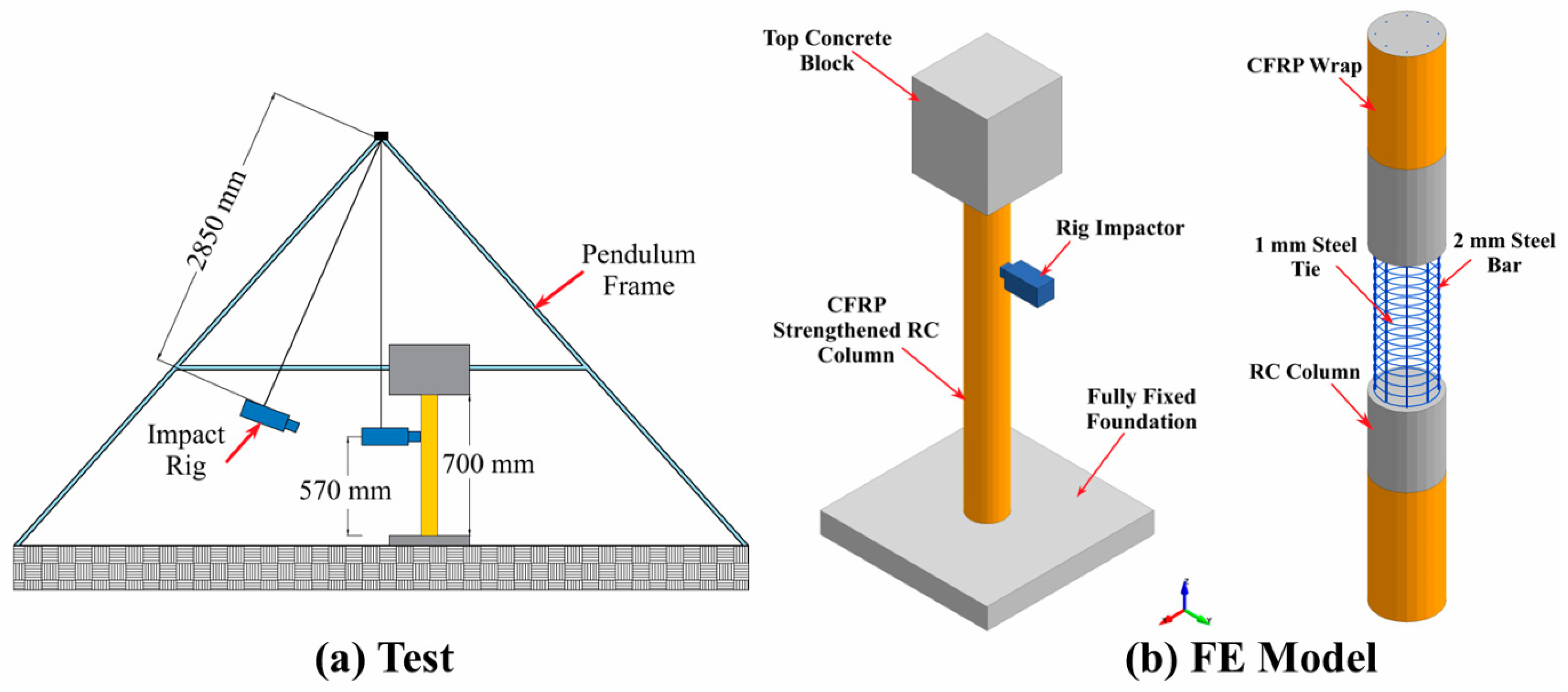
- Yan, J.; Liu, Y.; Xu, Z.; Li, Z.; Huang, F. Experimental and numerical analysis of CFRP strengthened RC columns subjected to close-in blast loading. Int. J. Impact Eng. 2020, 146, 103720. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, L.; Fang, Q.; Kong, X.; Shi, Y.; Cui, J. Study of CFRP retrofitted RC column under close-in explosion. Eng. Struct. 2021, 227, 111431. [Google Scholar] [CrossRef]
- Ju, S.J.; Kwak, H.-G. A FE model to evaluate the resisting capacity of RC beams and columns under blast loading based on P-I diagram. Int. J. Impact Eng. 2022, 161, 104113. [Google Scholar] [CrossRef]
- Zhou, X.-Q.; Huang, B.-G.; Wang, X.-Y.; Xia, Y. Deep learning-based rapid damage assessment of RC columns under blast loading. Eng. Struct. 2022, 271, 114949. [Google Scholar] [CrossRef]
- Yang, D.; Yang, J.; Shi, J. Prediction and analysis of damage to RC columns under close-in blast loads based on machine learning and Monte Carlo method. Eng. Struct. 2024, 318, 118787. [Google Scholar] [CrossRef]
- ACI 318-19; Building Code Requirements for Structural Concrete (ACI 318-19) and Commentary. American Concrete Institute (ACI): Farmington Hills, MI, USA, 2019.
- Wang, J.; Yin, J.; Li, X.; Yi, J.; Wang, Z.; Li, X. Construction of a Dimensional Damage Model of Reinforced Concrete Columns under Explosion Loading. Appl. Sci. 2024, 14, 3659. [Google Scholar] [CrossRef]
- Zhu, Y.; Iv, N.; Hu, S.; Almustafa, M.; Nehdi, M.L. Interpretable natural gradient boosting model for probabilistic response evaluation of RC columns under blast loads. Structures 2025, 80, 109765. [Google Scholar] [CrossRef]
- Peng, J.-Z.; Pan, L.-J.; Wang, Z.-Q.; Gao, G.-F.; Wang, M.; Hu, J.; He, Y.; Wu, W.-T. Self-adaptive graph neural network for predicting blast-induced damage in RC columns across multiple scenarios. Eng. Struct. 2025, 337, 120505. [Google Scholar] [CrossRef]
- Liu, S.; Shi, Y.; Zhang, X.; Cui, J. Experimental investigation on the post-blast behaviors and damage indicators of RC columns. Eng. Struct. 2025, 342, 120902. [Google Scholar] [CrossRef]
- MacGregor, J.G.G. Reinforced Concrete: Mechanics and Design; Professional Technical Reference; Prentice-Hall: Englewood Cliffs, NJ, USA, 1996. [Google Scholar]
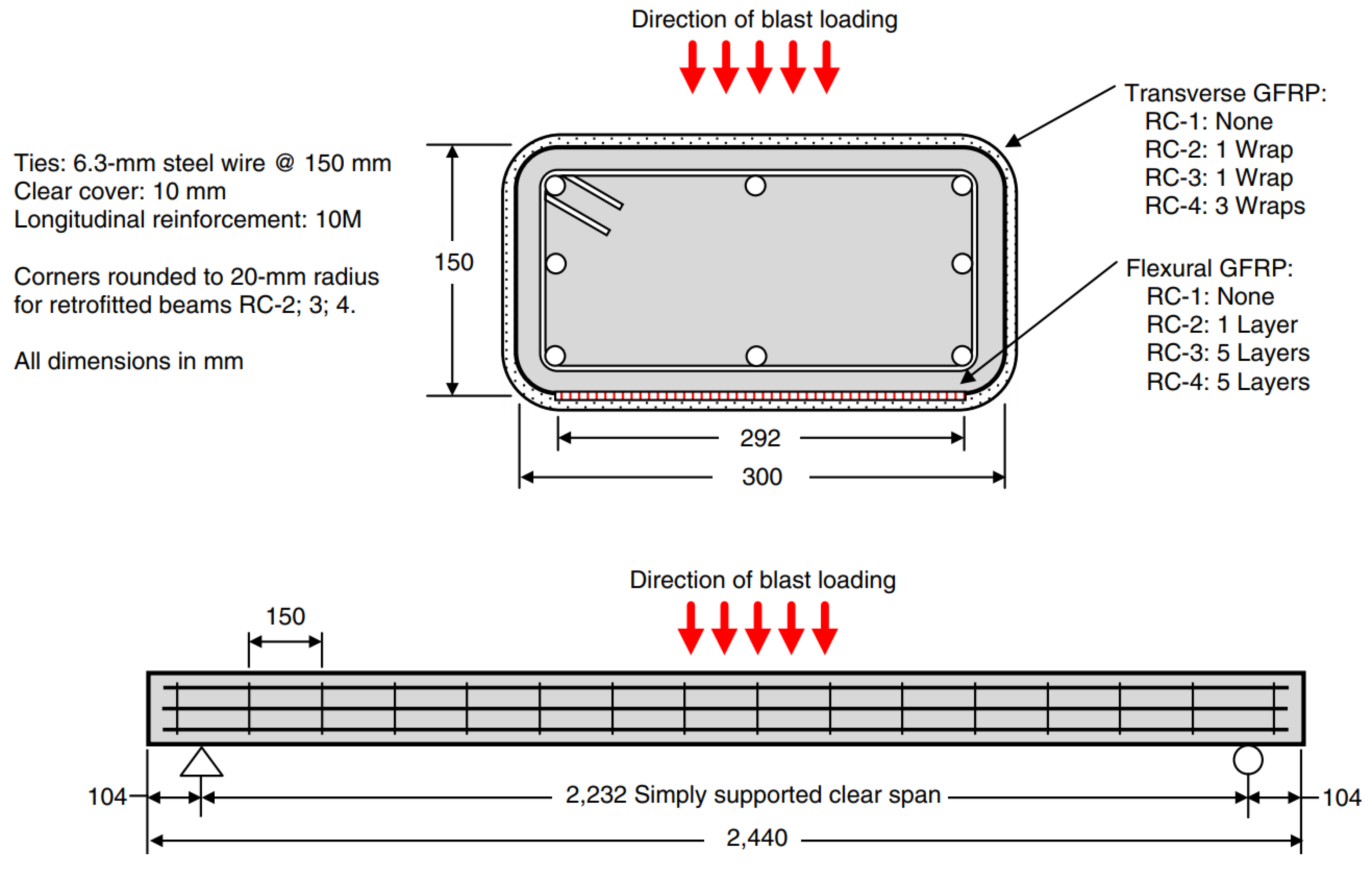
- Jacques, E.; Lloyd, A.; Imbeau, P.; Palermo, D.; Quek, J. GFRP-Retrofitted Reinforced Concrete Columns Subjected to Simulated Blast Loading. J. Struct. Eng. 2015, 141, 04015028. [Google Scholar] [CrossRef]
- To, Q.B.; Shin, J.; Lee, D.H.; Woo, S.; Lee, K. Parametric optimization and cost-efficient prediction of blast retrofit for AFRP-retrofitted RC columns using ML-driven finite element modeling. Compos. Struct. 2025, 371, 119498. [Google Scholar] [CrossRef]
- Roller, C.; Mayrhofer, C.; Riedel, W.; Thoma, K. Residual load capacity of exposed and hardened concrete columns under explosion loads. Eng. Struct. 2013, 55, 66–72. [Google Scholar] [CrossRef]
- Guo, Z.; Chen, W.; Yanyan, Z.; Huihui, Z. Post fire blast-resistances of RPC-FST columns using improved Grigorian model. Int. J. Impact Eng. 2017, 107, 80–95. [Google Scholar] [CrossRef]
- ISO 834-1:1999; Fire-Resistance Tests—Elements of Building Construction—Part 1: General Requirements. International Organization for Standardization: Geneva, Switzerland, 1999.
- Zhang, F.; Wu, C.; Zhao, L.X.; Li, X.Z. Numerical modelling of concrete-filled double-skin steel square tubular columns under blast loading. J. Perform. Constr. Facil. 2015, 29, 157–178. [Google Scholar] [CrossRef]
- Zhang, F.; Wu, C.; Zhao, X.-L.; Heidarpour, A.; Li, Z. Experimental and numerical study of blast resistance of square CFDST columns with steel-fibre reinforced concrete. Eng. Struct. 2016, 149, 50–63. [Google Scholar] [CrossRef]
- Wang, W.; Wu, C.; Li, J. Numerical Simulation of Hybrid FRP-Concrete-Steel Double-Skin Tubular Columns under Close-Range Blast Loading. J. Compos. Constr. 2018, 22, 04018036. [Google Scholar] [CrossRef]
- Li, M.; Zong, Z.; Hao, H.; Zhang, X.; Lin, J.; Xie, G. Experimental and numerical study on the behaviour of CFDST columns subjected to close-in blast loading. Eng. Struct. 2019, 184, 203–220. [Google Scholar] [CrossRef]
- Ben Rhouma, M.; Maazoun, A.; Aminou, A.; Belkassem, B.; Tysmans, T.; Lecompte, D. Damage Assessment of Laboratory-Scale Reinforced Concrete Columns Under Localized Blast Loading. Buildings 2025, 15, 1003. [Google Scholar] [CrossRef]
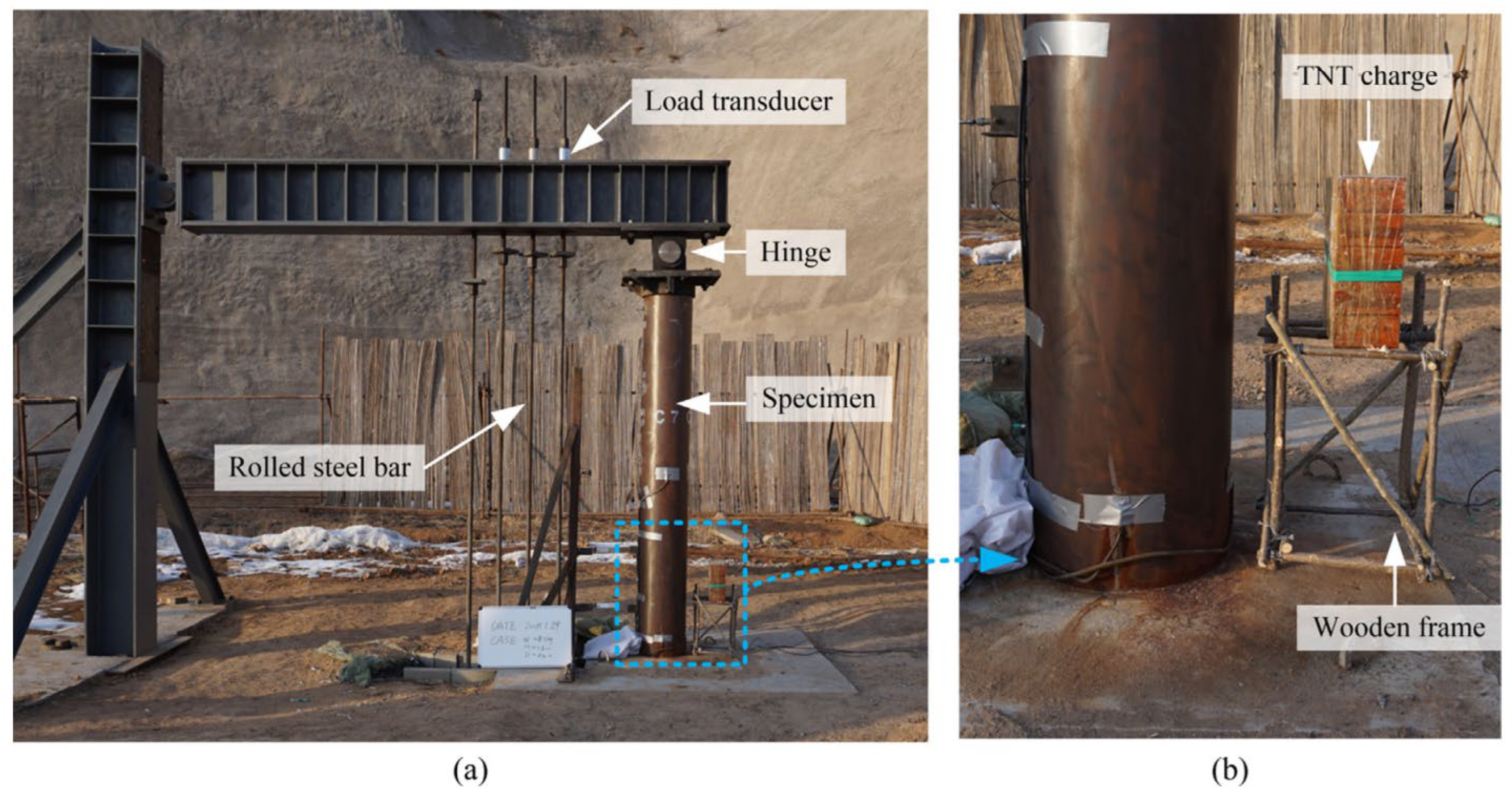
- Alomari, Q.A.; Linzell, D.G. Performance Assessment of Fire-Damaged and CFRP-Repaired Bridge Columns Under Single Unit Truck Impact and Blast. Fire 2025, 8, 227. [Google Scholar] [CrossRef]
- Li, H.; Li, M.; Li, L.; Cui, F.; Chen, Q. Effect of non-uniform chloride-induced corrosion on the time-varying blast fragility of aging RC columns. Structures 2025, 78, 109351. [Google Scholar] [CrossRef]












| Blast Overpressure (kPa) | Approximate Stand-Off Distance Range (m) | Typical Damage/Injury Description | Representative Structural or Human Response | Indicative Explosion Intensity |
|---|---|---|---|---|
| <2 kPa | >45 m | Minor window cracking or displacement of lightweight panels | Light glazing damage; negligible structural effect | Very Low: Peripheral blast or distant explosion |
| 2–5 kPa | 30–45 m | Cracked or shattered windows, minor facade damage | Brittle materials (glass, tiles) fracture; finishes may detach | Low Intensity: Far-field explosion |
| 5–10 kPa | 17–30 m | Wall cracks and slight failure of weak masonry | Unreinforced masonry experiences spalling or cracking | Moderate Intensity: External blast near small structures |
| 10–30 kPa | 6–17 m | Severe cracking and partial collapse of light buildings | Non-engineered or lightly reinforced buildings lose stability | Medium Intensity: Close-range explosion in open area |
| 30–70 kPa | 3–6 m | Partial structural failure of framed buildings | RC or steel frames undergo local yielding; interior walls collapse | High Intensity: Near-field explosion impacting small buildings |
| 70–250 kPa | 1–3 m | Complete failure of ordinary buildings; serious to fatal injuries from debris and overpressure | Load-bearing elements fail; eardrum rupture and lung injury possible | Severe Intensity: Close proximity explosion |
| 250–1400 kPa | <1.5 m | Catastrophic structural failure; near-instant human lethality | RC members fracture; severe internal trauma and lung rupture | Extreme Intensity: Immediate blast zone |
| >1400 kPa | <1 m (within fireball radius) | Total destruction; complete loss of structural integrity | No survivability; elements pulverized and disintegrated | Very Extreme: Detonation zone |
| S. No. | Design Standard/Manual | Key Points and Observations |
|---|---|---|
| 1 | TM-5-855-1 [8] | Offers procedures for designing and analyzing protective structures against conventional weapons. Useful for planning hardened facilities. |
| 2 | TM-5-1300 [9] | Focuses on methods to design structures to withstand blast waves and flying debris, considering blast parameters and structural response. |
| 3 | UFC 3-340-02 [10] | Predicts close-range and far-field blast loads using shock and gas dynamics. Incorporates dynamic increase factors (DIFs) and provides design approaches based on both flexural and shear failure. |
| 4 | UFC 4-010-01 [25] | Suggests practical measures to ensure defense buildings can withstand terrorist attacks. Emphasizes enforceable and implementable strategies. |
| 5 | FEMA 427 [26] | Offers a broad qualitative approach to reduce damage from terrorist explosions, including threats from chemical, biological, and radiological sources. |
| 6 | FEMA 428 [29] | Predicts expected overpressure on structures from vehicle-borne explosives, considering both horizontal and vertical distances. |
| 7 | ASCE [30] | Provides guidance for blast-resistant design specifically for petrochemical facilities. |
| 8 | ASCE/SEI 59-11 [19] | Uses SDOF analysis for far-field blast loads. Includes DIFs and focuses on flexural failure-based design. |
| 9 | ASCE [27] | Explains concepts and analysis techniques for progressive collapse of redundant or integrated structural systems under explosive events. |
| 10 | NCHRP 12-72 [31] | Offers methods and retrofit guidelines to protect critical bridges from terrorist attacks, highlighting effective structural design approaches. |
| Failure Type | Damage Characteristics | Damage Illustration |
|---|---|---|
| Minor Flexure | No permanent displacement observed, with only a few flexural cracks. Corresponds to a ductility ratio up to 3. |  |
| Moderate Flexure | Noticeable flexural cracks developing, showing increased deformation. Ductility ratio ranges between 3 and 10. |  |
| Severe Flexure | Extensive cracking and near collapse conditions. Ductility ratio rises from 10 to the verge of failure. |  |
| RC Member | Damage Classifications Based on Scaled Distance | ||
|---|---|---|---|
| Severe Spalling (Contact and Very Near Blasts) | Mix of Local and Overall Failure (Near Blasts) | Widespread Flexural Damage (Far-Field Blasts) | |
| Column |  |  |  |
| Case (A) | Case (B) | Case (C) | |
 |  | --- | |
| Case (D) | Case (E) | ||
| Beam |  |  |  |
| Case (F) | Case (G) | Case (H) | |
| Slab |  |  |  |
| Case (I) | Case (J) | Case (K) | |
| No. | Researchers | Year | Investigation | Column Type & Support | Span (mm) | Geometry & Size (mm) | λ | Concrete Cover (mm) | f′c 28-day (MPa) | Explosive | Blast Type | Strengthening Technique |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Shi et al. [15] | 2007 | Numerical | Axially loaded, Bottom fixed, Top hinged | Not specified | Not specified | Not specified | Not specified | Not specified | Not specified | Reflected pressure time history (positive phase only) | - |
| 2 | Shi et al. [16] | 2008 | Analytical | Axially loaded, Bottom fixed, Top hinged | Not specified | Rectangular, size not specified | - | Not specified | Not specified | Not specified | Close-in blast | - |
| 3 | Roller et al. [107] | 2013 | Experimental | Free-standing, Isolated footing | Not specified | Circular, Ø150 | - | Not specified | 40; 110 | PETN (spherical) | Contact & close-in | Thin layer of SIFCON, DUCON, UHPC |
| 4 | Astarlioglu et al. [74] | 2013 | Numerical | RC column, Simply Supported & Fixed | 3660 | Square, 406 × 406 | Not specified | Not specified | 27.6 | Not specified (blast loads idealized as triangular pulses, CONWEP for beams) | Close-in | – |
| 5 | Fujikake & Aemlaor [73] | 2013 | Experimental | Free-standing, Isolated footing | 1200 | Square, 180 × 180 | 6.67 | 30 | 51.60; 90.30 | Composite 4 | Contact | - |
| 6 | Jayasooriya et al. [56] | 2014 | Numerical | Axially loaded, Bottom fixed, Top restrained in axial direction | 4700 | Square, 1000 × 1000 | 4.70 | Not specified | 48 | TNT | Close-in | Seismic reinforcement over confining regions; steel core in RC column |
| 7 | Astarlioglu & Krauthammer [75] | 2014 | Numerical | Simply & fixed supports | 3660 | Square, 406 × 406 | 8.87 | Not specified | 27.60; 164.10 | Not specified | Idealized blast | UHPFRC |
| 8 | Aoude et al. [36] | 2015 | Experimental | Axially loaded, Partially fixed supports | 2468 | Square, 152 × 152 | 16.23 | 16 | 130 | Shock tube | Simulated blast | CRC; steel fibers |
| 9 | Zhang et al. [110] | 2015 | Numerical | Axially loaded, Pinned & fixed supports | 2500 | Hollow circular & square, Do = 210, Di = 100 | 11.90 | - | 29 | TNT | Close-in | - |
| 10 | Cui et al. [3] | 2015 | Numerical | Axially loaded, Bottom fixed, Top hinged | 3600 | Square, 400 × 400 | 9 | Not specified | 40 | TNT | Close-in | - |
| No. | Researchers | Year | Investigation | Column Type & Support | Span (mm) | Geometry & Size (mm) | λ | Concrete Cover (mm) | f′c 28-day (MPa) | Explosive | Blast Type | Strengthening Technique |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | Jacques et al. [105] | 2015 | Experimental | Not specified | 2440 | Rectangular, 300 × 150 | 16.27 | Not specified | 38.50; 32.80; 30.80; 30.40 | Shock tube | Simulated blast | GFRP wrapping |
| 12 | Burrell et al. [82] | 2015 | Experimental | Axially loaded, Partially fixed supports | 2468 | Square, 152 × 152 | 16.23 | Not specified | 54.70 | Shock tube | Simulated blast | SFRC; seismic reinforcement |
| 13 | Xu et al. [76] | 2016 | Experimental | Axially loaded, Steel test bench with pneumatic jack | 2500 | Square, 200 × 200 | 12.50 | 35 | 148 | Double-end-initiation cylindrical rock emulsion | Close-in explosion | UHPFRC; HSRC; Seismic reinforcement over confining regions |
| 14 | Zhang et al. [111] | 2016 | Experimental | Axially loaded, Steel reaction structure | 2500 | Hollow square, Ls = 210, Li = 110 | 11.90 | - | 170 | TNT | Close-in explosion | - |
| 15 | Zhang et al. [77] | 2016 | Experimental | Axially loaded, Steel test bench with hydraulic jack | 2500 | Hollow circular & square, Do = 210, Di = 110 | 11.90 | - | 170 | Rock emulsion | Close-in explosion | UHPC concrete core |
| 16 | Guo et al. [108] | 2017 | Experimental | Axially loaded, Steel test bench with pneumatic jack | 2500 | Circular, Ø194 | 12.88 | - | 116.20 | TNT | Close-in explosion | RPC |
| 17 | Li et al. [83] | 2017 | Numerical | Fully restrained at both ends | 2900 | Segmental square, 400 × 400 | 7.25 | Not specified | 40 | TNT | Close-in blast | ED bars |
| 18 | Li et al. [84] | 2017 | Experimental | Axially loaded, Steel test bench with hydraulic jack | 2500 | Square, 200 × 200 | 12.50 | 35 | 130; 148 | Double-end-initiation cylindrical rock emulsion | Close-in explosion | Twisted steel fiber (2.50%); Micro steel fiber (2.50%) |
| 19 | Kyei & Braimah [2] | 2017 | Experimental | Axially loaded, Concrete structure | 3000 | Square, 300 × 300 | 10 | 40 | 30 | ANFO | Close-in explosion | Seismic/confining reinforcement over top, bottom, mid-height regions |
| 20 | Hu et al. [85] | 2018 | Experimental | Axially loaded, Steel test bench with pneumatic jack | Not specified | Not specified | - | Not specified | Not specified | Spherical & cylindrical double-end-initiation rock emulsion | Close-in explosion | - |
| No. | Researchers | Year | Investigation | Column Type & Support | Span (mm) | Geometry & Size (mm) | λ | Concrete Cover (mm) | f′c 28-day (MPa) | Explosive | Blast Type | Strengthening Technique |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 21 | Wang et al. [112] | 2018 | Numerical | Axially loaded, Bottom fixed, Top hinged | 2500 | Hollow circular, Do = 210, Di = 100 | 11.90 | - | 40 | TNT | Close-in blast | FRP & steel tubes |
| 22 | Chen et al. [78] | 2019 | Experimental | Axially loaded, Steel test bench with pneumatic jack | 2500 | Square, 200 × 200 | 12.50 | Not specified | 50.16 | Double-end-initiation cylindrical rock emulsion | Close-in detonation | - |
| 23 | Li et al. [113] | 2019 | Experimental | Axially loaded, Steel reaction structure | 2500 | Hollow circular, Do = 325, Di = 159 | 7.69 | - | 41.90 | TNT | Close-in explosion | - |
| 24 | Rajkumar et al. [23] | 2020 | Numerical | Axially loaded, Bottom fixed, Top hinged | 900 | Square, 85 × 85 | 10.58 | Not specified | 42 | Composite 4 | Close-in blast | Seismic reinforcement |
| 25 | Alsendi & Eamon [90] | 2020 | Numerical | Axially loaded, Bottom fixed, Top hinged | 5000 | Square, 900 × 900 | 5.56 | 50 | 28; 42; 55 | Not specified | Close-in blast | SFRP composite wrapping |
| 26 | Dua et al. [69] | 2020 | Experimental | Free-standing, Isolated footing | 3300 | Square & rectangular: 300 × 300; 300 × 500; 300 × 700; 300 × 900 | 11 | Not specified | 25 | TNT | Contact explosion | - |
| 27 | Do et al. [4] | 2020 | Numerical | Axially loaded, Bottom fixed, Top hinged | 1500 | Segmental circular, Ø150 | 10 | Not specified | Not specified | Hemispherical TNT | Close-in explosion | ED bar |
| 28 | Pathak et al. [91] | 2020 | Numerical | Axially loaded, Bottom fixed, Top hinged | Not specified | Square, 914.40 × 914.40; 1219.20 × 1219.20 | - | Not specified | 68.94 | Not specified | Close-in blast | FRP jackets |
| 29 | Yan et al. [94] | 2020 | Experimental | -, Concrete base | 1700 | Square, 150 × 150 | 11.33 | 20 | 31 | TNT | Close-in explosion | Woven carbon-FRP sheets |
| 30 | Hu et al. [95] | 2021 | Experimental | Axially loaded, Steel test bench with pneumatic jack | 2500 | Square, 200 × 200 | 12.50 | Not specified | 50.16 | Double-end-initiation cylindrical rock emulsion | Close-in detonation | Carbon-FRP strips (0.167 mm) |
| No. | Researchers | Year | Investigation | Column Type & Support | Span (mm) | Geometry & Size (mm) | λ | Concrete Cover (mm) | f′c 28-day (MPa) | Explosive | Blast Type | Strengthening Technique |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 31 | Ju & Kwak [96] | 2022 | Numerical | RC beams & columns, simply supported | 2000, 1100, 3000 | 2000 × 1000 × 100; 2000 × 400 × 100; 1100 × 100 × 100; Square, 3000 × 1000 × 1000 | <20 | – | 32–40 | 0.36–8.30 kg TNT | Close-in | End reinforcement (parametric) |
| 32 | Yan et al. [86] | 2022 | Experimental | RC column, fixed base (lab setup) | 1200 | Square, 200 × 200 | – | – | 58.5 | 9 g 2# emulsion explosive (0.7 TNT eq.) | Contact (borehole) | – |
| 33 | Zhou et al. [97] | 2022 | Numerical + Deep Learning | RC column, fixed base & head (Case II); horizontal foundation (Case I) | 3660 (Case I), 900 (Case II) | Square: 400 × 400, 85 × 85 | Not specified | – | 40 (Case I), 42 (Case II) | TNT 25 kg (Case I), C4 7.1 kg ≈ 8 kg TNT (Case II), simulations 0.115–12,000 kg | Close-in | – |
| 34 | Wu et al. [88] | 2023 | Experimental + Numerical | RC column, both ends fixed with 100 mm fixtures | 1700 | Square, 150 × 150 | Not specified | 20 | 31.3 | TNT, 0.4 kg | Close-in (0.5 m) | – |
| 35 | Yang et al. [98] | 2024 | Numerical + Data-driven | not specified | – | Square, 450 × 450 | – | – | 30–60 (avg. 45) | – | Close-in blast | – |
| 36 | Wang et al. [100] | 2024 | Numerical | RC column, fixed at base (rigid support) | 3900 | Square, 400 × 400 | Not specified | 20 | 35 | TNT, 1–5 kg | Close-in | – |
| 37 | Zhu et al. [101] | 2025 | Numerical (ML, trained on experimental data) | RC column, fixed boundary | Not specified | Mix of square/circular, 2–3 m height | – | – | 25.8–166.0 | Shock tube & live blast | Close-in | – |
| 38 | Peng et al. [102] | 2025 | Numerical + ML | RC column (fixed support assumed) | Not specified | Not specified (3D RC column model) | Not specified | Not specified | 20.13 MPa | TNT | Close-in & Contact | None |
| 39 | Liu et al. [103] | 2025 | Experimental | RC column, fixed base with axial translation allowed at top | 2400 mm (clear height) | Square, 200 × 200 mm | Not specified | 15 mm | 29.4 MPa (cube strength) | Simulated blast (drop-weight equivalent TNT 3.94–19.52 kg) | Far-field (simulated) | None (baseline RC) |
| 40 | Li et al. [116] | 2025 | Numerical | RC Column, Both Ends Fixed | 5000 | Square, 600 × 600 | Not specified | 40 | 42 | TNT, 1000 kg | Close-in (air-blast) | – |
| No. | Researchers | Year | Investigation | Column Type & Support | Span (mm) | Geometry & Size (mm) | λ | Concrete Cover (mm) | f′c 28-day (MPa) | Explosive | Blast Type | Strengthening Technique |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 41 | To et al. [106] | 2025 | Numerical | Exterior RC column, fixed support | – | Rectangular 300 × 500 | – | – | 26.5–34.75 | 7.1 kg C4 | Close-in (1.07 m standoff) | AFRP jacketing |
| 42 | Kim et al. [79] | 2025 | Numerical | RC column, fixed base with footing & header | – | Square, 400 × 400 | – | – | 42 (validated model) | 680 kg TNT | Close-in to Far-field | – |
| 43 | Rhouma et al. [114] | 2025 | Experimental + Numerical | Circular RC, simply supported | 1800 | Circular, Ø100 | Not specified | 10 | 22.4 ± 1.6 | 30 g C4 + 1 g TNT detonator | Close-in | – |
| 44 | Shen et al. [80] | 2025 | Experimental + Numerical | RC column, fixed ends | 1500 | Square 200 × 200 | ~7.5 | 10 | 40.53 | Emulsion (1–6 kg TNT eq.) | Close-in airburst | – |
| 45 | Alomari & Linzell [115] | 2025 | Numerical | RC circular bridge column, fixed at base | – | Circular, D = 750, 1050, 1350 | Not specified | – | 28 | Modeled air blast (charge details not specified) | Close-in | CFRP full, partial, intermittent wraps (0.5–2.0 mm) + Hybrid NSM bars |
| 46 | Zhang & Niu [87] | 2025 | Experimental | RC, RCAC, RFRCAC; Fixed support | 1800 | Square 200 × 200 | – | 25 | 47.85 (RC), 46.05 (RCAC), 55.18 (RFRCAC) | 2 kg TNT | Close-in (0.4–1.0 m) | Hybrid fibers (0.05% basalt + 0.05% polypropylene) |
| No. | Researchers | Year | Exp./Num Verified | Correlation | Software Used | Damage Model | Type of Response | Research Gap/Future Recommendations |
|---|---|---|---|---|---|---|---|---|
| 1 | Shi et al. [15] | 2007 | Yes | Good | ANSYS AUTODYN | - | Time lag; reflected blast pressure; impulse | - |
| 2 | Shi et al. [16] | 2008 | Yes | Good | SDOF method | - | P-I diagrams; damage index; damage degree | - |
| 3 | Roller et al. [107] | 2013 | No | - | - | - | Maximum residual load-carrying capacity, damage, cracking | 1. Yield of explosive not mentioned. 2. Maximum charge affecting the core column needs further tests. 3. Residual axial capacity not compared with virgin capacity. |
| 4 | Astarlioglu et al. [74] | 2013 | Yes | Reasonable | DSAS, ABAQUS, CONWEP | Modified Drucker–Prager Cap (in ABAQUS), resistance function (DSAS) | Flexure, tension membrane, direct shear | Need experimental validation of full-scale RC columns; study axial load influence further for blast design. |
| 5 | Fujikake & Aemlaor [73] | 2013 | No | - | - | - | Residual compressive & flexural resistance; damage modes | 1. Key parameters like maximum displacement, stresses, and damage indices not studied. 2. Residual axial/flexural resistance not compared with virgin capacity. |
| 6 | Jayasooriya et al. [56] | 2014 | Yes | Good | LS-DYNA | Mat_Concrete_Damage_Rel3 | Displacement; damage; residual load | Variation in stresses in column materials not reported. |
| 7 | Astarlioglu & Krauthammer [75] | 2014 | No | - | - | - | Mid-span displacement | 1. Column behavior under blast not well understood; experimental study recommended. 2. Comparative study of blast damage recommended. |
| 8 | Aoude et al. [36] | 2015 | Yes | Close | SDOF method | - | Maximum displacement; residual displacement; damage | Possible causes of rupture of longitudinal steel with fiber content >4% not discussed. |
| 9 | Zhang et al. [110] | 2015 | Yes | Good | LS-DYNA | Karagozian & Case Concrete (KCC, Mat_Concrete_Damage_Rel3) | Maximum mid-span deflection | Blast response under contact explosions with similar parametric studies could be investigated. |
| 10 | Cui et al. [3] | 2015 | Yes | Good | LS-DYNA | Mat_Concrete_Damage_Rel3 | Spall damage; damage index | Study could be extended for explosive charges >6.0 kg TNT. |
| No. | Researchers | Year | Exp./Num Verified | Correlation | Software Used | Damage Model | Type of Response | Research Gap/Future Recommendations |
|---|---|---|---|---|---|---|---|---|
| 11 | Jacques et al. [105] | 2015 | Yes | Close | SDOF method | - | Maximum displacement; residual displacement; damage | 1. Reason for choosing GFRP not mentioned. 2. Higher strength FRP should also be considered. |
| 12 | Burrell et al. [82] | 2015 | Yes | Close | SDOF method | - | Damage; maximum and residual displacements | Transverse reinforcement had higher yield than longitudinal steel, but conclusions were not clearly drawn. |
| 13 | Xu et al. [76] | 2016 | No | - | - | - | Maximum and residual displacements; damage; failure modes | Confining reinforcement over mid-height should be considered to study its influence on displacement and damage. |
| 14 | Zhang et al. [111] | 2016 | Yes | Good | LS-DYNA | Mat_Concrete_Damage_Rel3 | Damage; mid-span deflection | Stress distribution in core concrete and steel tubes not discussed. |
| 15 | Zhang et al. [77] | 2016 | Yes | Reasonable | LS-DYNA | Mat_Concrete_Damage_Rel3 | Peak overpressure; impulse; damage; displacement | Only obvious conclusions were presented by the authors. |
| 16 | Guo et al. [108] | 2017 | Yes | Close | LS-DYNA | Modified Girgorian & Mat_Concrete_Damage_Rel3 | Maximum mid-span displacement; failure modes; plastic deformation; damage; temperature | No reference column without fire loading was considered under blast. |
| 17 | Li et al. [83] | 2017 | Yes | Close | LS-DYNA | Mat_Concrete_Damage_Rel3 | Spall damage; displacement | 1. Stress distribution in column materials not discussed. 2. Cost comparison of segmental columns not provided. |
| 18 | Li et al. [84] | 2017 | No | - | - | - | Residual strength; damage; blast overpressure | Blast performance under different explosive charges studied, but same standoff distance; further parametric study needed. |
| 19 | Kyei & Braimah [2] | 2017 | Yes | Good | LS-DYNA | Karagozian & Case Concrete (KCC, Mat_Concrete_Damage_Rel3) | Maximum transverse displacement; damage profile; support rotation | 1. Effect of additional transverse reinforcement (diameter variation) over different regions should be investigated. 2. Stress distribution in reinforcements not presented. |
| 20 | Hu et al. [85] | 2018 | Yes | Reasonable | ANSYS AUTODYN | - | Blast reflected peak overpressure; impulse | Weather effects (temperature, humidity, wind) should be accounted for in experiments and numerical studies. |
| No. | Researchers | Year | Exp./Num Verified | Correlation | Software Used | Damage Model | Type of Response | Research Gap/Future Recommendations |
|---|---|---|---|---|---|---|---|---|
| 21 | Wang et al. [112] | 2018 | Yes | Reasonable | LS-DYNA | - | Mid-span deflection; hoop strain distribution; residual deflection | Stresses in column materials not discussed. |
| 22 | Chen et al. [78] | 2019 | Yes | Good | LS-DYNA | Mat_Concrete_Damage_Rel3 | Peak & residual deflection; plastic damage | Weather conditions (temperature, humidity, wind) may influence blast response; should be reported and incorporated in numerical studies. |
| 23 | Li et al. [113] | 2019 | Yes | Good | LS-DYNA | Karagozian & Case Concrete (KCC, Mat_Concrete_Damage_Rel3) | Denting deformation; damage; failure modes; plastic strain; damage dissipation energy | 1. Local axial deformation at top/bottom and lateral displacement due to buckling not considered. 2. No comparison with conventional circular RC column of equivalent capacity. 3. Parametric studies on concrete strength & steel tube thickness needed. |
| 24 | Rajkumar et al. [23] | 2020 | Yes | Close | LS-DYNA | Mat_Concrete_Damage_Rel3 | Peak deflection | Effect of additional mid-span confining reinforcement on blast performance should be investigated. |
| 25 | Alsendi & Eamon [90] | 2020 | Yes | Favorable | LS-DYNA | Mat_Concrete_Damage_Rel3; Johnson-Holmquist-Cook | Vertical displacement; plastic strain; blast load resistance | 1. Selection rationale for SFRP composite wrapping not explained. 2. Effect of increased concrete strength with SFRP application should be studied. |
| 26 | Dua et al. [69] | 2020 | Yes | Close | LS-DYNA | Mat_Concrete_Damage_Rel3 | Damage/crack patterns; reflected pressure; displacement; damage index | 1. Damage index may not reflect true damage (columns tested without axial load). 2. Comparison of square & rectangular columns under different axial capacities not relevant. 3. Stress variation in reinforcements not presented. |
| 27 | Do et al. [4] | 2020 | Yes | Reasonable | LS-DYNA | Mat_Concrete_Damage_Rel3 | Stress distribution; damage; failure mode | Selection of longitudinal & transverse reinforcements for PCSC column not justified; steel bar weight much higher than steel tube segment. |
| 28 | Pathak et al. [91] | 2020 | No | - | LS-DYNA | Mat_Concrete_Damage_Rel3 | Maximum shear stress; effective plastic strain | 1. Unusually low diameter of longitudinal bars not justified. 2. Maximum displacement and damage not reported. |
| 29 | Yan et al. [94] | 2020 | Yes | Close | SDOF approach | - | Stress histories; displacement; damage | Axial load not considered in the study. |
| 30 | Hu et al. [95] | 2021 | Yes | Close | LS-DYNA | Mat_Concrete_Damage_Rel3 | Displacement; plastic strain; residual bearing capacity | 1. CFRP strip wrapping scheme not mentioned. 2. Effect of CFRP on contact detonation performance should be studied. 3. Reasons for better performance of column A-type not discussed. |
| No. | Researchers | Year | Exp./Num Verified | Correlation | Software Used | Damage Model | Type of Response | Research Gap/Future Recommendations |
|---|---|---|---|---|---|---|---|---|
| 31 | Ju & Kwak [96] | 2022 | Yes | Good | FE model, CONWEP loading | Tri-linear M–φ + shear stress–slip | Mid-span displacement, P–I diagram | Need to address computational efficiency, large-scale 3D modeling, and full-scale experimental validation |
| 32 | Yan et al. [86] | 2022 | Yes | Reasonable | – | Empirical via dimensional analysis | Damaged zone, bending deflection, fragment distribution | Section size, blast-hole parameters, and explosive mass not considered; recommended further tests & numerical models |
| 33 | Zhou et al. [97] | 2022 | Yes | Good | LS-DYNA, PyTorch, Keras | K&C Concrete Model, PLASTIC_KINEMATIC Steel | Damage index, failure mode (BF, SF, BSF) | Need for far-range blast data, inclusion of strengthened/retrofitted RC columns |
| 34 | Wu et al. [88] | 2023 | Yes | Good | ANSYS/LS-DYNA 2020R2 | *MAT_CONCRETE_DAMAGE_REL3 (MAT72), *MAT_PLASTIC_KINEMATIC | Mid-span displacement, failure mode | Study different geometries, axial loads, and strengthening methods |
| 35 | Yang et al. [98] | 2024 | Yes | Good | Python (Scikit-learn, CatBoost, XGBoost) | Residual axial capacity (D-index) | Global/local damage & collapse | Larger-scale experimental validation; inclusion of diverse reinforcement layouts; dataset expansion for generalization |
| 36 | Wang et al. [100] | 2024 | Yes | Reasonable | LS-DYNA 18.2 | Dimensional analysis + disturbance model | Mid-height displacement, disturbance | Extend to axial loads, larger-scale RC frames, strengthening strategies |
| 37 | Zhu et al. [101] | 2025 | Yes | Good | Python (NGBoost) | Probabilistic displacement model | Dataset expansion (geometry, axial load), inclusion of strengthening cases | Datasets should be extended to cover a wider range of geometries, higher levels of axial loading, and alternative strengthening methods to ensure broader use in real-world conditions. |
| 38 | Peng et al. [102] | 2025 | Yes (compared with literature benchmarks) | Close | Abaqus/CAE | CDP, JWL EOS | Nodal displacement, Damage Index | Extend model to extreme scenarios, include stress/energy dissipation for physics-informed predictions |
| 39 | Liu et al. [103] | 2025 | Yes | Close agreement between displacement, energy-based and residual capacity indicators | – (purely experimental) | Empirical damage indicator (displacement + energy absorption) | Bending-shear failure, residual capacity degradation, modal frequency reduction | Need for larger dataset, calibration of regression models, further validation under varied ALRs |
| 40 | Li et al. [116] | 2025 | Yes (validated with literature) | Good | LS-DYNA | MAT_72R3 (Concrete_Damage_Rel3), MAT_03 (Plastic_Kinematic) | Time-varying blast fragility, P-I curves, displacement, capacity loss | Future work should include experimental validation of P-I models and study combined corrosion mechanisms (sulfate, carbonation) for more realistic predictions. |
| No. | Researchers | Year | Exp./Num Verified | Correlation | Software Used | Damage Model | Type of Response | Research Gap/Future Recommendations |
|---|---|---|---|---|---|---|---|---|
| 41 | To et al. [106] | 2025 | Yes | Close | LS-DYNA | CDP for concrete, MAT55 for AFRP, Park–Ang model | Displacement, ductility ratio, damage demand | Extend to CFRP/GFRP/hybrids, include multi-hazard (blast + seismic), interpretability (SHAP) for ML |
| 42 | Kim et al. [79] | 2025 | Yes | Good | LS-DYNA | K&C Concrete (MAT_072), Bilinear Steel (MAT_003) | Ductility demand (μmax), Residual strength index (D) | Integration of displacement- and strength-based criteria; future work with energy-based demand and geometric/material variability |
| 43 | Rhouma et al. [114] | 2025 | Yes | Good | LS-DYNA | Karagozian & Case (K&C) | Deflection, crack propagation, rotation | Extend to full-scale RC columns, study strengthening methods, validate under varying reinforcement ratios and blast intensities |
| 44 | Shen et al. [80] | 2025 | Yes | Good | LS-DYNA | RHT (concrete), JWL (TNT) | Displacement, rotation, capacity loss | Internal explosions, progressive collapse analysis needed |
| 45 | Alomari & Linzell [115] | 2025 | Yes | Good | LS-DYNA | MAT-159 (CSC-Concrete), MAT-24 (Steel), MAT-54 (CFRP) | Displacement, cracking, residual capacity | Full-scale experimental validation, design code development, optimization for large diameters |
| 46 | Zhang & Niu [87] | 2025 | – | – | – (purely experimental) | – | Displacement, cracking, spalling | Lack of numerical verification; effect of larger charge weights and corrosion durability in marine conditions |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anas, S.M.; Al-Dala’ien, R.N.; Benzerara, M.; Al-Ezzi, M.J. Computational and Experimental Insights into Blast Response and Failure Mechanisms of Square, Rectangular and Circular Reinforced Concrete Columns: A State-of-the-Art Review. Buildings 2025, 15, 3928. https://doi.org/10.3390/buildings15213928
Anas SM, Al-Dala’ien RN, Benzerara M, Al-Ezzi MJ. Computational and Experimental Insights into Blast Response and Failure Mechanisms of Square, Rectangular and Circular Reinforced Concrete Columns: A State-of-the-Art Review. Buildings. 2025; 15(21):3928. https://doi.org/10.3390/buildings15213928
Chicago/Turabian StyleAnas, S. M., Rayeh Nasr Al-Dala’ien, Mohammed Benzerara, and Mohammed Jalal Al-Ezzi. 2025. "Computational and Experimental Insights into Blast Response and Failure Mechanisms of Square, Rectangular and Circular Reinforced Concrete Columns: A State-of-the-Art Review" Buildings 15, no. 21: 3928. https://doi.org/10.3390/buildings15213928
APA StyleAnas, S. M., Al-Dala’ien, R. N., Benzerara, M., & Al-Ezzi, M. J. (2025). Computational and Experimental Insights into Blast Response and Failure Mechanisms of Square, Rectangular and Circular Reinforced Concrete Columns: A State-of-the-Art Review. Buildings, 15(21), 3928. https://doi.org/10.3390/buildings15213928









