Seismic Performance of a Brazilian RC Frame Structure Designed Considering Different Scenarios Based on Eurocodes 2 and 8

Abstract

In low to medium-seismicity countries, seismic design is often not mandatory. Furthermore, zoning is frequently adopted to justify simplified calculations based on force methods without capacity criteria. However, risk analysis should merge vulnerability, threat, and exposure. So even regions with low seismicity can face potentially high consequences due to earthquakes. This is the case of Brazil, where seismic provisions were lacking until 2006 when the first standard was approved, being updated in 2023. Therefore, this study selected a typical RC frame configuration and focuses on assessing the differences in seismic performance between the provisions outlined in EN1992-1-1/EN1998-1 and ABNT NBR15421. The research highlights how different requirements affect low and medium-seismicity regions. Hence, the methodology and conclusions can serve as a guide for decision-making in other countries regarding impact and effectiveness. There are considered different scenarios of design, seismicity, and ductility class. The nonlinear static Pushover analysis was conducted and also validated with nonlinear dynamic Time-history analysis. The assessment of the results is based on the design assumptions, capacity curves, collapse mechanism, IDA curves, PSDM, damage limit states and cost-benefits. Non-seismic design structures had a premature brittle collapse. The global ductility condition was the main key to changing into a ductile mechanism, and seismic detailing was the variable that addresses the ductility level.

1. Introduction and Literature Review

The evaluation of the seismic structural behavior mainly focuses on how a structure responds to dynamic excitation and the resulting plastic mechanisms. Seismic actions are considered the most destructive among all natural threats due to their random and unpredictable nature [1]. Hence, it is essential to have well defined and effective earthquake-resistant design processes to ensure structural safety. According to [2,3,4,5], ductility has become more important than resistance for seismic design since the 1980s, because structural stiffness is a better predictor of structural damage than strength. Although traditional building design methods rely on force-based design methodologies generally producing safe structures, they do not guarantee uniform damage [6]. Moreover, it is not practical to design a structure to maintain the elastic regime during an earthquake. In reality, buildings are expected to deform under inelastic behavior. Therefore, the aim is to maintain deformation and energy dissipation mechanisms that prevent total collapse, ensuring the desired levels of functionality and safety are maintained [7].

Brazil is located in the central region of the South American tectonic plate, which is generally considered to be more geologically stable than border plate regions regarding earthquakes. However, medium or low-magnitude seismic are not uncommon in the country, even though high-magnitude earthquakes are rare [8]. Hence, there is still a possibility of seismic activity, and if earthquakes occur in regions with specific geological and geotechnical conditions, they can become catastrophic due to amplification. As a result, the seismic effect cannot be ruled out, and it is essential to consider the location and depth of the earthquake’s focus and the surrounding geological conditions. It means that intraplate earthquakes can also release significant stress, resulting in high-damage earthquakes [9,10]. Although strong intraplate earthquakes are rare, they are still possible in Brazil [11]. Yet, Refs. [12,13] report Brazilian seismic events that caused significant damage.

In recent decades, the consideration of seismicity has significantly affected the design, maintenance, and rehabilitation of structures on a global level [14,15]. This impact is based on the concept of seismic risk, which is described as the potential for damage or loss that a region may suffer after a seismic event [16,17]. Seismic risk is determined probabilistically as a function of threat, exposure, and vulnerability and concerns the capacity for loss of life, injuries, destruction, or damage to property that may occur in a system, society, or community within a specific period [18,19]. Thus, despite the considerations made above about the threat, this is not the only determining factor for seismic rules. In fact, taking into account exposure and vulnerability as metrics offers a more comprehensive analysis of the potential impact on society [20]. This means that even regions with a low frequency of high-intensity earthquakes and mostly low and medium-magnitude earthquakes, like Brazil, can still have a significant seismic risk due to exposure and vulnerability factors. So, this scenario can significantly enhance the consequences of these earthquakes, making them potentially devastating.

Considering the aforementioned relevance of seismic provisions, it is important to note that the Brazilian standard for the design of earthquake-resistant structures, ABNT NBR15421 [21] , was created in 2006 and recently updated in 2023. As part of the update, some modifications have been done in the seismic zones by adding regions with non-trivial seismic activity. This modification is based on recent national studies that have improved the understanding of the seismic threat scenario in Brazil. Besides, major international seismic standards have been intensifying their design measures and including performance tools, which has motivated the development of several national studies aimed at understanding Brazilian seismic risk [22,23,24,25,26,27,28,29,30,31,32].

Although many efforts have been made in the past twenty years to rehabilitate and maintain existing structures, the management of structures also involves designing new ones. Therefore, a definitive conclusion on the seismic safety and performance of Brazilian buildings remains elusive, indicating the need for further research, mainly concerning the improvement of the Brazilian seismic design normative process.

Most of the Brazilian buildings are reinforced concrete frame structures. The location where the plastic hinges are formed in these structures plays a crucial role in the structure’s behavior [33,34]. It helps to identify the primary and secondary elements in the energy dissipation. While designing RC frames, special attention is given to columns and beams, as they are the most vulnerable elements. According to [35], the poor performance of RC frames during earthquakes can be attributed to the formation of plastic hinges in the structure’s columns. This often leads to collapse due to the rupture of the columns before the beams yield. Therefore, it is essential for seismic design to define a collapse mechanism based not just on withstand but also on the structure’s capacity.

Brazilian design standards predominantly rely on force-based design (FBD) principles, which are focused on preventing local component failures. However, this approach does not adequately ensure the structures have the necessary dissipative capacity or verify the collapse mechanisms. As a result, the buildings have brittle failure and exhibit a lack of ductility. In terms of seismic loads, there is no differentiation between ductility classes, nor are there specific detailing requirements for structural elements or global ductility considerations to direct primary elements toward potential failure. Although recent risk assessments conducted within Brazil indicate a concerning scenario [22,23,24,25,26,27,28,29,30,31,32], this study represents the first critical evaluation of the Brazilian design approach in a seismic context while also elucidating the collapse mechanisms that may arise. Moreover, this research is pioneering as it systematically contrasts the Brazilian design method with an international approach through the application of nonlinear analyses.

This article aims to contribute to improving the low and medium-seismic countries codes, particularly, but not only, the Brazilian seismic design standard process. In order to do so, this research selected a typical RC frame configuration and focuses on investigating the application of seismic rules in RC frames based on the Eurocodes. It is evaluated the impact on ductility capacity and seismic performance for a low-rise reinforced concrete building as designed following the EN 1992-1-1 [36] and EN 1998-1 [37]. Regarding the focus of this paper, there are considered different scenarios of design, seismicity, and ductility class. Non-linear static Pushover analysis are carried out on finite element models of six-story reinforced concrete buildings to assess and compare their resultant performance. The nonlinear dynamic Time-history analysis is also performed but in order to validate the results. Thereby, the main differences between the Brazilian design process are confronted with Eurocode’s regulations. The former adopts FBD exclusively, and the latter involves capacity-based design (CBD). CBD concerns global and local ductility conditions in order to ensure a global ductile failure mechanism, distinguishing it from local brittle one.

The main outcomes of this study include a performance comparison of the design premises, identifying the point where the scenario is inserted in the performance scale and damage limit states, determining the ductility capacity of the structure as well as the established collapse mechanism. Even though the case study is conducted in Brazil, the methodology and conclusions of this research can be stretched out to other countries around the world, as the research highlights how different requirements affect low and medium-seismicity regions. Hence, the methodology and conclusions can serve as a guide for decision-making in other countries regarding impact and effectiveness for updates and development of seismic standardization.

2. Brazilian and European Seismic Design Standards

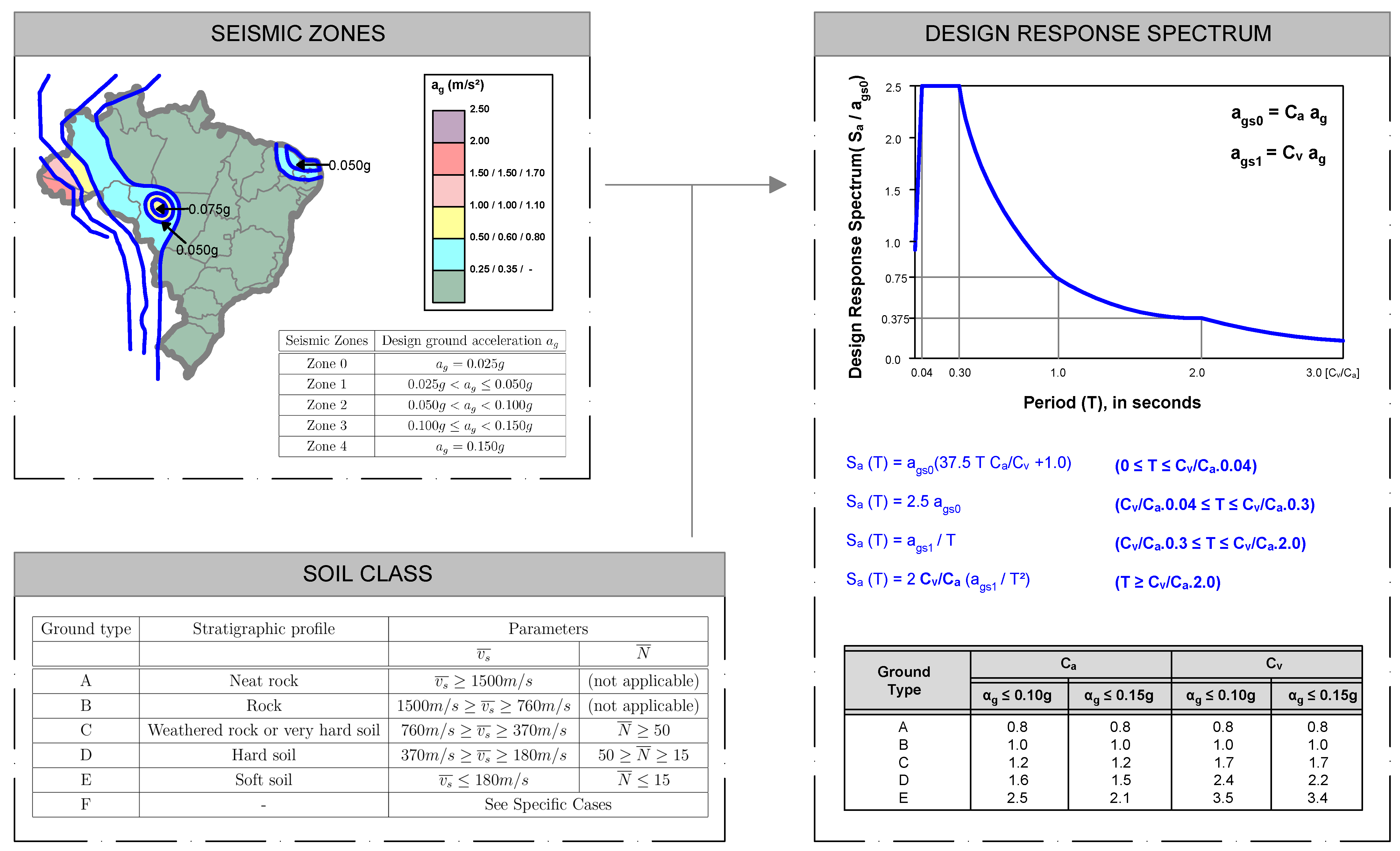
In Brazil, the seismic design of concrete structures is ruled by two standards: ABNT NBR6118—Design of concrete structures (2023) [38] and ABNT NBR15421—Design of seismic resistant structures (2023) [21]. Both codes only follow FBD. The latter code assumes an elastic response of the structure to seismic action with constant mechanical characteristics. In order to account for energy dissipation due to seismicity, the material’s elastoplastic behavior is adopted through the use of response modification and overstrength factors, in addition to displacement amplification coefficients. A design response spectrum is determined by combining seismic zones and soil class, as shown in Figure 1.

However, no regulations are applied to evaluate the capacity of structures and ensure their ductile behavior during seismic events. The seismic zones play a key role in determining the appropriate seismic design method. For areas classified as Zone 0, the design ground acceleration $a_g$ is $a_g=0.025$ g, and structures are exempt from anti-seismic requirements. For Zone 1 regions, where $0.025$ g $<a_g\le 0.050$ g, a simplified method that relies on horizontal forces in both directions must be applied. Thus, seismic design is mandatory only for Zone 2, 3, and 4, where $a_g>0.050$ g, and the design is determined by either the method of equivalent forces or spectral analysis.

Besides the current code lacks tools for evaluating the structure’s capacity, it also does not provide rules for defining ductile mechanisms and seismic detailing. On one hand, the 2006 version of ABNT NBR15241 introduced ductility classes to define the elastoplastic factors; on the other hand, due to the lack of specific details and correlation with seismic detailing, this was removed in the 2023 update. As a result, the present national design process is based on a low ductility class, and engineers have to rely on their judgment to refer to foreign standards for a higher ductility project.

The foreign seismic code selected for analysis and comparison of structural assumptions was Eurocode 8—Design of structures for seismic resistance (2004) [37], associated with the respective European concrete standard Eurocode 2—Design of concrete structures (2004) [36]. Whereas, in addition to ensuring structural resistance through a FBD, EN 1998-1:2004 conceptualizes the entire design process based on capacity design. EN 1998-1:2004 and ABNT NBR15421:2023 have similar approaches in terms of FBD, as the design response spectrum is defined in both cases based on seismic zones and soil class. Yet the ground type classification is very similar for both codes, it is necessary to add a comment for seismic zones. Since the Eurocodes apply to 28 countries, seismic zones are presented in the national annexes. Nevertheless, Figure 2 compares seismic zones for Brazil and Portugal, with the latter being covered by EN 1998-1:2004. Despite the similarities between the seismic accelerations of both countries that one can infer from Figure 2, the seismic rules adopted by the seismic design of these countries are significantly different. This contrast is noteworthy as EN 1998-1:2004 design methodology defines a series of capacity requirements to ensure a structure’s ductility behavior.

The EN 1998-1:2004 applies capacity-based rules in the design of structural systems, whereby the primary elements are selected, designed, and detailed to ensure energy dissipation when subjected to large deformations. The other structural elements are designed with sufficient strength to support the energy dissipation system aforementioned. This code outlines several restrictions and requirements for capacity design, including the presentation of performance requirements and conformity classifications for the development of the collapse mechanism. The collapse mechanism is predicted by determining plastic hinge zones in specific structural elements, which establishes a hierarchy of energy dissipation and capacity gain in the inelastic regime. As soon as the aim is to avoid rupture and failure due to brittle collapse.

Providing structural ductility insurance is the main goal of EN 1998-1:2004, which is achieved by adopting conditions of global ductility, local ductility, and specific seismic detailing. The global ductility condition is directly related to the structure’s collapse mechanism and involves implementing the Strong Column—Weak Beam design rule. According to EN 1998-1:2004, the value of 1.3 for the ratio between the bending moments of columns and beams from the same node must be used for 90% of all structure nodes, except for the roof floor. The local ductility condition defines, for the design process, bending as mandatory than shear, which is the most common design criterion for reinforced concrete structures. By adopting these conditions, EN 1998-1:2004 aims to ensure the safety and durability of structures during seismic activity.

Finally, one of the key factors in designing structures for capacity and ensuring ductility is the seismic detailing. Plastic hinge formation in areas with appropriate detailing establishes the collapse mechanism, enabling the structure to withstand seismic action effectively. The European standard EN 1998-1:2004 defines three ductility classes: Ductility Class Low (DCL), Ductility Class Medium (DCM), and Ductility Class High (DCH). For regions with very low seismicity ($a_g<0.040$ g and $a_{g}S<0.050$ g) or low seismicity ($a_g<0.080$ g and $a_{g}S<0.100$ g), DCL is applied as the ductility class, and the basic provisions of EN 1992-1-1:2004 are maintained. No seismic detailing is required for DCL. However, for other cases, engineers must adopt at least the DCM class. It is up to the engineer’s discretion to choose the DCH class, which is recommended for essential buildings like schools, hospitals, and structures vital for the society’s maintenance. The detailing provisions for DCM and DCH classes include limiting the eccentricities of the element’s sections, defining minimum sizes for structural elements, criteria regarding spacing, minimum diameter, rates, and the minimum number of reinforcement bars for both longitudinal and transverse reinforcement.

Furthermore, EN 1998-1:2004 applies the behavior factor q as an elastoplastic coefficient to adjust the efforts taking into account the non-linear response of the structure. Figure 3 shows a comparison between the design response spectrum for RC frames of the two versions of the national seismic code and action types 1 and 2 specified in EN 1998-1:2004. It should be noted that as Eurocodes are developed for more than 28 countries, certain parameters are defined by national annexes. In this work, all parameters referring to national annexes were considered to correspond to Portugal. This decision was taken based on the inherited construction scenario, the similarity in seismic zones as shown in Figure 2, and the studies [23,25].

To achieve a thorough comprehension and consistent implementation of EN 1998-1:2004 methodology, it is essential to utilize EN 1992-1-1:2004 in conjunction. This approach was adopted in the methodology of the current study. As an example, the consideration of the physical nonlinearity of reinforced concrete elements can be applied as a cracking coefficient to the stiffness of the structure. In Brazilian design, the reduction of inertia caused by physical nonlinearity is expressed as a percentage of the elastic stiffness of the structural elements. The percentage varies depending on the type of element. For slabs, it is 30%; for asymmetrical reinforcement beams, it is 40%; for symmetrical reinforcement beams, it is 50%; and for columns, it is 80%. This decrease in stiffness applies to the design of all reinforced concrete structures, regardless of whether they need to meet seismic requirements. In contrast, the Eurocodes specify a 50% reduction in inertia for all structural elements exclusively in EN 1998-1:2004, there are no reductions for applying EN 1992-1-1:2004 alone.

In this section, it was explored the general aspects of applying both Brazilian and European seismic codes. This provides support for the work methodology. The next section briefly explains the meaning of collapse mechanisms for structural assessment, mainly from a seismic point of view.

3. Collapse Mechanisms

The energy dissipation capacity and ductility of a structure are directly related to the number and location of the plastic hinges. These hinges are critical as they mark the areas where the material undergoes plastic deformation. Plastic hinge formations can lead to different failure modes, depending on their number and location. Therefore, the collapse mechanisms of a structure are governed by the relative strength of different elements [39,40]. Thus, the failure of different structural components impacts the overall structure safety and behavior in different ways. Besides, the definition of an optimized strength and vulnerability hierarchy can result in structural capacity and ductility increases. Regarding energy dissipation, the more floors mobilized, the greater the resistant capacity of the structure. As a result, an improvement scenario for design is settled as failure mechanisms are established in elements that do not compromise structure stability and also ensure the inelastic response performance [41].

Failure modes of structures can be categorized into three main mechanisms, namely local, soft-story, and global [39,42]. Local and soft-story failure mechanisms should be avoided for the design of structures, as they lead to lower energy dissipation and ductility. Global failure, on the other hand, is a permissible mechanism that guarantees increased energy dissipation and ductility when it involves the Strong Column-Weak Beam structural premise. This is due to a more uniform distribution of drift.

Concerning the hierarchy of commitment of different structural components for buildings, it is important to note that failure mechanisms are conditioned by the formation of plastic hinges primarily in columns or beams. In cases where these plastic zones are first formed at the beams, it is called the beam-sway mechanism. However, if they are formed at the columns primarily, it is called the story-sway mechanism. As columns are elements of lower ductility and essential for ensuring the overall stability of a building, the loss of resistant capacity in these components can cause the structure’s brittle collapse, which happens through the formation of a mechanism called soft-story [30].

Beam-sway mechanism structures have a higher energy dissipation capacity for lower ductility when compared to story-sway ones. This results in a more uniform drift distribution and better seismic performance, as stated by [39,43,44]. Moreover, the formation of plastic hinges in the beams affects only small sections of the structure, while the formation of inelastic zones in the columns leads to the progressive collapse of the entire building, characterizing a more severe consequence [42].

Therefore, the structure collapse mechanism must be settled in the design process, so that the formation of plastic hinges occurs in elements of interest, ensuring the use of the structure’s ductile capacity to gain performance. In the case of buildings, it involves designing the structural systems in a way that allows the beams to yield before the columns. This work evaluates design and detailing recommendations, with the resulting structure collapse mechanisms serving as indicators for seismic design.

4. Materials and Methods

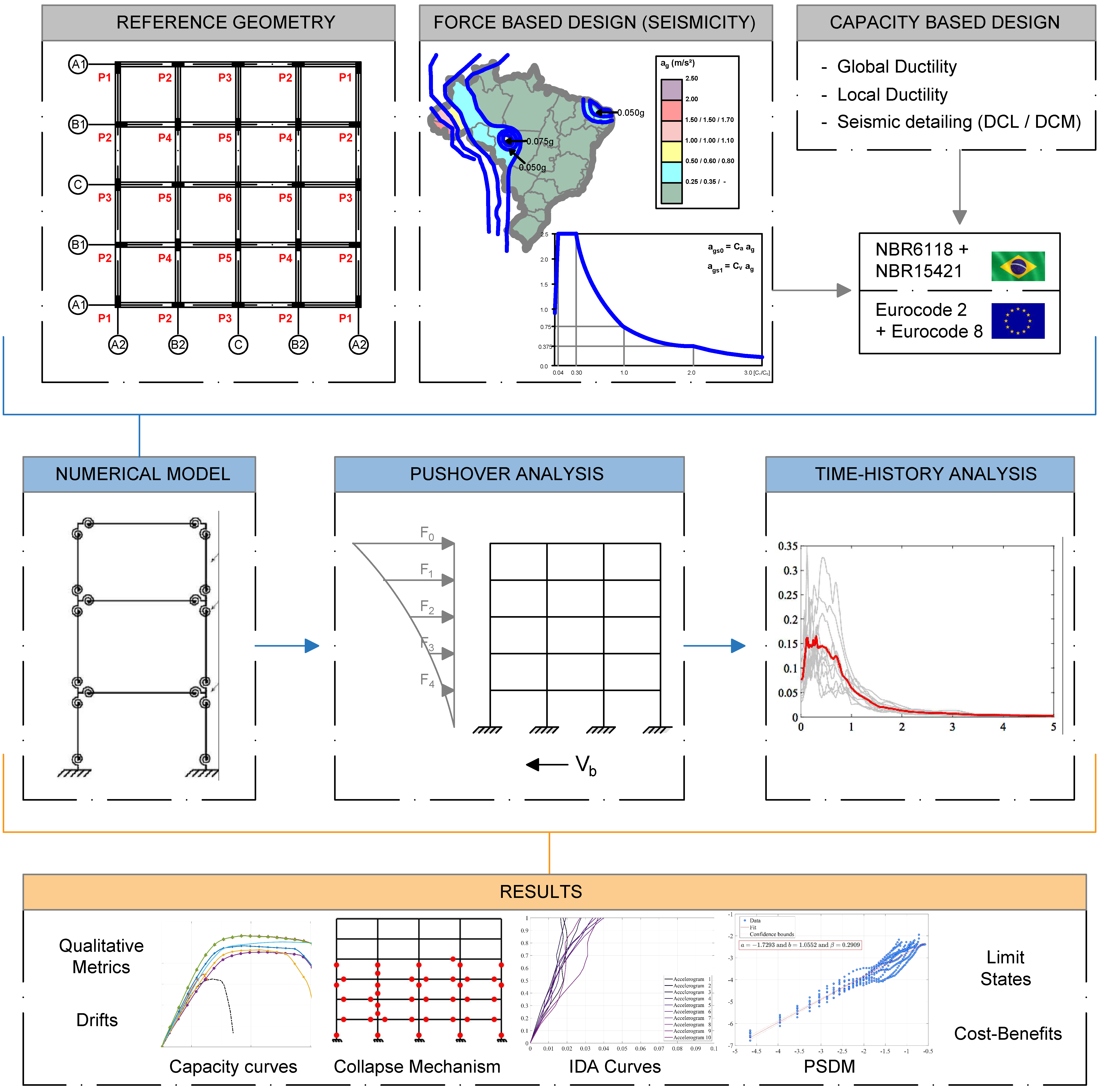
A summary of the methodology applied in this work is depicted in Figure 4 and reported in the following sections. Firstly, a low-rise reinforced concrete building with both plan and elevation regularity was selected as the reference geometry. The force-based design was carried out for seismic actions in Zones 0, 1, and 2 from ABNT NBR15421:2023. The capacity-based rules investigated were the ones preconized in the EN 1998-1:2004, namely global ductility, local ductility, and seismic detailing. Eight seismic design models were developed, considering different scenarios of design, seismicity, ductility, and detailing. TQS^® v.2023 [45] and ETABS^® v.2023 [46] softwares were used for seismic design, while Opeensees v.3.3.1 [47] was adopted for developing numerical models using a lumped plasticity methodology. In order to evaluate the seismic performance, nonlinear static Pushover analyses were conducted, following modal and uniform load patterns as suggested in EN 1998-1:2004. The nonlinear dynamic Time-history analysis were also performed but in order to validate the results. Finally, the models were assessed based on their collapse mechanism, resultant capacity curve, comparisons concerning ductility gain, drift, IDA curves, PSDM, limit states measures and cost-benefits.

4.1. Reference Geometry

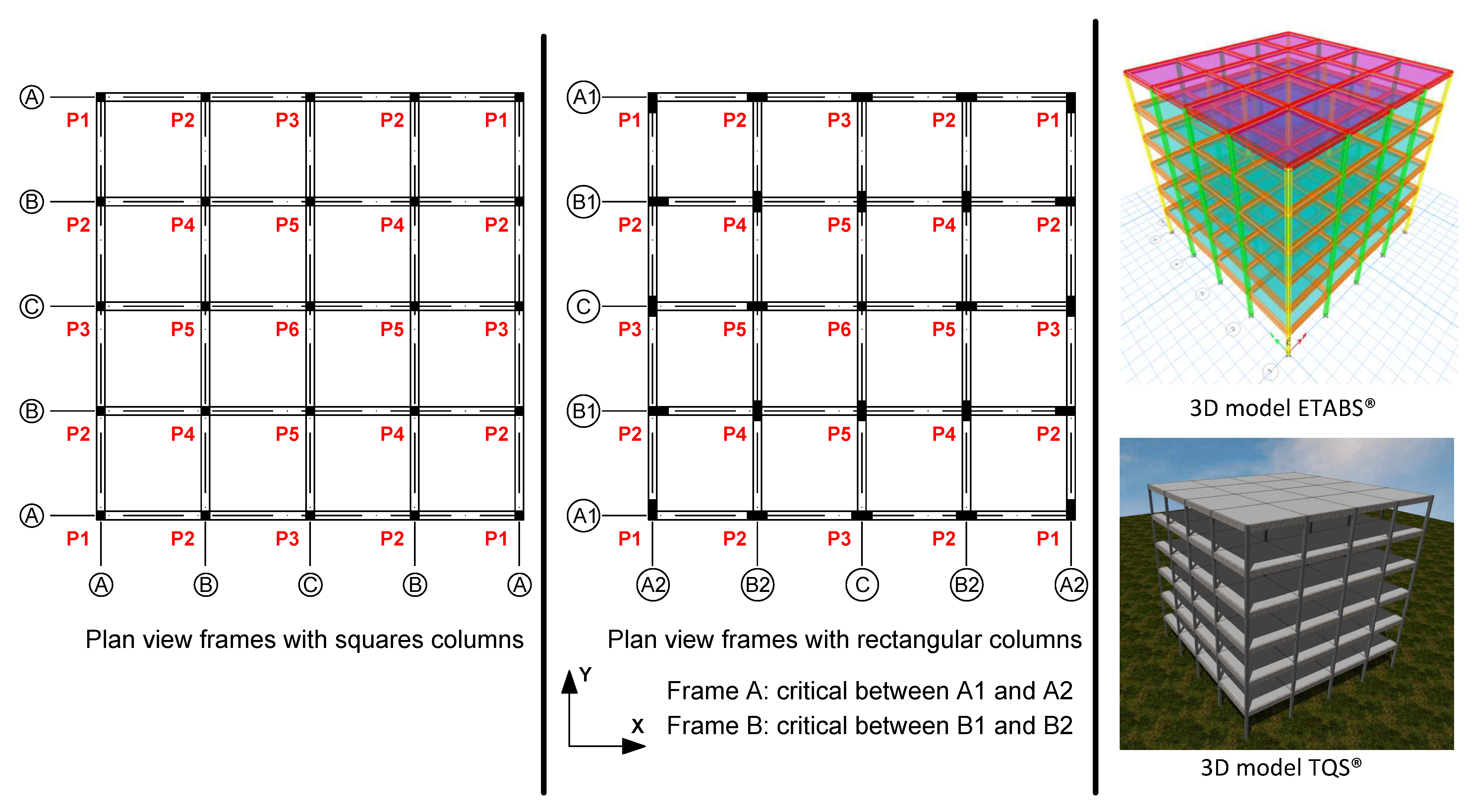
The reference geometry used for seismic design evaluation is a six-story reinforced concrete building, as illustrated in Figure 5. The structure was chosen as regular in both plan and elevation. This decision was taken since EN 1998-1:2004 has different rules for earthquake design regarding the structure’s regularity, and this study aims to investigate initial solutions to improve Brazilian seismic design. The selection of a six-story mid-rise building was based on [48] seismic vulnerability study, which also draws conclusions about the representativeness of this geometry in the Brazilian structural scenario. Figure 5 displays the plan view reference geometry, as well as the 3D model created using TQS^® [45] and ETABS^® [46].

A characteristic concrete compressive strength and steel yield strength of 30 MPa and 500 MPa, respectively, are adopted in the model. The floor slabs are 20 cm thick with a permanent overload of $1.0 {\mathrm{kN}/\mathrm{m}}^2$, as well as an accidental one of $3.0 {\mathrm{kN}/\mathrm{m}}^2$. The covering slabs are 12 cm thick with only an accidental overload of $1.50 {\mathrm{kN}/\mathrm{m}}^2$. To ensure the slabs meet the required thickness standards, they were checked for minimum values according to EN 1992-1-1:2004 and ABNT NBR6118:2023. These overload were adopted based on ABNT NBR6120—Design loads for structures (2019) [49]. The geometry has five frame lines in each direction with four 5-m spans each. The floor height is $3.24$ m for all stories, and the coverings were specified by ABNT NBR6118:2023. The corresponding values are $2.5$ cm for slabs and $3.0$ cm for beams and columns. These values were validated with those prescribed by European codes. In addition to self-weight, walls were considered above all beams.

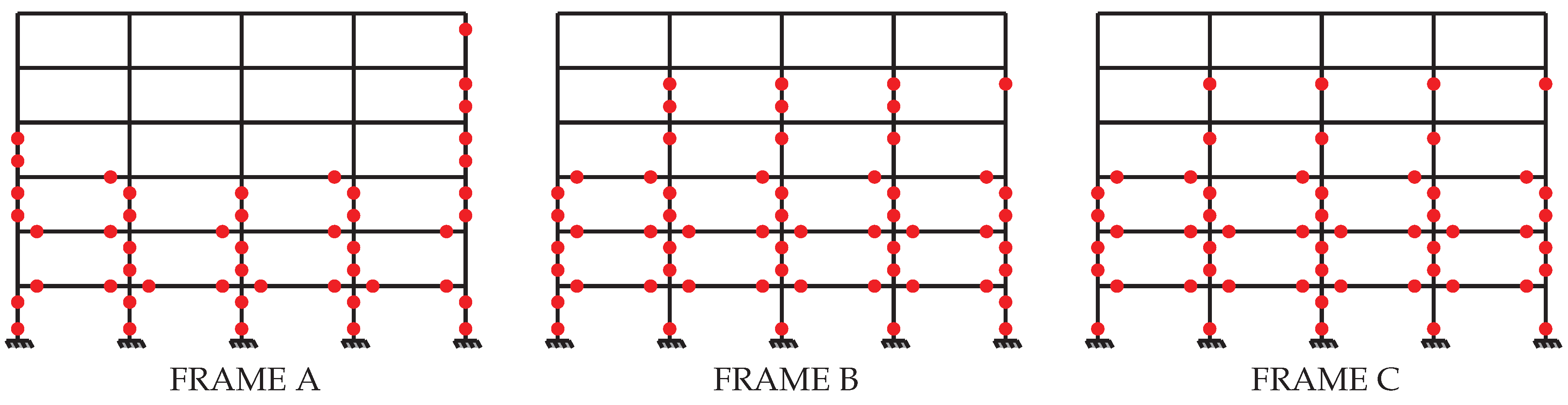
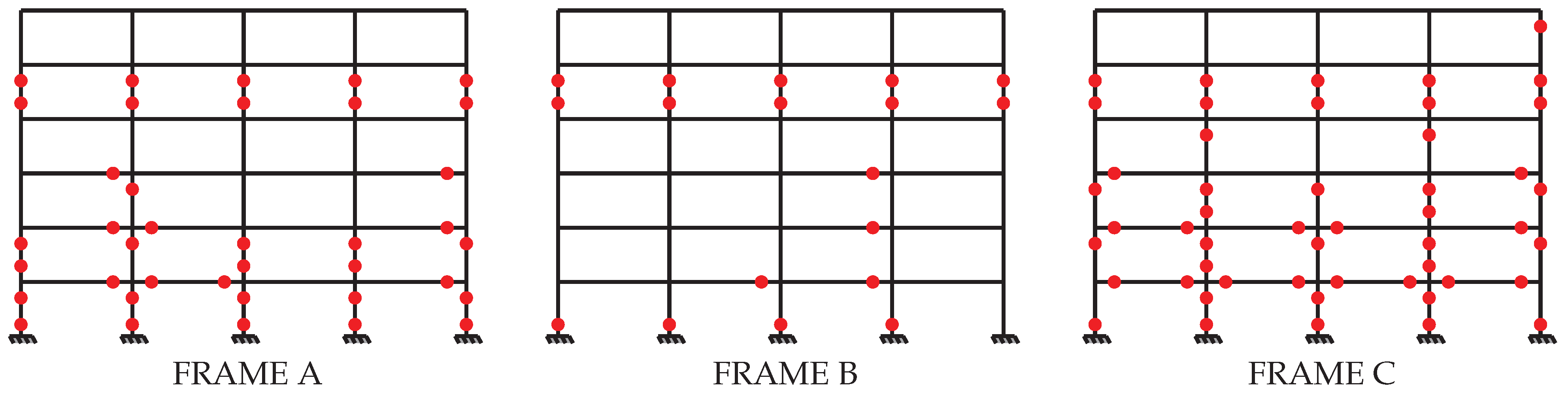
The building design considered two types of beams, namely roof beams and floor beams. The external and internal beams of each floor have the same size and detailing. The columns were reinforced from top to bottom with cross-sectional configurations that met the resistance criteria, ensuring safety, but also optimizing capacity versus demand. It should be noted that square column sections were used for designs based only on gravitational loads. However, rectangular columns were used for seismic design when dimensions exceeded 40 cm. As shown in Figure 5, a symmetrical scheme was adopted for rectangular columns in order to ensure structural regularity and to simplify the analysis to only three different frame lines per direction. For the results, it is introduced the critical frames A, B, and C considering both directions of the structure.

4.2. Seismic Actions and Force-Based Design

As discussed in Section 2, the force-based design application is quite similar between Brazilian and European standards. In this work, purely seismic analyses are carried out, without considering the effect of wind. This is because the Brazilian standard ABNT NBR8681—Actions and safety in structures (2003) [50] allows engineers to ignore the combination factors to variable actions for exceptional combinations where the primary action is seismic. Additionally, even though both lateral actions can cause entirely different behaviors in the structure, they are often misconstrued by engineers as overlapping. Hence, due to the difference in the low seismic accelerations of Brazilian seismic zones and high wind speeds, engineers frequently assume that wind design can make the structure withstand an earthquake, which is not true [23].

Seismic zones in Figure 2 indicate the predominance of Zone 0, 1, and 2 for highly vulnerable regions nationwide. Concerning the study’s application beyond possible future updates in the earthquake zones, three seismicity zones were determined. These regions were chosen and evaluated based on the extreme seismic acceleration in the corresponding category. Zone 0 has an $a_g=0.025$ g, Zone 1 $a_g=0.050$ g and Zone 2 $a_g=0.075$ g. Ground type is also very important for spectral analysis. Regarding its national predominance, Type D soil was adopted in this study. This sorting corresponds to European Soil Class C. The former is described as altered rock or very stiff soil, the latter as deep deposits of compact/moderately compact sand, pebbles (gravel), or hard clay. The main geotechnical properties of both soil classes are the average speed of the surface shear wave between 180 m/s and 370 m/s, and the average number of blows in SPT test is between 15 and 50.

4.3. Capacity-Based Design: Ductility and Seismic Detailing

The importance of capacity methodology for seismic design, as per Eurocodes, was discussed in the literature review of this paper. The study focused on the capacity-based rules suggested in EN 1998-1:2004, including global ductility, local ductility, and seismic detailing. Local ductility is ensured regarding bending as mandatory than shear, which is the most common design criterion for RC frames and is even applied to Brazilian codes. However, national Brazilian codes do not specify rules for global ductility and seismic detailing, which are the main focus of this study.

The EN 1998-1:2004 recommends a global ductility condition for structural design, which follows the Strong Column—Weak Beam premiss. This means that the objective is to create a collapse mechanism where beams are weak elements and columns are strong ones. As per the guidelines stated in this paper, the ratio between the bending moments of columns and beams from the same node is defined as 1.3, as established by EN 1998-1:2004. It is important to note that this value must be respected for 90% of all structural nodes, except for the roof floor.

Concerning seismic detailing, the DCL and DCM ductility classes of EN 1998-1:2004 were considered. On one hand, DCL follows EN 1992-1-1:2004 detailing, on the other hand, DCM has specific seismic rules outlined in EN 1998-1:2004. To determine the minimum ductility class, EN 1998-1:2004 considers the level of seismic activity in the area. In this work, $S=1.6$ was adopted as a soil parameter. Zone 0 has $a_g=0.025$ g, which is classified as a region of very low seismicity ($a_g<0.040$ g and $a_{g}S<0.050$ g). Zone 1 has $a_g=0.050$ g and is considered a low seismicity area ($a_g<0.080$ g and $a_{g}S<0.100$ g). For both zones, the minimum ductility class is DCL, and the EN 1992-1-1:2004 seismic detailing is sufficient. However, Zone 2 has $a_g=0.075$ g, so at least the DCM class becomes mandatory ($a_{g}S=0.12 \mathrm{g}>0.10$ g), including seismic detailing.

Moreover, this paper adopts the seismic detailing prescriptions established by the DCM class. These include limiting the eccentricities of the element’s sections, defining minimum sizes for structural elements, criteria regarding spacing, minimum diameter, rates, and the minimum number of reinforcement bars for both longitudinal and transverse reinforcement.

4.4. Study Case Models

From the aforementioned context, 8 models were defined for analysis.

Table 1. Study case models.

Model Label	RC Code	Seismic Code	Ductility Class	Zone	Design Software	Global Ductility Condition (SCWB)
Z0_DCL_NBR6118	NBR6118	-	DCL	0	TQS	NO
Z0_DCL_EC2	EC2	-	DCL	0	ETABS	NO
Z0_DCM_EC2_EC8-NSCWB	EC2	EC8	DCM	0	ETABS	NO (NSCWB)
Z0_DCM_EC2_EC8-WSCWB	EC2	EC8	DCM	0	ETABS	YES (WSCWB)
Z1_DCM_EC2_EC8-NSCWB	EC2	EC8	DCM	1	ETABS	NO (NSCWB)
Z1_DCM_EC2_EC8-WSCWB	EC2	EC8	DCM	1	ETABS	YES (WSCWB)
Z2_DCM_EC2_EC8-NSCWB	EC2	EC8	DCM	2	ETABS	NO (NSCWB)
Z2_DCM_EC2_EC8-WSCWB	EC2	EC8	DCM	2	ETABS	YES (WSCWB)

summarizes their main information as well as their respective nomenclature. It is important to note that the main research focus was on finding solutions to improve seismic design in Brazil. To achieve this, seven models applying European standards were considered, besides the control model, the one adopting only Brazilian standards.

4.5. Numerical Model

In this work, the OpenSees Software [47] was used for numerical modeling in Finite Elements. As the reference geometry is a regular structure, the eight design models were analyzed using the three frame lines A, B, and C described in Section 4.1, with a 2D model.

Regarding structural components, three plasticity models can be used to simulate the nonlinear behavior of RC frames. These models are continuous, fiber, or concentrated. According to [51], while continuous and fiber models are capable of accurately capturing the effects of concrete cracking and reinforcing bar yielding, they are unable to replicate the strength manipulation effects associated with reinforcing bar buckling, bond bonding, and shear failure causing strain softening. As these effects are more critical for assessing structural collapse, concentrated plasticity models have gained popularity for simulating the inelastic response of buildings [40]. Hence, a concentrated plasticity model was adopted in this study, following previous work as [52,53,54]. Figure 6 illustrates the components used in this modeling and the trilinear idealization of the resistant moment response curve for the plastic rotations of the section.

The components were modeled using linear elastic elements with non-linear springs at their ends, and they were connected by infinitely stiffness linear-elastic elements in the joint region. The elasticBeamColumn material was used for the linear elastic elements, which considered the modulus of elasticity, area, and cross-section moment of inertia. The joints of beams and columns are represented by elastic elements with the same length, and they are infinitely rigid. Nonlinear springs were modeled using the uniaxialMaterial IMKPeakOriented material from the OpenSees library, applied to a zero-length element, and following the model developed by [55,56].

Figure 6. Representation of the Finite Element Model for the Lumped Plasticity Model and the idealized trilinear end moment versus chord rotation (adapted from [31,57]).

Figure 6. Representation of the Finite Element Model for the Lumped Plasticity Model and the idealized trilinear end moment versus chord rotation (adapted from [31,57]).

These elements compose the lumped plasticity model, which consists of a monotonic curve and hysteretic degradation to capture the post-peak behavior of cyclic analyses that are associated with concrete crushing and buckling of reinforcement at large cyclic displacements [57]. This monotonic curve was represented in Figure 6 by the trilinear idealization of the ultimate moment $\left(M\right)$ and rotation ($\theta$) response for an equivalent column. The five base parameters of this curve are yield moment $M_Y$; initial elastic effective stiffness secant at the yield point $K_E$; maximum moment $M_C$; plastic rotation of the flow to peak ${\theta }_{cap,pl}$; post-peak plastic rotation ${\theta }_{pc}$. The equations for the model parameters can be conferred in [31,57].

Additionally, it should be noted that concentrated plasticity modeling was picked up for this study also considering its wide and current use in recent national studies on fragility and seismic vulnerability, such as [28,31].

It is noteworthy that the $P-{\mathsf{\Delta }}_{effect}$ on the columns was included using geometric transformations, and soil-structure interaction was not considered. Neglecting soil–structure interaction is a common practice for seismic performance and design studies. The conventional fixed-base assumption is a standard practice to decouple the structural and geotechnical models, aiming for purity in characterizing the superstructure’s inherent behavior. However, neglecting this interaction can add some bias and interfere in the accuracy of seismic predictions, especially for structures founded on deformable soils.

The effects of soil-structure interaction and the impact of soil properties on spectral analysis were addressed in [58]. The study emphasizes the seismic pounding importance for the seismic performance evaluation of RC frames, highlighting both the amplification and attenuation effects, as well as the variations in the fundamental natural period. Regarding this manuscript scope in evaluate different design methods for the same base geometry, the widely used simplification was considered valid. Furthermore, adopting the soil-structure interaction would imply adding many subsurface uncertainties to the analysis.

4.6. Nonlinear Static Pushover Analysis

Pushover analysis consists of a nonlinear static analysis conducted under constant gravitational loads and gradually applied horizontal load increments. The main objective is to generate the capacity curve, which represents the total shear force at the base of the structure as a function of the displacement of the control node, usually considered at the top of the building [59]. This analysis allows the explicit calculation of the structure’s ductility and the definition of deformation states directly related to damage to structural components. Therefore, it is also possible to estimate the expected plastic mechanisms and damage distribution, as the non-linear structural model enables the formation of plastic hinges in ductile members [7].

The load distribution used in the Pushover analysis followed the recommendations of both EN 1998-1:2004 and the FEMA-356 manual [60]. It consisted of two load patterns—uniform and modal. The uniform pattern was based on a mode that considered lateral forces proportional to mass. For the modal pattern, the FEMA-356 manual was followed, which stated that if the mass participation of the first mode of vibration was greater than 75%, the pattern of horizontal lateral loads should be proportional to the shape of this mode.

For regular buildings, EN 1998-1:2004 suggests using two flat models for Pushover analysis, one for each main direction. As the reference geometry was regular both in plan and elevation, analyses were carried out for the three different frame lines in each direction. The results presented correspond to the critical frame line for each frame of type A, B, or C. For all models and frames analyzed, the first mode of vibration of the structure had a modal participation in the range of 75.62–83.64%. Therefore, the second load pattern was adopted based on the structure’s fundamental mode.

4.7. Nonlinear Dynamic Time History Analysis

In this case study, pushover analysis was adopted as the primary methodology, based on the regularity and predominant modal participation of the first vibration mode. Besides that the main research objective was to evaluate the evolution of the collapse mechanism. Wherefore, pushover analysis is regarded as a straightforward and cost-effective approach, as highlighted by [61], a key reference in the field of seismic engineering. The author states that nonlinear static pushover analysis should only be replaced with a more rigorous method, such as nonlinear dynamic time history analysis, in cases where there are limitations such as significantly higher mode contributions, irregularities, torsion, or time-varying demands.

However, to enhance this paper, the results and conclusions were validated applying time-history dynamic analyses. For this purpose, seismic event records compatible with the design spectras were selected as illustrated in Figure 7, and a Probabilistic Seismic Demand Model (PSDM) was developed using Incremental Dynamic Analysis (IDA). Additional details regarding the records selection can be found in [62]. It is important to note that time-history dynamic analyses were solely used for validation purposes; the entire methodology presented in this article is primarily based on pushover analysis.

According to reference [63], acceleration records used in dynamic analyses should ideally reflect the seismic activity of the study region, meaning they must be compatible with the corresponding tectonic environment. References [64,65] further emphasize the importance of selecting records that feature magnitudes and distances consistent with events that accurately represent the seismic risk in the area.

Reference [19] states that, due to the nonlinear dynamic analyses being employed for seismic performance, the seismic demand should be characterized using Probabilistic Seismic Demand Models (PSDM), which rely on a suitable intensity measure. The PSDM was derived through linear regression based on the correspondence between structure critical components and the ground motion intensity defined by the logarithmic power model referenced in [66].

Three main methodologies are commonly used to obtain the Probabilistic Seismic Demand Model (PSDM): Incremental Dynamic Analysis (IDA), Multiple Stripe Analysis, and Cloud Analysis. In this study, IDA was adopted due to the benefits highlighted by [67]. This approach involves scaling earthquake records to uniformly increase and decrease the amplitude of the initial accelerogram. The spectral acceleration with 5% damping corresponding to the structure’s first vibration mode period ($S_a\left(T1\right)$) was selected as the intensity measure utilized, as the study was conducted only for buildings. And the Interstory Drift was chosen as the monitoring parameter. According to [68], scaling does not change the duration or shape of the response spectrum; it only affects the amplitude while keeping the frequency content unchanged. Therefore, the definitions employed in this analysis are justified, and further details can be found in [62].

4.8. Results Assessment

Regarding the methodology described above and the eight models Pushover Analysis was conducted, the results were assessed using the following metrics. Firstly, the seismic design and detailing at local levels were compared by examining component sections and reinforcement characteristics. This was done qualitatively to determine whether the structural assumptions adopted in each model had a considerable impact on the resulting cross-sections and reinforcement characteristics. As quantitative metrics and global model analysis, it was investigated the collapse mechanism established in each model and the corresponding capacity curve. This was done to check whether the ductility improvement was capable of changing the collapse mechanism. Based on nonlinear dynamic time history, dynamic instability was evaluated using IDA curves, and PSDM verified the convergence and dispersion of the designs with seismic behavior. Finally, considerations were made about the limit states, displacement, drift achieved, cost-benefits, being the explanations presented below.

In this work, the Damage Limit States based on the Hazus FEMA manual [69] are adopted to classify and define the performance levels established in the ATC-40 [70]. The six-story bare reinforced concrete structure defined as reference geometry is classified as C1M. The Damage Limit States are Slight Structural Damage, Moderate Structural Damage, Extensive Structural Damage, and Complete Structural Damage.

Table 2. Limit States qualitative description (adapted from [69]).

Limit States	Description
Slight Structural Damage	Flexural or shear-type hairline cracks in some beams and columns near joints or within joints.
Moderate Structural Damage	Most beams and columns exhibit hairline cracks. In ductile frames, some of the frame elements have reached yield capacity indicated by larger flexural cracks and some concrete spalling. Nonductile frames may exhibit larger shear cracks and spalling.
Extensive Structural Damage	Some of the frame elements have reached their ultimate capacity indicated in ductile frames by large flexural cracks, spalled concrete, and buckled main reinforcement; nonductile frame elements may have suffered shear failures or bond failures at reinforcement splices, or broken ties or buckled main reinforcement in columns which may result in partial collapse.
Complete Structural Damage	Structure is collapsed or in imminent danger of collapse due to brittle failure of nonductile frame elements or loss of frame stability. Approximately 13% (low-rise), 10% (mid-rise), or 5% (high-rise) of the total area of C1 buildings with Complete damage is expected to be collapsed.

and

Table 3. Limit States quantitative description for C1M strucutres (adapted from [69]).

Seismic Design Level	Drift Ratio Threshold of Limit States
	Slight	Moderate	Extensive	Complete
Pre-Code	0.0027	0.0043	0.0107	0.0267
Low-Code	0.0033	0.0053	0.0133	0.0333
Moderate-Code	0.0033	0.0058	0.0156	0.0400

show, respectively, the C1M qualitative and quantitative standards for these limits. To apply the quantitative limits, it is necessary to distinguish by level of seismic design. Therefore, the correspondence with the models evaluated in this work is also indicated next. Pre-code: Z0_DCL_NBR6118. Low-Code: Z0_DCL_EC2. Moderate-Code: Z0_DCM_EC2_EC8-NSCWB, Z0_DCM_EC2_EC8-WSCWB, Z1_DCM_EC2_EC8-NSCWB, Z1_DCM_EC2_EC8-WSCWB, Z2_DCM_EC2_EC8-NSCWB, Z2_DCM_EC2_EC8-WSCWB.

5. Results and Discussion

5.1. Qualitative Metrics

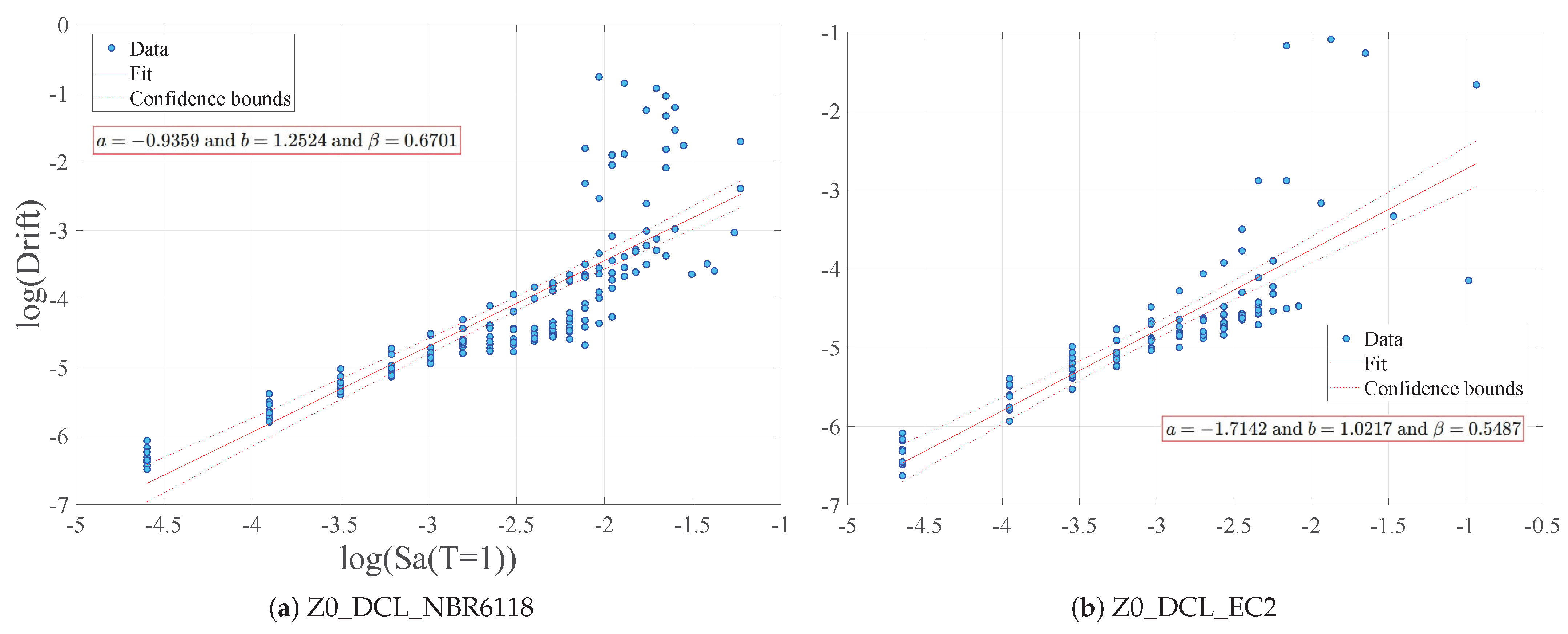
As presented in the Methodology Section 4.8, the results were assessed by qualitative and quantitative metrics. Firstly, seismic design and detailing were compared at local levels by examining component sections and reinforcement characteristics. For this purpose,

Table 4. Sections adopted in the columns after design.

Label	Section	Longitudinal Reinforcement		Stirrup Spacing/Critical
	[cm] × [cm]	$n_{\mathit{bars}}{\mathit{\varphi }}_{\mathit{diameter}}$[mm]	${\mathit{\rho }}_l$[%]	[cm]
1	20 × 30	$8\varphi 10.0$	1.05	20/6
2	20 × 35	$8\varphi 12.5$	1.40	20/6
3	20 × 40	$8\varphi 12.5$	1.23	20/6
4	20 × 40	$8\varphi 16.0$	2.01	20/6
5	25 × 25	$4\varphi 8.0$	0.32	16/-
6	25 × 25	$4\varphi 10.0$	0.50	20/-
7	25 × 25	$4\varphi 12.5$	0.79	25/-
8	25 × 25	$4\varphi 16.0$	1.29	25/-
9	25 × 25	$8\varphi 10.0$	1.01	20/8
10	25 × 40	$10\varphi 12.5$	1.23	20/8
11	25 × 45	$8\varphi 16.0$	1.43	20/8
12	25 × 45	$8\varphi 20.0$	2.23	20/8
13	25 × 45	$10\varphi 12.5$	1.09	20/8
14	25 × 45	$10\varphi 16.0$	1.79	20/8
15	30 × 30	$4\varphi 12.5$	0.55	25/-
16	30 × 30	$4\varphi 16.0$	0.89	30/-
17	30 × 30	$8\varphi 12.5$	1.09	20/10
18	30 × 50	$8\varphi 16.0$	1.07	20/11
19	30 × 50	$8\varphi 20.0$	1.68	20/11
20	30 × 50	$10\varphi 16.0$	1.34	20/11
21	35 × 35	$4\varphi 16.0$	0.66	32/-
22	35 × 35	$8\varphi 16.0$	1.31	20/12
23	40 × 40	$4\varphi 16.0$	0.50	32/-
24	40 × 40	$4\varphi 20.0$	0.79	20/-
25	40 × 40	$8\varphi 16.0$	1.01	20/12

and

Table 5. Sections adopted in the beams after design.

Models	Beam Type	Section [cm] × [cm]	Longitudinal Reinforcement			Transversal Reinforcement
			Top	Bottom	ρl [%]	Spacing	Critical Spacing
			${\mathit{n}}_{\mathit{bars}}{\mathit{\varphi }}_{\mathit{diameter}}$[mm]			[cm]
Z0_DCL_EC2	Roof	25 × 35	$3\varphi 12.5$	$3\varphi 12.5$	1.10	23	-
	Floor	25 × 50	$3\varphi 20.0$	$3\varphi 16.0$	1.20	23	-
Z0_DCL_NBR6118	Roof	19 × 30	$3\varphi 12.5$	$4\varphi 10.0$	1.20	17	-
	Floor	19 × 45	$3\varphi 20.0$	$3\varphi 12.5$	1.53	12	-
All Other Models	Roof	25 × 35	$4\varphi 12.5$	$3\varphi 12.5$	1.00	23	8
	Floor	25 × 50	$4\varphi 20.0$	$3\varphi 16.0$	1.50	18	12

provide information about column and beam components, while Figure 8 and Figure 9 show the correspondence between the column’s cross-sections in Table 4 and frame model lines. It is worth noting that the Z0_DCL_EC2 and Z0_DCL_NBR6118 models have square sections for columns, while the other six models have rectangular ones. All columns and beams have transversal reinforcement of 2-legged $\varphi 6.3$ mm bars, and the spacing is determined in the following tables. For models where EN 1998-1:2004 is adopted, two spacing values are presented—one for the critical zones named critical spacing and the other for the non-critical zone of the components, named just as spacing.

Based on the qualitative analysis of the data presented in Table 4 and Table 5, and Figure 8 and Figure 9, the following inferences can be made. Considering the design for the Zone 0 scenario and DCL ductility class, models Z0_DCL_EC2 and Z0_DCL_NBR6118, it resulted in square sections for columns. On one hand, for the external frame A, the EN 1992-1-1:2004 model has a smaller amount of reinforcement. On the other hand, for the internal frames, the ABNT NBR6118:2023 design resulted in more resistant sections. The B and C frame lines are very similar for both models and overall, the results between the two models are close.

The second comparison was carried out regarding the seismic detailing assumptions of three models: Z0_DCL_EC2, Z0_DCM_EC2_EC8-NSCWB, and Z0_DCM_EC2_EC8-WSCWB. The purpose was to assess the impact of the change in ductility class on seismic design. The first observation is that square columns are no longer a viable design option due to the significant increase in section size. In model Z0_DCM_EC2_EC8-NSCWB, section size was increased from 30 cm × 30 cm with a longitudinal reinforcement rate of 0.55% to 20 cm × 40 cm with a longitudinal reinforcement rate of 1.23%. In model Z0_DCM_EC2_EC8-WSCWB, this change was up to 25 cm × 45 cm section size with a longitudinal reinforcement rate of 1.09%. One significant difference between the seismic detailing assumptions of DCL and DCM class is the need for intermediate bars in the longitudinal reinforcement in each direction of the column. Therefore, configurations of four bars are no longer accepted, and the minimum number of bars required is eight. Finally, it was found that the application of the global ductility condition increased section size and reinforcement. This indicates that ductility is more restrictive and mandatory than strength for seismic design according to EN 1998-1:2004. This conclusion is further supported by the capacity curve analyses and evaluations that follow.

In the third verification, it was compared models Z1_DCM_EC2_EC8-NSCWB with Z1_DCM_EC2_EC8-WSCWB and also models Z2_DCM_EC2_EC8-NSCWB with Z2_DCM_EC2_EC8-WSCWB. Similar to what was presented for Zone 0, the models that adopted the global ductility condition resulted in more resistant sections to the columns. This effect is so noticeable that the models Z1_DCM_EC2_EC8-WSCWB and Z2_DCM_EC2_EC8-WSCWB are very similar, indicating minimum ductility required by EN 1998-1:2004 in the DCM class would cover the increase in strength required by the rise in seismicity. However, models Z1_DCM_EC2_EC8-NSCWB and Z2_DCM_EC2_EC8-NSCWB are not similar, which reinforces the statement about ductility importance.

Finally, regarding the beams, a small variance is noted between models designed by European codes. The only noteworthy variation is in the additional reinforcement required by the EN 1998-1:2004 DCM class for the longitudinal reinforcement in the upper part of the beam. Compared to model Z0_DCL_NBR6118, the latter results in less resistant beams in both the concrete section and reinforcement.

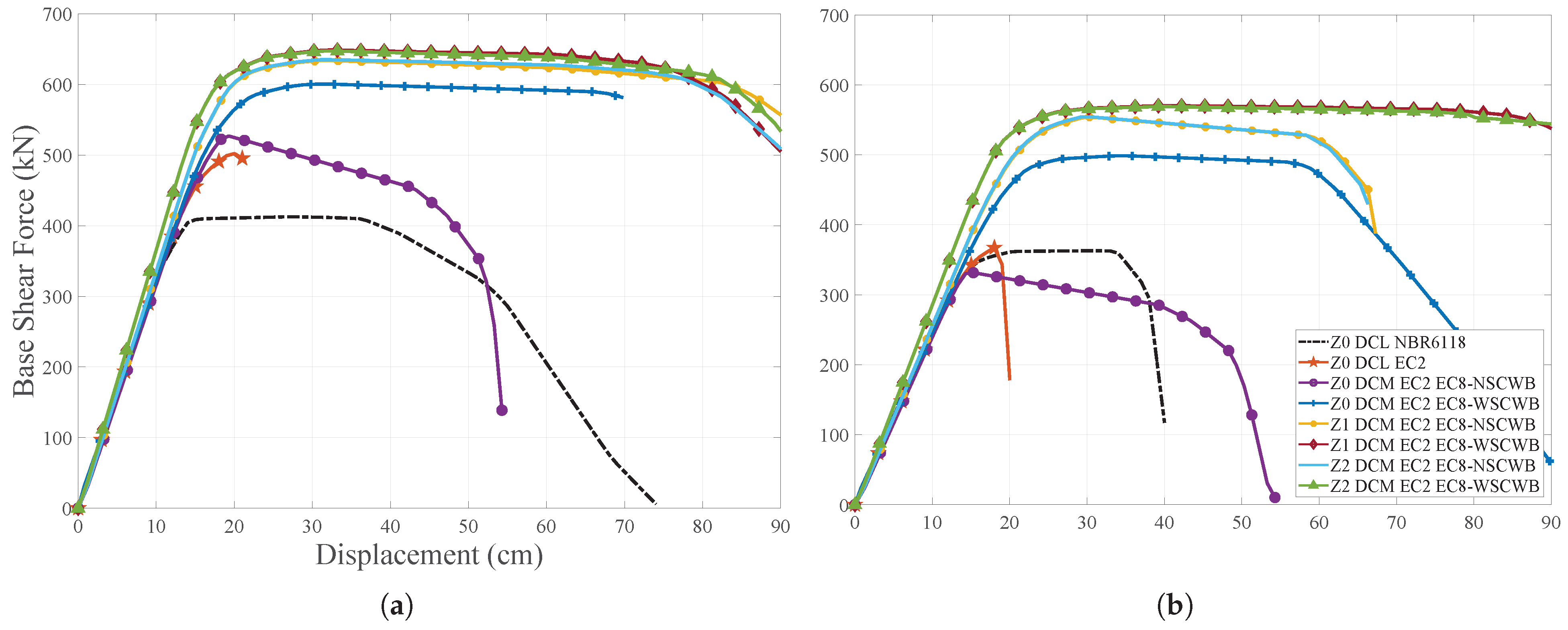
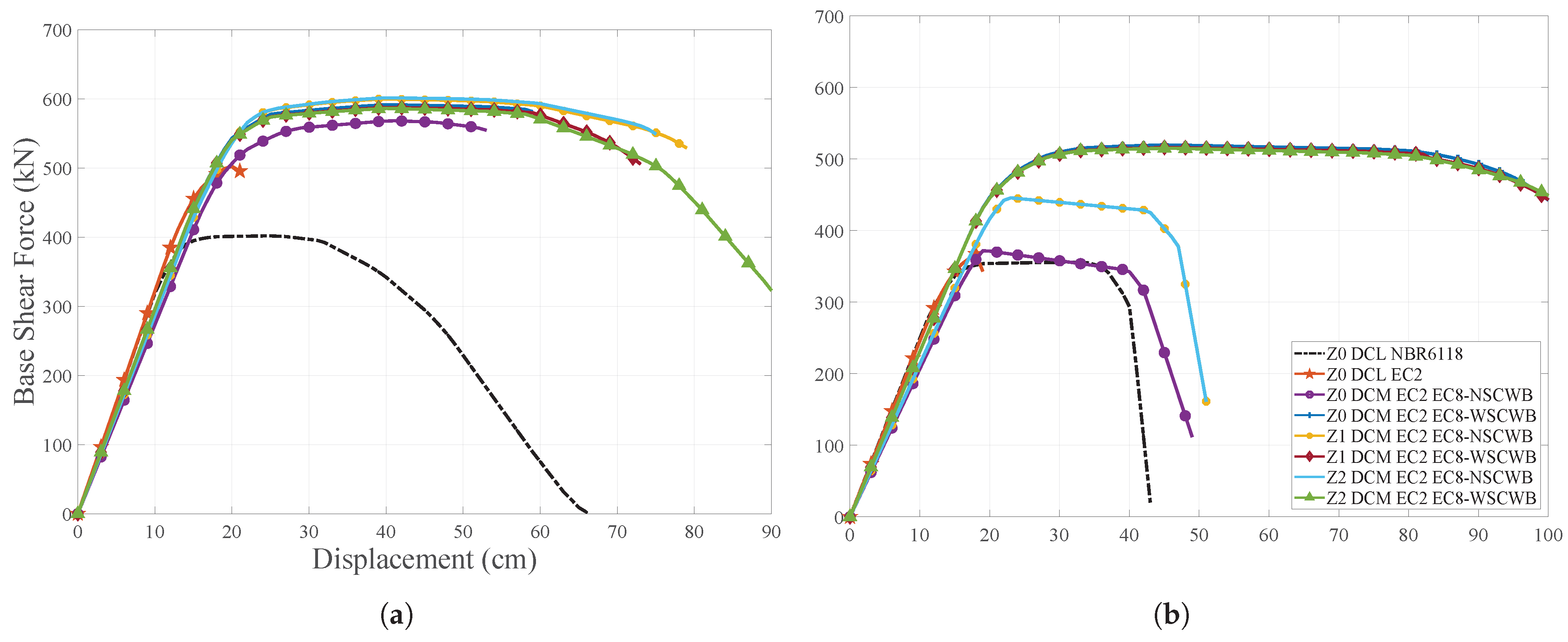
5.2. Capacity Curves

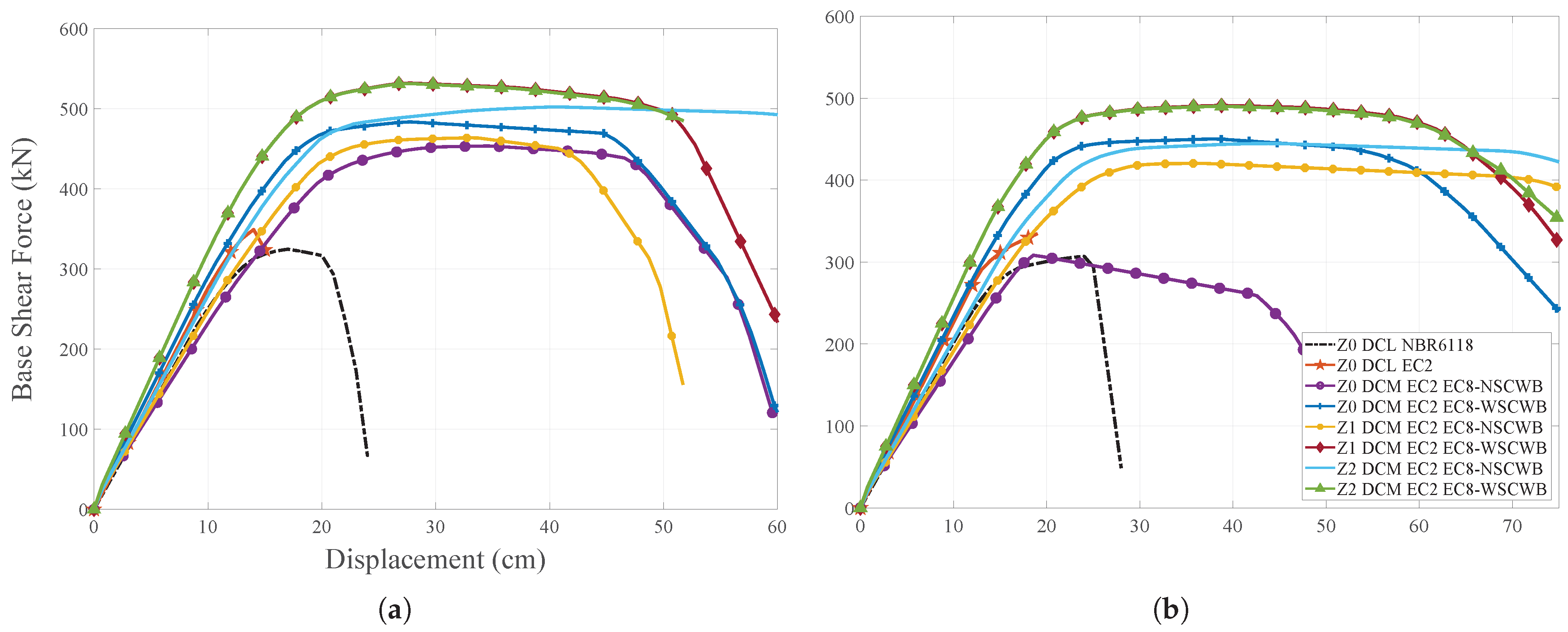
Figure 10, Figure 11 and Figure 12 illustrate the capacity curves of the structure’s frames due to Pushover for uniform and modal load patterns. It is evident from all the graphs that the designs Z0_DCL_EC2 and Z0_DCL_NBR6118, which lack any seismic resistance criteria, exhibit a brittle type of collapse mechanism, without utilizing the ductility of the structure. Additionally, as expected, the elastic force is insufficient for the frame to withstand an earthquake. Therefore, for all frames, the structure collapses for a displacement in the range of 20 cm and 30 cm, with a shear force at the base of approximately 60% less than that achieved by other models.

Regarding the load patterns, it was found that the capacity of the structure is lower for the modal pattern in all frames. Therefore, it is important to indicate that for all frames of all analysed models, 24 in total, the structure’s vibration modes had an equivalent shape, including mobilization of more than 90% in the first mode. Another important finding is that the model with the lowest capacity among the design models that considered the application of anti-seismic requirements by EN 1998-1:2004 is Z0_DCM_EC2_EC8-NSCWB. This result supports the one presented in the qualitative analysis, as it is a model where the global ductility condition is not implemented and the seismic action is the lowest, making the generated frames less resistant.

As mentioned in the qualitative criterion, a second verification was conducted to assess the impact of adopting seismic detailing. The following models were compared: Z0_DCL_EC2, Z0_DCM_EC2_EC8-NSCWB, and Z0_DCM_EC2_EC8-WSCWB. For all frames, it was observed that there were few differences in terms of maximum elastic strength between Z0_DCL_EC2 and Z0_DCM_EC2_EC8-NSCWB. However, the collapse mechanism changed significantly from brittle to ductile type. As a result, the ultimate displacement doubled to the elastic one, which was in the range of 40 cm to 50 cm. Furthermore, the structure’s capacity increased significantly due to the adoption of the global ductility condition, which will be further explored.

The third analysis examines the impact of adopting the Strong Column—Weak Beam structural premise on the structure’s ductility gain. To do this, it was compared model Z1_DCM_EC2_EC8-NSCWB with Z1_DCM_EC2_EC8-WSCWB and Z2_DCM_EC2_EC8-NSCWB with Z2_DCM_EC2_EC8-WSCWB. For all frames, the structure has a capacity gain of approximately 20% for the maximum base shear force, and there is a significant increase in the inelastic response, leading to considerable amplification of the ductile mechanism. The similarity between the frames resulted from the design for the models Z1_DCM_EC2_EC8-WSCWB and Z2_DCM_EC2_EC8-WSCWB also becomes clear from the capacity curves. This is because, despite representing different zones with different levels of seismic acceleration, the condition of global ductility becomes more mandatory than resistance.

5.3. Collapse Mechanism

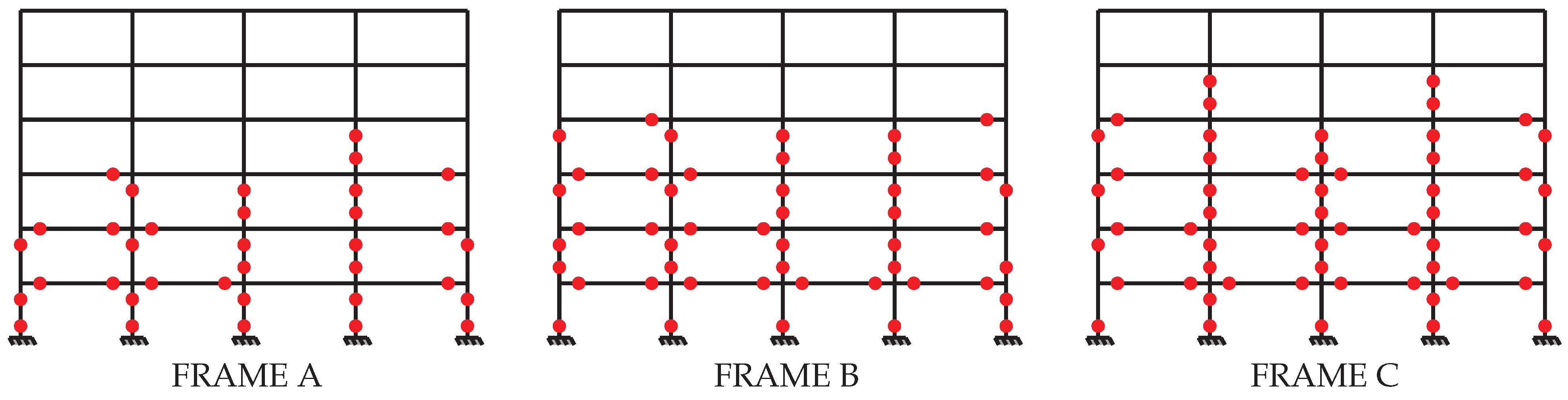
Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25 and Figure 26 present the collapse mechanisms of the evaluated structures based on the design model. The data is organized by frame, indicating the springs of the model that achieved yielding by at least one load pattern. It is important to note that Pushover was conducted for a displacement of 1 m and the mechanisms were verified in their main steps corresponding to 15%, 30%, 50%, and 100% of this displacement. In this section two different discussions are held, the former regarding the collapse mechanism achieved in each model at step 100% for the three frames (Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20), the latter concerning the collapse mechanism developed over the four steps for one specific frame of some selected models (Figure 21, Figure 22, Figure 23, Figure 24, Figure 25 and Figure 26).

Considering the first discussion, Figure 13 and Figure 14 show the plastic mechanisms formed in the models that did not follow seismic requirements, namely Z0_DCL_NBR6118 and Z0_DCL_EC2. It is important to note that for all frames, the columns yielded for the first five stories. In the case of the second structure, even the roof was in the inelastic stage. One significant difference between the two models is that the Eurocodes-based one had fewer beams involved in the collapse, while the Brazilian one mobilized at least the first three floors. This is reflected in the ductile capacity discussed by the capacity curves. However, it is important to note that the desired collapse mechanism for seismic structures regards the preponderant involvement of beams, which was not achieved in the absence of seismic detailing and global ductility conditions.

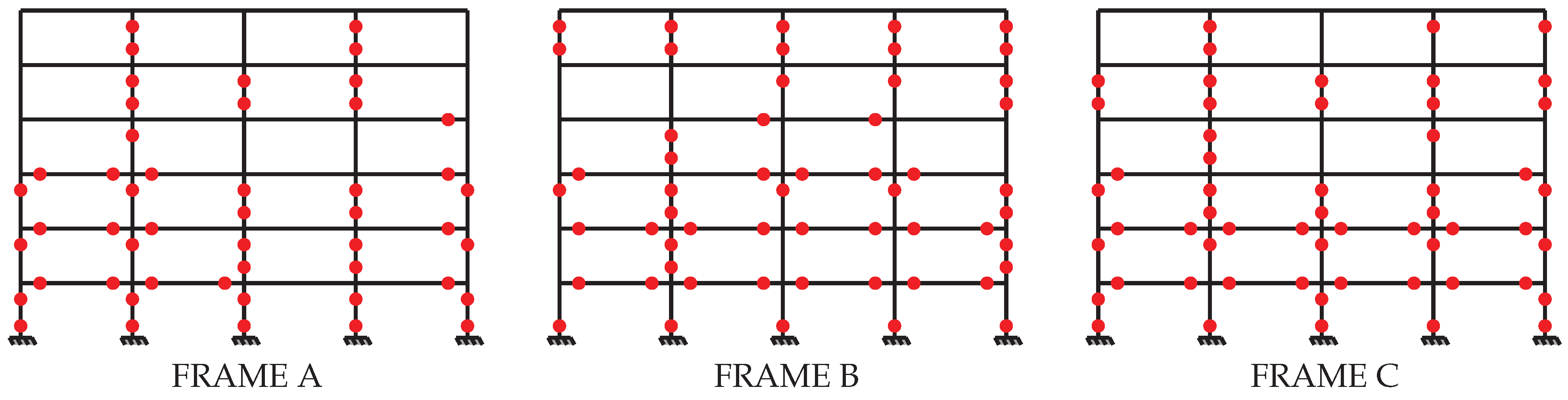
The next point in this analysis was carried out according to Figure 14, Figure 15 and Figure 16, which respectively represent the models Z0_DCL_EC2, Z0_DCM_EC2_EC8-NSCWB and Z0_DCM_EC2_ EC8-WSCWB. The aim was to identify the influence of seismic detailing on the collapse mechanism. As per the capacity curves and qualitative description, the adoption of seismic detailing resulted in a gain in the structure’s ductility, with greater mobilization of the beams in the collapse mechanism. However, the number of yielding columns is only reduced with the adoption of the global ductility condition. This can be verified by comparing Figure 17 with Figure 18 and Figure 19 with Figure 20, corresponding to the models without and with global ductility condition in Zones 1 and 2.

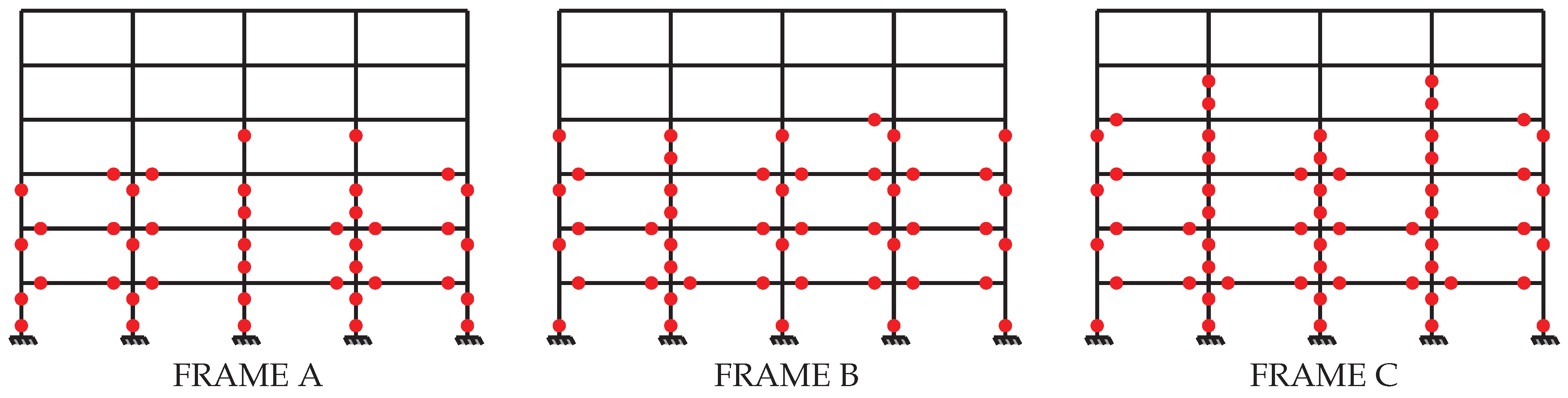
The second discussion was held regarding the collapse mechanism evaluation in four main steps, corresponding to 15%, 30%, 50%, and 100% of the final displacement. In order to select the most interesting results, Figure 10, Figure 11 and Figure 12 are analysed to choose the models and frames for this comparison. Firstly, Frame B is selected as it presents the most varied data on the collapse mechanism. Thus, according to Figure 11, six models of interest are selected to evaluate the association between the capacity curve and the collapse mechanism. Namely these models are: Z0_DCL_NBR6118, Z0_DCL_EC2, Z0_DCM_EC2_EC8-NSCWB, Z0_DCM_EC2_EC8-WSCWB, Z1_DCM_EC2_EC8-WSCWB and Z2_DCM_EC2_EC8-WSCWB. So, it is possible to investigate the difference between the brittle and ductile mechanisms, the global ductility condition and seismic detailing.

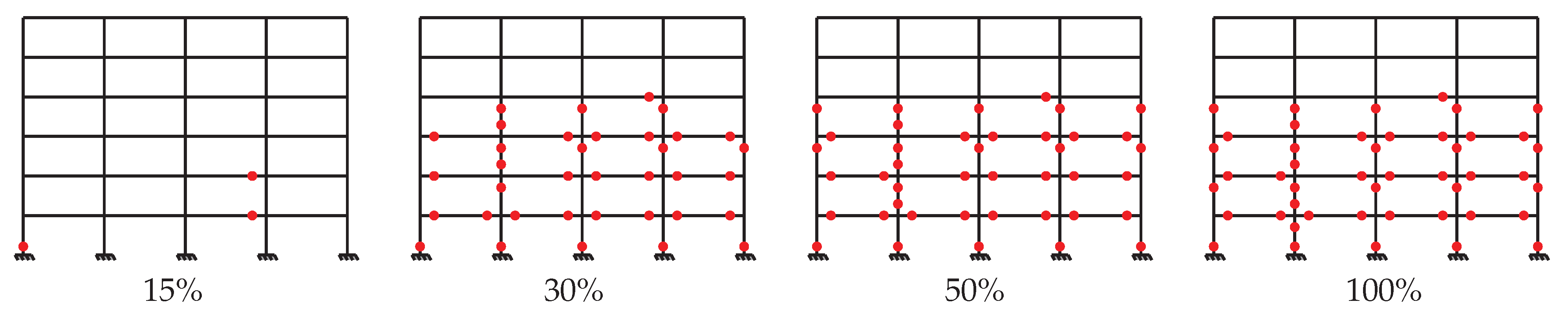
Although the models which don’t include anti-seismic requirements, Z0_DCL_NBR6118 and Z0_DCL_EC2, have a predominance of the formation of plastic hinges in columns, the evolution of this mechanism is very different as illustrated in Figure 21 and Figure 22. On one hand, the Z0_DCL_EC2 model presents a purely brittle mechanism where the columns are mobilized and involved in energy dissipation from the first step. On the other hand, in the Z0_DCL_NBR6118 model the beams of the first three floors are mobilized in the first stages of the analysis, which provides some initial ductility to the structure, in accordance with the results from the capacity curves.

The results for the Z0_DCM_EC2_EC8-NSCWB structure indicate the importance of seismic detailing in changing the collapse mechanism. Since, comparing Figure 21, Figure 22 and Figure 23, it is remarkable the difference in collapse mechanism from this structure to the ones without anti-seismic requirements. Whilst the Z0_DCM_EC2_EC8-NSCWB model shows a collapse mechanism with a small ductile baseline, the number of plastic hinges formed was lower. Conversely, it should be noted that Figure 23 illustrates a soft-story collapse mechanism for the fifth floor, highlighting the importance of adopting the global ductility condition for a more uniform behaviour of the structure. Figure 24 supports this conclusion since it demonstrates a mechanism next to the one expected for seismic design. In seismic design, the yielding of the beams in the first load steps stands out, in order to achieve desired levels of ductility capacity for the structure.

Finally, Figure 25 and Figure 26 corroborate with the last conclusion presented based on Figure 24. Furthermore, it is highlighted the impact of the global ductility condition in the design, since the collapse mechanism established for zones with different seismicity are similar in this case. Once again the global ductility condition shows as mandatory than strength for seismic design, enabling the energy dissipation required.

5.4. Nonlinear Dynamic Time History Analysis

As outlined in Methodology Section 4.7, the time-history dynamic analyses were conducted and incorporated to enhance this paper and further validate the results. Therefore, this section provides a brief overview of the results, while a detailed description of the selection criteria for the seismic records used can be found in reference [62]. It is important to note, as shown in Figure 7, that ten signals with distinct energy content and shapes, but compatible spectra, were selected. These ten signals were scaled using IDA to a range of 0.05–3.00 g in 0.05 g steps to generate the seismic event history for this study.

Figure 27 displays the results of the IDA curves that correlate the monitoring measurement interstory drift with the demand parameter $S_a\left(T1\right)$ for the seismic action models in Zone 0: Z0_DCL_NBR6118, Z0_DCL_EC2, Z0_DCM_EC2_EC8-NSCWB, and Z0_DCM_EC2_EC8-WSCWB. It can be seen that for the two non-seismically designed models, Z0_DCL_NBR6118 and Z0_DCL_EC2, the IDA curves exhibited dynamic instability. In these cases, the interstory drift increases indefinitely without reaching a limit for the same demand level, indicating a horizontal behavior. This performance is typically associated with collapse and suggests a brittle failure mode.

In contrast, the model Z0_DCM_EC2_EC8-NSCWB demonstrates a noticeable behavior change compared to the non-seismic models. Specifically, some IDA curves for this model are not horizontal, indicating that it is less dynamically unstable and reflects a collapse condition with lower ductility. Finally, the model Z0_DCM_EC2_EC8-WSCWB, which incorporates the global ductility condition, shows IDA curves that continuously increase for both the demand and the monitored parameter, without any horizontal plateau. This behavior is indicative of a structure with significant ductility and energy dissipation capacity, aligning with the expected performance of structures designed for seismic scenarios.

The associated PSDMs were developed from the IDA. Figure 28 illustrates the PSDM results based on the power methodology of [66] for the seismic action models of Zone 0. Since each design resulted in structures with different vibration periods, the spectral acceleration with 5% damping corresponding to a period of 1 s ($S_a(T=1)$) was used as the demand parameter for coherent comparisons between the models. This approach ensures consistency when evaluating the models. From the linear regression obtained through the PSDM, the resulting values for the median and dispersion of the demand are analyzed using the parameters: $a,b,\beta$.

Inferences regarding the fit of the regression to the model results can be made directly from the dispersion parameter $\beta$. Specifically, models that are not dimensioned for seismic activity exhibit significant associated dispersions (such as Z0_DCL_NBR6118 and Z0_DCL_EC2). These dispersions are mitigated by adopting ductility classes and seismic criteria (e.g., Z0_DCM_EC2_EC8-NSCWB). However, only the assumption of the SCWB (Z0_DCM_EC2_EC8-WSCWB) greatly reduces these dispersions, resulting in structures that behave more in line with expectations under seismic effects.

5.5. Limit States

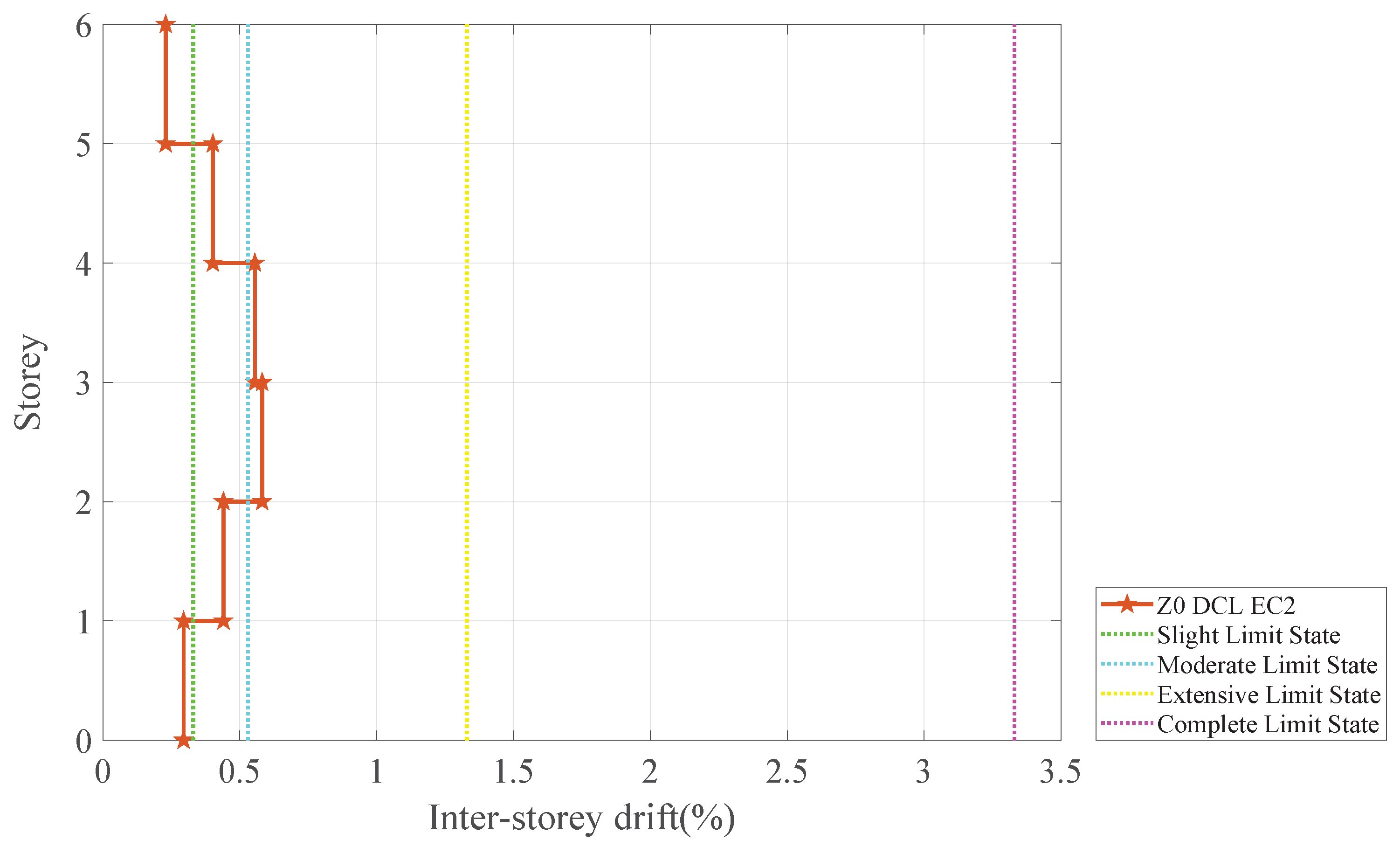
The Hazus FEMA manual [69] was used to verify the limit states outlined in the Methodology Section 4.8. For the capacity assessment, the intensity measurement selected was inter-story drift. Firstly, the distribution of inter-story drift was analyzed for each floor and each model, as illustrated in Figure 29. The definition of the structure’s collapse point is critically significant for determining the step at which the intensity of measurement was recorded. This assessment was conducted using two established criteria. The first criterion is associated with the post-peak point of the capacity curve where there is a 20% reduction in the maximum base shear, indicating an 80% structural response. The second criterion complements this fundamental one; in instances of brittle and abrupt failures, exemplified by the Z0_DCL_EC2 model in Figure 10, the step considered was the final one in the analysis. Conversely, in cases of ductile failures, where the analysis ceased—as illustrated by the Z0_DCM_EC2_EC8-WSCWB and Z1_DCM_EC2_EC8-WSCWB models in Figure 11 and Figure 12 respectively—the ultimate analytical step was also adopted. It is important to note that the critical value was considered for each model among the three evaluated frames.

The first evaluation in the Figure 29 is about the high inter-story drift values obtained for the models Z0_DCM_EC2_EC8-WSCWB, Z1_DCM_EC2_EC8-WSCWB, and Z2_DCM_EC2_EC8-WSCWB on the first and second floors. These three models share the common feature of adopting the global ductility condition through the Strong Column–Weak Beam structural approach. Based on this design principle, the columns are designed to withstand bending moments that are greater than those of the beams connected at the same nodes. Consequently, this outcome aligns with the expected ductility increase. Thus, this result converges to the expected ductility gain, demonstrated and discussed both in the yield levels of the capacity curves in Figure 10, Figure 11 and Figure 12 and in the collapse mechanisms in Figure 16, Figure 18 and Figure 20, which encompass a greater mobilization of structural elements for gradual energy dissipation on each floor.

It should be emphasized that the results presented sought to explore the full capacity of the analyzed models. However, for design purposes, EN 1998-1:2004 establishes in Section 4.4.3.2 that inter-story drift values should be limited, taking into account potential damage to secondary and non-structural elements. The higher inter-story drift values observed on the second and third floors are to be expected, since the first floor is significantly stiffer due to the influence of the foundation, which contrasts with the flexibility of the second and third floors. This effect becomes even more pronounced when there is a change in the cross-section of the column elements between subsequent floors. Therefore, such changes should generally be avoided; however, in some cases this may be necessary to adopt the SCWB principle, such as those analyzed in this research in Z0_DCM_EC2_EC8-WSCWB, Z1_DCM_EC2_EC8-WSCWB, and Z2_DCM_EC2_EC8-WSCWB models.

After the initial overall discussion regarding inter-story drifts, the limit states assessment detailed in the Methodology Section 4.8 was conducted. It should be noted that, in order to apply the quantitative limits, it is necessary to distinguish between seismic design levels. Therefore, the correspondence with the models evaluated in this work was Pre-code: Z0_DCL_NBR6118 in Figure 30. Low-code: Z0_DCL_EC2 in Figure 31. Moderate-code in Figure 32: Z0_DCM_EC2_EC8-NSCWB, Z0_DCM_EC2_EC8-WSCWB, Z1_DCM_EC2_EC8-NSCWB, Z1_DCM_EC2_EC8-WSCWB, Z2_DCM_EC2_EC8-NSCWB, Z2_DCM_EC2_EC8-WSCWB.

Previously, it was shown that the Pre-code Z0_DCL_NBR6118 model has a brittle collapse mechanism without ductility (Figure 10, Figure 11 and Figure 12) and with disordered mobilization of components in energy dissipation (Figure 13 and Figure 21). This result is consistent with the inter-story drift distribution presented in Figure 30, in which only the sixth floor remained in the Slight Limit State, the fifth in the Moderate Limit State, the fourth and third in the Extensive Limit State, and only the first and second in the Complete Limit State. This type of inter-story drift behavior also indicates a brittle collapse mechanism without ductility, since the floors were not mobilized in energy dissipation in order to reach the Complete Limit State for most floors of the analyzed structure. The more ductile the structure, the greater the expected inter-story drifts, indicating the energy dissipation capacity of the structure.

Similar behavior was also observed for the Low-code Z0_DCL_EC2 structure, with the latter being even more critical, since the collapse occurred even more abruptly than the Pre-code Z0_DCL_NBR6118 model (Figure 10, Figure 11 and Figure 12). In addition to the total absence of yield and ductility, the collapse mechanism of the structure (Figure 14 and Figure 22) indicates that few beams were mobilized, namely only the first floor, which justifies the abrupt brittle behavior. This result is also consistent with the inter-story drift distribution presented in Figure 31, in which only the sixth and first floors remained in the Slight Limit State, the fifth and second in the Moderate Limit State, and the fourth and third in the Extensive Limit State. None of the floors achieved the Complete Limit State, another indicator of how the structure was not designed to mobilize its components for energy dissipation. It should be emphasized that not only are the different limit states noticeable, but also the shape of the inter-story drift distribution. This is because in the Pre-code model in Figure 30, greater displacements are observed in the two lower floors, while in the Low-code model in Figure 31, the greatest displacements are concentrated at mid-height of the structure.

Finally, the models suited as Moderate-code and illustrated in Figure 32 were analyzed: Z0_DCM_EC2_EC8-NSCWB, Z0_DCM_EC2_EC8-WSCWB, Z1_DCM_EC2_EC8-NSCWB, Z1_DCM_EC2_EC8-WSCWB, Z2_DCM_EC2_EC8-NSCWB, and Z2_DCM_EC2_EC8-WSCWB. When comparing models that adopt the SCWB structural premise with those that do not, for the same seismic acceleration, it becomes clear—consistent with previous discussions in the capacity curves and collapse mechanisms—that this assumption significantly impacts the collapse mechanism, shifting it from brittle to ductile. Furthermore, the inter-story drifts reveal a pattern change, as discussed earlier in this section. The WSCWB models reached the Complete Limit State for the two lower floors. Notably, for the upper floors, the WSCWB models consistently exhibit higher inter-story drift values compared to the NSCWB models.

Another conclusion to be addressed is that only three structures, each with just one floor, reached the Slight Limit State. These structures belong to the models with lower seismic acceleration and are of the NSCWB type (Z0_DCM_EC2 EC8-NSCWB and Z1_DCM_EC2 EC8-NSCWB). Aside from the Z0_DCM_EC2 EC8-NSCWB model, which has four floors in the Moderate Limit State and two in the Slight Limit State, most floors in the other models reached the Extensive Limit State, for those that did not achieve the Complete Limit State. This reinforces the conclusion that a model’s ductility correlates with increased inter-story drift values obtained from the analysis and a more critical damage state. The enhanced performance and energy dissipation of the structure indicate that greater energy dissipation and mobilization of the structural components occur.

5.6. Cost-Benefits

In the previous sections, the results were assessed based on the structural behavior of the model. To ensure compliance with normative methods, this section includes a straightforward cost-benefit analysis. Ductility factor ($\mu$) was adopted as a benefit metric, which relates the ultimate displacement achieved by the structure to the cracking displacement. For the cost metrics, we recorded the volume of concrete (${\mathrm{m}}^3$), the amount of reinforcement (kg), and the ratio between reinforcement and concrete required (kg/${\mathrm{m}}^3$).

Table 6. Cost metrics for cost-benefit analysis.

Model Label	Concrete		Reinforcement		Reinforcement/Concrete [kg/m3]
	Volume	Ratio	Volume	Ratio
	[m3]	[%]	[kg]	[%]
Z0_DCL_NBR6118	138.06	0.00	16723.69	0.00	121.14
Z0_DCL_EC2	185.49	34.36	17,927.83	7.20	96.65
Z0_DCM_EC2_EC8-NSCWB	184.75	33.82	24,661.17	47.46	133.48
Z0_DCM_EC2_EC8-WSCWB	194.86	41.14	24,850.28	48.59	127.53
Z1_DCM_EC2_EC8-NSCWB	188.64	36.64	24,553.63	46.82	130.16
Z1_DCM_EC2_EC8-WSCWB	199.72	44.66	25,676.69	53.53	128.56
Z2_DCM_EC2_EC8-NSCWB	192.40	39.36	24,850.76	48.60	129.16
Z2_DCM_EC2_EC8-WSCWB	199.72	44.66	25,239.77	50.92	126.38

presents the results of the cost metrics, including a comparison between the several designs and the reference model (Z0_DCL_NBR6118).

Table 7. Benefits metrics for cost-benefit analysis.

Model Label	${\mathit{F}}_{\mathit{y}}$ [kN]	${\mathit{\delta }}_{\mathit{y}}$ [cm]	${\mathit{F}}_{\mathit{u}}$ [kN]	${\mathit{\delta }}_{\mathit{u}}$ [cm]	$\mathit{\mu }$
Z0_DCL_NBR6118	318.87	15.01	316.86	20.01	1.33
Z0_DCL_EC2	349.35	14.01	349.35	0.00	0.00
Z0_DCM_EC2_EC8-NSCWB	371.82	19.02	342.48	40.02	2.10
Z0_DCM_EC2_EC8-WSCWB	467.01	19.73	469.35	44.73	2.27
Z1_DCM_EC2_EC8-NSCWB	442.34	22.03	425.15	43.03	1.95
Z1_DCM_EC2_EC8-WSCWB	540.84	20.02	579.79	59.02	2.95
Z2_DCM_EC2_EC8-NSCWB	442.34	22.03	425.15	43.03	1.95
Z2_DCM_EC2_EC8-WSCWB	540.84	20.02	574.40	59.02	2.95

displays the benefit metrics for each model, which include ultimate force ($F_u$), ultimate displacement (${\delta }_u$), cracking force ($F_y$), cracking displacement (${\delta }_y$), and the ductility factor ($\mu$).

Based on the cost-benefit analysis, it can be seen that the concrete volume cost metric for the Z0_DCL_EC2 model increased by 34.36%. In contrast, the models that include the SCWB (Z1_DCM_EC2_EC8-WSCWB and Z2_DCM_EC2_EC8-WSCWB) experienced a significant increase of 44.66% in the same metric, representing the highest increase in concrete volume. Regarding reinforcement, the Z0_DCL_EC2 model showed a relatively modest increase of 7.20%. In comparison, the Z1_DCM_EC2_EC8-WSCWB and Z2_DCM_EC2_EC8-WSCWB models had much larger increases of 53.53% and 50.92%, respectively. It is important to note that the NSCWB models had values similar to those of the SCWB models for the same seismicity classification. These findings suggest that the adoption of the DCM is directly related to the volume of reinforcement required for the structure, while the SCWB primarily affects the volume of concrete.

The reinforcement-to-concrete ratio has been quantified as 121.14 kg/${\mathrm{m}}^3$ for the Z0_DCL_NBR6118 model and 96.65 kg/${\mathrm{m}}^3$ for the Z0_DCL_EC2. For the remaining models, the values were approximately 130.00 kg/${\mathrm{m}}^3$. This analysis indicates that the ratio applicable to ABNT NBR15421 design, in the absence of seismic load considerations, is comparable to that of models adhering to the EN 1998-1:2004 with DCM. Nonetheless, despite this apparent similarity, it is important to note the significant increase in material consumption that has been previously emphasized.

The evaluated benefit metric was the ductility factor ($\mu$). The Z0_DCL_EC2 model exhibited zero ductility, as its failure was abrupt and brittle. Although the reference model Z0_DCL_NBR6118 presented an intrinsic ductility factor of 33%, a review of the capacity curves in Figure 10 and Figure 11 reveals that its collapse mechanism was also characterized as brittle. The models that incorporated SCWB displayed a substantial ductility gain of approximately 300% ($\mu =3$) for zones Z1 and Z2, and a gain of 227% for zone Z0. On the other hand, models that did not adopt SCWB achieved a ductility gain of approximately 200% ($\mu =2$) across all evaluated zones.

6. Conclusions

This paper addressed an initial investigation into seismic provisions to Brazilian structures based on European codes. The main focus relies on evaluating and determining the importance of adopting certain structural rules based on EN 1992-1-1:2004 for Brazilian seismic design, particularly in terms of ductility. There were considered different scenarios of design, seismicity, and ductility class. To assess and compare the performance of six-story reinforced concrete buildings, non-linear static Pushover analysis was carried out on finite element models and also validated with nonlinear dynamic Time-history analysis. The study compared the Brazilian design process with the regulations in Eurocodes. The former adopts FBD exclusively, and the latter involves CBD with global and local ductility conditions. Based on the simulation results, the following conclusions can be drawn:

• The main impacts on the designed structural components occurred for the columns. Regarding the beams, a minor variance is shown due to the different solutions presented. The only noteworthy difference concerns the additional reinforcement required by the DCM class for the longitudinal reinforcement in the upper part of the beam. However, it’s important to note that as the design process is global, small variations may occur.
• As for the load pattern applied in the Pushover analysis, the most critical structural response was based on the first vibration for the 24 frames analysed.
• Models that do not adhere to anti-seismic requirements exhibit a brittle failure mechanism, which is primarily controlled by the columns. Such models can only withstand up to a quarter of the displacement that can be achieved if ductility rules are adopted. Moreover, the base shear force is also quantified at 60% for the same reference.
• Seismic detailing adoption based on Eurocode implied doubling the inelastic response of the structure, changing the collapse mechanism from brittle to ductile. Thereby, this highlights the importance of seismic detailing for Brazilian projects and suggests that future studies be conducted in this direction for an optimal relationship with the national scenario. Among the most critical premises evaluated are the adoption of intermediate bars in the configuration of the longitudinal reinforcement, and the implementation of smaller spacings between stirrups in critical areas of the structure where yielding is expected.
• The Strong Column—Weak Beam structural premise, also known as the global ductility condition, is an important rule that ensures a ductile collapse mechanism with high energy dissipation. This condition quadruples the inelastic response of the structure for the models analysed, making it a crucial premise for seismic design. Also, among the premises studied in this paper, this is more restrictive and mandatory than strength for seismic design, which means that similar sections are required for regions with different seismicity. This rate between the resistant moments determines the greater mobilization of beams compared to columns for the same node, which helps to expand the plastic mechanism across the floor beams and generate ductility gain. This makes it a potential tool for national study, highlighting the importance of investigating optimal values for Brazil.
• The nonlinear dynamic time-history analysis enabled the validation of the results obtained from the pushover analysis. Regarding the model’s characteristics in terms of regularity, vibration mode participation, and the objective of evaluating collapse mechanisms, the pushover analysis proved sufficient and consistent, with a low computational cost. However, the authors emphasize the limitation in extrapolating this conclusion to different case studies.
• According to the Hazus FEMA manual [69], the assessment of Limit States showed that structures with higher ductility tend to have greater inter-story drift due to energy mobilization and dissipation. As a result, ductile models tend to be classified as having complete structural damage. Furthermore, the models that adopted the global ductility condition showed greater inter-story drifts, reflecting the desired energy dissipation capacity for a structure under seismic design.
• The cost-benefit analysis indicates that the performance improvement significantly outweighs the associated costs. The models employing EN 1998-1:2004 and DCM exhibited an increase in concrete volume ranging from 34% to 45%, and 50% for the reinforcement. Furthermore, the ductility enhancement was substantial, with SCWB models demonstrating a 300% improvement, while NSCWB models experienced 200%. Despite the increase in overall volume, the reinforcement-to-concrete volume ratio of the EN 1998-1:2004 and DCM models remained close to the reference model.
• Specifically for ABNT NBR15421, it is advisable to conduct a thorough review of the design methodology for seismic actions and to incorporate tools that will ensure the structure’s capacity and ductility. The importance of a global ductility condition, such as SCWB, is highlighted in order to effectively manage collapse mechanisms and guarantee energy dissipation. Furthermore, the implementation of specific seismic detailing is recommended to reinforce plastic hinge zones in accordance with the corresponding demand.

It should be noted that the conclusions presented above are derived from the evaluated reference geometry. Extrapolating these results to other structures and design standards should be approached with caution and meticulous consideration.