Numerical Investigation on the Diffusion and Ventilation Characteristics of Hydrogen-Blended Natural Gas Leakage in Indoor Spaces

Abstract

The blending of hydrogen significantly impacts the diffusion and safety characteristics of natural gas within indoor environments. This study employs ANSYS Fluent 2021 R1 to numerically investigate the diffusion and ventilation characteristics of hydrogen-blended natural gas (HBNG) leakage in indoor spaces. A physical and mathematical model of gas leakage from pipelines is established to study hazardous areas, flammable regions, ventilation characteristics, alarm response times, safe ventilation rates, and the concentration distribution of leaked gas. The effects of hydrogen blending ratio (HBR), ventilation conditions, and space dimensions on leakage diffusion and safety are analyzed. Results indicate that HBNG leakage forms vertical concentration stratification in indoor spaces, with ventilation height being negatively correlated with gas concentration and flammable regions. In the indoor space conditions of this study, by improving ventilation conditions, the hazardous area can be reduced by up to 92.67%. Increasing HBR substantially expands risk zones—with pure hydrogen producing risk volumes over five times greater than natural gas. Mechanical ventilation significantly enhances indoor safety. Safe ventilation rates escalate with hydrogen content, providing quantitative safety criteria for HBNG implementation. The results underscore the critical influence of HBR and ventilation strategy on risk assessment, providing essential insights for the safe indoor deployment of HBNG.

1. Introduction

Driven by the global carbon neutrality agenda [1,2], Hydrogen is globally regarded as one of the most promising energy carriers due to its clean combustion [3,4], high efficiency [5], zero-carbon emissions [6], and abundant availability [7]. Currently, the predominant methods for hydrogen transportation include liquid hydrogen tank trucks [8], high-pressure hydrogen cylinder tube trailers [9], and liquid hydrogen barges [10,11]. However, these approaches are limited by low transportation efficiency and high costs [12]. An emerging alternative is blending hydrogen into natural gas pipelines for downstream utilization, which presents a novel pathway for hydrogen energy deployment [13,14,15,16,17].

The global deployment of HBNG projects has grown substantially in recent years [18,19,20]. Notable examples include France’s 2014 GRHYD project, which successfully demonstrated the technical feasibility of HBNG pipeline transportation [21]. In 2019, the UK’s HyDeploy project confirmed the viability of blending hydrogen into natural gas pipelines at a 20% volumetric ratio [22]. The same year, China’s Liaoning Chaoyang HBNG demonstration project successfully applied HBNG for residential energy supply [23]. In 2021, the United States launched its largest HBNG project, “HyBlend,” aiming to achieve fuel decarbonization [24]. These projects collectively focus on two key aspects: (1) the adaptability of existing natural gas infrastructure for hydrogen transport and (2) end-use equipment compatibility with HBNG [25].

Compared to natural gas, hydrogen demonstrates significantly higher flammability and explosiveness, characterized by a broader flammability range [26], greater diffusivity [27], and lower minimum ignition energy [28]. These properties render HBNG more susceptible to deflagration and other hazardous scenarios compared to natural gas [29]. Furthermore, hydrogen modifies the leakage behavior and diffusion characteristics of gas mixtures [30], potentially exacerbating leakage and explosion risks in indoor gas applications [31], thereby raising significant safety concerns. To address these risks, researchers worldwide have investigated gas leakage diffusion and explosion characteristics in confined spaces. For instance, Xing et al. [32] performed explosion experiments with methane-air mixtures in a chamber, demonstrating that obstacles enhance explosion overpressure, with magnitude variations depending on ignition location. Brady et al. [33] carried out hydrogen leakage diffusion and explosion experiments in a garage model, examining the effects of ventilation on hydrogen dispersion and catalytic ignition sources on explosion risks. Their findings indicated that catalytic ignition sources significantly increase hydrogen explosion risks while correctly matching ventilation with leakage rates and effectively mitigating explosion hazards. Marangon et al. [34] experimentally studied leakage and diffusion of hydrogen-methane mixtures (10% and 30% hydrogen) in enclosed spaces, observing initially non-uniform concentration distributions that gradually homogenize over time. Hajji et al. [35] focused on hydrogen leakage in residential garages, systematically analyzing ventilation effects on dispersion patterns and establishing fundamental characteristics of hydrogen diffusion in such environments.

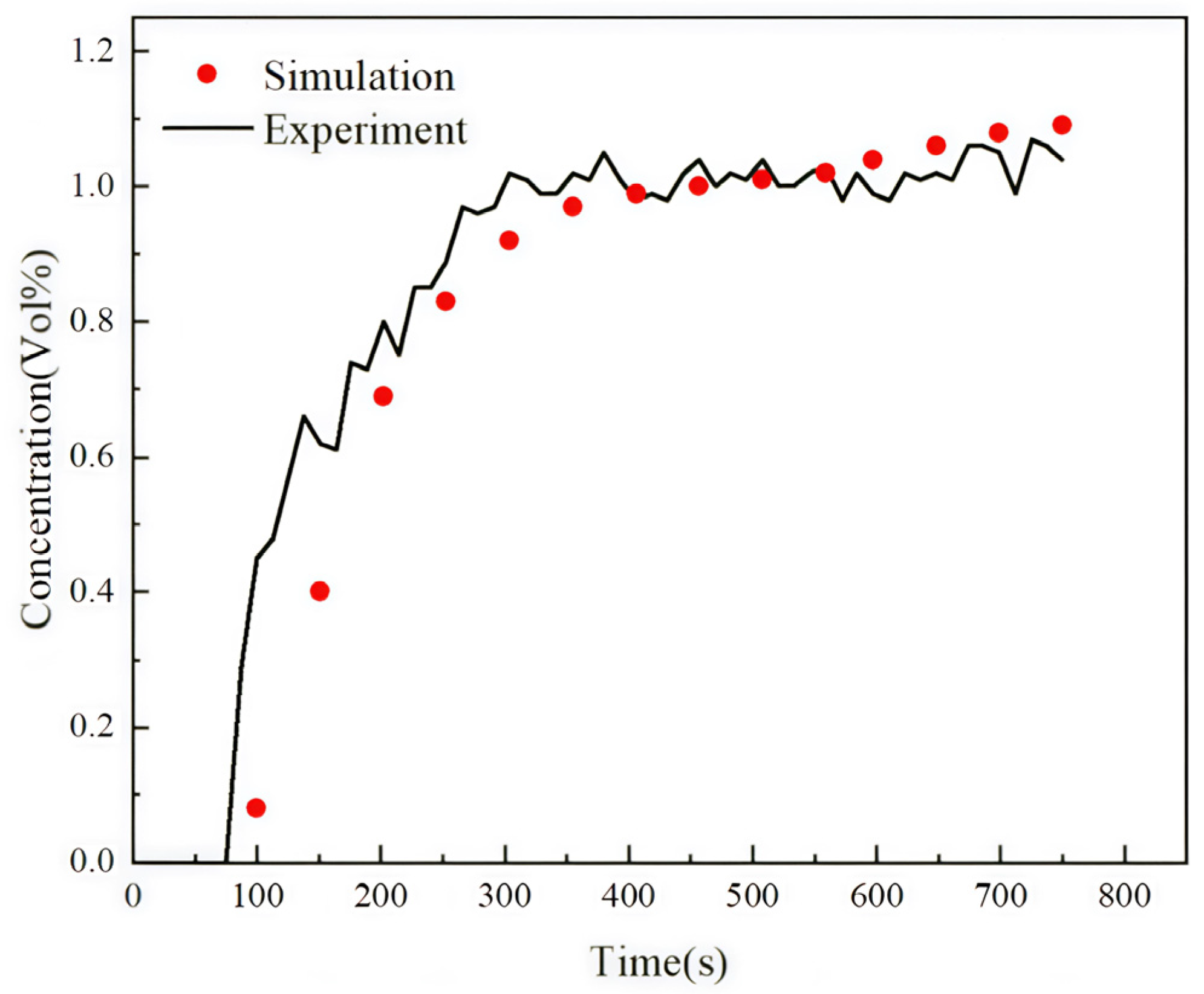
The rapid development of computational fluid dynamics (CFD) has established numerical simulation as a powerful methodology for investigating gas leakage phenomena [36]. This approach eliminates the safety concerns inherent in experimental studies while enabling comprehensive analysis of HBNG leakage and explosion characteristics across diverse conditions through parameter variation. Several studies have demonstrated the effectiveness of this approach. Su et al. [37] developed a household kitchen model using Fluent R19.2 to evaluate how various factors influence HBNG concentration distribution, explosion risks, and alarm response times. Their simulations revealed that at constant leakage rates, increasing the HBR substantially reduces both the alarm response time and the time to reach the lower explosion limit, while mechanical ventilation effectively mitigates gas accumulation. Cen et al. [38] employed Fluent to simulate indoor gas leakage and diffusion dynamics, ultimately determining the minimum required ventilation area for typical northeastern Chinese residential buildings. Li et al. [39] created a sealed container model using CFD to analyze leakage patterns, diffusion behavior, and flammable zone distribution for natural gas with varying HBRs. Their results indicated that at HBRs below 20%, HBNG exhibits leakage and diffusion characteristics comparable to pure methane. Lu et al. [40] utilized the FLACS 9.0 to investigate how horizontal baffles at ventilation openings affect hydrogen concentration and ventilation efficiency. Their findings demonstrated that strategically placed baffles at ventilation inlets and outlets enhance airflow velocity while reducing interior hydrogen concentrations. The study further identified an optimal baffle height corresponding to peak ventilation efficiency.

The rapid advancement of the hydrogen energy industry has conclusively demonstrated the technical feasibility of HBNG. In the near future, hydrogen is anticipated to be delivered to residential consumers primarily through HBNG, with its main end-use application being indoor combustion for energy supply [41]. However, current research exhibits two significant gaps: (1) limited consideration of varying HBRs as leakage sources and (2) insufficient focus on indoor environments as the study setting. Both experimental and numerical investigations of HBNG leakage and diffusion in indoor spaces remain notably scarce. To address these research gaps, the present study systematically examines HBNG leakage diffusion characteristics and associated safety risks in indoor environments. A numerical model of a representative indoor space is developed and experimentally validated to ensure reliability. The investigation focuses on three critical aspects: (1) the influence of HBR variations, (2) ventilation effects on leakage and diffusion patterns, and (3) the consequent impacts on indoor safety. Furthermore, the ventilation rate to ensure indoor safety is proposed.

2. Physical and Mathematical Model

2.1. Physical Mode

A numerical investigation was conducted to examine HBNG leakage and diffusion characteristics in indoor spaces. This study employed a three-dimensional physical model representing a residential space measuring 12 m (length) × 4 m (width) × 3 m (height), simplifying the internal structure. The modeled space consists of three distinct areas: (1) a kitchen compartment (3 m × 1.85 m × 3 m) and (2) two adjacent rooms (each 4 m × 4 m × 3 m). Figure 1 illustrates the complete geometric configuration of the computational domain. The HBNG leakage source was positioned at coordinates (6.6, 1.55, 1) within the kitchen space, representing a typical residential gas appliance location.

2.2. Mathematical Model

Prior to numerical simulation, the following simplifying assumptions were adopted:

(1)

No chemical interactions occur between HBNG and air.

(2)

The leakage process is adiabatic (no heat transfer with surroundings).

(3)

Both HBNG and air are modeled as incompressible ideal gases.

(4)

A constant mass flow rate is maintained during leakage with turbulent flow conditions.

These assumptions form the basis for the governing equations implemented in the computational model [42]. This model is applicable to physical mixing and flow dynamics under low pressure conditions, which include:

(1)

The general differential form of the Continuity Equation for Fluid Flow (Mass Conservation Equation):

$${\displaystyle \frac{\partial \rho }{\partial t}}+{\displaystyle \frac{\partial (\rho u_i)}{\partial x_i}}=0$$

(1)

where $\rho$ is the fluid density (kg/m³); $t$ is time (s); $u_i$ is the velocity component of the fluid in the i-direction (m/s, i = x, y, z); $x_i$ represents the coordinate direction of fluid motion (i = x, y, z).

(2)

Mass Conservation Equation for Incompressible Ideal Gases:

$${\displaystyle \frac{\partial (\rho u_i)}{\partial x_i}}=0$$

(2)

(3)

The differential form of the Energy Conservation Equation for Fluid Flow:

$${\displaystyle \frac{\partial (\rho T)}{\partial t}}+{\displaystyle \frac{\partial (\rho u_{j}T)}{\partial x_j}}={\displaystyle \frac{1}{c_p}}{\displaystyle \frac{\partial }{\partial x_j}}\left(k_i{\displaystyle \frac{\partial T}{\partial x_j}}\right)+{\displaystyle \frac{c_{pv}-c_{pa}}{c_p}}\left[\left({\displaystyle \frac{{\mu }_t}{{\sigma }_p}}\right){\displaystyle \frac{\partial \omega }{\partial x_j}}\right]{\displaystyle \frac{\partial T}{\partial x_j}}$$

(3)

where $T$ is the temperature of the leaking fluid (K); $c_p$ is the specific heat capacity of the gas mixture at constant pressure (J/(kg·K)); $k_i$ is the thermal conductivity of the leaking fluid; $c_{pv},c_{pa}$ are the specific heat capacities of the mixed gas and air (J/(kg·K)); ${\mu }_t$ is the turbulent viscosity of the leaking fluid (Pa·s); $\omega$ is the mass fraction of the leaking fluid (kg/s); $u_j$ represents the velocity component in the j-direction (m/s, j = x, y, z)

(4)

The differential form of the Momentum Conservation Equation for Fluid Flow:

$${\displaystyle \frac{\partial (\rho u_i)}{\partial t}}+{\displaystyle \frac{\partial (\rho u_i{u}_j)}{\partial x_j}}=-{\displaystyle \frac{\partial p}{\partial x_i}}+{\displaystyle \frac{\partial {\tau }_{ij}}{\partial x_j}}+F_i$$

(4)

where $p$ is the absolute pressure of the leaking fluid (Pa); ${\tau }_{ij}$ represents the shear stress component acting on the plane parallel to the i-axis (N/m², i = x, y, z); $F_i$ represents the mass force acting on the fluid in the i-direction (N, i = x, y, z).

(5)

The differential form of the Species Transport Equation for Fluid Flow:

$${\displaystyle \frac{\partial (\rho c_s)}{\partial t}}+{\displaystyle \frac{\partial (\rho u_i{c}_s)}{\partial x_i}}={\displaystyle \frac{\partial }{\partial x_i}}\left(D_i\rho {\displaystyle \frac{\partial c_s}{\partial x_i}}\right)$$

(5)

where $c_s$ is the volume concentration of species s in the leaking fluid (kg/m³); $D_i$ is the diffusion coefficient of the leaking fluid component in the gas mixture.

(6)

Ideal Gas Equation of State

Since the pressure of HBNG is relatively low in this study, it can be considered an incompressible ideal gas, satisfying the ideal gas equation:

$$PV=mRT$$

(6)

where $P$ is the absolute pressure of the gas (Pa); $V$ is the volume occupied by the gas (m³); $m$ is the mass of the gas (kg); $R$ is the gas constant (J/(kg·K)); $T$ is the temperature of the gas (K).

(7)

Turbulence Equations

The Realizable k-ε turbulent model with standard wall function is applied in this study, which includes the turbulent kinetic energy equation and the turbulent dissipation rate equation:

$${\displaystyle \frac{\partial (\rho k)}{\partial t}}+{\displaystyle \frac{\partial }{\partial x_i}}(\rho k{u}_i)={\displaystyle \frac{\partial }{\partial x_i}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_k}}\right){\displaystyle \frac{\partial k}{\partial x_i}}\right]+G_k+G_b-\rho \epsilon -Y_m+S_k$$

(7)

$${\displaystyle \frac{\partial (\rho \epsilon )}{\partial t}}+{\displaystyle \frac{\partial }{\partial x_i}}(\rho \epsilon u_i)={\displaystyle \frac{\partial }{\partial x_i}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_{\epsilon }}}\right){\displaystyle \frac{\partial \epsilon }{\partial x_i}}\right]+\rho C_1{S}_{\epsilon }-\rho C_2{\displaystyle \frac{{\epsilon }^2}{k+\sqrt{\nu \epsilon }}}-C_{1\epsilon }{\displaystyle \frac{\epsilon }{k}}{C}_{3\epsilon }{G}_b+S_{\epsilon }$$

(8)

where $k$ is the turbulent kinetic energy; $\epsilon$ is the turbulent dissipation rate; $Y_m$ represents the effects of compressible flow on turbulent dissipation; $G_k,G_b$ are the production terms for buoyancy and mean velocity gradients, respectively; $\mu$ is the dynamic viscosity; ${\sigma }_k,{\sigma }_{\epsilon }$ are the empirical constants for k and ε, with values of 1 and 1.2, respectively; $C_{3\epsilon }$ is a function of velocity gradient relative to gravity; $C_2,C_{1\epsilon }$ are empirical constants, with values of 1.90 and 1.44, respectively; $C_1$ is a model function for variable-speed flow in swirl-dominated regions; $S_k$ is the source term for turbulent kinetic energy; $S_{\epsilon }$ is the source term for turbulent dissipation rate.

2.3. Boundary Conditions

ANSYS Fluent 2021 R1 is used for numerical simulations, with detailed boundary condition settings provided in

Table 1. Boundary Condition Settings.

Domain Boundary	Boundary Type	Parameter Setting
Leak hole	mass-flow-inlet	Flow rate, mole fraction composition, gauge pressure, turbulence
Inner Door	Interior (close), wall (open)	——
Exterior Walls, Exterior Doors, Interior Walls	wall	——
External Window	Wall (close), pressure-outlet (natural ventilation)	Pressure, turbulence
Natural ventilation opening	pressure-outlet (natural ventilation)	Pressure, turbulence
Mechanical exhaust outlet	velocity-inlet (mechanical ventilation)	Pressure, turbulence

.

3. Numerical Simulation

3.1. Mesh Generation

ICEM CFD 2021 R1is employed to generate unstructured mesh for the three-dimensional indoor spaces model. Elements near the leakage source and its surrounding area are refined to improve accuracy. The mesh generated within the computational domain representing is shown in Figure 2.

3.2. Numerical Methods

The simulations utilize the SIMPLE algorithm for pressure-velocity coupling. A second-order upwind scheme is implemented for both temporal and spatial discretization to maintain solution accuracy. The relaxation factors for all discretized equations retain their default values as specified in the computational software. The detailed model and discretization scheme settings are presented in

Table 2. Model and discrete scheme settings.

Item	Settings in ANSYS Fluent
Turbulence model	Realizable k-ε
Wall surface	Standard wall functions
Pressure-velocity coupling	SIMPLE
The spatial discretization of Time and Space	second-order upwind

.

3.3. Calculation Parameters

The simulations utilize the SIMPLE algorithm for pressure-velocity coupling. A second-order upwind scheme is implemented for both temporal and spatial discretization to maintain solution accuracy. The relaxation factors for all discretized equations retain their default values as specified in the computational software. The detailed model and discretization scheme settings are presented in Table 2.

(1)

The simulated accident scenario involves continuous HBNG leakage resulting from hose detachment at a gas appliance connection point. The leakage occurs through a 9 mm diameter pipe opening under an operating pressure of 2 kPa. The mass flow rate during leakage is calculated using the following equation:

$$q_{m,n}={\displaystyle \frac{\pi D^2}{4}}\sqrt{{\displaystyle \frac{n\left(p_1^{\raisebox{1ex}{$n+1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}-p_2^{\raisebox{1ex}{$n+1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}\right)}{(n+1)p_1^{\raisebox{1ex}{$1-n$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}R{T}_1(\frac{\lambda L}{2D}+\frac{1}{n}\ln \frac{p_1}{p_2})}}}$$

(9)

where $q_{m,n}$ is the mass flow rate of gas leakage (kg/s); $p_1$ is the pressure of the gas pipeline (Pa); $p_2$ is the pressure of the gas leakage (Pa); $D$ is the diameter of leakage pipe (m); $T$ is the temperature of gas inside the pipe (K); $\lambda$ is the pipeline friction coefficient; $L$ is the length of the pipeline (distance from entrance to leakage point) (m); $n$ is the polytropic index of gas.

(2)

The explosive limit refers to the concentration range of combustible gas in the air within which flame propagation occurs upon ignition. Specifically, the lower explosive limit (LEL) represents the minimum gas concentration (vol%) required to sustain combustion, calculated as:

$$L_l={\displaystyle \frac{100}{{\displaystyle \sum \frac{y_i}{L_i}}}}$$

(10)

where $L_l$ is the Explosive limit of the target gas (%); $y_i$ is the Volume fraction of components in the gas mixture (%); $L_i$ is the Explosive limit of components in the gas mixture (%).

Table 3. Calculated parameter results.

HBR (%)	0	10	20	50	Pure Hydrogen
Leakage flow rate (m3/h)	2.496	2.615	2.764	3.396	7.016
Leakage velocity (m/s)	10.905	11.426	12.075	14.834	30.651
LEL	5	4.88	4.76	4.44	4
Alarm threshold (25% LEL)	1.25	1.22	1.19	1.11	1

presents the comparative leakage characteristics for different HBRs, including flow rate, velocity, and lower explosion limit (LEL) values. The numerical simulation incorporates the gas leakage flow rates directly from these experimental measurements to ensure model fidelity.

3.4. Simulation Conditions

(1)

Simulation conditions

The simulation conditions are set in

Table 4. Numerical Simulation Conditions for HBNG Leakage and Diffusion in Indoor Spaces.

No.			1	2	3	4	5	6	7	Remarks
	HBR (%)		0	5	10	20	30	50	Pure Hydrogen
1	Ventilation Condition	Close	√	√	√	√	√	√	√
2		Window Open				√				Kitchen
3		Window Open				√				Room 2
4	Diffusion Space	Kitchen				√
5		Entire Space				√
6	Ventilation Opening Position	Position1				√				Central (5.6, 0, 2.3)
7		Position2				√				Central (6.5, 0, 2.3)
8		Position3				√				Central (7.4, 0, 2.3)
9		Position4				√				Central (6.5, 0, 1.5)
10		Position5				√				Central (6.5, 0, 0.7)
11	Ventilation Area	Area 1	√			√		√	√	Area 0.5 m × 0.4 m
12		Area 2						√		Area 0.5 m × 0.8 m
13		Area 3						√		Area 0.5 m × 1.2 m
14	Ventilation Rate	Rate 1	√		√	√		√
15		Rate 2	√		√	√		√
16		Rate 3	√		√	√		√
17		Rate 4	√
18		Rate 5	√		√			√		Rate 5–10

based on the study of HBNG leakage and diffusion characteristics in indoor spaces.

(2)

Monitoring points

The monitoring points coordinates are set according to

Table 5. Location of monitoring points.

No.	Location (m)	No.	Location (m)
P1	(6.50, 0.90, 2.70)	P8	(6.50, 1.50, 1.70)
P2	(7.0, 1.75, 2.70)	P9	(6.50, 0.90, 1.70)
P3	(5.30, 1.50, 2.20)	P10	(6.50, 0.90, 0.30)
P4	(7.70, 1.50, 2.20)	P11	(10.0, 2.0, 2.70)
P5	(6.50, 0.30, 2.20)	P12	(6.0, 2.90, 2.70)
P6	(5.30, 0.30, 1.70)	P13	(2.0, 2.0, 2.70)
P7	(7.70, 0.30, 1.70)

, forming the monitoring point layout diagram shown in Figure 3. The entire computational domain (all zones) is initialized, with all gas parameters set to zero and the temperature set to 293 K. In contrast, other parameters remain at their default values.

4. Model Validations

4.1. Analysis of Mesh Sensitivity

The mesh quality significantly influences the simulation results, while excessive mesh elements elevate computational time and storage demands [43]. To identify the optimal mesh resolution, the model is assessed under the scenario of HBNG leakage in a sealed indoor environment. To achieve mesh sensitivity tests, five different mesh configurations were generated: a coarse mesh with 456,249 elements, a relatively coarse mesh with 761,804 elements, a fine mesh with 1,067,397 elements, an extra-fine mesh with 1,501,892 elements and an over-refined mesh with 1,915,416 elements,

Table 6. Mesh Element Counts with error.

Mesh	No. of Elements	Average Error (%)
Coarse	456,249	7.9
Relatively coarse	761,804	5.4
Fine	1,067,397	4.5
Extra-Fine	1,501,892	4.3
Over-refined	1,915,416	2.1

demonstrates how numerical errors diminish with increasing mesh refinement.

Figure 4 illustrates the temporal variation in methane concentration at monitoring points P1 and P6 for different mesh densities. The methane concentration trends remain consistent across varying elements, with the concentration curves for mesh density 1,067,397 and 1,501,892 demonstrating strong agreement. Based on computational time and storage considerations, the fine mesh with 1,067,397 elements is adopted as it satisfies both accuracy and efficiency requirements. All numerical simulations in this study employ this mesh density.

4.2. Validation of Mathematical Model

The accuracy of the established numerical model is verified using experimental data from HBNG leakage tests (Table 5, No.5) conducted in the kitchen. As illustrated in Figure 4, four gas sensors are positioned in the kitchen to measure gas concentration, corresponding to locations P3, P4, P6, and P7. The leakage source is situated at coordinates (6.6, 1.55, 1), with a diameter of 9 mm and a leakage pressure of 2 kPa. As shown in Figure 5, a comparison between the numerically simulated gas concentration at P6 and the experimental results over a 750 s leakage duration demonstrates good agreement. The deviation between the simulation and experimental results remains below 5%, confirming the reliability of the proposed numerical model and computational method for analyzing the leakage and diffusion of HBNG in indoor spaces.

5. Results and Discussion

5.1. The Concentration Distribution of HBNG

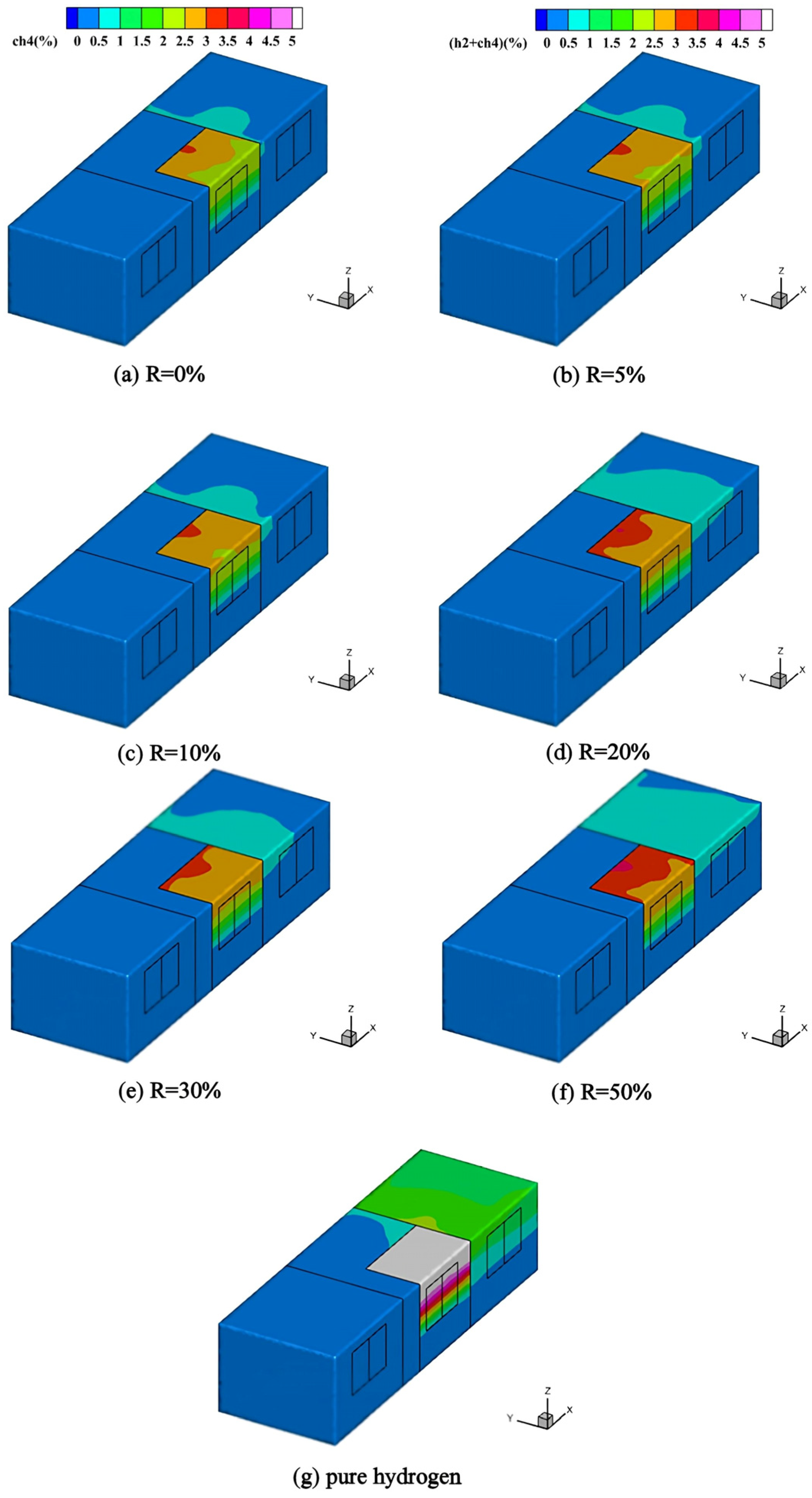
Condition 1 from Table 3 serves as an example to analyze the effect of HBR on the concentration diffusion of HBNG. Figure 6 presents the diffusion contours of different HBRs in indoor spaces at 300 s after leakage. The 3–4% gas concentration region is predominantly located above the leakage source. As HBR increases, the 3–4% concentration region expands along the ceiling, exhibiting a downward diffusion trend. A comparison between Figure 6a,g reveals that the hazardous area and the flammable concentration coverage area of HBNG are significantly larger than those of natural gas. These results demonstrate that increasing the HBR elevates the risk associated with HBNG leakage.

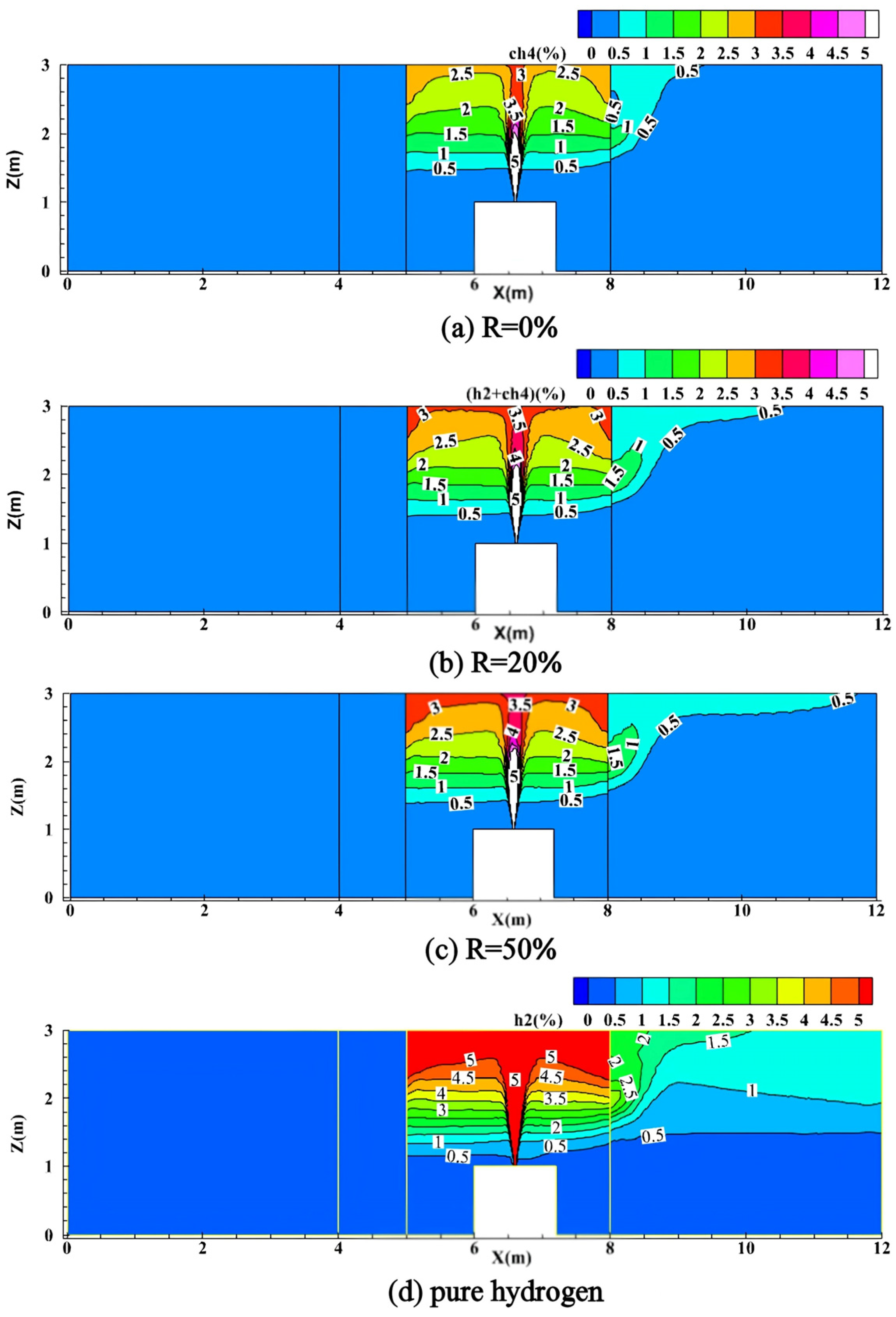
The gas concentration distribution following HBNG leakage in indoor spaces is illustrated by a vertical slice along the X-Z plane at the leakage source, as shown in Figure 7. The leakage process for different HBRs exhibits a confined jet diffusion pattern, with gas concentration above the leakage source being higher than in other regions. The maximum concentrations for 0%, 20%, 50% HBR, and pure hydrogen are 2.5%, 3.5%, 3.5%, and 5.0%, respectively, whereas the corresponding concentrations in Room 2 measure 1%, 1.5%, 2%, and 3%.

As HBR increases, the concentration stratification gradually diminishes. Vertically, the gas concentration rises with indoor height, exhibiting a distinct stratification effect. Horizontally, the gas concentration decreases with distance from the leakage source, with higher concentrations observed near the walls adjacent to the leakage source compared to the central region. The maximum diffusion distance for HBR of 0%, 20%, 50%, and pure hydrogen are 2.4 m, 4 m, 5 m, and 5.4 m.

The results presented in Figure 7c,d demonstrate that increasing HBR leads to significant expansion of the hazardous area where the concentration exceeds the alarm threshold (25% LEL). At R = 50% and pure hydrogen, the concentration reaches the lower explosion limit (LEL) within 300 s after leakage. Furthermore, in the kitchen, a flammable region (gas concentration ≥ LEL) forms at elevations above 2.0 m, indicating that elevated HBR levels substantially enhance the leakage and diffusion risks of HBNG in confined spaces.

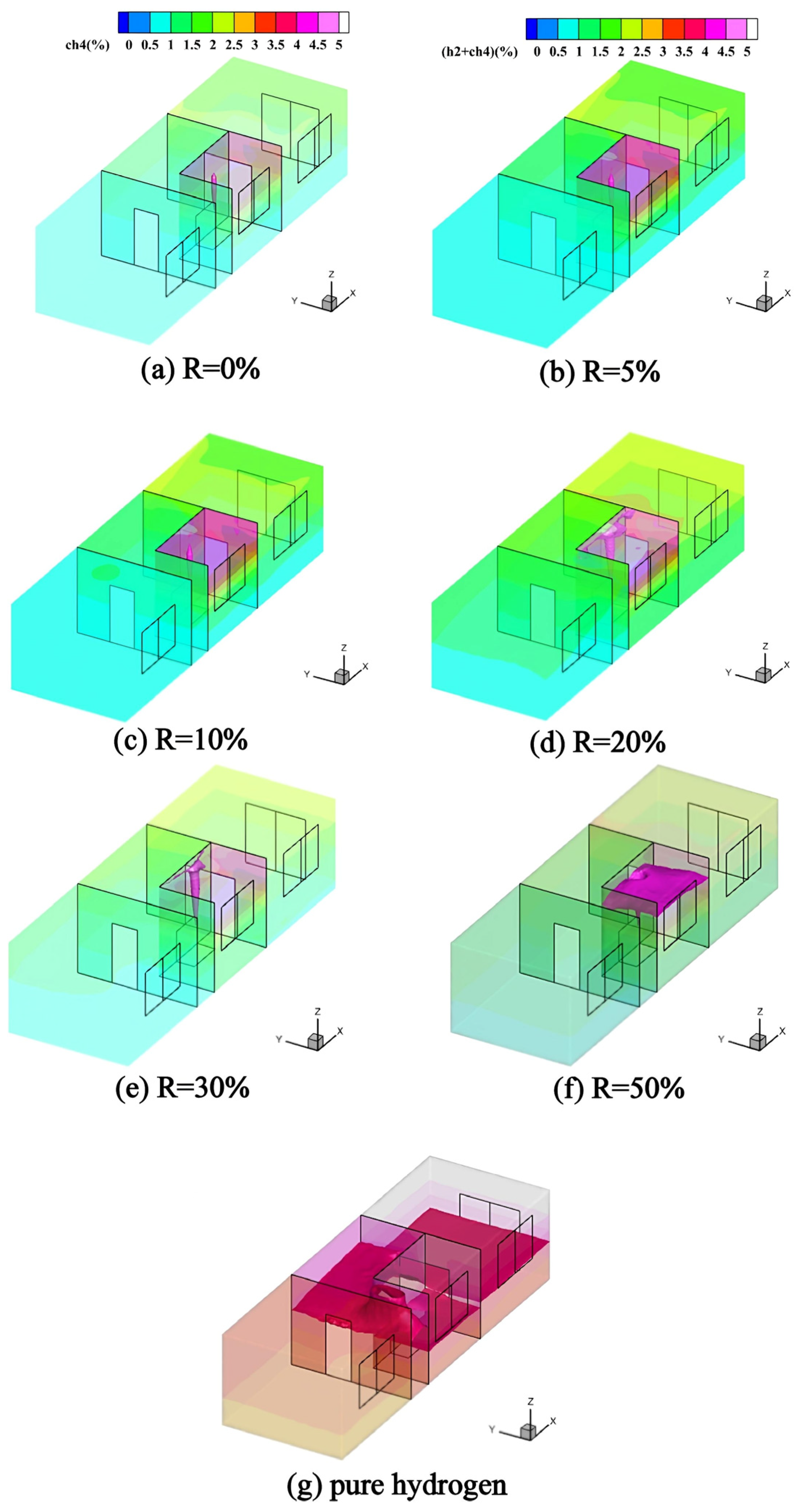
To further examine the influence of time on the leakage and diffusion process, Figure 8 displays the distribution of the flammable region for HBNG at 2400 s. Over time, the indoor flammable region (indicated by red-purple areas in the figure) gradually expands beyond the kitchen into adjacent spaces. For 0–50% HBR, the flammable region remains predominantly confined within the kitchen. In contrast, the flammable region for pure hydrogen exhibits substantial expansion, encompassing most of the kitchen, Room 2, and the corridor. These results demonstrate that as HBR increases, the flammable region following leakage enlarges, resulting in a greater risk of gas leakage hazards in indoor spaces. Notably, R ≥ 50% presents a significantly elevated safety risk.

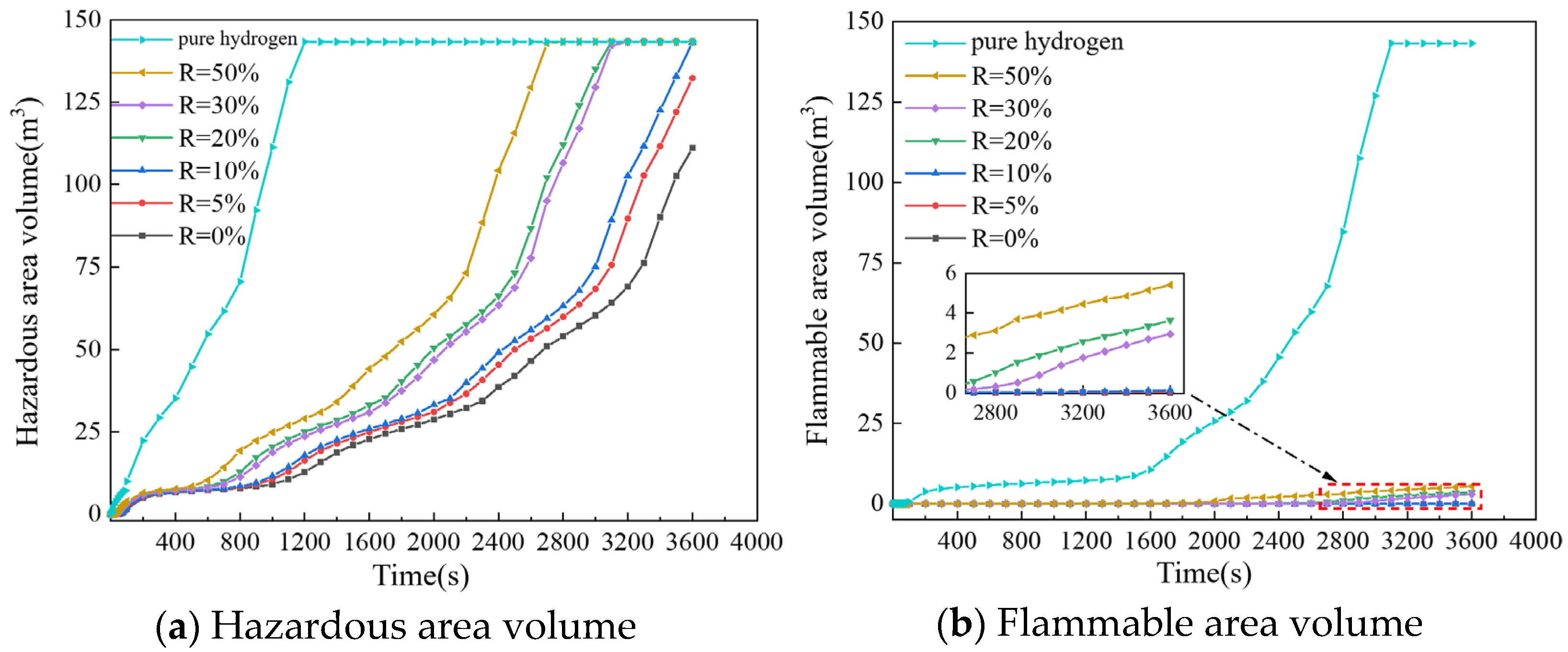
Figure 9 illustrates the variations in hazardous areas and LEL volume within confined indoor spaces under different HBRs of HBNG. As depicted in Figure 9a, increasing the HBR leads to a gradual reduction in the duration during which the entire indoor space remains classified as hazardous. At R = 50%, the hazardous condition persists for 2700 s, while for pure hydrogen, this duration decreases to 1200 s, corresponding to a 55.6% reduction.

As shown in Figure 9b, for R < 20%, the difference in the indoor flammable region compared to pure natural gas leakage remains negligible. However, when R ≥ 20%, the volume of the flammable region increases substantially. The most pronounced effect occurs with pure hydrogen, where the time required for the entire indoor space to become a fully flammable region decreases significantly.

5.2. Influence of Ventilation Location and Area on Diffusion Characteristics

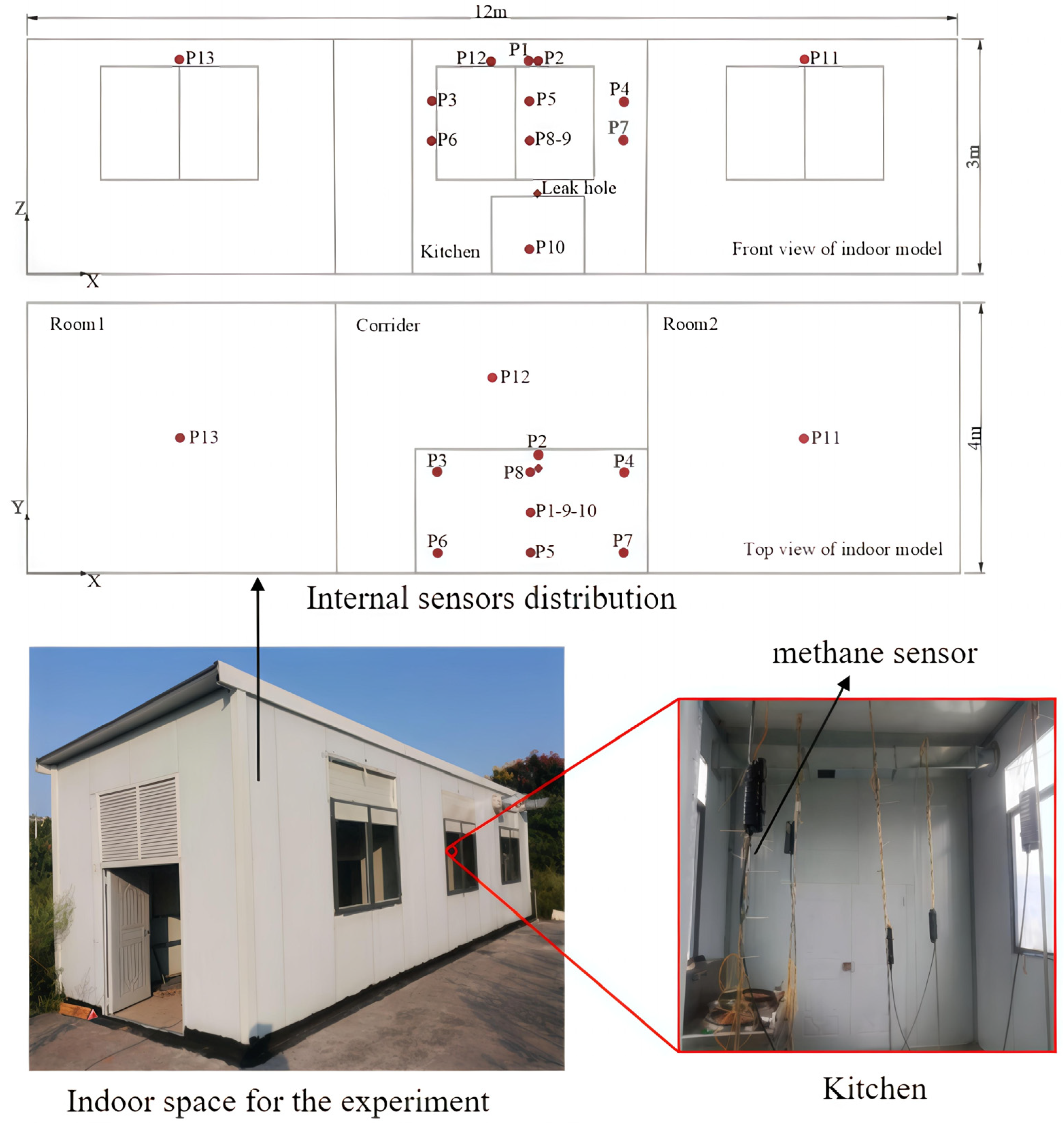
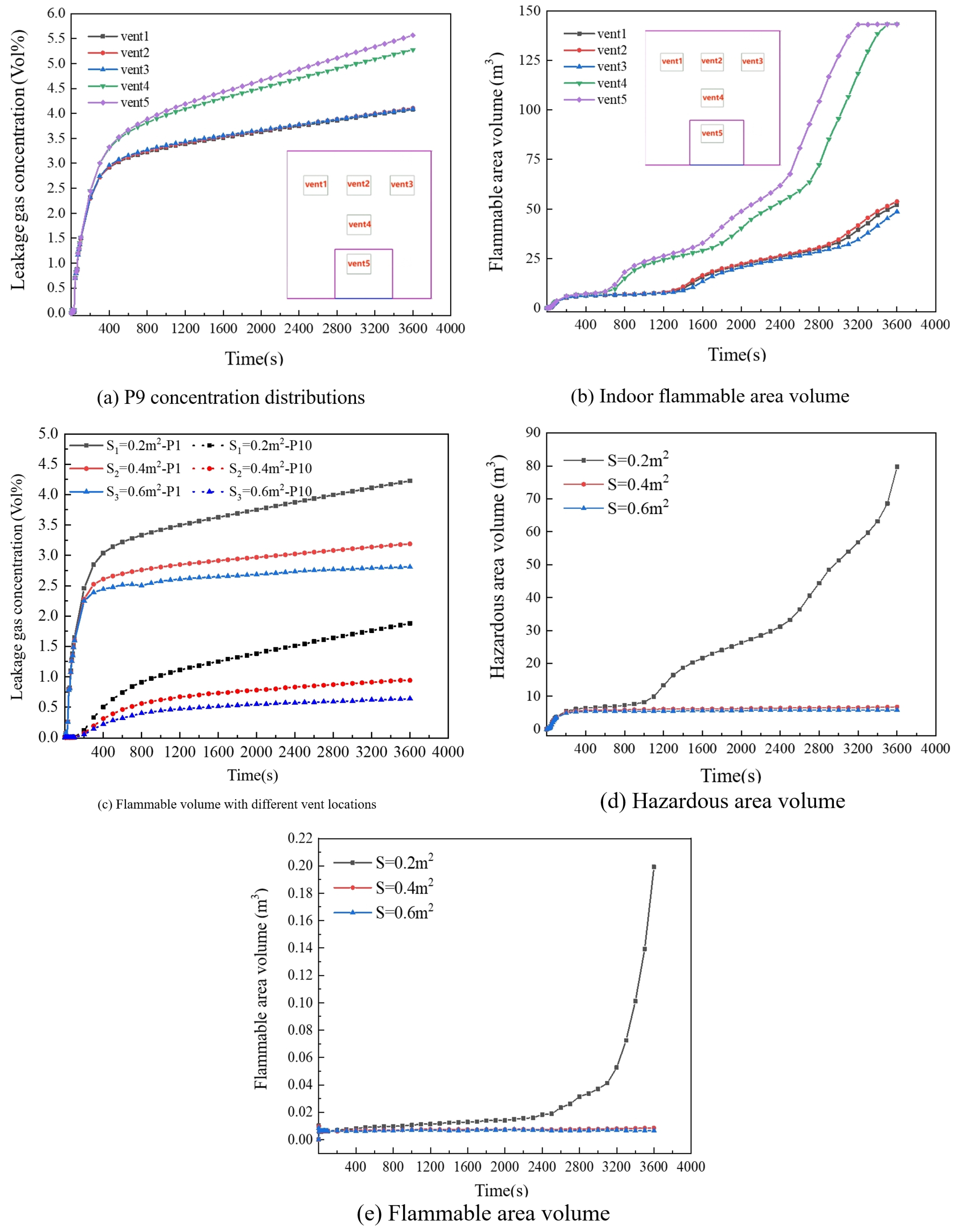
To investigate the influence of different positions of ventilation openings located on the exterior wall near kitchen windows on ventilation effectiveness. Figure 10a depicts the variation in gas concentration at P9 (6.5, 0.9, 2.7) for different natural ventilation opening positions. Altering the horizontal position of the ventilation openings (vent 1, 2, 3; area 0.2 m²) results in gas concentration curves that follow a similar temporal trend and nearly coincide. At 3600 s, the gas concentration reaches 84% of LEL, substantially exceeding the gas alarm threshold. In contrast, adjusting the vertical height of the ventilation openings (vent 2, 4, 5) reveals that the concentration at vent 2 remains consistently below the LEL. However, at vent 4 and vent 5, the concentration surpasses the LEL at approximately 2500 s. Figure 10b presents the variation in flammable region volume for different ventilation positions. The flammable region volume gradually increases when the ventilation openings are set at positions 2, 4, and 5.

Figure 10c presents the concentration variations at P1 (kitchen) and P10 (room 2) under different ventilation opening areas at R = 50%. At 3600 s, the gas concentration at P1 decreases by 24.58% and 44.6% for opening areas of 0.4 m² and 0.6 m², respectively. This indicates a negative correlation between indoor gas concentration and ventilation opening area, with gas concentration gradually decreasing as the ventilation area increases. However, the marginal benefit of increasing the ventilation area diminishes beyond a certain threshold. While greater ventilation areas accelerate the establishment of indoor-outdoor airflow equilibrium, merely expanding the opening size proves insufficient for maintaining gas concentrations below the alarm threshold throughout the entire indoor space.

Figure 10d,e illustrates the variations in the hazardous area and flammable gas volume for different ventilation areas at R = 50%. Increasing the ventilation area from the initial 0.2 m² to 0.4 m² and 0.6 m² reduces the hazardous area and flammable gas volume by 91.51%, 92.67%, 95.73%, and 96.74%, respectively. Additionally, the indoor flammable gas region is almost completely eliminated. Altering the ventilation position yields a maximum reduction of 66.65% in the hazardous gas region volume. In comparison, modifying the ventilation opening area achieves a maximum reduction of 92.67%. These results demonstrate that the ventilation area significantly influences gas concentration and flammable region distribution.

Figure 11 demonstrates that the concentration contour exceeds the alarm threshold under fixed ventilation conditions (Vent 2 position, 0.2 m² area) for different HBRs in HBNG (Red Zone: An area where the gas cloud concentration exceeds the alarm threshold (1.11%)). The results indicate that when the ventilation position and area remain constant, the spatial extent of concentrations exceeding the alarm threshold decreases as HBR increases, following the order: pure hydrogen > 50% > 20% > 0%. The hazardous area volume with HBR of 20%, 50%, and pure hydrogen increased by 1.89, 2.65, and 5.04 times, respectively, compared to natural gas. This demonstrates that HBR higher, the indoor safety risk greater.

It is recommended that indoor spaces utilizing HBNG adopt optimized ventilation strategies, including increased opening areas and elevated vent placement. This approach capitalizes on hydrogen’s buoyancy to enhance safety without substantially increasing construction costs.

5.3. Influence of Ventilation Method on Diffusion Characteristics

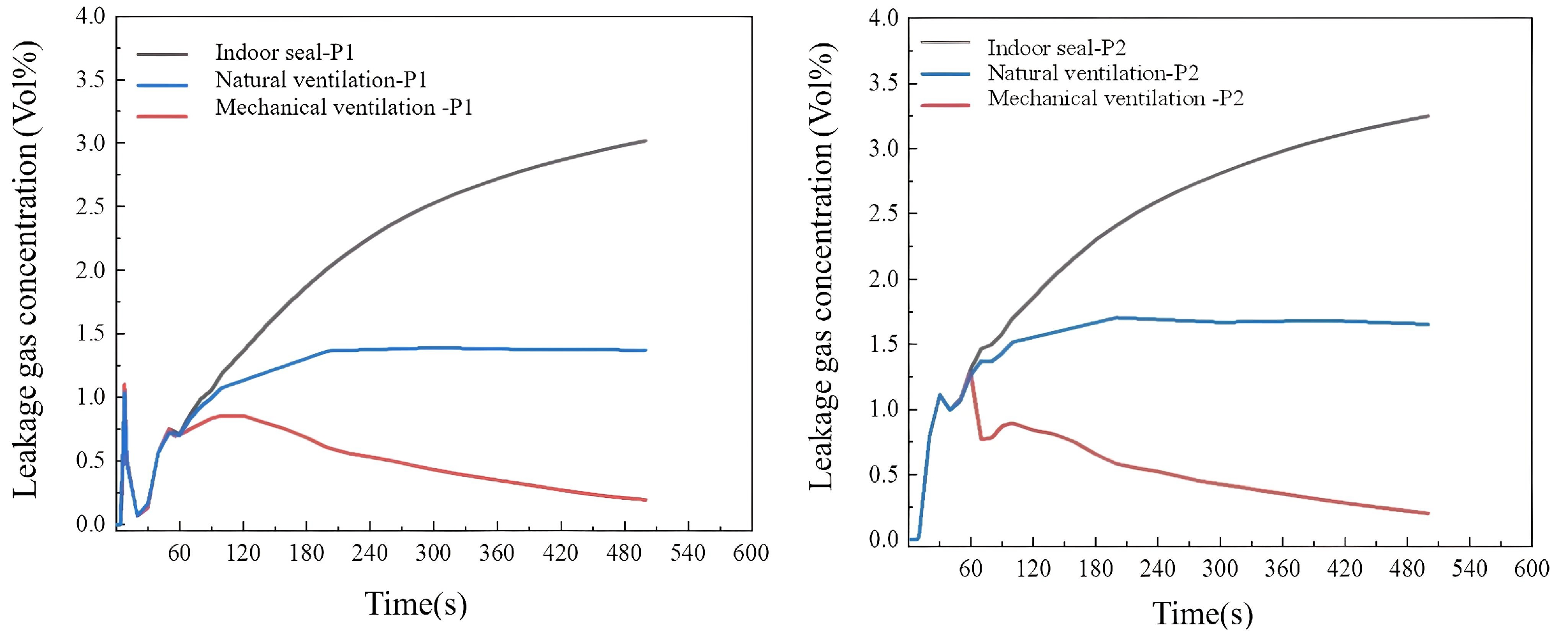
The effects of natural ventilation and mechanical ventilation (ventilation rate: 1134 m³/h) on HBNG leakage and diffusion are analyzed in Figure 12, which shows the concentration variations over time at P1 (6.5, 0.9, 2.7) and P2 (7, 1.75, 2.7) under different ventilation conditions at R = 20%. P2 corresponds to the designated installation location of the indoor gas alarm. Mechanical ventilation initiates automatically when the gas concentration at P2 reaches the alarm threshold.

In sealed conditions, the gas concentration exhibits a gradual increase following an HBNG leakage event. Under natural ventilation (ventilation area: 1.34 m²), the indoor gas concentration initially rises before stabilizing, yet remains above the alarm threshold. By contrast, when mechanical ventilation is activated, the gas concentration at all monitoring points decreases below the alarm threshold within 60 s.

Figure 13a,b,h presents the hazardous area variation at R = 20% and 400 s under different ventilation conditions. The results demonstrate that the hazardous area volume reaches its maximum in enclosed indoor spaces and its minimum under mechanical ventilation. Compared to enclosed indoor conditions, natural ventilation reduces the hazardous area volume by 53.29%, while mechanical ventilation achieves a 99.76% reduction.

Consequently, automatic mechanical ventilation systems interlocked with gas detectors should be required as a core component of the safety standard for homes using HBNG. Mandating these systems in all new construction and retrofit projects must be considered by policymakers, drawing a parallel to existing commercial kitchen regulations, to ensure rapid hazard response.

5.4. Determination of Safety Ventilation Rate

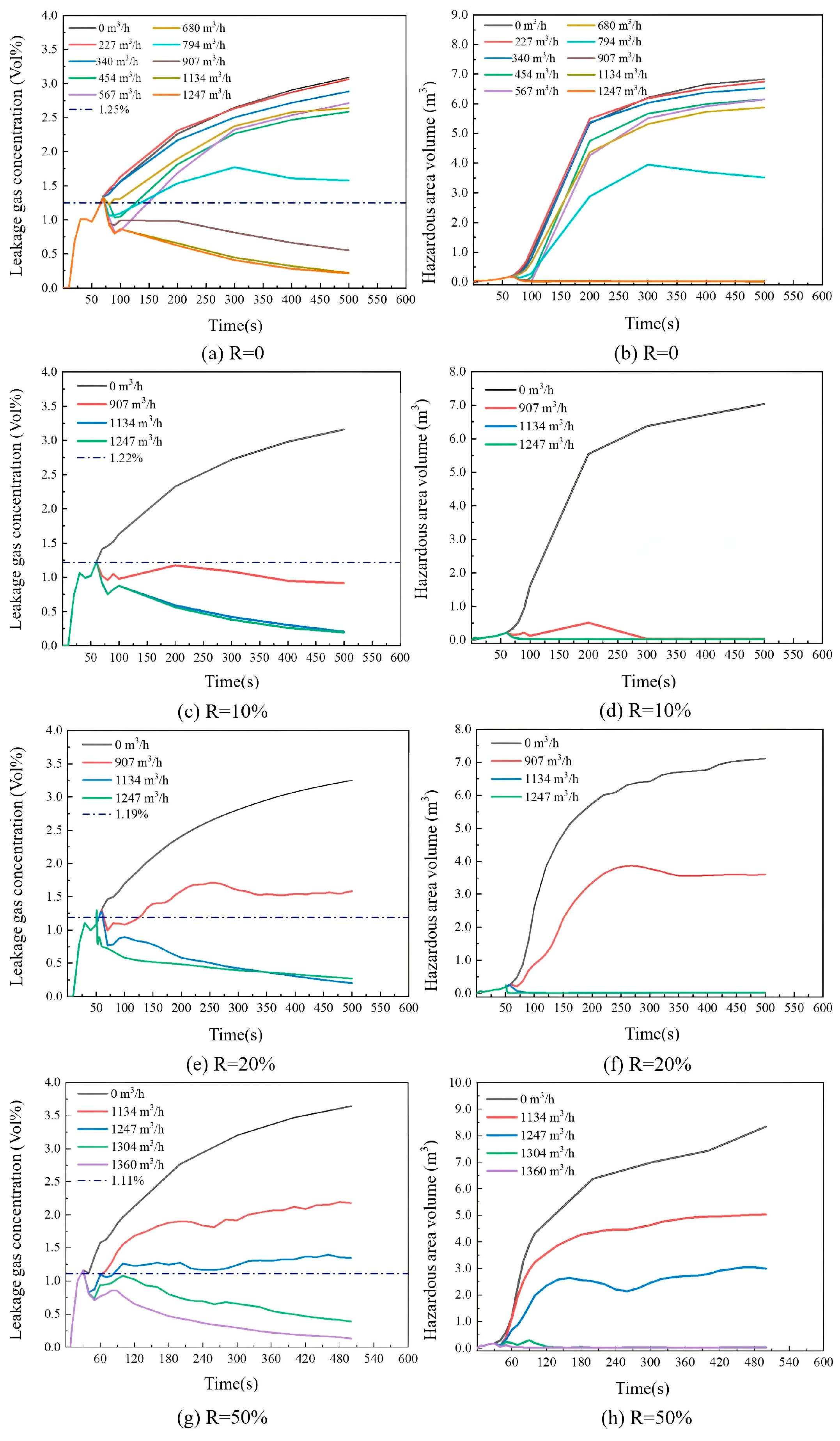
To examine the impact of ventilation rate during continuous leakage, Figure 13c–f,h displays the volume contour of hazardous areas at various time intervals under a ventilation rate of 1304 m³/h with R = 50%. The results indicate that the hazardous area volume progressively increases from 10 s to 30 s, peaking at 30 s when P2 attains the alarm concentration. Following the activation of mechanical ventilation, the hazardous area within the indoor space diminishes gradually over time. By the 240 s, the hazardous area has persisted solely above the leakage source.

To further determine the safe ventilation rate—defined as the rate at which the indoor gas concentration remains consistently below the alarm threshold while nearly eliminating the flammable region—for different HBRs leakage scenarios, the safety criterion is established based on the P2 concentration being lower than the alarm threshold (Table 3).

Figure 14 presents the variations in P2 concentration and the corresponding changes in indoor hazardous areas. Analysis of Figure 14a,b demonstrates that a ventilation rate of 907 m³/h maintains safe conditions for natural gas leakage. Similarly, Figure 14c,d confirm that 907 m³/h also constitutes a safe ventilation rate for R = 10%. However, Figure 14e,f reveal that a higher ventilation rate of 1134 m³/h is required for R = 20%, while Figure 14g,h indicate that 1304 m³/h is necessary to ensure safety at R = 50%.

The variation patterns of leakage concentration and hazardous areas for different HBRs exhibit trends similar to those of natural gas as ventilation rates change. When HBR is constant, indoor gas concentration and hazardous areas decrease with increasing ventilation rate. However, further increases in ventilation yield diminishing reductions in indoor gas concentration once the ventilation rate reaches a level commensurate with the indoor space volume. When the ventilation rate remains constant, higher HBRs lead to gradual increases in indoor gas concentration and hazardous areas. Additionally, the alarm response time at P2 advances, with response times for 10%, 20%, and 50% HBRs occurring 9.1%, 24.24%, and 59.1% earlier than that of natural gas. The safe ventilation rates for different HBRs are presented in

Table 7. Safe ventilation rate of HBNG.

HBR (%)	0	10	20	50
Safe ventilation rate (m3/h)	907	907	1134	1304

. We emphasize that the safe ventilation rate was obtained within the context of our model, and the proposed methodology is meant to guide its determination.

6. Conclusions

This study numerically investigates the leakage, diffusion, and safety of HBNG in indoor spaces. The effects of HBR, ventilation opening position, mode, area, and rate on leakage diffusion and indoor safety are analyzed. The main conclusions are as follows:

• Following an HBNG leak, the gas initially accumulates at the top of the indoor space and then spreads outward along the ceiling and downward along the walls. The diffusion range expands with increasing HBR. Gas concentration rises with vertical height, exhibiting distinct stratification, with higher concentrations near the walls adjacent to the leakage point compared to the central region.
• Ventilation height exerts a more significant influence on gas concentration and flammable volume than horizontal positioning. Higher ventilation openings correlate with reduced gas concentration and smaller flammable regions. Adjusting ventilation position and area decreases the indoor hazardous area by 66.65% and 92.67%, respectively. At a fixed ventilation configuration, the hazardous volume for HBRs of 20%, 50%, and pure hydrogen exceeds that of natural gas by factors of 1.89, 2.65, and 5.04.
• Mechanical ventilation effectively mitigates indoor gas concentration, maintaining a safe environment during leakage. Increasing the ventilation rate to match the space size yields diminishing returns in further improving indoor safety.
• A method for determining the safe ventilation rate is proposed. For HBRs of 0%, 10%, 20%, and 50%, the required safe ventilation rates are 907 m³/h, 907 m³/h, 1134 m³/h, and 1304 m³/h, respectively, under the studied conditions.