A Novel Optimal Control Method for Building Cooling Water Systems with Variable Speed Condenser Pumps and Cooling Tower Fans
Abstract
1. Introduction
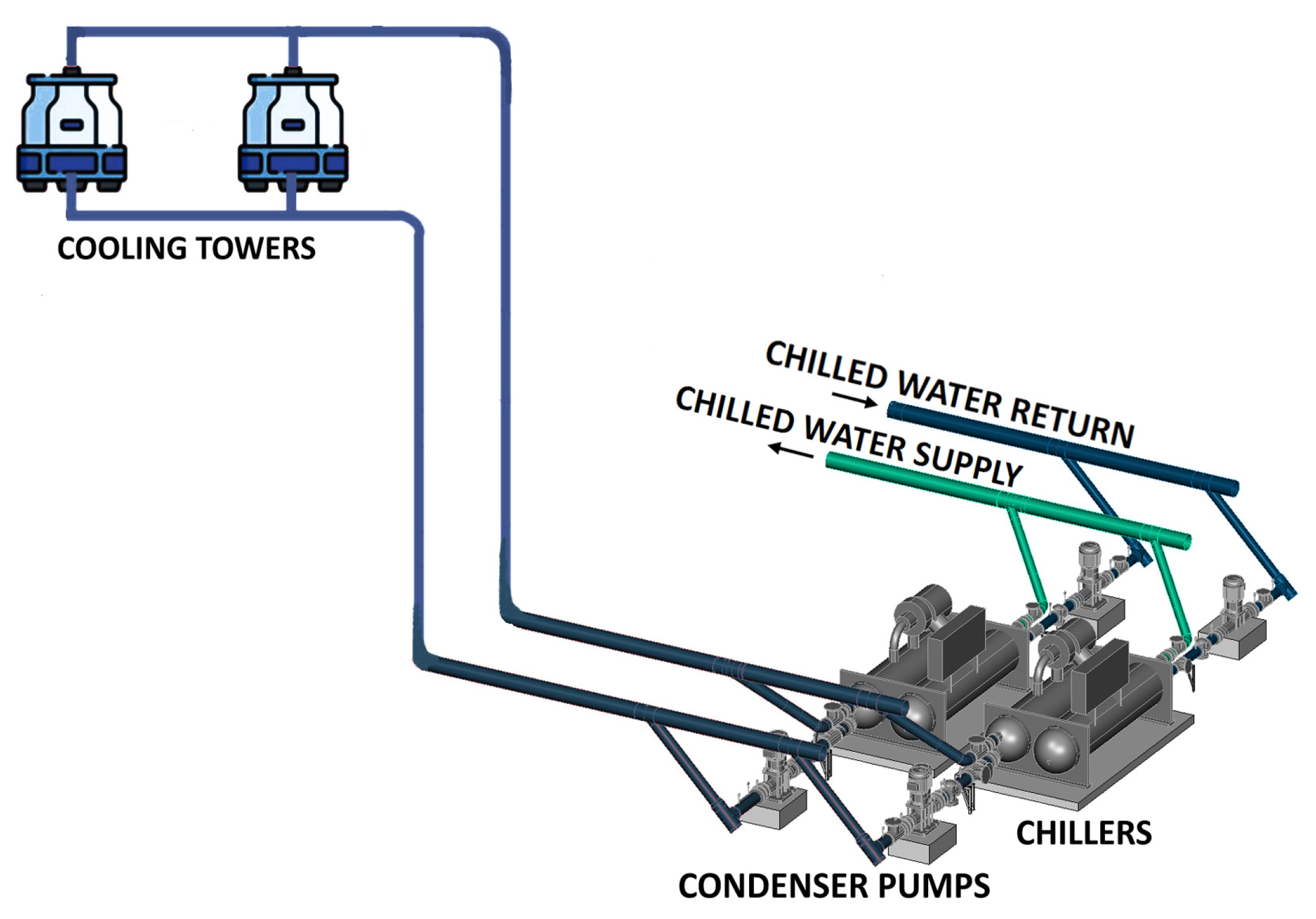
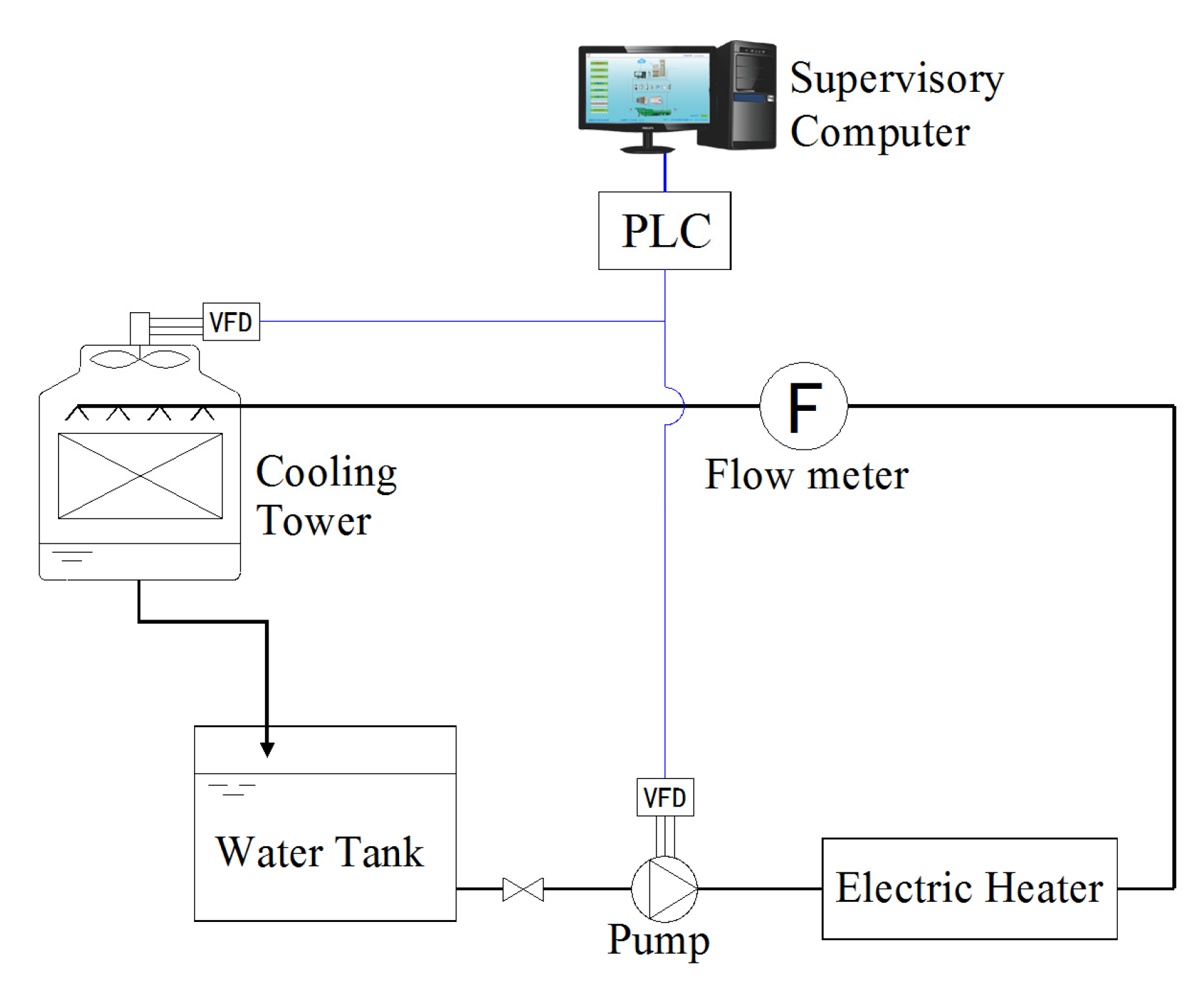
2. Description of the Studied Cooling Water System
3. Formulation of the Optimal Control Method
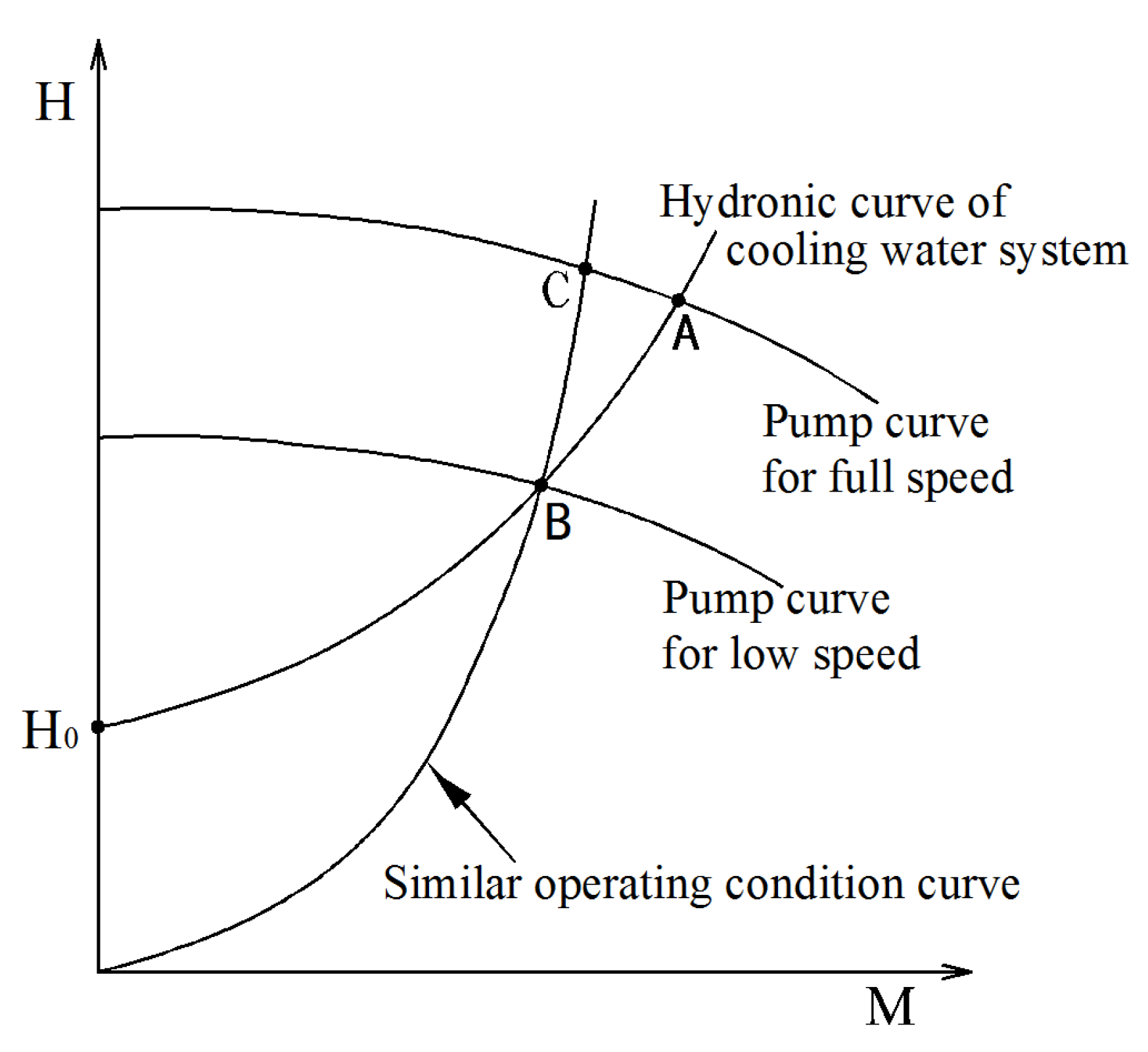
3.1. Control Strategy
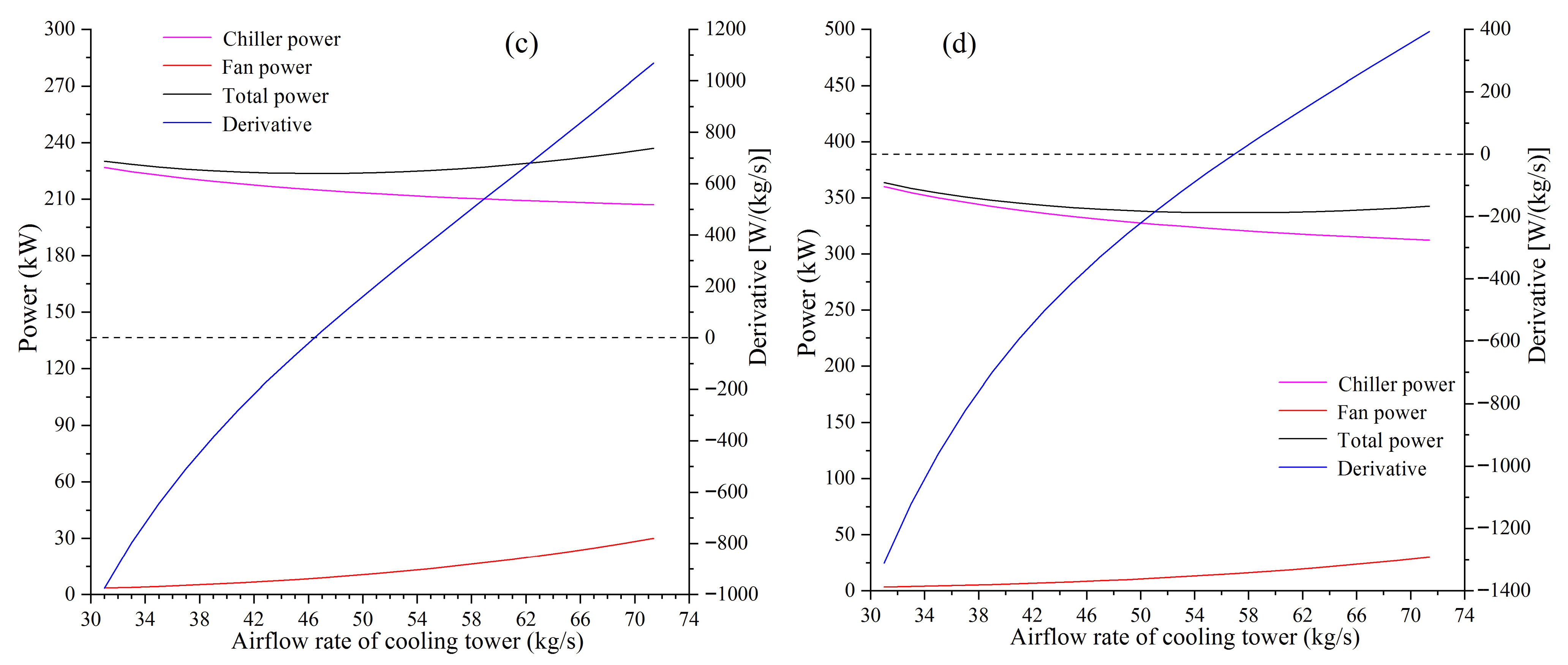
3.2. Calculation Method for the Derivative of Total Power
4. Validation and Performance of the Proposed Optimal Control Strategy
4.1. Determination of the Parameters of Chiller and Pump Models
4.2. Validation Results
4.3. Performance Analysis
5. Implementation of the Direct Optimal Control Method
5.1. Optimization Algorithms and Direct Control Method
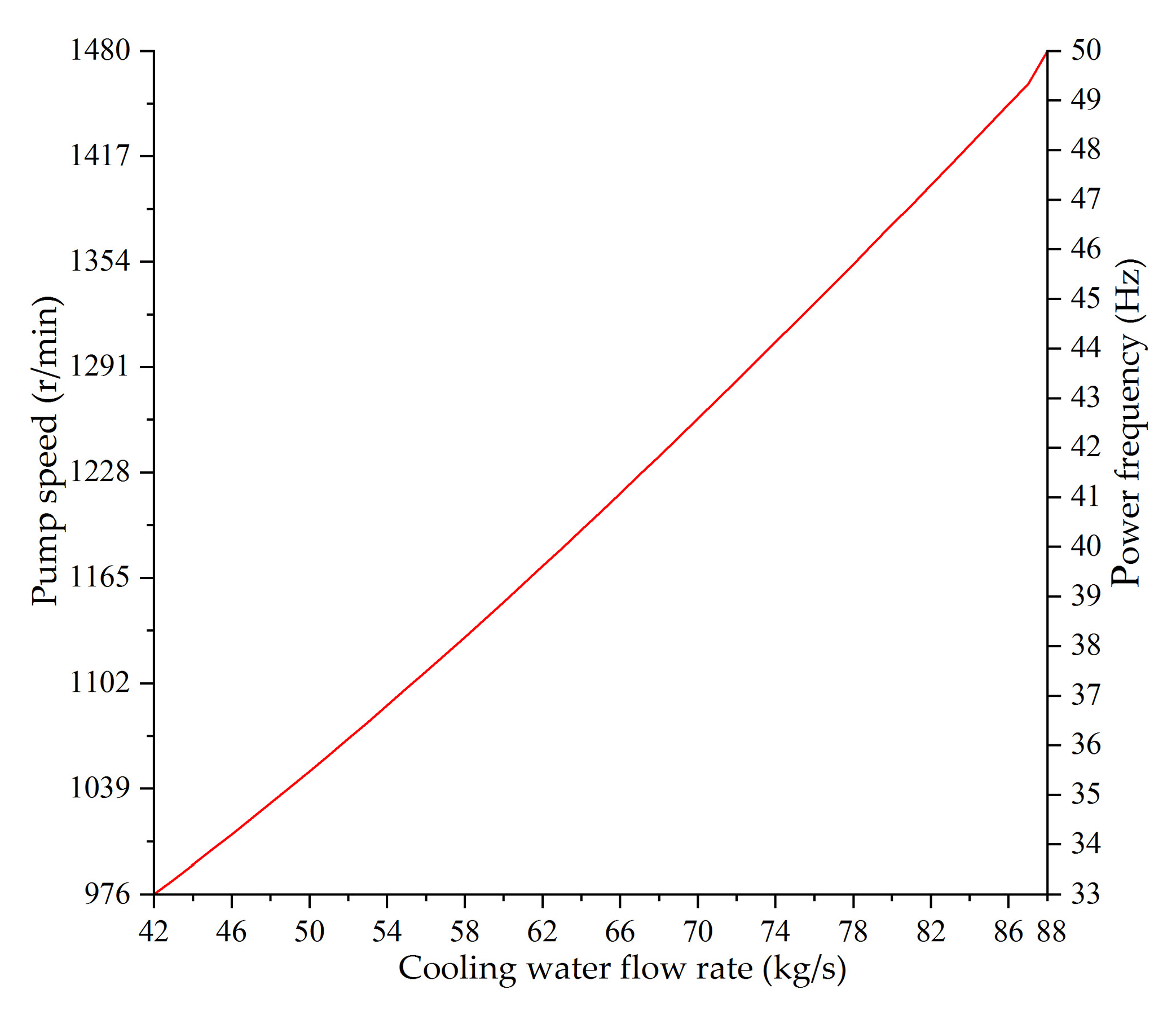
5.2. Experiment Validation of the Direct Control Method for Condenser Pumps and Fans
6. Conclusions
- The impact of changes in IWTC on the optimal CWFR can be neglected, and it is feasible to decouple water flow rate optimization and airflow rate optimization. The total power approaches a minimum when the derivative of total power with respect to water/air flow rate approaches zero.
- The power-saving rate has much to do with the PLR of the chiller plant. The lower the plant PLR is, the higher the power-saving rate is. The total power can be reduced by 13.2% at a plant PLR of 20% compared to the constant speed pump/fan mode.
- The flow rate of condenser pumps is not proportional to pump speed and power frequency. In the direct optimal control method, the optimal CWFR and ARCT are transformed to corresponding power frequencies of pumps and fans. Experimental results show that the optimization results can be obtained immediately and VFDs can regulate their output frequencies to be equal to the optimized power frequencies for pump and fan taking 4~8 s of time.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CWFR | Cooling water flow rate |
| ARCT | Airflow rate of cooling tower |
| PID | Proportional–integral–derivative |
| PLR | Part-load ratio |
| VFD | Variable-frequency drive |
| IWTC | Inlet water temperature of condenser |
| COP | Coefficient of performance |
| NMBE | Normalized mean bias error |
| CVRMSE | Coefficient of variation of the rootmeansquared error |
| PLC | Programmable logic controller |
References
- Coa, A.; Keane, M.M.; Torrens, J.I.; Corry, E. Building operation and energy performance: Monitoring, analysis and optimisation toolkit. Appl. Energy 2013, 101, 310–316. [Google Scholar] [CrossRef]
- Pérez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008, 40, 394–398. [Google Scholar] [CrossRef]
- Liang, X.; Chen, S.; Zhu, X.; Jin, X.; Du, Z. Domain knowledge decomposition of building energy consumption and a hybrid data-driven model for 24-h ahead predictions. Appl. Energy 2023, 344, 121244. [Google Scholar] [CrossRef]
- Shanghai Committee of Municipal and Rural Construction. Monitoring and Analysis Report of Building Energy Consumption and Carbon Emissions in Shanghai; Shanghai Committee of Municipal and Rural Construction: Shanghai, China, 2023. [Google Scholar]
- Cao, Y.; Wang, C.; Wang, S.; Fu, X.; Ming, X.G. Energy modeling and optimization of building condenser water systems with all-variable speed pumps and tower fans: A case study. Build. Simul. 2024, 17, 1085–1111. [Google Scholar] [CrossRef]
- Xue, Q.; Jin, X.Q.; Jia, Z.Y.; Lyu, Y.; Du, Z.M. Optimal control strategy of multiple chiller system based on background knowledge graph. Appl. Energy 2024, 375, 124132. [Google Scholar] [CrossRef]
- Liang, X.B.; Liu, Y.; Chen, S.L.; Li, X.L.; Jin, X.Q.; Du, Z.M. Physics-informed neural network for chiller plant optimal control with structure-type and trend-type prior knowledge. Appl. Energy 2025, 390, 125857. [Google Scholar] [CrossRef]
- Hu, B.; Guo, Y.H.; Huang, W.J.; Jin, J.X.; Zou, M.X.; Zhu, Z.K. Energy-saving optimization of HVAC Systems using an antlion optimizer with enhancements. Buildings 2024, 14, 2842. [Google Scholar] [CrossRef]
- Zhang, D.; Luh, P.B.; Fan, J. Chiller plant operation optimization: Energy-efficient primary-only and primary–secondary systems. IEEE Trans. Autom. Sci. Eng. 2018, 15, 341–355. [Google Scholar] [CrossRef]
- Karami, M.; Wang, L. Particle swarm optimization for control operation of an all-variable speed water-cooled chiller plant. Appl. Therm. Eng. 2018, 130, 962–978. [Google Scholar] [CrossRef]
- Lu, L.; Cai, W.; Soh, Y.C. HVAC system optimization—Condenser water loop. Energy Convers. Manag. 2004, 45, 613–630. [Google Scholar] [CrossRef]
- Yao, Y.; Lian, Z.W.; Hou, Z.J. Optimal operation of a large cooling system based on an empirical model. Appl. Therm. Eng. 2004, 24, 2303–2321. [Google Scholar] [CrossRef]
- Wang, L.; Lee, E.W.M.; Yuen, R. A practical approach to chiller plants’ optimisation. Energy Build. 2018, 169, 332–343. [Google Scholar] [CrossRef]
- He, K.; Fu, Q.M.; Lu, Y.; Wang, Y.Z.; Luo, J.; Wu, H.J.; Chen, J.P. Predictive control optimization of chiller plants based on deep reinforcement learning. J. Build. Eng. 2023, 76, 107158. [Google Scholar] [CrossRef]
- Kang, W.H.; Yoon, Y.; Lee, J.H.; Song, K.W.; Chae, Y.T.; Lee, K.H. In-situ application of an ANN algorithm for optimized chilled and condenser water temperatures set-point during cooling operation. Energy Build. 2021, 233, 110666. [Google Scholar]
- Ma, Z.; Wang, S.; Xu, X.; Xiao, F. A supervisory control strategy for building cooling water systems for practical and real-time applications. Energy Convers. Manag. 2008, 49, 2324–2336. [Google Scholar] [CrossRef]
- Yu, F.W.; Chan, K.T. Optimization of water-cooled chiller system with load-based speed control. Appl. Energy 2008, 85, 931–950. [Google Scholar]
- Jiang, X.; Long, W.; Li, M. Optimum control strategy for all-variable speed chiller plant. J. Cent. South Univ. 2011, 18, 573–579. [Google Scholar]
- Huang, S.; Zuo, W.; Sohn, M.D. Improved cooling tower control of legacy chiller plants by optimizing the condenser water setpoint. Build. Environ. 2017, 111, 33–46. [Google Scholar]
- Jiang, W.; Reddy, T.A. Reevaluation of the Gordon-Ng performance models for water-cooled chillers. ASHRAE Trans. 2003, 109 Pt 2, 4655. [Google Scholar]
- American Society of Heating, Refrigerating and Air-conditioning Engineers (ASHRAE). Energy estimating and modeling methods. In ASHRAE Handbook—Fundamentals; ASHRAE Inc.: Atlanta, GA, USA, 2009. [Google Scholar]
- Gordon, J.M.; Ng, K.C. Cool Thermodynamics; Cambridge International Science Publishing: Cambridge, UK, 2000. [Google Scholar]
- Jin, G.-Y.; Cai, W.-J.; Lu, L.; Lee, E.L.; Chiang, A. A simplified modeling of mechanical cooling tower for control and optimization of HVAC systems. Energy Convers. Manag. 2007, 48, 355–365. [Google Scholar] [CrossRef]
- Park, S.K.; Moon, H.J.; Min, K.C.; Hwang, C.; Kim, S. Application of a multiple linear regression and an artificial neural network model for the heating performance analysis and hourly prediction of a large-scale ground source heat pump system. Energy Build. 2018, 165, 206–215. [Google Scholar] [CrossRef]
- GB/T 18430.1-2024; National Standard. Water Chilling (Heat Pump) Packages Using the Vapor Compression Cycle. Standards Press of China: Beijing, China, 2024. (In Chinese)
- Rishel, J.; Durkin, T.; Kincaid, B. HVAC Pump Handbook, 2nd ed.; McGraw-Hill Professional: New York, NY, USA, 2006. [Google Scholar]

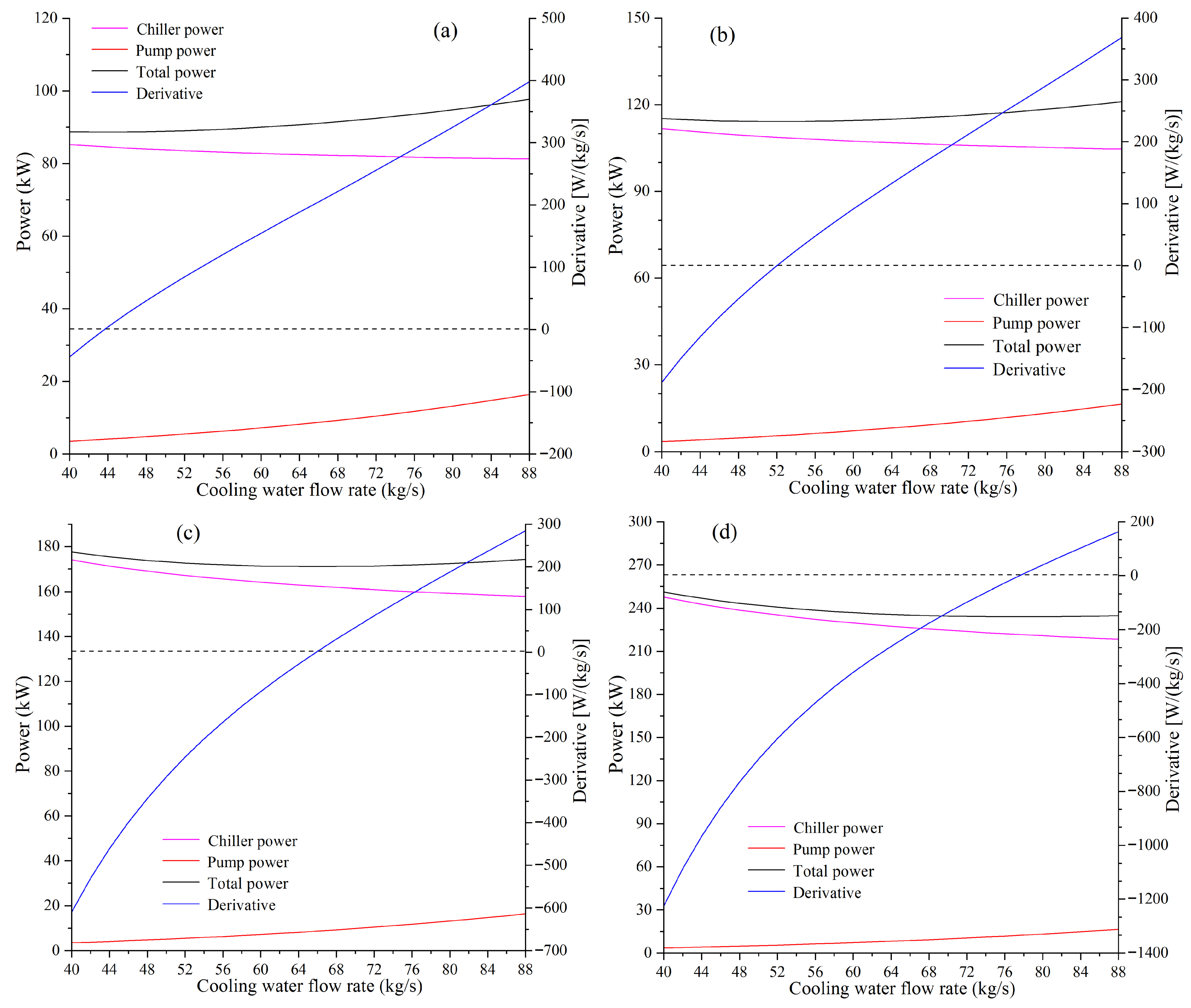
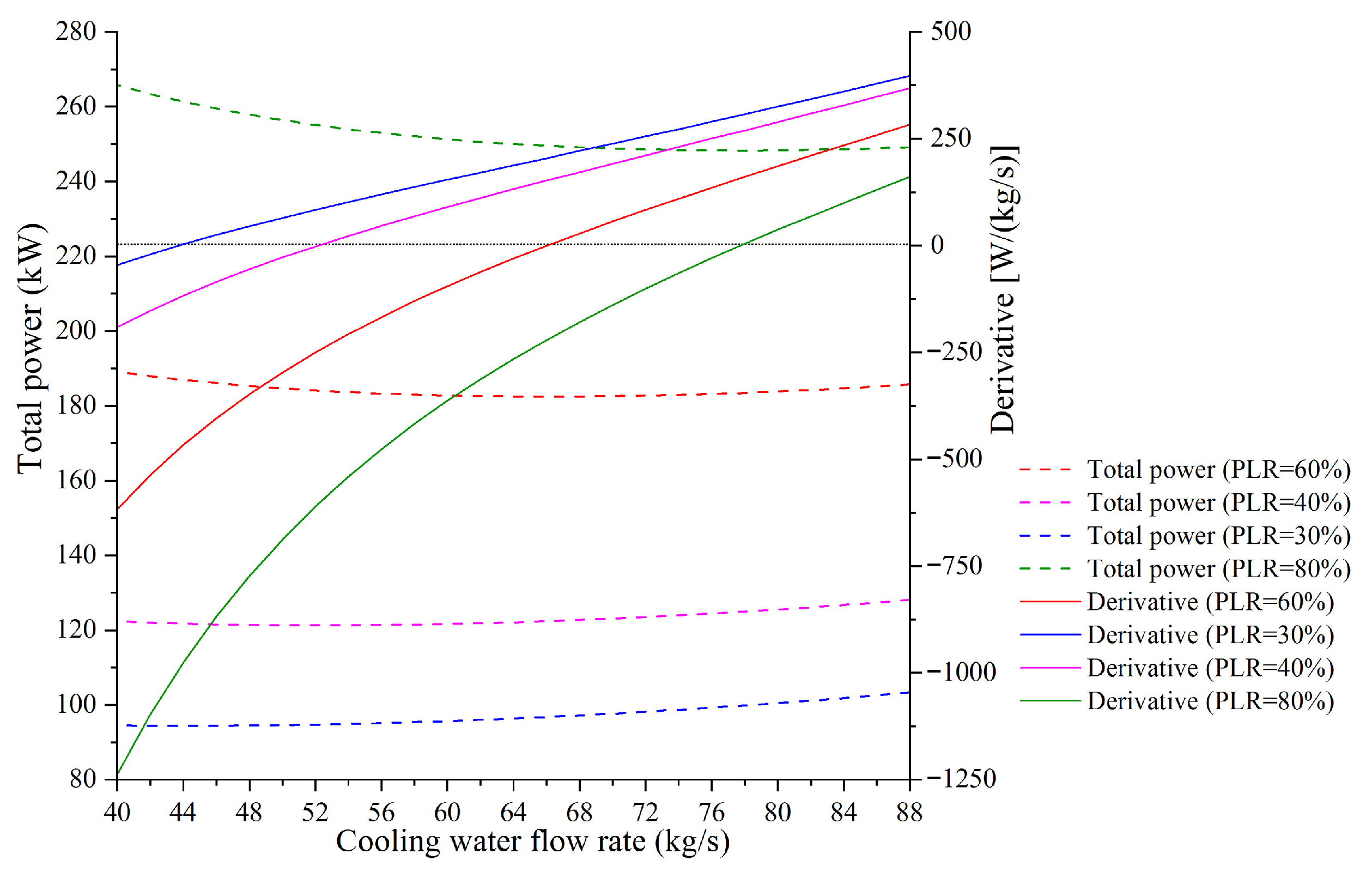
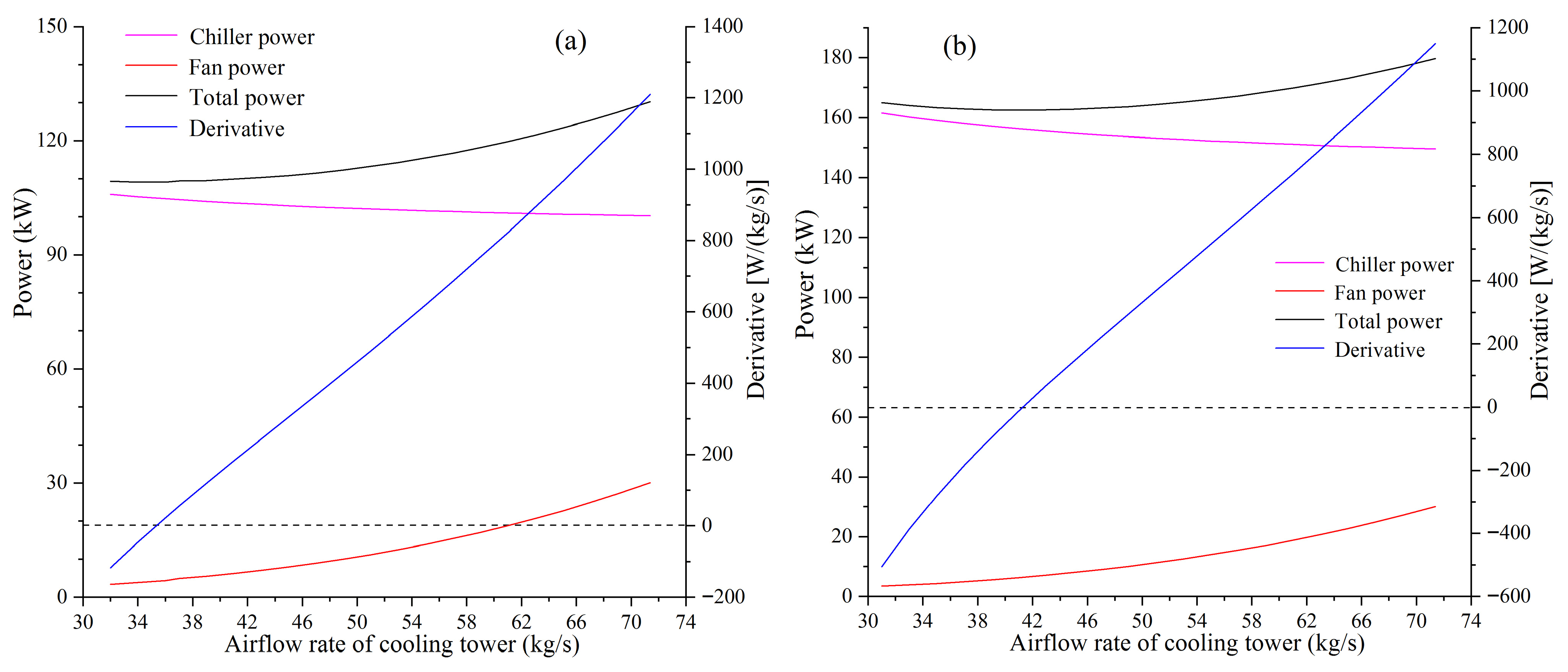


| Model | C1 | C2 | C3 | NMBE | CVRMSE |
|---|---|---|---|---|---|
| Model for the conditions of PLR at 40~100% | −0.026569 | 436.793687 | 0.0054616 | −4.8789 × 10−4 | 0.0218 |
| Model for the conditions of PLR at 15~40% | 0.0195159 | 223.754763 | 0.0063577 | 5.8995 × 10−6 | 0.0282 |
| Operating Condition 1 | Operating Condition 2 | Operating Condition 3 | Operating Condition 4 | ||
|---|---|---|---|---|---|
| Plant PLR | 60% | 40% | 30% | 20% | |
| Chiller PLR | 60% | 80% | 60% | 40% | |
| Number of operating chillers | 2 | 1 | 1 | 1 | |
| Number of operating cooling towers | 2 | 2 | 2 | 2 | |
| Optimal CWFR (kg/s) | 66 | 78 | 66 | 52 | |
| Optimal airflow rate (kg/s) | 57 | 46.5 | 41.4 | 35.7 | |
| Variable-speed pump/fan mode | Chiller power (kW) | 321.2 | 214.7 | 156.2 | 104.7 |
| Pump power (kW) | 17.4 | 12.5 | 8.7 | 5.5 | |
| Fan power (kW) | 15.4 | 8.9 | 6.3 | 4.3 | |
| Total power (kW) | 354 | 236.1 | 171.2 | 114.5 | |
| Constant-speed pump/fan mode | Chiller power (kW) | 308 | 216.7 | 154 | 100.6 |
| Pump power (kW) | 32.8 | 16.4 | 16.4 | 16.4 | |
| Fan power (kW) | 30 | 15 | 15 | 15 | |
| Total power (kW) | 370.8 | 248.1 | 185.4 | 132 | |
| Total power saved (kW) | 16.8 | 12 | 14.2 | 17.5 | |
| Power-saving rate | 4.53% | 4.84% | 7.66% | 13.23% | |
| Set Values of Chiller Load (kW) | Number of Searches for Optimal CWFR (Times) | Number of Searches for Optimal ARCT (Times) | Optimal CWFR (kg/s) | Optimal ARCT (kg/s) | Optimized Power Frequency of Pump (Hz) | Optimized Power Frequency of Fans (Hz) |
|---|---|---|---|---|---|---|
| 528 | 45 | 42 | 44 | 30 | 33.27 | 21 (fixed at 25 Hz) |
| 704 | 36 | 37 | 52 | 36 | 36.10 | 25 |
| 880 | 29 | 34 | 59 | 38 | 38.51 | 26.61 |
| 1055 | 23 | 31 | 66 | 41 | 40.69 | 28.71 |
| 1232 | 17 | 29 | 71 | 43 | 42.95 | 30.11 |
| 1407 | 11 | 26 | 78 | 46 | 45.29 | 32.21 |
| 1583 | 6 | 24 | 82 | 48 | 47.29 | 33.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Guan, L.; Yang, C.; Ge, P.; Xia, J. A Novel Optimal Control Method for Building Cooling Water Systems with Variable Speed Condenser Pumps and Cooling Tower Fans. Buildings 2025, 15, 3568. https://doi.org/10.3390/buildings15193568
Chen X, Guan L, Yang C, Ge P, Xia J. A Novel Optimal Control Method for Building Cooling Water Systems with Variable Speed Condenser Pumps and Cooling Tower Fans. Buildings. 2025; 15(19):3568. https://doi.org/10.3390/buildings15193568
Chicago/Turabian StyleChen, Xiao, Lingjun Guan, Chaoyue Yang, Peihong Ge, and Jinrui Xia. 2025. "A Novel Optimal Control Method for Building Cooling Water Systems with Variable Speed Condenser Pumps and Cooling Tower Fans" Buildings 15, no. 19: 3568. https://doi.org/10.3390/buildings15193568
APA StyleChen, X., Guan, L., Yang, C., Ge, P., & Xia, J. (2025). A Novel Optimal Control Method for Building Cooling Water Systems with Variable Speed Condenser Pumps and Cooling Tower Fans. Buildings, 15(19), 3568. https://doi.org/10.3390/buildings15193568





