Optimisation of Interlayer Bond Strength in 3D-Printed Concrete Using Response Surface Methodology and Artificial Neural Networks
Abstract
1. Introduction
- 1.
- Build an RSM quadratic model to characterise interpretable main effects, curvature, and interactions, with full ANOVA and diagnostics;
- 2.
- Develop and tune an ANN regressor to capture non-linearities beyond quadratic forms and benchmark its predictive accuracy against RSM;
- 3.
- Perform a comparative evaluation of models using parity plots and coefficient of determination , and visualise areas of agreement and discrepancy through contour surfaces;
- 4.
- Conduct desirability-based optimisation (single- and bi-factor planes) to identify practically feasible optima in the , TimeGap) space;
- 5.
- Perform ANN-based sensitivity analysis using partial dependence plots (PDPs) to identify and rank the relative influence of material and process variables on bond strength;
- 6.
- Provide model-informed guidance for print-process control and mix design specific to interlayer interface performance.
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Response Surface Methodology
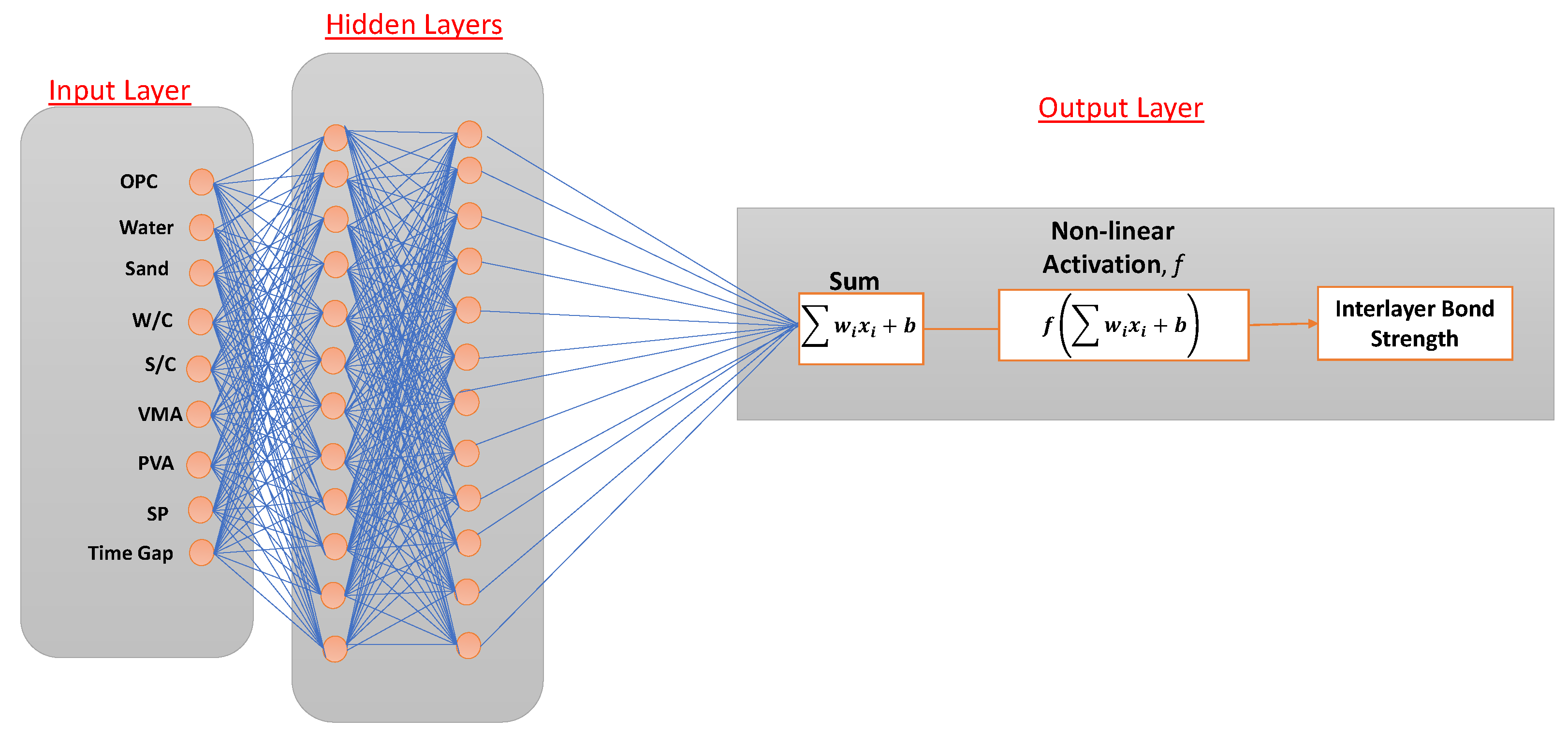
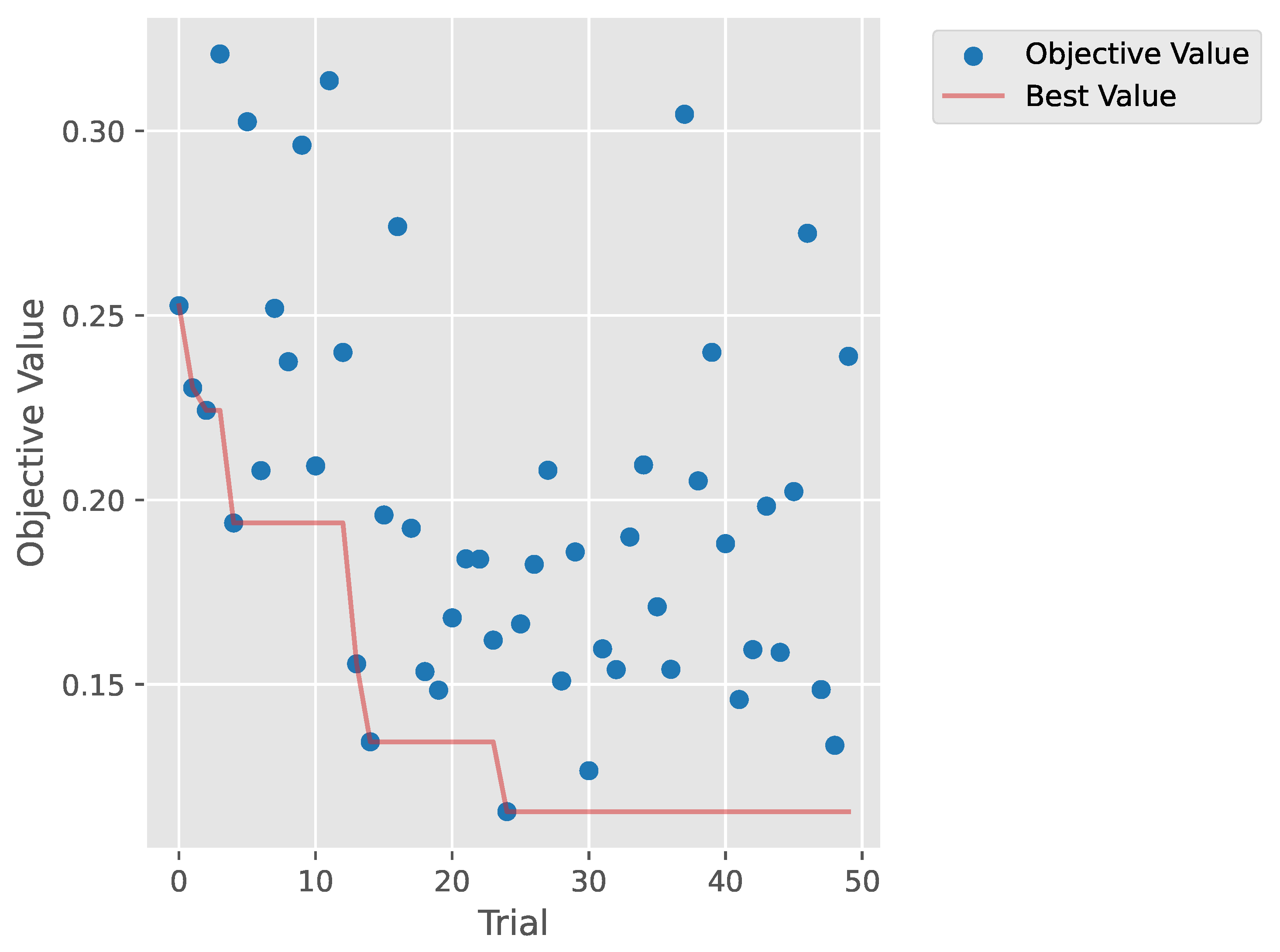
2.2.2. Artificial Neural Network
3. Results and Discussion
3.1. Response Surface Methodology Modelling
3.2. Artificial Neural Network Modelling
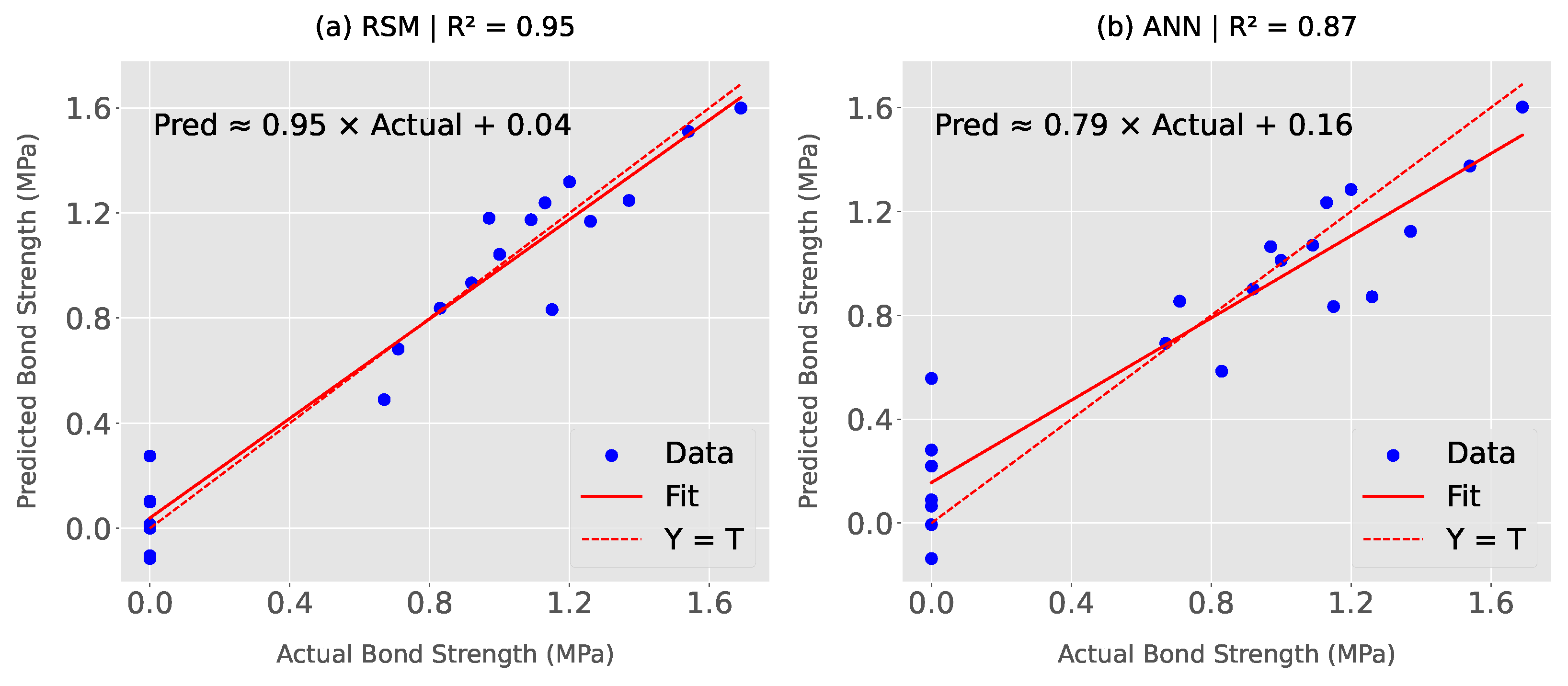
3.3. Model Performance Comparison
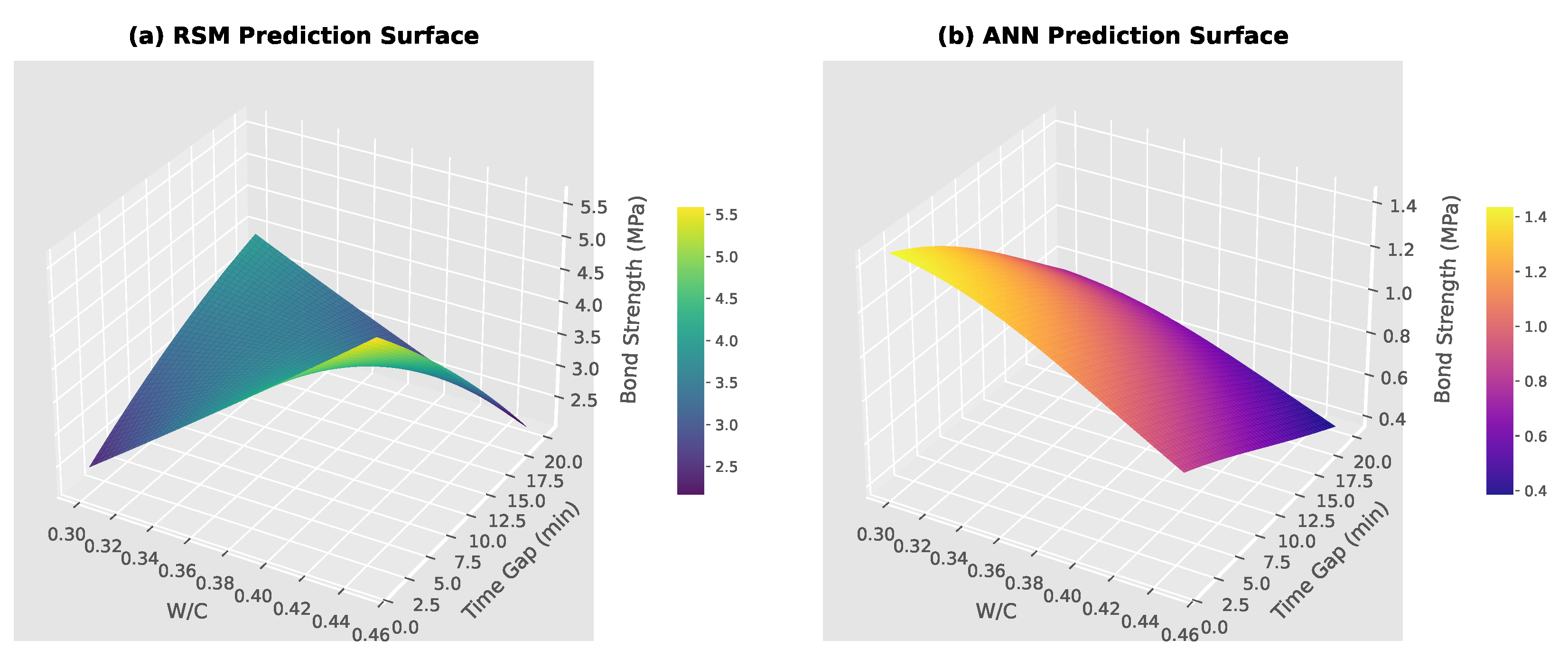
3.4. Comparison of Response Surfaces and Contour Maps
3.5. Desirability and Multi-Objective Optimisation
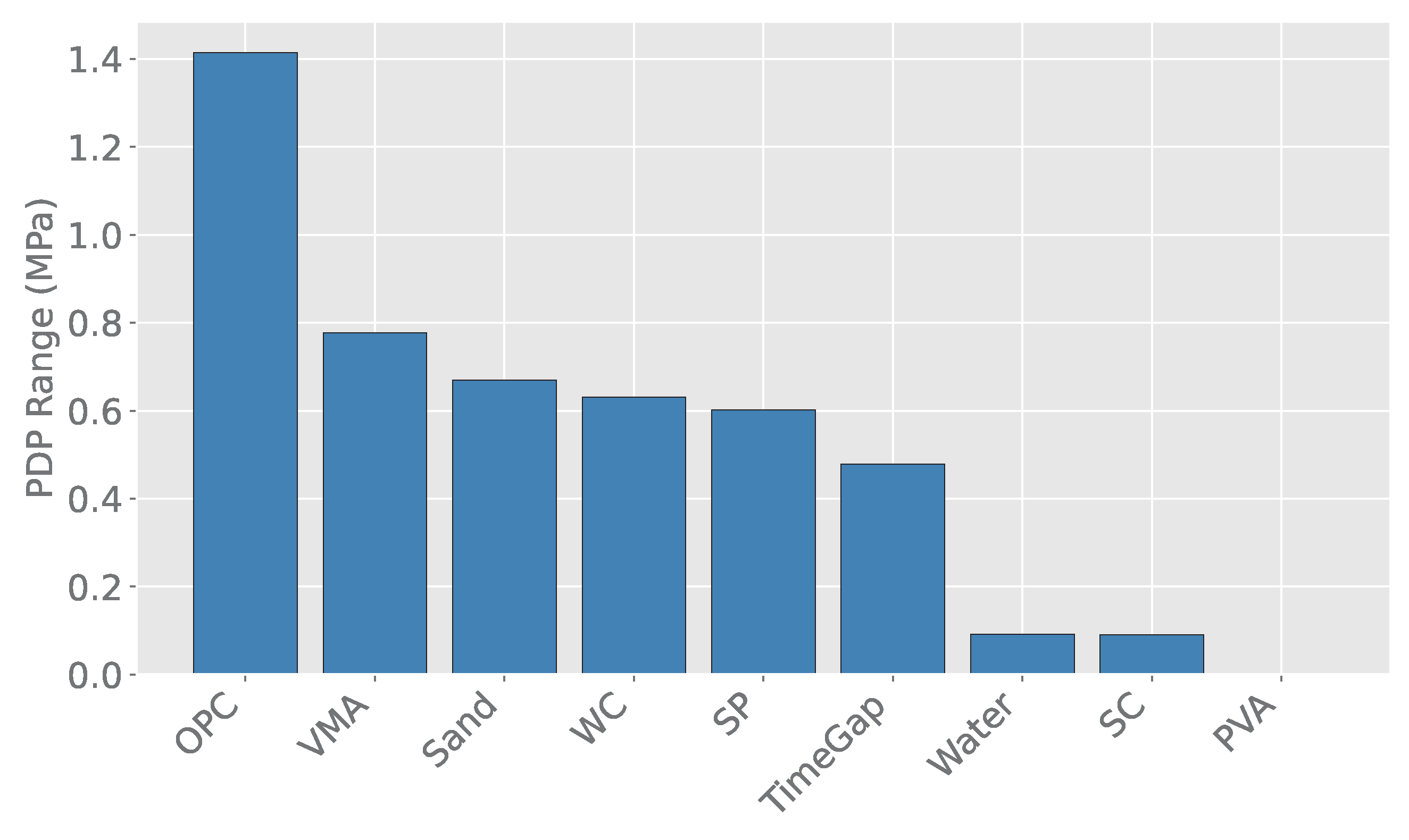
3.6. Sensitivity Analysis
4. Limitations and Future Work
5. Conclusions
- 1.
- The RSM model provided accurate and interpretable predictions of bond strength, achieving a high coefficient of determination () and low prediction error (maximum absolute errors = 0.16 MPa). ANN captured complex non-linearities but showed reduced predictive stability due to the limited dataset (, maximum absolute errors = 0.29 MPa).
- 2.
- Desirability-based optimisation identified that maintaining a low W/C ratio and minimising the interlayer time gap are critical to enhancing interlayer bond strength. Optimal values predicted by RSM suggested a W/C ratio of approximately 0.45 and a time gap below 5 min.
- 3.
- Sensitivity analysis using PDP confirmed that OPC content and W/C ratio are the most influential variables, followed by superplasticiser dosage and silica content, while water content, viscosity-modifying agent, and time gap have moderate effects. Sand and fibre content are less influential within the studied range.
- 4.
- The combined use of RSM and ANN provides complementary benefits: RSM delivers interpretable models for mix design, while ANN offers flexibility for non-linear behaviour when sufficiently large and diverse datasets are available.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| ANOVA | Analysis of Variance |
| MAE | Mean Absolute Error |
| OPC | Ordinary Portland Cement |
| PDP | Partial Dependence Plot |
| PVA | Polyvinyl Alcohol |
| RSM | Response Surface Methodology |
| RMSE | Root Mean Squared Error |
| SC | Silica Content |
| S/C | Sand–Cement Ratio |
| SP | Superplasticiser |
| VMA | Viscosity-Modifying Agent |
| W/C | Water–Cement Ratio |
References
- Bos, F.; Menna, C.; Pradena, M.; Kreiger, E.; da Silva, W.L.; Rehman, A.; Weger, D.; Wolfs, R.; Zhang, Y.; Ferrara, L.; et al. The realities of additively manufactured concrete structures in practice. Cem. Concr. Res. 2022, 156, 106746. [Google Scholar] [CrossRef]
- Li, Z.; Hojati, M.; Wu, Z.; Piasente, J.; Ashrafi, N.; Duarte, J.; Radlińska, A. Fresh and hardened properties of extrusion-based 3D-printed cementitious materials: A review. Sustainability 2020, 12, 5628. [Google Scholar] [CrossRef]
- Shahzad, Q.; Umair, M.; Waqar, S. Bibliographic analysis on 3D printing in the building and construction industry: Printing systems, material properties, challenges, and future trends. J. Sustain. Constr. Mater. Technol. 2022, 7, 198–220. [Google Scholar] [CrossRef]
- Pemas, S.; Sougioultzi, K.; Kouroutzidou, C.; Stefanidou, M.; Konstantinidis, A.; Pechlivani, E. Enhancing clay-based 3D-printed mortars with polymeric mesh reinforcement techniques. Polymers 2024, 16, 2182. [Google Scholar] [CrossRef] [PubMed]
- Shaw, R.; Maurya, K.; Maity, D. 3D concrete printing: A road map for future of automated construction in India. In Proceedings of the 36th National Convention of Civil Engineers & National Conference on Innovation, Mechanization and Modern Techniques in Civil Engineering, Ranchi, India, 23–24 October 2021. [Google Scholar] [CrossRef]
- Satish, S.; Umar, T. Bridging innovation and practice: Assessing the readiness for 3D printing in construction. Eng. Constr. Archit. Manag. 2025. [Google Scholar] [CrossRef]
- Firoozi, A.; Firoozi, A. 3D printing in civil engineering: Pioneering affordable housing solutions. J. Civ. Eng. Urban. 2024, 14, 63–75. [Google Scholar] [CrossRef]
- Kantaros, A.; Zacharia, P.; Drosos, C.; Papoutsidakis, M.; Pallis, E.; Ganetsos, T. Smart infrastructure and additive manufacturing: Synergies, advantages, and limitations. Appl. Sci. 2025, 15, 3719. [Google Scholar] [CrossRef]
- Tay, Y.W.D.; Ting, G.H.A.; Qian, Y.; Panda, B.; He, L.; Tan, M.J. Time gap effect on bond strength of 3D-printed concrete. Virtual Phys. Prototyp. 2018, 14, 104–113. [Google Scholar] [CrossRef]
- Lee, H.; Kim, J.; Moon, J.; Kim, W.; Seo, E. Evaluation of the mechanical properties of a 3D-printed mortar. Materials 2019, 12, 4104. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, S.; Kim, J.; Jeong, H.; Han, S.; Kim, K. Interlayer bond strength of 3D printed concrete members with ultra high performance concrete (UHPC) mix. Buildings 2024, 14, 2060. [Google Scholar] [CrossRef]
- Kloft, H.; Krauss, H.W.; Hack, N.; Herrmann, E.; Neudecker, S.; Varady, P.A.; Lowke, D. Influence of process parameters on the interlayer bond strength of concrete elements additive manufactured by Shotcrete 3D Printing (SC3DP). Cem. Concr. Res. 2020, 134, 106078. [Google Scholar] [CrossRef]
- Putten, J.; De Schutter, G.; De Tittelboom, K. Surface modification as a technique to improve inter-layer bonding strength in 3D-printed cementitious materials. RILEM Tech. Lett. 2019, 4, 33–38. [Google Scholar] [CrossRef]
- Shahzad, Q.; Li, F. Interfacial bond effects on the shear strength and damage in 3D-printed concrete structures: A combined experimental and numerical study. Eng. Fract. Mech. 2025, 315, 110840. [Google Scholar] [CrossRef]
- Hager, I.; Golonka, A.; Putanowicz, R. 3D printing of buildings and building components as the future of sustainable construction? Procedia Eng. 2022, 151, 292–299. [Google Scholar] [CrossRef]
- Peng, W.; Xia, H.; Wu, J.; Fang, Z.; Zhang, X. Dynamic boronate ester chemistry facilitating 3D printing interlayer adhesion and modular 4D printing of polylactic acid. Adv. Funct. Mater. 2025, 35, 2503682. [Google Scholar] [CrossRef]
- Qi, P.; Wang, Z.; Yu, R.; Pei, Q.; Yang, Q.; Wang, C.; Yang, L. Optimization design and regression model analysis of mechanical properties of 3D printed concrete. J. Build. Eng. 2025, 108, 112998. [Google Scholar] [CrossRef]
- Wang, C.; Lian, J.; Fang, Y.; Fan, G.; Yang, Y.; Huang, W.; Shi, S. Rheological optimization of 3D-printed cementitious materials using response surface methodology. Materials 2025, 18, 3933. [Google Scholar] [CrossRef]
- Jawad, H.H.; Kordani, N.; Bagheri, A.; Derazkola, H.A. Optimization of 3D printing parameters for enhanced mechanical strength: Effects of glass fiber reinforcement and fill ratio using RSM and ANOVA. J. Compos. Sci. 2025, 9, 63. [Google Scholar] [CrossRef]
- Patil, S.; Ramesh, B.; Sathish, T.; Saravanan, A. RSM-based modelling for predicting and optimizing the rheological and mechanical properties of fibre-reinforced laterized self-compacting concrete. Heliyon 2024, 10, e25973. [Google Scholar] [CrossRef]
- Cui, W.; Ji, D.; Shen, L.; Su, S.; Shi, X.; Liu, J.; Bai, Z.; Sun, Y.; Gong, J.; Tao, Y. A neural network-based model for assessing 3D printable concrete performance in robotic fabrication. Results Eng. 2025, 27, 105970. [Google Scholar] [CrossRef]
- Arif, M.; Jan, F.; Rezzoug, A.; Afridi, M.A.; Luqman, M.; Khan, W.A.; Kujawa, M.; Alabduljabbar, H.; Khan, M. Data-driven models for predicting compressive strength of 3D-printed fiber-reinforced concrete using interpretable machine learning algorithms. Case Stud. Constr. Mater. 2024, 21, e03935. [Google Scholar] [CrossRef]
- Sheiati, S.; Ranjbar, N.; Frellsen, J. Neural network predictions of the simulated rheological response of cement paste in the FlowCyl. Neural Comput. Appl. 2021, 33, 13027–13037. [Google Scholar] [CrossRef]
- Peng, L.; Miao, X.; Zhu, J.-X.; Zhang, M.-Q.; Zheng, X.-Q.; Li, H.-Y.; Wang, Y.; Jiang, X.; Huang, B.-T. Hybrid machine learning and multi-objective optimization for intelligent design of green and low-carbon concrete. Sustain. Mater. Technol. 2025, 45, e01605. [Google Scholar] [CrossRef]
- Azhagarsamy, S.; Pannirselvam, N. Optimizing mechanical properties of recycled aggregate concrete with graphene oxide and steel fibers: A predictive approach using ANN and RSM. Results Eng. 2025, 26, 104875. [Google Scholar] [CrossRef]
- Ombres, L.; Aiello, M.A.; Cascardi, A.; Verre, S. Modeling of Steel-Reinforced Grout Composite System-to-Concrete Bond Capacity Using Artificial Neural Networks. J. Compos. Constr. 2024, 28, 04024034. [Google Scholar] [CrossRef]
- Moelich, G.M.; Kruger, J.; Combrinck, R. Modelling the interlayer bond strength of 3D printed concrete with surface moisture. Cem. Concr. Res. 2021, 150, 106559. [Google Scholar] [CrossRef]
- Zandifaez, P.; Asadi Shamsabadi, E.; Akbar Nezhad, A.; Zhou, H.; Dias-da-Costa, D. AI-assisted optimisation of green concrete mixes incorporating recycled concrete aggregates. Constr. Build. Mater. 2023, 391, 131851. [Google Scholar] [CrossRef]
- Luo, D.; Wang, K.; Wang, D.; Sharma, A.; Li, W.; Choi, I.H. Artificial intelligence in the design, optimization, and performance prediction of concrete materials: A comprehensive review. npj Mater. Sustain. 2025, 3, 14. [Google Scholar] [CrossRef]
- Zheng, W.; Shui, Z.; Xu, Z.; Gao, X.; Zhang, S. Multi-objective optimization of concrete mix design based on machine learning. J. Build. Eng. 2023, 76, 107396. [Google Scholar] [CrossRef]
- Getachew, E.M.; Taffese, W.Z.; Espinosa-Leal, L.; Yehualaw, M.D. Machine learning applications in sustainable construction materials: A scientometrics review of global trends, themes, and future directions. Sustainability 2025, 17, 8453. [Google Scholar] [CrossRef]
- Anjali, R.; Venkatesan, G. Optimization and prediction of mechanical properties of composite concrete with crumb rubber using RSM and hybrid DNN–HHO algorithm. J. Build. Eng. 2024, 84, 108486. [Google Scholar] [CrossRef]
- Mousavi, M.; Bengar, H.A.; Mousavi, F.; Mahdavinia, P.; Bengar, M.A. Interlayer bond strength prediction of 3D printable concrete using artificial neural network: Experimental and modeling study. Structures 2025, 71, 108147. [Google Scholar] [CrossRef]
- Bittmann, T. A practical guide from Ordinary Least Squares to causal machine learning. Int. Food Agribus. Manag. Rev. 2025, 1, 1–30. [Google Scholar] [CrossRef]
- Jensen, W.A. Response Surface Methodology: Process and Product Optimization Using Designed Experiments 4th edition. J. Qual. Technol. 2017, 49, 186–188. [Google Scholar] [CrossRef]
- Fard, S.; Zainuddin, Z. The universal approximation capabilities of 2pi-periodic approximate identity neural networks. In Proceedings of the 2013 International Symposium on Computational and Business Intelligence, Guangzhou, China, 7–8 December 2013; pp. 793–798. [Google Scholar] [CrossRef]
- Fard, S.; Zainuddin, Z. Universal approximation property of weighted approximate identity neural networks. Proc. Sci. 2015, 259, 7. [Google Scholar] [CrossRef]
- Lazrak, A.; Boudéhenn, F.; Bonnot, S.; Fraisse, G.; Leconte, A.; Papillon, P.; Souyri, B. Development of a dynamic artificial neural network model of an absorption chiller and its experimental validation. Renew. Energy 2016, 86, 1009–1022. [Google Scholar] [CrossRef]
- Khan, A.Q.; Awan, H.A.; Rasul, M.; Siddiqi, Z.A.; Pimanmas, A. Optimized artificial neural network model for accurate prediction of compressive strength of normal and high strength concrete. Clean. Mater. 2023, 10, 100211. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; KDD ’19. pp. 2623–2631. [Google Scholar] [CrossRef]
- Wu, D.; Wang, J.; Tong, M.; Chen, K.; Zhang, Z. Performance optimization of FA-GGBS geopolymer based on response surface methodology. Polymers 2023, 15, 1881. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Zhang, G.; Qin, T.; Yu, L.; Li, T.; Guan, X. Experimental research on mix ratio of construction waste cemented filling material based on response surface methodology. Adv. Mater. Sci. Eng. 2022, 2022, 8274733. [Google Scholar] [CrossRef]
- Cui, H.; Peng, H.; Yang, W.; Yang, H.; Zhang, C.; Zheng, D. Effect of thermal cycles and curing age on bonding strength of cement mortar using manufactured sand. Buildings 2024, 14, 783. [Google Scholar] [CrossRef]
- Khuri, A.I. A general overview of response surface methodology. Biom. Biostat. Int. J. 2017, 5, 87–93. [Google Scholar] [CrossRef]
- Almarzooq, H.; Waheed, U. Automating hyperparameter optimization in geophysics with optuna: A comparative study. Geophys. Prospect. 2024, 72, 1778–1788. [Google Scholar] [CrossRef]
- Mairpady, A.; Mourad, A.; Mozumder, M. Statistical and machine learning-driven optimization of mechanical properties in designing durable HDPE nanobiocomposites. Polymers 2021, 13, 3100. [Google Scholar] [CrossRef] [PubMed]
- Nakhaei, M.; Mostafapour, A.; Naderi, G. Optimization of mechanical properties of PP/EPDM/clay nanocomposite fabricated by friction stir processing with response surface methodology and neural networks. Polym. Compos. 2016, 38, E80–E90. [Google Scholar] [CrossRef]
- Betiku, E.; Okunsolawo, S.; Ajala, S.; Odedele, O. Performance evaluation of artificial neural network coupled with genetic algorithm and response surface methodology in modeling and optimization of biodiesel production process parameters from shea tree (Vitellaria paradoxa) nut butter. Renew. Energy 2015, 76, 408–417. [Google Scholar] [CrossRef]
- Lingam, D.; Ananthanarayanan, R.; Jeevanantham, A. Analysis and prediction of the mechanical properties of cold rolled Al-Li preforms using statistical and artificial neural network models. Eng. Res. Express 2025, 7, 015583. [Google Scholar] [CrossRef]
- Sridhar, J.; Balaji, S.; Dhanapal, J.; Awoyera, P. Prediction of the mechanical properties of fibre-reinforced quarry dust concrete using response surface and artificial neural network techniques. Adv. Civ. Eng. 2023, 2023, 8267639. [Google Scholar] [CrossRef]
- Reza, A.; Chen, L. Optimization and modeling of ammonia nitrogen removal from high strength synthetic wastewater using vacuum thermal stripping. Processes 2021, 9, 2059. [Google Scholar] [CrossRef]
- Pardede, D.; Hayadi, B.; Iskandar, I. Kajian literatur multi layer perceptron seberapa baik performa algoritma ini. J. ICT Appl. Syst. 2022, 1, 23–35. [Google Scholar] [CrossRef]
- Taki, O.; Rhazi, K.; Mejdoub, Y. Stirling engine optimization using artificial neural networks algorithm. ITM Web Conf. 2023, 52, 02010. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimisation Using Designed Experiments, 4th ed.; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Mashrei, M.A.; Seracino, R.; Rahman, M.S. Application of artificial neural networks to predict the bond strength of FRP-to-concrete joints. Constr. Build. Mater. 2013, 40, 812–821. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines, 3rd ed.; Pearson: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Montgomery, D.C.; Runger, G.C.; Hubele, N.F. Engineering Statistics, 5th ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Altharan, Y.; Shamsudin, S.; Lajis, M.; Al-Alimi, S.; Yusuf, N.; Alduais, N.; Zhou, W. Optimizing strength of directly recycled aluminum chip-based parts through a hybrid rsm-ga-ann approach in sustainable hot forging. PLoS ONE 2024, 19, e0300504. [Google Scholar] [CrossRef] [PubMed]
- Khalid, A.; Hamza, H.; Mirjalili, S.; Hosny, K. MOCOVIDOA: A novel multi-objective coronavirus disease optimization algorithm for solving multi-objective optimization problems. Neural Comput. Appl. 2023, 35, 17319–17347. [Google Scholar] [CrossRef] [PubMed]
- Khodadadi, N.; Abualigah, L.; Al-Tashi, Q.; Mirjalili, S. Multi-objective chaos game optimization. Neural Comput. Appl. 2023, 35, 14973–15004. [Google Scholar] [CrossRef]
- Moosbauer, J.; Herbinger, J.; Casalicchio, G.; Lindauer, M.; Bischl, B. Explaining hyperparameter optimization via partial dependence plots. Adv. Neural Inf. Process. Syst. 2021, 34, 2280–2291. [Google Scholar]
- Correia, A.; Oliveira, P.; Lemos, L. Strength assessment of chemically stabilised soft soils. Proc. Inst. Civ. Eng.-Geotech. Eng. 2019, 172, 218–227. [Google Scholar] [CrossRef]
- Baltazar, L.G.; Henriques, F.M.A.; Reis, D.; Cidade, M.T. Yield Stress in Injection Grouts for Strengthening of Stone Masonry Walls. In Proceedings of the Iberian Meeting on Rheology (IBEREO 2019); Galindo-Rosales, F.J., Campo-Deaño, L., Afonso, A.M., Alves, M.A., Pinho, F.T., Eds.; Springer: Cham, Switzerland, 2020; pp. 170–174. [Google Scholar] [CrossRef]
- Zhou, J.; Ban, C.; Zhou, H.; Ren, J.; Liu, Z. Experimental study on the shear strength and failure mechanism of cemented soil–concrete interface. Materials 2023, 16, 4222. [Google Scholar] [CrossRef]
- Mizobuchi, S.; Kato, T.; Yamada, B.; Kan, K.; Ohtani, M.; Kobiro, K. Influence of the nanostructural characteristics of inorganic fillers on the physical properties of resin cements. Dent. Mater. J. 2023, 42, 291–299. [Google Scholar] [CrossRef]
- Ebonghas, I.P.; Odokonyero, L.C. Integrated experimental and microstructural analysis of basalt fiber-reinforced cemented soils: Multivariable strength prediction and residual behavior assessment. 2025. Preprints. [Google Scholar] [CrossRef]
- Chen, Y.; Jansen, K.; Zhang, H.; Rodríguez, C.; Gan, Y.; Çopuroğlu, O.; Schlangen, E. Effect of printing parameters on interlayer bond strength of 3D printed limestone-calcined clay-based cementitious materials: An experimental and numerical study. Constr. Build. Mater. 2020, 262, 120094. [Google Scholar] [CrossRef]
- Yuan, Q.; Gao, C.; Huang, T.; Zuo, S.; Yao, H.; Zhang, K.; Liu, J. Factors influencing the properties of extrusion-based 3D-printed alkali-activated fly ash-slag mortar. Materials 2022, 15, 1969. [Google Scholar] [CrossRef]
- Raphael, B.; Senthilnathan, S.; Patel, A.; Bhat, S. A review of concrete 3D printed structural members. Front. Built Environ. 2023, 8, 1034020. [Google Scholar] [CrossRef]
- Ng, W.; Goh, G.; Ten, J.; Yeong, W. Progress and opportunities for machine learning in materials and processes of additive manufacturing. Adv. Mater. 2024, 36, 23010006. [Google Scholar] [CrossRef]
- Ning, X.; Liu, T.; Wu, C.; Wang, C. 3D printing in construction: Current status, implementation hindrances, and development agenda. Adv. Civ. Eng. 2021, 2021, 6665333. [Google Scholar] [CrossRef]
- Nguyen, P.; Zhang, Y.; Zhang, Z.; Yang, C. Multi-objective optimisation of fused filament fabrication of acrylonitrile butadiene styrene for enhancing mechanical performance and build time. Int. J. Adv. Manuf. Technol. 2025, 137, 5431–5449. [Google Scholar] [CrossRef]
- Zhu, A. Navigating the path to responsible AI: Interpretable models and ethical implications. Highlights Sci. Eng. Technol. 2024, 85, 830–835. [Google Scholar] [CrossRef]



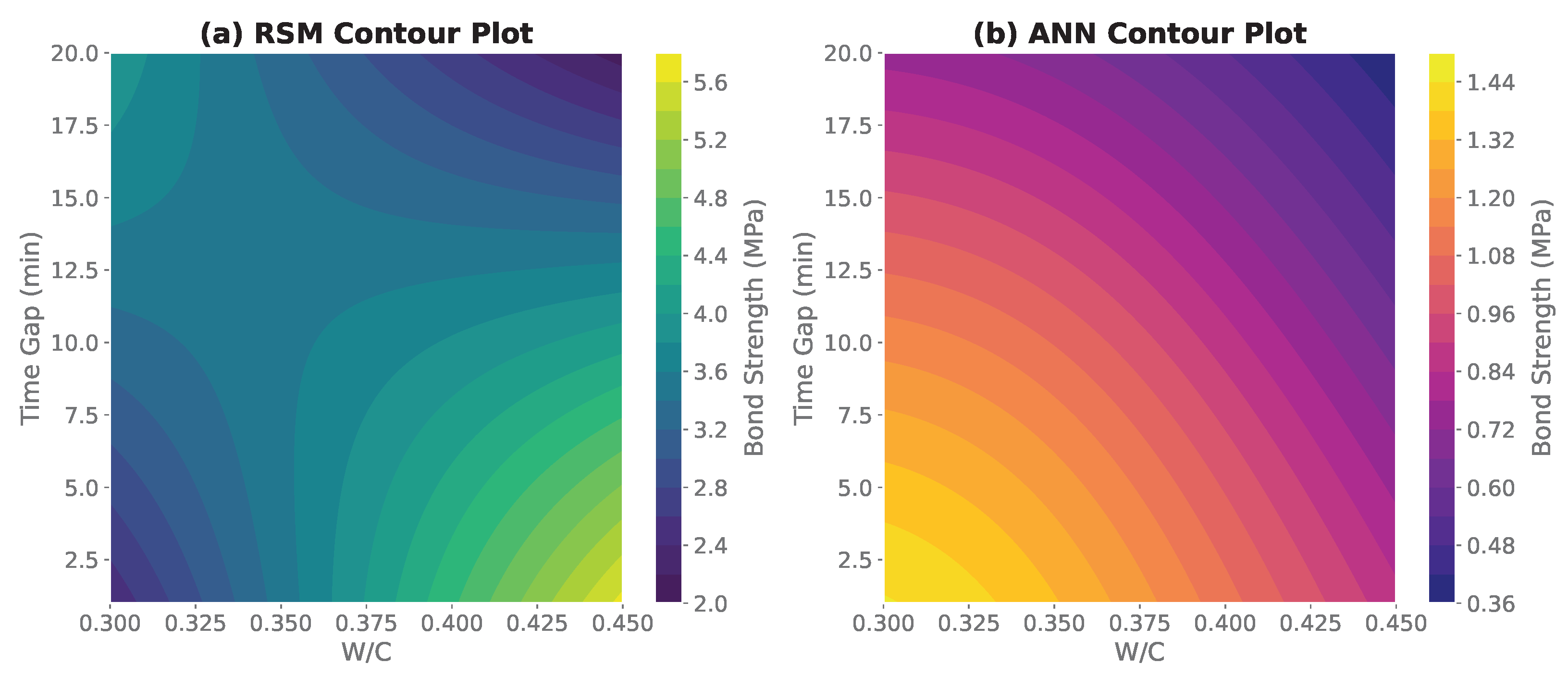
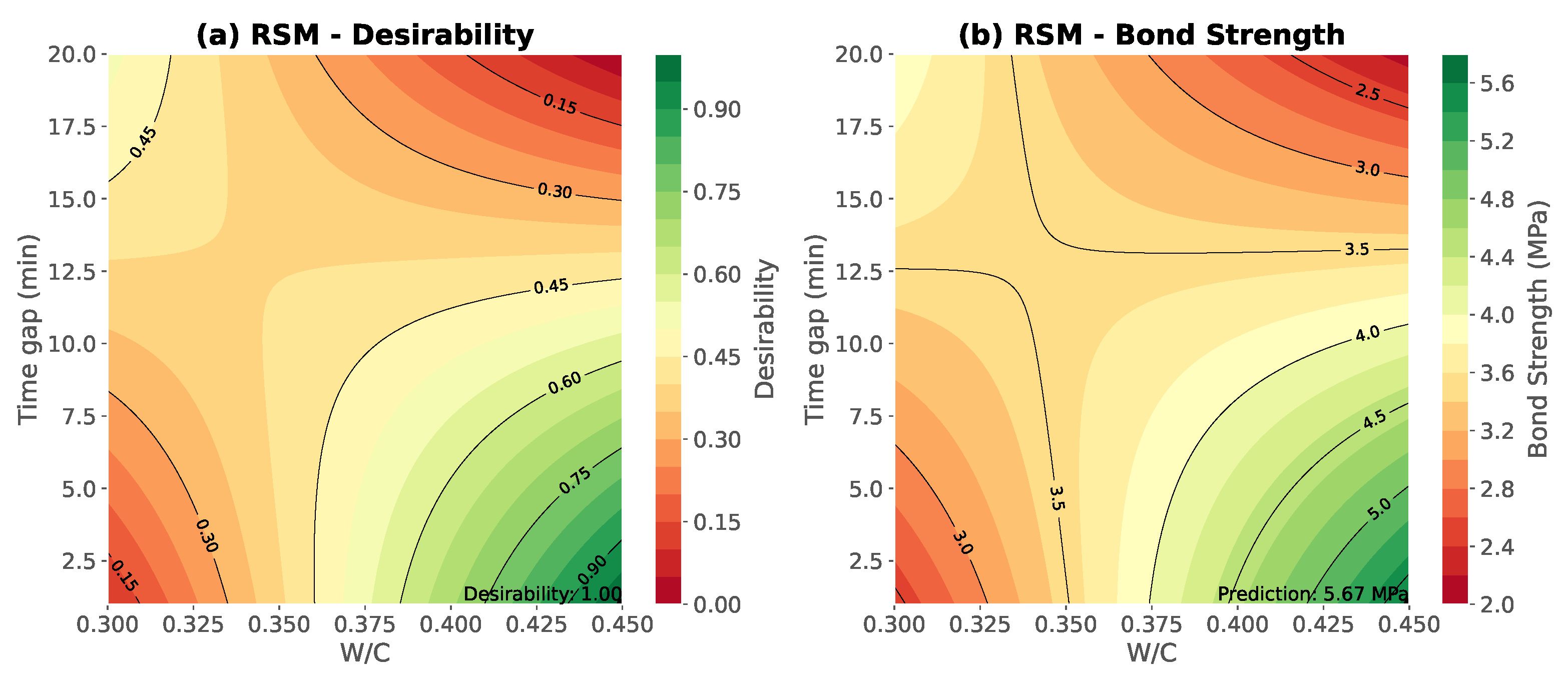
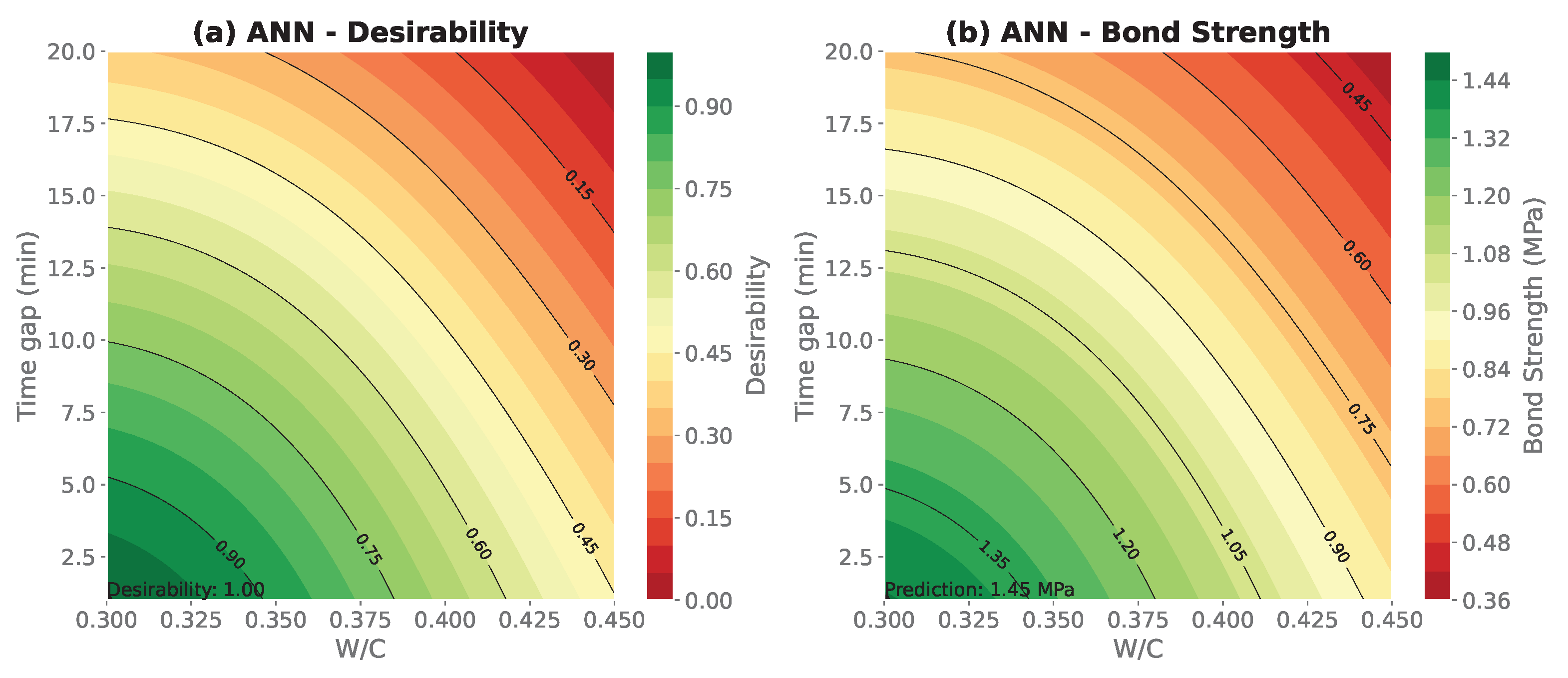
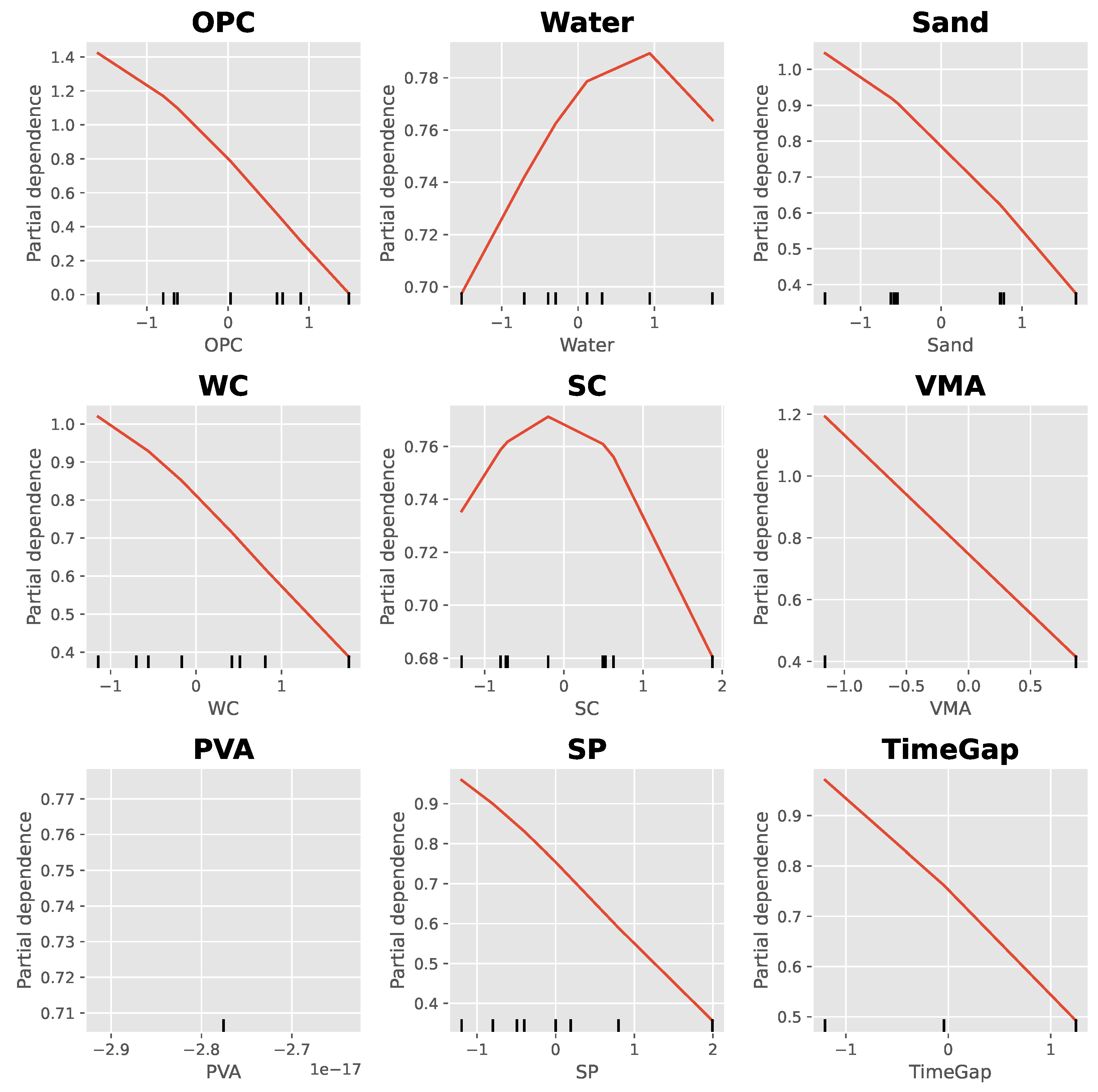
| Source | Sum Sq | df | F | p-Value |
|---|---|---|---|---|
| WC | 2.6582 | 1 | 65.225 | 0.000021 |
| SC | 1.4030 | 1 | 34.426 | 0.000239 |
| SP | 2.7581 | 1 | 67.677 | 0.000018 |
| Time Gap | 0.0092 | 1 | 0.226 | 0.645941 |
| 0.1189 | 1 | 2.919 | 0.121741 | |
| 0.4391 | 1 | 10.774 | 0.009494 | |
| 0.1300 | 1 | 3.190 | 0.107744 | |
| 0.1095 | 1 | 2.686 | 0.135643 | |
| WC:SC | 0.0774 | 1 | 1.900 | 0.201331 |
| WC:SP | 0.1860 | 1 | 4.565 | 0.061369 |
| WC:Time Gap | 0.2509 | 1 | 6.156 | 0.034922 |
| SC:SP | 0.2435 | 1 | 5.975 | 0.037097 |
| SC:Time Gap | 0.2837 | 1 | 6.960 | 0.026992 |
| SP:Time Gap | 0.0414 | 1 | 1.016 | 0.339798 |
| Residual | 0.3668 | 9 | – | – |
| Hyperparameter | Optimal Value |
|---|---|
| Number of units (Layer 1) | 70 |
| Number of units (Layer 2) | 40 |
| Activation function | tanh |
| Solver | adam |
| Regularisation parameter () | |
| Initial learning rate | 0.00923 |
| Early stopping | False |
| Specimen No. | RSM | ANN | ||
|---|---|---|---|---|
| Predicted (MPa) | Abs. Error (MPa) | Predicted (MPa) | Abs. Error (MPa) | |
| 1 | −0.12 | 0.12 | 0.28 | 0.28 |
| 2 | 0.10 | 0.10 | 0.07 | 0.07 |
| 3 | 0.02 | 0.02 | −0.14 | 0.14 |
| 4 | 1.51 | 0.03 | 1.37 | 0.17 |
| 5 | 1.18 | 0.21 | 1.06 | 0.09 |
| 6 | 0.49 | 0.18 | 0.69 | 0.02 |
| 7 | 1.60 | 0.09 | 1.60 | 0.09 |
| 8 | 1.32 | 0.12 | 1.28 | 0.08 |
| 9 | 0.68 | 0.03 | 0.85 | 0.14 |
| 10 | 1.24 | 0.11 | 1.23 | 0.10 |
| 11 | 1.25 | 0.12 | 1.12 | 0.25 |
| 12 | 0.93 | 0.01 | 0.90 | 0.02 |
| 13 | 1.17 | 0.08 | 1.07 | 0.02 |
| 14 | 1.17 | 0.09 | 0.87 | 0.39 |
| 15 | 0.84 | 0.01 | 0.58 | 0.25 |
| 16 | 1.04 | 0.04 | 1.01 | 0.01 |
| 17 | 0.83 | 0.32 | 0.83 | 0.32 |
| 18 | 0.28 | 0.28 | 0.56 | 0.56 |
| 19 | 0.00 | 0.00 | 0.22 | 0.22 |
| 20 | 0.10 | 0.10 | 0.09 | 0.09 |
| 21 | −0.10 | 0.10 | −0.01 | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simwanda, L.; David, A.B.; Perampalam, G.; Olalusi, O.B.; Sykora, M. Optimisation of Interlayer Bond Strength in 3D-Printed Concrete Using Response Surface Methodology and Artificial Neural Networks. Buildings 2025, 15, 3794. https://doi.org/10.3390/buildings15203794
Simwanda L, David AB, Perampalam G, Olalusi OB, Sykora M. Optimisation of Interlayer Bond Strength in 3D-Printed Concrete Using Response Surface Methodology and Artificial Neural Networks. Buildings. 2025; 15(20):3794. https://doi.org/10.3390/buildings15203794
Chicago/Turabian StyleSimwanda, Lenganji, Abayomi B. David, Gatheeshgar Perampalam, Oladimeji B. Olalusi, and Miroslav Sykora. 2025. "Optimisation of Interlayer Bond Strength in 3D-Printed Concrete Using Response Surface Methodology and Artificial Neural Networks" Buildings 15, no. 20: 3794. https://doi.org/10.3390/buildings15203794
APA StyleSimwanda, L., David, A. B., Perampalam, G., Olalusi, O. B., & Sykora, M. (2025). Optimisation of Interlayer Bond Strength in 3D-Printed Concrete Using Response Surface Methodology and Artificial Neural Networks. Buildings, 15(20), 3794. https://doi.org/10.3390/buildings15203794









