Machine Learning-Based Surrogate Ensemble for Frame Displacement Prediction Using Jackknife Averaging
Abstract
1. Introduction
- JMA1: Classical surrogates—PRS, RBF, and SVR.
- JMA2: Tree-based models—XGB, LGBM, and RF.
- JMA3: Hybrid combination—all six models.
- We benchmark the predictive performance of six representative surrogate models on a large-scale, realistic structural simulation dataset.
- We design and compare three model averaging strategies (JMA1, JMA2, and JMA3) to evaluate the benefits of homogeneous versus hybrid ensembles.
- We show that JMA-based ensembles consistently achieve superior accuracy, robustness, and generalization.
2. Problem Definition and Data Description
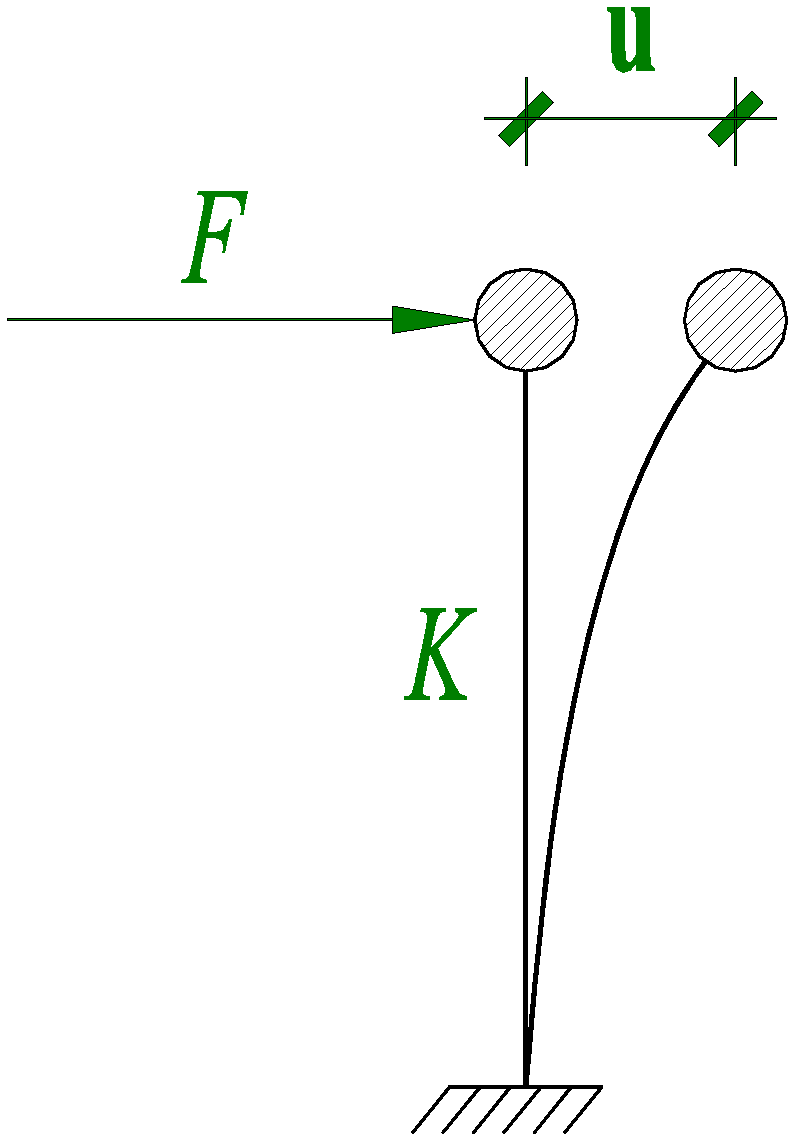
2.1. Problem Definition
- A_indices: A array of integer-valued row and column indices of non-zero entries in K;
- A_values: A array containing the corresponding non-zero values of K;
- b: A length-n vector representing the right-hand-side load vector F;
- x: A length-n vector representing the displacement solution , obtained by solving the linear system.
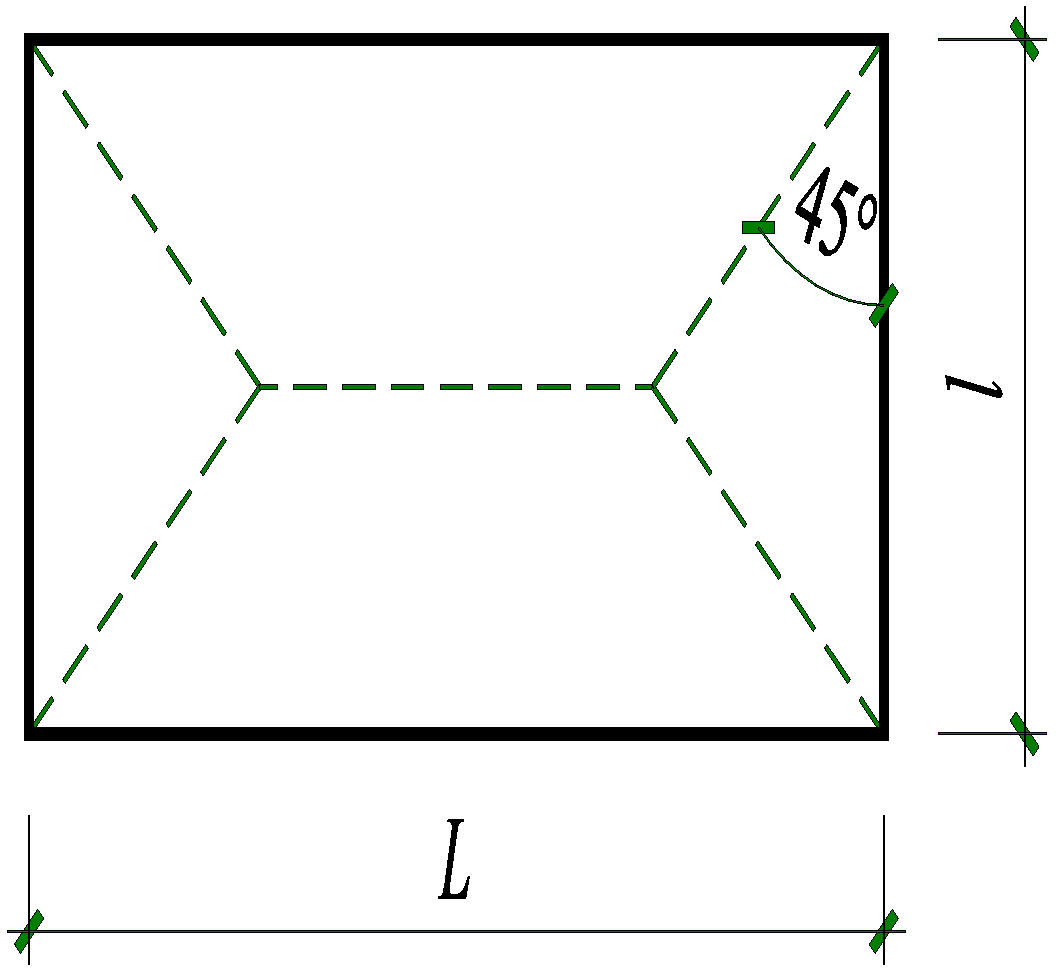
2.2. Feature Construction
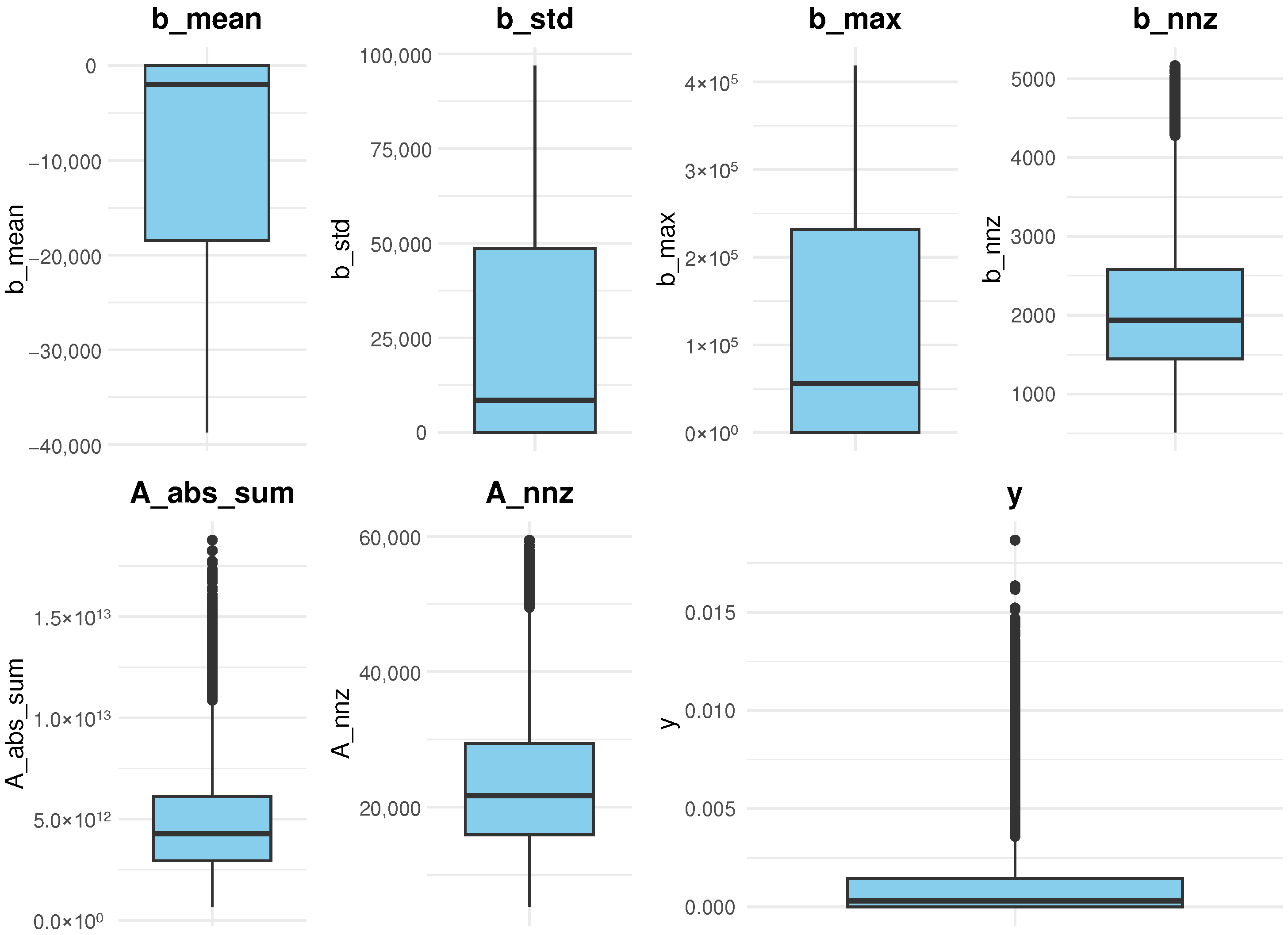
- b_mean, b_std, b_max, and b_nnz: The mean, standard deviation, maximum absolute value, and number of non-zero entries in the force vector F;
- A_abs_sum and A_nnz: The total sum of absolute values and the number of non-zero entries in the stiffness matrix K.
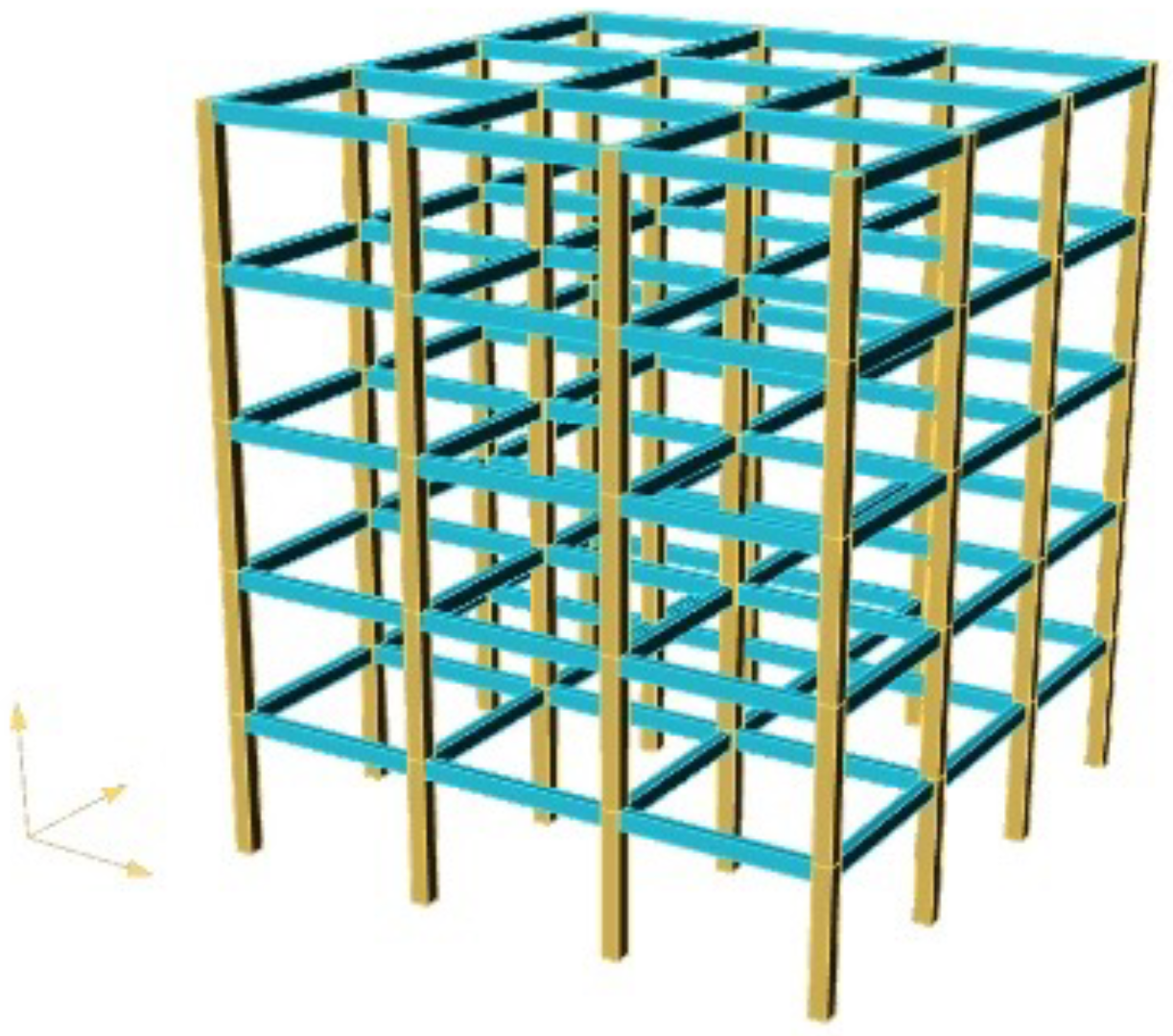
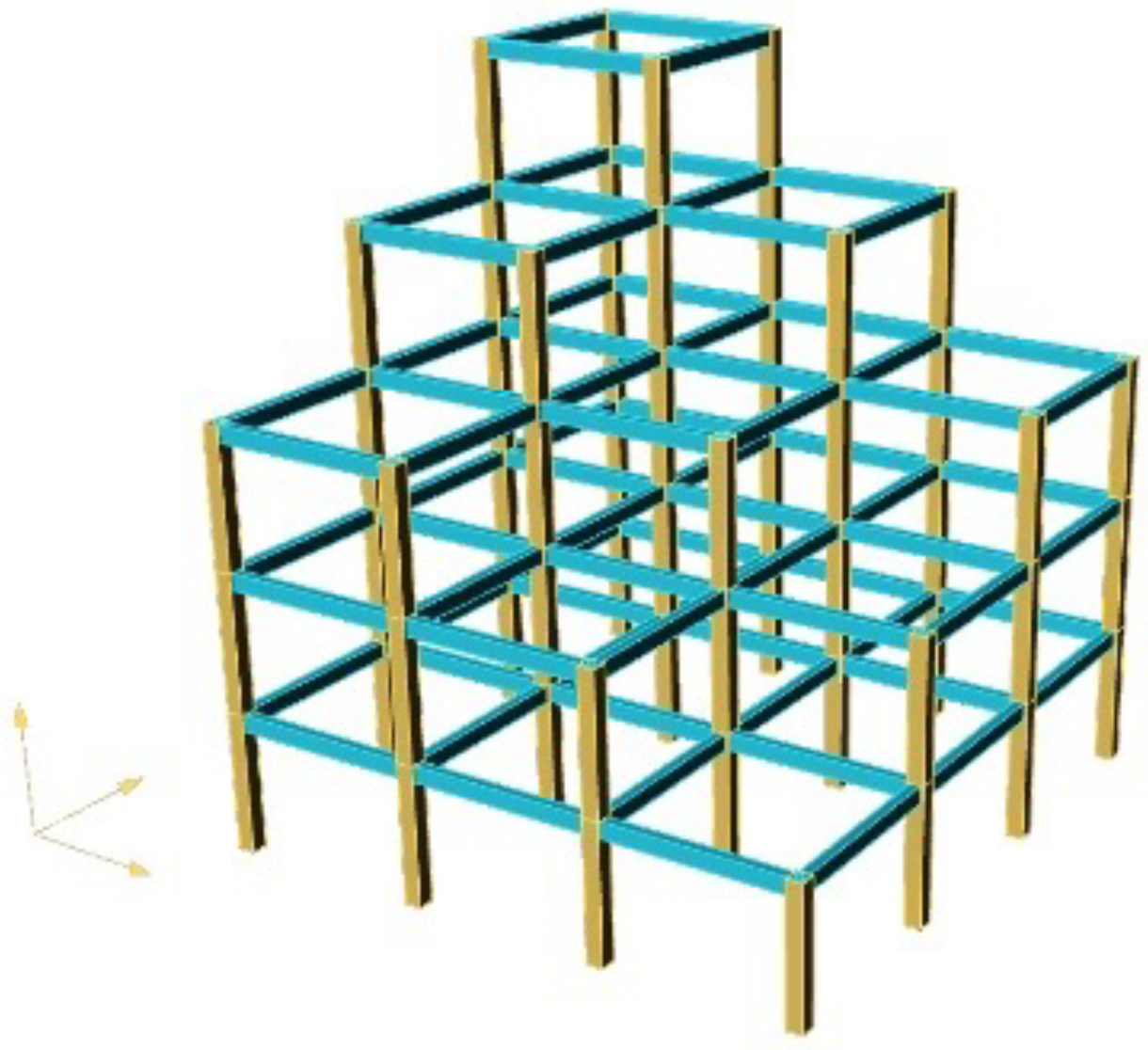
2.3. Use Case Motivation
2.4. Dataset Description
2.5. Exploratory Analysis of Data Distribution
3. Related Models
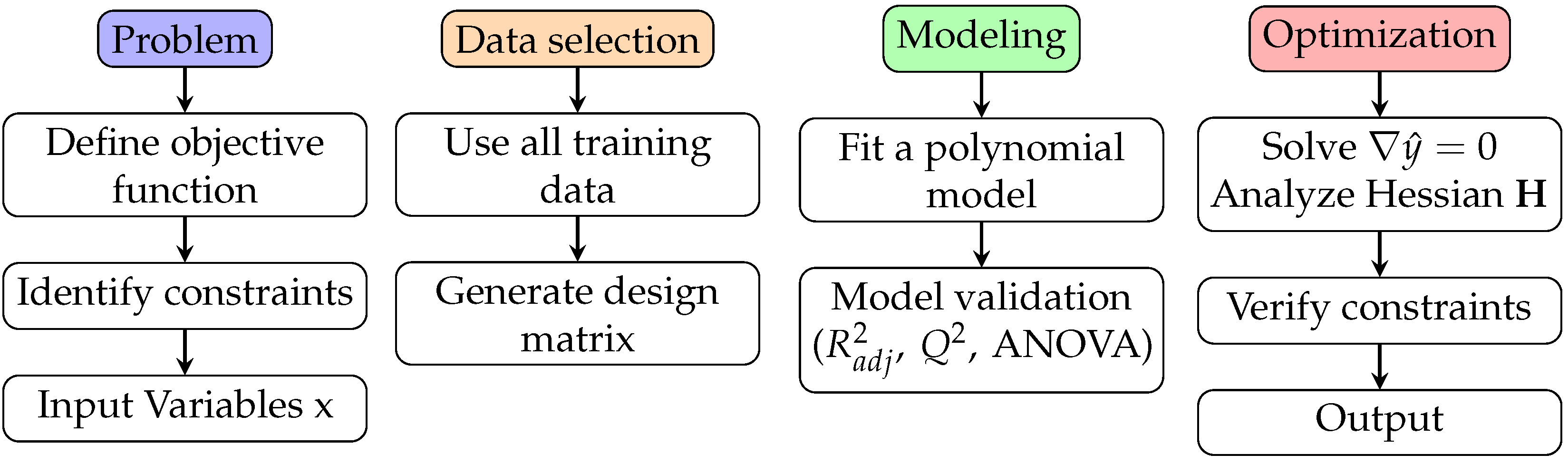
3.1. PRS Model
- Problem definition: Identify the modeling objective, input variables, and constraints.
- Data selection: Use all available training data without experimental design subsampling.
- Model fitting: Fit a full quadratic polynomial regression using the ordinary least squares method.
- Model validation: Assess goodness of fit using criteria such as adjusted (), predictive , and analysis of variance (ANOVA).
- Analysis or optimization: Apply the surrogate model for optimization, sensitivity analysis, or uncertainty quantification as required.
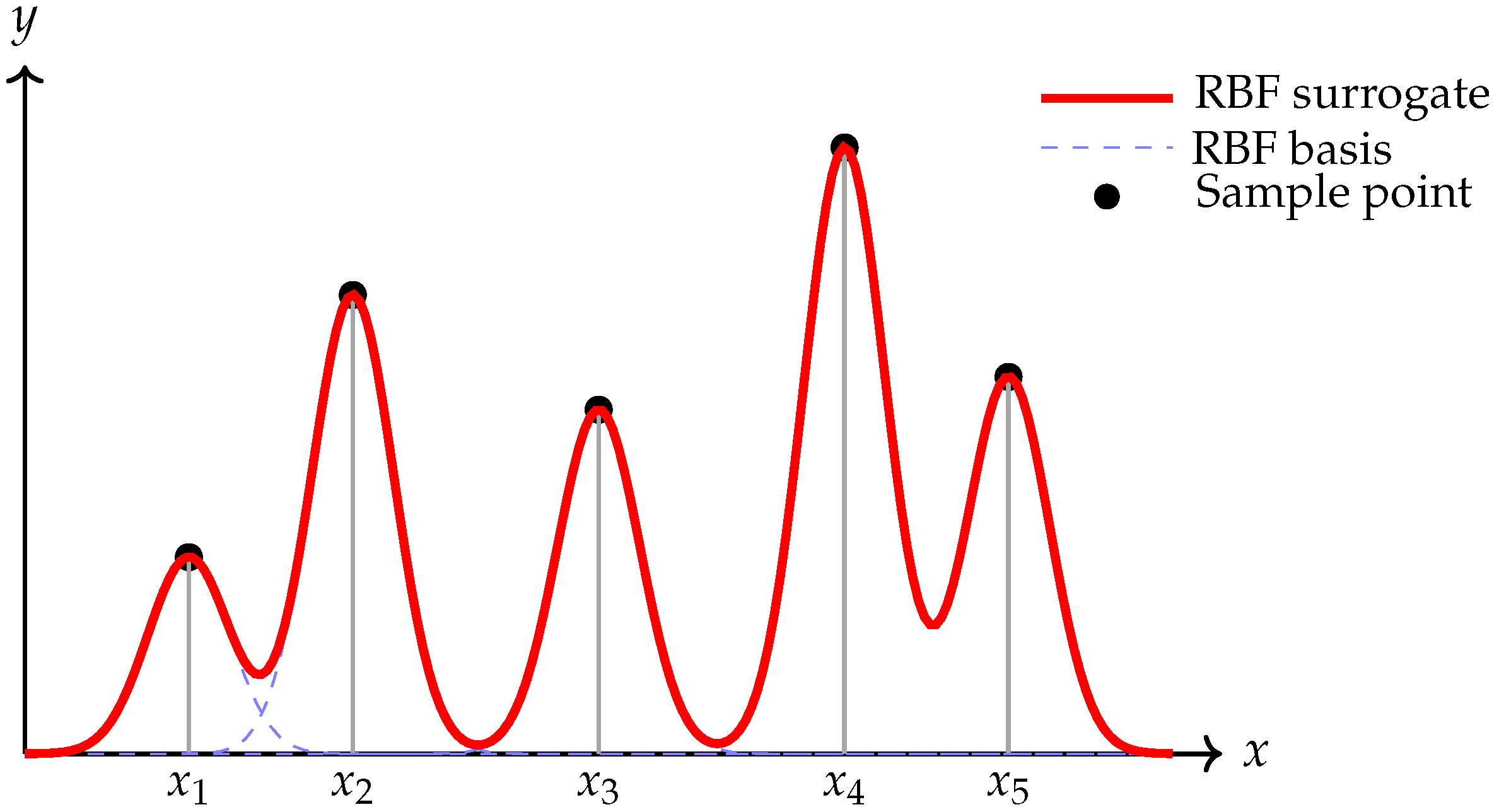
3.2. RBF Surrogates
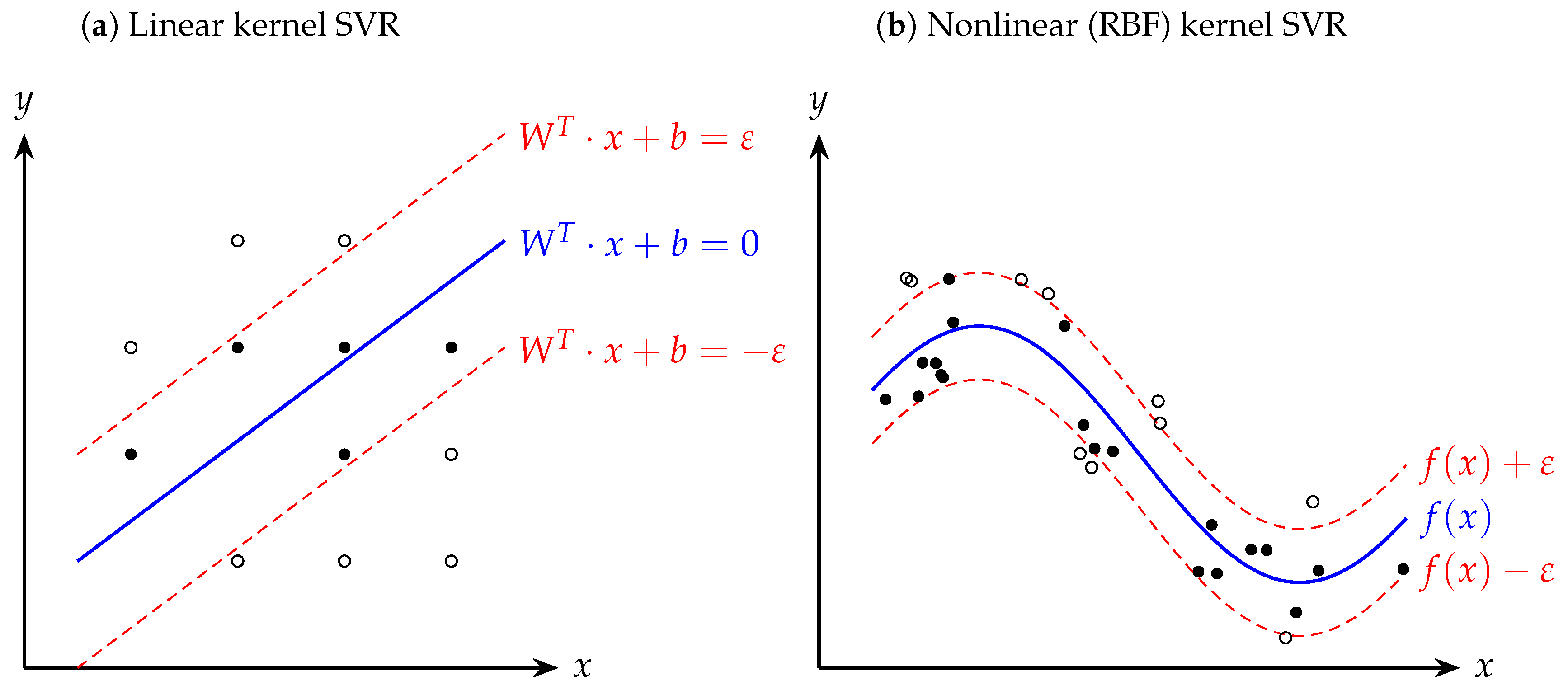
3.3. SVR
3.4. XGB
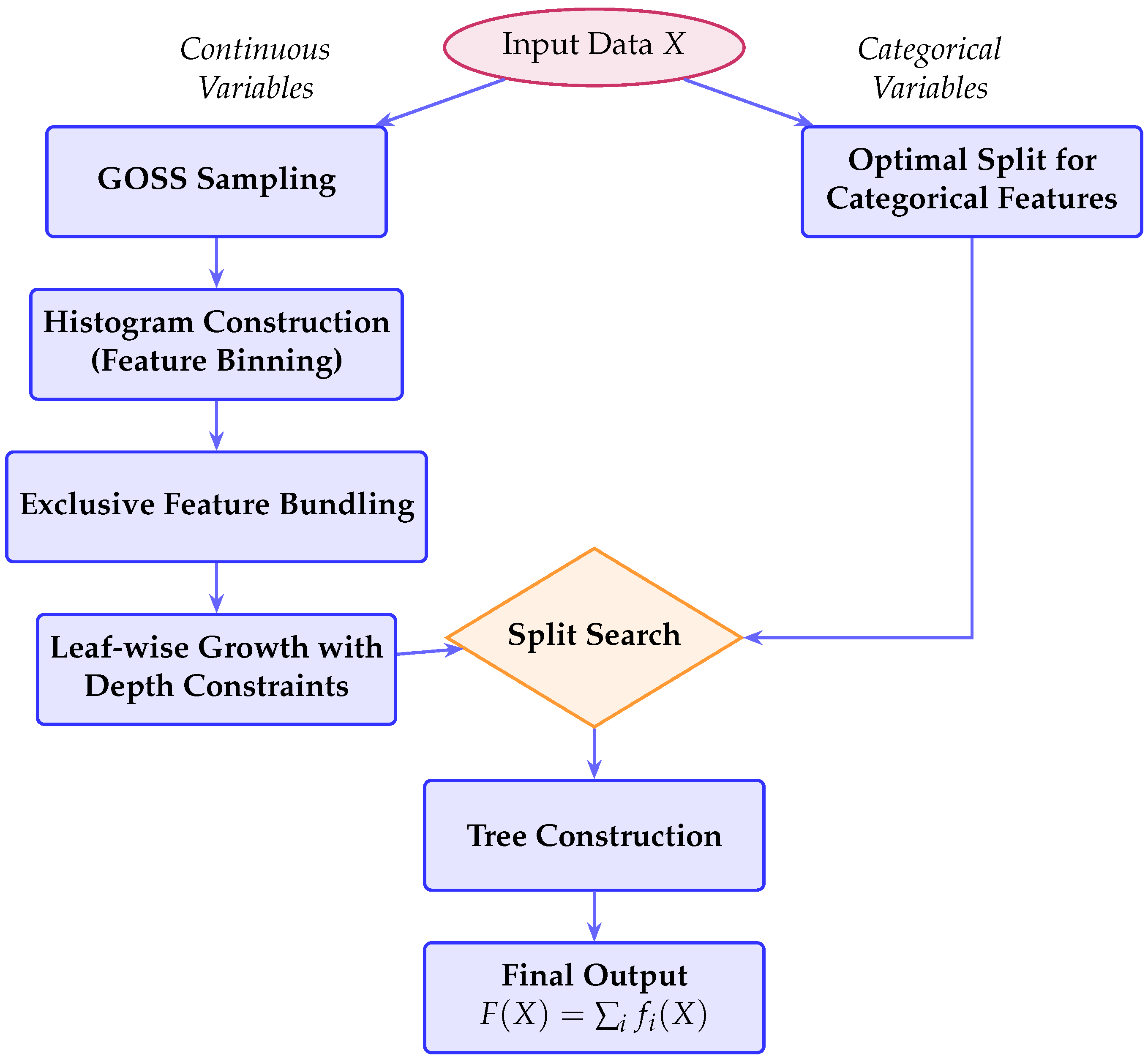
3.5. LGBM
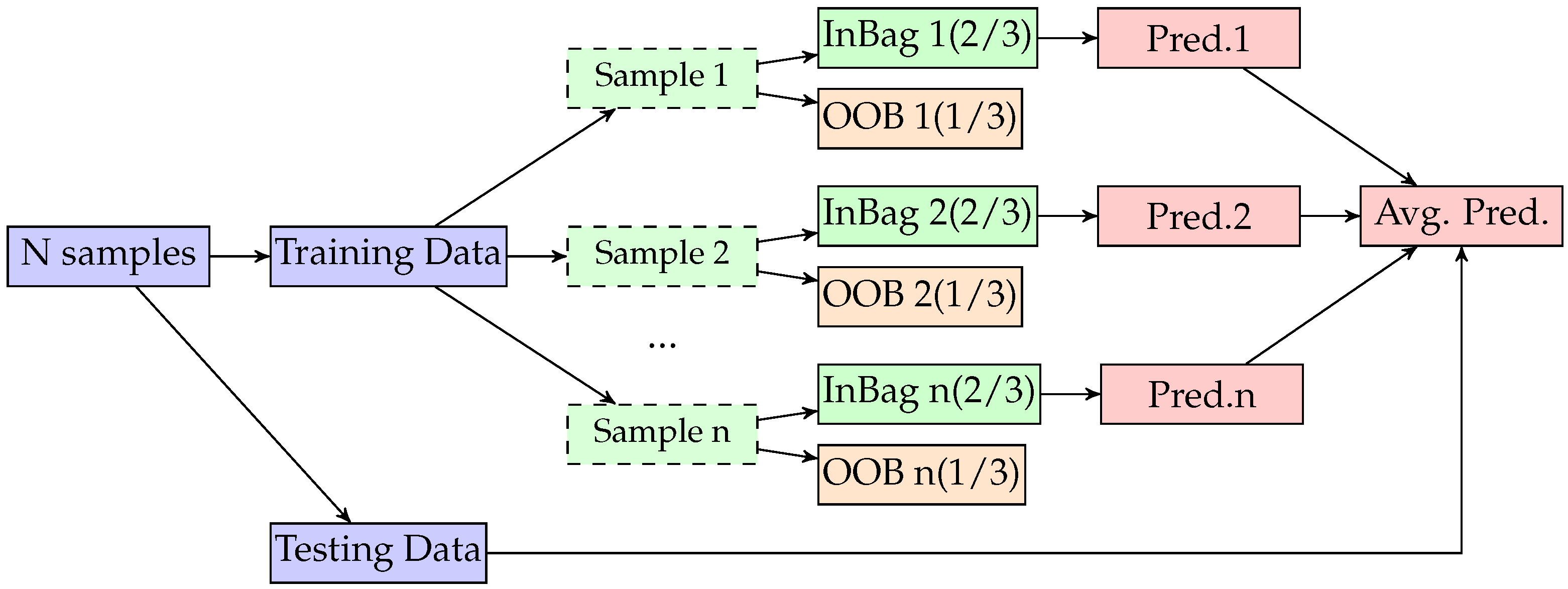
3.6. RF
4. Methodology
4.1. Problem Setup and Base Models
- Classical surrogate models:
- −
- PRS: A second-order global polynomial regression.
- −
- SVR: With radial basis function kernel.
- −
- RBF: Using thin-plate spline basis.
- Tree-based ensemble models:
- −
- XGB: An efficient implementation of gradient boosting.
- −
- LGBM: Optimized for speed and memory efficiency.
- −
- RF: Ensemble of bagged decision trees with variance reduction.
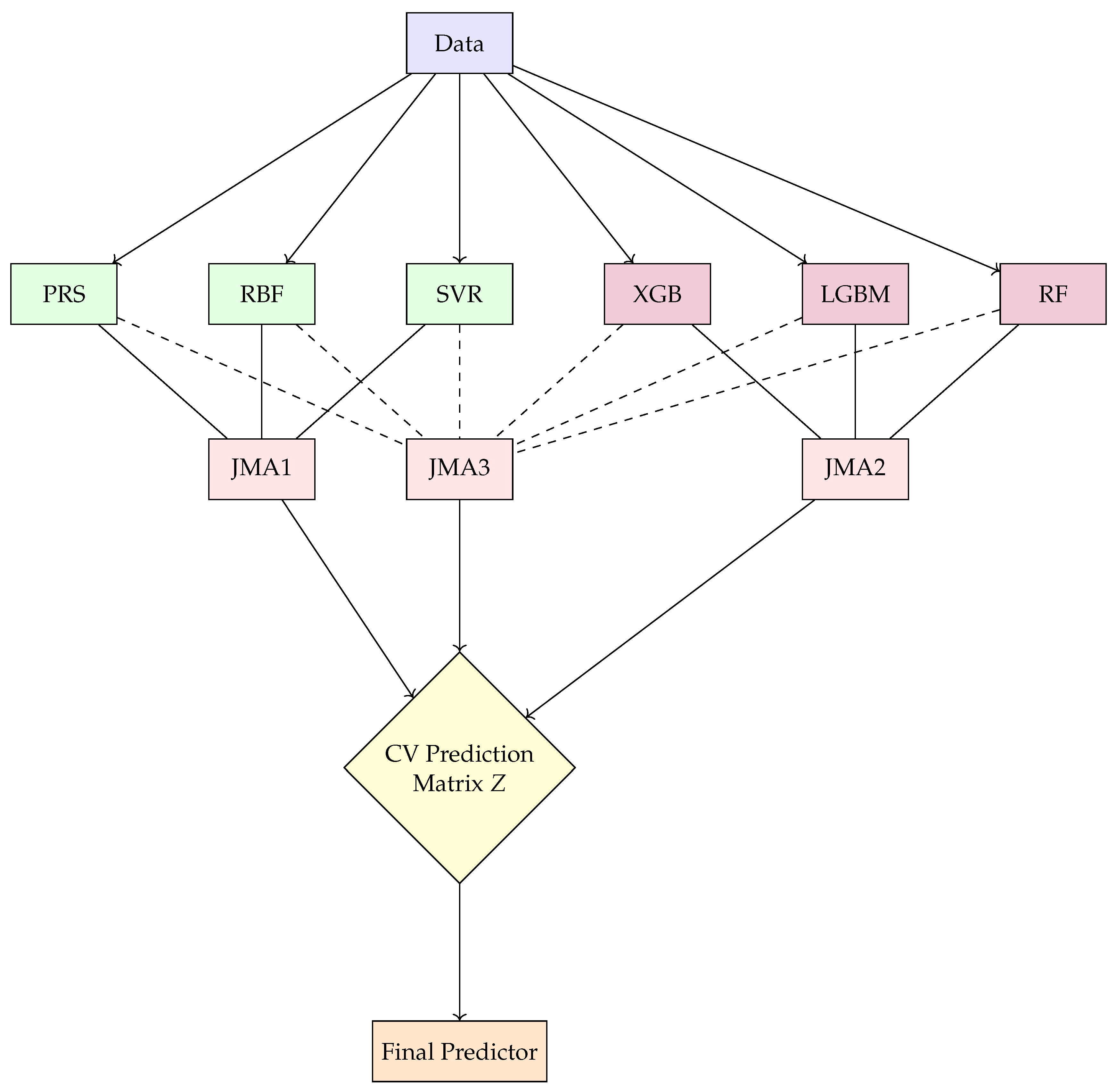
4.2. JMA Framework
- Extract feature vectors and response values from the simulation data.
- Train PRS, RBF, and SVR models on a subset of training data.
- Obtain out-of-fold predictions using k-fold cross-validation and compute JMA weights.
- Combine the three models using JMA to form the final ensemble predictor.
- Evaluate the prediction accuracy on a held-out test set.
| Algorithm 1 JMA for surrogate modeling |
| Require: Training data , base learners , number of folds K |
| Ensure: Final predictor |
| 1: Split data into K folds |
| 2: for each base model to K do |
| 3: for each fold to K do |
| 4: Train on |
| 5: Predict for all |
| 6: end for |
| 7: Collect predictions to form column of matrix Z |
| 8: end for |
| 9: Solve the following quadratic program: |
| 10: Form final JMA predictor: |
5. Experiments
5.1. Experimental Setup
- PRS: Second-order polynomial regression including all pairwise interactions;
- SVR: SVR with an RBF kernel, implemented via e1071 with default parameters;
- RBF: Thin-plate spline RBF interpolator trained on the full 2000-sample set;
- XGB: XGB with 50 boosting rounds and default tree depth;
- LGBM: LGBM with 50 iterations and default learning rate;
- RF: RF with 50 trees and depth-limited construction.
- JMA1: Averaging PRS, RBF, and SVR;
- JMA2: Averaging XGB, LGBM, and RF;
- JMA3: Averaging all six base models.
5.2. Evaluation Metrics and Experimental Results
5.2.1. Evaluation Metrics
- RMSE:RMSE measures the magnitude of prediction errors, giving greater weight to larger discrepancies due to the squared term. Thus, it is sensitive to significant deviations and particularly suitable for assessing models where large prediction errors are highly undesirable.
- MAE:MAE quantifies the average absolute prediction error without emphasizing outliers. Compared to RMSE, MAE provides a more balanced representation of a model’s typical prediction accuracy and is less sensitive to extreme observations.
- :where denotes the mean of the observed responses. measures the proportion of variance in the dependent variable explained by the predictive model. A value close to 1 indicates high predictive capability, whereas negative values suggest that the model underperforms compared to a simple mean-based predictor.
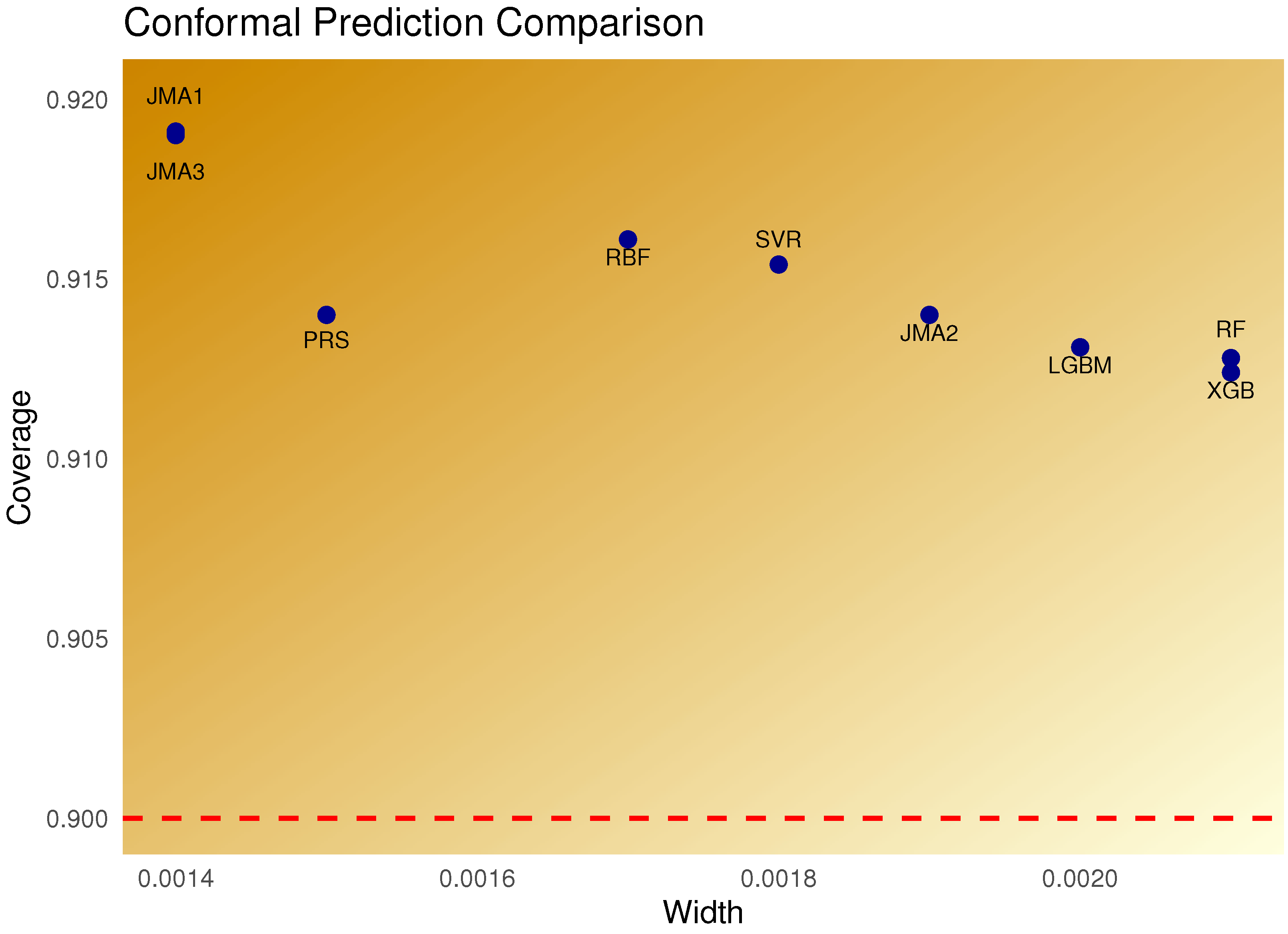
- CP Evaluation MetricsTo evaluate the predictive uncertainty of each model, we adopt two standard metrics commonly used in the CP literature: CR and IW.
- −
- CR measures the proportion of true response values that fall within the predicted confidence interval :where is the indicator function and n is the number of test samples.
- −
- IW quantifies the sharpness of the predicted intervals:
A reliable conformal predictor should attain a CR close to the nominal level (e.g., 90%) while maintaining a narrow width W to ensure interval efficiency.
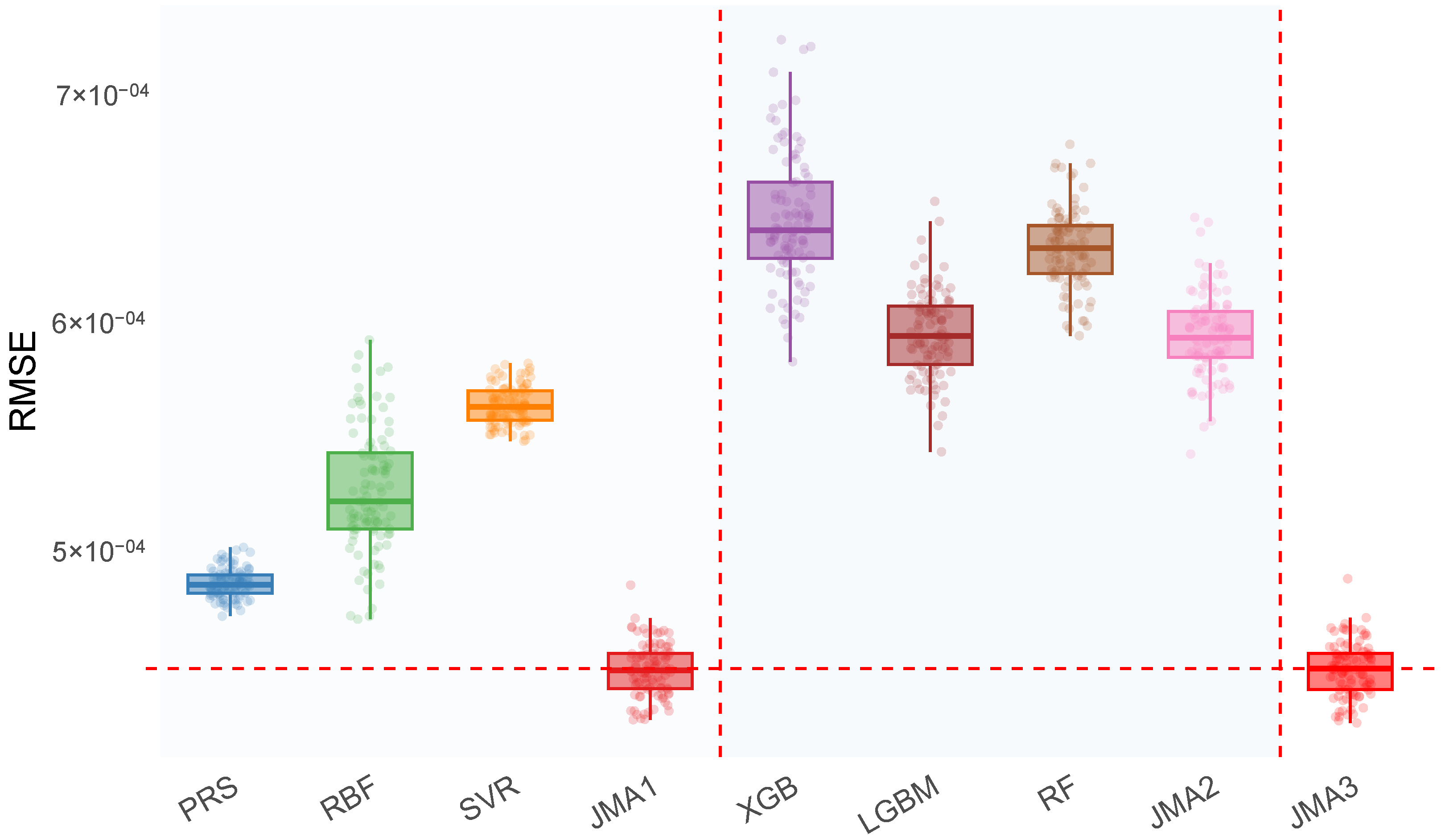
5.2.2. Results and Analysis
5.3. Summary and Discuss
6. Conclusions
- JMA consistently outperforms individual surrogate models in terms of RMSE and MAE on held-out test data;
- The ensemble approach shows greater robustness, characterized by lower prediction variance and the highest number of wins across trials;
- By leveraging out-of-fold predictions to estimate model weights, JMA remains computationally efficient even in high-dimensional and sparse feature spaces.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals, 6th ed.; Elsevier: Oxford, UK, 2005. [Google Scholar]
- Bathe, K.J. Finite Element Procedures; Klaus-Jürgen Bathe: Watertown, MA, USA, 2006. [Google Scholar]
- Hadidi, A.; Azar, B.F.; Rafiee, A. Efficient response surface method for high-dimensional structural reliability analysis. Struct. Saf. 2017, 68, 15–27. [Google Scholar] [CrossRef]
- Gudipati, V.K.; Cha, E.J. Surrogate modeling for structural response prediction of a building class. Struct. Saf. 2021, 89, 102041. [Google Scholar] [CrossRef]
- Ghosh, J.; Padgett, J.E.; Dueñas-Osorio, L. Surrogate modeling and failure surface visualization for efficient seismic vulnerability assessment of highway bridges. Probabilistic Eng. Mech. 2013, 34, 189–199. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Buhmann, M.D. RBFs: Theory and Implementations; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Ye, J.; Stewart, E.; Zhang, D.; Chen, Q.; Roberts, C. Method for Automatic Railway Track Surface Defect Classification and Evaluation Using a Laser-Based 3D Model. IET Image Process. 2020, 14, 2701–2710. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.C.; Kaufman, L.; Smola, A.; Vapnik, V. SVR Machines. Adv. Neural Inf. Process. Syst. 1997, 9, 155–161. [Google Scholar]
- Toh, G.; Park, J. Review of vibration-based structural health monitoring using deep learning. Appl. Sci. 2020, 10, 1680. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Volume 22, pp. 785–794. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3146–3154. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hansen, B.E. Jackknife Model averaging, asymptotic risk, and minimax efficiency. J. Econom. 2012, 167, 52–67. [Google Scholar] [CrossRef]
- Lu, X.; Su, L. Jackknife model averaging for quantile regressions. J. Econom. 2015, 188, 40–58. [Google Scholar] [CrossRef]
- Cheung, Y.-W.; Wang, W. A jackknife model averaging analysis of RMB misalignment estimates. J. Int. Commer. Econ. Policy 2020, 11, 2050007. [Google Scholar] [CrossRef]
- Zhang, X.; Zou, G.; Wan, A.T. Model averaging by jackknife criterion in models with dependent data. J. Econom. 2013, 174, 82–94. [Google Scholar] [CrossRef]
- Ando, T.; Li, K.-C. A model-averaging approach for high-dimensional regression. J. Am. Stat. Assoc. 2014, 109, 254–265. [Google Scholar] [CrossRef]
- You, K.; Wang, M.; Zou, G. Jackknife model averaging for composite quantile regression. J. Syst. Sci. Complex. 2024, 37, 1604–1637. [Google Scholar] [CrossRef]
- He, B.; Ma, S.; Zhang, X.; Zhu, L.-X. Rank-based greedy model averaging for high-dimensional survival data. J. Am. Stat. Assoc. 2023, 118, 2658–2670. [Google Scholar] [CrossRef]
- Grementieri, L.; Finelli, F. StAnD: A Dataset of Linear Static Analysis Problems. arXiv 2022, arXiv:2201.05356. [Google Scholar] [CrossRef]
- Box, G.E.P.; Wilson, K.B. On the Experimental Attainment of Optimum Conditions. J. R. Stat. Soc. Ser. B (Methodol.) 1951, 13, 1–45. [Google Scholar] [CrossRef]
- Dackermann, U.; Smith, W.A.; Randall, R.B. Damage identification based on response-only measurements using cepstrum analysis and artificial neural networks. Struct. Health Monit. 2014, 13, 430–444. [Google Scholar] [CrossRef]
- Cheng, K.; Lu, Z. Adaptive Bayesian SVR model for structural reliability analysis. Reliab. Eng. Syst. Saf. 2021, 206, 107286. [Google Scholar] [CrossRef]
- Kazemi, F.; Çiftçioğlu, A.Ö.; Shafighfard, T.; Asgarkhani, N.; Jankowski, R. RAGN-R: A multi-subject ensemble machine-learning method for estimating mechanical properties of advanced structural materials. Comput. Struct. 2025, 308, 107657. [Google Scholar] [CrossRef]
- Yang, J.; Hao, Y.; Peng, D.; Shi, J.; Zhang, Y. Machine learning-based methods for predicting the structural damage and failure mode of RC slabs under blast loading. Buildings 2025, 15, 1221. [Google Scholar] [CrossRef]
- Li, S.; Jin, N.; Dogani, A.; Yang, Y.; Zhang, M.; Gu, X. Enhancing LightGBM for industrial fault warning: An innovative hybrid algorithm. Processes 2024, 12, 221. [Google Scholar] [CrossRef]
- Aslam, F. Advancing Credit Card Fraud Detection: A Review of Machine Learning Algorithms and the Power of Light Gradient Boosting. Am. J. Comput. Sci. Technol. 2024, 7, 9–12. [Google Scholar] [CrossRef]
- Prajisha, C.; Vasudevan, A.R. An efficient intrusion detection system for MQTT-IoT using enhanced chaotic salp swarm algorithm and LightGBM. Int. J. Inf. Secur. 2022, 21, 1263–1282. [Google Scholar] [CrossRef]
- Wang, D.-N.; Li, L.; Zhao, D. Corporate finance risk prediction based on LightGBM. Inf. Sci. 2022, 602, 259–268. [Google Scholar] [CrossRef]
- Zhang, D.; Gong, Y. The Comparison of LightGBM and XGBoost Coupling Factor Analysis and Prediagnosis of Acute Liver Failure. IEEE Access 2020, 8, 220990–221003. [Google Scholar] [CrossRef]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition (ICDAR’95), Montreal, QC, Canada, 14–16 August 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 278–282. [Google Scholar]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Chapman & Hall/CRC: Boca Raton, FL, USA, 1984. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Fernández-Delgado, M.; Cernadas, E.; Barro, S.; Amorim, D. Do We Need Hundreds of Classifiers to Solve Real-World Classification Problems? J. Mach. Learn. Res. 2014, 15, 3133–3181. [Google Scholar]
- Ziegler, A.; König, I.R. Mining Data with Random Forests: Current Options for Real-World Applications. WIREs Data Min. Knowl. Discov. 2014, 4, 55–63. [Google Scholar] [CrossRef]
- Vatani, A.; Jafari-Asl, J.; Ohadi, S.; Safaeian Hamzehkolaei, N.; Afzali Ahmadabadi, S.; Correia, J.A.F.O. An Efficient Surrogate Model for Reliability Analysis of the Marine Structure Piles. Proc. Inst. Civ. Eng.-Marit. Eng. 2023, 176, 176–192. [Google Scholar] [CrossRef]
- Zhou, Q.; Ning, Y.; Zhou, Q.; Luo, L.; Lei, J. Structural Damage Detection Method Based on Random Forests and Data Fusion. Struct. Health Monit. 2013, 12, 48–58. [Google Scholar] [CrossRef]
- Lei, X.; Sun, L.; Xia, Y.; He, T. Vibration-Based Seismic Damage States Evaluation for Regional Concrete Beam Bridges Using Random Forest Method. Sustainability 2020, 12, 5106. [Google Scholar] [CrossRef]
- Trinchero, R.; Larbi, M.; Torun, H.M.; Canavero, F.G.; Swaminathan, M. Machine Learning and Uncertainty Quantification for Surrogate Models of Integrated Devices with a Large Number of Parameters. IEEE Access 2018, 7, 4056–4066. [Google Scholar] [CrossRef]
- Esteghamati, M.Z.; Flint, M.M. Developing Data-Driven Surrogate Models for Holistic Performance-Based Assessment of Mid-Rise RC Frame Buildings at Early Design. Eng. Struct. 2021, 245, 112971. [Google Scholar] [CrossRef]
- Vovk, V.; Gammerman, A.; Shafer, G. Algorithmic Learning in a Random World; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Shafer, G.; Vovk, V. A tutorial on conformal prediction. J. Mach. Learn. Res. 2008, 9, 371–421. [Google Scholar]
- Borrotti, M. Quantifying Uncertainty with Conformal Prediction for Heating and Cooling Load Forecasting in Building Performance Simulation. Energies 2024, 17, 4348. [Google Scholar] [CrossRef]



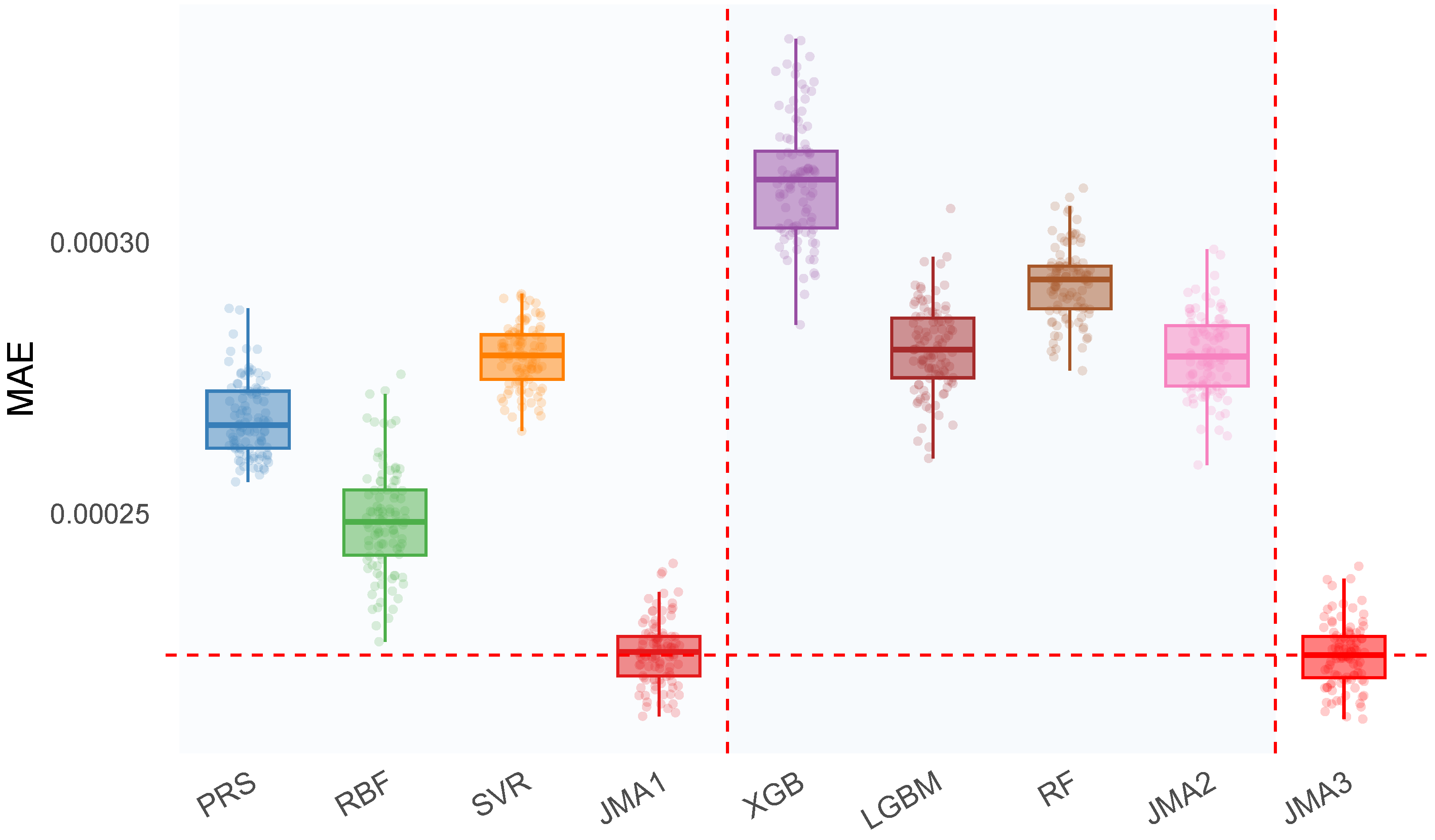
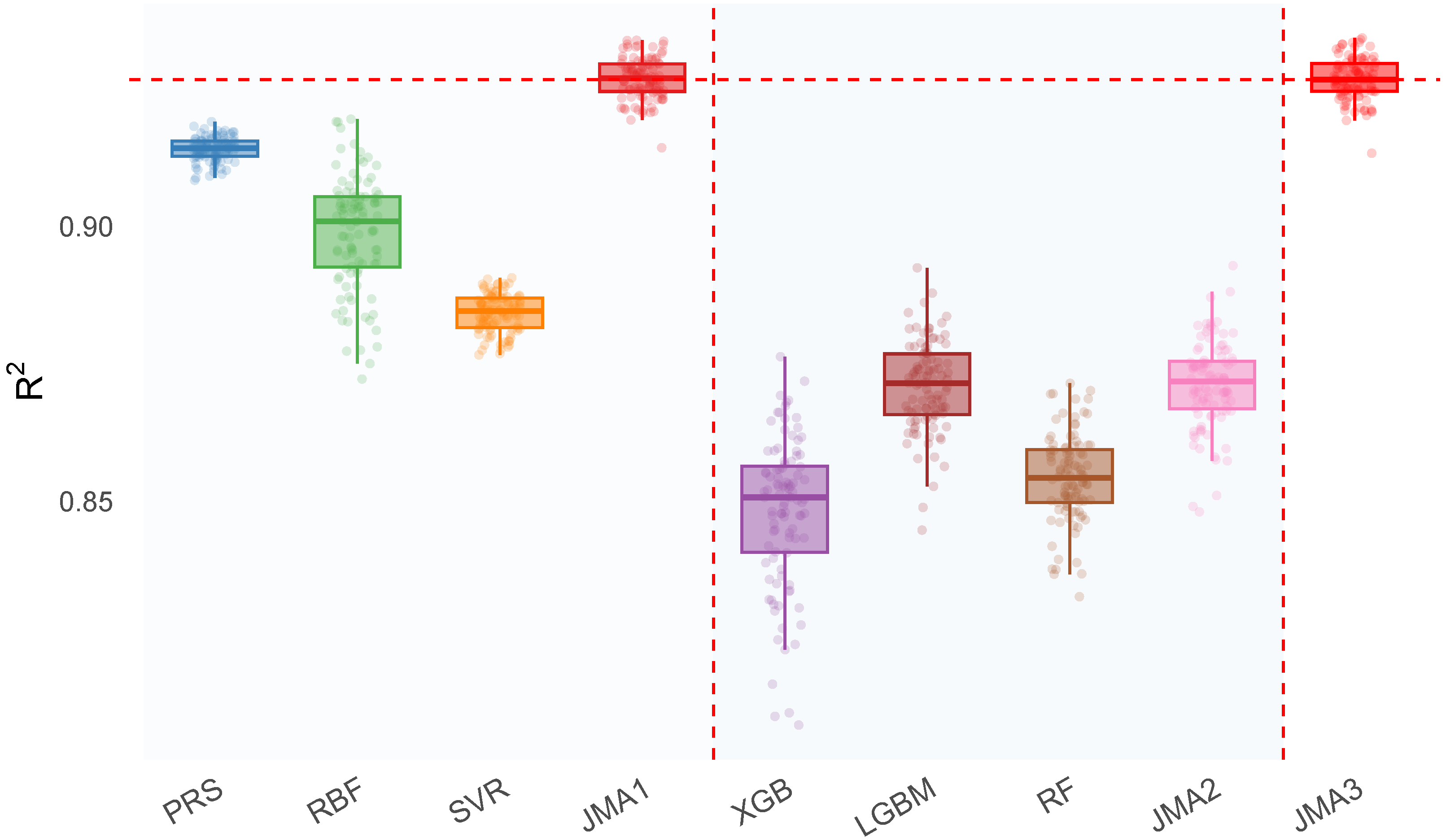
| Method | RMSE () | MAE () | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Median | SD | Mean | Median | SD | Mean | Median | SD | |
| PRS | 0.486 | 0.485 | 0.006 | 0.267 | 0.266 | 0.007 | 0.914 | 0.914 | 0.002 |
| RBF | 0.526 | 0.521 | 0.027 | 0.249 | 0.248 | 0.010 | 0.900 | 0.901 | 0.010 |
| SVR | 0.564 | 0.563 | 0.008 | 0.279 | 0.279 | 0.006 | 0.884 | 0.885 | 0.003 |
| JMA1 | 0.448 | 0.448 | 0.011 | 0.225 | 0.225 | 0.006 | 0.927 | 0.927 | 0.004 |
| XGB | 0.645 | 0.646 | 0.029 | 0.311 | 0.312 | 0.011 | 0.848 | 0.851 | 0.014 |
| LGBM | 0.595 | 0.594 | 0.019 | 0.280 | 0.280 | 0.008 | 0.871 | 0.872 | 0.008 |
| RF | 0.633 | 0.633 | 0.017 | 0.293 | 0.293 | 0.007 | 0.854 | 0.854 | 0.008 |
| JMA2 | 0.595 | 0.594 | 0.018 | 0.279 | 0.279 | 0.007 | 0.871 | 0.871 | 0.008 |
| JMA3 | 0.448 | 0.448 | 0.012 | 0.224 | 0.224 | 0.006 | 0.927 | 0.927 | 0.004 |
| Model | CR | IW |
|---|---|---|
| PRS | 0.9140 | 0.0015 |
| RBF | 0.9161 | 0.0017 |
| SVR | 0.9154 | 0.0018 |
| XGB | 0.9124 | 0.0021 |
| LGBM | 0.9131 | 0.0020 |
| RF | 0.9128 | 0.0021 |
| JMA1 | 0.9190 | 0.0014 |
| JMA2 | 0.9140 | 0.0019 |
| JMA3 | 0.9191 | 0.0014 |
| Method | PRS | SVR | RBF | JMA1 | XGB | LGBM | RF | JMA2 | JMA3 |
|---|---|---|---|---|---|---|---|---|---|
| Time (s) | 0.002 | 0.081 | 10.183 | 30.602 | 0.034 | 0.021 | 0.223 | 1.388 | 31.466 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Wang, J.; Wu, N. Machine Learning-Based Surrogate Ensemble for Frame Displacement Prediction Using Jackknife Averaging. Buildings 2025, 15, 2872. https://doi.org/10.3390/buildings15162872
Zhao Z, Wang J, Wu N. Machine Learning-Based Surrogate Ensemble for Frame Displacement Prediction Using Jackknife Averaging. Buildings. 2025; 15(16):2872. https://doi.org/10.3390/buildings15162872
Chicago/Turabian StyleZhao, Zhihao, Jinjin Wang, and Na Wu. 2025. "Machine Learning-Based Surrogate Ensemble for Frame Displacement Prediction Using Jackknife Averaging" Buildings 15, no. 16: 2872. https://doi.org/10.3390/buildings15162872
APA StyleZhao, Z., Wang, J., & Wu, N. (2025). Machine Learning-Based Surrogate Ensemble for Frame Displacement Prediction Using Jackknife Averaging. Buildings, 15(16), 2872. https://doi.org/10.3390/buildings15162872








