Research on the Safety Judgment of Cuplok Scaffolding Based on the Principle of Image Recognition
Abstract
1. Introduction
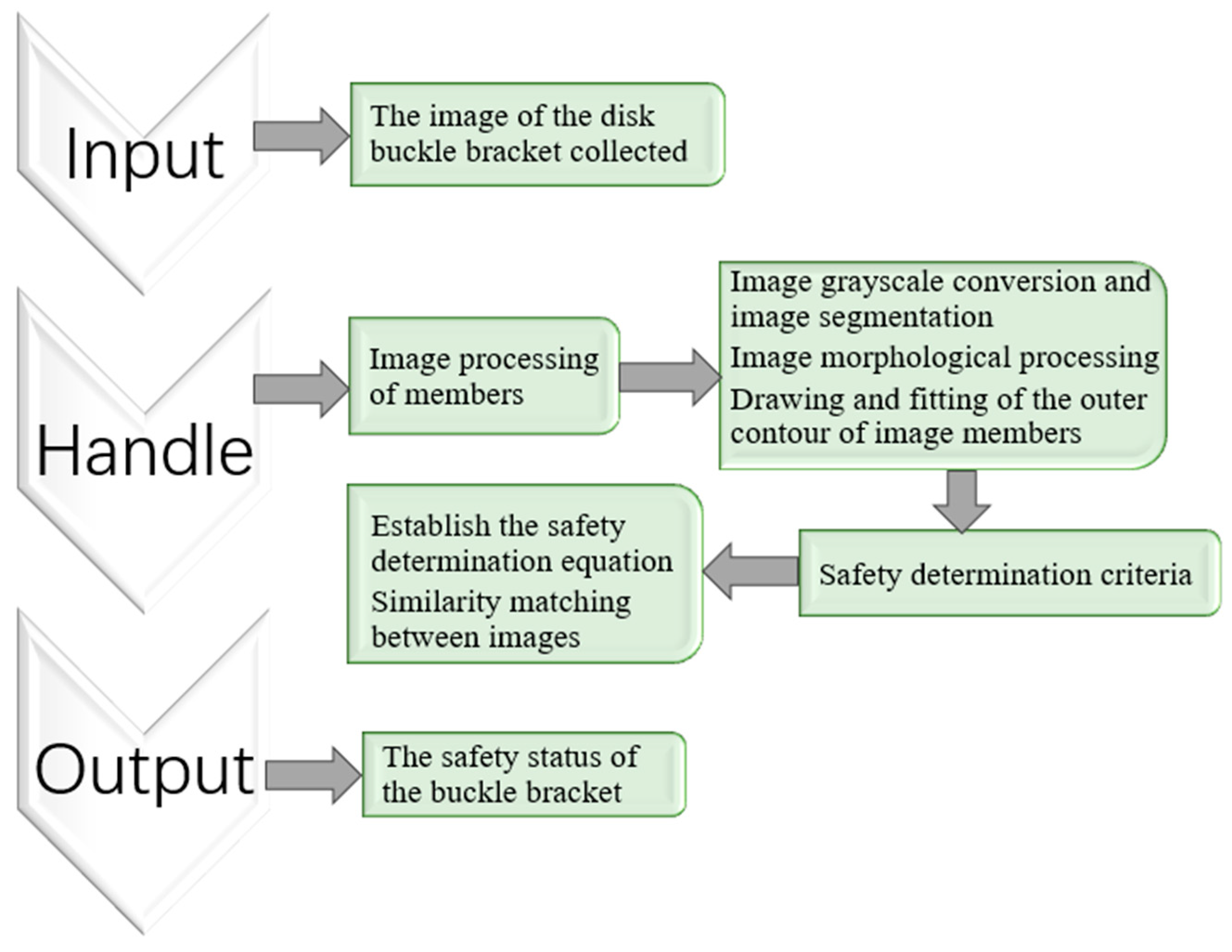
2. Cuplok Scaffolding Safety Evaluation Framework
3. Image Processing of Cuplok Scaffolding Systems
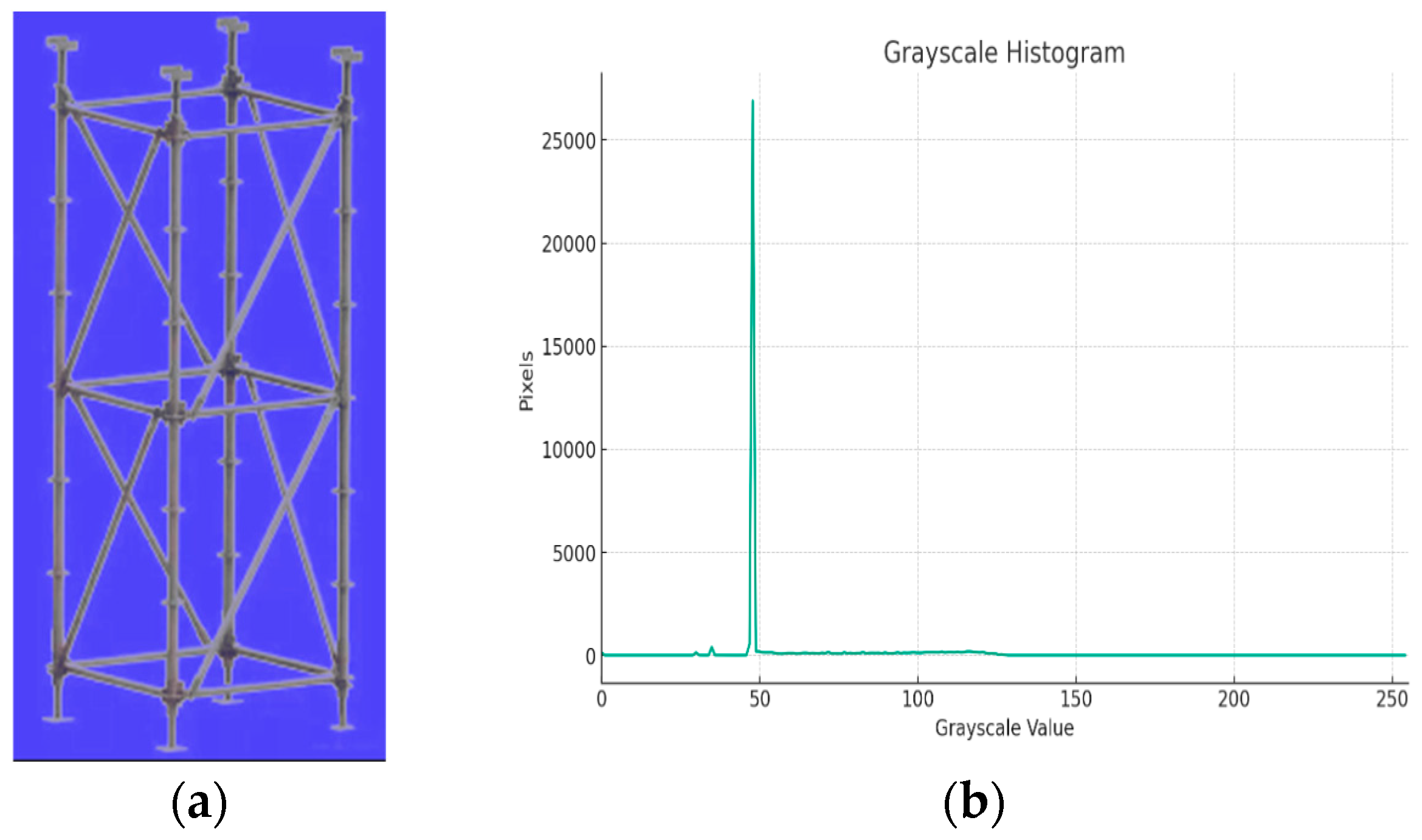
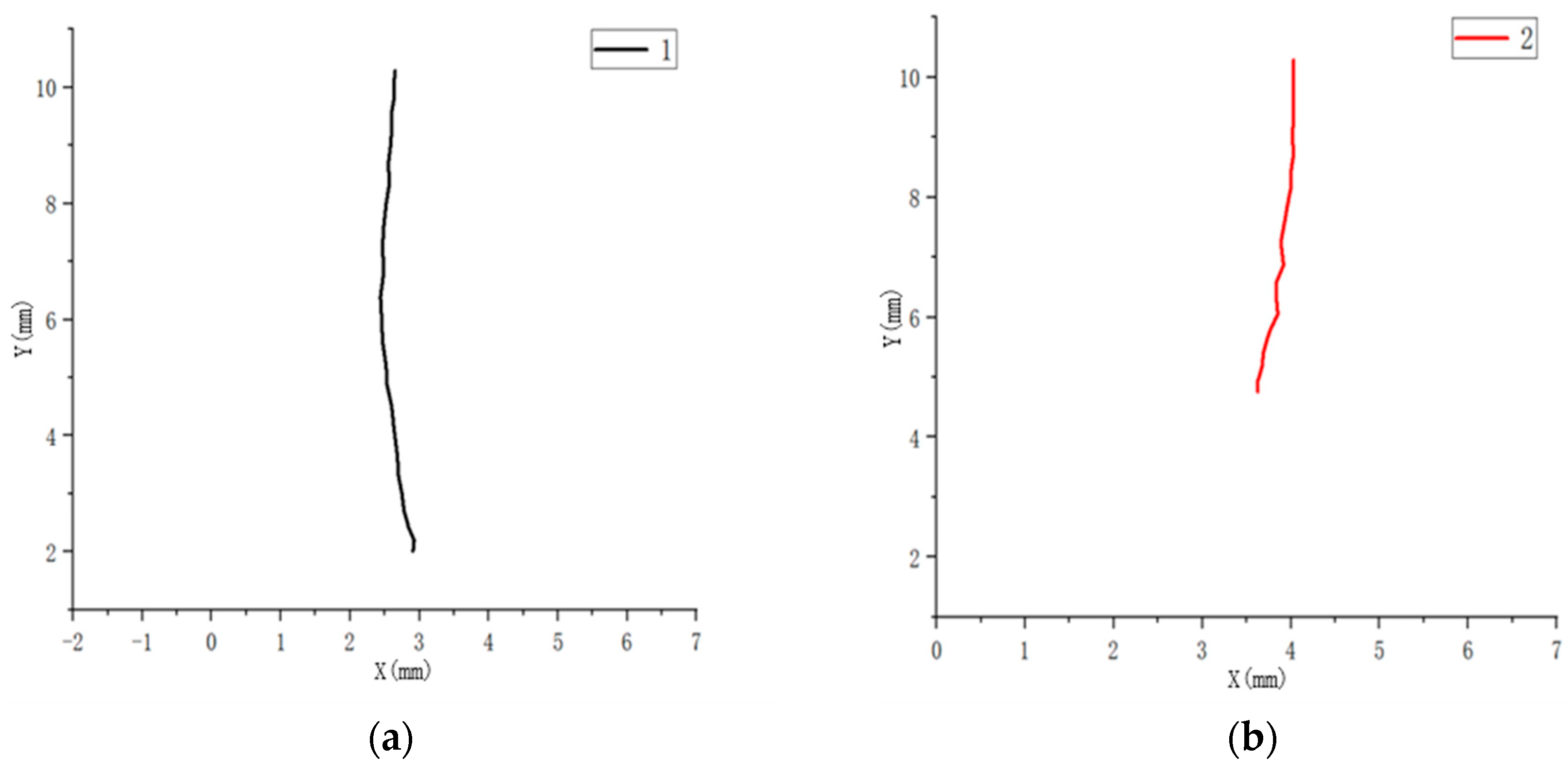
3.1. Image Grayscale Processing
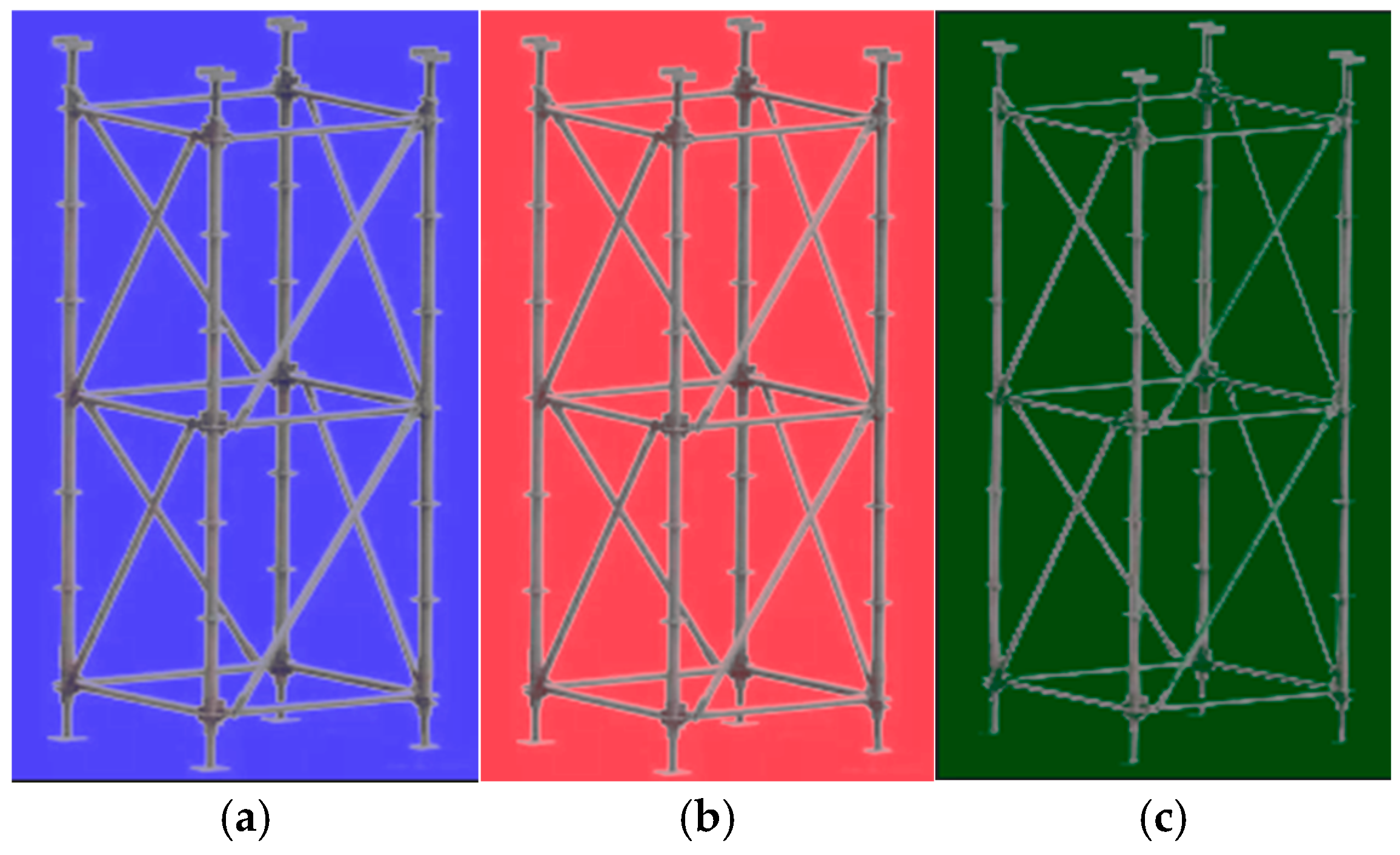
3.2. Image Feature Analysis and Segmentation Processing
- Under the same light brightness and among the background color factor differences of each member, compared with the blue and green backgrounds, the color factor difference under the red background was the largest. It can be seen that for the color of the cuplok scaffold system, when there was a large amount of red in the background, the buckle bracket system was the easiest to distinguish.
- It can be known from Rod 1, Rod 3, and Rod 4 that as the brightness of the light increases, the color factor difference keeps decreasing and decreases linearly. However, compared with Rod 3, the decrease in amplitude of Rod 1 and Rod 4 was faster. And the color factor difference is lower under the green and blue background; however, against the background of red and blue, member 2 suddenly showed a significant decrease in abruptness. It can be seen that when shooting the rods, a certain distance should be maintained.
- Under the same light brightness and the same color, the color factor difference between member 1 and member 4 was the largest, while that between member 2 and member 3 was the smallest. Members 1 and 2 were at the closer positions of the image, while members 2 and 3 were further back. It can be concluded that due to the influence of distance, the closer the disk cuplok scaffold members are, the greater the color factor difference, and the easier it is to segment.
3.3. Image Denoising and Morphological Processing
3.4. Image Transformation Processing
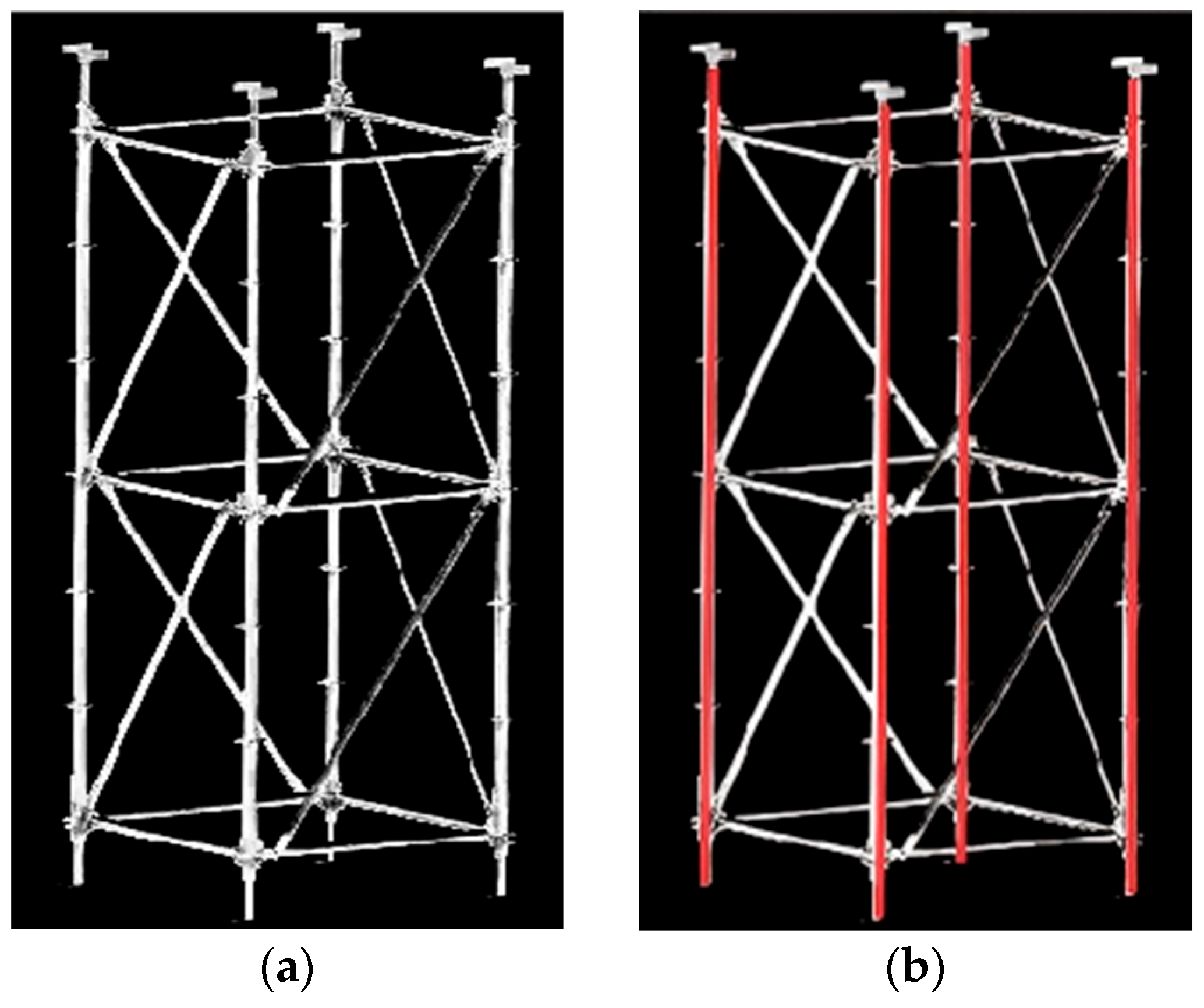
3.5. Discrete and Integrated Processing of Vertical Rods
4. Linearization of the Image of the Cuplok Scaffold
4.1. Image Binarization Processing
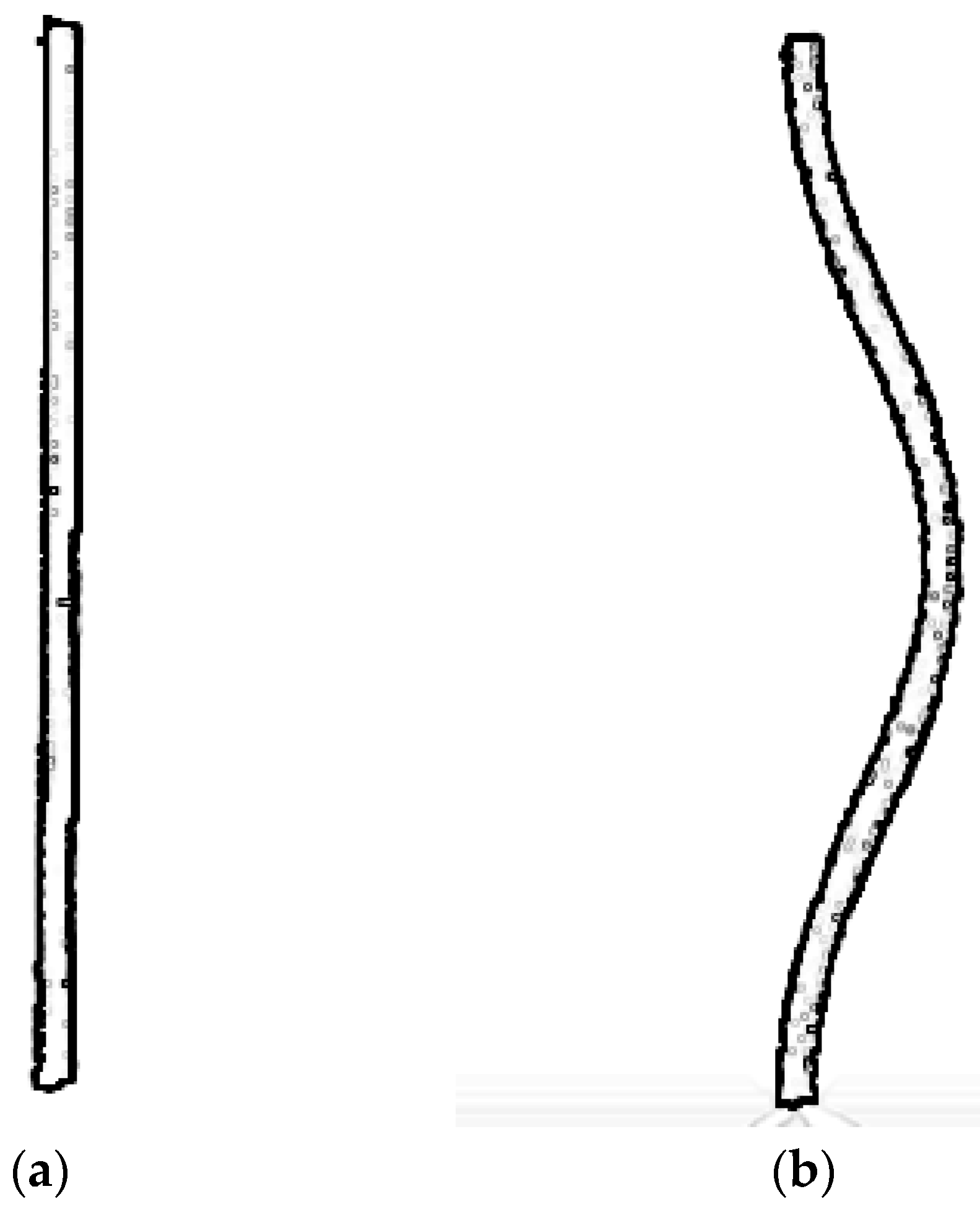
4.2. Extraction of Outer Contour
4.3. Based on Open Cv Numerical Curve Fitting
5. The Image Safety Determination Criterion of the Cuplok Scaffold Is Established
The Safety Determination Criterion Based on Bending Energy Is Established
- 1.
- The number of curve bends ().
- 2.
- The ratio of arc length to major axis ().
- 3.
- The ratio of the radius of curvature of the coordinate point to the major axis.
- First, calculate the bending times of the identified structural members and the contour curves of the numerical model, respectively, and then compare them.When , this point is considered to have experienced a bend;When 80% of the points (namely16 points) are successfully matched, it is considered that the number of curve bends is successfully matched.
- Next, the identified bracket poles and the contour curves of the model examples are matched for the second feature. When the relative error between the two is less than 10%, it is considered that the characteristic value of the ratio of the arc length to the major axis of the two is successfully matched.When , it is considered that this point matches successfully;When 80% of the points (namely 16 points) are successfully matched, it is considered that the number of curve bends is successfully matched.
- The comparison of the curvature radius and the ratio of the major axis of the contour curves of the identified support poles and model examples. When at least 80% of the coordinate points satisfy a relative error of less than 10%, the feature matching is considered successful.When , it is considered that this point matches successfully.When 80% of the points (i.e., 16 points) are successfully matched, it is considered that the number of curve bends is successfully matched. When the matching of the three features is successful, the corresponding recognition of the numerical curve of the identified deformed support and the buckling mode calculated by the model example is achieved.
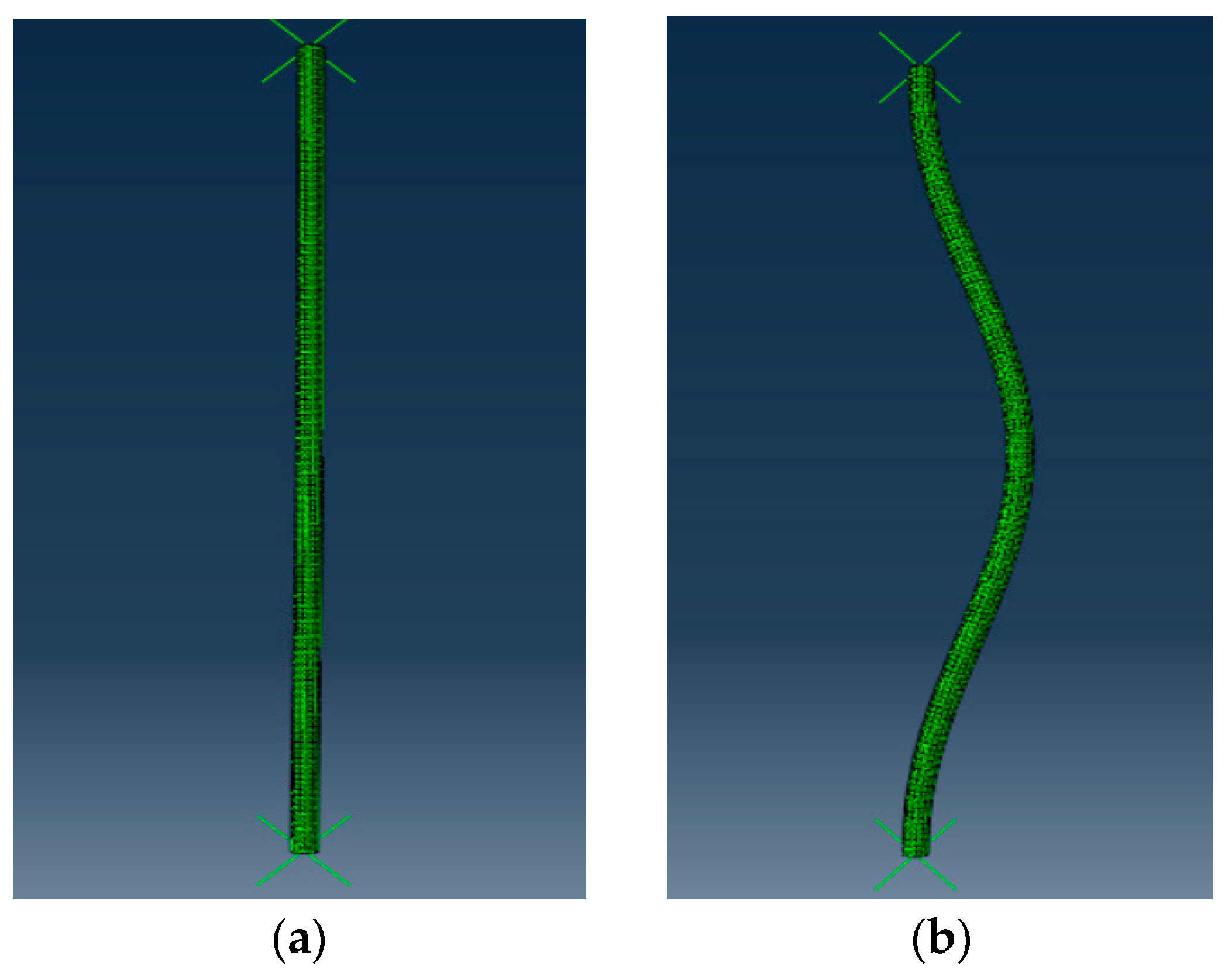
6. Image Case and Result Analysis of Cuplok Scaffold
6.1. Image Case Processing
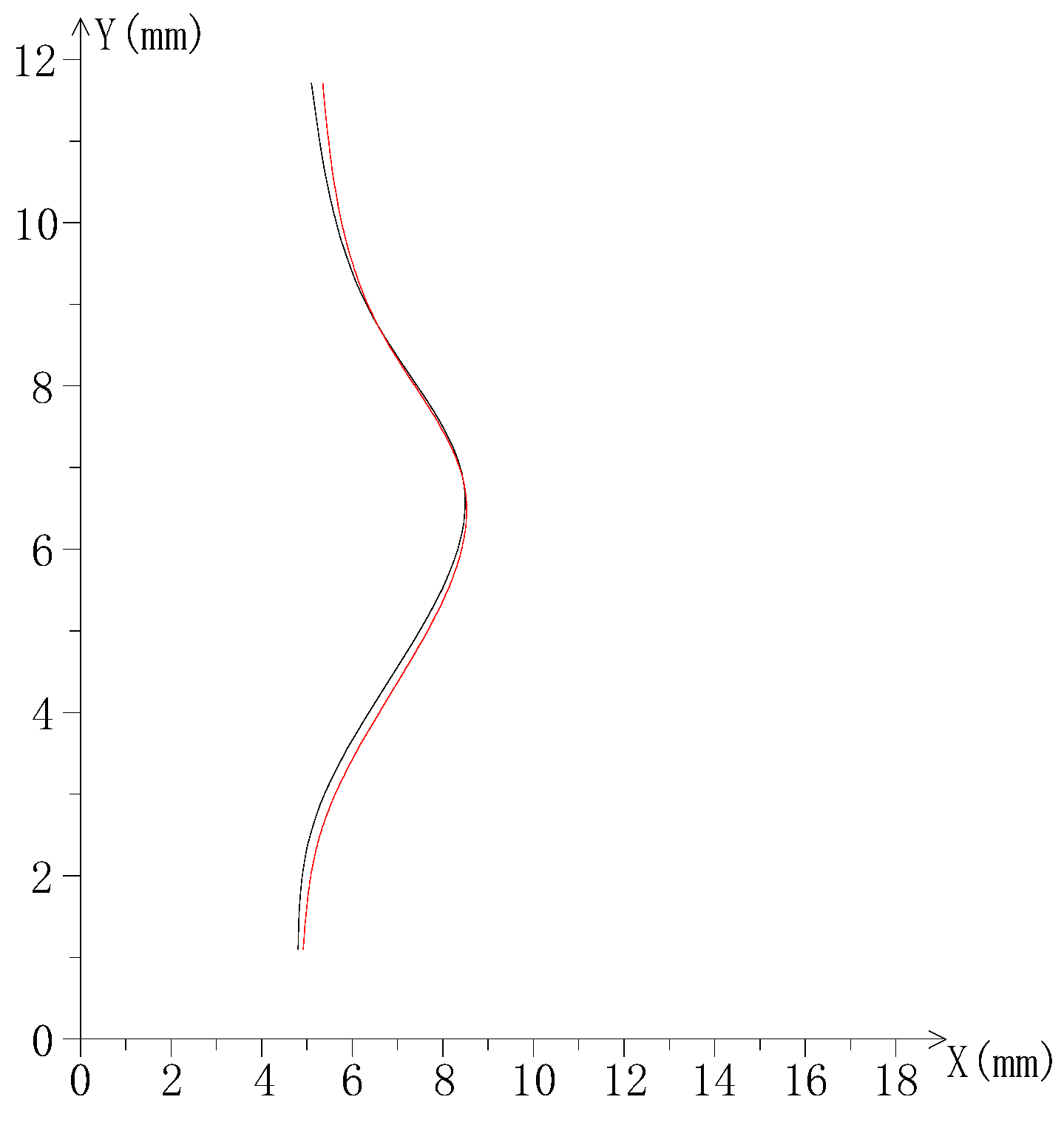
6.2. Analysis of Image Matching Results
7. Conclusions
- For the collected images of the cuplok scaffold, a set of effective image processing technical methods was proposed to realize the recognition of the cuplok scaffold system in a complex background.
- Based on Open CV, the outer contour of the structural members was proposed through binarized images, and the least square method was used to fit the outer contour to fit the linear curve of the deformed support. This has improved the efficiency for subsequent similarity matching.
- The safety determination criterion of the cuplok scaffold was proposed. The results of the experimental case show that this safety determination method has better accuracy, and the accuracy rate of evaluating the force magnitude reaches 80%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gui, Z.J.; Zhang, J.D.; Feng, X.N.; Liu, D. Application of Socket-Type Disk Buckle Steel Pipe Supports in Bridge Engineering. Highw. Traffic Sci. Technol. 2018, 35, 76–81. [Google Scholar]
- Xie, H.B.; Wang, G.L. Analysis of the Causes of Safety Accidents and Preventive Measures of Steel Pipe Formwork Supports in Bridge Construction. Highway 2010, 9, 175–179. [Google Scholar]
- Jiang, S.Q.; Min, W.Q.; Wang, S.H. Review and Prospect of Image Recognition Technology for Intelligent Interaction. Comput. Res. Dev. 2016, 53, 113–122. [Google Scholar]
- Gong, R.K.; Liu, J. Research on maize disease recognition based on image processing. Mod. Electron. Tech. 2021, 44, 149–152. [Google Scholar]
- Zhao, J.L.; Jin, Y.; Ye, H.C.; Huang, W.; Dong, Y.; Fan, L.; Jiang, J. Remote sensing monitoring of areca yellow leaf disease based on UAV multispectral images. Trans. Chin. Soc. Agric. Eng. 2020, 36, 54–61. [Google Scholar]
- Yi, X.; Xiao, Q.; Zeng, F.; Yin, H.; Li, Z.; Qian, C.; Chen, B.T. Computed tomography radiomics for predicting pathological grade of renal cell carcinoma. Front. Oncol. 2021, 10, 570396. [Google Scholar] [CrossRef]
- Bandara, M.S.; Gurunayaka, B.; Lakraj, G.; Pallewatte, A.; Siribaddana, S.; Wansapura, J. Ultrasound based radiomics features of chronic kidney disease. Acad. Radiol. 2022, 29, 229–235. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X. Research on Real-time Monitoring Method and Application of External Scaffolding Safety Based on Mobile IT. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2014. [Google Scholar]
- Yang, Z.; Yuan, Y.; Zhang, M.; Zhao, X.; Zhang, Y.; Tian, B. Safety distance identification for crane drivers based on mask R-CNN. Sensors 2019, 19, 2789. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.L.; Chen, W.F.; Chen, H.J.; Yen, T.; Kao, Y.G.; Lin, C.Q. A monitoring method for scaffold-frame shoring systems for elevated concrete formwork. Comput. Struct. 2000, 78, 681–690. [Google Scholar] [CrossRef]
- Chen, Y.R.; Liu, L.J.; Duan, C.Y. Study on the Mechanical Characteristic and Safety Measures of Bowl-scaffold. Procedia-Soc. Behav. Sci. 2013, 96, 304–309. [Google Scholar] [CrossRef]
- Zhao, J.P.; Liu, X.X.; Zhang, X.Z. Hazard Image Recognition Technology for External Scaffolding Based on Improved YOLOv5s. China Saf. Sci. J. 2023, 33, 60–66. [Google Scholar] [CrossRef]
- Zhang, M.Y.; Cao, Z.Y.; Zhao, X.F.; Yang, Z. Research on Safety Helmet Wearing Detection for Construction Workers Based on Deep Learning. J. Saf. Environ. 2019, 19, 535–541. [Google Scholar]
- Li, H.; Wang, Y.B.; Yi, P.; Wang, T.; Wang, C.L. Research on Safety Helmet Recognition in Complex Work Scenarios Based on Deep Learning. J. Saf. Sci. Technol. 2021, 17, 175–181. [Google Scholar]
- Wang, Z.; Zhou, J.; Zhou, Y.; Chen, B.; Xu, X.; Zhu, H. Exploration of Perimeter Guardrail Identification Method Based on CNN Algorithm and UAV Technology. J. Inf. Technol. Civ. Eng. Archit. 2021, 13, 29–37. [Google Scholar]
- Liu, C.; Sui, H.; Wang, J.; Ni, Z.; Ge, L. Real-Time Ground-Level Building Damage Detection Based on Lightweight and Accurate YOLOv5 Using Terrestrial Images. Remote Sens. 2022, 14, 2763. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J.; Faster, R.C.N.N. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Redmon, J.; Divvala, S.K.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Lou, L.T.; He, H.L. An OTSU Threshold Optimization Algorithm Based on Image Grayscale Transformation. J. South-Cent. Minzu Univ. (Nat. Sci. Ed.) 2021, 40, 325–330. [Google Scholar]
- Zhang, L.N. Color Image Gray Method Research. Ph.D. Thesis, Lanzhou University, Lanzhou, China, 2024. [Google Scholar]
- Bhunia, A.K.; Bhattacharyya, A.; Banerjee, P.; Roy, P.P.; Murala, S. A novel feature descriptor for image retrieval by combining modified color histogram and diagonally symmetric co-occurrence texture pattern. Pattern Anal. Appl. 2019, 23, 1–21. [Google Scholar] [CrossRef]
- Li, E.; Zhang, W. Smoke Image Segmentation Algorithm Suitable for Low-Light Scenes. Fire 2023, 6, 217. [Google Scholar] [CrossRef]
- Ma, W.; Zhang, P.C.; Huang, L.; Zhu, J.W.; Lian, Y.T.; Xiong, J.; Jin, F. Improved Yolov5 and Image Morphology Processing Based on UAV Platform for Dike Health Inspection. Int. J. Web Serv. Res. (IJWSR) 2023, 20, 1–13. [Google Scholar] [CrossRef]
- Grigoriev, S.N.; Zakharov, O.V.; Lysenko, V.G.; Masterenko, D.A. An efficient algorithm for areal morphologicalfiltering. Meas. Tech. 2024, 66, 906–912. [Google Scholar] [CrossRef]
- Liu, J.L. Application of Mathematical Morphology in Digital Image Processing. Integr. Circuit Appl. 2022, 39, 75–77. [Google Scholar] [CrossRef]
- Salanghouch, H.S.; Kabir, E.; Fakhimi, A. Finding Particle Size Distribution from Soil Images Using Circular Hough Transform. Int. J. Civ. Eng. 2025, 23, 1521–1533. [Google Scholar] [CrossRef]
- Li, P.S.; Li, J.D.; Wu, L.W.; Hu, J.P. Convolution kernel initialization method based on image characteristics. J. Ji Lin Univ. (Sci. Ed.) 2021, 59, 587–594. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, J.; Gao, J. An algorithm for building contour inference fitting based on multiple contour point classification processes. Int. J. Appl. Earth Obs. Geoinf. 2024, 133, 104126. [Google Scholar] [CrossRef]
- Amato, U.; Della Vecchia, B. Iterative rational least squares fitting. Georgian Math. J. 2019, 28, 1–14. [Google Scholar] [CrossRef]
- Zhu, G.A.; Wang, J.X. Research on Human Sitting Posture Recognition Method Based on Zhang-Suen Algorithm. Digit. World 2020, 1–46. [Google Scholar]

















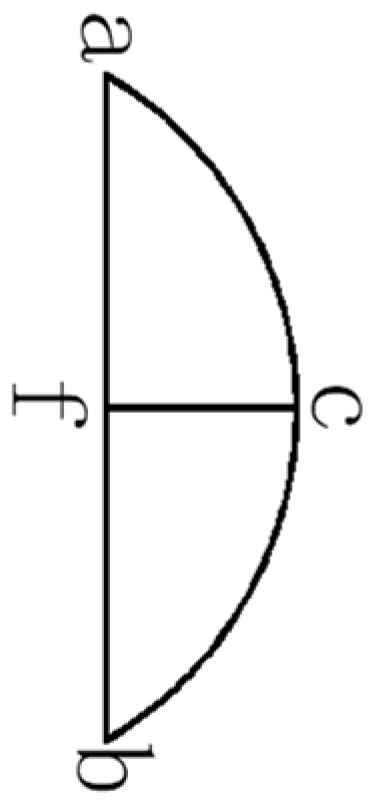



| Category of Rods | Point Sequence | R | G | B | Color Factor |
|---|---|---|---|---|---|
| Member 1 | 1 | 251 | 221 | 125 | 1.45 |
| 2 | 255 | 220 | 125 | 1.47 | |
| 3 | 251 | 221 | 132 | 1.42 | |
| Member 2 | 4 | 253 | 243 | 108 | 1.20 |
| 5 | 255 | 243 | 110 | 1.21 | |
| 6 | 255 | 243 | 108 | 1.31 | |
| Member 3 | 7 | 251 | 223 | 138 | 1.03 |
| 8 | 252 | 220 | 135 | 1.03 | |
| 9 | 255 | 230 | 138 | 1.02 | |
| Member 4 | 10 | 251 | 221 | 125 | 1.45 |
| 11 | 251 | 221 | 125 | 1.45 | |
| 12 | 252 | 220 | 132 | 1.43 |
| Background | R | G | B | Color Factor |
|---|---|---|---|---|
| red | 17 | 53 | 27 | 0.43 |
| green | 17 | 53 | 27 | 0.43 |
| blue | 76 | 67 | 244 | 0.58 |
| Rod 1 | 100% | 90% | 90% |
| Rod 2 | 90% | 80% | 85% |
| Rod 3 | 85% | 80% | 80% |
| Rod 4 | 100% | 95% | 90% |
| Serial Number | Actual Axial Force | Identify Axial Force | Accuracy Rate |
|---|---|---|---|
| Rod 1 | 15 kN | 13.7 kN | 89% |
| Rod 2 | 15 kN | 13 kN | 87% |
| Rod 3 | 15 kN | 12.45 kN | 83% |
| Rod 4 | 15 kN | 13.65 kN | 91% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, J.; Bai, S.; Ruan, G.; Gryniewicz, M. Research on the Safety Judgment of Cuplok Scaffolding Based on the Principle of Image Recognition. Buildings 2025, 15, 3737. https://doi.org/10.3390/buildings15203737
Xue J, Bai S, Ruan G, Gryniewicz M. Research on the Safety Judgment of Cuplok Scaffolding Based on the Principle of Image Recognition. Buildings. 2025; 15(20):3737. https://doi.org/10.3390/buildings15203737
Chicago/Turabian StyleXue, Jiang, Shuile Bai, Guanhao Ruan, and Marcin Gryniewicz. 2025. "Research on the Safety Judgment of Cuplok Scaffolding Based on the Principle of Image Recognition" Buildings 15, no. 20: 3737. https://doi.org/10.3390/buildings15203737
APA StyleXue, J., Bai, S., Ruan, G., & Gryniewicz, M. (2025). Research on the Safety Judgment of Cuplok Scaffolding Based on the Principle of Image Recognition. Buildings, 15(20), 3737. https://doi.org/10.3390/buildings15203737






