Mud Spurt Distance and Filter Cake Hydraulic Conductivity of Slurry Shield
Abstract
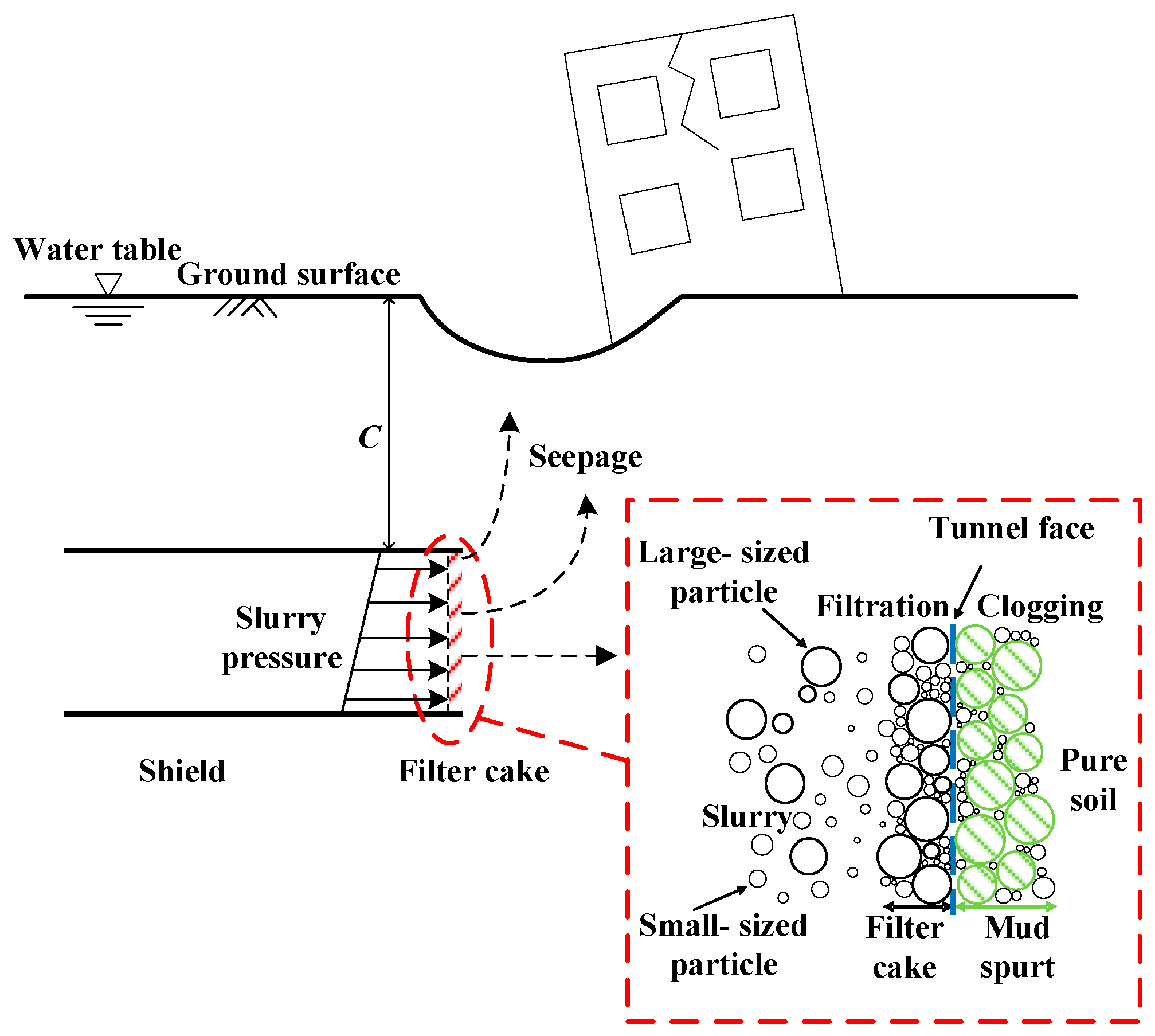
1. Introduction
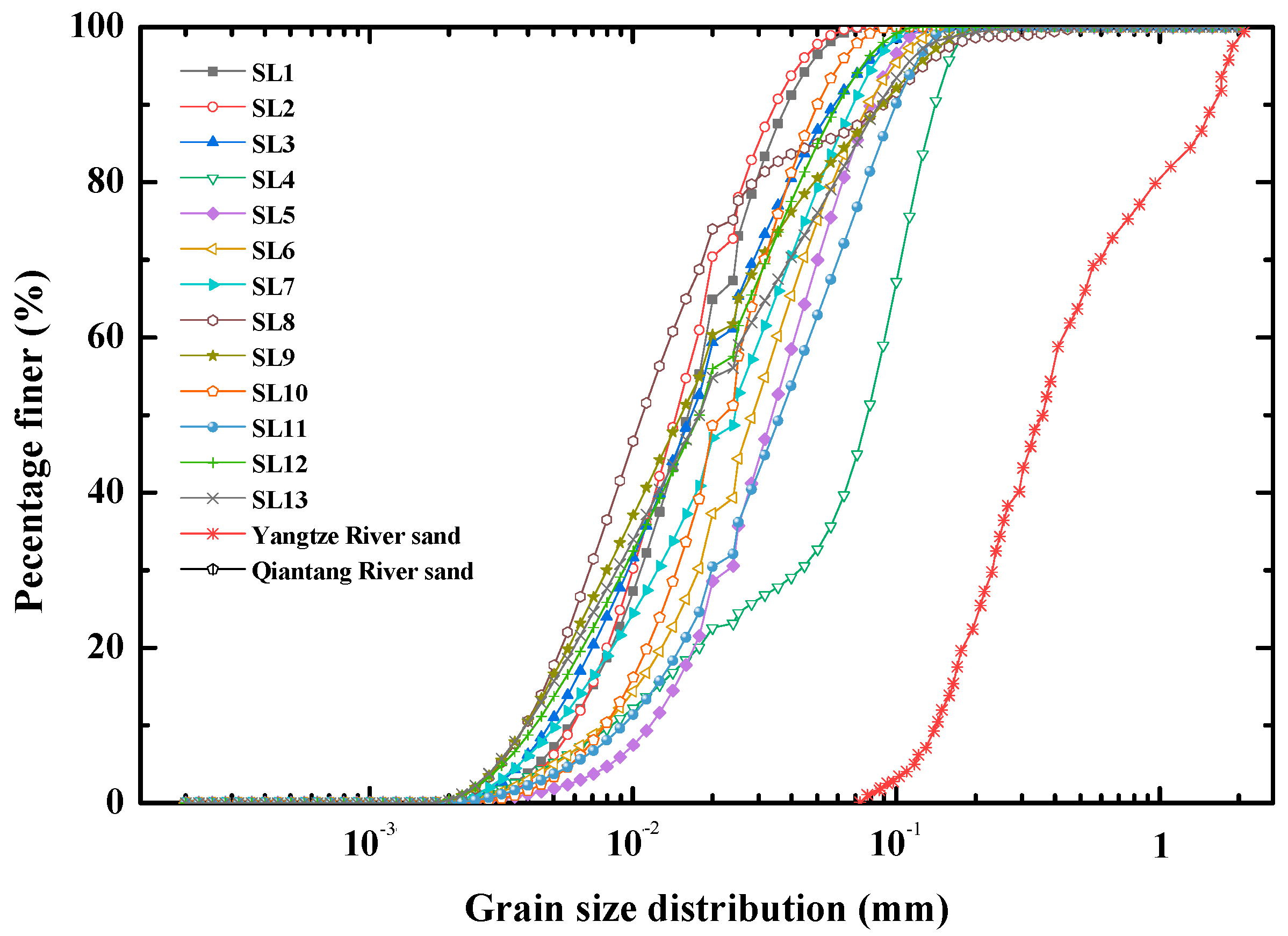
2. Materials
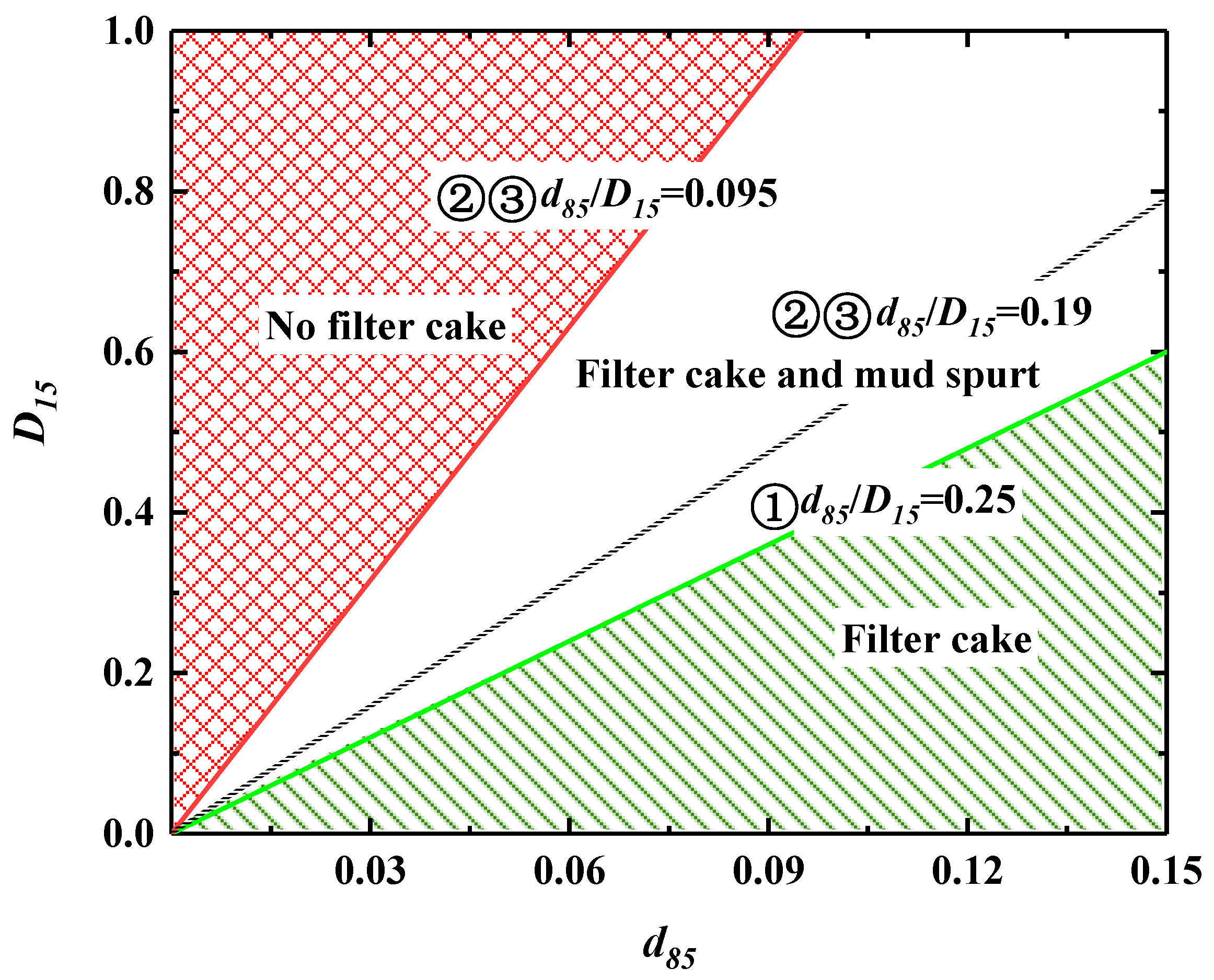
3. The Criteria of Filter Cake Formation
4. Mud Spurt Distance Model
4.1. Mud Spurt Model
4.2. Calculation of Mud Spurt Model
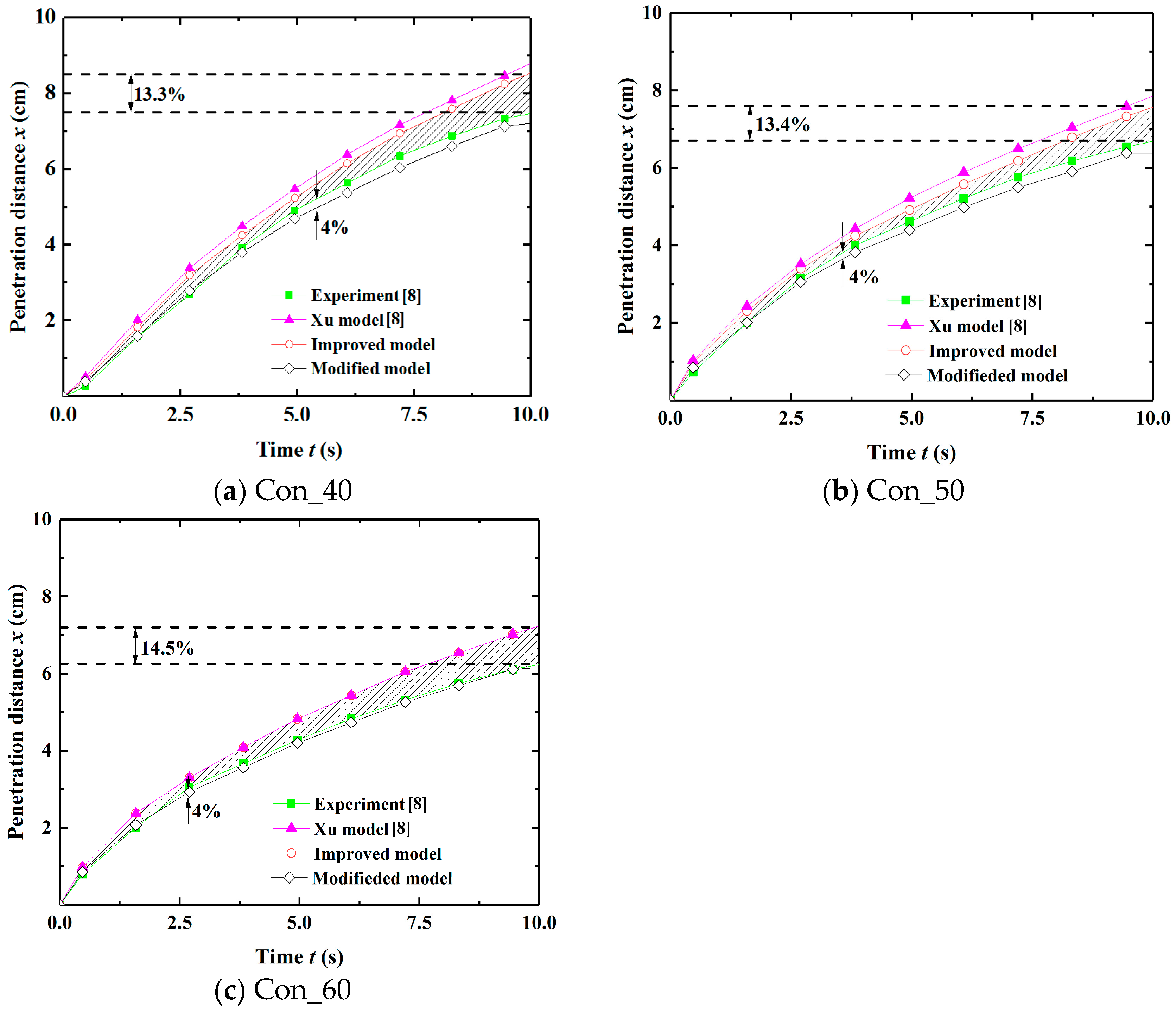
4.3. Validation of Mud Spurt Model
4.4. Mud Spurt Model with Filter Cake
5. Hydraulic Conductivity and Thickness of Filter Cake
5.1. Filtration Theory
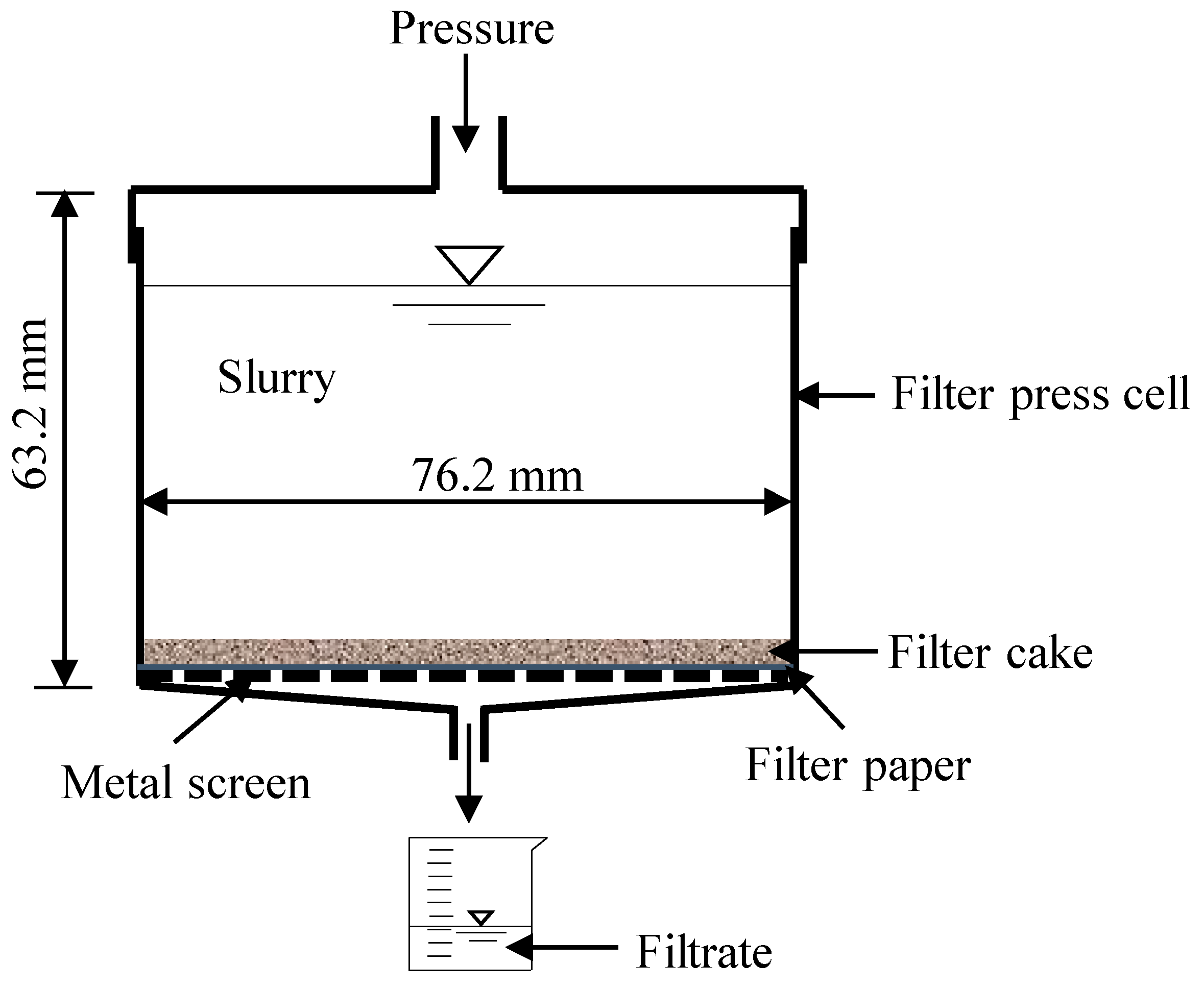
5.2. Modified Fluid Loss Test
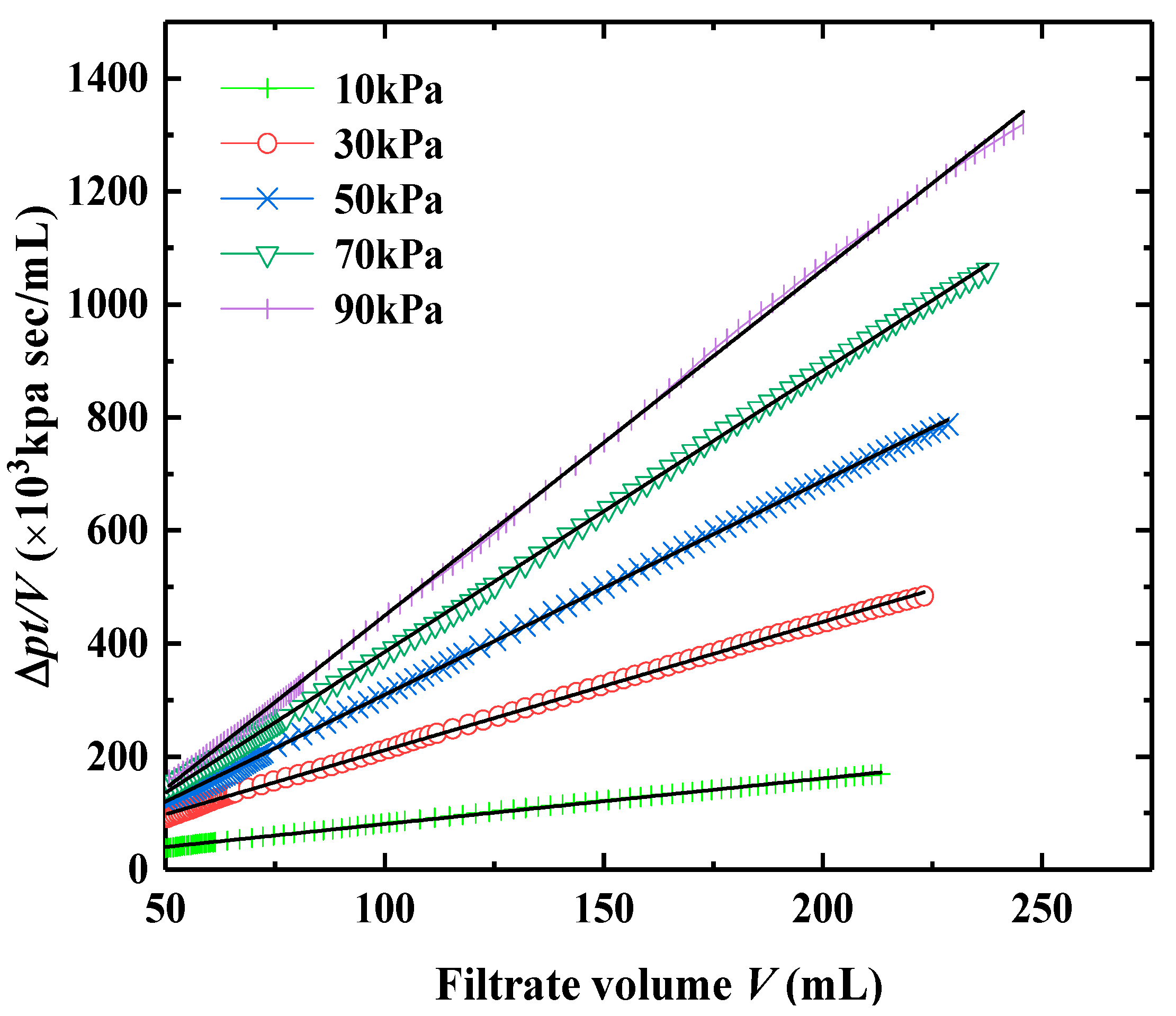
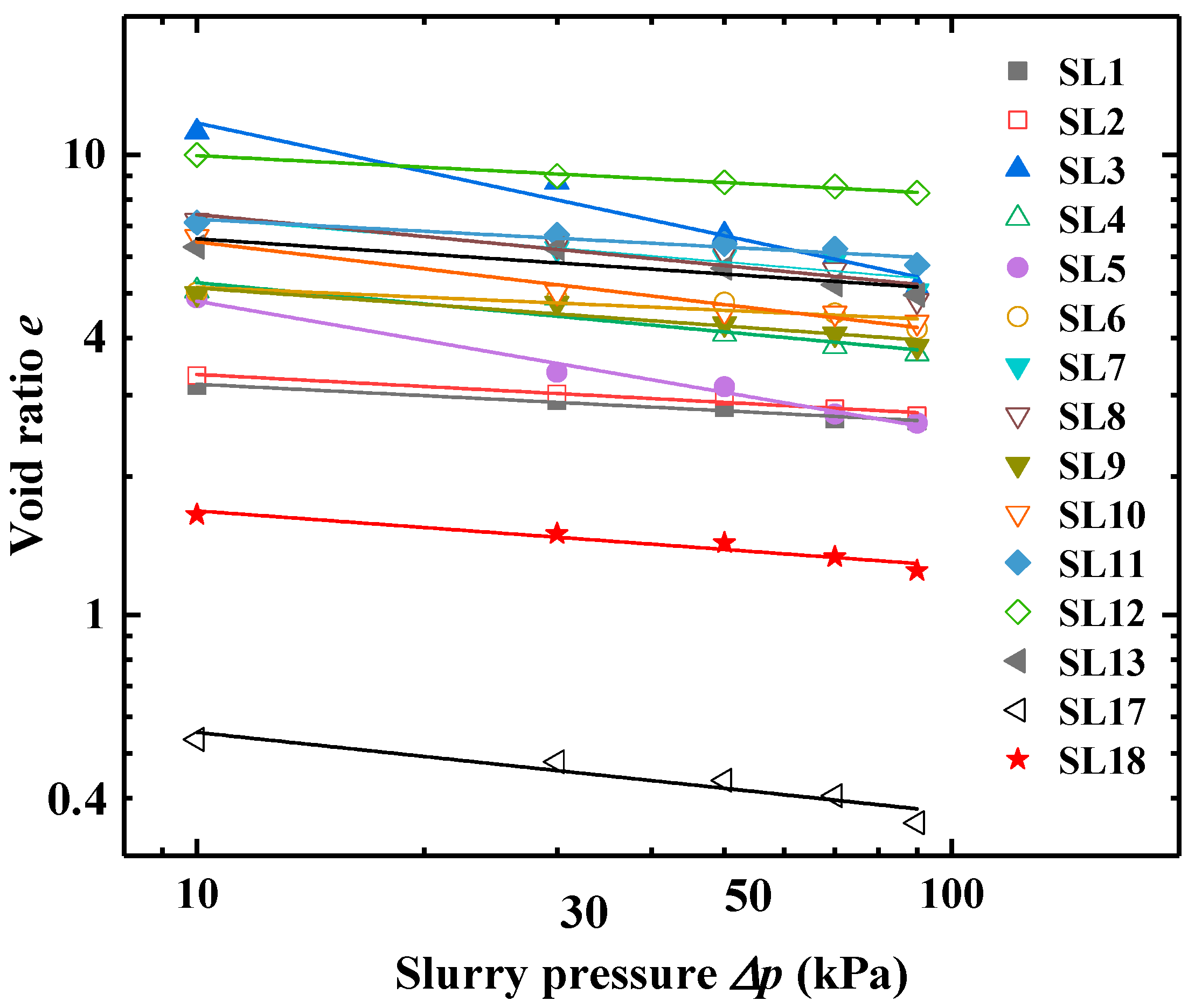
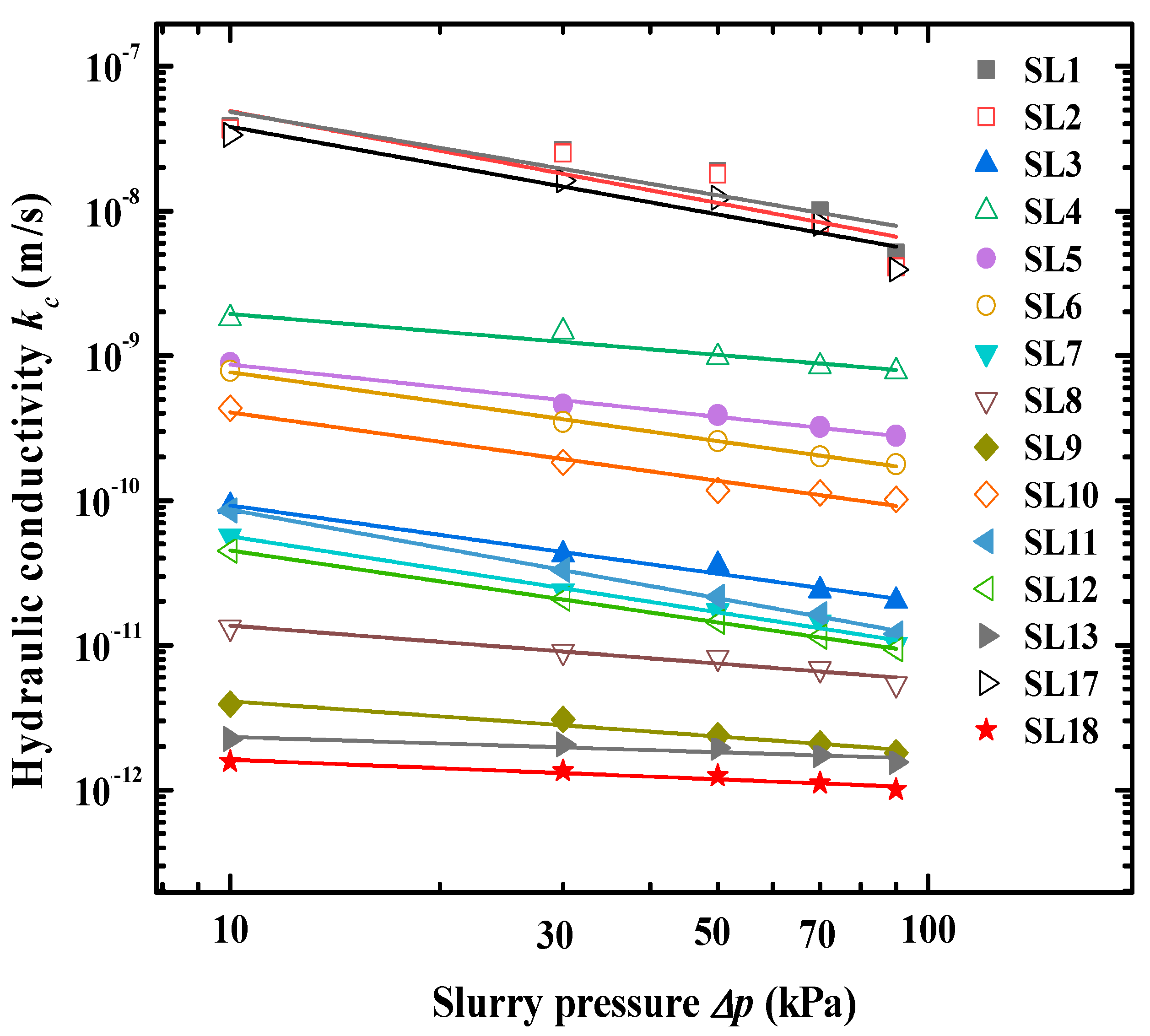
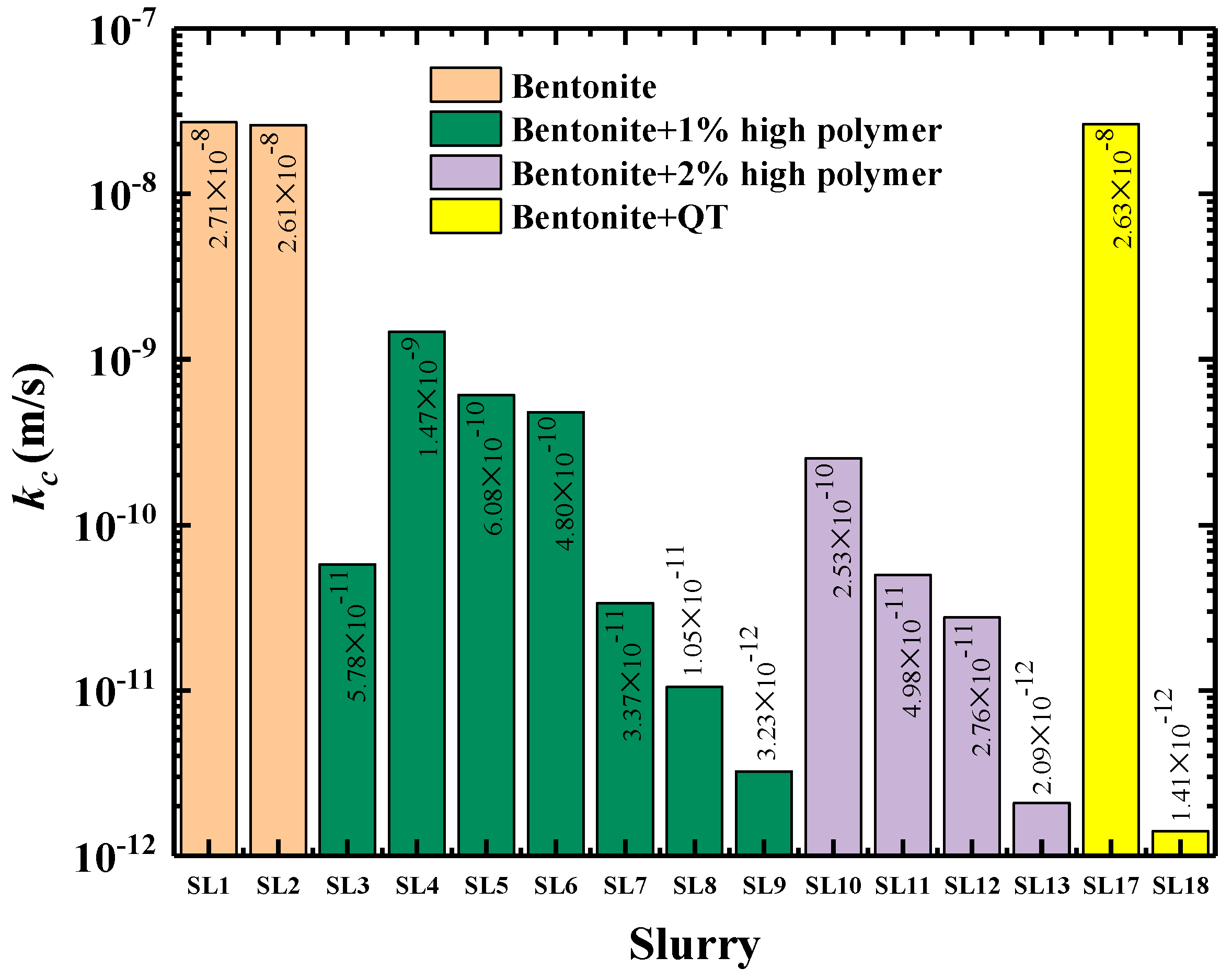
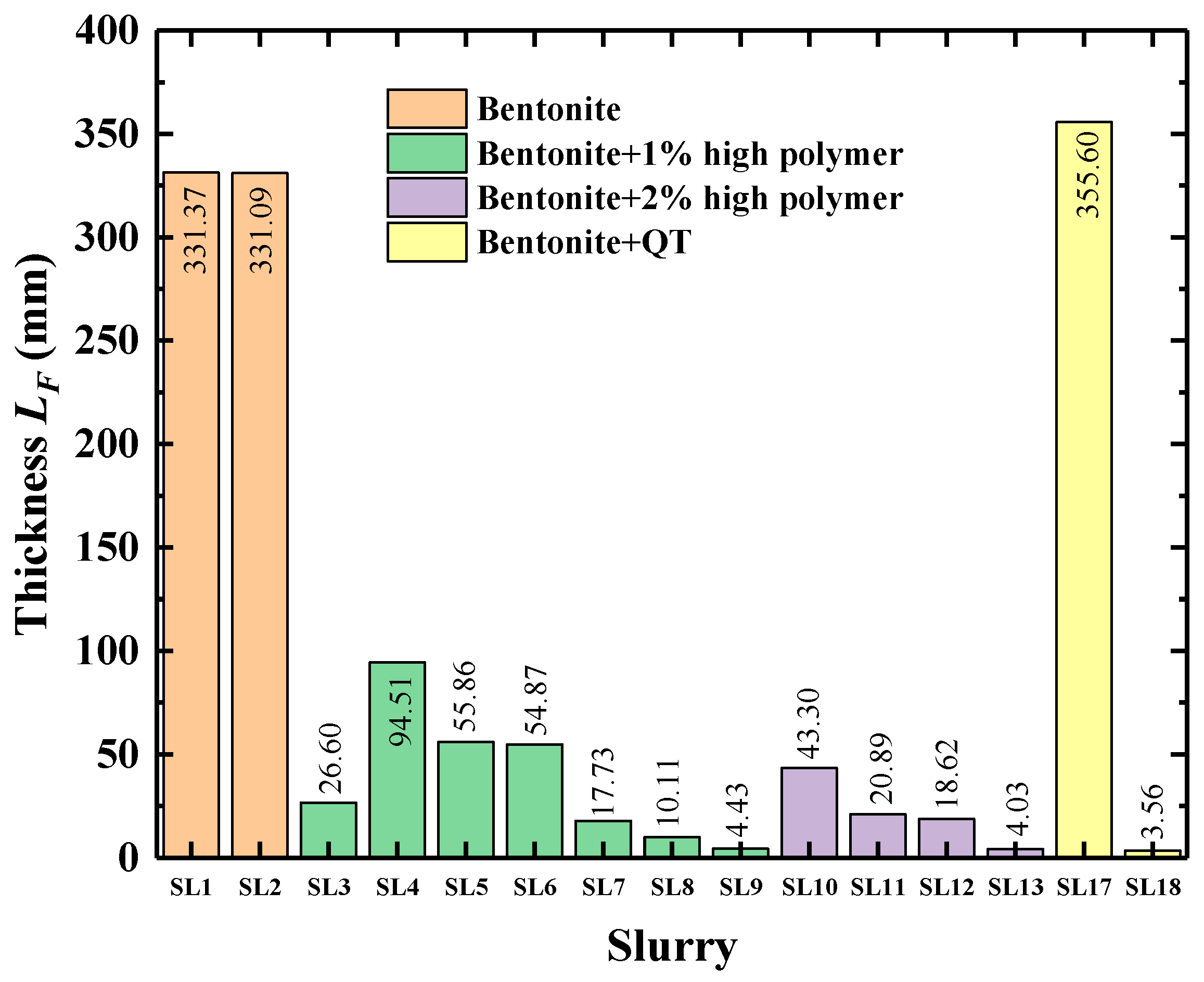
5.3. Test Results
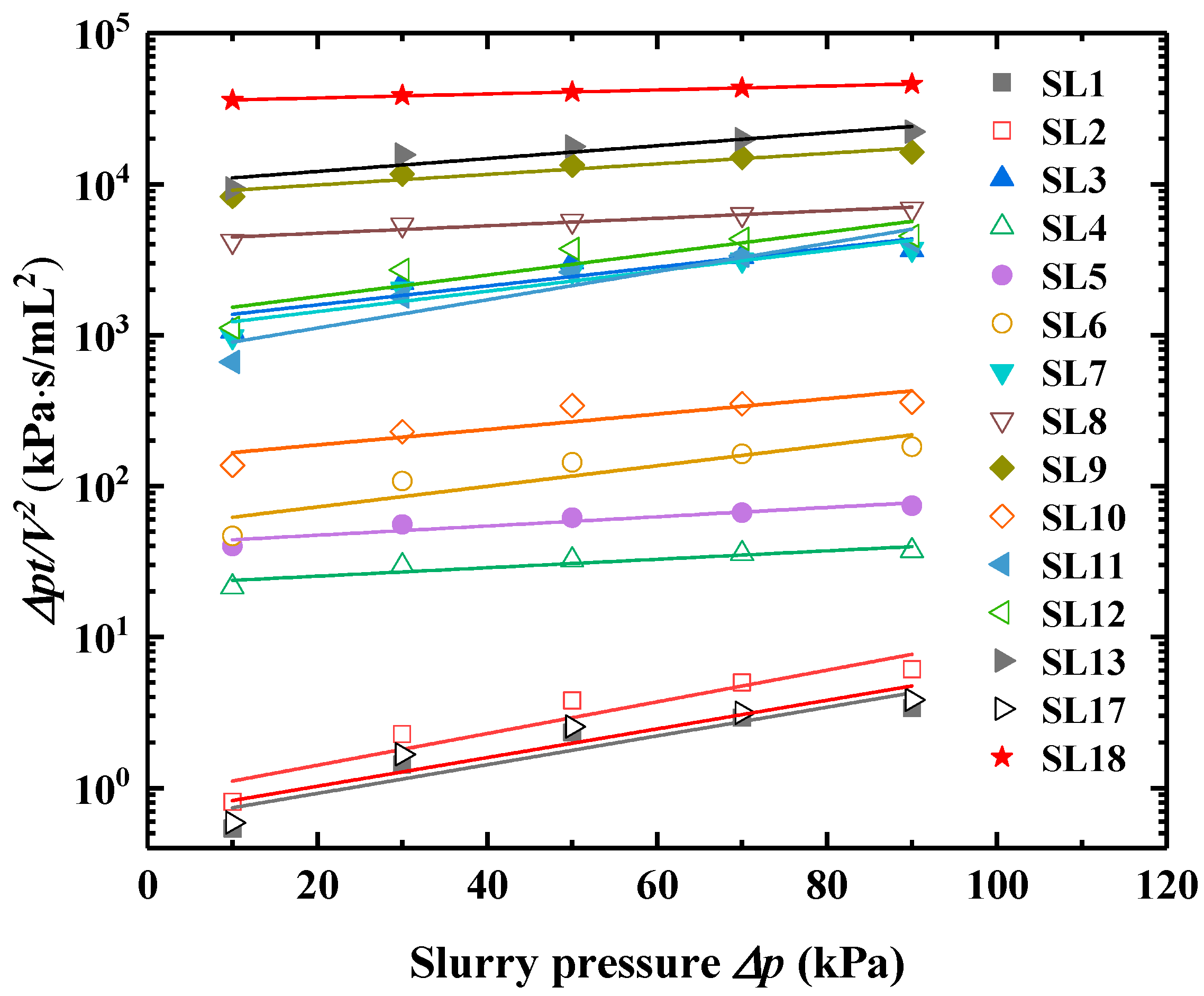
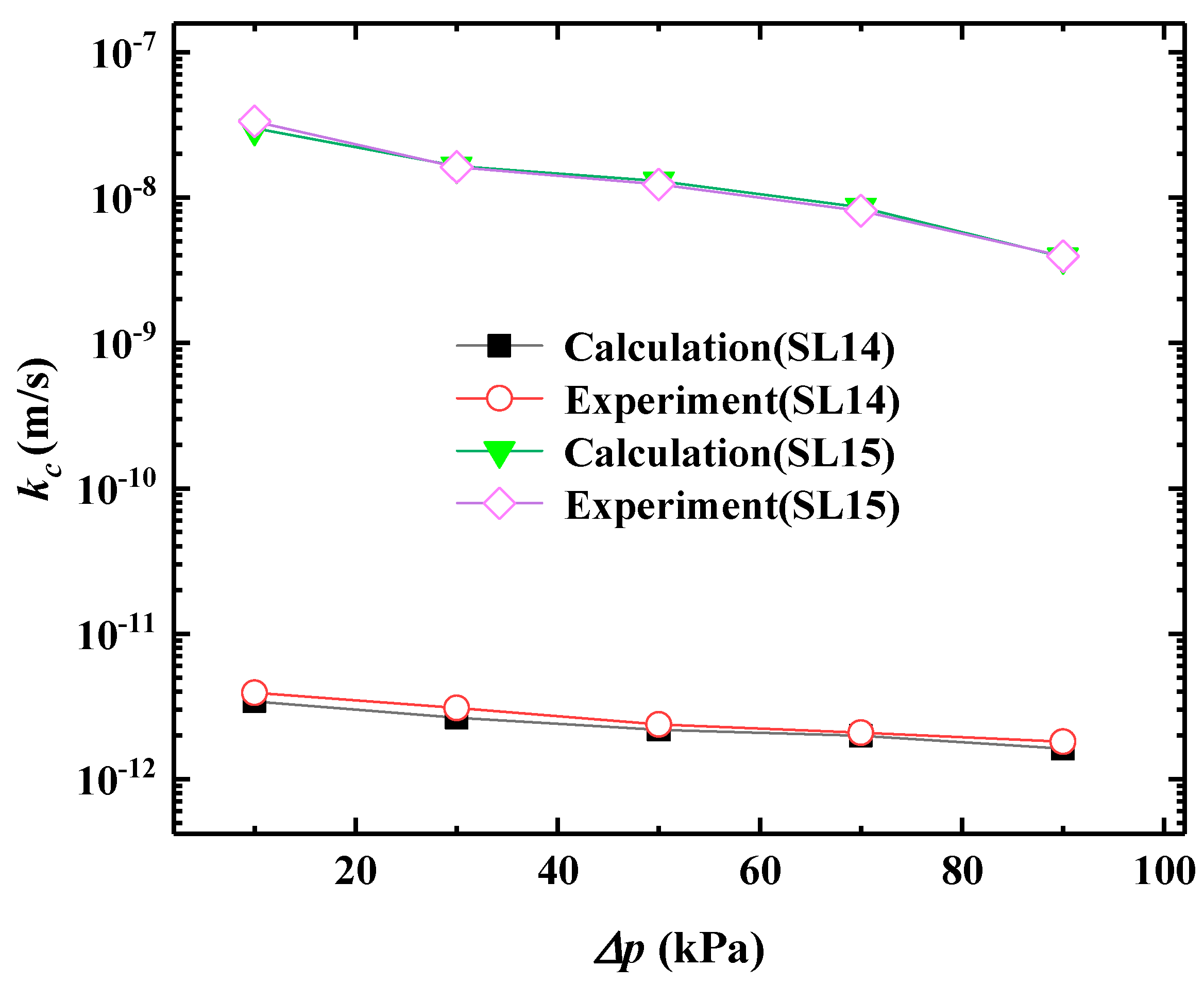
5.4. Filter Cake Hydraulic Conductivity
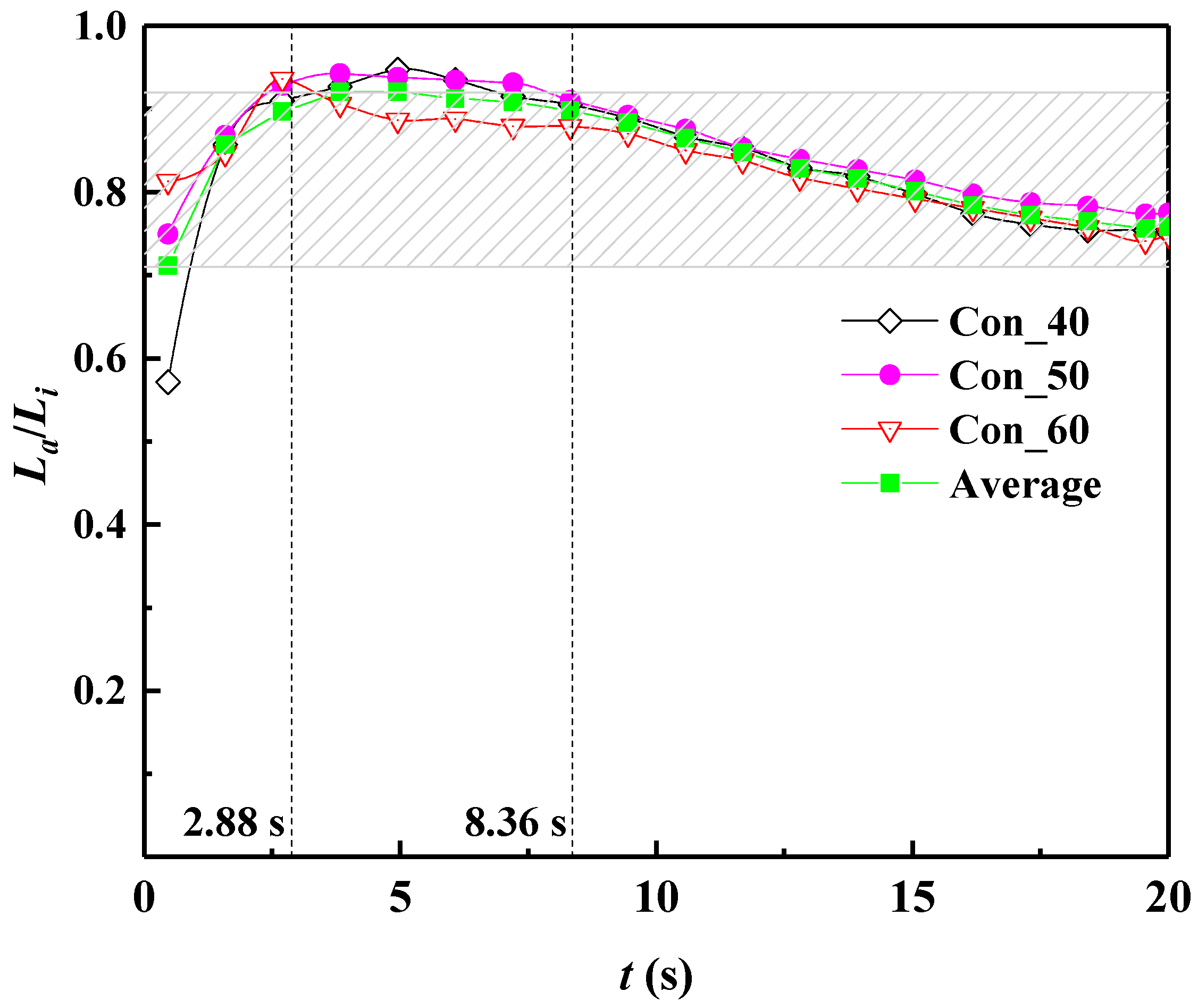
5.5. Relationship Between Dynamic Filter Cake Hydraulic Conductivity and Thickness
6. Discussion
7. Conclusions
- (1)
- Practical criterion for filter cake formation was established based on the readily measurable particle sizes (sand D15 and slurry d85). The novelty of this criterion lies in its simplicity and direct applicability in engineering practice, providing a rapid and reliable method for preliminary assessment of slurry-ground compatibility during the design phase, which surpasses the need for complex laboratory tests.
- (2)
- A novel mud spurt model was proposed and validated. Its primary novelty and advantage are its practicality; it predicts slurry penetration distance using parameters obtainable from standard geotechnical surveys and basic slurry property tests, effectively eliminating the dependency on time-consuming and specialized infiltration column tests required by previous models. The model demonstrates a high level of accuracy, with an error of approximately 6% compared to experimental data. This magnitude of error is considered fully acceptable for preliminary design and process control in tunneling engineering, where factors of safety are typically designed to accommodate uncertainties far exceeding this range, thus confirming the model’s robustness and suitability as a design tool.
- (3)
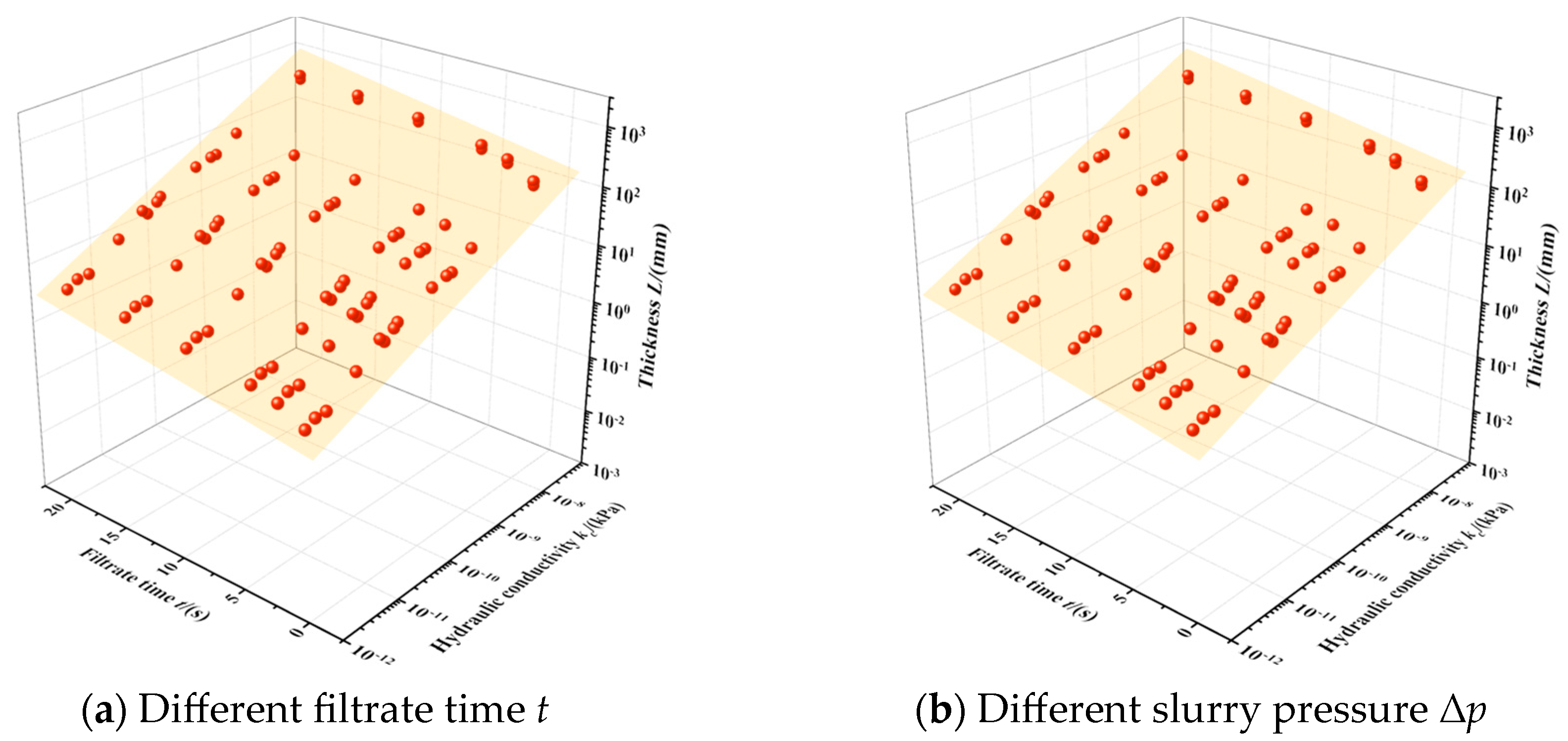
- Based on modified fluid loss (MFL) tests, constitutive model parameters for 15 different slurries were determined. The novelty here is the creation of a comprehensive and generalized dataset and predictive equations that enable the calculation of filter cake hydraulic conductivity and void ratio under any arbitrary slurry pressure. This moves beyond case-specific results, providing a valuable foundation for optimizing slurry recipes in various ground conditions.
- (4)
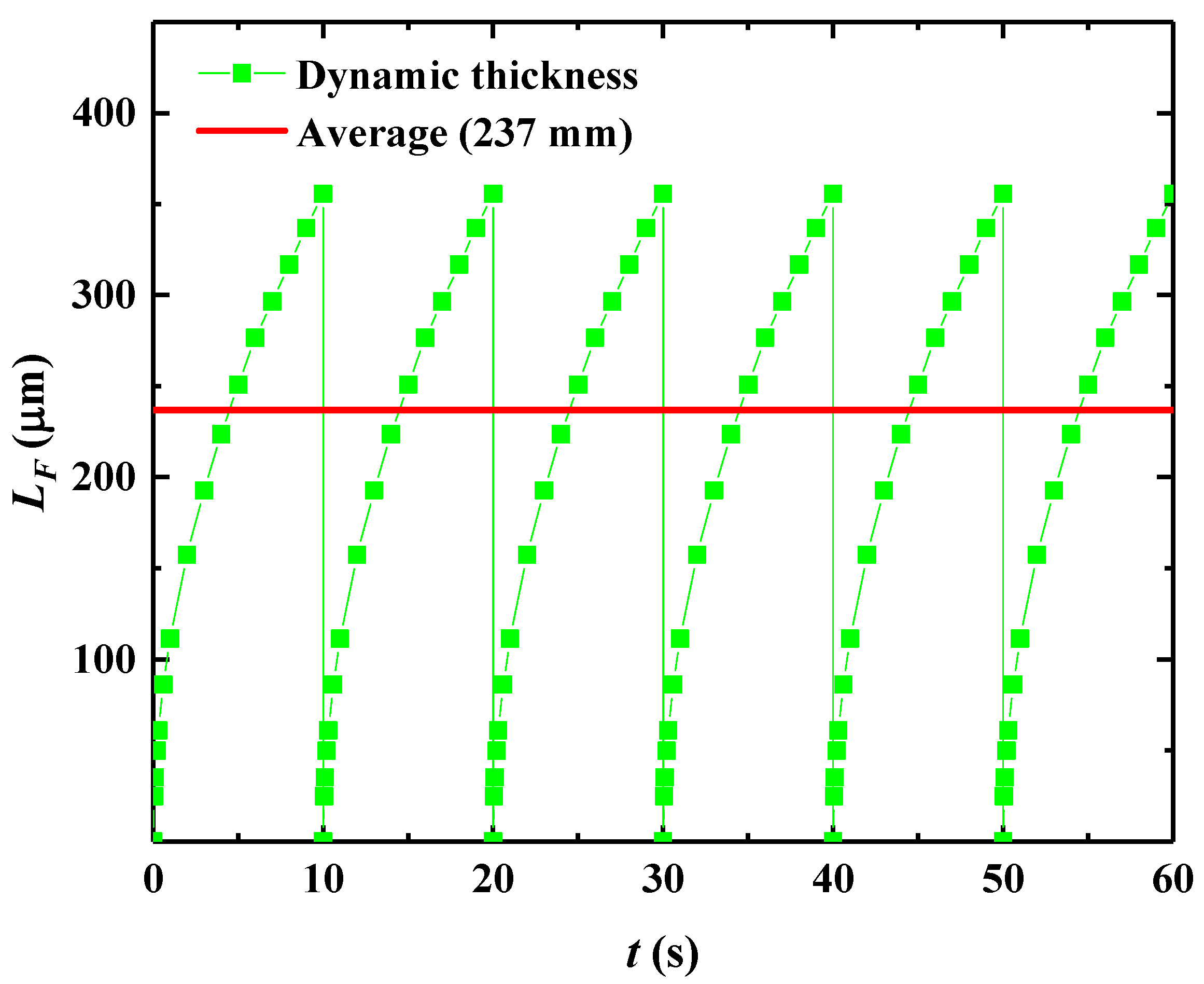
- The evolution of filter cake thickness during the dynamic excavation process was analyzed. A significant practical outcome of this analysis is the proposal of a simplified engineering approximation: the average filter cake thickness during a cutterhead rotation cycle can be reasonably estimated as two-thirds of the maximum thickness. It is crucial to state that this “2/3 rule” is derived from the analytical integration of the filter cake growth model in this study and serves as a practical, conservative approximation for stability evaluation. Future research involving direct in situ measurements can further validate this relationship across a wider range of conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cui, W.; Liu, D.; Song, H.F.; Pu, G.-J. Development and experimental study on environmental slurry for slurry shield tunneling. Constr. Build. Mater. 2019, 216, 416–423. [Google Scholar] [CrossRef]
- Mao, J.H.; Yuan, D.J.; Jin, D.L.; Liu, S. Influence of Cutting Tools on Filter Cake Formation during Slurry Shield Tunnelling. KSCE J. Civ. Eng. 2021, 25, 2261–2274. [Google Scholar] [CrossRef]
- Lin, Y.F.; Fang, Y.; He, C.; Wang, W. Experimental study on degree of match between slurry and ground based on particle retention rate. Tunn. Undergr. Space Technol. 2021, 116, 104105. [Google Scholar] [CrossRef]
- Li, Y.C.; Tong, X.; Chen, Y.; Wen, Y.-D.; Pan, Q. Non-monotonic piezocone dissipation curves of backfills in a soil-bentonite slurry trench cutoff wall. J. Zhejiang Univ.-Sci. A 2018, 19, 277–288. [Google Scholar] [CrossRef]
- Cui, Y.; Duong, T.V.; Tang, A.M.; Dupla, J.-C.; Calon, N.; Robinet, A. Investigation of the hydro-mechanical behaviour of fouled ballast. J. Zhejiang Univ.-Sci. A 2013, 14, 244–255. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Wei, G.; Lin, Z.; Wei, X.; Yan, Z.; Yan, J.; Shen, X. Numerical Study of Excavation Face Active Instability in Upward Shield Tunneling. Buildings 2025, 15, 3371. [Google Scholar] [CrossRef]
- Chen, F.; Xiong, H.; Yin, Z.Y.; Chen, X. Impermeable and mechanical stability of filter cake under different infiltration conditions via CFD-DEM. Acta Geotech. 2023, 18, 4115–4140. [Google Scholar] [CrossRef]
- Xu, T.; Bezuijen, A. Experimental study on the mechanisms of bentonite slurry penetration in. Tunn. Undergr. Space Technol. 2019, 93, 103052. [Google Scholar] [CrossRef]
- Broere, W. Tunnel Face Stability & New CPT Application. Ph.D. Thesis, Delft University of Technology, Delft, Netherlands, 2001. [Google Scholar]
- Talmon, A.; Masthergen, D.R. Invasion of pressurized clay suspensions into granular soil. J. Porous Media 2013, 16, 351–365. [Google Scholar] [CrossRef]
- Watanabe, T.; Yamazaki, H. Giant size slurry shield is a success in Tokyo. Tunn. Tunn. 1981, 13, 13–17. [Google Scholar]
- Min, F.L.; Zhu, W.; Han, X. Filter cake formation for slurry shield tunnelling in highly permeable sand. China J. Highw. Transp. 2013, 87, 423–430. [Google Scholar]
- Yin, X.S.; Chen, R.P.; Li, Y.; Qi, S. A column system for modeling bentonite slurry infiltration in sands. J. Zhejiang Univ.-Sci. A 2016, 17, 818–827. [Google Scholar] [CrossRef]
- Yin, X.S.; Chen, R.P.; Men, F.Y.; Ding, Z.; Cui, Y.; Hedayat, A.; Mooney, M. Face stability of slurry-driven shield with permeable filter cake. Tunn. Undergr. Space Technol. 2021, 111, 103841. [Google Scholar] [CrossRef]
- Yang, Y.; Yuan, D.; Du, C.; Jin, D.; Hao, J. Calculation method for the formation time of dynamic filter cake in slurry shield tunneling. Front. Struct. Civ. Eng. 2024, 18, 1337–1349. [Google Scholar] [CrossRef]
- Yin, Z.; Zhang, X.; Zheng, D.; Zhang, Q. Experimental study on infiltration behavior of slurry containing excavated sand into saturated sand. Phys. Fluids 2024, 36, 16. [Google Scholar] [CrossRef]
- Guo, S.; Li, R.; Zhang, M.; Zhang, Q.; Li, X.; Li, X.; Liu, Y.; Zheng, D. Experimental and mechanistic investigation of synergistic effects of particle size distribution and xanthan gum on rheological and infiltration properties of bentonite slurries. Phys. Fluids 2025, 37, 086608. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Yin, T. A Coupled CFD-DEM Simulation of Slurry Infiltration and Filter Cake Formation during Slurry Shield Tunneling. Infrastructures 2018, 3, 15. [Google Scholar] [CrossRef]
- Yin, T.; Zhang, Z.X.; Huang, X.; Shire, T.; Hanley, K.J. On the morphology and pressure-filtration characteristics of filter cake formation: Insight from coupled CFD-DEM simulations. Tunn. Undergr. Space Technol. 2021, 111, 103586. [Google Scholar] [CrossRef]
- Cheng, H.; Wu, N.; Shi, Y.; Wang, B. Influence of Permeability of Filter Cake on Face Stability of Slurry Shield-Driven Tunnels in Sandy Gravel Stratum. In Proceedings of the 10th International Conference on Hydraulic and Civil Engineering & Engineering Safety and Disaster Prevention Forum, Nanjing, China, 18–20 March 2025; pp. 1495–1508. [Google Scholar]
- Liu, J. CFD-DEM Simulation of Slurry Particle Infiltration in Granular Soils. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2025. [Google Scholar]
- Liu, J.; Hanley, K.J. CFD–DEM Comparison of Slurry Infiltration in Laboratory Column Tests and in Real-World Tunnelling. Comput. Geotech. 2024, 176, 106816. [Google Scholar] [CrossRef]
- Ayasrah, M.; Qiu, H.; Zhang, X.; Daddow, M. Prediction of Ground Settlement Induced by Slurry Shield Tunnelling in Granular Soils. Civ. Eng. J. 2020, 6, 2273–2289. [Google Scholar] [CrossRef]
- Razakamanantsoa, A.R.; Barast, G.; Djeran, M.I. Hydraulic performance of activated calcium bentonite treated by polyionic charged polymer. Appl. Clay Sci. 2012, 59, 103–114. [Google Scholar] [CrossRef]
- Tien, C. Principle of Filtration; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Zumsteg, R.; Puzrin, A.M.; Anagnostou, G. Effects of slurry on stickiness of excavated clays and clogging of equipment in fluid supported excavations. Tunn. Undergr. Space Technol. 2016, 58, 197–208. [Google Scholar] [CrossRef]
- Min, F.L.; Du, J.R.; Zhang, N.; Chen, X.; Lv, H.; Liu, L.; Yu, C. Experimental study on property change of slurry and filter cake of slurry shield under seawater intrusion. Tunn. Undergr. Space Technol. 2019, 88, 290–299. [Google Scholar] [CrossRef]
- Terzaghi, K.; Peck, R.B. Soil Mechanics in Engineering Practice; John Wiley & Sons: New York, NY, USA, 1951. [Google Scholar]
- Sherard, J.L.; Dunnigan, L.P.; Talbot, J.R. Basic properties of sand and gravel filters. J. Geotech. Eng. 1984, 110, 684–700. [Google Scholar] [CrossRef]
- Krause, T. Schildvortrieb Mit Flüssigkeits und Erdgestützter Ortsbrust; Universität Braunschweig: Braunschweig, Germany, 1987. [Google Scholar]
- Bezuijen, A.; Steeneken, S.P.; Ruigrok, J.A.T. Monitoring and analysing pressures around a TBM. In Proceedings of the 13th International Conference on Underground Construction, Prague, Czech Republic, 23–25 May 2016. [Google Scholar]
- Ye, F.; Yang, T.; Mao, J.H. Half-spherical surface diffusion model of shield tunnel backfill grouting based on infiltration effect. Tunn. Undergr. Space Technol. 2019, 59, 274–281. [Google Scholar] [CrossRef]
- Kim, J.S.; Lee, I.M.; Jang, J.H.; Choi, H. Groutability of cement-based grout with consideration of viscosity and filtration phenomenon. Int. J. Numer. Anal. Methods Geomech. 2010, 33, 1771–1797. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Z.X.; Zhang, G.J. Laboratory study on face stability mechanism of slurry shields. China J. Geotech. Eng. 2007, 29, 1074–1079. [Google Scholar]
- Ruth, B. Study in filtration. Ind. Eng. Chem. 1935, 27, 708–723. [Google Scholar] [CrossRef]
- Fehervari, A.; Gates, W.P.; Patti, A.F. Potential hydraulic barrier performance of cyclic organic carbonate modified bentonite complexes against hyper-salinity. Geotext. Geomembr. 2016, 44, 748–760. [Google Scholar] [CrossRef]
- Chung, J.; Daniel, D.E. Modified fluid loss test as an improved measure of hydraulic conductivity for bentonite. Geotech. Test. J. 2008, 31, 243–251. [Google Scholar] [CrossRef]
- Liu, X.Y.; Wang, F.M.; Yuan, D.J.; Fang, H.Y.; Zhang, S.L. Range of support pressures for slurry shield and analysis of its influence factors. Chin. J. Geotech. Eng. 2019, 41, 908–917. [Google Scholar]

| Typical Analysis | Percentage (%) | Typical Characteristics | Typical |
|---|---|---|---|
| Al2O3 | 13.74 | Sodium bentonite | Test Results |
| TiO2 | 0.15 | Fine Content (<0.075 mm) | 100% |
| SiO2 | 69.12 | Clay Content | 83.2% |
| Fe2O3 | 0.90 | Specific Gravity | 2.55 |
| MgO | 2.73 | Liquid Limit | 242.8% |
| CaO | 1.13 | Plastic Limit | 72.6% |
| K2O | 0.98 | Plasticity Index Ip | 170.2 |
| Na2O | 0.89 | Free Swell (mL/2 g) | 12.0 |
| LOi | 10.32 | pH | 7 |
| Hardness | 1–2 | ||
| Color | Canary Yellow | ||
| Adsorptivity | 8–15 |
| Slurry | Bentonite /(g/L) | Adding Material | Material Content/(%) | Russian Funnel Viscosity/(s) | Marsh Funnel Viscosity/(s) | ρ/ (g/cm3) | τy/ (pa) | μ/ (mpa·s) | d85 | d50 |
|---|---|---|---|---|---|---|---|---|---|---|
| SL1 | 50 | - | 0 | 16 ± 0.3 | 30 ± 2.1 | 1.030 ± 0.018 | 0.150 ± 0.006 | 1.50 ± 0.06 | 0.0331 | 0.0163 |
| SL2 | 70 | - | 0 | 17 ± 0.5 | 31 ± 1.6 | 1.035 ± 0.012 | 0.160 ± 0.002 | 1.90 ± 0.03 | 0.0305 | 0.0146 |
| SL3 | 50 | APAM (25 M) | 1.0 | 253 ± 10.1 | 472 ± 22.7 | 1.030 ± 0.014 | 8.94 ± 0.224 | 33.65 ± 1.04 | 0.0478 | 0.0167 |
| SL4 | 50 | CPAM (16 M) | 1.0 | 19 ± 0.4 | 38 ± 2.5 | 1.030 ± 0.020 | 0.100 ± 0.001 | 5.80 ± 0.28 | 0.1351 | 0.0798 |
| SL5 | 50 | PAA-Na (1.2 k) | 1.0 | 19 ± 0.5 | 34 ± 1.3 | 1.030 ± 0.011 | 0.510 ± 0.016 | 3.40 ± 0.07 | 0.0698 | 0.0338 |
| SL6 | 50 | PAA-Na (15 k) | 1.0 | 22 ± 0.7 | 40 ± 3.0 | 1.030 ± 0.015 | 1.280 ± 0.024 | 6.05 ± 0.08 | 0.0669 | 0.0290 |
| SL7 | 50 | CMC (41 k) | 1.0 | 23 ± 0.7 | 41 ± 2.3 | 1.030 ± 0.019 | 2.200 ± 0.084 | 9.15 ± 0.46 | 0.0596 | 0.0246 |
| SL8 | 50 | CMC (57 k) | 1.0 | 264 ± 8.4 | 291 ± 10.8 | 1.030 ± 0.013 | 32.040 ± 0.160 | 63.35 ± 1.58 | 0.0509 | 0.0109 |
| SL9 | 50 | CMC-Na (8 k) | 1.0 | 31 ± 0.9 | 51 ± 2.1 | 1.030 ± 0.021 | 2.960 ± 0.065 | 19.40 ± 0.72 | 0.0635 | 0.0153 |
| SL10 | 50 | PAA-Na (1.2 k) | 2.0 | 20 ± 0.4 | 36 ± 2.2 | 1.030 ± 0.016 | 0.870 ± 0.035 | 5.95 ± 0.09 | 0.0448 | 0.0218 |
| SL11 | 50 | PAA-Na (15 k) | 2.0 | 23 ± 0.4 | 38 ± 1.2 | 1.030 ± 0.012 | 3.120 ± 0.047 | 6.45 ± 0.26 | 0.0872 | 0.0365 |
| SL12 | 50 | CMC (41 k) | 2.0 | 29 ± 0.5 | 51 ± 4.0 | 1.030 ± 0.019 | 3.730 ± 0.123 | 7.75 ± 0.22 | 0.0499 | 0.0179 |
| SL13 | 50 | CMC-Na (8 k) | 2.0 | 114 ± 4.4 | 163 ± 9.6 | 1.030 ± 0.015 | 19.210 ± 0.538 | 56.50 ± 1.07 | 0.0702 | 0.0178 |
| SL14 | 50 | QT | 13.7 | 17 ± 0.4 | 31 ± 1.4 | 1.100 ± 0.015 | 0.200 ± 0.003 | 3.50 ± 0.12 | 0.0335 | 0.0143 |
| SL15 | 50 | QT | 13.7 | 49 ± 1.7 | 114 ± 9.1 | 1.100 ± 0.021 | 8.640 ± 0.302 | 34.95 ± 1.61 | 0.0745 | 0.0292 |
| CMC-Na | 1.0 |
| Number | Author | Index | Filter Cake | Filter Cake and Mud Spurt | No Filter Cake |
|---|---|---|---|---|---|
| ① | Terzaghi and Peck [28] | d85/D15 | d85/D85 ≥ 0.25 | ||
| ② | Sherard et al. [29] | d85/D15 | d85/D15 ≥ 0.19 | 0.095 < d85/D15 < 0.19 | d85/D15 ≤ 0.095 |
| ③ | Min et al. [12] | d85/D15 | d85/D15 ≥ 0.19 | 0.095 < d85/D15 < 0.19 | d85/D15 ≤ 0.095 |
| ④ | Talmon & Masthergen [10] | Dpore/d50 | Dpore/d50 < 3 | 3 ≤ Dpore/d50 < 14 | Dpore/d50 ≥ 14 |
| Slurry | τy/(Pa) | L/(m) | kb/(m/s) | kb’/(m/s) |
|---|---|---|---|---|
| Con_40 | 0.50 | 1.563 | 8.0 × 10−5 | 7.5 × 10−5 |
| Con_50 | 0.87 | 1.042 | 5.0 × 10−5 | 4.5 × 10−5 |
| Con_60 | 2.00 | 0.434 | 4.0 × 10−5 | 4.0 × 10−5 |
| Slurry | α | k0/(m/s) | δ | e0 |
|---|---|---|---|---|
| SL1 | 0.84 | 3.4 × 10−7 | 0.075 | 3.763 |
| SL2 | 0.90 | 3.9 × 10−7 | 0.098 | 4.202 |
| SL3 | 0.67 | 4.3 × 10−10 | 0.350 | 26.308 |
| SL4 | 0.40 | 4.9 × 10−9 | 0.152 | 7.490 |
| SL5 | 0.51 | 2.8 × 10−9 | 0.283 | 9.230 |
| SL6 | 0.68 | 3.7 × 10−9 | 0.071 | 6.064 |
| SL7 | 0.73 | 3.0 × 10−10 | 0.136 | 9.963 |
| SL8 | 0.37 | 3.2 × 10−11 | 0.270 | 16.908 |
| SL9 | 0.34 | 9.1 × 10−12 | 0.118 | 6.736 |
| SL10 | 0.67 | 1.9 × 10−9 | 0.195 | 10.418 |
| SL11 | 0.92 | 7.9 × 10−10 | 0.086 | 8.824 |
| SL12 | 0.71 | 2.3 × 10−10 | 0.083 | 12.075 |
| SL13 | 0.15 | 3.3 × 10−12 | 0.109 | 8.454 |
| SL14 | 0.82 | 3.2 × 10−7 | 0.173 | 0.828 |
| SL15 | 0.19 | 2.5 × 10−12 | 0.119 | 2.217 |
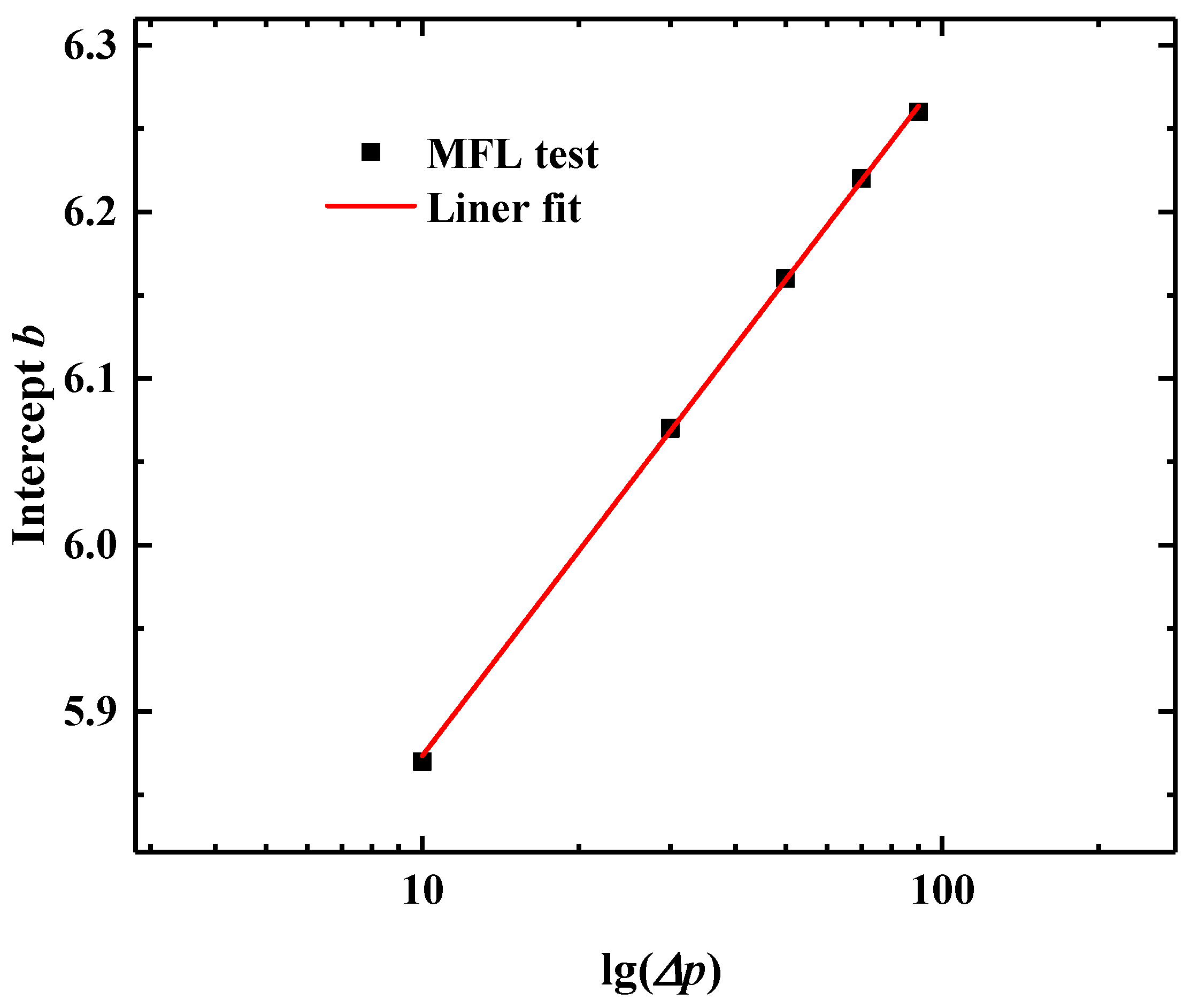
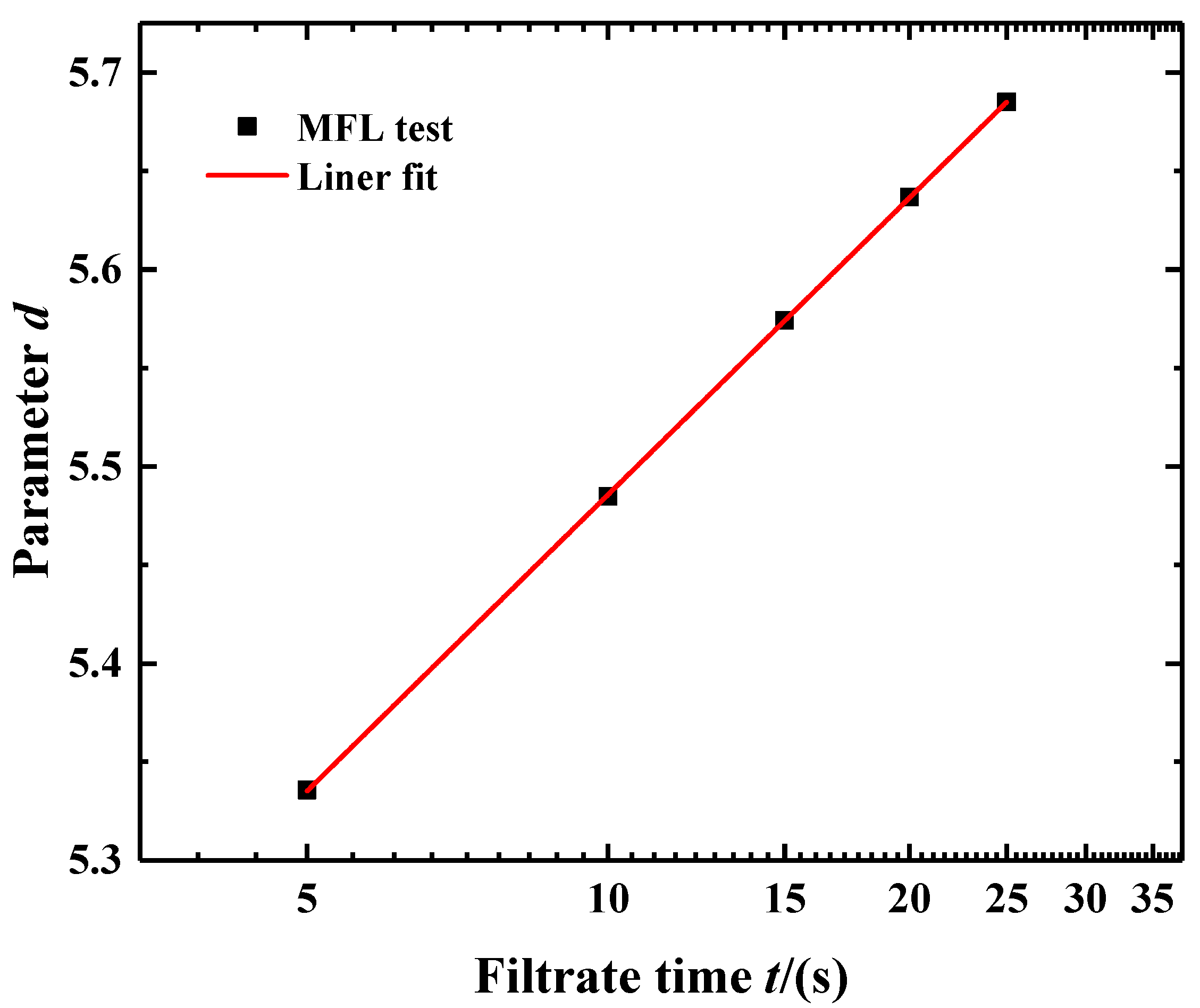
| Condition | Slurry Pressure/(kPa) | t/(s) | a | b | R2 |
|---|---|---|---|---|---|
| 1 | 10 | 10 | 0.456 | 5.87 | 0.99 |
| 2 | 20 | 10 | 0.456 | 6.00 | 0.99 |
| 3 | 30 | 10 | 0.456 | 6.07 | 0.99 |
| 4 | 50 | 10 | 0.456 | 6.16 | 0.99 |
| 5 | 70 | 10 | 0.456 | 6.22 | 0.99 |
| 6 | 90 | 10 | 0.456 | 6.26 | 0.99 |
| 7 | 20 | 20 | 0.456 | 6.15 | 0.99 |
| 8 | 20 | 15 | 0.456 | 6.09 | 0.99 |
| 9 | 20 | 5 | 0.456 | 5.85 | 0.99 |
| 10 | 20 | 3 | 0.456 | 5.74 | 0.99 |
| 11 | 20 | 1 | 0.456 | 5.50 | 0.99 |
| Slurry | Mud Spurt/(cm) | Hydraulic Conductivity/(m/s) | Thickness/(μm) |
|---|---|---|---|
| SL1 | 6.3 ± 0.1 | (2.71 ± 0.20) × 10−8 | 331 ± 1.4 |
| SL2 | 5.8 ± 0.1 | (2.61 ± 0.21) × 10−8 | 331 ± 1.4 |
| SL5 | 4.7 ± 0.1 | (6.08 ± 0.29) × 10−10 | 55 ± 0.6 |
| SL6 | 3.7 ± 0.1 | (4.80 ± 0.30) × 10−10 | 54 ± 0.6 |
| SL7 | 3.1 ± 0.1 | (3.37 ± 0.22) × 10−11 | 17 ± 0.1 |
| SL9 | 2.3 ± 0.1 | (3.23 ± 0.10) × 10−12 | 4 ± 0.1 |
| SL10 | 3.8 ± 0.1 | (2.53 ± 0.15) × 10−10 | 43 ± 0.2 |
| SL11 | 3.5 ± 0.1 | (4.98 ± 0.41) × 10−11 | 20 ± 0.1 |
| SL12 | 3.3 ± 0.1 | (2.76 ± 0.18) × 10−11 | 18 ± 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, X.; Zhu, Y.; Wei, G.; Cui, Y.; Ding, Z. Mud Spurt Distance and Filter Cake Hydraulic Conductivity of Slurry Shield. Buildings 2025, 15, 3699. https://doi.org/10.3390/buildings15203699
Yin X, Zhu Y, Wei G, Cui Y, Ding Z. Mud Spurt Distance and Filter Cake Hydraulic Conductivity of Slurry Shield. Buildings. 2025; 15(20):3699. https://doi.org/10.3390/buildings15203699
Chicago/Turabian StyleYin, Xinsheng, Yanhua Zhu, Gang Wei, Yunliang Cui, and Zhi Ding. 2025. "Mud Spurt Distance and Filter Cake Hydraulic Conductivity of Slurry Shield" Buildings 15, no. 20: 3699. https://doi.org/10.3390/buildings15203699
APA StyleYin, X., Zhu, Y., Wei, G., Cui, Y., & Ding, Z. (2025). Mud Spurt Distance and Filter Cake Hydraulic Conductivity of Slurry Shield. Buildings, 15(20), 3699. https://doi.org/10.3390/buildings15203699






