Creep Performance and Viscoelastic Constitutive Relationship of Structural Acrylic Connected Using Bulk Polymerization Technique
Abstract
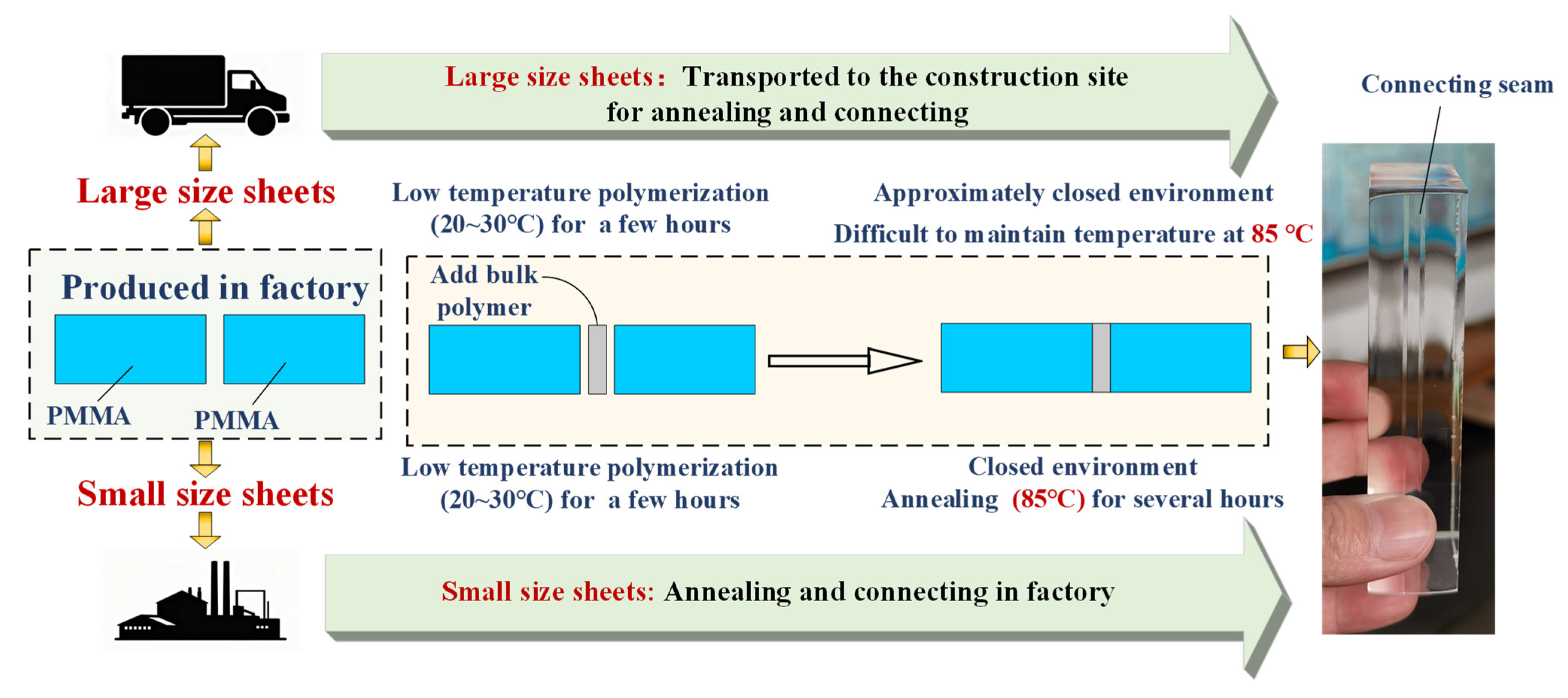
1. Introduction
2. Experimental Test
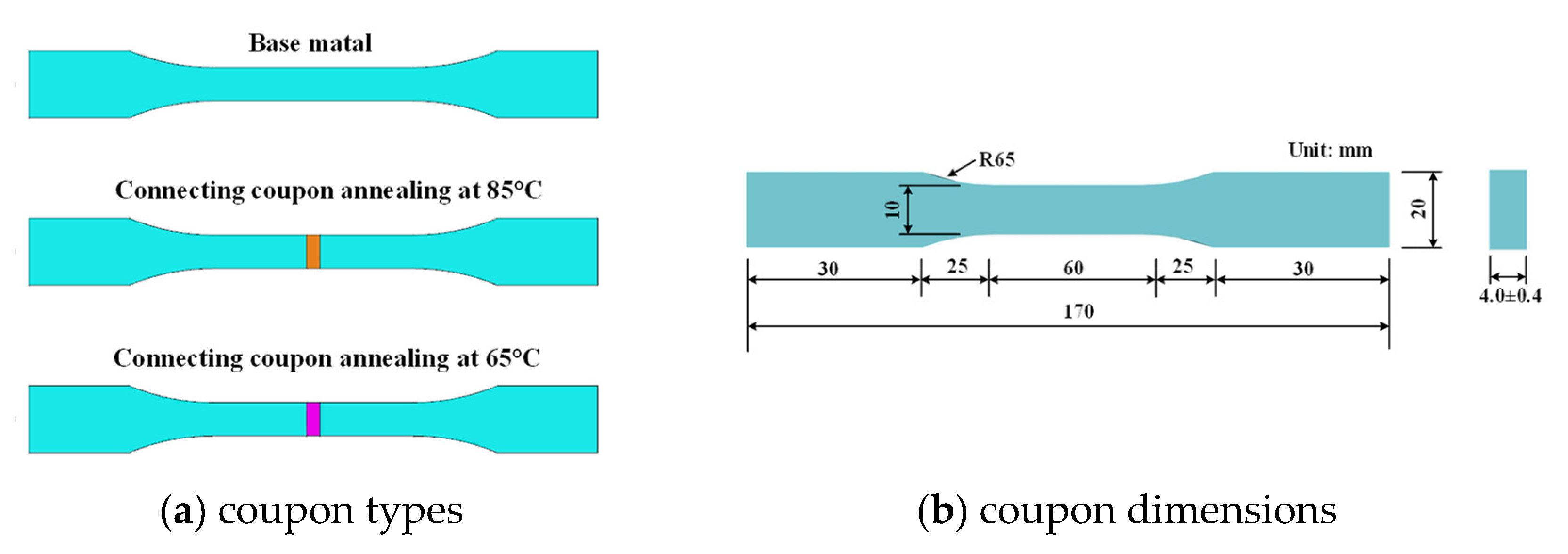
2.1. Coupon Design
2.2. Short-Term Uniaxial Tensile Test
2.3. Creep Test
2.3.1. Test Program
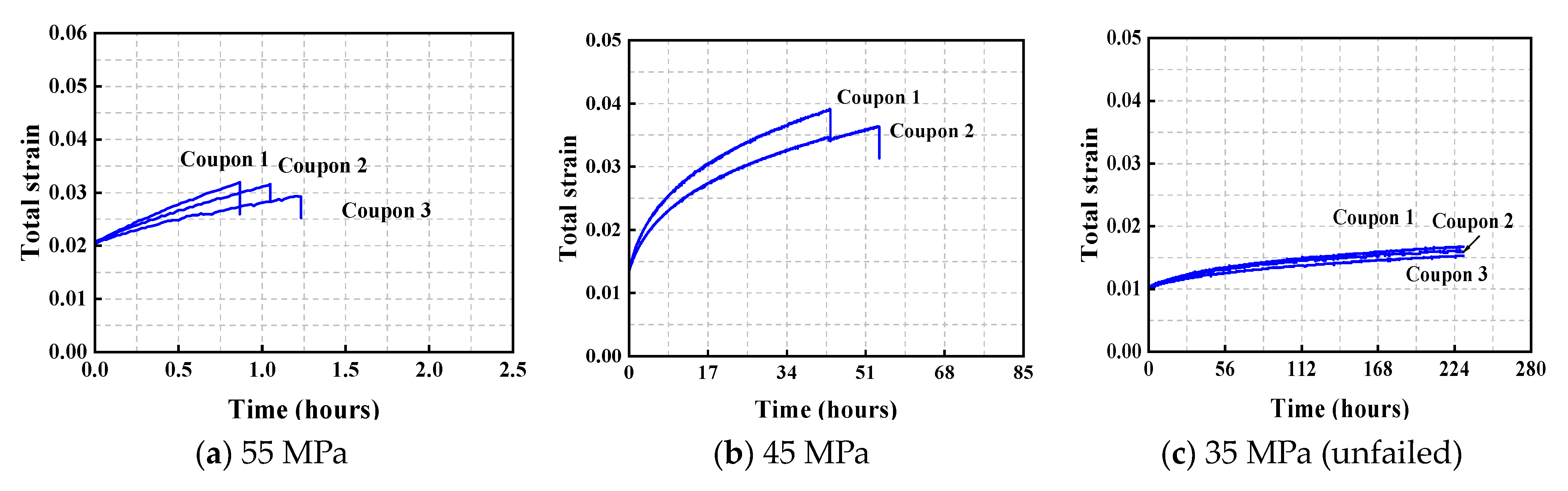
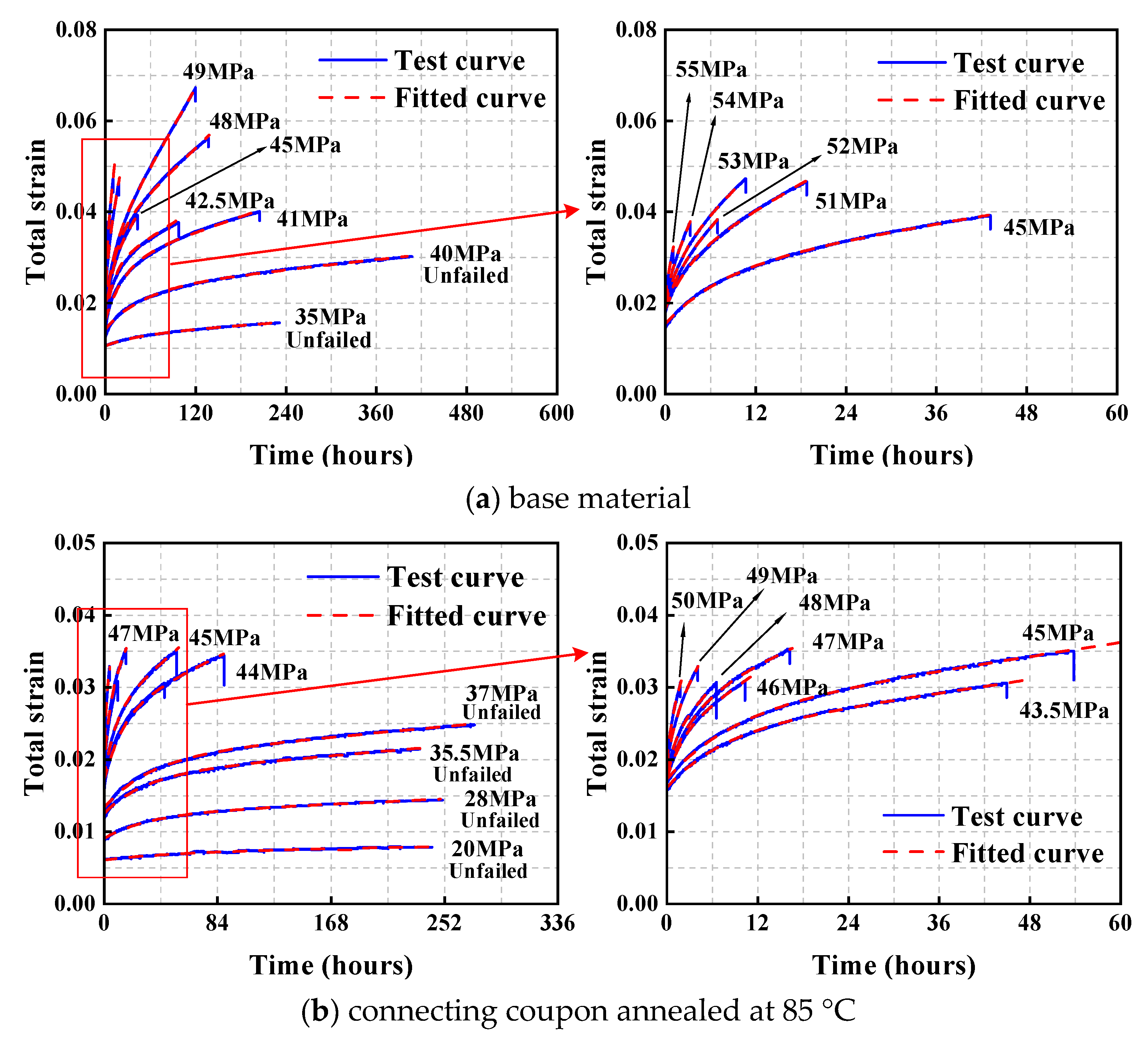
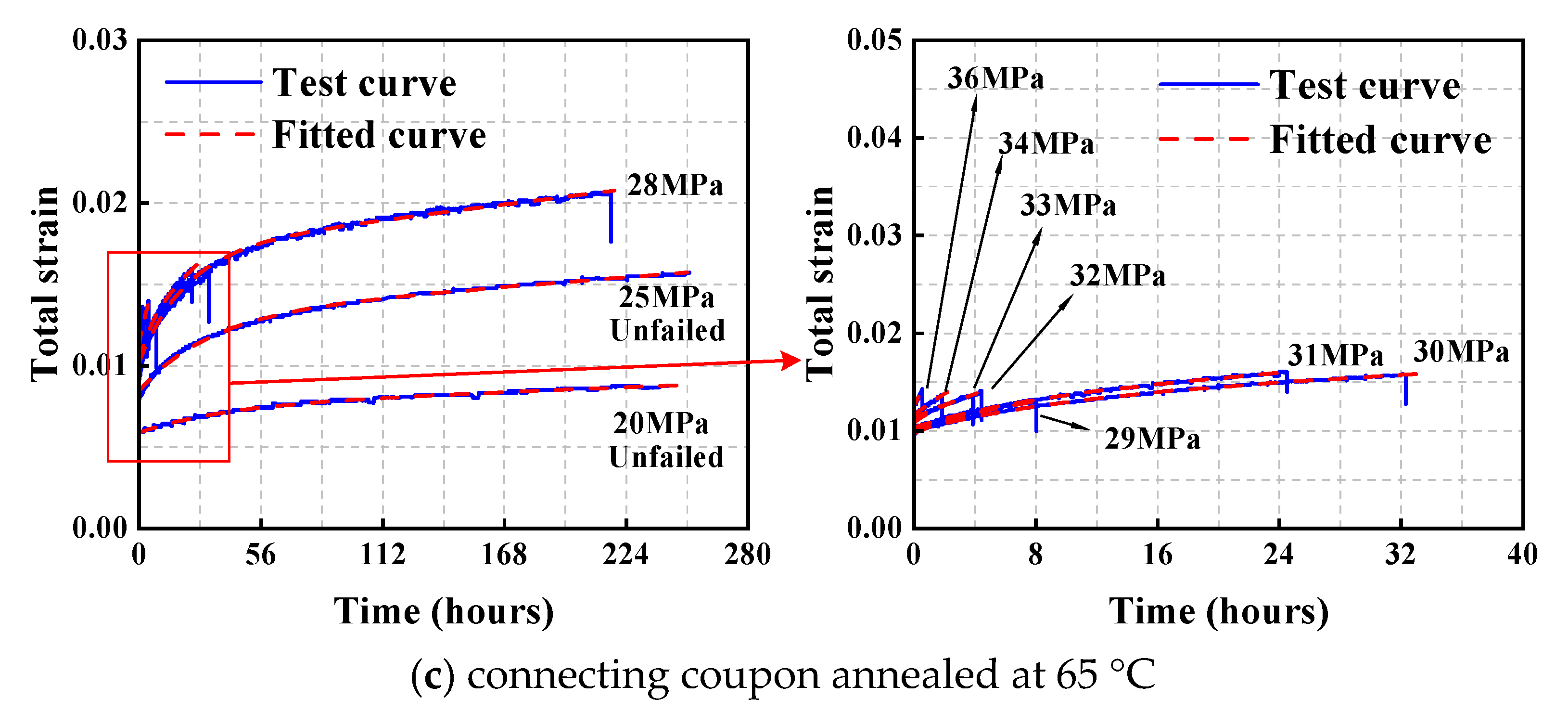
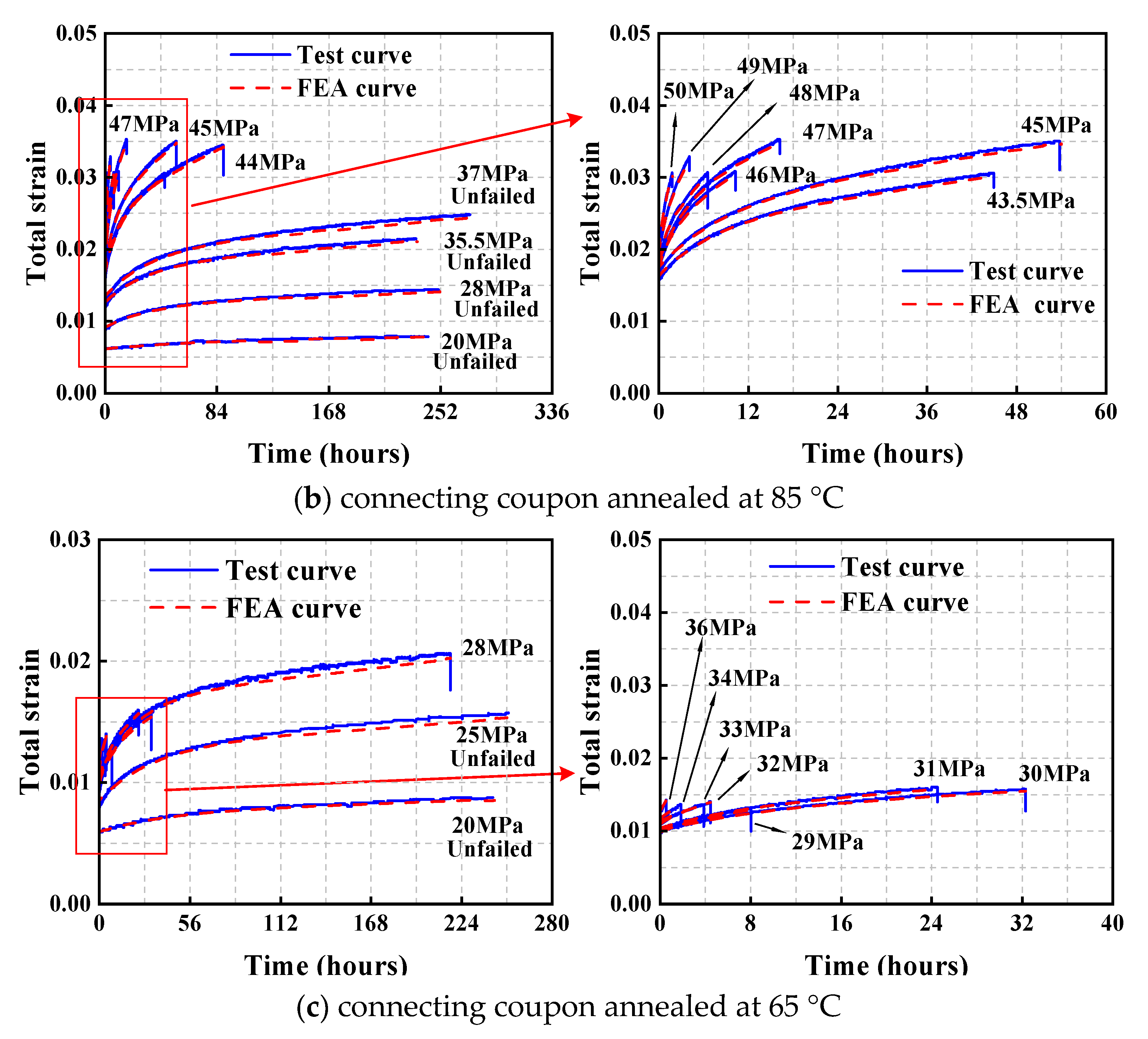
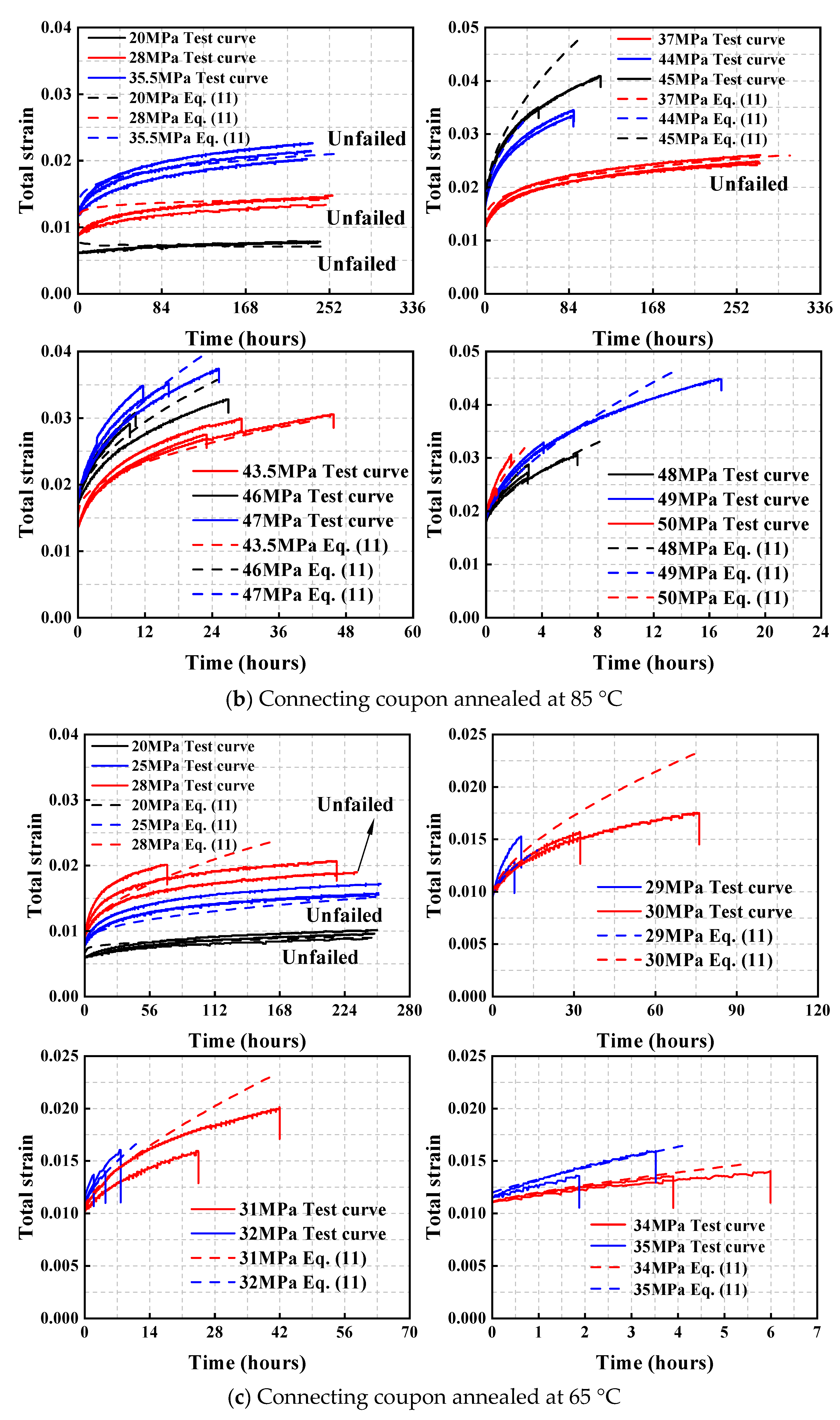
2.3.2. Creep Curves
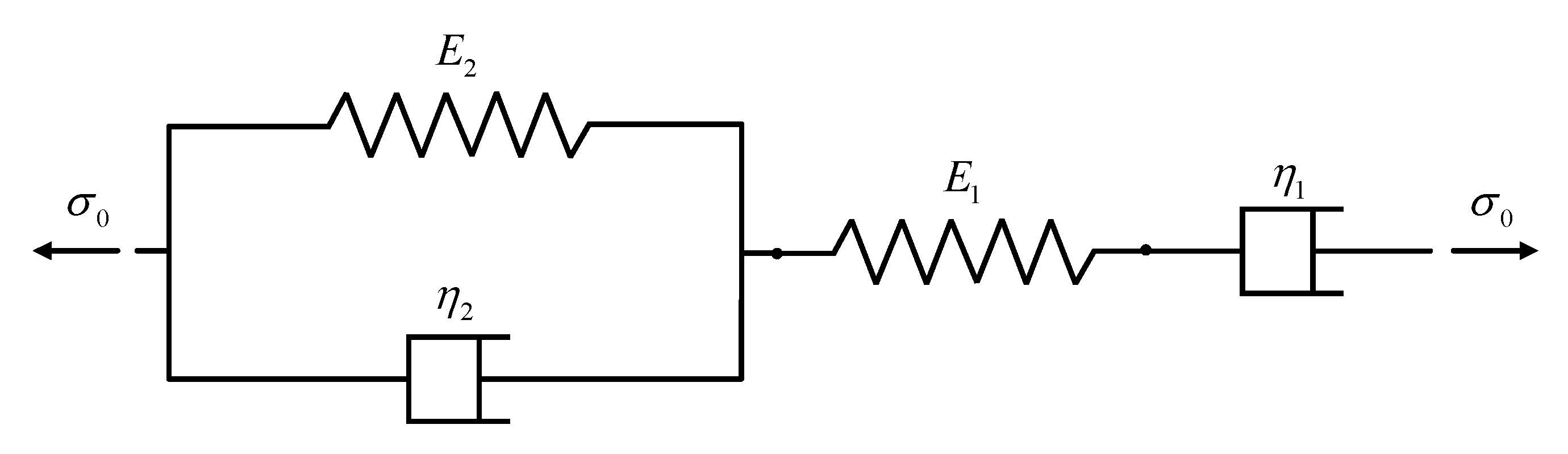
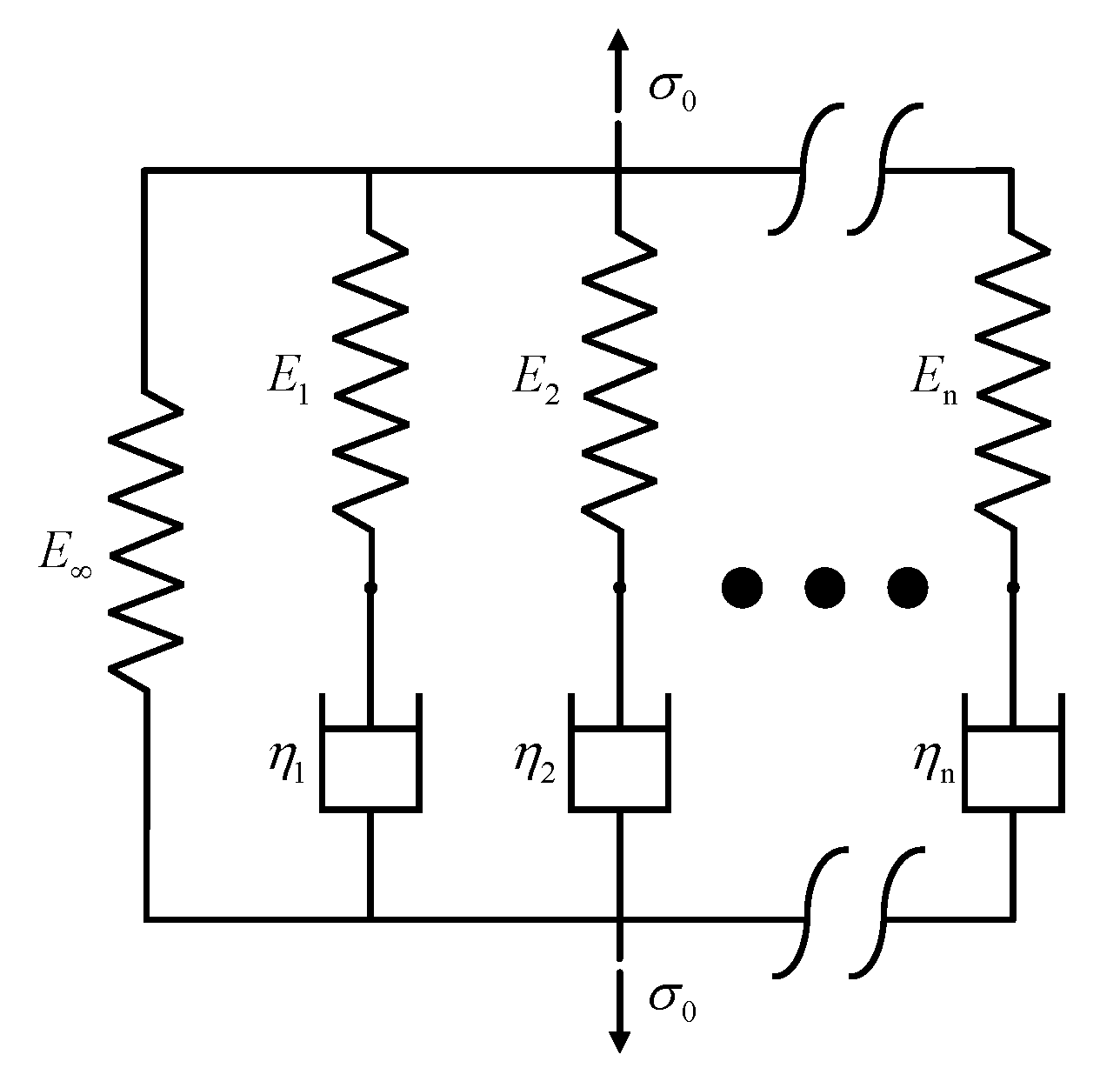
3. Burgers Model and Finite Element Analysis
3.1. Determination of Parameters in Burgers Model
3.2. Prony Series
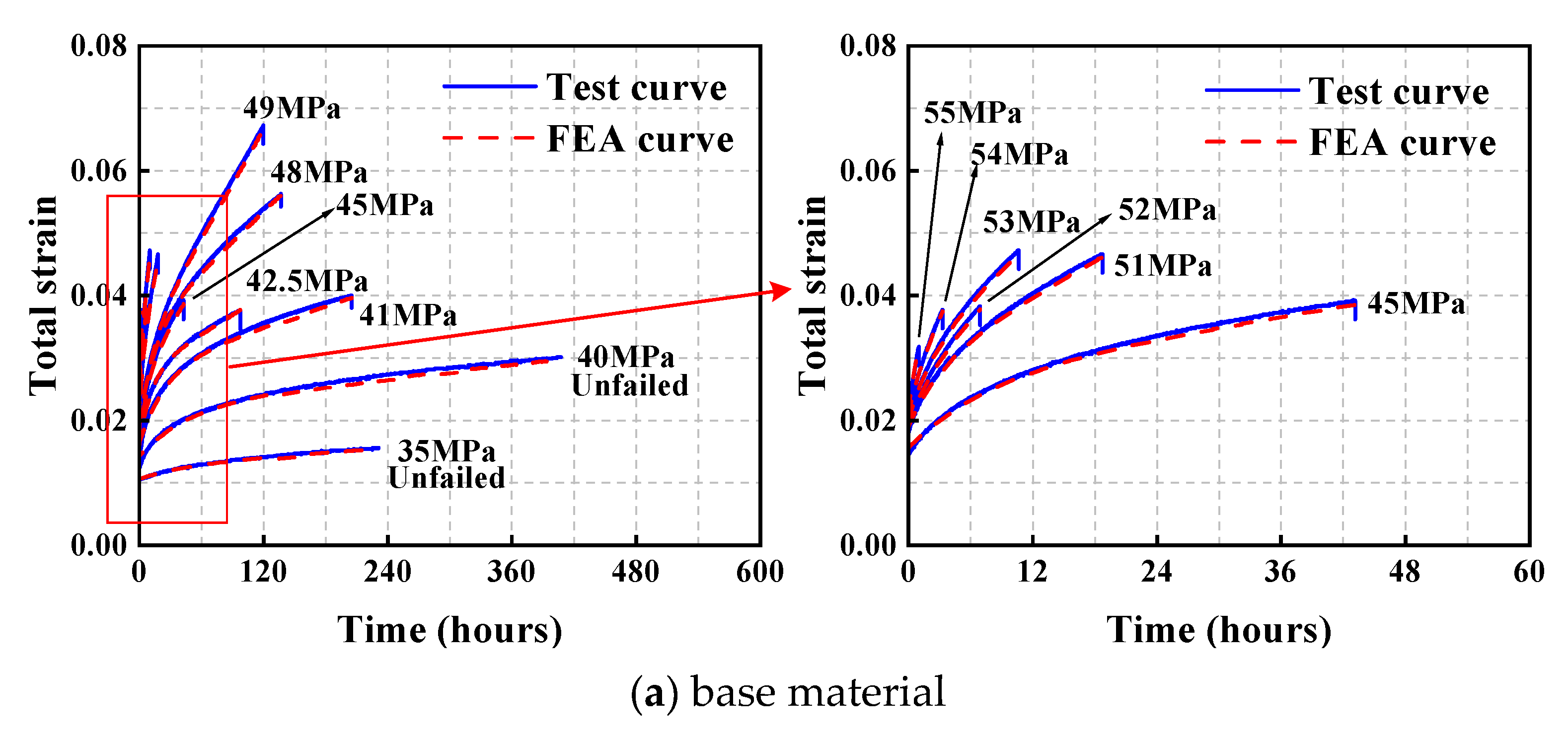
3.3. Finite Element Analysis
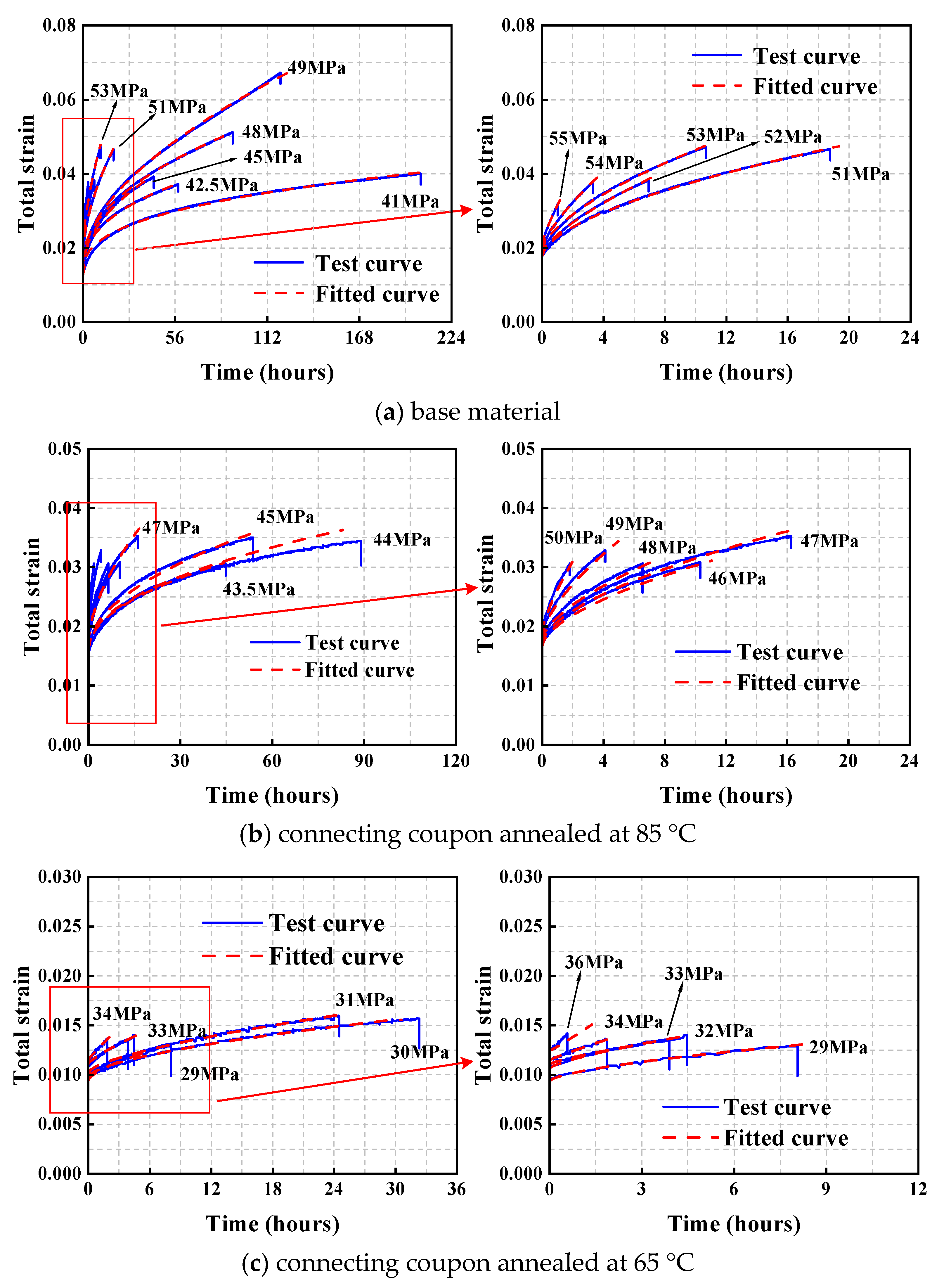
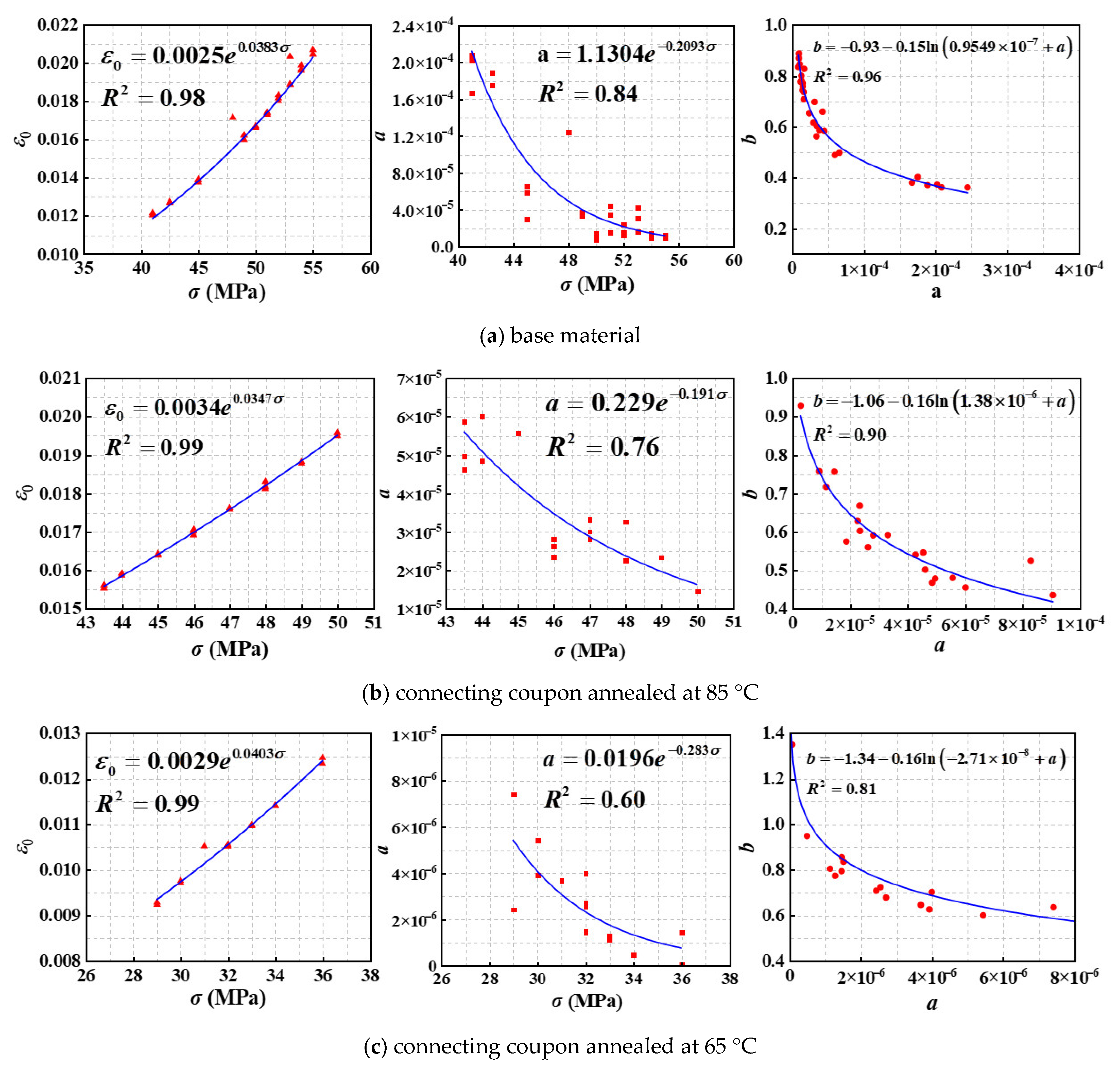
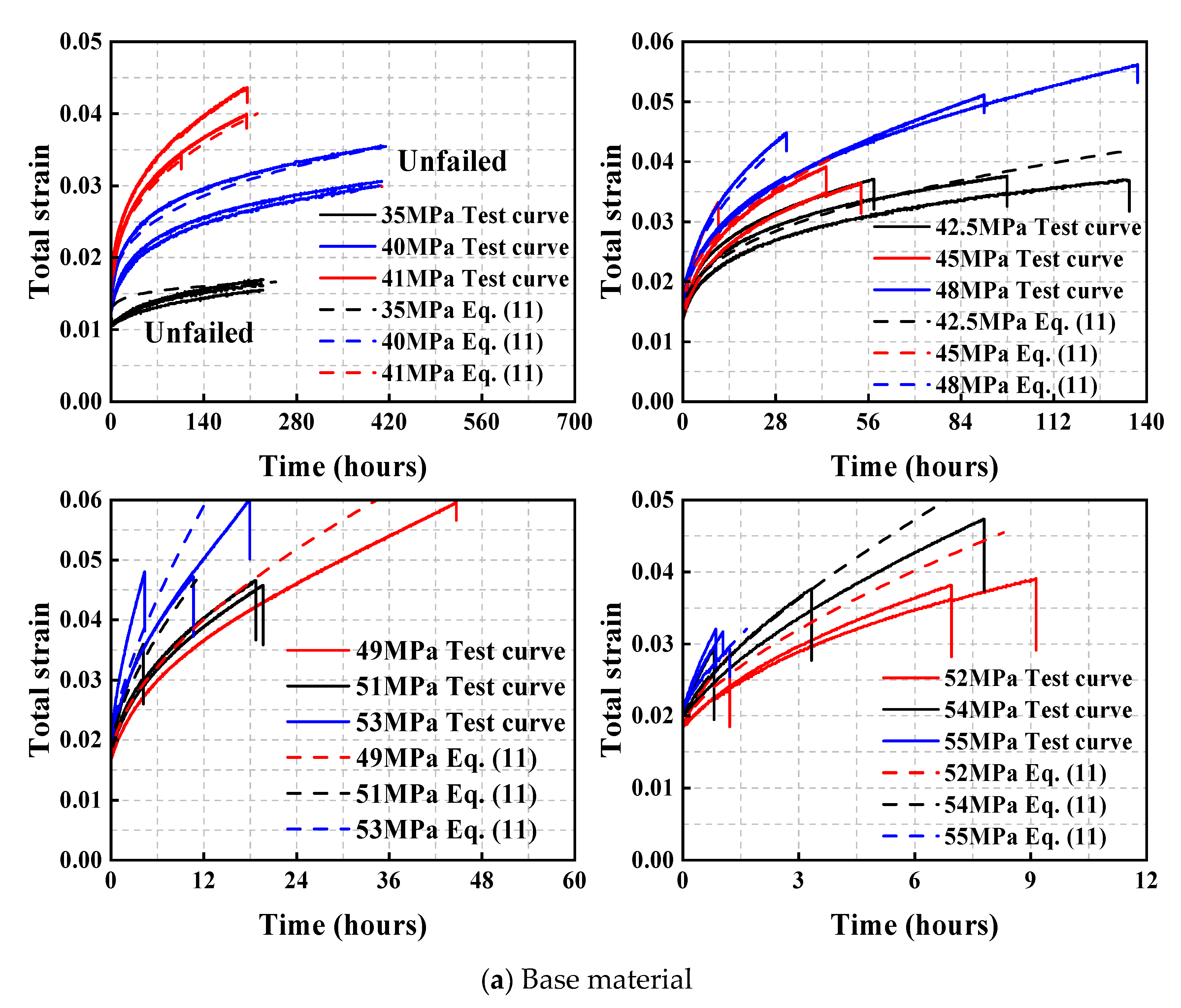
4. Findley Model
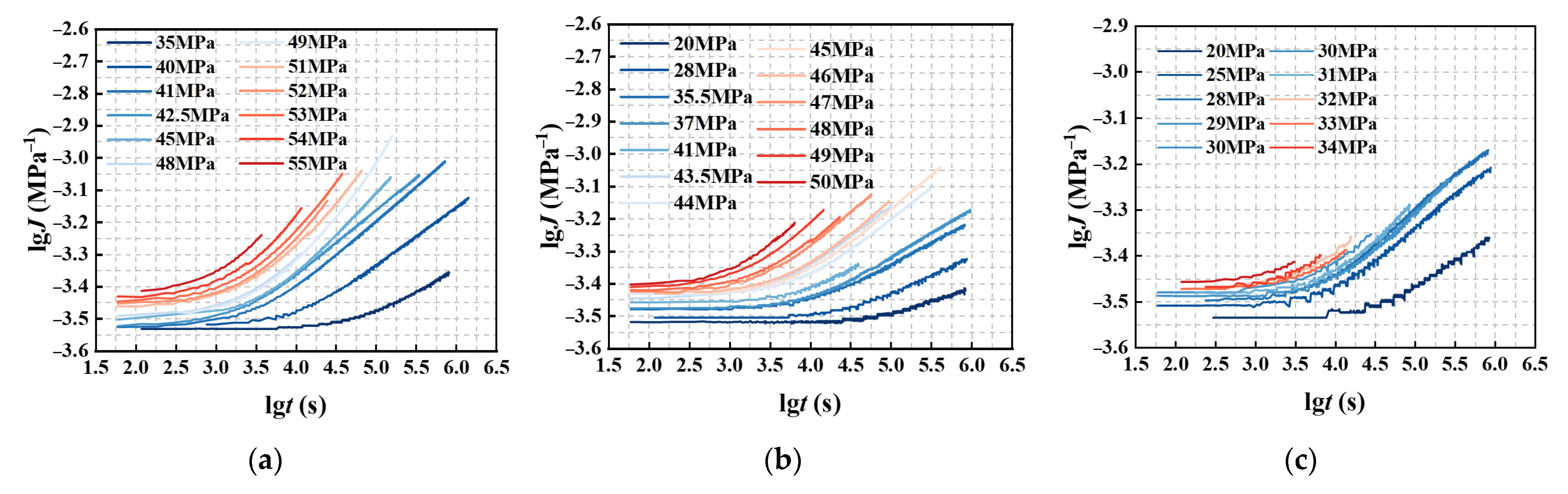
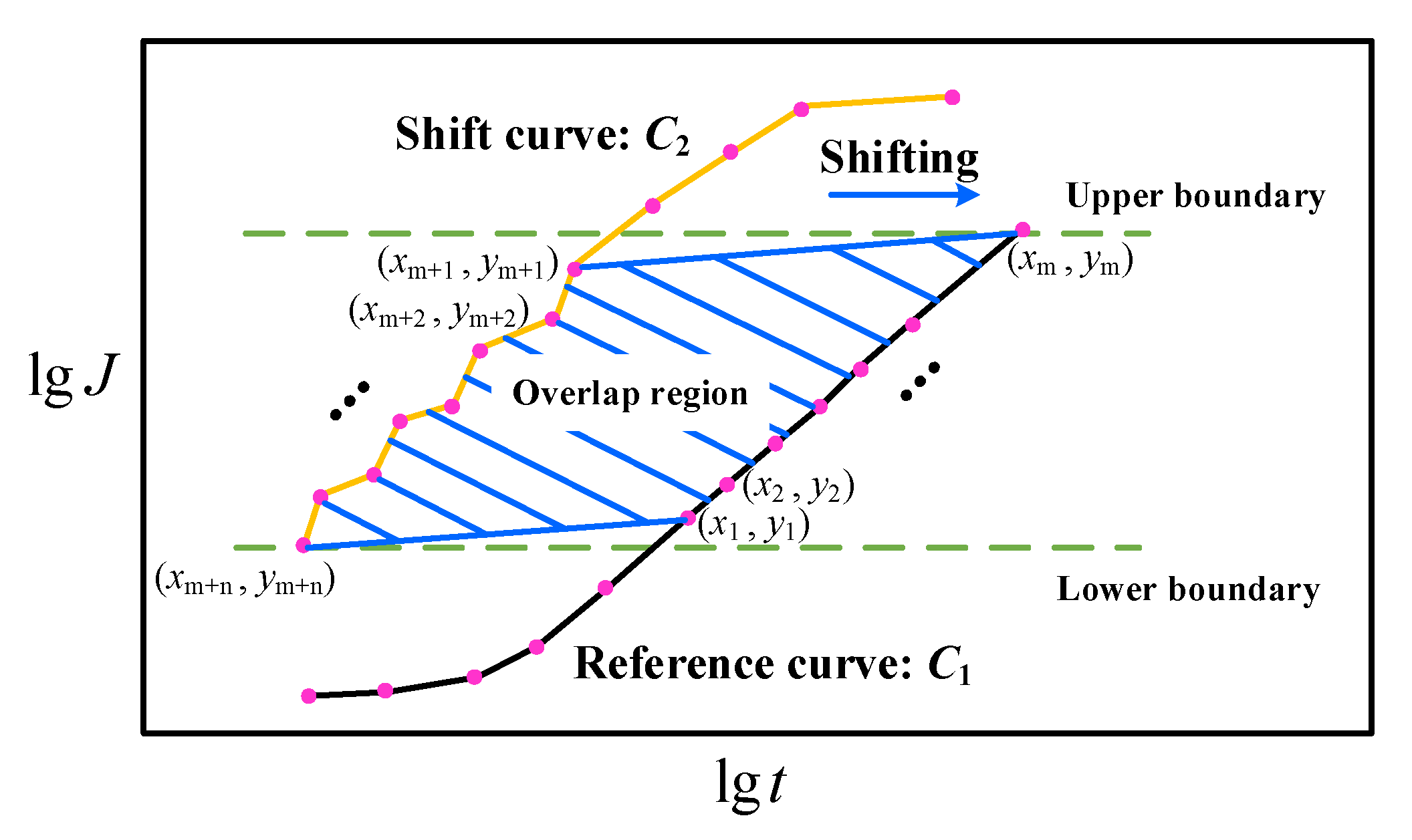
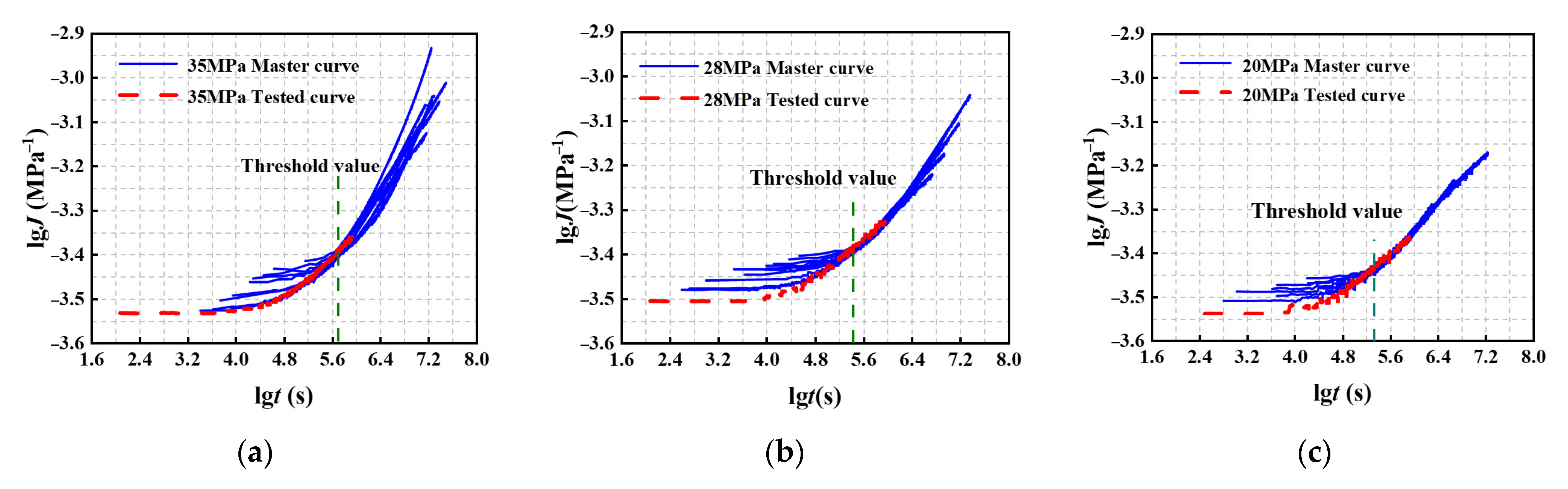
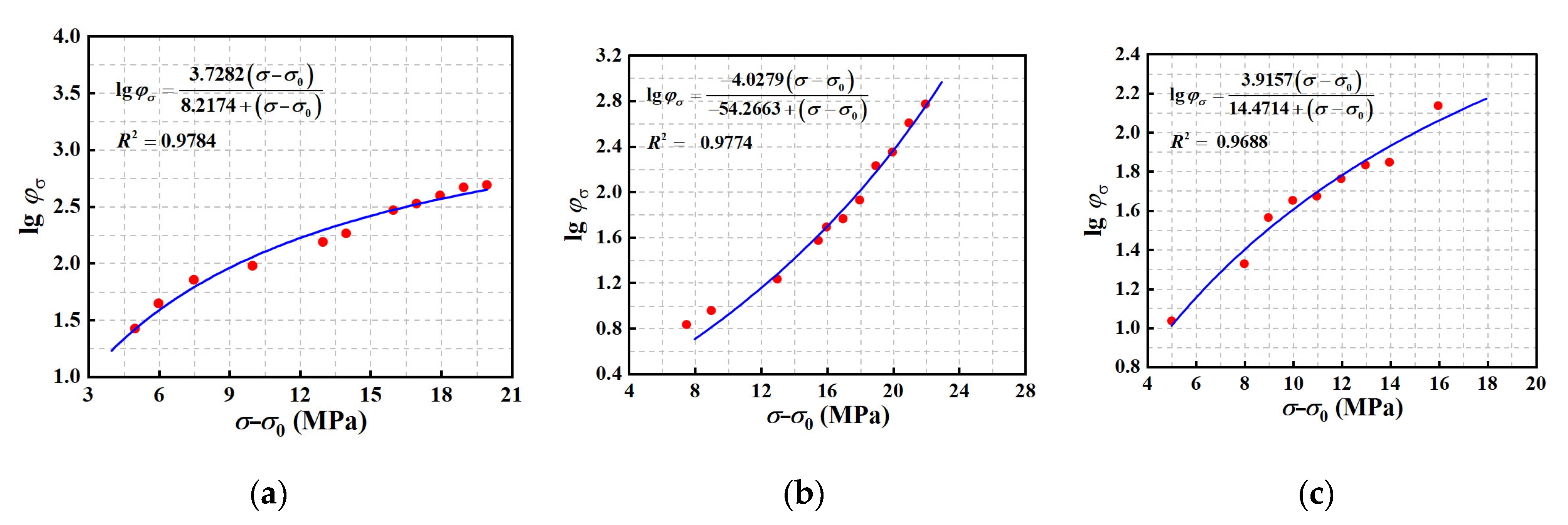
5. Verification of Time–Stress Superposition Principle (TSSP)
6. Conclusions
- (1)
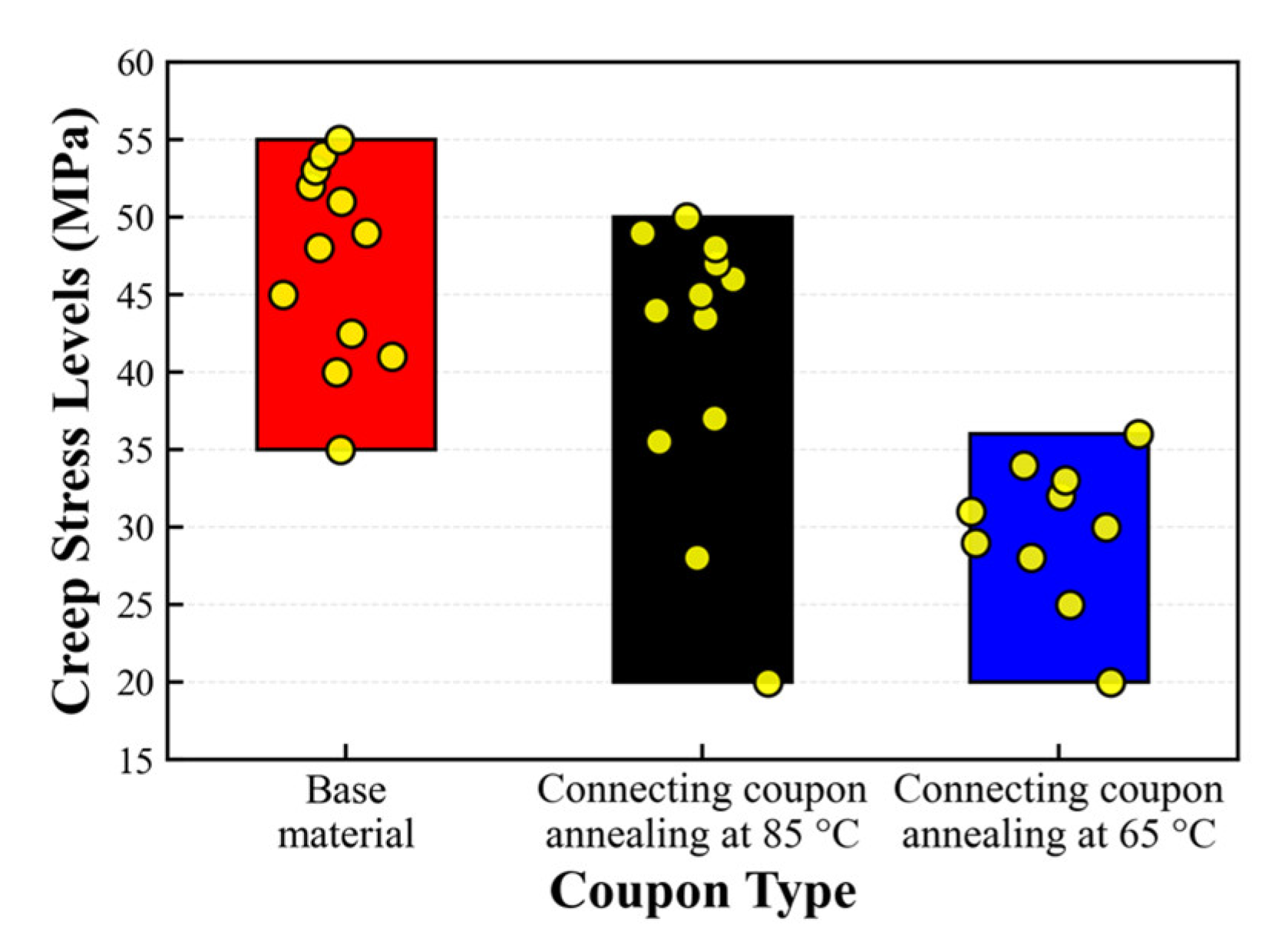
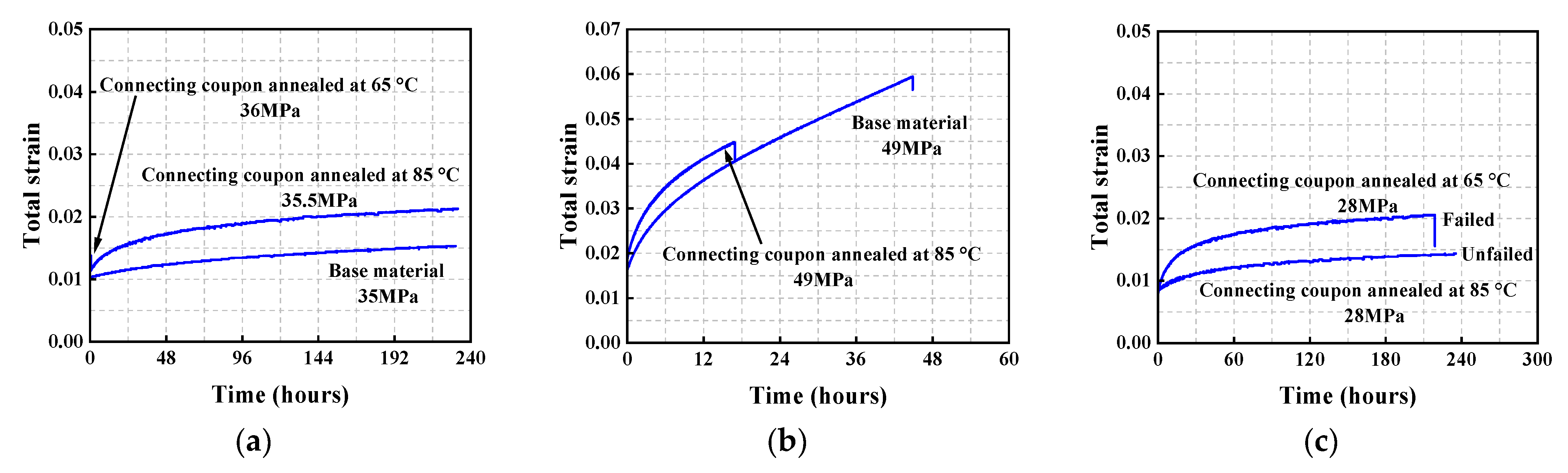
- Bulk polymerization degrades the mechanical performance of structural acrylic. The ultimate strength of the connecting coupon annealed at 65 °C is significantly lower than that of the connecting coupon annealed at 85 °C, indicating that annealing temperature profoundly affects the quality of bulk polymerization.
- (2)
- The creep curves of the tested coupons have primary and secondary stages, whereas the tertiary stages were not found. The Burgers model effectively characterizes the viscoelastic behavior of both the structural acrylic base material and connecting coupons. The Prony series converted from the parameters in the Burgers model can be directly used in the Abaqus software for the creep analysis. The close correlation between FEA predictions and experimental results validates the effectiveness of both the Burgers model and its Prony series equivalent in capturing the creep characteristics of structural acrylic.
- (3)
- Although the physical interpretation of the parameters in the Findley model remains unclear, the model demonstrates remarkable accuracy in characterizing creep behavior. Equation (11) proposed in this study on the basis of the Findley model provides a reliable framework for predicting creep curves of both structural acrylic base material and connecting coupons.
- (4)
- The TSSP demonstrates applicability to both structural acrylic base material and connecting coupons annealed at 85 °C and 65 °C, with respective minimum time thresholds of 501,187 s, 316,227 s, and 199,526 s. Through curve fitting analysis, Equation (15) has been established as an effective predictor of the shift factor for structural acrylic.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tsai, S.N.; Chiag, H.T. Repair Effects of Offcut-Carbon-Fiber-Powder-Modified PU-PMMA Copolymer on Flexure-After-Impact Behaviors of Composite Laminate. Heliyon 2025, 11, e41476. [Google Scholar] [CrossRef]
- Zheng, Z.B.; Chen, S.Y.; Liu, X.D.; Wang, Y.; Bian, Y.; Feng, B.; Zhao, R.; Qiu, Z.; Sun, Y.; Zhang, H.; et al. A Bioactive Polymethylmethacrylate Bone Cement for Prosthesis Fixation in Osteoporotic Hip Replacement Surgery. Mater. Des. 2021, 209, 109966. [Google Scholar] [CrossRef]
- Zhou, W.; Huang, J.X.; Huang, W.; Liu, D. Dynamic Fracture Testing of Polymethylmethacrylate (PMMA) Single-Edge Notched Beam. Polym. Test. 2020, 91, 106833. [Google Scholar] [CrossRef]
- Vu, T.V.; Sim, J.H.; Choi, J.; Jeong, H.; Park, S.; Kim, S.; Baek, S.; Lee, H.; Kang, Y. Conformational Energy Inversion in PMMA Crystals Prepared via Thermal Quenching with Entropy Diluents. Polymer 2025, 326, 128318. [Google Scholar] [CrossRef]
- Ube, T.; Aoki, H.; Ito, S.; Horinaka, J.-I.; Takigawa, T. Conformation of Single PMMA Chain in Uniaxially Stretched Film Studied by Scanning Near-Field Optical Microscopy. Polymer 2007, 48, 6221–6225. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Wang, Y.Q.; Du, X.X.; Zhang, T.; Heng, Y. Study on the Fracture Properties of the PMMA Structure for the JUNO Central Detector. KSCE J. Civ. Eng. 2019, 23, 2584–2597. [Google Scholar] [CrossRef]
- GB/T 7134-2008; Poly (Methyl Methacrylate) Cast Sheets. Standards Press of China: Beijing, China, 2008. (In Chinese)
- Cai, S.M.; Chen, Y.M.; Liu, Q.X. Development and Validation of Fractional Constitutive Models for Viscoelastic-Plastic Creep in Time-Dependent Materials: Rapid Experimental Data Fitting. Appl. Math. Model. 2024, 132, 645–678. [Google Scholar] [CrossRef]
- Poynting, J.H.; Thomson, J.J. Properties of Matter; C. Griffin and Co.: London, UK, 1902. [Google Scholar] [CrossRef]
- Williams, M.L. Structural Analysis of Viscoelastic Materials. AIAA J. 1964, 2, 785–808. [Google Scholar] [CrossRef]
- Li, X.Z.; Sha, A.M.; Jiao, W.X.; Song, R.M.; Cao, Y.S.; Li, C.; Liu, Z.Z. Fractional derivative Burgers models describing dynamic viscoelastic properties of asphalt binders. Constr. Build. Mater. 2023, 408, 133552. [Google Scholar] [CrossRef]
- Jalocha, D.; Constantinescu, A.; Neviere, R. Revisiting the Identification of Generalized Maxwell Models from Experimental Results. Int. J. Solids Struct. 2015, 67–68, 169–181. [Google Scholar] [CrossRef]
- Plazek, D.J.; Plazek, C.T. A History of Andrade Creep and the Investigation of the Dielectric Dipolar Andrade Creep. J. Non-Cryst. Solids 2021, 560, 120625. [Google Scholar] [CrossRef]
- Xiao, H.R.; Cai, L.X.; Han, G.Z. A Novel Theoretical Model for Obtaining Norton’s Law of Creep Materials Using Different Small Specimens. Int. J. Mech. Sci. 2024, 261, 108677. [Google Scholar] [CrossRef]
- Dong, S.L.; Gong, Z.; Chen, Z.Y.; Qu, Y.; Chen, R.; Liu, S.; Li, G. High Temperature Tensile Creep Behavior and Microstructure Evolution of Ti60 Alloy Rolled Sheet. Mater. Today Commun. 2024, 41, 110805. [Google Scholar] [CrossRef]
- Xu, S.X.; Gao, H.X.; Qiu, P.; Shen, W.; Cai, Y.; Liu, D. Stability Analysis of Acrylic Glass Pressure Cylindrical Shell Considering Creep Effect. Thin-Walled Struct. 2022, 181, 110033. [Google Scholar] [CrossRef]
- Mahdavi, R.; Goodarzi, V.; Jafari, S.H.; Saeb, M.R.; Shojaei, S. Experimental Analysis and Prediction of Viscoelastic Creep Properties of PP/EVA/LDH Nanocomposites Using Master Curves Based on Time–Temperature Superposition. J. Appl. Polym. Sci. 2018, 135, 46725. [Google Scholar] [CrossRef]
- Luo, W.B.; Wang, C.H.; Hu, X.L.; Yang, T.Q. Long-term creep assessment of viscoelastic polymer by time-temperature-stress superposition. Acta Mech. Solida Sin. 2012, 25, 571–578. [Google Scholar] [CrossRef]
- Jazouli, S.; Luo, W.; Bremand, F.; Vu-Khanh, T. Application of Time–Stress Equivalence to Nonlinear Creep of Polycarbonate. Polym. Test. 2005, 24, 463–467. [Google Scholar] [CrossRef]
- Wang, B.; Fancey, K.S. Application of Time–Stress Superposition to Viscoelastic Behavior of Polyamide 6,6 Fiber and Its “True” Elastic Modulus. J. Appl. Polym. Sci. 2017, 134, 44971. [Google Scholar] [CrossRef]
- Yang, Z.Q.; Wang, H.; Ma, X.F.; Shang, F.; Ma, Y.; Shao, Z.; Hou, D. Flexural Creep Tests and Long-Term Mechanical Behavior of Fiber-Reinforced Polymeric Composite Tubes. Compos. Struct. 2018, 193, 154–164. [Google Scholar] [CrossRef]
- Zhou, F.; Hou, S.J.; Qian, X.H.; Chen, Z.; Zheng, C.; Xu, F. Creep Behavior and Lifetime Prediction of PMMA Immersed in Liquid Scintillator. Polym. Test. 2016, 53, 323–328. [Google Scholar] [CrossRef]
- Wang, C.H.; Luo, W.B.; Liu, X.; Chen, X.; Jiang, L.; Yang, S. Application of Time-Temperature-Stress Equivalence to Nonlinear Creep in Poly(methyl methacrylate). Mater. Today Commun. 2019, 21, 100710. [Google Scholar] [CrossRef]
- GB/T 1040.1-2006; Plastics—Determination of Tensile Properties—Part 1: General Principles. Standards Press of China: Beijing, China, 2006. (In Chinese)
- GB/T 11546.1-2008; Plastics—Determination of Creep Behavior—Part 1: Tensile Creep. Standards Press of China: Beijing, China, 2008. (In Chinese)
- Wang, Z.Y.; Liu, Y.H.; Wang, Y.Q.; Huang, M.; Xiao, J.X.; Cheng, W. Creep Model of Base Material and Bulk Polymerization Connected Coupons of Structural Acrylic. J. Southeast Univ. (Nat. Sci. Ed.) 2025, 55, 1035–1043. (In Chinese) [Google Scholar] [CrossRef]
- Gutierrez-Lemini, D. Engineering Viscoelasticity; Oil States Industries: Arlington, TX, USA, 2014. [Google Scholar] [CrossRef]
- Luo, R.; Lv, H.J.; Liu, H.Q. Development of Prony Series Models Based on Continuous Relaxation Spectrums for Relaxation Moduli Determined Using Creep Tests. Constr. Build. Mater. 2018, 168, 758–770. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Birgisson, B.; Lytton, R.L. Weak Form Equation-Based Finite-Element Modeling of Viscoelastic Asphalt Mixtures. J. Mater. Civ. Eng. 2016, 28, 04015115. [Google Scholar] [CrossRef]
- Barbero, E.J. Finite Element Analysis of Composite Materials with Abaqus; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar] [CrossRef]
- Wang, C.; Anupam, K.; Kasbergen, C.; Erkens, S. Frequency Range Optimization for Linear Viscoelastic Characterization of Burger’s Model. Int. J. Mech. Sci. 2025, 285, 109817. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Gu, X.Y.; Lv, J.X.; Zhu, Z.; Zou, X. Numerical Analysis of the Rheological Behaviors of Basalt Fiber Reinforced Asphalt Mortar Using ABAQUS. Constr. Build. Mater. 2017, 157, 392–401. [Google Scholar] [CrossRef]
- Amjadi, M.; Fatemi, A. Creep Behavior and Modeling of High-Density Polyethylene (HDPE). Polym. Test. 2021, 94, 107031. [Google Scholar] [CrossRef]
- Gao, D.D.; Wang, P.B.; Li, M.; Luo, W. Modelling of Nonlinear Viscoelastic Creep Behaviour of Hot-Mix Asphalt. Constr. Build. Mater. 2015, 95, 329–336. [Google Scholar] [CrossRef]
- Liu, X.; Luo, W.B.; Li, M. A Novel Approach for Constructing Master Curves of Rheological Simple Material. Chin. J. Solid Mech. 2015, 36, 223–232. (In Chinese) [Google Scholar] [CrossRef]

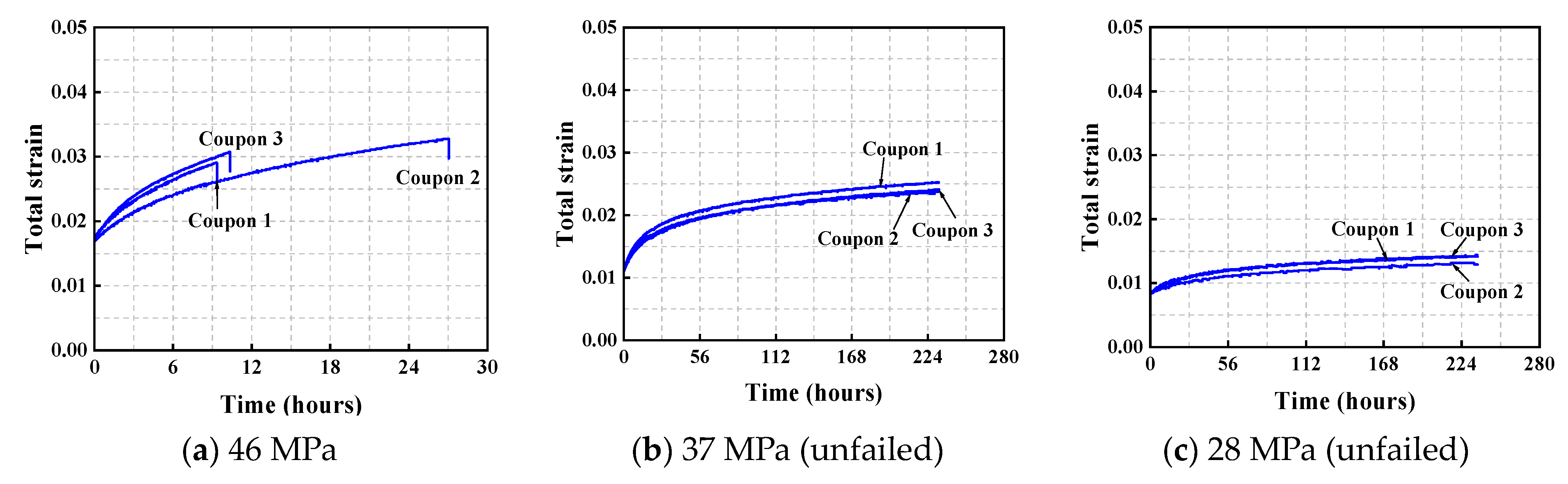
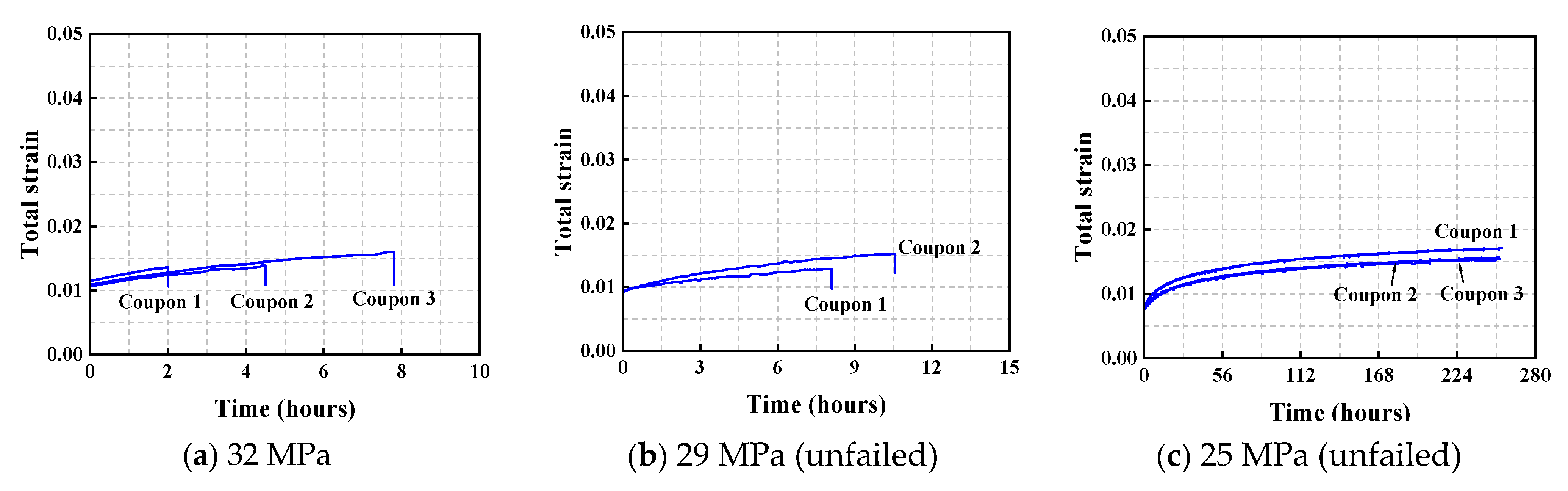
| The Type of Coupon | Young’s Modulus (GPa) | True Ultimate Strength (MPa) | Ultimate Strain |
|---|---|---|---|
| Base material | 3.36 ± 0.22 | 74.4 ± 4.3 | 0.054 ± 0.014 |
| Connecting coupon annealed at 85 °C | 3.34 ± 0.31 | 64.3 ± 3.6 | 0.032 ± 0.007 |
| Connecting coupon annealed at 65 °C | 3.41 ± 0.53 | 52.8 ± 1.4 | 0.022 ± 0.001 |
| Coupon Type | The Creep Stress Levels |
|---|---|
| Base material | 35 MPa, 40 MPa, 41 MPa, 42.5 MPa, 45 MPa, 48 MPa, 49 MPa, 51 MPa, 52 MPa, 53 MPa, 54 MPa, 55 MPa |
| Connecting coupon annealed at 85 °C | 20 MPa, 28 MPa, 35.5 MPa, 37 MPa, 43.5 MPa, 44 MPa, 45 MPa, 46 MPa, 47 MPa, 48 MPa, 49 MPa, 50 MPa |
| Connecting coupon annealed at 65 °C | 20 MPa, 25 MPa, 28 MPa, 29 MPa, 30 MPa, 31 MPa, 32 MPa, 33 MPa, 34 MPa, 36 MPa |
| Type | ||||||
|---|---|---|---|---|---|---|
| Base material | 35 | 3424 | 14,829 | 1.05 × 1010 | 2.55 × 109 | 0.9989 |
| 40 | 2907 | 4534 | 7.81 × 109 | 8.05 × 108 | 0.9978 | |
| 41 | 2619 | 3209 | 2.60 × 109 | 2.94 × 108 | 0.9980 | |
| 42.5 | 2770 | 3430 | 1.44 × 109 | 1.44 × 108 | 0.9977 | |
| 45 | 2990 | 3756 | 5.77 × 108 | 1.05 × 108 | 0.9995 | |
| 48 | 2612 | 2971 | 1.08 × 109 | 1.65 × 108 | 0.9986 | |
| 49 | 2767 | 3404 | 6.08 × 109 | 1.58 × 108 | 0.9998 | |
| 51 | 2796 | 4867 | 1.92 × 108 | 5.81 × 107 | 0.9994 | |
| 52 | 2860 | 7077 | 1.02 × 108 | 4.87 × 107 | 0.9999 | |
| 53 | 2768 | 4903 | 1.18 × 108 | 4.11 × 107 | 0.9999 | |
| 54 | 2726 | 11,195 | 4.95 × 107 | 3.67 × 107 | 0.9994 | |
| 55 | 2666 | 22,863 | 2.42 × 107 | 2.95 × 107 | 0.9995 | |
| Connecting coupon annealed at 85 °C | 20 | 3398 | 19,874 | 2.09 × 1010 | 3.91 × 109 | 0.9817 |
| 28 | 3161 | 8523 | 1.14 × 1010 | 1.01 × 109 | 0.9975 | |
| 35.5 | 2887 | 6548 | 8.10 × 109 | 7.29 × 108 | 0.9969 | |
| 37 | 2822 | 5359 | 7.60 × 109 | 6.56 × 108 | 0.9978 | |
| 43.5 | 2738 | 5654 | 1.02 × 109 | 1.51 × 108 | 0.9993 | |
| 44 | 2634 | 4560 | 1.71 × 109 | 2.33 × 108 | 0.9989 | |
| 45 | 2634 | 4802 | 1.01 × 109 | 1.54 × 108 | 0.9992 | |
| 46 | 2705 | 7256 | 2.29 × 108 | 5.69 × 107 | 0.9998 | |
| 47 | 2642 | 4866 | 3.53 × 108 | 6.38 × 107 | 0.9994 | |
| 48 | 2672 | 9250 | 1.54 × 108 | 4.44 × 107 | 0.9988 | |
| 49 | 2595 | 7240 | 9.91 × 107 | 3.40 × 107 | 0.9998 | |
| 50 | 2578 | 6176 | 7.79 × 107 | 2.28 × 107 | 0.9985 | |
| Connecting coupon annealed at 65 °C | 20 | 3461 | 12,292 | 1.36 × 1010 | 1.72 × 109 | 0.9933 |
| 25 | 2998 | 5341 | 8.60 × 109 | 6.25 × 108 | 0.9973 | |
| 28 | 2781 | 4040 | 5.95 × 109 | 3.12 × 108 | 0.9954 | |
| 29 | 3043 | 14,270 | 5.42 × 109 | 1.97 × 108 | 0.9949 | |
| 30 | 3061 | 8494 | 1.45 × 109 | 3.15 × 108 | 0.9988 | |
| 31 | 3062 | 11,157 | 9.05 × 108 | 2.80 × 108 | 0.9969 | |
| 32 | 3001 | 30,878 | 2.33 × 108 | 1.72 × 108 | 0.9905 | |
| 33 | 2989 | 42,707 | 2.65 × 108 | 2.67 × 108 | 0.9964 | |
| 34 | 2990 | 88,379 | 1.31 × 108 | 2.71 × 108 | 0.9725 | |
| 36 | 2916 | 31 | 7.37 × 108 | 4.81 × 107 | 0.9619 |
| Type | Stress Levels (MPa) | Prony Series Parameters | ||||
|---|---|---|---|---|---|---|
| (MPa) | ||||||
| Base material | 35 | 3424 | 0.7979 | 0.2021 | 3.80 × 106 | 1.38 × 105 |
| 40 | 2907 | 0.5900 | 0.4100 | 4.48 × 106 | 1.07 × 105 | |
| 41 | 2619 | 0.5253 | 0.4747 | 1.84 × 106 | 4.93 × 104 | |
| 42.5 | 2770 | 0.5311 | 0.4689 | 9.61 × 105 | 2.27 × 104 | |
| 45 | 2990 | 0.5166 | 0.4834 | 3.59 × 105 | 1.50 × 104 | |
| 48 | 2612 | 0.4963 | 0.5037 | 8.05 × 105 | 2.86 × 104 | |
| 49 | 2767 | 0.4931 | 0.5069 | 4.20 × 105 | 2.43 × 104 | |
| 51 | 2796 | 0.5819 | 0.4181 | 1.13 × 105 | 7.27 × 103 | |
| 52 | 2860 | 0.6512 | 0.3488 | 5.23 × 104 | 4.69 × 103 | |
| 53 | 2768 | 0.5785 | 0.4215 | 6.99 × 104 | 5.10 × 103 | |
| 54 | 2726 | 0.7521 | 0.2479 | 2.33 × 104 | 2.55 × 103 | |
| 55 | 2666 | 0.8676 | 0.1324 | 1.03 × 104 | 1.14 × 103 | |
| Connecting coupon annealed at 85 °C | 20 | 3398 | 0.8470 | 0.1530 | 7.23 × 106 | 1.67 × 105 |
| 28 | 3161 | 0.7199 | 0.2801 | 4.99 × 106 | 8.59 × 104 | |
| 35.5 | 2887 | 0.6821 | 0.3179 | 4.08 × 106 | 7.66 × 104 | |
| 37 | 2822 | 0.6415 | 0.3585 | 4.15 × 106 | 7.93 × 104 | |
| 43.5 | 2738 | 0.6519 | 0.3481 | 5.62 × 105 | 1.77 × 104 | |
| 44 | 2634 | 0.6104 | 0.3896 | 1.05 × 106 | 3.17 × 104 | |
| 45 | 2634 | 0.6203 | 0.3797 | 6.03 × 105 | 2.04 × 104 | |
| 46 | 2705 | 0.7006 | 0.2994 | 1.19 × 105 | 5.60 × 103 | |
| 47 | 2642 | 0.6183 | 0.3817 | 2.11 × 105 | 8.31 × 103 | |
| 48 | 2672 | 0.7522 | 0.2478 | 7.54 × 104 | 3.67 × 103 | |
| 49 | 2595 | 0.6987 | 0.3013 | 5.32 × 104 | 3.37 × 103 | |
| 50 | 2578 | 0.6679 | 0.3321 | 4.40 × 104 | 2.53 × 103 | |
| Connecting coupon annealed at 65 °C | 20 | 3461 | 0.7705 | 0.2295 | 5.07 × 106 | 1.09 × 105 |
| 25 | 2998 | 0.6283 | 0.3717 | 4.52 × 106 | 7.42 × 104 | |
| 28 | 2781 | 0.5819 | 0.4181 | 3.65 × 106 | 4.53 × 104 | |
| 29 | 3043 | 0.8045 | 0.1955 | 2.19 × 105 | 1.12 × 104 | |
| 30 | 3061 | 0.7118 | 0.2882 | 6.55 × 105 | 2.68 × 104 | |
| 31 | 3062 | 0.7608 | 0.2392 | 3.82 × 105 | 1.94 × 104 | |
| 32 | 3001 | 0.9000 | 0.1000 | 8.57 × 104 | 5.03 × 103 | |
| 33 | 2989 | 0.9258 | 0.0742 | 9.53 × 104 | 5.83 × 103 | |
| 34 | 2990 | 0.9625 | 0.0375 | 4.53 × 104 | 2.96 × 103 | |
| 36 | 2916 | 0.0094 | 0.9906 | 2.52 × 107 | 1.53 × 104 | |
| Type | Shift Factor at Corresponding Stress Level | ||||||
|---|---|---|---|---|---|---|---|
| Base material | Stress level | 35 MPa | 40 MPa | 41 MPa | 42.5 MPa | 45 MPa | 48 MPa |
| Shift factor | 0 | 1.417469 | 1.637511 | 1.847392 | 1.971217 | 2.180772 | |
| Stress level | 49 MPa | 51 MPa | 52 MPa | 53 MPa | 54 MPa | 55 MPa | |
| Shift factor | 2.257238 | 2.46118 | 2.520115 | 2.592012 | 2.665671 | 2.686152 | |
| Connecting coupon annealed at 85 °C | Stress level | 28 MPa | 35.5 MPa | 37 MPa | 41 MPa | 43.5 MPa | 44 MPa |
| Shift factor | 0 | 0.825744 | 0.949047 | 1.227911 | 1.568961 | 1.686544 | |
| Stress level | 45 MPa | 46 MPa | 47 MPa | 48 MPa | 49 MPa | 50 MPa | |
| Shift factor | 1.758884 | 1.924178 | 2.227396 | 2.347765 | 2.602786 | 2.770233 | |
| Connecting coupon annealed at 65 °C | Stress level | 20 MPa | 25 MPa | 28 MPa | 29 MPa | 30 MPa | 31 MPa |
| Shift factor | 0 | 1.031863 | 1.324451 | 1.541804 | 1.649485 | 1.670194 | |
| Stress level | 32 MPa | 33 MPa | 34 MPa | 36 MPa | |||
| Shift factor | 1.759538 | 1.816737 | 1.844731 | 2.847703 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Liu, Y.; Zhang, B.; Wang, Y.; Xiao, J.; Cheng, W.; Huang, M.; Song, Y. Creep Performance and Viscoelastic Constitutive Relationship of Structural Acrylic Connected Using Bulk Polymerization Technique. Buildings 2025, 15, 3691. https://doi.org/10.3390/buildings15203691
Wang Z, Liu Y, Zhang B, Wang Y, Xiao J, Cheng W, Huang M, Song Y. Creep Performance and Viscoelastic Constitutive Relationship of Structural Acrylic Connected Using Bulk Polymerization Technique. Buildings. 2025; 15(20):3691. https://doi.org/10.3390/buildings15203691
Chicago/Turabian StyleWang, Zongyi, Yuhao Liu, Bailun Zhang, Yuanqing Wang, Jianxia Xiao, Wei Cheng, Ming Huang, and Yulong Song. 2025. "Creep Performance and Viscoelastic Constitutive Relationship of Structural Acrylic Connected Using Bulk Polymerization Technique" Buildings 15, no. 20: 3691. https://doi.org/10.3390/buildings15203691
APA StyleWang, Z., Liu, Y., Zhang, B., Wang, Y., Xiao, J., Cheng, W., Huang, M., & Song, Y. (2025). Creep Performance and Viscoelastic Constitutive Relationship of Structural Acrylic Connected Using Bulk Polymerization Technique. Buildings, 15(20), 3691. https://doi.org/10.3390/buildings15203691







