Creep and Fatigue Life Prediction of Bulk-Polymerized Spliced Acrylic
Abstract
1. Introduction
2. Experimental Test
2.1. Coupon Design
2.2. Short-Term Tensile Test
2.3. Creep and Fatigue Failure Test
3. Analysis of Test Results
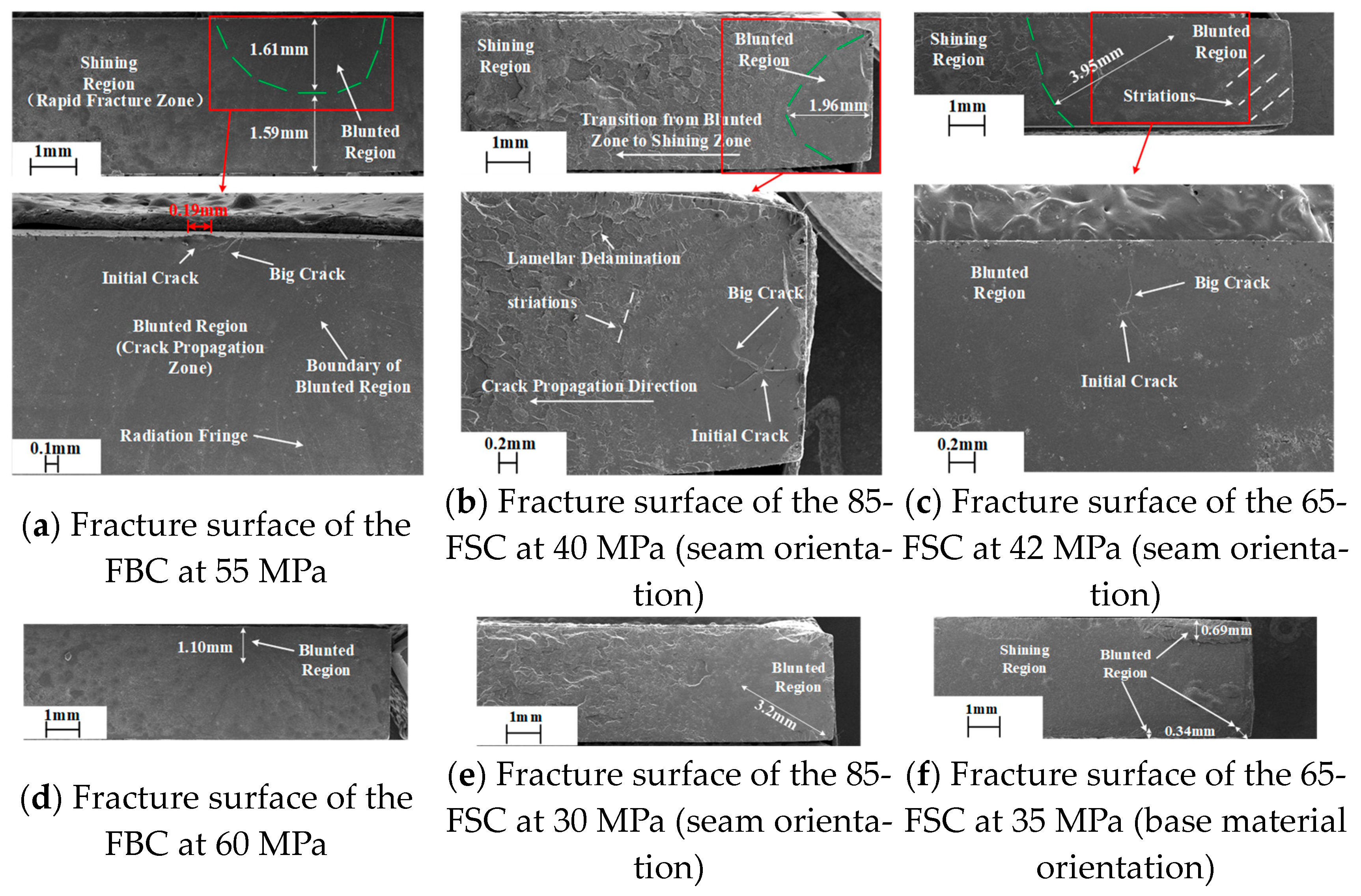
3.1. Coupon Fracture Morphology
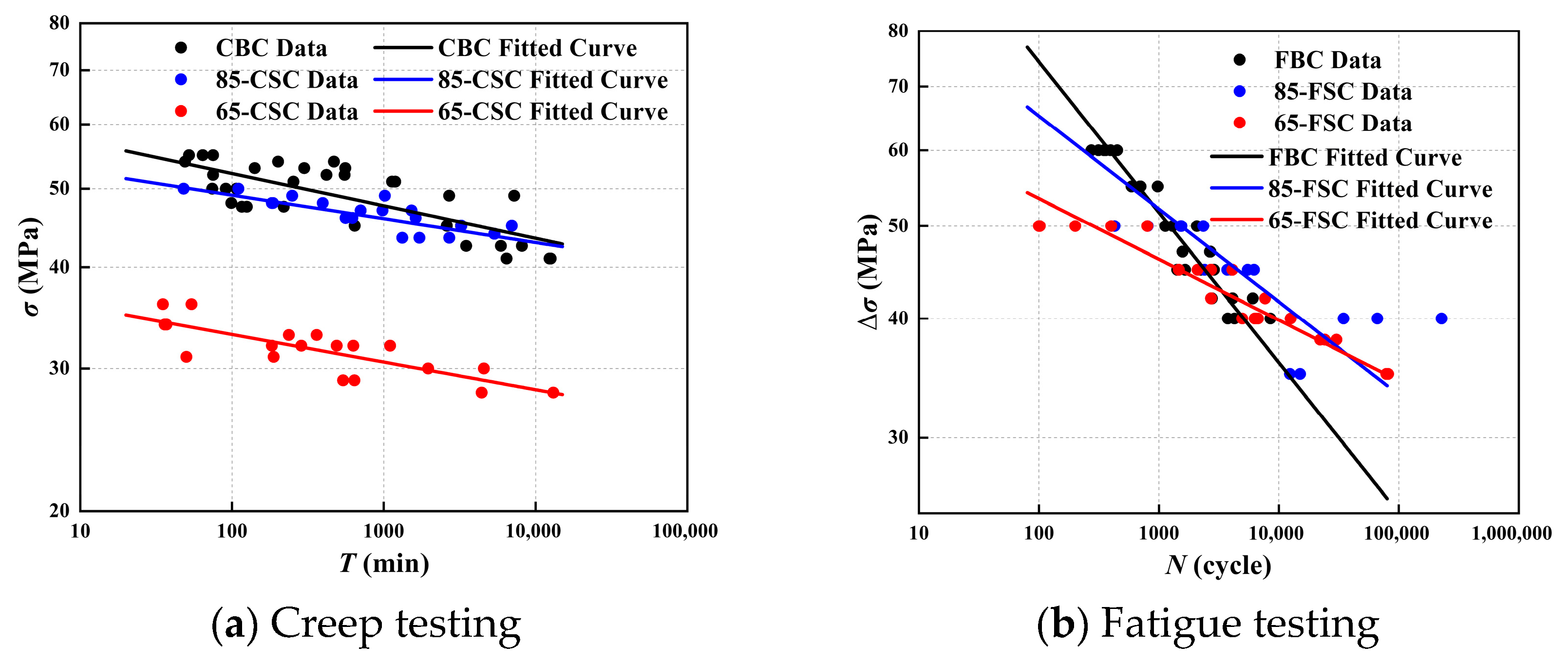
3.2. Creep and Fatigue Fracture Life
4. Statistical Analysis of Creep and Fatigue Life
4.1. Life Prediction Curves
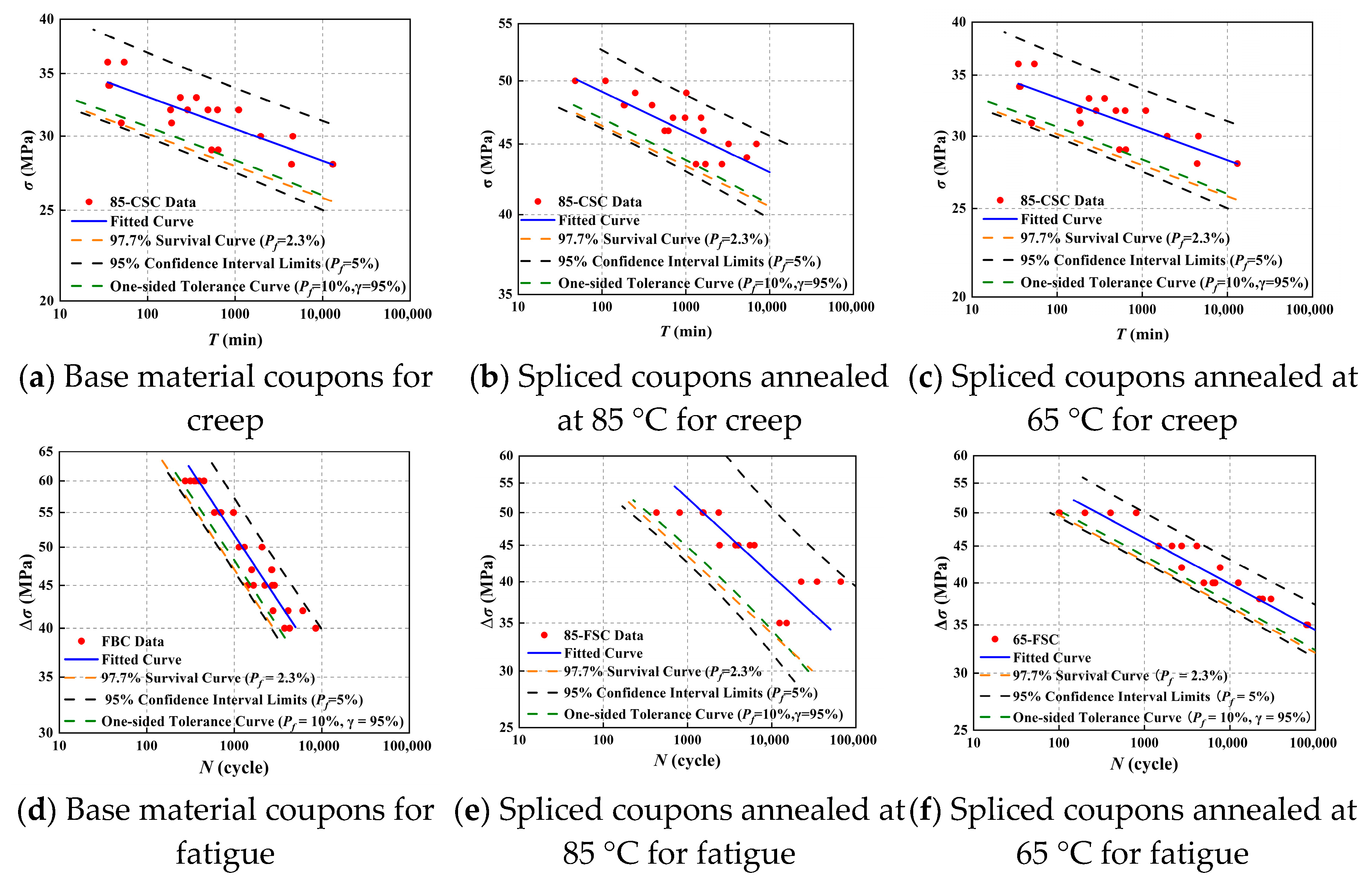
4.2. 97.7% Survival Curve
4.3. 95% Confidence Interval Limits
4.4. One-Sided Tolerance Curve
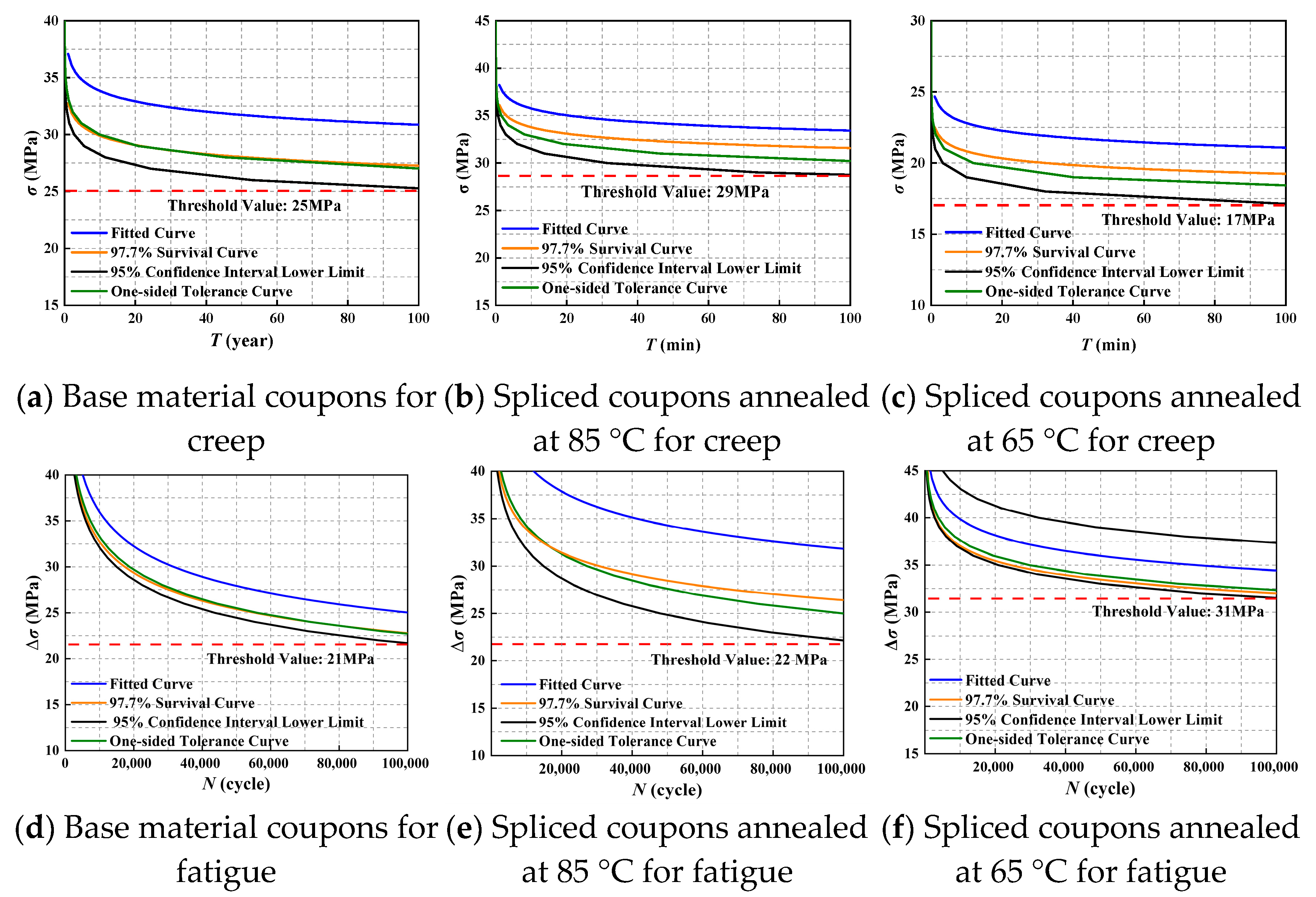
4.5. Life Threshold Value
5. SEM Fracture Analysis
5.1. Creep Fracture Surface
5.2. Fatigue Fracture Surface
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- GB/T 2680-2021; Glass in Building—Determination of Light Transmittance, Solar Direct Transmittance, Total Solar Energy Transmittance, Ultraviolet Transmittance and Related Glazing Factors. Standards Press of China: Beijing, China, 2021. (In Chinese)
- Reggente, M.; Harhash, M.; Kriegel, S.; He, W.; Masson, P.; Faerber, J.; Pourroy, G.; Palkowski, H.; Carradò, A. Resin-Free Three-Layered Ti/PMMA/Ti Sandwich Materials: Adhesion and Formability Study. Compos. Struct. 2019, 218, 107–119. [Google Scholar] [CrossRef]
- Shi, Z.L.; Zhao, G.Q.; Wang, G.L.; Zhang, L.; Wei, C.; Chai, J. Development of Ultralight, Tough and Hydrophobic Polymethylmethacrylate/Polyvinylidene Fluoride Shape Memory Foams for Heat Insulation Applications. Mater. Des. 2023, 225, 111527. [Google Scholar] [CrossRef]
- Pawar, E. A Review Article on Acrylic PMMA. IOSR J. Mech. Civ. Eng. 2016, 13, 1–4. [Google Scholar] [CrossRef]
- Wang, J.; Xu, Y.J.; Zhang, W.H. Finite Element Simulation of PMMA Aircraft Windshield Against Bird Strike Using a Rate and Temperature Dependent Nonlinear Viscoelastic Constitutive Model. Compos. Struct. 2014, 108, 21–30. [Google Scholar] [CrossRef]
- Du, Y.M.; Pei, P.H.; Suo, T.; Gao, G. Large Deformation Mechanical Behavior and Constitutive Modeling of Oriented PMMA. Int. J. Mech. Sci. 2023, 257, 108520. [Google Scholar] [CrossRef]
- Guo, H.; Lu, C.; Chen, Y.; Tao, J.; Chen, L. Thermal-Mechanical Coupling Behavior of Directional Polymethylmethacrylate under Tension and Compression. Polymers 2018, 10, 1279. [Google Scholar] [CrossRef]
- Weon, J.I.; Creasy, T.S.; Sue, H.J. Mechanical Behavior of Polymethylmethacrylate with Molecules Oriented via Simple Shear. Polym. Eng. Sci. 2005, 45, 249–256. [Google Scholar] [CrossRef]
- Gao, Z.Z.; Liu, Z.Q.; Liu, W.; Yue, Z.F. Experimental and Constitutive Investigation on Tensile and Compressive Behavior of MDYB-3 at Different Temperatures and Loading Rates. Int. J. Polym. Mater. Polym. Biomater. 2011, 60, 340–350. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology. Molecular and Microscopic Structure of Oriented Polymers and Their Influence on Mechanical Behavior; NIST Special Publication 960-16e3; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1985. [Google Scholar]
- Reynolds Polymer Technology. Jewel Changi Airport. Reynolds Polymer. 2019. Available online: https://www.reynoldspolymer.com/projects/jewel-changi-airport/ (accessed on 30 April 2025).
- Xu, X.J.; Wang, Z.; Chen, S.M. Solar Neutrino Physics. Prog. Part. Nucl. Phys. 2023, 131, 104043. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Liu, Y.H.; Chen, S.M.; Wang, Y.; Wang, Z.; Huang, M. Structural Design of the Acrylic Vessel for the Jinping Neutrino Experiment. J. Instrum. 2024, 19, P07041. [Google Scholar] [CrossRef]
- Wilson, J.D. Thermally-Driven Scintillator Flow in the SNO+ Neutrino Detector. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2023, 1055, 168430. [Google Scholar] [CrossRef]
- Qian, X.H.; Ma, X.Y.; Heng, Y.K.; He, W.; Tang, H.; Hou, S.; Pei, Y. Application of Non-Contact Strain Measurement Based on CCD Camera in PMMA Material Constitutive Model. Mater. Res. Express 2021, 8, 095305. [Google Scholar] [CrossRef]
- Guo, W.W.; Zhang, X.Q.; Su, J. Fatigue Damage Mechanism Analyses of Oriented Sheets of Polymethyl Methacrylate Glasses. Key Eng. Mater. 2011, 462, 36–41. [Google Scholar] [CrossRef]
- Okeke, C.P.; Thite, A.N.; Durodola, J.F.; Greenrod, M.T. Fatigue Life Prediction of Polymethyl Methacrylate (PMMA) Polymer under Random Vibration Loading. Procedia Struct. Integr. 2019, 17, 589–595. [Google Scholar] [CrossRef]
- Adibeig, M.R.; Hassanifard, S.; Vakili-Tahami, F. Optimum Creep Lifetime of Polymethyl Methacrylate (PMMA) Tube Using Rheological Creep Constitutive Models Based on Experimental Data. Polym. Test. 2019, 75, 107–116. [Google Scholar] [CrossRef]
- Zhou, F.; Hou, S.J.; Qian, X.H.; Chen, Z.; Zheng, C.; Xu, F. Creep Behavior and Lifetime Prediction of PMMA Immersed in Liquid Scintillator. Polym. Test. 2016, 53, 323–328. [Google Scholar] [CrossRef]
- Yin, W.H.; Xie, Z.Y.; Yin, Y.M.; Yi, J.; Liu, X.; Wu, H.; Wang, S.; Xie, Y.; Yang, Y. Aging Behavior and Lifetime Prediction of PMMA under Tensile Stress and Liquid Scintillator Conditions. Adv. Ind. Eng. Polym. Res. 2019, 2, 82–87. [Google Scholar] [CrossRef]
- Liu, W.; Yao, X.; Ma, Y.; Chen, X.; Guo, G.; Ma, L. Prediction on Fatigue Life of U-Notched PMMA Plate. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 300–312. [Google Scholar] [CrossRef]
- Huang, A.F.; Yao, W.X.; Chen, F. Analysis of Fatigue Life of PMMA at Different Frequencies Based on a New Damage Mechanics Model. Math. Probl. Eng. 2014, 1, 352676. [Google Scholar] [CrossRef]
- He, Z.H.; Wang, F.; Gaidai, O.; Qu, W.; Li, C. Lifetime Assessment of Deep-Sea Manned Cabin with PMMA Pressure-Resistant Hull Prior to Micro-Cracks. Ocean Eng. 2024, 306, 118119. [Google Scholar] [CrossRef]
- Said, B.L.; Hentati, H.; Wali, M.; Ayadi, B.; Alhadri, M. Damage Investigation in PMMA Polymer: Experimental and Phase-Field Approaches. Polymers 2024, 16, 3304. [Google Scholar] [CrossRef]
- Ahmed, M.A.M.; Jurczak, K.M.; Lynn, N.S.; Mulder, J.-P.S.H.; Verpoorte, E.M.J.; Nagelkerke, A. Rapid Prototyping of PMMA-Based Microfluidic Spheroid-on-a-Chip Models Using Micromilling and Vapour-Assisted Thermal Bonding. Sci. Rep. 2024, 14, 2831. [Google Scholar] [CrossRef]
- Lauterwasser, B.D.; Kramer, E.J. Microscopic Mechanisms and Mechanics of Crazing Growth and Fracture. Philos. Mag. A 1979, 38, 469–495. [Google Scholar] [CrossRef]
- Yan, Y.; Sun, Y.; Su, J.; Li, B.; Zhou, P. Crazing Initiation and Growth in Polymethyl Methacrylate under Effects of Alcohol and Stress. Polymers 2023, 15, 1375. [Google Scholar] [CrossRef] [PubMed]
- Sezavar, A.; Zebarjad, S.M.; Sajjadi, S.A. A Study on the Effect of Nano Alumina Particles on Fracture Behavior of PMMA. Technologies 2015, 3, 94–102. [Google Scholar] [CrossRef]
- GB/T 1040.2-2022; Plastics—Determination of Tensile Properties—Part 2: Test Conditions for Moulding and Extrusion Plastics. Standards Press of China: Beijing, China, 2022. (In Chinese)
- ASTM D638-22; Standard Test Method for Tensile Properties of Plastics. ASTM International: West Conshohocken, PA, USA, 2022.
- Wang, Z.Y.; Liu, Y.H.; Zhang, B.L.; Wang, Y.Q.; Xiao, J.X. Creep Life Analysis of Acrylic Base Material and Bulk Polymerized Connected Coupons Annealed at Different Temperatures. J. Southeast Univ. Nat. Sci. Ed. 2025, in press. Available online: https://link.cnki.net/urlid/32.1178.n.20250609.1341.002 (accessed on 6 August 2025). (In Chinese).
- GJB 2033-94; Test Method for Fatigue of Aircraft Transparent Materials. General Equipment Department of the PLA: Beijing, China, 1994. (In Chinese)
- ASTM E739-15; Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (S-N) and Strain-Life (ε-N) Fatigue Data. ASTM International: West Conshohocken, PA, USA, 2015.
- Yang, X.H. Fatigue and Fracture, 2nd ed.; Huazhong University of Science and Technology Press: Wuhan, China, 2020. [Google Scholar]
- Jiao, D.; Qu, T.R.; Zhang, Z.F. Macroscopic Bifurcation and Fracture Mechanism of Polymethyl Methacrylate. Adv. Eng. Mater. 2015, 17, 1454–1464. [Google Scholar] [CrossRef]
- Atkins, A.G.; Lee, C.S.; Caddell, R.M. Time-Temperature Dependent Fracture Toughness of PMMA. J. Mater. Sci. 1975, 10, 1381–1393. [Google Scholar] [CrossRef]
- Kuleyin, H.; Gümrük, R.; Çalişkan, S. The Effect of ABS Fraction on the Fatigue Behavior of PMMA/ABS Polymer Blends. Mater. Today Commun. 2022, 33, 104139. [Google Scholar] [CrossRef]
- Simsiriwong, J.; Shrestha, R.; Shamsaei, N.; Lugo, M.; Moser, R.D. Effects of Microstructural Inclusion on Fatigue Life of Polyether Ether Ketone (PEEK). J. Mech. Behav. Biomed. Mater. 2015, 51, 388–397. [Google Scholar] [CrossRef]
- Gómez, E.C.; Almaraz, M.G.D.; Juarez, J.C.V. Crack Initiation and Propagation on CT Specimens of Two Polymers (ABS and PMMA) under Cyclic Constant Displacement Loading. Theor. Appl. Fract. Mech. 2019, 100, 55–64. [Google Scholar] [CrossRef]
- Ravi-Chandar, K.; Yang, B. On the Role of Microcracks in the Dynamic Fracture of Brittle Materials. J. Mech. Phys. Solids 1997, 45, 535–563. [Google Scholar] [CrossRef]
- Kopp, J.B.; Girardot, J. Dynamic Fracture in a Semicrystalline Biobased Polymer: An Analysis of the Fracture Surface. Int. J. Fract. 2020, 226, 121–132. [Google Scholar] [CrossRef]

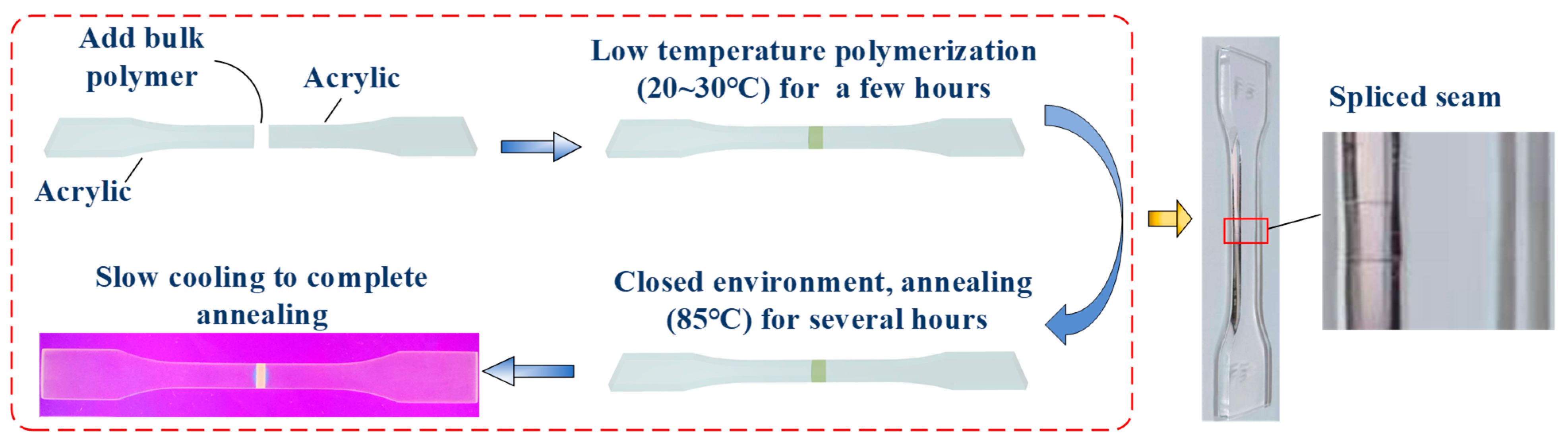




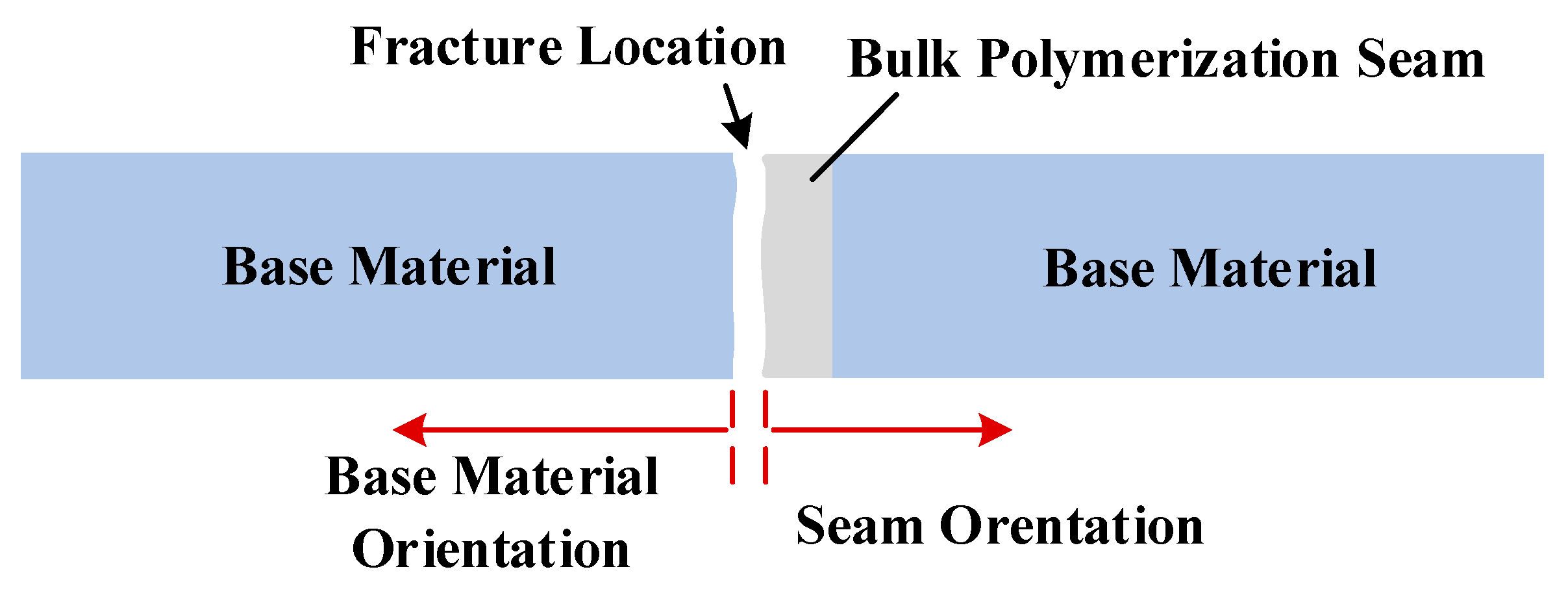
| Coupon Type | Ultimate Strength (MPa) | Elastic Modulus (GPa) |
|---|---|---|
| Base material coupon | 74.4 ± 4.3 | 3.36 ± 0.22 |
| 85 °C annealing spliced coupon | 64.3 ± 3.6 | 3.34 ± 0.31 |
| 65 °C annealing spliced coupon | 52.8 ± 1.4 | 3.41 ± 0.53 |
| Type | Creep Stress (MPa) | Creep Life (min) | Creep Stress (MPa) | Creep Life (min) |
|---|---|---|---|---|
| CBC | 41 | 6438; 12,574; 12,361 | 50 | 91; 107; 74 |
| 42.5 | 3492; 8132; 5905 | 51 | 254; 1132; 1188 | |
| 45 | 643; 2602; 3229 | 52 | 75; 552; 419 | |
| 47 | 125; 116; 219 | 53 | 141; 299; 558 | |
| 48 | 99 | 54 | 49; 201; 469 | |
| 49 | 2675; 7233 | 55 | 52; 75; 64 | |
| 85-CSC | 43.5 | 1323; 2700; 1717 | 47 | 704; 980; 1523 |
| 44 | 5368; 5347 | 48 | 186; 396; 183 | |
| 45 | 3245; 6974 | 49 | 1015; 249 | |
| 46 | 560; 1622; 620 | 50 | 110; 48 | |
| 65-CSC | 28 | 4410; 13,075 | 32 | 183; 286; 489; 1100; 630; 361 |
| 29 | 539; 640 | 33 | 361; 237 | |
| 30 | 4564; 1958 | 34 | 36; 37 | |
| 31 | 188; 50 | 36 | 35; 54 |
| Type | Stress Amplitude (MPa) | Fatigue Life (Cycle) | Stress Amplitude (MPa) | Fatigue Life (Cycle) |
|---|---|---|---|---|
| CBC | 40 | 3754; 8504; 4274 | 50 | 1303; 2074; 1131 |
| 42 | 4116; 6062; 2771 | 55 | 592; 696; 704; 977; 980 | |
| 45 | 1421; 2233; 1421; 2712; 1878; 1657 | 60 | 397; 450; 314; 274; 361; 350 | |
| 47 | 2666; 1578; 2689 | - | - | |
| 85-CSC | 35 | 12,401; 15,022 | 45 | 6221; 5510; 3713; 4009; 2402 |
| 40 | 66,201; 22,401; 34,601 | 50 | 1521; 428; 807; 2346; 1542 | |
| 65-CSC | 35 | 78,742; 81,400 | 42 | 2728; 2718; 7683 |
| 38 | 22,127; 24,157; 30,247 | 45 | 2101; 4101; 1468; 2728; 2718 | |
| 40 | 6301; 6699; 6547; 12,549; 4956 | 50 | 801; 401; 201; 102; 100 |
| Coupon Type | Life Prediction Equation | s | r | R2 |
| CBC | 0.67 | −0.763 | 0.582 | |
| 85-CSC | 0.42 | −0.825 | 0.680 | |
| 65-CSC | 0.58 | −0.804 | 0.646 | |
| FBC | 0.13 | −0.947 | 0.898 | |
| 85-FSC | 0.37 | −0.810 | 0.657 | |
| 65-FSC | 0.25 | −0.952 | 0.906 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Liu, Y.; Zhang, B.; Wang, Y.; Xiao, J.; Song, Y.; Cheng, W. Creep and Fatigue Life Prediction of Bulk-Polymerized Spliced Acrylic. Buildings 2025, 15, 3677. https://doi.org/10.3390/buildings15203677
Wang Z, Liu Y, Zhang B, Wang Y, Xiao J, Song Y, Cheng W. Creep and Fatigue Life Prediction of Bulk-Polymerized Spliced Acrylic. Buildings. 2025; 15(20):3677. https://doi.org/10.3390/buildings15203677
Chicago/Turabian StyleWang, Zongyi, Yuhao Liu, Bailun Zhang, Yuanqing Wang, Jianxia Xiao, Yulong Song, and Wei Cheng. 2025. "Creep and Fatigue Life Prediction of Bulk-Polymerized Spliced Acrylic" Buildings 15, no. 20: 3677. https://doi.org/10.3390/buildings15203677
APA StyleWang, Z., Liu, Y., Zhang, B., Wang, Y., Xiao, J., Song, Y., & Cheng, W. (2025). Creep and Fatigue Life Prediction of Bulk-Polymerized Spliced Acrylic. Buildings, 15(20), 3677. https://doi.org/10.3390/buildings15203677







