CGV-Net: Tunnel Lining Crack Segmentation Method Based on Graph Convolution Guided Transformer
Abstract
1. Introduction
- 1.
- This paper proposes a graph neural network-guided Vision Transformer (ViT) tunnel crack segmentation module, CGV, designed for modeling tunnel lining cracks. The module is capable of simultaneously learning both local crack features and contextual information, thereby enhancing the accuracy of tunnel lining crack structure modeling. This approach further improves the performance of crack recognition and segmentation, leading to more precise and effective results in complex tunnel environments.
- 2.
- This paper proposes a graph-based representation method for tunnel lining cracks, which facilitates data interaction between different local regions by learning the features from the final layer of the encoder. This approach enhances the model’s reasoning capability for complex crack structures, improving the accuracy and robustness of crack segmentation in challenging environments.
- 3.
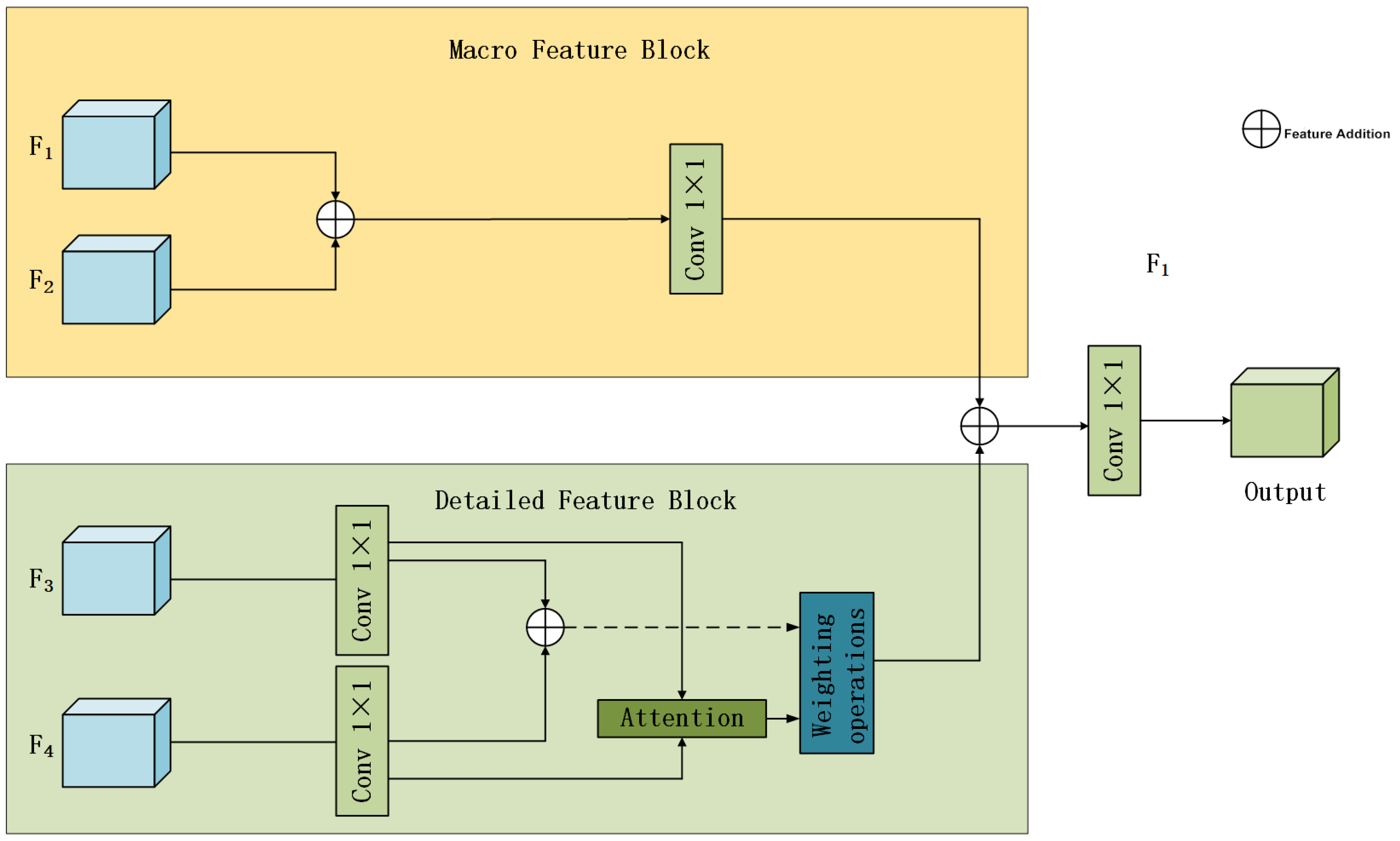
- This paper proposes a multi-scale Detailed-Macro Feature Fusion (DMFF) module, which performs different feature fusion operations on feature layers of varying scales. This approach effectively compensates for the loss of critical data during the encoding and decoding stages, further enhancing the accuracy and robustness of crack segmentation.
- 4.
- A comprehensive dataset covering various crack types and complex backgrounds in operational tunnel linings has been constructed. This dataset is designed to provide a richer and more diverse set of training and testing samples for tunnel crack recognition and segmentation tasks. The aim is to enhance the model’s generalization ability in complex scenarios, improving its performance in real-world applications.
2. Method
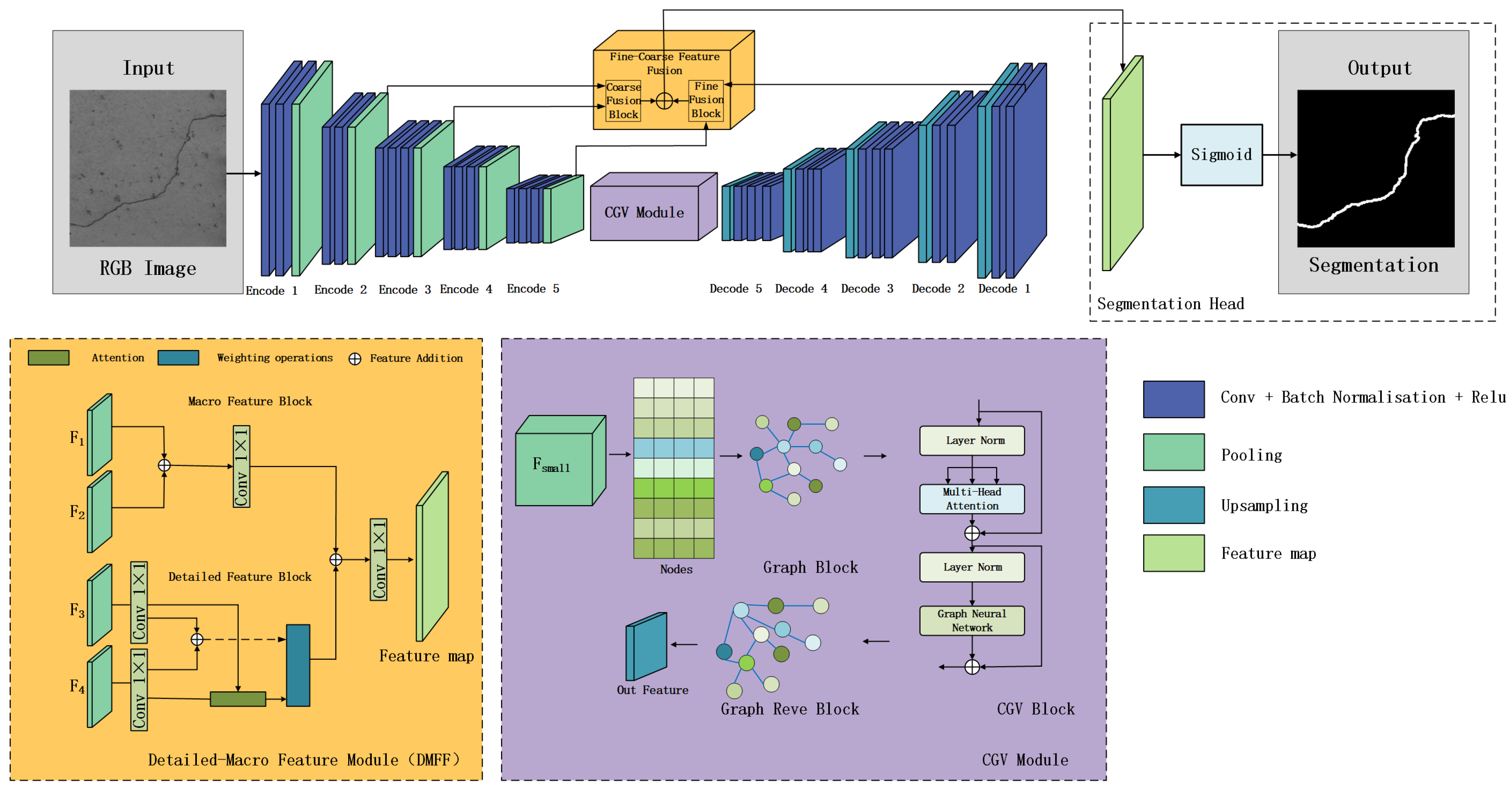
2.1. CGV-Net
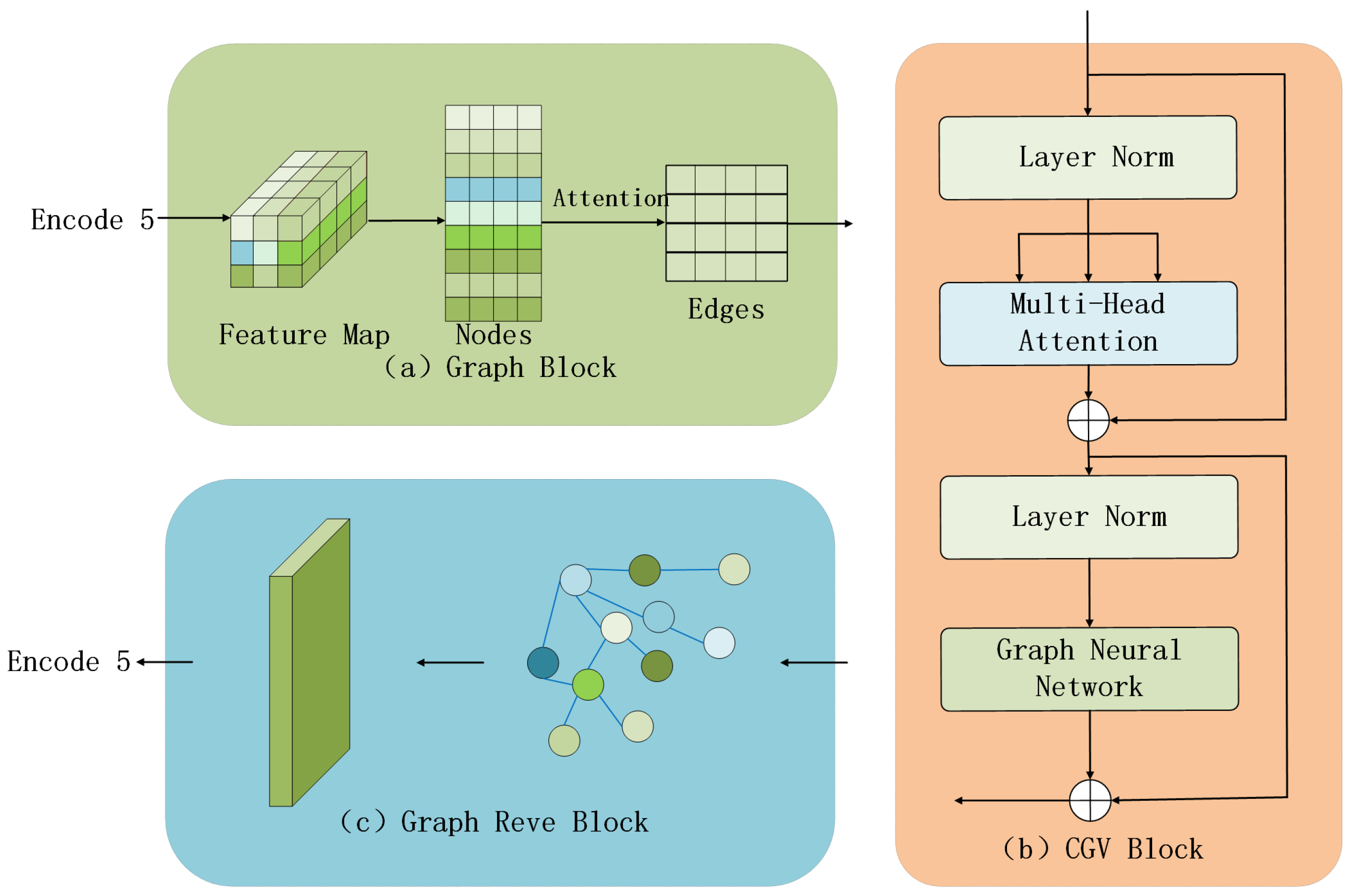
2.2. Neural Network Guided Vision Transformer
2.2.1. The Structural Construction of the Diagram
2.2.2. Graph Reasoning
2.2.3. Multi-Scale Feature Fusion
3. Experimental Setup
3.1. Experimental Environment
3.2. Dataset
3.3. Evaluation Metrics
4. Results and Discussion
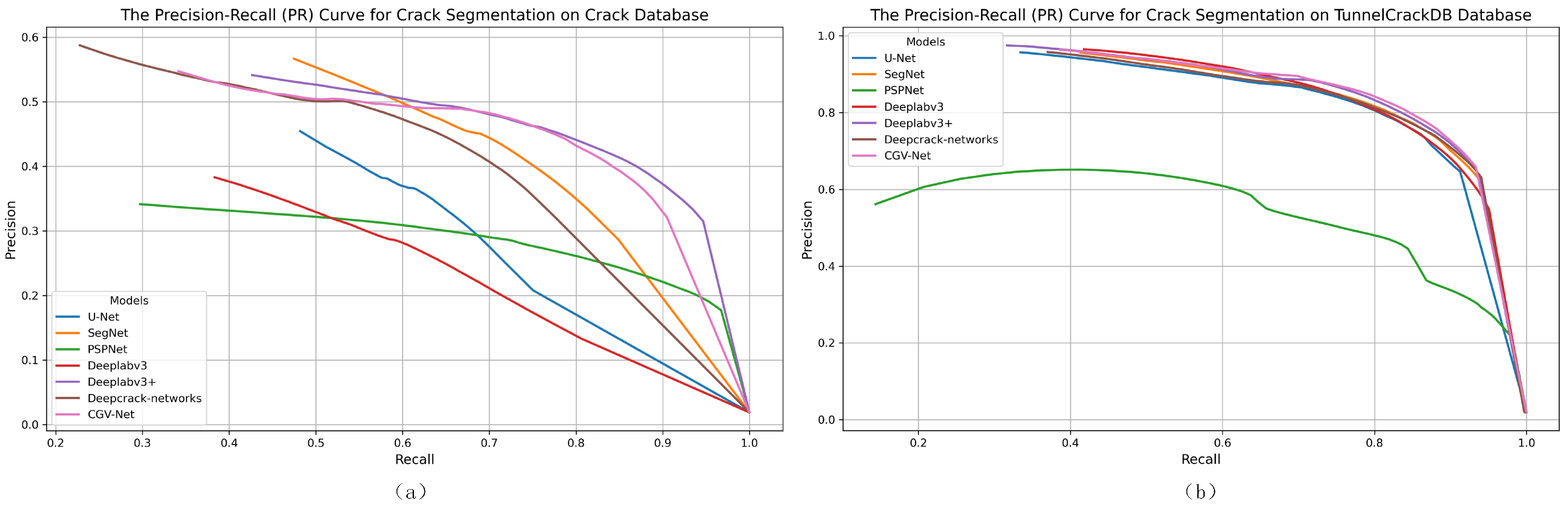
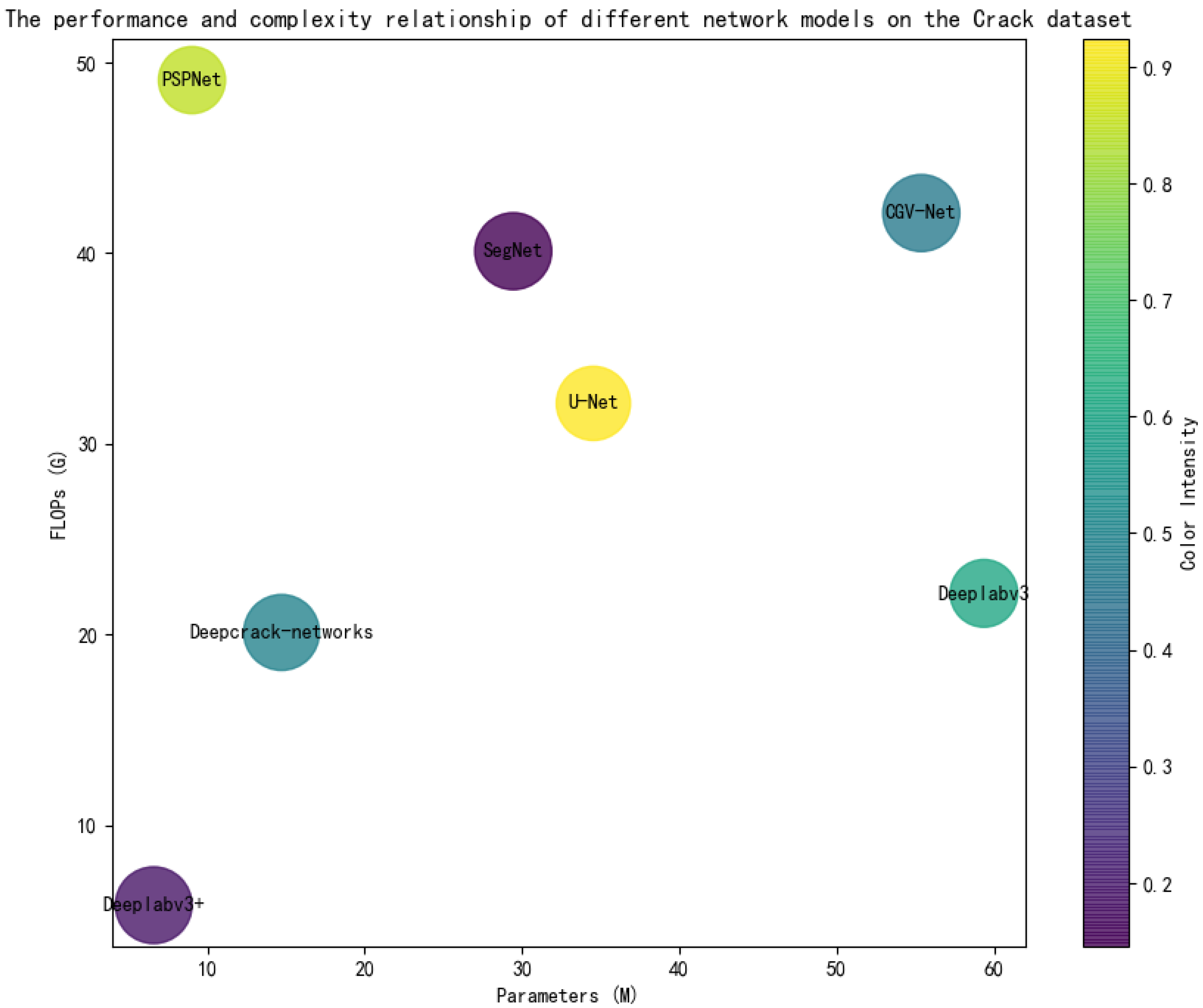
4.1. Comparative Experiments
4.2. Ablation Experiment
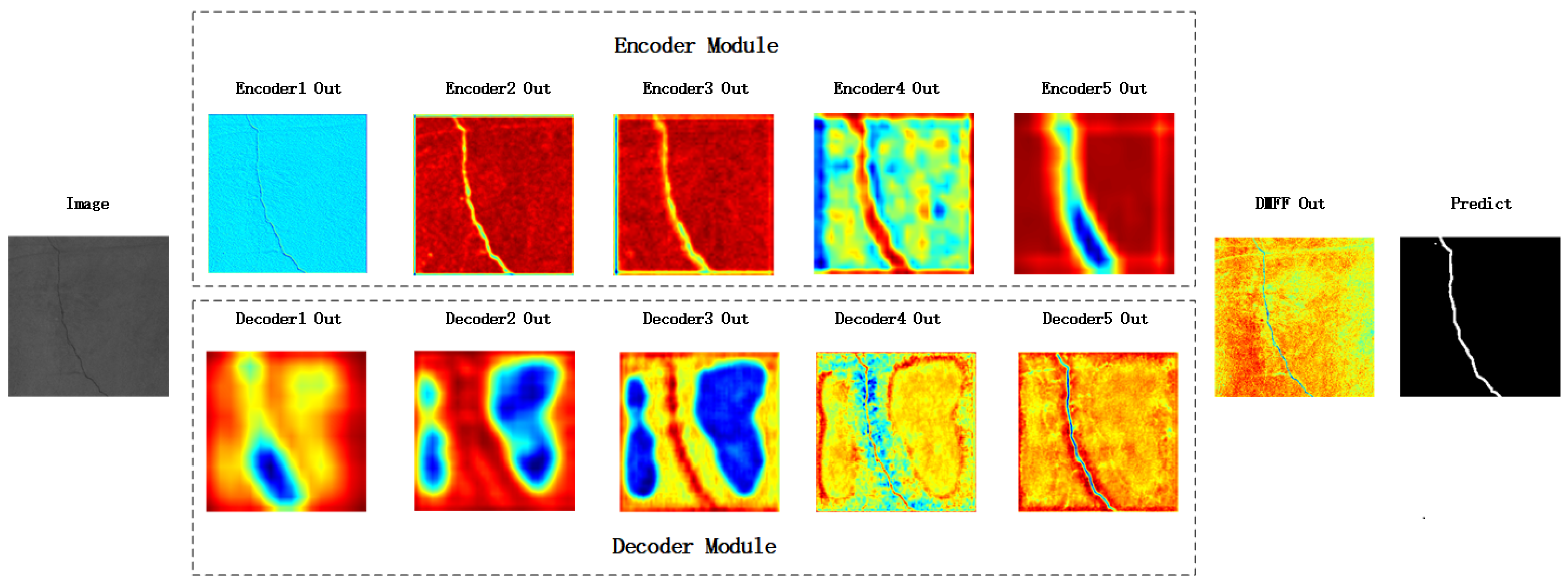
4.3. Experimental Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qiu, J.; Liu, D.; Zhao, K.; Lai, J.; Wang, X.; Wang, Z.; Liu, T. Influence spatial behavior of surface cracks and prospects for prevention methods in shallow loess tunnels in China. Tunn. Undergr. Space Technol. 2024, 143, 105453. [Google Scholar] [CrossRef]
- Xu, H.; Wang, M.; Liu, C.; Li, F.; Xie, C. Automatic detection of tunnel lining crack based on mobile image acquisition system and deep learning ensemble model. Tunn. Undergr. Space Technol. 2024, 154, 106124. [Google Scholar] [CrossRef]
- Chen, L.L.; Li, J.; Wang, Z.F.; Wang, Y.Q.; Li, J.C.; Li, L. Sustainable health state assessment and more productive maintenance of tunnel: A case study. J. Clean. Prod. 2023, 396, 136450. [Google Scholar] [CrossRef]
- Rosso, M.M.; Aloisio, A.; Randazzo, V.; Tanzi, L.; Cirrincione, G.; Marano, G.C. Comparative deep learning studies for indirect tunnel monitoring with and without Fourier pre-processing. Integr. Comput.-Aided Eng. 2023, 31, 213–232. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, X.L.; Feng, S.J.; Zhang, W.; Hu, K.; Da, Y.W. Intelligent segmentation and quantification of tunnel lining cracks via computer vision. Struct. Health Monit. 2024. [Google Scholar] [CrossRef]
- Wang, R.; Chen, R.Q.; Guo, X.X.; Liu, J.X.; Yu, H.Y. Automatic recognition system for concrete cracks with support vector machine based on crack features. Sci. Rep. 2024, 14, 20057. [Google Scholar] [CrossRef]
- Rosso, M.M.; Marasco, G.; Aiello, S.; Aloisio, A.; Chiaia, B.; Marano, G.C. Convolutional networks and transformers for intelligent road tunnel investigations. Comput. Struct. 2023, 275, 106918. [Google Scholar] [CrossRef]
- Jiang, F.; Wang, G.; He, P.; Zheng, C.; Xiao, Z.; Wu, Y. Application of canny operator threshold adaptive segmentation algorithm combined with digital image processing in tunnel face crevice extraction. J. Supercomput. 2022, 78, 11601–11620. [Google Scholar] [CrossRef]
- Long, S.; Yang, T.; Qian, Y.; Wu, Y.; Xu, F.; Tang, Q.; Guo, F. GPR Imagery Based Internal Defect Evaluation System for Railroad Tunnel Lining Using Real-time Instance Segmentation. IEEE Sens. J. 2024, 24, 35997–36010. [Google Scholar] [CrossRef]
- Lei, M.; Liu, L.; Shi, C.; Tan, Y.; Lin, Y.; Wang, W. A novel tunnel-lining crack recognition system based on digital image technology. Tunn. Undergr. Space Technol. 2021, 108, 103724. [Google Scholar] [CrossRef]
- A, R.M.N.; K, S.S. Predicting the settlement of geosynthetic-reinforced soil foundations using evolutionary artificial intelligence technique. Geotext. Geomembr. 2021, 49, 1280–1293. [Google Scholar]
- Zhao, S.; Zhang, D.; Xue, Y.; Zhou, M.; Huang, H. A deep learning-based approach for refined crack evaluation from shield tunnel lining images. Autom. Constr. 2021, 132, 103934. [Google Scholar] [CrossRef]
- Dang, L.M.; Wang, H.; Li, Y.; Park, Y.; Oh, C.; Nguyen, T.N.; Moon, H. Automatic tunnel lining crack evaluation and measurement using deep learning. Tunn. Undergr. Space Technol. 2022, 124, 104472. [Google Scholar] [CrossRef]
- Razveeva, I.; Kozhakin, A.; Beskopylny, A.N.; Stel’makh, S.A.; Shcherban’, E.M.; Artamonov, S.; Pembek, A.; Dingrodiya, H. Analysis of Geometric Characteristics of Cracks and Delamination in Aerated Concrete Products Using Convolutional Neural Networks. Buildings 2023, 13, 3014. [Google Scholar] [CrossRef]
- Wang, H.; Li, Y.; Dang, L.M.; Lee, S.; Moon, H. Pixel-level tunnel crack segmentation using a weakly supervised annotation approach. Comput. Ind. 2021, 133, 103545. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, G.; Zhang, D.; Tan, D.; Huang, H. A hybrid attention deep learning network for refined segmentation of cracks from shield tunnel lining images. J. Rock Mech. Geotech. Eng. 2023, 15, 3105–3117. [Google Scholar] [CrossRef]
- Lin, Q.; Li, W.; Zheng, X.; Fan, H.; Li, Z. DeepCrackAT: An effective crack segmentation framework based on learning multi-scale crack features. Eng. Appl. Artif. Intell. 2023, 126, 106876. [Google Scholar] [CrossRef]
- Chen, S.; Feng, Z.; Xiao, G.; Chen, X.; Gao, C.; Zhao, M.; Yu, H. Pavement Crack Detection Based on the Improved Swin-Unet Model. Buildings 2024, 14, 1442. [Google Scholar] [CrossRef]
- Qin, S.; Qi, T.; Deng, T.; Huang, X. Image segmentation using Vision Transformer for tunnel defect assessment. Comput.-Aided Civ. Infrastruct. Eng. 2024, 39, 3243–3268. [Google Scholar] [CrossRef]
- Zhou, Z.; Yan, L.; Zhang, J.; Zheng, Y.; Gong, C.; Yang, H.; Deng, E. Automatic segmentation of tunnel lining defects based on multiscale attention and context information enhancement. Constr. Build. Mater. 2023, 387, 131621. [Google Scholar] [CrossRef]
- Tao, H.; Liu, B.; Cui, J.; Zhang, H. A convolutional-transformer network for crack segmentation with boundary awareness. In Proceedings of the 2023 IEEE International Conference on Image Processing (ICIP), Kuala Lumpur, Malaysia, 8–11 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 86–90. [Google Scholar]
- Pu, R.; Ren, G.; Li, H.; Jiang, W.; Zhang, J.; Qin, H. Autonomous concrete crack semantic segmentation using deep fully convolutional encoder–decoder network in concrete structures inspection. Buildings 2022, 12, 2019. [Google Scholar] [CrossRef]
- Wang, A.; Togo, R.; Ogawa, T.; Haseyama, M. Defect detection of subway tunnels using advanced U-Net network. Sensors 2022, 22, 2330. [Google Scholar] [CrossRef]
- Kang, D.; Benipal, S.S.; Gopal, D.L.; Cha, Y.J. Hybrid pixel-level concrete crack segmentation and quantification across complex backgrounds using deep learning. Autom. Constr. 2020, 118, 103291. [Google Scholar] [CrossRef]
- Huang, H.; Zhao, S.; Zhang, D.; Chen, J. Deep learning-based instance segmentation of cracks from shield tunnel lining images. Struct. Infrastruct. Eng. 2022, 18, 183–196. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, L.; Zhang, B.; Dai, X.; Ye, J.; Sun, B.; Liu, N.; Wang, Z.; Zhao, Y. Tunnel lining detection and retrofitting. Autom. Constr. 2023, 152, 104881. [Google Scholar] [CrossRef]
- Liu, Z.; Cao, Y.; Wang, Y.; Wang, W. Computer vision-based concrete crack detection using U-net fully convolutional networks. Autom. Constr. 2019, 104, 129–139. [Google Scholar] [CrossRef]
- Chen, T.; Cai, Z.; Zhao, X.; Chen, C.; Liang, X.; Zou, T.; Wang, P. Pavement crack detection and recognition using the architecture of segNet. J. Ind. Inf. Integr. 2020, 18, 100144. [Google Scholar] [CrossRef]
- Zhu, X.; Cheng, Z.; Wang, S.; Chen, X.; Lu, G. Coronary angiography image segmentation based on PSPNet. Comput. Methods Programs Biomed. 2021, 200, 105897. [Google Scholar] [CrossRef]
- Fu, H.; Meng, D.; Li, W.; Wang, Y. Bridge crack semantic segmentation based on improved Deeplabv3+. J. Mar. Sci. Eng. 2021, 9, 671. [Google Scholar] [CrossRef]
- Chen, H.; Lin, H. An effective hybrid atrous convolutional network for pixel-level crack detection. IEEE Trans. Instrum. Meas. 2021, 70, 5009312. [Google Scholar] [CrossRef]





| Total | Longitude | Circular | Oblique | Network | Intersecting | Craze | |
|---|---|---|---|---|---|---|---|
| Train set | 794 | 152 | 138 | 132 | 104 | 122 | 146 |
| Valid set | 89 | 19 | 17 | 13 | 11 | 11 | 18 |
| Test set | 99 | 23 | 20 | 16 | 14 | 12 | 14 |
| Total | 982 | 194 | 175 | 161 | 129 | 145 | 178 |
| Precision | Recall | F1 | mIoU | |
|---|---|---|---|---|
| U-Net [27] | 43.55% | 55.78% | 48.92% | 45.32% |
| SegNet [28] | 47.06% | 66.35% | 55.05% | 52.74% |
| PSPNet [29] | 35.64% | 67.39% | 46.62% | 45.50% |
| Deeplabv3 [15] | 36.36% | 54.52% | 43.63% | 42.07% |
| Deeplabv3+ [30] | 46.79% | 71.94% | 56.70% | 55.43% |
| Deepcrack-net [31] | 45.66% | 63.19% | 53.02% | 51.26% |
| CGV-Net | 47.11% | 73.27% | 57.32% | 56.14% |
| Precision | Recall | F1 | mIoU | |
|---|---|---|---|---|
| U-Net [27] | 63.56% | 65.69% | 64.61% | 63.41% |
| SegNet [28] | 79.43% | 82.89% | 81.12% | 79.96% |
| PSPNet [29] | 51.51% | 71.59% | 59.91% | 58.32% |
| Deeplabv3 [15] | 79.45% | 81.81% | 80.61% | 7962% |
| Deeplabv3+ [30] | 80.84% | 83.03% | 81.92% | 80.83% |
| Deepcrack-net [31] | 78.93% | 83.00% | 80.92% | 79.51% |
| CGV-Net | 81.15% | 83.54% | 82.33% | 81.24% |
| Precision | Recall | F1 | mIoU | |
|---|---|---|---|---|
| Baseline | 79.43% | 82.89% | 82.07% | 80.36% |
| Baseline+CGV | 80.11% | 82.94% | 81.51% | 80.57% |
| Baseline+DMFF | 80.81% | 81.79% | 81.30% | 80.48% |
| Baseline+CGV+DMFF (CGV-Net) | 81.15% | 83.54% | 82.33% | 81.24% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Ren, T.; Lan, Z.; Yang, Y.; Liu, R.; Xu, Y. CGV-Net: Tunnel Lining Crack Segmentation Method Based on Graph Convolution Guided Transformer. Buildings 2025, 15, 197. https://doi.org/10.3390/buildings15020197
Liu K, Ren T, Lan Z, Yang Y, Liu R, Xu Y. CGV-Net: Tunnel Lining Crack Segmentation Method Based on Graph Convolution Guided Transformer. Buildings. 2025; 15(2):197. https://doi.org/10.3390/buildings15020197
Chicago/Turabian StyleLiu, Kai, Tao Ren, Zhangli Lan, Yang Yang, Rong Liu, and Yuantong Xu. 2025. "CGV-Net: Tunnel Lining Crack Segmentation Method Based on Graph Convolution Guided Transformer" Buildings 15, no. 2: 197. https://doi.org/10.3390/buildings15020197
APA StyleLiu, K., Ren, T., Lan, Z., Yang, Y., Liu, R., & Xu, Y. (2025). CGV-Net: Tunnel Lining Crack Segmentation Method Based on Graph Convolution Guided Transformer. Buildings, 15(2), 197. https://doi.org/10.3390/buildings15020197





