Optimisation and Mechanical Behaviour Analysis of Splice Joints in Prefabricated H-Shaped Steel Beams
Abstract
1. Introduction
2. Experimental Investigation
2.1. Experimental Design
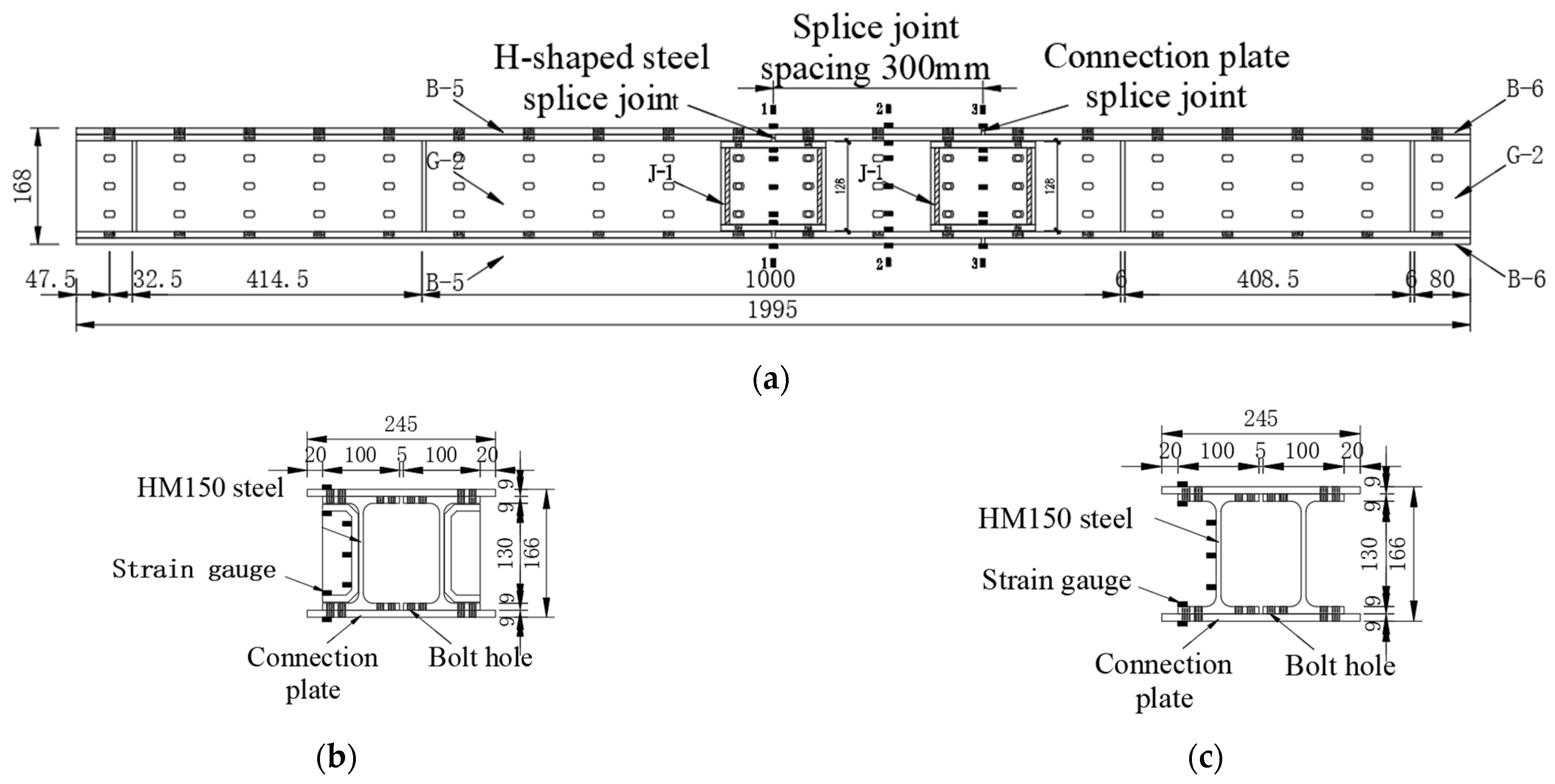
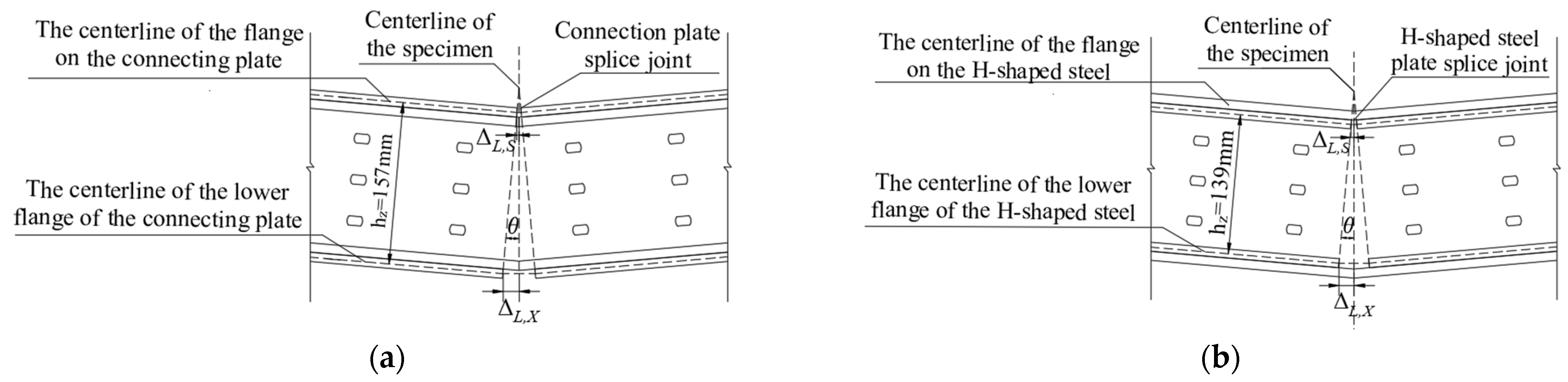
2.1.1. Splice Joint Overview and Specimen Design
2.1.2. Material Properties of Specimens
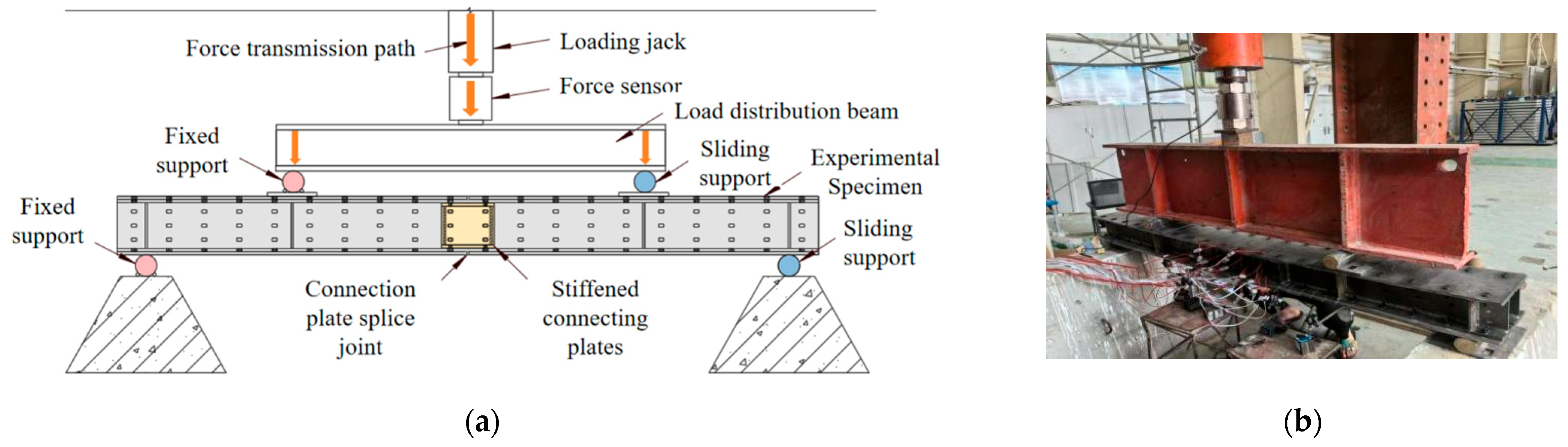
2.1.3. Loading Equipment and Measurement System
2.1.4. Experimental Observations
2.1.5. Failure Modes Analysis
2.2. Experimental Results Analysis
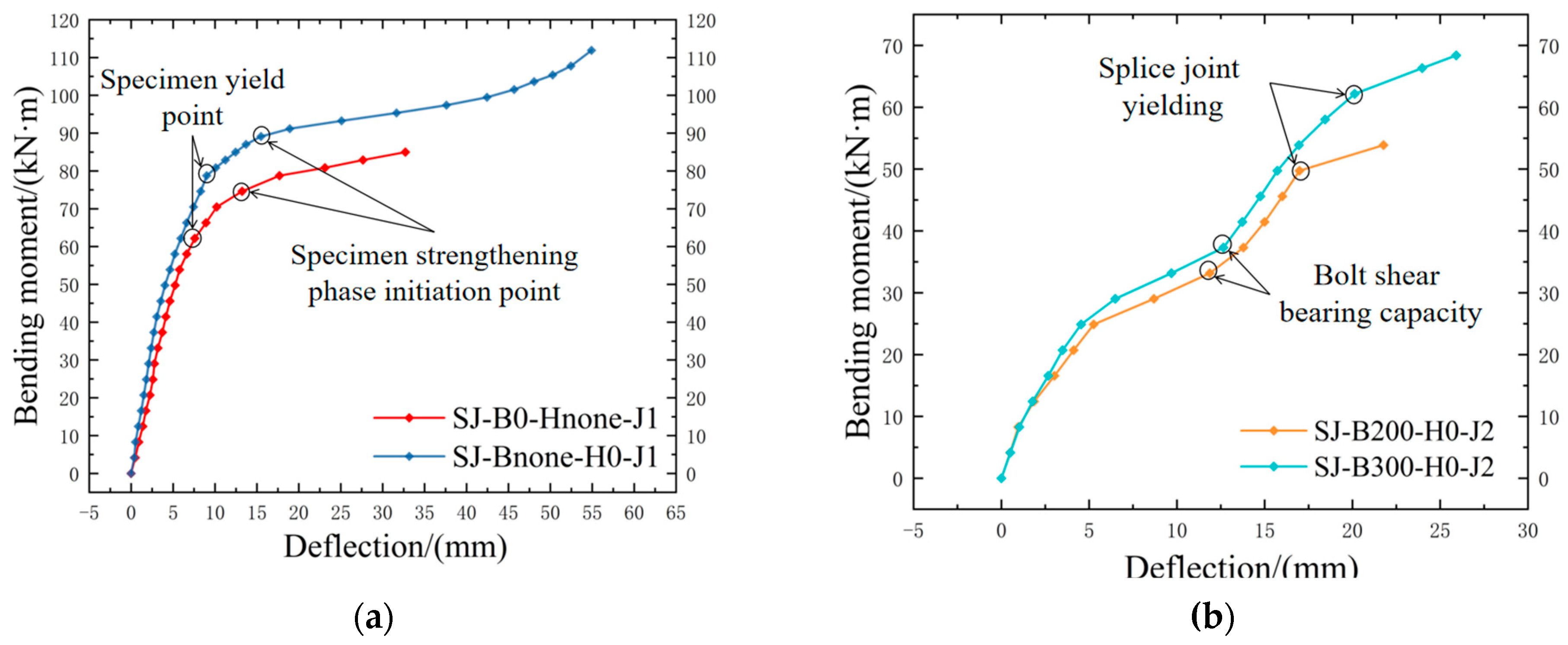
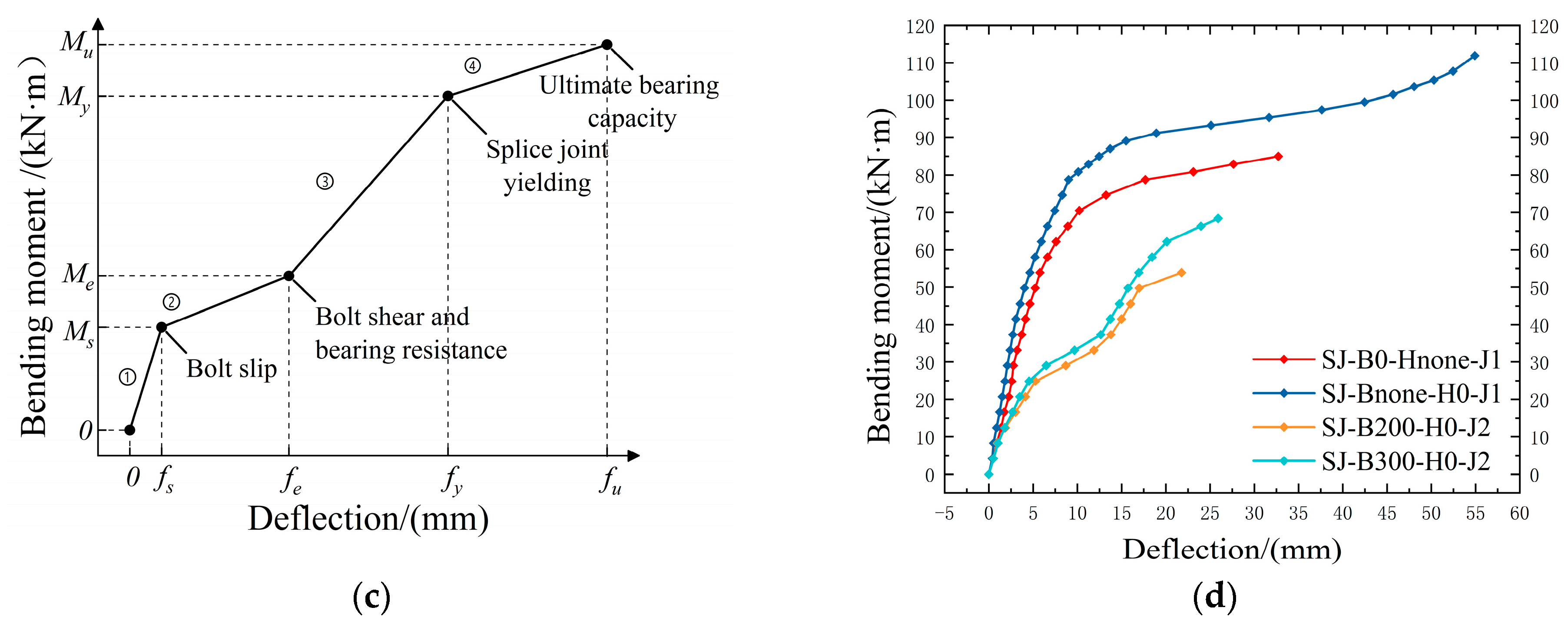
2.2.1. Load Versus Mid-Span Deflection Curves
2.2.2. Flexural Bearing Capacity Analysis
- (1)
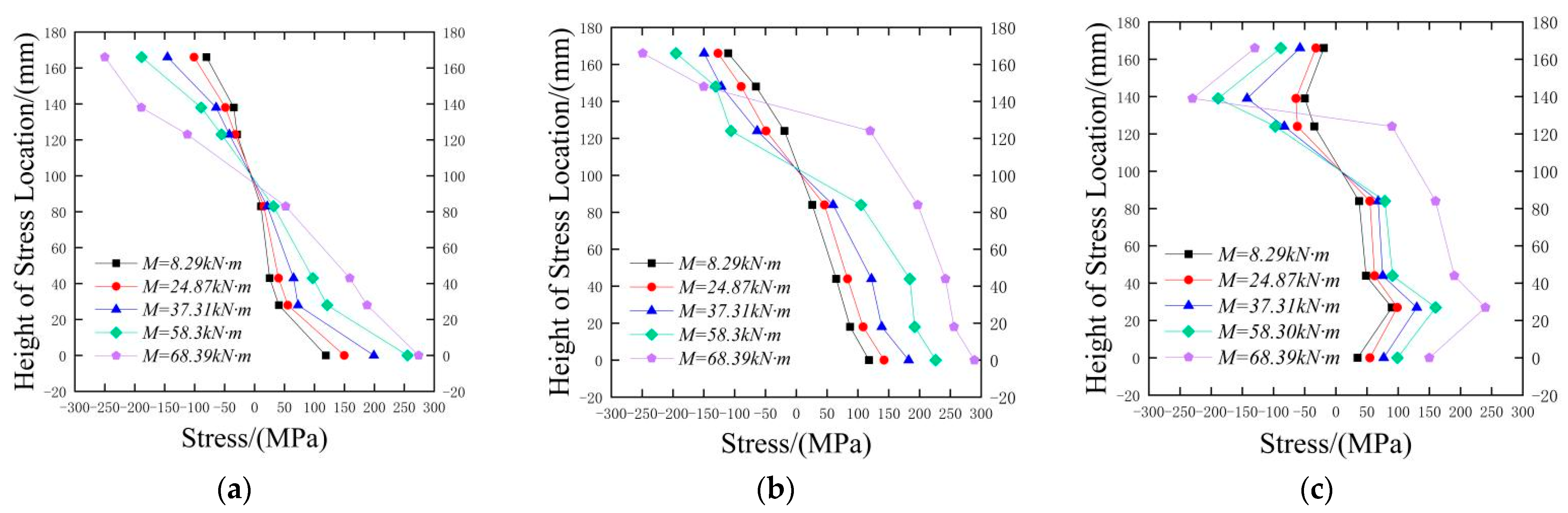
- In single-splice-joint specimens, both the connecting plate splice joint and the H-shaped steel splice joint decrease bearing capacity relative to joint-free specimens. Nonetheless, specimens with joints at the H-shaped steel section displayed superior performance.
- (2)
- Double-splice-joint specimens exhibit more intricate failure mechanisms. Reducing the proximity between the connecting plate and H-shaped steel splice joints significantly compromises the flexural bearing capacity. This phenomenon arises from increased stress concentration at adjacent joints, resulting in elevated shear forces and bearing pressures on the bolts.
- (3)
- Enhancing inter-joint spacing significantly improves the failure bending moment, demonstrating that optimal splice joint separation effectively boosts flexural performance.
2.2.3. Stress Analysis
3. Finite Element Model Validation and Parametric Analysis
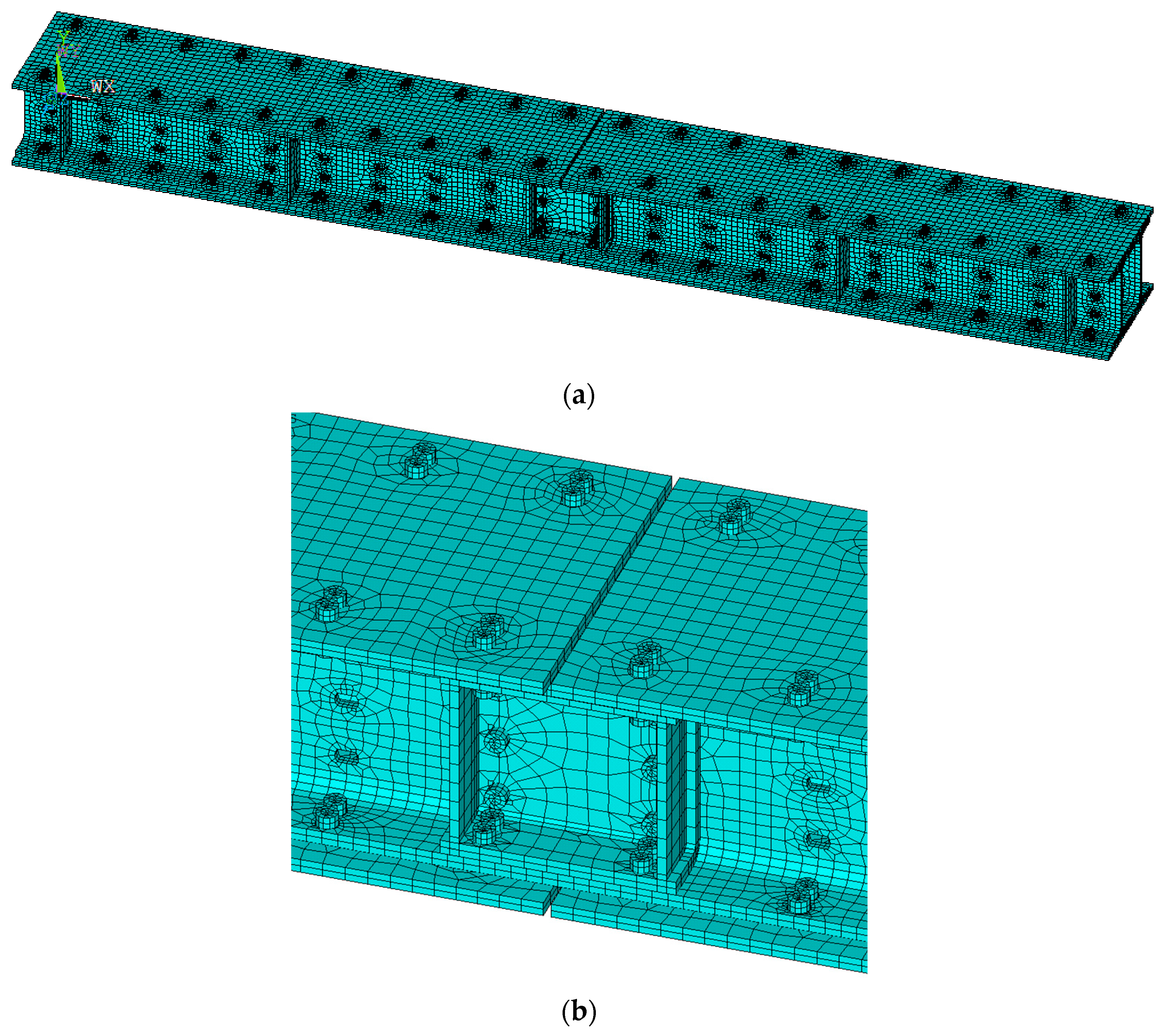
3.1. Finite Element Model Development
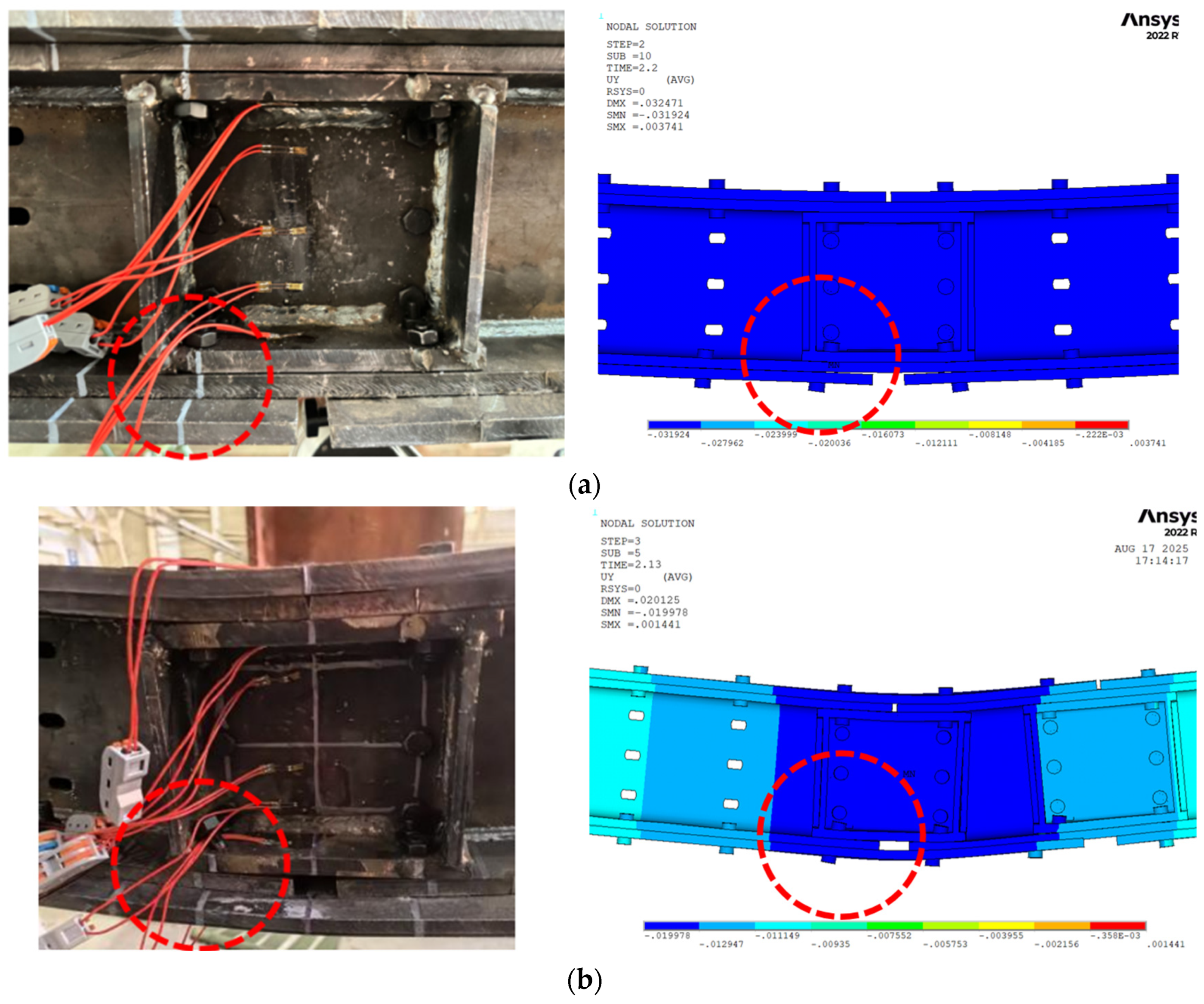
3.2. Quantitative Comparison of Numerical Simulation and Experimental Results
4. Deflection Calculation at Splice Joints
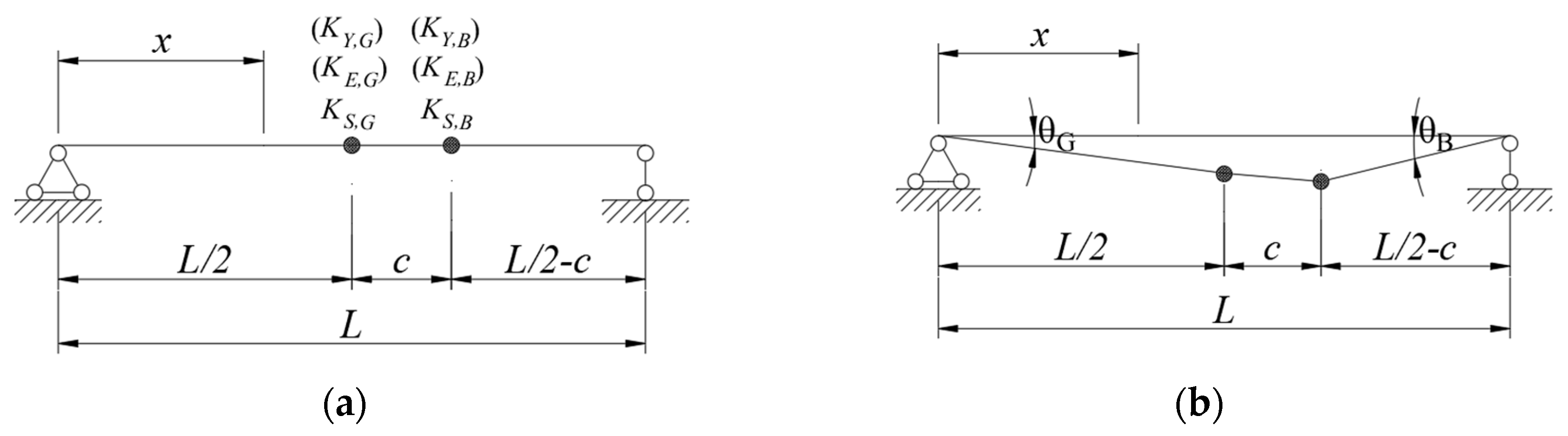
4.1. Single Splice Joint Deflection
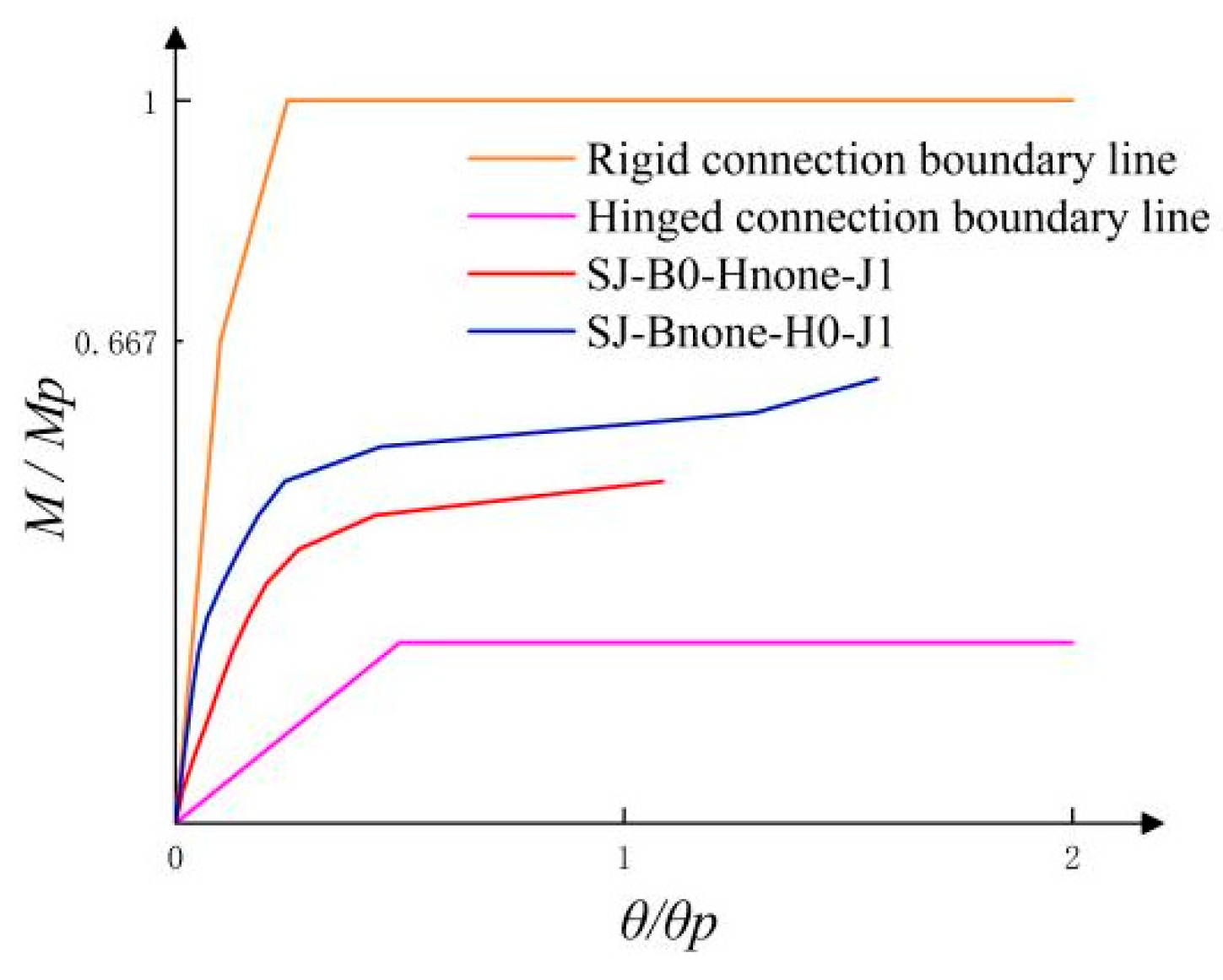
4.1.1. Stiffness Characterisation and Classification
4.1.2. Deflection Calculation Formulas
4.2. Deflection Calculation in Double-Splice-Joint Specimens
5. Conclusions
- (1)
- Mechanical testing of prefabricated H-shaped steel beams was performed alongside finite element modelling to validate the results. The close correspondence between experimental outcomes and simulation data across all specimens confirms the reliability of the testing methodology. This demonstrates the capability of the tests to accurately characterise the mechanical behaviour of prefabricated H-shaped steel beams under actual loading conditions, providing a robust analytical tool for subsequent design optimisation.
- (2)
- Specimens featuring double splice joints demonstrate a substantial reduction in bending load-bearing capacity and stiffness compared to those with single splice joints. Using the single H-shaped steel assembly as a reference, the ultimate bending load-bearing capacity decreases by approximately 24.07% when employing single connection plates. When both splice joints are present simultaneously, the specimen’s ultimate bending load-bearing capacity declines by 39.89% to 51.88%. Notably, specimens with two splice joints spaced 200 mm apart (SJ-B200-H0-J2) exhibit the lowest bending load-bearing capacity. Consequently, engineering practices should avoid positioning two splice joints in adjacent or overlapping locations. As the distance between the two splice joints increases, the specimen’s bending load-bearing capacity markedly improves.
- (3)
- During testing, the double-shear joint specimen undergoes four deformation phases under load: 1. Bolt friction compression stage; 2. Bolt slip stage; 3. Component coordinated stress stage; and 4. Yield stage. Under pure bending loads, components at the joint assembly site fail first, preventing the observation of a significant plastic deformation phase in the specimen.
- (4)
- Both connection plate splice joints and HM150 steel section splice joints are classified as semi-rigid joints. Based on experimental data and numerical simulation results, corner calculation formulas for single splice joints under pure bending loads that account for angular deformation effects were developed, along with deflection calculation formulas. Additionally, rotational spring nodes were introduced to simulate the converted rotational stiffness of splice joints. Furthermore, a deflection calculation formula for double splice joint specimens during elastic deformation stages was proposed. All calculated values aligned with the experimental results.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HSFG | High-Strength Friction Grip |
| FEA | Finite Element Analysis |
| EC3 | European Council on Computing in Construction |
References
- Khan, K.; Chen, Z.; Liu, J.; Javed, K. State-of-the-Art on Technological Developments and Adaptability of Prefabricated Industrial Steel Buildings. Appl. Sci. 2023, 13, 685. [Google Scholar] [CrossRef]
- Huang, Z.; Zhou, H.; Tang, H.; Zhang, D.; Zhao, Y.; Yu, J.; Luo, M.; Wang, Y.; Lin, B. Process-based evaluation of carbon emissions from the on-site construction of prefabricated steel structures: A case study of a multistory data center in China. J. Clean. Prod. 2024, 439, 140579. [Google Scholar] [CrossRef]
- Liu, J.; Liu, H.; Liu, Y. A Sustainability-Oriented Framework for Life Cycle Environmental Cost Accounting and Carbon Financial Optimization in Prefabricated Steel Structures. Sustainability 2025, 17, 4296. [Google Scholar] [CrossRef]
- Habib, A.; Al Houri, A.; Alibrahim, B.; Habib, M. Behavior and sustainability benefits of modular steel buildings. Int. J. Sustain. Eng. 2025, 18, 2459715. [Google Scholar] [CrossRef]
- Zhang, X.; Nie, Y.; Qian, K.; Xie, X.; Zhao, M.; Zhao, Z.; Zheng, X.Y. Experimental Investigation of the Seismic Behavior of a Multi-Story Steel Modular Building Using Shaking Table Tests. Buildings 2025, 15, 2661. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, W.; Du, Y.; Zhang, W.; Zhou, H.; Wang, R.; Li, W.; Zhang, P.; Huang, X.; Cao, Z.; et al. Application of BIM Collaborative Design Technology in Intelligent Buildings for Prefabricated Steel Structures. Procedia Comput. Sci. 2024, 247, 310–319. [Google Scholar] [CrossRef]
- Lu, Y.; Liang, S.; Zhu, X.; Wu, D.; Yang, J.; Wang, W.; Sun, B. Eccentric compression behaviour of precast H-shaped steel support in foundation pit engineering. J. Constr. Steel Res. 2025, 234, 109740. [Google Scholar] [CrossRef]
- Lu, Y.; Liang, S.; Zhu, X.; Sun, B.; Wang, W.; Chen, Y.; Ji, X. Axial compressive stability of precast H-shaped steel support in foundation pit engineering. J. Constr. Steel Res. 2025, 230, 109540. [Google Scholar] [CrossRef]
- SEI/ASCE 8-02; Specification for the Design of Cold-Formed Stainless Steel Structural Members. American Society of Civil Engineers (ASCE): Reston, VA, USA, 2002. Available online: https://ascelibrary.org/doi/pdf/10.1061/9780784405567.fm (accessed on 12 June 2024).
- Wu, X.; Wang, Y.; Ji, S.; Liu, M.; Wang, D. Numerical study on the mechanical behaviors of a new type of steel shear-connection horizontal joint in prefabricated shear wall structure. Buildings 2023, 13, 3000. [Google Scholar] [CrossRef]
- Chu, Y.; Zhang, H.; Gong, Y. Experimental study on shear performance of the new steel-bolt vertical joint. Structures 2024, 64, 106554. [Google Scholar] [CrossRef]
- Xie, J.; Zhang, W. Numerical analysis on steel bracing members with bolted gusset plate connections. J. Constr. Steel Res. 2024, 222, 108960. [Google Scholar] [CrossRef]
- Li, J.; Mou, B.; Wang, Z. Cyclic behavior of column-to-column connections in novel prefabricated H-shaped steel beam to CFST column joint. J. Constr. Steel Res. 2023, 200, 107657. [Google Scholar] [CrossRef]
- Zhang, W.; Xie, J.; Liu, Y.; Ding, Y. Experimental investigation on steel bracing members with bolted gusset plate connections. J. Build. Eng. 2023, 76, 107133. [Google Scholar] [CrossRef]
- Yin, L.; Niu, Y.; Quan, G.; Gao, H.; Ye, J. A numerical investigation of new types of bolted joints for cold-formed steel moment-resisting frame buildings. J. Build. Eng. 2023, 65, 105738. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Z.; An, Q. Analysis of Seismic Performance and Applicable Height of a Cooperative Modular Steel Building. Buildings 2024, 14, 678. [Google Scholar] [CrossRef]
- Bao, Y.; Yang, F.; Li, X.; Ma, T.; Ma, J. Numerical study on seismic performance of concrete-filled steel tube column-steel beam joints with replaceable T-type connectors. Structures 2025, 79, 109606. [Google Scholar] [CrossRef]
- Liu, X.; Meng, Q.; Xu, L.; Liu, Y.; Tian, X. Modular Steel Buildings Based on Self-Locking-Unlockable Connections Seismic Performance Analysis. Buildings 2025, 15, 678. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, Y.; Yan, P.; Zhang, L.; Liu, Y.; Chen, Y.; Fu, B.; Zhou, Y. Numerical investigation on seismic performance of drilled flange connection for steel frames. Soil Dyn. Earthq. Eng. 2025, 190, 109122. [Google Scholar] [CrossRef]
- Feng, R.; Zhan, H.; Meng, S.; Zhu, J. Experiments on H-shaped high-strength steel beams with perforated web. Eng. Struct. 2018, 177, 374–394. [Google Scholar] [CrossRef]
- Feng, R.; Liu, J.; Chen, Z.; Roy, K.; Chen, B.; Lim, J.B. Numerical investigation and design rules for flexural capacities of H-section high-strength steel beams with and without web openings. Eng. Struct. 2020, 225, 111278. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, S.; Feng, S.; Fan, D.; Zhang, F.; Cao, H. Study on the Bending Performance of Prefabricated H-Shaped Steel Beams with Different Bolt Hole Types. Buildings 2024, 14, 2988. [Google Scholar] [CrossRef]
- Luo, L.; Fu, H.; Zhang, Y.; Xie, X. Experimental study on the overall stability of corroded H-Shaped steel beams. Buildings 2022, 12, 1923. [Google Scholar] [CrossRef]
- Yu, Z.W.; Li, H.; Ho, J.C.M.; Ma, T.Y.; Bao, W.; Zhang, J.Z. Axial compressive behavior of corroded H-shaped steel columns. J. Constr. Steel Res. 2024, 218, 108726. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, J.; Wang, B.; Gao, Y. Post-buckling shear capacity of the corroded end panels of H-shaped steel beams. Thin-Walled Struct. 2023, 184, 110499. [Google Scholar] [CrossRef]
- Yuan, J.; Wang, S.; Fan, Y.; Wu, G. Data analysis of mechanical properties of steel specimens under four-point bending load. In Proceedings of the 2024 IEEE 4th International Conference on Information Technology, Big Data and Artificial Intelligence (ICIBA), Chongqing, China, 6–8 December 2024; IEEE: Piscataway, NJ, USA, 2024; Volume 4, pp. 1481–1486. [Google Scholar]
- Zhang, B.; Zhou, C.; Zhang, S.; Peng, Y.; Li, Y. Effects of FRP fiber orientations on four-point bending behaviour of FRP-concrete-steel tubular beams: Experimental study and modeling. Eng. Struct. 2025, 322, 119191. [Google Scholar] [CrossRef]
- GB/T 228. 1-2010; Metallic Materials: Tensile Testing: Part 1: Method of Test at Room Temperature. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2012.
- GB/T 1041-2008; Metallic Materials—Bend Test Method. China Standards Press: Beijing, China, 2008.
- GB 50017-2017; Code for Design of Steel Structures. China Architecture & Building Press: Beijing, China, 2018; pp. 22–27.
- GB/T 1228-2006; National Technical Committee of Standardization for Fasteners, High-Strength Large Hexagon Head Bolts for Steel Structures. Standards Press of China: Beijing, China, 2006; pp. 2–4.
- JGJ82-2011; Technical Specification for High-Strength Bolted Connections in Steel Structures. China Architecture & Building Press: Beijing, China, 2021; pp. 8–9.
- BS EN 1993-1-8; 2005 Eurocode 3: Design of Steel Structures-Part 1.8: Design of Joints. European Committee for Standardization: London, UK, 2005.
- Shi, G.; Chen, X.; Wang, D.Y. Experimental study of a ultra-large capacityend-plate joints. J. Constr. Steel Res. 2017, 128, 354–361. [Google Scholar] [CrossRef]
- Guo, B.; Sun, N.; Yang, D. Research progress on calculation methods of elastic critical moment for simply supported beams. J. Shandong Jianzhu Univ. 2017, 32, 69–77. [Google Scholar]
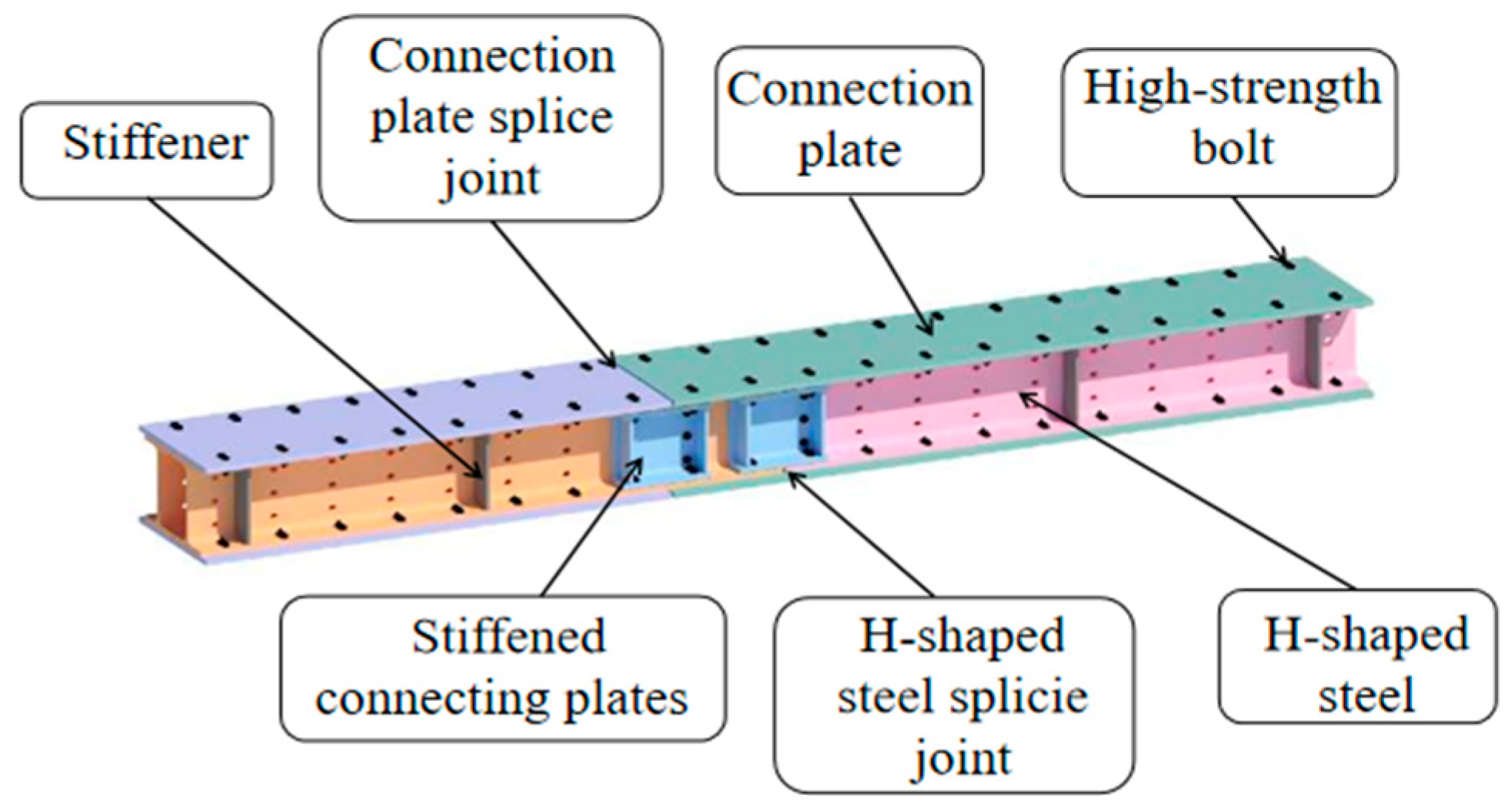
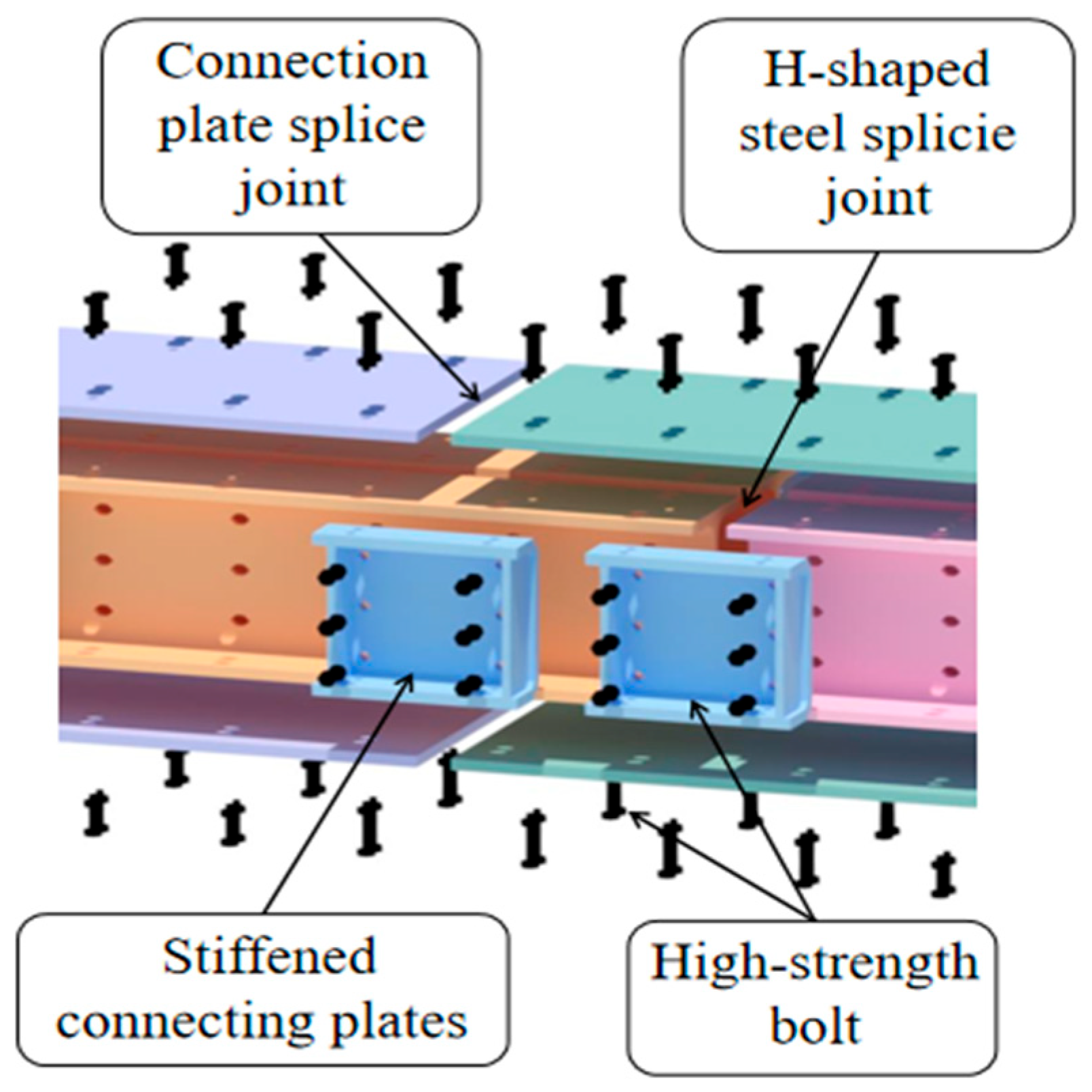
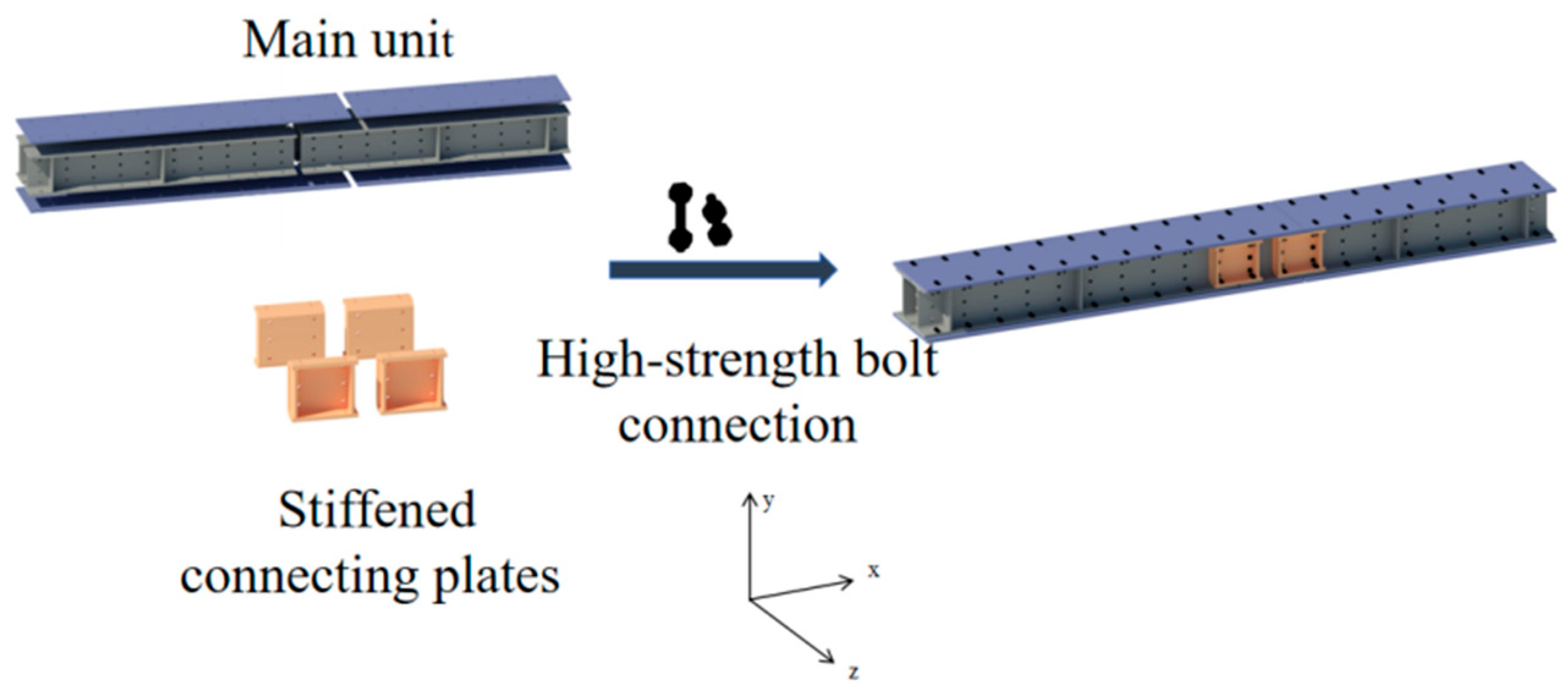
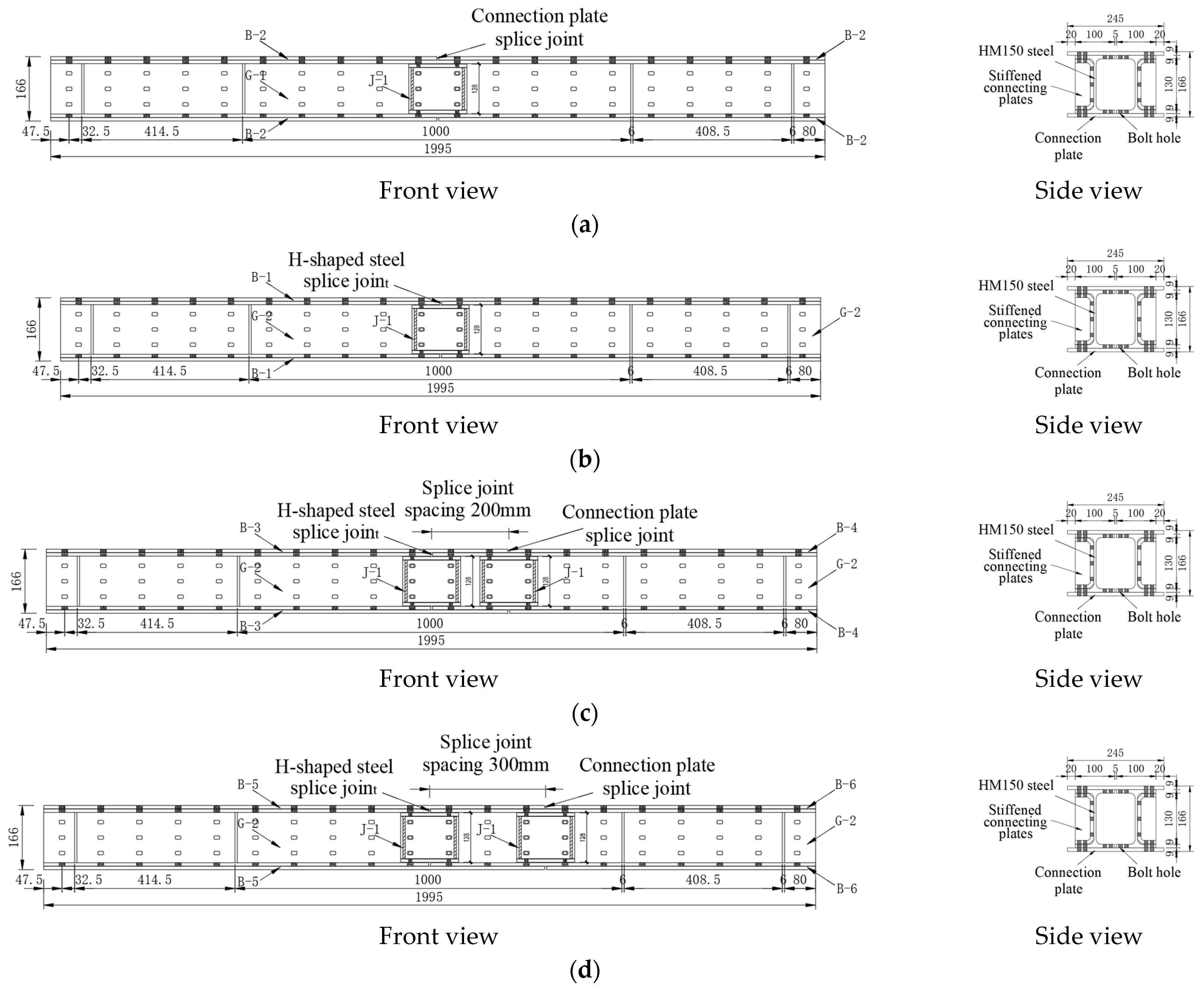





| Name of Specimen | Component Composition | |||
|---|---|---|---|---|
| Connecting Plate/mm | HM150 Steel/mm | |||
| SJ-B0-Hnone-J1 | B-2 × 4 | 995 mm | G-1 × 2 | 1995 mm |
| SJ-Bnone-H0-J1 | B-1 × 2 | 1995 mm | G-2 × 4 | 995 mm |
| SJ-B200-H0-J2 | B-3 × 2 | 1195 mm | G-2 × 4 | 995 mm |
| B-4 × 2 | 795 mm | |||
| SJ-B300-H0-J2 | B-5 × 2 | 1295 mm | G-2 × 4 | 995 mm |
| B-6 × 2 | 695 mm | |||
| Name of Specimen | Connecting Plate | HM150 Steel | Fasten the Connecting Plate | ||
|---|---|---|---|---|---|
| Splice Joint Settings | Distance Between Joint and Mid-Span of Specimen in mm | Splice Joint Settings | Distance Between Joint and Mid-Span of Specimen in mm | ||
| SJ-B0-Hnone-J1 | Set | 0 | Not Set | -- | Set |
| SJ-Bnone-H0-J1 | Not Set | -- | Set | 0 | Set |
| SJ-B200-H0-J2 | Set | 200 | Set | 0 | Set × 2 |
| SJ-B300-H0-J2 | Set | 300 | Set | 0 | Set × 2 |
| Sample Number | Sample Location | Thickness/mm | Length (l0)/mm | Yield Strength/MPa | Ultimate Strength/MPa | Modulus of Elasticity/MPa | Elongation /% |
|---|---|---|---|---|---|---|---|
| H | H-shaped steel | 9 | 100 | 260 | 390 | 255 | 20.2 |
| B | Connection plate | 9 | 100 | 255 | 390 | 248 | 23.7 |
| L | Stiffener | 6 | 80 | 245 | 430 | 256 | 19.6 |
| Name of Specimen | Maximum Bearing Capacity Bending Moment Mp /kN·m | SJ-Bnone-H0-J1 Ultimate Bearing Capacity Reduction Coefficient/% | Maximum Bearing Capacity Bending Moment Maximum y Displacement Value/mm | Destructive Patterns |
|---|---|---|---|---|
| SJ-B0-Hnone-J1 | 84.97 | 24.07 | 32.72 | High strength bolt fracture |
| SJ-Bnone-H0-J1 | 111.92 | 0 | 54.92 | High strength bolt fracture |
| SJ-B200-H0-J2 | 53.86 | 51.88 | 21.78 | High strength bolt breaks at the joint of the connecting plate |
| SJ-B300-H0-J2 | 68.39 | 38.89 | 25.97 | High strength bolt breaks at the joint of the connecting plate |
| Name of Specimen | Maximum Bearing Capacity Bending Moment Mp /kN·m | SJ-Bnone-H0-J1 Ultimate Bearing Capacity Reduction Coefficient /% | Maximum Bearing Capacity Bending Moment Maximum y Displacement Value /mm | Destructive Patterns |
|---|---|---|---|---|
| SJ-B0-Hnone-J1 | 82.90 | 23.08 | 31.92 | Consistent with the experiment |
| SJ-Bnone-H0-J1 | 107.77 | 0 | 53.16 | Consistent with the experiment |
| SJ-B200-H0-J2 | 53.86 | 50.02 | 19.98 | Consistent with the experiment |
| SJ-B300-H0-J2 | 66.32 | 38.46 | 24.82 | Consistent with the experiment |
| Name of Specimen | End of Test | ANSYS Bear Fruit | Ultimate Bending Moment Reduction Coefficient | Maximum Displacement Reduction Coefficient | ||
|---|---|---|---|---|---|---|
| Experimentalmaximum Bearing Capacity Bending Moment Mp /kN·m | The Maximum y Displacement Value of the Bearing Capacity Limit Bending Moment y/mm | ANSYS Maximum Bearing Capacity Bending Moment Ma/kN·m | The Maximum y Displacement Value of the Bearing Capacity Limit Bending Moment y’/mm | /% | /% | |
| SJ-B0-Hnone-J1 | 84.97 | 32.73 | 82.90 | 31.92 | 2.43 | 2.47 |
| SJ-Bnone-H0-J1 | 111.92 | 54.92 | 107.77 | 53.16 | 3.71 | 3.21 |
| SJ-B200-H0-J2 | 53.86 | 21.78 | 53.86 | 19.98 | 0 | 8.26 |
| SJ-B300-H0-J2 | 68.39 | 25.97 | 66.32 | 24.82 | 3.03 | 4.43 |
| Average value | 2.293 | 4.593 | ||||
| Name of Specimen | The Plastic Ultimate Bending Moment Borne by the Node Mp /kN·m | The Angle of the Node at the Plastic Bending Moment Mp of the Node θp /rad | Elastic Bending Moment of the Node Mk /kN·m | The Node Rotation Angle at the Elastic Bending Moment Mk of the Node θk /rad | Initial Rotational Stiffness Sj,ini /kN·m·rad−1 |
|---|---|---|---|---|---|
| SJ-B0-Hnone-J1 | 82.90 | 0.04843 | 55.27 | 0.008394 | 6585 |
| SJ-Bnone-H0-J1 | 107.77 | 0.06979 | 71.84 | 0.008026 | 8951 |
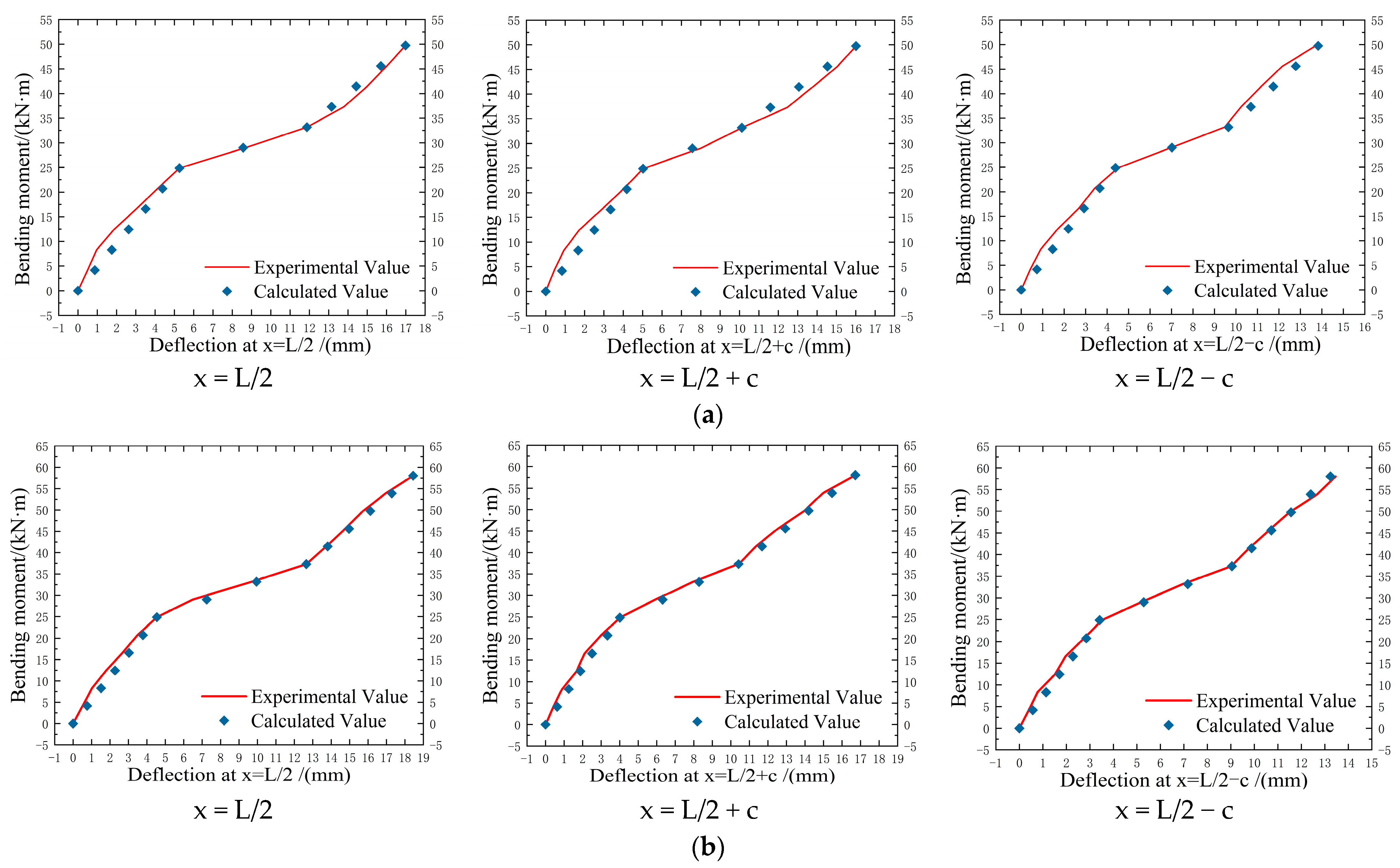
| Name of Specimen | The Elastic-Stage Bending Moment My /kN·m | ω1max /mm | ω2max /mm | ωymax /mm | End of Test/mm | The Difference Between the Formula and the Model /% |
|---|---|---|---|---|---|---|
| SJ-B0-Hnone-J1 | 62.175 | 3.1 | 4.32 | 7.42 | 7.59 | 2.3 |
| SJ-Bnone-H0-J1 | 78.755 | 3.92 | 4.4 | 8.32 | 9.01 | 7.65 |
| Name of Specimen | SJ-B200-H0-J2 | SJ-B300-H0-J2 |
|---|---|---|
| KS,G/kN·m·rad−1 | 2824 | 3437 |
| KE,G/kN·m·rad−1 | 611 | 759 |
| KY,G/kN·m·rad−1 | 1768 | 1989 |
| KS,B/kN·m·rad−1 | 2763 | 3362 |
| KE,B/kN·m·rad−1 | 763 | 858 |
| KY,B/kN·m·rad−1 | 1399 | 1545 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Lv, J.; Fan, D.; Feng, S.; Yu, S. Optimisation and Mechanical Behaviour Analysis of Splice Joints in Prefabricated H-Shaped Steel Beams. Buildings 2025, 15, 3610. https://doi.org/10.3390/buildings15193610
Zhang X, Lv J, Fan D, Feng S, Yu S. Optimisation and Mechanical Behaviour Analysis of Splice Joints in Prefabricated H-Shaped Steel Beams. Buildings. 2025; 15(19):3610. https://doi.org/10.3390/buildings15193610
Chicago/Turabian StyleZhang, Xin, Jiahan Lv, Dawei Fan, Shuaike Feng, and Shenlu Yu. 2025. "Optimisation and Mechanical Behaviour Analysis of Splice Joints in Prefabricated H-Shaped Steel Beams" Buildings 15, no. 19: 3610. https://doi.org/10.3390/buildings15193610
APA StyleZhang, X., Lv, J., Fan, D., Feng, S., & Yu, S. (2025). Optimisation and Mechanical Behaviour Analysis of Splice Joints in Prefabricated H-Shaped Steel Beams. Buildings, 15(19), 3610. https://doi.org/10.3390/buildings15193610





