A Data-Driven Battery Energy Storage Regulation Approach Integrating Machine Learning Forecasting Models for Enhancing Building Energy Flexibility—A Case Study of a Net-Zero Carbon Building in China
Abstract
1. Introduction
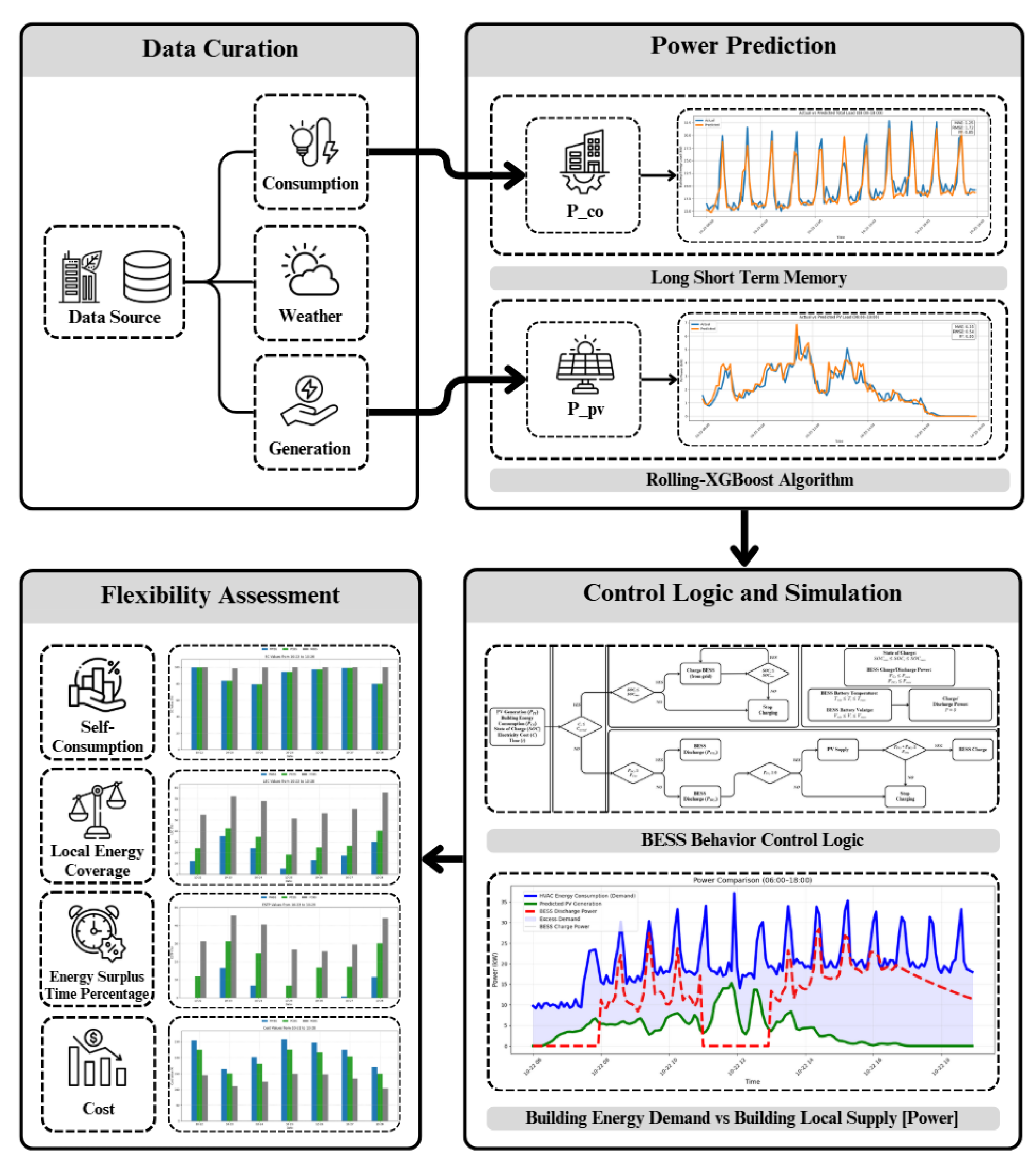
2. Methodology
2.1. Case Study Building
2.2. Data Curation and Energy Prediction Model
2.2.1. LSTM Method for Building Energy Demand Prediction
2.2.2. Rolling-XGB Method for PV Generation Prediction
2.3. Design of Energy Storage Regulation Strategy
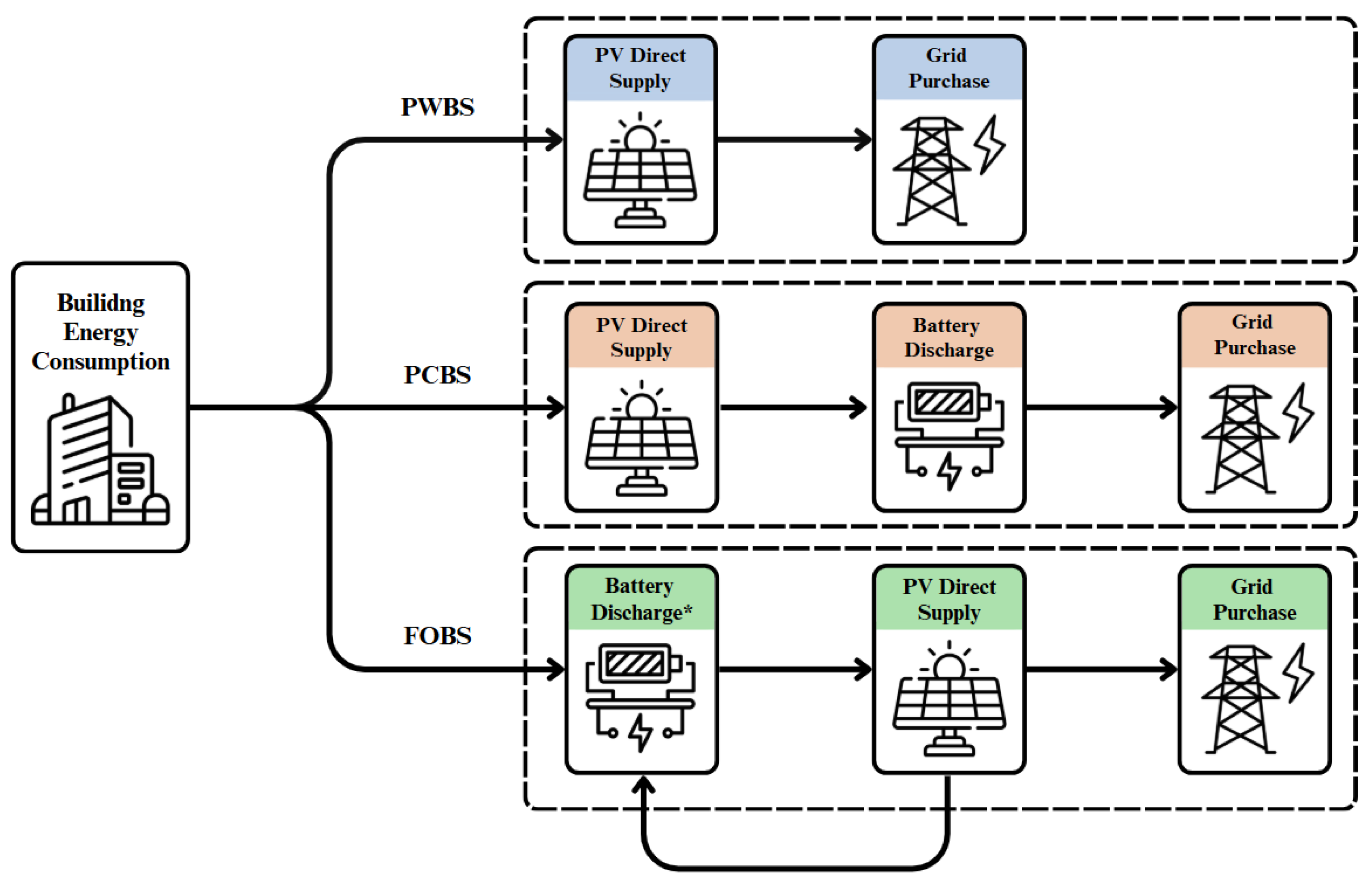
2.3.1. Building Energy Flow Framework
2.3.2. Overview of Strategy Groups
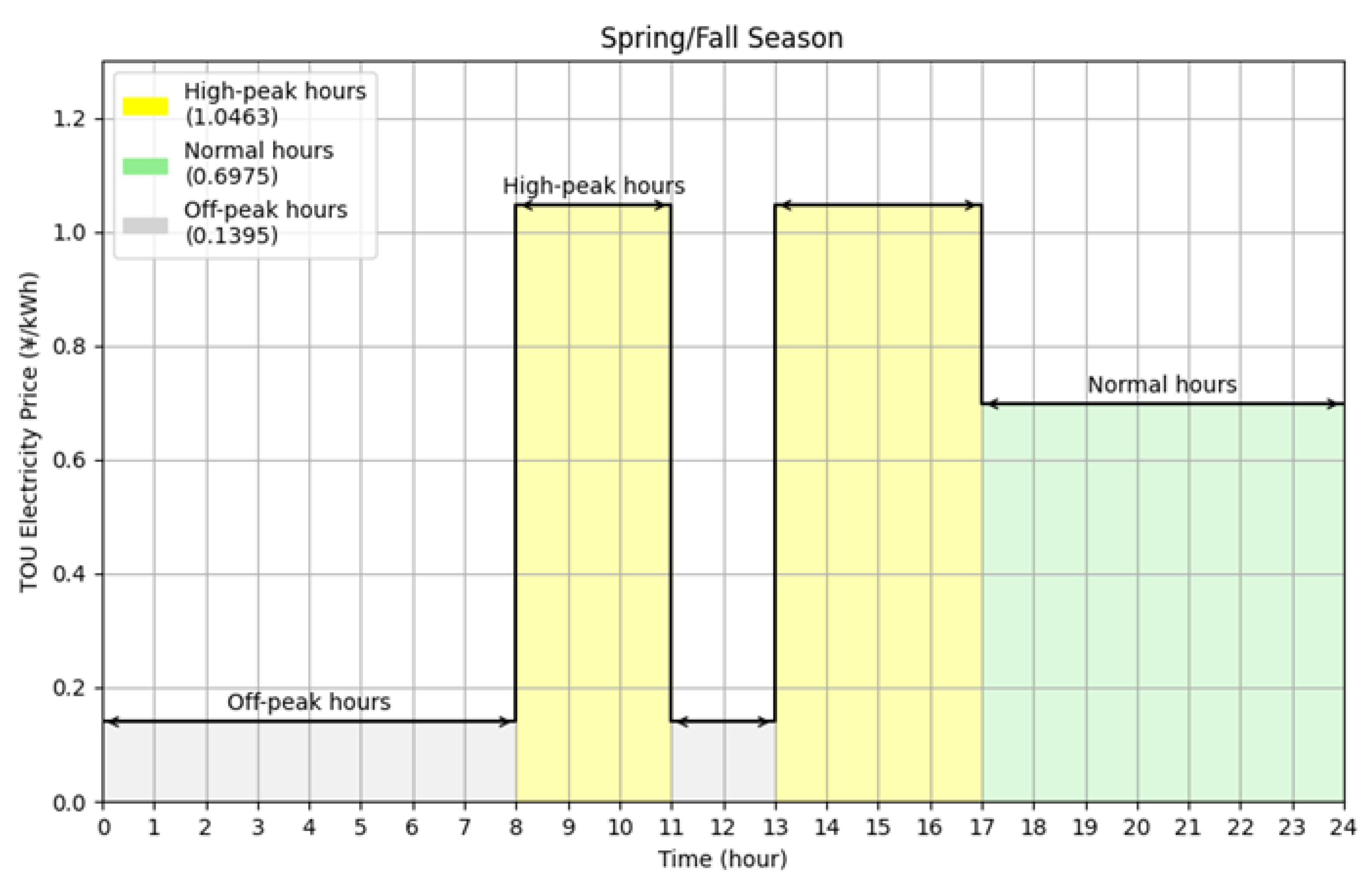
2.3.3. Time-Sharing Tariff Policy in Ningbo
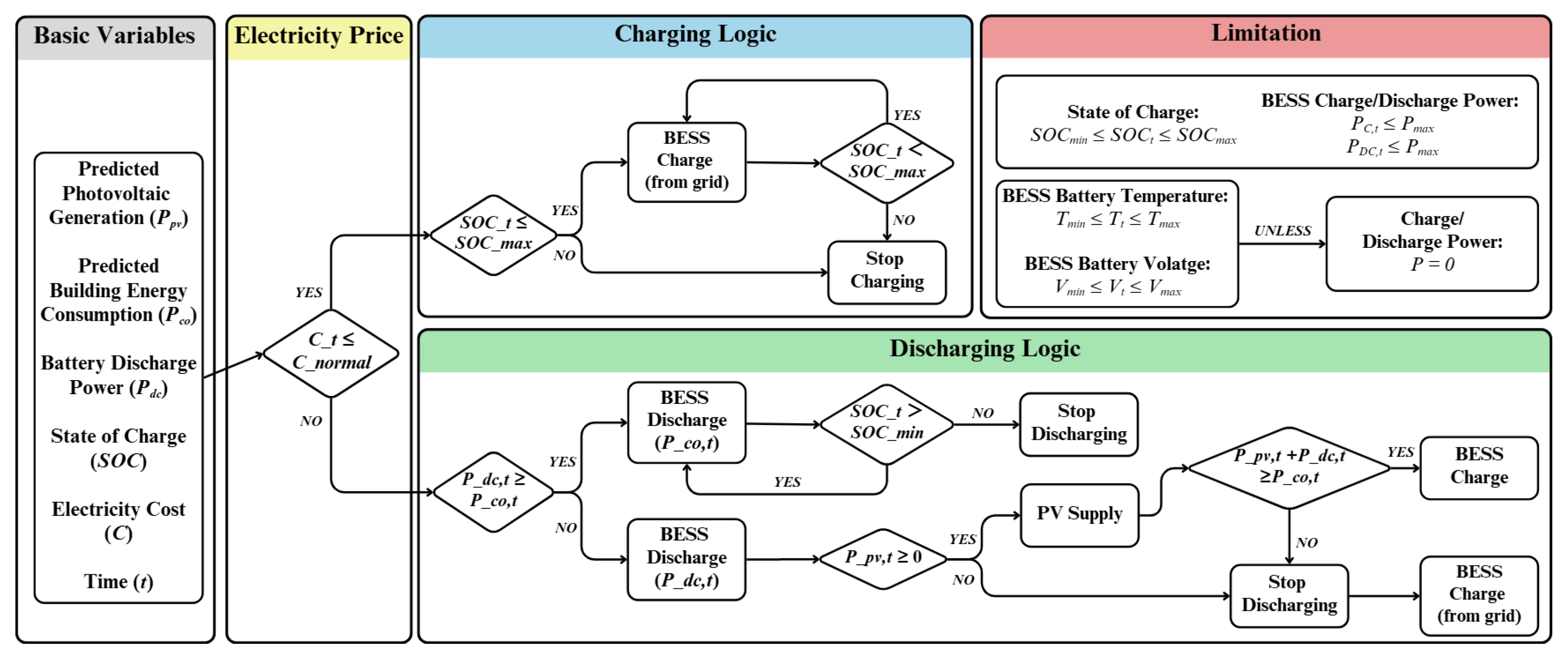
2.3.4. Modeling Battery Energy Storage Constraints for Simulation and Control
2.3.5. Control Logic and Strategy Implementation
2.4. Building Energy Flexibility Assessment Approach
3. Results and Discussion
3.1. Building Energy Consumption Prediction Results
3.2. PV Generation Power Prediction Results
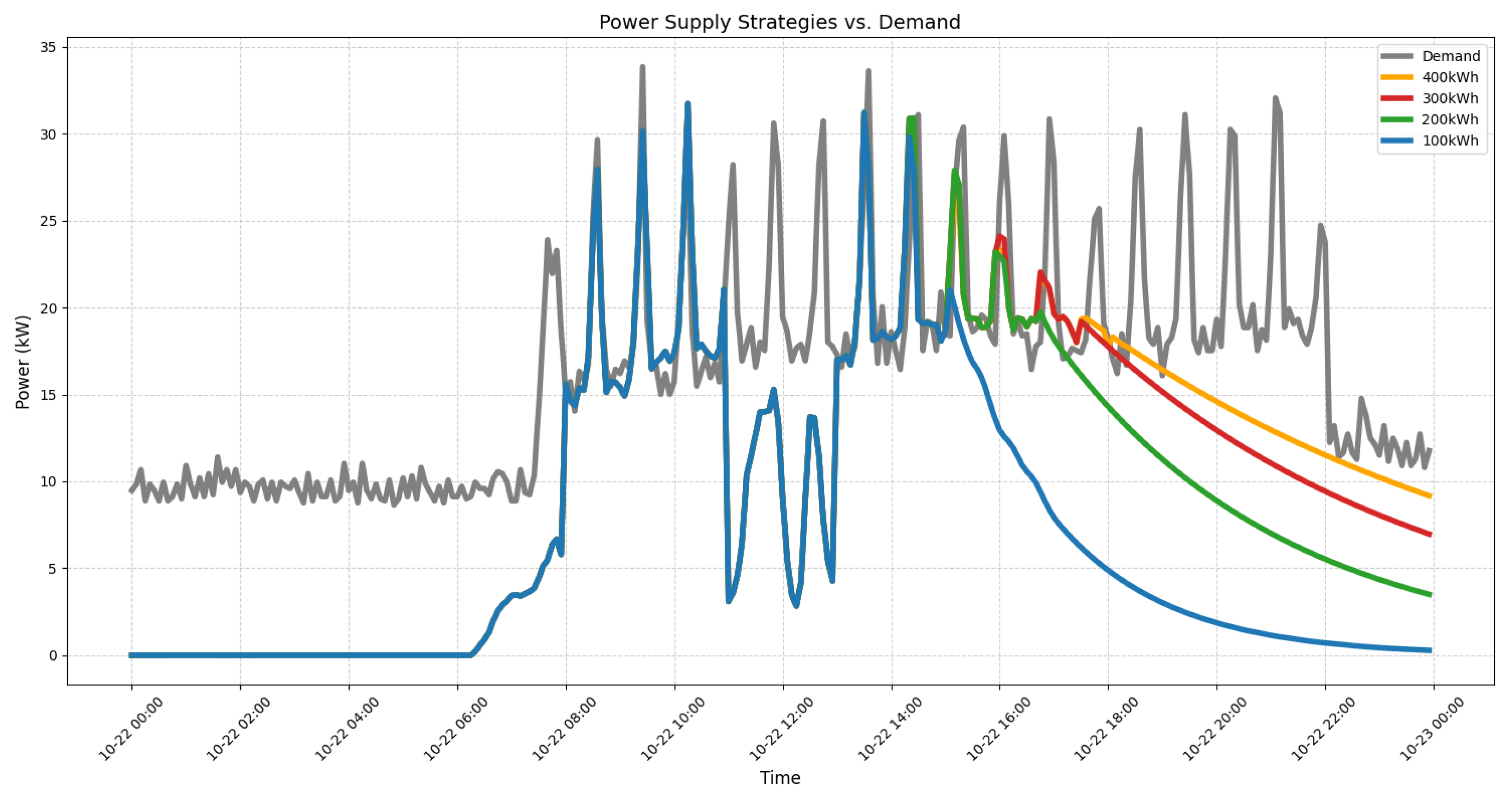
3.3. Comparison of Different Capacities of BESS
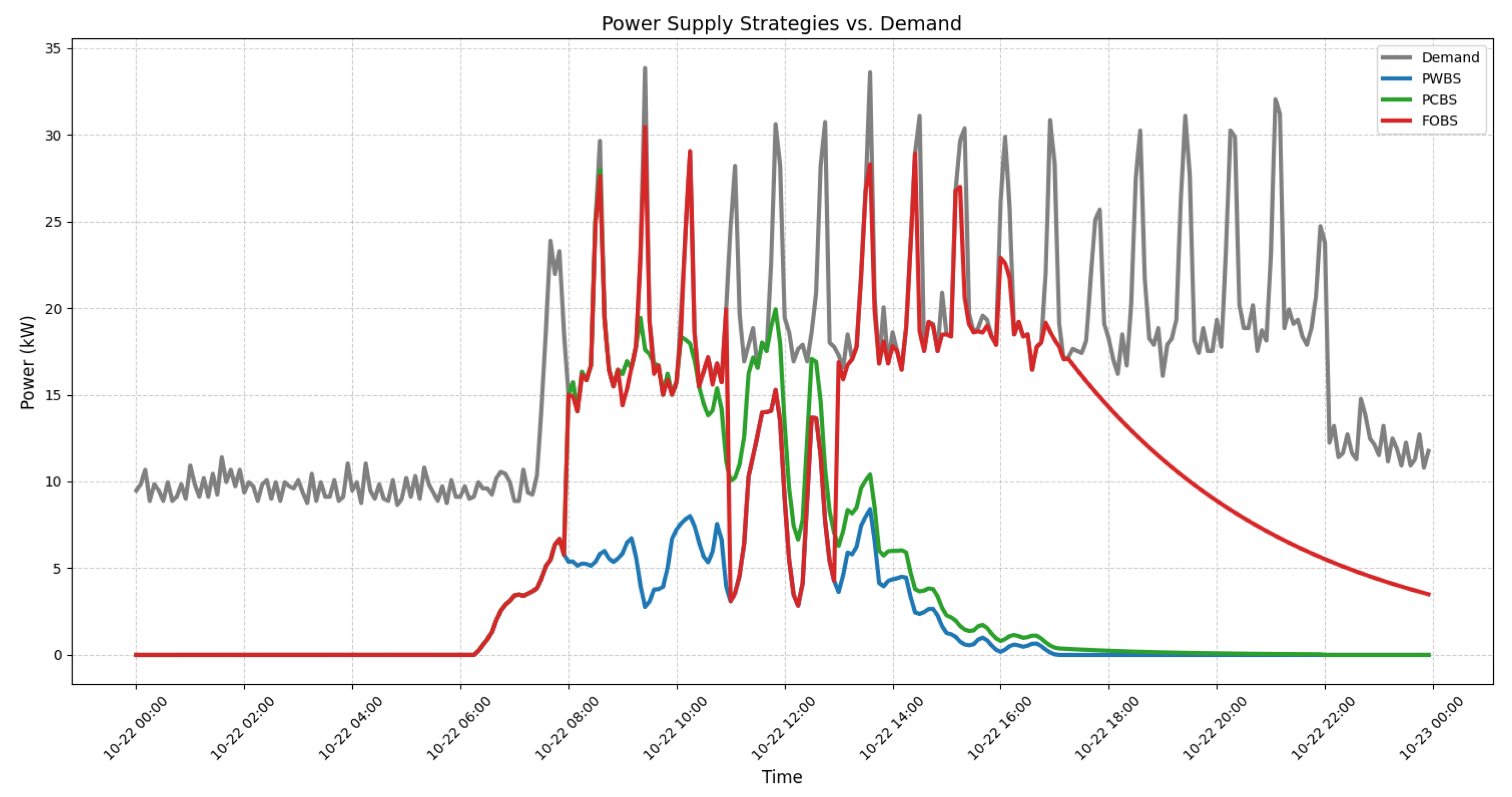
3.4. BESS Behavior Analysis
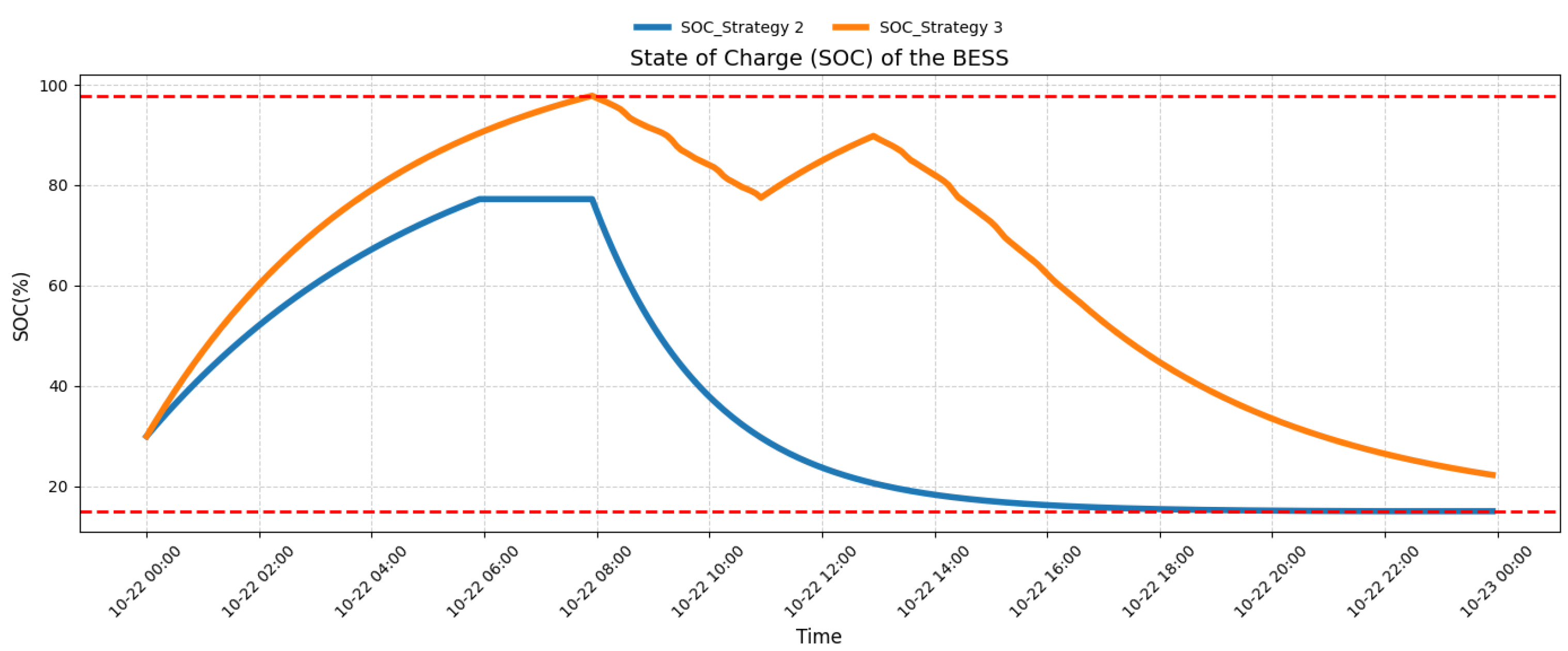
3.4.1. SOC and Charging/Discharging Power
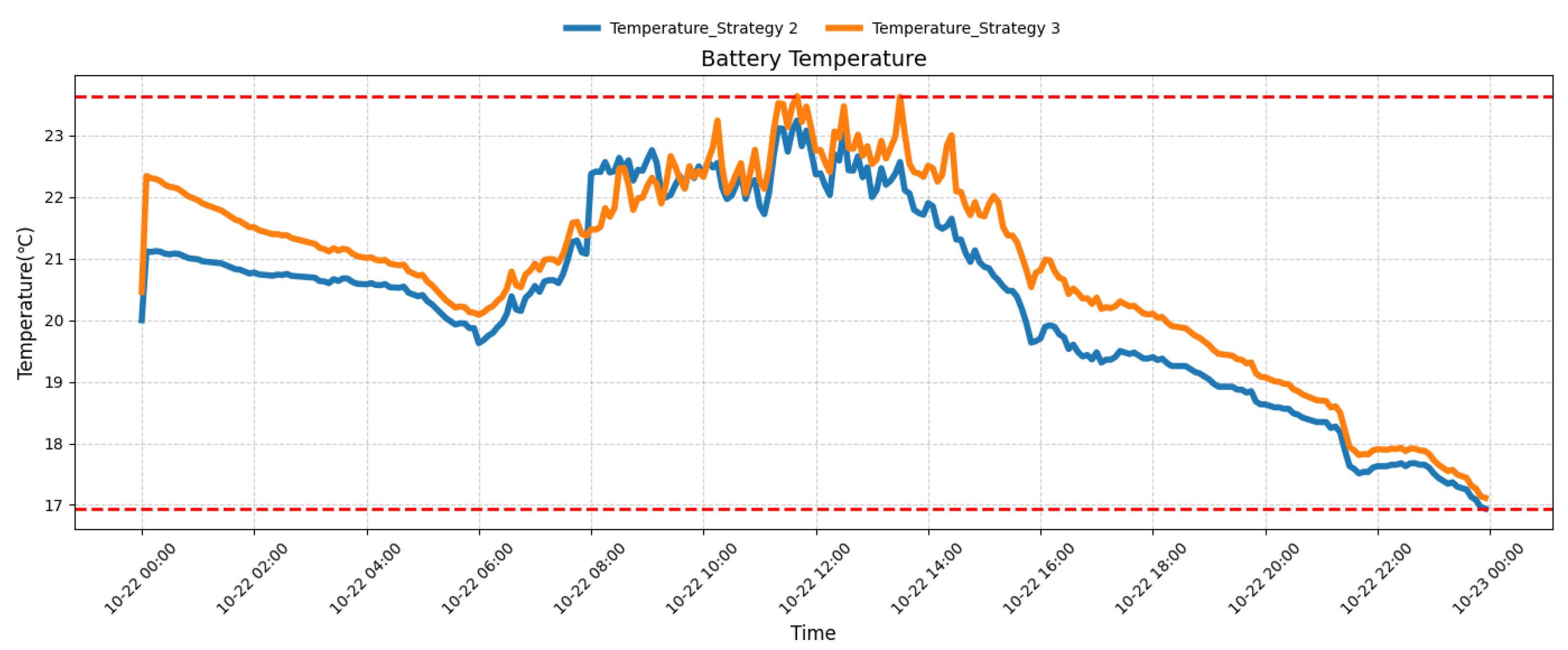
3.4.2. Temperature and Voltage
3.5. Comparison of Key Indicators
3.6. Comparative Discussion of Methods and Results
4. Conclusions and Future Work
- Enhance forecasting: Develop more accurate load prediction methods using hybrid or deep learning models to improve control decisions.
- Broaden system scope: Incorporate flexible loads such as HVAC or EV charging to expand demand-side flexibility potential.
- Evaluate long-term impacts: Analyze battery degradation and life-cycle costs to assess sustained economic and environmental benefits.
- Validate in practice: Implement pilot studies in varied building types and climates to test the real-world applicability of both strategies and flexibility assessment frameworks.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Motherway, B.; Bilodeau, J.; Cohen, J.; Mooney, E.; Rozite, V.; Slade, M. Energy Efficiency 2024; International Energy Agency: Paris, France, 2024. [Google Scholar]
- Liang, W.; Li, H.; Zhan, S.; Chong, A.; Hong, T. Energy flexibility quantification of a tropical net-zero office building using physically consistent neural network-based model predictive control. Adv. Appl. Energy 2024, 14, 100167. [Google Scholar] [CrossRef]
- Infield, D.G. Accommodation of high renewable energy penetration in power systems. In Proceedings of the 11th IET International Conference on Advances in Power System Control, Operation and Management (APSCOM 2018), Hong Kong, China, 11–15 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Masson, G.; Jäger-Waldau, A.; Kaizuka, I.; Lindahl, J.; Donoso, J.; de l’Epine, M. Snapshot of Global PV Markets—2023. In Proceedings of the 2024 IEEE 52nd Photovoltaic Specialist Conference (PVSC), Seattle, WA, USA, 9–14 June 2024. [Google Scholar]
- Aktaş, A. Chapter 10—The importance of energy storage in solar and wind energy, hybrid renewable energy systems. In Advances in Clean Energy Technologies; Azad, A.K., Ed.; Academic Press: Cambridge, MA, USA, 2021; pp. 377–403. [Google Scholar] [CrossRef]
- Kong, D.; Jing, J.; Gu, T.; Wei, X.; Sa, X.; Yang, Y.; Zhang, Z. Theoretical Analysis of Integrated Community Energy Systems (ICES) Considering Integrated Demand Response (IDR): A Review of the System Modelling and Optimization. Energies 2023, 16, 4129. [Google Scholar] [CrossRef]
- Sheha, M.; Mohammadi, K.; Powell, K. Solving the duck curve in a smart grid environment using a non-cooperative game theory and dynamic pricing profiles. Energy Convers. Manag. 2020, 220, 113102. [Google Scholar] [CrossRef]
- Zahedi, A. Sustainable power supply using solar energy and wind power combined with energy storage. Energy Procedia 2014, 52, 642–650. [Google Scholar] [CrossRef][Green Version]
- Liu, J.; Chen, X.; Yang, H.; Shan, K. Hybrid renewable energy applications in zero-energy buildings and communities integrating battery and hydrogen vehicle storage. Appl. Energy 2021, 290, 116733. [Google Scholar] [CrossRef]
- Kong, D.; Cheshmehzangi, A.; Zhang, Z.; Ardakani, S.P.; Gu, T. Urban building energy modeling (UBEM): A systematic review of challenges and opportunities. Energy Effic. 2023, 16, 69. [Google Scholar] [CrossRef]
- Jia, S.; Sheng, K.; Huang, D.; Hu, K.; Xu, Y.; Yan, C. Design optimization of energy systems for zero energy buildings based on grid-friendly interaction with smart grid. Energy 2023, 284, 129298. [Google Scholar] [CrossRef]
- Prasad, M.B.; Ganesh, P.; Kumar, K.V.; Mohanarao, P.A.; Swathi, A.; Manoj, V. Renewable Energy Integration in Modern Power Systems: Challenges and Opportunities. E3S Web Conf. 2024, 591, 03002. [Google Scholar] [CrossRef]
- Bampoulas, A.; Saffari, M.; Pallonetto, F.; Mangina, E.; Finn, D.P. A fundamental unified framework to quantify and characterise energy flexibility of residential buildings with multiple electrical and thermal energy systems. Appl. Energy 2021, 282, 116096. [Google Scholar] [CrossRef]
- Bucking, S.; Dermardiros, V. Distributed evolutionary algorithm for co-optimization of building and district systems for early community energy masterplanning. Appl. Soft Comput. 2018, 63, 14–22. [Google Scholar] [CrossRef]
- Qiao, B.; Dong, J.; Xu, W.; Li, J.; Lu, F. Research and Demonstration of Operation Optimization Method of Zero-Carbon Building’s Compound Energy System Based on Day-Ahead Planning and Intraday Rolling Optimization Algorithm. Buildings 2025, 15, 836. [Google Scholar] [CrossRef]
- Ma, Z.; Arici, M.; Shahsavar, A. Building Energy Flexibility and Demand Management; Academic Press: San Diego, CA, USA, 2023. [Google Scholar]
- Coraci, D.; Brandi, S.; Hong, T.; Capozzoli, A. An innovative heterogeneous transfer learning framework to enhance the scalability of deep reinforcement learning controllers in buildings with integrated energy systems. Build. Simul. 2024, 17, 739–770. [Google Scholar] [CrossRef]
- Li, H.; Hong, T. On data-driven energy flexibility quantification: A framework and case study. Energy Build. 2023, 296, 113381. [Google Scholar] [CrossRef]
- Chung, W. Review of building energy-use performance benchmarking methodologies. Appl. Energy 2011, 88, 1470–1479. [Google Scholar] [CrossRef]
- Chung, W.; Hui, Y.V.; Lam, Y.M. Benchmarking the energy efficiency of commercial buildings. Appl. Energy 2006, 83, 1–14. [Google Scholar] [CrossRef]
- Tang, H.; Wang, S. Energy flexibility quantification of grid-responsive buildings: Energy flexibility index and assessment of their effectiveness for applications. Energy 2021, 221, 119756. [Google Scholar] [CrossRef]
- Jensen, S.Ø.; Marszal-Pomianowska, A.; Lollini, R.; Pasut, W.; Knotzer, A.; Engelmann, P.; Stafford, A.; Reynders, G. IEA EBC Annex 67 Energy Flexible Buildings. Energy Build. 2017, 155, 25–34. [Google Scholar] [CrossRef]
- Neukomm, M.; Nubbe, V.; Fares, R. Grid-Interactive Efficient Buildings; U.S. Dept. of Energy (USDOE): Washington, DC, USA; Navigant Consulting, Inc.: Chicago, IL, USA, 2019.
- Lopes, R.A.; Chambel, A.; Neves, J.; Aelenei, D.; Martins, J. A Literature Review of Methodologies Used to Assess the Energy Flexibility of Buildings. Energy Procedia 2016, 91, 1053–1058. [Google Scholar] [CrossRef]
- Lund, P.D.; Lindgren, J.; Mikkola, J.; Salpakari, J. Review of energy system flexibility measures to enable high levels of variable renewable electricity. Renew. Sustain. Energy Rev. 2015, 45, 785–807. [Google Scholar] [CrossRef]
- Stinner, S.; Huchtemann, K.; Müller, D. Quantifying the operational flexibility of building energy systems with thermal energy storages. Appl. Energy 2016, 181, 140–154. [Google Scholar] [CrossRef]
- De Coninck, R.; Helsen, L. Quantification of flexibility in buildings by cost curves—Methodology and application. Appl. Energy 2016, 162, 653–665. [Google Scholar] [CrossRef]
- Le Dréau, J.; Heiselberg, P. Energy flexibility of residential buildings using short term heat storage in the thermal mass. Energy 2016, 111, 991–1002. [Google Scholar] [CrossRef]
- Reynders, G.; Diriken, J.; Saelens, D. Generic characterization method for energy flexibility: Applied to structural thermal storage in residential buildings. Appl. Energy 2017, 198, 192–202. [Google Scholar] [CrossRef]
- Saberi-Derakhtenjani, A.; Barbosa, J.D.; Rodriguez-Ubinas, E. Energy Flexibility Strategies for Buildings in Hot Climates: A Case Study for Dubai. Buildings 2024, 14, 3008. [Google Scholar] [CrossRef]
- Barchi, G.; Miori, G.; Moser, D.; Papantoniou, S. A Small-Scale Prototype for the Optimization of PV Generation and Battery Storage through the Use of a Building Energy Management System. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Chen, Y.; Trifkovic, M. Optimal scheduling of a microgrid in a volatile electricity market environment: Portfolio optimization approach. Appl. Energy 2018, 226, 703–712. [Google Scholar] [CrossRef]
- Tziovani, L.; Kolios, P.; Hadjidemetriou, L.; Kyriakides, E. Energy scheduling in non-residential buildings integrating battery storage and renewable solutions. In Proceedings of the 2018 IEEE International Energy Conference (ENERGYCON), Limassol, Cyprus, 3–7 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Darbandsari, A.; Askarzadeh, A.R. Optimal Energy Management of a Smart Building Considering Rooftop Photovoltaic, Electric Vehicles and Schedulable Loads. In Proceedings of the 2022 9th Iranian Conference on Renewable Energy & Distributed Generation (ICREDG), Mashhad, Iran, 23–24 February 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Manrique Delgado, B.; Ruusu, R.; Hasan, A.; Kilpeläinen, S.; Cao, S.; Sirén, K. Energetic, Cost, and Comfort Performance of a Nearly-Zero Energy Building Including Rule-Based Control of Four Sources of Energy Flexibility. Buildings 2018, 8, 172. [Google Scholar] [CrossRef]
- Zhao, Y. Using Machine Learning to Optimize Building Energy Consumption Prediction and Generate Energy-saving Strategies. In Proceedings of the 2024 International Conference on Intelligent Algorithms for Computational Intelligence Systems (IACIS), Hassan, India, 23–24 August 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Zhou, X.; Lin, W.; Kumar, R.; Cui, P.; Ma, Z. A data-driven strategy using long short term memory models and reinforcement learning to predict building electricity consumption. Appl. Energy 2022, 306, 118078. [Google Scholar] [CrossRef]
- Zhou, M.; Li, X.; Zhong, Z. Research on Photovoltaic Power Generation Power Prediction Based on RF-XGBoost Model. In Proceedings of the 2023 IEEE 6th International Conference on Information Systems and Computer Aided Education (ICISCAE), Dalian, China, 23–25 September 2023; pp. 544–549. [Google Scholar] [CrossRef]
- Zhu, J.; Li, M.; Luo, L.; Zhang, B.; Cui, M.; Yu, L. Short-term PV power forecast methodology based on multi-scale fluctuation characteristics extraction. Renew. Energy 2023, 208, 141–151. [Google Scholar] [CrossRef]
- Li, T.; Zhang, Y.; Zhu, Z.; Bai, L.; Meng, F.; Yang, G. A Comparative Study of Photovoltaic Power Prediction Models Based on BP and XGBoost. In Proceedings of the 2024 6th International Conference on Robotics, Intelligent Control and Artificial Intelligence (RICAI), Nanjing, China, 6–8 December 2024; pp. 567–570. [Google Scholar] [CrossRef]
- Nastić, F.; Jurišević, N.; Nikolić, D.; Končalović, D. Harnessing open data for hourly power generation forecasting in newly commissioned photovoltaic power plants. Energy Sustain. Dev. 2024, 81, 101512. [Google Scholar] [CrossRef]
- Zou, Z.; Xu, J.; Mi, C.; Cao, B.; Chen, Z. Evaluation of Model Based State of Charge Estimation Methods for Lithium-Ion Batteries. Energies 2014, 7, 5065–5082. [Google Scholar] [CrossRef]
- Meng, J.; Ricco, M.; Luo, G.; Swierczynski, M.; Stroe, D.-I.; Stroe, A.-I.; Teodorescu, R. An Overview and Comparison of Online Implementable SOC Estimation Methods for Lithium-Ion Battery. IEEE Trans. Ind. Appl. 2018, 54, 1583–1591. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, X. Overview of lithium-ion battery SOC estimation. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 2454–2459. [Google Scholar] [CrossRef]






| Ref. | Modeling Method | Control/Optimization Strategy | Evaluation Metrics or Case Study | Key Findings |
|---|---|---|---|---|
| [2] | Physically consistent neural network combined with a prediction model | PV + BESS integration with dynamic pricing control | Net-zero energy office building in Singapore | PV and BESS improve energy flexibility; dynamic pricing aids control decisions |
| [16] | Physics-based simulations and data-driven models | Single- and multi-objective optimization | Net-zero energy buildings with PV and storage | Demonstrates modeling and enhancement of energy flexibility |
| [17] | Transfer learning + DRL | Rule-based controller, DRL with online TL | Co-simulation with PV and BESS models | Proposes scalable TL strategy for DRL; shows action selection logic and model setup |
| [18] | Data-driven framework for flexibility quantification | Model Predictive Control (MPC) | Residential DR use cases; KPI-based framework | Defines a 7-step process for flexibility quantification using KPIs |
| Indicators [Ref.] | Short Review | Equation Examples |
|---|---|---|
| Ramp-up capability, power capacity and energy [26] | A framework for quantifying building energy systems for thermal storage in terms of time, power and energy is proposed. | |
| Flexibility energy and related energy cost [27] | Bottom-up approach to flexible quantification of commercial buildings, including cost curves | |
| Flexibility Factor [28] | Evaluate the potential of a building to regulate its heating power and define a control strategy to test the flexibility potential | |
| Available structure storage capacity [29] | Flexibility analysis of structural thermal energy storage provision under active demand response | |
| Self-consumption, storage capacity and storage efficiency [13] | Presentation of a quantitative framework for basic energy flexibility for the assessment of multicomponent electrical and thermal systems. |
| Energy Consumption () | Energy Generation () | Ratio of Generation to Consumption (%) | ||
|---|---|---|---|---|
| HVAC | Non-HVAC | Total | PV | PV/Total |
| 4315.26 | 7788.47 | 12,103.73 | 3563.14 | 29.44 |
| Photovoltaic System | Battery Energy Storage System | ||
|---|---|---|---|
| Parameter | Value | Parameter | Value |
| Total Area | 284.24 m2 | State of Charge | 15–100% |
| Voltage | 292–403 V | ||
| Peak Power | 60 kW | Nominal Capacity | 100 kWh |
| Maximum Power | 50 kW | ||
| Efficiency | 20.32% | Efficiency | 96% |
| Temperature | 0–40 °C | ||
| Scenario | Strategy |
|---|---|
| PWBS [PV Without Battery Storage] | PV Direct Supply + Grid Purchase |
| PCBS [PV with Current Battery Strategy] | PV Direct Supply + Battery Discharge[current] + Grid Purchase |
| FOBS [Forecast-based Optimized Battery Strategy] | Large Battery Capacity + Battery Discharge [predicted] + PV Direct Replenish + Grid Purchase considering TOU Policy |
| KPI | Definition | Applicability |
|---|---|---|
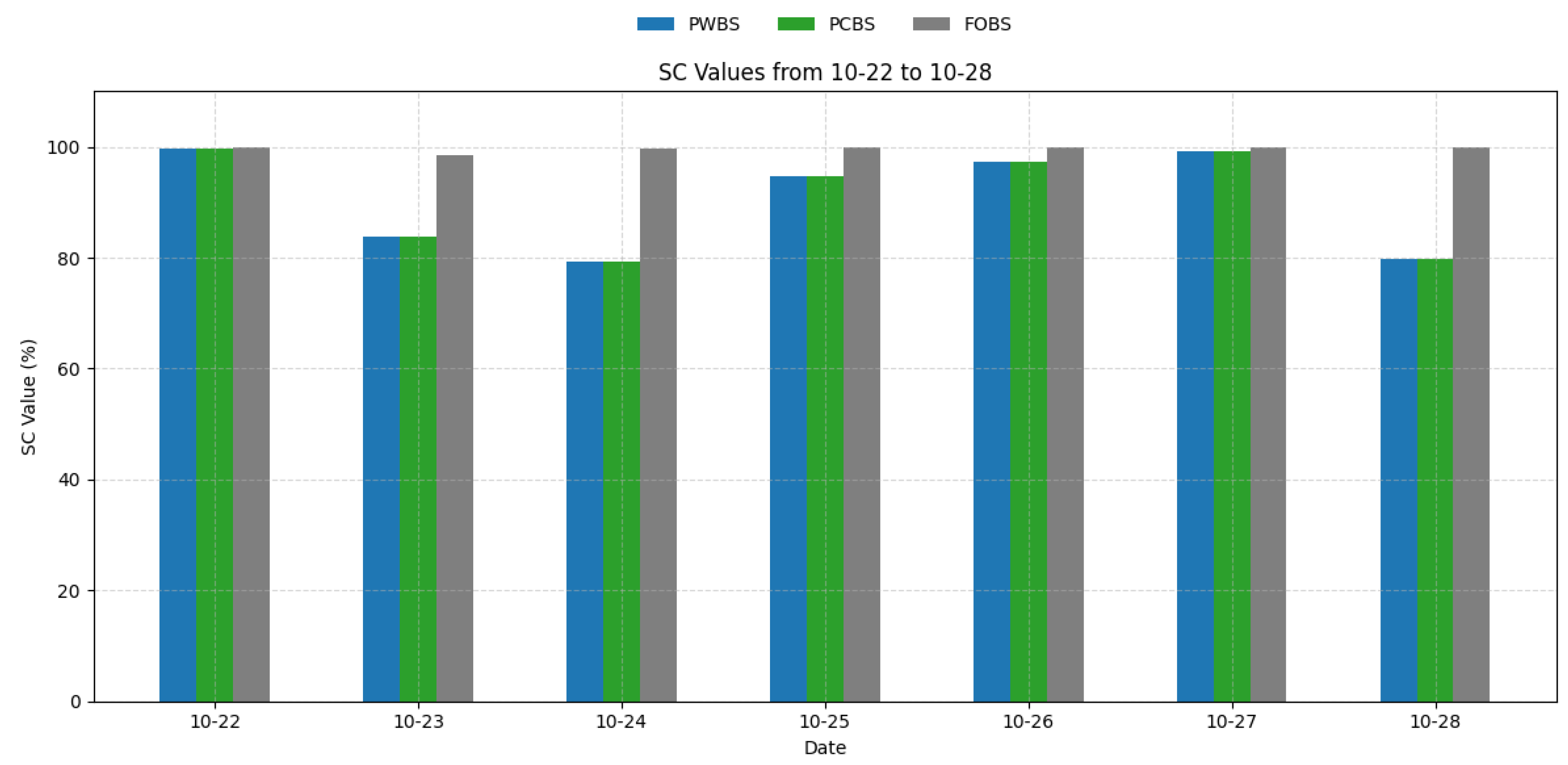
| Self-Consumption (SC) | For buildings with PV power generation and BESS, it is possible to reflect the efficiency of the building’s use of its renewable energy supply. | |
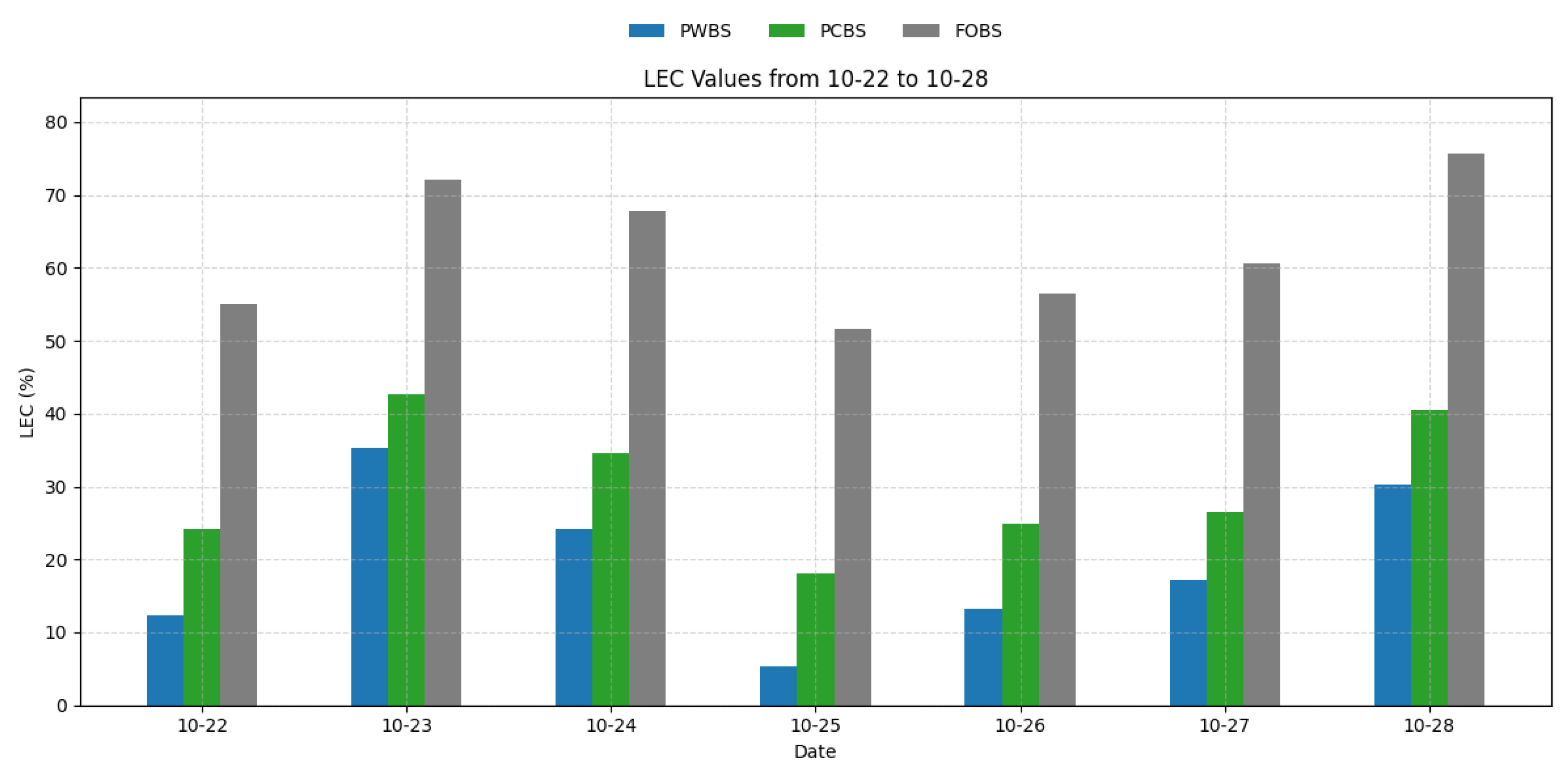
| Local Energy Coverage (LER) | The ratio of energy supplied by the local energy system (including on-site renewable energy supply and the energy stored from the grid in advance) to its total energy demand. | |
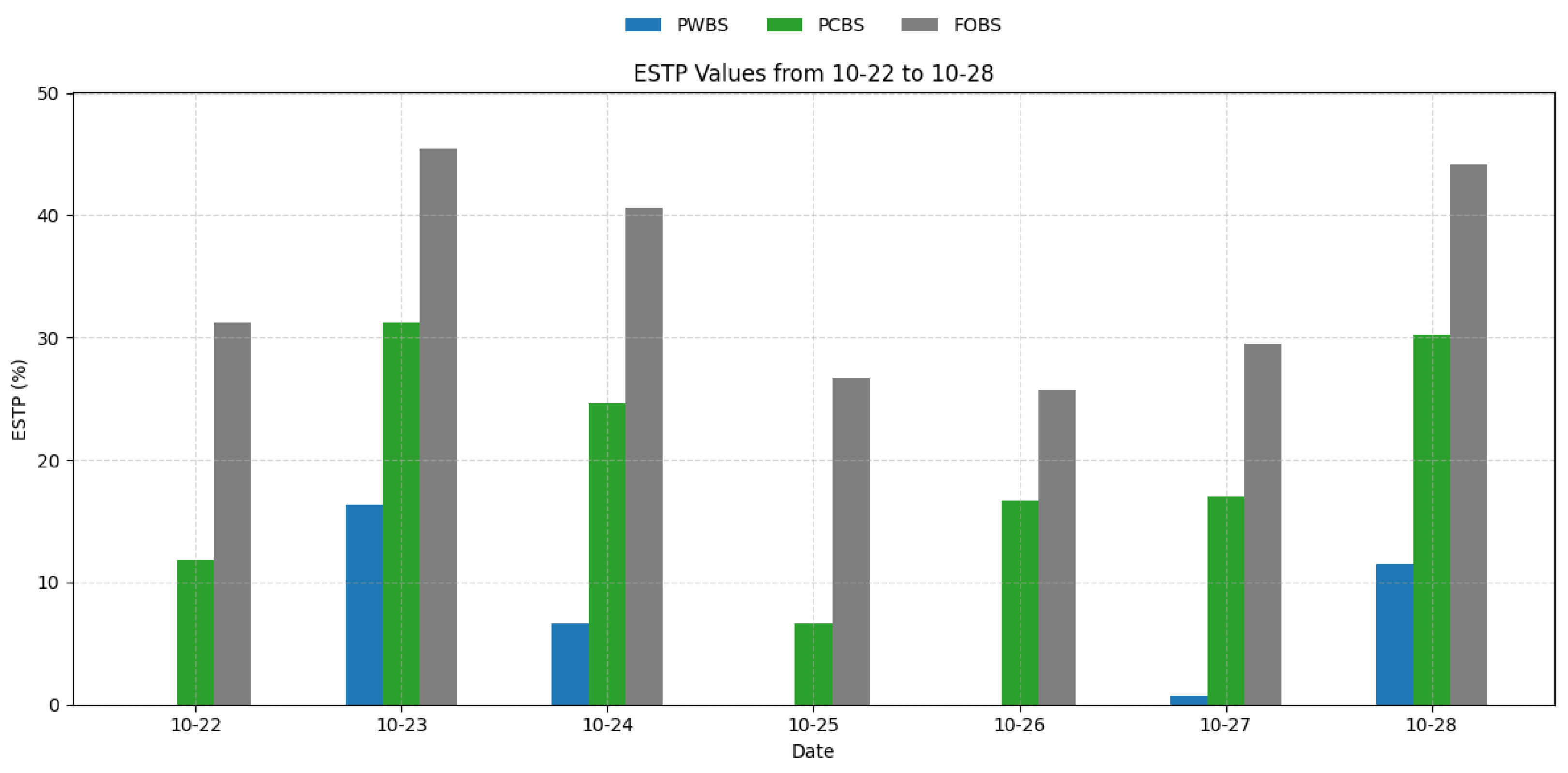
| Energy Surplus Time Percentage (ESTP) | Reflects the effectiveness of energy scheduling in the time dimension. |
| Date | MAE of P_consumption (kW) | RMSE of P_consumption (kW) | R2 of P_consumption |
|---|---|---|---|
| 22 October 2024 | 1.27 | 2.06 | 0.90 |
| 23 October 2024 | 1.10 | 1.58 | 0.93 |
| 24 October 2024 | 1.11 | 1.53 | 0.92 |
| 25 October 2024 | 1.16 | 1.67 | 0.92 |
| 26 October 2024 | 1.21 | 1.94 | 0.92 |
| 27 October 2024 | 1.12 | 1.75 | 0.91 |
| 28 October 2024 | 1.19 | 1.72 | 0.92 |
| Average | 1.166 | 1.750 | 0.917 |
| Date | MAE of P_PV (kW) | RMSE of P_PV (kW) | R2 of P_PV |
|---|---|---|---|
| 22 October 2024 | 0.61 | 1.46 | 0.80 |
| 23 October 2024 | 2.49 | 5.44 | 0.74 |
| 24 October 2024 | 2.24 | 5.98 | 0.69 |
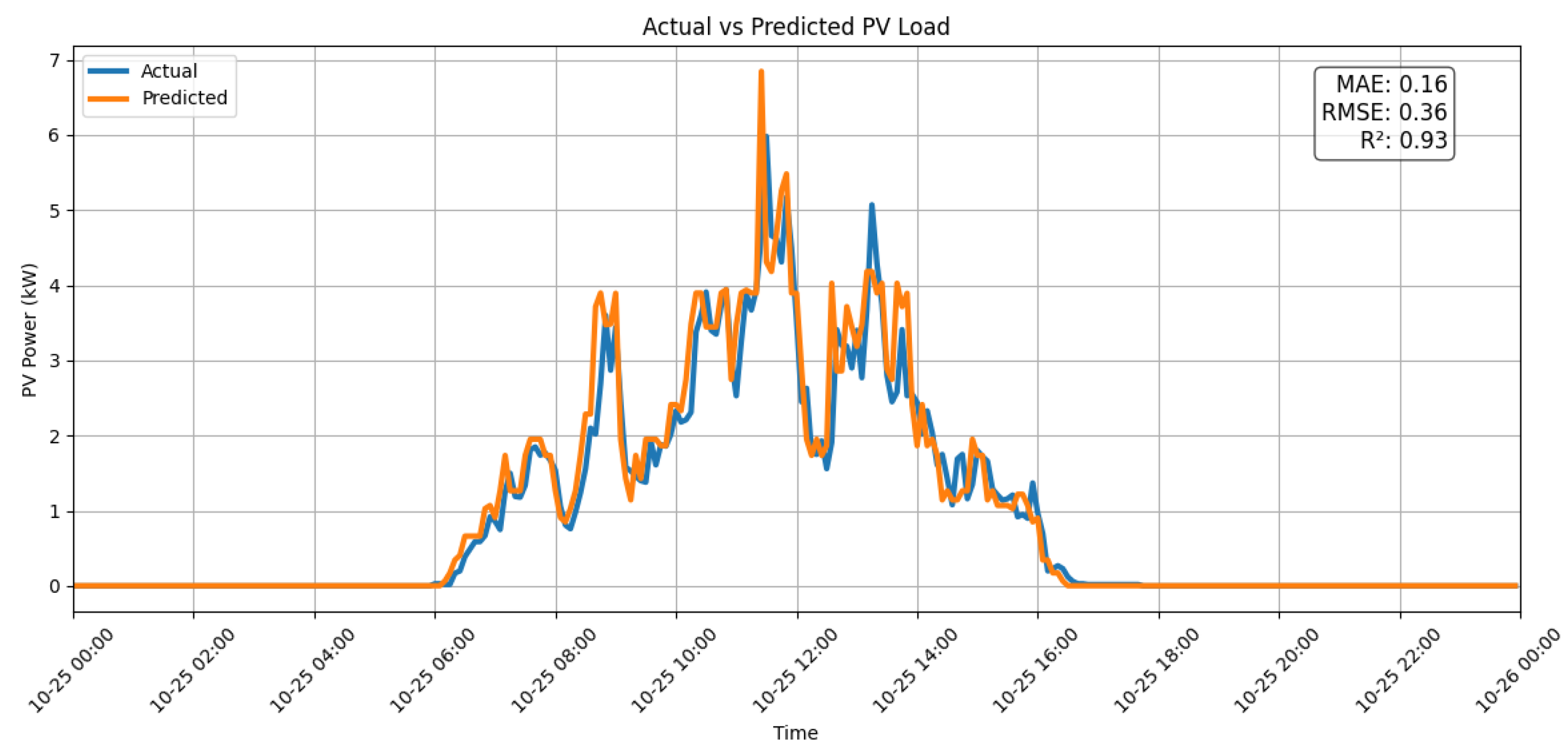
| 25 October 2024 | 0.16 | 0.36 | 0.93 |
| 26 October 2024 | 0.45 | 1.14 | 0.91 |
| 27 October 2024 | 0.62 | 1.52 | 0.89 |
| 28 October 2024 | 2.03 | 4.92 | 0.75 |
| Average | 1.229 | 2.974 | 0.816 |
| Date | PWBS | PCBS | FOBS |
|---|---|---|---|
| 22 October 2024 | 99.63% | 99.63% | 100.00% |
| 23 October 2024 | 83.86% | 83.86% | 98.39% |
| 24 October 2024 | 79.31% | 79.31% | 99.56% |
| 25 October 2024 | 94.68% | 94.68% | 100.00% |
| 26 October 2024 | 97.39% | 97.39% | 100.00% |
| 27 October 2024 | 99.28% | 99.28% | 100.00% |
| 28 October 2024 | 79.85% | 79.85% | 100.00% |
| Average | 90.57% | 90.57% | 99.71% |
| Date | PWBS | PCBS | FOBS | |||
|---|---|---|---|---|---|---|
| LEC | ESTP | LEC | ESTP | LEC | ESTP | |
| 22 October 2024 | 12.29% | 0.00% | 24.16% | 11.81% | 55.02% | 31.25% |
| 23 October 2024 | 35.39% | 16.32% | 42.69% | 31.25% | 72.01% | 45.49% |
| 24 October 2024 | 24.09% | 6.60% | 34.52% | 24.65% | 67.71% | 40.63% |
| 25 October 2024 | 5.26% | 0.00% | 18.00% | 6.60% | 51.61% | 26.74% |
| 26 October 2024 | 13.28% | 0.00% | 24.94% | 16.67% | 56.49% | 25.69% |
| 27 October 2024 | 17.12% | 0.69% | 26.55% | 17.01% | 60.67% | 29.51% |
| 28 October 2024 | 30.34% | 11.46% | 40.46% | 30.21% | 75.75% | 44.10% |
| Average | 19.68% | 5.01% | 30.19% | 19.74% | 62.75% | 34.77% |
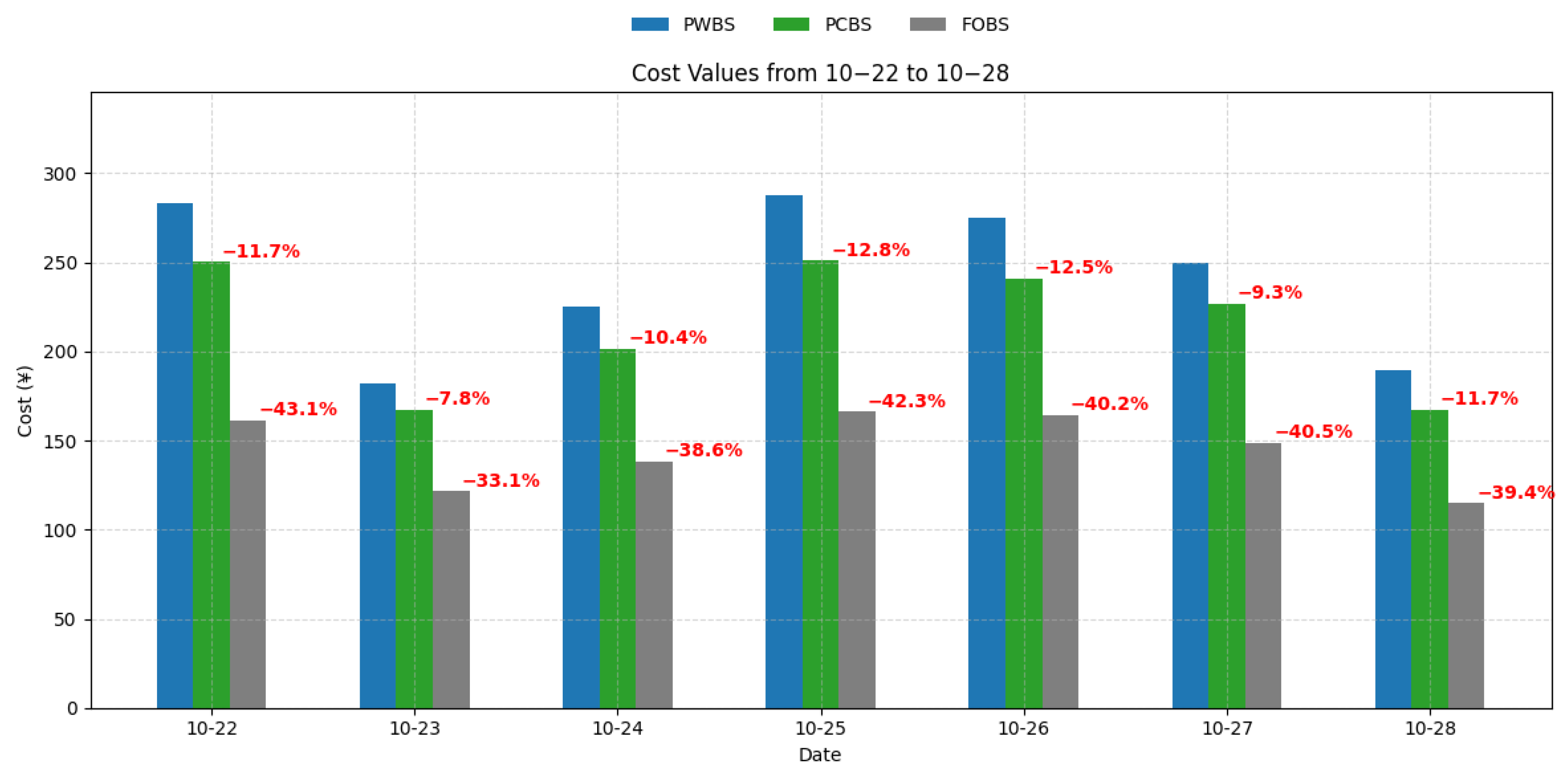
| Date | PWBS (CNY) | PCBS (CNY) | FOBS (CNY) |
|---|---|---|---|
| 22 October 2024 | 283.51 | 250.22 | 161.42 |
| 23 October 2024 | 181.70 | 167.45 | 121.60 |
| 24 October 2024 | 224.96 | 201.51 | 138.14 |
| 25 October 2024 | 287.85 | 251.04 | 166.09 |
| 26 October 2024 | 275.22 | 240.73 | 164.48 |
| 27 October 2024 | 250.00 | 226.69 | 148.82 |
| 28 October 2024 | 189.37 | 167.18 | 114.80 |
| Average | 283.51 | 250.22 | 161.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Kong, D.; Chen, Z.; Zhang, Z.; Du, D.; Zhu, Z. A Data-Driven Battery Energy Storage Regulation Approach Integrating Machine Learning Forecasting Models for Enhancing Building Energy Flexibility—A Case Study of a Net-Zero Carbon Building in China. Buildings 2025, 15, 3611. https://doi.org/10.3390/buildings15193611
Yang Z, Kong D, Chen Z, Zhang Z, Du D, Zhu Z. A Data-Driven Battery Energy Storage Regulation Approach Integrating Machine Learning Forecasting Models for Enhancing Building Energy Flexibility—A Case Study of a Net-Zero Carbon Building in China. Buildings. 2025; 15(19):3611. https://doi.org/10.3390/buildings15193611
Chicago/Turabian StyleYang, Zesheng, Dezhou Kong, Zhexuan Chen, Zhiang Zhang, Dengfeng Du, and Ziyue Zhu. 2025. "A Data-Driven Battery Energy Storage Regulation Approach Integrating Machine Learning Forecasting Models for Enhancing Building Energy Flexibility—A Case Study of a Net-Zero Carbon Building in China" Buildings 15, no. 19: 3611. https://doi.org/10.3390/buildings15193611
APA StyleYang, Z., Kong, D., Chen, Z., Zhang, Z., Du, D., & Zhu, Z. (2025). A Data-Driven Battery Energy Storage Regulation Approach Integrating Machine Learning Forecasting Models for Enhancing Building Energy Flexibility—A Case Study of a Net-Zero Carbon Building in China. Buildings, 15(19), 3611. https://doi.org/10.3390/buildings15193611







