Computational Fluid Dynamics Approach to Aeroelastic Stability in Cable-Stayed Bridges
Abstract
1. Introduction
- Modal analysis of a finite element (FE) model to determine natural frequencies and mode shapes.
- CFD simulations of a two-dimensional deck section, subjected to a steady wind speed U = 20 m/s and varying angles of attack (AoA) from −10° to +10°, using the RANS k-ω SST turbulence model with a wall function Y+ = 30.
- Aeroelastic assessment of the structure against the four principal instability mechanisms—vortex shedding, galloping, torsional divergence, and classical flutter—using the static aerodynamic coefficients (CD, CL, CM) derived from CFD.
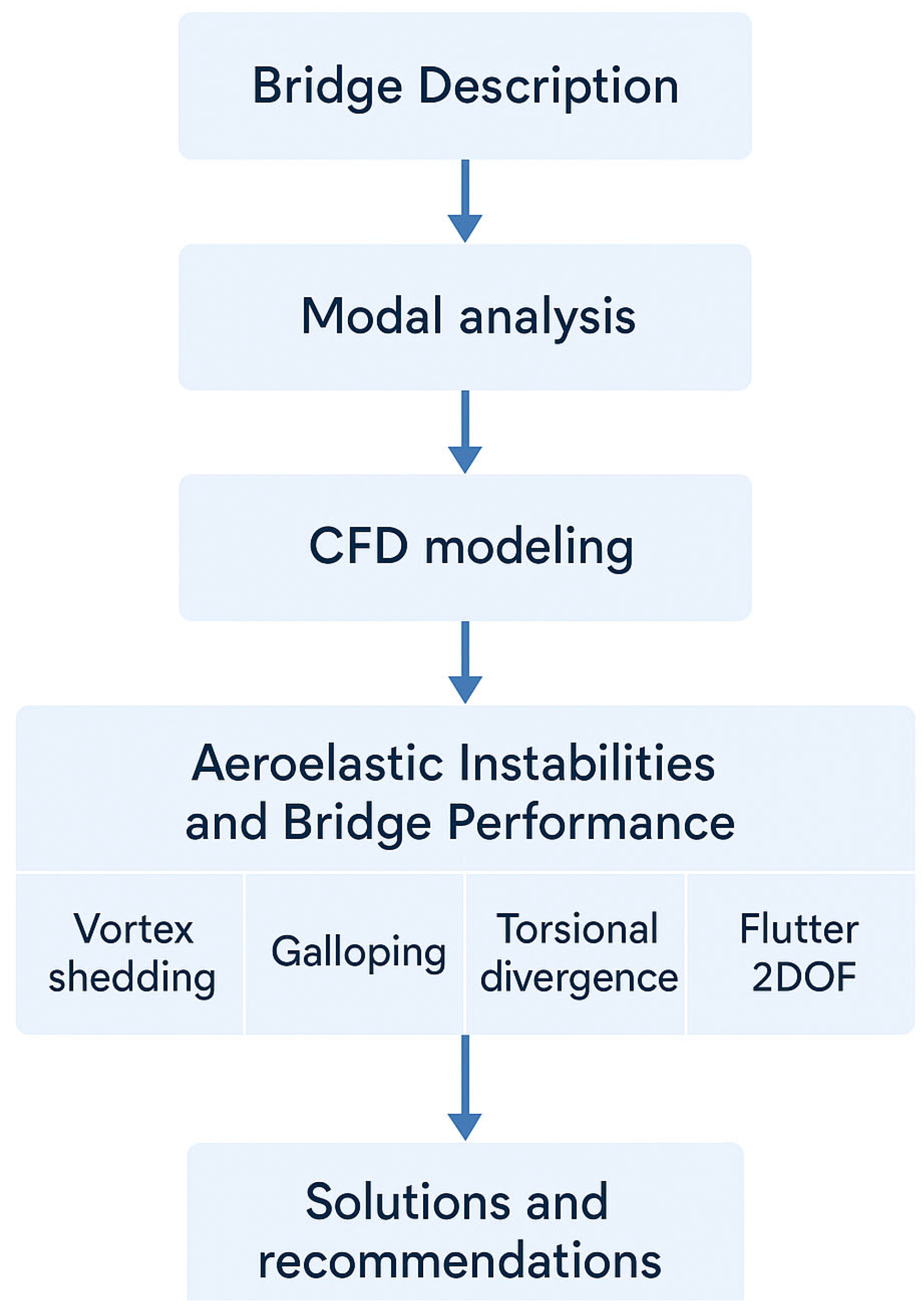
2. Bridge Description
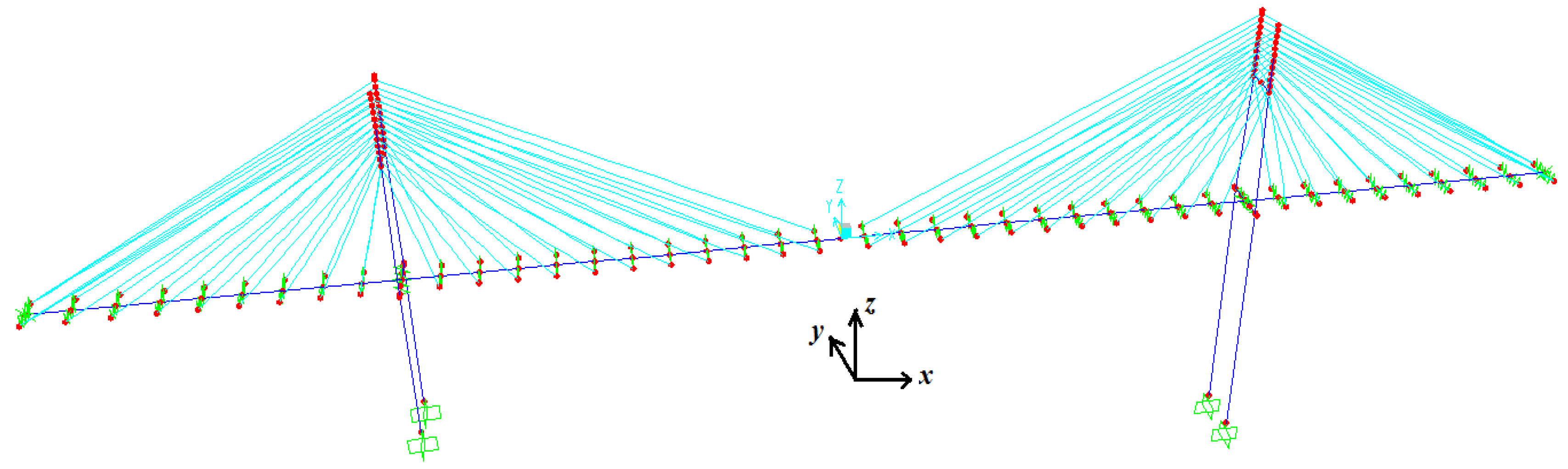
3. Modal Analysis
3.1. Modal Frequencies
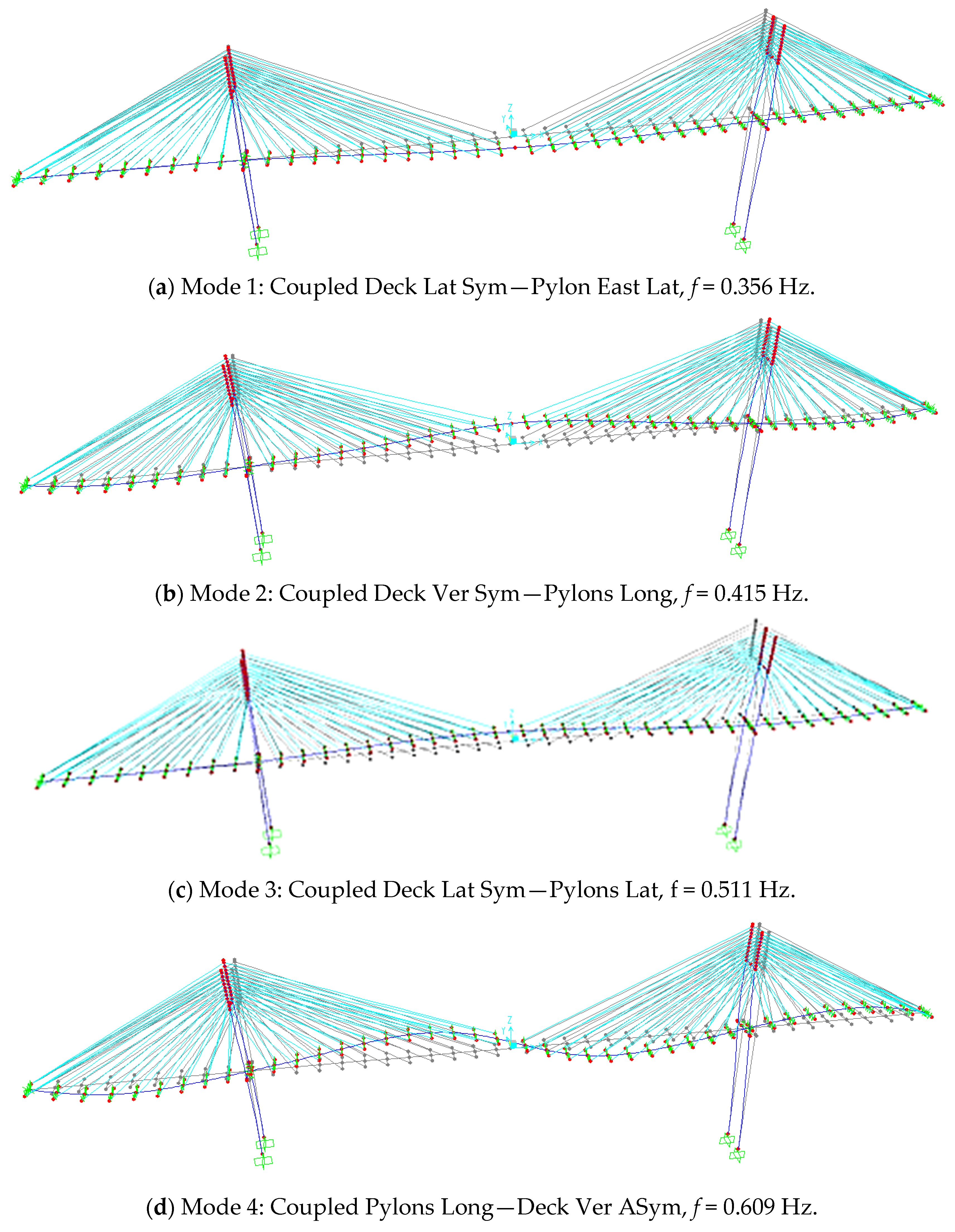
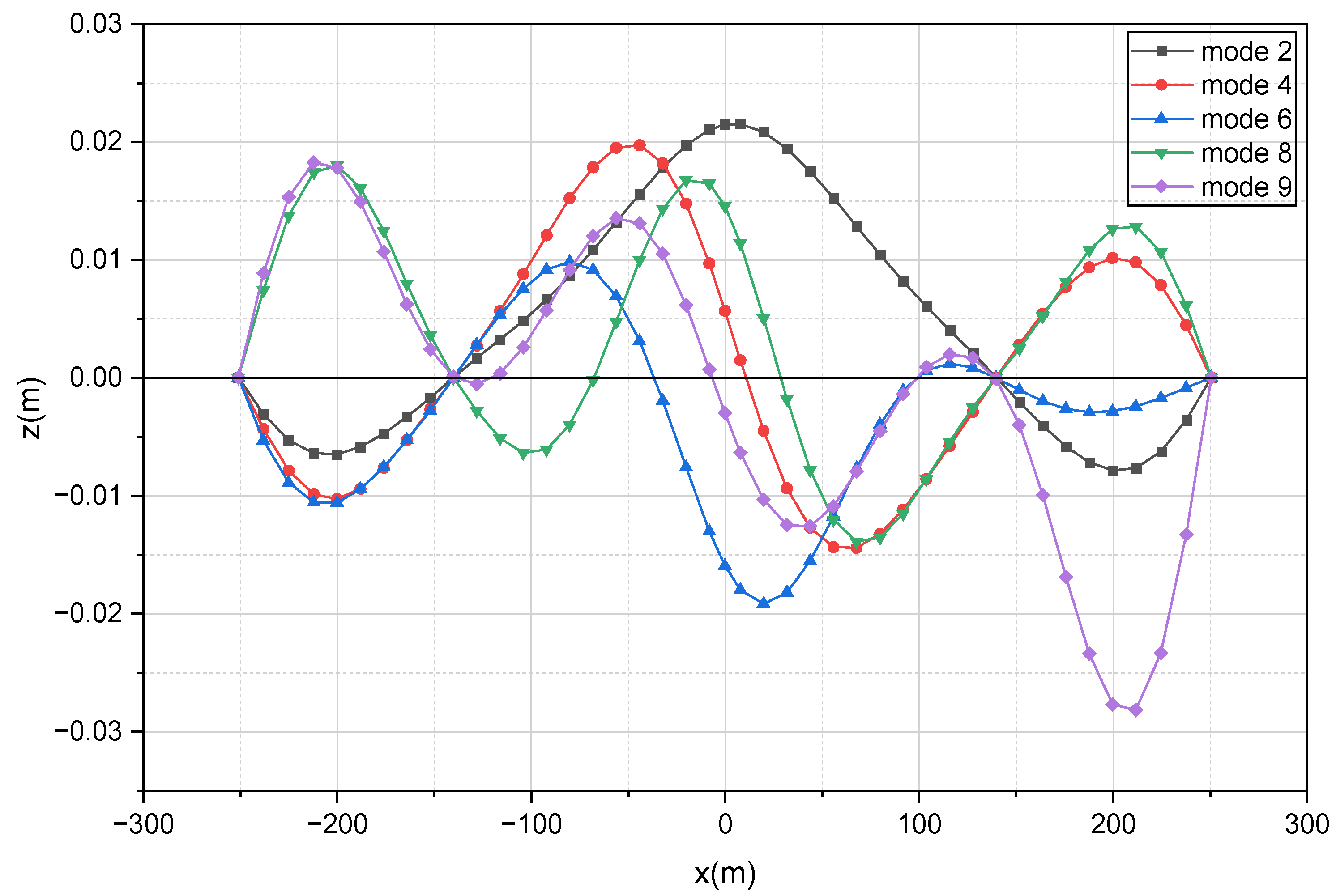
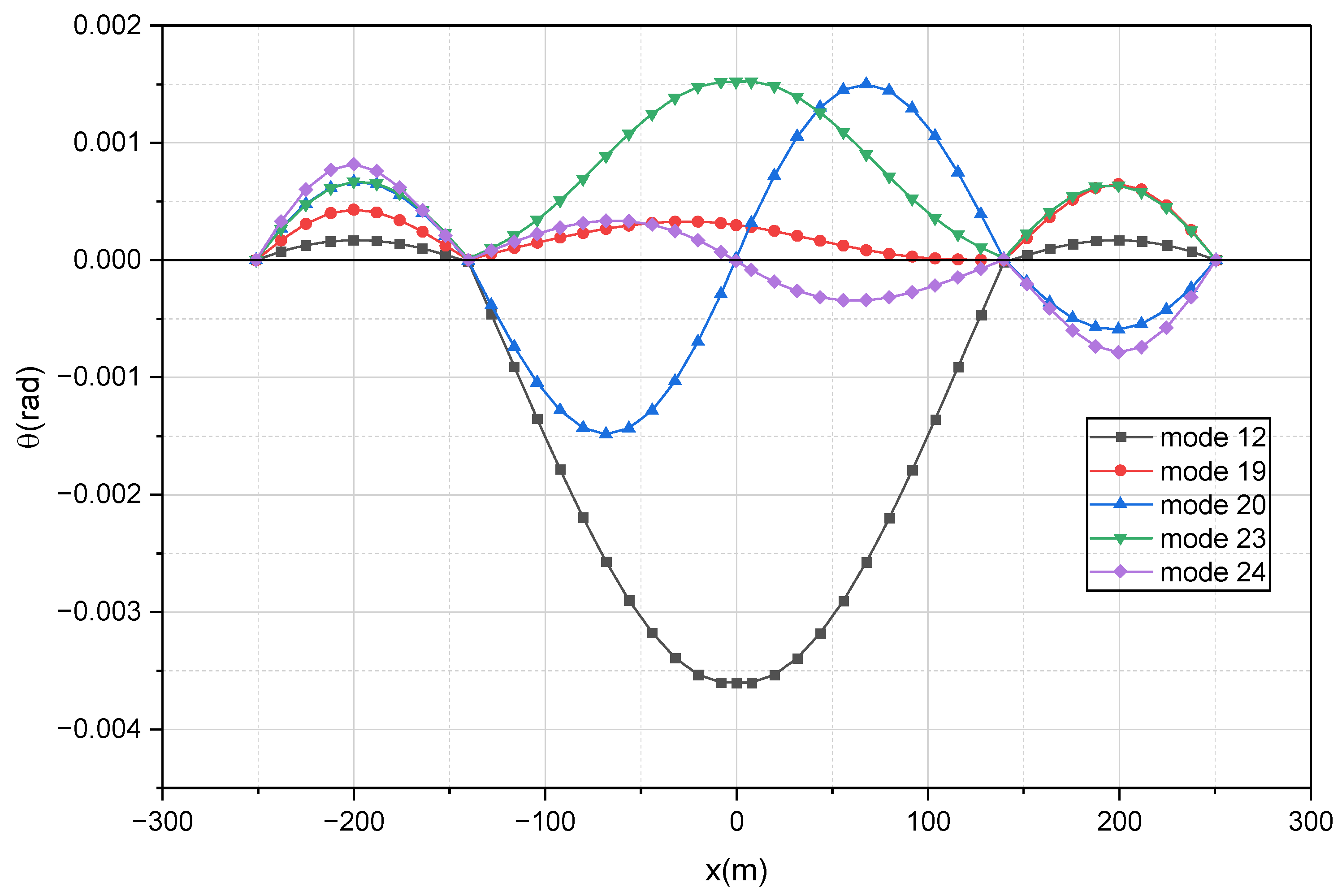
3.2. Vibration Mode Shapes
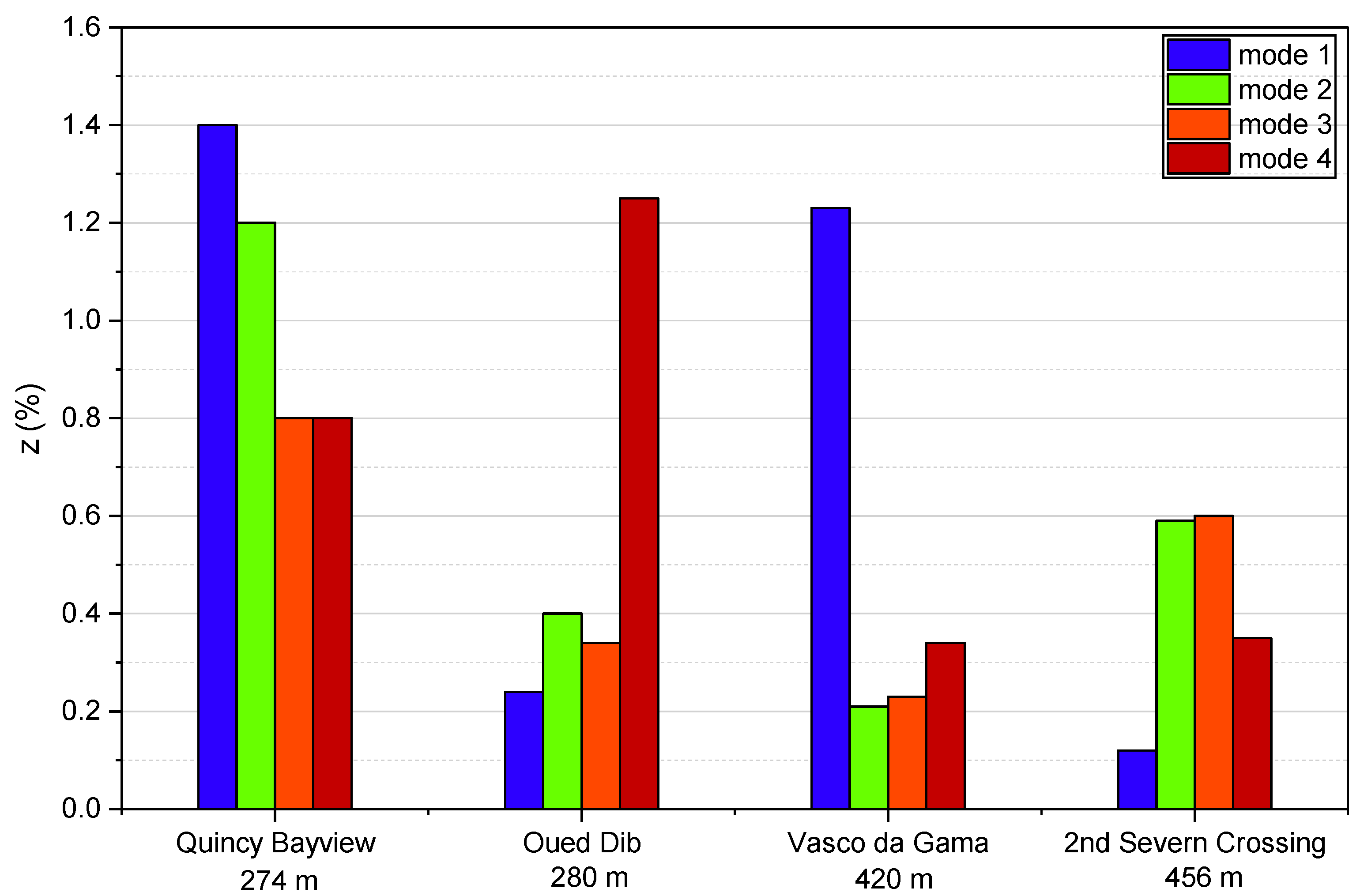
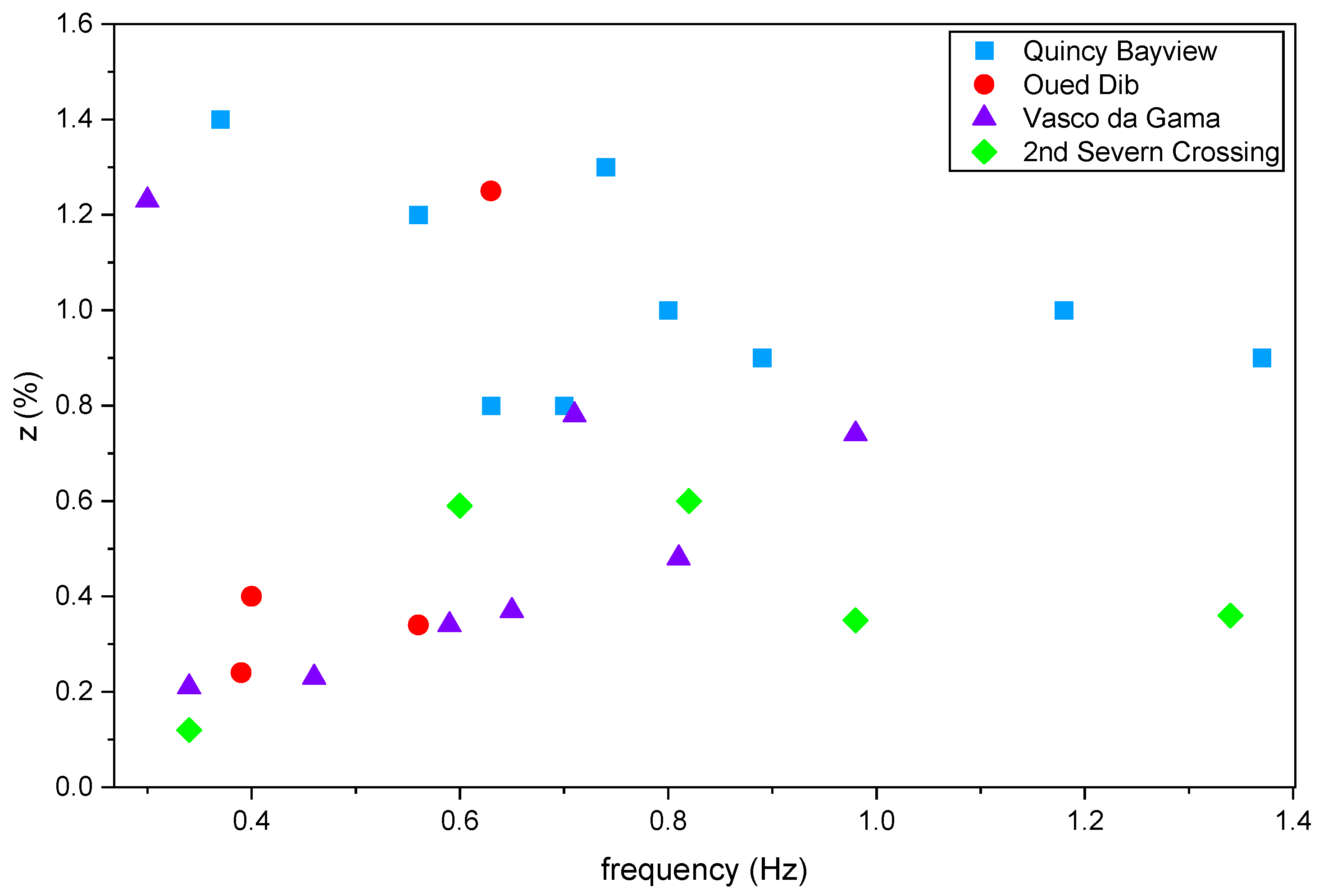
3.3. Estimation of the Modal Damping
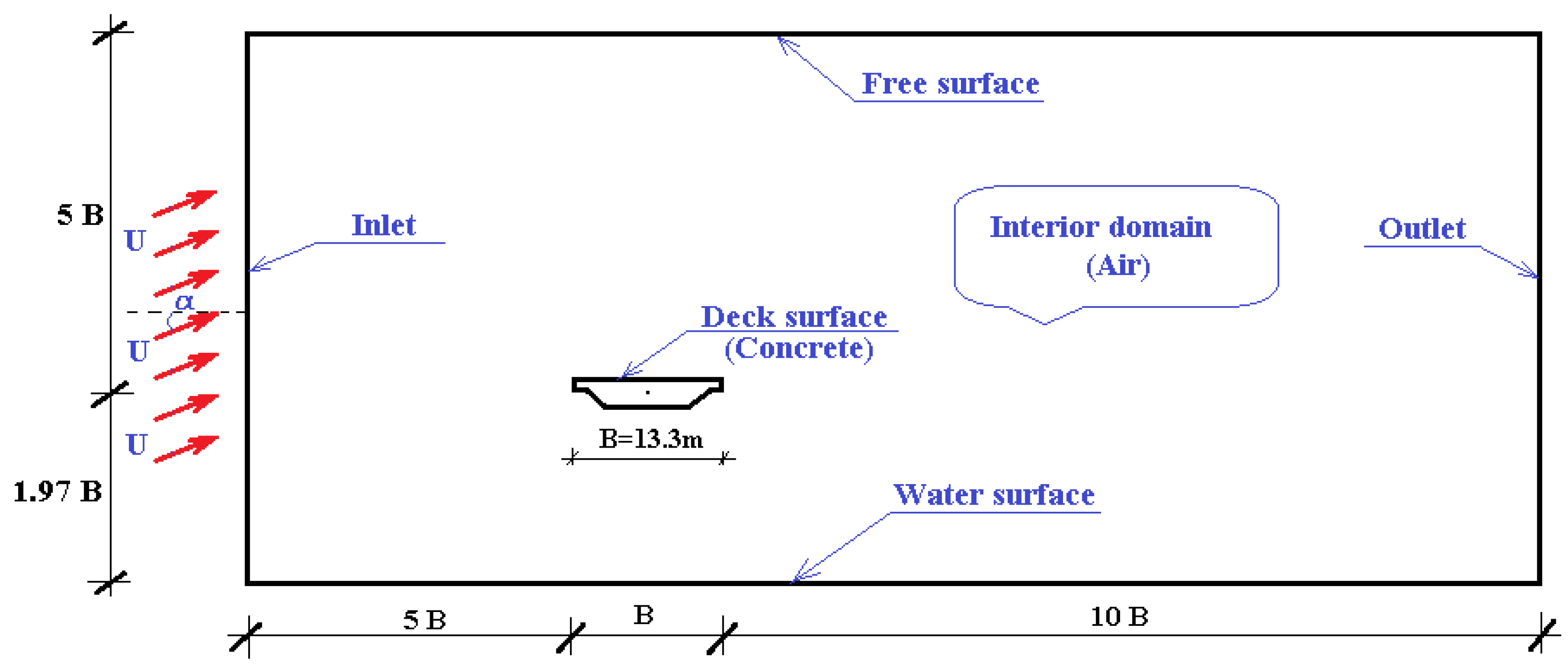
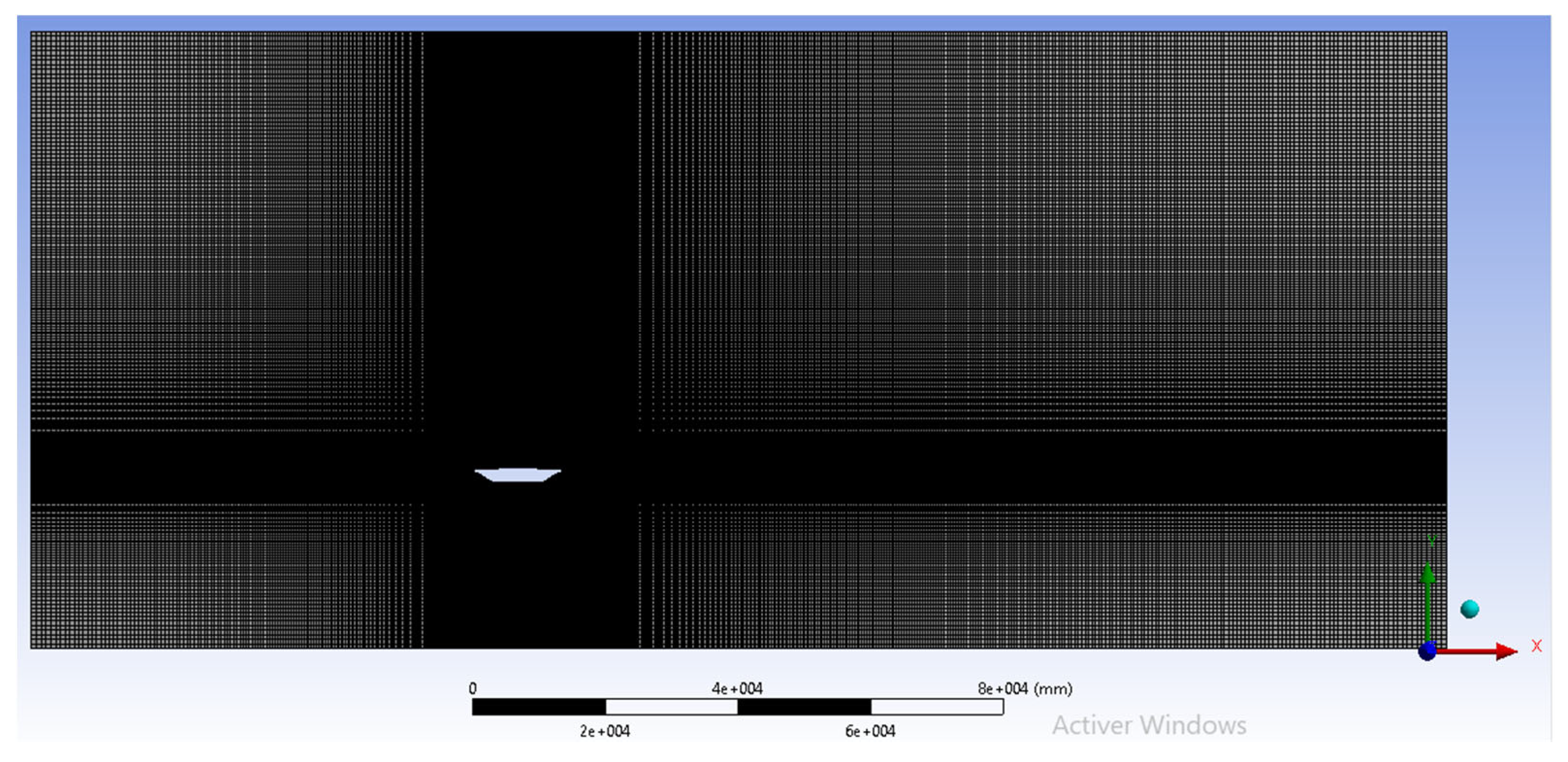
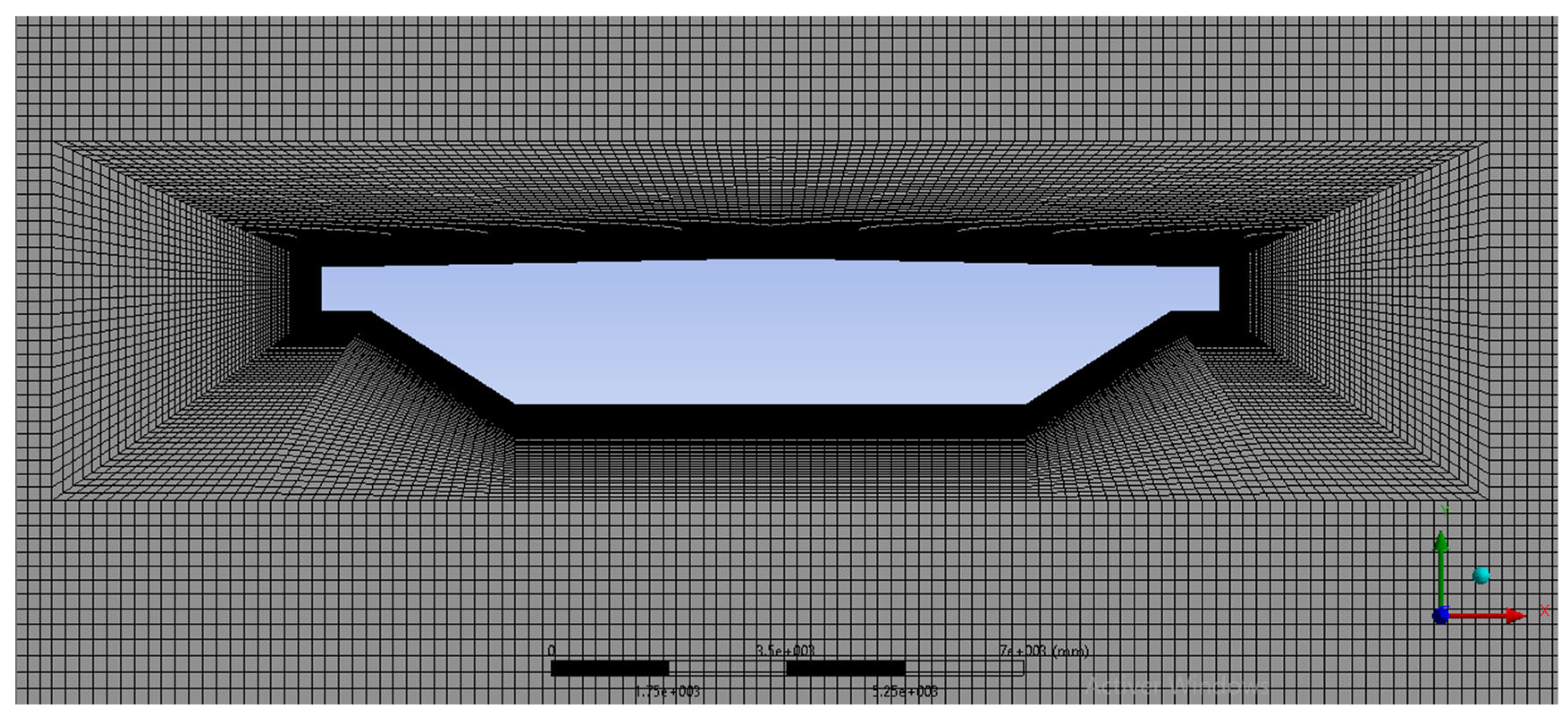
4. CFD Modeling
4.1. CFD Set-Up
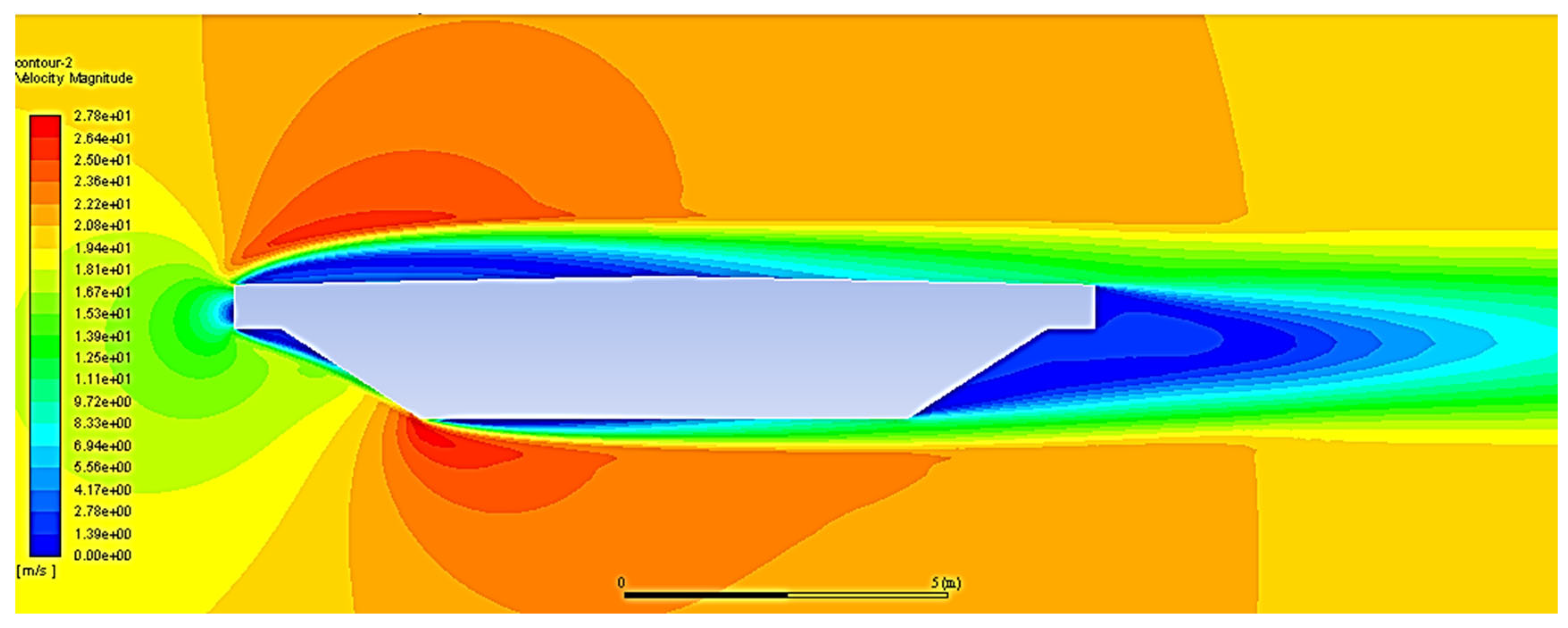
4.2. CFD Results
5. Aeroelastic Instabilities and Bridge Performance
5.1. Vortex Shedding
5.2. Flutter in a Single Vibration Mode
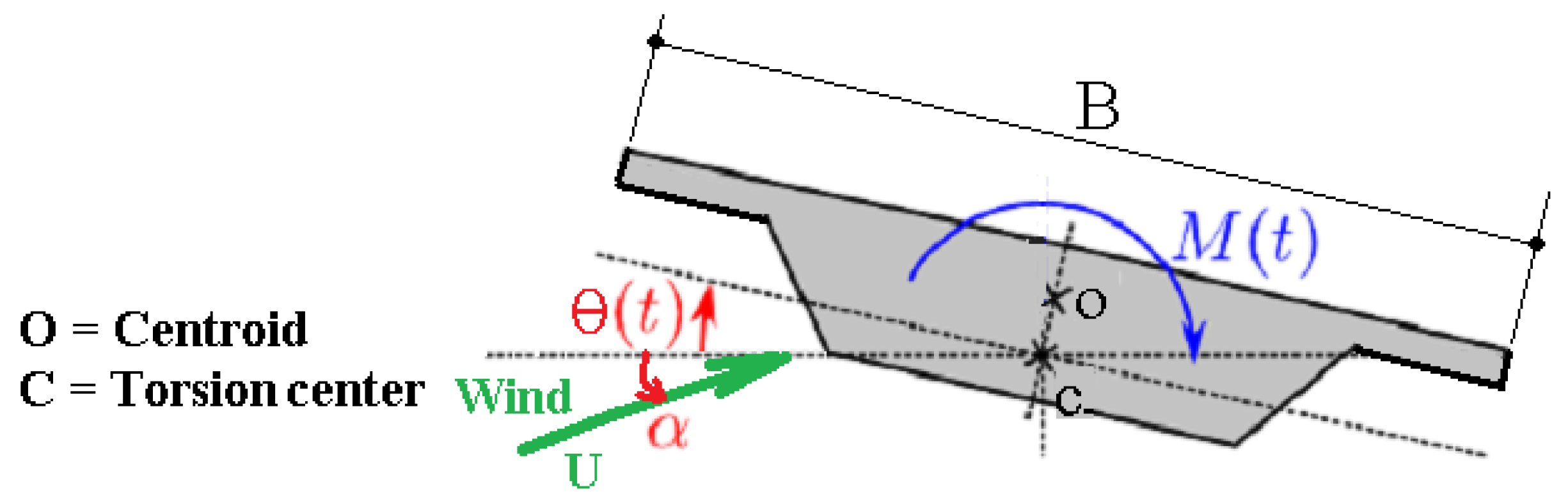
5.2.1. Galloping
5.2.2. Torsional Divergence
5.3. Flutter with Two Degrees of Freedom
5.4. Study Limitations
- Potential fatigue due to nearly continuous vortex shedding vibrations remains a concern and should be carefully monitored.
- The CFD simulations were conducted in steady-state conditions, which may not capture unsteady flow phenomena such as buffeting or transient gust effects.
- Only the deck section was modeled in CFD, without explicitly considering the influence of pylons, cables, and traffic loading.
- Aeroelastic checks were performed using linear assumptions; nonlinear effects, especially under extreme wind events, were not fully addressed.
- The analysis was limited to a single wind speed (U = 20 m/s) for static coefficient extraction, whereas variable wind intensities and turbulence spectra could affect stability margins.
6. Conclusions and Outlook
- The modal analysis in the vertical direction gave results in very good agreement with ambient vibration measurements, with a maximum deviation of 3.7% of the natural frequencies.
- The Oued Dib Bridge, when compared with four other bridges, exhibits good consistency in its modal behavior. The separation between its torsional and bending natural frequencies, with a ratio of 1.6, places it outside the risk associated with two-degree-of-freedom flutter. This demonstrates the good structural design of this bridge.
- Cable-stayed bridges exhibit low structural damping, which makes them vulnerable to wind effects. In addition, this type of structure shows strong coupling between vibration modes, which makes it impossible to use Rayleigh’s law to calculate modal damping.
- CFD analysis highlighted flow separation, vortex initiation, and backflow regions around the bluff deck section, confirming its susceptibility to vortex-induced phenomena.
- The adopted wall function value of Y+ = 30 proved appropriate for capturing boundary-layer behavior at high Reynolds numbers (Re = 1.77 × 107).
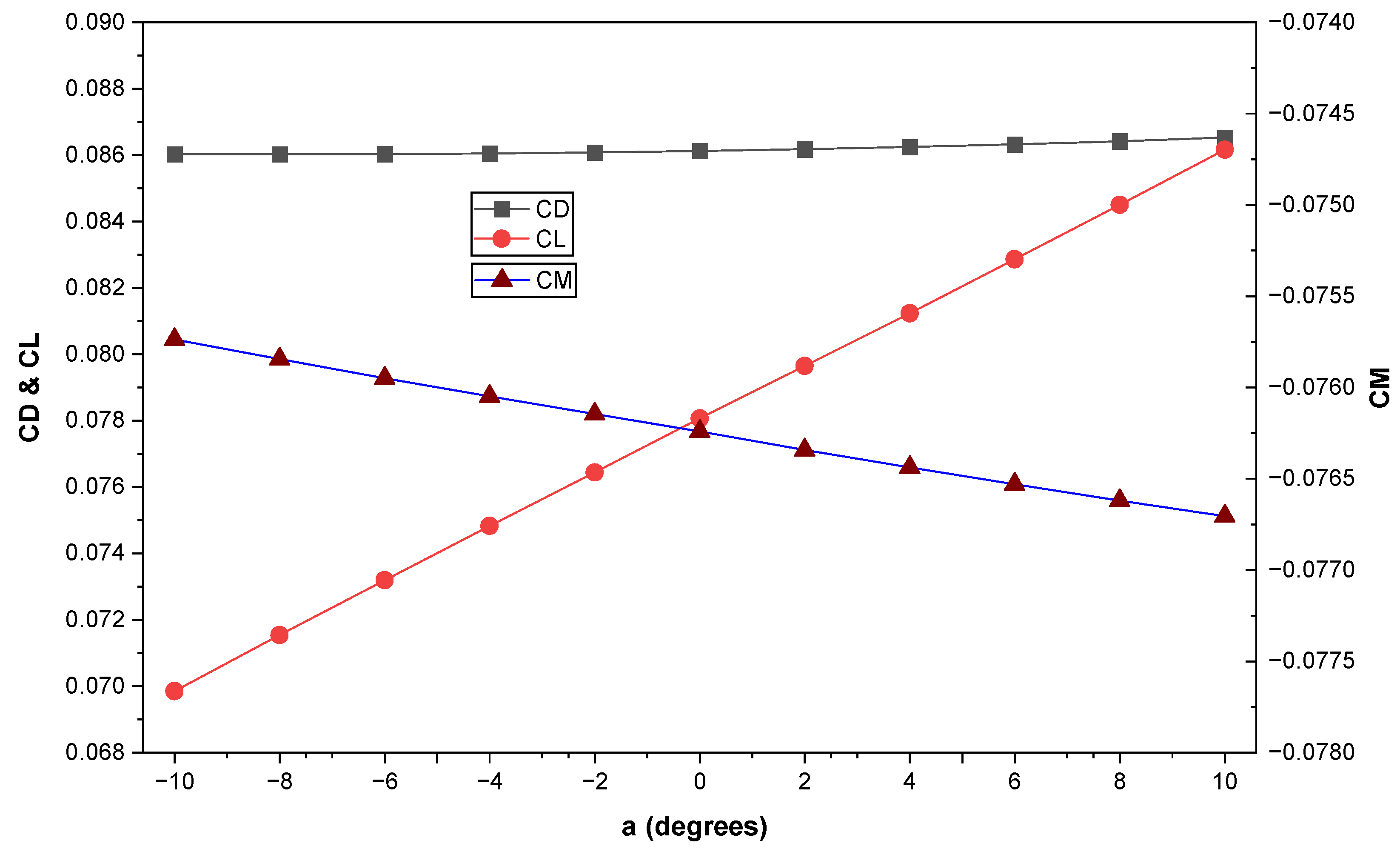
- The coefficient curve CM(α) decreased with AoA, consistent with typical bluff-body decks, unlike streamlined profiles where it increases. The negative sign of the derivative CM’(α) places the structure outside the risk of torsional divergence and two-degree-of-freedom flutter.
- Aeroelastic checks confirmed no risk of vortex shedding resonance, galloping, torsional divergence, or classical flutter under the design wind speed (Umax = 33.3 m/s).
- Extend CFD simulations to unsteady (URANS or LES) approaches to better capture vortex shedding dynamics and buffeting responses.
- Investigate the combined aeroelastic behavior of the deck and stay cables, particularly under rain–wind excitation, which can accelerate cable fatigue.
- Explore aerodynamic countermeasures, such as deck edge modifications or fairings, to mitigate vortex-induced vibrations.
- Perform aeroelastic studies under traffic loading, as moving vehicles can significantly alter the aerodynamic response of the bridge.
- Validate CFD results with wind tunnel experiments to further confirm accuracy and reliability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| U | wind speed [m/s] |
| α | wind angle of attack [°] |
| ρ | air density [Kg/m3] |
| μ | dynamic viscosity of air [Kg/m.s] |
| B | bridge deck width [m] |
| D | bridge deck thickness [m] |
| m | mass of the deck per unit length [Kg/m] |
| J | torsional constant of the deck per unit length [Kg.m2/m] |
| fz, fθ | ordinary frequencies in the vertical and rotational directions, respectively [Hz] |
| ωz, ωθ | circular frequencies in the vertical and rotational directions, respectively [rad/s] |
| ξ | damping ratio |
Abbreviations
| Sym | Symmetric mode |
| Asym | Asymmetric mode |
| Lat | Lateral mode shape |
| Long | Longitudinal mode shape |
| Ver | Vertical mode shape |
| Tor | Torsional mode shape |
References
- Zhang, B.; Zhu, L. Experimental and Computational Analysis of Large-Amplitude Flutter in the Tacoma Narrows Bridge: Wind Tunnel Testing and Finite Element Time-Domain Simulation. Buildings 2025, 15, 2800. [Google Scholar] [CrossRef]
- Wang, D.; Sun, M.; Ma, R.; Shen, X. Numerical Modeling of Ice Accumulation on Three-Dimensional Bridge Cables under Freezing Rain and Natural Wind Conditions. Symmetry 2022, 14, 396. [Google Scholar] [CrossRef]
- Deng, Y.; Li, L.; Li, S.; Hu, W. Experimental study on features and control of wind-induced instability of parallel dual main cables of ultra-long-span suspension bridge in construction phases. Eng. Struct. 2025, 333, 120141. [Google Scholar] [CrossRef]
- Li, S.; Wang, P.; Wu, Y.; Zou, Y.; Yang, Q.; Tian, J.; Zhou, Y. Experiment study on vortex-induced vibration of variable cross-section bridge tower considering alongwind and acrosswind coupling effect. Eng. Struct. 2025, 327, 119678. [Google Scholar] [CrossRef]
- Guo, H.; Tian, S.; Li, J. The Vortex-Induced Vibration Characteristics of the Water-Conveying Truss Pipeline Cable-Stayed Bridge. Appl. Sci. 2025, 15, 9437. [Google Scholar] [CrossRef]
- Chen, X.; Yu, H.; Yu, H.; Zhao, P.; Li, M. Aerodynamic Loading and Wind-Induced Vibration Characteristics of Bridge Girders with Typical Asymmetric Configurations. Buildings 2025, 15, 2824. [Google Scholar] [CrossRef]
- Holmes, J.D. Wind Loading of Structures, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Larsen, A. Aerodynamics of the Tacoma Narrows Bridge-60 years later. Struct. Eng. Int. 2000, 10, 243–248. [Google Scholar] [CrossRef]
- Green, D.; Unruh, W.G. The failure of the Tacoma Bridge: A physical model. Am. J. Phys. 2006, 74, 706–716. [Google Scholar] [CrossRef]
- Song, D.; Kim, W.; Kwon, O.K.; Choi, H. Vertical and torsional vibrations before the collapse of the Tacoma Narrows Bridge in 1940. J. Fluid Mech. 2022, 949, A11. [Google Scholar] [CrossRef]
- Hu, C.; Zhao, L.; Ge, Y. Wind-induced instability mechanism of Old Tacoma Narrows Bridge from aerodynamic work perspective. J. Bridge Eng. 2022, 27, 04022029. [Google Scholar] [CrossRef]
- Ammann, O.H.; Woodruff, G.B. The Failure of the Tacoma Narrows Bridge; Federal Works Agency: Washington, DC, USA, 1941. [Google Scholar]
- Scanlan, R.H. The Action of Flexible Bridges under Wind, I: Flutter Theory. J. Sound Vib. 1978, 60, 187–199. [Google Scholar] [CrossRef]
- Scanlan, R.H. Motion-related body-force functions in two-dimensional low-speed flow. J. Fluids Struct. 2000, 14, 49–63. [Google Scholar] [CrossRef]
- Scanlan, R. Problematic in Formulation of Wind-Force Model for Bridge Decks. J. Struct. Eng. Asce 1993, 119, 1433–1446. [Google Scholar] [CrossRef]
- Scanlan, R.H.; Beliveau, J.G.; Budlong, K.S. Indicial Aerodynamic Functions for Bridge Decks. J. Eng. Mech. Div. 1974, 100, 657–672. [Google Scholar] [CrossRef]
- Huston, D.R.; Bosch, H.R.; Scanlan, R.H. The Effects of Fairings and of Turbulence on the Flutter Derivatives of a Notably Unstable Bridge Deck. J. Wind. Eng. Ind. Aerodyn. 1988, 29, 339–349. [Google Scholar] [CrossRef]
- Diana, G.; Resta, F.; Rocchi, D. A New Numerical Approach to Reproduce Bridge Aerodynamic Non-Linearities in Time Domain. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 1871–1884. [Google Scholar] [CrossRef]
- Diana, G.; Rocchi, D.; Argentini, T.; Muggiasca, S. Aerodynamic Instability of a Bridge Deck Section Model: Linear and Nonlinear Approach to Force Modeling. J. Wind. Eng. Ind. Aerodyn. 2010, 98, 363–374. [Google Scholar] [CrossRef]
- Diana, G.; Rocchi, D.; Argentini, T. An Experimental Validation of a Band Superposition Model of the Aerodynamic Forces Acting on Multi-Box Deck Sections. J. Wind. Eng. Ind. Aerodyn. 2013, 113, 40–58. [Google Scholar] [CrossRef]
- Gao, G.; Zhu, L.; Han, W.; Li, J. Nonlinear Post-Flutter Behavior and Self-Excited Force Model of a Twin-Side-Girder Bridge Deck. J. Wind. Eng. Ind. Aerodyn. 2018, 177, 227–241. [Google Scholar] [CrossRef]
- Diana, G.; Resta, F.; Zasso, A.; Belloli, M.; Rocchi, D. Forced Motion and Free Motion Aeroelastic Tests on a New Concept Dynamometric Section Model of the Messina Suspension Bridge. J. Wind. Eng. Ind. Aerodyn. 2004, 92, 441–462. [Google Scholar] [CrossRef]
- Náprstek, J.; Pospíšil, S.; Hračov, S. Analytical and Experimental Modelling of Non-Linear Aeroelastic Effects on Prismatic Bodies. J. Wind. Eng. Ind. Aerodyn. 2007, 95, 1315–1328. [Google Scholar] [CrossRef]
- Gao, G.; Zhu, L.; Wang, F.; Bai, H.; Hao, J. Experimental Investigation on the Nonlinear Coupled Flutter Motion of a Typical Flat Closed-Box Bridge Deck. Sensors 2020, 20, 568. [Google Scholar] [CrossRef]
- Bucher, C.G.; Lin, Y.K. Stochastic Stability of Bridges Considering Coupled Modes. J. Eng. Mech. 1988, 114, 384–400. [Google Scholar] [CrossRef]
- Bucher, C.G.; Lin, Y.K. Stochastic Stability of Bridges Considering Coupled Modes: II. J. Eng. Mech. 1989, 115, 384–400. [Google Scholar] [CrossRef]
- Wu, T.; Kareem, A. Modeling Hysteretic Nonlinear Behavior of Bridge Aerodynamics via Cellular Automata nested neural network. J. Wind. Eng. Ind. Aerodyn. 2011, 99, 378–388. [Google Scholar] [CrossRef]
- Bleich, F. Dynamic instability of truss-stiffened suspension bridges under wind action. Trans. Am. Soc. Civ. Eng. 1949, 114, 1177–1222. [Google Scholar] [CrossRef]
- Bisplinghoff, R.L.; Ashley, H. Principles of Aeroelasticity; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Scanlan, R.H.; Tomko, J.J. Airfoil and bridge deck flutter derivatives. J. Eng. Mech. Div. 1971, 97, 1717–1737. [Google Scholar] [CrossRef]
- Wilson, J.C.; Gravelle, W. Modelling of a cable-stayed bridge for dynamic analysis. Earthq. Eng. Struct. Dyn. 1991, 20, 707–721. [Google Scholar] [CrossRef]
- Kumar, S.; Nallasivam, K. Modal analysis of natural dynamic frequency for a double deck cable-stayed steel bridge by using finite element method. Discov. Civ. Eng. 2024, 1, 115. [Google Scholar] [CrossRef]
- Wen, Y.; Zhou, Z. Qualification of the Ernst formula for modeling the sag effect of super-long stay cables in the long-span railway cable-stayed bridges. Structures 2022, 45, 99–109. [Google Scholar] [CrossRef]
- EN 1337; Structural Bearings. European Committee for Standardization: Brussels, Belgium, 2004.
- Yamaguchi, H.; Ito, M. Mode-dependence of structural damping in cable-stayed bridges. J. Wind Eng. Ind. Aerodyn. 1997, 72, 289–300. [Google Scholar] [CrossRef]
- Kibboua, A.; Farsi, M.N.; Chatelain, J.L.; Guillier, B.; Bechtoula, H.; Mehani, Y. Modal analysis and ambient vibration measurements on Mila-Algeria cable stayed bridge. Struct. Eng. Mech. 2008, 29, 171–186. [Google Scholar] [CrossRef]
- Pridham, B.A.; Wilson, J.C. A reassessment of dynamic characteristics of the Quincy Bayview Bridge using output-only identification techniques. Earthq. Engng. Struct. Dyn. 2005, 34, 787–805. [Google Scholar] [CrossRef]
- Zhong, R.; Zong, Z.; Niu, J.; Liu, Q.; Zheng, P. A multiscale finite element model validation method of composite cable-stayed bridge based on Probability Box theory. J. Sound Vib. 2016, 370, 111–131. [Google Scholar] [CrossRef]
- Cunha, A.; Caetano, E.; Delgado, R. Dynamic Tests on Large Cable-Stayed Bridge. J. Bridge Eng. 2001, 6, 54–62. [Google Scholar] [CrossRef]
- Macdonald, J.H.G.; Daniell, W.E. Variation of modal parameters of a cable-stayed bridge identified from ambient vibration measurements and FE modelling. Eng. Struct. 2005, 27, 1916–1930. [Google Scholar] [CrossRef]
- Lefaucheur, D.; Bouchon, E. Conception des Ponts à Haubans, Un Savoir Faire Français; Cerema: Bron, France, 2016. [Google Scholar]
- RNV. Snow and Wind Regulation; National Center of Integrated Studies and Research of Building: Algiers, Algeria, 2013. [Google Scholar]
- EN 1991-1-4; Eurocode 1: Actions on Structures—Part 1–4: General Actions—Wind Actions. European Committee for Standardization: Brussels, Belgium, 2005.
- Gulich, D.; Tebaldi, M.; Sierra-Sosa, D. Automatic Quantification of Atmospheric Turbulence Intensity in Space-Time Domain. Sensors 2025, 25, 1483. [Google Scholar] [CrossRef]
- Franke, J.; Hellsten, A.; Schlunzen, K.H.; Carissimo, B. The COST 732 Best Practice Guideline for CFD simulation of flows in the urban environment: A summary. Int. J. Environ. Pollut. 2011, 44, 419–427. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Jeong, W.; Liu, S.; Bogunovic Jakobsen, J.; Ong, M.C. Unsteady RANS simulations of flow around a twin-box bridge girder cross section. Energies 2019, 12, 2670. [Google Scholar] [CrossRef]
- Hernández, S.; Nieto, F.; Jurado, J.A.; Pérez, I. Bluff body aerodynamics of simplified bridge decks for aeroelastic optimization. In Proceedings of the 7th International Colloquium on Bluff Body Aerodynamics and Applications, Shanghai, China, 2–6 September 2012. [Google Scholar]
- Dong, X.; Zhao, L.; Cui, W.; Peng, Y.; Ge, Y. Aerodynamics and aeroelastic performance of a rigid-frame bridge with a bluff body girder subjected to short-rise-time gusts. Eng. Struct. 2022, 263, 114376. [Google Scholar] [CrossRef]
- Potts, D.A.; Marcollo, H.; Jayasinghe, K. Strouhal number for vortex-induced vibration excitation of long slender structures. J. Offshore Mech. Arct. Eng. 2022, 144, 041906. [Google Scholar] [CrossRef]
- Pan, T.; Li, T.; Li, C.; Yan, Z.; Li, Q. Frequency lock-in mechanism in the presence of blockage effects. Phys. Fluids 2024, 36, 077132. [Google Scholar] [CrossRef]
- Cremona, C. Comportement au Vent des Ponts; Presses de l’Ecole Nationale des Ponts et Chaussées: Paris, France, 2002. [Google Scholar]
- Chen, C.; Mannini, C.; Bartoli, G.; Thiele, K. Experimental study and mathematical modeling on the unsteady galloping of a bridge deck with open cross section. J. Wind Eng. Ind. Aerodyn. 2020, 203, 104170. [Google Scholar] [CrossRef]
- Ma, Z.; Li, J.; Liu, S.; Li, H.; Wang, F. Research on an Improved Method for Galloping Stability Analysis Considering Large Angles of Attack. Appl. Sci. 2023, 13, 5390. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, J.; Zeng, J.; Zhang, Z. Wind-induced asymmetry torsional divergence of long-span bridges: Mechanism, three-dimensional and turbulence effects. Int. J. Struct. Stab. Dyn. 2023, 23, 2350042. [Google Scholar] [CrossRef]

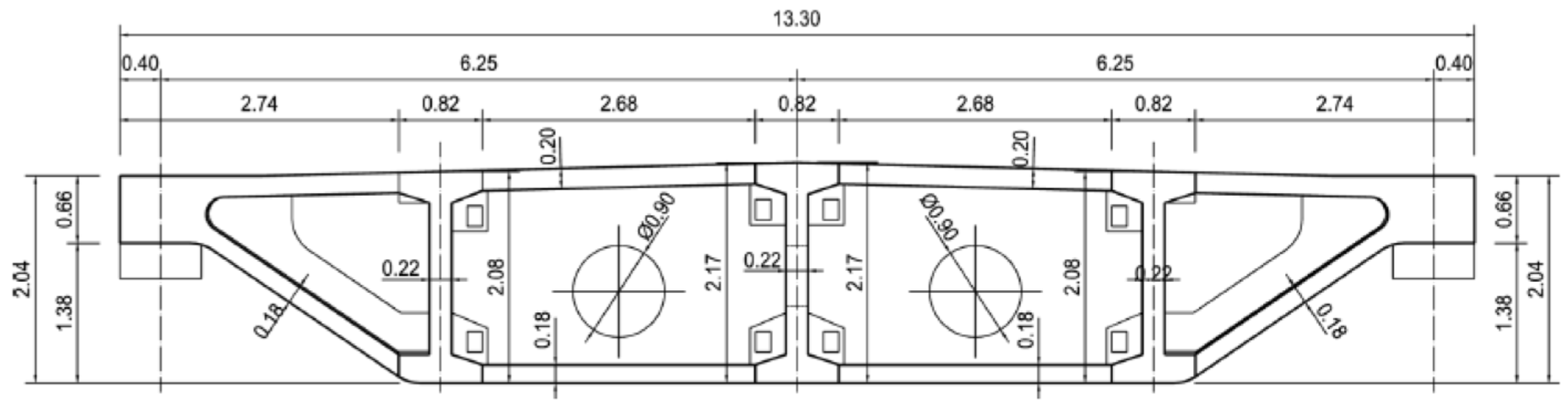












| Mechanical Characteristics | Deck | Pylons | Cables |
|---|---|---|---|
| Young’s modulus (GPa) | 39.0 | 39.0 | 210.0 |
| Poisson’s ratio | 0.2 | 0.2 | 0.3 |
| Weight density (kN/m3) | 25 | 25 | 80 |
| Mode Index | Frequency (Hz) | Principal Component | Other Components |
|---|---|---|---|
| 1 | 0.356 | Deck Lat Sym | Pylon East Lat |
| 2 | 0.415 | Deck Vert Sym | Pylons Long |
| 3 | 0.511 | Deck Lat Sym | Pylons Lat |
| 4 | 0.609 | Pylons Long | Deck Vert ASym |
| 5 | 0.634 | Pylon West Lat | Deck Lat Sym |
| 6 | 0.824 | Pylon East Long | Deck Vert ASym |
| 7 | 0.960 | Pylon East Lat | Deck Lat ASym |
| 8 | 1.064 | Pylons Long | Deck Vert Sym |
| 9 | 1.171 | Pylons Long | Deck Vert ASym |
| 10 | 1.210 | Pylons Lat | Deck Lat ASym |
| 11 | 1.286 | Deck Vert Sym | Pylons Long |
| 12 | 1.309 | Deck Tor Sym | --- |
| Direction | Measurement (Hz) | FE Model (Hz) | Error (%) |
|---|---|---|---|
| Lat1 | 0.390 | 0.356 | 8.7 |
| Lat2 | 0.550 | 0.511 | 7.1 |
| Ver1 | 0.400 | 0.415 | 3.7 |
| Ver2 | 0.630 | 0.609 | 3.3 |
| Long1 | 0.380 | 0.415 | 9.2 |
| Long2 | 0.560 | 0.609 | 8.7 |
| N° | Name | Country | Deck Material | Main Span L (m) | Side Spans L′ (m) | Deck Wide B (m) | 1st Vert Mode (Hz) | 1st Lat Mode (Hz) | 1st Tor Mode (Hz) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Quincy Bayview | USA | composite | 274 | 2 × 134 | 14.2 | 0.37 | 0.56 | 0.56 |
| 2 | Oued Dib | Algeria | concrete | 280 | 2 × 111 | 13.3 | 0.40 | 0.39 | 0.64 |
| 3 | Guanhe | China | composite | 340 | 2 × 150 | 34.0 | 0.38 | 0.39 | 0.63 |
| 4 | Vasco da Gama | Portugal | concrete | 420 | 2 × 204.6 | 31.0 | 0.34 | 0.30 | 0.47 |
| 5 | 2nd Severn Crossing | UK | composite | 456 | 2 × 245.3 | 34.6 | 0.35 | 0.34 | 0.56 |
| Quincy Bayview L = 274 m | Oued Dib L = 280 m | Vasco da Gama L = 420 m | 2nd Severn Crossing L = 456 m | ||||
|---|---|---|---|---|---|---|---|
| f [Hz] | ξ [%] | f [Hz] | ξ [%] | f [Hz] | ξ [%] | f [Hz] | ξ [%] |
| 0.37 | 1.4 | 0.39 | 0.24 | 0.30 | 1.23 | 0.34 | 0.12 |
| 0.56 | 1.2 | 0.4 | 0.4 | 0.34 | 0.21 | 0.6 | 0.59 |
| 0.63 | 0.8 | 0.56 | 0.34 | 0.46 | 0.23 | 0.82 | 0.60 |
| 0.7 | 0.8 | 0.63 | 1.25 | 0.59 | 0.34 | 0.98 | 0.35 |
| 0.74 | 1.3 | - | - | 0.65 | 0.37 | 1.34 | 0.36 |
| 0.8 | 1.0 | - | - | 0.71 | 0.78 | - | - |
| 0.89 | 0.9 | - | - | 0.81 | 0.48 | - | - |
| 1.18 | 1.0 | - | - | 0.98 | 0.74 | - | - |
| 1.37 | 0.9 | - | - | - | - | - | - |
| Boundary | Velocity (U) | Pressure (P) |
|---|---|---|
| Inlet | U = 20 m/s; α = variable | Zero gradient |
| Outlet | Zero gradient | P = 0 |
| Deck surface | Ux = 0; Uy = 0; roughness= 0.3 mm | Zero gradient |
| Water surface | Ux = 0; Uy = 0; roughness = 0 | Zero gradient |
| Free surface | Zero gradient | Zero gradient |
| α (°) | CD | CL | CM |
|---|---|---|---|
| −10.0 | 0.086031 | 0.069853 | −0.075736 |
| −8.0 | 0.086031 | 0.071542 | −0.075845 |
| −6.0 | 0.086036 | 0.073197 | −0.075949 |
| −4.0 | 0.086052 | 0.074833 | −0.076048 |
| −2.0 | 0.086088 | 0.076442 | −0.076145 |
| 0.0 | 0.086128 | 0.078070 | −0.076241 |
| 2.0 | 0.086181 | 0.079649 | −0.076342 |
| 4.0 | 0.086253 | 0.081237 | −0.076438 |
| 6.0 | 0.086329 | 0.082864 | −0.076530 |
| 8.0 | 0.086419 | 0.084508 | −0.076619 |
| 10.0 | 0.086529 | 0.086167 | −0.076705 |
| Mode Index | fvs (Hz) | Ucr,v (m/s) |
|---|---|---|
| mode 2 | 0.415 | 8.47 |
| mode 4 | 0.609 | 12.42 |
| mode 6 | 0.824 | 16.81 |
| mode 8 | 1.064 | 21.71 |
| mode 9 | 1.171 | 23.89 |
| ξ = 0.4% | δs = 0.025 | m = 21,540 Kg/mL Sc = 211.26 | ρ = 1.225 Kg/m3 | D = 2.04 m |
| Sc = 211.26 | aG = 4.7 | f1,z = 0.415 Hz UC,G = 76.11 m/s | D = 2.04 m | Umax = 33.3 m/s |
| B = 13.3 m | J = 40,694 Kg.m | ρ = 1.225 Kg/m3 | C’M(0) = −0.00286 Ucr,fl = 1143 m/s | fθ = 1.309 Hz | fz = 1.402 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Louhibi, Z.S.M.; Chioukh, N.; Daoud, S.M.; Harrat, Z.R.; Harirchian, E.; Mansour, W. Computational Fluid Dynamics Approach to Aeroelastic Stability in Cable-Stayed Bridges. Buildings 2025, 15, 3509. https://doi.org/10.3390/buildings15193509
Louhibi ZSM, Chioukh N, Daoud SM, Harrat ZR, Harirchian E, Mansour W. Computational Fluid Dynamics Approach to Aeroelastic Stability in Cable-Stayed Bridges. Buildings. 2025; 15(19):3509. https://doi.org/10.3390/buildings15193509
Chicago/Turabian StyleLouhibi, Zouhir S. M., Nadji Chioukh, Sidi Mohammed Daoud, Zouaoui R. Harrat, Ehsan Harirchian, and Walid Mansour. 2025. "Computational Fluid Dynamics Approach to Aeroelastic Stability in Cable-Stayed Bridges" Buildings 15, no. 19: 3509. https://doi.org/10.3390/buildings15193509
APA StyleLouhibi, Z. S. M., Chioukh, N., Daoud, S. M., Harrat, Z. R., Harirchian, E., & Mansour, W. (2025). Computational Fluid Dynamics Approach to Aeroelastic Stability in Cable-Stayed Bridges. Buildings, 15(19), 3509. https://doi.org/10.3390/buildings15193509








