Research on the Punching Shear Performance of Steel Grid–UHPC Composite Bridge Decks
Abstract
1. Introduction
2. Experimental Work
2.1. Geometric Dimensioning of Test Specimens
2.2. Material Property
2.2.1. UHPC
2.2.2. T-Shaped Steel and Rebar
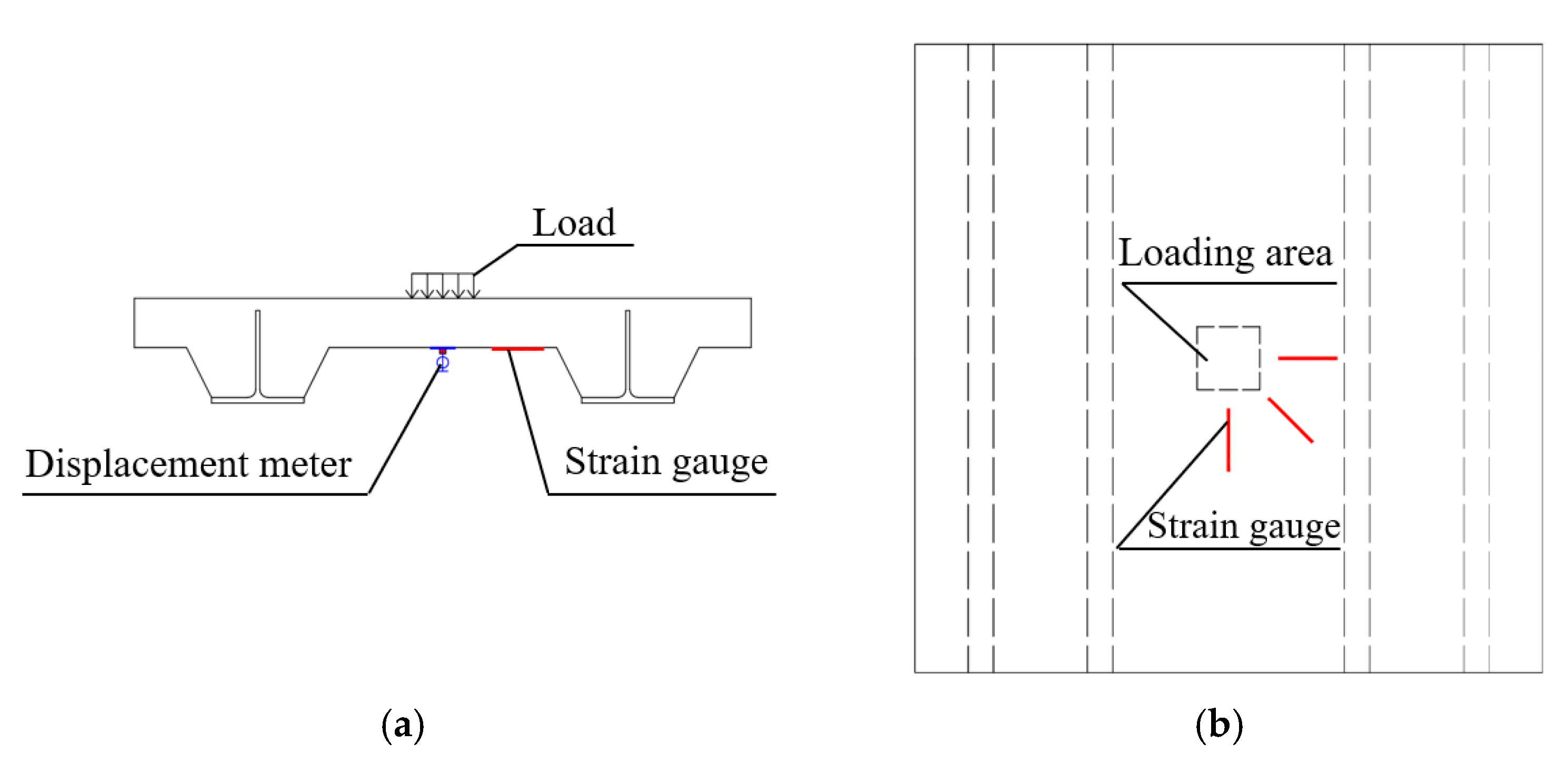
2.3. Loading Device and Measuring Device
3. Finite Element Model
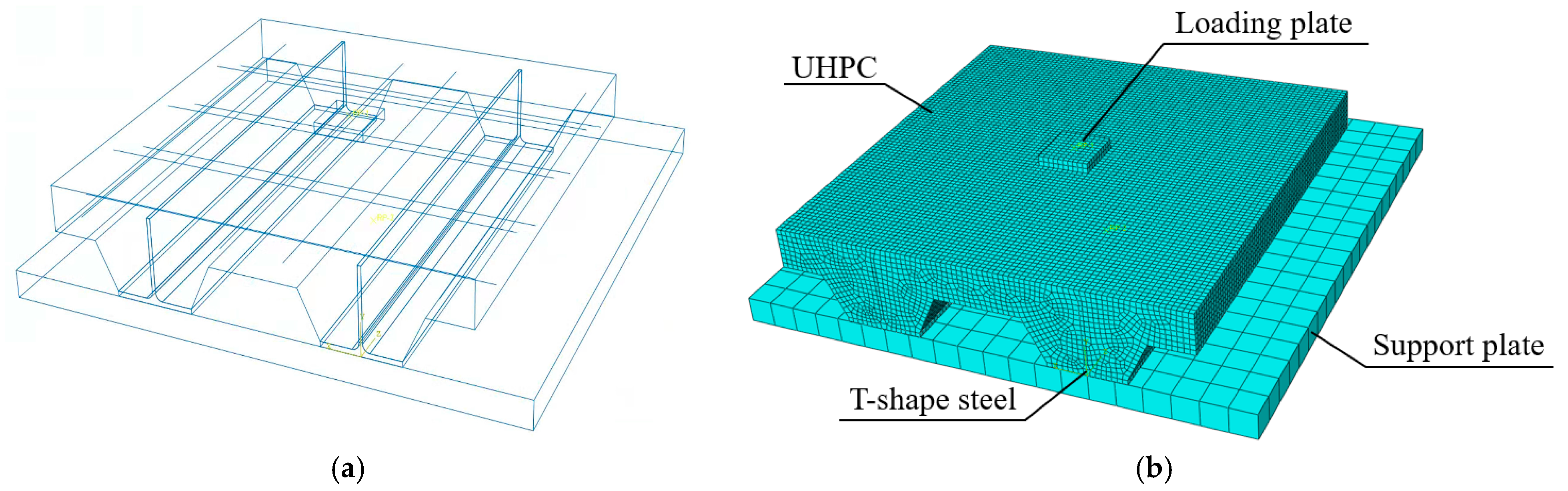
3.1. Finite Element Model and Mesh Division
3.2. Boundary Conditions
3.3. Material Parameters
4. Comparison Between Finite Element Analysis and Experimental Results
4.1. Specimen CQD4
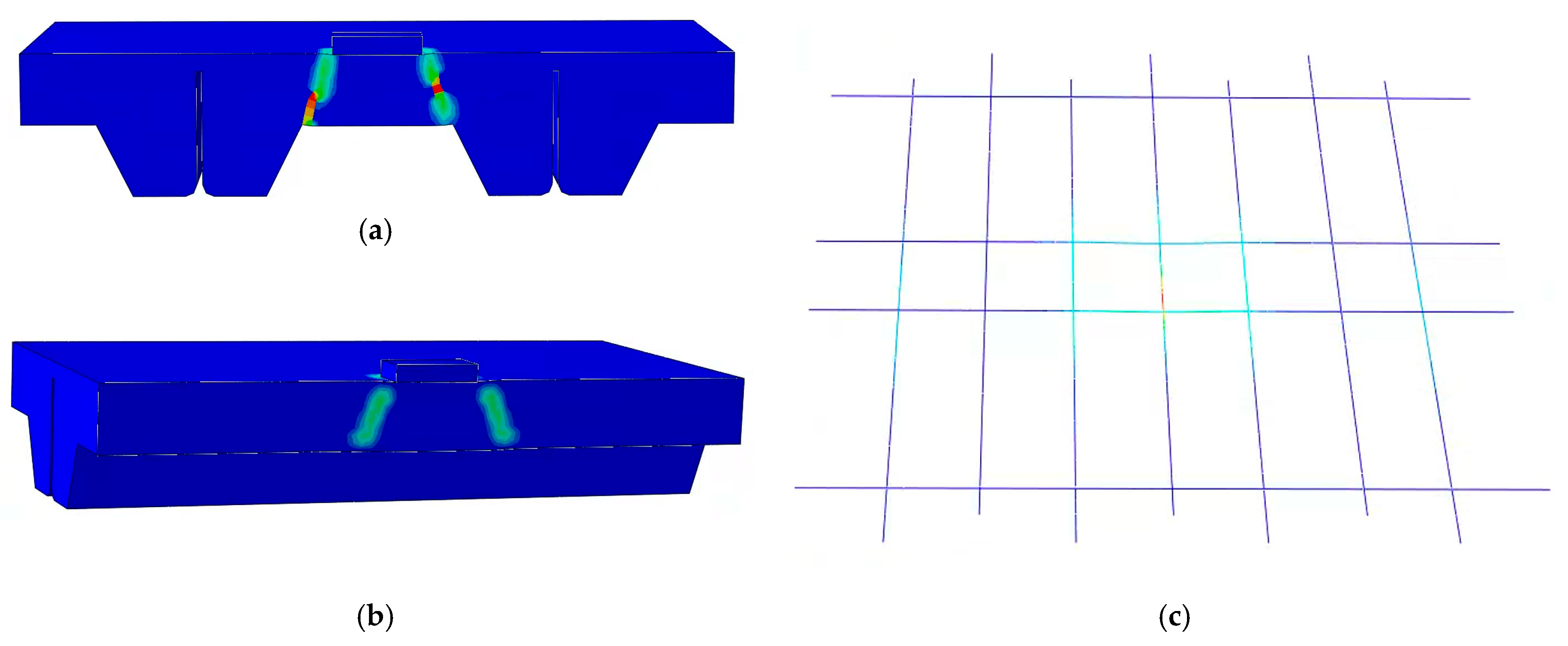
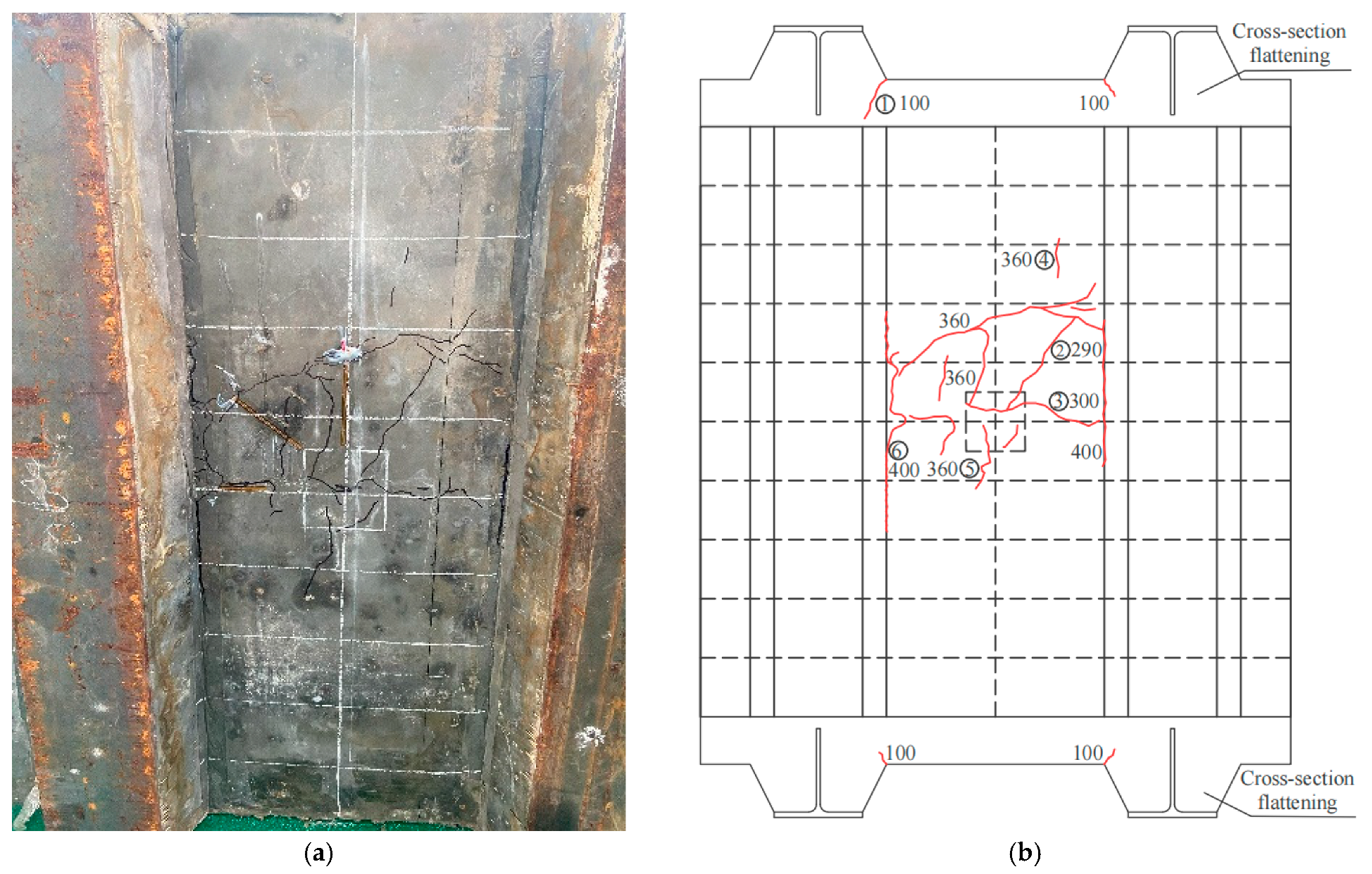
4.1.1. Experimental Phenomenon
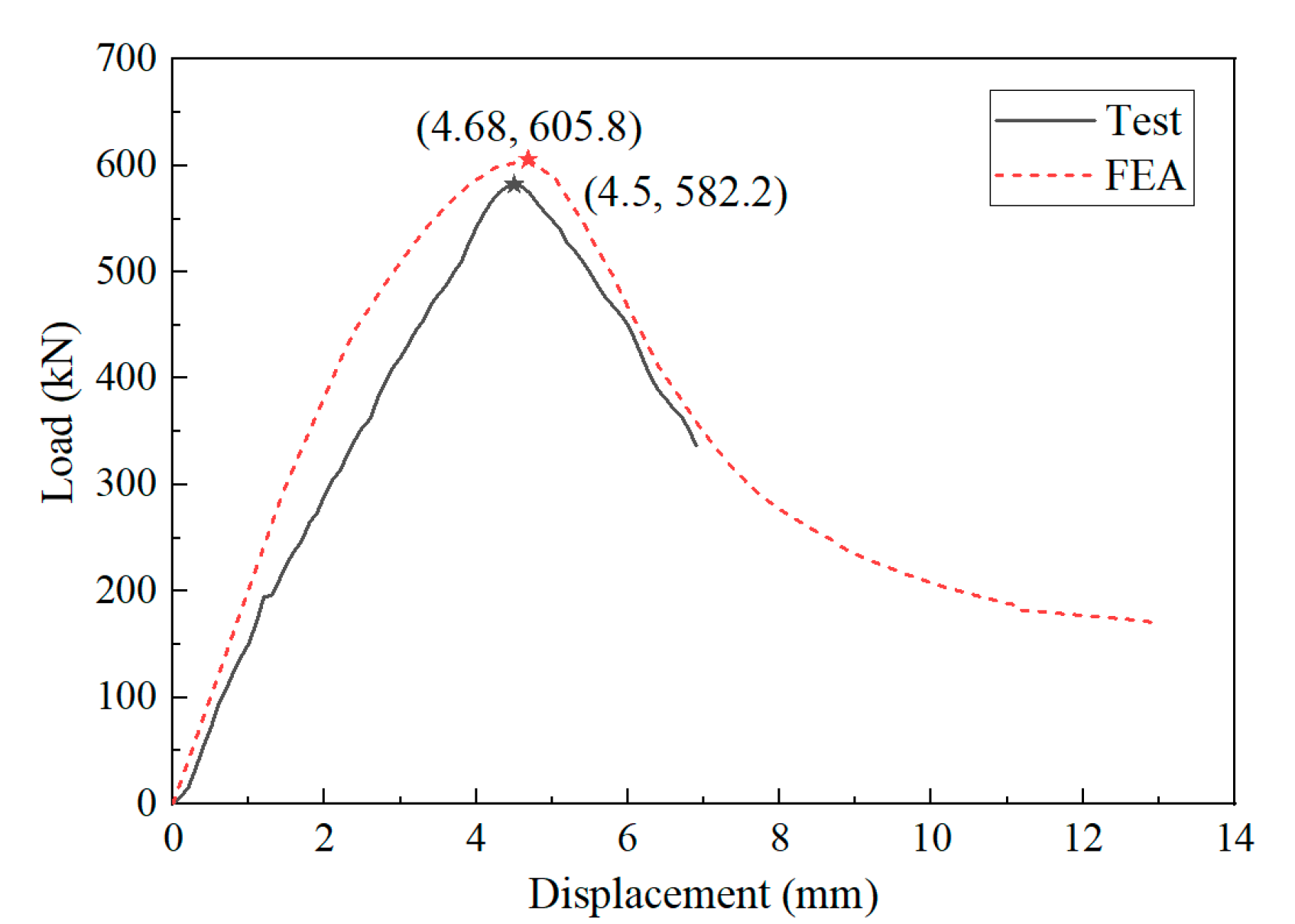
4.1.2. Comparison and Analysis
4.2. Specimen CQD6
4.2.1. Experimental Phenomenon
4.2.2. Comparison and Analysis
5. Parameter Analysis
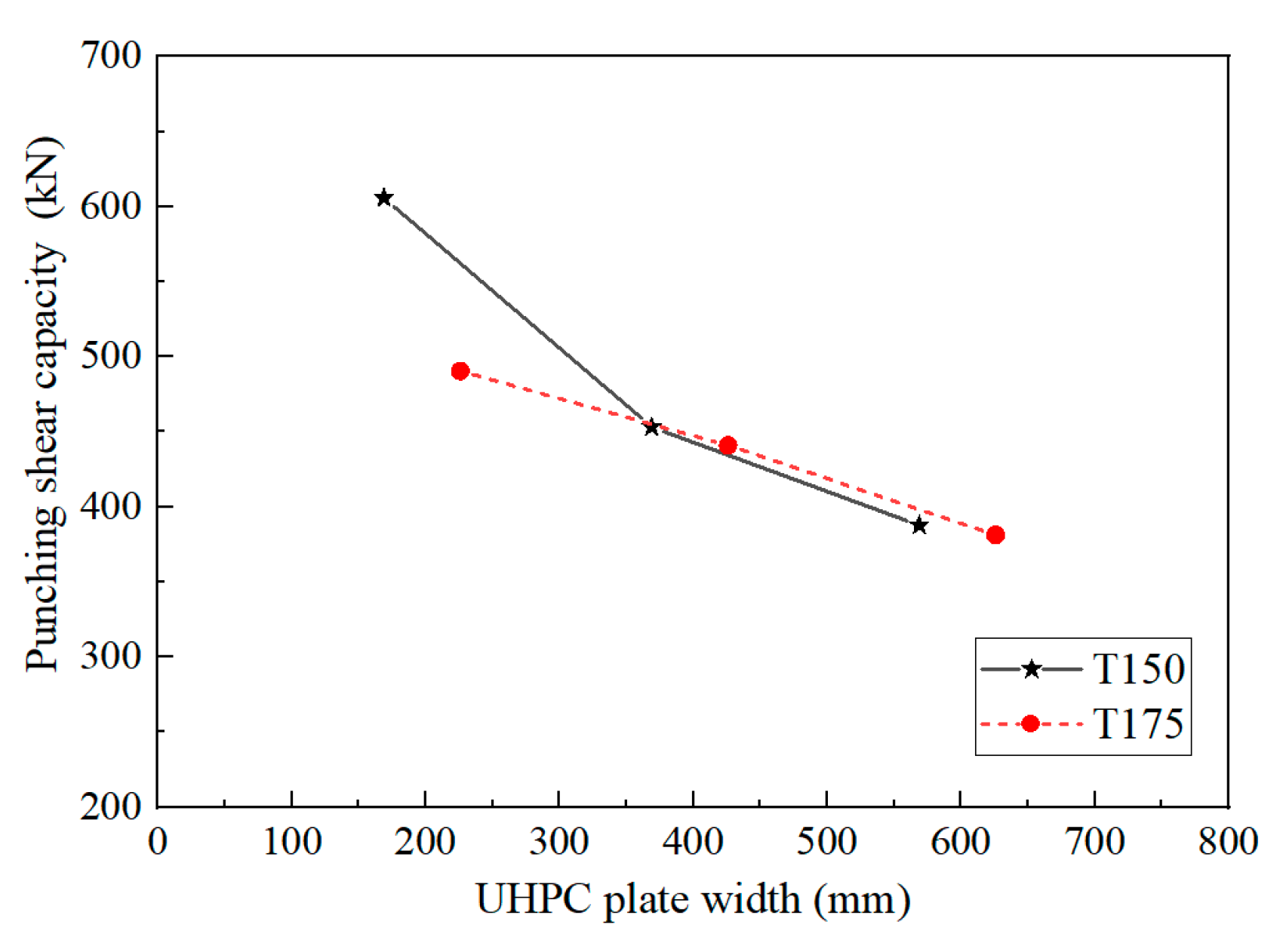
5.1. UHPC Plate Width
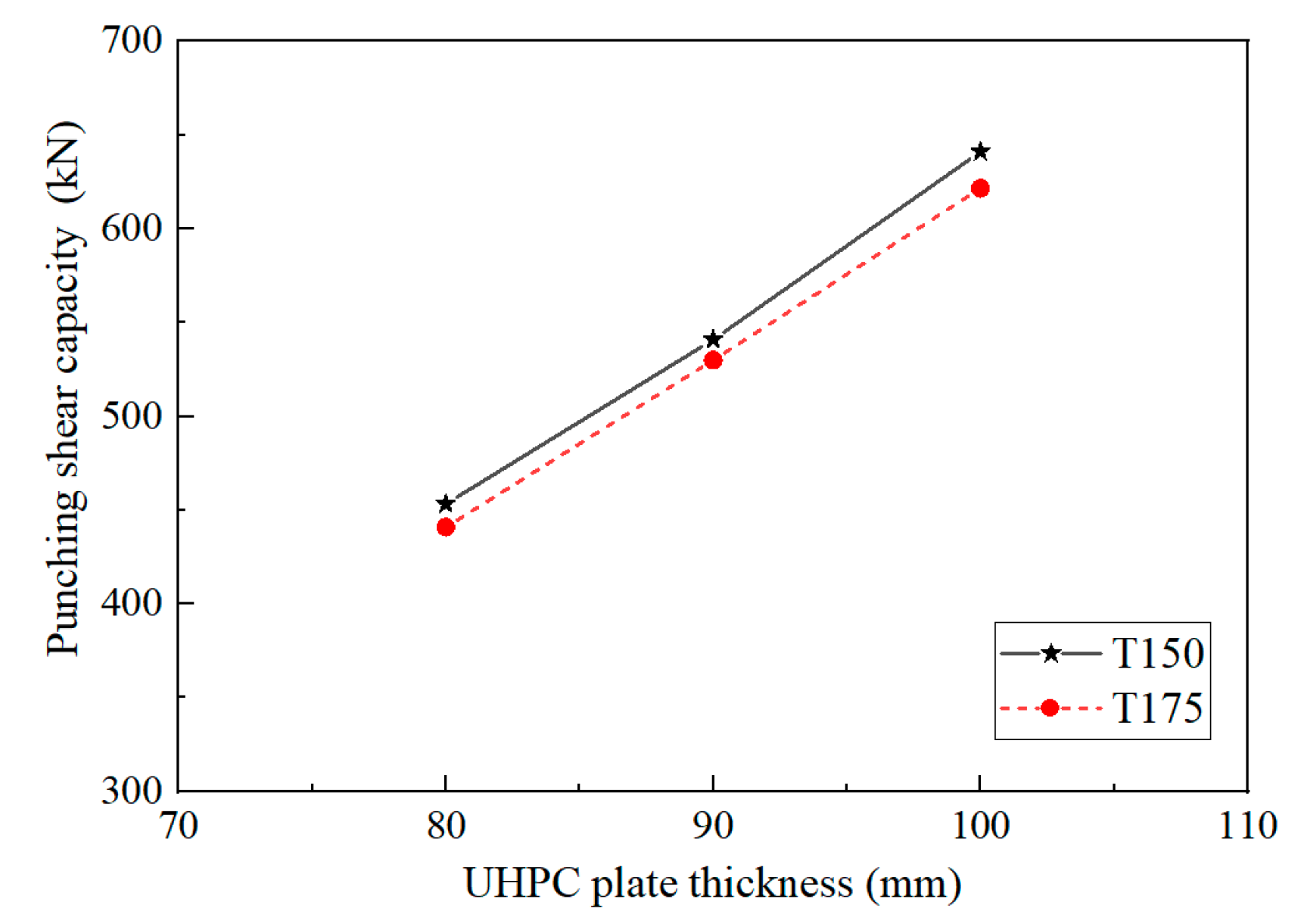
5.2. UHPC Plate Thickness
6. Punching Shear Capacity
6.1. Existing Formulas of Punching Shear Capacity for Plates
6.1.1. Chinese Standard-GB 50010-2010
6.1.2. Chinese Standard-JTG 3362-2018
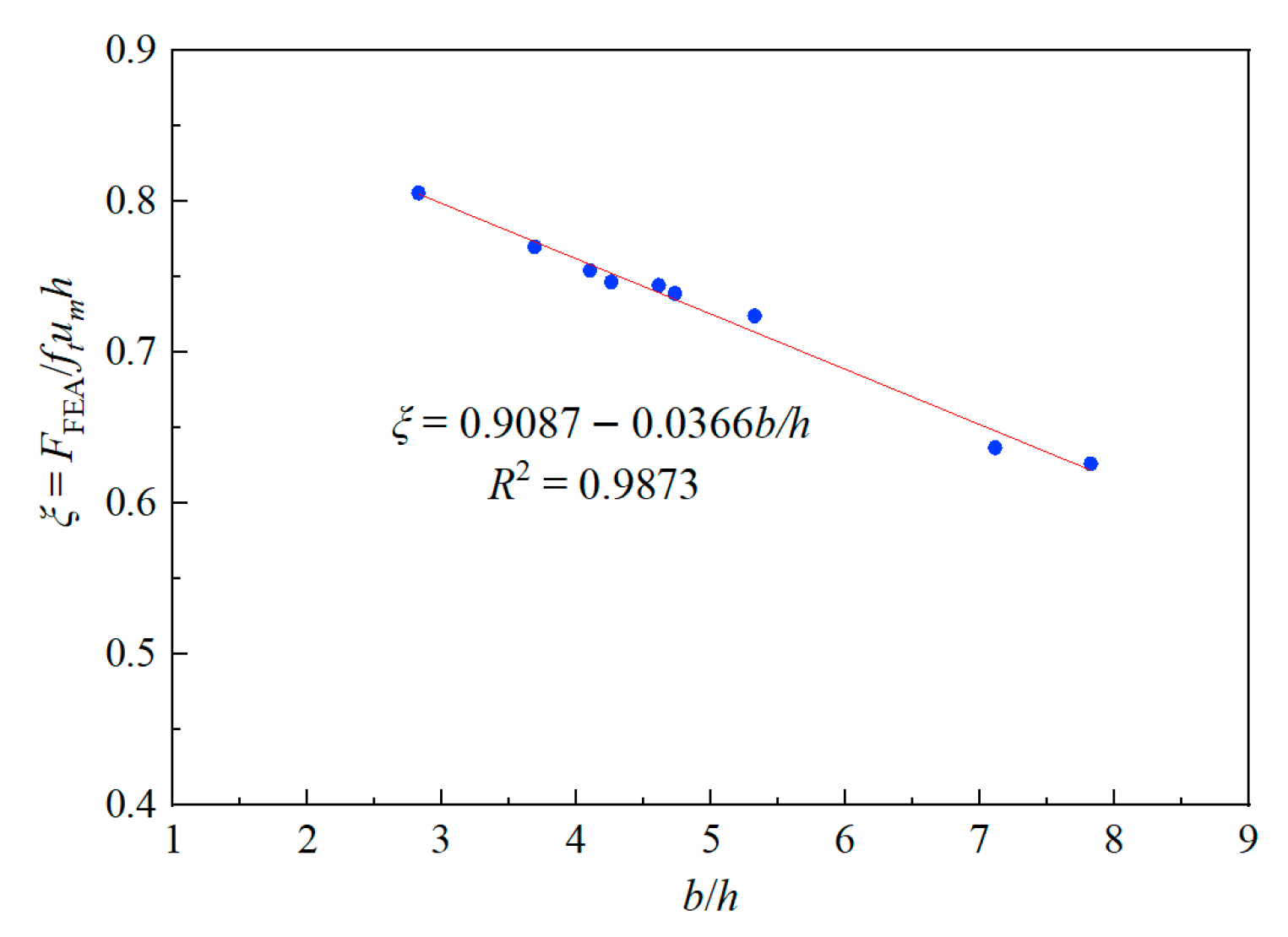
6.2. Contrastive Analysis of the Existing Formulas and FEA Results
7. Conclusions
- (1)
- The new steel grid–UHPC composite bridge deck exhibits two distinct punching shear failure modes: conventional failure mode and unconventional failure mode. Under identical conditions and test specimen parameters, the punching shear capacity associated with the unconventional failure mode is approximately 35% higher than that of the conventional failure mode.
- (2)
- The width and thickness of UHPC plate significantly influence the punching shear capacity of the steel grid–UHPC composite bridge deck. In contrast, the type of T-shape steel exhibits a negligible effect. For the composite bridge decks experiencing conventional punching shear failure mode, the bearing capacity decreases approximately linearly with increasing UHPC plate width, whereas it increases approximately linearly with increasing UHPC plate thickness.
- (3)
- Based on the formula for calculating the punching shear capacity of conventional plates in Chinese standards, this paper introduces a correction coefficient that accounts for the width-to-thickness ratio of UHPC plate and proposes an improved calculation method applicable for determining the punching shear capacity of steel grid–UHPC composite bridge decks under conventional punching shear failure mode condition.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, X.; Nematollahi, B.; Chougan, M.; Xiao, J. Approaches to reduce cost and environmental impacts of UHPC production: A review. Case Stud. Constr. Mater. 2025, 22, e04644. [Google Scholar] [CrossRef]
- Zhu, Y.; Hussein, H.; Kumar, A.; Chen, G. A review: Material and structural properties of UHPC at elevated temperatures or fire conditions. Cem. Concr. Compos. 2021, 123, 104212. [Google Scholar] [CrossRef]
- Shao, X.; Yi, D.; Huang, Z.; Zhao, H.; Chen, B.; Liu, M. Basic performance of the composite deck system composed of orthotropic steel deck and ultrathin RPC layer. J. Bridge Eng. 2013, 18, 417–428. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhang, Q.; Bao, Y.; Deng, P.; Li, M. Flexural behavior of corrugated steel-UHPC composite bridge decks. Eng. Struct. 2021, 246, 113066. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, H.; Ding, H.; Ren, P. Study on the interface shear performance of corrugated steel-UHPC composite bridge decks with stud shear connectors. KSCE J. Civ. Eng. 2025, 100286. [Google Scholar] [CrossRef]
- Zareef, M.A.E.; Abdulrahaman, A.G.; Alnemari, A. Experimental investigation of punching shear behaviour of ultra-high performance self-compacting concrete slabs. Case Stud. Constr. Mater. 2023, 19, e02307. [Google Scholar] [CrossRef]
- Jeffrey, J.; Brunton, J.; Bank, C.L.; Oliva, M.G. Punching shear failure in double-layer pultruded FRP grid reinforced concrete bridge decks. Adv. Struct. Eng. 2012, 15, 601–613. [Google Scholar] [CrossRef]
- Awad, R.; Ateyat, A.A.; Junaid, M.T.; Al-Sadoon, Z.; Altoubat, S.; Maalej, M.; Barakat, S. Punching shear capacity of fiber-reinforced concrete suspended slabs: Database analysis and models assessments. J. Build. Eng. 2024, 83, 108433. [Google Scholar] [CrossRef]
- Lampropoulos, A.; Tsioulou, O.; Mina, A.; Nicolaides, D.; Petrou, M.F. Punching shear and flexural performance of ultra-high performance fibre reinforced concrete (UHPFRC) slabs. Eng. Struct. 2023, 281, 115808. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, H.; Gao, D.; Li, C. Experimental study on punching shear bearing capacity of BFRP bars reinforced two-way concrete slabs under concentrated load. Structures 2025, 71, 108072. [Google Scholar] [CrossRef]
- Ahmed, F.R.; Numan, B.S.A. Failure characteristics and critical punching perimeter of high strength concrete panels. Int. J. Eng. Trend. Tech. 2014, 13, 367–372. [Google Scholar] [CrossRef]
- Metwally, I.M.; Issa, M.S.; El-Betar, S.A. Punching shear resistance of normal and high strength reinforced concrete flat slabs. Civ. Eng. Res. 2008, 30, 982–1003. [Google Scholar]
- Ramadan, M.; Ors, D.M.; Farghal, A.M.; Afifi, A.; Zaher, A.H. Punching shear behavior of HSC & UHPC post tensioned flat slabs—An experimental study. Results Eng. 2023, 17, 100882. [Google Scholar] [CrossRef]
- Inácio, M.M.G.; Almeida, A.F.O.; Faria, D.M.V.; Lúcio, V.J.G.; Ramos, A.P. Punching of high strength concrete flat slabs without shear reinforcement. Eng. Struct. 2015, 103, 275–284. [Google Scholar] [CrossRef]
- Ngab, A.S.; Shahin, M.S. Simple equation for predicting the punching shear capacity of normal and high strength concrete flat plates. Int. J. Eng. Res. Technol. 2021, 10, 678–688. [Google Scholar] [CrossRef]
- Elsanadedy, H.M.; Al-Salloum, Y.A.; Alsayed, S.H. Prediction of punching shear strength of HSC interior slab-column connections. KSCE J. Civ. Eng. 2013, 17, 473–485. [Google Scholar] [CrossRef]
- ACI Committee 318. Building Code Requirements for Structural Concrete (ACI 318M-14) and Commentary (ACI 318RM-14); American Concrete Institute: Farmington Hills, MI, USA, 2014. [Google Scholar]
- CSA A23.3-14; Design of Concrete Structures. Canadian Standard Association: Mississauga, ON, Canada, 2014.
- IS 456: 2000; Indian Standard Code of Practice for Plain and Reinforced Concrete, Fourth Revision. Bureau of Indian Standards: New Delhi, India, 2000.
- Eurocode 2. BS EN 1992-1-1: 2004; Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Standard: Brussels, Belgium, 2004.
- Habeeb, M.; Al-Azzawi, A.A.; Al-Zwainy, M.F. Punching shear behavior of LWA bubble deck slab with different types of shear reinforcement. J. King Saud Univ.-Eng. Sci. 2020, 33, 15–22. [Google Scholar] [CrossRef]
- Jia, Y.; Chiang, J.C. Finite element analysis of punching shear of reinforced concrete slab–column connections with shear reinforcement. Appl. Sci. 2022, 12, 9584. [Google Scholar] [CrossRef]
- Zheng, Y.; Sun, C.; Deng, T.; Yang, J.; Lu, Z. Arching action contribution to punching failure of GFRP-reinforced concrete bridge deck slabs. Arabian J. Sci. Eng. 2014, 39, 8609–8625. [Google Scholar] [CrossRef]
- Amir, S.; Veen, C.; Walraven, J.C.; Boer, A. Experiments on punching shear behavior of prestressed concrete bridge decks. ACI Struct. J. 2016, 113, 627–636. [Google Scholar] [CrossRef]
- JTG 3362-2018; Specifications for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts. Ministry of Transport of the People’s Republic of China: Beijing, China, 2018.
- GB/T 1499.2-2018; Steel for the Reinforcement of Concrete—Part 2: Hot Rolled Ribbed Bars. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2018.
- GB/T 50081-2019; Standard for Test Methods of Concrete Physical and Mechanical Properties. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2019.
- GB/T 228.1-2010; Metallic Materials-Tensile Testing—Part 1: Method of Test at Room Temperature. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2010.
- Boulbes, R.J. Troubleshooting Finite-Element Modeling with Abaqus: With Application in Structural Engineering Analysis. Fransa 2020, 1, 439. [Google Scholar]
- Shan, B. Experimental Research on the Basic Mechanical Properties of Reactive Powder Concrete. Master’s Thesis, Hunan University, Changsha, China, 2002. [Google Scholar]
- Zhang, Z.; Shao, X.; Li, W.; Zhu, P.; Chen, H. Axial tensile behavior test of ultra high performance concrete. China J. Highway Transport. 2015, 28, 50–58. [Google Scholar] [CrossRef]
- Li, L.; Ye, M.; Hu, F.; Liao, R.; Tang, J.; Shao, X. Experimental study on the flexural behavior of a prefabricated large-cantilevered prestressed UHPC thin-walled bent cap. China Civ. Eng. J. 2020, 53, 92–104. [Google Scholar] [CrossRef]
- GB 50010-2010; Code for Design of Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2010.
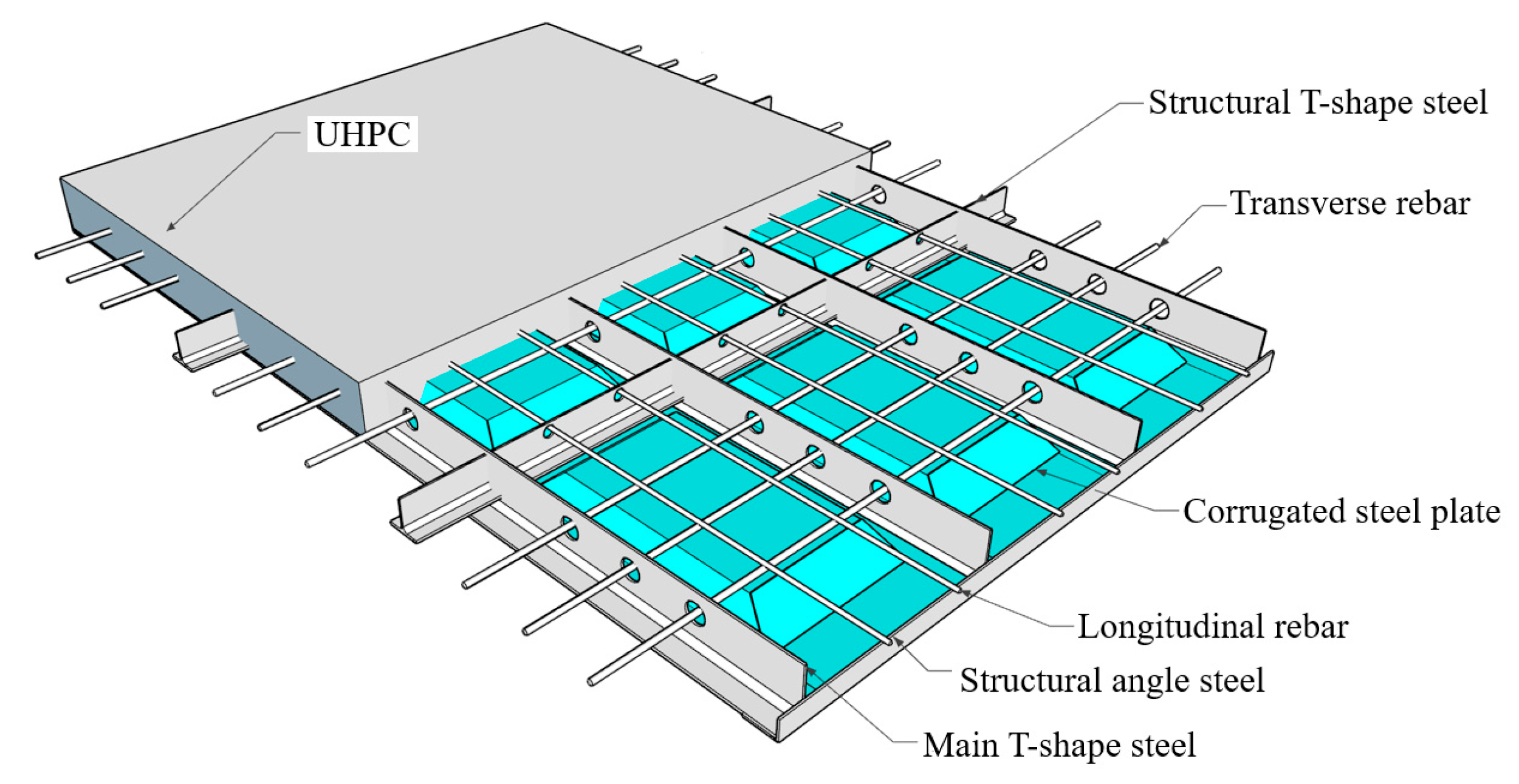

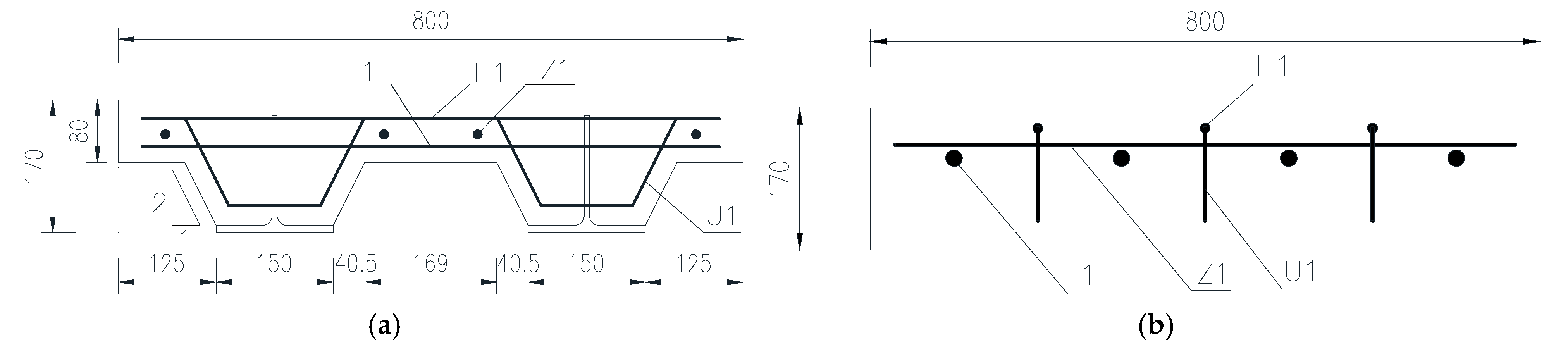
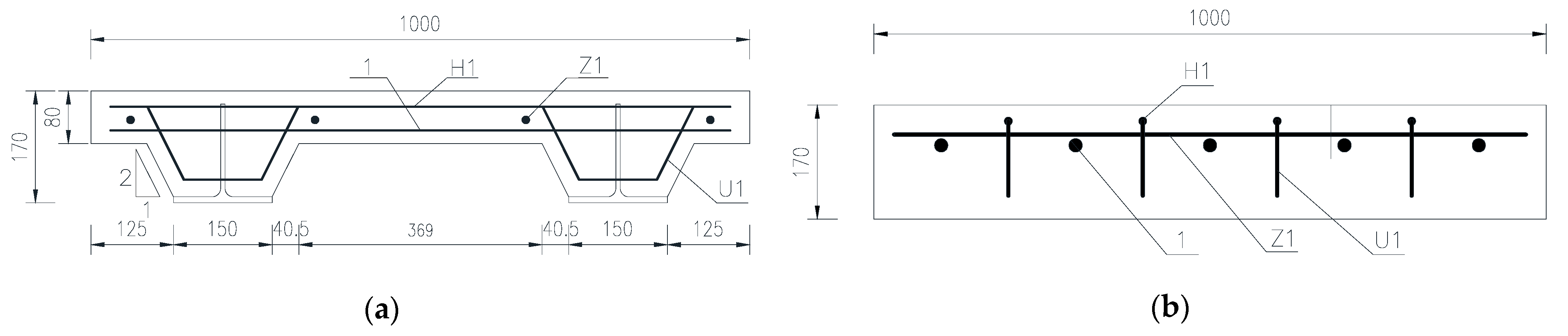




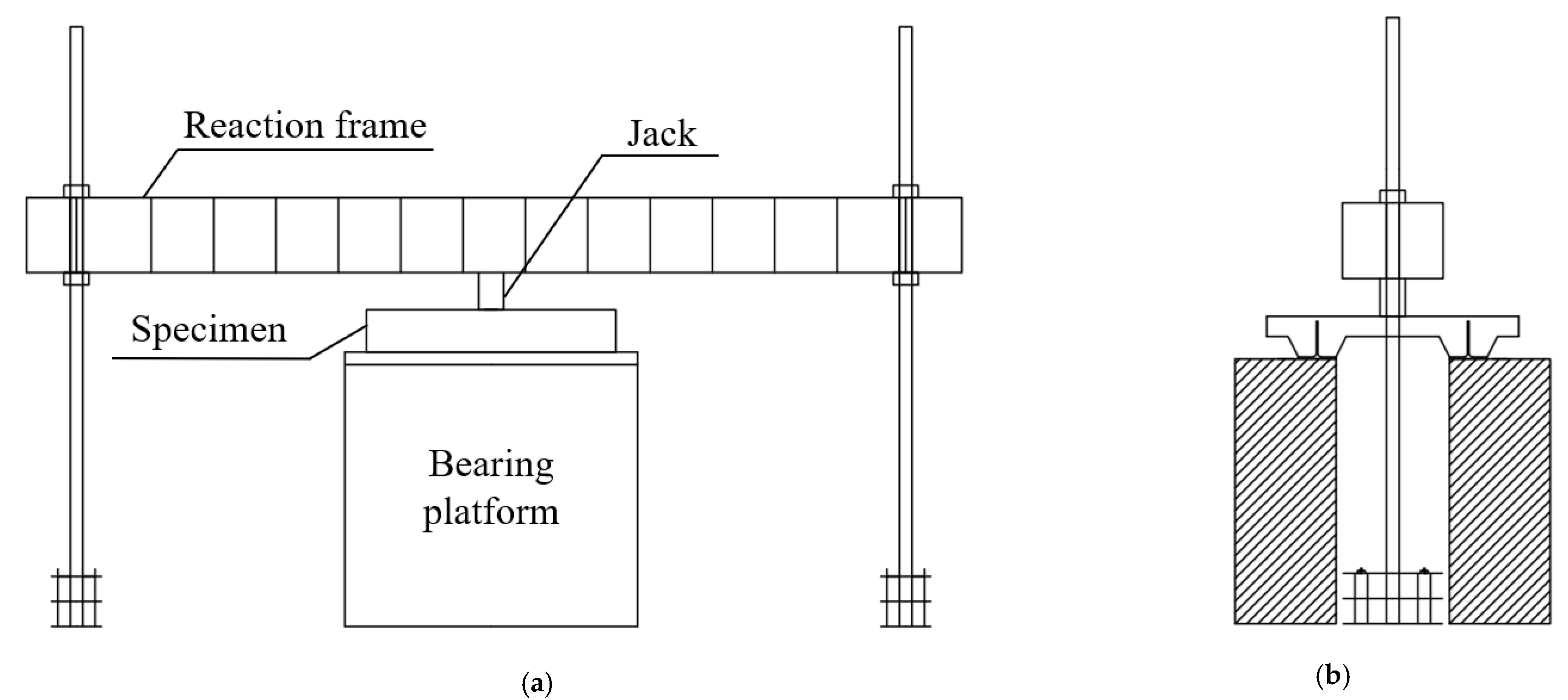










| Specimens | Length (mm) | Width (mm) | Thickness (mm) | UHPC Plate Thickness (mm) | Two T-Shape Steel Spacing (mm) | T-Shape Steel (mm) Height × Width × Web Thickness × Flange Thickness |
|---|---|---|---|---|---|---|
| CQD4 | 800 | 800 | 170 | 80 | 400 | 150 × 150 × 6.5 × 9 |
| CQD6 | 1000 | 1000 | 170 | 80 | 600 | 150 × 150 × 6.5 × 9 |
| Premix | Water-Reducing Admixture | Water | Steel Fiber |
|---|---|---|---|
| 2071.4 | 13 | 184.7 | 181 |
| Concrete Strength Grade | Average Compressive Strength of Cubic Blocks Measured Over a 28-Day Curing Period | Average Compressive Strength of Cubic Blocks During the Test Period | Mean Value of Axial Compressive Strength | Mean Value of Axial Tensile Strength | Elastic Modulus |
|---|---|---|---|---|---|
| C120 | 137.9 | 153.0 | 105.6 | 11.89 | 59,642 |
| Grade | Yield Strength | Ultimate Strength | Elastic Modulus |
|---|---|---|---|
| Q355B | 357 | 566 | 213,642 |
| HRB400 | 425 | 631 | 212,753 |
| FE Models | UHPC Plate Width (mm) | UHPC Plate Thickness (mm) | T-Shape Steel (mm) Height × Width × Web Thickness × Flange Thickness | Punching Shear Capacity (kN) | Failure Mode |
|---|---|---|---|---|---|
| T150W169T80 (CQD4) | 169 | 80 | 150 × 150 × 6.5 × 9 | 605.8 | Unconventional |
| T150W369T80 (CQD6) | 369 | 80 | 150 × 150 × 6.5 × 9 | 453.2 | Conventional |
| T150W369T90 | 369 | 90 | 150 × 150 × 6.5 × 9 | 540.9 | Conventional |
| T150W369T100 | 369 | 100 | 150 × 150 × 6.5 × 9 | 641.0 | Conventional |
| T150W569T80 | 569 | 80 | 150 × 150 × 6.5 × 9 | 387.7 | Conventional |
| T175W226T80 | 226 | 80 | 175 × 175 × 7 × 11 | 490.5 | Conventional |
| T175W426T80 | 426 | 80 | 175 × 175 × 7 × 11 | 440.9 | Conventional |
| T175W426T90 | 426 | 90 | 175 × 175 × 7 × 11 | 529.9 | Conventional |
| T175W426T100 | 426 | 100 | 175 × 175 × 7 × 11 | 621.6 | Conventional |
| T175W626T80 | 626 | 80 | 175 × 175 × 7 × 11 | 381.2 | Conventional |
| FE Models | Width-to-Thickness | FEA | Equations (1) and (4) | Equations (5) and (6) | Percentage | ||
|---|---|---|---|---|---|---|---|
| Ratio of UHPC Plate | Result (kN) | Result (kN) | Error | Result (kN) | Error | Improvement | |
| T150W169T80 (CQD4) | 2.1 | 605.8 | 426.1 | −29.7% | 506.1 | −16.5% | 18.8% |
| T150W369T80 (CQD6) | 4.6 | 453.2 | 426.1 | −6.0% | 450.4 | −0.6% | 5.7% |
| T150W369T90 | 4.1 | 540.9 | 501.9 | −7.2% | 543.9 | 0.6% | 8.4% |
| T150W369T100 | 3.7 | 641.0 | 582.6 | −9.1% | 643.9 | 0.5% | 10.5% |
| T150W569T80 | 7.1 | 387.7 | 426.1 | 9.9% | 394.7 | 1.8% | −7.4% |
| T175W226T80 | 2.8 | 490.5 | 426.1 | −13.1% | 490.2 | −0.1% | 15.0% |
| T175W426T80 | 5.3 | 440.9 | 426.1 | −3.3% | 434.5 | −1.4% | 2.0% |
| T175W426T90 | 4.7 | 529.9 | 501.9 | −5.3% | 527.3 | −0.5% | 5.1% |
| T175W426T100 | 4.3 | 621.6 | 582.6 | −6.3% | 626.5 | 0.8% | 7.5% |
| T175W626T80 | 7.8 | 381.2 | 426.1 | 11.8% | 378.8 | −0.6% | −11.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Wang, P.; Ren, P.; Ding, H. Research on the Punching Shear Performance of Steel Grid–UHPC Composite Bridge Decks. Buildings 2025, 15, 3398. https://doi.org/10.3390/buildings15183398
Liu S, Wang P, Ren P, Ding H. Research on the Punching Shear Performance of Steel Grid–UHPC Composite Bridge Decks. Buildings. 2025; 15(18):3398. https://doi.org/10.3390/buildings15183398
Chicago/Turabian StyleLiu, Sumei, Peng Wang, Pengfei Ren, and Hanshan Ding. 2025. "Research on the Punching Shear Performance of Steel Grid–UHPC Composite Bridge Decks" Buildings 15, no. 18: 3398. https://doi.org/10.3390/buildings15183398
APA StyleLiu, S., Wang, P., Ren, P., & Ding, H. (2025). Research on the Punching Shear Performance of Steel Grid–UHPC Composite Bridge Decks. Buildings, 15(18), 3398. https://doi.org/10.3390/buildings15183398






