Debris Simulation in Controlled Demolition of Tall Building Structures: Solid Model-Based Approach
Abstract
1. Introduction
2. Materials and Methods
3. Model Validation and Insights from FEM and AEM
4. Parametric Studies: Structural System and General Information
4.1. Results of Debris Propagation in the 20-Storey Building: Influence of Time Interval
- At 100 ms interval, the maximum horizontal debris distance reached approximately −42.39 m.
- At 300 ms interval, debris spread was around −39.9 m.
- At 500 ms interval, debris spread was about −36.4 m.
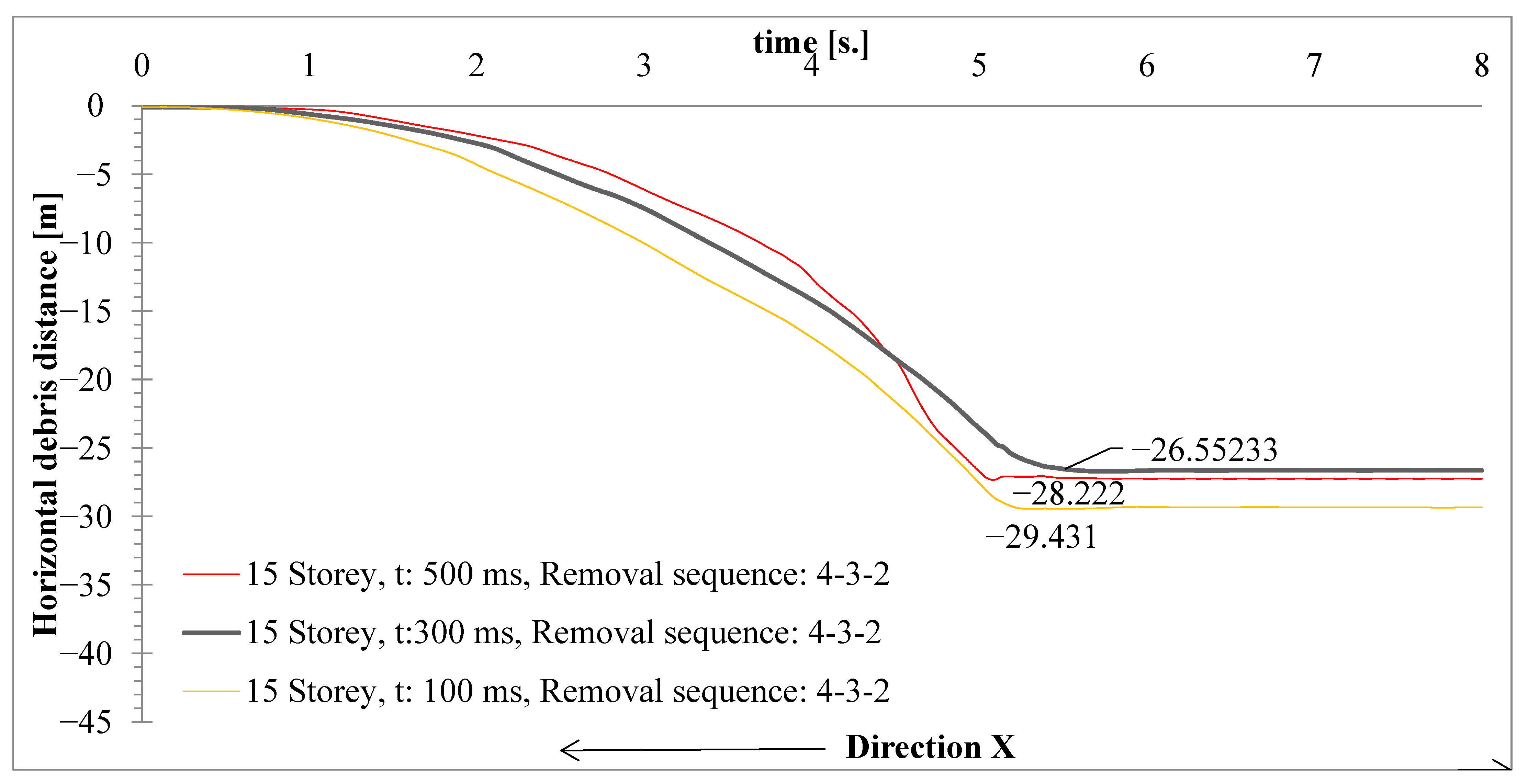
4.2. Results of Debris Propagation in the 15-Storey Building: Influence of Time Interval
- At 100 ms interval, the debris reached approximately −29.43 m.
- At 300 ms interval, it was around −28.22 m.
- At 500 ms interval, it was about −26.55 m.
- In both the 20-storey and 15-storey models, the maximum debris dispersion occurred under the 100 ms interval scenario, indicating a more aggressive collapse pattern caused by rapid sequential failure.
- The 300 ms and 500 ms scenarios exhibited relatively reduced horizontal debris spread, with the 300 ms interval providing an optimal balance between collapse progression and debris containment.
- For the 15-storey structure, although the 100 ms interval still produced the largest debris spread, the differences in debris distances among the three time intervals were less pronounced. This suggests that factors such as structural stiffness and mass distribution reduce the sensitivity of debris propagation to timing variations.
5. Results and Discussions on Modified Collapse Sequences Under 300 Millisecond (ms) Delay
- (a)
- The 100 ms interval leads to maximum debris dispersion,
- (b)
- The 500 ms interval, although offering more time between removals, results in longer durations during which the non-demolished sections remain structurally unsupported, risking unintended collapse or instability. Thus, a 300 ms interval represents an optimal compromise, maintaining controlled collapse progression while limiting excessive debris spread and preserving short-term structural stability of the remaining sections during demolition.
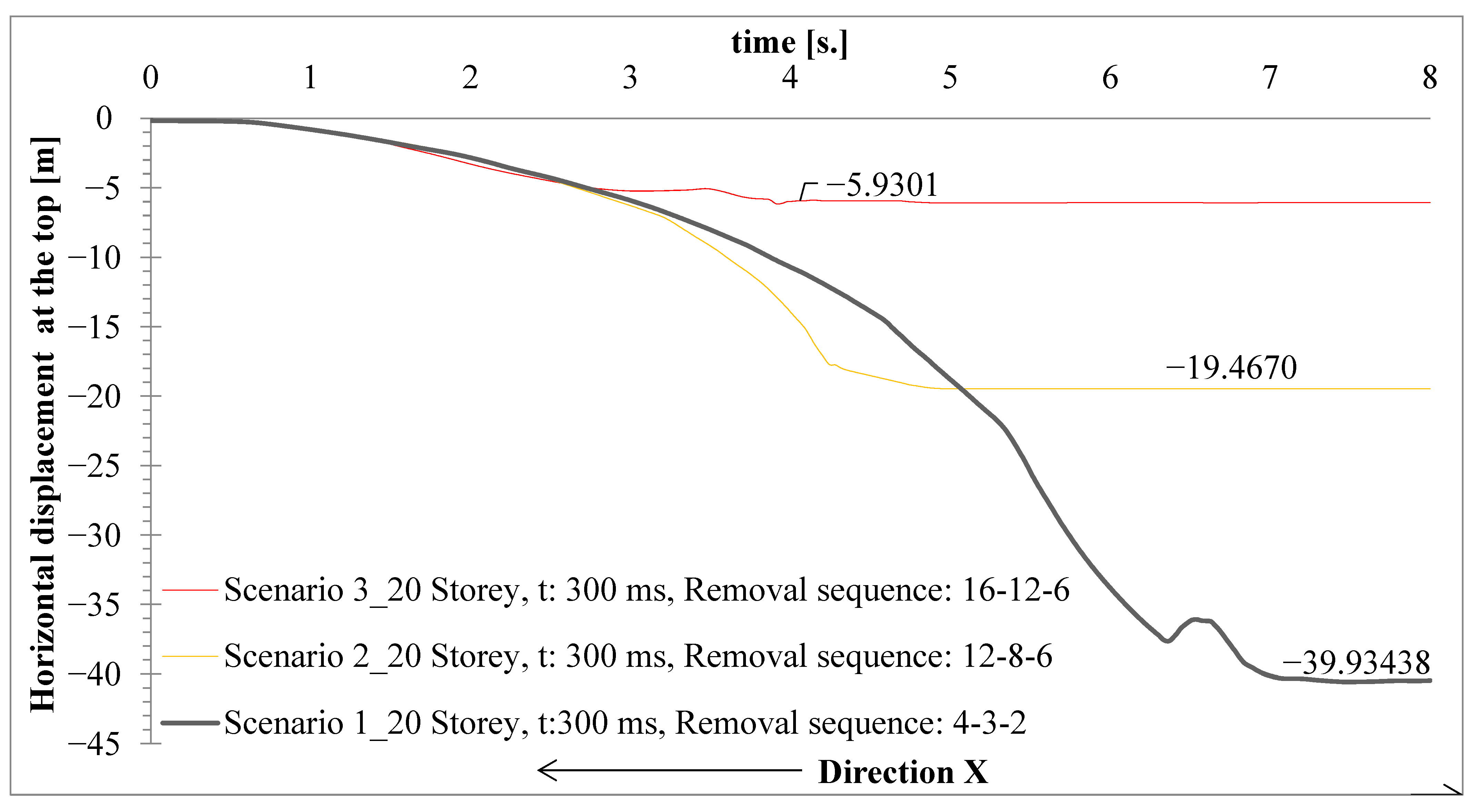
- Scenario 1: Under the 4–3–2 removal sequence, the debris distance reached approximately −39.9 m.
- Scenario 2: For the 12–8–6 sequence, debris distance was reduced to about −19.46 m.
- Scenario 3: The 16–12–6 sequence further decreased the debris spread to around −5.93 m.
Limitations of the Study
6. Conclusions
- Rapid column removals (e.g., 100 ms) cause the most extensive horizontal debris dispersion, especially in taller structures.
- A 300 ms delay offers a balance between progressive failure realism and debris containment.
- The sequence of removal significantly influences collapse behavior; evenly spaced, higher-level removals (as in Scenario 3) reduce debris extent.
- Excessively long removal intervals risk destabilizing remaining structural parts, demonstrating the need for an optimized timing window.
- Vertical positioning and the number of columns removed per sequence directly affect debris footprint size, confirming the necessity of scenario-specific demolition planning.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FEM | Finite Element Method |
| AEM | Applied Element Method |
| ms | millisecond |
| t | time |
| s | second |
| m | meter |
| RC | Reinforced Concrete |
References
- Yuzbasi, J. Controlled demolition: Novel monitoring and experimental validation of blast-induced full-scale existing high-rise building implosion using numerical finite element simulations. J. Civ. Struct. Health Monit. 2024, 15, 891–914. [Google Scholar] [CrossRef]
- Michaloudis, G.; Blankenhorn, G.; Mattern, S.; Schweizerhof, K. Modelling structural failure with finite element analysis of controlled demolition of buildings by explosives using LS-DYNA. In High Performance Computing in Science and Engineering’09: Transactions of the High Performance Computing Center, Stuttgart (HLRS) 2009; Springer: Berlin/Heidelberg, Germany, 2010; pp. 539–551. [Google Scholar] [CrossRef]
- Yuzbasi, J. Experimental verification of full-scale silo structure demolition: Investigating successive column removal with finite element method and progressive collapse simulation through blast load. Struct. Concr. 2024, 25, 4408–4427. [Google Scholar] [CrossRef]
- Karasin, I.B. Comparative analysis of the 2023 Pazarcık and Elbistan Earthquakes in Diyarbakır. Buildings 2023, 13, 2474. [Google Scholar] [CrossRef]
- Işık, E. Structural failures of adobe buildings during the February 2023 Kahramanmaraş (Türkiye) earthquakes. Appl. Sci. 2023, 13, 8937. [Google Scholar] [CrossRef]
- Elnashai, A.S.; Di Sarno, L. Fundamentals of Earthquake Engineering: From Source to Fragility; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Di Sarno, L. Effects of multiple earthquakes on inelastic structural response. Eng. Struct. 2015, 56, 673–681. [Google Scholar] [CrossRef]
- Ivanov, M.L.; Chow, W.K. Structural damage observed in reinforced concrete buildings in Adiyaman during the 2023 Türkiye Kahramanmaras Earthquakes. In Structures; Elsevier: Amsterdam, The Netherlands, 2023; Volume 58, p. 105578. [Google Scholar] [CrossRef]
- Yuzbasi, J. Post-Earthquake Damage assessment: Field observations and recent developments with recommendations from the Kahramanmaraş earthquakes in Türkiye on February 6th, 2023 (Pazarcık M7. 8 and Elbistan M7. 6). J. Earthq. Eng. 2024, 1–26. [Google Scholar] [CrossRef]
- Büyüksaraç, A.; Işık, E.; Bektaş, Ö.; Avcil, F. Achieving intensity distributions of 6 February 2023 Kahramanmaraş (Türkiye) earthquakes from peak ground acceleration records. Sustainability 2024, 16, 599. [Google Scholar] [CrossRef]
- Wang, T.; Chen, J.; Zhou, Y.; Wang, X.; Lin, X.; Wang, X.; Shang, Q. Preliminary investigation of building damage in Hatay under February 6, 2023 Türkiye earthquakes. Earthq. Eng. Eng. Vib. 2023, 22, 853–866. [Google Scholar] [CrossRef]
- Kobbekaduwa, D.; Yang, P.; Nanayakkara, O.; Krevaikas, T.; Di Sarno, L. Experimental study on corroded reinforced concrete columns repaired with textile-reinforced mortar (TRM) and organic corrosion inhibitors. Constr. Build. Mater. 2025, 491, 142702. [Google Scholar] [CrossRef]
- Pei, S.; Van De Lindt, J.W.; Barbosa, A.; Berman, J.; McDonnell, E.; Dolan, J.D.; Blomgren, H.-E.; Zimmerman, R.B.; Huang, D.; Wichman, S. Experimental seismic response of a resilient 2-story mass-timber building with post-tensioned rocking walls. J. Struct. Eng. 2019, 145, 04019120. [Google Scholar] [CrossRef]
- Zarate Garnica, G.I.; Lantsoght, E.O.L.; Yang, Y. Monitoring structural responses during load testing of reinforced concrete bridges: A review. Struct. Infrastruct. Eng. 2022, 18, 1558–1580. [Google Scholar] [CrossRef]
- Di Sarno, L.; Albuhairi, D.; Medeiros, J.M.P. Exploring innovative resilient and sustainable bio-materials for structural applications: Hemp-fibre concrete. In Structures; Elsevier: Amsterdam, The Netherlands, 2024; Volume 68, p. 107096. [Google Scholar] [CrossRef]
- Yuzbasi, J. Research and Practice on Demolition of Structures Worldwide in the 21st Century: Exploring Methods Using Mechanics of Solid Bodies with Object Tracking Validation. In Proceedings of the CIBv 2024—Civil Engineering and Buildings Services; Tuns, I., Muntean, R., Gălățanu, T., Cazacu, C., Conțiu, M., Eds.; Springer: Cham, Switzerland, 2025; Volume 665. [Google Scholar] [CrossRef]
- Kocakaplan Sezgin, S.; SAYGILI, Ö. Architectural Heritage After the February 6th Kahramanmaras Earthquakes: Preliminary Observations on Historical Masonry Structures. Afyon Kocatepe Üniv. Fen Ve Mühendis. Bilim. Derg. 2025, 25, 621–634. [Google Scholar] [CrossRef]
- Thomsen, A.; Schultmann, F.; Kohler, N. Deconstruction, demolition and destruction. Build. Res. Inf. 2011, 39, 327–332. [Google Scholar] [CrossRef]
- Yankelevsky, D.Z.; Schwarz, S.; Brosh, B. Full scale field blast tests on reinforced concrete residential buildings–from theory to practice. Int. J. Prot. Struct. 2013, 4, 565–590. [Google Scholar] [CrossRef]
- Schenker, A.; Anteby, I.; Gal, E.; Kivity, Y.; Nizri, E.; Sadot, O.; Michaelis, R.; Levintant, O.; Ben-Dor, G. Full-scale field tests of concrete slabs subjected to blast loads. Int. J. Impact Eng. 2008, 35, 184–198. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, Z.; Ke, C. Study on Dynamic Response and Progressive Collapse Resistance of Space Steel Frame Under Impact Load. Buildings 2025, 15, 1888. [Google Scholar] [CrossRef]
- Jiang, L.; Zhao, C.; Zhang, S.; Qiu, M.; Zhang, R.; Li, Y.; Zhang, W.; Yu, S. Failure Mechanisms of Basalt Fiber Concrete Under Splitting Tensile Tests and DEM Simulations. Buildings 2025, 15, 3035. [Google Scholar] [CrossRef]
- Zhang, Z.; Davis, L.; Malomo, D. Distinct Element macro-crack networks for expedited discontinuum seismic analysis of large-scale URM structures. J. Build. Eng. 2024, 97, 110962. [Google Scholar] [CrossRef]
- Devanand, K.; Ghiassi, B.; Faramarzi, A.; Mehravar, M. Particle-Based DEM to Assess Masonry Behaviour Under Compression. In Proceedings of the 18th International Brick and Block Masonry Conference, Birmingham, UK, 21–24 July 2024; Springer Nature: Cham, Switzerland, 2024; pp. 254–271. [Google Scholar] [CrossRef]
- Chen, X.; Liang, Z.; Chan, A.H. Simulating the damage of rubble stone masonry walls using FDEM with a detailed micro-modelling approach. Comput. Part. Mech. 2024, 11, 2839–2855. [Google Scholar] [CrossRef]
- Yuzbasi, J.; Arslan, H.M. Applied element method and Finite element method for progressive collapse assessment: A comparative study on the influence of slab types, thicknesses, and damping via three incremental column removals. In Structures; Elsevier: Amsterdam, The Netherlands, 2025; Volume 73, p. 108358. [Google Scholar] [CrossRef]
- Chen, G.; Cheng, X.; Diao, M.; Li, Y.; Lu, Y. Progressive collapse resistance of one-way wet-connected precast concrete beam-slab-column substructures: Experimental and numerical investigations. Eng. Struct. 2025, 344, 121288. [Google Scholar] [CrossRef]
- Guo, M.; Huang, H.; Yang, S.; Huang, M. Experimental and numerical investigation on progressive collapse resistance of three-dimensional RC structures. Eng. Fail. Anal. 2025, 167, 108954. [Google Scholar] [CrossRef]
- Song, M.; Wang, Z.; Chen, X.; Liu, B.; Huang, S.; He, J. Numerical Investigation of Progressive Collapse Resistance in Fully Bonded Prestressed Precast Concrete Spatial Frame Systems with and Without Precast Slabs. Buildings 2025, 15, 2743. [Google Scholar] [CrossRef]
- Tan, K.H. Experimental study on progressive collapse behaviour of intact and slightly earthquake-damaged exterior precast concrete joints, and finite element modelling of building performance. Eng. Struct. 2025, 333, 120146. [Google Scholar] [CrossRef]
- Savin, S.; Kolchunov, V.; Fedorova, N.; Tuyen Vu, N. Experimental and Numerical Investigations of RC Frame Stability Failure under a Corner Column Removal Scenario. Buildings 2023, 13, 908. [Google Scholar] [CrossRef]
- Fascetti, A.; Kunnath, S.K.; Nisticò, N. Robustness evaluation of RC frame buildings to progressive collapse. Eng. Struct. 2015, 86, 242–249. [Google Scholar] [CrossRef]
- Izzuddin, B.A. Robustness by design–Simplified progressive collapse assessment of building structures. Stahlbau 2010, 79, 556–564. [Google Scholar] [CrossRef]
- Al-Sadoon, Z.A.; Junaid, M.T.; Al-Sabouni, U.; Dabous, S.A.; Almaghari, H. Resilience of code compliant reinforced concrete buildings to progressive collapse: A numerical analysis investigation. Results Eng. 2024, 24, 102982. [Google Scholar] [CrossRef]
- Huang, H.; Huang, M.; Zhang, W.; Guo, M.; Chen, Z.; Li, M. Progressive collapse resistance of multistory RC frame strengthened with HPFL-BSP. J. Build. Eng. 2021, 43, 103123. [Google Scholar] [CrossRef]
- Elsanadedy, H.M.; Almusallam, T.H.; Abbas, H.; Al-Salloum, Y.A. Innovative Retrofitting for Disaster Resilience: Optimizing Steel Plate Grade and Scheme in RC Non-Seismic Frames to Prevent Progressive Collapse. Buildings 2025, 15, 3325. [Google Scholar] [CrossRef]
- Mokashi, V.M.; Jadhav, H.S. Progressive collapse analysis and seismic performance of irregular RC structures: A probabilistic approach. Asian J. Civ. Eng. 2024, 25, 4911–4921. [Google Scholar] [CrossRef]
- Ferraioli, M.; Laurenza, B.; Lavino, A.; De Matteis, G. Progressive collapse analysis and retrofit of a steel-RC building considering catenary effect. J. Constr. Steel Res. 2024, 213, 108364. [Google Scholar] [CrossRef]
- Ding, L.; Dai, X.; Gan, Y.; Zeng, Y. Impact of Reinforcement Corrosion on Progressive Collapse Behavior of Multi-Story RC Frames. Buildings 2025, 15, 2534. [Google Scholar] [CrossRef]
- Costanzo, S.; Cassiano, D.; D’Aniello, M. Robustness of Steel Moment-Resisting Frames Under Column Loss Scenarios with and without Prior Seismic Damage. Buildings 2025, 15, 2490. [Google Scholar] [CrossRef]
- Wang, Z.; Yin, J.; Wang, Z.; Yi, J. Dynamic Response and Anti-Collapse Analysis of Multi-Column Demolition Mode in Frame Structures. Buildings 2025, 15, 1525. [Google Scholar] [CrossRef]
- Yuzbasi, J. Progressive Collapse Analysis of Steel Structures. Cukurova Univ. J. Fac. Eng. 2025, 40, 429–444. [Google Scholar]
- Gnedin, N.Y.; Semenov, V.A.; Kravtsov, A.V. Enforcing the Courant–Friedrichs–Lewy condition in explicitly conservative local time stepping schemes. J. Comput. Phys. 2018, 359, 93–105. [Google Scholar] [CrossRef]
- Higaki, T.; Tanabe, Y.; Hashimoto, H.; Iida, T. Step-by-step enhancement of a graph neural network-based surrogate model for Lagrangian fluid simulations with flexible time step sizes. Appl. Ocean Res. 2025, 154, 104424. [Google Scholar] [CrossRef]
- Meguro, K.; Tagel-Din, H. Applied Element Method: A New Efficient Tool for Design of Structure Considering Its Failure Behavior; Institution of Industrial Science (IIS), The University of Tokyo: Tokyo, Japan, 2001; pp. 1–20. [Google Scholar]
- Meguro, K.; Tagel-Din, H. Applied element method for structural analysis: Theory and application for linear materials. Struct. Eng. Earthq. Eng. JSCE 2000, 17, 15. [Google Scholar] [CrossRef] [PubMed]
- Tagel-Din, H.; Meguro, K. Applied element method for dynamic large deformation analysis of structures. Struct. Eng. Earthq. Eng. JSCE 2000, 17, 215–224. [Google Scholar] [CrossRef] [PubMed]
- Tagel-Din, H.; Meguro, K. Applied element method for simulation of nonlinear materials: Theory and application for RC structures. Struct. Eng. Earthq. Eng. JSCE 2000, 17, 137–148. [Google Scholar]
- Christy, D.L.; Pillai, T.M.; Nagarajan, P.; Manimaran, L. Determination of Crack Pattern in Concrete Structures Using Applied Element Method. Mater. Sci. Forum 2019, 969, 303–308. [Google Scholar] [CrossRef]
- Yuzbasi, J. Applied element method: Earthquake simulation analysis of soft story and weak story in building structures using solid mechanics. In Proceedings of the CIBv 2024—Civil Engineering and Buildings Services; Springer Nature: Cham, Switzerland, 2024; pp. 695–712. [Google Scholar] [CrossRef]












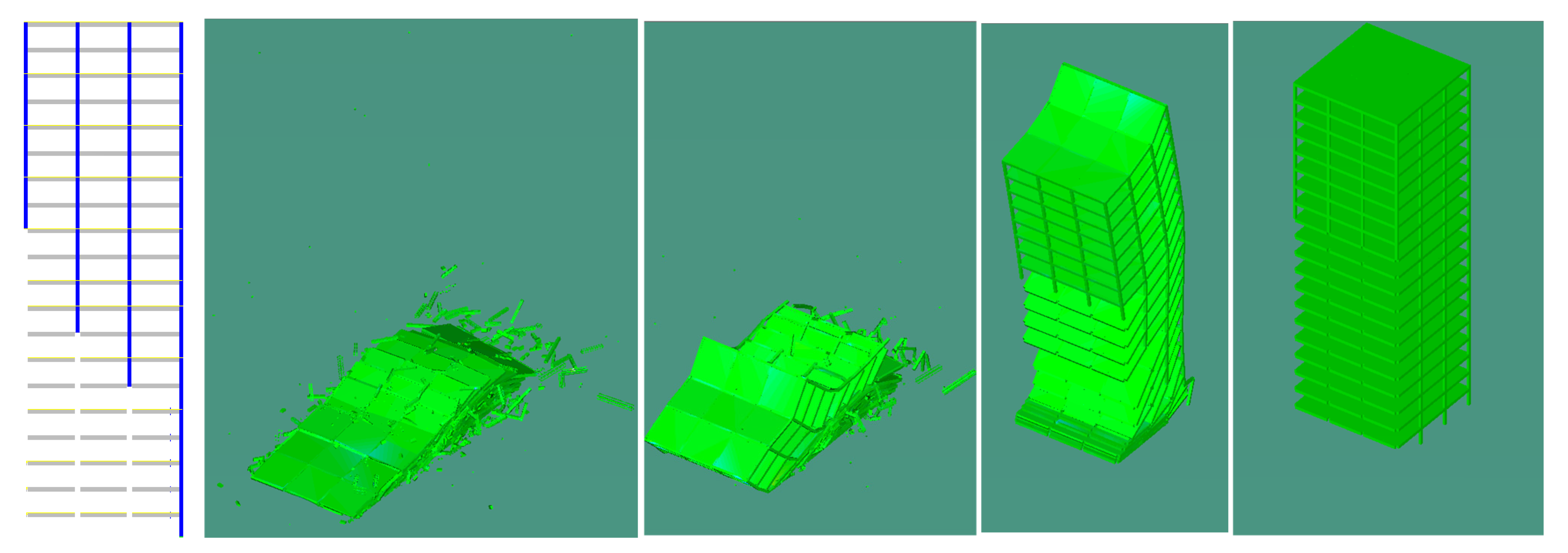

| Category | Parameter | Description |
|---|---|---|
| Numerical method | Applied Element Method (AEM) | Used for detailed collapse simulation |
| Collapse type | Progressive Collapse | Sequential column removal scenarios |
| Slab Strategy | Thin Structure Correction Factor (TSCF) | Applied to capture out-of-plane flexural behavior |
| Model type | Solid model with rebar | Reinforced concrete with detailed meshing |
| Validation reference | Real demolition footage | Used for visual comparison with model |
| Validation method | Visual validation | Comparison using fixed-camera and drone imagery |
| Highlighted zones | Rear (Blue), Front (Orange) | Emphasized for debris spread similarity |
| Parameter | 15-Storey Model | 20-Storey Model |
|---|---|---|
| Story height | 3.0 m | 3.0 m |
| Total building height | 45.0 m | 60.0 m |
| Typical span length | 6.0 m | 6.0 m |
| Column cross-section | 120 × 120 cm | 120 × 120 cm |
| Beam cross-section | 75 × 90 cm | 75 × 90 cm |
| Slab thickness | 20 cm | 20 cm |
| Reinforcement ratio (vertical members) | 4% | 4% |
| Concrete grade | C40 | C40 |
| Steel grade | S420 | S420 |
| Scenario Time Interval | Axis 1 Trigger Time | Axis 2 Trigger Time | Axis 3 Trigger Time |
|---|---|---|---|
| 100 ms | 0 ms | 100 ms | 200 ms |
| 300 ms | 0 ms | 300 ms | 600 ms |
| 500 ms | 0 ms | 500 ms | 1000 ms |
| Scenario | 1st Removal | 2nd Removal | 3rd Removal |
|---|---|---|---|
| S1 | Storey 4 | Storey 3 | Storey 2 |
| S2 | Storey 12 | Storey 8 | Storey 6 |
| S3 | Storey 16 | Storey 12 | Storey 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuzbasi, J. Debris Simulation in Controlled Demolition of Tall Building Structures: Solid Model-Based Approach. Buildings 2025, 15, 3396. https://doi.org/10.3390/buildings15183396
Yuzbasi J. Debris Simulation in Controlled Demolition of Tall Building Structures: Solid Model-Based Approach. Buildings. 2025; 15(18):3396. https://doi.org/10.3390/buildings15183396
Chicago/Turabian StyleYuzbasi, Julide. 2025. "Debris Simulation in Controlled Demolition of Tall Building Structures: Solid Model-Based Approach" Buildings 15, no. 18: 3396. https://doi.org/10.3390/buildings15183396
APA StyleYuzbasi, J. (2025). Debris Simulation in Controlled Demolition of Tall Building Structures: Solid Model-Based Approach. Buildings, 15(18), 3396. https://doi.org/10.3390/buildings15183396






