A Precision Measurement Method for Rooftop Photovoltaic Capacity Using Drone and Publicly Available Imagery

Abstract

Against the global backdrop of energy transition, the precise assessment of urban rooftop photovoltaic (PV) system capacity is recognized as crucial for optimizing the energy structure and enhancing the sustainable utilization efficiency of spatial resources. Publicly available aerial imagery is characterized by non-orthorectified issues; direct utilization is known to lead to geometric distortions in rooftop PV and errors in capacity prediction. To address this, a dual-optimization framework is proposed in this study, integrating monocular vision-based 3D reconstruction with a lightweight linear model. Leveraging the orthogonal characteristics of building structures, camera self-calibration and 3D reconstruction are achieved through geometric constraints imposed by vanishing points. Scale distortion is suppressed via the incorporation of a multi-dimensional geometric constraint error control strategy. Concurrently, a linear capacity-area model is constructed, thereby simplifying the complexity inherent in traditional multi-parameter fitting. Utilizing drone oblique photography and Google Earth public imagery, 3D reconstruction was performed for 20 PV-equipped buildings in Wuhan City. Two buildings possessing high-precision field survey data were selected as typical experimental subjects for validation. The results demonstrate that the 3D reconstruction method reduced the mean absolute percentage error (MAPE)—used here as an estimator of measurement uncertainty—of PV area identification from 10.58% (achieved by the 2D method) to 3.47%, while the coefficient of determination (R²) for the capacity model reached 0.9548. These results suggest that this methodology can provide effective technical support for low-cost, high-precision urban rooftop PV resource surveys. It has the potential to significantly enhance the reliability of energy planning data, thereby contributing to the efficient development of urban spatial resources and the achievement of sustainable energy transition goals.

1. Introduction

Against the macro background of globally accelerating the low-carbon transition of the energy structure and actively implementing decarbonization strategic goals, the construction of sustainable energy systems has become a core issue in urban development [1]. Distributed photovoltaic (PV) systems, particularly urban rooftop PV systems, are increasingly emerging as a crucial vehicle for cities to achieve a cleaner and low-carbon energy supply, alongside the intensive utilization of space resources [2]. This prominence stems from their significant advantages: a highly flexible deployment mode compatible with built environments, considerable potential for scaled application, and an almost negligible occupation of valuable land resources [3,4]. Within this context, the high-precision and high-efficiency assessment of the actual installed capacity of existing rooftop PV installations carries significance that extends far beyond simple resource accounting. It not only constitutes fundamental data essential for scientifically planning regional energy structures, optimizing power dispatch and consumption, and supporting the sustainable transformation of urban energy systems, but also, as it directly quantifies the energy output efficiency of cities’ finite three-dimensional spatial resources (especially rooftop space), represents a core technical challenge. Addressing it is essential for enhancing the sustainable development and utilization efficiency of urban spatial resources [5].

This study focuses on the high-precision estimation of the installed capacity of existing urban rooftop photovoltaic (PV) systems [6]. Similar to research emphasizing PV resource potential prediction [3,4,7,8], reliance is placed on publicly available imagery (e.g., satellite images and aerial drone photography) for the image recognition of PV components. However, the widely utilized public data sources prevalent in current mainstream works (e.g., Malof et al. [9,10], Mayer et al. [11]) still face two critical bottlenecks hindering accuracy improvement. Firstly, non-orthorectified projection effects, primarily caused by the image acquisition perspective (such as satellite side-looking imaging or drone oblique photography), lead to significant geometric distortions in the imagery. Buildings and PV arrays are distorted due to perspective relationships, manifesting as facade tilting and roof compression or stretching. Secondly, there exists high uncertainty in the imaging methodology. These images are often derived from complex sources with unknown acquisition parameters. Specifically, critical metadata—including shooting angle, flight altitude, camera orientation, and focal length parameters—is not publicly available. Furthermore, the imagery is obtained from diverse times, devices, and platforms. This irregularity makes it difficult to establish a universal geometric correction model, thereby increasing the uncontrollability of systematic errors. If the recognition results from such non-orthorectified imagery are directly utilized for estimating urban rooftop PV capacity, significant systematic errors will inevitably be introduced. The root cause of this error lies in the geometric distortion induced by non-orthorectified projection: roof areas may be stretched or compressed within the imagery due to building tilt and height differentials, resulting in severe distortion of scale information along the direction perpendicular to the imaging line-of-sight. Empirical studies have demonstrated that the extent of facade projection deformation (expressed as the ratio of projected facade area to actual area) is significantly positively correlated (Pearson correlation coefficients of 0.870, 0.909, and 0.843 for the north, south, and east facades, respectively; see Section 3.1) with photovoltaic area estimation errors associated with 2D methods. This phenomenon is discussed in Section 3.1 of this paper. This core issue severely constrains the overall accuracy and credibility of large-scale urban rooftop PV surveys. Conducting these surveys with low-cost, accessible imagery becomes less reliable under these geometric distortions. Consequently, it impedes the accurate assessment of urban sustainable energy potential.

To address the issue of non-orthorectification errors, various approaches have been explored. For instance, Liang et al. used orthorectified imagery [12], and Li et al. applied LiDAR technology [13]. These methods provide high-precision geometric information. However, their high acquisition costs and complex processing workflows pose significant obstacles for city-wide applications. Consequently, their scalability is limited. Consequently, their application is hindered in supporting sustainable large-scale census operations. In summary, progress has been made in identifying urban rooftop PV systems through deep learning methods [5,9,10,14,15]. However, the two-dimensional outlines identified by these approaches still fail to resolve the geometric distortions introduced by non-orthorectified projection. As a result, the error in installed capacity estimation remains substantial.

A recent study by So et al. [6] shares our objective of utilizing publicly available imagery for low-cost assessment. Nonetheless, their method estimates capacity by fitting a model based on the visible (2D) surface area and color information of PV arrays, deliberately ignoring the 3D tilt angle. This simplification, while innovative, introduces a high dependency on image acquisition conditions (e.g., solar-PV relative position) and PV module types, making it potentially less robust and generalizable across diverse datasets characterized by complex imagery and varied PV installations.

To address these challenges, this study leverages image visual information [16,17] and introduces a monocular vision-based 3D reconstruction technique leveraging vanishing points (a technique extensively explored and preliminarily applied in autonomous driving and robotics domains [18,19,20,21]). This approach is combined with a lightweight linear capacity prediction model to establish a dual-optimization framework [6]. The framework is designed to achieve low-cost, high-precision extraction of existing photovoltaic (PV) areas on urban rooftops, thereby enabling accurate capacity prediction. The core innovations of this framework are manifested in the following aspects:

(1)

A single publicly available aerial/satellite image is employed, significantly reducing surveying costs compared to technologies such as LiDAR.

(2)

Based on the Hankou University case study, the correlation between facade projection and PV area estimation error is quantified for the first time, revealing the systematic error source inherent in 2D methods.

(3)

To rectify the non-orthorectified issues prevalent in public imagery, a novel camera calibration and 3D reconstruction method is developed. This method leverages prior knowledge of building orthogonal structures and vanishing point geometric constraints to eliminate perspective distortion.

(4)

A closed-loop error optimization process incorporating multi-dimensional geometric constraints (with a 5% residual threshold) is designed. This process mitigates scale distortion induced by image quality deficiencies and annotation errors, thereby ensuring PV reconstruction accuracy.

(5)

A manufacturer-data-driven linear capacity-area model (trained on 215 samples) is constructed, circumventing the parameter complexity associated with traditional physical modeling.

To verify the reliability of the framework, this study utilized typical buildings in Wuhan City as empirical subjects. Combined with UAV oblique photography data, the technical advantages of the proposed method in PV area identification and capacity prediction were validated. This framework is demonstrated to provide a cost-accuracy balanced solution for urban rooftop photovoltaic power capacity assessment [1,9]. It is thereby considered to effectively support urban energy planning and the implementation of the “dual carbon” goals. Furthermore, a replicable and scalable methodological paradigm is established for large-scale, sustainable urban rooftop PV resource surveys based on publicly available satellite remote sensing imagery, significantly enhancing the feasibility of decarbonization strategy implementation.

The discussion in this paper follows the logical framework of “problem-driven, methodological innovation, and empirical verification”. Section 1 systematically explains the research objective of achieving cost-accuracy balanced extraction of existing rooftop PV areas and capacity prediction, which is conducted using publicly available aerial imagery. Subsequently, to address the non-orthorectified issues inherent in public imagery (where the correlation between facade projection and PV area estimation error was quantified based on a typical case in Section 3.1), a dual optimization framework integrating monocular 3D reconstruction and a lightweight linear model is proposed. Section 2 provides a detailed exposition of the technical workflow. Section 3 presents the results and discussion.

2. Methodology

2.1. Dataset

2.1.1. Photovoltaic Array Image Dataset

Images of 20 effective photovoltaic buildings in Wuhan were collected in this study. The image data are comprised of publicly available Google Earth [22] imagery and self-collected high-resolution drone images. Among these, drone data were acquired with a DJI Mavic 3 Classic drone (SZ DJI Technology Co., Ltd., Shenzhen, China), which is equipped with a 4/3-inch CMOS image sensor with 20 million effective pixels, an 84° field of view, and an equivalent focal length of 24 mm.

The publicly available satellite imagery was sourced from Google Earth Pro (version 7.3.6.10201, Google LLC, Mountain View, CA, USA). The images were accessed between August 2022 and April 2025, and the capture dates for the individual building images vary within this period. The specific imagery used for each building is the most recent cloud-free version available on the platform at the time of our study. The use of this imagery for academic research is in accordance with Google’s Terms of Service, permitted under “Fair Use” for non-commercial, educational purposes.

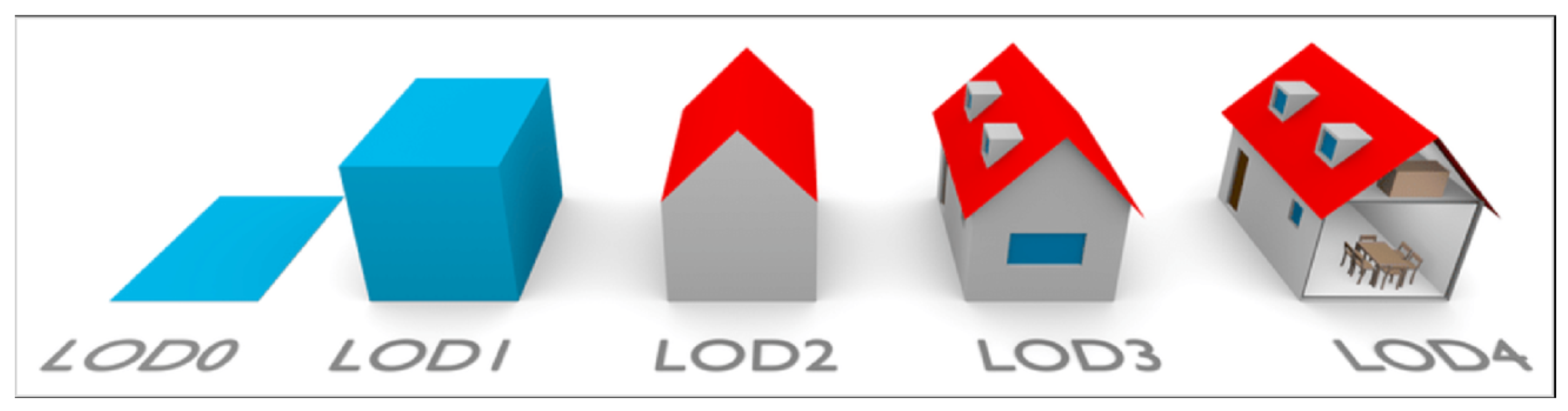
This study focuses on the assessment of photovoltaic (PV) systems on building rooftops. The inherent orthogonal structural features of buildings (such as mutually perpendicular walls and roof edges) are employed as geometric constraints for camera calibration; these features simultaneously constitute the key criteria for building screening. The accuracy of 3D reconstruction is benchmarked against the requirements for PV area estimation. An LOD1 (Level of Detail 1) basic block model, where roofs are simplified and represented as rectangles, is demonstrated to effectively support the geometric error optimization process. This approach ensures the required accuracy, while computational efficiency is significantly enhanced. The LOD specifications for the 3D building models are illustrated in Figure 1.

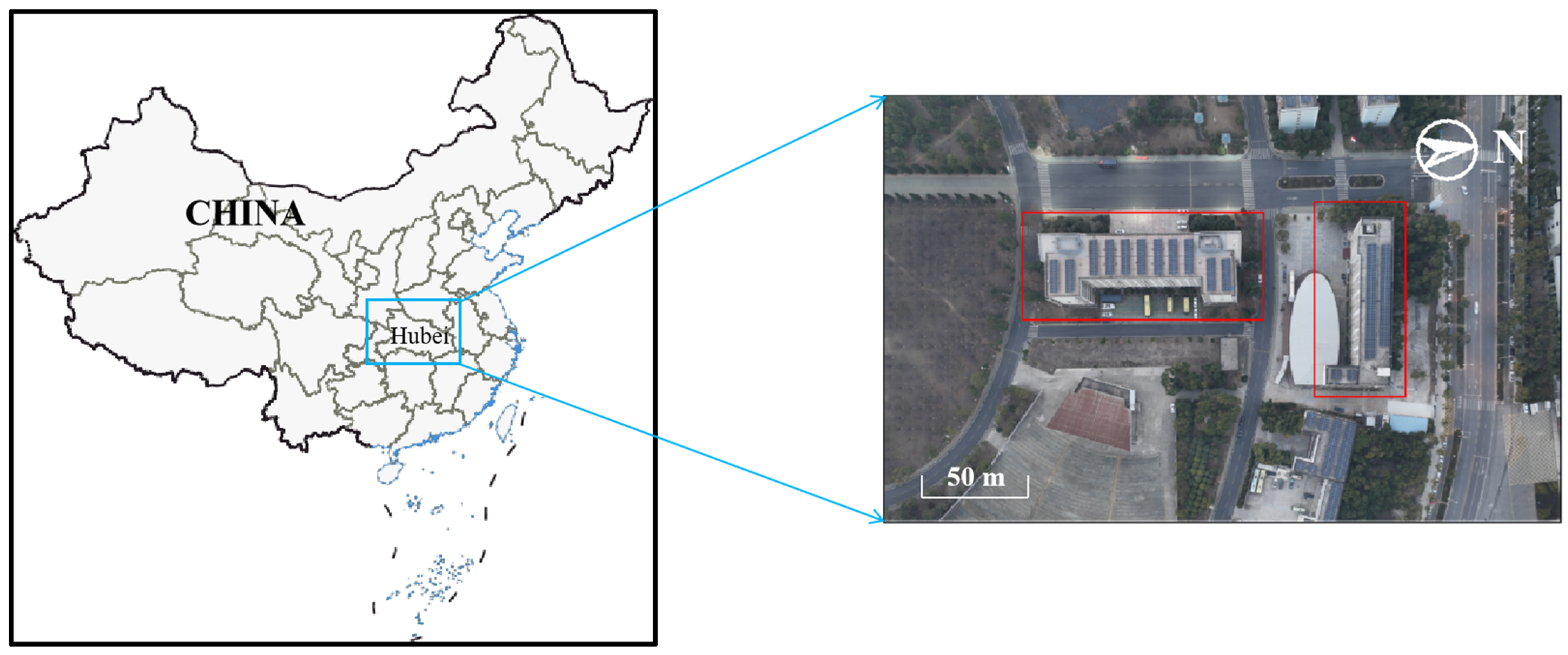
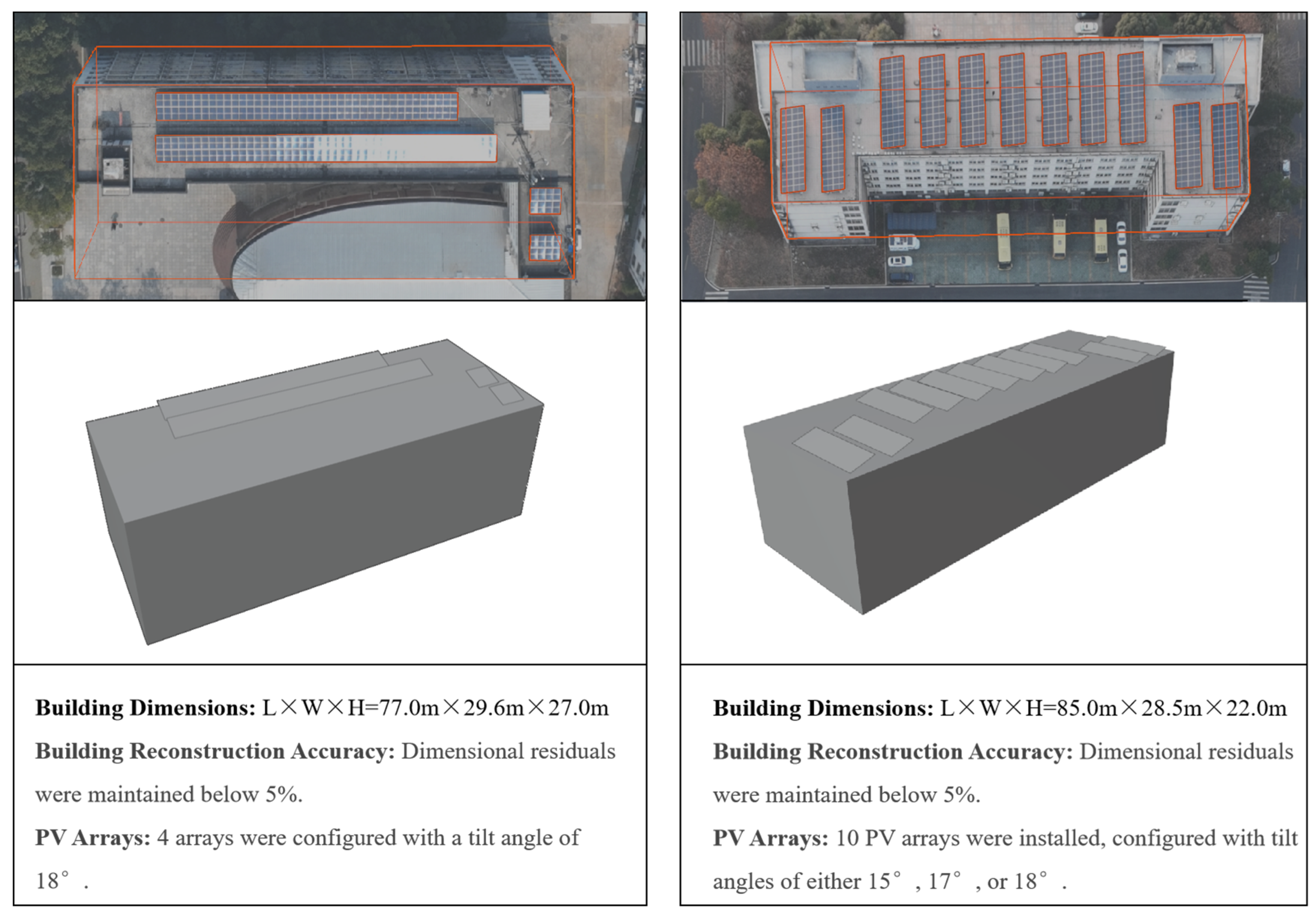
During the experiment, the Comprehensive Building and No. 3 Teaching Building of Hankou University in Wuhan were selected as typical experimental subjects. High-definition images of these two buildings are shown in Figure 2. An ideal geometric reference for 3D reconstruction is provided by their low occlusion rate and prominent structural features, and subsequent accuracy verification is effectively supported. The remaining 18 buildings were used for qualitative assessment and method development.

Key geometric parameters of the buildings and PV components were obtained in detail through field surveys (e.g., roof dimensions, building height, PV tilt angle, and orientation). Among these, roof dimensions, PV dimensions, and building height were used as benchmark data for model validation, while the tilt angle and orientation were employed as known parameters to support the 3D modeling process.

The photographic altitude was set at 250 m relative to the roof plane. This altitude was determined to balance the requirements for image resolution and three-dimensional feature capture, resulting in a ground resolution of 2.7 cm for the captured photovoltaic (PV) rooftops. High-definition images with varying degrees of non-orthogonality were acquired through multi-angle non-orthographic photography. Ultimately, a standardized dataset was constructed, containing images of the PV arrays along with their precise dimensions and the corresponding building dimensions.

The UAV flights were conducted in compliance with local regulations for low-altitude, lightweight UAV operations, which were permitted for this academic research project.

2.1.2. Capacity-Area Manufacturer Dataset

The capacity model was constructed based on product technical parameter manuals from 19 mainstream PV manufacturers, which encompass technical specifications for over 200 different PV module models. Key indicators were defined as power capacity and dimensional specifications. During data processing, power units (W) and area units (m²) were standardized. The Interquartile Range (IQR) method was employed to identify and remove outliers, resulting in 215 valid samples. This standardized database provides reliable support for modeling and analyzing the capacity–area relationship.

2.2. Study Framework

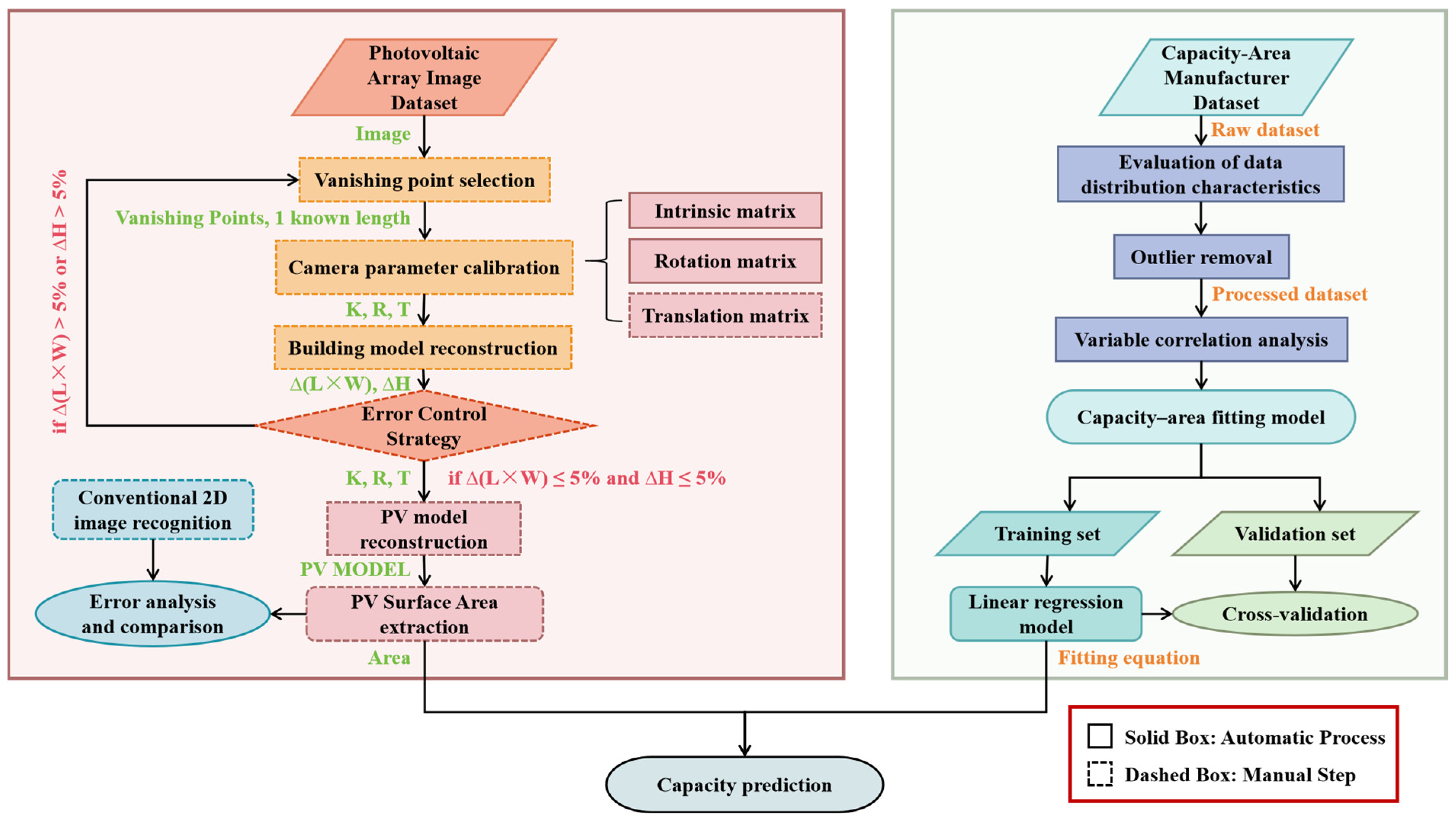
Our technical framework addresses the core challenges of assessing urban rooftop PV capacity from a single non-orthorectified aerial image. As illustrated in Figure 3, the framework primarily comprises four core modules: camera parameter calibration, 3D reconstruction with error control, precise PV area extraction, and lightweight capacity estimation. The detailed workflow is described as follows:

Input Data Preparation: A single non-orthorectified aerial image (e.g., publicly available satellite imagery from Google Earth or UAV oblique photography imagery) is input, along with a limited number of easily obtainable key building geometric parameters. These parameters include building footprint dimensions (L × W), height (H), and PV module installation tilt angle (θ) and orientation. They are typically acquired through simple on-site surveys or publicly available sources. The source of these priors is as follows: the footprint dimensions (L × W) were obtained by measuring the polygon outlines of buildings on publicly available web-mapping services (e.g., Baidu Maps, which provides a built-in distance measurement tool). The building height (H) was acquired from open urban 3D model databases. In the absence of specific installation data, the PV tilt angle (θ) can be set based on regional common practice or default values, and the orientation is typically assumed to be south-facing for sites in the Northern Hemisphere. These priors represent a pragmatic approach to data acquisition that leverages commonly accessible sources.

Camera Self-Calibration: Leveraging the ubiquitous orthogonal structural features inherent to buildings (such as mutually perpendicular walls and roof edges), groups of parallel lines corresponding to three orthogonal directions are selected within the input image. Their corresponding vanishing points (VPs) are computed. Utilizing the geometric orthogonality constraints between the vanishing points, combined with a known dimensional constraint of one building side (e.g., the building base length), the camera’s intrinsic matrix (K) and extrinsic matrices (rotation matrix R and translation vector T) are solved, thereby completing camera self-calibration (Section 2.3).

3D Reconstruction and Error Control: Using the calibrated camera parameters (K, R, T), preliminary 3D reconstruction is performed via the collinearity equations (Equation (1)). To mitigate calibration error accumulation and ensure the geometric accuracy of the reconstructed model, an error-closed-loop iterative strategy is introduced, incorporating multi-dimensional geometric constraints: The reconstructed model’s roof dimensions (L, W) and building height (H) are projected back onto the 2D image plane and aligned with the corresponding features in the input image. Simultaneously, the reconstructed key geometric parameters are compared against the input measured/known parameters (L × W, H), and the residual is calculated (Equation (18)). If the residual exceeds the preset threshold (ε = 5%), the vanishing point selection is revised or the dimensional constraints are optimized, initiating iterative optimization until the accuracy requirement is met (Section 2.4).

PV Array 3D Reconstruction and Area Extraction: Based on the optimized camera parameters and the reconstructed building roof plane, leveraging the known PV module tilt angle (θ) and orientation parameters (typically south-facing), the PV array model is precisely reconstructed in 3D space. Model parameters are finely adjusted to ensure its projected contours are precisely aligned with the edges of the PV modules in the input imagery (Section 2.5). Finally, the surface area (α) of the aligned PV array is extracted directly within the 3D modeling environment.

Lightweight Capacity Estimation: The accurately extracted PV surface area (α) is input into a pre-constructed lightweight linear capacity model (Equation (19)). This model, established based on statistical analysis of large-scale PV manufacturer data, utilizes surface area as the sole independent variable and directly outputs the estimated installed capacity (c) of the PV system (Section 2.6).

This workflow achieves inversion from 2D imagery to 3D information through monocular vision geometric constraints, effectively correcting projection distortion in non-orthorectified imagery. Combined with the error control strategy to ensure accuracy, it ultimately enables robust capacity estimation via a concise linear model. Consequently, an efficient and low-cost technical pathway is provided for city-scale PV resource surveys.

2.3. Vanishing-Point Constrained Camera Calibration

Three-dimensional spatial information is inferred from two-dimensional images, which constitutes the core objective of camera calibration [23,24,25,26,27]. During the monocular vision imaging process, points in 3D space are mapped onto a two-dimensional pixel plane via the collinearity condition equations. The mathematical expression is provided by:

$$\mathit{s}\left[\begin{array}{c}\mathit{i}\\ \mathit{j}\\ 1\end{array}\right]=\mathit{K}\left[\mathit{R}\left|\mathit{T}\right.\right]\left[\begin{array}{c}\mathit{x}\\ \mathit{y}\\ \begin{array}{c}\mathit{z}\\ 1\end{array}\end{array}\right]$$

(1)

In the equation, s represents the scale factor (dimensionless), K denotes the intrinsic matrix, R and T are the rotation matrix and translation vector (extrinsic parameters), respectively, (i, j) represents the pixel coordinates, and (x, y, z) denotes the world coordinates.

The problem involves describing and computing the transformations between the world, camera, and image plane coordinate systems. Define the world coordinate system as R_O (O, x, y, z), the camera coordinate system as R_C (C, i, j, k), and the image plane coordinate system as R_S (S, i, j). The world coordinate system R_O is transformed into the camera coordinate system R_C via the extrinsic matrix [R | T]. Subsequently, the camera coordinate system R_C is transformed into the image plane coordinate system R_S via the intrinsic matrix K.

In this study, the open-source tool fspy (version 1.0.3; stuffmatic, Stockholm, Sweden) [28] is used for calibration, with the orthogonal structural features of building facades being utilized to select three orthogonal pixel points in monocular images, and the corresponding three sets of vanishing points are calculated. Secondly, known dimensional constraints of the building (specifically, the actual length of one side) are combined to solve the camera’s intrinsic parameters (intrinsic matrix K) and extrinsic parameters (including rotation matrix R and translation vector T). A schematic diagram of the camera calibration process based on vanishing points is provided in Figure 4.

2.3.1. Calculating the Intrinsic Matrix

As shown in Figure 4, the projection center is denoted as C, and its projection onto the image plane is point P. The image contains three mutually orthogonal sets of parallel lines, whose corresponding vanishing points are v₁, v₂, and v₃. These vanishing points are represented in homogeneous coordinates as (v_x, v_y, 1). Corresponding to the three orthogonal directions (x/y/z axes), these vanishing points satisfy the following constraint in the camera coordinate system:

$${{\mathit{v}}_{\mathit{i}/{\mathit{R}}_{\mathit{C}}}}^T·{\mathit{v}}_{\mathit{j}/{\mathit{R}}_{\mathit{C}}}=0( \mathit{i} \ne \mathit{j} \mathrm{and} \mathit{i}, \mathit{j} \in \left\{1, 2, 3\right\})$$

(2)

And:

$${\mathit{v}}_{/{\mathit{R}}_{\mathit{C}}}={\mathit{K}}^{-1}·{\mathit{v}}_{/{\mathit{R}}_{\mathit{S}}}$$

(3)

Therefore:

$${{\mathit{v}}_{\mathit{i}/{\mathit{R}}_{\mathit{S}}}}^T{\mathit{K}}^{-T}{\mathit{K}}^{-1}{\mathit{v}}_{\mathit{j}/{\mathit{R}}_{\mathit{S}}}=0$$

(4)

where K is the intrinsic matrix:

$$\mathit{K}=\left[\begin{array}{ccc}\mathit{f}& 0& {\mathit{u}}_0\\ 0& \mathit{f}& {\mathit{v}}_0\\ 0& 0& 1\end{array}\right]$$

(5)

We derive the equation:

$$\left({\mathit{v}}_{\mathit{ix}}{-\mathit{u}}_0\right)\left({\mathit{v}}_{\mathit{jx}}-{\mathit{u}}_0\right)+\left({\mathit{v}}_{\mathit{iy}}-{\mathit{v}}_0\right)\left({\mathit{v}}_{\mathit{jy}}-{\mathit{v}}_0\right)+{\mathit{f}}^2=0 ( \mathit{i} \ne \mathit{j} )$$

(6)

For the combination of three orthogonal vanishing points, we can establish three equations to solve for the parameters f, u₀, and v₀, ultimately determining the intrinsic matrix K.

2.3.2. Calculating the Rotation Matrix

Taking the vanishing point v₁ corresponding to the x-axis in the camera coordinate system R_O as an example, it represents a point at infinity in the real world projected onto the image plane. It is represented in homogeneous coordinates as ${\left(\begin{array}{ccc}1& 0& \begin{array}{cc}0& 0\end{array}\end{array}\right)}_{/{\mathit{R}}_{\mathit{O}}}$. Its collinearity equation is expressed as:

$$\begin{array}{c} \mathit{s}{\mathit{v}}_{1/{\mathit{R}}_{\mathit{S}}}=\mathit{K}\left[\mathit{R}\left|\mathit{T}\right.\right]{\mathit{X}}_{\infty /{\mathit{R}}_{\mathit{O}}}\hfill \\ =\mathit{K}\left[\begin{array}{ccc}{\mathit{r}}_1& {\mathit{r}}_2& {\mathit{r}}_3\end{array}\left|\mathit{T}\right.\right]\left[\begin{array}{c}1\\ 0\\ \begin{array}{c}0\\ 0\end{array}\end{array}\right]\hfill \end{array}$$

(7)

Therefore:

$$\mathit{s}{\mathit{v}}_{1/{\mathit{R}}_{\mathit{S}}}=\mathit{K}{\mathit{r}}_1$$

(8)

${\mathit{r}}_1$ is normalized:

$${\mathit{r}}_1={\displaystyle \frac{{\mathit{K}}^{-1}{\mathit{v}}_{1/R_S}}{‖{\mathit{K}}^{-1}{\mathit{v}}_x‖}}=\left[\begin{array}{c}{\displaystyle \frac{v_{1x}-u_0}{\sqrt{{\left(v_{1x}-u_0\right)}^2+{\left(v_{1y}-v_0\right)}^2+f^2}}}\\ {\displaystyle \frac{v_{1y}-v_0}{\sqrt{{\left(v_{1x}-u_0\right)}^2+{\left(v_{1y}-v_0\right)}^2+f^2}}}\\ {\displaystyle \frac{f}{\sqrt{{\left(v_{1x}-u_0\right)}^2+{\left(v_{1y}-v_0\right)}^2+f^2}}}\end{array}\right]$$

(9)

Similarly, the rotation vectors $r_2$ and $r_3$ corresponding to the y-axis and z-axis, respectively, can be calculated using the vanishing points v₂ and v₃.

$$\begin{gathered} {\mathit{r}}_2={\displaystyle \frac{{\mathit{K}}^{-1}{\mathit{v}}_{2/R_S}}{‖{\mathit{K}}^{-1}{\mathit{v}}_y‖}} \\ {\mathit{r}}_3={\displaystyle \frac{{\mathit{K}}^{-1}{\mathit{v}}_{3/R_S}}{‖{\mathit{K}}^{-1}{\mathit{v}}_{\mathit{z}}‖}} \end{gathered}$$

(10)

Ultimately, the rotation matrix is given by:

$$\mathit{R}=\left[\begin{array}{ccc}{\mathit{r}}_1& {\mathit{r}}_2& {\mathit{r}}_3\end{array}\right]$$

(11)

2.3.3. Calculating the Translation Vector

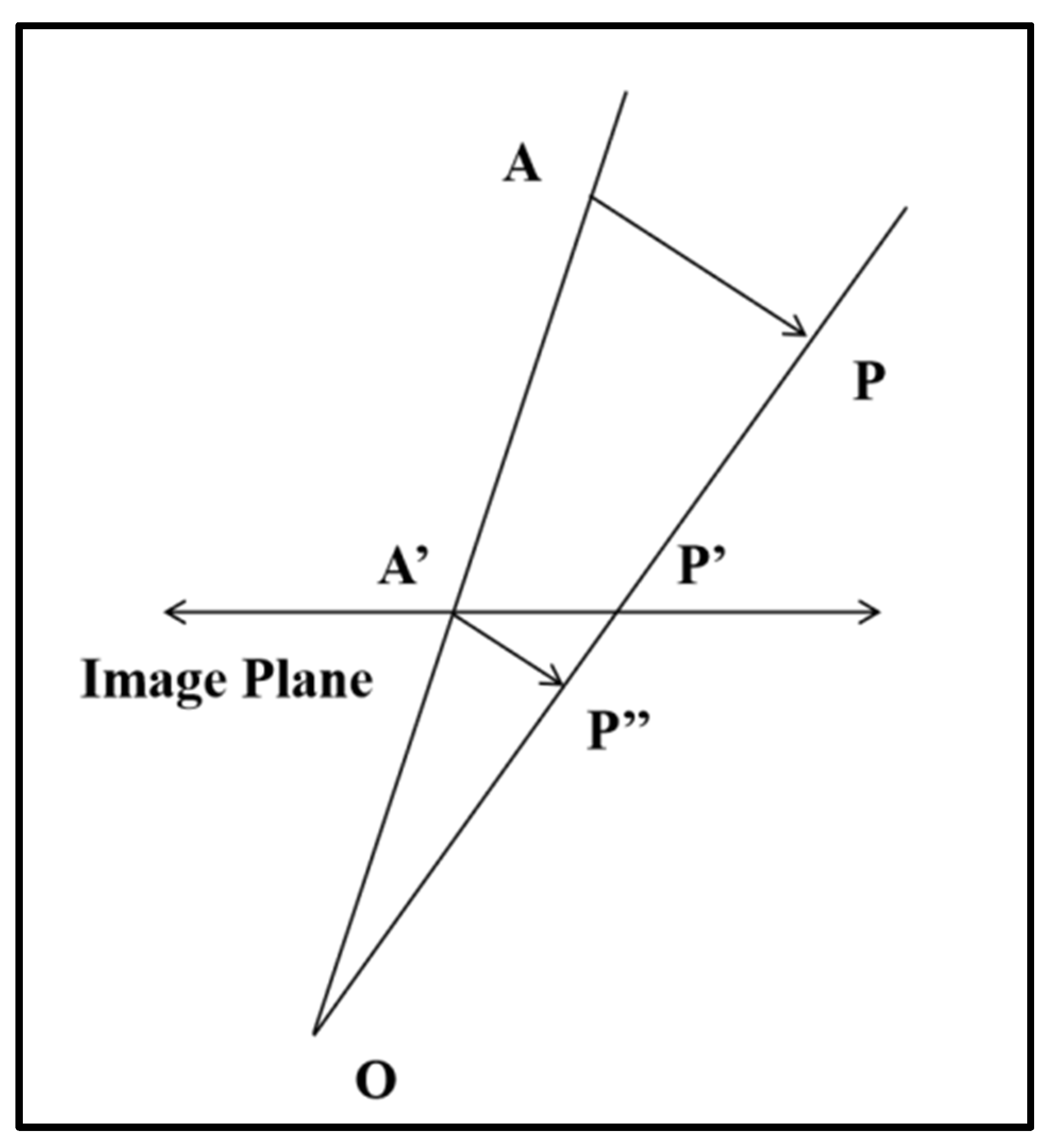
As shown in Figure 5, let point A′ denote the perspective projection of point A, and vector $\overrightarrow{{\mathit{A}}^{\prime }{\mathit{P}}^{\prime }}$ denote the perspective projection of vector $\overrightarrow{\mathit{AP}}$. Vector $\overrightarrow{\mathit{AP}}$ is parallel to the x-axis of the world coordinate system R_O and originates from its origin O. To determine the translation vector T, we assume the length of $\overrightarrow{\mathit{AP}}$ is known; otherwise, the translation vector can only be determined up to an unknown scale factor.

We can write:

$${\overrightarrow{\mathit{AP}}}_{/{\mathit{R}}_{\mathit{O}}}= \mathit{l} · \mathit{u} ;{ \overrightarrow{\mathit{AP}}}_{/{\mathit{R}}_{\mathit{C}}} = \mathit{R} · {\overrightarrow{\mathit{AP}}}_{/{\mathit{R}}_{\mathit{O}}}$$

(12)

Let P″ denote the intersection point of line (OP) and line D passing through A with direction vector $\overrightarrow{\mathit{AP}}$. Then:

$${{\mathit{P}}^{″}}_{/{\mathit{R}}_{\mathit{C}}}={\left(\mathit{OP}\right)}_{/{\mathit{R}}_{\mathit{C}}}\bigcap \mathit{D}={\left(\mathit{OP}\text{'}\right)}_{/{\mathit{R}}_{\mathit{C}}}\bigcap \mathit{D}$$

(13)

Since triangles OA′P″ and OAP are similar, we obtain:

$${\displaystyle \frac{‖{\overrightarrow{{\mathit{A}}^{\prime }{\mathit{P}}^{″}}}_{/{\mathit{R}}_{\mathit{C}}}‖}{‖{\overrightarrow{\mathit{AP}}}_{/{\mathit{R}}_{\mathit{C}}}‖}}={\displaystyle \frac{‖{\overrightarrow{{\mathit{OA}}^{\prime }}}_{/{\mathit{R}}_{\mathit{C}}}‖}{‖{\overrightarrow{\mathit{OA}}}_{/{\mathit{R}}_{\mathit{C}}}‖}}$$

(14)

or

$$‖{\overrightarrow{\mathit{OA}}}_{/{\mathit{R}}_{\mathit{C}}}‖={\displaystyle \frac{‖{\overrightarrow{{\mathit{OA}}^{\prime }}}_{/{\mathit{R}}_{\mathit{C}}}‖·‖{\overrightarrow{\mathit{AP}}}_{/{\mathit{R}}_{\mathit{C}}}‖}{‖{\overrightarrow{{\mathit{A}}^{\prime }{\mathit{P}}^{″}}}_{/{\mathit{R}}_{\mathit{C}}}‖}}$$

(15)

Therefore:

$${\overrightarrow{\mathit{OA}}}_{/{\mathit{R}}_{\mathit{C}}}=‖{\overrightarrow{\mathit{OA}}}_{/{\mathit{R}}_{\mathit{C}}}‖·{\displaystyle \frac{{\overrightarrow{{\mathit{OA}}^{\prime }}}_{/{\mathit{R}}_{\mathit{C}}}}{‖{\overrightarrow{{\mathit{OA}}^{\prime }}}_{/{\mathit{R}}_{\mathit{C}}}‖}}$$

(16)

The translation vector is given by:

$$\mathit{T} = {\mathit{R}}^{-1} ·{{\displaystyle \stackrel{⇢}{OA}}}_{/{\mathit{R}}_{\mathit{C}}}$$

(17)

Similarly, if the length of a line segment parallel to any other coordinate axis (y or z) of R_O is known, the translation vector T can be solved using the same principle.

2.4. Error Control Strategy

The conversion from the 2D image plane coordinate system to the 3D world coordinate system is enabled by the initial parameters obtained via the vanishing point calibration method (intrinsic matrix K and extrinsic matrix [R | T]) through the collinearity equations. Given that point selection accuracy is critical for vanishing-point-based calibration and that errors can be accumulated progressively during the parameter estimation process—ultimately affecting the geometric precision of the reconstructed 3D model [9]—a robust error control strategy based on multi-dimensional geometric constraints is proposed in this study. Publicly available, redundant geometric information commonly accessible for urban buildings—such as building footprint dimensions and height data—is leveraged in the core idea of this strategy to compute residuals and iteratively optimize the initially calibrated parameters. The propagation of single-point errors is effectively suppressed, and the overall scale accuracy of the reconstructed model is ensured by this approach [20]. The specific steps are outlined as follows.

Based on the initial calibration parameters, the building’s 3D model was reconstructed from the monocular image using the open-source 3D modeling software Blender (version 2.83.19, Blender Foundation, Amsterdam, The Netherlands) [29]. By interactively adjusting the parameters of the reconstructed model—specifically, the rooftop dimensions (length L and width W) and building height (H)—the projected contours of the model in the two-dimensional image plane (including rooftop edge lines and building footprint outlines) were precisely aligned with the corresponding features in the input image. This step effectively leveraged the identifiable geometric outlines of buildings in the image as strong constraints, with potential errors in camera calibration parameters being mapped and corrected into the observable and adjustable parameter space of the 3D model [25].

The key geometric parameters of the reconstructed model are compared with publicly available measured data. The outline size residual Δ(L × W) and height residual ΔH are calculated:

$$\begin{gathered} ∆\left(\mathit{L}\times \mathit{W}\right)={\displaystyle \frac{\left|{\mathit{L}}_{\mathit{pre}}·{\mathit{W}}_{\mathit{pre}}-{\mathit{L}}_{\mathit{real}}·{\mathit{W}}_{\mathit{real}}\right|}{{\mathit{L}}_{\mathit{real}}·{\mathit{W}}_{\mathit{real}}}} \\ ∆\mathit{H}={\displaystyle \frac{\left|{\mathit{H}}_{\mathit{pre}}-{\mathit{H}}_{\mathit{real}}\right|}{{\mathit{H}}_{\mathit{real}}}} \end{gathered}$$

(18)

The residual threshold is set as $\mathsf{ϵ} = 5\%$, taking into account typical measurement errors in building dimensions, acceptable accuracy levels for engineering applications, and the efficiency of model optimization. The current set of camera calibration parameters is deemed valid only when both the residual error in the building’s footprint dimensions $∆\left(\mathit{L} \times \mathit{W}\right)$ and the height residual $∆\mathit{H}$ are strictly below this threshold. If either error exceeds the threshold, the process returns to the camera calibration stage, where vanishing point selection is adjusted or geometric constraints on building dimensions are refined.

The residual threshold of ε = 5% was selected based on a trade-off between reconstruction accuracy and operational feasibility. This value was chosen to be stricter than typical uncertainties in the readily available prior data to ensure it meaningfully improved the model, while being loose enough to be achievable without excessive manual iteration for the majority of buildings in our dataset.

A formal quantitative sensitivity analysis of this threshold (e.g., testing ε = 3% or 8%) would require fully automating the vanishing point selection and model adjustment steps to avoid introducing human variability. While such an ablation study is a valuable direction for future work with an automated pipeline, the chosen value of 5% proved to be robust and effective in practice, as evidenced by the low final MAPU achieved (3.47%).

2.5. PV Array 3D Reconstruction and Area Extraction

Based on the validated or optimized camera calibration parameters, the 3D reconstruction process incorporates key field-surveyed information, including the tilt angle θ and orientation of the photovoltaic (PV) modules, which are typically tilted southward [30,31]. These empirically obtained parameters are treated as known constraints and are directly input into the 3D modeling software Blender. Specifically, the tilt angle θ is used to precisely define the angle between the surface normal of the PV modules and the horizontal rooftop plane, while the orientation parameter (commonly south-facing) determines the azimuth of the PV modules on the roof plane, ensuring that the reconstructed PV array accurately reflects the real-world installation in spatial posture. The open-source 3D modeling software Blender is employed to reconstruct rooftop PV arrays from monocular images.

Using the reconstructed rooftop plane as the spatial reference baseline, the lowest edge of the photovoltaic (PV) array model—typically the edge adjacent to the rooftop mounting base—is strictly constrained to align with this reference plane, thereby simulating the actual installation condition. Subsequently, the edge length parameters of the PV panels are finely adjusted to ensure that their projected boundaries in the two-dimensional image coordinate system precisely match the visually identifiable edges of the PV modules in the original image [23]. This sequence of spatial geometric constraints constitutes a critical step in mitigating scale distortions of PV components caused by perspective projection and oblique viewing angles in monocular imagery.

The surface area data of the aligned PV array are extracted via the 3D modeling software. Figure 6 illustrates the geometric alignment process and the reconstructed building and PV array models. By leveraging spatial geometric constraints, scale distortions caused by non-orthogonal projection in monocular imagery are effectively mitigated by this method, providing high-precision surface area input for capacity prediction.

2.6. Capacity Fitting Model

A Pearson correlation analysis was performed on the manufacturer capacity–area dataset, and a remarkably high correlation coefficient of 0.9599 (p = 2.1590 × 10⁻¹¹⁷) between module area and power generation capacity was revealed. This provides strong statistical support for constructing a linear regression model and validates the feasibility of utilizing the “power capacity per unit area” parameter [5,6].

Based on this analysis, a lightweight linear prediction model is established:

$$\mathit{c} = \mathit{\gamma }\mathit{\alpha } + {\mathit{\gamma }}_0$$

(19)

where $\mathit{c}$ represents the power capacity of the PV module (W), $\mathit{\gamma }$ denotes the power capacity per unit area parameter (W/m²), $\mathit{\alpha }$ is the surface area of the PV module (m²), and ${\mathit{\gamma }}_0$ is the model intercept (W). Although theoretically the intercept approaches zero, retaining this parameter enhances model flexibility [5].

3. Results and Discussion

3.1. Impact of Facade Distortion on PV Area Prediction

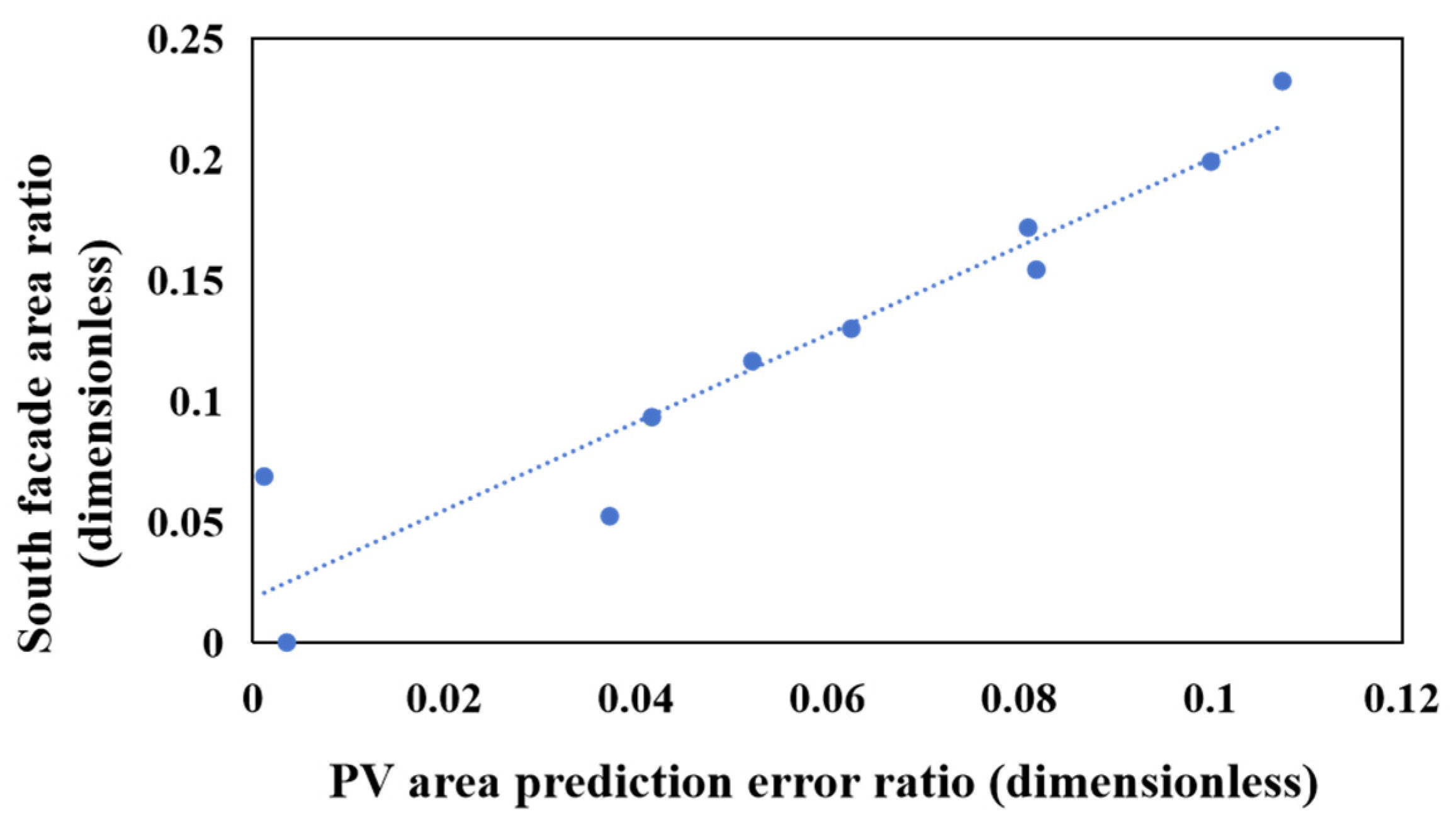
To quantitatively assess the error contribution of building facade distortion under non-orthorectified projection to rooftop photovoltaic (PV) area prediction, the facade area ratio (i.e., the ratio of projected facade area to its actual area) and the relative error of PV area prediction (i.e., the relative difference between PV area estimated using a purely 2D projection method and the actual PV area) were extracted along directions of Teaching Building No. 3 at Hankou University. The correlation between these two variables was then calculated to evaluate their relationship.

The Pearson correlation coefficients calculated for all samples were 0.870 for the north facade, 0.909 for the south facade, and 0.843 for the east facade, indicating that as the degree of facade projection distortion increases, the systematic error in photovoltaic area estimation using 2D methods also significantly increases. This strong correlation suggests that geometric distortions caused by the tilt or height differences of various building facades are a major source of error in conventional 2D extraction methods.

Taking the south facade as an example, an ordinary least squares (OLS) linear regression was performed on the data presented in Figure 7.

$${\mathit{∆}}_{\mathit{PV}} = 0.5126{\mathit{∆}}_{\mathit{facade}} + 0.0063$$

(20)

The analysis yielded a highly significant relationship (p < 0.001 for β) with the following parameters: slope β = 0.5126 (95% CI: [0.3572, 0.6297]; SE = 0.0591), and intercept α = 0.0063. The coefficient of determination R² was 0.8971.

A Breusch–Pagan test was conducted to assess heteroskedasticity (LM statistic = 1.2438, p = 0.2647), indicating that the null hypothesis of homoscedasticity cannot be rejected at the 5% significance level. This supports the use of standard OLS assumptions for this relationship.

This result indicates that for every 0.1 increase in the facade area ratio, the relative uncertainty of the 2D estimation method increases by approximately 5.1 percentage points on average.

Specifically, for every 0.1 increase in the facade area ratio, the relative error of the 2D estimation method increases by approximately 5.1% on average. This further confirms that building tilt and height differences cause stretching or compression of rooftop areas in non-orthorectified imagery. Such geometric effects make it challenging for 2D methods that directly utilize aerial images—while ignoring non-orthorectification errors—to accurately recover the true dimensions of rooftop planes, especially where scale information perpendicular to the imaging line of sight is severely distorted. In contrast, the 3D reconstruction approach proposed in this study effectively mitigates the interference of facade projection distortion on rooftop dimension estimation by restoring the three-dimensional spatial geometry.

3.2. PV Area Recognition Accuracy and Uncertainty Analysis

To quantitatively evaluate the effectiveness of the 3D reconstruction method, the Mean Absolute Percentage Error (MAPE) is employed as the core metric to estimate the uncertainty in area prediction. The performance differences between the proposed 3D reconstruction method and a conventional 2D method (which directly utilizes aerial imagery while ignoring non-orthographic errors) are compared when applied to the PV module image dataset.

To establish a baseline for comparison, the performance of the proposed 3D reconstruction method was evaluated against a conventional 2D method. This 2D baseline involved the manual polygonal delineation of PV array boundaries directly on the original, non-orthorectified input imagery (i.e., without applying any geometric correction). Crucially, to enable a direct and fair comparison, the scale for this 2D method was derived in an analogous way to the 3D method: it was calibrated using the same known dimensions of a building segment (e.g., the length of a roof edge) that served as the control for the 3D reconstruction. The area in pixels was converted to physical units (m²) by first establishing a pixel-to-meter ratio from this known reference length. This approach represents a common yet geometrically naive practice that directly utilizes imagery while ignoring perspective distortion, thereby highlighting the specific advantage of our 3D framework in correcting these geometric errors.

As presented in Figure 8, the mean MAPE of the 2D method, indicating its higher uncertainty, was recorded as 10.58%, while the proposed 3D method with the 5% error control strategy achieved a significantly reduced mean MAPE of 3.47%. The error frequency distribution table further demonstrates that the 2D method exhibited a significantly higher proportion of high-error samples, while the results of the proposed method were concentrated within the low-error range. These findings indicate that 3D reconstruction substantially enhances the stability and accuracy of area identification by correcting geometric distortions induced by non-orthogonal projection. Furthermore, the error reduction is primarily attributed to the error control strategy integrated into the 3D reconstruction process. This strategy, leveraging vanishing point constraints and multi-dimensional geometric constraints, effectively suppressed scale biases caused by non-orthorectified projection in monocular imagery.

This significant reduction in estimation uncertainty—from 10.58% to 3.47%—strongly demonstrates that the major geometric distortions caused by non-orthorectified projection, particularly the rooftop plane’s perspective foreshortening and scaling biases induced by building facade tilt and height variations, are successfully corrected by the 3D reconstruction process. The high consistency between the 3D method’s predicted areas and the actual areas is visually illustrated in Figure 9, with data points closely clustered around the reference line y = x. In contrast, obvious outliers are exhibited by the 2D method’s points.

3.3. Capacity Model Performance

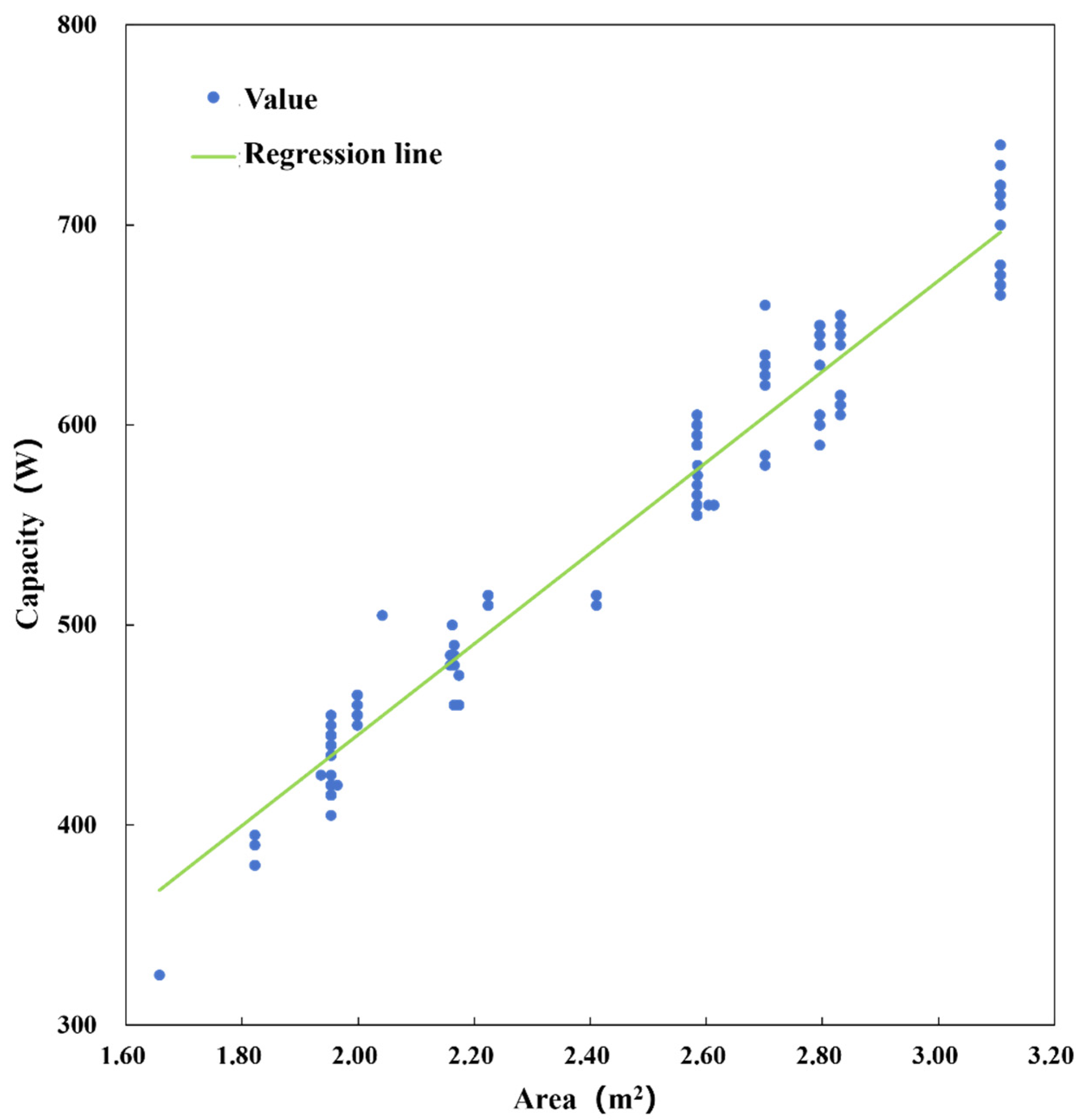
A total of 215 data points comprising photovoltaic (PV) module areas and their corresponding power capacities were collected in this study. To mitigate the influence of outliers on the regression model, a multi-stage outlier removal procedure was designed: first, univariate extreme values in area and capacity were removed using the interquartile range (IQR) rule; second, multivariate extreme samples were further filtered by using the Z-score method; third, samples with residuals exceeding ±2 standard deviations from an initial linear regression model were excluded; finally, observations with excessive influence were identified and removed based on Cook’s Distance from ordinary least squares (OLS) regression, with a threshold of 4/n being used.

After this procedure, 202 samples were retained, corresponding to a removal rate of 6.0%. Subsequent examination of the excluded samples revealed that all corresponded to atypical modules with power-to-area ratios deviating significantly from mainstream products, including colored photovoltaic glass, photovoltaic tiles, and obsolete models. Therefore, these were considered non-representative extreme values and were justifiably excluded.

Figure 10 presents a comparison of the dataset before and after outlier removal, demonstrating that data cleaning substantially improved the model’s stability and predictive accuracy.

Based on the cleaned dataset, a linear regression model was constructed relating photovoltaic (PV) module surface area ($\mathit{\alpha }$) to power generation capacity ($\mathit{c}$):

$$\mathit{c} = \mathit{\gamma }\mathit{\alpha } + {\mathit{\gamma }}_0$$

where $\mathit{\gamma }$ represents the capacity per unit area parameter (W/m²), and ${\mathit{\gamma }}_0$ denotes the model intercept (W). Although the intercept is theoretically expected to approach zero, retaining this parameter is found to enhance the model’s flexibility in practical applications.

As demonstrated in Figure 11, a high level of consistency was demonstrated by the model. A coefficient of determination (R²) of 0.9548 was achieved, with a mean squared error (MSE) of 426.79 W² and a mean absolute error (MAE) of 18.86 W, indicating excellent predictive capability. The specific regression equation derived is:

$$\mathit{c} = 226.95\mathit{\alpha } - 8.7663$$

(21)

Although the model intercept (γ₀ = $-$8.7663 W) is non-zero, it is statistically insignificant (p-value = 0.2316 > 0.05; 95% CI: $-$28.5453, 6.9494). This indicates that forcing the regression through the origin (i.e., setting γ₀ = 0) would not materially change the model’s predictions or conclusions; while retaining it enhances model flexibility.

To validate the model’s generalizability, a five-fold cross-validation approach was further adopted. Robust generalization capability for unseen data is indicated by

Table 1. Results of five-fold cross-validation.

Fold	R2	MSE (W2)	MAE (W)
1	0.9589	391.75	18.18
2	0.9584	454.46	19.13
3	0.9326	516.55	20.29
4	0.9427	458.44	19.86
5	0.9590	431.49	19.33
Mean	0.9503 ± 0.0108	450.54 ± 40.63	19.36 ± 0.71

Note: The dataset was randomly partitioned into five folds for cross-validation.

, which shows that the average cross-validated R² is 0.9503 ± 0.0108.

It is important to note that this linear capacity-area model is derived from and is therefore applicable to the types of standard photovoltaic modules represented in the technical specifications of the 19 mainstream manufacturers included in our dataset. Its application to atypical module designs (e.g., colored PV glass, solar tiles, or flexible thin-film modules with significantly different power-to-area ratios) may require additional validation or model adjustment.

An important consideration for the long-term application of the proposed capacity-area model is its sensitivity to the continuous evolution of photovoltaic technology. The linear relationship (Equation (19)) and its parameter γ (W/m²) are empirically derived from the prevailing market technologies at the time of the study. The emergence of new, high-efficiency module designs (e.g., perovskite-silicon tandems, heterojunction cells) with significantly higher power densities could indeed alter this relationship, potentially reducing the model’s accuracy if not updated.

However, the framework itself is designed to be adaptable, not static. The simplicity of the linear model is a key advantage here; it can be rapidly recalibrated with a new set of manufacturer datasheets. Future work could automate this process by periodically scraping the latest technical specifications from manufacturer websites. Thus, while the specific numerical value of γ may change over time, the understanding that a strong, linear capacity-area relationship exists and the methodology for extracting the area α remain the core, enduring contributions of this work. The proposed method provides a powerful tool for generating snapshots of PV capacity at a city scale, with the understanding that its predictive core (the linear coefficient) requires periodic updates to reflect technological progress, much like any other data-driven model in a rapidly advancing field.

3.4. Analysis of Measurement Uncertainty

In accordance with the Guide to the Expression of Uncertainty in Measurement (GUM), an analysis of the measurement uncertainty was conducted to evaluate the reliability of the proposed method. The overall measurement process is complex and non-linear, involving the 3D reconstruction of the PV array and subsequent area extraction. The key quantity of interest is the surface area α (in m²) of the photovoltaic array.

Measurement Model:

The measured area α is a function of multiple input quantities: the input image data (I), the camera parameters (K, R, T) estimated through calibration, the prior geometric constraints (M_prior, e.g., building height H, footprint dimensions L × W), and the manual intervention points (M_man, e.g., vanishing point selection, PV boundary delineation).

Identification of Major Uncertainty Sources:

The main contributors to the combined standard uncertainty of the area measurement u_c(α) include:

(1)

Uncertainty in camera calibration (u_cal): Arises from the selection of vanishing points and linear features in the image. This component also encompasses residual optical distortions not fully corrected by the calibration model.

(2)

Uncertainty in prior dimensions (u_prior): Associated with the accuracy of the easily obtainable building geometric parameters (e.g., H, L, W). This is a Type B uncertainty estimate.

(3)

Uncertainty in manual delineation (u_man): Related to the manual selection of PV array boundaries in the image for both the 2D baseline and the final alignment in the 3D model.

(4)

Uncertainty from the linear capacity model (u_model): Although not directly affecting the area measurement α, this contributes to the final capacity uncertainty. It is quantified by the standard error of the regression fit to the manufacturer’s data.

Combined Uncertainty Estimate:

Due to the non-linearity of the overall measurement function, a Monte Carlo simulation would be required for a rigorous propagation of uncertainties. However, for the practical purpose of this study, the validation process against high-accuracy field measurements provides an empirical estimate of the total uncertainty. The Mean Absolute Percentage Uncertainty (MAPU)—previously reported as MAPE—of 3.47% for the 3D method is therefore put forward as a pragmatic estimate of the relative combined standard uncertainty u_c,rel(α) for the PV area measurement:

u_c,rel(α) ≈ MAPU = 3.47%

This value encapsulates the net effect of all the uncertainty sources listed above and provides a direct measure of the precision achievable with the proposed method under the conditions of this experiment.

4. Conclusions

The core challenge of geometric distortion and systematic errors caused by prevalent non-orthorectified projection when publicly available aerial imagery is utilized for urban rooftop photovoltaic (PV) capacity assessment is addressed in this study. A dual-optimization framework integrating monocular vision-based 3D reconstruction with a lightweight linear capacity model is proposed and validated. The core contributions and advantages of this framework are summarized as follows:

High-Precision, Low-Cost 3D Reconstruction: By innovatively leveraging orthogonal structural priors of urban buildings, camera self-calibration and building 3D reconstruction are achieved through vanishing point geometric constraints from a single non-orthorectified image. Combined with a multi-dimensional error control strategy utilizing redundant measured geometric data (footprint dimensions, height) at a 5% residual threshold, geometric distortions are effectively corrected by this approach. It reduces the mean absolute percentage error (MAPE) —our measure of measurement uncertainty—to 3.47% (substantially outperforming the 10.58% error of 2D methods). Requiring only easily accessible public imagery and minimal building geometric priors, this method dramatically lowers the cost barrier for high-precision 3D data acquisition.

Efficient, Robust Capacity Prediction: Based on statistical analysis of large-scale manufacturer data, a lightweight linear capacity prediction model using PV surface area as the sole independent variable is constructed. While high predictive accuracy (R² = 0.9548) is ensured, complex physical modeling is completely circumvented. This model exhibits high computational efficiency and facilitates straightforward engineering deployment. Its exceptional generalization capability and robustness are confirmed by rigorous five-fold cross-validation (mean R² = 0.9503 ± 0.0108).

In summary, our findings indicate that this framework may provide a viable technical solution for city-scale rooftop PV resource surveys, potentially integrating high precision, low cost, and strong engineering applicability. It appears to be particularly well-suited for efficiently utilizing massive public aerial/satellite imagery (e.g., Google Earth) to conduct rapid, large-scale resource potential assessments, thereby furnishing reliable data support for urban energy planning and the achievement of “dual carbon” goals.

Future work will focus on: (1) developing more robust automatic vanishing point detection algorithms to reduce manual intervention; (2) exploring automation and intellectualization of the multi-dimensional geometric constraint error control process (e.g., introducing optimization algorithms for automatic parameter iteration) to further enhance efficiency and accuracy.