Next Article in Journal
Experimental and Theoretical Studies on Shear Performance of Corrugated Steel–Concrete Composite Arches Considering the Shear–Compression Ratio
Previous Article in Journal
Lifecycle Assessment of Seismic Resilience and Economic Losses for Continuous Girder Bridges in Chloride-Induced Corrosion
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Buildings
Volume 15
Issue 18
10.3390/buildings15183317
buildings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Damping and Microstructure of Graphene/Carbon Nanotube-Modified Cement Composites

by
Bin Liu
1,2,
Jiyang Wang
3,4,*,
Zheng Wei
5,
Yu Peng
3,6 and
Jingwei Wu
3
1
Department of Construction Engineering, Zhejiang College of Construction, Hangzhou 311231, China
2
Faculty of Engineering, Science and Technology, Infrastructure University Kuala Lumpur, Kajang 43000, Selangor, Malaysia
3
Institute of Advanced Engineering Structures, Zhejiang University, Hangzhou 310058, China
4
Center for Balance Architecture, Zhejiang University, Hangzhou 310007, China
5
Zhejiang Provincial Transportation Engineering Management Center, Hangzhou 310007, China
6
The Architectural Design & Research Institute of Zhejiang University Co., Ltd., Hangzhou 310007, China
*
Author to whom correspondence should be addressed.
Buildings 2025, 15(18), 3317; https://doi.org/10.3390/buildings15183317
Submission received: 10 August 2025 / Revised: 8 September 2025 / Accepted: 10 September 2025 / Published: 13 September 2025
(This article belongs to the Section Building Materials, and Repair & Renovation)
Browse Figures
Versions Notes

Abstract

The development of lightweight, high-damping building materials is critical for enhancing the seismic resilience of civil infrastructure. This study introduces a novel approach to synergistically improve the damping and mechanical properties of cementitious composites by incorporating one-dimensional carbon nanotubes (CNTs) or two-dimensional graphene nanoplatelets (GNPs). The novelty lies in (1) a direct comparison of 1D versus 2D carbon nanomaterials efficacy within a vibration-relevant frequency range (0.5–2 Hz); (2) the use of the Ca(OH)2 orientation index, derived from X-ray diffraction (XRD), to link microstructural texturing with macroscopic dynamic performance; and (3) establishing clear mechanistic link between carbon nanomaterials dispersion, pore structure evolution, and the resultant balance between stiffness and damping. Dynamic mechanical analysis identified an optimal dosage of 0.1% by weight for both nanomaterials. Comprehensive microstructural characterization (SEM, MIP, XRD, TGA/DTG) revealed that the carbon nanomaterials act as nucleation sites, promoting cement hydration and refining the pore structure. This structural enhancement concurrently improved mechanical strength and energy dissipation capacity. The primary damping mechanism was identified as interfacial friction and slippage at the nanofiller–matrix interface. These findings provide fundamental insights for the rational design of high-performance cementitious composites and offer an evidence-based pathway for creating advanced seismic-resistant materials.

1. Introduction

Graphene is a two-dimensional nanomaterial of carbon atoms arranged in sp2 hybridized orbitals, forming a hexagonal honeycomb lattice. It boasts an exceptionally high specific surface area (2630 m2/g) [1], with tensile strength and Young’s modulus reaching up to 125 GPa [2] and 1.1 TPa [3], respectively. Graphene nanoplatelets (GNPs) are two-dimensional nanomaterials consisting of multiple stacked graphene layers, with diameters in the micrometer range and thicknesses of up to 100 nm. Carbon nanotubes (CNTs), on the other hand, are one-dimensional nanofiber materials formed by rolling GNPs into seamless cylindrical structures.
GNPs and CNTs have recently been incorporated into cementitious materials to enhance their properties. Wang et al. [4] observed that in cementitious composites doped with GNPs, the number of pores larger than 200 nm decreased, while the number of pores smaller than 50 nm increased. Similarly, Han et al. [5] observed that doping 0.2% CNTs into cement mortar significantly decreased the permeability coefficient of the composites. Du et al. [6] demonstrated that the addition of 0.6% GNPs to cement mortar reduced the permeability coefficient by 64%, the chloride diffusion coefficient by 70%, and the chloride mobility coefficient by 31%. Furthermore, Wang et al. [4] found that the compressive and flexural strengths of cementitious composites increased by 27.4% and 25.2%, respectively, when doped with 0.05% GNPs. Similarly, Hawreen et al. [7] reported that the compressive and flexural strengths of composites doped with 0.05% CNTs improved by 23% and 29%, respectively. Other studies [8,9,10,11,12,13] have consistently demonstrated that improvements in pore structure, mechanical properties, and durability are primarily attributed to the nano-filling effect of graphene materials, which refine larger pores into smaller ones. In addition, the large specific surface area of graphene materials serves as nucleation sites for cement hydration, thereby promoting hydration reactions and generating more hydration products, which significantly enhance the densification of cementitious composites [14,15]. Moreover, the bridging effect of CNTs effectively mitigates the formation and propagation of microcracks, further contributing to the improved performance of cementitious composites [16].
In addition to the aforementioned research on the effects of graphene materials on the basic mechanical properties of cementitious composites, scholars, both domestically and internationally, have conducted studies on the damping enhancement of cementitious materials, particularly in response to dynamic loads such as those caused by vehicles, wind, and earthquakes. For instance, polymer cementitious composites have been shown to significantly improve material damping due to the viscous damping properties of polymers [17,18]. However, this improvement is often accompanied by reductions in stiffness, strength, and durability [19,20,21,22]. Similarly, cementitious composites doped with micrometer-sized fibers can enhance damping through interfacial debonding and interfacial Coulomb damping mechanisms [23,24,25]. Nevertheless, the effectiveness of these fibers is highly dependent on their dosage. High dosages can lead to uneven mixing, reduced fluidity, and an increase in pores and defects, which pose significant challenges to their practical application in cementitious composites [26]. Graphene materials, due to their unique size and properties, can overcome the issues associated with the fracture and macro-agglomeration of micrometer-sized fibers, as well as the reduction in mechanical properties caused by fiber doping. For example, Liew et al. [27] conducted dynamic mechanical tests on CNT-reinforced cement mortar and found that CNTs, when homogeneously dispersed using the Triton X-100 noncovalent wrapping dispersion in solution (TNWDIS) method, improved the loss factor of cement mortar composite by 25.9%. Similarly, Long et al. [28] investigated the damping performance of graphene oxide (GO)-reinforced cement mortar. They observed that the addition of GO increased the loss factor of cementitious composites by 77% and the energy storage modulus by 52%. Although significant progress has been made by scholars, both domestically and internationally, in applying CNTs and GO to enhance the damping properties of cementitious materials, the mechanisms underlying the synergistic enhancement of damping and mechanical properties in cementitious composites using graphene materials of different dimensions (e.g., GNPs and CNTs) and the characterization of their microstructures remain unclear.
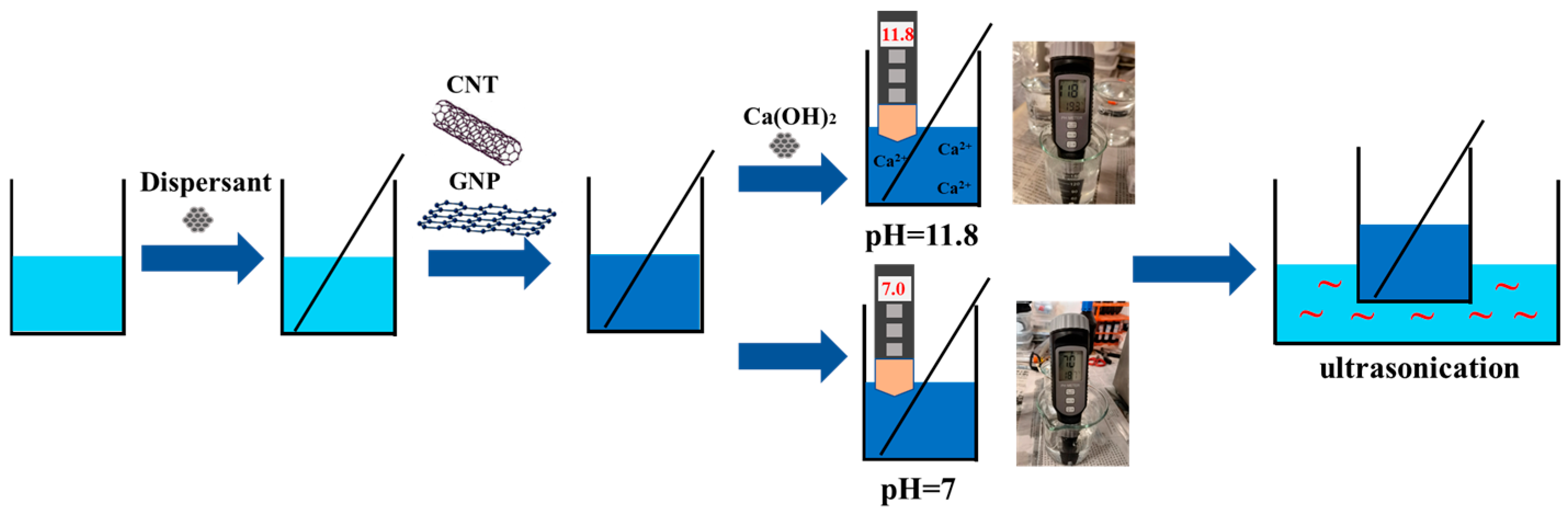
Therefore, in this study, five types of graphene cementitious composite specimens with varying dosages were designed to investigate the enhancement mechanisms of graphene materials with different dimensions (1D and 2D) on the damping characteristics of cementitious composites. It is worth noting that this study was conducted on cement paste composites, and deliberately excluded aggregates to create a simplified system that allows for a fundamental investigation of the intrinsic interactions between nanomaterials and the cement binder, without confounding effects from aggregate interfaces. First, the optimal dispersant types for dispersing CNTs and GNPs were determined. Subsequently, comparative tests were conducted to examine the damping characteristics, mechanical properties, pore structure, and micro-morphology of cementitious composites incorporating GNPs and CNTs. The interactions between GNPs, CNTs, and the cement matrix were elucidated through phase analysis, along with the mechanisms underlying the improvement in damping. The originality and primary contributions of this work are threefold: First, we provide a systematic, head-to-head comparison of how one-dimensional (1D) CNTs and two-dimensional (2D) GNPs affect the dynamic modulus and damping of cement composites, focusing on the low-frequency range (0.5–2 Hz) most relevant to civil engineering structures. Second, we introduce a link between a microstructural feature and the macroscopic dynamic mechanical response, offering a new analytical perspective on material performance. Third, we deconstruct the governing mechanisms by correlating nanoparticle dispersion with quantifiable changes in pore size distribution and the resultant synergy or trade-off between stiffness and damping. The findings provide valuable insights for developing cementitious composites with excellent damping and mechanical properties, offering a foundational understanding before extending to more complex concrete systems.

2. Experimental Program

2.1. Raw Materials

The raw materials used in this study included cement, GNPs, CNTs, water, and dispersants. The cement was a reference cement provided by the Institute of Cement Science and New Building Materials Science of the China General Research Institute of Building Materials, with its chemical and mineralogical compositions detailed in Table 1. Deionized water was used throughout the tests. The CNTs and GNPs were supplied by Nanjing Xianfeng Nanomaterials Science and Technology Co., Ltd., Nanjing, China, and their technical parameters are listed in Table 2. Three types of dispersants were used: (I) MELFLUX 2651F, a polycarboxylic acid-based superplasticizer produced by BASF, Ludwigshafen, Germany; (II) MELMENT F10, a melamine-based superplasticizer also produced by BASF, Ludwigshafen, Germany; and (III) PVP10, provided by SIGMA, Tokyo, Japan. The specific properties of these dispersants are presented in Table 3 and Table 4, respectively.

2.2. Dispersion of Graphene Materials

To achieve stable dispersions of GNPs and CNTs, a combination of dispersants and ultrasonication was employed in this study. The dispersion mechanism involves the adsorption of negatively charged dispersants onto the surface of graphene materials, imparting a negative charge that generates electrostatic repulsion and thereby promotes dispersion [6,29]. To identify the most effective dispersant for graphene materials, three commonly used dispersants were evaluated: polycarboxylate superplasticizer (PCE) [30,31], melamine dispersant (MS) [32,33], and PVP10 (PVP) [27]. Their effects on the dispersion of CNTs and GNPs were studied to determine the optimal dispersants for preparing CNTs/GNPs cementitious composites.
Since the cement matrix is alkaline, previous research by Mendoza et al. [34] demonstrated that the presence of Ca2+ ions in the cement pore solution, along with the high pH, can weaken the binding of dispersants to graphene materials. This reduces dispersion stability, leading to significant agglomeration of graphene materials in alkaline environments. To better simulate the actual conditions of graphene material dispersion in a cement matrix, this study utilized both Ca(OH)2 solution (pH = 11.8) [35] and deionized water (pH = 7) as dispersion media. The design of the dispersant to graphene-based nano-carbon additives (GNCAs) ratios is shown in Table 5. The concentration of graphene materials in the solution was consistent with that used in the subsequent preparation of specimens with graphene material suspensions. The amount of Ca(OH)2 required to prepare 100 mL of a pH = 11.8 solution was calculated using Equation (1).
pH = −lg[H+]·pOH = −lg[OH−]·pH + pOH = 14
To evaluate the dispersion effect, a UV–vis spectrophotometer was primarily used to assess the dispersion quality and stability of the graphene materials [36].
The preparation process for the graphene material suspension is illustrated in Figure 1, and the specific steps are as follows: First, water and dispersant were added to a beaker and stirred with a glass rod until the dispersant was fully dissolved. Next, GNPs, CNTs, and Ca(OH)2 were added sequentially, and the pH value of the solution was measured using a pH meter. Ca(OH)2 was added last to prevent premature reactions between Ca2+ ions and the graphene material, which could reduce the dispersion effect [37].
The suspension was then ultrasonicated using an ultrasonic instrument (Jiekang PS-20, 40 kHz, 120 W, Shenzhen, China) for 2 h. As prolonged ultrasonic vibration increases the temperature, and temperatures exceeding 45 °C can cause flocculation and agglomeration of the dispersant [38], which negatively impacts the dispersion of graphene materials, the suspension was cooled for 10 min after every 1 h of ultrasonication, and the water in the ultrasonic instrument was replaced.
After ultrasonication, the suspension was tested for absorbance using a UV–vis spectrophotometer (Thermo Fisher Scientific, Waltham, MA, USA) in the wavelength range of 250 nm–600 nm. Over time, GNP and CNT particles in the suspension tend to aggregate and settle to the bottom. The stability of the suspension was assessed by measuring its absorbance at regular intervals (30 min, 60 min, 120 min, 240 min, 480 min, and 10 days). These measurements help identify the most suitable dispersant for graphene materials.

2.3. Specimen Preparation

Ramezani M et al. [39] demonstrated that a lower water–cement ratio typically reduces the agglomeration caused by graphene suspensions added to cement. Based on this finding, this study designed cementitious composite specimens with varying dosages of graphene materials, maintaining a uniform water–cement ratio of 0.25. The detailed mix proportions are presented in Table 6. As shown in Table 6, five sets of specimens were prepared, with identical dosages of cement, water, and dispersing agent across all sets. The “Ref” set served as the control set without any graphene materials, while the “CNT” and “GNP” sets represented specimens doped with CNTs and GNPs, respectively. Additionally, the “01” and “03” sets corresponded to specimens containing graphene materials at 0.1% and 0.3% dosages, respectively.
The preparation process was as follows: first, the graphene dispersion was mixed with the pre-weighed cement at a low speed of 140 rpm for 2 min, followed by high-speed mixing at 280 rpm for 3 min. The thoroughly mixed graphene–cementitious composites were then poured into molds of two dimensions: 40 mm × 40 mm × 160 mm and 2.5 mm × 8 mm × 60 mm. The molds were vibrated on a high-frequency vibration table for 30 s to eliminate air bubbles generated during pouring. Subsequently, the specimens were wrapped in plastic film and cured at ambient temperature for 24 h to prevent water loss. After demolding, all specimens were placed in a curing room maintained at a temperature of 20 ± 2 °C and a relative humidity of 95% for 28 days.
The fabrication and curing processes were conducted following the Test Procedure for Cement and Cement Concrete for Highway Engineering (JTG 3420-2020) [40]. For each set, three specimens were prepared for mechanical property testing (see Figure 2a), and six specimens were prepared for damping property testing (see Figure 2b).

2.4. Test Methods

2.4.1. Mechanical Test Method

The compressive and flexural strength tests were conducted using a 25 T high-performance fatigue testing machine (Instron 8802, High Wycombe, UK). The loading rates were set to 144 kN/min and 3 kN/min, respectively, as recommended by the Chinese specification JTG 3420-2020 [40]. The specimens used for testing measured 40 mm × 40 mm × 160 mm, as shown in Figure 2a. The flexural strength test was performed first, following the center-point loading method. After the flexural test, the two fractured halves of the specimen were used for the compressive strength test. For the compressive test, the compression surfaces were the original molded sides of the specimen, with a compression area of 40 mm × 40 mm.

2.4.2. Damping Test Method

The damping test was performed using a dynamic thermo-mechanical analyzer (DMA) (TA Q800, Newcastle, WA, USA), as shown in Figure 3. The DMA is specifically designed to evaluate the dynamic mechanical properties of materials as a function of temperature, time, frequency, or stress under controlled temperature conditions. During the test, a sinusoidal alternating stress (σ) with a predetermined amplitude was applied to a specimen with dimensions of 2.5 mm × 8 mm × 60 mm (see Figure 2b and Figure 4). This stress induced a sinusoidal strain (ε) in the material, with the strain response of the viscoelastic material exhibiting a phase lag (δ) relative to the applied stress. Based on the magnitude of the phase lag (δ), materials can be classified into three categories: (1) ideal elastic materials, with a phase lag of 0°; (2) ideal viscous materials, with a phase lag of 45°; and (3) viscoelastic materials, with a phase lag between 0° and 45°. The phase lag is directly proportional to the material’s damping capacity, where larger phase lags indicate greater damping properties.
The composite modulus (M*), storage modulus (E′), loss modulus (E″), and loss factor (tan δ) of the specimen were calculated using Equations (2)–(7).
ε = ε0 sin ωt
σ = σ0 sin (ωt + δ)
M* = σ0/ε0
E′= σ0 cos δ/ε0
E″ = σ0 sin δ/ε0
tan δ = E″/E′
Here, ω represents the angular frequency, δ is the phase difference, t is time, ε0 is the peak strain, and σ0 is the peak stress. The composite modulus M* is defined as the ratio of peak stress σ0 to peak strain ε0. The storage modulus E′ reflects the elastic component of the material’s viscoelastic behavior, quantifying the energy stored during elastic deformation. The loss modulus E″ represents the viscous component, capturing the energy dissipated as heat due to viscous deformation. The loss factor tan δ, defined as the ratio of the loss modulus to the storage modulus (E″/E′), indicates the balance between viscous and elastic responses. A higher loss factor corresponds to greater energy dissipation, independent of the specimen’s size. The relationships among E′, E″, M*, and δ are illustrated in Figure 4.
The damping performance tests were conducted at room temperature, with the amplitude and frequency parameters selected to align with the conditions widely used in previous studies [27,41,42]. The test frequency range (0.5 Hz–2.5 Hz) was designed to cover the natural frequency range (0.5 Hz–1 Hz) of most multi-story building structures under 100 m in height in China [43]. During the experiments, six specimens for each mix proportion were tested to evaluate the damping performance of GNP/CNT cementitious composites at various frequencies (0.5 Hz–2 Hz) under a fixed amplitude of 7 μm.

2.4.3. Pore Structure Test Method

The pore structure of the specimens was analyzed using the mercury intrusion porosimetry (MIP) method with an Autopore IV 9510 instrument (Norcross, GA, USA). Before testing, undamaged portions of the specimens remaining after the mechanical experiments were dried in an oven at 60 °C for 24 h to remove pore water. The Autopore IV 9510 was employed to determine the porosity, pore-specific surface area, and pore size distribution of the cementitious composites. During the test, the mercury contact angle was set to 130°, the surface tension was 485 N/m, and the inlet pressure was increased incrementally from 3.7 kPa to 414 MPa. An equilibration time of 10 s was maintained for each pressure increment. This method allowed precise measurement of the pore size distribution, porosity, and specific surface area of the cementitious composites.

2.4.4. Microcosmic Observation

The surface micromorphology of graphene–cementitious composites was analyzed using a Quanta FEG 650 scanning electron microscope (SEM, Waltham, MA, USA). Specimens, measuring less than 1 cm, were extracted from fractured sections after mechanical property tests. Before observation, the specimens were dried in an oven at 60 °C for 24 h to remove internal moisture. To preserve the original fracture surface morphology, the dried specimens were cut into appropriate shapes without surface polishing. The specimens were then mounted on a sample stage, fixed with conductive adhesive, and coated with a thin layer of gold. To prevent distortion of the microstructural images caused by high accelerating voltage, a low accelerating voltage of 20 kV was consistently applied, with the working distance maintained between 10 and 15 mm.

2.4.5. Thermogravimetric Analysis

Thermogravimetric analysis (TGA) was performed using a TGA/DSC3+ analyzer (METTLER TOLEDO, Zurich, Switzerland). Before testing, fractured samples from the mechanical property tests were immersed in anhydrous ethanol to halt hydration. The samples were then dried in an oven at 60 °C for 24 h. After drying, the samples were ground into a fine powder using a mortar and pestle with anhydrous ethanol and passed through a 0.08 mm square-hole sieve. Approximately 10 mg of the powdered sample was used for the test. The sample was heated from 50 °C to 1000 °C at a constant rate of 10 °C/min under a nitrogen flow of 100 mL/min.

2.4.6. X-Ray Diffraction

The test was conducted using a Panalytical Empyrean X-ray diffractometer (Almelo, The Netherlands). After drying, the powdered samples were evenly distributed in the specimen holder, pressed, and compacted with a glass plate to ensure the surface was level with the glass. The specimen holder was then placed at the center of the goniometer. The angular range was continuously scanned from 10° to 80° with a step size of 0.02626° and an accuracy of 0.0001°. Each step had a duration of 18.87 s.

3. Test Results and Discussion

3.1. Dispersion of GNP/CNT

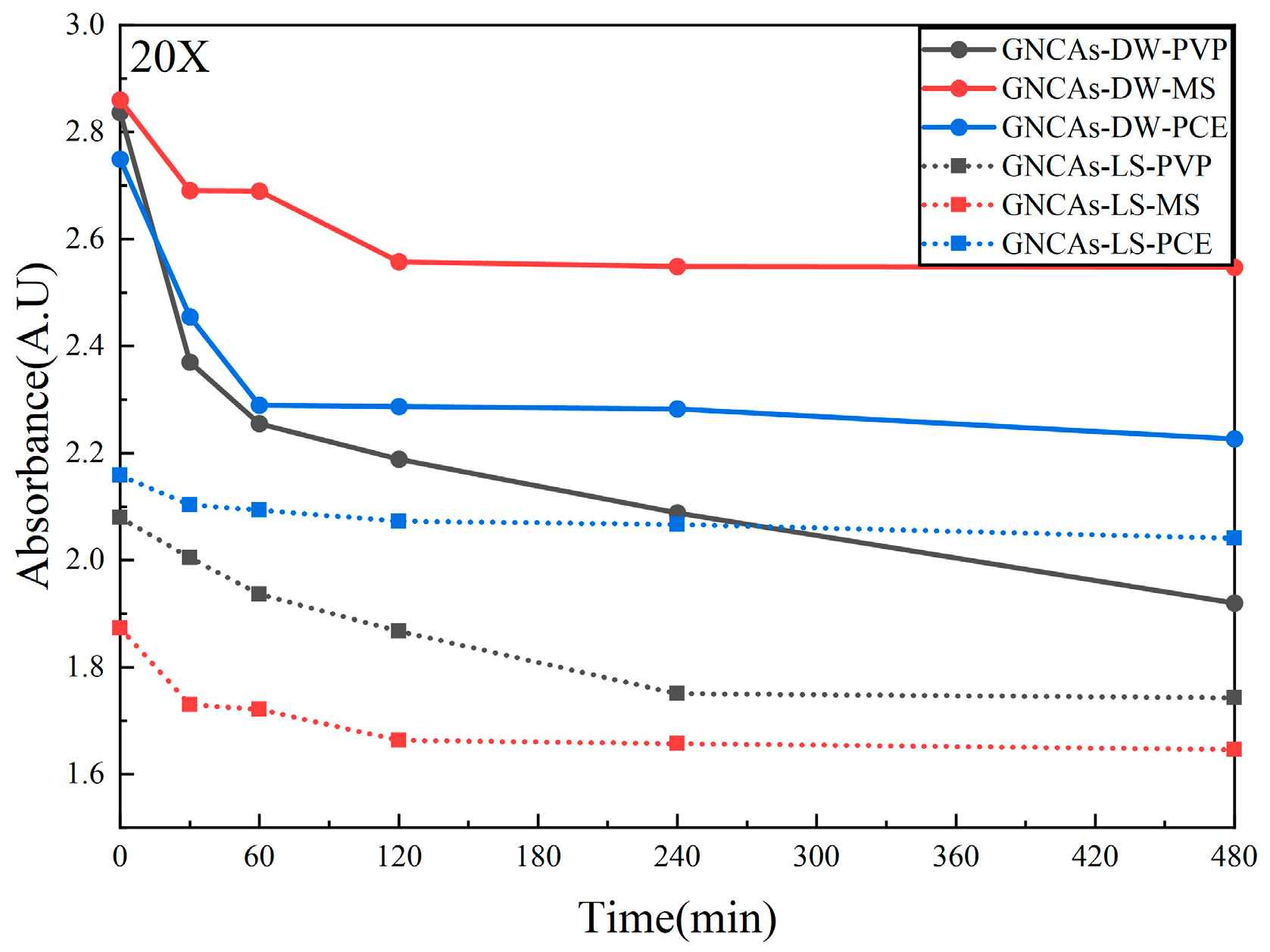
The UV–vis absorption spectrum of the graphene material suspension exhibits a characteristic peak at a wavelength of approximately 260 nm [44]. Following the Lambert–Beer law, the suspension’s optical absorbance is linearly related to the concentration of particles within the solution [45], where higher absorbance values indicate improved dispersion of the graphene material. The absorbance at 260 nm was measured over time using UV–vis spectroscopy to evaluate the suspension’s stability. Before measurement, the suspension was diluted by a factor of 20 to ensure the signal intensity remained within the instrument’s detection range. The resulting plot of absorbance versus settling time is presented in Figure 5.
As shown in Figure 5, the dispersions prepared by 2 h of ultrasonication in deionized water (pH = 7) with the addition of PVP10, MS, and PCE demonstrated effective dispersing capabilities. During the initial 60 min of the resting process, all three dispersions exhibited a notable decline in absorbance, with reductions of 20.5% (PVP10), 6% (MS), and 16.7% (PCE), respectively. After 480 min of standing, the graphene material suspension dispersed with the MS exhibited the highest stability, while the suspension dispersed with PVP10 showed the lowest stability, as evidenced by a significant decrease in absorbance over time.
In a Ca(OH)2 solution (pH = 11.8), the suspension dispersed using the PCE exhibited the highest absorbance after 2 h of ultrasonic dispersion. This result indicates that, under alkaline conditions, the PCE outperforms both the MS and PVP10 in dispersing graphene materials. Furthermore, the absorbance of the suspensions dispersed by the three agents decreased by 34.5% (MS), 29.2% (PVP10), and 21.4% (PCE) compared with their respective values in deionized water (pH = 7). This suggests that the presence of Ca2+ ions significantly impairs the dispersing efficiency of the agents for graphene materials. Notably, the suspension dispersed with the PCE exhibited the smallest decrease in absorbance (−5.4%) over 480 min of standing, demonstrating superior stability. These findings align with the results reported by Zhao et al. [46], which highlight the enhanced dispersion and stability of graphene materials achieved by PCE in alkaline environments with high concentrations of Ca2+ ions.
To evaluate the effectiveness of the selected dispersants in maintaining the stability of graphene material suspensions over both short- and long-term periods, the absorbance of alkaline graphene suspensions (pH = 11.8) dispersed by the three dispersants was measured after 10 days of resting. The results reveal that the suspension dispersed with the PCE exhibited a significantly higher absorbance compared with the other two dispersants (see Figure 6), indicating superior long-term stability.
Through the evaluation of the dispersibility of three commonly used dispersants for graphene materials in both alkaline and neutral environments, it was determined that the PCE exhibited superior dispersing performance. Moreover, the PCE demonstrated the highest dispersing stability in alkaline environments with high concentrations of Ca2+ ions. Based on these findings, the PCE was selected as the optimal dispersant for graphene materials in the preparation of subsequent specimens.

3.2. Microscopic Morphology Analysis

To elucidate the microstructure of the composites, SEM observations were conducted, with representative micrographs presented in Figure 7. It is important to note that the following interpretations are based on morphology. Figure 7b,c show composites with 0.1% and 0.3% CNTs, respectively, and show extensive C–S–H formation surrounding the nanotubes. CNTs are embedded within hydration products and help fill capillary pores in the cement matrix, an effect that becomes more pronounced with increasing CNT dosage. Nevertheless, localized CNT agglomeration into micrometer-scale clusters generates highly porous domains that act as nucleation sites for hexagonal prismatic portlandite crystals. Figure 7d,e illustrate the morphology and dispersion of GNPs in the cement slurry. Similar to CNTs, the two-dimensional, lamellar GNPs occupy pore space; however, their larger lateral dimensions enable them to bridge and fill larger voids than CNTs. As shown in Figure 7d, the geometry of GNPs more effectively arrests crack propagation in their vicinity relative to CNTs, indicating that GNPs can suppress microcrack initiation and growth, thereby enhancing peak load capacity and dynamic resistance. Although SEM provides only localized views, the extensive GNP–cement interfaces afforded by nanoscale GNPs impede crack development and serve as sites for load transfer and energy dissipation, which likely contributes to the improved mechanical performance of GNP–cementitious composites.
By contrast, Figure 7e shows that inadequately dispersed GNPs tend to curl, fold, and agglomerate within the matrix, producing interlayer gaps between stacked sheets. These gaps can increase the critical pore size of GNP–cementitious composites and degrade their properties. Thus, achieving uniform GNP dispersion is essential to minimize agglomeration and may further improve both mechanical and damping performance. For definitive phase identification and a more detailed microstructural characterization, future studies may incorporate SEM-EDS analysis.

3.3. Pore Structure Analysis

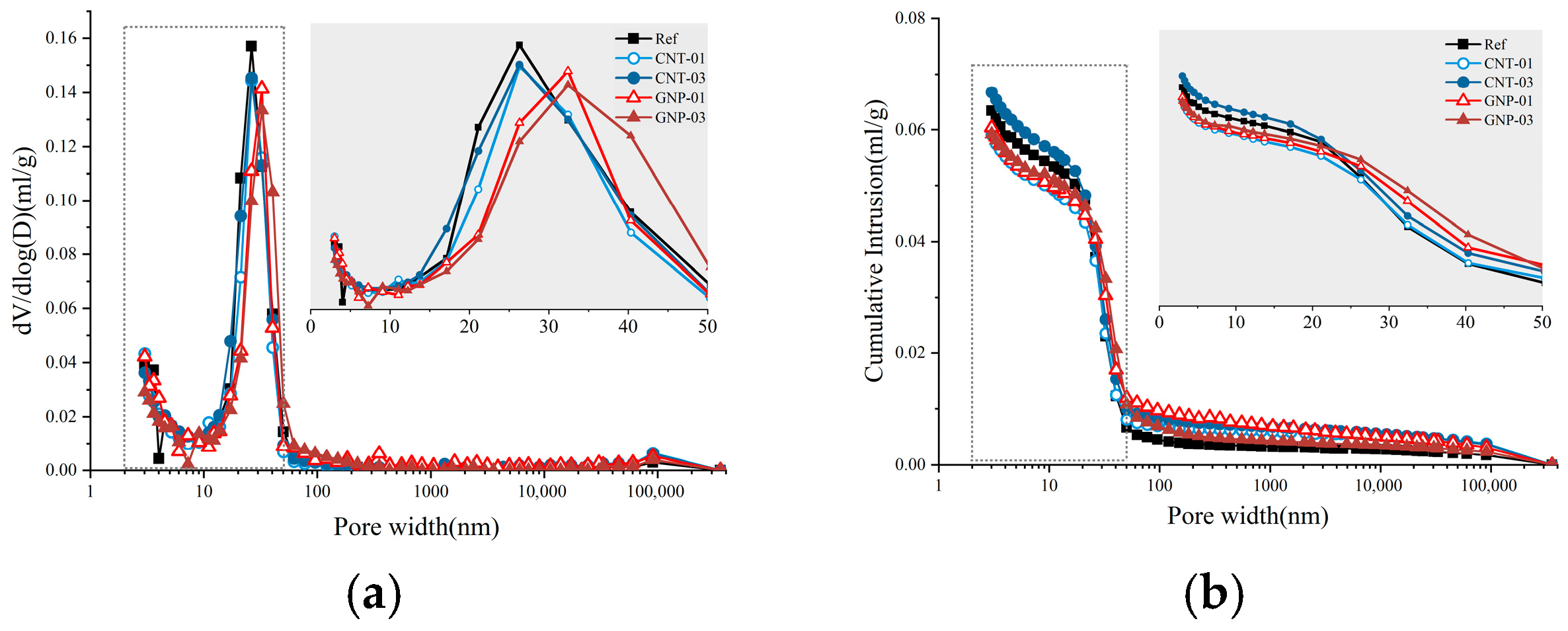
The pore structure of graphene-enhanced cementitious composites was characterized by mercury intrusion porosimetry (MIP). Summary metrics—total porosity, average pore size, critical pore size, and pore-size distribution—are listed in Table 7, and the corresponding differential and cumulative distributions are shown in Figure 8. As indicated in Table 7, adding 0.1% CNTs or 0.1% GNPs reduced porosity by 5.8% and 5.4%, respectively, implying comparable matrix-filling effects for both graphene-based additives.
The pore-size distributions, however, reveal distinct roles. In CNT-modified composites, the fraction of pores with diameters below 20 nm increases, whereas in GNP-modified composites, the proportion of 50–200 nm pores grows. This divergence reflects the materials’ geometries: CNTs are more effective at occupying finer capillary pores, while the larger lateral dimensions of GNPs favor filling and bridging of larger voids, thereby redistributing pore classes. Notably, the average and critical pore sizes remain essentially unchanged with CNT addition, but both parameters increase with GNP addition.
For GNP-03 (0.3 wt.%), total porosity decreases while the threshold pore size increases to 32.4 nm, and the fractions of 50–200 nm and >200 nm pores grow significantly (Table 7), indicating pore coarsening. This phenomenon is consistent with 2D-flake-specific effects: stacking-induced interlayer slit pores and GNP–matrix interfacial gaps that eliminate fine capillaries while introducing fewer but larger mesopores. SEM at the magnifications used cannot resolve 30–200 nm slit pores; therefore, we interpret this as the combined consequence of flake stacking and interfacial effects rather than solely visible agglomeration.
When the CNT dosage is increased to 0.3%, the composite porosity rises by 4.3% relative to the control. This reversal is consistent with that found when exceeding the optimal CNT content (previously identified as 0.048% [47]), which promotes self-agglomeration, diminishes effective pore filling, and ultimately increases percolating void space.

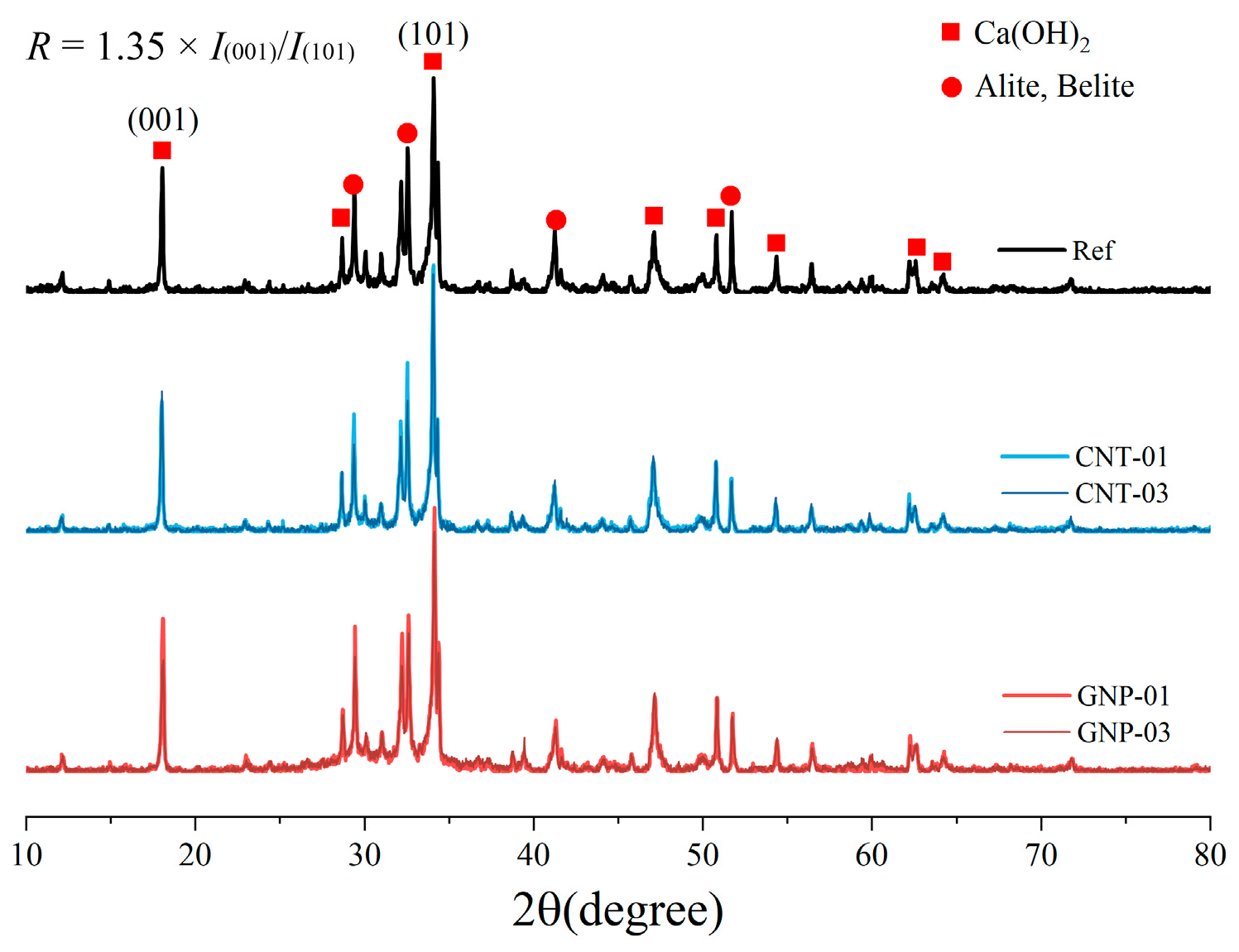
3.4. XRD Analysis

Figure 9 shows the 28-day XRD patterns of graphene cementitious composites. A qualitative analysis of these patterns provides insight into the hydration process. As is typical, the patterns are dominated by sharp diffraction peaks corresponding to residual unhydrated clinker phases (alite, C3S, and belite, C2S) and primary crystalline hydration products, mainly calcium hydroxide (Ca(OH)2, or portlandite) and traces of calcium carbonate (CaCO3, likely from minor carbonation). The progression of hydration is marked by the gradual consumption of the clinker phases and the simultaneous formation of amorphous C–S–H gel, which is visible as a broad, diffuse halo.
Upon incorporating GNPs and CNTs, a noticeable increase in the Ca(OH)2 peak intensity is observed relative to the control group. This suggests that the nanocarbons accelerate the hydration of the clinker phases, leading to a greater quantity of crystalline Ca(OH)2 at 28 days. It is worth noting that no distinct diffraction peaks for GNPs or CNTs were detected, which is expected given their low dosage and is consistent with the previous studies of Horszczaruk et al. [48].
Ca(OH)2 typically crystallizes as layered hexagonal plates, and its preferred orientation strongly affects paste mechanics. The influence of GNPs/CNTs on Ca(OH)2 texture can be assessed via an orientation index derived from XRD data [49]; lower values generally correlate with a denser microstructure and improved performance [50,51]. Thus, the orientation coefficient offers a proxy for the mechanical benefits imparted by GNPs/CNTs. Following Grandet and Ollivier [52], and using the Ca(OH)2 (001) plane at 2θ ≈ 18.1° as the reference, the orientation index R for the (101) plane at 2θ ≈ 34.0° is given by Equation (8), as follows:
R = 1.35 × I(001)/I(101)
where I(001) and I(101) represent the diffraction peak intensities of Ca(OH)2 crystals. For randomly oriented crystals, R = 1; values of R > 1 indicate preferred orientation, with larger R reflecting stronger texture and, typically, inferior mechanical performance. As shown in Figure 10, the orientation coefficient of the reference paste (Ref) is 1.22, whereas the values for CNT-01, CNT-03, GNP-01, and GNP-03 are 1.01, 1.04, 1.16, and 1.10, respectively. These results indicate that appropriate GNP/CNT additions decrease the preferred orientation of Ca(OH)2 (lower R), thereby densifying the matrix and improving mechanical properties, consistent with the measured mechanical outcomes.

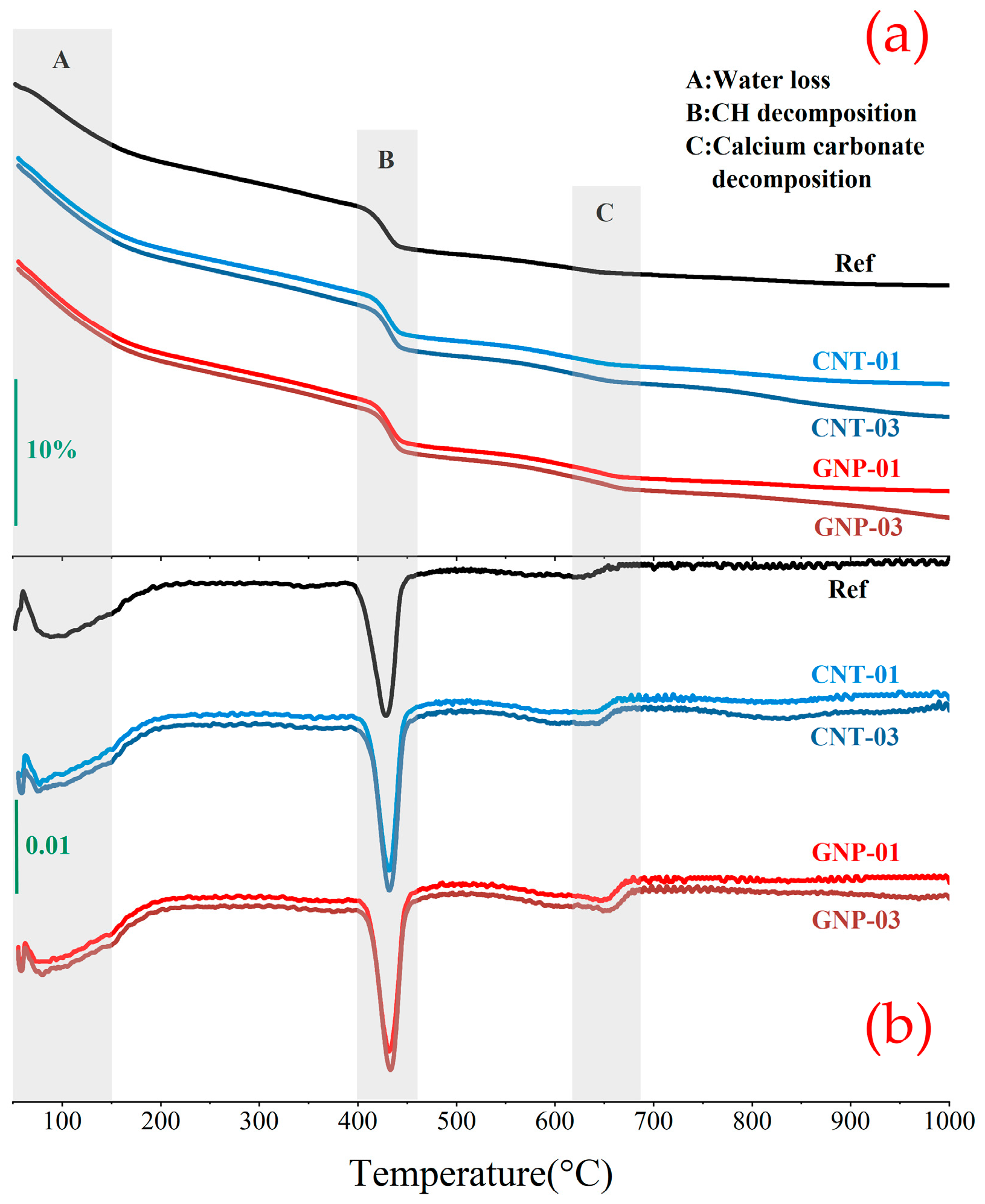
3.5. Thermogravimetric Analysis (TGA)

Figure 10 shows the thermogravimetric (TG) curves of GNP/CNT–cementitious composites, exhibiting three distinct mass-loss stages. In cement-based systems, mass loss between 50–100 °C reflects evaporation of pore water and physically adsorbed water, while loss between 105–200 °C is associated with release of crystalline water from minor phases (e.g., gypsum). Despite pre-drying at 60 °C, Stage A still accounts for about 6% mass loss (Figure 10), largely because interlayer water in C–S–H is difficult to remove completely [53,54]. Stage B (400–500 °C) corresponds to the dehydroxylation of portlandite [Ca(OH)2], and Stage C (625–700 °C) primarily reflects the decarbonation of calcite (CaCO3) formed by carbonation of a fraction of Ca(OH)2 and C–S–H [55].
The degree of cement hydration is directly correlated with the Ca(OH)2 content at Stage B, and the Ca(OH)2 content in the cement matrix can be determined using Equation (9), as follows:
C H % = M C a ( O H ) 2 / M 500 × 74 / 18 × 100 %
where M C a ( O H ) 2 denotes the mass loss attributable to Ca(OH)2 within 400–500 °C, and M500 is the mass at 500 °C. The factor 74/18 converts the mass of released water to the equivalent mass of Ca(OH)2, corresponding to the molar masses of Ca(OH)2, where 74 and 18 are the molar masses of Ca(OH)2 and H2O, respectively.
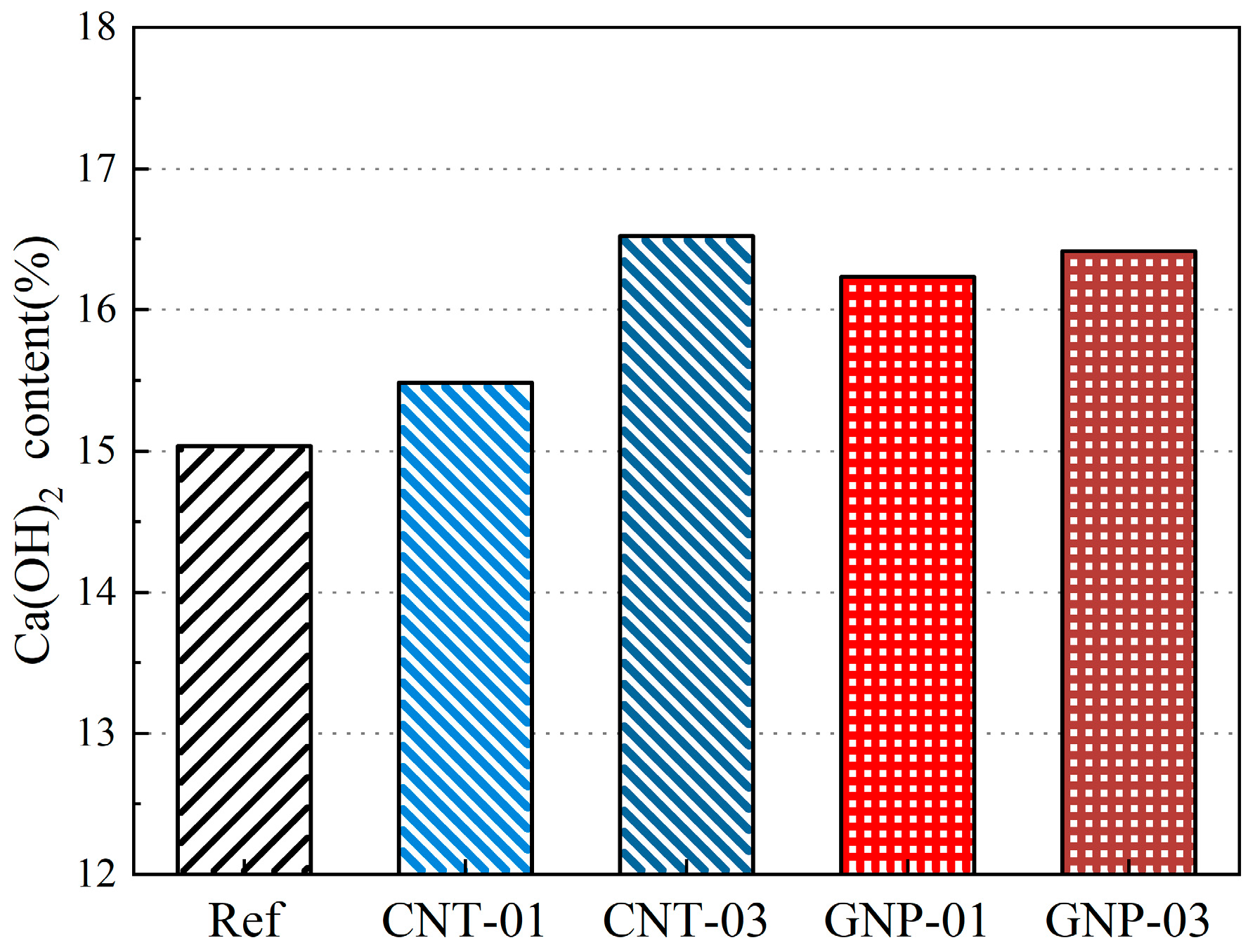
Figure 11 illustrates the percentage content of Ca(OH)2 at 28 days, revealing that the CNT-03 cementitious composites exhibit the highest degree of hydration. The incorporation of both GNP and CNT enhances cement hydration, which aligns with the XRD results. This effect can be attributed to the ability of carbon nanotubes and graphene nanosheets to provide heterogeneous nucleation sites for the growth of hydration products (see Figure 7), thereby accelerating the hydration process. These findings are consistent with the results of Fakhim and Abedi [15,56], who have reported that an increased degree of hydration improves the mechanical properties of cementitious composites and refines the pore structure of the cement matrix.
As is well-established, C–S–H gel is a predominantly amorphous or poorly crystalline phase. Consequently, in XRD patterns, it does not produce sharp, distinct diffraction peaks but is instead characterized by a broad, diffuse scattering hump, typically observed in the 2θ range of 25–35°. Additionally, the detection of certain phases (such as minor calcite content) by TGA may not correspond directly to XRD observations due to differences in detection limits and sensitivities between the two analytical techniques mentioned above.

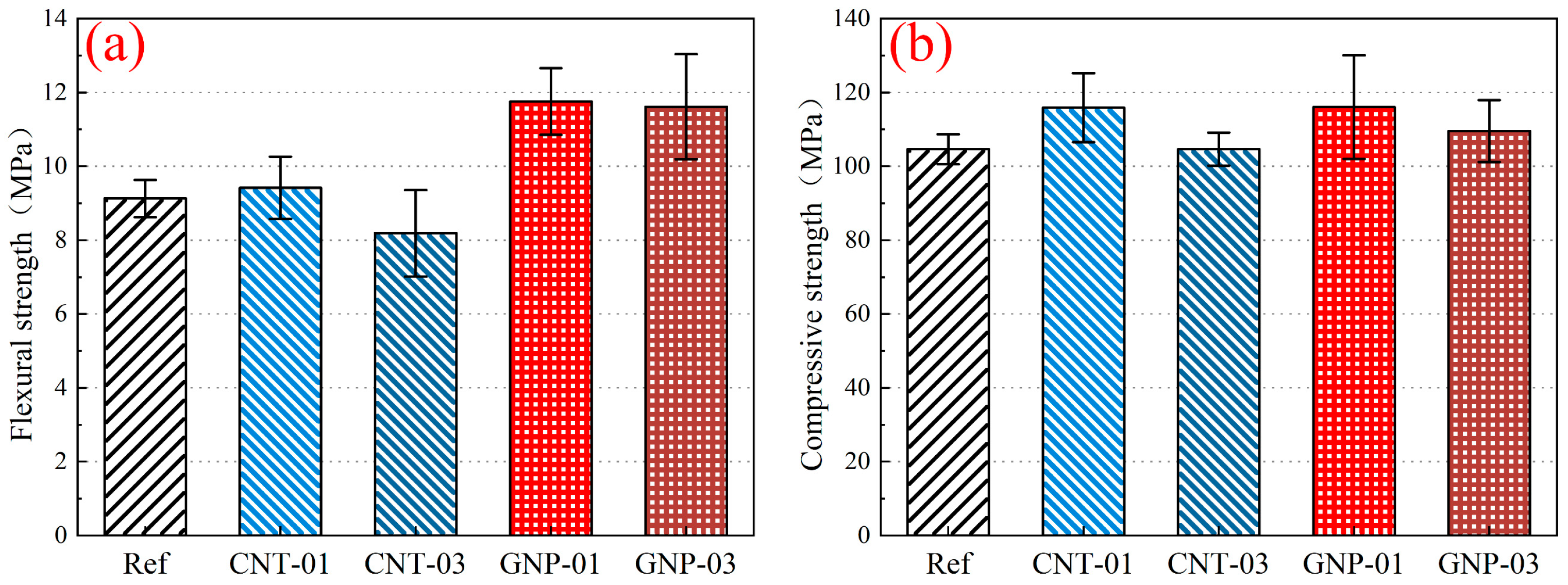
3.6. Mechanical Performance

Figure 12 shows the 28-day flexural and compressive strengths of graphene-modified cementitious composites. Relative to the control (flexural: 9.1 MPa; compressive: 104.6 MPa), adding 0.1% CNTs increased flexural strength to 9.4 MPa (+3.3%) and compressive strength to 115.8 MPa (+10.7%), while 0.1% GNPs raised flexural strength to 11.7 MPa (+28.6%) and compressive strength to 116.0 MPa (+10.9%). These enhancements are consistent with Abedi et al. [15].
The enhancement mechanisms are twofold: physical reinforcement and chemical influence on hydration. However, the final mechanical strength is predominantly governed by the physical mechanisms. The superior performance of GNPs, particularly at the 0.1% dosage, is attributed to their unique 2D plate-like morphology. These well-dispersed flakes are highly effective at deflecting and bridging microcracks, thereby inhibiting crack propagation and enhancing load-transfer efficiency [57,58]. From a chemical perspective, the 2D geometry of GNPs also provides superior nucleation sites for C–S–H formation—the primary strength-bearing phase in cement [59]. In contrast, 1D CNTs promote general bulk hydration, producing more Ca(OH)2 (a weaker crystalline by-product) without the targeted, dense C–S–H growth observed with GNPs.
Conversely, increasing the dosage to 0.3% (as in CNT-03 and GNP-03) led to decreased strength due to nanomaterial agglomeration, which introduces weak zones and stress concentrations within the matrix. This explains why CNT-03 shows lower strength than GNP-01 despite higher Ca(OH)2 content: the detrimental impact of agglomeration-induced defects outweighs any hydration benefits, and CNTs lack the geometric advantage for efficient C–S–H templating. Therefore, dispersion quality, crack-resistance effectiveness, and preferential C–S–H nucleation are the primary determinants of composite strength.

3.7. Damping Performance

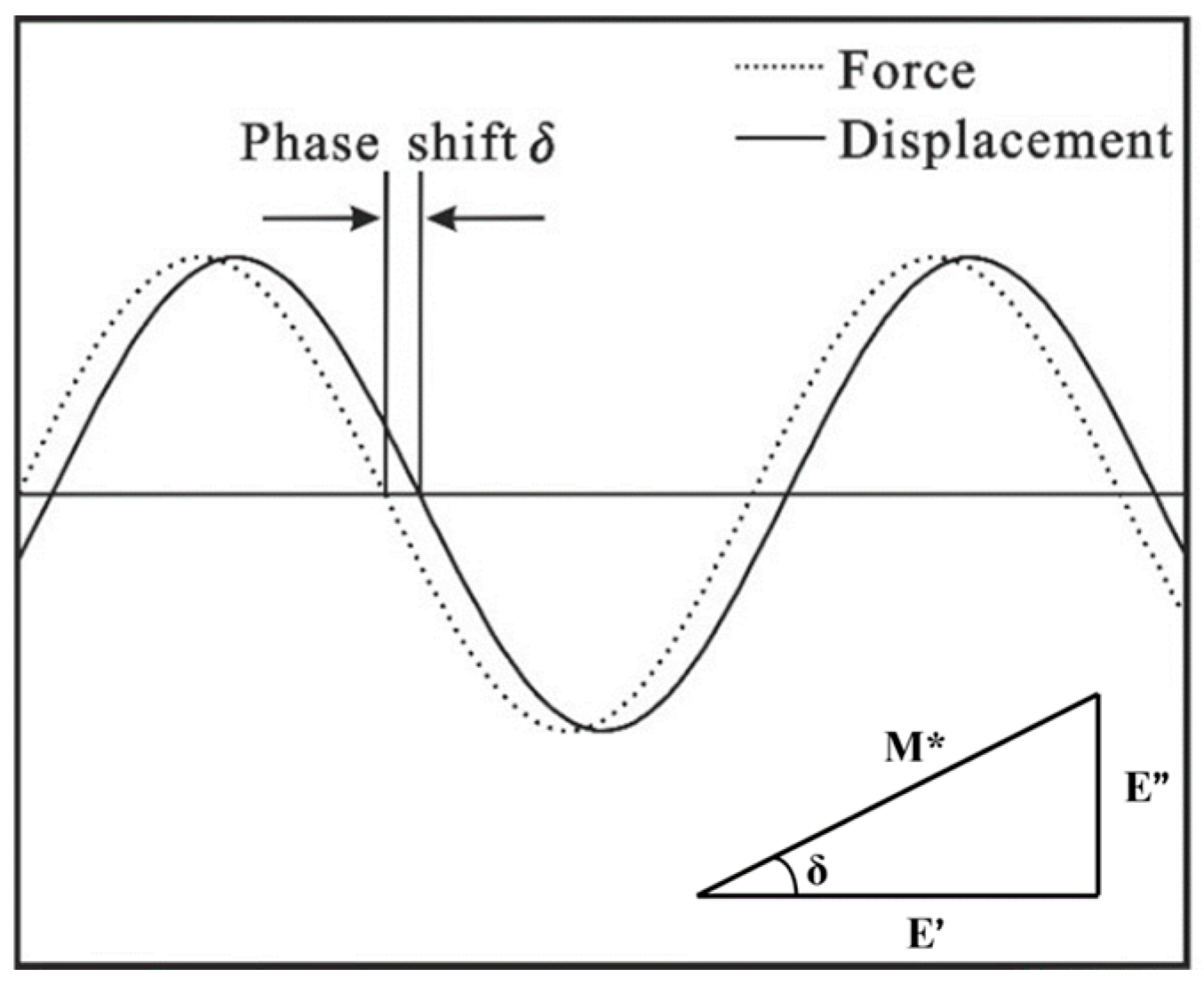
To avoid plastic deformation and fracture, specimens were subjected to low-amplitude harmonic loading. The damping behavior of graphene–cementitious composites was evaluated at frequencies of 0.5–2 Hz under a constant displacement amplitude of 7 μm. Damping performance was characterized by the loss factor (tan δ) and the storage modulus (E′) [28,60]. In practice, effective damping requires a high loss factor together with sufficient stiffness (i.e., elevated E′), ensuring both energy dissipation and load-bearing capacity.
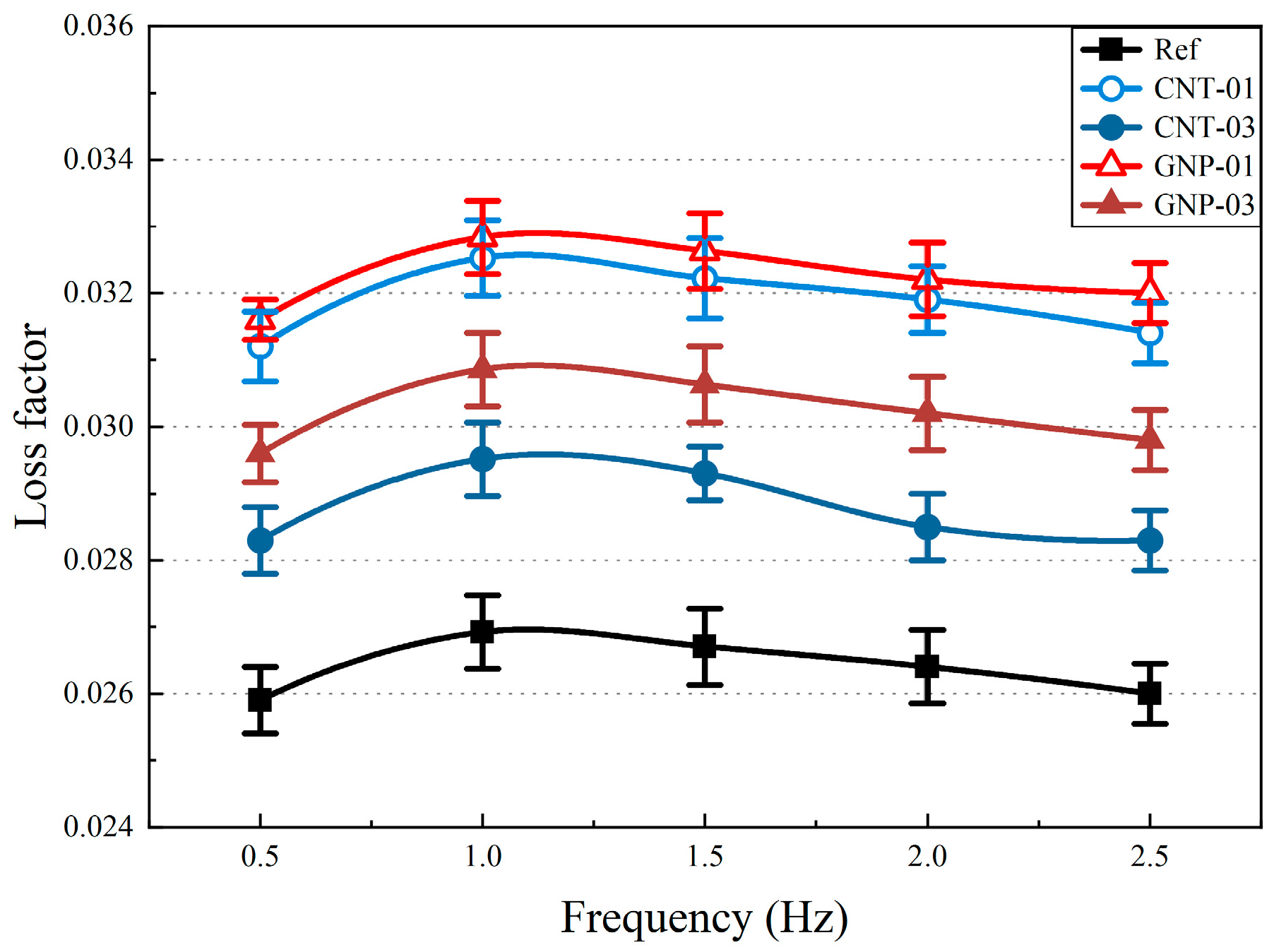
Figure 13 illustrates the frequency dependence of the loss factor tan δ for all composites. A prominent damping peak is observed at 1 Hz across all specimens, after which tan δ gradually decreases. This peak signifies an enhancement in viscoelastic damping due to the nanofillers. At 1 Hz, the loss factor increases by up to 21.9% (GNP-01), 20.8% (CNT-01), 14.5% (GNP-03), and 9.6% (CNT-03), relative to the reference. This behavior is attributed to intrinsic material behavior rather than experimental artifacts. All measurements were conducted within the linear viscoelastic region at a maximum displacement amplitude of 7 μm, and the testing environment was isolated to minimize external interference. The clear composition-dependent variation in peak intensity further rules out systemic artifacts and points to a material-based origin. Consistent with prior work [61,62], the enhanced damping arises from energy dissipation via frictional sliding at the nanocarbon–matrix interface and relative motion within the nanostructures themselves (i.e., inter-wall for CNTs and inter-layer for GNPs). These mechanisms convert mechanical work into heat through localized debonding and slip.
The storage modulus (E′)—the elastic energy stored per loading cycle and a close approximation to the dynamic Young’s modulus under small-strain harmonic loading—was measured at 1 Hz (Figure 14). Compared with the control, incorporating 0.1% GNPs and 0.1% CNTs increased E′ by 11.8% and 5.3%, respectively, indicating that a low nanocarbon dosage effectively stiffens the cement matrix. This enhancement accords with the poroelastic dependence of modulus on microstructure: in porous solids, E′ decreases as porosity increases [63]. SEM, MIP, TGA, and XRD in this study show that the high specific surface area of GNPs/CNTs provides additional nucleation sites, accelerates hydration, and—together with a filling effect—reduces total porosity and refines the pore network, thereby densifying the matrix and elevating E′. At a higher dosage (0.3%), however, insufficient dispersion leads to agglomeration and defect formation, which increase effective porosity and hinder local hydration; consequently, the storage modulus declines relative to the 0.1% mixes.

3.8. Discussion

The incorporation of GNPs and CNTs increases the loss factor (tan δ), storage modulus (E′), and thus the small-strain damping capacity of graphene–cementitious composites. SEM, MIP, XRD, and TG/DTG analyses indicate the complementary mechanisms:
(1)
Interfacial role
Damping in fiber-reinforced cementitious materials scales with the number and quality of matrix–fiber interfaces [64]. Nanoscale GNPs and CNTs introduce orders-of-magnitude more interfacial area than micrometer-scale fibers [1,65], enhancing frictional energy dissipation [66,67]. Interfacial bonding is decisive. In this study, GNPs/CNTs were not acid-functionalized and thus lacked surface functional groups, weakening chemical and mechanical anchorage to hydration products; interfacial gaps at GNP–cement contacts (Figure 7d,e) corroborate this. While stronger bonding improves damping [66], weak chemical/van der Waals/interlocking bonds can be disrupted under vibration, generating additional frictional contacts that dissipate energy [27]. Under cyclic loading, the dense population of nanocarbon–matrix interfaces functions as the primary locus of frictional loss.
(2)
Relative slip (debonding and sliding)
The large modulus mismatch between graphene reinforcements (≈1.1 TPa for GNPs; ≈2.1 TPa for CNTs) [3,68] and the cement matrix (≈30 GPa) induces interfacial shear and nonuniform stresses under load [67], promoting local debonding and relative slip. Debonding dissipates substantially more energy than steady interfacial sliding alone [24]. SEM evidence of CNT pull-out/slip in cement pastes substantiates this pathway [9]. Post-debonding, sliding friction along GNP surfaces and CNT outer walls under cyclic strain converts mechanical work to heat, enabling stress redistribution and additional energy dissipation.
(3)
Intrinsic material properties
GNPs and CNTs combine high stiffness with recoverable deformation, facilitating load transfer while accommodating interfacial shear [1,65]. Their multilayer architectures enable interwall/interlayer shear (multiwalled CNTs; multilayer GNPs), providing internal friction under dynamic loading [61,62]. These intrinsic features further augment vibrational energy dissipation, thereby improving overall damping performance.
(4)
TGA, MIP, and DMA Correlation
The microstructural changes revealed by XRD provide a strong foundation for understanding the macroscopic dynamic properties. The increased C–S–H formation and higher degree of hydration (from TGA-derived Ca(OH)2 content) directly explain the increase in storage modulus (E′), as more solid binder phase is available to carry load.
Furthermore, the pore structure refinement observed in MIP for the 0.1 wt.% samples correlates well with the enhanced mechanical performance. The reduced Ca(OH)2 orientation (lower R index) in these samples suggests a more tortuous and interlocked microstructure, which restricts pore connectivity and contributes to both higher stiffness and more effective energy dissipation pathways.
The superior damping capacity (tan δ) of the GNP samples, especially at 0.1 wt.%, can be attributed to the following two primary mechanisms now supported by evidence: (1) increased interfacial friction and slip between the large-surface-area GNP sheets and the surrounding C–S–H matrix, and (2) potential energy dissipation from friction between adjacent, overlapping GNP layers. CNTs, with their lower surface area and different geometry, offer fewer slip planes, resulting in a less pronounced damping enhancement. At 0.3 wt.%, the agglomeration of nanoparticles (seen in SEM and inferred from MIP pore coarsening) creates stress concentrations and voids, which compromise the matrix’s integrity and reduce the efficiency of interfacial load transfer and energy dissipation, explaining the drop in both E′ and tan δ compared with the 0.1 wt.% optimum.

4. Conclusions

This study comparatively evaluated the effects of one-dimensional CNTs and two-dimensional GNPs on the damping and mechanical properties of cementitious composites. Microstructural and phase characterizations support the following conclusions:
(1)
Dispersion and stability: PVP10, melamine-based superplasticizer, and polycarboxylate-based superplasticizer effectively disperse both CNTs and GNPs. Among these, the polycarboxylate-based superplasticizer provided the highest suspension stability in an alkaline, Ca2+-rich environment (pH = 11.8).
(2)
Hydration, pore structure, and mechanical properties: Both CNTs and GNPs promote cement hydration, refine the pore structure of the cement matrix, and reduce porosity. At suitable dosages, they strengthen and toughen the matrix. Owing to their two-dimensional, lamellar morphology and high aspect ratio, GNPs more effectively deflect and arrest cracks and facilitate load transfer/dissipation, yielding a more pronounced reinforcement than CNTs. Specifically, 0.1% GNPs increased compressive and flexural strengths by 10.9% and 28.6%, respectively. Similarly, 0.1% CNTs increased compressive and flexural strengths by 10.7% and 3.3%, respectively.
(3)
Damping properties: Both CNTs and GNPs significantly enhance the damping performance of cementitious composites, as evidenced by increases in the loss factor and energy storage modulus. For composites doped with 0.1% GNPs, the loss factor and energy storage modulus increased by 21.9% and 11.8%, respectively. Similarly, for composites doped with 0.1% CNTs, the loss factor and energy storage modulus increased by 20.8% and 5.3%, respectively. Microstructural analysis revealed that the improvement in damping performance is primarily attributed to interfacial interactions within the cement matrix, energy dissipation caused by debonding and slip due to differences in elastic modulus, and the intrinsic properties of the graphene materials.
Overall, graphene nanomaterials—particularly GNPs—show strong potential for multifunctional cementitious composites with superior mechanical performance and damping capacity.

Author Contributions

B.L.: Investigation, funding acquisition, and writing—original draft preparation. J.W. (Jiyang Wang): Funding acquisition, investigation, writing—review, and supervision. Z.W.: Validation, and writing—review and edit. Y.P.: Investigation, and data analysis. J.W. (Jingwei Wu): Investigation and validation. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Industry–University Cooperation Collaborative Education Project of Zhejiang Province (2021-383), the Construction Research Project of Zhejiang Province, China (2024K362), and the Basic Public Welfare Research Project of Zhejiang Province, China (LGG22E080004).

Data Availability Statement

The raw/processed data required to reproduce these findings cannot be shared at this time, as the data also form part of an ongoing study. The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.

Acknowledgments

The authors would like to acknowledge the support received from the Center for Balance Architecture and the Architectural Design & Research Institute Co., Ltd. of Zhejiang University in the research project.

Conflicts of Interest

Author Yu Peng was employed by the company The Architectural Design & Research Institute of Zhejiang University Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

  1. Zhu, Y.; Murali, S.; Cai, W.; Li, X.; Suk, J.W.; Potts, J.R.; Ruoff, R.S. Graphene and graphene oxide: Synthesis, properties, and applications. Adv. Mater. 2010, 22, 3906–3924. [Google Scholar] [CrossRef]
  2. Stoller, M.D.; Park, S.J.; Zhu, Y.; An, J.; Ruoff, R.S. Graphene-Based Ultracapacitors. Nano Lett. 2008, 8, 3498–3502. [Google Scholar] [CrossRef]
  3. Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
  4. Wang, B.; Shuang, D. Effect of graphene nanoplatelets on the properties, pore structure and microstructure of cement composites. Mater. Express 2018, 8, 407–416. [Google Scholar] [CrossRef]
  5. Han, B.; Yang, Z.; Shi, X.; Yu, X. Transport Properties of Carbon-Nanotube/Cement Composites. J. Mater. Eng. Perform. 2013, 22, 184–189. [Google Scholar] [CrossRef]
  6. Du, H.; Pang, S. Enhancement of barrier properties of cement mortar with graphene nanoplatelet. Cem. Concr. Res. 2015, 76, 10–19. [Google Scholar] [CrossRef]
  7. Hawreen, A.; Bogas, J.A.; Dias, A.P.S. On the mechanical and shrinkage behavior of cement mortars reinforced with carbon nanotubes. Constr. Build. Mater. 2018, 168, 459–470. [Google Scholar] [CrossRef]
  8. Nochaiya, T.; Chaipanich, A. Behavior of multi-walled carbon nanotubes on the porosity and microstructure of cement-based materials. Appl. Surf. Sci. 2011, 257, 1941–1945. [Google Scholar] [CrossRef]
  9. Wang, J.; Tao, J.; Li, L.; Zhou, C.; Zeng, Q. Thinner fillers, coarser pores? A comparative study of the pore structure alterations of cement composites by graphene oxides and graphene. Compos. Part A-Appl. Sci. Manuf. 2020, 130, 105750. [Google Scholar] [CrossRef]
  10. Hu, Y.; Luo, D.; Li, P.; Li, Q.; Sun, G. Fracture toughness enhancement of cement paste with multi-walled carbon nanotubes. Constr. Build. Mater. 2014, 70, 332–338. [Google Scholar] [CrossRef]
  11. Liu, J.; Fu, J.; Yang, Y.; Gu, C. Study on dispersion, mechanical and microstructure properties of cement paste incorporating graphene sheets. Constr. Build. Mater. 2019, 199, 1–11. [Google Scholar] [CrossRef]
  12. Wang, B.; Deng, S. Effect and mechanism of graphene nanoplatelets on hydration reaction, mechanical properties and microstructure of cement composites. Constr. Build. Mater. 2019, 228, 116720. [Google Scholar] [CrossRef]
  13. Du, H.; Gao, H.J.; Pang, S.D. Improvement in concrete resistance against water and chloride ingress by adding graphene nanoplatelet. Cem. Concr. Res. 2016, 83, 114–123. [Google Scholar] [CrossRef]
  14. Mendoza, O.; Sierra, G.; Tobón, J.I. Effect of the reagglomeration process of multi-walled carbon nanotubes dispersions on the early activity of nanosilica in cement composites. Constr. Build. Mater. 2014, 54, 550–557. [Google Scholar] [CrossRef]
  15. Abedi, M.; Fangueiro, R.; Camões, A.; Correia, A.G. Evaluation of CNT/GNP’s synergic effects on the Mechanical, Microstructural, and durability properties of a cementitious composite by the novel dispersion method. Constr. Build. Mater. 2020, 260, 120486. [Google Scholar] [CrossRef]
  16. Zhang, H.; Cao, S.; Yilmaz, E. Carbon nanotube reinforced cementitious tailings composites: Links to mechanical and microstructural characteristics. Constr. Build. Mater. 2023, 365, 130123. [Google Scholar] [CrossRef]
  17. Bowland, A.G. Comparison and Analysis of the Strength, Stiffness, and Damping Characteristics of Concrete with Rubber, Latex, and Carbonate Additives. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2011. [Google Scholar]
  18. Nadal Gisbert, A.; Gadea Borrell, J.M.; Parres García, F.; Julia Sanchis, E.; Crespo Amoros, J.E.; Segura Alcaraxz, J.; Salas Vicente, F. Analysis behaviour of static and dynamic properties of Ethylene-Propylene-Diene-Methylene crumb rubber mortar. Constr. Build. Mater. 2014, 50, 671–682. [Google Scholar] [CrossRef]
  19. Zhang, L.; Feng, M.; Liu, B.; Geng, G.; Lin, B. Multi-scale study on the crack resistance and energy dissipation mechanism of modified rubberized concrete. Constr. Build. Mater. 2024, 457, 139448. [Google Scholar] [CrossRef]
  20. Najim, K.B.; Hall, M.R. Mechanical and dynamic properties of self-compacting crumb rubber modified concrete. Constr. Build. Mater. 2012, 27, 521–530. [Google Scholar] [CrossRef]
  21. Hernández-Olivares, F.; Barluenga, G.; Bollati, M.; Witoszek, B. Static and dynamic behaviour of recycled tyre rubber-filled concrete. Cem. Concr. Res. 2002, 32, 1587–1596. [Google Scholar] [CrossRef]
  22. Pham, T.; Davis, J.; Ha, N.; Pournasiri, E.; Shi, F.; Hao, H. Experimental investigation on dynamic properties of ultra-high-performance rubberized concrete (UHPRuC). Constr. Build. Mater. 2021, 307, 125104. [Google Scholar] [CrossRef]
  23. Yan, L.; Jenkins, C.H.; Pendleton, R.L. Polyolefin fiber-reinforced concrete composites: Part I. Damping and frequency characteristics. Cem. Concr. Res. 2000, 30, 391–401. [Google Scholar] [CrossRef]
  24. Yan, L.; Jenkins, C.H.; Pendleton, R.L. Polyolefin fiber-reinforced concrete composites: Part II. Damping and interface debonding. Cem. Concr. Res. 2000, 30, 403–410. [Google Scholar] [CrossRef]
  25. Giner, V.T.; Baeza, F.J.; Ivorra, S.; Zornoza, E.; Galao, O. Effect of steel and carbon fiber additions on the dynamic properties of concrete containing silica fume. Mater. Des. 2012, 34, 332–339. [Google Scholar] [CrossRef]
  26. Islam, S.M.; Hussain, R.R.; Morshed, M.A.Z. Fiber-reinforced concrete incorporating locally available natural fibers in normal- and high-strength concrete and a performance analysis with steel fiber-reinforced composite concrete. J. Compos. Mater. 2012, 46, 111–122. [Google Scholar] [CrossRef]
  27. Liew, K.M.; Kai, M.F.; Zhang, L.W. Mechanical and damping properties of CNT-reinforced cementitious composites. Compos. Struct. 2017, 160, 81–88. [Google Scholar] [CrossRef]
  28. Long, W.; Wei, J.; Xing, F.; Khayat, K. Enhanced dynamic mechanical properties of cement paste modified with graphene oxide nanosheets and its reinforcing mechanism. Cem. Concr. Compos. 2018, 93, 127–139. [Google Scholar] [CrossRef]
  29. Du, H.; Pang, S.D. Dispersion and stability of graphene nanoplatelet in water and its influence on cement composites. Constr. Build. Mater. 2018, 167, 403–413. [Google Scholar] [CrossRef]
  30. Wang, Q.; Zhan, D.; Qi, G.; Wang, Y.; Zheng, H. Impact of the microstructure of polycarboxylate superplasticizers on the dispersion of graphene. New Carbon Mater. 2020, 35, 547–558. [Google Scholar] [CrossRef]
  31. Birenboim, M.; Nadiv, R.; Alatawna, A.; Buzaglo, M.; Schahar, G.; Lee, J.; Kim, G.; Peled, A.; Regev, O. Reinforcement and workability aspects of graphene-oxide-reinforced cement nanocomposites. Compos. Part B Eng. 2019, 161, 68–76. [Google Scholar] [CrossRef]
  32. Tao, J.; Wang, X.; Wang, Z.; Zeng, Q. Graphene nanoplatelets as an effective additive to tune the microstructures and piezoresistive properties of cement-based composites. Constr. Build. Mater. 2019, 209, 665–678. [Google Scholar] [CrossRef]
  33. Tao, J.; Wang, J.; Zeng, Q. A comparative study on the influences of CNT and GNP on the piezoresistivity of cement composites. Mater. Lett. 2020, 259, 126858. [Google Scholar] [CrossRef]
  34. Mendoza, O.; Sierra, G.; Tobón, J.I. Influence of super plasticizer and Ca(OH)2 on the stability of functionalized multi-walled carbon nanotubes dispersions for cement composites applications. Constr. Build. Mater. 2013, 47, 771–778. [Google Scholar] [CrossRef]
  35. Haga, K.; Sutou, S.; Hironaga, M.; Tanaka, S.; Nagasaki, S. Effects of porosity on leaching of Ca from hardened ordinary Portland cement paste. Cem. Concr. Res. 2005, 35, 1764–1775. [Google Scholar] [CrossRef]
  36. Gao, Y.; Jing, H.; Chen, S.; Du, M.; Chen, W.; Duan, W. Influence of ultrasonication on the dispersion and enhancing effect of graphene oxide–carbon nanotube hybrid nanoreinforcement in cementitious composite. Compos. Part B Eng. 2019, 164, 45–53. [Google Scholar] [CrossRef]
  37. Lu, Z.; Hanif, A.; Ning, C.; Shao, H.; Yin, R.; Li, Z. Steric stabilization of graphene oxide in alkaline cementitious solutions: Mechanical enhancement of cement composite. Mater. Des. 2017, 127, 154–161. [Google Scholar] [CrossRef]
  38. Yan, Y.; Piao, L.; Kim, S.; Li, W.; Zhou, H. Effect of Pluronic block copolymers on aqueous dispersions of graphene oxide. RSC Adv. 2015, 5, 40199–40204. [Google Scholar] [CrossRef]
  39. Ramezani, M.; Kim, Y.; Sun, Z. Modeling the mechanical properties of cementitious materials containing CNTs. Cem. Concr. Compos. 2019, 104, 103347. [Google Scholar] [CrossRef]
  40. JTG 3420-2020; Testing Methods of Cement and Concrete for Highway Engineering. Ministry of Transport of the People’s Republic of China: Beijing, China, 2020. (In Chinese)
  41. Zhang, W.; Wu, P.; Zhang, Y.; Zeng, W.; Yang, F. The effect of carbon nanotubes on the mechanical and damping properties of macro-defect-free cements. Sci. Eng. Compos. Mater. 2020, 27, 28–40. [Google Scholar]
  42. Li, W.; Ji, W.; Liu, Y.; Xing, F.; Liu, Y. Damping property of a cement-based material containing carbon nanotube. J. Nanomater. 2015, 2015, 371404. [Google Scholar] [CrossRef]
  43. Xu, P.; Xiao, C.; Li, J. Study on relationship between natural vibration periods and heights of structures for high-rise buildings and its reference range. China Civ. Eng. J. 2014, 47, 1–11. (In Chinese) [Google Scholar]
  44. Grossiord, N.; Regev, O.; Loos, J.; Meuldijk, J.; Koning, C. Time-dependent study of the exfoliation process of carbon nanotubes in aqueous dispersions by using UV−visible spectroscopy. Anal. Chem. 2005, 77, 5135–5139. [Google Scholar] [CrossRef]
  45. Potgieter, J.; Strydom, C. Determination of the clay index of limestone with methylene blue adsorption using a UV-VIS spectrophotometric method. Cem. Concr. Res. 1999, 29, 1815–1817. [Google Scholar] [CrossRef]
  46. Zhao, L.; Guo, X.; Liu, Y.; Ge, C.; Chen, Z.; Guo, L.; Shu, X.; Liu, J. Investigation of dispersion behavior of GO modified by different water reducing agents in cement pore solution. Carbon 2018, 127, 255–269. [Google Scholar] [CrossRef]
  47. Konsta-Gdoutos, M.; Metaxa, Z.; Shah, S. Multi-scale mechanical and fracture characteristics and early-age strain capacity of high performance carbon nanotube/cement nanocomposites. Cem. Concr. Compos. 2010, 32, 110–115. [Google Scholar] [CrossRef]
  48. Horszczaruk, E.; Mijowska, E.; Kalenczuk, R.; Aleksandrzak, M.; Mijowska, S. Nanocomposite of cement/graphene oxide—Impact on hydration kinetics and Young’s modulus. Constr. Build. Mater. 2015, 78, 234–242. [Google Scholar] [CrossRef]
  49. Han, B.; Zheng, Q.; Sun, S.; Dong, S.; Zhang, L.; Yu, X.; Ou, J. Enhancing mechanisms of multi-layer graphenes to cementitious composites. Compos. Part A Appl. Sci. Manuf. 2017, 101, 143–150. [Google Scholar] [CrossRef]
  50. Ye, Q.; Zhang, Z.; Kong, D.; Chen, R. Influence of nano-SiO2 addition on properties of hardened cement paste as compared with silica fume. Constr. Build. Mater. 2007, 21, 539–545. [Google Scholar]
  51. Meng, T.; Yu, Y.; Qian, X.; Zhan, S.; Qian, K. Effect of nano-TiO2 on the mechanical properties of cement mortar. Constr. Build. Mater. 2012, 29, 241–245. [Google Scholar] [CrossRef]
  52. Grandet, J.; Ollivier, J. Etude de la formation du monocarboaluminate de calcium hydrate au contact d’un granulat calcaire dans une pate de ciment portland. Cem. Concr. Compos. 1980, 10, 759–770. [Google Scholar] [CrossRef]
  53. Zhang, Q.; Zeng, Q.; Zheng, D.; Wang, J.; Xu, S. Oven dying kinetics and status of cement-based porous materials for in-lab microstructure investigation. Adv. Cem. Res. 2018, 30, 204–215. [Google Scholar] [CrossRef]
  54. Zhou, C.; Ren, F.; Zeng, Q.; Xiao, L.; Wang, W. Pore-size resolved water vapor adsorption kinetics of white cement mortars as viewed from proton NMR relaxation. Cem. Concr. Res. 2018, 105, 31–43. [Google Scholar] [CrossRef]
  55. Villain, G.; Thiery, M.; Platret, G. Measurement methods of carbonation profiles in concrete: Thermogravimetry, chemical analysis and gammadensimetry. Cem. Concr. Res. 2007, 37, 1182–1192. [Google Scholar] [CrossRef]
  56. Fakhim, B.; Hassani, A.; Rashidi, A.; Ghodousi, P. Predicting the impact of multiwalled carbon nanotubes on the cement hydration products and durability of cementitious matrix using artificial neural network modeling technique. Sci. World J. 2013, 2013, 103713. [Google Scholar] [CrossRef]
  57. Han, B.; Zhang, L.; Zeng, S.; Dong, S.; Yu, X.; Yang, R.; Ou, J. Nano-core effect in nano-engineered cementitious composites. Compos. Part A Appl. Sci. Manuf. 2017, 95, 100–109. [Google Scholar] [CrossRef]
  58. Wang, B.; Pang, B. Mechanical property and toughening mechanism of water reducing agents modified graphene nanoplatelets reinforced cement composites. Constr. Build. Mater. 2019, 226, 699–711. [Google Scholar] [CrossRef]
  59. Durczak, K.; Pyzalski, M.; Brylewski, T.; Sujak, A. Effect of variable synthesis conditions on the formation of ye’elimite-aluminate-calcium (YAC) cement and its hydration in the presence of portland cement (OPC) and several accessory additives. Materials 2023, 16, 6052. [Google Scholar] [CrossRef]
  60. Foray-Thevenin, G.; Vigier, G.; Vassoille, R.; Orange, G. Characterization of cement paste by dynamic mechanical thermo-analysis: Part I: Operative conditions. Mater. Charact. 2006, 56, 129–137. [Google Scholar] [CrossRef]
  61. Yu, P.; Wang, Z.; Lu, S.; Lai, P. Effects of carbon nanofibers and carboxyl functionalized multi-walled carbon nanotubes on mechanical damping behavior of cement paste. J. Nanosci. Nanotechnol. 2019, 19, 163–169. [Google Scholar] [CrossRef]
  62. Ruan, Y.; Zhou, D.; Sun, S.; Wu, X.; Yu, X.; Hou, J.; Dong, X.; Han, B. Self-damping cementitious composites with multi-layer graphene. Mater. Res. Express 2017, 4, 075605. [Google Scholar] [CrossRef]
  63. Yang, C.; Huang, R. Double inclusion model for approximate elastic moduli of concrete material. Cem. Concr. Res. 1996, 26, 83–91. [Google Scholar] [CrossRef]
  64. Chandra, R.; Singh, S.; Gupta, K. Damping studies in fiber-reinforced composites—A review. Compos. Struct. 1999, 46, 41–51. [Google Scholar] [CrossRef]
  65. Wong, E.; Sheehan, P.; Lieber, C. Nanobeam mechanics: Elasticity, strength, and toughness of nanorods and nanotubes. Science 1997, 277, 1971–1975. [Google Scholar] [CrossRef]
  66. Zhou, X.; Shin, E.; Wang, K.; Bakis, C. Interfacial damping characteristics of carbon nanotube-based composites. Compos. Sci. Technol. 2004, 64, 2425–2437. [Google Scholar] [CrossRef]
  67. Zou, D.; Liu, T.; Teng, J. Improving the damping ability by the addition of Nano SiO2 to the concrete materials. In Proceedings of the SPIE 2009, Second International Conference on Smart Materials and Nanotechnology in Engineering, Weihai, China, 20 October 2009; Volume 7493, p. 74933C. [Google Scholar]
  68. Yu, M.; Lourie, O.; Dyer, M.; Moloni, K.; Kelly, T.; Ruoff, R. Strength and breaking mechanism of multiwalled carbon nanotubes under tensile load. Science 2000, 287, 637–640. [Google Scholar] [CrossRef] [PubMed]
Buildings 15 03317 g001
Figure 1. Flowchart of dispersion. Note: The red wavy lines represent water waves.
Figure 1. Flowchart of dispersion. Note: The red wavy lines represent water waves.
Buildings 15 03317 g001
Buildings 15 03317 g002
Figure 2. Photographs of specimens (a) for mechanical tests and (b) for damping tests.
Figure 2. Photographs of specimens (a) for mechanical tests and (b) for damping tests.
Buildings 15 03317 g002
Buildings 15 03317 g003
Figure 3. Photographs of the DMA instrument.
Figure 3. Photographs of the DMA instrument.
Buildings 15 03317 g003
Buildings 15 03317 g004
Figure 4. Relationship between applied sinusoidal force, displacement, phase lag, and modulus. Note: The space between the opposing arrows indicates the phase shift.
Figure 4. Relationship between applied sinusoidal force, displacement, phase lag, and modulus. Note: The space between the opposing arrows indicates the phase shift.
Buildings 15 03317 g004
Buildings 15 03317 g005
Figure 5. Absorbance at 260 nm vs. time for GNCA dispersions in water and lime solution after 2 h of sonication.
Figure 5. Absorbance at 260 nm vs. time for GNCA dispersions in water and lime solution after 2 h of sonication.
Buildings 15 03317 g005
Buildings 15 03317 g006
Figure 6. UV–vis spectra of GNCAs/lime solution at 10 days.
Figure 6. UV–vis spectra of GNCAs/lime solution at 10 days.
Buildings 15 03317 g006
Buildings 15 03317 g007
Figure 7. Typical SEM images of the GNP/CNT–cementitious composites: (a) Ref, (b) CNT-01, (c) CNT-03, (d) GNP-01, and (e) GNP-03. Note: The red curve indicates the cracks, while the arrow points to the substance mentioned in this figure.
Figure 7. Typical SEM images of the GNP/CNT–cementitious composites: (a) Ref, (b) CNT-01, (c) CNT-03, (d) GNP-01, and (e) GNP-03. Note: The red curve indicates the cracks, while the arrow points to the substance mentioned in this figure.
Buildings 15 03317 g007
Buildings 15 03317 g008
Figure 8. Pore size distribution of specimens: (a) pore size distribution curve and (b) cumulative pore size distribution curve.
Figure 8. Pore size distribution of specimens: (a) pore size distribution curve and (b) cumulative pore size distribution curve.
Buildings 15 03317 g008
Buildings 15 03317 g009
Figure 9. XRD analysis of composites at 28 days.
Figure 9. XRD analysis of composites at 28 days.
Buildings 15 03317 g009
Buildings 15 03317 g010
Figure 10. Thermogravimetric analysis on 28-day GNP/CNT-modified cement paste: (a) TG curves and (b) DTG curves.
Figure 10. Thermogravimetric analysis on 28-day GNP/CNT-modified cement paste: (a) TG curves and (b) DTG curves.
Buildings 15 03317 g010
Buildings 15 03317 g011
Figure 11. Ca(OH)2 content in percentage at 28 days.
Figure 11. Ca(OH)2 content in percentage at 28 days.
Buildings 15 03317 g011
Buildings 15 03317 g012
Figure 12. (a) Flexural and (b) compressive strengths of the GNP/CNT–cementitious composites.
Figure 12. (a) Flexural and (b) compressive strengths of the GNP/CNT–cementitious composites.
Buildings 15 03317 g012
Buildings 15 03317 g013
Figure 13. Loss factors of GNP/CNT–cementitious composites.
Figure 13. Loss factors of GNP/CNT–cementitious composites.
Buildings 15 03317 g013
Buildings 15 03317 g014
Figure 14. Storage modulus of GNP/CNT–cementitious composites.
Figure 14. Storage modulus of GNP/CNT–cementitious composites.
Buildings 15 03317 g014
Table 1. Chemical and mineral compositions of cement (%).
Table 1. Chemical and mineral compositions of cement (%).
Chemical CompositionPercentageMineral CompositionPercentage
SiO222.78C3S54.72
Al2O34.65C2S21.18
Fe2O33.54C3A6.34
CaO64.78C4AF10.76
MgO2.22
SO30.34
NaOeq0.52
f-CaO0.98
Table 2. Physical properties of GNPs and CNTs.
Table 2. Physical properties of GNPs and CNTs.
PropertiesCNTsGNPs
DiameterOuter: 8–15 nm, inner:3–5 nm5–10 μm
Thickness/3–10 nm
Length~50 μm/
Aspect ratio~1000~0.001
Specific surface area>140 m2/g31.657 m2/g
Tap density0.15 g/cm30.075 g/cm3
Electrical conductivity>100 S/cm500–1000 S/cm
Table 3. Properties of polycarboxylate superplasticizer and melamine dispersant.
Table 3. Properties of polycarboxylate superplasticizer and melamine dispersant.
ParameterPolycarboxylate SuperplasticizerMelamine Dispersant
AppearanceLight yellow powderWhite power
Packing density0.3–0.6 g/cm30.45–0.75 g/cm3
Loss on dying<2%<4%
pH value6.5–8.5 (20 °C 20% solution)9–11.4 (20 °C 20% solution)
Table 4. Properties of PVP 10.
Table 4. Properties of PVP 10.
AppearanceSolubilitypH ValueK-Value (Viscosity Value)
White powder100 mg/mL, H2O3–7 (5% solution)13–19
Table 5. Experimental design for dispersant types.
Table 5. Experimental design for dispersant types.
Sample IDDispersant (g)Deionized Water (mL)GNPs (g)CNTs (g)Ca(OH)2 (g)
PCEMSPVP
GNCA-DW-PCE0.2--1000.20.2-
GNCA-DW-MS-0.2-1000.20.2-
GNCA-DW-PVP--0.21000.20.2-
GNCA-LS-PCE0.2--1000.20.20.023
GNCA-LS-MS-0.2-1000.20.20.023
GNCA-LS-PVP--0.21000.20.20.023
GNCA-DW-PCE: GNCAs in deionized water (pH = 7) with polycarboxylate superplasticizer; GNCA-DW-MS: GNCAs in deionized water (pH = 7) with melamine dispersant; GNCA-DW-PVP: GNCAs in deionized water (pH = 7) with PVP10; GNCA-LS-PCE: GNCAs in lime solution (pH = 11.8) with polycarboxylate superplasticizer; GNCA-LS-MS: GNCAs in lime solution (pH = 11.8) with melamine dispersant; GNCA-LS-PVP: GNCAs in lime solution (pH = 11.8) with PVP10.
Table 6. Mix proportions of CNT/GNP cementitious composites.
Table 6. Mix proportions of CNT/GNP cementitious composites.
Sample IDContents (%)CNT/GNP (g)Dispersant (g)Cement (g)Water (mL)
Ref0093000750
CNT-010.1393000750
CNT-030.3993000750
GNP-010.1393000750
GNP-030.3993000750
Table 7. Representative MIP results of the CNT(GNP)–cement composites.
Table 7. Representative MIP results of the CNT(GNP)–cement composites.
Sample ID
RefCNT-01CNT-03GNP-01GNP-03
Porosity (%)13.2712.5413.8412.5612.71
Mean pore size (nm)16.3016.0016.7016.3018.50
Threshold pore size (nm)26.3026.3026.3032.4032.40
Pore distribution (%)<20 nm25.0326.5527.6925.9621.73
20–50 nm64.4259.7157.3554.3260.08
50–200 nm4.733.063.725.999.48
>200 nm5.8210.6811.2413.738.71
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Liu, B.; Wang, J.; Wei, Z.; Peng, Y.; Wu, J. Damping and Microstructure of Graphene/Carbon Nanotube-Modified Cement Composites. Buildings 2025, 15, 3317. https://doi.org/10.3390/buildings15183317

AMA Style

Liu B, Wang J, Wei Z, Peng Y, Wu J. Damping and Microstructure of Graphene/Carbon Nanotube-Modified Cement Composites. Buildings. 2025; 15(18):3317. https://doi.org/10.3390/buildings15183317

Chicago/Turabian Style

Liu, Bin, Jiyang Wang, Zheng Wei, Yu Peng, and Jingwei Wu. 2025. "Damping and Microstructure of Graphene/Carbon Nanotube-Modified Cement Composites" Buildings 15, no. 18: 3317. https://doi.org/10.3390/buildings15183317

APA Style

Liu, B., Wang, J., Wei, Z., Peng, Y., & Wu, J. (2025). Damping and Microstructure of Graphene/Carbon Nanotube-Modified Cement Composites. Buildings, 15(18), 3317. https://doi.org/10.3390/buildings15183317

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop