Lifecycle Assessment of Seismic Resilience and Economic Losses for Continuous Girder Bridges in Chloride-Induced Corrosion
Abstract
1. Introduction
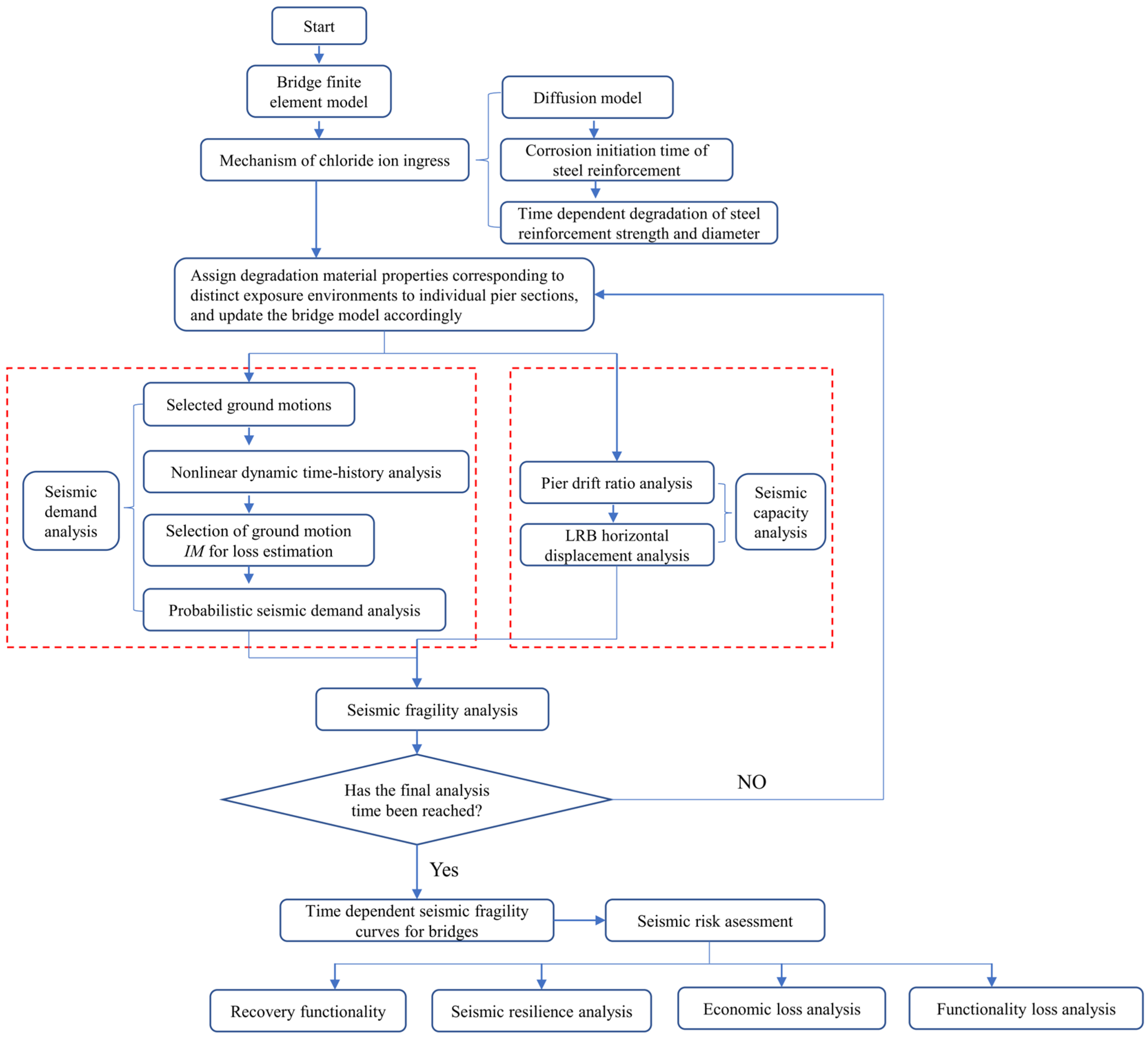
2. Probabilistic Modeling of Deterioration
2.1. Diffusion Process
2.2. Corrosion of Reinforcing Steel
3. Seismic Fragility Analysis of Bridges
4. Seismic Resilience Assessment
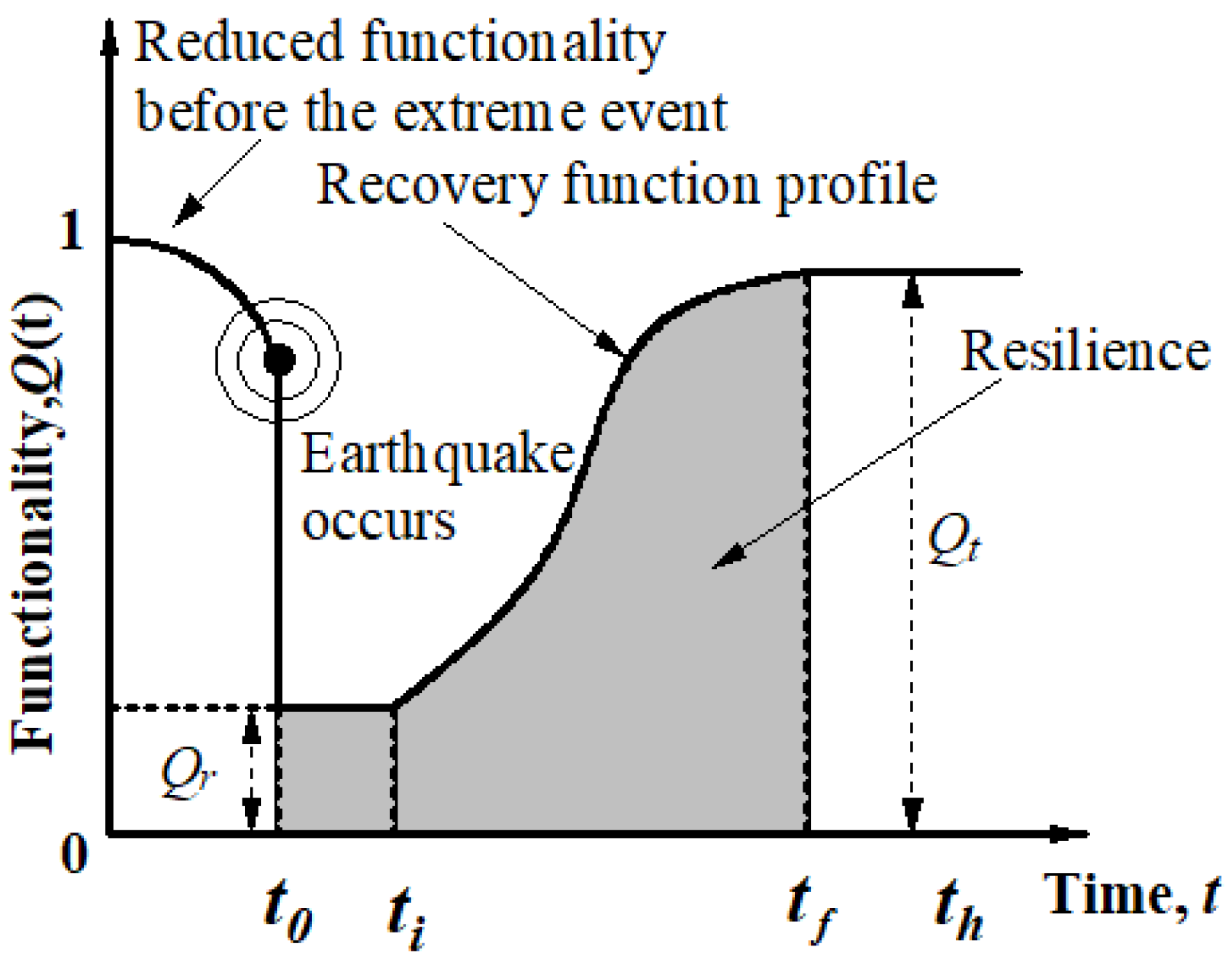
4.1. Definition of Resilience
4.2. Time-Variant Seismic Capacity and Functionality
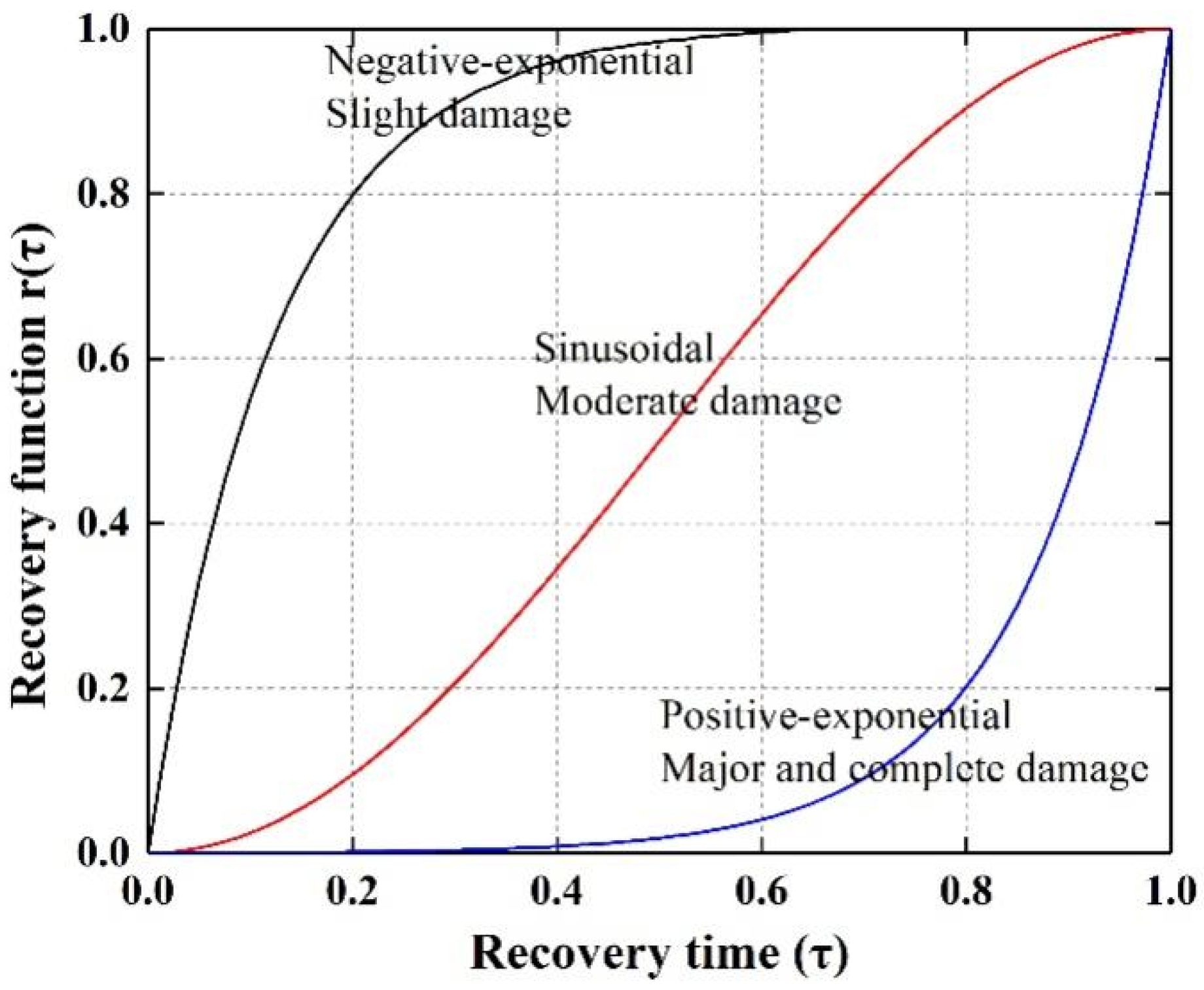
4.3. Recovery Functionality
4.4. Resilience Improvement
5. Economic Loss Assessment
6. Example Bridge and Selection of Ground Motions
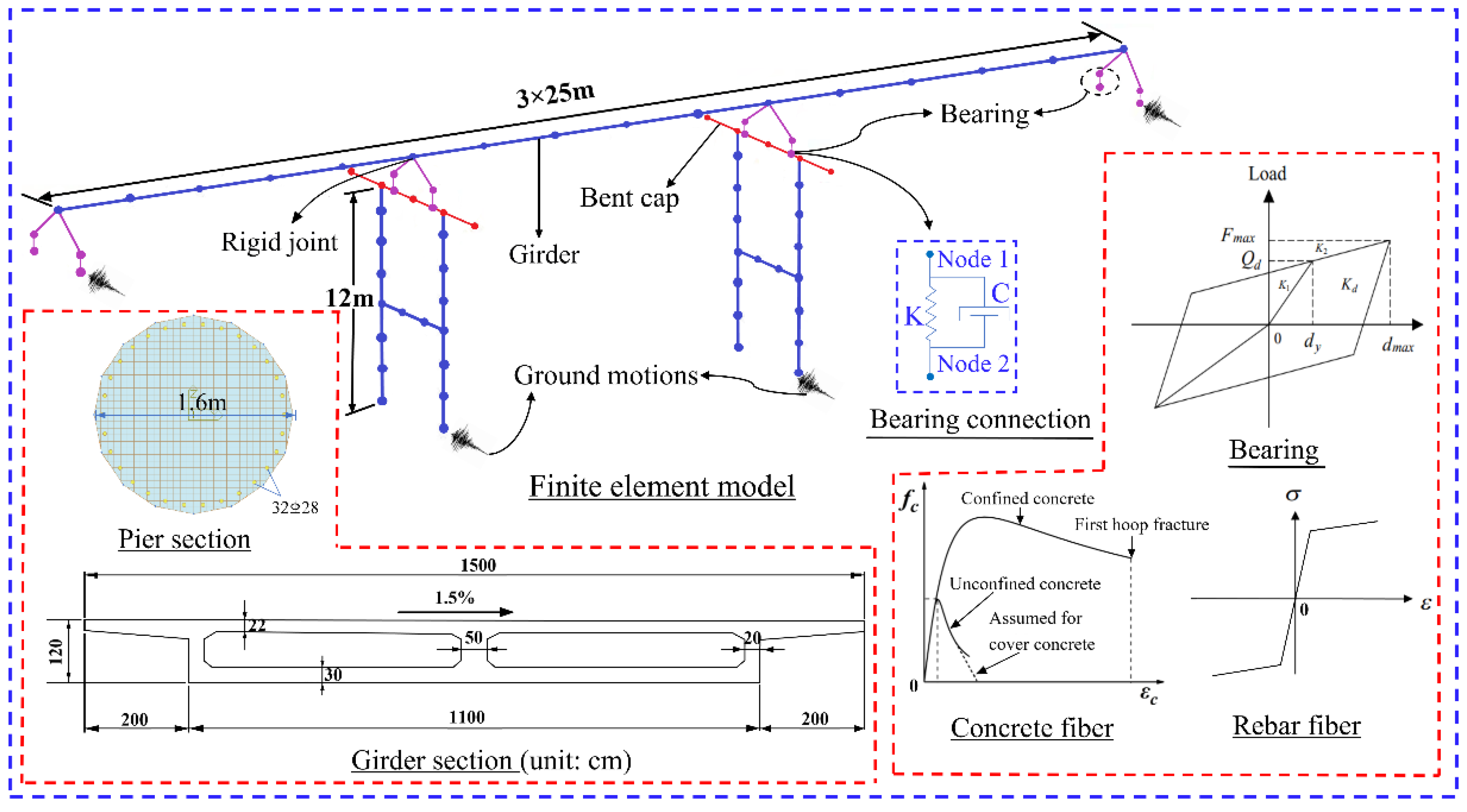
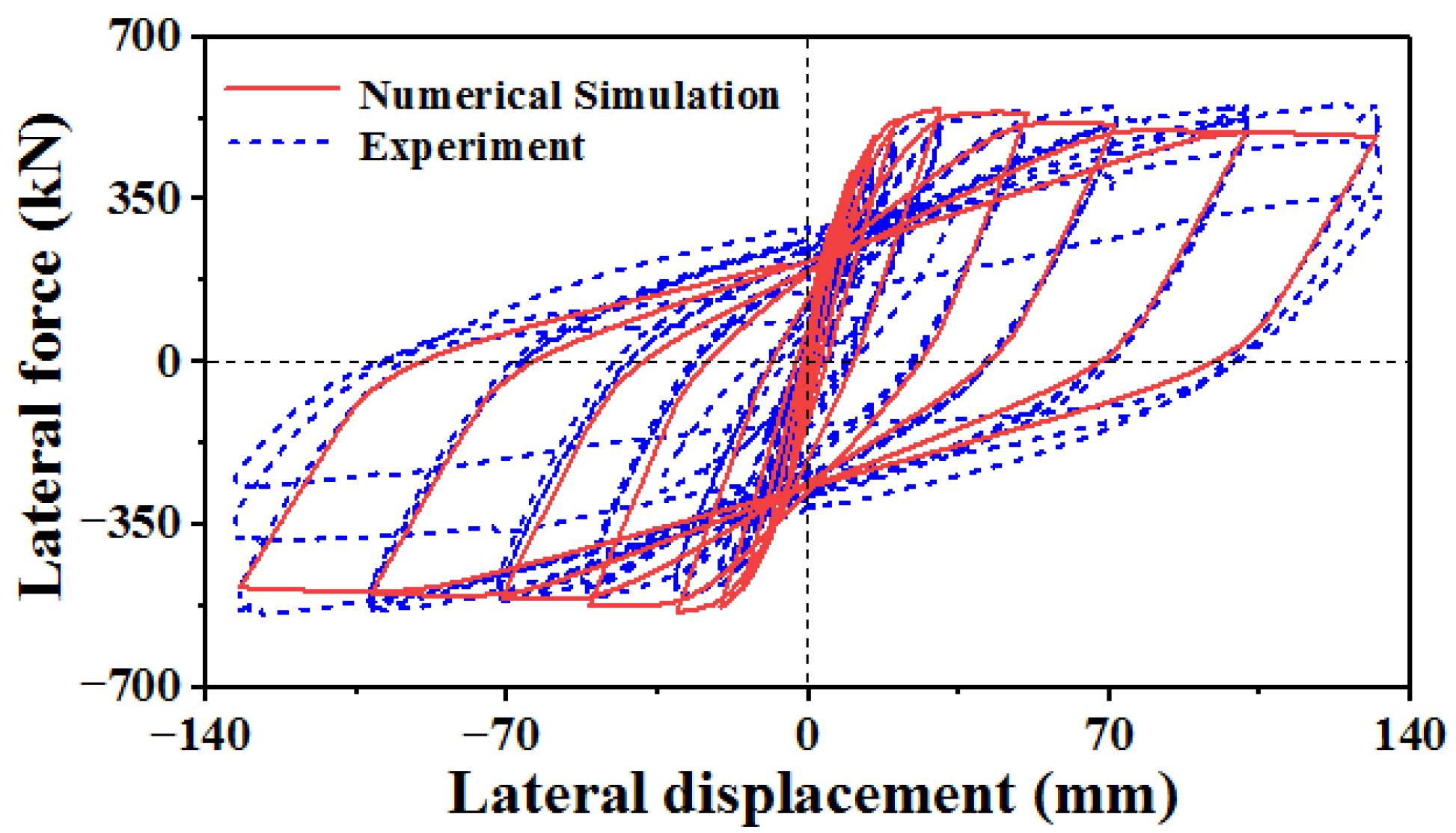
6.1. Finite Element Analysis of a Representative Bridge Structure
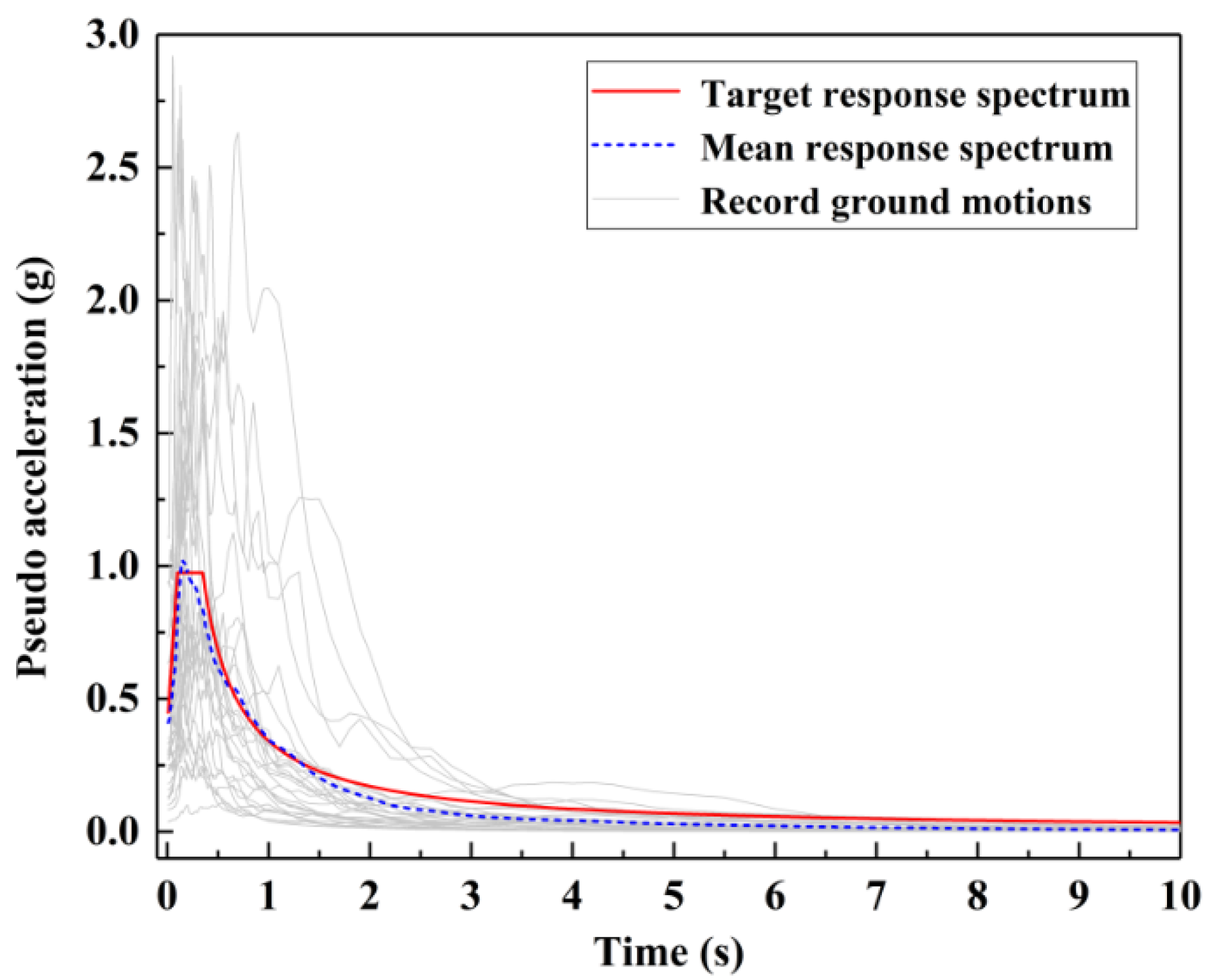
6.2. Selection of Ground Motions
7. Results and Discussion
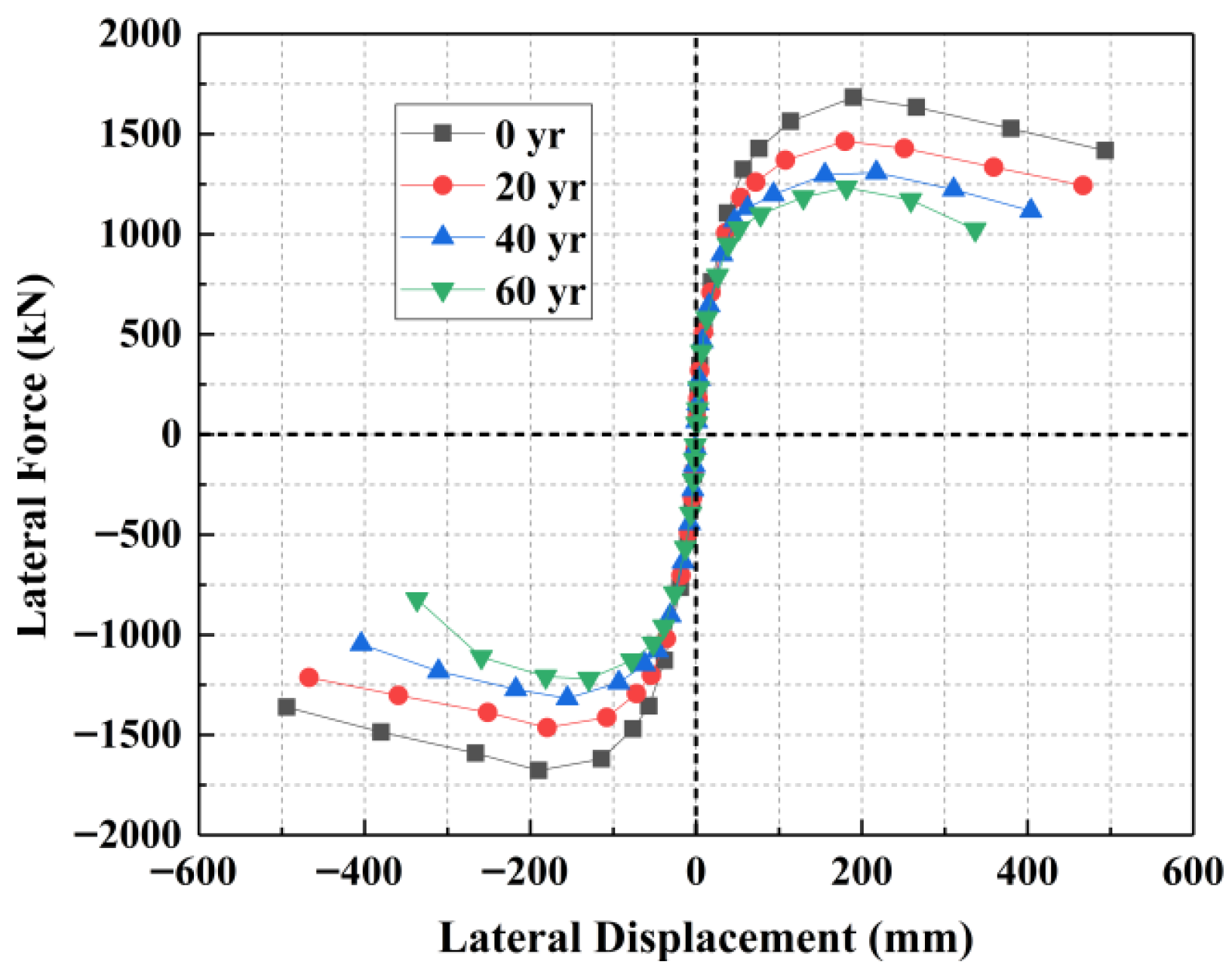
7.1. Seismic Performance of a Representative Bridge Structure
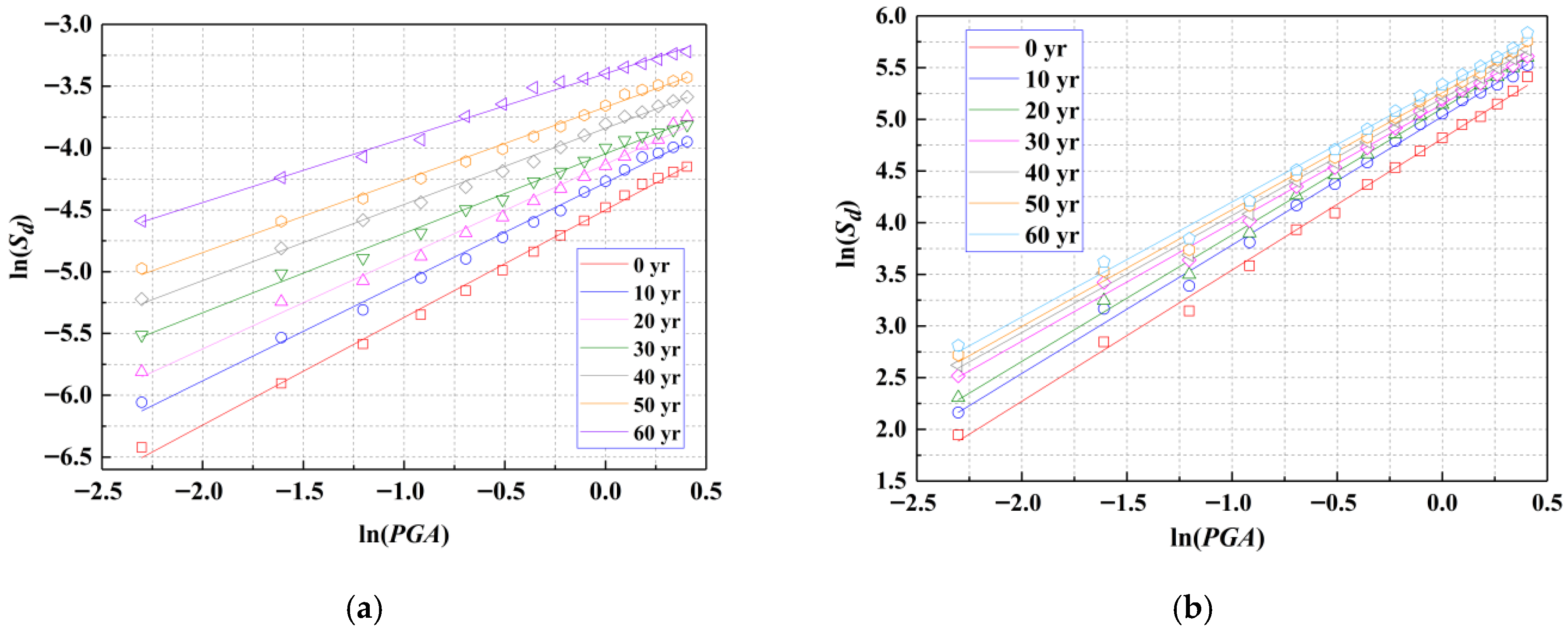
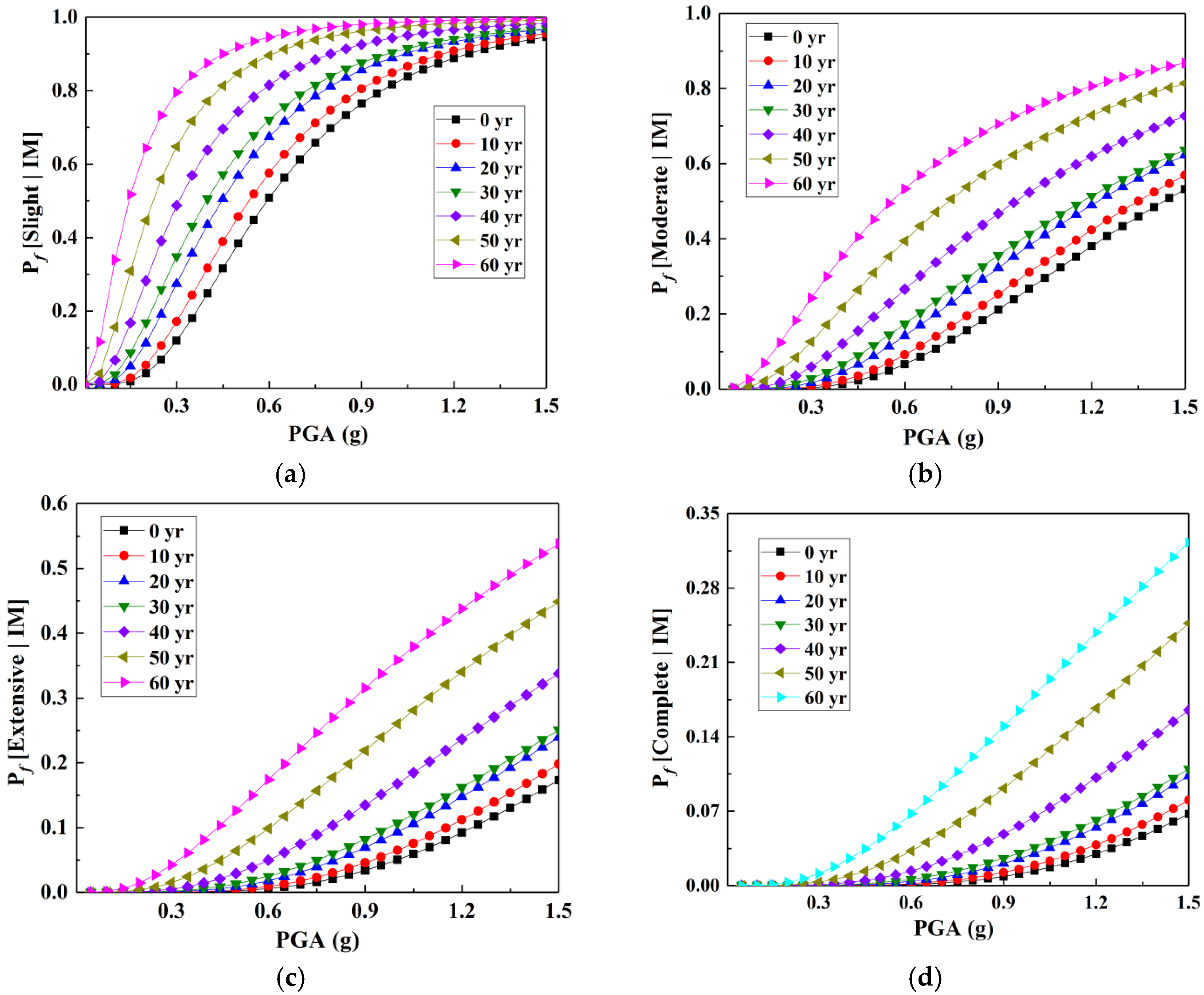
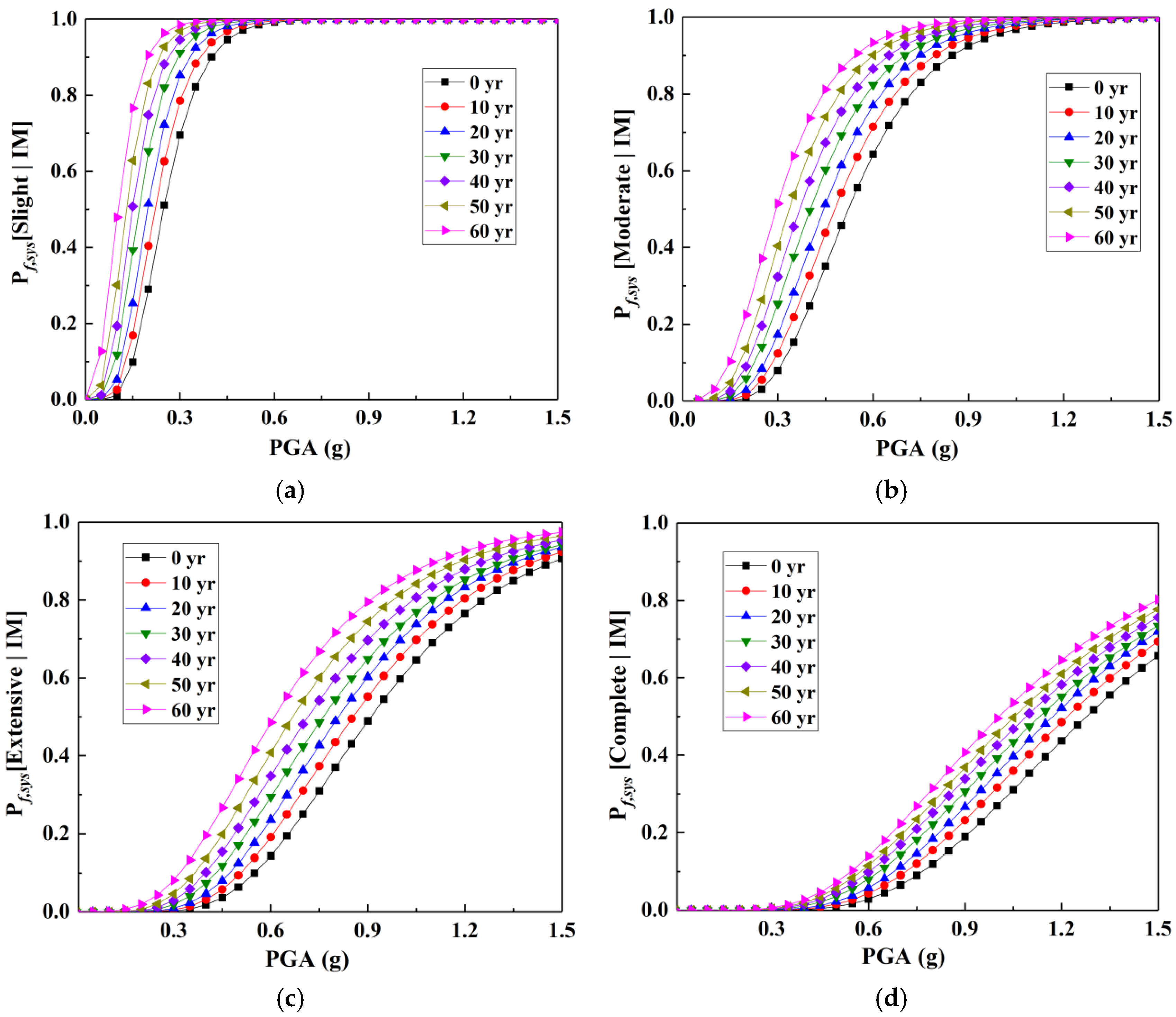
7.2. Seismic Fragility of Sample Bridge
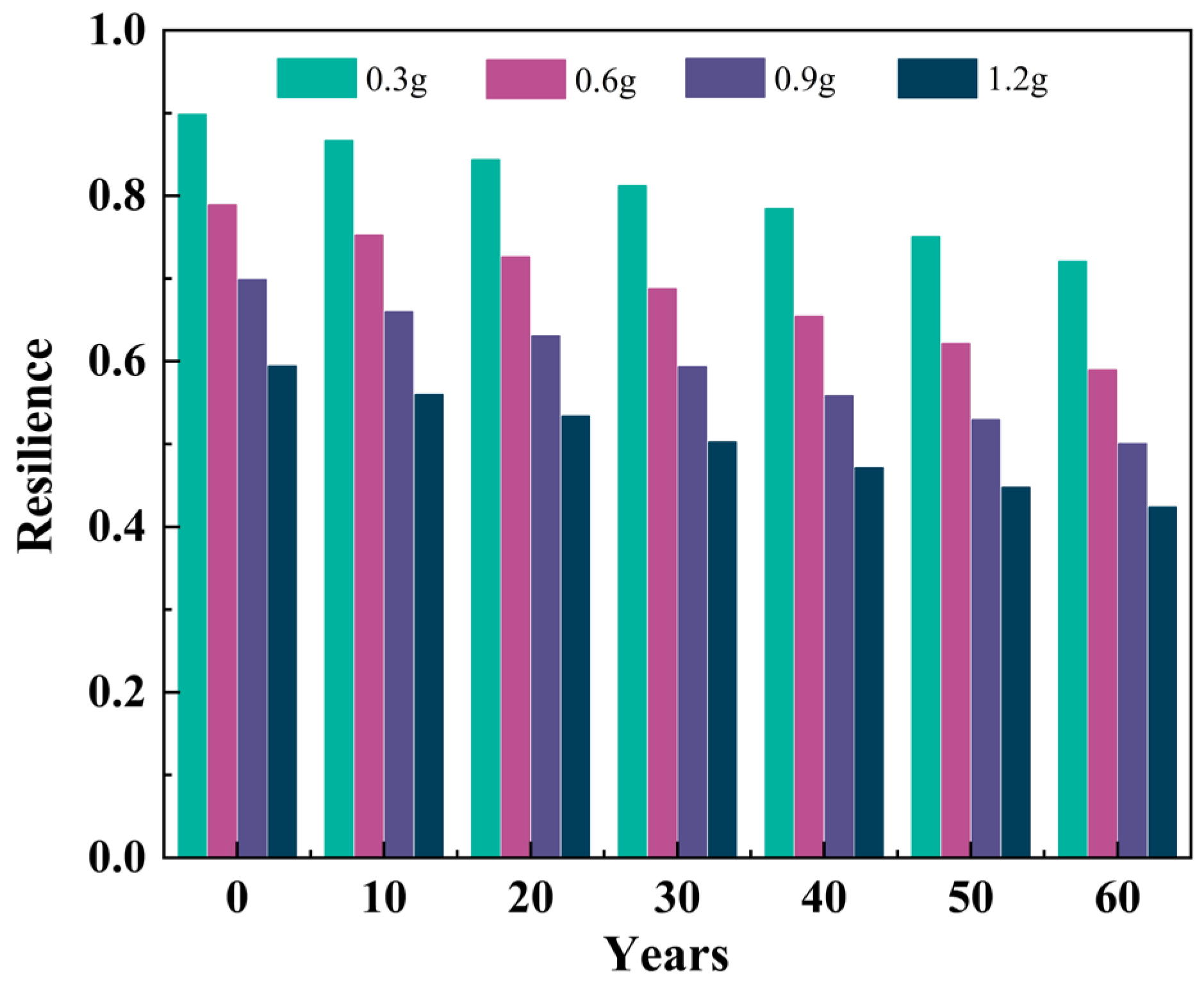
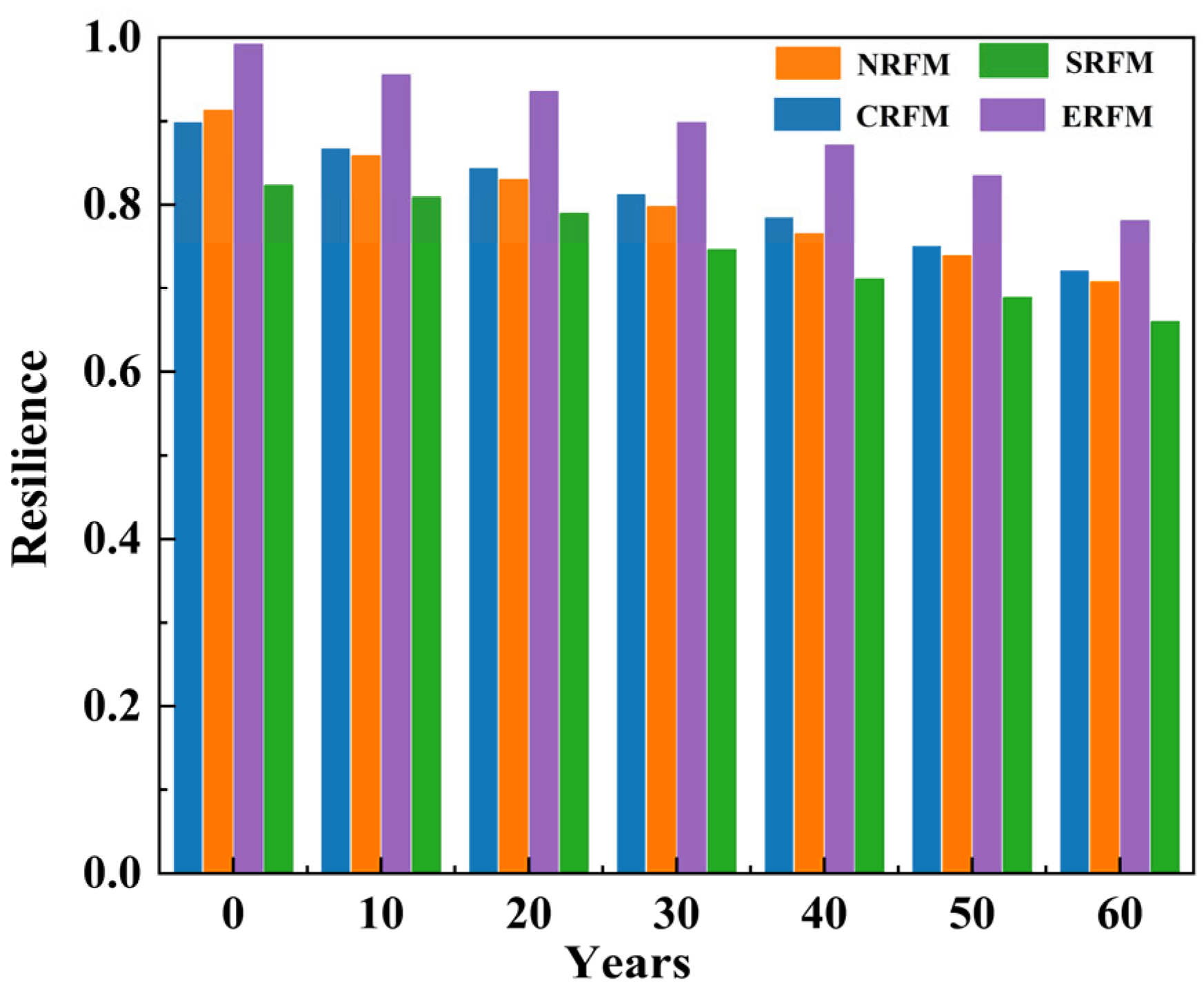
7.3. Assessment of Resilience
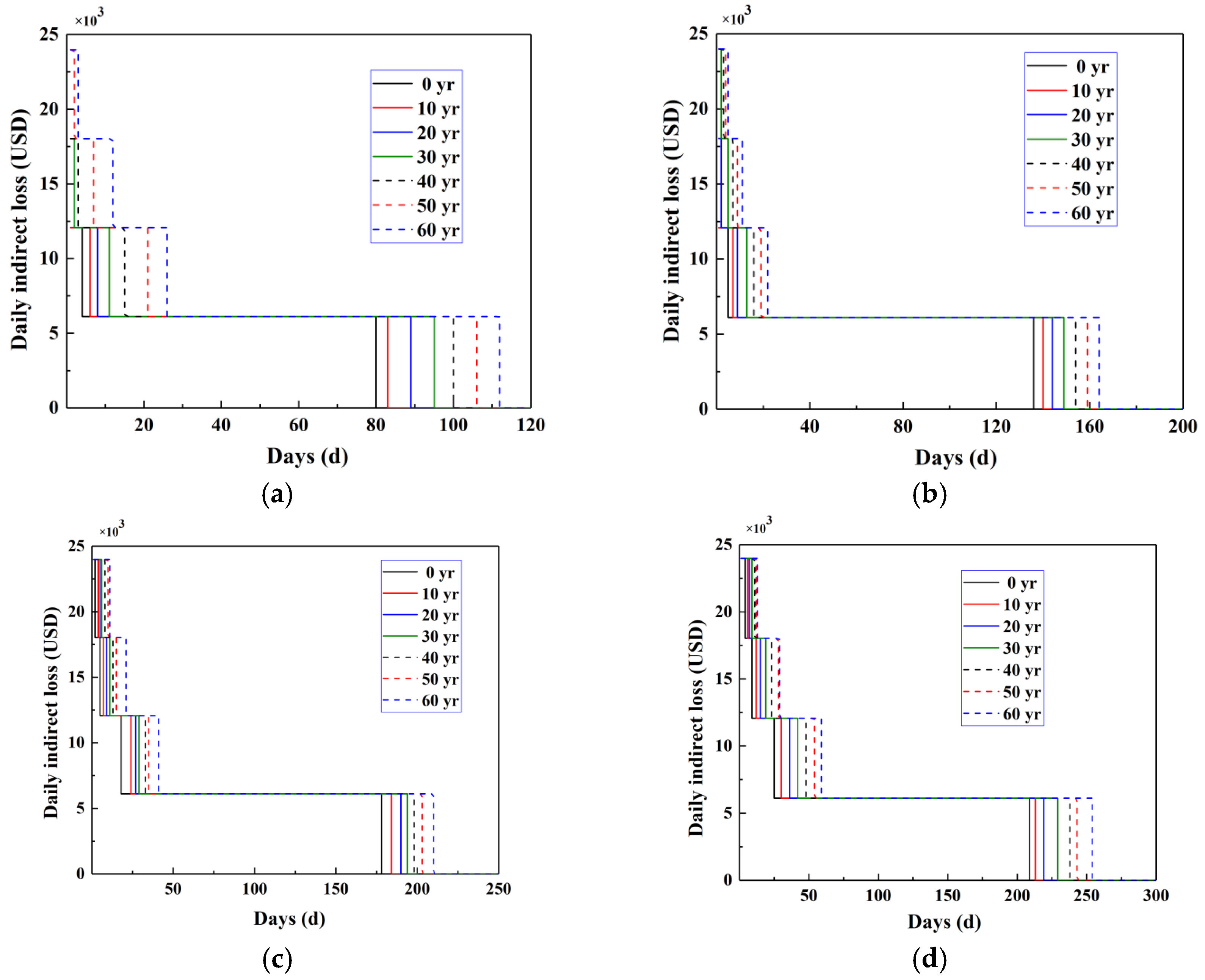
7.4. Assessment of Economic Losses
8. Conclusions
- (1)
- A highly reliable fragility prediction model (R2 > 0.95) was established through multivariate analysis of seismic damage indicators. Statistical fragility profiles indicate that chloride attack substantially elevates structural susceptibility, particularly for piers rather than bearings. The interaction between chloride deterioration and seismic acceleration intensifies the recovery function Q(t) impairment, accelerating performance decline. Post-seismic rehabilitation measures, featuring targeted damage repair and stiffness augmentation, effectively restored operational capacity within required timeframes.
- (2)
- Nonlinear resilience degradation patterns were identified to both ground motion severity and chloride exposure time. Analytical results quantify that 0.3 g PGA enhancements reduce RI by 11.4–18.2%, while ten-year chloride exposure intervals lead to more moderate 2.7–6.2% reductions. NRFM refines existing ERFM and SRFM approaches by integrating probabilistic failure analysis. Verification against CRFM shows discrepancies ≤ 2.4% in stochastic analyses, confirming the method’s reliability.
- (3)
- Financial analysis demonstrated significant indirect cost amplification due to seismic intensity and corrosion duration, with each decade of chloride penetration increasing secondary expenses by $58,000–$108,000. Indirect impacts consistently outweighed direct damages, substantially influencing rehabilitation scheduling and resource allocation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| № | Earthquake | Year | Station Name | Mw | Mechanism | Rrup (km) | Vs30 (m/s) |
|---|---|---|---|---|---|---|---|
| 1 | Northern Calif | 1952 | Ferndale City Hall | 5.2 | strike slip | 43.28 | 219.31 |
| 2 | Southern Calif | 1952 | San Luis Obispo | 6 | strike slip | 73.41 | 493.5 |
| 3 | Central Calif | 1954 | Hollister City Hall | 5.3 | strike slip | 25.81 | 198.77 |
| 4 | Imperial Valley | 1955 | El Centro Array #9 | 5.4 | strike slip | 14.88 | 213.44 |
| 5 | San Francisco | 1957 | Golden Gate Park | 5.28 | Reverse | 11.02 | 874.72 |
| 6 | Central Calif | 1960 | Hollister City Hall | 5 | strike slip | 9.02 | 198.77 |
| 7 | Northern Calif | 1960 | Ferndale City Hall | 5.7 | strike slip | 57.21 | 219.31 |
| 8 | Hollister | 1961 | Hollister City Hall | 5.6 | strike slip | 19.56 | 198.77 |
| 9 | Lytle Creek | 1970 | Castaic-Old Ridge Route | 5.33 | Reverse Oblique | 103.39 | 450.28 |
| 10 | Lytle Creek | 1970 | Cedar Springs Pumphouse | 5.33 | Reverse Oblique | 22.94 | 477.22 |
| 11 | Lytle Creek | 1970 | Cedar Springs_Allen Ranch | 5.33 | Reverse Oblique | 19.35 | 813.48 |
| 12 | Lytle Creek | 1970 | LA-Hollywood Stor FF | 5.33 | Reverse Oblique | 73.67 | 316.46 |
| 13 | Lytle Creek | 1970 | Lake Hughes #1 | 5.33 | Reverse Oblique | 90.42 | 425.34 |
| 14 | Lytle Creek | 1970 | Santa Anita Dam | 5.33 | Reverse Oblique | 42.52 | 667.13 |
| 15 | Lytle Creek | 1970 | Wrightwood-6074 Park Dr | 5.33 | Reverse Oblique | 12.14 | 486 |
| 16 | San Fernando | 1971 | Anza Post Office | 6.61 | Reverse | 173.16 | 360.45 |
| 17 | San Fernando | 1971 | Carbon Canyon Dam | 6.61 | Reverse | 61.79 | 235 |
| 18 | San Fernando | 1971 | Cedar Springs_Allen Ranch | 6.61 | Reverse | 89.72 | 813.48 |
| 19 | San Fernando | 1971 | Cholame-Shandon Array #2 | 6.61 | Reverse | 218.13 | 184.75 |
| 20 | San Fernando | 1971 | Lake Hughes #12 | 6.61 | Reverse | 19.3 | 602.1 |
| 21 | San Fernando | 1971 | Maricopa Array #1 | 6.61 | Reverse | 193.91 | 303.79 |
| 22 | San Fernando | 1971 | Pasadena-CIT Athenaeum | 6.61 | Reverse | 25.47 | 415.13 |
| 23 | San Fernando | 1971 | Pasadena-Old Seismo Lab | 6.61 | Reverse | 21.5 | 969.07 |
| 24 | San Fernando | 1971 | San Diego Gas and Electric | 6.61 | Reverse | 205.77 | 354.06 |
| 25 | San Fernando | 1971 | San Juan Capistrano | 6.61 | Reverse | 108.01 | 459.37 |
| 26 | San Fernando | 1971 | San Onofre-So Cal Edison | 6.61 | Reverse | 124.79 | 442.88 |
| 27 | San Fernando | 1971 | Santa Anita Dam | 6.61 | Reverse | 30.7 | 667.13 |
| 28 | San Fernando | 1971 | Castaic-Old Ridge Route | 6.61 | Reverse | 22.63 | 450.28 |
| 29 | San Fernando | 1971 | Bakersfield-Harvey Aud | 6.61 | Reverse | 113.02 | 241.41 |
| 30 | San Fernando | 1971 | UCSB-Fluid Mech Lab | 6.61 | Reverse | 124.41 | 322.42 |
References
- Mehta, P.K. Durability of concrete-fifty ages of progress. ACI SP 1991, 126, 1–31. [Google Scholar]
- Li, C.Q.; Melchers, R.E. Time-dependent risk assessment of structural deterioration caused by reinforcement corrosion. ACI Struct. J. 2005, 102, 754–762. [Google Scholar] [CrossRef]
- Council, ASCE Advisory. 2013 Report Card for America’s Infrastructure; Reston Va American Society of Civil Engineers: Reston, VA, USA, 2013; pp. 1–4. [Google Scholar]
- Qeshta, I.M.; Hashemi, M.J.; Gravina, R.; Setunge, S. Review of resilience assessment of coastal bridges to extreme wave-induced loads. Eng. Struct. 2019, 185, 332–352. [Google Scholar] [CrossRef]
- Dong, Y.; Frangopol, D.M. Performance-based seismic assessment of conventional and base-isolated steel buildings including environmental impact and resilience. Earthq. Eng. Struct. Dyn. 2016, 45, 739–756. [Google Scholar] [CrossRef]
- Dong, Y.; Frangopol, D.M. Probabilistic life-cycle cost-benefit analysis of portfolios of buildings under flood hazard. Eng. Struct. 2017, 142, 290–299. [Google Scholar] [CrossRef]
- Frangopol, D.M.; Dong, Y.; Sabatino, S. Bridge life-cycle performance and cost: Analysis, prediction, optimisation and decision-making. Struct. Infrastruct. Eng. 2017, 13, 1239–1257. [Google Scholar] [CrossRef]
- Chandrasekaran, S.; Banerjee, S. Retrofit optimization for resilience enhancement of bridges under multihazard scenario. J. Struct. Eng. 2016, 142, C4015012. [Google Scholar] [CrossRef]
- Gidaris, I.; Padgett, J.E.; Barbosa, A.R.; Chen, S.; Cox, D.; Webb, B.; Cerato, A. Multiple-hazard fragility and restoration models of highway bridges for regional risk and resilience assessment in the United States: State-of-the-art review. J. Struct. Eng. 2017, 143, 04016188. [Google Scholar] [CrossRef]
- Pang, Y.; Wang, X. Enhanced endurance-time-method (EETM) for efficient seismic fragility, risk and resilience assessment of structures. Soil Dyn. Earthq. Eng. 2021, 147, 106731. [Google Scholar] [CrossRef]
- Bocchini, P.; Frangopol, D.M. A stochastic computational framework for the joint transportation network fragility analysis and traffic flow distribution under extreme events. Probabilistic Eng. Mech. 2011, 26, 182–193. [Google Scholar] [CrossRef]
- Shafieezadeh, A.; Burden, L.I. Scenario-based resilience assessment framework for critical infrastructure systems: Case study for seismic resilience of seaports. Reliab. Eng. Syst. Saf. 2014, 132, 207–219. [Google Scholar] [CrossRef]
- Kazmi, S.Q.A.; Naqvi, S.A.A.; Hussain, E.; Ahmed, S. Resilience Assessment Framework for an Urban Road Network Subjected to Disruptions. KSCE J. Civ. Eng. 2023, 27, 5350–5361. [Google Scholar] [CrossRef]
- Vishwanath, B.S.; Banerjee, S. Life-Cycle Resilience of Aging Bridges under Earthquakes. J. Bridge Eng. 2019, 24, 04019106. [Google Scholar] [CrossRef]
- Pang, Y.; Wei, K.; He, H.; Wang, W. Assessment of lifetime seismic resilience of a long-span cable-stayed bridge exposed to structural corrosion. Soil Dyn. Earthq. Eng. 2022, 157, 107275. [Google Scholar] [CrossRef]
- Motlagh, Z.S.; Dehkordi, M.R.; Eghbali, M.; Samadian, D. Evaluation of seismic resilience index for typical RC school buildings considering carbonate corrosion effects. Int. J. Disaster Risk Reduct. 2020, 46, 101511. [Google Scholar] [CrossRef]
- Dong, Y.; Frangopol, D.M.; Saydam, D. Time-variant sustainability assessment of seismically vulnerable bridges subjected to multiple hazards. Earthq. Eng. Struct. Dyn. 2013, 42, 1451–1467. [Google Scholar] [CrossRef]
- Biondini, F.; Camnasio, E.; Titi, A. Seismic resilience of concrete structures under corrosion. Earthq. Eng. Struct. Dyn. 2015, 44, 2445–2466. [Google Scholar] [CrossRef]
- Nettis, A.; Nettis, A.; Ruggieri, S.; Uva, G. Corrosion-induced fragility of existing prestressed concrete girder bridges under traffic loads. Eng. Struct. 2024, 314, 118302. [Google Scholar] [CrossRef]
- Alipour, A.; Shafei, B.; Shinozuka, M. Performance evaluation of deteriorating highway bridges located in high seismic areas. J. Bridge Eng. 2011, 16, 597–611. [Google Scholar] [CrossRef]
- Ghosh, J.; Padgett, J.E. Aging considerations in the development of time-dependent seismic fragility curves. J. Struct. Eng. 2010, 136, 1497–1511. [Google Scholar] [CrossRef]
- Szweda, Z.; Gołaszewski, J.; Ghosh, P.; Lehner, P.; Konečný, P. Comparison of Standardized Methods for Determining the Diffusion Coefficient of Chloride in Concrete with Thermodynamic Model of Migration. Materials 2023, 16, 637. [Google Scholar] [CrossRef]
- Bertolini, L. Steel corrosion and service life of reinforced concrete structures. Struct. Infrastruct. Eng. 2008, 4, 123–137. [Google Scholar] [CrossRef]
- Collepardi, M.; Marcialis, A.; Turriziani, R. Penetration of chloride ions into cement pastes and concretes. J. Am. Ceram. Soc. 1972, 55, 534–535. [Google Scholar] [CrossRef]
- DuraCrete. Modelling of Degradation, DuraCrete-Probabilistic Performance Based Durability Design of Concrete Structures; EU-Brite EuRam III, Contract BRPR-CT95–0132, Project BE95–1347/R4–5; Civieltechnisch Centrum Uitvoering Research: Gouda, The Netherlands, 1998. [Google Scholar]
- DuraCrete. Statistical Quantification of the Variables in the Limit State Functions, DuraCrete-Probabilistic Performance Based Durability Design of Concrete Structures; EU-Brite EuRam III, Contract BRPR-CT95–0132, Project BE95–1347/R9; Civieltechnisch Centrum Uitvoering Research: Gouda, The Netherlands, 2000. [Google Scholar]
- Du, Y.G.; Clark, L.A.; Chan, A.H.C. Residual capacity of corroded reinforcing bars. Mag. Concr. Res. 2005, 57, 135–147. [Google Scholar] [CrossRef]
- Karim, K.R.; Yamazaki, F. A simplified method of constructing fragility curves for highway bridges. Earthq. Eng. Struct. Dyn. 2003, 32, 1603–1626. [Google Scholar] [CrossRef]
- Sfahani, M.G.; Guan, H. An extended cloud analysis method for seismic fragility assessment of highway bridges. Earthq. Struct. 2018, 15, 605–616. [Google Scholar] [CrossRef]
- Yu, X.H.; Lv, D.G. Probabilistic seismic demand analysis and seismic fragility analysis based on a cloud-stripe method. Eng. Mech. 2016, 33, 68–76. [Google Scholar]
- Cornell, C.A.; Jalayer, F.; Hamburger, R.O.; Foutch, D.A. Probabilistic basis for 2000 sac federal emergency management agency steel moment frame guidelines. J. Struct. Eng. 2002, 128, 526–533. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency (FEMA), The Department of Homeland Security (DHS). Multi-hazard loss estimation methodology earthquake model. In HAZUS®MH MR4 Technical Manual; National Institute of Building Sciences: Washington, DC, USA, 2003. [Google Scholar]
- Choi, E.; DesRoches, R.; Nielson, B. Seismic fragility of typical bridges in moderate seismic zones. Eng. Struct. 2004, 26, 187–199. [Google Scholar] [CrossRef]
- Nielson, B.G.; DesRoches, R. Seismic fragility methodology for highway bridges using a component level approach. Earthq. Eng. Struct. Dyn. 2007, 36, 823–839. [Google Scholar] [CrossRef]
- Lu, J.; Li, Z.; Teng, J. Seismic Resilience Evaluation of High-Rise Frame-Core Tube Structure Considering Structural Network Performance Loss and Repair Path. Buildings 2025, 15, 23. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency (FEMA), The Department of Homeland Security (DHS). Multi-hazard loss estimation methodology earthquake model. In HAZUS®MH 2.1 Technical Manual; National Institute of Building Sciences: Washington, DC, USA, 2012. [Google Scholar]
- Werner, S.D.; Taylor, C.E.; Cho, S.; Lavoie, J.P.; Huyck, C.K.; Eitzel, C.; Eguchi, R.T. REDARS 2 Methodology and Software for Seismic Risk Analysis of Highway Systems (MCEER-06-SP08); Multidisciplinary Center for Earthquake Engineering Research: Buffalo, NY, USA, 2006. [Google Scholar]
- Applied Technology Council. Earthquake Damage Evaluation Data for California, ATC-13; Applied Technology Council: Redwood City, CA, USA, 1999. [Google Scholar]
- Federal Emergency Management Agency (FEMA), The Department of Homeland Security (DHS). Multi-hazard loss estimation methodology earthquake model. In HAZUS®MH MR5 Technical Manual; National Institute of Building Sciences: Washington, DC, USA, 2011. [Google Scholar]
- Cimellaro, G.P.; Reinhorn, A.M.; Bruneau, M. Seismic resilience of a hospital system. Struct. Infrastruct. Eng. 2010, 6, 127–144. [Google Scholar] [CrossRef]
- Camnasio, E. Lifetime Performance and Seismic Resilience of Concrete Structures Exposed to Corrosion. Ph.D. Thesis, Politecnico di Milano, Milan, Italy, 2013. [Google Scholar]
- Zheng, Y.; Dong, Y.; Li, Y. Resilience and life-cycle performance of smart bridges with shape memory alloy (SMA)-cable-based bearings. Constr. Build. Mater. 2018, 158, 389–400. [Google Scholar] [CrossRef]
- Dong, Y.; Frangopol, D.M. Risk and resilience assessment of bridges under mainshock and aftershocks incorporating uncertainties. Eng. Struct. 2015, 83, 198–208. [Google Scholar] [CrossRef]
- Dassault Systèmes. ABAQUS Theory Manual, Version 6.16. Software Documentation. Dassault Systèmes: Providence, RI, USA, 2016.
- Mander, J.B. Seismic Design of Bridge Columns; University of Canterbury: Christchurch, New Zealand, 1983. [Google Scholar]
- AASHTO. Guide Specification for Seismic Isolation Design, 4th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2014. [Google Scholar]
- Li, H.N.; Li, C. Research progress on life-cycle based bridge structural seismic performance evaluation and design method. China J. Highw. Transp. 2014, 27, 32–45. [Google Scholar] [CrossRef]
- Pacific Earthquake Engineering Research Center. PEER Ground Motion Database-PEER Center. Available online: https://ngawest2.berkeley.edu/ (accessed on 3 March 2024).
- Calderone, A.J.; Lehman, D.E.; Moehle, J.P. Behavior of Reinforced Concrete Bridge Columns Having Varying Aspect Ratios and Varying Lengths of Confinement; PEER 2000/08; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2000. [Google Scholar]




| Parameters | Notation | Mean | CV | Distribution |
|---|---|---|---|---|
| Recovery time increasing ratio | θt | 1.6 b | N/A | N/A |
| Unit reconstruction cost per square meter for piers (USD/m2) | c1 | 100,000 b | 0.2 | LN b |
| Unit refurbishment cost for an individual isolation bearing (USD) | c2 | 10,000 b | 0.2 | LN b |
| The ratio of maintenance costs for the j-th damage state | βj | N/A | N/A | N/A |
| The cross-sectional area of the i-th pier element | Ai | N/A | N/A | N/A |
| The probability of the j-th damage state of the i-th pier element at a specified IM | Pi,j | N/A | N/A | N/A |
| The probability of the j-th damage state of the kth bearing element at a given IM | Pk,j | N/A | N/A | N/A |
| The total number of bearing units | m | N/A | N/A | N/A |
| The total number of pier units | n | N/A | N/A | N/A |
| The cost-augmenting factor of the i-th pier element | θc | 2.2 b | N/A | N/A |
| Duration of chloride ion exposure (years) | ŋ | N/A | N/A | N/A |
| The growth rate of chloride ion erosion repair costs | λc | 1.3 b | N/A | N/A |
| Mean daily traffic | MDT | 19,750 c | N/A | N/A |
| Daily truck traffic ratio | T | 0.13 c | N/A | N/A |
| Length of detour distance (km) | Ld | 2 c | N/A | N/A |
| Length of the transport link incorporating the bridge (km) | Ll | 6 c | N/A | N/A |
| Freight load factor for haulage vehicles | otruck | 1.05 c | N/A | N/A |
| Cost of ownership for private passenger vehicles (USD/km) | ccar | 0.4 a | 0.2 | LN a |
| Passenger car occupancy rate | ocar | 1.5 c | N/A | N/A |
| Monetary remuneration for car drivers (USD/h) | cscd | 11.91 a | 0.3 | LN a |
| Monetary remuneration for truck drivers (USD/h) | cstd | 29.87 a | 0.3 | LN a |
| Mean travel speed on the deviated route (km/h) | Sde | 50 a | 0.2 | LN a |
| Benchmark operating speed on the unimpaired link (km/h) | S0 | 80 a | 0.2 | LN a |
| Cost of ownership for commercial trucking operations (USD/km) | ctruck | 0.57 a | 0.2 | LN a |
| Mean travel speed on the degraded segment (km/h) | Sda | 65 b | 0.2 | LN b |
| Pre-Yield Stiffness (kN/m) | Equivalent Stiffness (kN/m) | Post-Yield Stiffness (kN/m) | Yield Force (kN) |
|---|---|---|---|
| 21,800 | 4500 | 3400 | 200 |
| Component | Damage Index | No Damage | Slight Damage | Moderate Damage | Major Damage | Complete Damage |
|---|---|---|---|---|---|---|
| Pier | Drift ratio θc | 0~0.007 | 0.007~0.015 | 0.015~0.025 | 0.025~0.05 | >0.05 |
| Bearing | Displacement δ (mm) | 0~25 | 25~50 | 50~100 | 100~150 | >150 |
| Component | Years | a | b | χ2 | R2 |
|---|---|---|---|---|---|
| Pier | 0 | −4.503 | 0.871 | 0.0216 | 0.9967 |
| 10 | −4.281 | 0.801 | 0.0252 | 0.9954 | |
| 20 | −4.131 | 0.747 | 0.0331 | 0.9931 | |
| 30 | −4.046 | 0.644 | 0.0201 | 0.9944 | |
| 40 | −3.839 | 0.616 | 0.0123 | 0.9962 | |
| 50 | −3.669 | 0.588 | 0.0133 | 0.9953 | |
| 60 | −3.398 | 0.521 | 0.0161 | 0.9932 | |
| Bearing | 0 | 4.813 | 1.271 | 0.109 | 0.9922 |
| 10 | 5.028 | 1.244 | 0.0546 | 0.9959 | |
| 20 | 5.106 | 1.225 | 0.0448 | 0.9965 | |
| 30 | 5.146 | 1.147 | 0.0436 | 0.9961 | |
| 40 | 5.203 | 1.133 | 0.0551 | 0.9950 | |
| 50 | 5.257 | 1.131 | 0.0491 | 0.9955 | |
| 60 | 5.314 | 1.113 | 0.0468 | 0.9956 |
| Years | Pier Drift Ratio (%) | LRB Horizontal Displacement (mm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.3 g | 0.6 g | 0.9 g | 1.2 g | 1.5 g | 0.3 g | 0.6 g | 0.9 g | 1.2 g | 1.5 g | |
| 0 | 0.375 | 0.681 | 1.018 | 1.368 | 1.612 | 21 | 60 | 109 | 152 | 183 |
| 10 | 0.407 | 0.750 | 1.097 | 1.468 | 1.736 | 26 | 67 | 117 | 157 | 192 |
| 20 | 0.493 | 0.845 | 1.190 | 1.553 | 1.814 | 28 | 70 | 121 | 160 | 199 |
| 30 | 0.536 | 0.889 | 1.240 | 1.620 | 1.916 | 32 | 75 | 126 | 163 | 203 |
| 40 | 0.687 | 1.055 | 1.447 | 1.862 | 2.028 | 33 | 77 | 130 | 168 | 209 |
| 50 | 0.814 | 1.259 | 1.698 | 2.120 | 2.344 | 34 | 79 | 132 | 171 | 214 |
| 60 | 1.032 | 1.520 | 1.956 | 2.404 | 2.622 | 37 | 83 | 135 | 177 | 221 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, G.; Yao, G.; Jia, H.; Zheng, S.; Yao, Y. Lifecycle Assessment of Seismic Resilience and Economic Losses for Continuous Girder Bridges in Chloride-Induced Corrosion. Buildings 2025, 15, 3315. https://doi.org/10.3390/buildings15183315
Peng G, Yao G, Jia H, Zheng S, Yao Y. Lifecycle Assessment of Seismic Resilience and Economic Losses for Continuous Girder Bridges in Chloride-Induced Corrosion. Buildings. 2025; 15(18):3315. https://doi.org/10.3390/buildings15183315
Chicago/Turabian StylePeng, Ganghui, Guowen Yao, Hongyu Jia, Shixiong Zheng, and Yun Yao. 2025. "Lifecycle Assessment of Seismic Resilience and Economic Losses for Continuous Girder Bridges in Chloride-Induced Corrosion" Buildings 15, no. 18: 3315. https://doi.org/10.3390/buildings15183315
APA StylePeng, G., Yao, G., Jia, H., Zheng, S., & Yao, Y. (2025). Lifecycle Assessment of Seismic Resilience and Economic Losses for Continuous Girder Bridges in Chloride-Induced Corrosion. Buildings, 15(18), 3315. https://doi.org/10.3390/buildings15183315







