Modeling the Fire Response of Reactive Powder Concrete Columns with Due Consideration of Transient Thermal Strain
Abstract
1. Introduction
2. FE Analysis
2.1. Material Properties
2.2. Temperature Field Model
2.2.1. Principle of Heat Transfer
- 1.
- Initial conditions
- 2.
- Boundary conditions
- The temperature function of the component surface is known;
- The heat flux density function on the component surface is known;
- The fluid temperature, thermal conductivity and radiation coefficient on the surface of the component are known.
- The heat transfer conditions at the contact surfaces between objects are known.
2.2.2. Temperature Field Calculation Model
- (1)
- Column Geometry and Model Setup
- (2)
- Reinforcement–Concrete Interaction
- (3)
- Mesh Size and Convergence Analysis
- (4)
- Element Types
- (5)
- Thermal Analysis Settings
- (6)
- Fire Exposure and Boundary Conditions
- (7)
- Fire Exposure Configuration
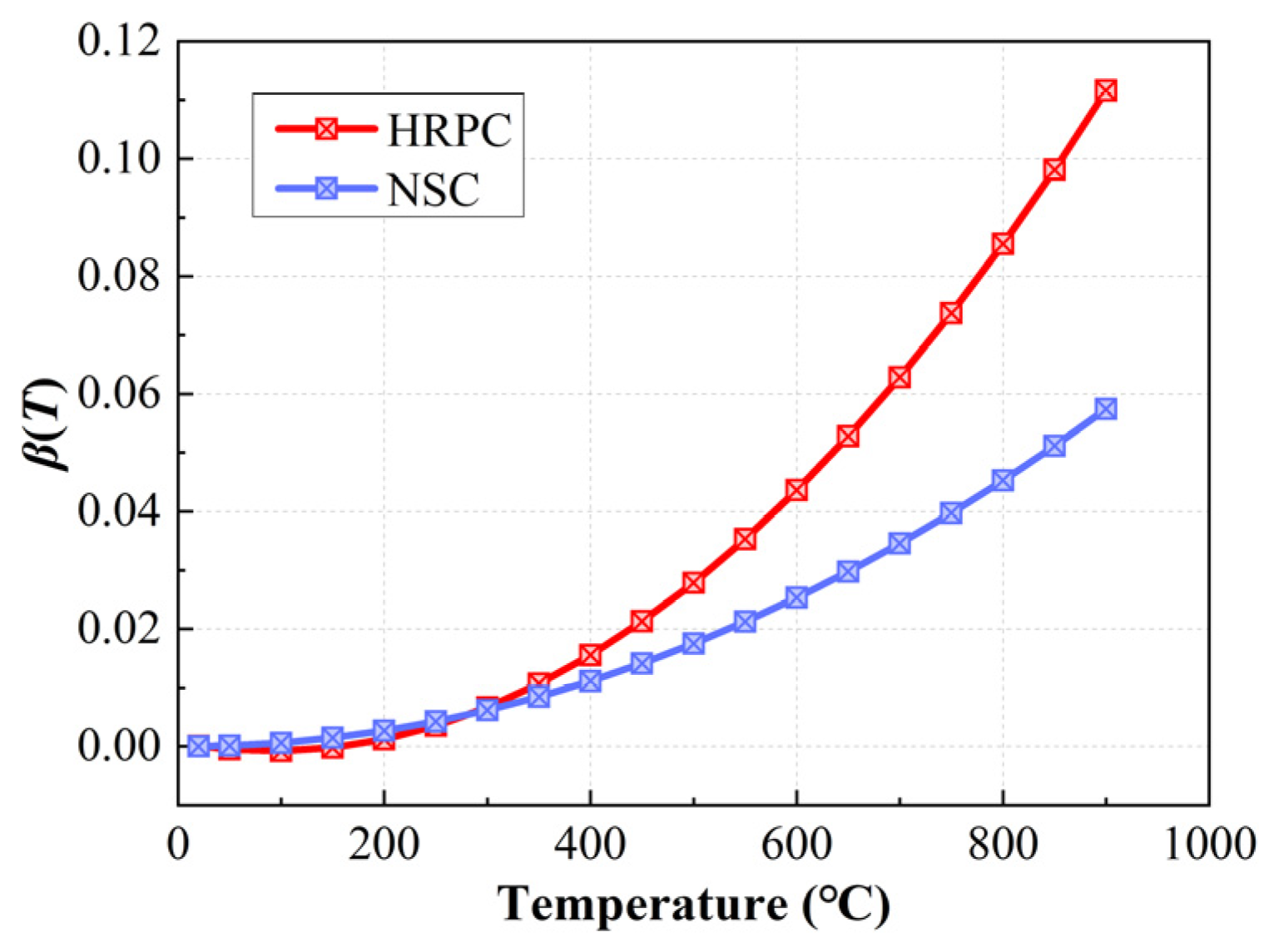
2.3. TS of RPC
2.4. RPC FE Model Considering TS
2.5. Thermal–Mechanical Coupling Model of RPC Column
2.6. Model Validation
2.6.1. Verification of NC Column
2.6.2. Verification of UHSC Columns
2.6.3. RPC Material Constitutive Verification
3. Effect of TS on Fire Resistance of RPC Columns
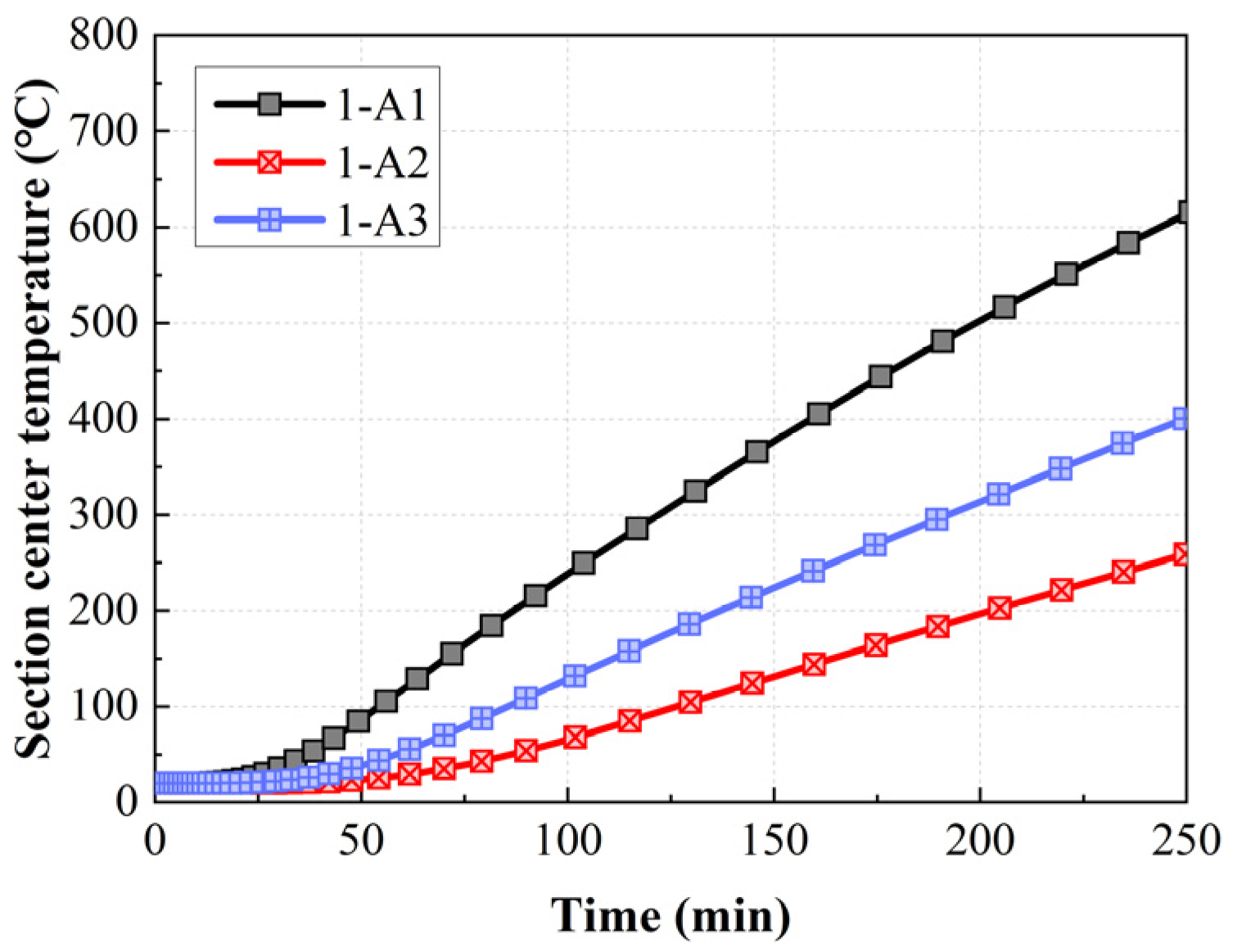
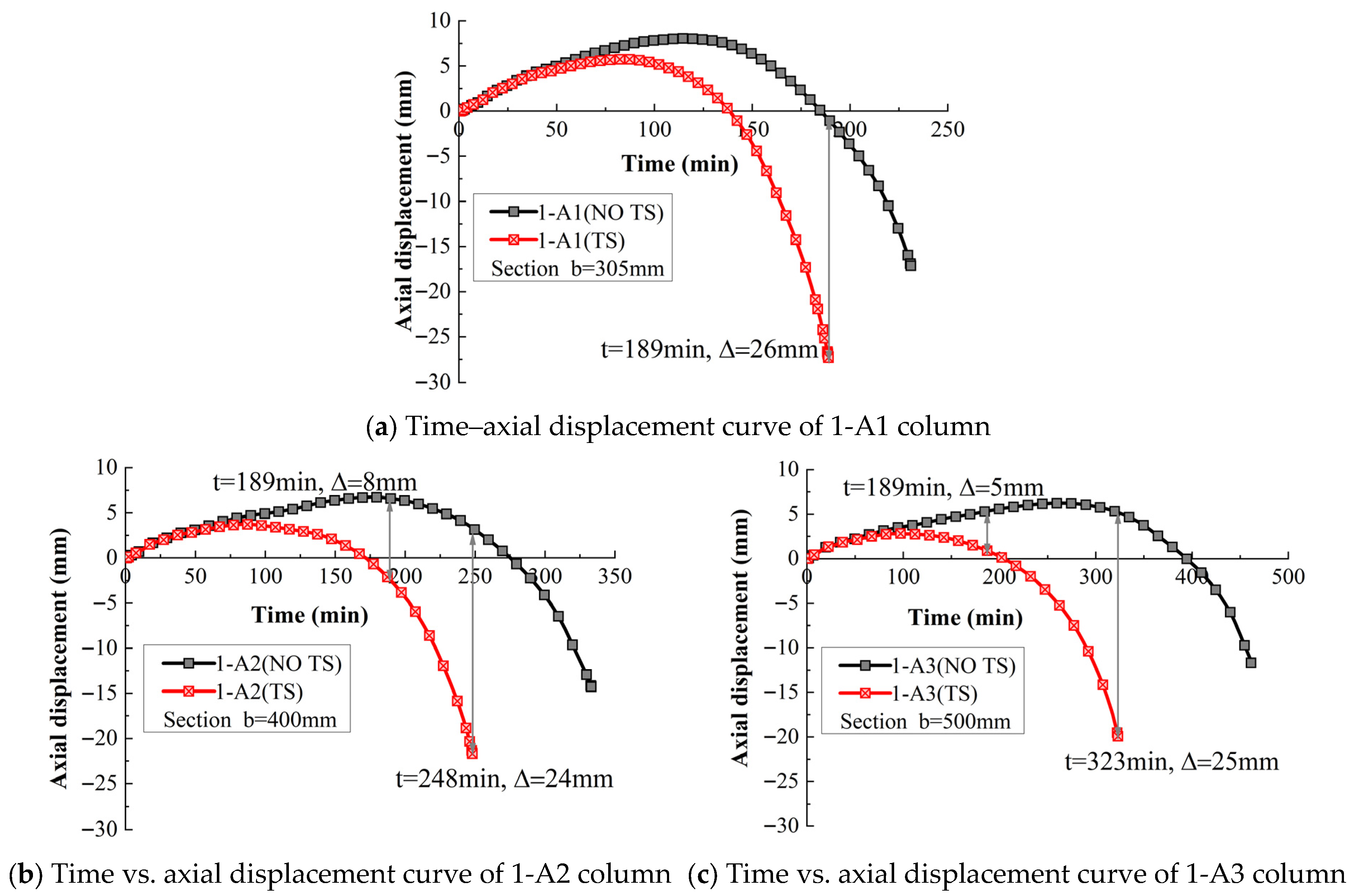
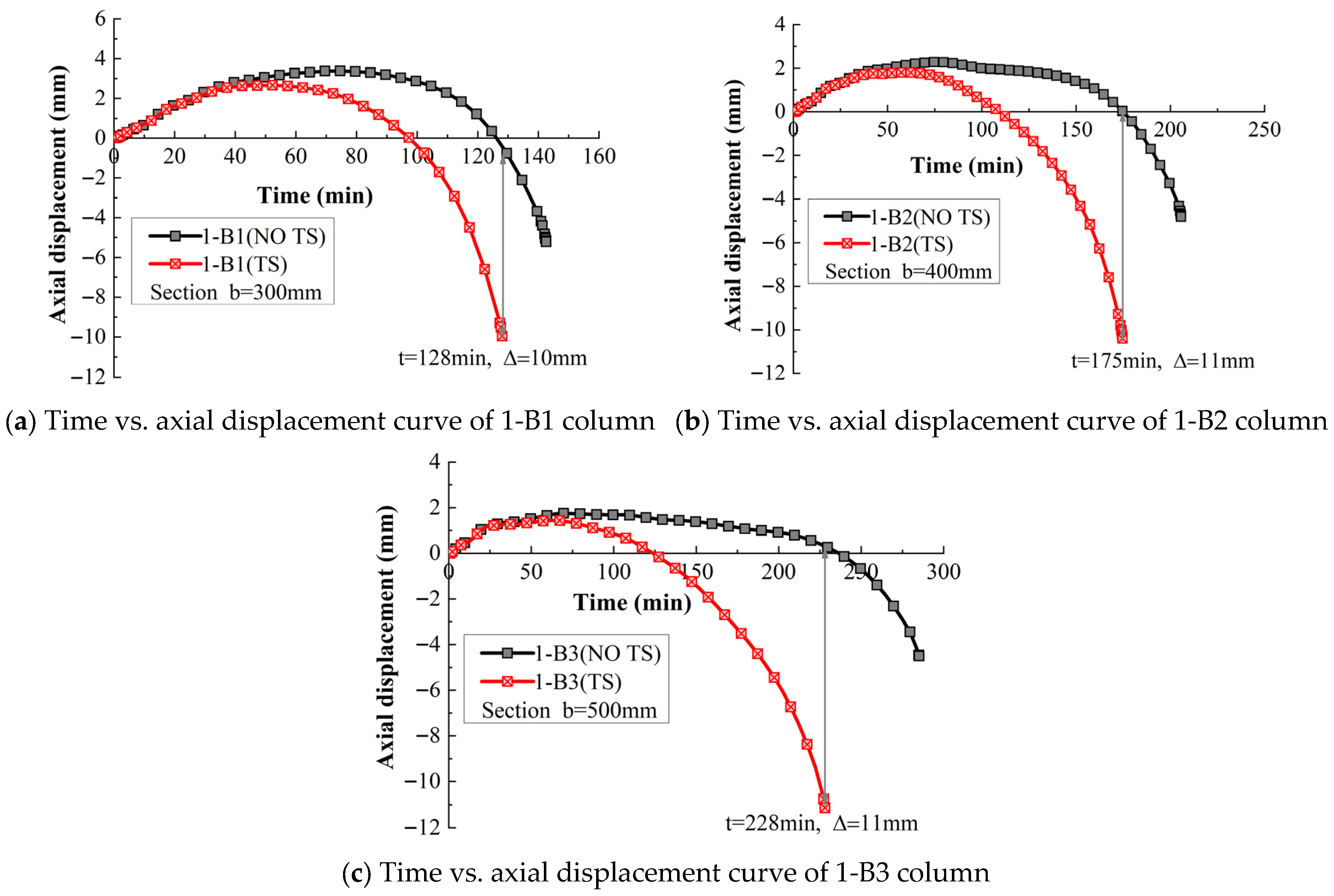
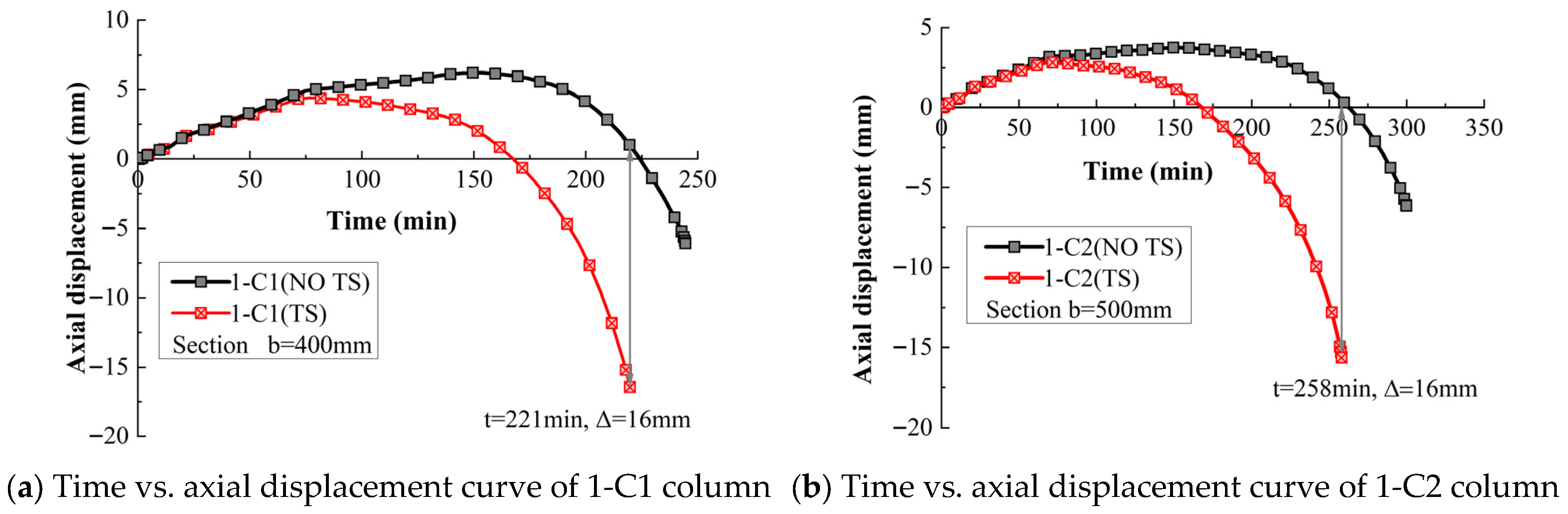
3.1. Effect of Section Size
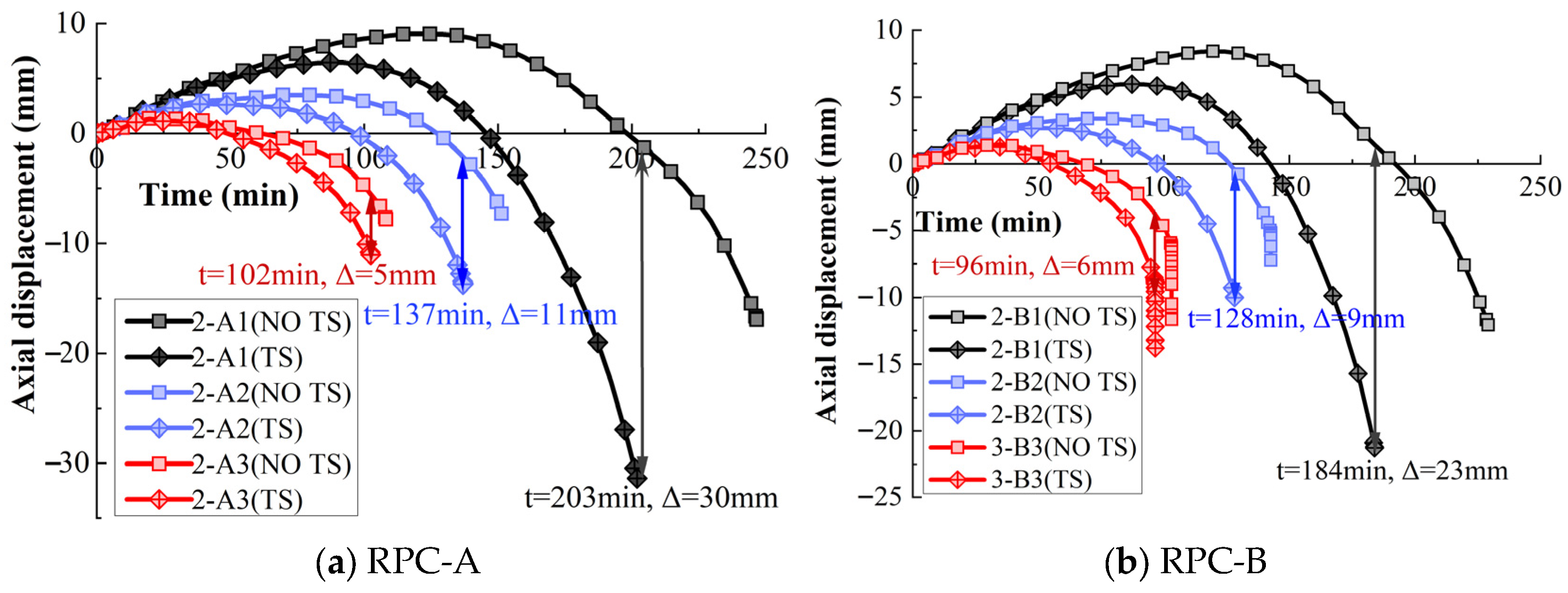
3.2. Effect of Load Level
- When the RPC column reaches fire resistance, although the temperature outside the RPC section is very high, the temperature of about 53% of the core area of the RPC section is lower than 600 °C, and the RPC TS of the low-temperature part has not been fully developed;
- The TS calculation model used in this study is mainly related to stress and temperature. The TS of RPC is proportional to the stress level and increases exponentially with the increase in temperature. The unit stress TS value [40] of RPC and NC was introduced, as expressed in Equation (16).
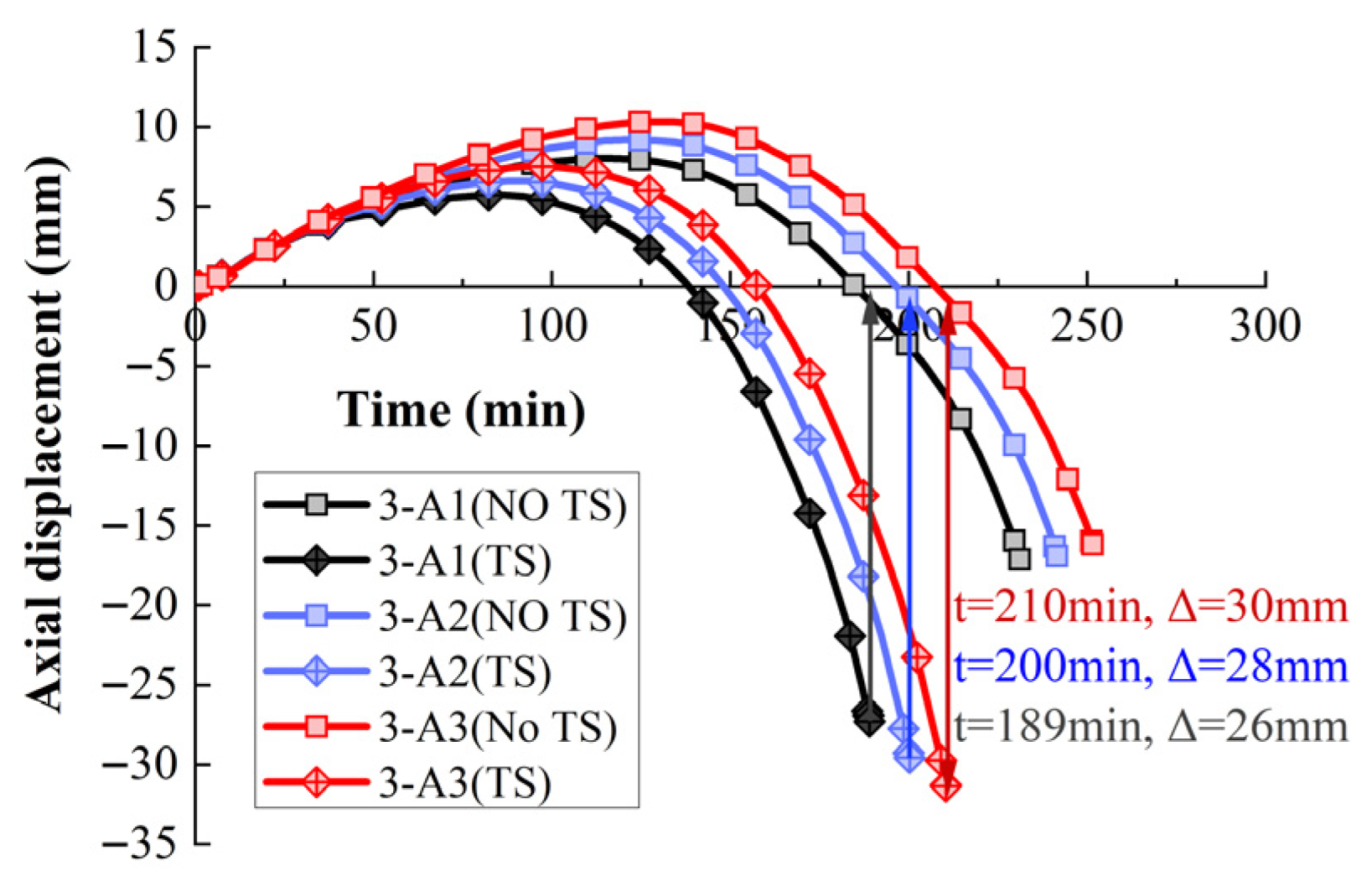
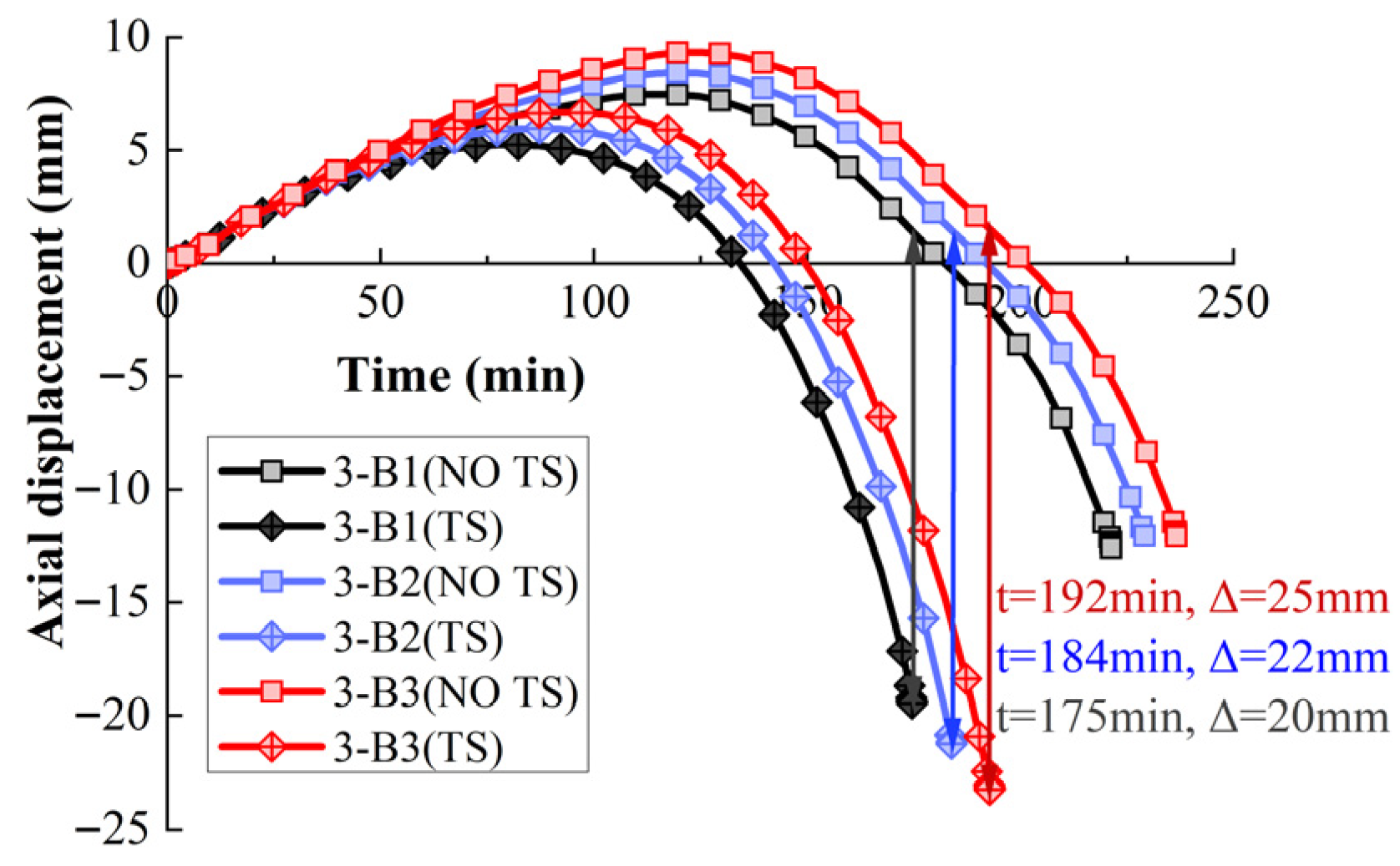
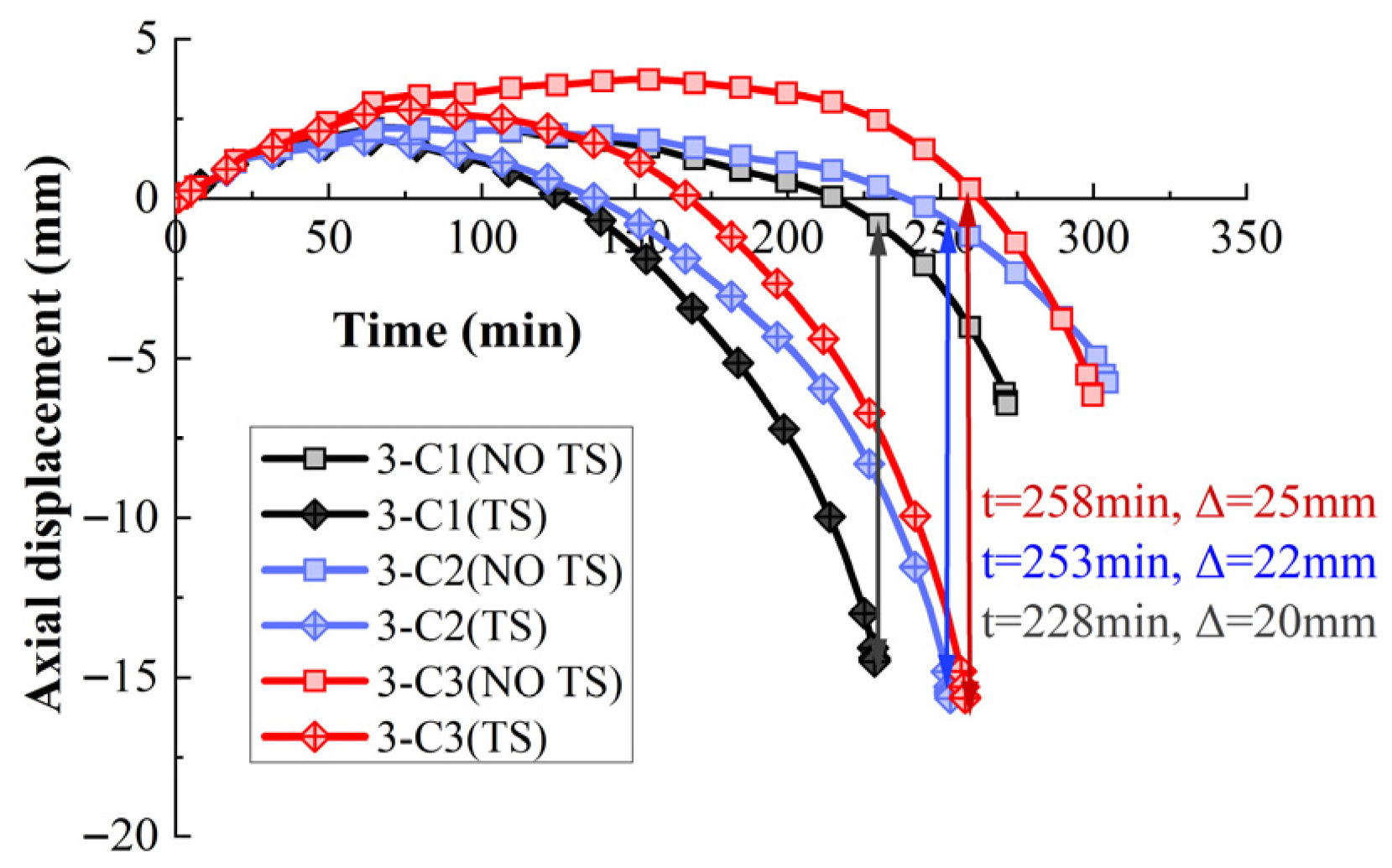
3.3. Effect of Reinforcement Ratio
3.4. Effect of Fire Conditions
3.5. Effect of Fire Side of RPC Columns
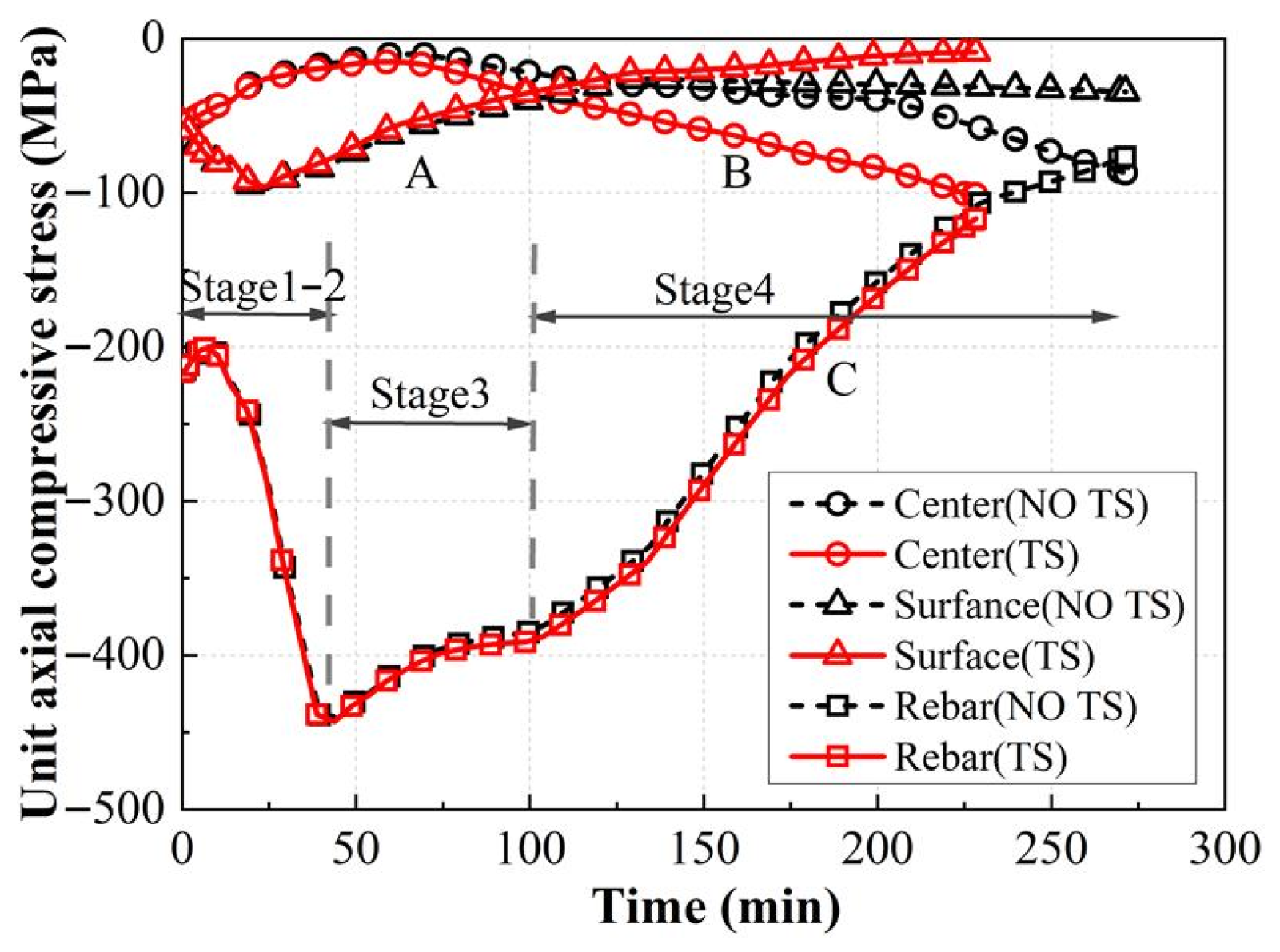
3.6. Effect of TS on Stress Redistribution
3.7. The Difference in Fire Resistance Between RPC Column and NC Column
4. Discussion
5. Conclusions
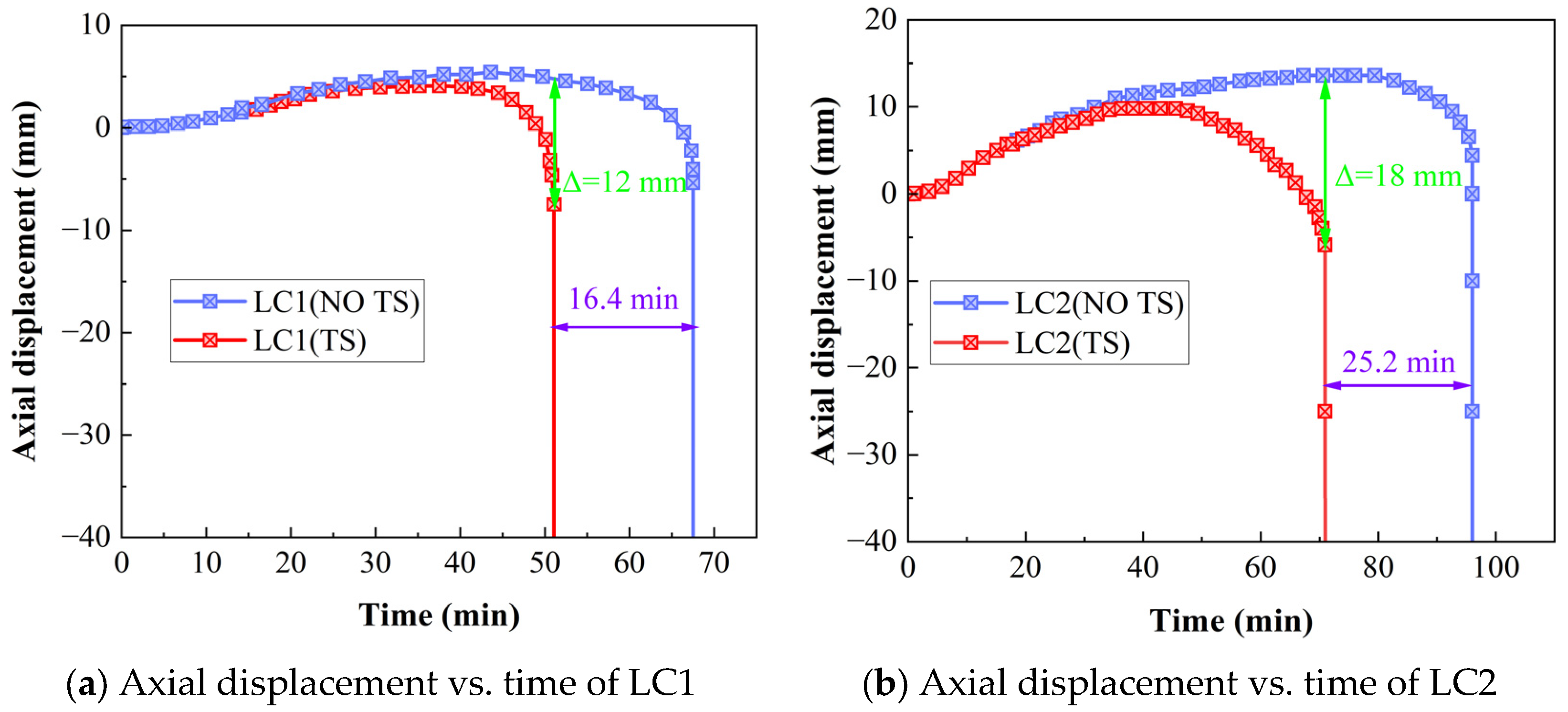
- The fire resistance of RPC columns and the influence of TS increase with the increase in cross-sectional dimensions. When the cross-sectional size increases from 305 mm to 500 mm, the influence of TS on the fire resistance limit of RPC columns rises from 22% to 43%. If the influence of TS is ignored, the maximum axial deformation error of the RPC column reaches 26 mm. Therefore, in the fire resistance design of large cross-section RPC columns, the influence of TS should be taken into account;
- When the exposure time is short, due to the more uniform cross-sectional temperature of the RPC column and the smaller temperature gradient, the influence of TS on the RPC column is lower than that on the NC column. When exposed to fire for a long time, the internal temperature of the RPC column cross-section fully develops, and TS begins to significantly affect the fire resistance performance of the RPC column. At this time, the influence of TS on the RPC column is greater than that on the NC column;
- The influence of TS on RPC columns is greater than that on NC columns. Under the same load, the impact of TS on the fire resistance performance of RPC columns is 26.2% and that on NC columns is 24.3%. If the influence of TS is not taken into account, it will lead to an overestimation of the axial deformation of the RPC column, with an axial deformation error of up to 18 mm;
- The presence of TS causes the RPC stress in the low-temperature area of the RPC column to increase under fire, while the stress of the reinforcing bars does not change significantly, resulting in a large stress gradient in the cross-section and accelerating the failure process of the RPC column;
- Under the temperature rise curves of ASTM E119, ISO 834, and hydrocarbon, respectively, the influence of TS on the fire resistance limit of RPC columns is 22%, 10.5%, and 38%. It can be seen that, under the hydrocarbon temperature rise curve, TS has the greatest impact on the fire resistance performance of RPC columns. Therefore, when designing RPC columns for high fire risk buildings such as chemical plants, the TS effect must be fully considered to ensure fire safety.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Richard, P.; Cheyrezy, M. Composition of reactive powder concretes. Cem. Concr. Res. 1995, 25, 1501–1511. [Google Scholar] [CrossRef]
- Cheyrezy, M. Structural applications of RPC. Concrete 1999, 33, 20–23. [Google Scholar]
- Pierre, Y.B.; Marco, C.R. Prestresses Pedestrian Bridge-World’s First Reactive Powder Concrete Structure. PCI J. 1999, 44, 60–71. [Google Scholar] [CrossRef]
- Zheng, W.; Wang, R.; Wang, Y. Experimental study on thermal parameter of reactive powder concrete. J. Build. Struct. 2014, 35, 107–114. (In Chinese) [Google Scholar] [CrossRef]
- Luo, B. Study on Explosive Spalling Rules and Mechanical Properties of Reactive Powder Concrete at Elevated Temperatures. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2013. (In Chinese). [Google Scholar]
- Ge, C. Effect of Pore Pressure and Fire Surface on High Temperature Burst of RPC. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2019. (In Chinese). [Google Scholar]
- Zheng, W.; Luo, B.; Wang, Y. Microstructure and mechanical properties of RPC containing PP fibres at elevated temperatures. Mag. Concr. Res. 2014, 66, 397–408. [Google Scholar] [CrossRef]
- Zheng, W.; Luo, B.; Wang, Y. Compressive and tensile properties of reactive powder concrete with steel fibres at elevated temperatures. Constr. Build. Mater. 2013, 41, 844–851. [Google Scholar] [CrossRef]
- Illston, J.M.; Sander, P.D. The effect of temperature change upon the creep of tortar under torsional loading. Mag. Concr. Res. 1973, 25, 136–144. [Google Scholar] [CrossRef]
- Anderberg, Y.; Thelandersson, S. Stress and deformation characteristics of concrete at high temperatures. 2. Experimental investigation and material behaviour model. Bull. Div. Struct. Mech. Concr. Constr. Bull. 1976, 54, 27–34. [Google Scholar]
- Schneider, U. Modelling of concrete behavior at high temperature. In Design of Structures Against Fire; Aston University Birmingham: Birmingham, UK, 1986; pp. 53–69. [Google Scholar]
- Wu, B.; Siulhu, L.; Liu, Q.; Chung, Y.; Ho, F. Creep Behavior of High-Strength Concrete with olypropylene Fibers at Elevated Temperatures. ACI Mater. J. 2010, 107, 176. [Google Scholar]
- Sanchayan, S.; Foster, S.J. High temperature behavior of hybrid steel-PVA fibre reinforced reactive powder concrete. Mater. Struct. 2016, 49, 769–782. [Google Scholar] [CrossRef]
- Abid, M.; Hou, X.; Zheng, W.; Hussain, R.R.; Cao, S.; Lv, Z. Creep behavior of steel fiber reinforced reactive powder concrete at high temperature. Constr. Build. Mater. 2019, 205, 321–331. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, H.; Zhu, H.; Wang, X.; Li, A. Research on Fire Resistance of Reinforced Concrete Columns with Different Curing Period. Struct. Eng. 2020, 36, 5. (In Chinese) [Google Scholar] [CrossRef]
- Kodur, V.K.R.; Cheng, F.P.; Wang, T.C.; Sultan, M.A. Effect of Strength and Fiber Reinforcement on Fire Resistance of High-Strength Concrete Columns. J. Struct. Eng. 2003, 129, 253–259. [Google Scholar] [CrossRef]
- Lee, J.H.; Sohn, Y.S.; Lee, S.H. Fire resistance of hybrid fibre-reinforced, ultra-high-strength concrete columns with compressive strength from 120 to 200 MPa. Mag. Concr. Res. 2012, 64, 539–550. [Google Scholar] [CrossRef]
- Choe, G.; Kim, G.; Gucunski, N.; Lee, S. Evaluation of the mechanical properties of 200 MPa ultra-high-strength concrete at elevated temperatures and residual strength of column. Constr. Build. Mater. 2015, 86, 159–168. [Google Scholar] [CrossRef]
- ISO 834; Fire-Resistance Tests-Elements of Building Construction. International Organization for Standardization: Geneva, Switzerland, 1975.
- Li, Y.; Du, P.; Tan, K.H. Fire resistance of ultra-high performance concrete columns subjected to axial and eccentric loading. Eng. Struct. 2021, 248, 113158. [Google Scholar] [CrossRef]
- Wu, B.; Xu, Y. Fire resistance of reinfoced concrete columns with +-Shaped cross section. Eng. Mech. 2008, 25, 3. [Google Scholar]
- Wu, B.; Chen, H. Analysis of Fire Endurance of Reinforced Concrete Columns with Sideway. J. Disaster Prev. Mitig. Eng. 2017, 37, 5. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, Y.; Yuan, G.; Wang, Y. Fire Response Analysis of Reinforced Concrete Slabs Considering Transient Strain. J. Hunan Univ. (Nat. Sci.) 2014, 41, 6. (In Chinese) [Google Scholar]
- Wei, Y.; Au, F.T.; Li, J.; Tsang, N.C. Effects of transient creep strain on post-tensioned concrete slabs in fire. Mag. Concr. Res. 2017, 69, 337–346. [Google Scholar] [CrossRef]
- Sadaoui, A.; Khennane, A. Effect of transient creep on the behaviour of reinforced concrete columns in fire. Eng. Struct. 2009, 31, 2203–2208. [Google Scholar] [CrossRef]
- Kodur, V.K.R.; Alogla, S.M. Effect of high-temperature transient creep on response of reinforced concrete columns in fire. Mater. Struct. 2017, 50, 27. [Google Scholar] [CrossRef]
- Alogla, S.; Kodur, V.K.R. Quantifying transient creep effects on fire response of reinforced concrete columns. Eng. Struct. 2018, 174, 885–895. [Google Scholar] [CrossRef]
- Ren, P.; Hou, X.; Rong, Q.; Zheng, W. Quantifying Fire Insulation Effects on the Fire Response of Hybrid-Fiber Reinforced Reactive Powder Concrete Beams. Fire Technol. 2020, 56, 1487–1525. [Google Scholar] [CrossRef]
- Hou, X.; Ren, P.; Rong, Q.; Zheng, W.; Zhan, Y. Comparative fire behavior of reinforced RPC and NSC simply supported beams. Eng. Struct. 2019, 185, 122–140. [Google Scholar] [CrossRef]
- Kodur, V.K.R.; Wang, T.C.; Cheng, F.P. Predicting the fire resistance behaviour of HSC columns. Cem. Concr. Compos. 2004, 26, 141–153. [Google Scholar] [CrossRef]
- Bo, W.; Zhou, H. Fire resistance of high strength concrete columns. J. South China Univ. Technol. (Nat. Sci. Ed.) 2006, 34, 11. (In Chinese) [Google Scholar]
- Lie, T.T. Fire Resistance of Circular Steel Columns Filled with Bar-Reinforced Concrete. J. Struct. Eng. 1994, 120, 1489–1509. [Google Scholar] [CrossRef]
- European Convention for Constructional Steelwork (ECCS). Technical Committee 3, and Fire safety of Steel Structures. In European Recommendations for the Fire Safety of Steel Structures: Calculation of the Fire Resistance of Load Bearing Elements and Structural Assemblies Exposed to the Standard Fire; Elsevier Science and Technology: Amsterdam, The Netherlands, 1983; Volume 3. [Google Scholar]
- Han, L. Concrete Filled Steel Tubular Structures—Theory and Practice, 3rd ed.; Science Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- ASTM E119-88; Standard Methods of Fire Tests on Building Construction and Materials. American Society for Testing and Materials: Philadelphia, PA, USA, 1990.
- Wang, G.; Xue, S. Calculation on TS of concrete. J. Beijing Univ. Technol. 2008, 34, 387–390. (In Chinese) [Google Scholar]
- BS EN 1992-1-2; Design of Concrete Structures: Part 1-2: General Rules: Structural Fire Design. British Standards Institution: London, UK, 2004.
- Hong, S.; Varma, A.H. Analytical modeling of the standard fire behavior of loaded CFT columns. J. Constr. Steel Res. 2009, 65, 54–69. [Google Scholar] [CrossRef]
- Gernay, T.; Millard, A.; Franssen, J.M. A multiaxial constitutive model for concrete in the fire situation: Theoretical formulation. Int. J. Solids Struct. 2013, 50, 3659–3673. [Google Scholar] [CrossRef]
- Guo, Z.; Shi, X. High Temperature Performance and Calculation of Reinforced Concrete; Tsinghua University Press: Beijing, China, 2003. [Google Scholar]
- Li, L. Study on the Stress Performance and Design Method of Reactive Powder Concrete Beams. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2010. (In Chinese). [Google Scholar]
- Ren, P. Research on Spalling Property and Fire Resistance Design Method of Reactive Powder Concrete Beams. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2022. (In Chinese). [Google Scholar]
- Lie, T.T.; Lin, T.D.; Abrams, M.S. Fire Resistance of Reinforced Concrete Columns; Division of Building Research, National Research Council of Canada: Ottawa, ON, Canada, 1987. [Google Scholar]
- Al-Bayati, E.S.N. Behavior of Reactive Powder Reinforced Concrete Beams Exposed to Fire. Ph.D. Thesis, Tikrit University, Tikrit, Iraq, 2017. [Google Scholar]
- American Concrete Institute. Building Code Requirements for Structural Concrete (ACI 318-14): Commentary on Building Code Requirements for Structural Concrete (ACI 318R-14): An ACI Report; American Concrete Institute: Farmington Hills, MI, USA, 2014. [Google Scholar]
- GA/T 714-2007; Rapid Rise Fire Test Methods of Fire Protection Materials for Structural Elements. China Standards Press: Beijing, China, 2007.
- GB50016-2014; Code for Fire Protection Design of Buildings. China Planning Press: Beijing, China, 2018.
- Liu, F. Fire Resistance of Concrete Filled RHS Columns Under Three-Surface Fire Loading. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2010. [Google Scholar]


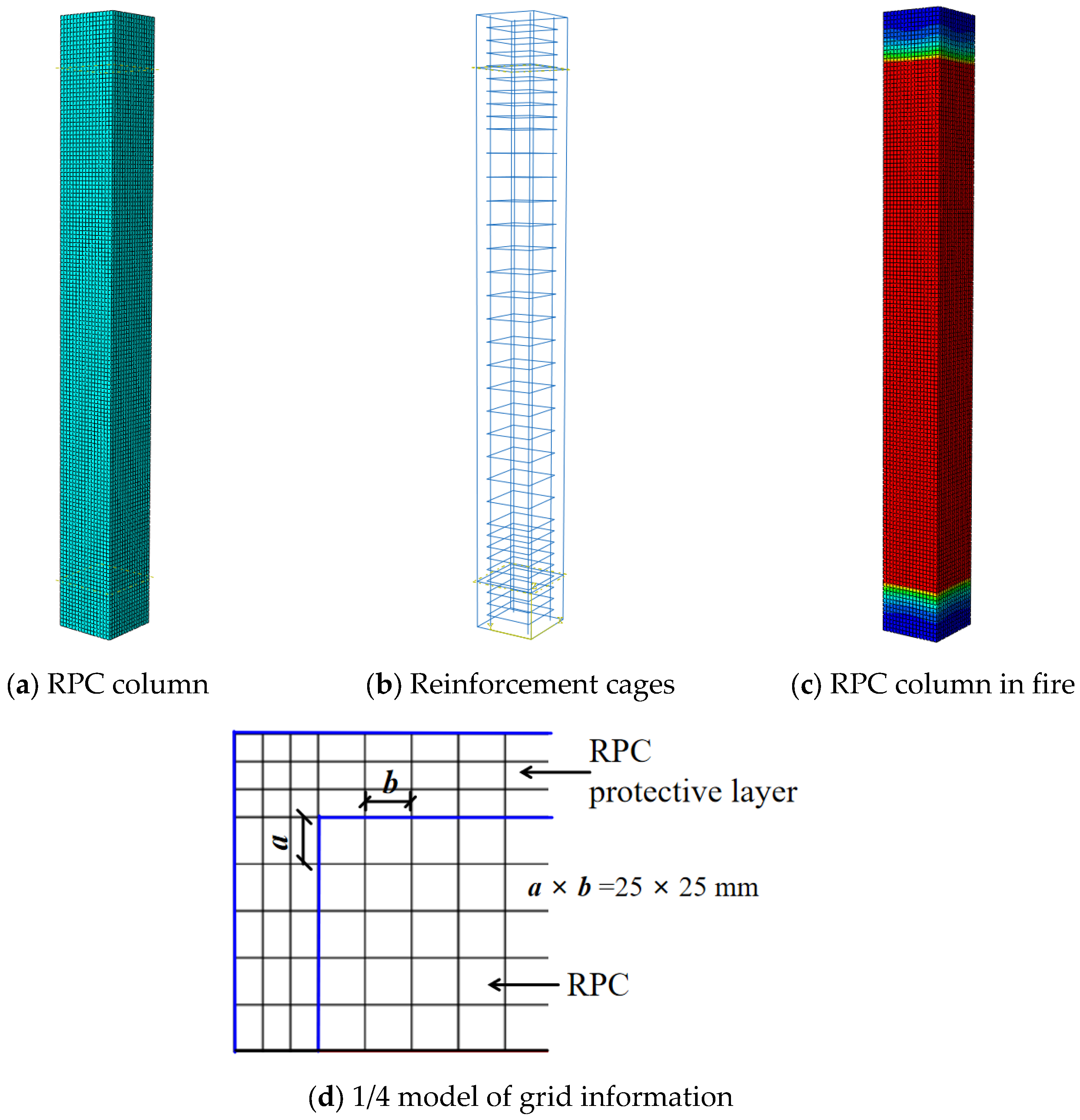
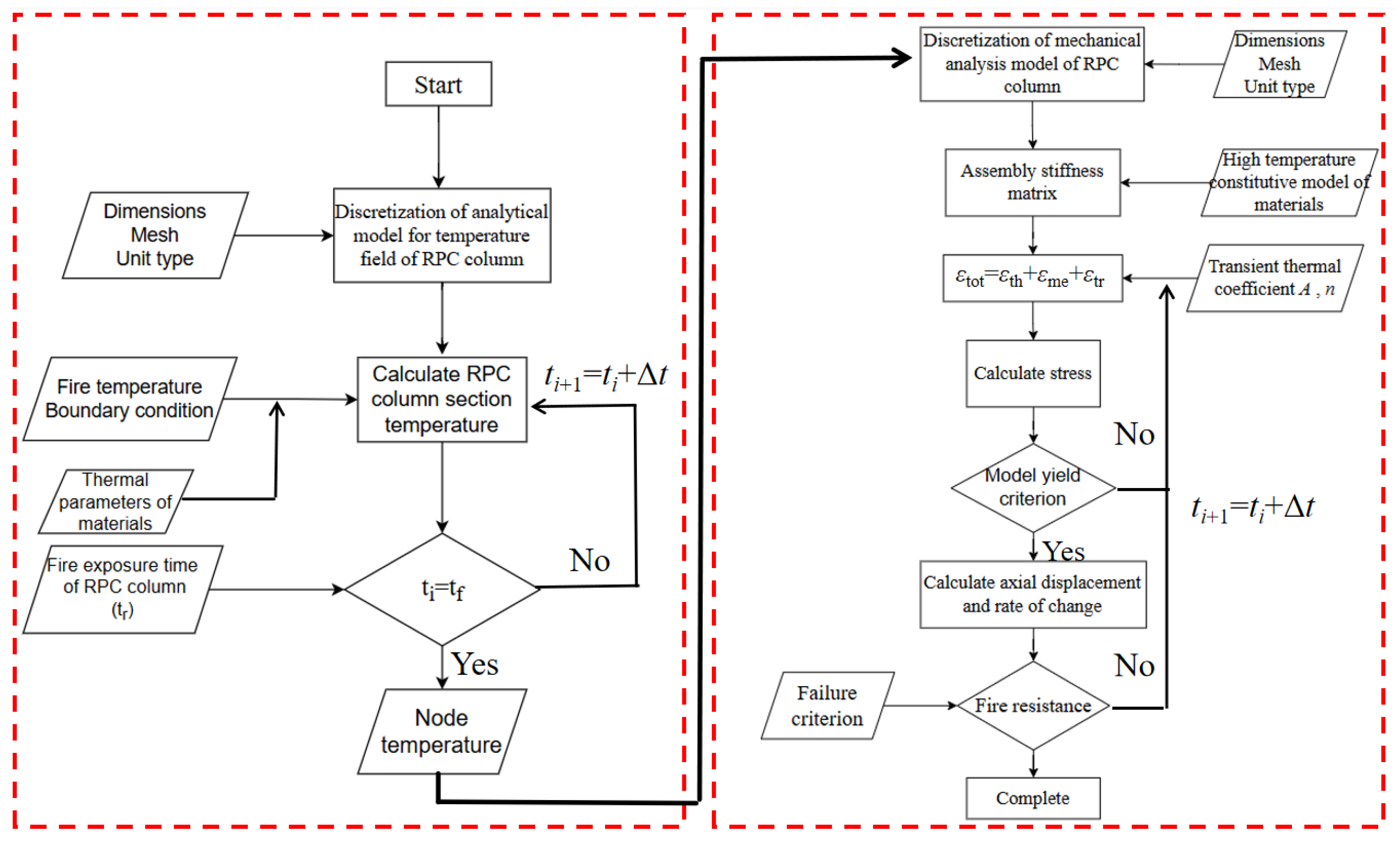

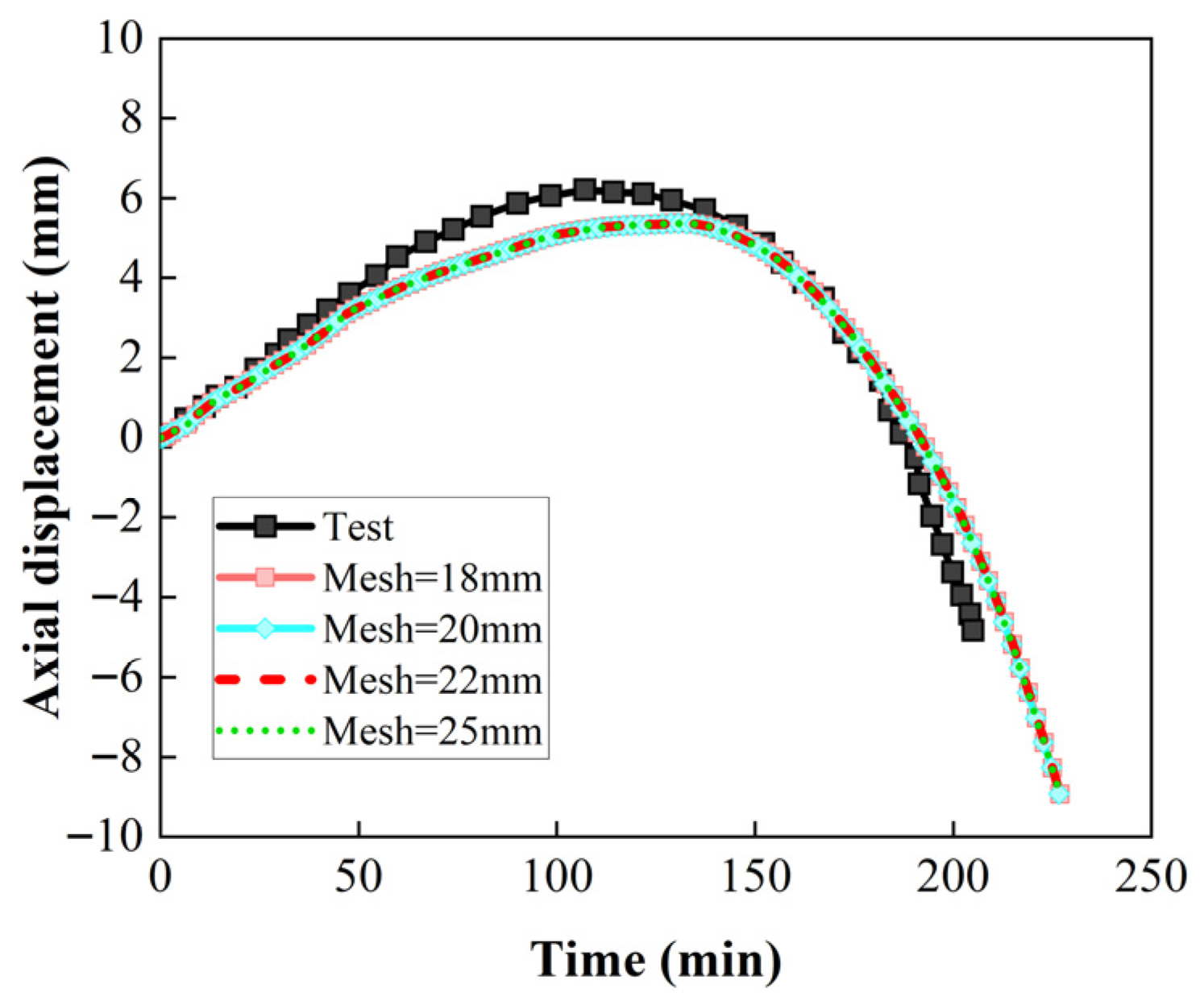
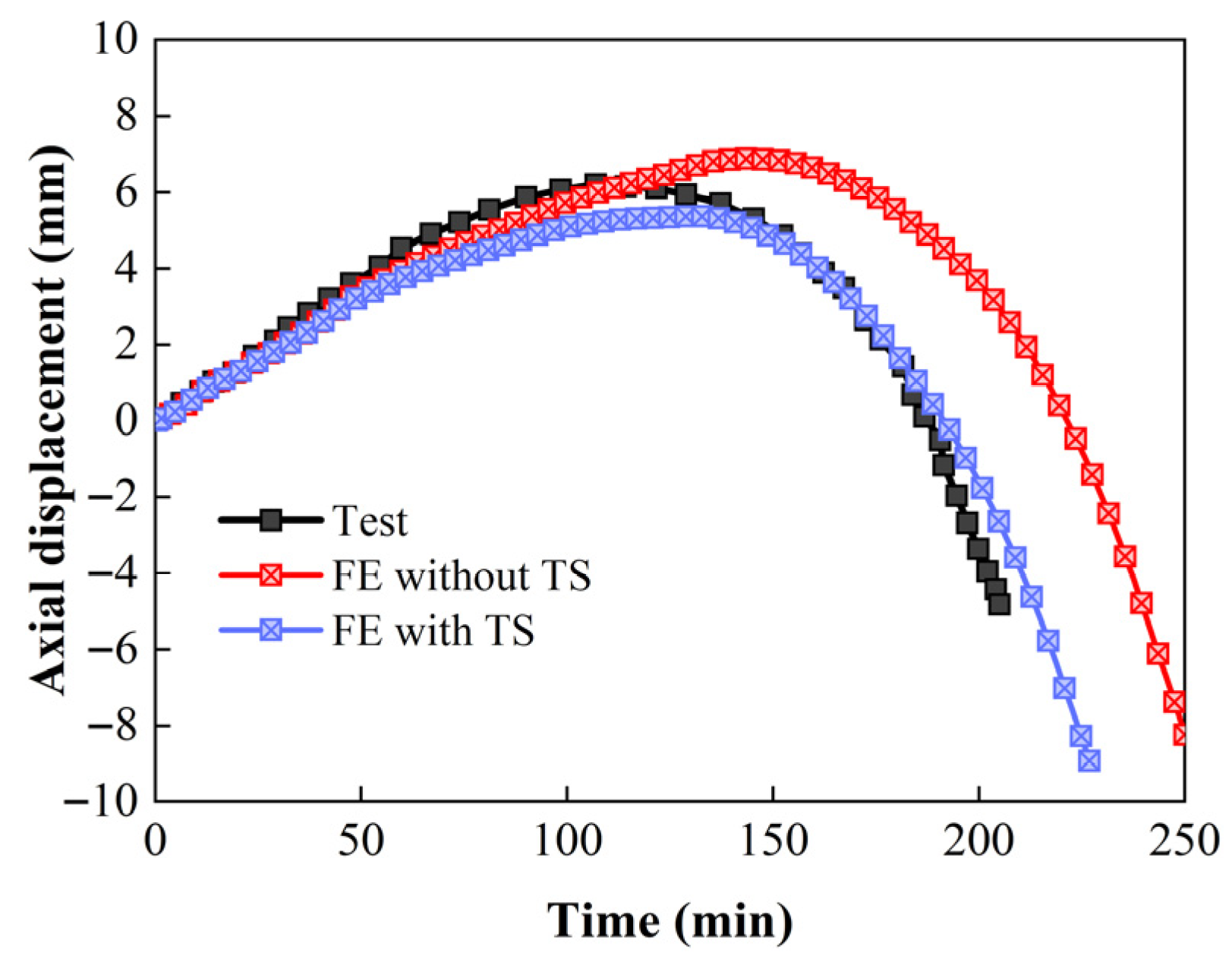
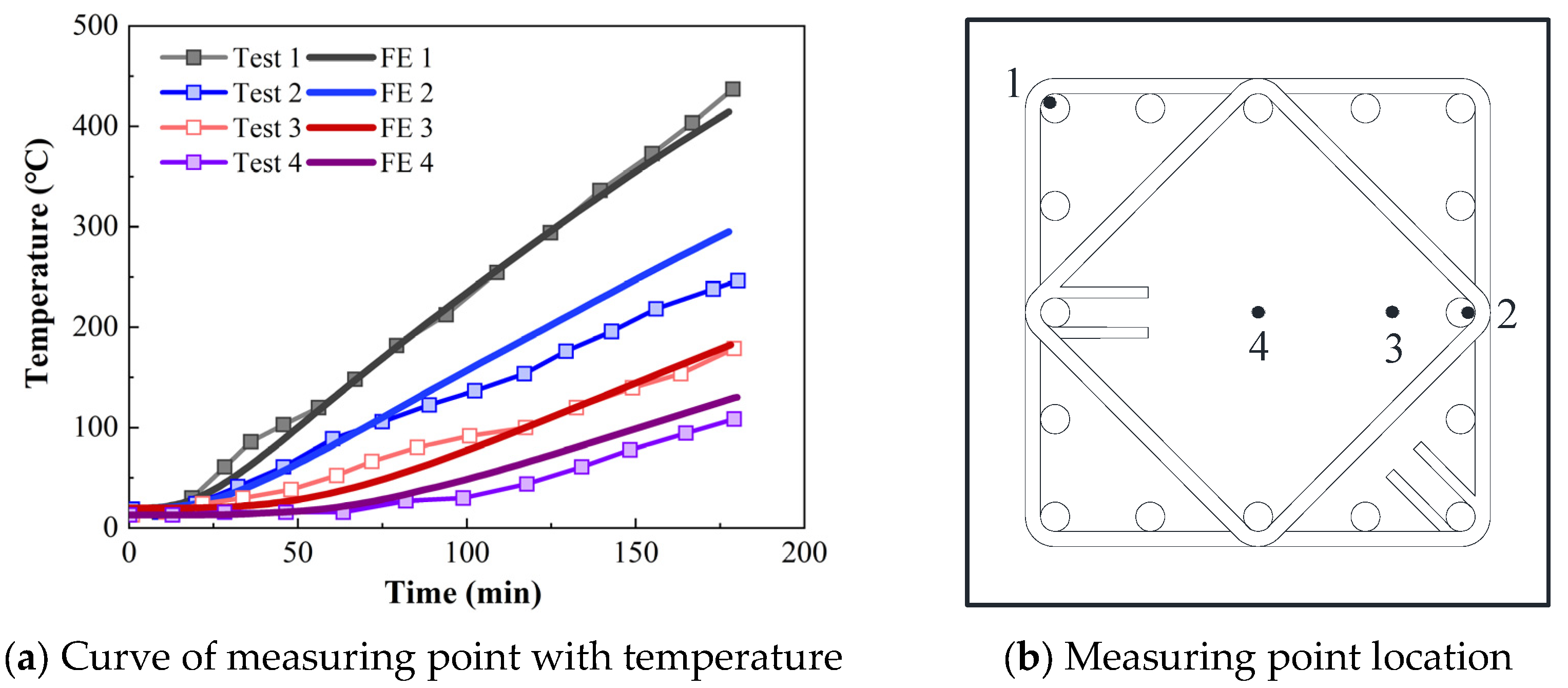
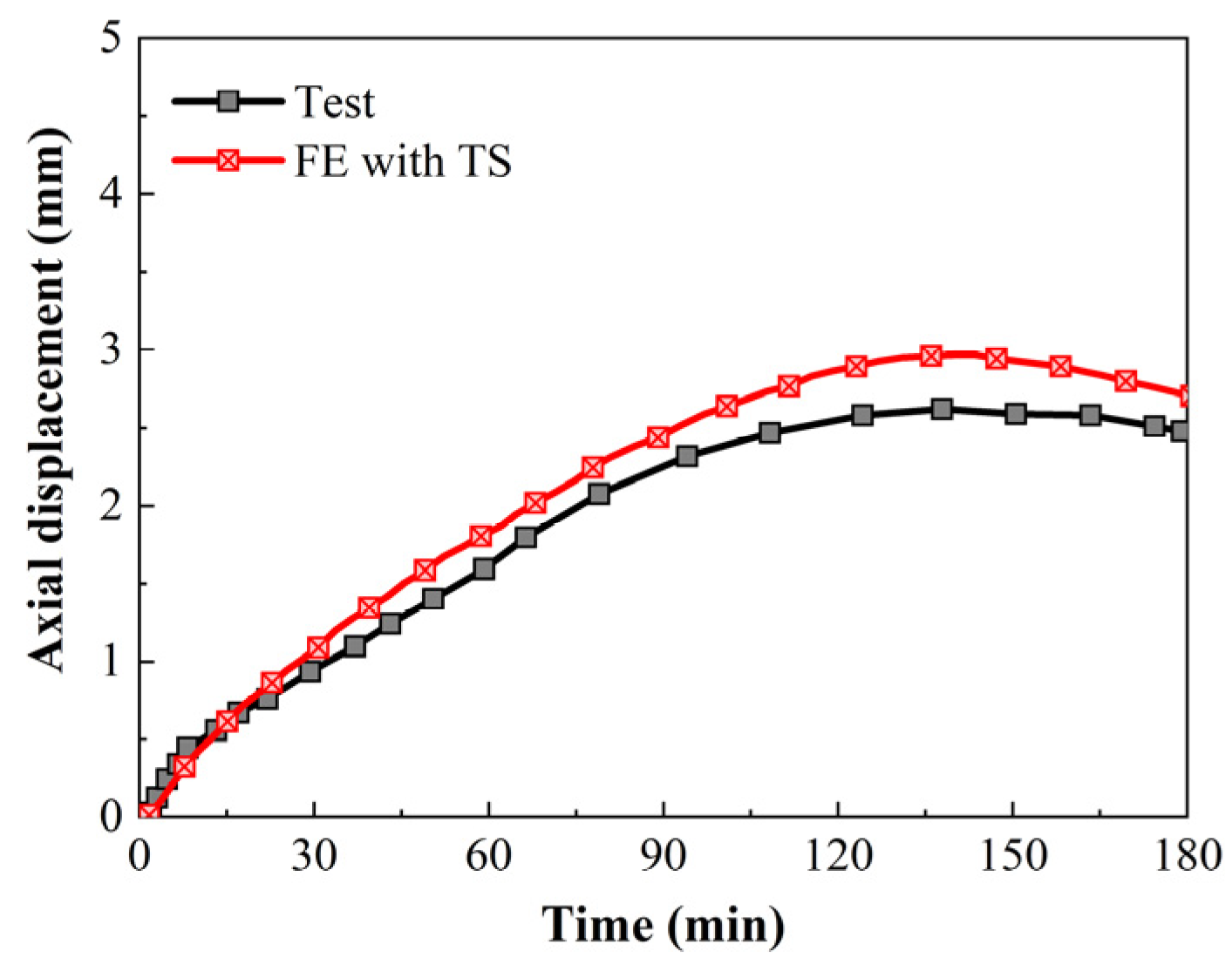
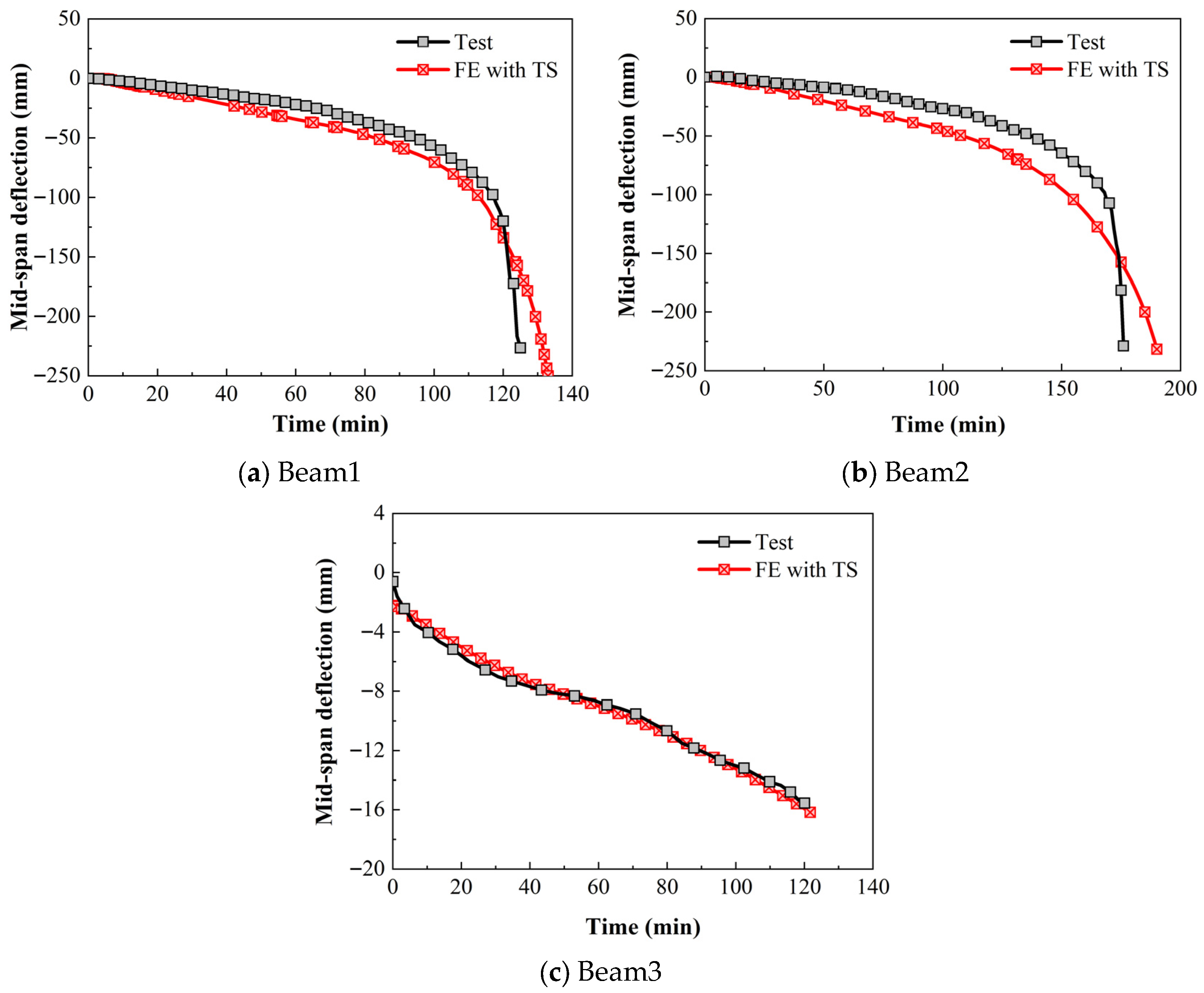

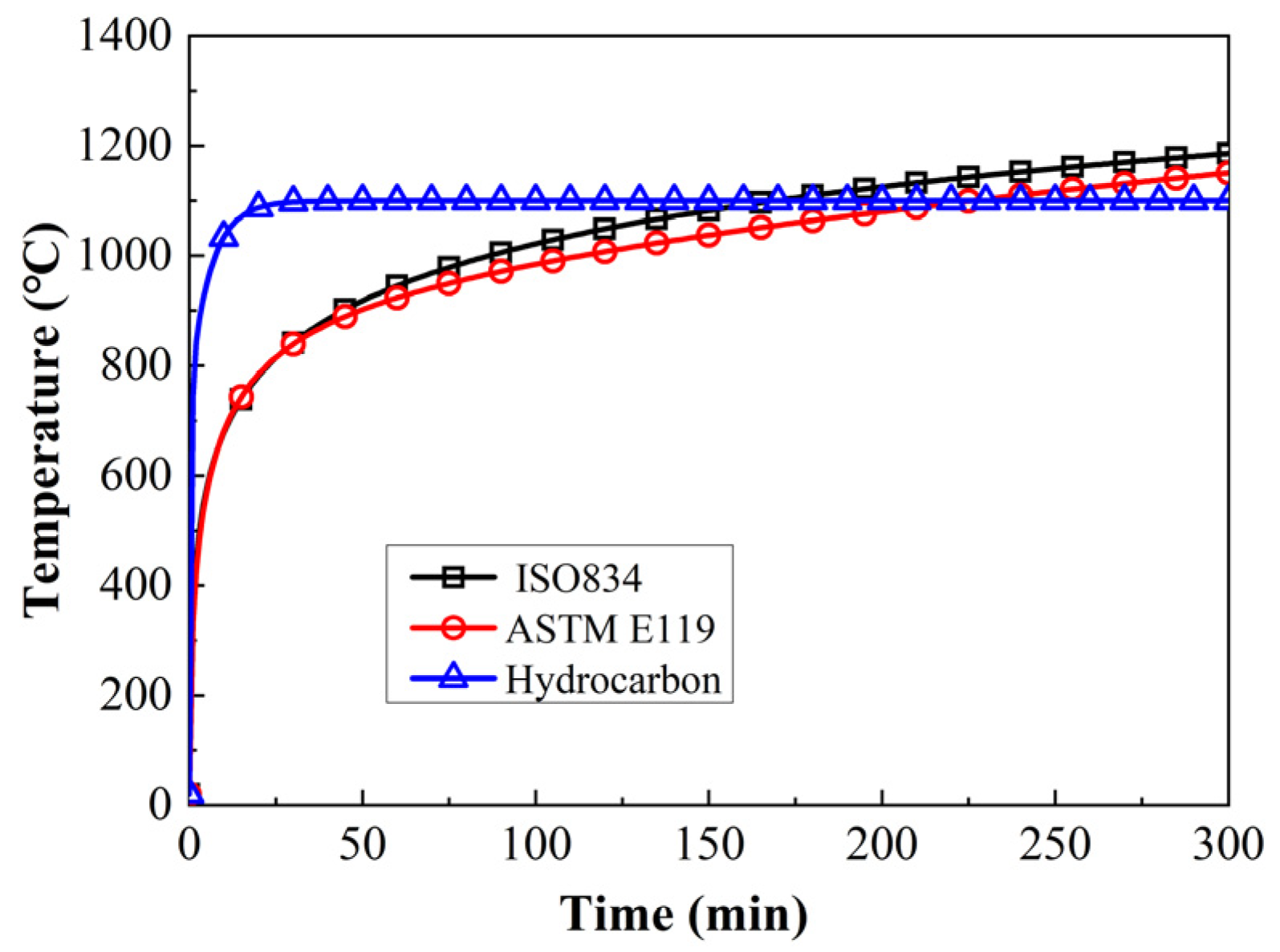
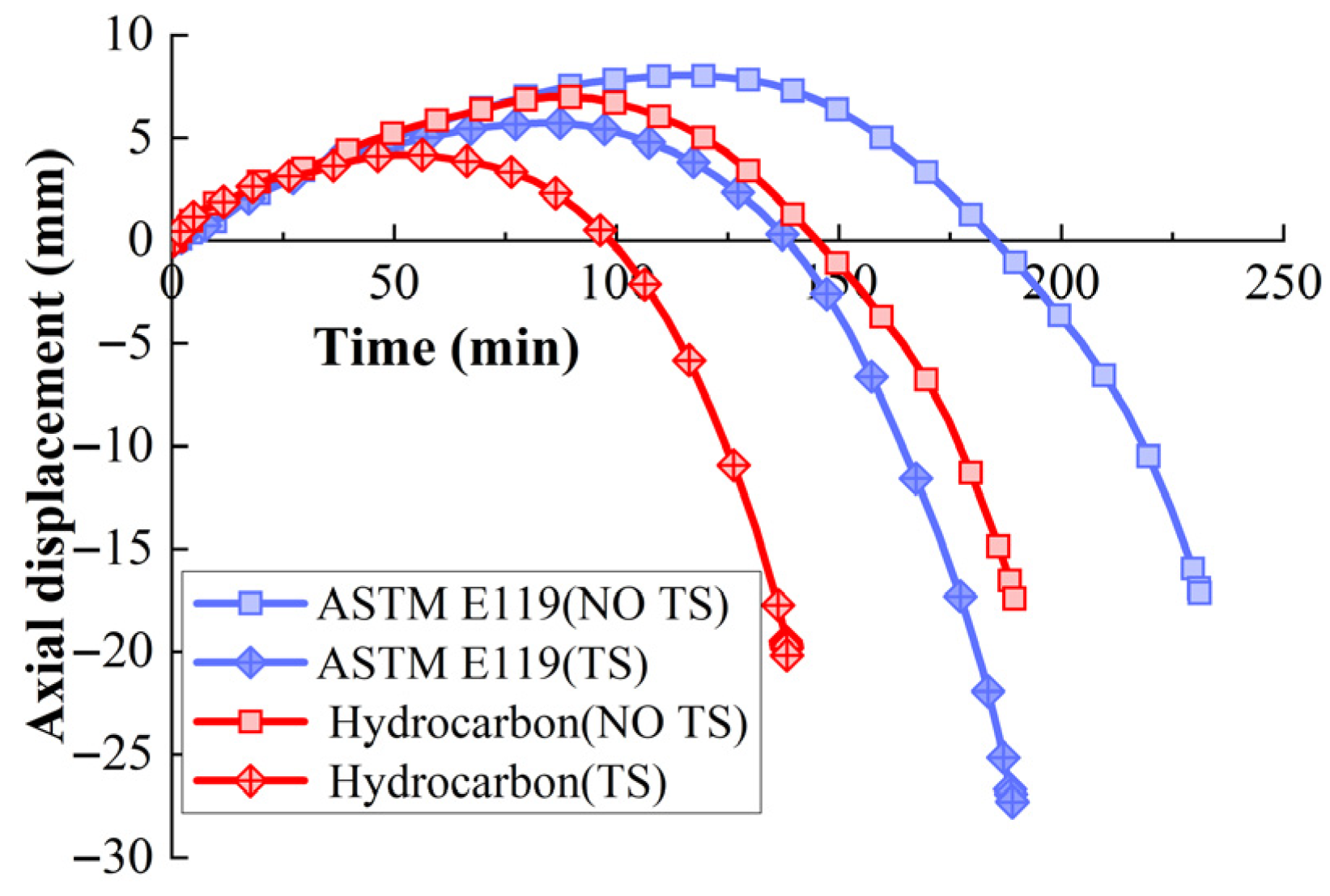
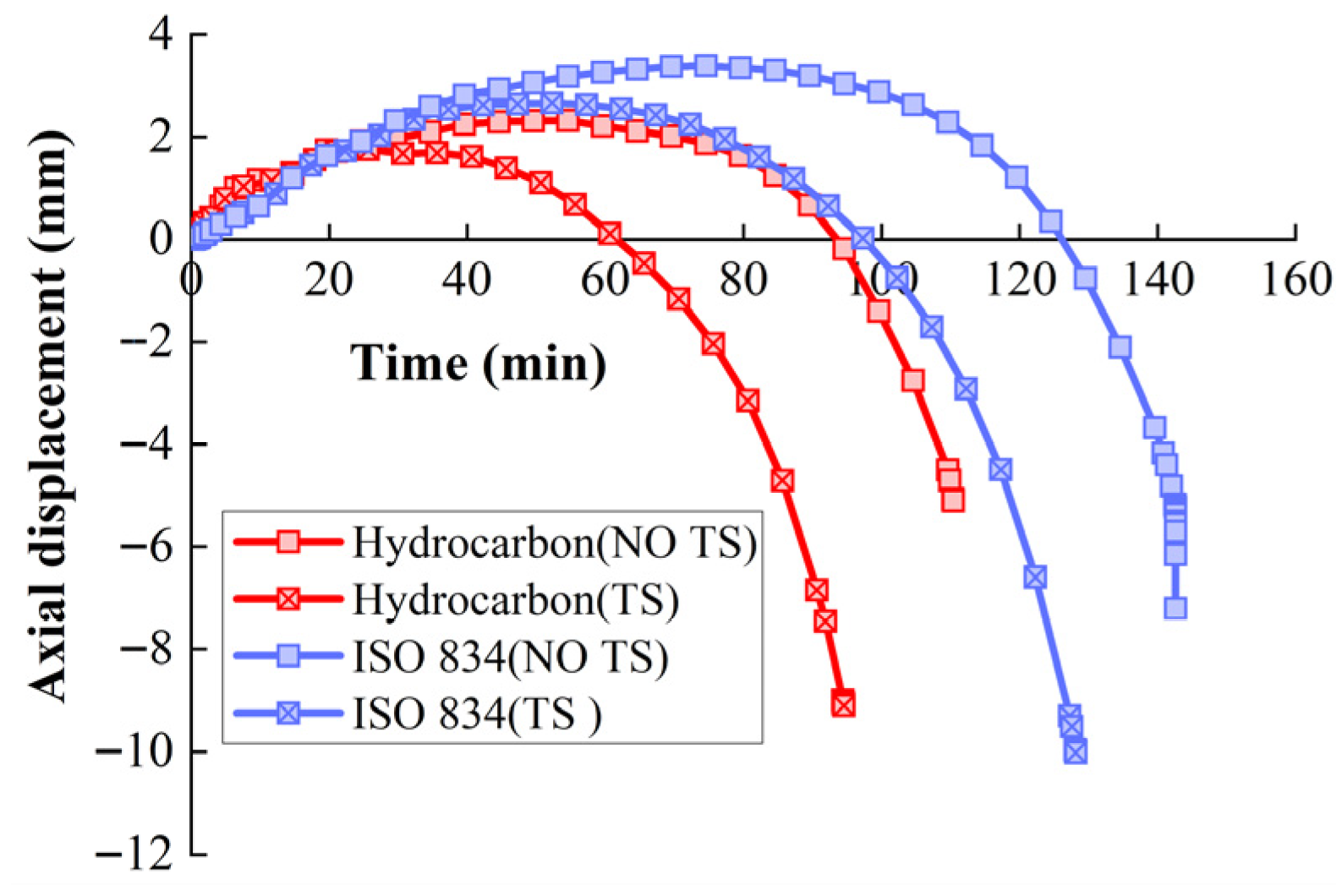
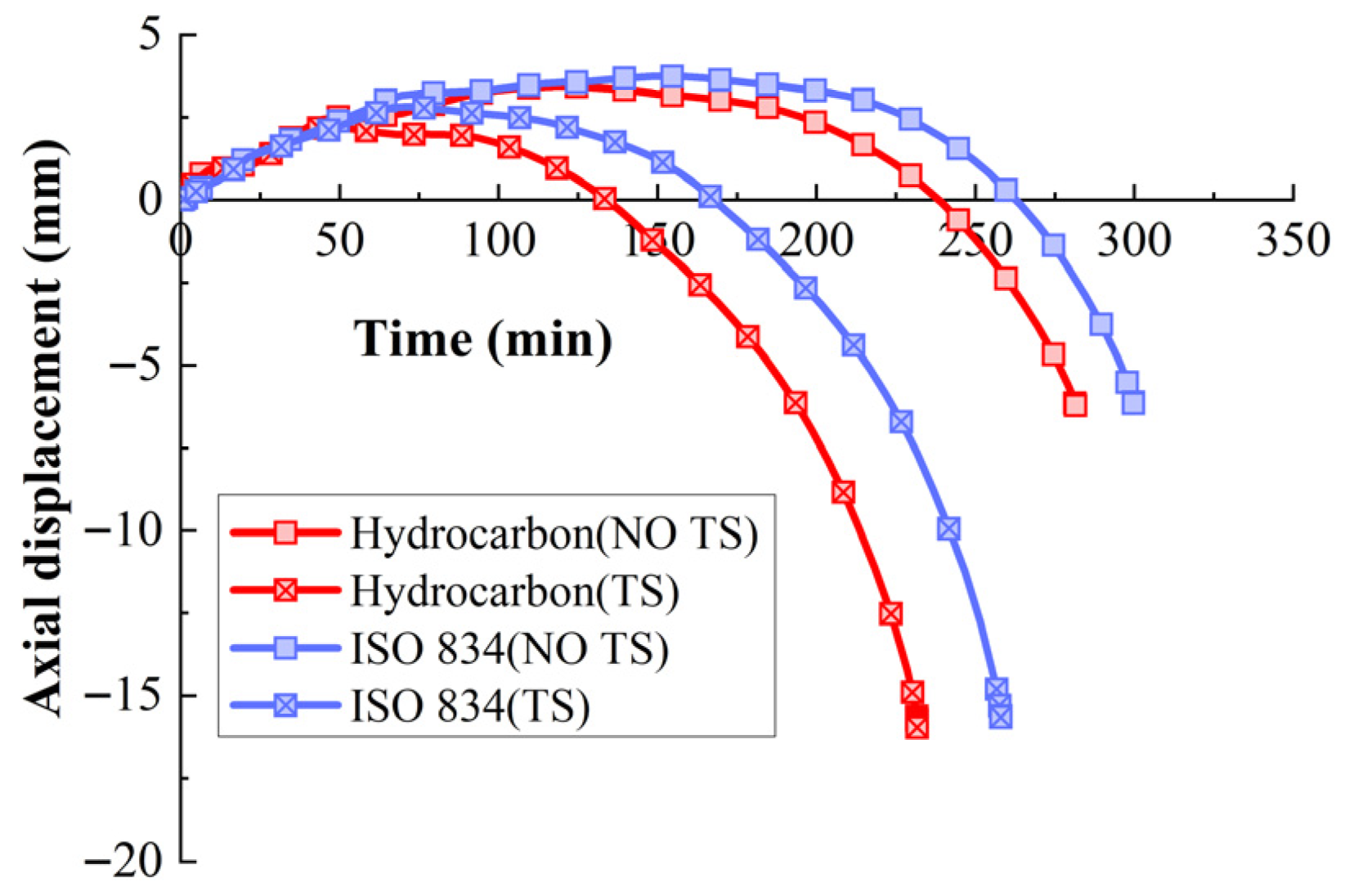

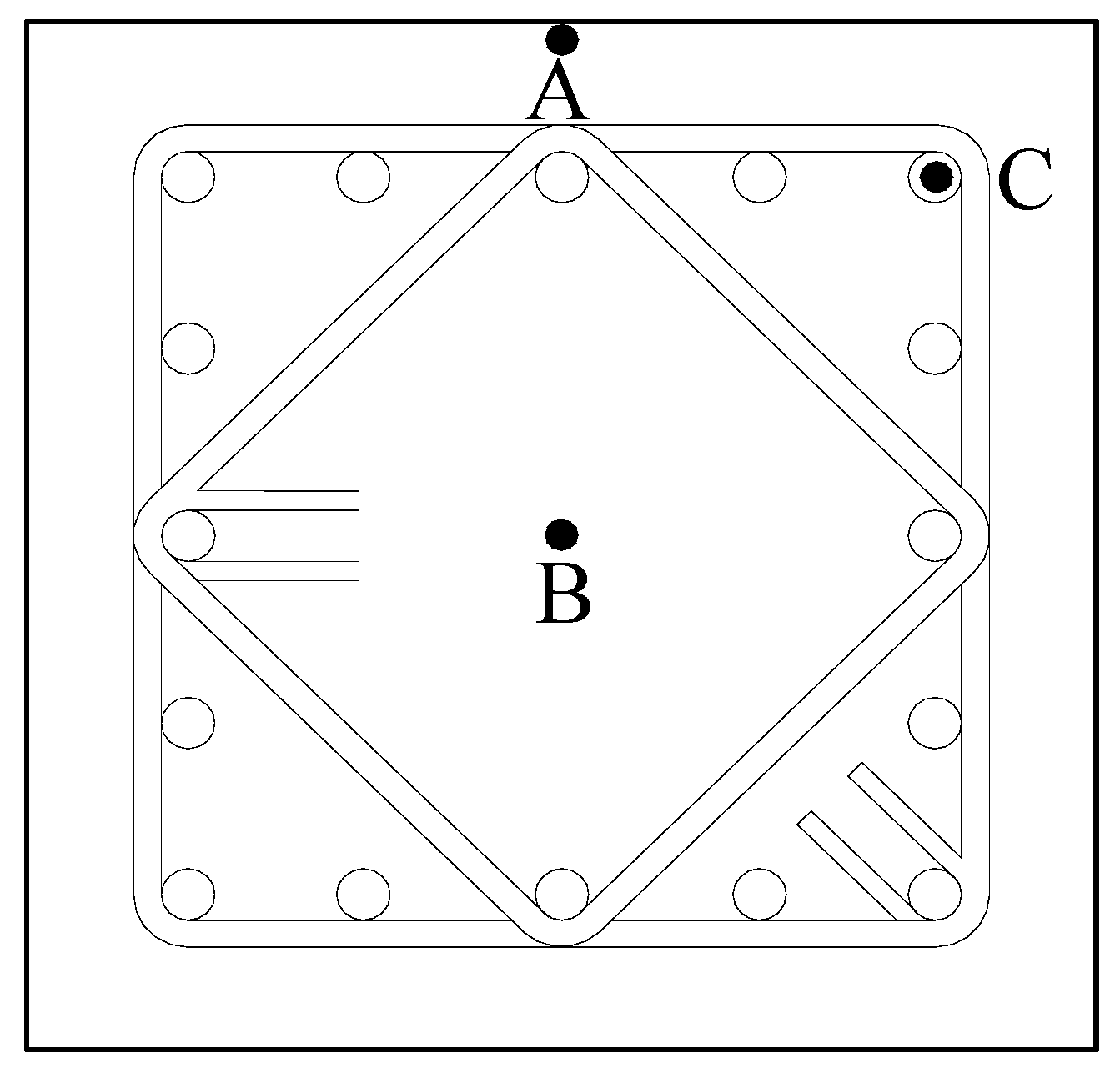
| Column A | Column B | Column C | |
|---|---|---|---|
| Section/mm | 305 × 305 | 300 × 300 | 500 × 500 |
| Length/m | 3.81 | 3.3 | 3.6 |
| RPC compressive strength/MPa | 150 | 150 | 200 |
| Longitudinal reinforcement /MPa | 354 | 500 | 500 |
| Rebar numbers—diameter /mm | 4–25 | 6–20 | 16–29 |
| Stirrup diameter—distance /mm | D8-75/150 | D8-250 | D13-100 |
| Concrete cover thickness /mm | 40 | 40 | 50 |
| Temperature rise curve | ASTM-E119 [35] | ISO-834 [19] | ISO-834 [19] |
| Fiber dosage | 0.2% PP fibers + 2% steel fibers | ||
| A | n | m | T |
|---|---|---|---|
| 5.42 × 10−17 | 1 | 0 | 20 |
| 5.42 × 10−18 | 1 | 0 | 100 |
| 7.48 × 10−16 | 1 | 0 | 200 |
| 4.11 × 10−15 | 1 | 0 | 300 |
| 9.59 × 10−15 | 1 | 0 | 400 |
| 1.72 × 10−14 | 1 | 0 | 500 |
| 2.69 × 10−14 | 1 | 0 | 600 |
| 3.88 × 10−14 | 1 | 0 | 700 |
| 9.96 × 10−14 | 1 | 0 | 800 |
| 5.83 × 10−13 | 1 | 0 | 900 |
| Description | Lie [43]-Column1 | Section Form |
|---|---|---|
| Section (mm) | 305 × 305 | 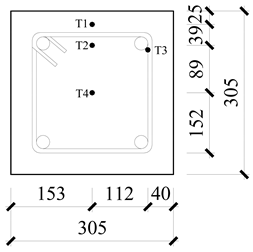 |
| Length (m) | 3.81 | |
| Concrete compressive strength fc (MPa) | 36.1 | |
| Concrete aggregate type | Siliceous | |
| Yield strength of longitudinal reinforcement (MPa) | 354 | |
| Rebar numbers/diameter (mm) | 4/25 | |
| Stirrup diameter and distance (mm) | D8/305 | |
| Concrete cover thickness (mm) | 40 | |
| Load (kN) | 1067 | |
| Load ratio | 0.32 | |
| Fire resistance (min) | 208 |
| Description | Hou/Beam 1 | Hou/Beam 2 | Ezzulddin/Beam 3 |
|---|---|---|---|
| Section/mm | 200 × 400 | 200 × 400 | 150 × 200 |
| Beam length/m | 4.9 | 4.9 | 2.0 |
| Number of rebar at beam top—diameter/mm Yield strength/MPa | 2D10 415 | 2D10 415 | 2D6 500 |
| Number of reinforcement at beam bottom—diameter/mm Yield strength/MPa | 3–25 463 | 3–25 463 | 2–8 500 |
| Stirrup diameter and spacing/mm Yield strength/MPa | D8@60 415 | D8@60 415 | D8@75 500 |
| Concrete cover thickness/mm | 25 mm | 35 mm | 30 mm |
| Load/kN | 50.9 kN | 49.6 kN | 22.1 kN·m |
| Temperature rising curve | ISO-834 | ISO-834 | ASTM-E119 |
| Heating time | 125 min | 176 min | 120 min |
| Tab | Section /mm2 | Column Length/m | Load Level % | Load/ kN | RPC fc/MPa | Longitudinal Rebars | Heating Curve | Cover Thickness/ mm |
|---|---|---|---|---|---|---|---|---|
| 1-A1 | 305 × 305 | 3.81 | 47 | 3007 | 150 | 4C25 | ASTM-E119 [35] | 40 |
| 1-A2 | 400 × 400 | 5094 | ||||||
| 1-A3 | 500 × 500 | 7898 | ||||||
| 1-B1 | 300 × 300 | 3.3 | 64 | 4050 | 150 | 6C20 | ISO834 [19] | 40 |
| 1-B2 | 400 × 400 | 7022 | ||||||
| 1-B3 | 500 × 500 | 10,842 | ||||||
| 1-C1 | 400 × 400 | 3.6 | 63 | 10,052 | 200 | 16C29 | ISO834 [19] | 50 |
| 1-C2 | 500 × 500 | 15,000 |
| Tab | Section (mm2) | Length (m) | Load Level % | Load/ kN | RPC fc/MPa | Longitudinal Rebars | Heating Curve | Cover Thickness/ mm |
|---|---|---|---|---|---|---|---|---|
| 2-A1 | 305 × 305 | 3.81 | 44 | 2790 | 150 | 4C25 | ASTM-E119 [35] | 40 |
| 2-A2 | 65 | 4186 | ||||||
| 2-A3 | 88 | 5580 | ||||||
| 2-B1 | 300 × 300 | 3.3 | 43 | 2700 | 150 | 6C20 | ISO834 [19] | 40 |
| 2-B2 | 64 | 4050 | ||||||
| 2-B3 | 85 | 5400 | ||||||
| 2-C1 | 500 × 500 | 3.6 | 42 | 1000 | 200 | 16C29 | ISO834 [19] | 50 |
| 2-C2 | 63 | 15,000 | ||||||
| 2-C3 | 84 | 2000 |
| Tab | Section (mm2) | Column Length (m) | Load Level (%) | Load (kN) | RPC fc (MPa) | Longitudinal Rebars | Heating Curve | Cover Thickness (mm) |
|---|---|---|---|---|---|---|---|---|
| 3-A1 | 305 × 305 | 3.81 | 47 | 3007 | 150 | 4C25 | ASTM-E119 [35] | 40 |
| 3-A2 | 6C25 | |||||||
| 3-A3 | 8C25 | |||||||
| 3-B1 | 300 × 300 | 3.3 | 43 | 2700 | 150 | 4C20 | ISO834 [19] | 40 |
| 3-B2 | 6C20 | |||||||
| 3-B3 | 8C20 | |||||||
| 3-C1 | 500 × 500 | 3.6 | 62 | 15,000 | 200 | 8C29 | ISO834 [19] | 50 |
| 3-C2 | 12C29 | |||||||
| 3-C3 | 16C29 |
| Tab | Section /mm2 | Column Length/m | Load Level % | Load/ kN | RPC fc/MPa | Longitudinal Rebars | Heating Curve | Cover Thickness/ mm |
|---|---|---|---|---|---|---|---|---|
| 4-A1 | 305 × 305 | 3.81 | 47 | 3007 | 150 | 4C25 | ASTM-E119 [35] | 40 |
| 4-A2 | Hydrocarbon [46] | |||||||
| 4-B1 | 300 × 300 | 3.3 | 64 | 4050 | 150 | 6C20 | ISO834 [19] | 40 |
| 4-B2 | Hydrocarbon [46] | |||||||
| 4-C1 | 500 × 500 | 3.6 | 62 | 15,000 | 200 | 16C29 | ISO834 [19] | 50 |
| 4-C2 | Hydrocarbon [46] |
| Tab | Section /mm2 | Column Length/m | Fire Side | Load/ kN | RPC fc/MPa | Longitudinal Rebars | Heating Curve | Cover Thickness/ mm |
|---|---|---|---|---|---|---|---|---|
| 5-A1 | 305 × 305 | 3.81 | 4 | 3007 | 150 | 4C25 | ASTM-E119 [35] | 40 |
| 5-A2 | 3 | |||||||
| 5-A3 | 2 | |||||||
| 5-A4 | 1 |
| Tab | Load Level % | Load/kN | Fire Resistance/(min) | Difference | Error Percentage % | ||
|---|---|---|---|---|---|---|---|
| TS | No TS | ||||||
| Section | 1-A1 | 47 | 3007 | 189 | 231 | 42 | 22 |
| 1-A2 | 5094 | 248 | 333 | 85 | 34 | ||
| 1-A3 | 7898 | 323 | 461 | 138 | 43 | ||
| 1-B1 | 64 | 4050 | 128 | 143 | 15 | 12 | |
| 1-B2 | 7022 | 175 | 206 | 31 | 18 | ||
| 1-B3 | 10,842 | 228 | 285 | 57 | 25 | ||
| 1-C1 | 63 | 10,052 | 221 | 244 | 23 | 10 | |
| 1-C2 | 15,000 | 258 | 300 | 42 | 16 | ||
| Load level | 2-A1 | 44 | 2790 | 203 | 247 | 44 | 22 |
| 2-A2 | 65 | 4186 | 137 | 152 | 15 | 11 | |
| 2-A3 | 88 | 5580 | 102 | 108 | 6 | 6 | |
| 2-B1 | 43 | 2700 | 184 | 229 | 45 | 25 | |
| 2-B2 | 64 | 4050 | 128 | 143 | 15 | 12 | |
| 2-B3 | 85 | 5400 | 96 | 103 | 7 | 7 | |
| 2-C1 | 42 | 10,000 | 362 | 497 | 135 | 37 | |
| 2-C2 | 63 | 15,000 | 258 | 300 | 42 | 16 | |
| 2-C3 | 84 | 20,000 | 192 | 219 | 27 | 14 | |
| Reinforcement ratio | 3-A1 | 47 | 3007 | 189 | 231 | 42 | 22 |
| 3-A2 | 200 | 241 | 41 | 21 | |||
| 3-A3 | 210 | 252 | 42 | 20 | |||
| 3-B1 | 43 | 2700 | 175 | 221 | 46 | 26 | |
| 3-B2 | 184 | 229 | 45 | 25 | |||
| 3-B3 | 192 | 237 | 45 | 23 | |||
| 3-C1 | 62 | 15,000 | 228 | 272 | 44 | 19 | |
| 3-C2 | 253 | 304 | 51 | 20 | |||
| 3-C3 | 258 | 300 | 42 | 16 | |||
| Heating curve | 4-A1 | 47 | 3007 | 189 | 231 | 42 | 22 |
| 4-A2 | 138 | 190 | 52 | 38 | |||
| 4-B1 | 64 | 4050 | 128 | 143 | 15 | 12 | |
| 4-B2 | 94 | 111 | 17 | 18 | |||
| 4-C1 | 62 | 15,000 | 258 | 300 | 42 | 16 | |
| 4-C2 | 231 | 282 | 51 | 22 | |||
| Fire side of RPC column | 5-A1 | 65 | 4186 | 137 | 152 | 15 | 11 |
| 5-A2 | 187 | 218 | 31 | 14 | |||
| 5-A3 | 300 | 300 | - | - | |||
| 5-A4 | 300 | 300 | - | - | |||
| Label | Longitudinal Bar/fy (MPa) | TS | Number of Bars—Diameter | Hooping Diameter—Spacing | fc | Length (mm) | Load (kN) | BC | FR (min) |
|---|---|---|---|---|---|---|---|---|---|
| LC1 | 355 | No | 4–25 | 8@150 | 50 | 3810 | 1150 | P-P | 67.5 |
| 355 | Yes | 4–25 | 8@150 | 50 | 3810 | 1150 | P-P | 51.1 | |
| LC2 | 355 | No | 4–25 | 8@150 | 150 | 3810 | 1150 | P-P | 96.1 |
| 355 | Yes | 4–25 | 8@150 | 150 | 3810 | 1150 | P-P | 70.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rong, Q.; Chang, Z.; Lyu, Z.; Hou, X. Modeling the Fire Response of Reactive Powder Concrete Columns with Due Consideration of Transient Thermal Strain. Buildings 2025, 15, 3287. https://doi.org/10.3390/buildings15183287
Rong Q, Chang Z, Lyu Z, Hou X. Modeling the Fire Response of Reactive Powder Concrete Columns with Due Consideration of Transient Thermal Strain. Buildings. 2025; 15(18):3287. https://doi.org/10.3390/buildings15183287
Chicago/Turabian StyleRong, Qin, Zeyu Chang, Zhihao Lyu, and Xiaomeng Hou. 2025. "Modeling the Fire Response of Reactive Powder Concrete Columns with Due Consideration of Transient Thermal Strain" Buildings 15, no. 18: 3287. https://doi.org/10.3390/buildings15183287
APA StyleRong, Q., Chang, Z., Lyu, Z., & Hou, X. (2025). Modeling the Fire Response of Reactive Powder Concrete Columns with Due Consideration of Transient Thermal Strain. Buildings, 15(18), 3287. https://doi.org/10.3390/buildings15183287







