Dynamic Response and Failure Mode of Reinforced Concrete Beams Subjected to Impact
Abstract
1. Introduction
2. Numerical Model Validation and Development
2.1. Introduction to Test Model
2.2. Material Model and Strain Rate Effect
2.3. Calibration of the Numerical Model
3. Results and Discussions
3.1. Failure Modes
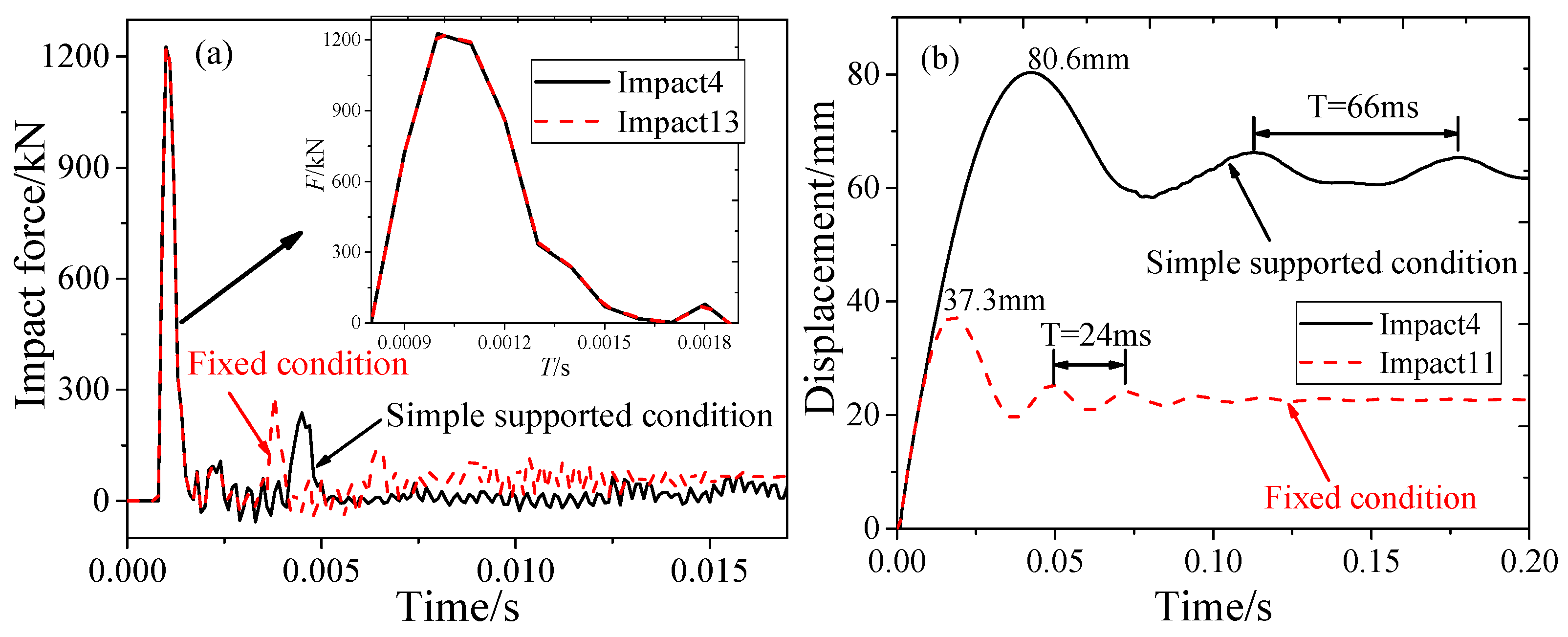
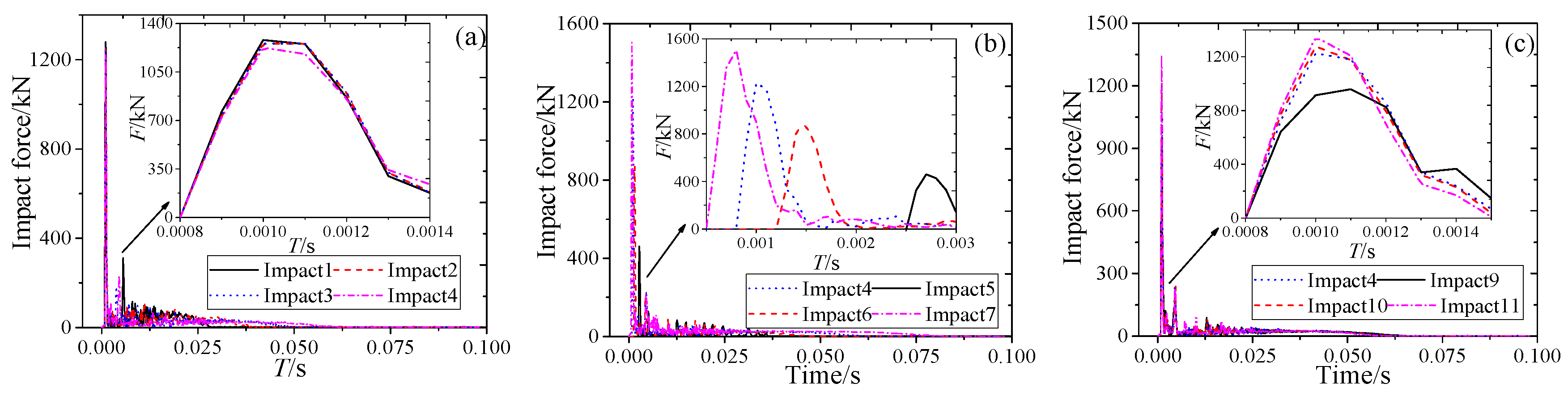
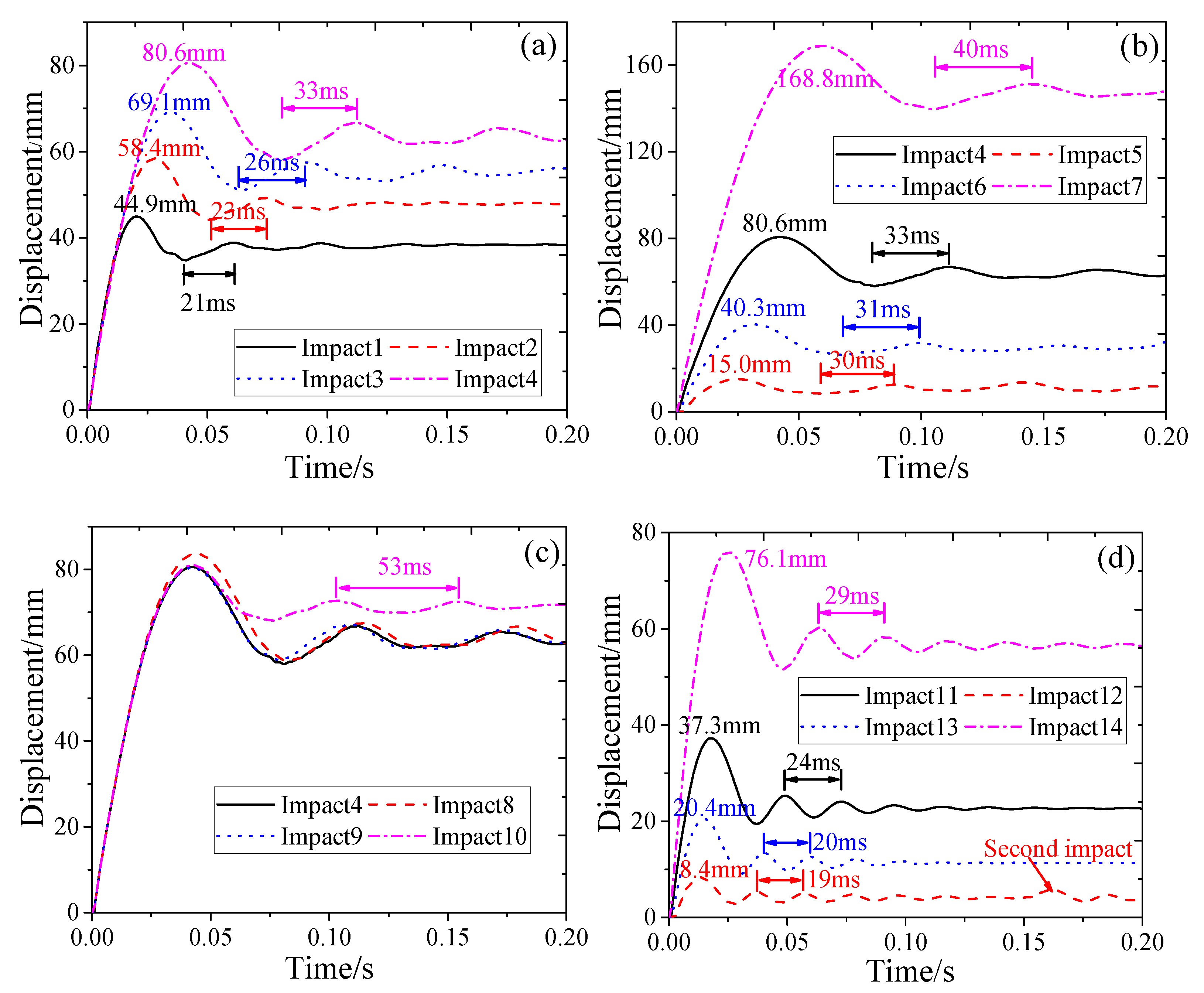
3.2. Impact Force and Displacement
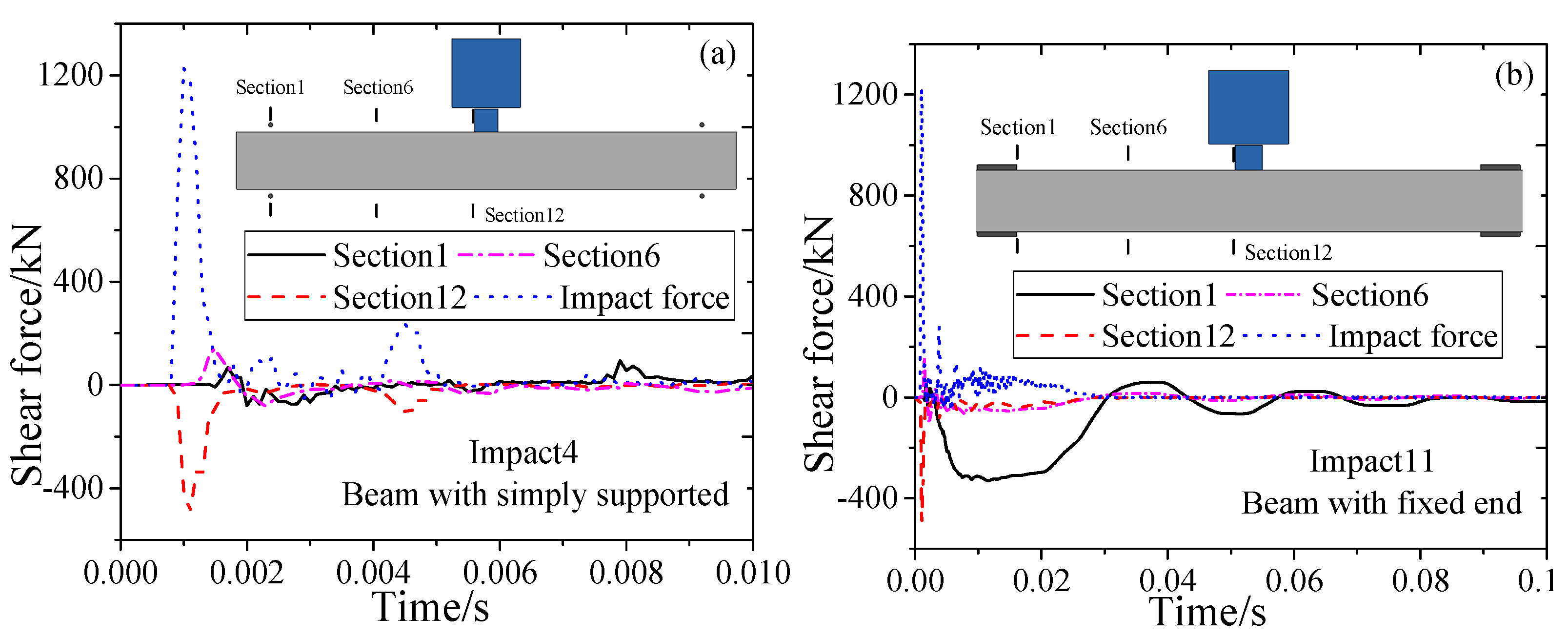
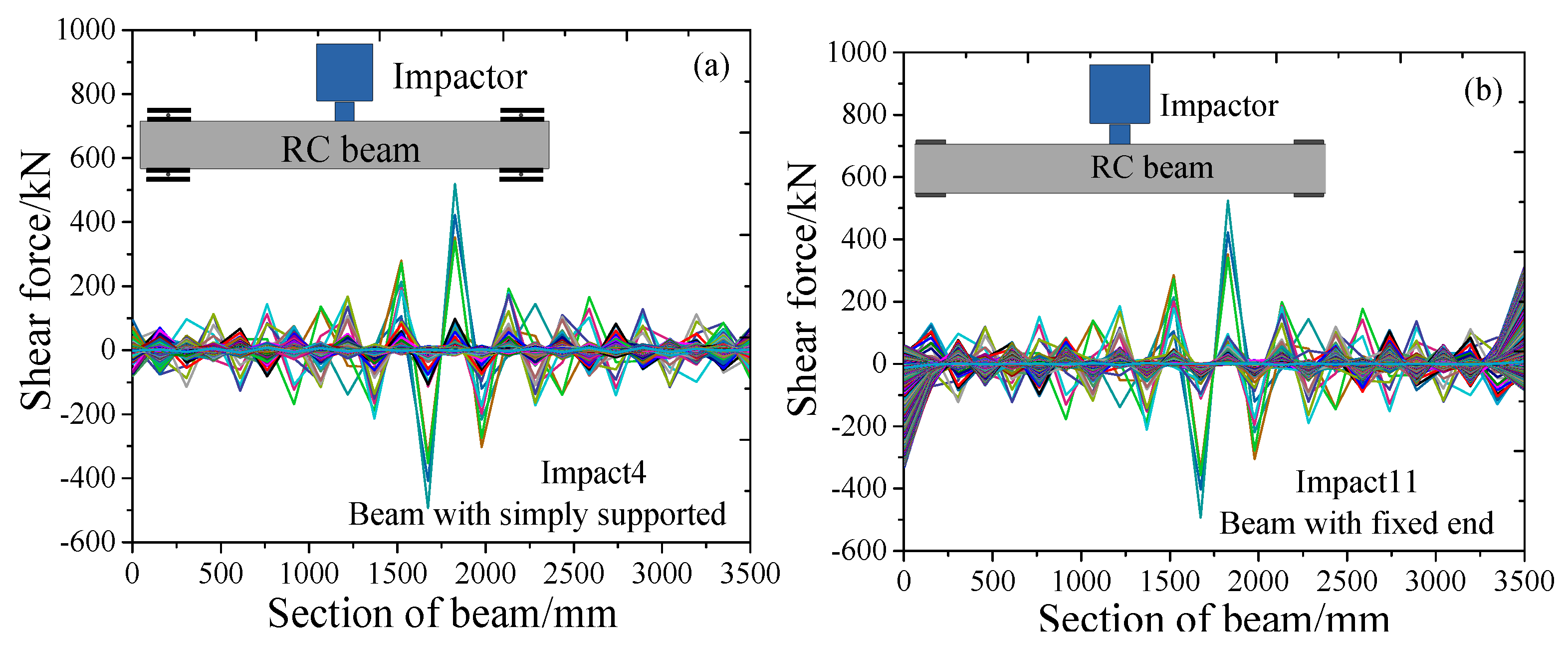
3.3. Shear Response
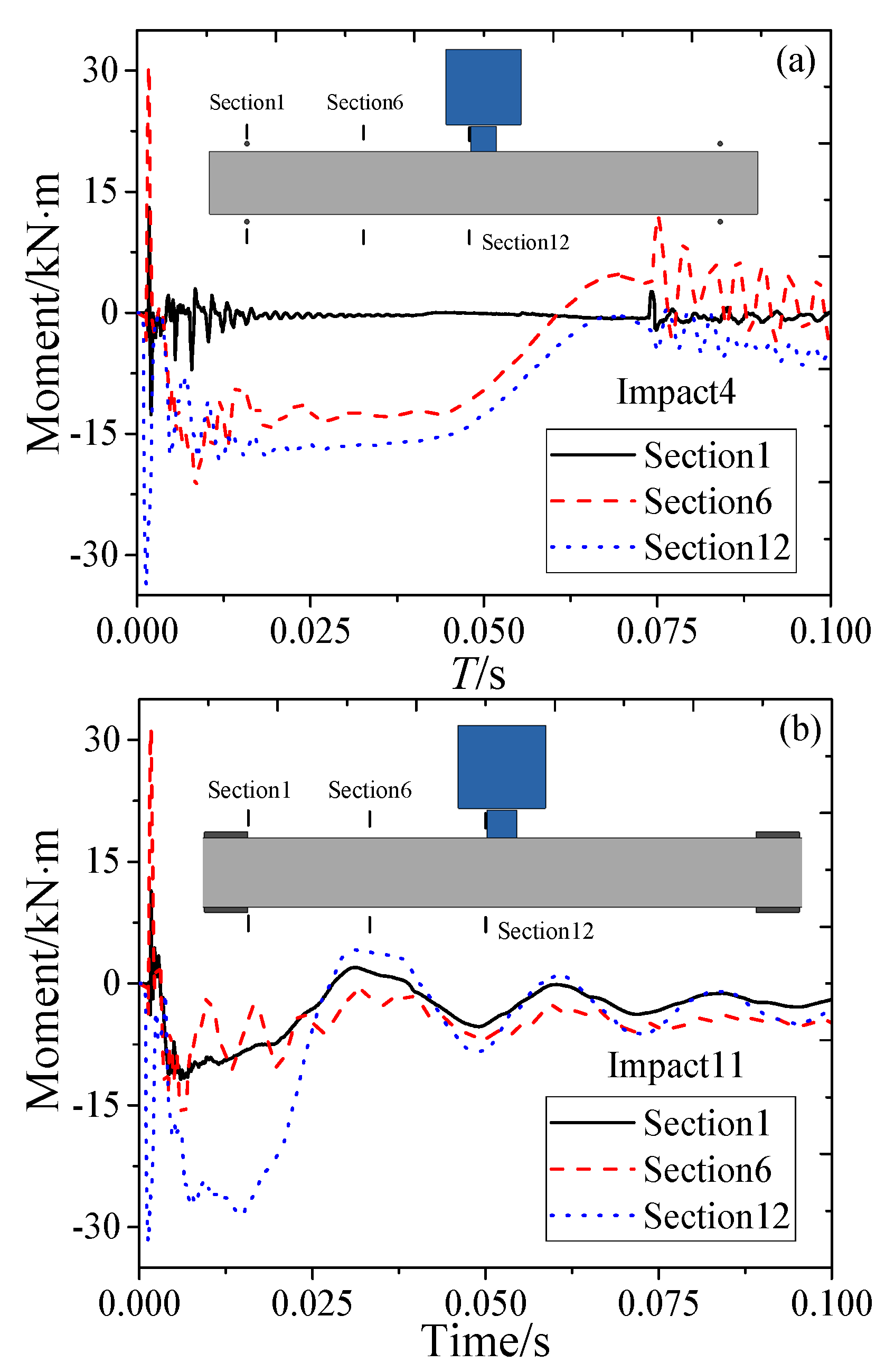
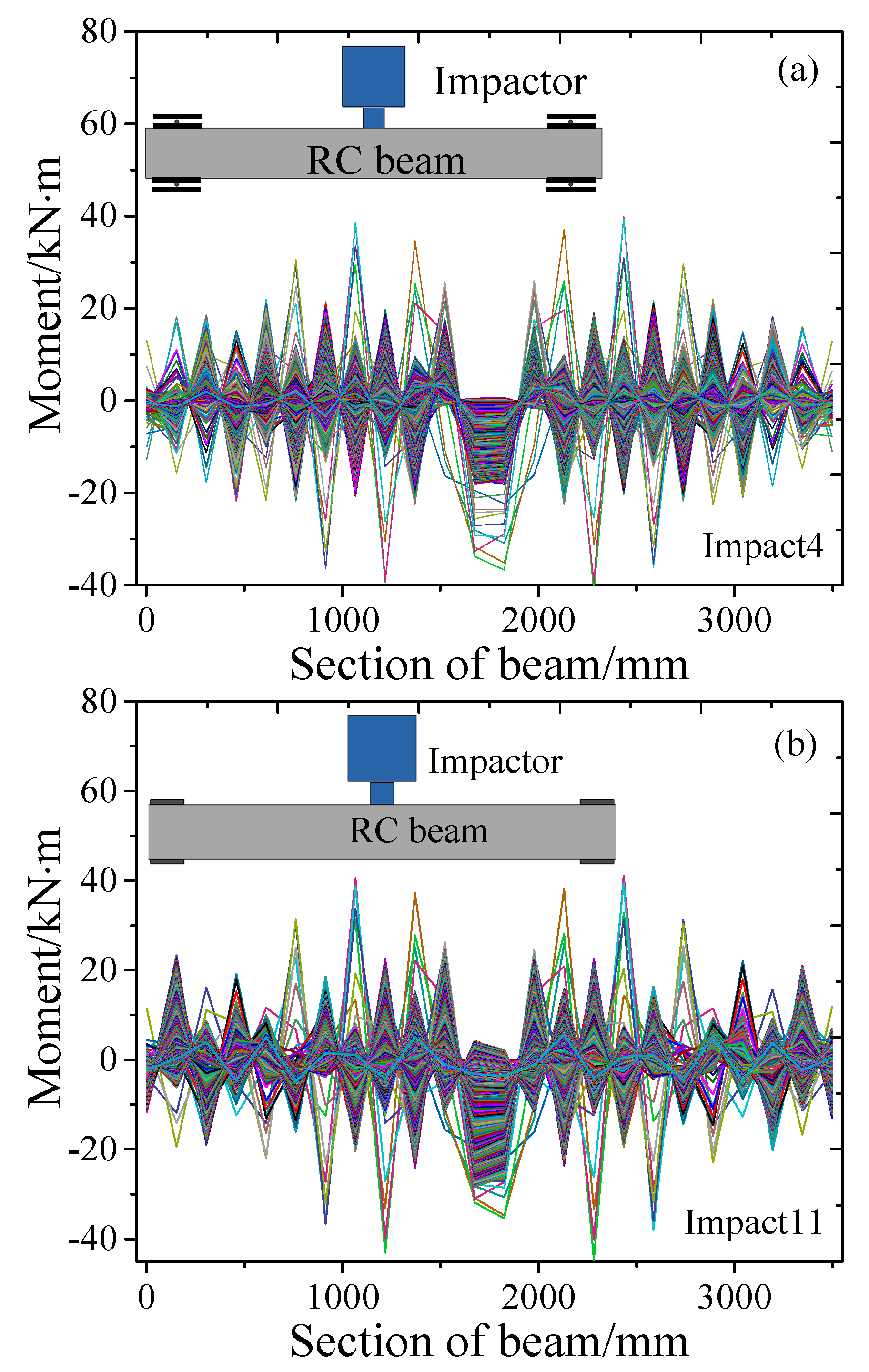
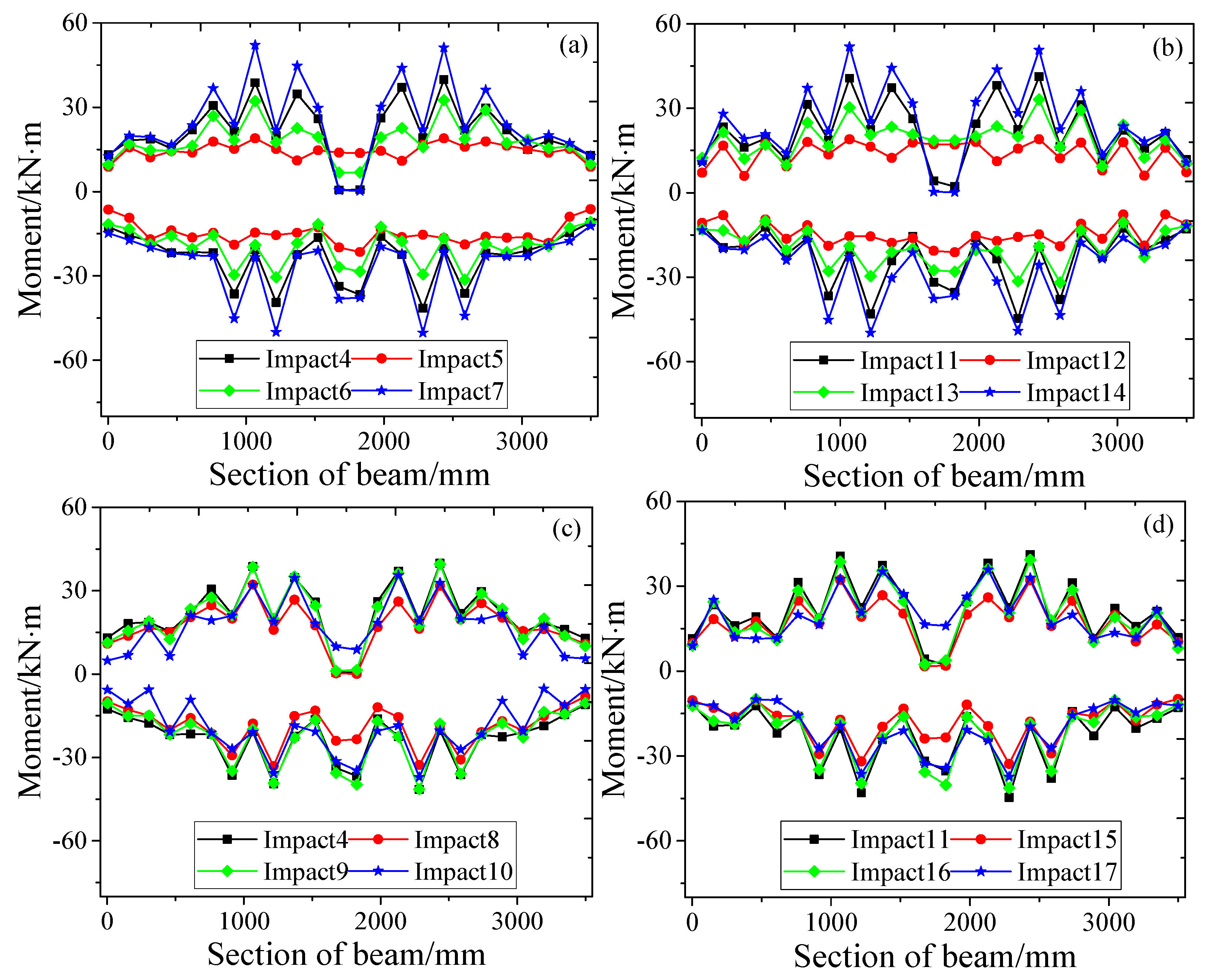
3.4. Bending Moment
4. Conclusions
- (1)
- Increasing the concrete strength decreases the damage degree of RC beams and changes the failure mode from bending–shear failure to bending failure under impact loading.
- (2)
- The boundary conditions of RC beams have no remarkable effect on the impact force of RC beams but have a noticeable effect on the peak displacement and residual displacement. The vibration period of fixed- boundary RC beams is significantly shorter than that of simply supported beams.
- (3)
- Under impact loads, the failure mode of the beams is subjected to a negative bending moment, and for fixed- boundary conditions, significant end shear leads to the formation of vertical cracks.
- (4)
- The bending moments of RC beams with simply supported and fixed- boundary conditions are similar, and the bending moment in the impact position is much greater than that in other areas.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wardhana, K.; Hadipriono, F. Analysis of recent bridge failures in the United States. J. Perform. Constr. Fac. 2003, 17, 144–150. [Google Scholar] [CrossRef]
- Harik, I.; Shaaban, A.; Gesund, H.; Valli, G.; Wang, S. United States Bridge Failures. J. Perform. Constr. Fac. 1990, 4, 272–277. [Google Scholar] [CrossRef]
- Pham, T.M.; Hao, H. Effect of the plastic hinge and boundary conditions on impact behavior of reinforced concrete beams. Int. J. Impact Eng. 2017, 102, 74–85. [Google Scholar] [CrossRef]
- Kishi, N.; Mikami, H.; Matsuoka, K.G. Impact behavior of shear failure type RC beams without shear rebar. Int. J. Impact Eng. 2002, 27, 955–968. [Google Scholar] [CrossRef]
- Kishi, N.; Mikami, H.; Ando, T. Impact resistant behavior of shear failure type RC beams under falling-weight impact loading. In Structures Under Shock and Impact VII; Jones, N., Brebbia, C.A., Rajendran, A.M., Eds.; WIT Press: Ashurst Lodge, UK, 2002; pp. 499–508. [Google Scholar]
- Mylrea, T.D. Effect of impact on reinforced concrete beams. ACI J. Proc. 1940, 36, 581–594. [Google Scholar] [CrossRef]
- Saatci, S.; Vecchio, F.J. Effects of shear mechanisms on impact behavior of rein-forced concrete beams. ACI Struct. J. 2009, 106, 78–86. [Google Scholar]
- Li, H.W.; Chen, W.S.; Hao, H. Influence of drop weight geometry and inter layer on impact behavior of RC beams. Int. J. Impact Eng. 2019, 131, 222–237. [Google Scholar] [CrossRef]
- Fan, W.; Liu, B.; Huang, X.; Sun, Y. Efficient modeling of flexural and shear behaviors in reinforced concrete beams and columns subjected to low-velocity impact loading. Eng. Struct. 2019, 195, 22–50. [Google Scholar] [CrossRef]
- Jones, N. Structural Impact; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Banthia, N.; Mindess, S.; Bentur, A.; Pigeon, M. Impact testing of concrete using a drop-weight impact machine. Exp. Mech. 1989, 29, 63–69. [Google Scholar] [CrossRef]
- Pham, T.M.; Hao, H. Plastic hinges and intertia force in RC beams under impact loads. Int. J. Impact Eng. 2017, 103, 1–11. [Google Scholar] [CrossRef]
- Cotsovos, D.; Stathopoulos, N.; Zeris, C. Behavior of RC beams subjected to high rates of concentrated loading. J. Struct. Eng. 2008, 134, 1839–1851. [Google Scholar] [CrossRef]
- Cotsovos, D. A simplified approach for assessing the load carrying capacity of reinforced concrete beams under concentrated load applied at high rates. Int. J. Impact Eng. 2010, 37, 907–917. [Google Scholar] [CrossRef]
- Gholipour, G.; Zhang, C.W.; Mousavi, A.A. Effects of axial load on nonlinear response of RC columns subjected to lateral impact load: Ship-pier collision. Eng. Fail. Anal. 2018, 91, 397–418. [Google Scholar] [CrossRef]
- Issac, P.; Darby, D.; Ibell, T.; Evernden, M. experimental investigation into the force propagation velocity due to hard impacts on reinforced concrete members. Int. J. Impact Eng. 2017, 100, 131–138. [Google Scholar] [CrossRef]
- Do, T.V.; Pham, T.M.; Hao, H. Dynamic responses and failure modes of bridge columns under vehicle collision. Eng Struct. 2018, 156, 243–259. [Google Scholar] [CrossRef]
- Pham, T.M.; Hao, Y.F.; Hao, H. Sensitivity of impact behavior of RC beams to contact stiffness. Int. J. Impact Eng. 2018, 112, 155–164. [Google Scholar] [CrossRef]
- Han, L.H.; Hou, C.C.; Zhao, X.L.; Rasmussen, K.J.R. Behaviour of high-strength concrete filled steel tubes under transverse impact loading. J. Constr. Steel Res. 2014, 92, 25–39. [Google Scholar] [CrossRef]
- Kishi, N.; Khasraghy, S.G.; Kon-No, H. Numerical simulation of reinforced concrete beams under consecutive impact loading. ACI Struct. J. 2011, 108, 444–452. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, X.; He, S.H. Numerical simulation of impact tests on reinforced concrete beams. Mater. Des. 2012, 39, 111–120. [Google Scholar] [CrossRef]
- Liao, W.Z.; Li, M.; Zhang, W.; Tian, Z.M. Experiment studies and numerical simulation of behavior of RC beams retrofitted with HSSWM-HPM under impact loading. Eng. Struct. 2017, 149, 131–146. [Google Scholar] [CrossRef]
- Liu, B.; Fan, W.; Guo, W.; Chen, B.; Liu, R. Experiment investigation and improved FE modeling of axially-loaded circular RC colums under lateral impact loading. Eng. Struct. 2017, 152, 619–642. [Google Scholar] [CrossRef]
- Aghdamy, S.; Thambiratnam, D.P.; Dhanasekar, M.; Saiedi, S. Effects of load-related parameters on the response of concrete-filled double-skin steel tube columns subjected to lateral impact. J. Constr. Steel Res. 2017, 138, 642–662. [Google Scholar] [CrossRef]
- Dogan, F.; Hadavinia, H.; Donchev, T.; Bhonge, P.S. Delamination of impacted composite structures by cohesive zone interface elements and tiebreak contact. Gentral Euro. J. Eng. 2012, 2, 612–626. [Google Scholar] [CrossRef]
- Sha, Y.; Hao, H. Laboratory tests and numerical simulations of barge impact on circular reinforced concrete piers. Eng. Struct. 2013, 46, 593–605. [Google Scholar] [CrossRef]
- Qian, K.; Weng, Y.H.; Li, B. Impact of two columns missing in dynamic response of RC flat slab structures. Eng. Struct. 2018, 177, 598–615. [Google Scholar] [CrossRef]
- Fan, W.; Xu, X.; Zhang, Z.Y.; Shao, X.D. Performance and sensitivity analysis of UHPFRC-strengthened bridge columns subjected to vehicle collisions. Eng. Struct. 2018, 173, 251–268. [Google Scholar] [CrossRef]
- Murray, Y.D.; Abu-Odeh, R.; Bligh, A. Evaluation of LS-DYNA concrete material model 159. In Report No. FHWA-HRT-05-063; Federal Highway Administration: Mclean, VA, USA, 2007. [Google Scholar]
- Meng, Y. Experiment and Numerical Simulation Study on Reinforced Concrete Beam Under Impact Loading; Hunan University: Changsha, China, 2012. [Google Scholar]
- Mosallam, A.; Elsanadedy, H.M.; Almusallam, T.H. Structural evaluation of reinforced concrete beams strengthened with innovative bolted/bonded advanced FRP composites sandwich panels. Compos. Struct. 2015, 124, 421–440. [Google Scholar] [CrossRef]
- Hao, H.; Hao, Y.; Li, J.; Chen, W. Review of the current practices in blast-resistant analysis and design of concrete structrures. Adv. Struct. Eng. 2016, 19, 1193–1223. [Google Scholar] [CrossRef]
- Malvar, L.J.; Ross, C.A. Review of strain rate effects for concrete in tension. ACI Mater. J. 1998, 95, 735–739. [Google Scholar] [CrossRef]
- Hao, Y.; Hao, H. Numerical evaluation of the influence of aggregates on concrete compressive strength at high strain rate. Int. J. Prot. Struct. 2011, 2, 177–206. [Google Scholar] [CrossRef]
- Hao, Y.; Hao, H.; Jiang, G.P.; Zhou, Y. Experimental confirmation of some factors influencing dynamic concrete compressive strength in high-speed impact tests. Cement Concr. Res. 2013, 52, 63–70. [Google Scholar] [CrossRef]
- Chen, W.; Hao, H.; Chen, S. Numerical analysis of prestressed reinforced concrete beam subjected to blast loading. Mater. Des. 2015, 65, 662–674. [Google Scholar] [CrossRef]
- Hao, Y.; Hao, H. Influence of the concrete DIF model on the numerical predictions of RC wall responses to blast loadings. Eng. Struct. 2014, 73, 24–38. [Google Scholar] [CrossRef]
- Comite Euro-International du Beton. CEB-FIB Model Code 1990; Redwood Book: Trowbridge, Wiltshire, UK, 1993. [Google Scholar]
- Malvar, L.J. Review of static and dynamic properties of steel reinforcing bars. ACI Mater. J. 1998, 95, 609–614. [Google Scholar] [CrossRef] [PubMed]
- Ditommaso, R.; Ponzo, F.C. Identifying Damage in Structures: Definition of Thresholds to Minimize False Alarms in SHM Systems. Buildings 2024, 14, 821. [Google Scholar] [CrossRef]
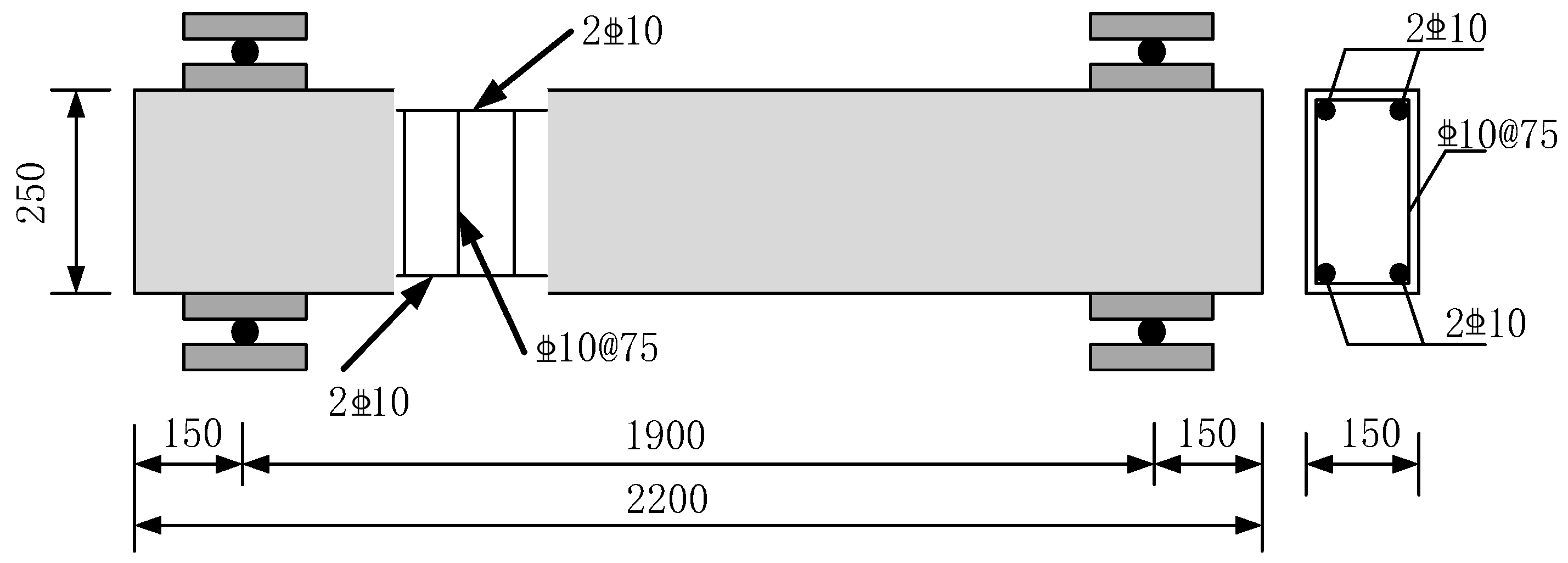
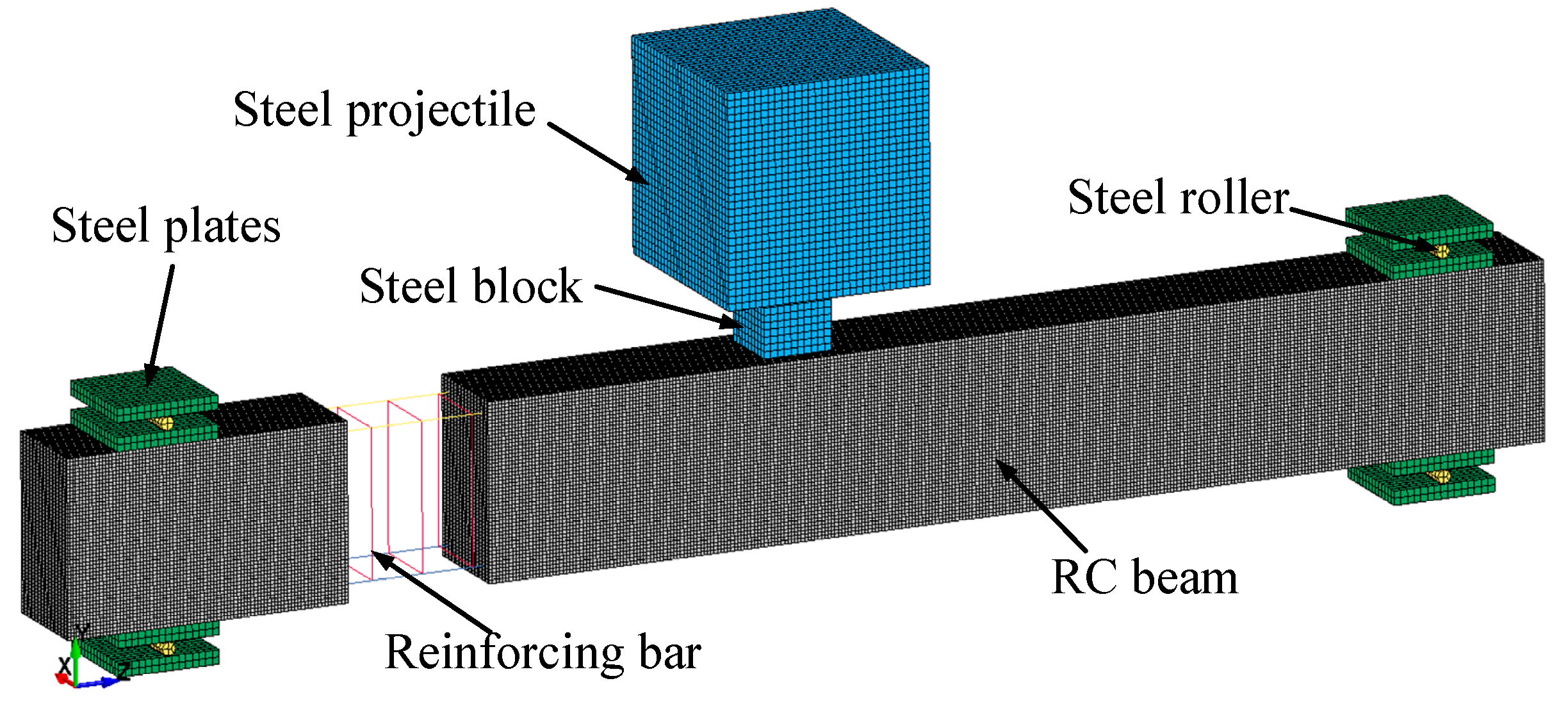
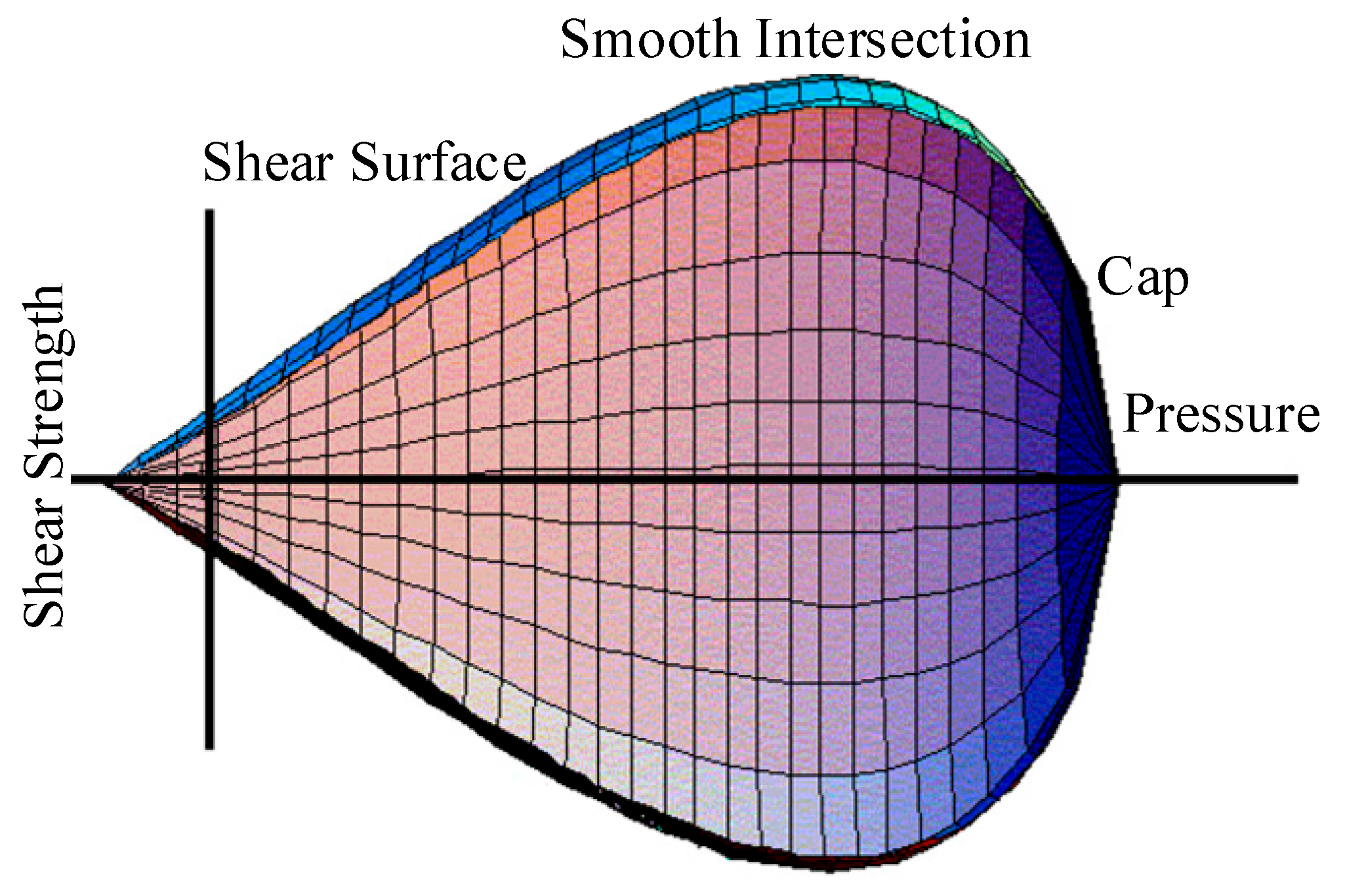


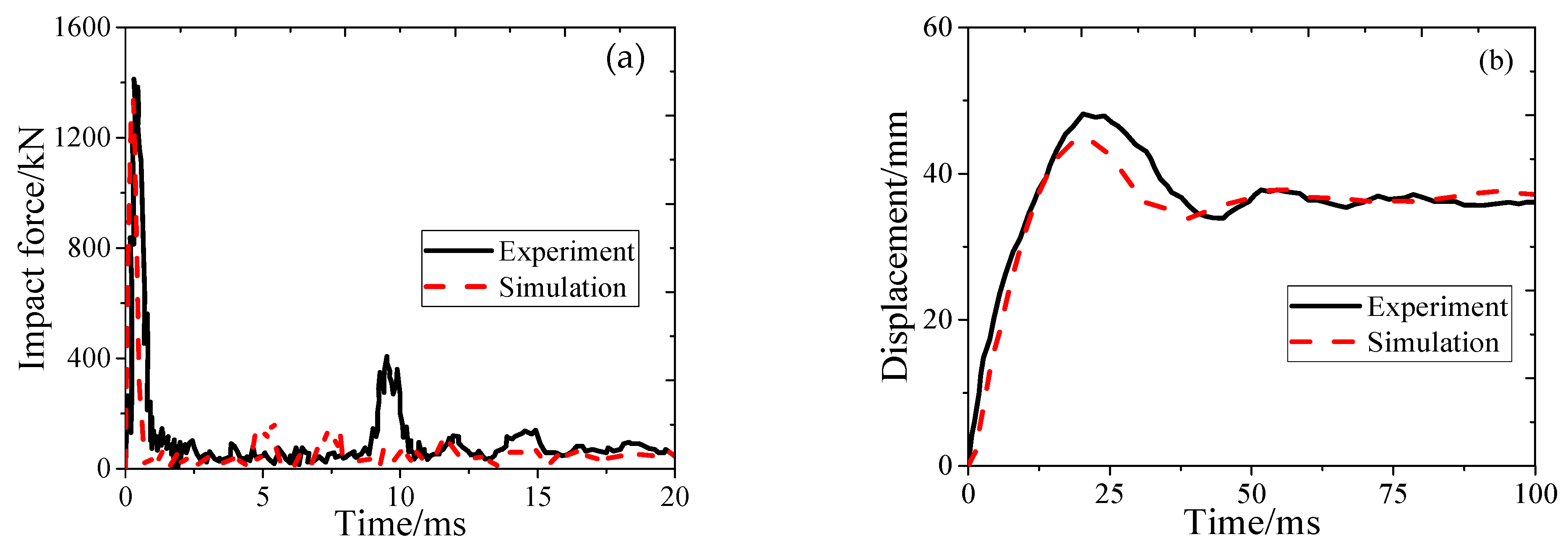
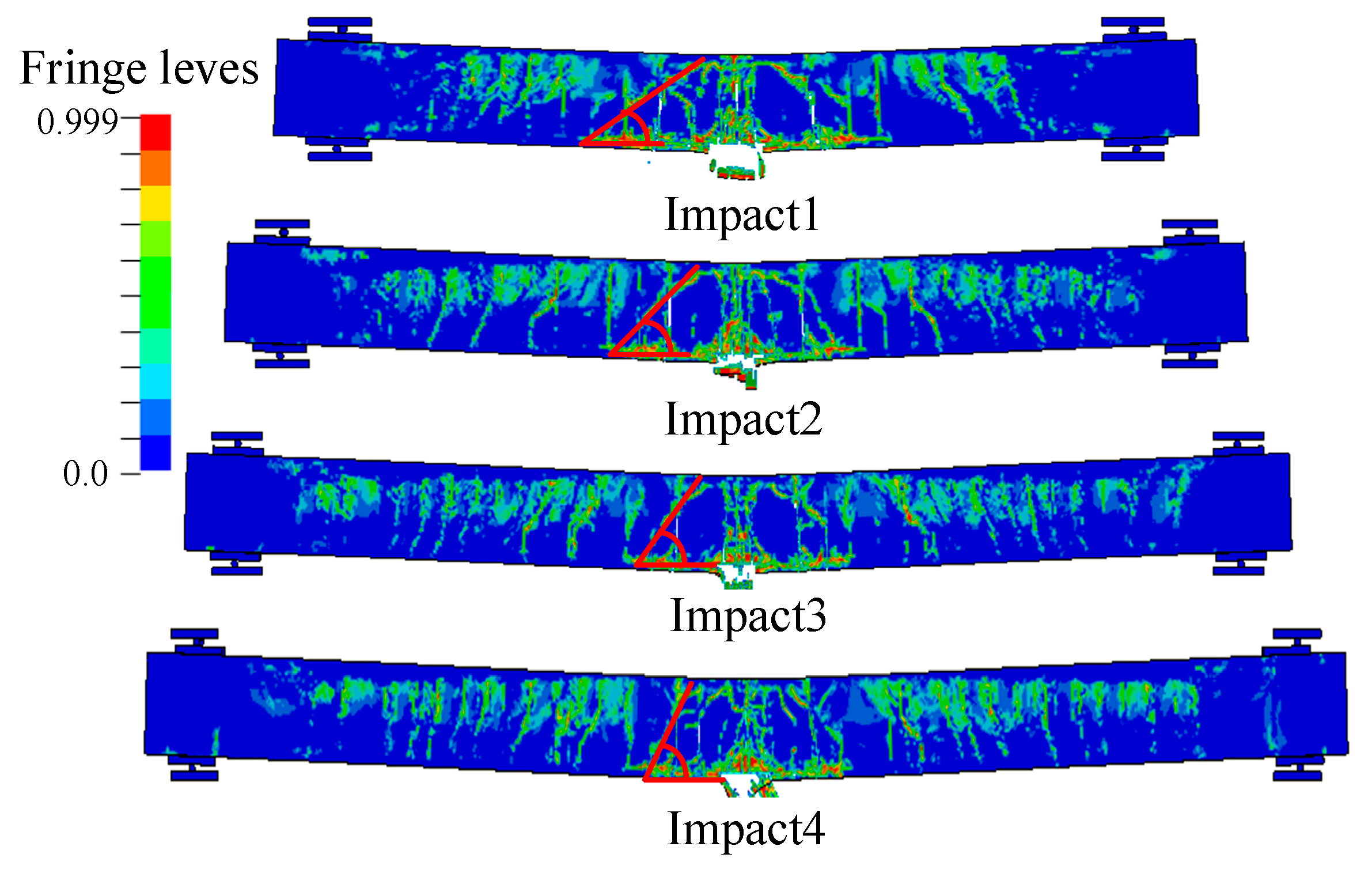
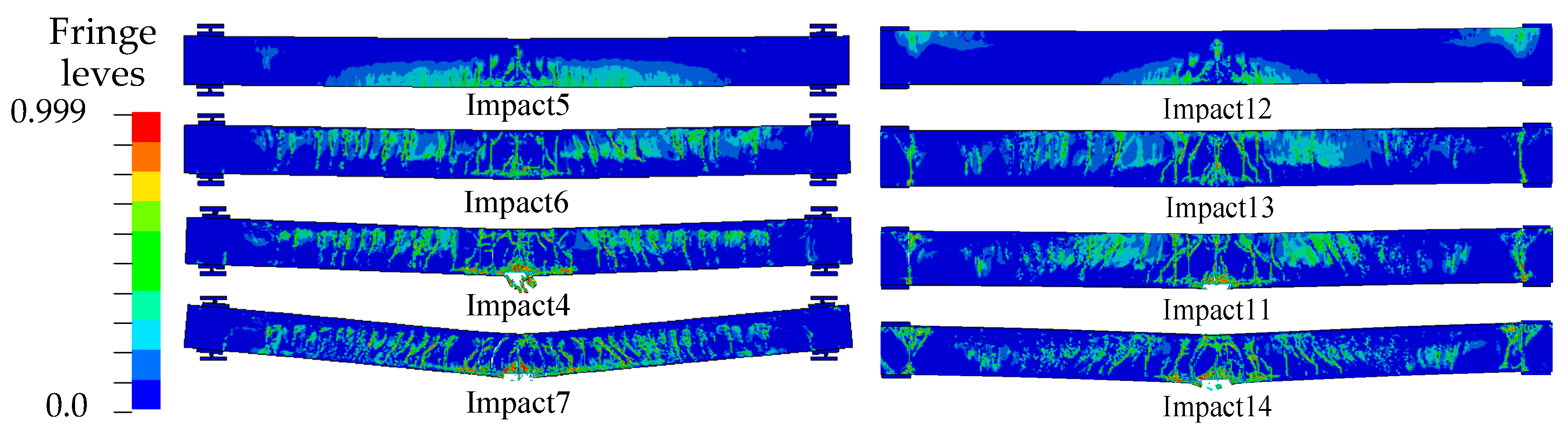


| Simulation | Clear Span (mm) | Impact Velocity (mm/s) | Boundary Condition | Concrete Strength (MPa) | Shear–Span Ratio |
|---|---|---|---|---|---|
| Impact 1 | 1900 | 6260 | Simply supported | 52 | 4.4 |
| Impact 2 | 2500 | 6260 | Simply supported | 52 | 5.8 |
| Impact 3 | 3000 | 6260 | Simply supported | 52 | 7.0 |
| Impact 4 | 3500 | 6260 | Simply supported | 52 | 8.1 |
| Impact 5 | 3500 | 2000 | Simply supported | 52 | 8.1 |
| Impact 6 | 3500 | 4000 | Simply supported | 52 | 8.1 |
| Impact 7 | 3500 | 9000 | Simply supported | 52 | 8.1 |
| Impact 8 | 3500 | 6260 | Simply supported | 30 | 8.1 |
| Impact 9 | 3500 | 6260 | Simply supported | 70 | 8.1 |
| Impact 10 | 3500 | 6260 | Simply supported | 90 | 8.1 |
| Impact 11 | 3500 | 6260 | Fixed end | 52 | 8.1 |
| Impact 12 | 3500 | 2000 | Fixed end | 52 | 8.1 |
| Impact 13 | 3500 | 4000 | Fixed end | 52 | 8.1 |
| Impact 14 | 3500 | 9000 | Fixed end | 52 | 8.1 |
| Impact 15 | 3500 | 6260 | Fixed end | 30 | 8.1 |
| Impact 16 | 3500 | 6260 | Fixed end | 70 | 8.1 |
| Impact 17 | 3500 | 6260 | Fixed end | 90 | 8.1 |
| Mid | Ro | Nplot | Incre | Irate | Erode | Recover | Iretrac |
|---|---|---|---|---|---|---|---|
| 159 | 2.4 × 10−9 | 1 | 0.000 | 1 | 1.1 | 0.000 | 0 |
| pred | |||||||
| 0.0 | |||||||
| g | k | alpha | theta | lambda | beta | nalpha | calpha |
| 30 | 15 | 15.9 | 0.38 | 10.5 | 1.929 × 10−2 | 0.0 | 0.0 |
| alpha1 | theta1 | lambda1 | beta1 | alpha2 | theta2 | lambda2 | beta2 |
| 0.74735 | 4.25 × 10−4 | 0.17 | 0.036 | 0.66 | 4.61 × 10−4 | 0.16 | 0.032 |
| Material | Material Model | Parameter | Value |
|---|---|---|---|
| Concrete | *MAT_159 (Mat_CSCM_CONCRETE) | Density | 2400 kg/m3 |
| Compressive strength | 52 MPa | ||
| Poisson’s ratio | 0.2 | ||
| Steel reinforcement | *MAT_024 (MAT_PIECEWISE_LINEAR_PLASTICITY) | Density | 7800 kg/m3 |
| Elastic modulus | 200 GPa | ||
| Yield strength | 550 MPa | ||
| Poisson’s ratio | 0.3 | ||
| Failure strain | 0.15 | ||
| Steel impactor, steel block, steel plates, and steel rollers | *MAT_001(ELASTIC) | Density | 7800 kg/m3 |
| Elastic modulus | 200 GPa | ||
| Poisson’s ratio | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Kang, Z.; Yu, G.; Wang, S.; Wu, M.; Bu, L.; Farooq, A.; Kai, C. Dynamic Response and Failure Mode of Reinforced Concrete Beams Subjected to Impact. Buildings 2025, 15, 3250. https://doi.org/10.3390/buildings15183250
Li J, Kang Z, Yu G, Wang S, Wu M, Bu L, Farooq A, Kai C. Dynamic Response and Failure Mode of Reinforced Concrete Beams Subjected to Impact. Buildings. 2025; 15(18):3250. https://doi.org/10.3390/buildings15183250
Chicago/Turabian StyleLi, Jianhe, Zichun Kang, Guo Yu, Shuai Wang, Min Wu, Lei Bu, Asim Farooq, and Chen Kai. 2025. "Dynamic Response and Failure Mode of Reinforced Concrete Beams Subjected to Impact" Buildings 15, no. 18: 3250. https://doi.org/10.3390/buildings15183250
APA StyleLi, J., Kang, Z., Yu, G., Wang, S., Wu, M., Bu, L., Farooq, A., & Kai, C. (2025). Dynamic Response and Failure Mode of Reinforced Concrete Beams Subjected to Impact. Buildings, 15(18), 3250. https://doi.org/10.3390/buildings15183250






