Application of an Automated Parameter Determination Framework to Boundary Value Problems
Abstract
1. Introduction
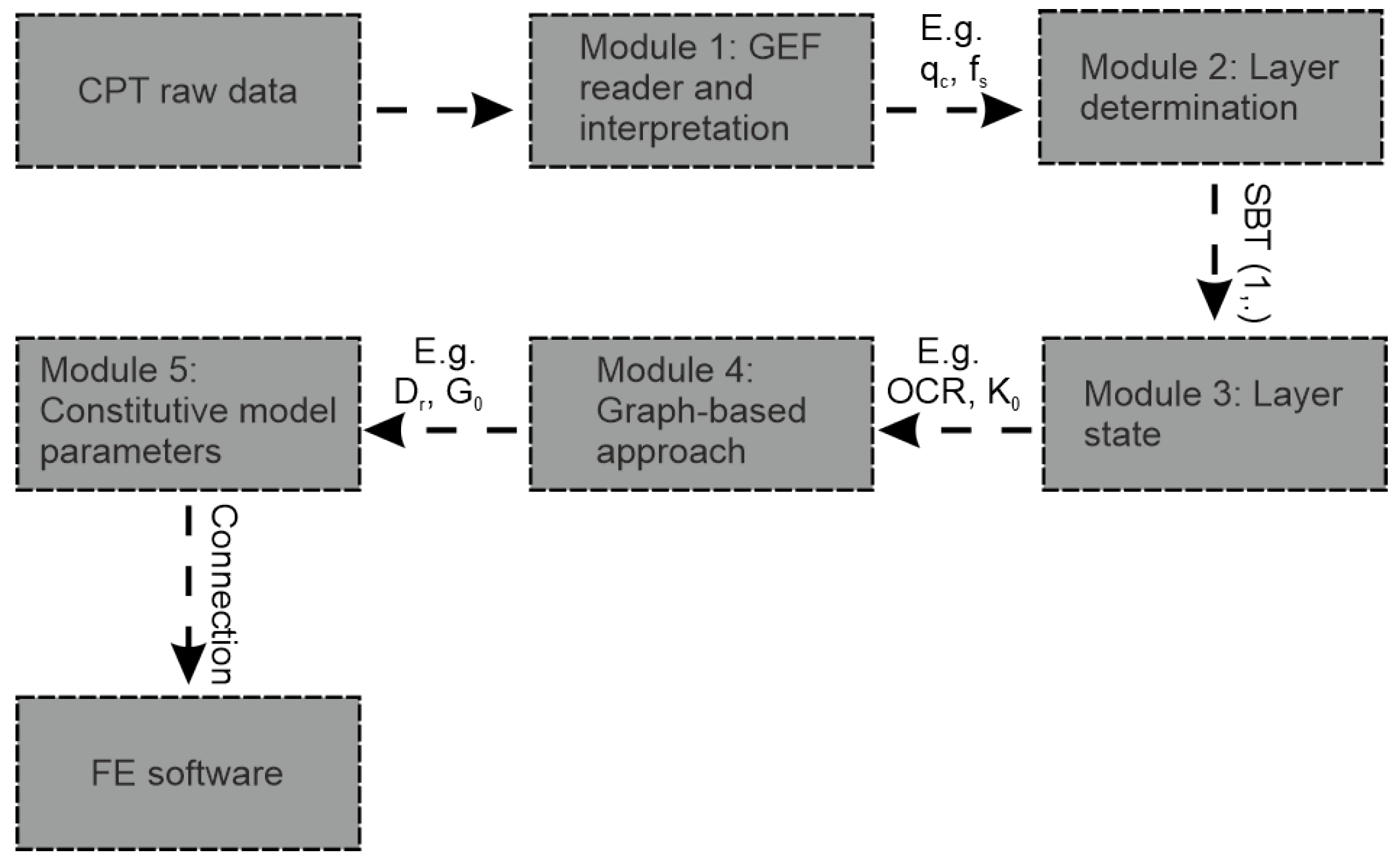
2. APD
2.1. APD Modules
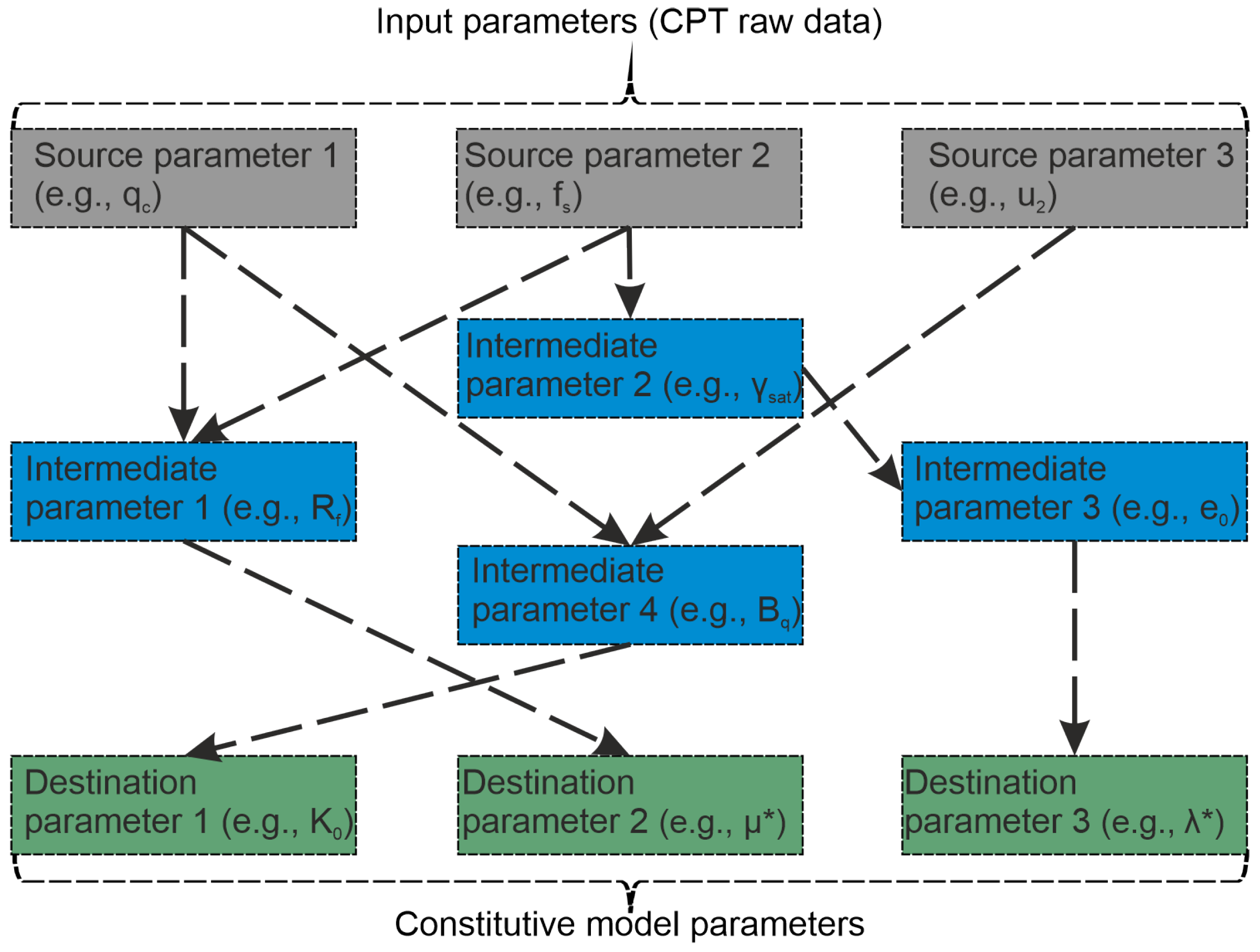
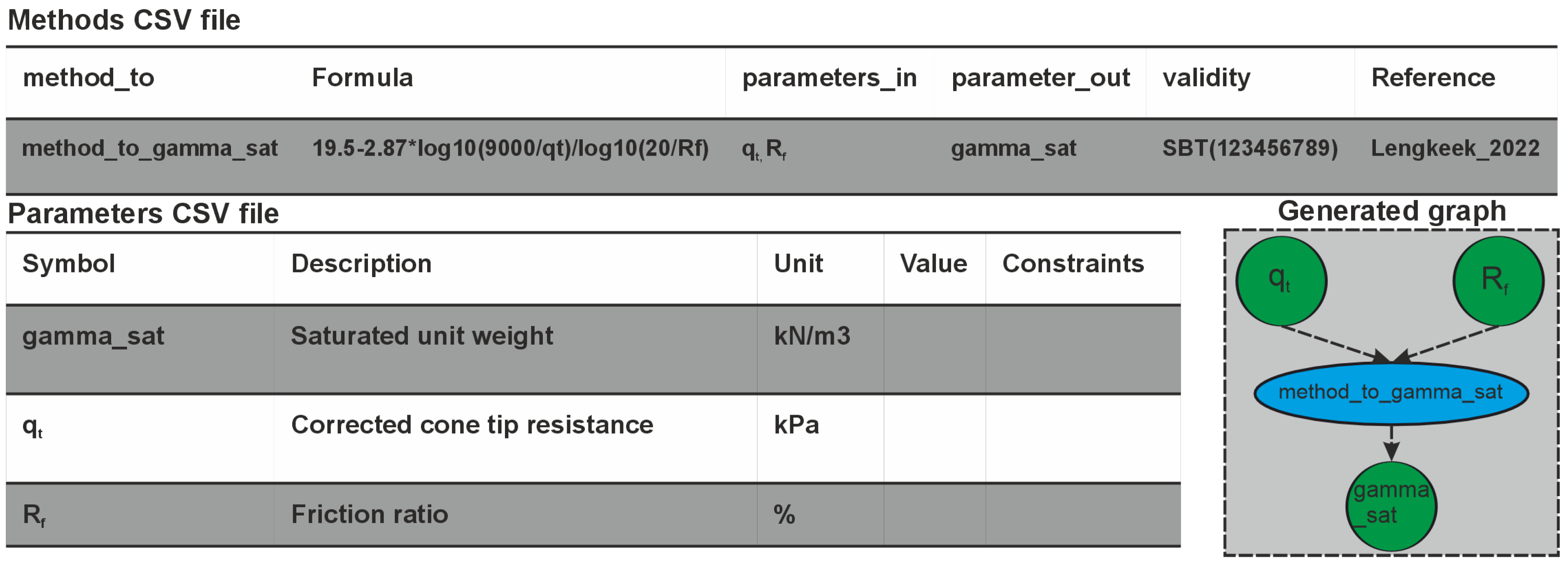
2.2. Graph-Based Approach
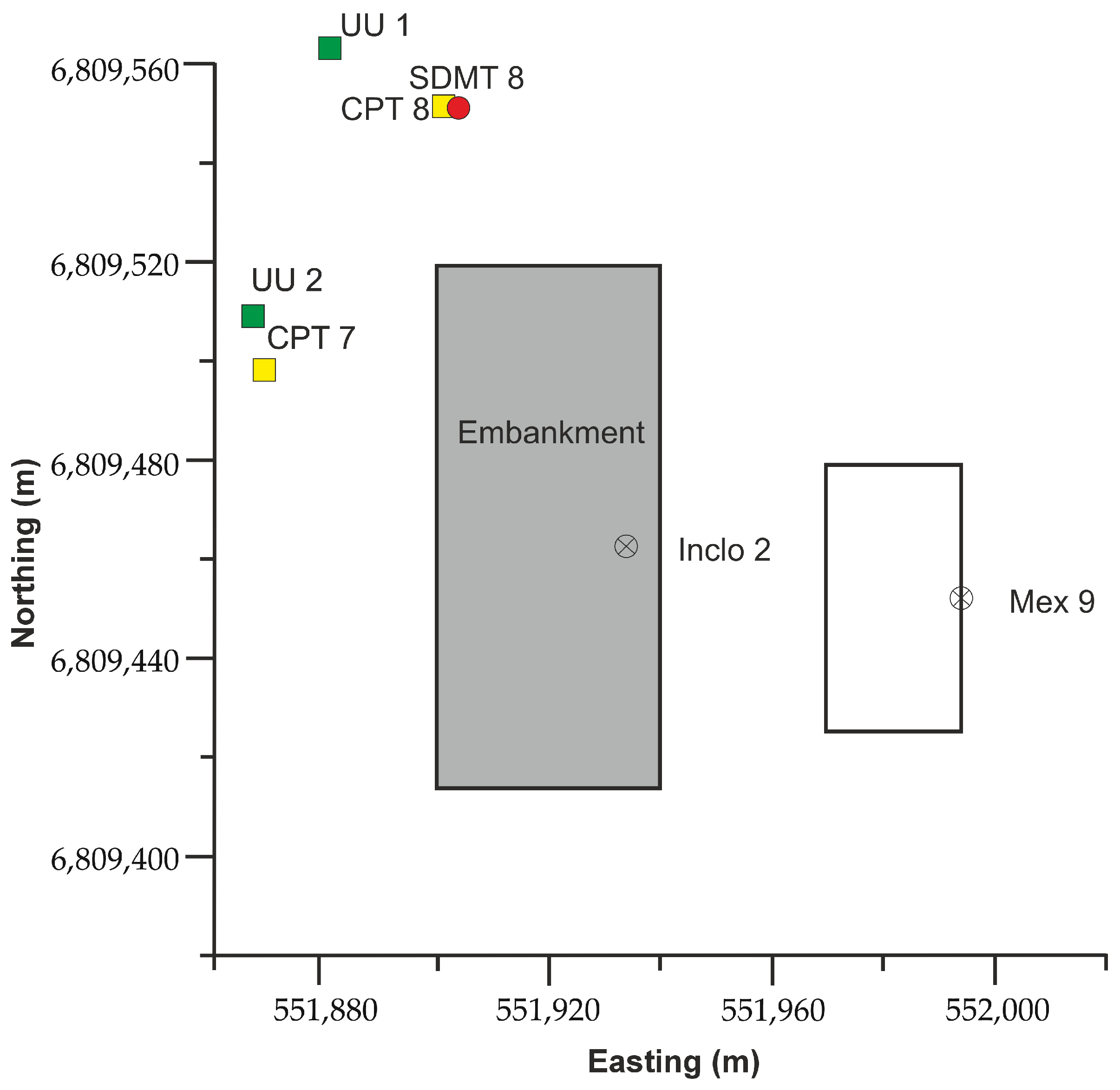
3. Test Site
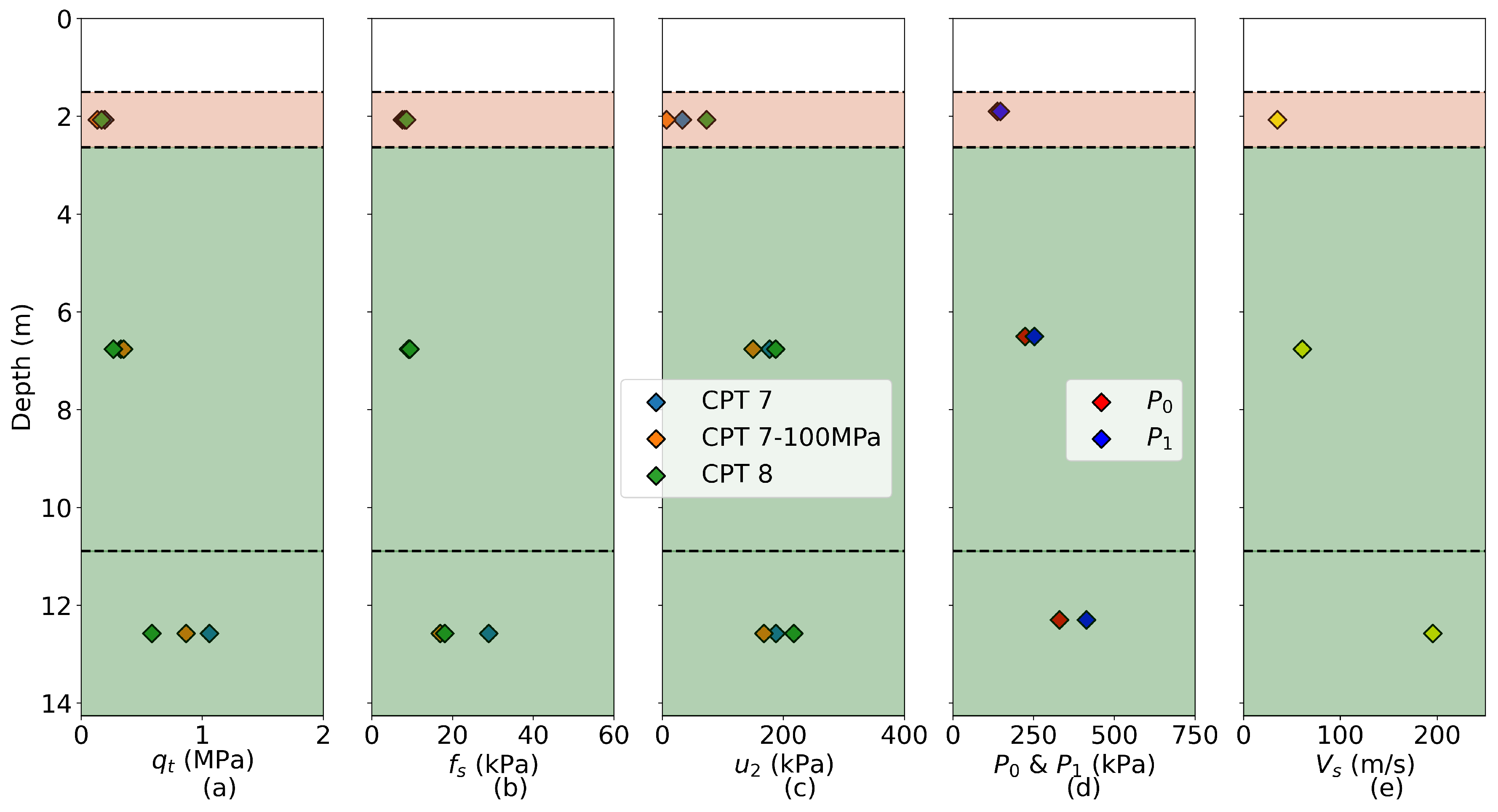
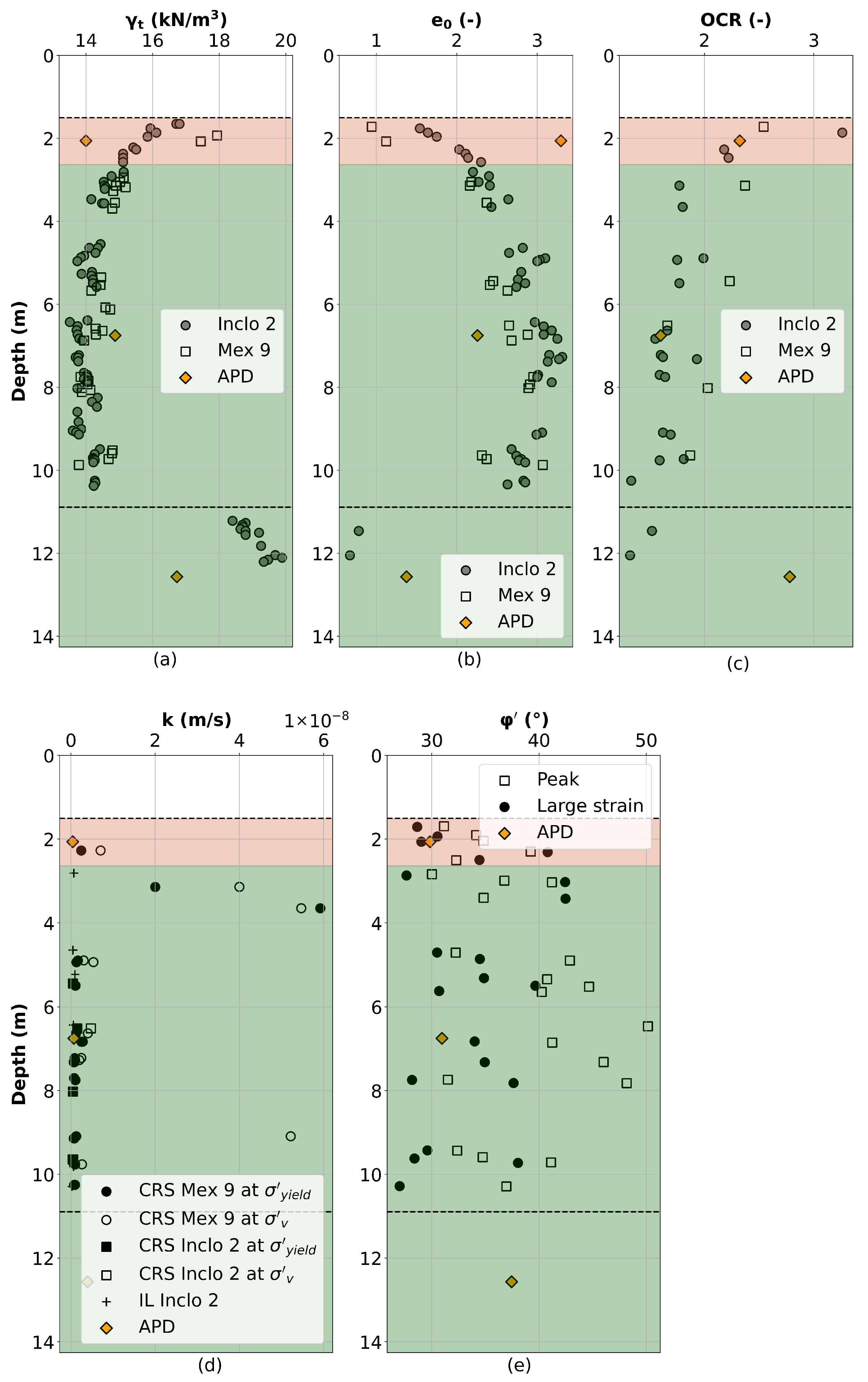
4. Application of APD to the Test Site
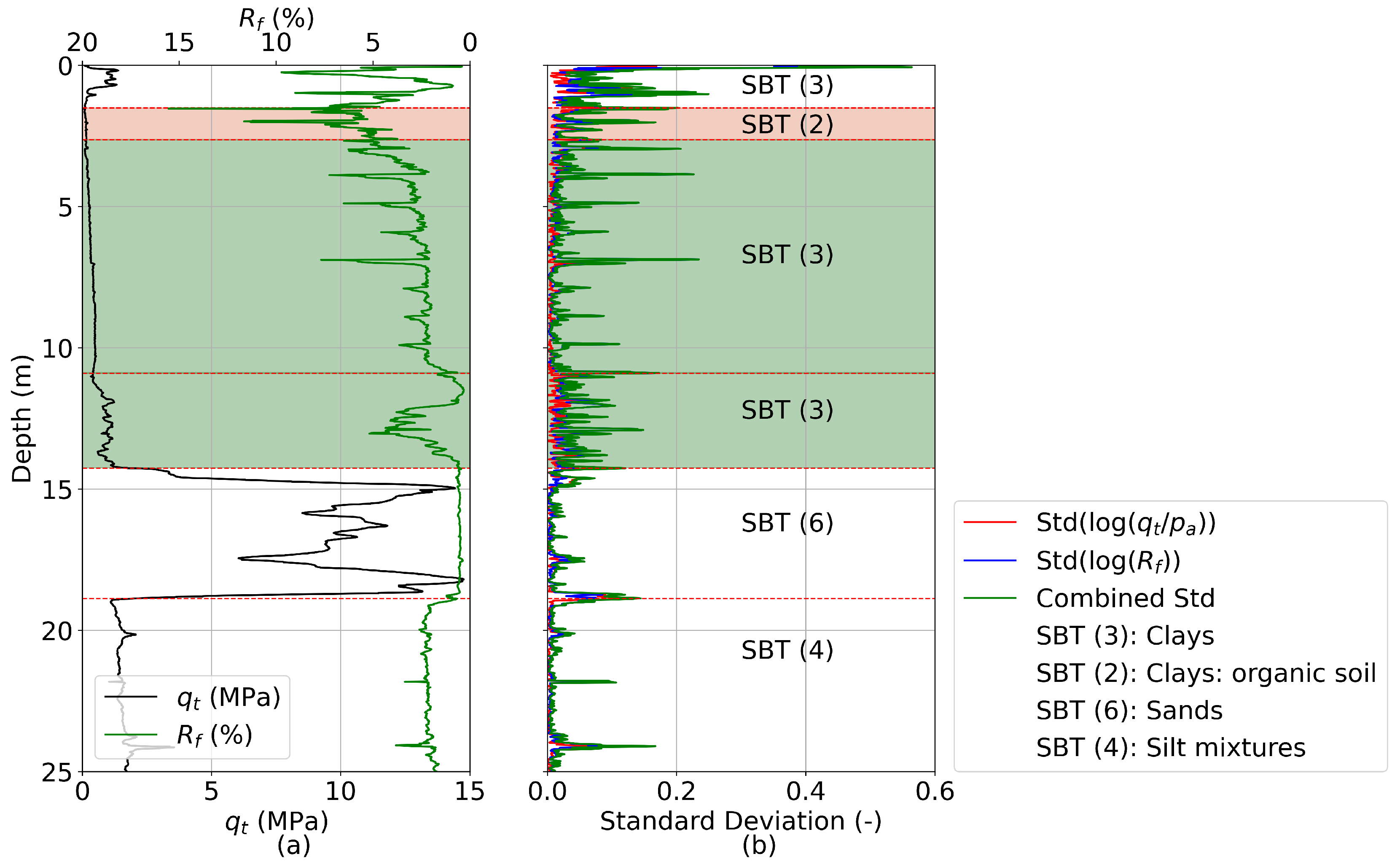
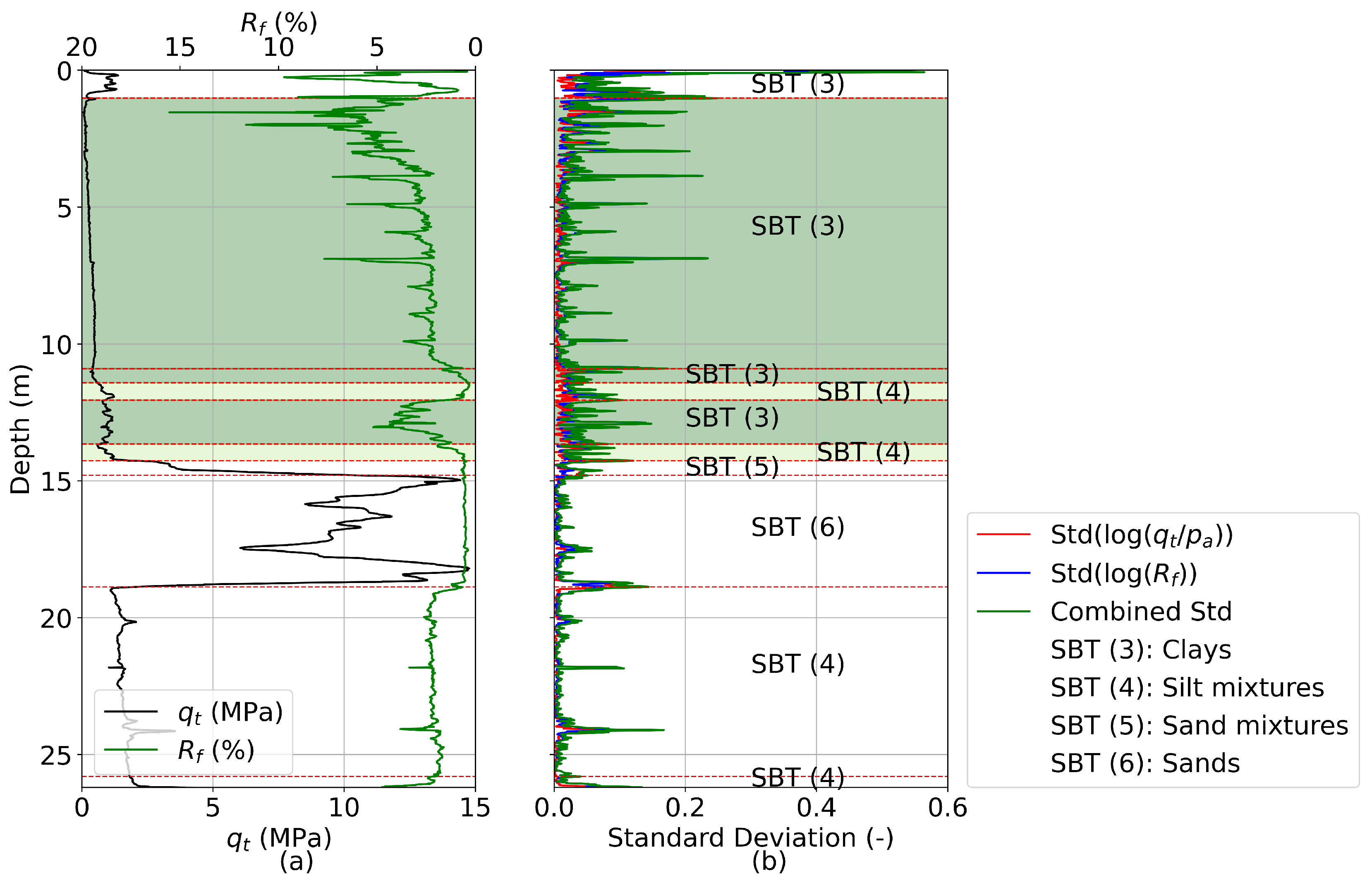
4.1. Stratification
- Preprocessing: Converts and to their logarithmic forms, i.e., and .
- Detection of fluctuations using a moving window: Computes moving standard deviations over a specified window of measurements (e.g., 7 points) for and , and combines them into a single metric—the combined standard deviation.
- Peak identification: Detects spikes in the combined standard deviation and retains only one peak within every meters, as specified by the user. The choice of significantly influences the number and thickness of the resulting layers; smaller values allow for a finer resolution, while larger values enforce a minimum layer thickness and suppress closely spaced transitions.
- Filtering of similar layers: For each detected peak, the two adjacent layers are identified, and their positions in Robertson’s modified non-normalised SBT chart [32] are determined. The distance between these positions is calculated and compared to a threshold value (typically in the range [0.1–0.3] [31]). If the distance is below the threshold, the layers are considered similar, and the peak is discarded.
4.2. Constitutive Model
4.3. Parameter Determination
- Index parameters: unit weight () and void ratio ().
- Stiffness parameters: modified compression index (), modified swelling index (), and modified creep index ().
- Strength parameters: effective friction angle () and effective cohesion ().
- Permeability (k)
- State parameters: overconsolidation ratio (OCR) and coefficient of earth pressure at rest ().
| Workflow | Method | Author | |
|---|---|---|---|
| CPT | ; | (15) | [43,44] |
| (16) | [45] | ||
| (17) | [46] | ||
| (18) | [47] | ||
| (19) | [48] | ||
| (20) | [49] | ||
| (21) | [49] | ||
| DMT | (22) | [50] | |
| (23) | [51] | ||
| (24) | [52] | ||
| (25) | [53] | ||
| (26) | [54] | ||
| (27) | [55] as cited in [54] | ||
| (28) | [56] | ||
| (29) | [1] |
- Modified compression index (): A direct method between CPT measurements and the compression ratio () is provided by [57]:where .Alternatively, several empirical correlations exist between the compression index () and common index parameters such as the plasticity index (), void ratio (), and liquid limit (). In this study, the following method between and from [58] is used:from which is calculated as follows:The plasticity index () can be estimated from CPT data using the method proposed by [59]:
- Modified swelling index (): is determined from according to [57]:
- Modified creep index (): Two methods for estimating the creep ratio () are presented in [57]:and is then computed as
4.4. Results
5. Boundary Value Problems
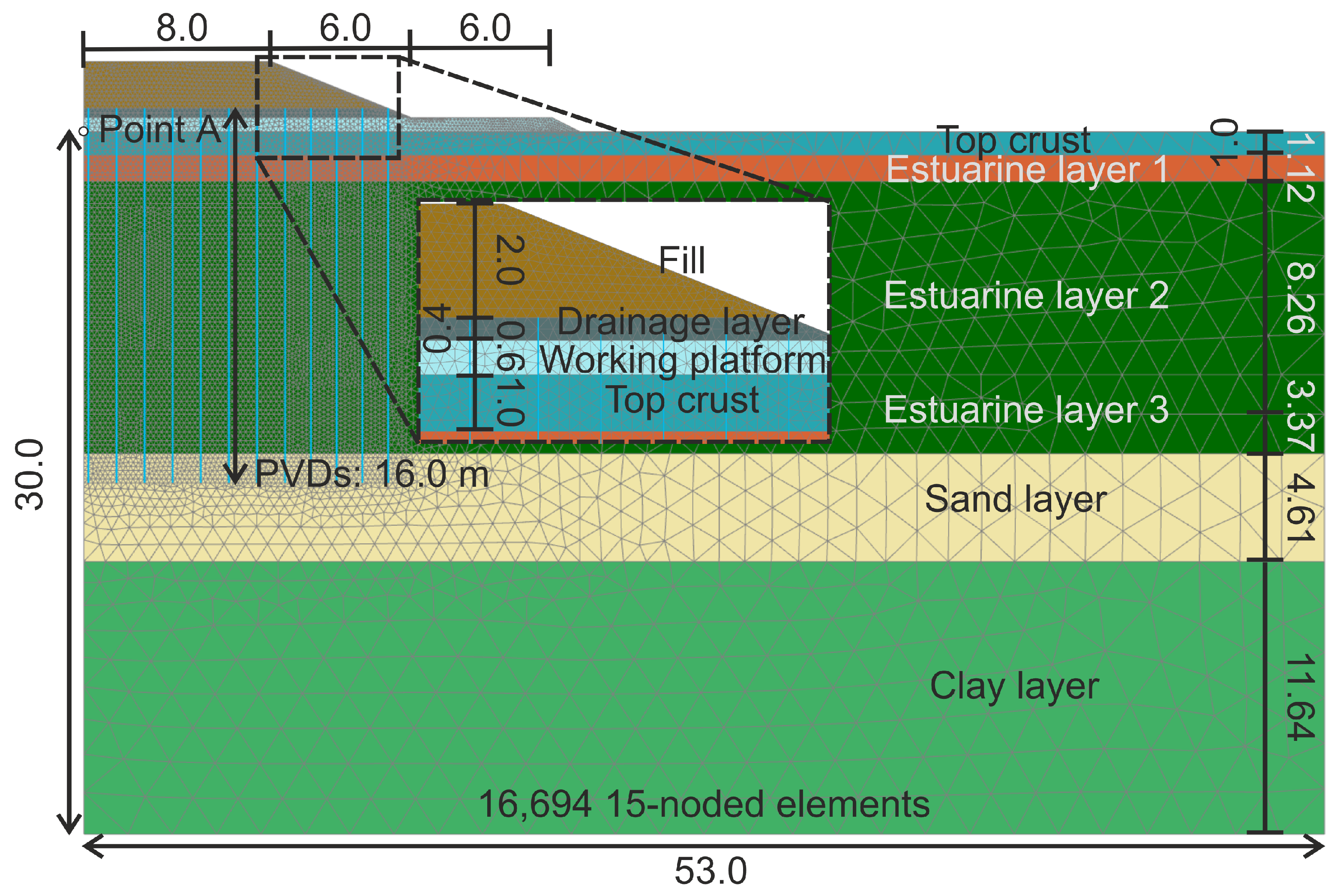
5.1. Long-Term Settlements of Embankment
- Initial phase;
- Installation of a 0.6 m working platform (see Figure 10)—duration: 3 days;
- Consolidation—duration: 14 days;
- Installation of a 0.4 m sand layer (see Figure 10)—duration: 8 days;
- Activation of PVDs—duration: 23 days;
- Construction of a 2.0 m embankment (see Figure 10)—duration: 16 days;
- Final consolidation—duration: 1026 days.
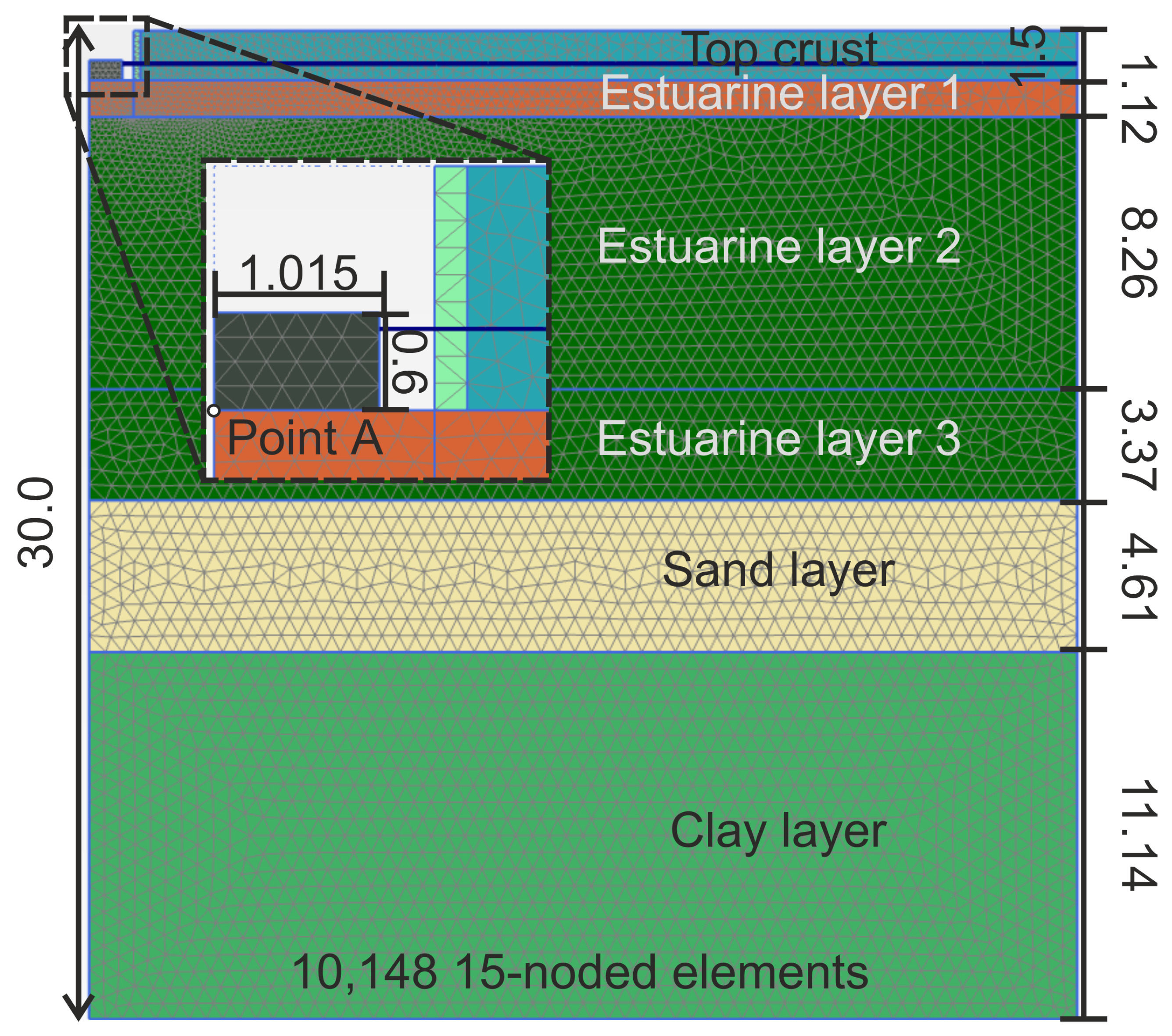
5.2. Failure Load of Shallow Footing
- Initial phase;
- Excavation;
- Construction of the footing;
- Consolidation-duration: 30 days;
- Application of load.
6. Discussion
6.1. Motivation of the Study
6.2. Initial Unit Weight
6.3. Uncertainty in the Obtained Values
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duan, W.; Cai, G.; Liu, S.; Puppala, A.J. Correlations between Shear Wave Velocity and Geotechnical Parameters for Jiangsu Clays of China. Pure Appl. Geophys. 2019, 176, 669–684. [Google Scholar] [CrossRef]
- Lunne, T.; Robertson, P.; Powell, J. Cone Penetration Testing in Geotechnical Practice, 1st ed.; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Mayne, P.W. Interpretation of geotechnical parameters from seismic piezocone tests. In Proceedings of the 3rd International Symposium on Cone Penetration Testing, Las Vegas, NV, USA, 13–14 May 2014. [Google Scholar]
- Marchetti, S.; Monaco, P.; Totani, G.; Calabrese, M. The Flat Dilatometer Test (DMT) in Soil Investigations—A Report by the ISSMGE Committee TC16; International Society for Soil Mechanics and Geotechnical Engineering (ISSMGE): London, UK, 2001. [Google Scholar]
- Mair, R.; Wood, D. Pressuremeter Testing: Methods and Interpretation; Elsevier Science: Kent, UK, 1987. [Google Scholar]
- Clarke, B. Pressuremeters in Geotechnical Design, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Brinkgreve, R.; Engin, E.; Engin, H. Validation of empirical formulas to derive model parameters for sands. In Proceedings of the 7th NUMGE 2010, Trodheim, Norway, 2–4 June 2010. [Google Scholar]
- Tao, Y.q.; Sun, H.l.; Cai, Y.q. Bayesian inference of spatially varying parameters in soil constitutive models by using deformation observation data. Int. J. Numer. Anal. Methods Geomech. 2021, 45, 1647–1663. [Google Scholar] [CrossRef]
- Van Berkom, I.; Brinkgreve, R.; Lengkeek, H.; de Jong, A. An automated system to determine constitutive model parameters from in situ tests. In Proceedings of the 20th International Conference on Soil Mechanics and Geotechnical Engineering, Sydney, Australia, 1–5 May 2022. [Google Scholar]
- Marzouk, I.; Brinkgreve, R.; Lengkeek, H.; Tschuchnigg, F. APD: An automated parameter determination system based on in-situ tests. Comput. Geotech. 2024, 176, 106799. [Google Scholar] [CrossRef]
- Marzouk, I.; Tschuchnigg, F.; Brinkgreve, R. Expansion of an automated system for determining soil parameters using in-situ tests. In Proceedings of the 10th European Conference on Numerical Methods in Geotechnical Engineering (NUMGE 2023), London, UK, 26–28 June 2023. [Google Scholar] [CrossRef]
- Marzouk, I.; Oberhollenzer, S.; Tschuchnigg, F. An automated system for determining soil parameters: Case study. In Proceedings of the 8th International Symposium on Deformation Characteristics of Geomaterials, Porto, Portugal, 3–6 September 2023. [Google Scholar] [CrossRef]
- Marzouk, I.; Tschuchnigg, F. A combined approach to Automated Parameter Determination (APD). In Proceedings of the 7th International Conference on Geotechnical and Geophysical Site Characterization, Barcelona, Spain, 18–24 June 2024. [Google Scholar] [CrossRef]
- Yu, H. CASM: A unified state parameter model for clay and sand. Int. J. Numer. Anal. Methods Geomech. 1998, 22, 621–653. [Google Scholar] [CrossRef]
- Marzouk, I.; Wijaya, A.E.; Schweiger, H.F.; Tschuchnigg, F. An automated system for determining soil parameters from in situ tests: Application to a sand site. Aims Geosci. 2025, 11, 489–516. [Google Scholar] [CrossRef]
- Marzouk, I.; Tschuchnigg, F. Bridging In Situ Testing and Constitutive Modelling: An Automated Approach to Soil Parameter Identification. Appl. Sci. 2025, 15, 7224. [Google Scholar] [CrossRef]
- Schanz, T.; Vermeer, P.; Bonnier, P. The hardening soil model: Formulation and verification. In Beyond 2000 in Computational Geotechnics; Routledge: London, UK, 1999; pp. 281–296. [Google Scholar]
- Benz, T. Small-Strain Stiffness of Soils and Its Numerical Consequences. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2007. [Google Scholar]
- Bentley System Inc. PLAXIS 2D (24.3); Bentley System Inc.: Exton, PA, USA, 2024. [Google Scholar]
- Marzouk, I.; Granitzer, A.; Rauter, S.; Tschuchnigg, F. A Case Study on Advanced CPT Data Interpretation: From Stratification to Soil Parameters. Geotech. Geol. Eng. 2024, 42, 4087–4113. [Google Scholar] [CrossRef]
- Gansner, E. Drawing Graph with Graphviz; AT&T Bell Laboratories: New York, NY, USA, 2011. [Google Scholar]
- Pineda, J.A.; Kelly, R.B.; Suwal, L.; Bates, L.; Sloan, S.W. The Ballina soft soil Field Testing Facility. Aims Geosci. 2019, 5, 509–534. [Google Scholar] [CrossRef]
- Kelly, R.B.; Pineda, J.A.; Bates, L.; Suwal, L.P.; Fitzallen, A. Site characterisation for the Ballina field testing facility. Géotechnique 2017, 67, 279–300. [Google Scholar] [CrossRef]
- Pineda, J.A.; Suwal, L.P.; Kelly, R.B.; Bates, L.; Sloan, S.W. Characterisation of Ballina clay. Géotechnique 2016, 66, 556–577. [Google Scholar] [CrossRef]
- Doherty, J.; Gourvenec, S.; Gaone, F.; Pineda, J.; Kelly, R.; O’Loughlin, C.; Cassidy, M.; Sloan, S. A novel web based application for storing, managing and sharing geotechnical data, illustrated using the national soft soil field testing facility in Ballina, Australia. Comput. Geotech. 2018, 93, 3–8. [Google Scholar] [CrossRef]
- Tschuchnigg, F.; Schweiger, H. Embankment and footing prediction by means of 2D and 3D finite element analyses. In Proceedings of the Embankment and Footing Prediction Symposium, Newcastle, Australia, 12–13 September 2016; pp. 360–390. [Google Scholar]
- Tschuchnigg, F.; Schweiger, H.F. Embankment prediction and back analysis by means of 2D and 3D finite element analyses. Comput. Geotech. 2018, 93, 104–114. [Google Scholar] [CrossRef]
- Rauter, S.; Tschuchnigg, F. CPT Data Interpretation Employing Different Machine Learning Techniques. Geosciences 2021, 11, 265. [Google Scholar] [CrossRef]
- Rauter, S.; Tschuchnigg, F. Identification of Soil Strata from In-Situ Test Data Using Machine Learning. In Proceedings of the Challenges and Innovations in Geomechanics, Turin, Italy, 30 August–2 September 2022; Barla, M., Di Donna, A., Sterpi, D., Insana, A., Eds.; Springer: Cham, Switzerland, 2022; pp. 37–44. [Google Scholar] [CrossRef]
- Oberhollenzer, S.; Premstaller, M.; Marte, R.; Tschuchnigg, F.; Erharter, G.H.; Marcher, T. Cone penetration test dataset Premstaller Geotechnik. Data Brief 2021, 34, 106618. [Google Scholar] [CrossRef]
- Brinkgreve, R.B.J.; Tschuchnigg, F.; Laera, A.; Brasile, R.S. Automated CPT interpretation and modelling in a BIM/Digital Twin environment. In Proceedings of the 10th European Conference on Numerical Methods in Geotechnical Engineering (NUMGE 2023), London, UK, 26–28 June 2023. [Google Scholar] [CrossRef]
- Robertson, P. Soil Behaviour Type from the CPT: An Update. In Proceedings of the 2nd International Symposium on Cone Penetration Testing, Huntington Beach, CA, USA, 9–11 May 2010; pp. 575–583. [Google Scholar]
- Kelly, R.; Sloan, S.; Pineda, J.; Kouretzis, G.; Huang, J. Outcomes of the Newcastle symposium for the prediction of embankment behaviour on soft soil. Comput. Geotech. 2018, 93, 9–41. [Google Scholar] [CrossRef]
- Vermeer, P.; Neher, H. A soft soil model that accounts for creep. In Proceedings of the Beyond 2000 in Computational Geotechnics—10 Years of PLAXIS International, Balkema, Rotterdam, The Netherlands, 18–20 March 1999; pp. 249–261. [Google Scholar]
- Robertson, P.; Cabal, K. Estimating soil unit weight from CPT. In Proceedings of the 2nd International Symposium on Cone Penetration Testing, Huntington Beach, CA, USA, 9–11 May 2010. [Google Scholar]
- Lengkeek, H.; Brinkgreve, R. CPT-based unit weight estimation extended to soft organic clays and peat: An update. In Cone Penetration Testing 2022; CRC Press: Boca Raton, FL, USA, 2022; pp. 503–508. [Google Scholar] [CrossRef]
- Mayne, P.; Cargil, E.; Greig, J. A CPT Design Parameter Manual; ConeTec Group: Richmond, BC, Canada, 2023. [Google Scholar]
- Marchetti, S.; Crapps, D.K. Flat Dilatometer Manual; Internal Report of G.P.E. Inc.; G.P.E. Inc.: Gainesville, FL, USA, 1981. [Google Scholar]
- Ozer, A.T.; Bartlett, S.F.; Lawton, E.C. CPTU and DMT for estimating soil unit weight of Lake Bonneville clay. In Proceedings of the 4th International Conference on Site Characterization 4, ISC-4, Porto de Galinhas, Brazil, 18–21 September 2012; pp. 291–296. [Google Scholar]
- Mayne, P.W. Stress-strain-strength-flow parameters from enhanced in situ tests. In Proceedings of the International Conference on In Situ Measurement of Soil Properties & Case Histories, Bali, Indonesia, 21–24 May 2001. [Google Scholar]
- Mayne, P.W. In-Situ Test Calibrations for Evaluating Soil Parameters. In Characterisation and Engineering Properties of Natural Soils; Taylor & Francis Group: London, UK, 2007; Volume 3, pp. 1601–1652. [Google Scholar]
- Burns, S.; Mayne, P.W. Small- and High-Strain Measurements of In Situ Soil Properties Using the Seismic Cone Penetrometer. Transp. Res. Rec. J. Transp. Res. Board 1996, 1548, 81–88. [Google Scholar] [CrossRef]
- Mayne, P.W.; Coop, M.; Springman, S.; Huang, A.B.; Zornberg, J. State-of-the-art paper (SOA-1): Geomaterial behavior and testing. In Proceedings of the 17th International Conference on Soil Mechanics and Geotechnical Engineering, Alexandria, Egypt, 5–9 October 2009. [Google Scholar]
- Mayne, P.W. Stress History of Soils from Cone Penetration Tests. Soils Rocks 2017, 40, 203–218. [Google Scholar] [CrossRef]
- Robertson, P. Interpretation of cone penetration tests—A unified approach. Can. Geotech. J. 2009, 46, 1337–1355. [Google Scholar] [CrossRef]
- Paniagua, P.; D’Ignazio, M.; L’Heureux, J.S.; Lunne, T.; Karlsrud, K. CPTU correlations for Norwegian clays: An update. Aims Geosci. 2019, 5, 82–103. [Google Scholar] [CrossRef]
- Chen, B.S.; Mayne, P.W. Statistical relationships between piezocone measurements and stress history of clays. Can. Geotech. J. 1996, 33, 488–498. [Google Scholar] [CrossRef]
- Schroeder, K.; Andersen, K.H.; Tjok, K.M. Laboratory Testing and Detailed Geotechnical Design of the Mad Dog Anchors. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 1–4 May 2006. [Google Scholar] [CrossRef]
- D’Ignazio, M.; Lunne, T.; Andersen, K.H.; Yang, S.; Di Buò, B.; Länsivaara, T. Estimation of preconsolidation stress of clays from piezocone by means of high-quality calibration data. Aims Geosci. 2019, 5, 104–116. [Google Scholar] [CrossRef]
- Marchetti, S. In Situ Tests by Flat Dilatometer. J. Geotech. Eng. Div. 1980, 106, 299–321. [Google Scholar] [CrossRef]
- Cao, L.F.; Peaker, S.M.; Ahmad, S. Use of Flat Dilatometer in Ontario. In Proceedings of the Fifth International Conference on Geotechnical and Geophysical Site Characterisation, Gold Coast, QLD, Australia, 5–9 September 2016; pp. 755–760. [Google Scholar]
- Powell, J.J.M.; Uglow, I.M. The Interpretation of the Marchetti Dilatometer Test in UK Clays; Telford (Thomas) Limited: London, UK, 1989. [Google Scholar]
- Monaco, P.; Amoroso, S.; Marchetti, S.; Marchetti, D.; Totani, G.; Cola, S.; Simonini, P. Overconsolidation and Stiffness of Venice Lagoon Sands and Silts from SDMT and CPTU. J. Geotech. Geoenviron. Eng. 2014, 140, 215–227. [Google Scholar] [CrossRef]
- Long, M.; L’Heureux, J.S. Shear wave velocity—SCPTU correlations for sensitive marine clays. In Cone Penetration Testing 2022; Gottardi, G., Tonni, L., Eds.; CRC Press: Boca Raton, FL, USA, 2022; pp. 515–520. [Google Scholar] [CrossRef]
- Mayne, P.; Robertson, P.K.; Lunne, T. Clay stress history evaluated from seismic piezocone tests. In Proceedings of the 1st. International Conference on Geotechnical Site Characterisation, Atlanta, GA, USA, 19–22 April 1998. [Google Scholar]
- L’Heureux, J.S.; Long, M. Relationship between Shear-Wave Velocity and Geotechnical Parameters for Norwegian Clays. J. Geotech. Geoenviron. Eng. 2017, 143, 04017013. [Google Scholar] [CrossRef]
- Lengkeek, H.J. Testing and Modeling of Sheet Pile Reinforced Dikes on Organic Soils: Insights from the Eemdijk Full-SCALE Failure Test. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2022. [Google Scholar] [CrossRef]
- Wroth, C.P.; Wood, D.M. The correlation of index properties with some basic engineering properties of soils. Can. Geotech. J. 1978, 15, 137–145. [Google Scholar] [CrossRef]
- Ramsey, N.; Tho, K. New methods for assessing Plasticity Index and Low-strain Shear Modulus in fine-grained offshore soils. In Cone Penetration Testing 2022; Gottardi, G., Tonni, L., Eds.; CRC Press: Boca Raton, FL, USA, 2022; pp. 657–663. [Google Scholar] [CrossRef]
- Mayne, P.W. Evaluating effective stress parameters andundrained shear strength of soft-firm clays from CPT and DMT. Aust. Geomech. J. 2016, 51, 27–55. [Google Scholar]
- Robertson, P. Estimating in-situ soil permeability from CPT and CPTu. In Proceedings of the 2nd International Symposium on Cone Penetration Testing, Huntington Beach, CA, USA, 9–11 May 2010. [Google Scholar]
- Mayne, P.; Kulhawy, F. Ko - OCR Relationships in Soil. J. Geotech. Eng. Div. 1982, 108, 851–872. [Google Scholar] [CrossRef]
- Kulhawy, F.; Mayne, P. Manual on Estimating Soil Properties for Foundation Design; Electric Power Research Institute: New York, NY, USA, 1990. [Google Scholar]
- Mayne, P. Updating our geotechnical curricula via a balanced approach of in-situ, laboratory, and geophysical testing of soil. In Proceedings of the 61st Annual Geotechnical Conference, Minnesota Geotechnical Society, University of Minnesota, St. Paul, MN, USA, 22 February 2013; pp. 65–86. [Google Scholar]
- Tavenas, F.; Jean, P.; Leblond, P.; Leroueil, S. The permeability of natural soft clays. Part II: Permeability characteristics. Can. Geotech. J. 1983, 20, 645–660. [Google Scholar] [CrossRef]
- Doherty, J.; Gourvenec, S.; Gaone, F. Insights from a shallow foundation load-settlement prediction exercise. Comput. Geotech. 2018, 93, 269–279. [Google Scholar] [CrossRef]
- Hird, C.C.; Pyrah, I.C.; Russel, D. Finite element modelling of vertical drains beneath embankments on soft ground. Géotechnique 1992, 42, 499–511. [Google Scholar] [CrossRef]
- Gaone, F.; Gourvenec, S.; Doherty, J. Large-scale shallow foundation load tests on soft clay—At the National Field Testing Facility (NFTF), Ballina, NSW, Australia. Comput. Geotech. 2018, 93, 253–268. [Google Scholar] [CrossRef]




| Workflow | Method | Author | |
|---|---|---|---|
| CPT | (1) | [35] | |
| (2) | [36] | ||
| (3) | [3] | ||
| (4) | [37] | ||
| DMT | from Marchetti’s chart | [38] | |
| (5) | [39] | ||
| (6) | [39] | ||
| (7) | [39] | ||
| (8) | [39] | ||
| (9) | [40] | ||
| (10) | [41] | ||
| (11) | [42] | ||
| (12) | [1] |
| Parameter | Estuarine Layer 1 | Estuarine Layer 2 | Estuarine Layer 3 |
|---|---|---|---|
| (kN/m3) | 13.99 | 14.87 | 16.72 |
| (-) | 3.295 | 2.256 | 1.373 |
| (-) | 0.1406 | 0.1366 | 0.1053 |
| (-) | 0.02249 | 0.02186 | 0.01685 |
| (-) | 0.01004 | ||
| (kPa) | 1.571 | 2.017 | 6.088 |
| (°) | 29.83 | 30.95 | 37.44 |
| (m/d) | |||
| (-) | 1.647 | 1.128 | 0.6867 |
| (-) | 0.7803 | 0.6528 | 0.8503 |
| OCR (-) | 2.322 | 1.6 | 2.779 |
| Parameter | Top Crust | Sand Layer | Deeper Clay Layer |
|---|---|---|---|
| (kN/m3) | 20 | 20.5 | 19 |
| (MPa) | 13 | 30 | 20 |
| (MPa) | 13 | 30 | 30 |
| (MPa) | 40 | 90 | 90 |
| m (-) | 0.7 | 0.5 | 0.9 |
| (kPa) | 100 | 100 | 100 |
| (-) | 0.2 | 0.2 | 0.2 |
| (MPa) | 83.3 | 187.5 | 187.5 |
| (-) | |||
| (kPa) | 3 | 0 | 8 |
| (°) | 30 | 34 | 27 |
| (m/d) | |||
| (-) | 0.625 | 0.5362 | 0.6940 |
| OCR (-) | 1.5 | 1.5 | 1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marzouk, I.; Tschuchnigg, F. Application of an Automated Parameter Determination Framework to Boundary Value Problems. Buildings 2025, 15, 3092. https://doi.org/10.3390/buildings15173092
Marzouk I, Tschuchnigg F. Application of an Automated Parameter Determination Framework to Boundary Value Problems. Buildings. 2025; 15(17):3092. https://doi.org/10.3390/buildings15173092
Chicago/Turabian StyleMarzouk, Islam, and Franz Tschuchnigg. 2025. "Application of an Automated Parameter Determination Framework to Boundary Value Problems" Buildings 15, no. 17: 3092. https://doi.org/10.3390/buildings15173092
APA StyleMarzouk, I., & Tschuchnigg, F. (2025). Application of an Automated Parameter Determination Framework to Boundary Value Problems. Buildings, 15(17), 3092. https://doi.org/10.3390/buildings15173092







