Damage Characteristics Analysis of High-Rise Frame-Core-Tube Building Structures in Soft Soil Under Earthquake Action
Abstract
1. Introduction
2. Model Overview
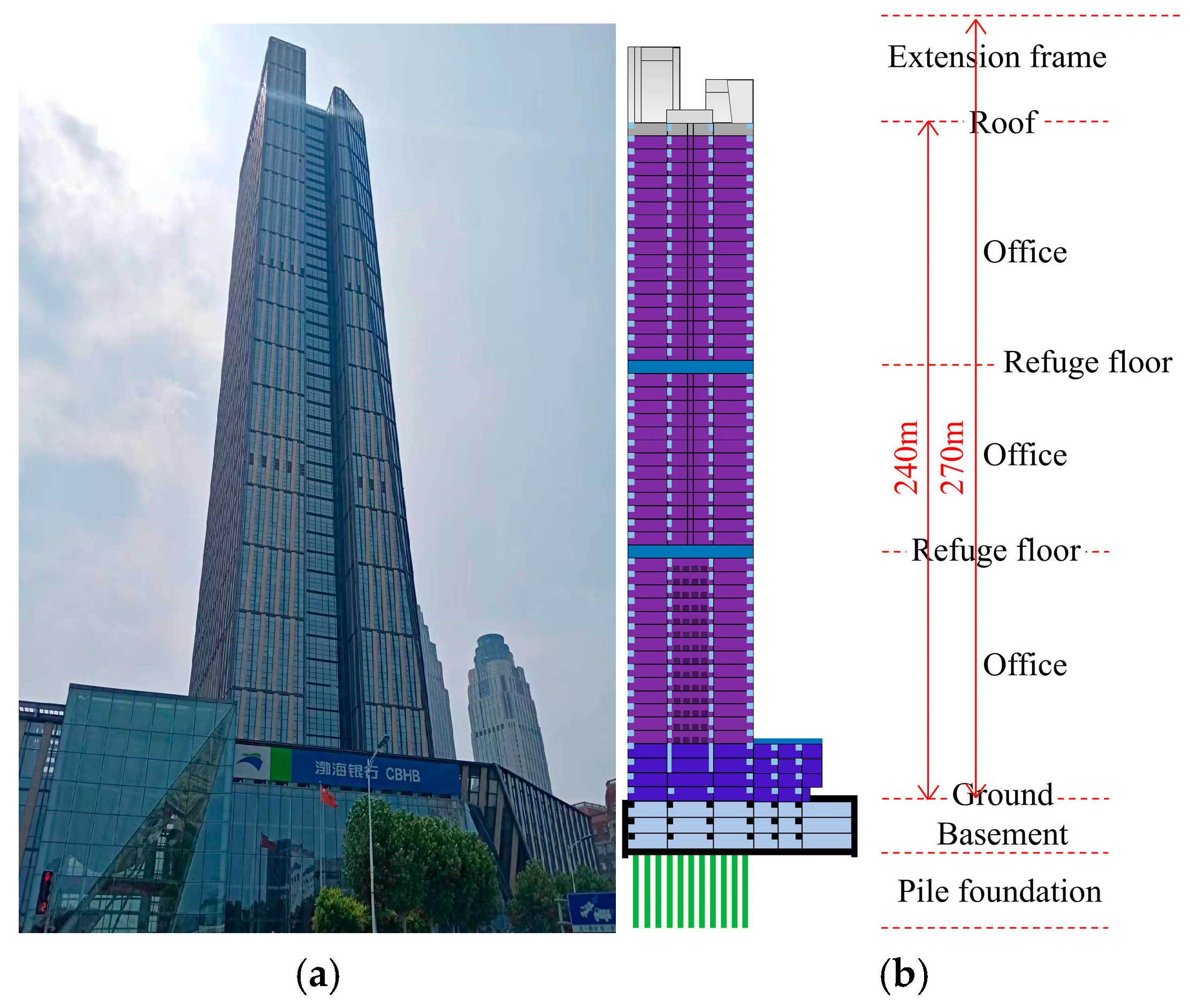
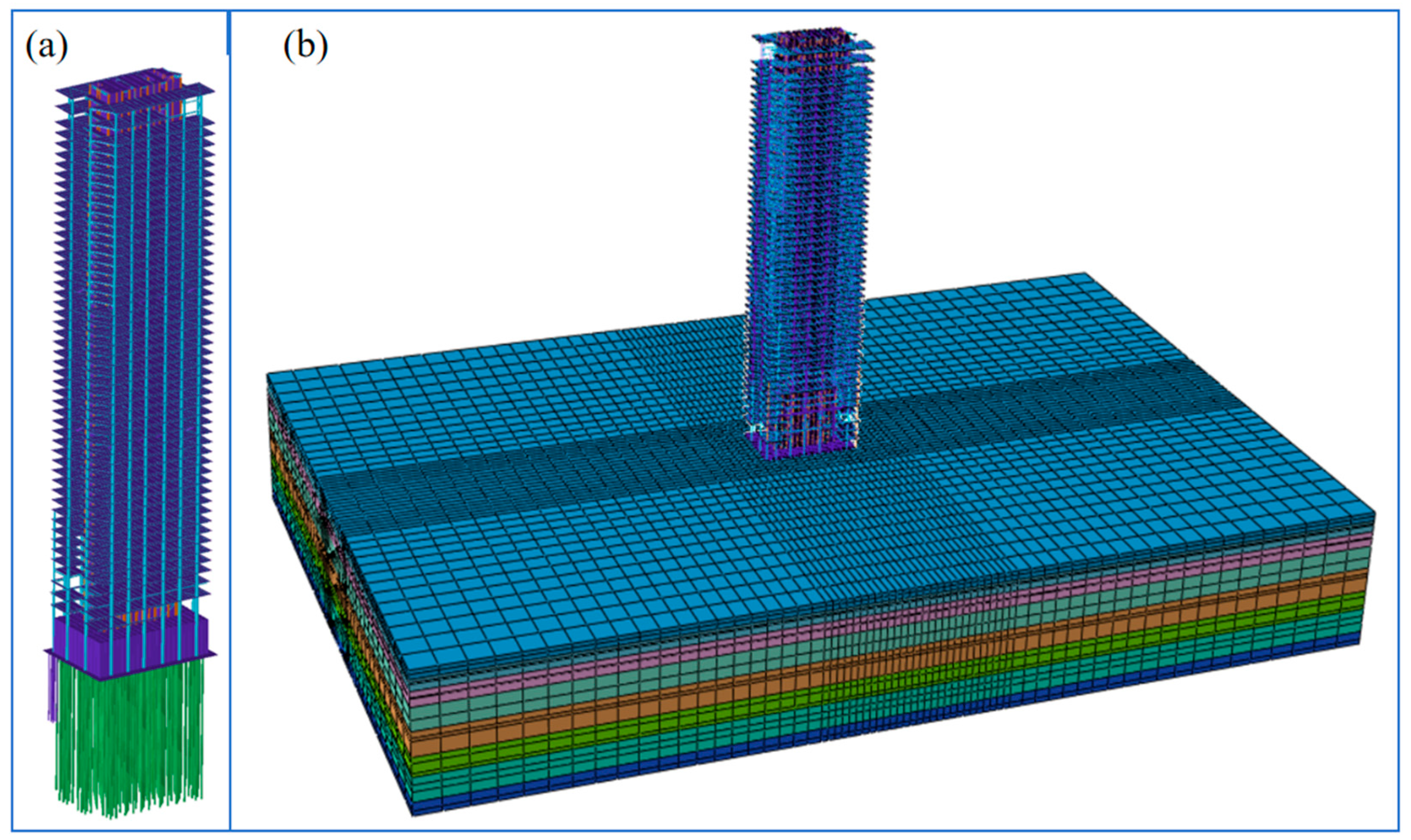
2.1. Brief Introduction to Building
2.2. Constitutive Model and Element Selection
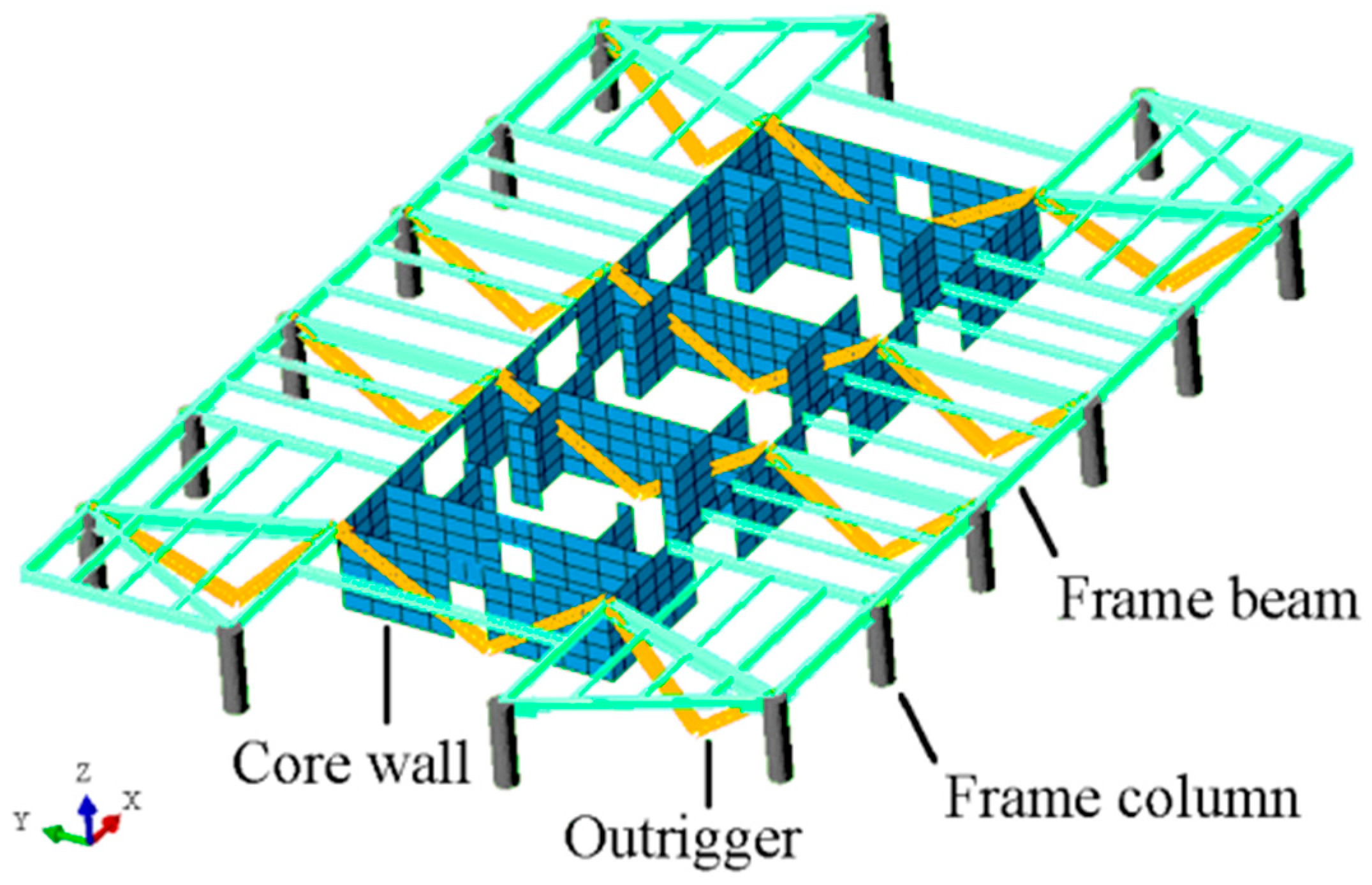
2.3. Finite Element Model
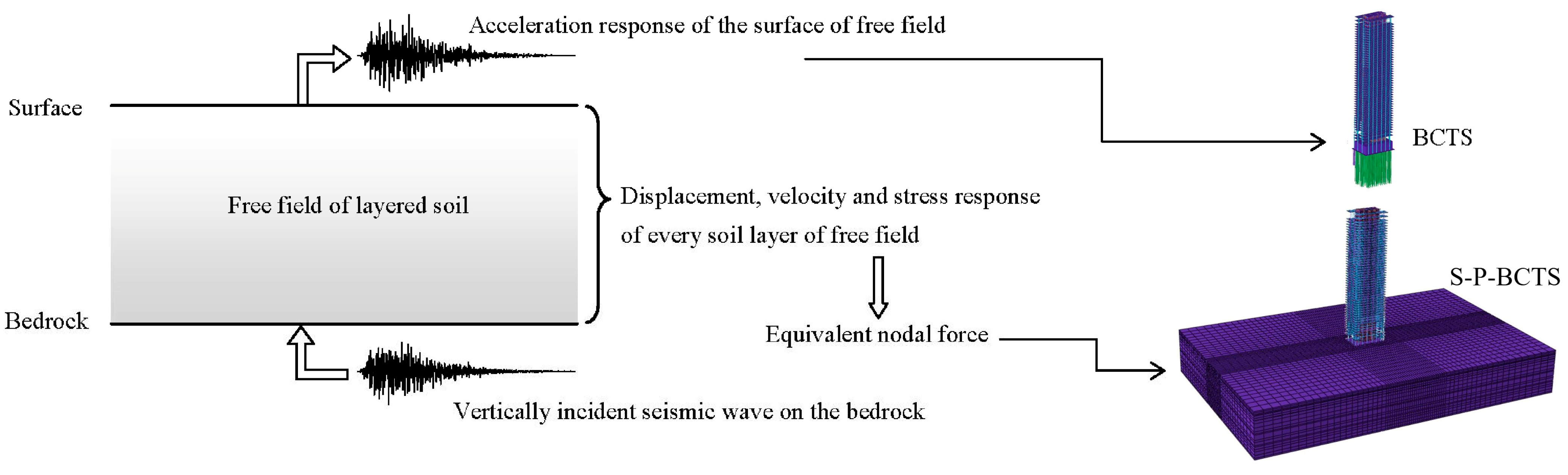
3. Model Boundary and Seismic Wave Input
3.1. Viscous-Spring Boundary
3.2. Equivalent Nodal Force Method
3.3. Verification of Accuracy
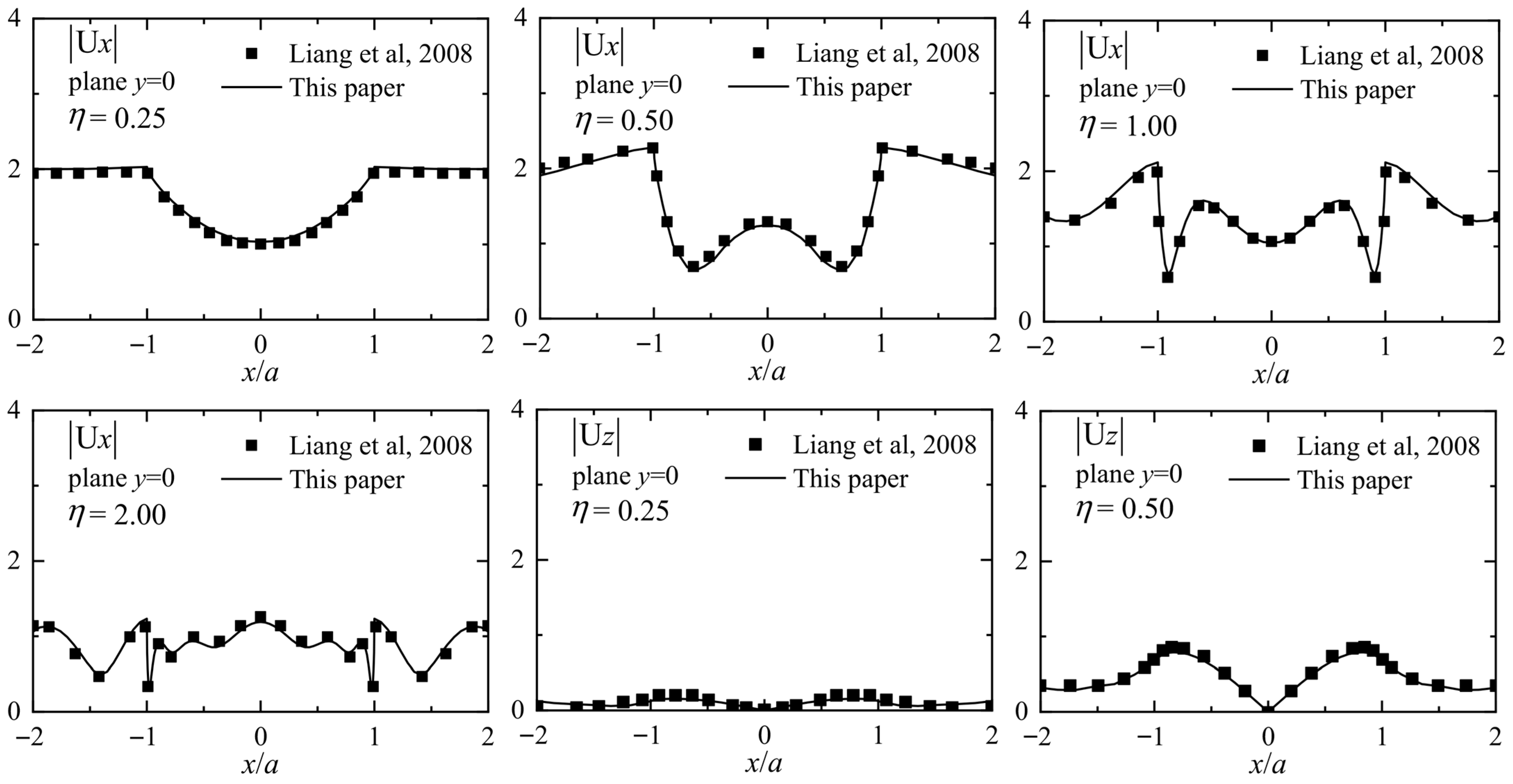
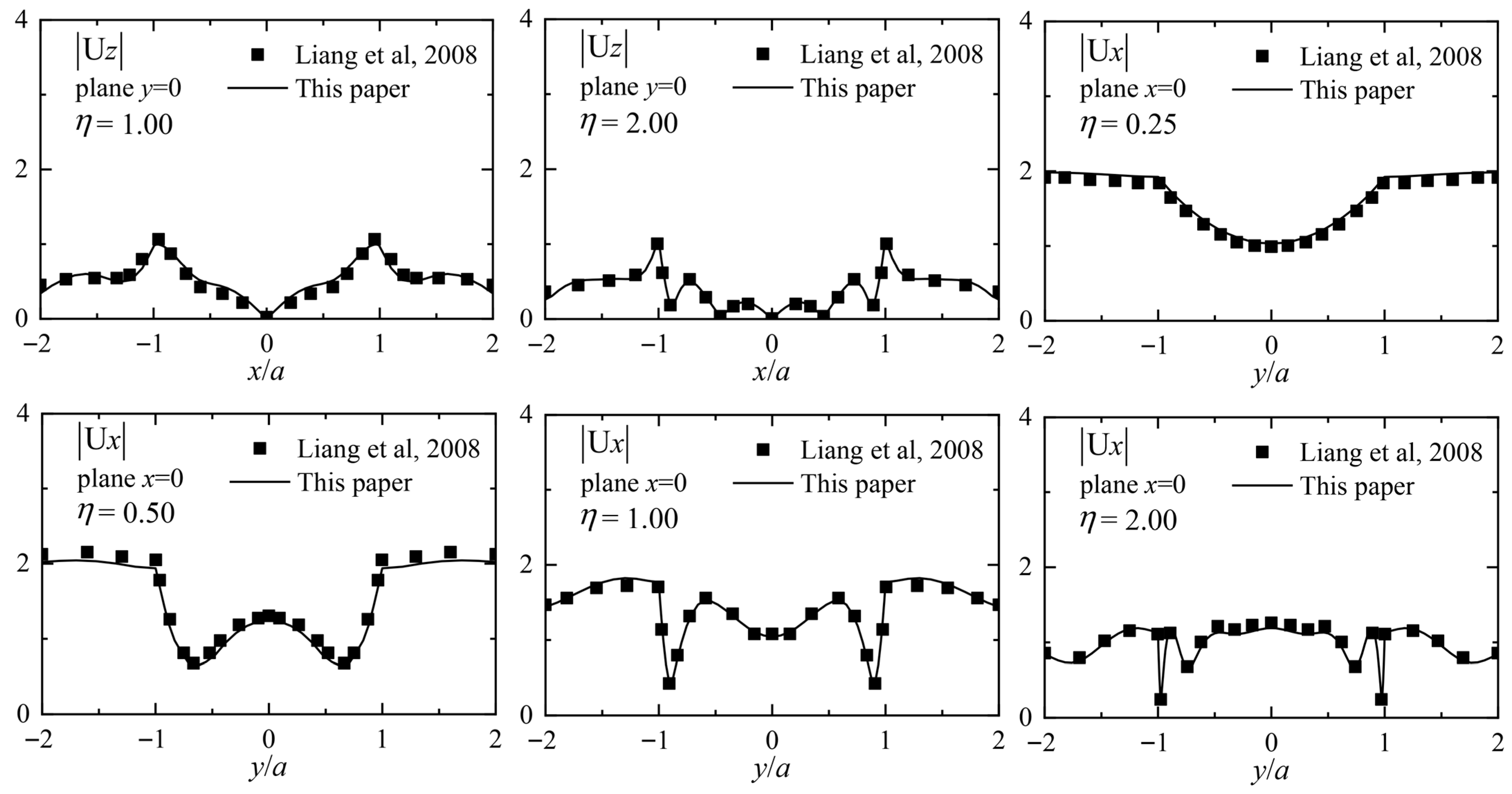
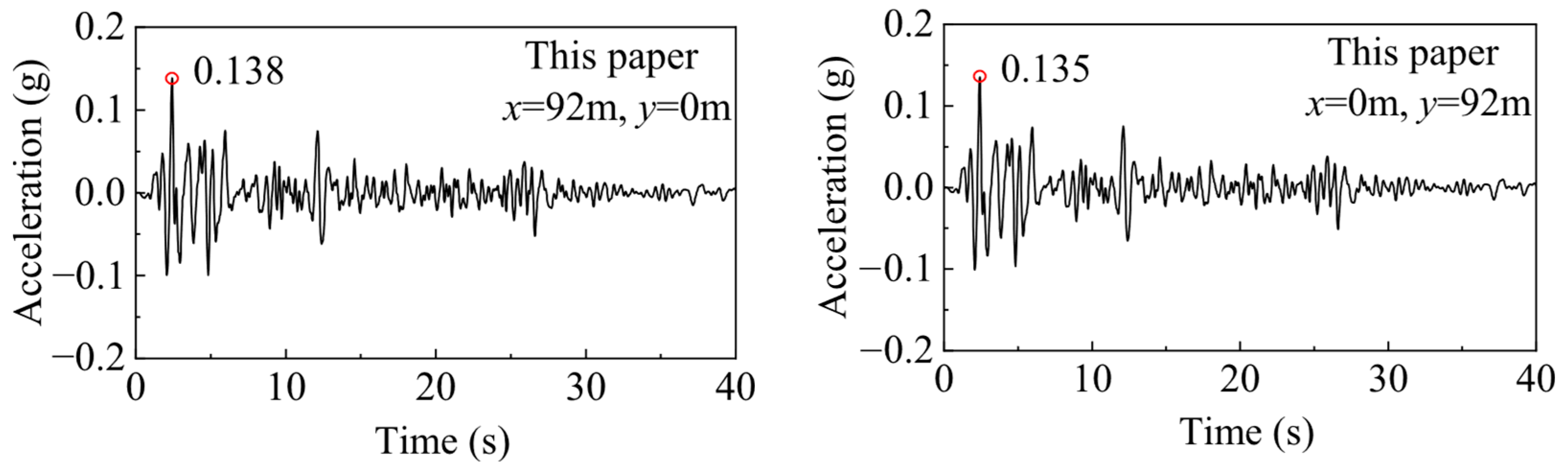
3.3.1. Linear Earthquake Response of a Hemispherical Canyon
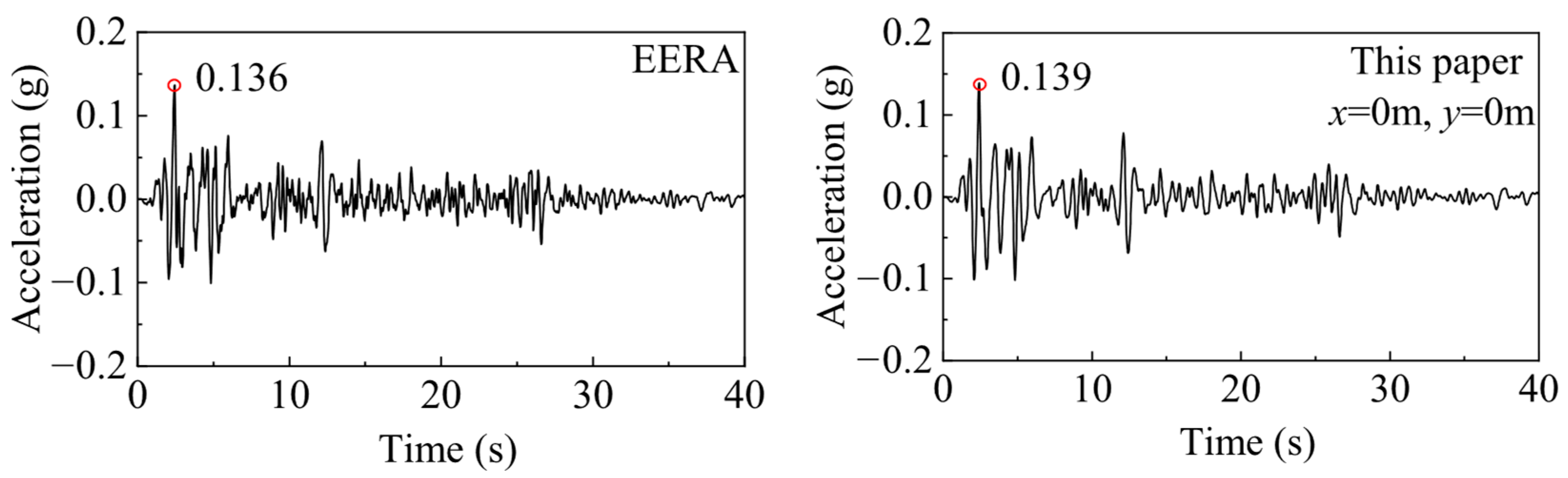
3.3.2. Nonlinear Earthquake Response of Three-Dimensional Free Field
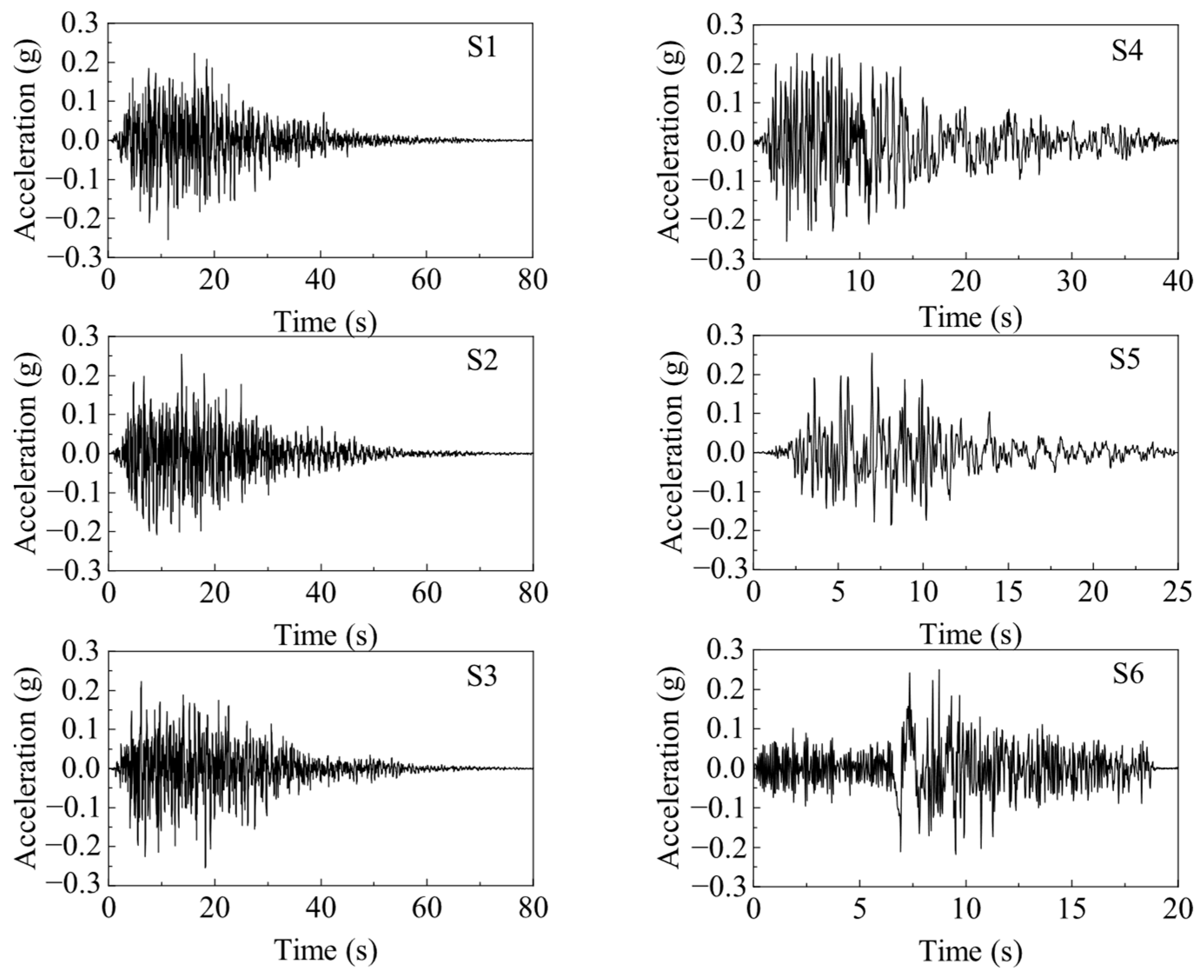
4. Results and Discussion
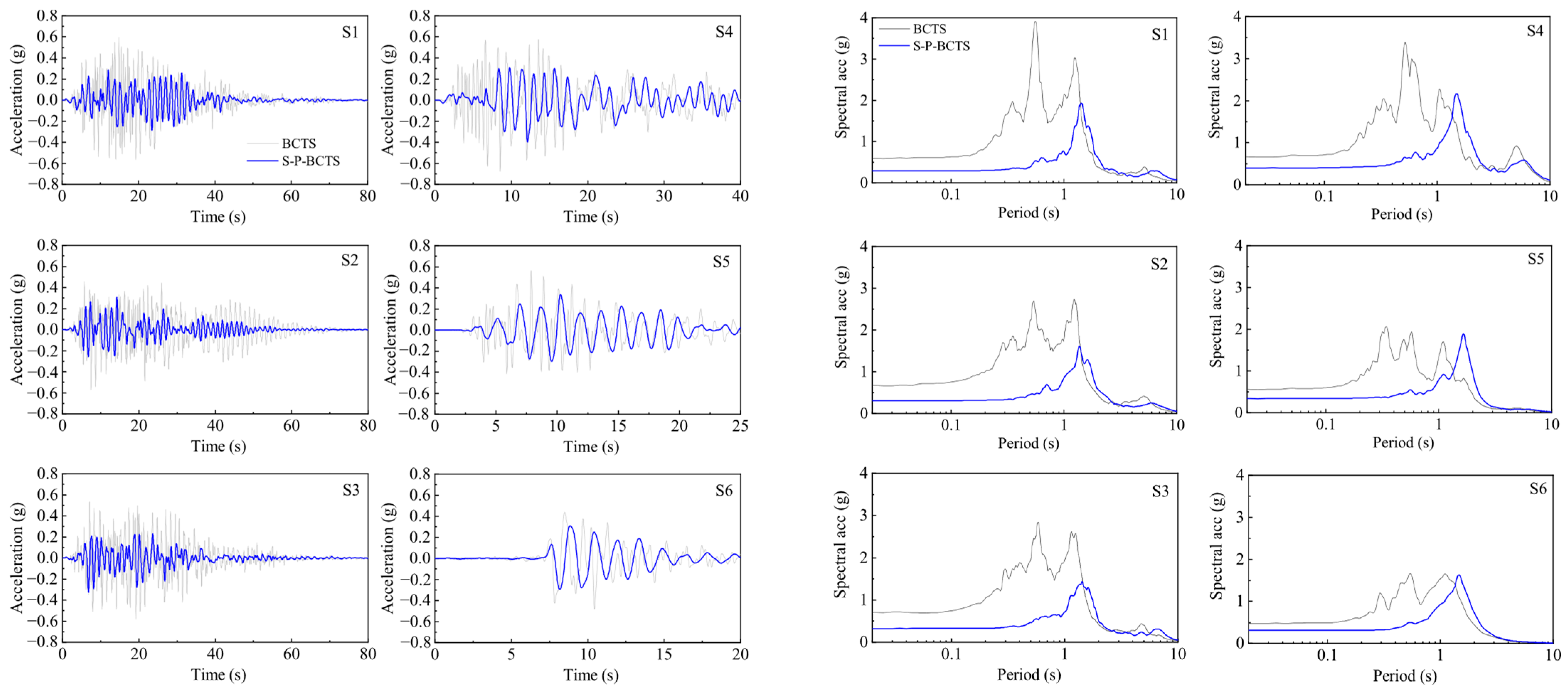
4.1. Top-Storey Acceleration
4.2. Lateral Displacement
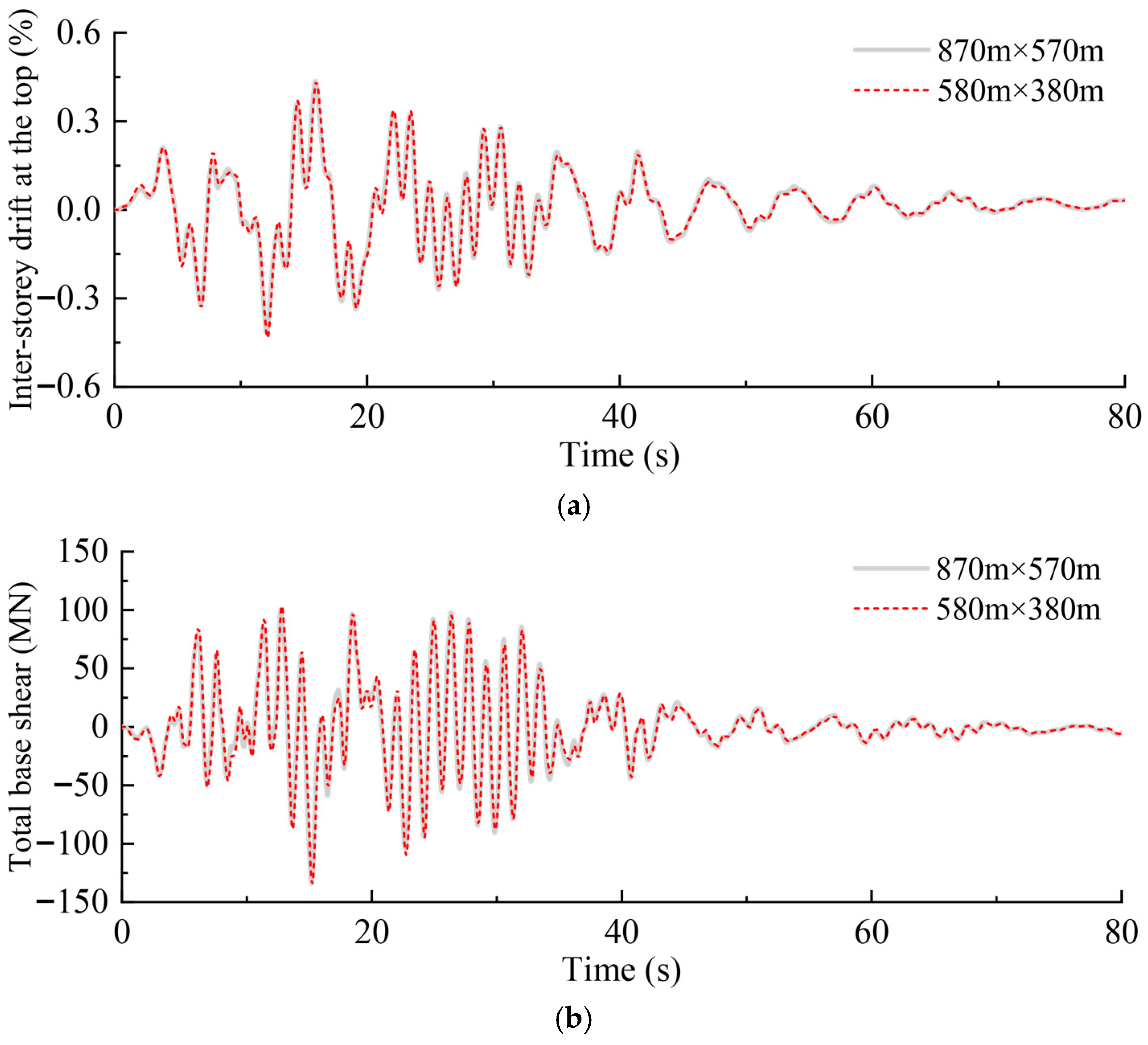
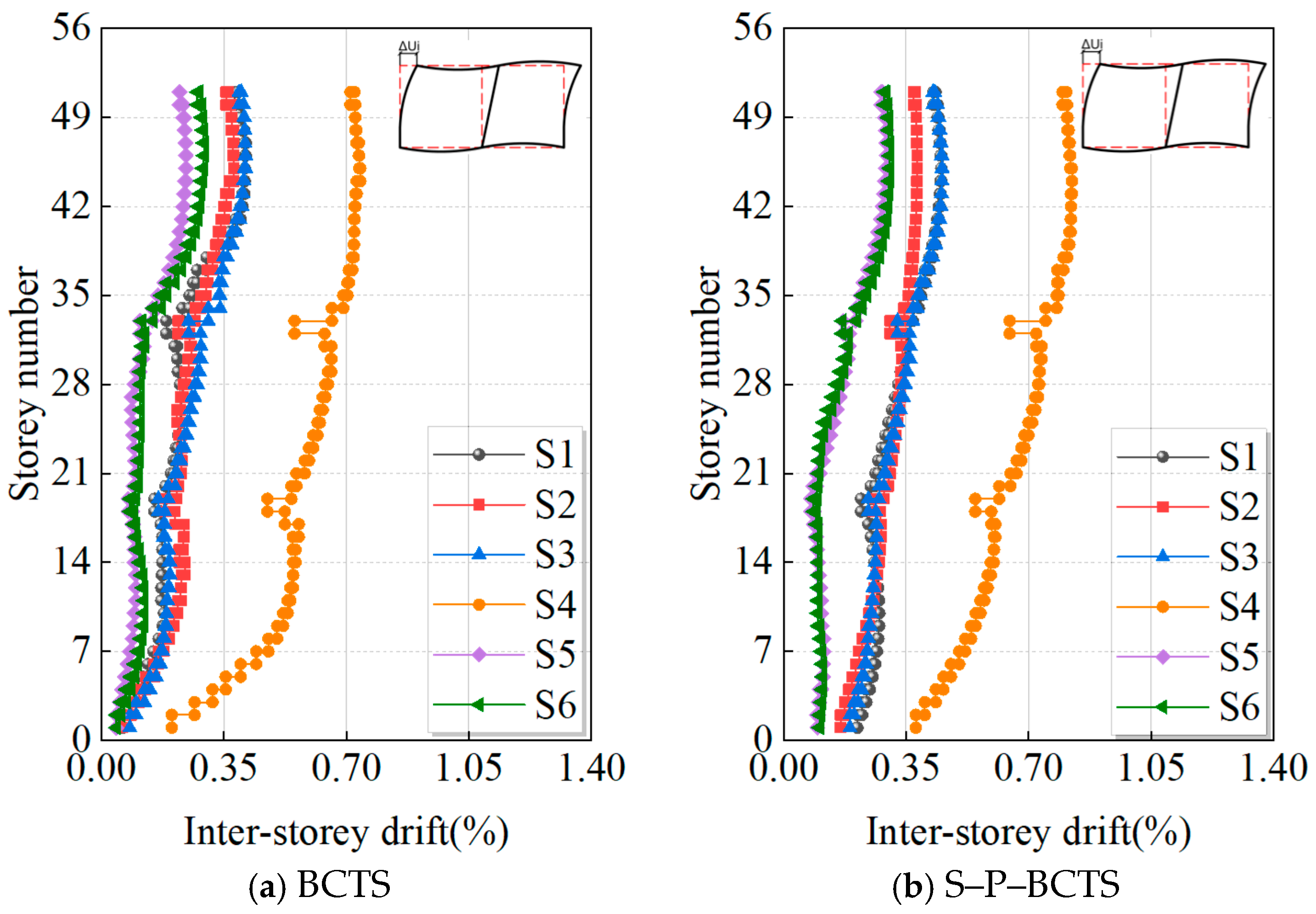
4.3. Inter-Storey Drift
4.4. Member Damage and Stress
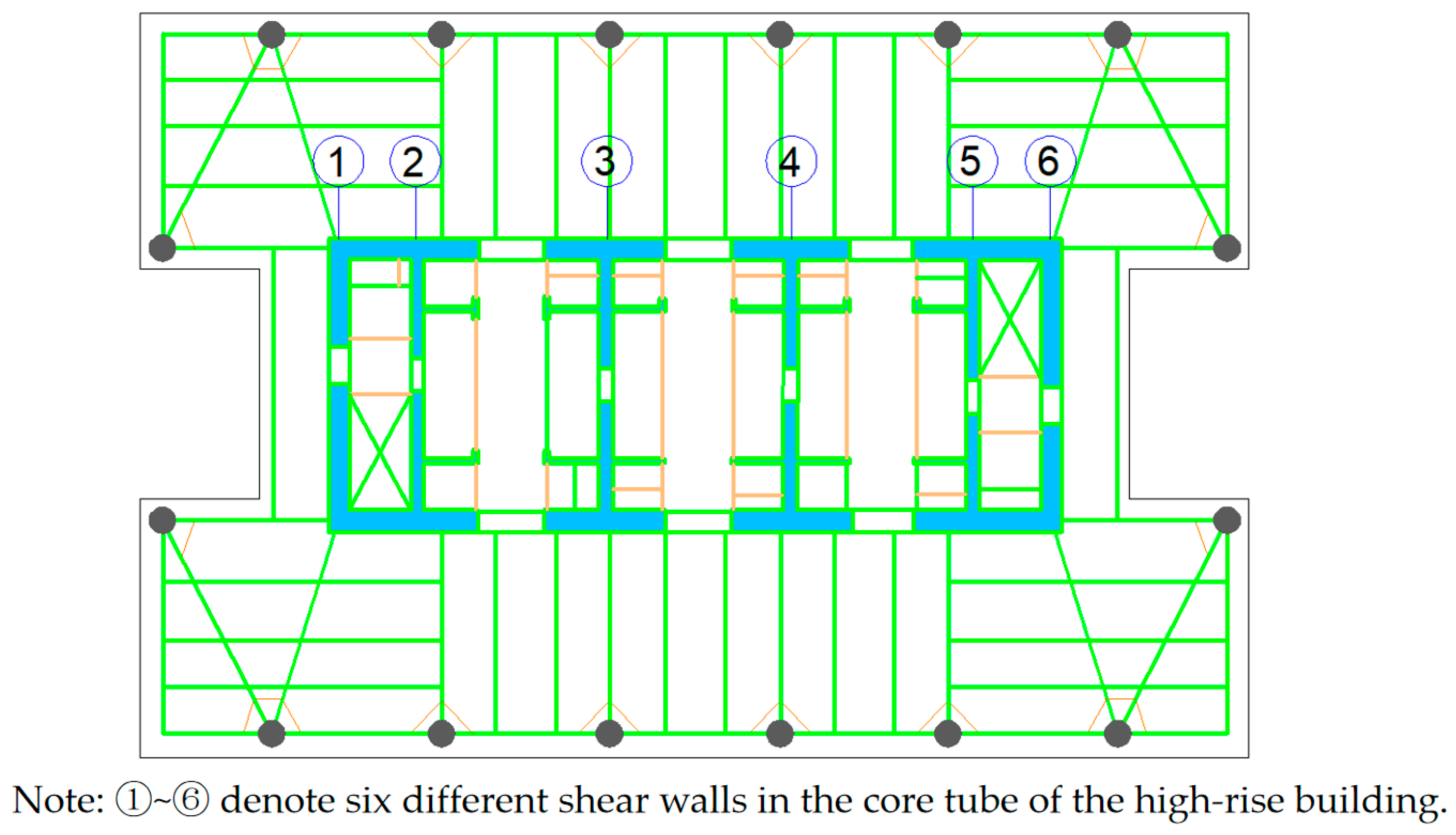
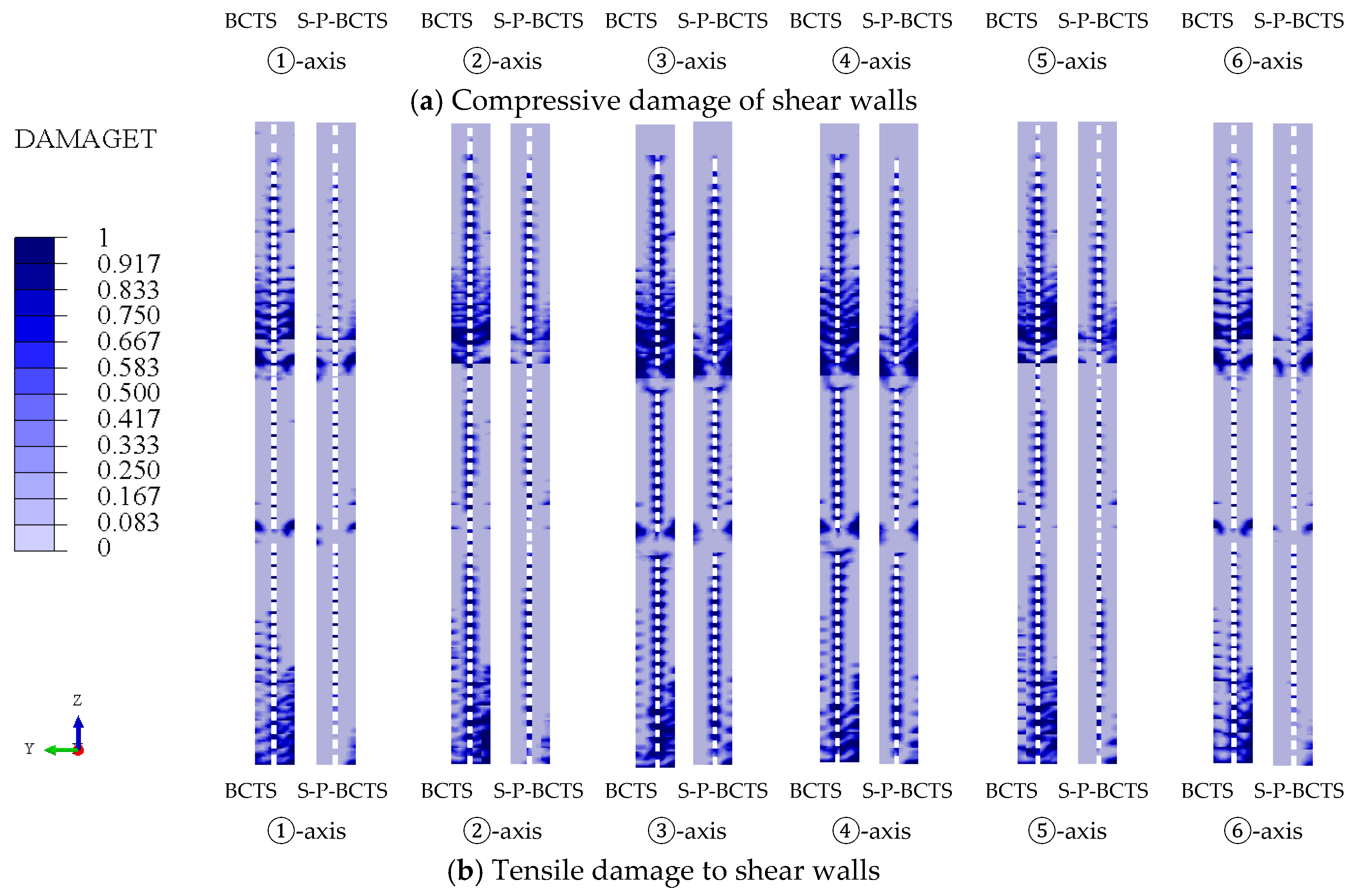
4.4.1. Core Wall Damage
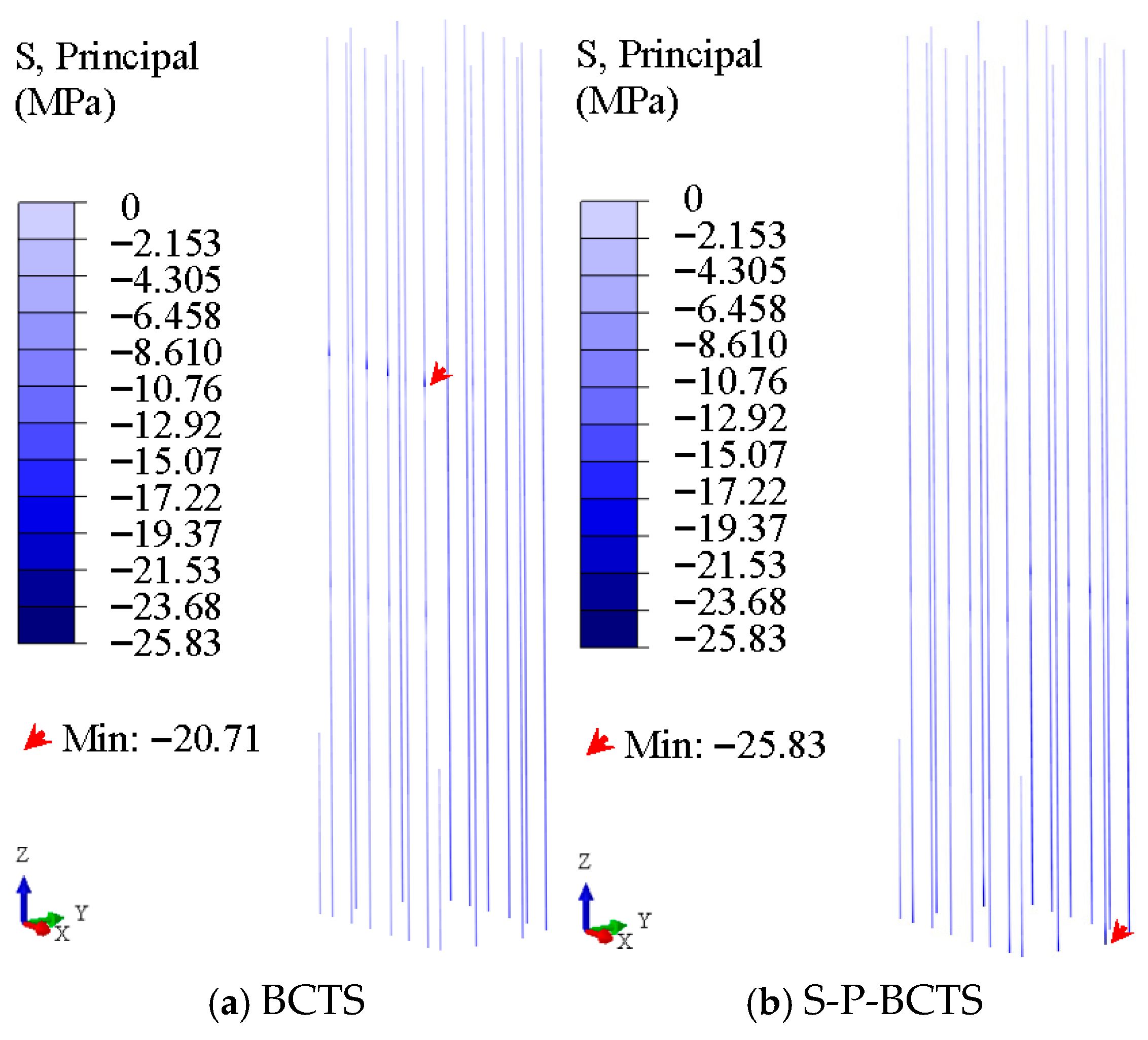
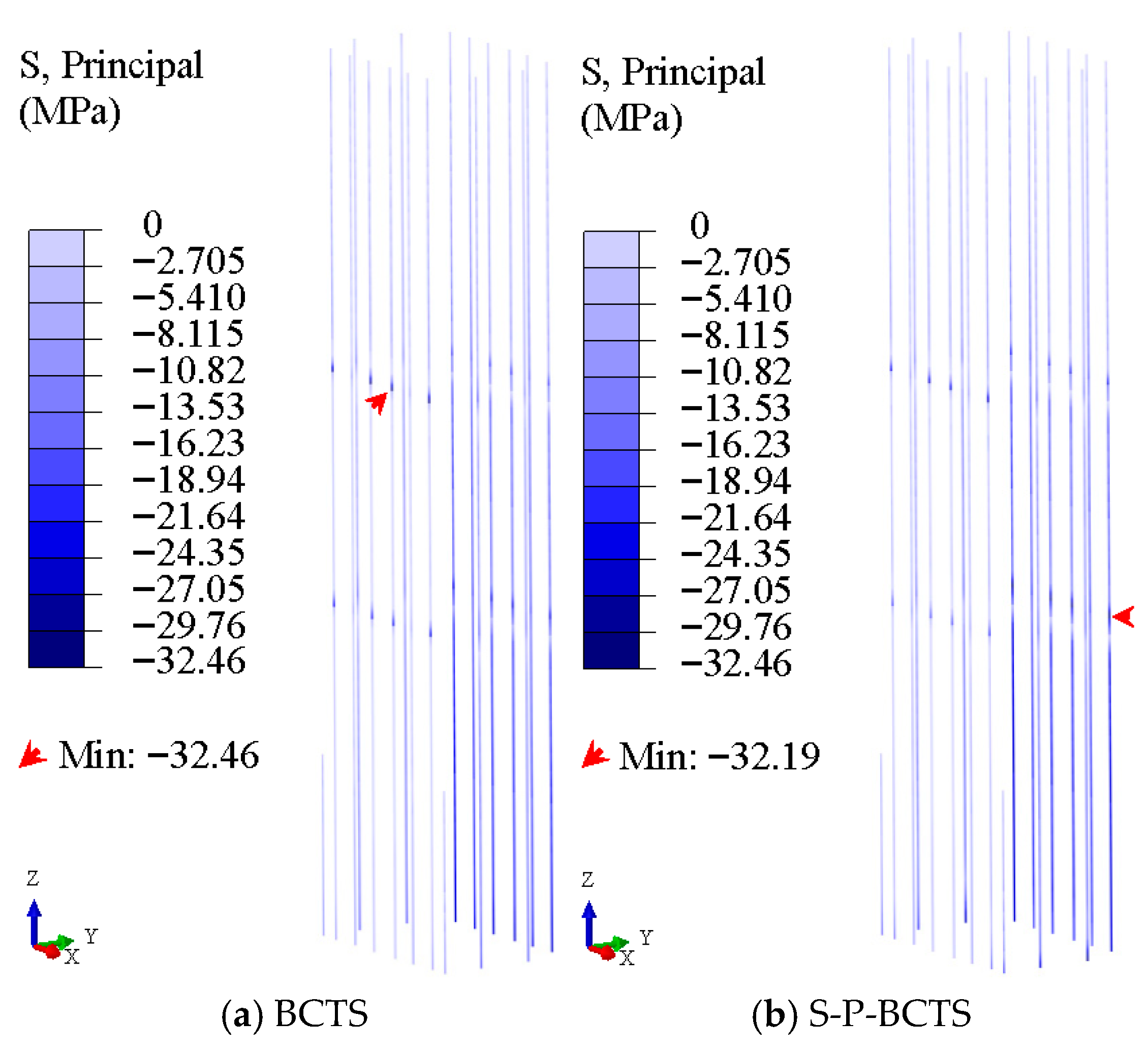
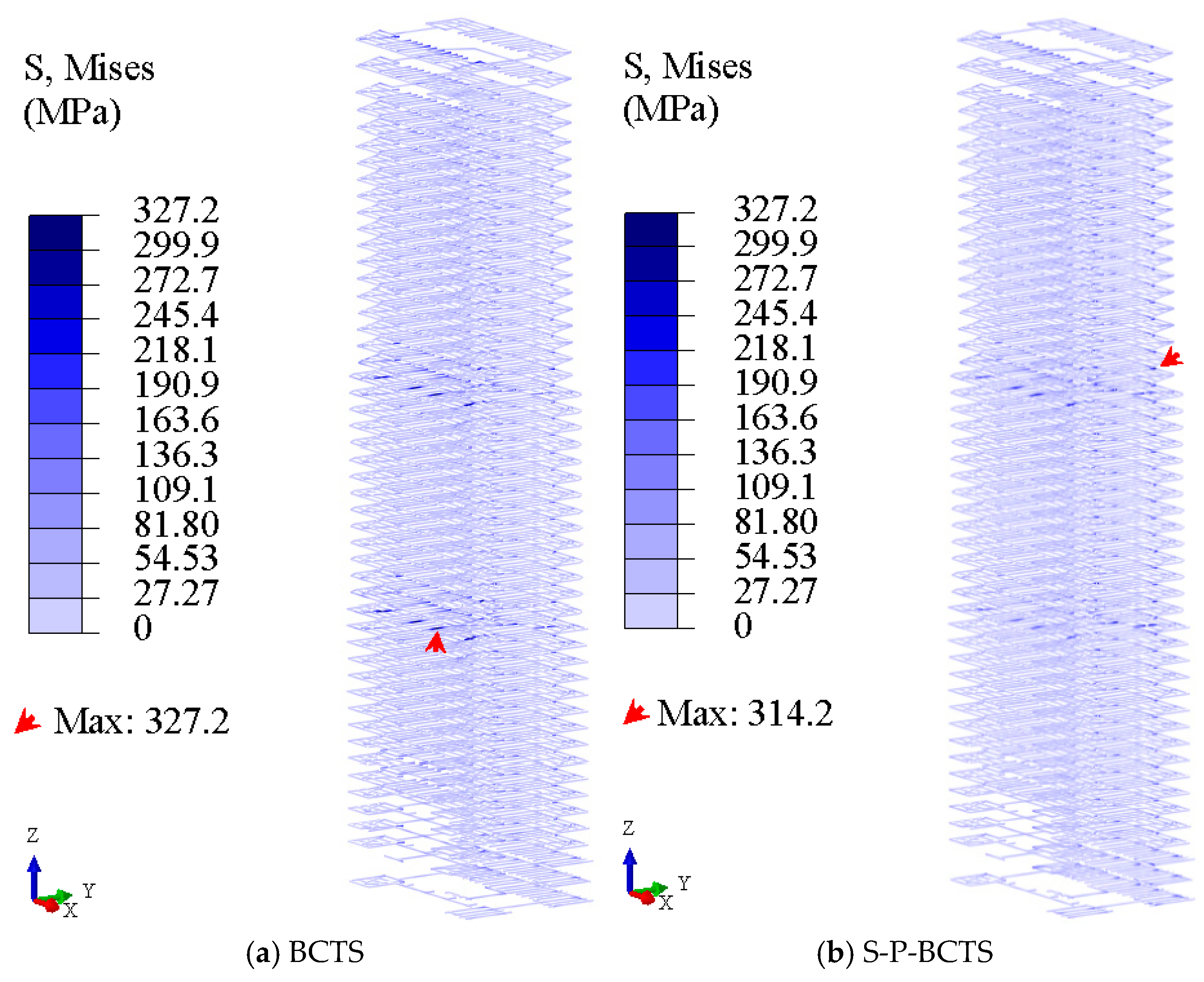
4.4.2. Frame Column Stress
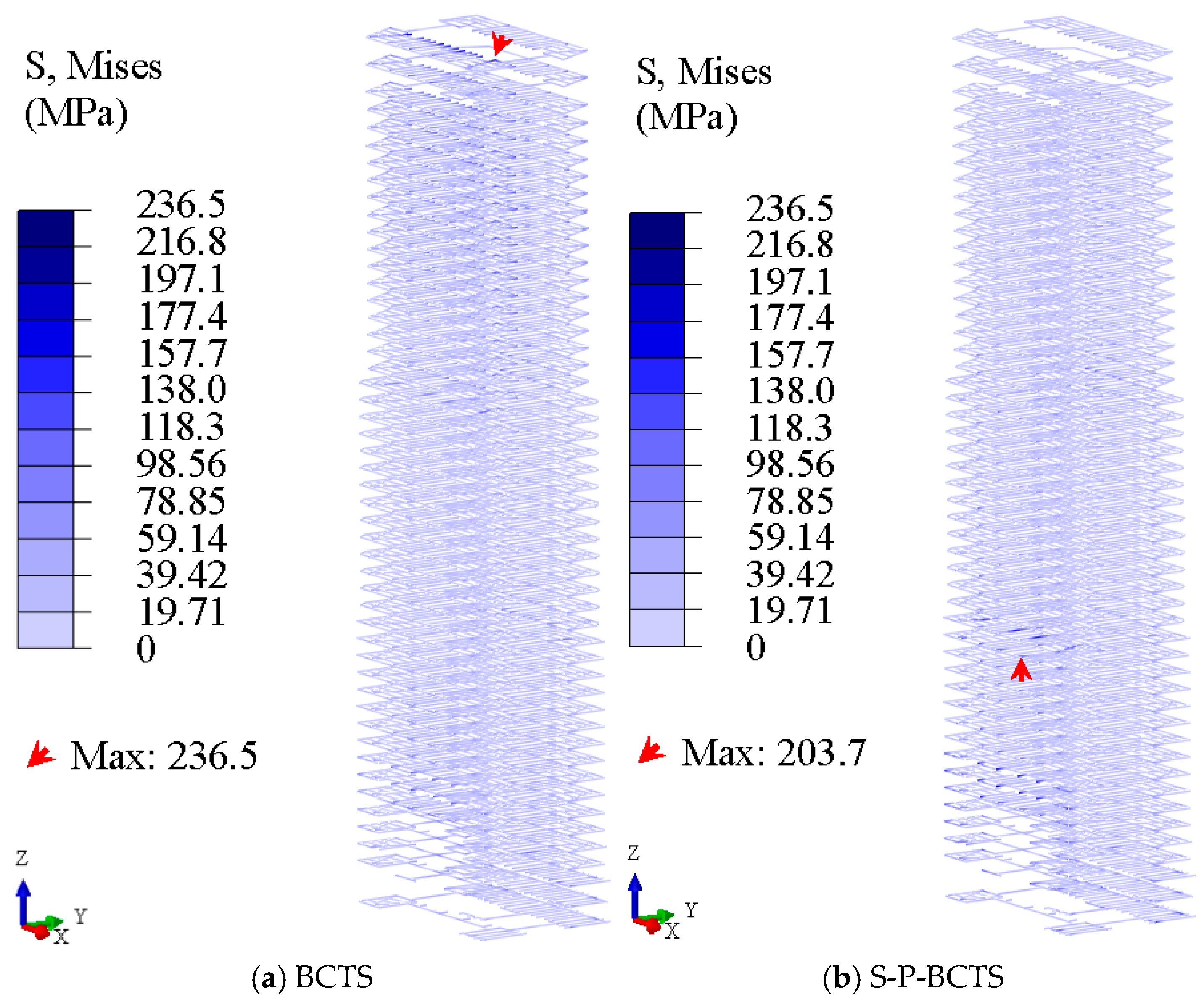
4.4.3. Frame Beam Stress
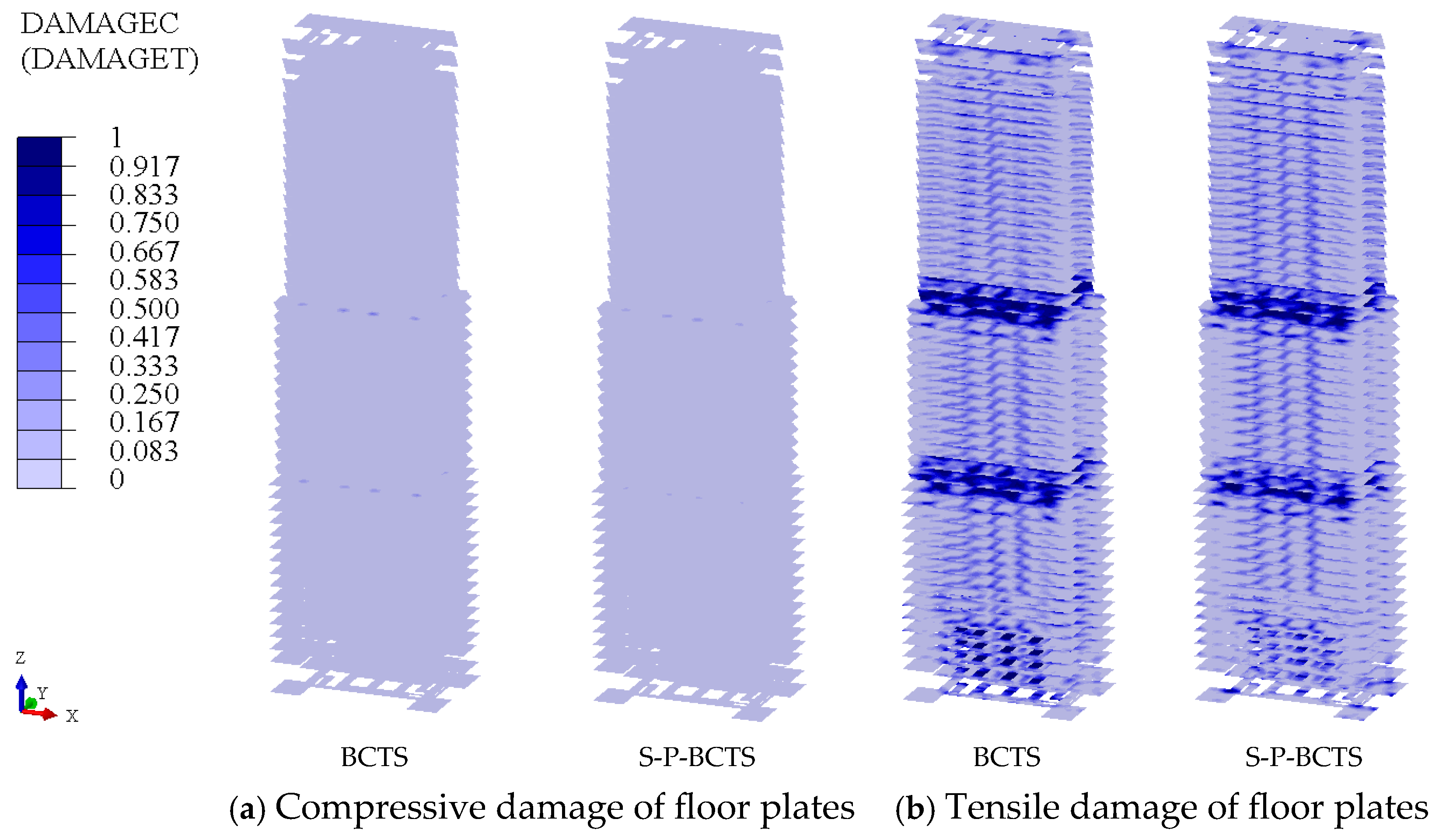
4.4.4. Floor Plate Damage
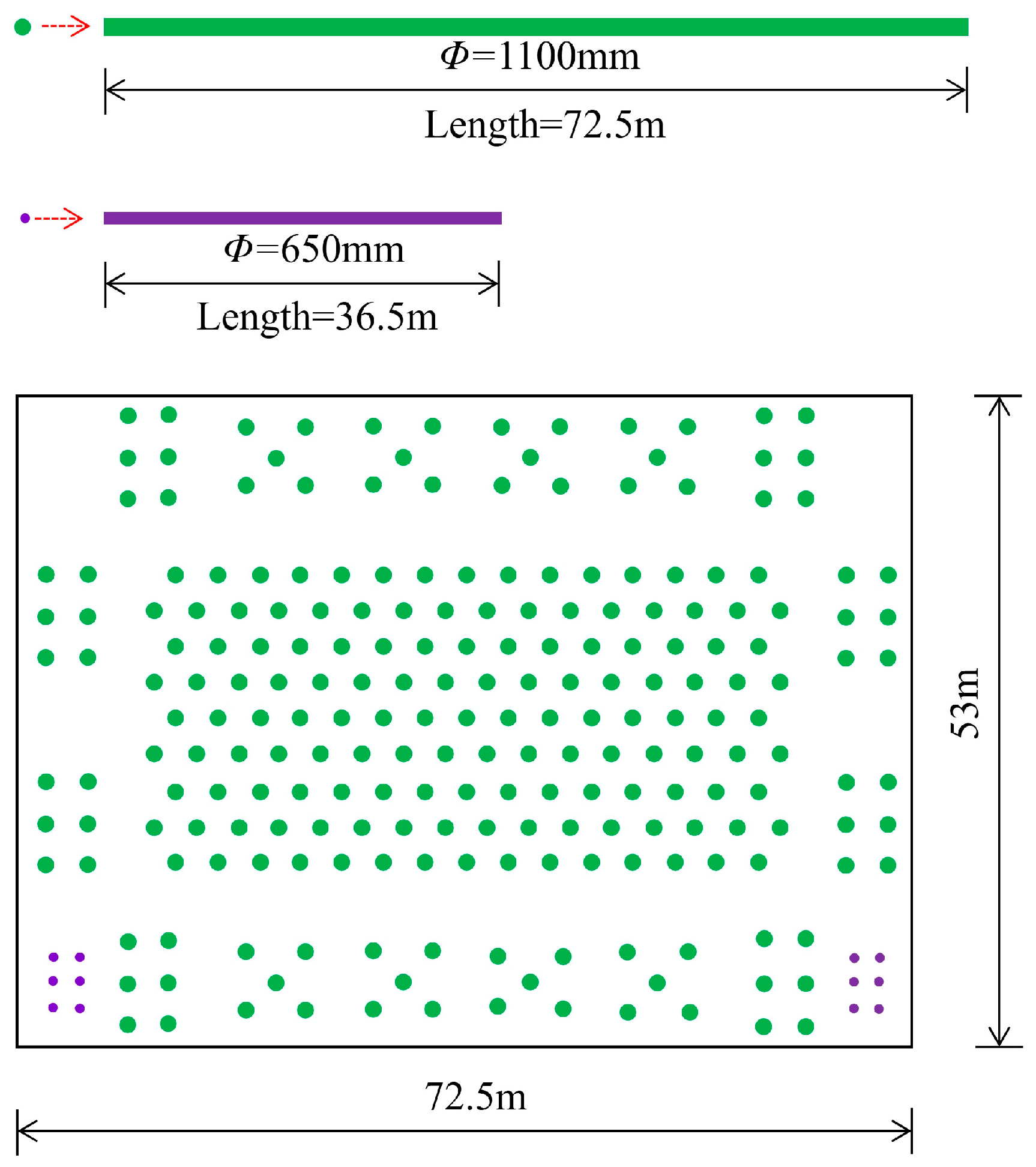
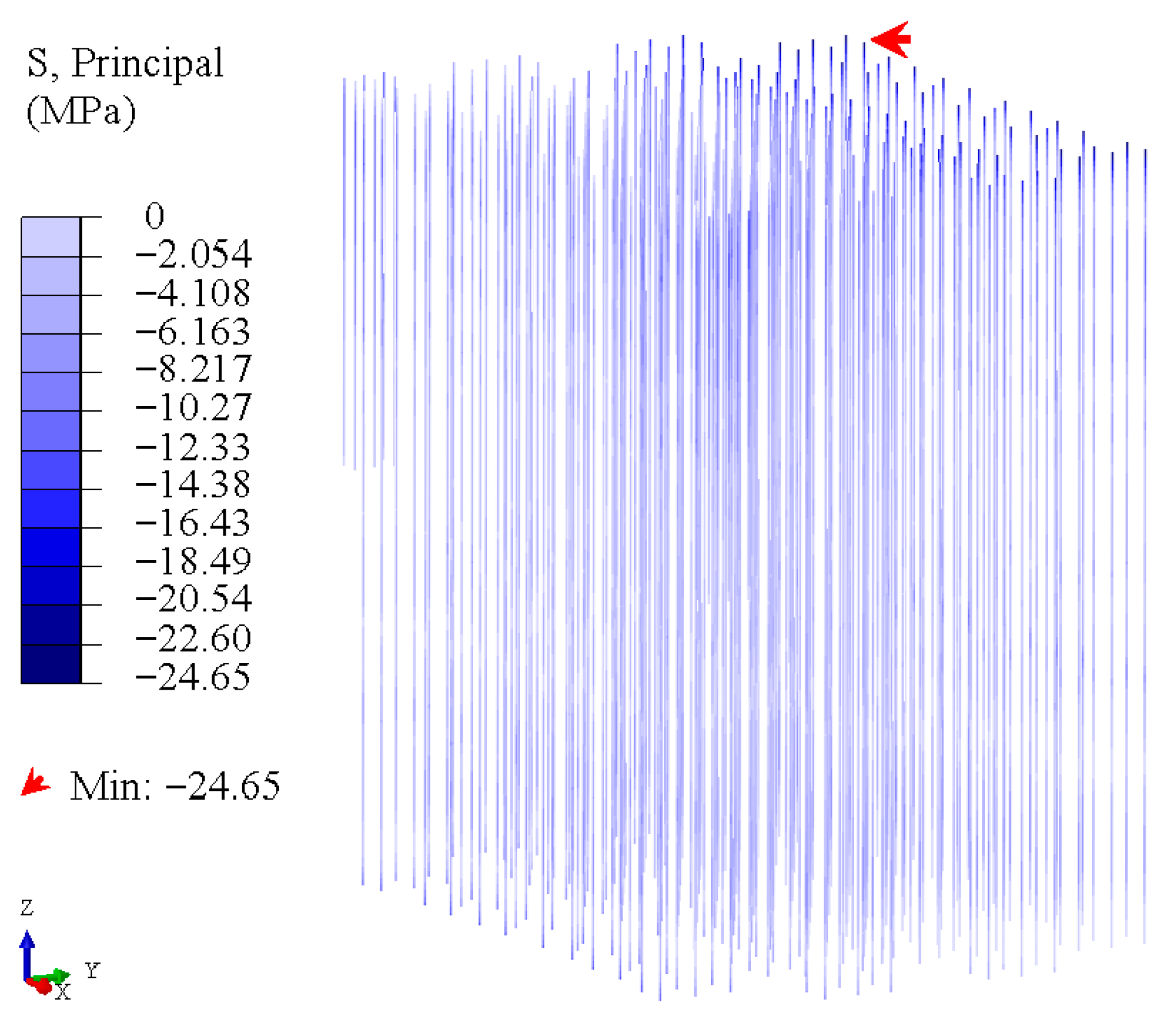
4.5. Pile Stress
5. Conclusions
- (1)
- For the top-storey acceleration, the peak value of the time histories decreases significantly. In addition, the short-period components of the response spectra decrease obviously, the predominant period of the response spectra prolongs clearly, and the peak value of the response spectra tends to decrease.
- (2)
- The lateral displacement and inter-storey drift increase significantly. The results in this paper show that the lateral displacement of the top storey and the maximum inter-storey drift obtained from the soil–pile–BCTS model can be as high as 1.79 and 1.22 times those obtained from the fixed-base above-ground BCTS model, respectively. The dynamic soil–pile–BCTS interaction should be fully considered in seismic analysis.
- (3)
- The total base shear decreases significantly. However, by observing the core wall and frame column base shear separately, it can be found that the core wall base shear also decreases significantly, but the frame column base shear increases significantly. The results in this paper show that the frame column base shear obtained from the soil–pile–BCTS model can be as high as 1.76 times that obtained from the fixed-base above-ground BCTS model. This amplification effect should be fully considered in the seismic design of the column.
- (4)
- The area of compressive damage and tensile damage of the core wall decreases significantly, the maximum Mises stress of the frame beam decreases, and the area of compressive damage and tensile damage of the floor plate decreases. However, the maximum principal compressive stress of the frame column may increase at the foot of the frame column. These mean that the dynamic soil–pile–BCTS interaction is beneficial to the seismic performance of the core wall, frame beam, and floor plate overall, but may be detrimental to the seismic performance of the frame column.
Author Contributions
Funding
Conflicts of Interest
References
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD). Technical Key Points of Special Examination of Seismic Fortification for Tall Building Engineering Beyond the Code-Specification. 2015. Available online: https://www.mohurd.gov.cn/gongkai/zc/wjk/art/2015/art_17339_220992.html (accessed on 21 May 2015).
- Kamal, M.; Inel, M. Correlation between Ground Motion Parameters and Displacement Demands of Mid-Rise RC Buildings on Soft Soils Considering SoilStructure-Interaction. Buildings 2021, 11, 125. [Google Scholar] [CrossRef]
- Li, W.; Li, Q.N. Performance-based seismic design of complicated tall building structures beyond the code specification. Struct. Des. Tall Spec. Build. 2012, 21, 578–591. [Google Scholar]
- Ma, X.; Liu, Z. Inffuence of Ground Motion Non-Gaussianity on Seismic Performance of Buildings. Buildings 2024, 14, 2364. [Google Scholar] [CrossRef]
- Zhao, G.; Zhang, L.; Liu, D.; Shen, K. Seismic Response Analysis of Double-Layer Isolation Structures in High-Rise Buildings. Buildings 2025, 15, 1292. [Google Scholar] [CrossRef]
- Penzien, J.; Scheffey, C.F.; Parmelee, R.A. Seismic analysis of bridges on long piles. J. Eng. Mech. Div. 1964, 90, 223–254. [Google Scholar] [CrossRef]
- Tokimatsu, M.; Mizuno, H.; Kakurai, M. Building damage associated with geotechnical problems. Soils Found. 1996, 36, 219–234. [Google Scholar] [CrossRef]
- Trifunac, M.D.; Ivanović, S.S.; Todorovska, M.I.; Novikova, E.I.; Gladkov, A.A. Experimental evidence for flexibility of a building foundation supported by concrete friction piles. Soil Dyn. Earthq. Eng. 1999, 18, 169–187. [Google Scholar] [CrossRef]
- Boulanger, R.W.; Curras, C.J.; Kutter, B.L.; Wilson, D.W.; Abghari, A. Seismic soil-pile-structure interaction experiments and analyses. J. Geotech. Geoenviron. Eng. 1999, 125, 750–759. [Google Scholar] [CrossRef]
- Tang, L.; Ling, X. Response of a RC pile group in liquefiable soil: A shake-table investigation. Soil Dyn. Earthq. Eng. 2014, 67, 301–315. [Google Scholar] [CrossRef]
- Cai, Y.X.; Gould, P.L.; Desai, C.S. Nonlinear analysis of 3D seismic interaction of soil–pile–structure systems and application. Eng. Struct. 2000, 22, 191–199. [Google Scholar] [CrossRef]
- Carbonari, S.; Dezi, F.; Leoni, G. Nonlinear seismic behaviour of wall-frame dual systems accounting for soil-structure interaction. Earthq. Eng. Struct. Dyn. 2012, 41, 1651–1672. [Google Scholar] [CrossRef]
- Lu, H.; Liang, P.; Shang, S. Computational analysis of dynamic layered soil-pile-structure interaction. Chin. J. Geotech. Eng. 2007, 29, 705–711. [Google Scholar]
- Rovithis, E.N.; Pitilakis, K.D.; Mylonakis, G.E. Seismic analysis of coupled soil-pile-structure systems leading to the definition of a pseudo-natural SSI frequency. Soil Dyn. Earthq. Eng. 2009, 29, 1005–1015. [Google Scholar] [CrossRef]
- Hokmabadi, A.S.; Fatahi, B.; Samali, B. Assessment of soil-pile-structure interaction influencing seismic response of mid-rise buildings sitting on floating pile foundations. Comput. Geotech. 2014, 55, 172–186. [Google Scholar] [CrossRef]
- Badry, P.; Satyam, N. Seismic soil structure interaction analysis for asymmetrical buildings supported on piled raft for the 2015 Nepal earthquake. J. Asian Earth Sci. 2017, 133, 102–113. [Google Scholar] [CrossRef]
- Padrón, L.A.; Aznárez, J.J.; Maeso, O. 3-D boundary element-finite element method for the dynamic analysis of piled buildings. Eng. Anal. Bound. Elem. 2011, 35, 465–477. [Google Scholar] [CrossRef]
- Lu, J.F.; He, C.Y. A model for the seismic analysis of a periodic viaduct when considering the pile-soil-structure interaction. Soil Dyn. Earthq. Eng. 2014, 56, 13–27. [Google Scholar] [CrossRef]
- JGJ 3-2010; Technical Specification for Concrete Structures of Tall Building. Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD): Beijing, China, 2011.
- Dassault Systèmes. 22.2.2 Models for metals subjected to cyclic loading. In Abaqus 6.11. Abaqus Analysis User’s Manual; Dassault Systèmes: Vélizy-Villacoublay, France, 2011. [Google Scholar]
- Dassault Systèmes. 22.6.3 Concrete damaged plasticity. In Abaqus 6.11. Abaqus Analysis User’s Manual; Dassault Systèmes: Vélizy-Villacoublay, France, 2017. [Google Scholar]
- Bardet, J.P.; Ichii, K.; Lin, C.H. EERA–A Computer Program for Equivalent Linear Earthquake Site Response Analyses of Layered Soil Deposits; University of Southern California: Los Angeles, CA, USA, 2000. [Google Scholar]
- China Academy of Building Research. User’s manual and technical specification of SATWE–Space finite element analysis and design software for multi-story and tall buildings with wall-element. Available online: https://uc.pkpm.cn/TrialCenterProDerail?trialCenterProductId=c8bb7833-b554-40ea-8ad1-95cc5b95e68c (accessed on 22 February 2021).
- Liang, J.; Cao, Z.; Zhou, D.; Zhao, H. Elastoplastic time-history analysis of a super high-rise building in Tianjin under rare earthquake. Ind. Constr. 2016, 46, 179–186. [Google Scholar]
- GB 50011-2010; Code for Seismic Design of Buildings: 4.1 Site. Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD): Beijing, China, 2010.
- Lysmer, J.; Kuhlemeyer, R.L. Finite dynamic model for infinite media. J. Eng. Mech. Div. 1969, 95, 859–878. [Google Scholar] [CrossRef]
- Liao, Z.P.; Wong, H.L.; Yang, B.P.; Yuan, Y.F. A transmitting boundary for transient wave analyses. Sci. Sin. Ser. A 1984, 27, 1063–1076. [Google Scholar]
- Deeks, A.J.; Randolph, M.F. Axisymmetric time-domain transmitting boundaries. J. Eng. Mech. 1994, 120, 25–42. [Google Scholar] [CrossRef]
- Liu, J.; Lu, Y. A direct method for analysis of dynamic soil-structure interaction based on interface idea. Dev. Geotech. Eng. 1998, 83, 261–276. [Google Scholar]
- Wang, Z.; Liu, J. Study on wave motion input and artificial boundary for problem of nonlinear wave motion in layered soil. Chin. J. Rock Mech. Eng. 2004, 23, 1169–1173. [Google Scholar]
- Gu, Y.; Liu, J.; Du, Y. 3D consistent viscous-spring artificial boundary and viscous-spring boundary element. Eng. Mech. 2007, 24, 31–37. [Google Scholar]
- Zhang, C.; Pan, J.; Wang, J. Influence of seismic input mechanisms and radiation damping on arch dam response. Soil Dyn. Earthq. Eng. 2009, 29, 1282–1293. [Google Scholar] [CrossRef]
- He, J.; Ma, H.; Zhang, B.; Chen, H. Method and realization of seismic motion input of viscous-spring boundary. Shuli Xuebao 2010, 41, 960–969. [Google Scholar]
- Liang, J.; Yu, J.; Zhang, J.; Ba, Z. Seismic response analysis of metro twin tunnels by the viscous-spring boundary. China Civ. Eng. J. 2014, 47, 274–279. [Google Scholar]
- Wang, Q.; Chen, J.; Li, J. Seismic response analysis of underground pipeline under obliquely incident seismic wave. J. Huazhong Univ. Sci. Technol. 2008, 25, 283–286. [Google Scholar]
- Huang, J.Q.; Du, X.L.; Liu, J.; Zhao, M. Impact of incident angles of P waves on the dynamic responses of long lined tunnels. Earthq. Eng. Struct. Dyn. 2016, 45, 2435–2454. [Google Scholar] [CrossRef]
- Liang, J.; Liu, Z.; Lee, V.W. Scattering of plane waves by a 3-D canyon in layered half-space. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Liang, J.; Liang, J.; Zhang, J.; Ba, Z. Nonlinear seismic response of 3D canyon in deep soft soils. Chin. J. Geotech. Eng. 2017, 39, 1196–1205. [Google Scholar]
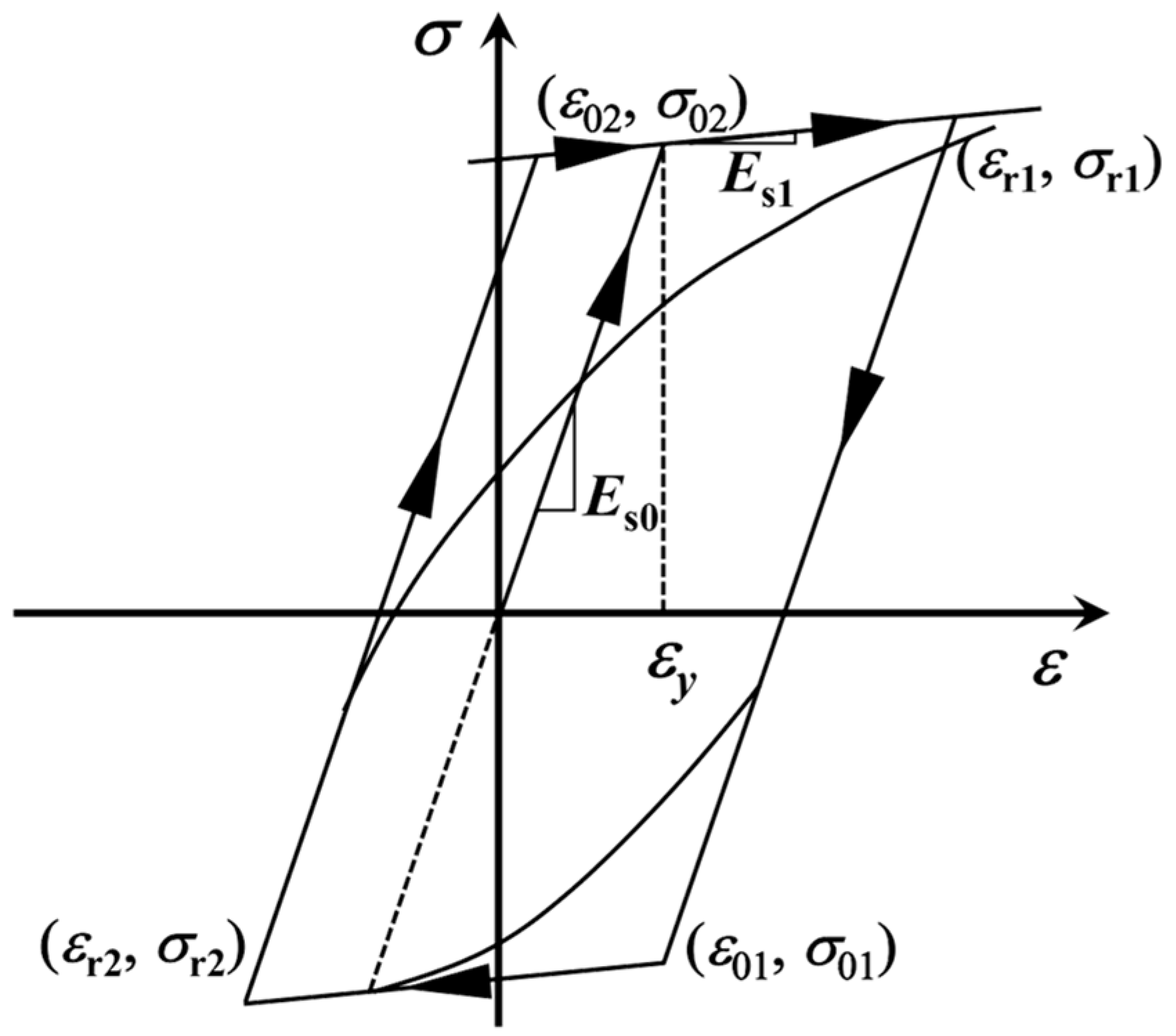

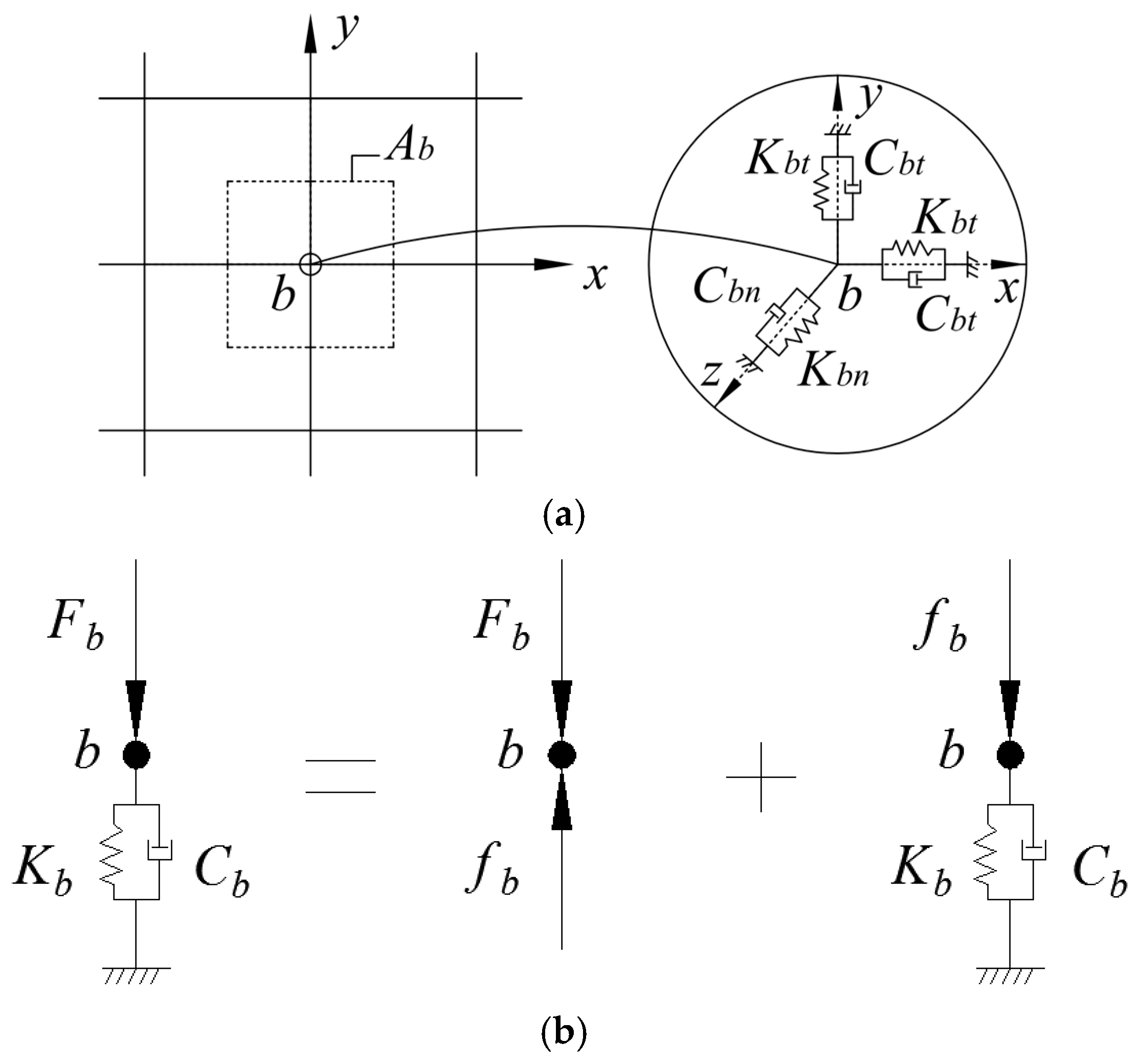





| Symbol Identification | Meaning of Symbols |
|---|---|
| Stress | |
| ϵ | Strain |
| Initial elastic modulus | |
| Tangent modulus in the plastic phase | |
| Compressive yield stress | |
| Ultimate compressive strength | |
| Compressive yield strain | |
| Ultimate compressive strain | |
| () | Yield initiation |
| () | Stress reversal state |
| Tensile damage variables | |
| Compressive damage variables | |
| Kbn | Normal spring stiffness of viscous-spring boundary |
| Kbt | Tangent spring stiffness of viscous-spring boundary |
| Cbn | Normal dashpot coefficients of viscous-spring boundary |
| Cbt | Tangent dashpot coefficients of viscous-spring boundary |
| G | Shear modulus of medium |
| cp | P-wave velocities of medium |
| cs | S-wave velocities of medium |
| υ | Poisson’s ratio of medium |
| ρ | Mass density of medium |
| Ab | Influence area of node b |
| αn | Normal correction factors of spring stiffness |
| αt | Tangent correction factors of spring stiffness |
| R | Distance from scattering wave source to boundary node |
| t | Time term |
| xb | x-coordinates of node b |
| yb | y-coordinates of node b |
| zb | z-coordinates of node b |
| u | Displacement at the boundary node b in the finite element model |
| τ | Stress at the boundary node b in the finite element model |
| uf | Displacement at the node b in the semi-infinite free field |
| τf | Stress at the node b in the semi-infinite free field |
| Fb | Equivalent nodal force imposed on the boundary node of finite element model |
| fb | Interior force between boundary node and spring-dashpot |
| Kb | Spring stiffness calculated by the converged soil parameters obtained from the free-field equivalent linear analysis |
| Cb | Dashpot coefficient calculated by the converged soil parameters obtained from the free-field equivalent linear analysis |
| uf | Converged displacement received from the free-field equivalent linear analysis |
| Velocity received from the free-field equivalent linear analysis | |
| τf | Stress responses received from the free-field equivalent linear analysis |
| a | Canyon radius |
| ω | Circular frequency of the incident harmonic wave |
| Shear wave velocity of the soil | |
| η | Dimensionless frequency |
| Soil particle density | |
| Water density | |
| n | Porosity |
| Maximum shear modulus |
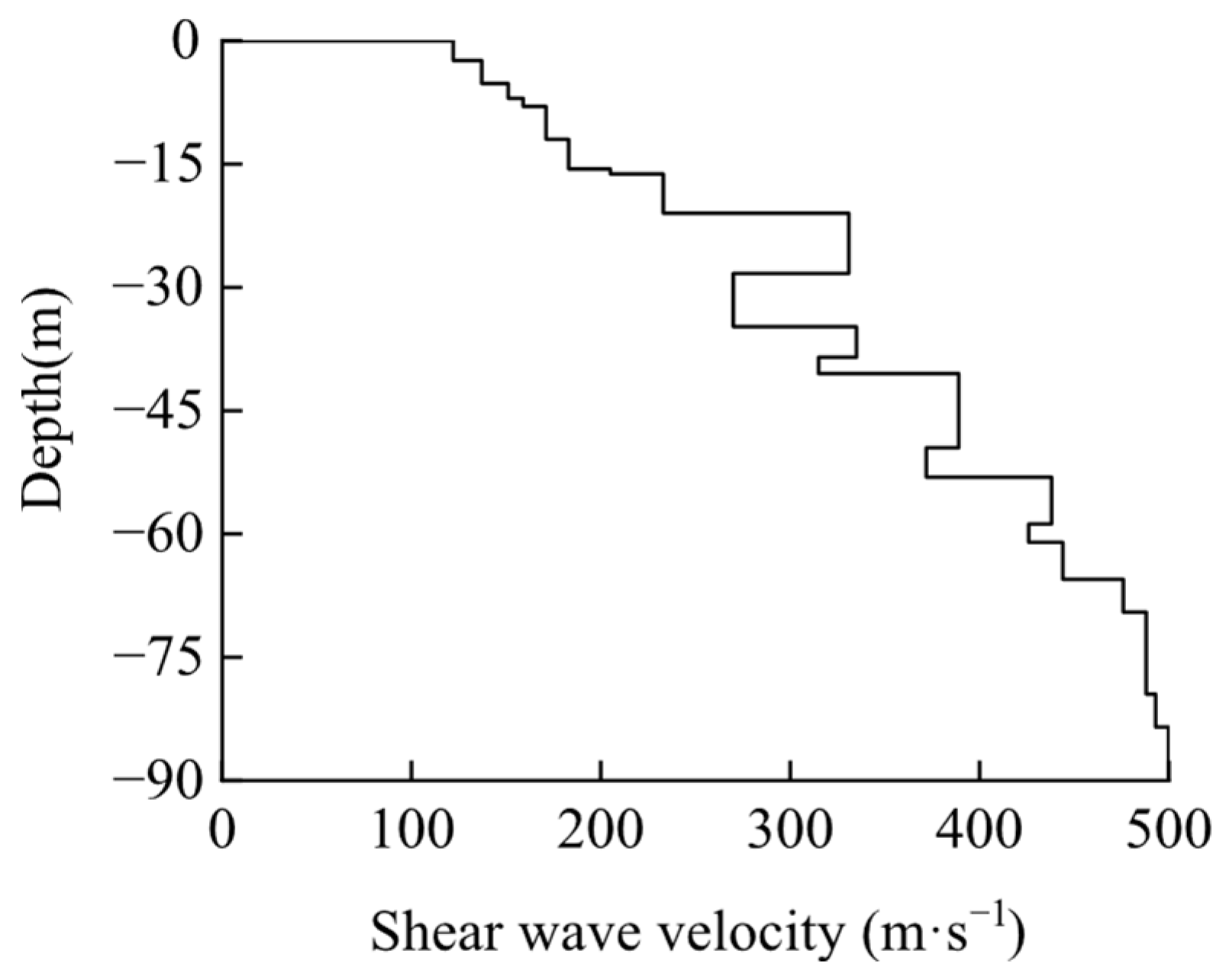
| Soil No. | ρs (kg·m−3) | ρf (kg·m−3) | n | Gmax (MPa) | υ |
|---|---|---|---|---|---|
| Ⅰ | 2477 | 1000 | 0.35 | 23.96 | 0.48 |
| Ⅱ | 2294 | 1000 | 0.32 | 29.28 | 0.35 |
| Ⅲ | 2493 | 1000 | 0.33 | 90.66 | 0.30 |
| Ⅳ | 2614 | 1000 | 0.30 | 200.50 | 0.34 |
| Ⅴ | 2397 | 1000 | 0.32 | 118.83 | 0.35 |
| Ⅵ | 2585 | 1000 | 0.35 | 188.54 | 0.26 |
| Ⅶ | 2463 | 1000 | 0.33 | 228.33 | 0.26 |
| Ⅷ | 2586 | 1000 | 0.30 | 347.24 | 0.30 |
| Ⅸ | 2485 | 1000 | 0.32 | 306.69 | 0.25 |
| Mode | Period (s) | Property | ||
|---|---|---|---|---|
| BCTS | S-P-BCTS | BCTS | S-P-BCTS | |
| 1 | 4.93 | 5.96 | First-order translation in y-direction | First-order translation in y-direction |
| 2 | 4.45 | 5.16 | First-order translation in x-direction | First-order translation in x-direction |
| 3 | 3.24 | 3.47 | First-order torsion | First-order torsion |
| 4 | 1.43 | 2.57 | Second-order translation in x-direction | Second-order translation in x-direction |
| 5 | 1.23 | 2.54 | Second-order translation in y-direction | Second-order translation in y-direction |
| 6 | 1.07 | 2.32 | Second-order torsion | Second-order torsion |
| 7 | 0.74 | 2.05 | Third-order translation in x-direction | First-order vertical vibration |
| 8 | 0.55 | 1.92 | Third-order torsion | Third-order translation in x-direction |
| 9 | 0.53 | 1.88 | Third-order translation in y-direction | Second-order vertical vibration |
| 10 | 0.47 | 1.82 | Fourth-order translation in x-direction | Third-order torsion |
| Seismic Wave | BCTS | S-P-BCTS |
|---|---|---|
| S1 | 0 | 1.63 |
| S2 | 0 | 1.87 |
| S3 | 0 | 1.64 |
| S4 | 0 | 3.65 |
| S5 | 0 | 1.05 |
| S6 | 0 | 1.60 |
| Seismic Wave | BCTS | S-P-BCTS |
|---|---|---|
| S1 | 1/242 (47th storey) | 1/222 (45th storey) |
| S2 | 1/264 (46th storey) | 1/262 (45th storey) |
| S3 | 1/242 (46th storey) | 1/220 (45th storey) |
| S4 | 1/135 (45th storey) | 1/121 (44th storey) |
| S5 | 1/414 (46th storey) | 1/339 (47th storey) |
| S6 | 1/341 (47th storey) | 1/329 (46th storey) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, J.; Sun, S.; Zhang, G.; Wang, D.; Yu, Y.; Wu, J.; Czech, K.R. Damage Characteristics Analysis of High-Rise Frame-Core-Tube Building Structures in Soft Soil Under Earthquake Action. Buildings 2025, 15, 3085. https://doi.org/10.3390/buildings15173085
Liang J, Sun S, Zhang G, Wang D, Yu Y, Wu J, Czech KR. Damage Characteristics Analysis of High-Rise Frame-Core-Tube Building Structures in Soft Soil Under Earthquake Action. Buildings. 2025; 15(17):3085. https://doi.org/10.3390/buildings15173085
Chicago/Turabian StyleLiang, Jiali, Shifeng Sun, Gaole Zhang, Dai Wang, Yong Yu, Jihu Wu, and Krzysztof Robert Czech. 2025. "Damage Characteristics Analysis of High-Rise Frame-Core-Tube Building Structures in Soft Soil Under Earthquake Action" Buildings 15, no. 17: 3085. https://doi.org/10.3390/buildings15173085
APA StyleLiang, J., Sun, S., Zhang, G., Wang, D., Yu, Y., Wu, J., & Czech, K. R. (2025). Damage Characteristics Analysis of High-Rise Frame-Core-Tube Building Structures in Soft Soil Under Earthquake Action. Buildings, 15(17), 3085. https://doi.org/10.3390/buildings15173085







