Numerical Assessment of Cast-in-Place Anchor Pullout Strength Regarding CCD Methodology

Abstract

Reliable anchorage of cast-in-place headed bolts in unreinforced concrete is vital in structural and industrial applications, where inaccurate strength predictions can compromise safety and efficiency. This study develops and validates an elastic–plastic concrete model within LS-DYNA to assess the tensile performance of headed anchors with varying embedment depth-to-diameter ratios. A parametric analysis is conducted, considering different concrete strengths, anchor sizes, and steel yield strengths. The results show notable deviations from the Concrete Capacity Design (CCD) method, particularly under high-strength concrete and reduced embedment ratios. The CCD method underestimates capacity at 30–40 MPa and overestimates it at 20 MPa. A correction coefficient is proposed to improve embedment depth estimation. The findings offer practical guidance for safer and more accurate anchor design.

1. Introduction

Cast-in-place anchors function as anchorage systems widely utilized in both structural and non-structural components of civil engineering projects to transfer external loads to concrete elements—for example, securing steel structures to concrete foundations or facilitating load transfer in concrete column–beam connections. 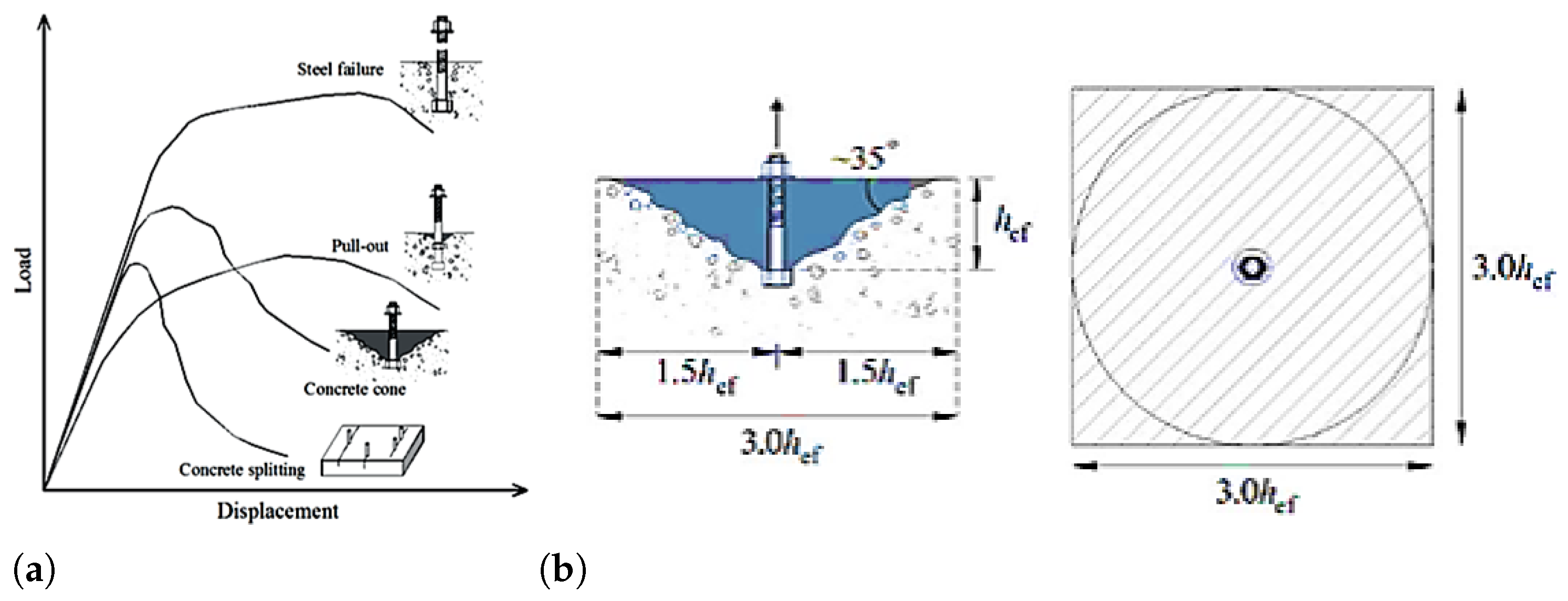Headed anchors are a type of cast-in-place anchor with a specific geometry that can act as suitable alternatives to hook anchors in order to decrease steel crowding in specially designed sections [1,2]. Previous theoretical and experimental studies have demonstrated that when a single cast-in-place headed anchor experiences tensile loads, it exhibits two types of failure behavior: ductile and brittle failure modes, as depicted in Figure 1a. In the load–displacement curves, both steel failure and pullout display the greatest displacement under peak loading, reflecting behavior typical of ductile failure. In cases of steel failure, the strength of a headed anchor is primarily governed by the cross-sectional area of the anchor head and the mechanical properties of the steel. Additionally, pullout failure depends on the embedment depth and cross-section. Brittle failure is observed in cases of concrete cone and concrete splitting. These failure modes demonstrate rapid declines at peak load due to the rapid and unstable propagation of concrete cracks. Cracking in the anchoring zone results from brittle failure, which arises directly from mobilizing the maximum tensile strength of the concrete. In general conditions, one of the parameters to achieve the required yield strength of concrete elements is ensuring an effective development length.

Under ideal conditions, a cast-in-place headed anchor subjected to tensile loading is expected to undergo maximum deformation at peak load at the point of failure. However, initially, the anchor should fail before the concrete loses its serviceability [3,4]. In recent decades, numerous experimental and numerical investigations have been conducted to develop accurate models for estimating the anchorage strength and identifying the failure modes of anchor bolts embedded in concrete structural elements. However, two main reference principles have been assumed for predicting and calculating the failure mechanism mode and strength of headed anchors. The first theoretical model, the concrete cone model, assumes a projected circular area and an inclination of 45-degree angle to the concrete surface, which was mentioned in ACI 349 [5]. The second model, known as the Concrete Capacity Design (CCD) approach, was proposed [3] to evaluate the tensile load-carrying capacity related to concrete cone fracture. The CCD method considers the formation of a concrete failure cone inclined at 35 degrees relative to the surface. This idealized failure region spans an approximate area of $3h_{ef}\times 3h_{ef}$ across the concrete face, as illustrated in Figure 1b.

Figure 1. Response of tension-loaded headed anchors and idealized projected area in CCD method. (a) Pullout response of anchors [6]. (b) Concrete cone area in CCD method [3].

Figure 1. Response of tension-loaded headed anchors and idealized projected area in CCD method. (a) Pullout response of anchors [6]. (b) Concrete cone area in CCD method [3].

To determine the nominal strength associated with the concrete cone failure of a cast-in-place single anchor subjected to tensile loading, the CCD method provides a predictive framework based on geometric and material parameters, as shown in Equation (1).

$$N_n=k\sqrt{f_c^{\prime }}{h}_{ef}^{1.5}$$

(1)

In this context, $N_n$ represents the mean nominal concrete cone strength factor, used to estimate the average breakout capacity of a headed anchor embedded in intact concrete, with a value of 16.8. The term $h_{ef}$ denotes the effective anchorage depth of the anchor, measured in millimeters. According to ACI 318-19 [7], the coefficient k used in calculating the ultimate tensile strength of a cast-in-place single anchor is 10, whereas for a post-installed anchor, it is 7. Considering the shallow ($h_{ef}\le 200$ mm) and deep anchorage depths of the anchor, which are determined by the relationship between anchorage depth and the distance to the nearest concrete surface, tests have shown that the shallow anchorage depth is characterized by cone failure, while the deep anchorage depth is associated with side blow-out failure [8]. According to Eligehausen et al. [6], an increase in anchorage depth leads to a steeper crack inclination within the failure cone. Moreover, the anchorage capacity of a headed anchor is enhanced when the surrounding concrete section is confined by parallel reinforcement. In contrast, longitudinal reinforcement has been shown to have no significant impact on anchorage capacity [9]. Observations regarding the effects of anchor head size and member thickness indicate that the ultimate tensile strength of the concrete cone increases with larger anchor head dimensions and greater concrete member thickness [4]. The CCD method has been observed to yield non-conservative predictions of tensile breakout capacity for short-headed anchors ($h_{ef}\le 100$ mm). Conversely, for deep anchors ($h_{ef}\ge 200$ mm), it provides overly conservative estimates [4]. Investigations into the effects of concrete compressive strength and anchor anchorage depth within the CCD framework have further revealed that seismic tensile strength is lower than the nominal values prescribed by current design codes. As a result, the revised k-value has been proposed to improve the accuracy of seismic strength predictions [10]. Finally, the anchorage strength provisions for headed anchors outlined in Chapter 17 of ACI 318-14 [11] were found to be excessively conservative, so new provisions were recommended and proposed for ACI 318-19 [7,12,13,14,15].

Recent investigations have confirmed the predictive accuracy of the CCD method in estimating the ultimate tensile capacity of cast-in-place anchors embedded in plain concrete, thereby reinforcing its validity for design applications. The primary contribution of this study is the development of a pullout model for cast-in-place headed anchors, grounded in the CCD methodology, to evaluate the ultimate tensile strength of anchor bolts embedded in plain concrete. The accuracy of the proposed model is critically examined, and its applicability is assessed through a series of tensile pullout analyses. Three parameters, namely the compressive strength of concrete, embedded depth, and the yield stress of steel, have been selected as key factors to measure the tensile anchorage strength. Section 1 outlines the key parameters affecting the anchorage behavior of headed anchors. Section 2 details the validation process of both the experimental pullout tests and the numerical model. In Section 3, the pullout behavior of cast-in-place headed anchors is examined, including the evaluation of ultimate anchor strength and the prediction of effective anchorage depth. Finally, Section 4 provides a summary of the key findings derived from the study.

2. Simulation Framework

This section focuses on modeling the pullout behavior of cast-in-place headed anchors using LS-DYNA, with validation performed through comparison of simulation results against experimental data. For this purpose, a laboratory specimen from a reference study by [4] was modeled for verification.

2.1. Reference Experiment

The experimental setup referenced in this study comprises a plain concrete box measuring $1300\times 1300$ mm, into which a single cast-in-place headed anchor is embedded. The steel headed anchor bolt is centrally located and features an effective anchorage depth of $h_{ef}=220$ mm. The anchor type used is an M36 standard threaded rod, with a shaft diameter of 36 mm, a head diameter of 55 mm, and a head thickness of 30 mm. Due to the thin plastic coating on the anchor, there is a complete absence of friction and adhesion between the rod and the concrete substrate. The yield strengths $\left(f_y\right)$ of the steel-headed anchor which is used for the rod and head sections are 900 and 1000 MPa, respectively. The selected model for validation in the reference tests is NPC330. The input data and models are reported in

Table 1. The details of the experimental model.

Model Name	${\mathit{f}}_{\mathit{c}}^{\mathbf{\prime }}$ (MPa)	${\mathit{h}}_{\mathit{ef}}$ (mm)	H (mm)	${\mathit{d}}_{\mathit{b}}$ (mm)	Anchor (mm)
NPC-330	$41.03$	220	330	36	$55\times 30$

. The test setup includes a steel support ring with an inner diameter of 880 mm on which the concrete slab was placed. The load was applied to the anchor shaft using a hydraulically operated actuator with displacement control.

2.2. Continuous Surface Cap Plasticity

One of the most important aspects of the present study is choosing a suitable concrete material that performs well under tensile load and demonstrates the algorithm of cracking in tension. However, among the various finite element software options available for simulation, LS-DYNA [16] stands out for its good accuracy, comprehensive library of concrete materials, and numerous interactions between concrete and steel anchors. A review of the concrete material models available in LS-DYNA identifies four primary plasticity-based formulations: MAT273 [17], MAT84 [18], MAT72 [19], and MAT159 [20,21]. Among these, MAT159 was selected for detailed analysis in the present study.

The CSCM concrete model, initially developed for roadside safety applications, represents a comprehensive material model for concrete within a finite element code, particularly in scenarios involving tensile loads. It includes an option for implementing peak strength through cap retraction. Figure 2 illustrates the characteristic shape of the CSCM yield surface. This model utilizes a multiplicative formulation that integrates the shear failure surface with a pressure-dependent hardening cap. As a cap-type plasticity model, CSCM ensures a smooth and continuous intersection between the failure envelope and the hardening cap. After an initial elastic phase, the concrete may undergo yielding and potential failure depending on the stress conditions. Yield behavior is governed by a three-dimensional yield surface, defined in terms of three stress invariants: the first invariant of the stress tensor $\left(J_1\right)$, and the second and third invariants of the deviatoric stress tensor ($J_2^{\prime }$ and $J_3^{\prime }$) [22]. These invariants are derived from the deviatoric stress tensor components ($S_{ij}$) and the hydrostatic pressure (P) as shown in Equation (2).

$$\begin{array}{c}\hfill J_1=3P,J_2^{\prime }={\displaystyle \frac{1}{2}}{S}_{ij}{S}_{ij},J_3^{\prime }={\displaystyle \frac{1}{3}}{S}_{ij}{S}_{jk}{S}_{ki}\end{array}$$

(2)

The yield criterion based on three stress invariants is derived from Equation (3) and is governed by the compaction-related hardening parameter k.

$$f(J_1,J_2^{\prime },J_3^{\prime },k)=J_2^{\prime }-R^2{F}_f^2{F}_c$$

(3)

Here, $F_f$ represents the shear failure surface, $F_c$ denotes the hardening cap, and R represents the Rubin three-invariant reduction factor. The cap hardening parameter, k, corresponds to the value of the pressure invariant at the intersection of the cap and shear surfaces. Concrete strength is represented by two distinct surface models: the shear failure surface and the cap surface. The shear surface model is primarily applicable under tensile stress conditions and low confining pressure, as described by Equation (4):

$$F_f\left(J_1\right)=\alpha -{\lambda }_{exp}^{-\beta J_1}+\theta J_1$$

(4)

In this formulation, the parameters $\alpha$, $\beta$, $\lambda$, and $\theta$ are calibrated by correlating the model response with experimental strength data obtained from tests on plain concrete cylinders. The integrated application of the shear and cap surface models addresses the behavior of concrete across low to high confining pressure regimes, as expressed in Equation (5).

$$F_c(J_1,k)=1-{\displaystyle \frac{(J_1-L_k)(\left|J_1-L_k\right|+J_1-L_k)}{2{(X_k-L_k)}^2}},L_k=\left\{\begin{array}{cc}k& k\ge k_0\\ k_0& k<k_0\end{array}\right\}$$

(5)

The function $F_c$ assumes a value of unity when $J_1\le L_k$. However, concrete demonstrates softening behavior in tensile and low-to-moderate compressive stress regimes. This softening is captured through the transformation of viscoplastic stress into damaged stress, as described by Equation (6).

$${\sigma }_{ij}^d=(1-d){\sigma }_{ij}^{vp}$$

(6)

The scalar damage parameter, denoted as d, induces a transformation of the viscoplastic stress tensor represented as ${\sigma }_{ij}^{vp}$, into the damaged stress tensor, denoted as ${\sigma }_{ij}^d$.

2.3. Numerical Simulation

In this section, the numerical model is developed. In the same direction, a Plastic–Kinematic material (MAT3) was selected to simulate the cast-in-place steel headed anchor. In this case, the anchor is modeled as a solid type and is subjected to a tensile load, which is adapted using the features of MAT3. The MAT3 material model in LS-DYNA is specifically designed to accurately represent the behavior of materials undergoing isotropic and kinematic hardening plasticity, while also providing the flexibility to incorporate rate effects. During the present study, isotropic hardening was considered and implemented in LS-DYNA by selecting ${\beta }_s=1$, as shown in Figure 3.

LS-DYNA offers a broad range of contact interaction definitions applicable to finite element models. When specifying contact between two solid element surfaces, the software provides two primary approaches: automatic and non-automatic. For explicit analyses, the automatic contact method is typically used, while non-automatic contacts are more common in implicit analyses [16]. In the present study, the interaction between the cast-in-place headed anchor and the surrounding concrete box is modeled using the CONTACT_AUTOMATIC_SURFACE_TO_SURFACE formulation. This contact definition establishes a bonded interaction between the anchor and concrete surfaces, utilizing the Slave and Master part assignment to monitor nodal positions and prevent interpenetration. According to the experimental setup, a round steel support featuring inner diameter of $4h_{ef}$ (880 mm) and outer diameter of $5h_{ef}$ (1100 mm) was placed directly on the concrete surface, as illustrated in Figure 4. The support was deliberately designed with sufficient dimensions to allow for the unrestricted formation of a concrete breakout cone, consistent with the CCD method. In the numerical simulation, this support is used to restrain vertical movement, and it is constrained in the x, y, and z directions as part of the boundary conditions. To simulate tensile loading on the headed anchor in LS-DYNA, the PRESCRIBED_MOTION_SET function is utilized. This function defines motion in the z-direction at the top nodes of the headed anchor to apply the tensile load. The type of loading is specified as displacement-controlled. A mesh overview of the model is presented in Figure 4.

A quasi-static analysis was performed using an explicit solver, with the pullout duration extended to approximately ten times the model’s natural period as Figure 5a to ensure dynamic effects were minimized. Based on the geometric configuration and mesh of the numerical model, the computed pullout strength is $345.2$ kN, whereas the experimentally measured pullout strength is 319 kN.

A comparison of force–displacement responses between the numerical and experimental results is presented in Figure 5b. The calculated error in pullout strength is approximately $8\%$ at the displacement corresponding to failure ($4.73$ mm). Both the experimental and numerical curves exhibit a generally smooth profile. As shown in the crack patterns in Figure 5c, fracture initiation is observed to occur sharply in both simulations. However, the post-collapse slope of the experimental curve, associated with energy dissipation, is noticeably steeper than that of the numerical counterpart. The formation of cone-shaped cracks between the anchor head and the concrete surface is responsible for the ultimate loss of load-carrying capacity. Observations from Figure 5c indicate that the cracks originating at the anchor head propagate at an inclination angle of approximately 35 degrees. Overall, the developed numerical models demonstrate strong agreement with the experimental data in terms of ultimate load capacity and pullout behavior.

3. Parametric Study

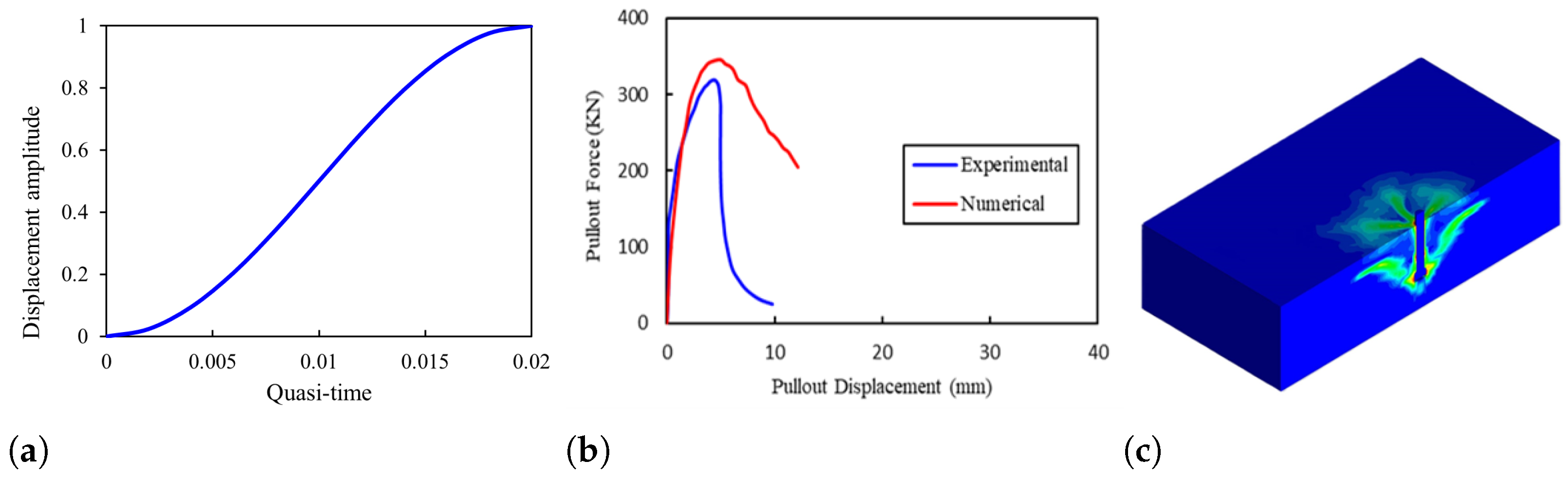
Accurately defining the true load-carrying capacity and ensuring adequate ductility of a cast-in-place headed anchor under tensile loading are critical for achieving optimal structural performance. Additionally, the ACI 318-19 [7] standard mentioned regulations to control the effective length and ultimate strength of anchorage, as well as the necessary protocols during implementation. The loading protocol adopted in this study was executed in phases using a monotonic displacement-controlled approach, continuing up to the point of failure displacement. This displacement-control approach was based on a motion set in the z-direction in LS-DYNA. The parameters considered in this study for the analysis are presented in

Table 2. The parametric space developed for cast-in-place anchor bolts with $d_b=20$ (mm) diameter.

Model	$\frac{{\mathit{h}}_{\mathit{ef}}}{{\mathit{d}}_{\mathit{b}}}$	${\mathit{h}}_{\mathit{ef}}$ (mm)	${\mathit{f}}_{\mathit{c}}^{\mathbf{\prime }}$ (MPa)	H (mm)	L (mm)
C20-D20-H5	5	100	20	200	600
C30-D20-H5	5	100	30	200	600
C40-D20-H5	5	100	40	200	600
C20-D20-H8	8	160	20	320	960
C30-D20-H8	8	160	30	320	960
C40-D20-H8	8	160	40	320	960
C20-D20-H10	10	200	20	400	1200
C30-D20-H10	10	200	30	400	1200
C40-D20-H10	10	200	40	400	1200
C20-D20-H12	12	240	20	480	1440
C30-D20-H12	12	240	30	480	1440
C40-D20-H12	12	240	40	480	1440

,

Table 3. The parametric space developed for cast-in-place anchor bolts with $d_b=25$ (mm) diameter.

Model	$\frac{{\mathit{h}}_{\mathit{ef}}}{{\mathit{d}}_{\mathit{b}}}$	${\mathit{h}}_{\mathit{ef}}$ (mm)	${\mathit{f}}_{\mathit{c}}^{\mathbf{\prime }}$ (MPa)	H (mm)	L (mm)
C20-D25-H5	5	125	20	250	750
C30-D25-H5	5	125	30	250	750
C40-D25-H5	5	125	40	250	750
C20-D25-H8	8	200	20	400	1200
C30-D25-H8	8	200	30	400	1200
C40-D25-H8	8	200	40	400	1200
C20-D25-H10	10	250	20	500	1500
C30-D25-H10	10	250	30	500	1500
C40-D25-H10	10	250	40	500	1500
C20-D25-H12	12	300	20	600	1800
C30-D25-H12	12	300	30	600	1800
C40-D25-H12	12	300	40	600	1800

and

Table 4. The parametric space developed for cast-in-place anchor bolts with $d_b=30$ (mm) diameter.

Model	$\frac{{\mathit{h}}_{\mathit{ef}}}{{\mathit{d}}_{\mathit{b}}}$	${\mathit{h}}_{\mathit{ef}}$ (mm)	${\mathit{f}}_{\mathit{c}}^{\mathbf{\prime }}$ (MPa)	H (mm)	L (mm)
C20-D30-H5	5	150	20	300	900
C30-D30-H5	5	150	30	300	900
C40-D30-H5	5	150	40	300	900
C20-D30-H8	8	240	20	480	1440
C30-D30-H8	8	240	30	480	1440
C40-D30-H8	8	240	40	480	1440
C20-D30-H10	10	300	20	600	1800
C30-D30-H10	10	300	30	600	1800
C40-D30-H10	10	300	40	600	1800
C20-D30-H12	12	360	20	720	2160
C30-D30-H12	12	360	30	720	2160
C40-D30-H12	12	360	40	720	2160

, consisting of various anchor diameters ($d_b)$, compressive concrete strength for the plain slab $\left(f_c^{\prime }\right)$, embedded depth $\left(h_{ef}\right)$, and the yield strength of the steel $\left(f_y\right)$. The interior and exterior diameter of the ring support $\left(L\right)$ depend on the embedded depth of each model. The height of the plain slab $\left(H\right)$ was chosen to be twice the embedded depth. Additionally, the nominal strength, calculated using Equation (1), is reported to support subsequent discussions. Cross-sectional dimensions of the headed anchor, as selected by chapter 25 of ACI 318-19 [7], states that it should be four times the anchor diameter.

3.1. Strength Measure

The concrete cone strength calculated using the ACI method $\left(N_b\right)$, the concrete cone strength from the CCD method $\left(N_c\right)$, the $beta$-factor which resulted from the numerical analysis, and the LS-DYNA results $\left(N_s\right)$ are presented in

Table 5. The pullout resistance of cast-in-place anchor bolts with $d_b=20$ (mm) diameter.

Model	${\mathit{N}}_{\mathit{b}}$ (kN)	${\mathit{N}}_{\mathit{c}}$ (kN)	${\mathit{N}}_{\mathit{s}}$ (kN)	$\frac{{\mathit{N}}_{\mathit{s}}}{{\mathit{N}}_{\mathit{c}}}$	$\mathit{\beta }$
C20-D20-H5	44.72	75.1	60.3	0.80	13.48
C30-D20-H5	54.8	92.0	100.2	1.09	18.30
C40-D20-H5	63.2	106.3	132.2	1.24	20.90
C20-D20-H8	90.5	152.1	130.8	0.86	14.45
C30-D20-H8	110.9	186.2	195.4	1.05	17.62
C40-D20-H8	128	215.04	253.2	1.18	19.78
C20-D20-H10	126.5	212.5	179.0	0.84	14.15
C30-D20-H10	154.9	260.3	267.2	1.03	17.25
C40-D20-H10	178.9	300.53	344.8	1.15	19.27
C20-D20-H12	166.3	279.3	244.0	0.87	14.67
C30-D20-H12	203.6	342.1	369.2	1.08	18.13
C40-D20-H12	235.15	395.05	480.0	1.22	20.41

,

Table 6. The pullout resistance of cast-in-place anchor bolts with $d_b=25$ (mm) diameter.

Model	${\mathit{N}}_{\mathit{b}}$ (kN)	${\mathit{N}}_{\mathit{c}}$ (kN)	${\mathit{N}}_{\mathit{s}}$ (kN)	$\frac{{\mathit{N}}_{\mathit{s}}}{{\mathit{N}}_{\mathit{c}}}$	$\mathit{\beta }$
C20-D25-H5	62.50	105.00	103.49	0.99	16.56
C30-D25-H5	76.55	128.60	164.82	1.28	21.53
C40-D25-H5	88.39	148.49	216.30	1.46	24.47
C20-D25-H8	126.49	212.51	190.00	0.89	15.02
C30-D25-H8	154.92	260.26	284.88	1.09	18.39
C40-D25-H8	178.89	300.53	375.30	1.25	20.98
C20-D25-H10	176.78	296.98	247.00	0.83	13.97
C30-D25-H10	216.51	363.73	385.30	1.06	17.80
C40-D25-H10	250.00	412.88	502.20	1.22	20.09
C20-D25-H12	232.38	390.40	336.70	0.86	14.49
C30-D25-H12	284.60	478.14	498.90	1.04	17.53
C40-D25-H12	328.63	559.49	662.80	1.18	20.17

and

Table 7. The pullout resistance of cast-in-place anchor bolts with $d_b=30$ (mm) diameter.

Model	${\mathit{N}}_{\mathit{b}}$ (kN)	${\mathit{N}}_{\mathit{c}}$ (kN)	${\mathit{N}}_{\mathit{s}}$ (kN)	$\frac{{\mathit{N}}_{\mathit{s}}}{{\mathit{N}}_{\mathit{c}}}$	$\mathit{\beta }$
C20-D30-H5	82.16	138.03	133.79	0.97	16.28
C30-D30-H5	100.62	169.05	210.66	1.25	20.94
C40-D30-H5	116.19	195.20	291.80	1.49	25.11
C20-D30-H8	166.28	279.35	294.40	1.05	17.71
C30-D30-H8	203.65	342.13	428.29	1.25	21.03
C40-D30-H8	235.15	395.05	583.30	1.48	24.81
C20-D30-H10	377.12	390.00	372.00	0.95	16.02
C30-D30-H10	232.38	478.20	545.40	1.14	19.16
C40-D30-H10	284.60	552.10	715.00	1.30	21.75
C20-D30-H12	305.47	513.19	493.61	0.96	16.16
C30-D30-H12	374.12	628.53	720.73	1.15	19.26
C40-D30-H12	432.00	725.76	928.70	1.28	21.50

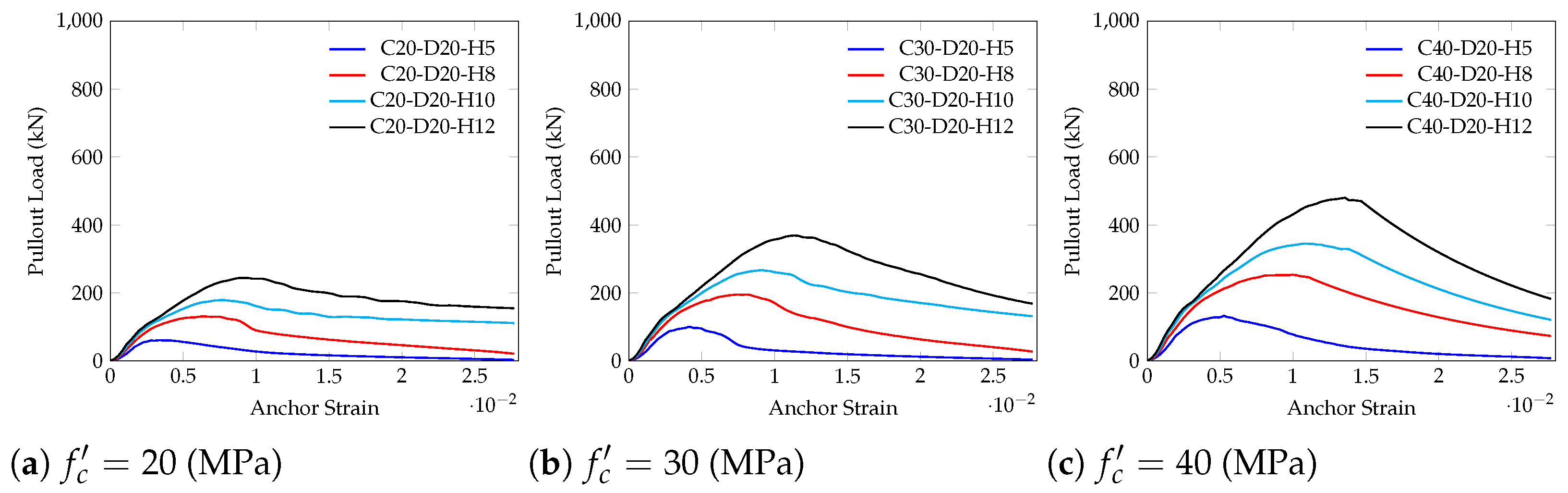
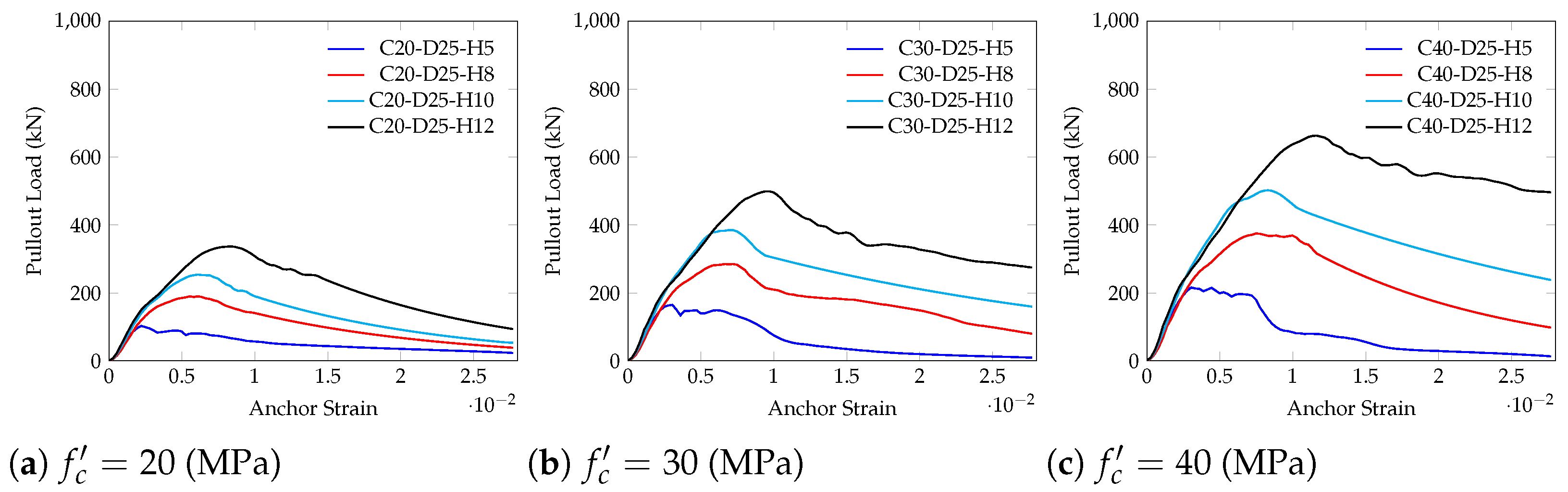
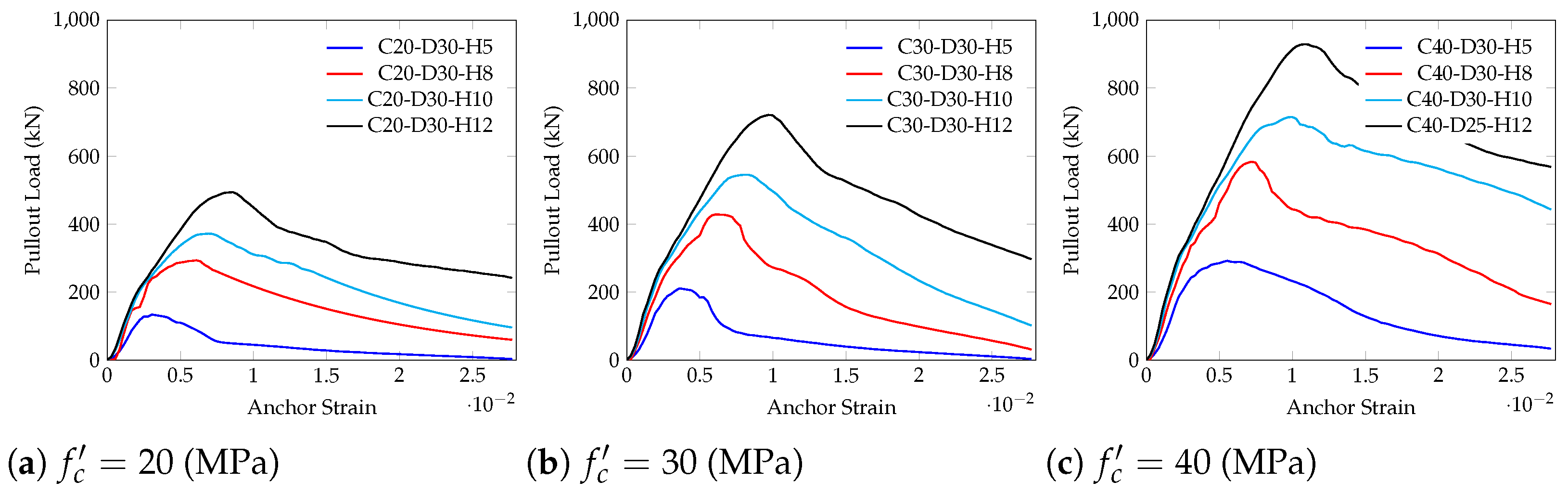
. Additionally, Figure 6, Figure 7 and Figure 8 illustrate the strength versus displacement curves from the pullout analyses conducted within the defined parametric space.

Upon reviewing the observations, the Concrete Capacity Design (CCD) method (Equation (1)) underestimates the concrete breakout capacity of anchor bolts embedded in plain concrete slabs with compressive strengths of 35 MPa and 45 MPa, while it overestimates the capacity for the concrete slab with a compressive strength of 20 MPa. According to the results for headed anchors, which demonstrate both overestimation and underestimation, there is no consistent trend observed in comparison to the CCD (Concrete Capacity Design) method. For headed anchor bolts embedded in plain concrete slabs with low embedment depth, a trend was shown where the pullout strength increased significantly as the embedment depth decreased in concrete slabs with 30 MPa and 40 MPa concrete strength. Remarkably, the anchor bolts with a size of 30 mm exhibited the most substantial difference. Actually, the manner of change and accuracy of convergence varied for each anchor size, according to the assumed parameters. Based on three different concrete compressive strength values, namely 20 MPa, 30 MPa, and 40 MPa, an average value of the $\beta$-factor is proposed for practical use, with $\beta =15.25$, $\beta =18.9$, and $\beta =21.6$, respectively.

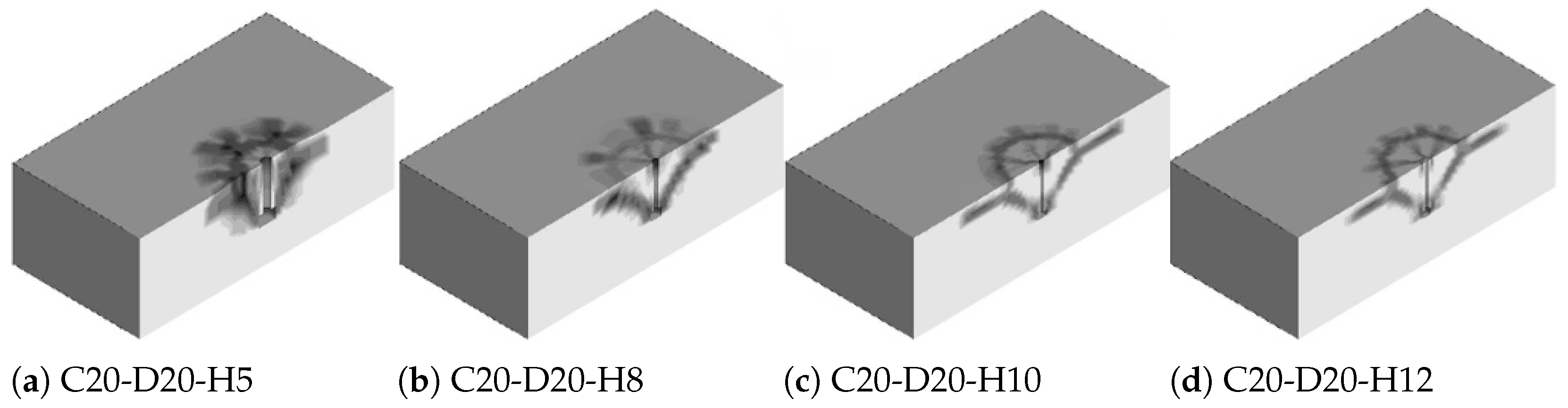
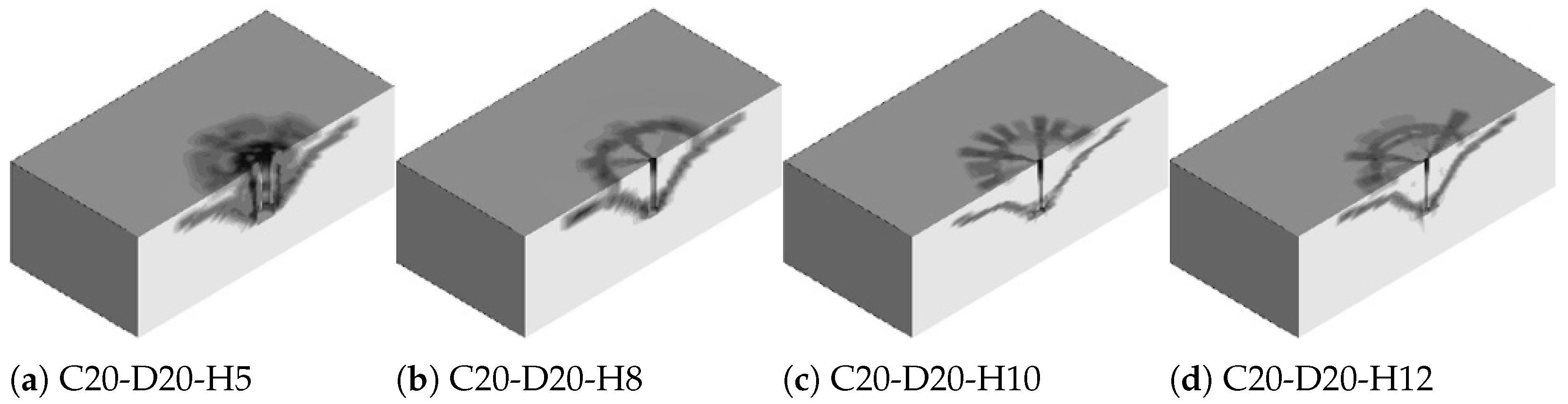
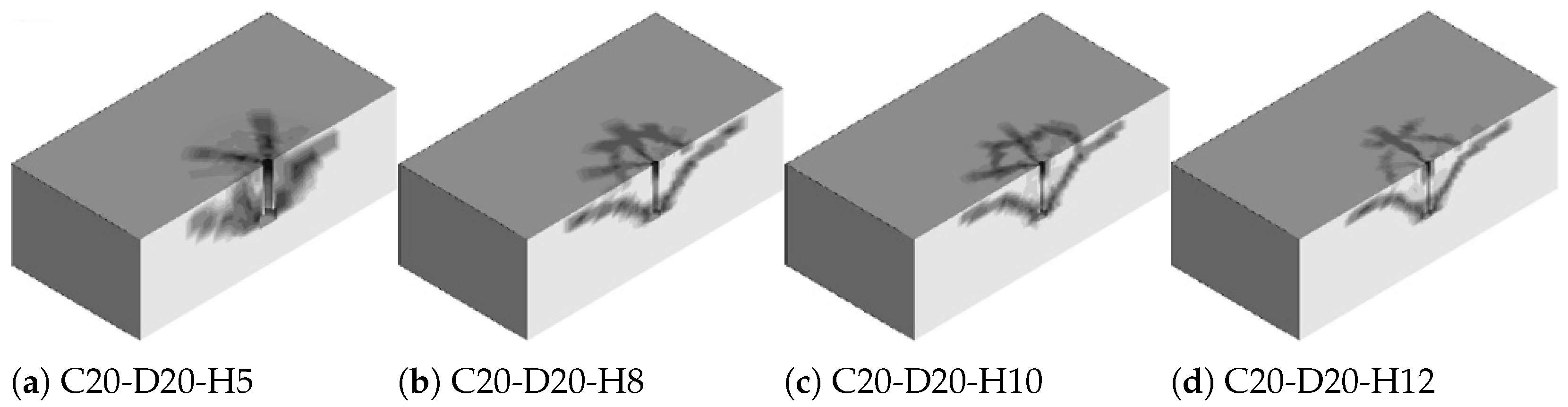
3.2. Crack Patterns

The cracking patterns observed in the modeled cast-in-place anchor bolts embedded within plain concrete slabs are illustrated in Figure 9, Figure 10 and Figure 11. According to the observations, the cracking process initiates at the anchor head region and subsequently progresses toward the concrete surface at an inclination angle of ${35}^{\circ }$–${45}^{\circ }$. The failure rate of the concrete and the associated failure pattern, as the effective depth increases, were effectively controlled, and a ductile behavior was noted. Furthermore, the observed failure pattern correlates with the pattern derived from the CCD method.

Based on observations, initially the damage initiates directly around the head of the anchor. Stress concentrations due to tensile forces cause local crushing and micro-cracking in the surrounding concrete. The cap plasticity model captures the onset of damage where compressive and tensile failure mechanisms interact at the anchor–concrete interface. Furthermore, as tensile load increases, cracks begin to propagate radially from the anchor head toward the concrete surface, forming the early shape of a breakout cone. The radial pattern indicates the formation of tensile cracks driven by the anchor’s uplift force. The cap yield surface adapts to the evolving stress state, simulating the coalescence of multiple cracks under mixed-mode failure. The breakout cone is now fully developed, characterized by a wide radial crack pattern reaching the free surface. The damage zone is distributed along a conical surface typical of concrete breakout failures. The propagation follows a roughly ${35}^{\circ }$–${45}^{\circ }$ angle from the anchor axis, consistent with empirical observations and analytical models like CCD.

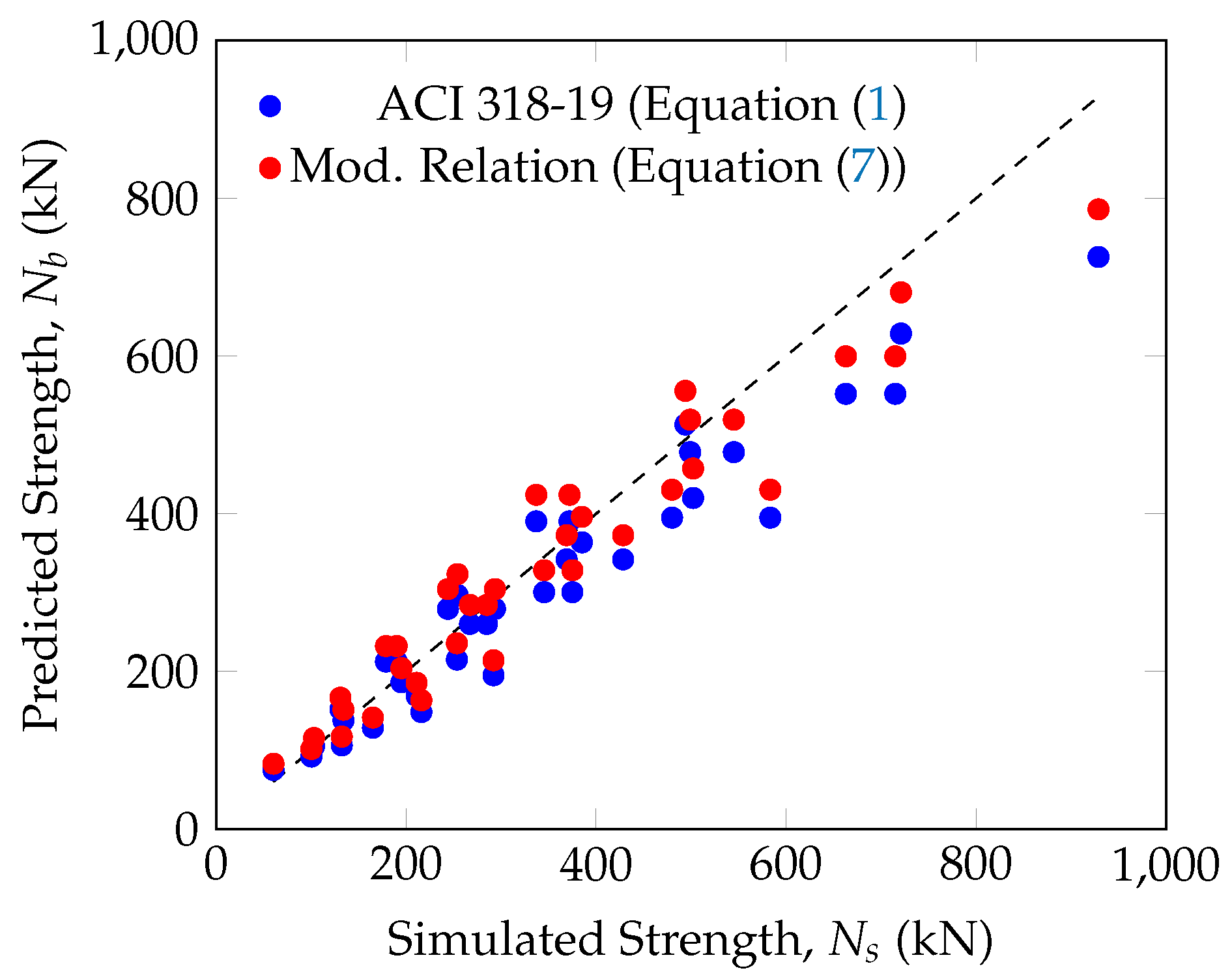
3.3. Modified Strength Prediction

Based on the obtained numerical results, a modified pullout strength prediction, $N_b^{\prime }$, is presented as Equation (7) according to logarithmic nonlinear regression and is compared with ACI 318-19 [7] $\left(N_s\right)$ as Figure 12. Regarding the trend of modified pullout strength $\left(N_b^{\prime }\right)$, its scatter with respect to simulated strength $\left(N_b\right)$ is significantly lower than the code-based strength. The $N_b^{\prime }$ initially shows greater convergence with the CCD method up to an anchorage depth. However, for deeper anchorage depths, the modified strength trend becomes upward.

$$N_b^{\prime }=19.86\sqrt{f_c^{\prime }}{h}_{ef}^{1.485}$$

(7)

Additionally, the smallest disparity between the results obtained from the Concrete Capacity Design (CCD) method and the LS-DYNA results is observed when the $h_{ef}=10d_b$ and the concrete compressive strength is 30 MPa. In the case of cast-in-place headed anchors with large size and concrete slabs with low strength (anchor size of 30 mm and $f_c^{\prime }=20$ MPa) under tensile loads, both overestimation and underestimation situations prevail, which needs review and more experimental studies for determine the final anchorage strength capacity. However, the headed anchor size of 25 mm with a concrete compressive strength of 30 MPa has the highest convergence to all assumed modes. The results confirm a notable loss and gain in strength, so in this way, modified strength prediction according to Equation (7) is recommended in design codes governing the tensile capacity of cast-in-place headed anchor bolts.

4. Conclusions

A numerical model based on the Concrete Capacity Design (CCD) approach was established to assess the tensile pullout behavior of cast-in-place headed anchors. The accuracy and validity of the developed model are confirmed through comparison with existing studies, demonstrating results within an acceptable range. A monotonic displacement–control stage is utilized as a loading protocol. Parametric studies were carried out on multiple anchorage concrete slabs, considering variations in concrete strength, anchor dimensions, and steel yield strength. Additionally, the overall geometry of the concrete specimens was assumed to be proportional to the anchorage depth of the headed anchors. The findings obtained from the analyses are summarized as follows:

• A notable discrepancy in pullout strength emerges at the final stage of monotonic loading when compared to predictions made by the CCD method. As the ratio of anchorage depth to anchor diameter decreases and concrete compressive strength increases, the divergence between the observed results and CCD estimates becomes increasingly evident. Specifically, the CCD method tends to underestimate the breakout capacity of anchor bolts embedded in plain concrete members with compressive strengths of 30 MPa and 40 MPa, while it overestimates the capacity for members with a compressive strength of 20 MPa. These inconsistencies highlight the need for a revision of the current design assumptions.
• Given the observed overestimation and underestimation of pullout strength by the CCD method across varying concrete strengths, a revision of the pullout strength $\left(N_b^{\prime }\right)$ within the CCD design model is recommended to improve predictive accuracy. The analysis results suggest pullout strength $N_b^{\prime }=19.86\sqrt{f_c^{\prime }}{h}_{ef}^{1.485}$. Due to the embedded depth-to-diameter ratio, the CCD method needs slight modification to consider the effect concrete strength parameter.
• The ratio of anchorage depth to anchor diameter significantly influences the degree of convergence between the numerical results and the CCD method across different concrete strengths. Anchors with deeper anchorage depths demonstrate greater alignment with CCD predictions compared to those with shallow anchorage. The highest level of convergence was observed for an anchorage depth of $h_{ef}=10d_b$ in 30 MPa concrete, particularly for cast-in-place headed anchors measuring 20 mm in size.
• Findings from the numerical analysis, which incorporated variations in concrete strength, steel yield strength, and anchorage depth of cast-in-place headed anchors in plain concrete slabs, led to the recommendation of a coefficient for predicting anchorage depth based on anchor dimensions. The force–displacement response indicated that the revised anchorage depth resulted in the highest displacement at peak load. Therefore, a revision to the design criteria is necessary to establish appropriate limits based on the yield strength of the steel.