Experimental Study on the Pullout Behavior of Helical Piles in Geogrid-Reinforced Dense Shahriyar Sand
Abstract
1. Introduction
2. Methodology
2.1. Testing Program
2.2. Dimensional Analysis
2.3. Helical Pile Model Design and Construction
2.4. Soil Testing Procedures
2.5. Geogrid Model
2.6. Soil Container Design and Soil Density
3. Experimental Setup
3.1. Experimental Setup for Axial Tensile Load Test
3.2. Design of Experiments
4. Results and Discussions
4.1. Pullout Test Results of Conventional Pile
4.1.1. Pullout Load–Displacement Curve of Conventional Pile
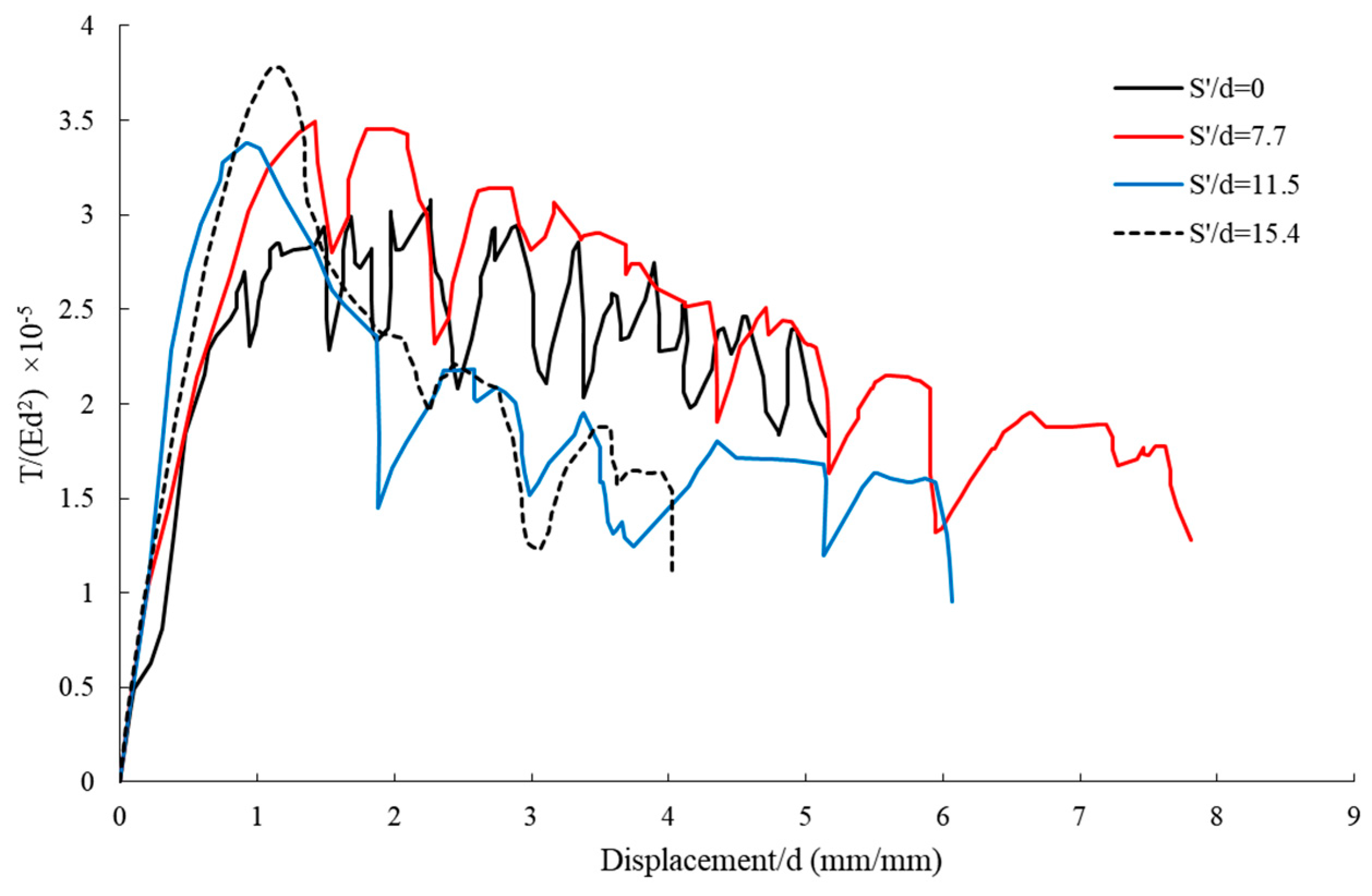
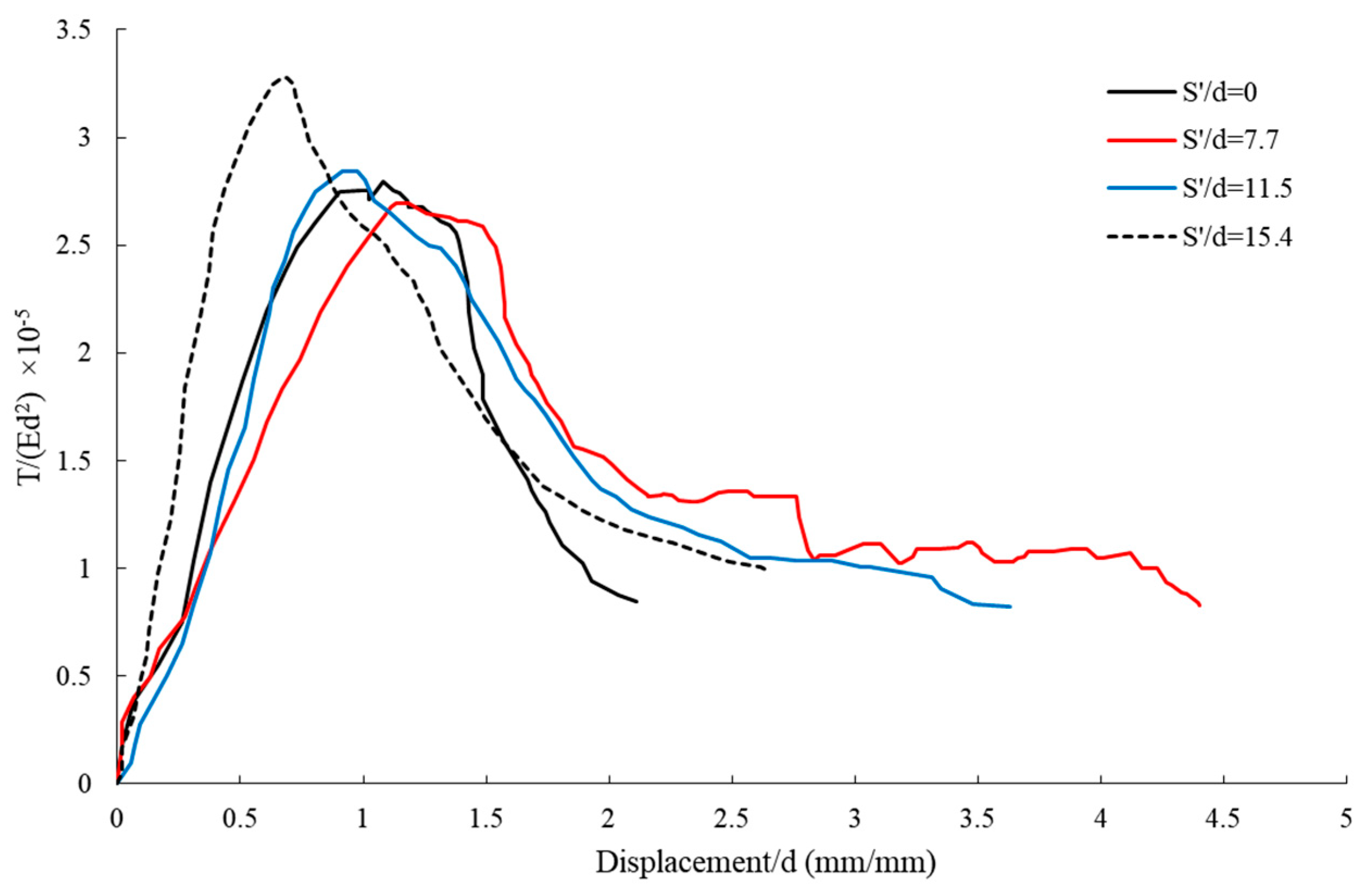
4.1.2. Effect of Geogrid Sheet Distance to Soil Surface on Pullout–Displacement Curves for CPs
4.2. Pullout–Displacement Curves for Helical Piles
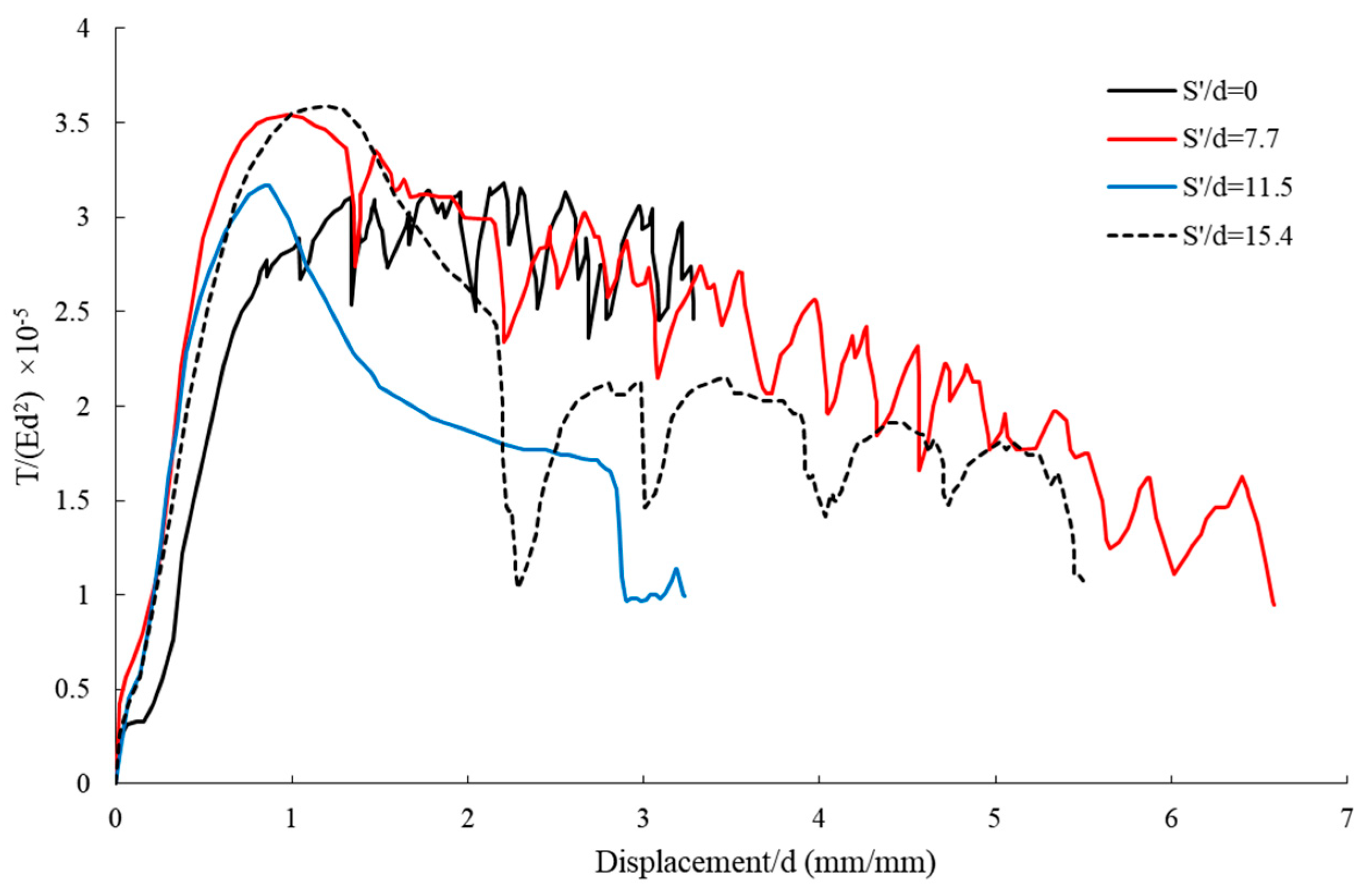
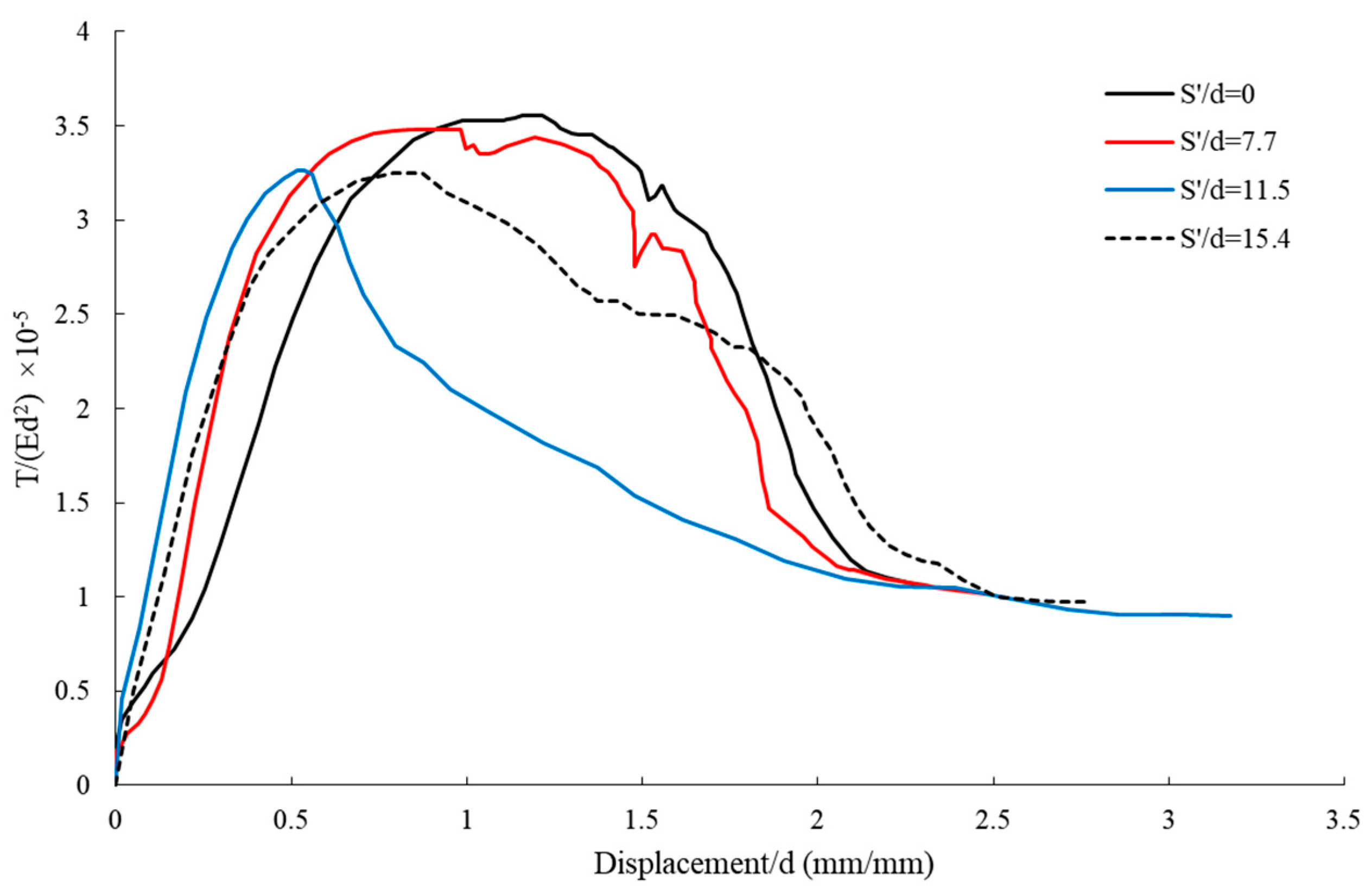
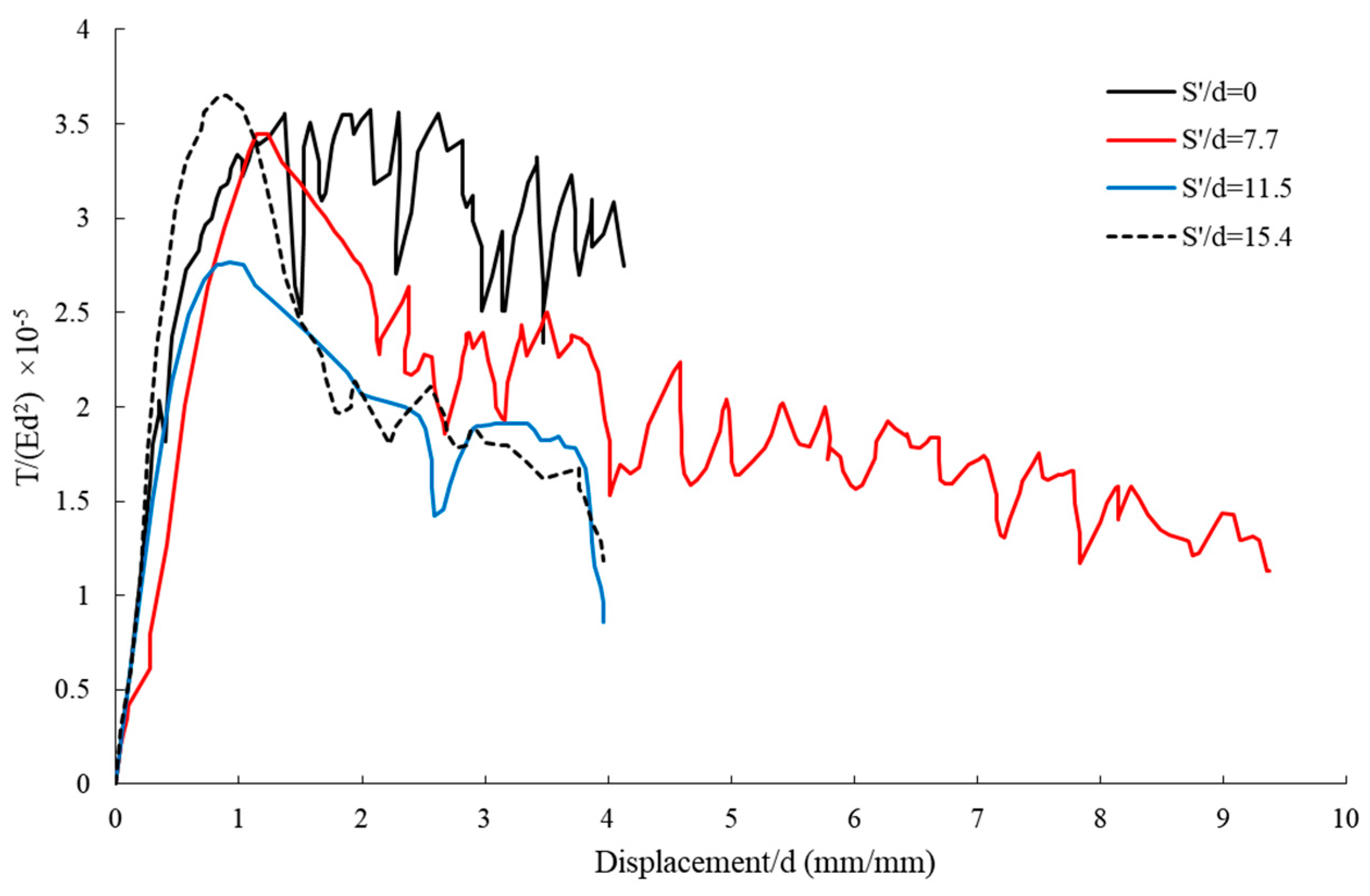
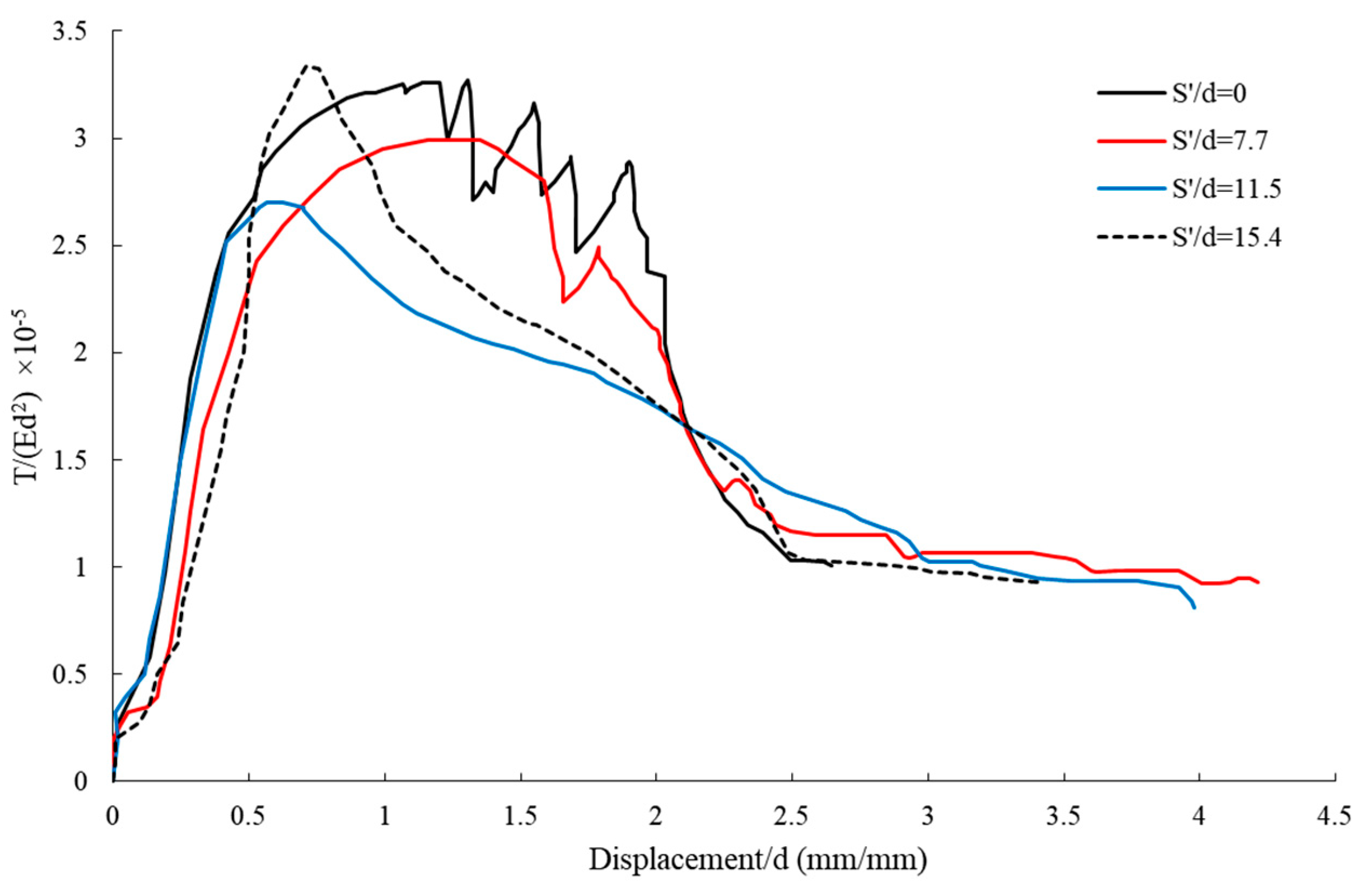
4.2.1. Effect of Geogrid Sheet Distance on Pullout–Displacement Curves for Piles
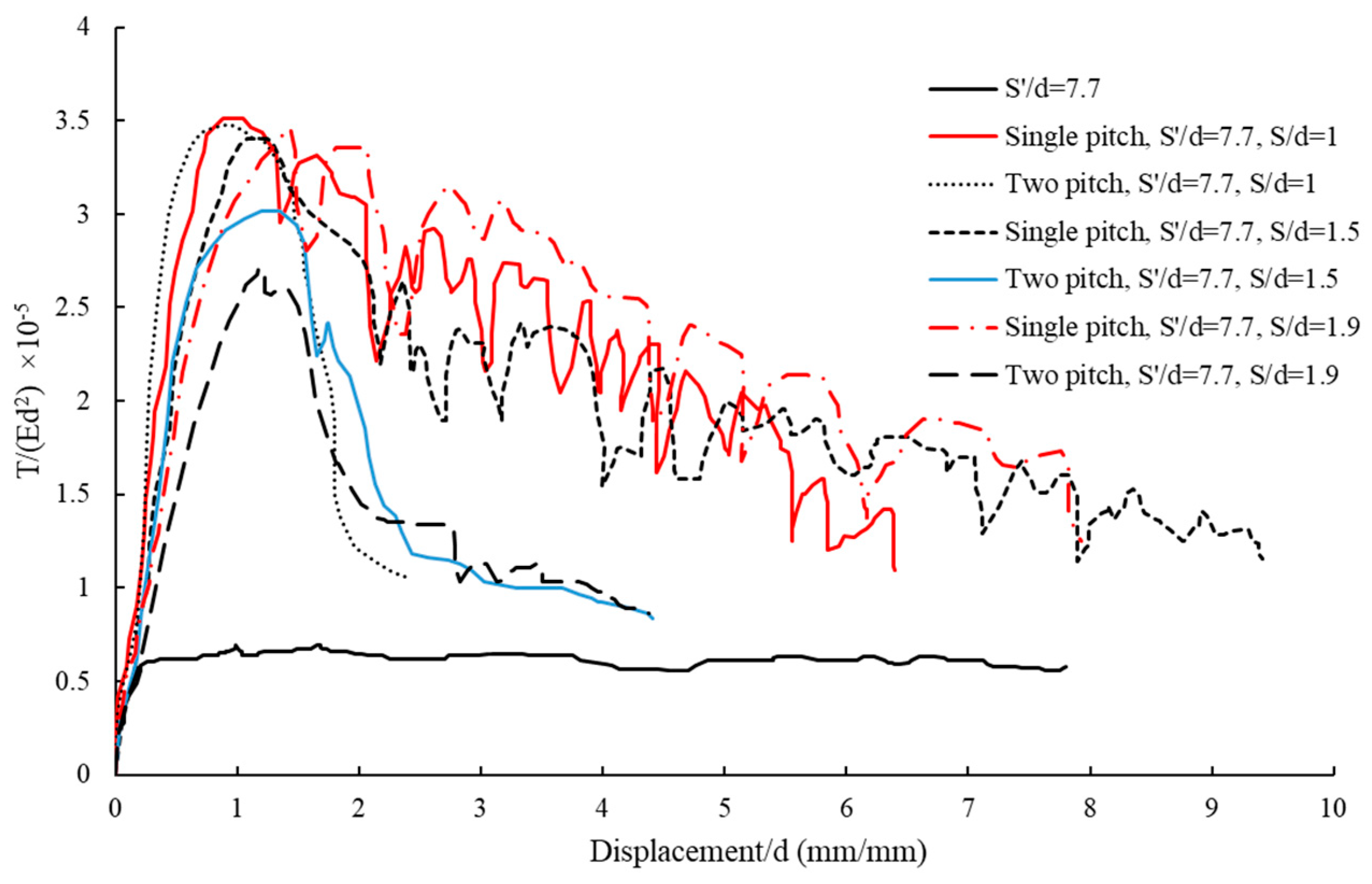
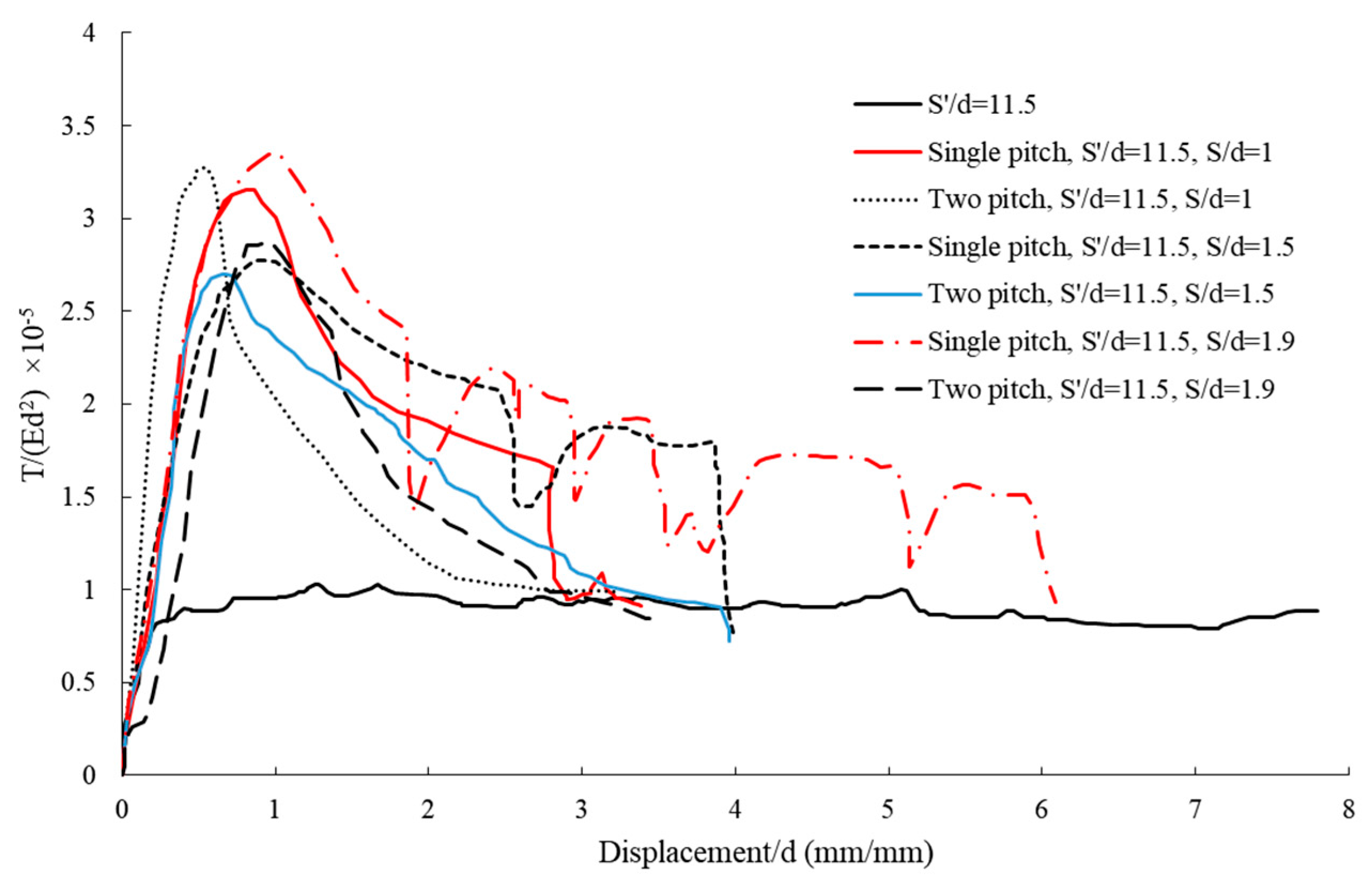
Comparison of Pullout–Displacement Curves for Single Blade HP with a Pitch of 13 mm
Comparison of Pullout–Displacement Curves for Double Blade HPs with a Pitch of 13 mm
Comparison of Pullout Capacity–Displacement for a Single-Blade Helical Pile with a Pitch of 20 mm
Comparison of Pullout Capacity–Displacement for a Double-Blade Helical Pile with a Pitch of 20 mm
Comparison of Pullout Capacity–Displacement for a Single-Blade Helical Pile with a Pitch of 25 mm
Comparison of Pullout Capacity–Displacement for a Double-Blade Helical Pile with a Pitch of 25 mm
4.2.2. Comparison of Pullout–Displacement Capacity for All Helical Piles with Different Blade Pitches
Comparison of Pullout–Displacement Capacity for All Helical Piles with Geogrids, 100 mm from the Ground Surface
Comparison of Pullout–Displacement Capacity for All Helical Piles with Geogrids, 150 mm from the Ground Surface
Comparison of Pullout–Displacement Capacity for All Helical Piles with Geogrids, 200 mm from the Ground Surface
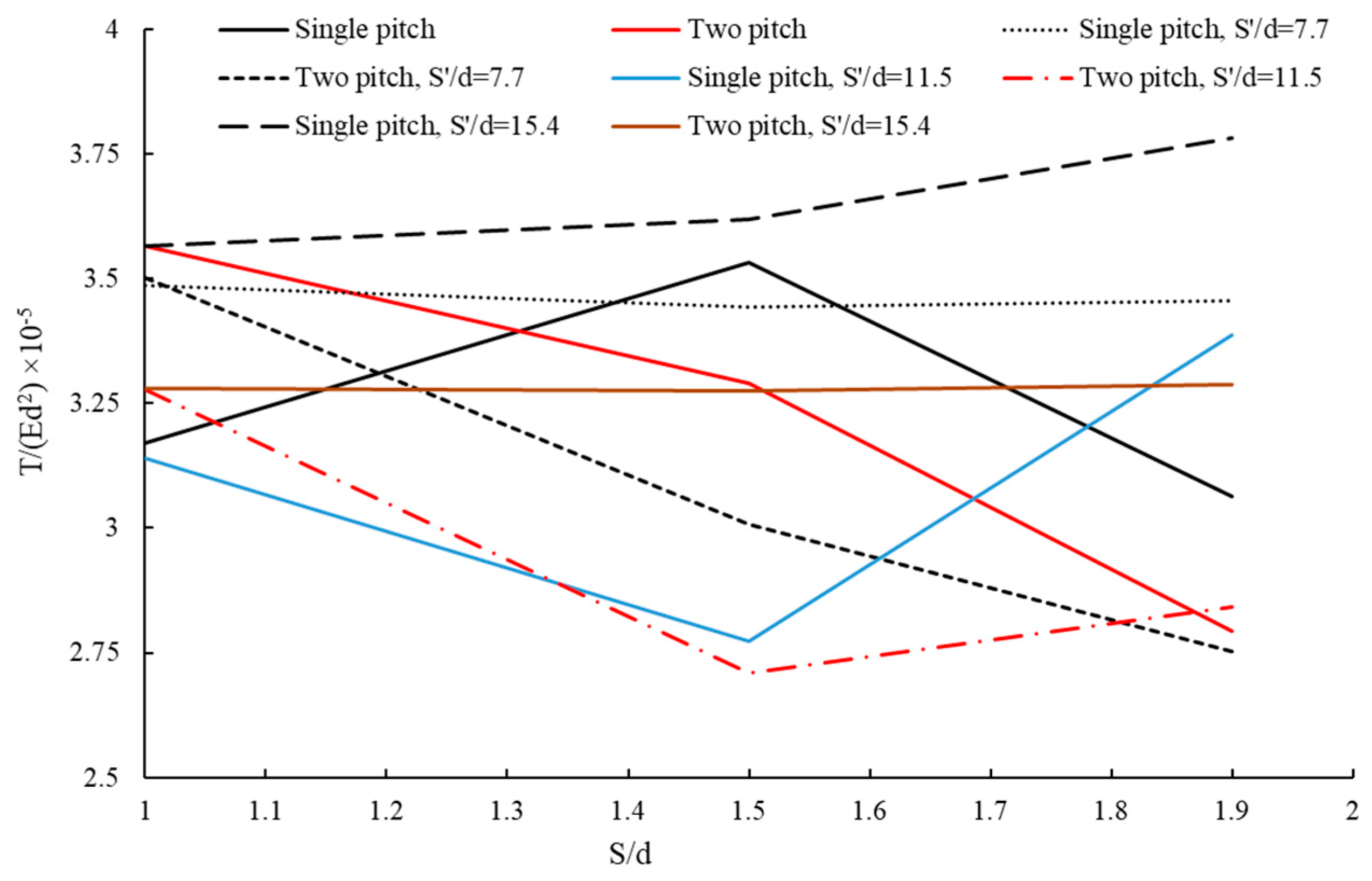
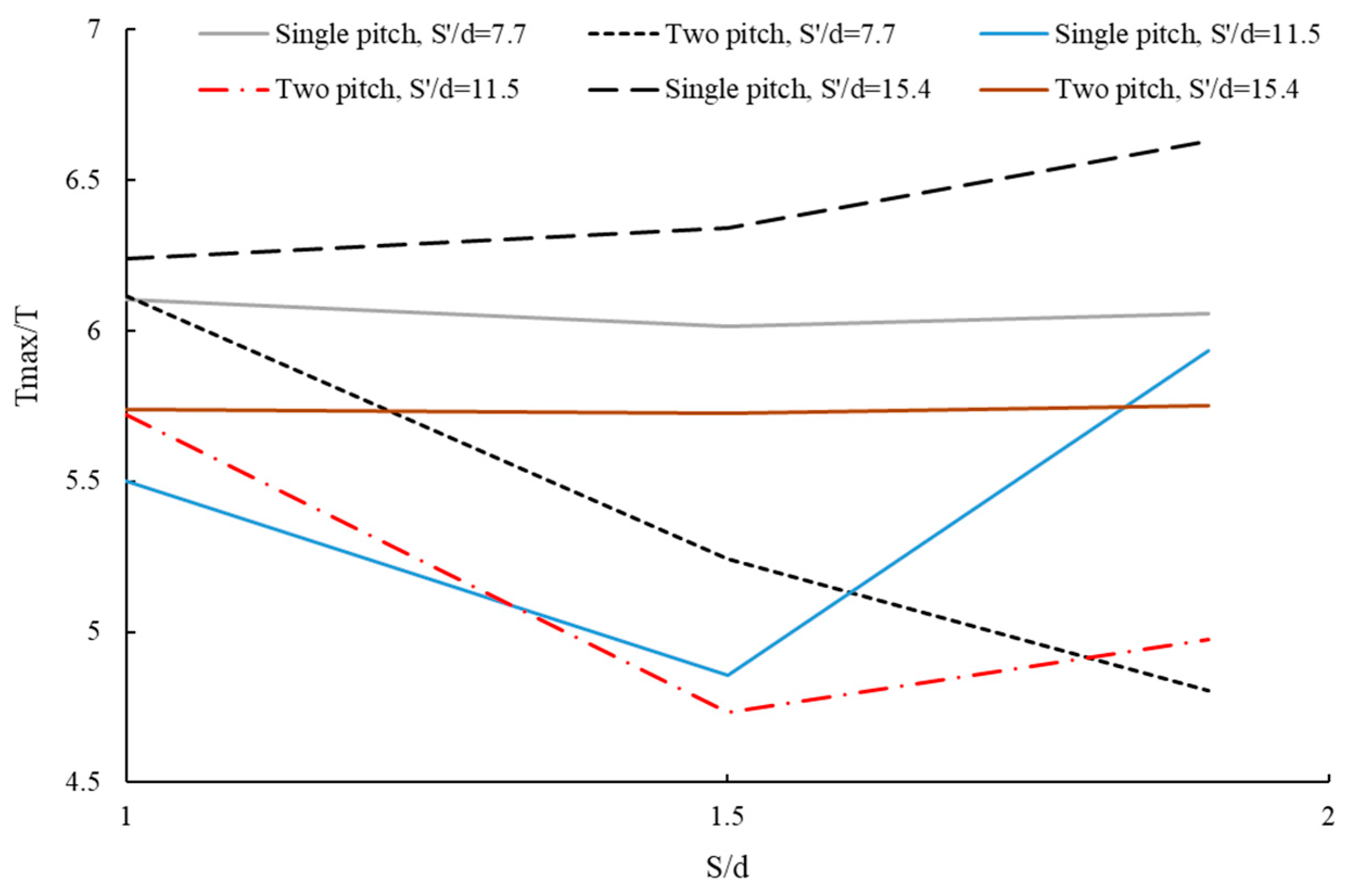
4.3. Comparison of Maximum Pullout Capacity–Blade Pitch of HPs
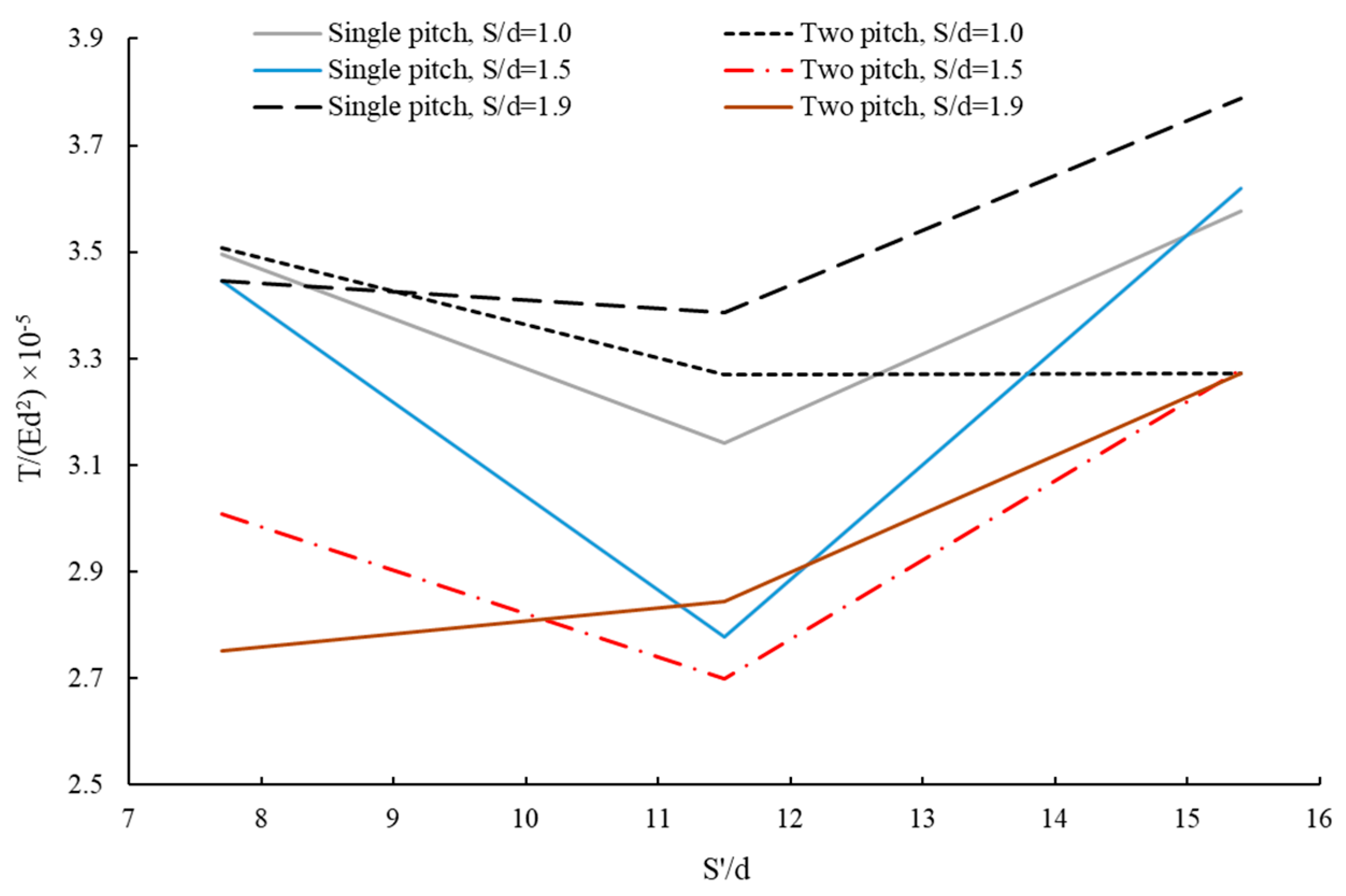
4.4. Comparison of Helical Pile Performance Based on Blade Pitch and Geogrid Placement
4.5. Synopsis of the Results
5. Limitations and Future Work
6. Conclusions
- Replacing conventional piles with HPs significantly increases pullout capacity—by an average of 345% and up to 518% in the best configuration—highlighting the superior load transfer mechanism of helical systems for tension-resisting foundations.
- Incorporating geogrid reinforcement improves both pullout resistance and stiffness, reducing displacement under load. The most effective configuration achieved a 62% reduction in displacement, improving overall serviceability and seismic performance.
- Geogrid depth strongly affects reinforcement efficiency. The maximum benefit occurs when the geogrid is placed at a “non-dimensional spacing of 0.47” (approximately 15.4 times the pile diameter from the surface), where soil confinement and load transfer to the geogrid are most effective.
- Increasing helix pitch generally improves pullout capacity by enlarging the bearing surface and enhancing soil interlock. However, this trend depends on pile configuration and geogrid placement, requiring careful optimization for specific projects.
- For projects in dense granular soils, single-blade HPs with larger pitch ratios (≈1.9) combined with geogrid reinforcement at optimized depth provide the highest pullout capacity. Double-blade HPs are advantageous where minimizing displacement is critical, such as in seismic zones or for structures sensitive to vertical movement. Geogrid layers should be placed within the active load transfer zone (near the upper third of pile embedment) to maximize reinforcement efficiency.
- The combined use of HPs and geogrids can deliver lighter, more economical, and more resilient foundation systems, especially in projects where uplift resistance is critical—such as transmission towers, anchored retaining structures, and offshore installations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Perko, H.A. Helical Piles: A Practical Guide to Design and Installation; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Sakr, M. Installation and performance characteristics of high capacity helical piles in cohesionless soils. DFI J. J. Deep. Found. Inst. 2011, 5, 39–57. [Google Scholar] [CrossRef]
- Sakr, M. Performance of helical piles in oil sand. Can. Geotech. J. 2009, 46, 1046–1061. [Google Scholar] [CrossRef]
- Spagnoli, G.; Gavin, K. Helical piles as a novel foundation system for offshore piled facilities. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 9–12 November 2015. [Google Scholar] [CrossRef]
- George, B.E.; Banerjee, S.; Gandhi, S.R. Helical Piles Installed in Cohesionless Soil by Displacement Method. Int. J. Geomech. 2019, 19, 04019074. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, P.; Ding, H.; Tian, Y.; Qi, X. The uplift capacity of single-plate helical pile in shallow dense sand including the influence of installation. Mar. Struct. 2020, 71, 102697. [Google Scholar] [CrossRef]
- Angurana, D.I.; Yadav, J.S.; Khatri, V.N.K. Estimation of uplift capacity of helical pile resting in cohesionless soil. Transp. Infrastruct. Geotechnol. 2024, 11, 833–864. [Google Scholar] [CrossRef]
- Annicchini, M.M.; Schiavon, J.A.; Tsuha, C.d.H.C. Effects of installation advancement rate on helical pile helix behavior in very dense sand. Acta Geotech. 2023, 18, 2795–2811. [Google Scholar] [CrossRef]
- da Silva, D.M.; Tsuha, C.d.H.C. Experimental investigation on the installation and loading performance of model-scale deep helical piles in very dense sand. Can. Geotech. J. 2021, 58, 1379–1395. [Google Scholar] [CrossRef]
- Garakani, A.A.; Serjoie, K.A. Ultimate bearing capacity of helical piles as electric transmission tower foundations in unsaturated soils: Analytical, numerical, and experimental investigations. Int. J. Geomech. 2022, 22, 04022194. [Google Scholar] [CrossRef]
- Asgari, A.; Arjomand, M.A.; Bagheri, M.; Ebadi-Jamkhaneh, M.; Mostafaei, Y. Assessment of experimental data and analytical method of helical pile capacity under tension and compressive loading in dense sand. Buildings 2025, 15, 2683. [Google Scholar] [CrossRef]
- Cerfontaine, B.; Ciantia, M.; Brown, M.; Sharif, Y. DEM study of particle scale and penetration rate on the installation mechanisms of screw piles in sand. Comput. Geotech. 2021, 139, 104380. [Google Scholar] [CrossRef]
- Chen, Y.; Deng, A.; Zhao, H.; Gong, C.; Sun, H.; Cai, J. Model and numerical analyses of screw pile uplift in dry sand. Can. Geotech. J. 2024, 61, 1144–1158. [Google Scholar] [CrossRef]
- Asgari, A.; Bagheri, M.; Hadizadeh, M. Advanced seismic analysis of soil-foundation-structure interaction for shallow and pile foundations in saturated and dry deposits: Insights from 3D parallel finite element modeling. Structures 2024, 69, 107503. [Google Scholar] [CrossRef]
- Asgari, A.; Ranjbar, F.; Bagheri, M. Seismic resilience of pile groups to lateral spreading in liquefiable soils: 3D parallel finite element modeling. Structures 2025, 74, 108578. [Google Scholar] [CrossRef]
- Shuman, N.M.; Khan, S.; Amini, F. Settlement based load capacity curve for single helix helical pile in c-ϕ soil. Soils Found. 2023, 63, 101265. [Google Scholar] [CrossRef]
- Asgari, A.; Ahmadtabar Sorkhi, S.F. Wind turbine performance under multi-hazard loads: Wave, wind, and earthquake effects on liquefiable soil. Results Eng. 2025, 26, 104647. [Google Scholar] [CrossRef]
- Ibsen, L.B.; Asgari, A.; Bagheri, M.; Barari, A. Response of monopiles in sand subjected to one-way and transient cyclic lateral loading. In Proceedings of the Geo-Shanghai 2014 International Conference, Shanghai, China, 26–28 May 2014; pp. 312–322. [Google Scholar] [CrossRef]
- Fateh, A.M.A.; Eslami, A.; Fahimifar, A. Direct CPT and CPTu methods for determining bearing capacity of helical piles. Mar. Georesources Geotechnol. 2017, 35, 193–207. [Google Scholar] [CrossRef]
- Rao, S.N.; Prasad, Y. Uplift behavior of screw anchors in sand. I: Dry sand. J. Geotech. Eng. 1992, 118, 1474–1476. [Google Scholar] [CrossRef]
- Jawad, Z.H.; Shakir, R.R. Behavior of Foundation Rested on Geogrid-Reinforced Soil: A Review. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1094, 012110. [Google Scholar] [CrossRef]
- Ahmad, H.; Mahboubi, A. Effect of the interfacial shearing stress of soil–geogrid interaction on the bearing capacity of geogrid-reinforced sand. Innov. Infrastruct. Solut. 2021, 6, 57. [Google Scholar] [CrossRef]
- Liu, J.; Pan, J.; Liu, Q.; Xu, Y. Experimental study on the interface characteristics of geogrid-reinforced gravelly soil based on pull-out tests. Sci. Rep. 2024, 14, 8669. [Google Scholar] [CrossRef]
- Wang, X.; Lu, J.; Wang, Z. Application of FRP screw anchor and geosynthetics in repairing of canal slope of expansive soils. In Proceedings of the 2010 International Conference on Mechanic Automation and Control Engineering, Wuhan, China, 26–28 June 2010; pp. 1430–1432. [Google Scholar] [CrossRef]
- Hasan, M.; Samadhiya, N.K. Performance of geosynthetic-reinforced granular piles in soft clays: Model tests and numerical analysis. Comput. Geotech. 2017, 87, 178–187. [Google Scholar] [CrossRef]
- Collin, J.G. U.S. state-of-practice for the design of the geosynthetic reinforced load transfer platform in column-supported embankments. In Soil Improvement; ASCE Library: Denver, CO, USA, 2007; pp. 1–12. [Google Scholar] [CrossRef]
- Le Hello, B.; Villard, P. Embankments reinforced by piles and geosynthetics—Numerical and experimental studies dealing with the transfer of load on the soil embankment. Eng. Geol. 2009, 106, 78–91. [Google Scholar] [CrossRef]
- Mooney, J.S.; Adamczak, S.; Clemence, S.P. Uplift capacity of helix anchors in clay and silt. In Uplift Behavior of Anchor Foundations in Soil; American Society of Civil Engineers: New York, NY, USA, 1985; pp. 48–72. [Google Scholar]
- Westine, P.S.; Dodge, F.T.; Baker, W. Similarity Methods in Engineering Dynamics: Theory and Practice of Scale Modeling; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Sedran, G.; Stolle, D.F.; Horvath, R.G. An investigation of scaling and dimensional analysis of axially loaded piles. Can. Geotech. J. 2001, 38, 530–541. [Google Scholar] [CrossRef]
- Buckingham, E. On physically similar systems; illustrations of the use of dimensional equations. Phys. Rev. 1914, 4, 345. [Google Scholar] [CrossRef]
- Chen, J.-J.; Zhang, L.; Zhang, J.-F.; Zhu, Y.-F.; Wang, J.-H. Field Tests, Modification, and Application of Deep Soil Mixing Method in Soft Clay. J. Geotech. Geoenvironmental Eng. 2013, 139, 24–34. [Google Scholar] [CrossRef]
- Sakr, M.; Bartlett, F. High capacity helical piles—A new dimension for bridge foundations. In Proceedings of the 8th International Conference on Short and Medium Span Bridges, Niagara Falls, ON, Canada, 3–6 August 2010. [Google Scholar]
- Sprince, A.; Pakrastinsh, L. Helical pile behaviour and load transfer mechanism in different soils. In Proceedings of the Modern Building Materials, Structures and Techniques, Vilnius, Lithuania, 19–21 May 2010; p. 1174. [Google Scholar]
- ASTM-D422; Standard Test Method for Particle-Size Analysis of Soils. ASTM International: West Conshohocken, PA, USA, 2007.
- ASTM-D854; Standard Test Methods for Specific Gravity of Soil Solids by Water Pycnometer. ASTM International: West Conshohocken, PA, USA, 2023.
- ASTM-D3080; Standard Test Method for Direct Shear Test of Soils Under Consolidated Drained Conditions. ASTM International: West Conshohocken, PA, USA, 2012.
- ASTM-D4254; Standard Test Methods for Minimum Index Density and Unit Weight of Soils and Calculation of Relative Density. ASTM International: West Conshohocken, PA, USA, 2016.
- ASTM-D4253; Standard Test Methods for Maximum Index Density and Unit Weight of Soils Using a Vibratory Table. ASTM International: West Conshohocken, PA, USA, 2016.
- ASTM-D2216-19; Standard Test Methods for Laboratory Determination of Water (Moisture) Content of Soil and Rock by Mass. ASTM International: West Conshohocken, PA, USA, 2019.
- ASTM-D2167-15; Standard Test Method for Density and Unit Weight of Soil in Place by the Rubber Balloon Method. ASTM International: West Conshohocken, PA, USA, 2015.
- ASTM-D3689/D3689M; Standard Test Methods for Deep Foundation Elements Under Static Axial Tensile Load. ASTM International: West Conshohocken, PA, USA, 2022.
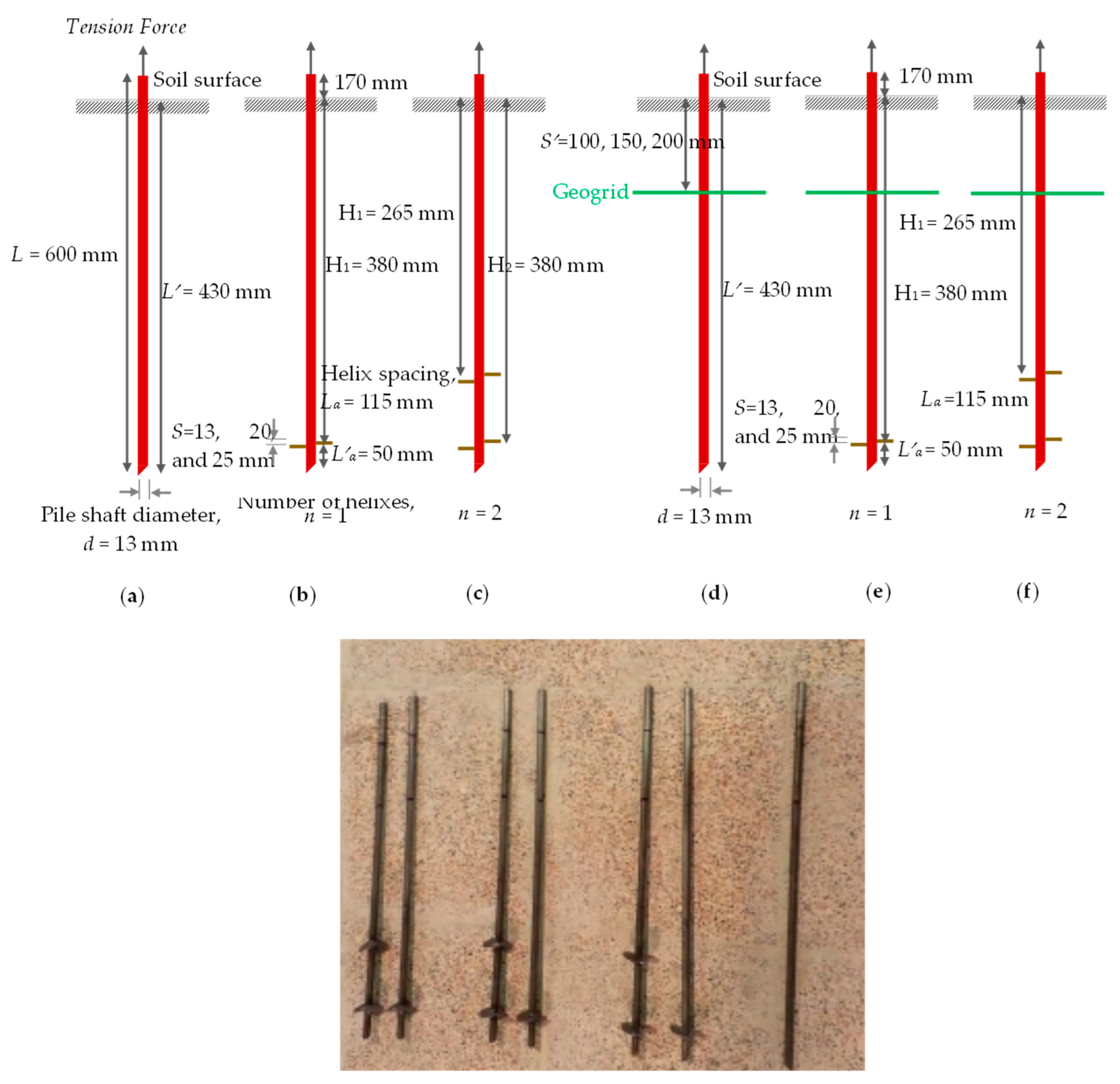
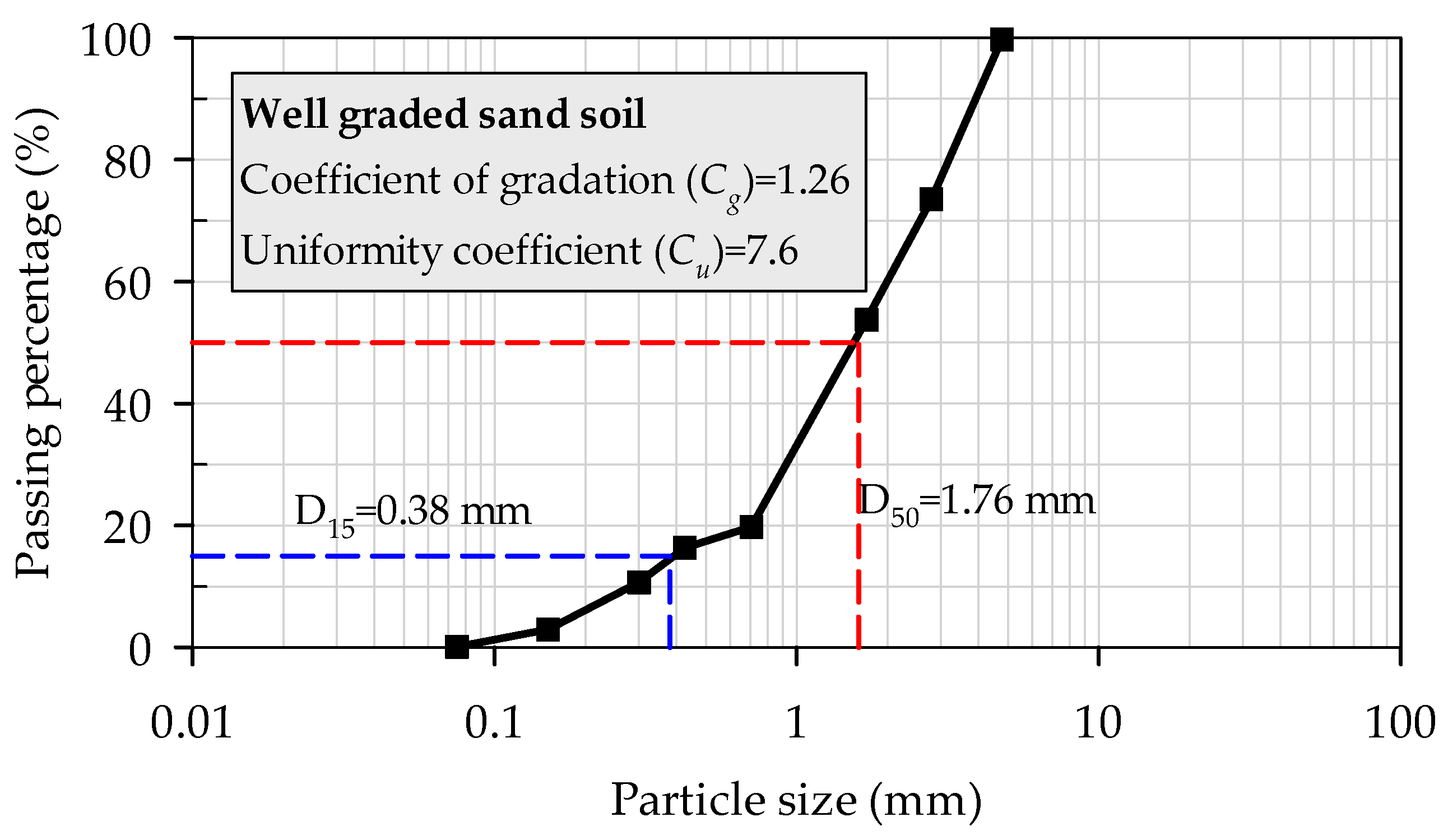


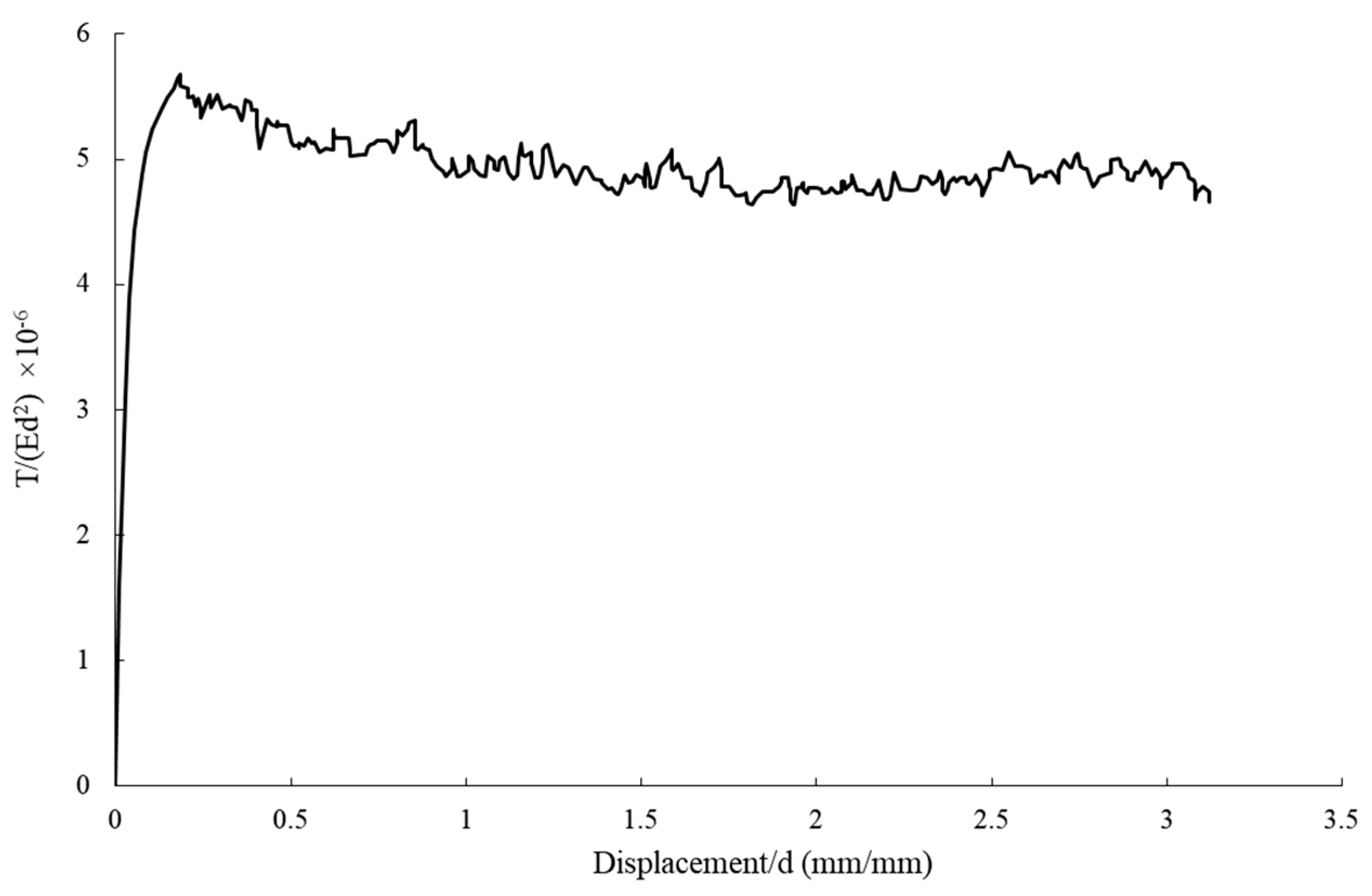
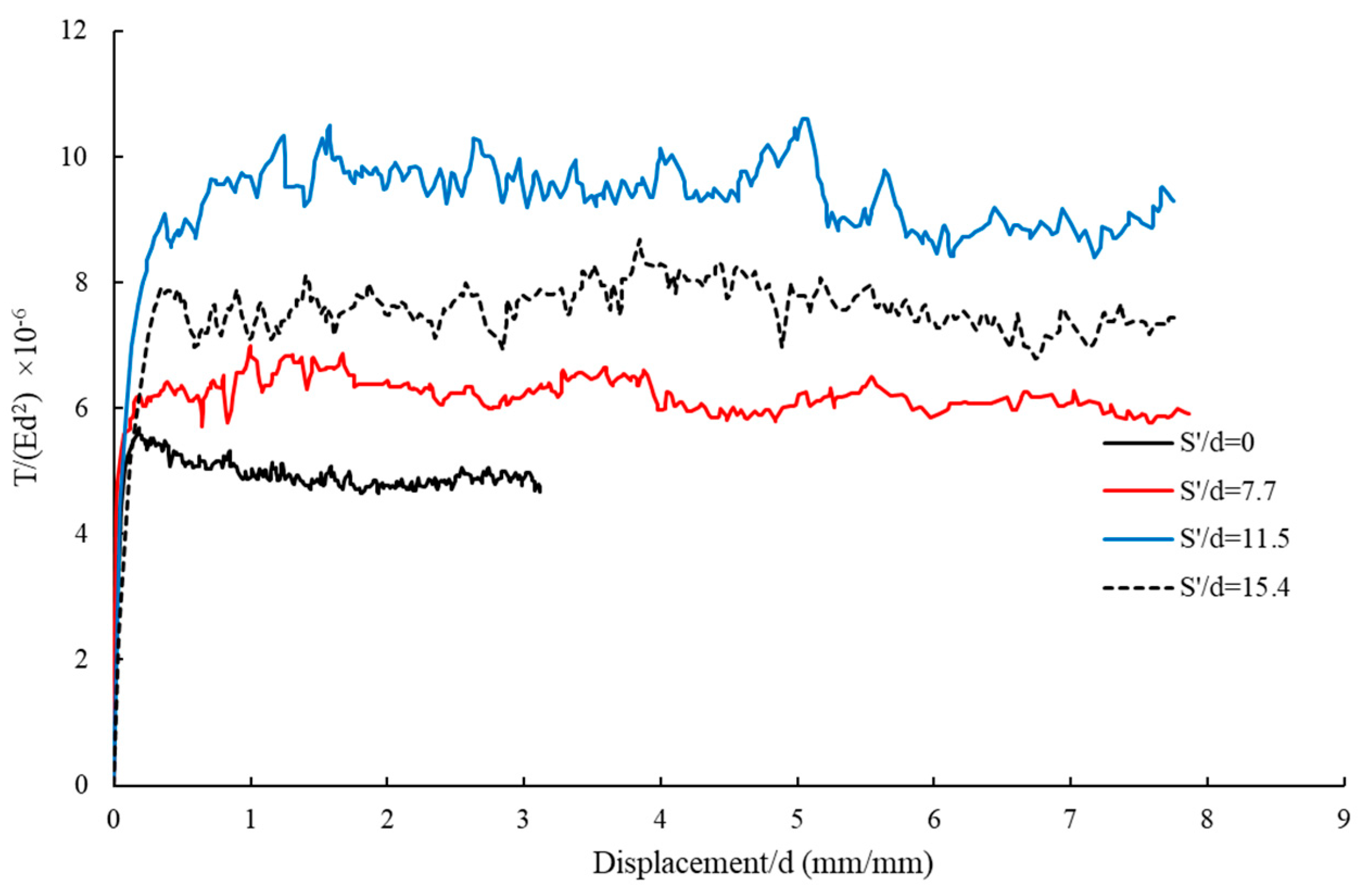

| Model No. | Number of Blades (n) | Blade Pitch (S) (mm) | Geogrid Distance from the Soil Surface () (mm) |
|---|---|---|---|
| 1 | 1 | 25 | 100 |
| 2 | 1 | 20 | 100 |
| 3 | 1 | 13 | 100 |
| 4 | 1 | 25 | 150 |
| 5 | 1 | 20 | 150 |
| 6 | 1 | 13 | 150 |
| 7 | 1 | 25 | 200 |
| 8 | 1 | 20 | 200 |
| 9 | 1 | 13 | 200 |
| 10 | 2 | 25 | 100 |
| 11 | 2 | 20 | 100 |
| 12 | 2 | 13 | 100 |
| 13 | 2 | 25 | 150 |
| 14 | 2 | 20 | 150 |
| 15 | 2 | 13 | 150 |
| 16 | 2 | 25 | 200 |
| 17 | 2 | 20 | 200 |
| 18 | 2 | 13 | 200 |
| 19 | 1 | 25 | - |
| 20 | 1 | 20 | - |
| 21 | 1 | 13 | - |
| 22 | 2 | 25 | - |
| 23 | 2 | 20 | - |
| 24 | 2 | 13 | - |
| 25 | - | - | 100 |
| 26 | - | - | 150 |
| 27 | - | - | 200 |
| 28 | - | - | - |
| Pile Type | Dimensionless Pitch (S/d) | Dimensionless Maximum Pullout Capacity (×10−5) | Dimensionless Displacement at Maximum Pullout |
|---|---|---|---|
| Conventional pile | - | 0.702 | 1.004 |
| Single-blade helical pile | 1 | 3.496 | 0.965 |
| Double-blade helical pile | 1 | 3.508 | 0.911 |
| Single-blade helical pile | 1.5 | 3.448 | 1.137 |
| Double-blade helical pile | 1.5 | 3.005 | 1.186 |
| Single-blade helical pile | 1.9 | 3.465 | 1.446 |
| Double-blade helical pile | 1.9 | 2.75 | 1.2 |
| Pile Type | Dimensionless Pitch of Blade (S/d) | Dimensionless Pullout (×10−5) | Dimensionless Displacement (ds/d) |
|---|---|---|---|
| Conventional pile | - | 1.069 | 5.051 |
| Single-blade helical pile | 1 | 3.148 | 0.818 |
| Double-blade helical pile | 1 | 3.276 | 0.507 |
| Single-blade helical pile | 1.5 | 2.779 | 0.950 |
| Double-blade helical pile | 1.5 | 2.709 | 0.584 |
| Single-blade helical pile | 1.9 | 3.391 | 0.967 |
| Double-blade helical pile | 1.9 | 2.845 | 0.909 |
| Pile Type | Dimensionless Pitch of Blade (S/d) | Dimensionless Pullout (×10−5) | Dimensionless Displacement (ds/d) |
|---|---|---|---|
| Conventional pile | - | 0.863 | 3.858 |
| Single-blade helical pile | 1 | 3.577 | 1.138 |
| Double-blade helical pile | 1 | 3.283 | 0.751 |
| Single-blade helical pile | 1.5 | 3.626 | 0.837 |
| Double-blade helical pile | 1.5 | 3.280 | 0.785 |
| Single-blade helical pile | 1.9 | 3.790 | 1.134 |
| Double-blade helical pile | 1.9 | 3.288 | 0.676 |
| Dimensionless Geogrid Spacing (S′/d) | Dimensionless Pitch of Blade (S/d) | Dimensionless Displacement (ds/d) | Dimensionless Pullout (×10−5) | ||||
|---|---|---|---|---|---|---|---|
| n | |||||||
| 2 | 1 | 0 | 2 | 1 | 0 | ||
| 0 | 1 | 1.12 | 2.158 | 0.188 | 3.573 | 3.169 | 0.573 |
| 7.7 | 1 | 0.911 | 0.965 | 1.004 | 3.508 | 3.496 | 0.702 |
| 11.5 | 1 | 0.507 | 0.818 | 5.051 | 3.276 | 3.148 | 1.069 |
| 15.4 | 1 | 0.751 | 1.138 | 3.858 | 3.283 | 3.577 | 0.8632 |
| 0 | 1.5 | 1.160 | 2.083 | 3.292 | 3.542 | ||
| 7.7 | 1.5 | 1.186 | 1.137 | 3.005 | 3.448 | ||
| 11.5 | 1.5 | 0.584 | 0.950 | 2.709 | 2.779 | ||
| 15.4 | 1.5 | 0.785 | 0.873 | 3.28 | 3.626 | ||
| 0 | 1.9 | 1.100 | 2.294 | 2.795 | 3.070 | ||
| 7.7 | 1.9 | 1.200 | 1.446 | 2.750 | 3.465 | ||
| 11.5 | 1.9 | 0.909 | 0.967 | 2.845 | 3.391 | ||
| 15.4 | 1.9 | 0.676 | 1.134 | 3.288 | 3.790 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ebadi-Jamkhaneh, M.; Arjomand, M.A.; Bagheri, M.; Asgari, A.; Nouhi Hefzabad, P.; Salahi, S.; Mostafaei, Y. Experimental Study on the Pullout Behavior of Helical Piles in Geogrid-Reinforced Dense Shahriyar Sand. Buildings 2025, 15, 2963. https://doi.org/10.3390/buildings15162963
Ebadi-Jamkhaneh M, Arjomand MA, Bagheri M, Asgari A, Nouhi Hefzabad P, Salahi S, Mostafaei Y. Experimental Study on the Pullout Behavior of Helical Piles in Geogrid-Reinforced Dense Shahriyar Sand. Buildings. 2025; 15(16):2963. https://doi.org/10.3390/buildings15162963
Chicago/Turabian StyleEbadi-Jamkhaneh, Mehdi, Mohammad Ali Arjomand, Mohsen Bagheri, Ali Asgari, Pouya Nouhi Hefzabad, Sahar Salahi, and Yashar Mostafaei. 2025. "Experimental Study on the Pullout Behavior of Helical Piles in Geogrid-Reinforced Dense Shahriyar Sand" Buildings 15, no. 16: 2963. https://doi.org/10.3390/buildings15162963
APA StyleEbadi-Jamkhaneh, M., Arjomand, M. A., Bagheri, M., Asgari, A., Nouhi Hefzabad, P., Salahi, S., & Mostafaei, Y. (2025). Experimental Study on the Pullout Behavior of Helical Piles in Geogrid-Reinforced Dense Shahriyar Sand. Buildings, 15(16), 2963. https://doi.org/10.3390/buildings15162963






